Как найти кинетическую энергию ядра атома - Исправление недочетов и поиск решений вместе с Examum.ru

Ядерные реакции

Энергетический выход ядерной реакции

Деление ядер

Цепная ядерная реакция

Термоядерная реакция

Как связаны кинетическая и ядерная энергии?

Как кинетическая энергия преобразуется в ядерную энергию?

Когда кинетическая энергия превращается в ядерную энергию?

Где происходит преобразование кинетической энергии в ядерную энергию?

Кинетическая энергия в формулу ядерной энергии

Кинетическая энергия для эффективности использования ядерной энергии

Примеры преобразования кинетической энергии в ядерную энергию

Часто задаваемые вопросы

Что вы имеете в виду под энергией связи?

Как рассчитать энергию связи атома?

расщепление

Fusion

Ядерного реактора

Вс

Радиоактивность

Ядерное топливо

Атомный взрыв

декомпозиция

Извержение вулкана

иррадиация

Ядерный рамановский эффект

метаморфизм

Допинг нейтронной трансмутации

Темы кодификатора ЕГЭ: ядерные реакции, деление и синтез ядер.

Темы кодификатора ЕГЭ: ядерные реакции, деление и синтез ядер.
Энергетический выход ядерной реакции
Деление ядер
Цепная ядерная реакция
Термоядерная реакция

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

В предыдущем листке мы неоднократно говорили о расщеплении атомного ядра на составные части. Но как этого добиться в действительности? В результате каких физических процессов можно разбить ядро?

Наблюдения радиоактивного распада в изменяющихся внешних условиях — а именно, при различных давлениях и температурах, в электрических и магнитных полях — показали, что скорость радиоактивного распада от этих условий не зависит. Никаких превращений химических элементов друг в друга все эти факторы вызвать не способны. Очевидно, изменения энергии тут слишком малы, чтобы повлиять на атомное ядро — так ветер, обдувающий кирпичный дом, не в состоянии его разрушить.

Но разрушить дом можно артиллерийским снарядом. И Резерфорд в 1919 году решил воспользоваться наиболее мощными «снарядами», которые имелись тогда в распоряжении. Это были alpha -частицы, вылетающие с энергией около 5 МэВ при радиоактивном распаде урана. (Как вы помните, это те самые снаряды, которыми он восемь лет назад бомбардировал лист золотой фольги в своих знаменитых опытах, породивших планетарную модель атома.)

Правда, превращений золота в другие химические элементы в тех экспериментах не наблюдалось. Ядро золота $^{197}_{phantom{1} 79}rm{Au}$ само по себе весьма прочное, да и к тому же содержит довольно много протонов; они создают сильное кулоновское поле, отталкивающее alpha -частицу и не подпускающее её слишком близко к ядру. А ведь для разбивания ядра alpha -снаряд должен сблизиться с ядром настолько, чтобы включились ядерные силы! Что ж, раз большое количество протонов мешает — может, взять ядро полегче, где протонов мало?

Резерфорд подверг бомбардировке ядра азота $^{14}_{phantom{1} 7}rm{N}$ и в результате осуществил первую в истории физики ядерную реакцию:

$^{14}_{vphantom{1}7}rm{N} + vphantom{1} ^{4}_{2}rm{He} rightarrow vphantom{1}^{17}_{phantom{1}8}rm{O} + vphantom{1}^{1}_{1}rm{H}.$ (1)

В правой части (1) мы видим продукты реакции — изотоп кислорода и протон.

Стало ясно, что для изучения ядерных реакций нужно располагать частицами-снарядами высоких энергий. Такую возможность дают ускорители элементарных частиц. Ускорители имеют два серьёзных преимущества перед естественными «радиоактивными пушками».

1. В ускорителях можно разгонять любые заряженные частицы. В особенности это касается протонов, которые при естественном распаде ядер не появляются. Протоны хороши тем, что несут минимальный заряд, а значит — испытывают наименьшее кулоновское отталкивание со стороны ядер-мишеней.

2. Ускорители позволяют достичь энергий, на несколько порядков превышающие энергию α-частиц при радиоактивном распаде. Например, в Большом адронном коллайдере протоны разгоняются до энергий в несколько ТэВ; это в миллион раз больше, чем 5 МэВ у alpha -частиц в реакции (1), осуществлённой Резерфордом.

Так, с помощью протонов, прошедших через ускоритель, в 1932 году удалось разбить ядро лития (получив при этом две alpha -частицы):

$^{7}_{3}rm{Li} + vphantom{1}^{1}_{1}rm{H} rightarrow vphantom{1}^{4}_{2}rm{He} + vphantom{1}^{4}_{2}rm{He}.$ (2)

Ядерные реакции дали возможность искусственного превращения химических элементов.

Кроме того, в продуктах реакций стали обнаруживаться новые, не известные ранее частицы. Например, при облучении бериллия alpha -частицами в том же 1932 году был открыт нейтрон:

$^{9}_{4}rm{Be} + vphantom{1}^{4}_{2}rm{He} rightarrow vphantom{1}^{12}_{phantom{1} 6}rm{O} + vphantom{1}^{1}_{0}rm{n}.$ (3)

Нейтроны замечательно подходят для раскалывания ядер: не имея электрического заряда, они беспрепятственно проникают внутрь ядра. (При этом ускорять нейтроны не надо — медленные нейтроны легче проникают в ядра. Нейтроны, оказывается, нужно даже замедлять, и делается это пропусканием нейтронов через обычную воду.) Так, при облучении азота нейтронами протекает следующая реакция:

$^{14}_{phantom{1} 7}rm{N} + vphantom{1}^{1}_{0}rm{n} rightarrow vphantom{1}^{11}_{phantom{1} 5}rm{B} + vphantom{1}^{4}_{2}rm{He}.$ (4)

к оглавлению ▴

Обсуждая энергию связи, мы видели, что в результате ядерных процессов масса системы частиц не остаётся постоянной. Это, в свою очередь, приводит к тому, что кинетическая энергия продуктов ядерной реакции отличается от кинетической энергии исходных частиц.

Прежде всего напомним, что полная энергия частицы массы складывается из её энергии покоя mc^2 и кинетической энергии :

Пусть в результате столкновения частиц и происходит ядерная реакция, продуктами которой служат частицы и :

(5)

Полная энергия системы частиц сохраняется:

то есть

(6)

Кинетическая энергия исходных частиц равна . Кинетическая энергия продуктов реакции равна . Энергетический выход ядерной реакции — это разность кинетических энергий продуктов реакции и исходных частиц:

Из (6) легко получаем:

(7)

Если Q > 0 , то говорят, что реакция идёт с выделением энергии: кинетическая энергия продуктов реакции больше кинетической энергии исходных частиц. Из (7) мы видим, что в этом случае суммарная масса продуктов реакции меньше суммарной массы исходных частиц.

Если же Q < 0 , то реакция идёт с поглощением энергии: кинетическая энергия продуктов реакции меньше кинетической энергии исходных частиц. Суммарная масса продуктов реакции в этом случае больше суммарной массы исходных частиц.

Таким образом, термины «выделение» и «поглощение» энергии не должны вызывать недоумение: они относятся только к кинетической энергии частиц. Полная энергия системы частиц, разумеется, в любой реакции остаётся неизменной.

Чтобы посчитать энергетический выход ядерной реакции (5), действуем по следующему алгоритму.

1. С помощью таблицы масс нейтральных атомов находим и m_Y , выраженные в а. е. м. (для нахождения массы ядра не забываем вычесть из массы нейтрального атома массу электронов).

2. Вычисляем массу исходных частиц, массу продуктов реакции и находим разность масс .

3. Умножаем Delta m на 931,5 и получаем величину , выраженную в МэВ.

Мы сейчас подробно рассмотрим вычисление энергетического выхода на двух примерах бомбардировки ядер лития $^{7}_{3}rm{Li}$ : сначала — протонами, затем — alpha -частицами.

В первом случае имеем уже упоминавшуюся выше реакцию (2):

$vphantom{1}^{7}_{3}rm{Li} + vphantom{1}^{1}_{1}rm{H} rightarrow vphantom{1}^{4}_{2}rm{He} + vphantom{1}^{4}_{2}rm{He}.$

Масса атома лития $^{7}_{3}rm{Li}$ равна 7,01601 а. е. м. Масса электрона равна а. е. м. Вычитая из массы атома массу трёх его электронов, получаем массу ядра лития $^{7}_{3}rm{Li}$ :

а. е. м.

Масса протона равна 1,00728 а. е. м., так что масса исходных частиц:

а. е. м.

Переходим к продуктам реакции. Масса атома гелия равна 4,00260 а. е. м. Вычитаем массу электронов и находим массу ядра гелия $vphantom{1}^{4}_{2}rm{He}$ :

а. е. м.

Умножая на , получаем массу продуктов реакции:

а. е. м.

Масса, как видим, уменьшилась ; это означает, что наша реакция идёт с выделением энергии. Разность масс:

а. е. м.

Выделившаяся энергия:

МэВ.

Теперь рассмотрим второй пример. При бомбардировке ядер лития alpha -частицами происходит реакция:

$vphantom{1}^{7}_{3}rm{Li} + vphantom{1}^{4}_{2}rm{He} rightarrow vphantom{1}^{10}_{phantom{1} 5}rm{B} + vphantom{1}^{1}_{0}rm{n}.$ (8)

Массы исходных ядер нам уже известны; остаётся сосчитать их суммарную массу:

а. е. м.

Из таблицы берём массу атома бора $vphantom{1}^{10}_{phantom{1} 5}rm{B}$ (она равна а. е. м.); вычитаем массу пяти электронов и получаем массу ядра атома бора:

а. е. м.

Масса нейтрона равна 1,00867 а. е. м. Находим массу продуктов реакции:

а. е. м.

На сей раз масса увеличилась , то есть реакция идёт с поглощением энергии.

Разность масс равна:

а. е. м.

Энергетический выход реакции:

МэВ.

Таким образом, в реакции (8) поглощается энергия 2,8 МэВ. Это означает, что суммарная кинетическая энергия продуктов реакции (ядра бора и нейтрона) на 2,8 МэВ меньше, чем суммарная кинетическая энергия исходных частиц (ядра лития и alpha -частицы). Поэтому чтобы данная реакция в принципе осуществилась, энергия исходных частиц должна быть не меньше 2,8 МэВ.

к оглавлению ▴

Бомбардируя ядра урана медленным нейтронами, немецкие физики Ган и Штрассман обнаружили появление элементов средней части периодической системы: бария, криптона, стронция, рубидия, цезия и т. д. Так было открыто деление ядер урана.

На рис. 1 мы видим процесс деления ядра (изображение с сайта oup.co.uk.). Захватывая нейтрон, ядро урана делится на два осколка, и при этом освобождаются два-три нейтрона.

Рис. 1. Деление ядра урана

Осколки являются ядрами радиоактивных изотопов элементов середины таблицы Менделеева. Обычно один из осколков больше другого. Например, при бомбардировке урана $vphantom{1}^{235}_{phantom{1} 92}rm{U}$ могут встречаться такие комбинации осколков (как говорят, реакция идёт по следующим каналам).

• Барий и криптон: $vphantom{1}^{235}_{phantom{1} 92}rm{U} + vphantom{1}^{1}_{0}rm{n} rightarrow vphantom{1}^{144}_{phantom{1} 56}rm{Ba} + vphantom{1}^{89}_{36}rm{Kr} + 3 vphantom{1}^{1}_{0}rm{n}.$

• Цезий и рубидий: $vphantom{1}^{235}_{phantom{1} 92}rm{U} + vphantom{1}^{1}_{0}rm{n} rightarrow vphantom{1}^{140}_{phantom{1} 55}rm{Cs} + 2vphantom{1}^{1}_{0}rm{n}.$

• Ксенон и стронций: $vphantom{1}^{235}_{phantom{1} 92}rm{U} + vphantom{1}^{1}_{0}rm{n} rightarrow vphantom{1}^{140}_{phantom{1} 54}rm{Xe} + vphantom{1}^{94}_{38}rm{Sr} + 2vphantom{1}^{1}_{0}rm{n}.$

В каждой из этих реакций выделяется очень большая энергия — порядка 200 МэВ. Сравните эту величину с найденным выше энергетическим выходом реакции (2), равным 17,4 МэВ! Откуда берётся такое количество энергии?

Начнём с того, что из-за большого числа протонов ( штуки), упакованных в ядре урана, кулоновские силы отталкивания, распирающие ядро, очень велики. Ядерные силы, конечно, ещё в состоянии удерживать ядро от распада, но могучий кулоновский фактор готов сказать своё слово в любой момент. И такой момент настаёт, когда в ядре застревает нейтрон (рис. 2 — изображение с сайта investingreenenergy.com).

Рис. 2. Деформация, колебания и разрыв ядра

Застрявший нейтрон вызывает деформацию ядра. Начнутся колебания формы ядра, которые могут стать столь интенсивными, что ядро вытянется в «гантельку». Короткодействующие ядерные силы, скрепляющие небольшое число соседних нуклонов перешейка, не справятся с силами электрического отталкивания половинок гантельки, и в результате ядро разорвётся.

Осколки разлетятся с огромной скоростью — около 1/30 скорости света. Они и уносят большую часть высвобождающейся энергии (около 170 МэВ из 200 ).

Деление тяжёлых ядер можно истолковать с точки зрения уже известного нам графика зависимости удельной энергии связи ядра от его массового числа (рис. 3).

Рис. 3. Деление тяжёлых ядер энергетически выгодно

Цветом выделена область , в которой удельная энергия связи достигает наибольшего значения 8,7 МэВ/нуклон. Это область наиболее устойчивых ядер. Справа от этой области удельная энергия связи плавно уменьшается до 7,6 МэВ/нуклон у ядра урана.

Процесс превращения менее устойчивых ядер в более устойчивые является энергетически выгодным и сопровождается выделением энергии. При делении ядра урана, как видим, удельная энергия связи повышается примерно на МэВ/нуклон; эта энергия как раз и выделяется в процессе деления. Умножив это на число нуклонов в ядре урана, получим приблизительно те самые 200 МэВ энергетического выхода, о которых говорилось выше.

к оглавлению ▴

Появление двух-трёх нейтронов в процессе деления ядра урана — важнейший факт. Эти нейтроны «первого поколения» могут попасть в новые ядра и вызвать их деление; в результате деления новых ядер возникнут нейтроны «второго поколения», которые попадут в следующие ядра и вызовут их деление; возникнут нейтроны «третьего поколения», которые приведут к делению очередных ядер и т. д. Так идёт цепная ядерная реакция, в ходе которой высвобождается колоссальное количество энергии.

Для протекания цепной ядерной реакции необходимо, чтобы число N_i высвободившихся нейтронов в очередном поколении было не меньше числа $N_{i-1}$ нейтронов в предыдущем поколении. Величина

$k = frac{displaystyle N_i}{displaystyle N_{i-1} vphantom{1^a}}$

называеся коэффициентом размножения нейтронов. Таким образом, цепная реакция идёт при условии k > 1 . Если k < 1 , то цепная реакция не возникает.

В случае k > 1 происходит лавинообразное нарастание числа освобождающихся нейтронов, и цепная реакция становится неуправляемой. Так происходит взрыв атомной бомбы.

В ядерных реакторах происходит управляемая цепная реакция деления с коэффициентом размножения k = 1 . Стационарное течение управляемой цепной реакции обеспечивается введением в активную зону реактора (то есть в ту область, где протекает реакция) специальных управляющих стержней, поглощающих нейтроны. При полностью введённых стержнях поглощение ими нейтронов настолько велико, что k < 1 и реакция не идёт. В процессе запуска реактора стержни постепенно выводят из активной зоны, пока выделяемая мощность не достигнет требуемого уровня. Этот уровень тщательно контролируется, и при его превышении включаются устройства, вводящие управляющие стержни назад в активную зону.

к оглавлению ▴

Наряду с реакцией деления тяжёлых ядер энергетически возможным оказывается и обратный в некотором смысле процесс — синтез лёгких ядер, то есть слияние ядер лёгких элементов (расположенных в начале периодической таблицы) с образованием более тяжёлого ядра.

Чтобы началось слияние ядер, их нужно сблизить вплотную — чтобы вступили в действие ядерные силы. Для такого сближения нужно преодолеть кулоновское отталкивание ядер, резко возрастающее с уменьшением расстояния между ними. Это возможно лишь при очень большой кинетической энергии ядер, а значит — при очень высокой температуре (в десятки и сотни миллионов градусов). Поэтому реакция ядерного синтеза называется термоядерной реакцией.

В качестве примера термоядерной реакции приведём реакцию слияния ядер дейтерия и трития (тяжёлого и сверхтяжёлого изотопов водорода), в результате которой образуется ядро гелия и нейтрон:

$vphantom{1}^{2}_{1}rm{H} + vphantom{1}^{3}_{1}rm{H} rightarrow vphantom{1}^{4}_{2}rm{He} + vphantom{1}^{1}_{0}rm{n}.$ (9)

Эта реакция идёт с выделением энергии, равной 17,6 МэВ (попробуйте сами провести расчёты и получить данную величину). Это очень много, если учесть, что в реакции участвуют всего нуклонов! В самом деле, в расчёте на один нуклон в реакции (9) выделяется энергия примерно 3,5 МэВ, в то время как при делении ядра урана выделяется «всего» МэВ на нуклон.

Таким образом, термоядерные реакции служат источником ещё большего количества энергии, чем реакции деления ядер. С физической точки зрения это понятно: энергия реакции ядерного деления есть в основном кинетическая энергия осколков, разогнанных электрическими силами отталкивания, а при ядерном синтезе энергия высвобождается в результате разгона нуклонов навстречу друг другу под действием куда более мощных ядерных сил притяжения.

Проще говоря, при делении ядер высвобождается энергия электрического взаимодействия, а при синтезе ядер — энергия сильного (ядерного) взаимодействия.

В недрах звёзд достигаются температуры, подходящие для синтеза ядер. Свет Солнца и далёких звёзд несёт энергию, выделяющуяся в термоядерных реакциях — при слиянии ядер водорода в ядра гелия и последующем слиянии ядер гелия в ядра более тяжёлых элементов, расположенных в средней части периодической системы. Направление термоядерного синтеза показано на рис. 4; синтез лёгких ядер энергетически выгоден, так как направлен в сторону увеличения удельной энергии связи ядра.

Рис. 4. Синтез лёгких ядер энергетически выгоден

Неуправляемая термоядерная реакция осуществляется при взрыве водородной бомбы. Сначала взрывается встроенная атомная бомба — это нужно для создания высокой температуры на первой ступени термоядерного взрыва. При достижении необходимой температуры в термоядерном горючем бомбы начинаются реакции синтеза, и происходит взрыв собственно водородной бомбы.

Осуществление управляемой термоядерной реакции остаётся пока нерешённой проблемой, над которой физики работают уже более полувека. Если удастся добиться управляемого течения термоядерного синтеза, то человечество получит в своё распоряжение фактически неограниченный источник энергии. Это чрезвычайно важная задача, стоящая перед нынешним и будущими поколениями — в свете угрожающей перспективы истощения нефтегазовых ресурсов нашей планеты.

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Ядерные реакции» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Подвижность частиц также отвечает за протекание ядерных реакций, но как происходит это преобразование кинетической энергии в ядерную, мы обсудим здесь.

Частицы, приближающиеся от дальнего источника, сообщают свою энергию атому при столкновении с ним. Получив дополнительную энергию, атом пытается поглотить эту энергию и связать ее вместе, чтобы преобразовать атомную структуру. В процессе он излучает часть энергии для стабилизации атомной структуры, которая называется ядерной энергией.

Кинетическая энергия и ядерная энергия взаимозависимы и обе производят источник тепловой энергии.

Генерация ядерной энергии происходит за счет кинетической энергии бомбардирующих частиц, которые обеспечивают дополнительную энергию атомам, что делает их нестабильными, высвобождая ядерную энергию, чтобы стать наиболее стабильными, которые снова перемещаются с кинетической энергией и вызывают дальнейшую ядерную реакцию. место.

Реакция, при которой выделяется ядерная энергия, протекает через радиоактивность, деление нейтронов или процесс синтеза. Вместе с выбросом частиц выделяется тепловая энергия.

Кинетическая энергия фактически отвечает за создание ядерной энергии.

Частица, приближающаяся издалека, передает кинетическую энергию ядрам атома, с которыми она сталкивается, что делает атом нестабильным, а лишняя заряженная масса связывается с частицей, которая высвобождает ядерную энергию, чтобы стать стабильным атомом.

Ядерная энергия находится в ядре ядер. Поскольку атом деформируется из-за воздействия кинетической энергии падающей частицы, вся атомная структура реформируется путем связывания частицы. Эквивалент энергия связи теряется из ядер при делении или синтезе атома.

Кинетический энергия одной частицы превращается в ядерную энергию при столкновении с ядрами другой частицы, и ядра становятся нестабильными.

Быстро движущаяся частица бомбардирует и связывается в ядре атома, и эта дополнительная доступная энергия высвобождается путем испускания фотонов и нейтронов или разделения на две части или слияния, чтобы стать стабильным атомом.

Ядерную энергию получают в больших масштабах с помощью ядерных реакторов.

Энергия связи находится в ядре ядра, которое высвобождается только при расщеплении ядер и при слиянии, высвобождающем энергию связи, высвобождая мелкие частицы для обретения стабильности.

Ядерная энергия сохраняется внутри ядер атома, и поэтому очевидно, что по мере захвата кинетической энергии ядрами ядра становятся нестабильными, высвобождая частицы из ядер и выделяя некоторую энергию.

Кинетическая энергия любого вещества определяется как KE=1/2mv.²

Поскольку частица движется со скоростью света, кинетическая энергия ядер равна KE=1/2mc.²

Ядра движутся со скоростью света и, следовательно, скорость ядер почти равна скорости света. Энергия, высвобождаемая после связывания, представляет собой ядерную энергию и определяется уравнением E=mc²

Е=2мкс²/2

Э=2К.Э

Следовательно, ядерная энергия получается в два раза больше кинетической энергии.

Эффективность – это количество энергии, отдаваемое при использовании подведенной энергии для выполнения работы. Здесь мы видели, что ядерная энергия, полученная из кинетической энергии бомбардирующей частицы, удваивается при высвобождении энергии связи.

Эффективность преобразования кинетической энергии в ядерную удваивается при преобразовании энергии.

Вот список кинетической энергии для примеров ядерной энергии:

Родительские ядра разделятся на два, когда ядерная энергия станет больше, и, следовательно, чтобы высвободить ядерную энергию из своего ядра, ядро разделится на два. Эта дополнительная энергия передается ядрам от частиц, бомбардирующих его с большого расстояния с большой кинетической энергией, и связывается с ним.

Два атомных ядра, движущиеся с большой скоростью с кинетической энергией, сближаются и бомбардируют друг друга, генерируемая энергия связи будет большой, и ядра, образующиеся таким образом, будут нестабильными. Таким образом, он освобождает привязку ядерная энергия пропуская частицы, чтобы стать стабильными ядрами.

Реакция деления происходит в ядерном реакторе, где родительские ядра делятся на два, высвобождая огромное количество энергии, которая используется для различных целей, таких как опреснение, образование водородного топлива, производство электроэнергии и т. д.

Ядерного реактора; Кредит изображения: pixabay

Наблюдения и советы этой статьи мы подготовили на основании опыта команды реакция синтеза видна на солнце что приводит к образованию солнечных вспышек. Высвобожденная энергия захватывается другим атомом и, как следствие, раздваивается и движется вместе с кинетической энергией, снова приводя к делению или слиянию атомов.

Все элементы подвергаются радиоактивности, которая аналогична разложению материи, и каждый из них имеет разные периоды полураспада в зависимости от состава материи. Фотоны, падающие на материю, обеспечивают тепловую энергию, которая связывается с ядрами атомов, составляющих материю, и пропускает выделяющие энергию частицы.

Ядерное топливо является чистым источником энергии и дает огромное количество энергии, не выделяя вредных газов в воздух. Сгорание топлива обеспечивает ядерную энергию для движения транспортных средств.

урановые топливные элементы; Кредит изображения: pixabay

Это высвобождает огромное количество ядерной энергии в воздух, что делает воздух очень плохим и нездоровым для дыхания. Кинетическая энергия, с которой он проходит через воздух, вызывает трение и истирание на поверхности материи.

Все органическое вещество подвергается разложению при падении на него лучистой энергии Солнца. Тепловая энергия, поступающая в материю от падающих фотонов, приводит к разрыву связей, разрушающих материю.

Кислая магма извергается из земной коры и стекает по горам, сливаясь с окружающей материей. Тепловая энергия отдается до тех пор, пока не остынет до температуры поверхности в данной местности.

Энергия, полученная от падающих фотонов в дневное время, увеличивает внутреннюю тепловую энергию системы, которая затем отдается объектом, если энергия, полученная составляющими его молекулами, становится очень большой.

В этом эффекте проявляется изменение длины волны падающего и рассеянного луча света. Электрон издалека летит и сталкивается с атомом, его ядра деформируются из-за воздействия сообщенной ему кинетической энергии и связываются вместе, высвобождая гамма-частицы.

Зерна, составляющие вещество породы, метаморфизировались, меняя размеры и текстуру зерен, образуя хорошо определенные минералы и состав.

В этом методе два разных изотопа легируют вместе, чтобы сформировать полупроводниковый материал. Из двух изотопов один образуется на основе радиоактивный распад.

Связывание в основном означает ограничение энергии.

Количество энергии, необходимое для того, чтобы атом мог связать, выпустив из него несколько частиц при деформации, чтобы сформировать стабильную атомную конфигурацию, называется энергией связи.

= 0,45 эВ.

Атомная масса атома изменяется при деформации.

Энергия связи равна энергии той массы, которая добавляется или выделяется при реакции и деформации, равной E= ∆mc²

Источник

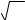
5.Основы ядерной физики

Обозначения, состав атомного ядра

Ядро обозначается тем же символом, что и нейтральный атом: ZA X или ZХA , где Х – символ химического элемента, Z – зарядовое число, равное числу протонов (заряженных частиц) в ядре, оно равно порядковому номеру в таблице Менделеева. Заряд ядра равен Zе, где е

– элементарный положительный заряд, численно равный заряду электрона, А – массовое число, численно равное числу протонов и нейтронов в ядре (числу нуклонов). Число нейтронов: N = А — Z. Свойства ядер зависят от как числа протонов, так и от числа нейтронов в них. Ядра атомов с одинаковым числом протонов, но разным числом

нейтронов называются изотопами (например, 63 Li , 73 Li ) и обладают

разными свойствами.

Ядра с одинаковым массовым числом А, но разным Z, называются изобарами. Они располагаются в разных клетках таблицы Менделеева.

В соответствии с гидродинамической (капельной) моделью ядра оно представляет собой сферическую каплю, состоящую из смеси

протонной (11 p ) и нейтронной ( 01n ) жидкости. Радиусы ядер определяются формулой

r = r0 3 A ,

где А – число нуклонов в ядре; r0 — коэффициент пропорциональности, его можно считать равным r0 = 1,4 10-15м. r0 по величине близка к

комптоновской длине волны π-мезона r0 ≈ ћ/mπc ≈ 1,4 10-15м. Единица длины в ядерной физике: 1 Фм (ферми) = 10-15м = 10-13см.

Эффективная площадь поперечного сечения ядра:

σ = π r2, где r — радиус ядра.

Ядро-капля и капля жидкости имеют общие физические свойства. Ядерные силы притяжения между нуклонами, как и силы взаимодействия между молекулами являются короткодействующими (в

118

пределах ядра). Ядерные силы обладают свойством насыщения (каждый нуклон взаимодействует только с ближайшими частицами). Ядерные силы обладают свойствами зарядовой независимости (p-p, n-n

и p-n).

Ядерные силы зависят от направления спинов взаимодействующих между собой нуклонов. Система из протона и нейтрона образует ядро (дейтрон, изотоп водорода 21 H ) лишь тогда, когда спины

протона и нейтрона параллельны (суммарный спин тогда ½ + ½ =1). Если спины антипараллельны, ядро не образуется.

Некоторые свойства нуклонов представлены в таблице 5.1.

Таблица 5.1

	Протон p	Нейтрон n	Электрон e
Масса покоя	m0p = 1,6726·10–27кг=	m0n = 1,6749·10–27кг=	m0e = 9,1·10–31кг=
	= 938,28 МэВ	= 939,57 МэВ	= 0,511 МэВ
Внутренний
момент	½	½	½
количества
движения (в
единицах ћ)
Статистика		Ферми — Дирака
Время жизни	>1025 лет	887±2 с	>4,3·1023 лет

Дефект массы и энергия связи

Точные измерения масс атомов (с помощью масс-спектрометров) показали, что сумма масс нуклонов, взятых отдельно, всегда на несколько десятых процента больше массы ядра, составленного из этих нуклонов:

M = Z mp + (A — Z) mn – Mя.

Здесь mp, mn и Mя соответственно массы протона, нейтрона и ядра. В таблицах обычно приводятся не массы ядер, а массы нейтральных атомов Mа = Mя + Z me, где me — масса электрона.

Тогда дефект массы

M = Z mp + Z me + (A — Z) mn – Mа = = Z mН + (A — Z) mn – Mа ,

где mН — масса атома водорода.

119

При образовании ядра должно выделяться некоторое количество энергии и обратно, чтобы разделить ядро на составные части, т.е. удалить нуклоны друг от друга до расстояния отсутствия их взаимодействия, затрачивается энергия, называемая энергией связи:

Есв = c2 М; где с – скорость света в вакууме.

Обычно энергию связи выражают в мегаэлектронвольтах (МэВ), если при этом размерность М в а.е.м., то формула для энергии связи приобретает вид

Есв = 931,5 аМэВ.е.м. M (а.е.м.)

Частное от деления энергии связи Есв на число нуклонов (А) называется удельной энергией связи , т.е. энергией, необходимой для удаления из ядра данного нуклона.

εсв = Eсв/А

Удельная энергия связи для большинства ядер имеет величину около 7 ÷ 8 МэВ/нуклон. Кривая зависимости удельной энергии связи

εсв от массового числа А представлена на рис. 5.1.

Рис. 5.1

Радиоактивность. Закон радиоактивного распада

Ядра некоторых изотопов, как естественных, так и искусственных, могут самопроизвольно превращаться в другие ядра. Эта способность к превращению называется радиоактивностью и

120

сопровождается испусканием некоторых частиц (альфа-распад, бета-распад, гамма-излучение).

Самопроизвольный распад атомных ядер подчиняется закону радиоактивного распада. Количество радиоактивных ядер изменяется по экспоненциальному закону:

N = N0e−λt ,

здесь N0 – число атомных ядер радиоактивного вещества в начальный момент времени, N — число нераспавшихся ядер в момент времени t, λ — постоянная распада, имеющая смысл вероятности распада ядра за секунду и равная доле ядер, распадающихся в единицу времени.

Величина τ = 1/λ, обратная постоянной распада, называется средним временем жизни данного изотопа. Если Т – период полураспада, то

	N0		= N0e−λT , то eλT = 2,	а	ln(eλT )= ln 2 = 0,693,
2
						1 = 0,693 .
т.е. λ Т = 0,693, а λ =
								τ	T
Тогда закон радиоактивного распада:
	N = N0e	−0,693t
		T	.
Для небыстро распадающихся веществ отношение числа ядер,
распадающихся в единицу времени N1 к N0
	N1		= λ ,		откуда N1	=	λN0 = А – активность	радиоактивного
	N0
	измеряется в беккерелях (Бк, с–1). Кроме того, используется
вещества,
Кюри (Kи) (1 Ku = 3,7 1010 актов распада в секунду).
									Альфа-распад
Альфа-распадом называется самопроизвольное превращение
ядра с испусканием альфа-частицы (ядра атома	гелия	24 He ).
Способность	к альфа-распаду наблюдается в основном у	изотопов

121

тяжелых элементов с порядковым номером Z > 82, например, у изотопа урана по схеме

23892 U α→23490Th+42 He

Спектр энергий α-частиц линейчатый, т.к. исходное (материнское) ядро и α-продукт обладают дискретными спектрами энергетических состояний. Энергии α-частиц различных изотопов лежат в пределах от 4 до 10,5 МэВ, что соответствует скоростям порядка 109 см/с.

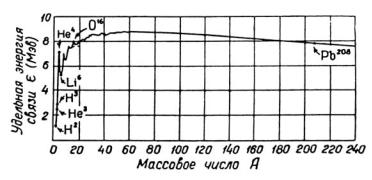
Суммарная потенциальная энергия электростатического отталкивания α-частиц от ядра и притяжение их к ядру под действием ядерных сил образует потенциальный барьер (рис.5.2).

			Потенциальный
			барьер


	d	Еα
–r	Глубина потен-	+r
		циальной ямы

Рис. 5.2. График потенциальной энергии

Опыт показывает, что энергия α-частиц (Еα) меньше высоты потенциального барьера. Например, для 23892 U Еα ~ 4,2 МэВ, а Еmax (потенциальный барьер) ~ 28,1 МэВ.

Квантово-механическая теория трактует вылет α-частицы из ядра как просачивание через потенциальный барьер ядра. Это явление называется туннельным эффектом и объясняется корпускулярноволновыми свойствами α-частицы.

122

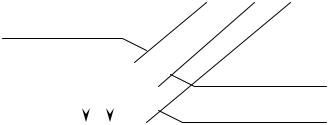
Часто дочернее ядро при α-распаде имеет несколько возбужденных уровней и испускает γ-кванты. Например,

23592 U α→23190Th+42He

εγ ~ 0,18 МэВ ÷ 0,38 МэВ, а энергия Еα ~ 4,58 МэВ ÷ 4,2 МэВ (рис.5.3).

				23892 U


	Еα=4,2 МэВ (4,2%)

εγ=0,38
МэВ			Еα=4,4 МэВ (85,6%)
Еγ=0,18 МэВ
			Еα=4,58 МэВ (10,2%)



		231Th
90
		Рис. 5.3

При движении в веществе α-частица тормозится и теряет энергию, в основном, на возбуждение и ионизацию атомов и молекул вещества.

Альфа-частица обладает малой проникающей способностью, поглощаясь, например, несколькими листочками бумаги, слоем алюминия толщиной 0, 05 мм и т.д..

Опасным является попадание радиоактивных загрязнений внутрь организма (вдыхание, заглатывание) При этом ионизационный эффект сказывается очень сильно, тогда как эффект внешнего облучения мал, α— частицы поглощаются одеждой или клетками кожного покрова.

Бета-распад

Бета-распадом называется самопроизвольное превращение ядра в другое ядро с тем же массовым числом А, но с зарядом, отличающимся от исходного (материнского) ядра на единицу. Различают три вида превращений:

123

1)электронный или бета-минус распад;

2)позитронный или бета-плюс распад;

3)электронный К-захват.

Соответственно:

1)	1 1 0 0	~
0 n→1p+−1e+0	νe (β–-распад);
2)	11 p→01n++10e+00νe (β+-распад);
3)	11 p+−10e→01n+00νe (К-захват).

1) превращение одного из нейтронов ядра в протон с вылетом электрона и электронного антинейтрино, например,

60	−e 60 0 0	~
27 Co →28 Ni+−1e+0	νe

происходит в естественно- и искусственно-радиоактивных ядрах, это превращение энергетически возможно и вне ядра

2) превращение одного из протонов ядра в нейтрон с вылетом позитрона и электронного нейтрино, например,

31	+e 31 0 0	νe
16S →15 P++1e+0

характерно для явления искусственной радиоактивности;

3) В результате электронного захвата заряд убывает на единицу, например,

7 Be+−0e→7 Li+0ν 4 1 3 0 e

Электронный захват сопровождается характеристическим рентгеновским излучением. Захват электрона с L-оболочки происходит в 100 раз реже, чем К-захват.

124

dN dЕ

Граница β-спектра

Еmax E

Рис. 5.4.

Спектр β-излучения является непрерывным (сплошным), энергия испускаемых частиц принимает все значения от нуля до Еmax (рис.5.4). Энергия, освобождаемая при электронном захвате, распределяется между ядром-продуктом и нейтрино. При прохождении через вещество β-частицы теряют свою энергию и тормозятся. Траектории β-частиц не прямолинейны. Интенсивность β-излучения уменьшается по экспоненциальному закону:

I = I0e−μl ,

где l — толщина поглотителя, μ — коэффициент поглощения в веществе, [μ] = м–1. При движении β-частиц в среде возникает тормозное излучение. Энергия фотонов тормозного излучения зависит от энергии β-частиц.

Ядерные реакции

Ядерными реакциями называются искусственные превращения атомных ядер, вызванные их взаимодействием с элементарными частицами или друг с другом. Как правило, в ядерных реакциях участвуют два ядра и две частицы. Символическая запись ядерной реакции:

X + a → Y + b или X (a,b) Y.

125

Ядерные реакции сопровождаются перестройкой атомных ядер, происходит более глубокое изменения вещества, чем при химических реакциях. Однако некоторые физические величины в реакции не меняются, имеют место законы сохранения:

1.Закон сохранения электрического заряда: ZХ + Zа = ZY + Zb.

2.Закон сохранения числа нуклонов: АХ + Аа = АY + Аb. 3.Сохраняются первые интегралы движения механики

применительно к ядрам и частицам: полная энергия, импульс, момент количества движения (частицы и ядра образуют замкнутую механическую систему).

Закон сохранения энергии выполняется в релятивистском понимании ЕХ + Еа = ЕY + Еb, при этом

Е = p2c2 + m02c4 =T + m0c2 ,

здесь m0 – масса покоя частиц, участвующих в реакции, р — модуль импульса.

Векторный закон сохранения импульса: pX + pa = pY + pb .

Полный момент количества движения ядер (частиц) равен векторной сумме собственного момента (спина) и орбитального момента.

Часто наблюдается, что сумма масс частиц, вступающих в реакции (МХ + Ма) не равна сумм масс (МY + Мb) частиц-продуктов реакции. В этом случае величина

Q = (МХ + Ма – МY – Мb)c2		или
			931,44[МэВ]

Q =	∑Mi исход − ∑M j конечн
	i	j

выражает энергетический баланс ядерной реакции и называется тепловым эффектом реакции или энергией реакции. Если Q > 0, реакция идет с выделением тепла (она экзотермическая), если Q < 0, то она эндотермическая. Эта реакция пойдет только тогда, когда энергия относительного движения МХ и Ма будет не меньше теплового эффекта реакции Q. При бомбардировке неподвижных ядер-мишеней Х частицами Ма, энергия последних должна превышать величину:

126

Eпор =	M a + M X	Q	= −	M a + M X	Q


	M X			M X

Энергия ядерной реакции может быть записана в виде:

Q = (Ta + TX) – (Tb + TY).

5.2.Примеры решения задач

Задача 5.1. Определить удельную энергию связи ядра 73 Li . Решение. Определим дефект массы ядра:

m = Z mp + (A – Z) mn – mя.

Так как в таблицах обычно приводятся массы нейтральных атомов, то mя = mа – Z me

m = Z mp + (A – Z) mn – mа + Z me = Z (mp + me) + (A – Z) mn ; ((mp + me) = mH — масса атома водорода).

Используя табличные данные

m = 3 1,00783 + 4 1,00867 – 7, 01601 = 0,04216 а.е.м. 1 а.е.м. = 1,67 10-27 кг.

Энергия связи

Eсв = mc2 = m(а.е.м.) 931,5 МэВ/ а.е.м. = 0,04216 931,5 = 39,27 МэВ.

Удельная энергия связи – энергия связи, приходящаяся на один нуклон А = 7

ε= ЕсвязиА = 397,27 = 5,61нуклонМэВ

Задача 5.2. Определить энергию, которую нужно затратить для отрыва нейтрона от ядра 2311 Na .

Решение. Отрыв нейтрона от ядра приводит к уменьшению числа нуклонов (массового числа) на единицу:

2311 Na→01n+2211Na .

Можно рассматривать энергию отрыва нейтрона от 2311 Na (E) как энергию связи (Eсв) нейтрона с ядром 2211 Na .

Тогда используем

E = Eсв = mc2

127

m = mn + m2211 Na − m2311 Na =1,00867 + 21,99444 − 22,9897 = = 0,01334 а.е.м.

E = Eсв = m 931,5 МэВ/ а.е.м. = 0,01334 931,5 = 12,43 МэВ.

Задача 5.3. Определить число нуклонов (А) в единице объема

ядра ZA X .

Решение. Концентрация нуклонов в ядре:

n =

; rя

– радиус ядра.

πr3

=1,3 10−15 A

3 1045

1044

нуклонов

4π 1,33 10−45

4 3,14 1,33

м3

Концентрация нуклонов одинакова для различных ядер.

Задача	5.4. Период полураспада радиоактивного	аргона
41 Ar равен	T	=110 мин. Определить время, в течение	которого
18	1 2

распадается 75% начального количества ядер.

Решение. Число распавшихся радиоактивных ядер в течение времени t равно:

N = N0 − N = N0 − N0e−λt = N0 (1−e−λt ).

По условию задачи	N = 0,75N0
0,75N0 = N0 (1−e−λt )
0,75 =1− e−λt
e−λt = 0,25
Логарифмируя, получим:
eλt = 4; λt = ln 4 t = ln 4
	λ		ln 2		ln 2
Период полураспада T	=	; λ =
		T
		1 2		λ
						1 2
Окончательно t =	ln 4	T	=	1,386	110 = 220 мин.
ln 2	0,693
	1 2

128

Задача 5.5. Определить начальную активность А0 радиоактивного магния 2712 Mg массой m = 0,2 мкг, а также активность

А по истечении 1 часа. Предполагается, что все атомы изотопа радиоактивны.

Решение. Начальная активность изотопа А0 = λ N0; λ— постоянная распада, N0 — количество ядер (атомов) в начальный момент

λ =

ln 2

; N

μ = 24,4

10−3

кг

— молярная масса

моль

1 2

магния, T1 2 =10 мин., NА – число Авогадро.

A	=	ln 2		mNA	=	6,93 10−1 2 10−10 6,02 1023	= 5,7 1012 Бк = 5,7ТБк
T		6 102 2,44 10−2
0			μ
		1 2

Активность изотопа изменяется со временем по закону:

	A = A e−λt .
		0								−ln 2 t
				ln 2						t
	Т.к. λ =		, то A = A e	T1 2 = A	(eln 2 )−T1 2 . Т.к. eln 2 = 2 , то

				T1 2		0			0

	−	t			A		12			12	10
A = A		T1 2				5,7 10		5,7 10	12
2		=		0		=			=		= 0,0891 10	=8,91 10 Бк =89 ГБк
	t		60
0							64
					2T1 2		210

Задача 5.6. Найти тепловой эффект реакции 94 Be+11p→63 Li+42He . Решение. Воспользуемся формулой

Q = mc2

Q = 931,5 m94 Be + mp − m63 Li − mα =

=931,5(9,01219 + 1,00783 – 6,01513 –4,0026) = 931,5·0,00229 =

=2,13 МэВ.

Реакция идет с выделением тепла.

Задача 5.7. Покоившееся ядро 21384 Po испустило α-частицу с кинетической энергией Tα =8,34 МэВ. При этом дочернее ядро

129

оказалось в основном состоянии. Найти полную энергию, освобождаемую в этом процессе. Какую долю этой энергии составляет кинетическая энергия дочернего ядра?

Решение. α-распад полония происходит согласно схеме:

21384 Po→42 He+20982Pb

Согласно закону сохранения импульса

prPb = prα , т.е. 2MPbTPb = 2mαTα или MPbTPb = mαTα .

Отсюда кинетическая энергия дочернего ядра (свинца)

TPb =Tα mα

MPb

Полная энергия, освобождаемая в процессе:

mα

4,0026

E =Tα +TPb =Tα 1

=8,34 1

=8,5 МэВ.

MPb

205,974

Доля кинетической энергии дочернего ядра:

Tα

mα

η=

0,019 =1,9% .

MPb

Tα 1

MPb

Задача 5.8. Вычислить порог реакции 73 Li (α,n)105B .

Решение. Реакция, о которой идет речь может быть записана в

виде

73 Li+42 He=01n+105B

Подсчитаем энергию реакции:

Q = 931,5 m63 Li + mα − mn − m105 Be =

= 931,5 МэВ/а.е.м.(7,01601 а.е.м.+4,0026 а.е.м. – 1,00867 а.е.м. –

– 10,01294 а.е.м. = 931,5 (– 0,003) = — 2,8 МэВ.

130

Следовательно, реакция эндотермическая. Для вычисления порога реакции воспользуемся формулой:

mα

Eпор = Qэнд 1

= 2,8 1

= 2,8

= 4,4 МэВ .

M Li

Задача 5.9. Какие ядра образуются из α-активного ядра радия 22688 Ra в результате пяти α- и четырех β-распадов?

Решение. Схема реакции:

226 Ra = AX +54 He + 4(−0 e+ 0ν~) 88 Z 2 1 0

Всоответствии с законом сохранения электрического заряда: 88 = Z + 5·2 + 4(–1) . Следовательно Z = 82.

Всоответствии с законом сохранения для А:

226 = А + 5·4 . Следовательно А = 206.

Тогда найденный неизвестный изотоп ZA X =20682 Pb – изотоп свинца.

Задача 5.10. Найти энергию реакции 94 Be+11H→63 Li+42He , если известно, что кинетические энергии протона TH = 5,45 МэВ, ядра гелия THe = 4 МэВи что α-частица вылетела под углом 90° к направлению

движения протона. Ядро	49 Be — неподвижно.
Решение. Энергия	реакции Q –	разность между суммой

кинетических энергий продуктов реакции и кинетической энергией протона

Q = TLi +Tα −TH

prH prLi

Кинетическая энергия ядра лития

неизвестна,	для	её	нахождения
воспользуемся	законом	сохранения
импульса (рис.5.5)
pH = pLi + pα		Рис. 5.5.
Отсюда pH2 = pLi2	+ pα2

r pα

131

Кинетические энергии ядер:

T = 2pm2 (T << mc2 )

2mLiTLi = 2mpTp + 2mαTα .
Отсюда:
T	=	mHTH + mαTα	=	4,00260 4 +1,00728 5,45	= 3,57 МэВ.

Li		mLi	6,01513

Тепловой эффект реакции:
Q = 3,57 + 4 − 5,45 = 2,12 МэВ.
Задача 5.11. Определить энергию, выделяющуюся при
образовании двух α-частиц в результате слияния ядер 21H и 63 Li ,	если
известно,	что удельные энергии связи (ε) в ядрах 21 H , 24 He, и	63 Li

равны соответственно 1,11; 7,08 и 5, 33 МэВ. Решение. Ядерная реакция (синтеза):

21H+63Li →242 He

Из нее следует

E= 2Eсв (42 He)− Eсв (21 H)− Eсв (63 Li)= 2 4ε(42 He)− 2ε(21 H)− 6ε(63 Li)=

=8 7,08 − 2 1,11− 6 5,33 = 22,44 МэВ.

5.3.Задачи для самостоятельного решения

При решении задач можете использовать значения масс покоя нейтральных атомов, а также масс покоя элементарных частиц и значения периодов полураспада радиоактивных изотопов, приведенные

вприложениях.

5.12.Определить массу ядра лития, если масса нейтрального атома лития равна 7,01601 а.е.м.

5.13.Какую часть массы нейтрального атома плутония составляет масса его электронной оболочки?

132

5.14. Определить атомные номера, массовые числа и химические символы ядер, которые получаются, если в ядрах 2Не3, 4Ве7, 8O15 протоны заменить нейтронами, а нейтроны протонами. Привести символическую запись получившихся ядер.

5.15. Определить диаметры следующих ядер: 1) 3Li6, 2) 13Al27, 3)

29Сu64, 4) 50Sn125, 5) 84Ро216.

5.16.Определить диаметры ядер калия (19К Найти соотношение сечений этих ядер.

5.17.Оценить, какую часть объема атома кобальта составляет67 .39

объем его ядра. Плотность кобальта ρ = 4500 кг/м3.

5.18.Показать, что средняя плотность < ρ > ядерного вещества одинакова для всех ядер. Оценить (по порядку величины) ее значение.

5.19.Два ядра 5В10 сблизились до расстояния, равного диаметру ядра. Считая, что масса и заряд равномерно распределены по объему

ядра, определить силу F1 гравитационного притяжения, силу F2 кулоновского отталкивания и отношение этих сил (F1/ F2 ).

5.20.Определить дефект массы m и энергию связи ядра атома тяжелого водорода. 31 H

5.21.Определить удельную энергию связи Eуд. ядра 6С12.

5.22.Во сколько раз сечение ядра нептуния 93Np234 больше сечения ядра стронция 38Sr88?

5.23.Найти удельную энергию связи ядер 1Н3 или 2Нe3. Какое из этих ядер более устойчиво?

5.24.Энергия связи ядра, состоящего из двух протонов и одного

нейтрона, равна 7,72 МэВ. Определить массу Ма нейтрального атома, имеющего это ядро.

5.25.Определить массу Ма нейтрального атома, если ядро этого

атома состоит из трех протонов и двух нейтронов и энергия связи

Есв = 26,3 МэВ.

5.26. Какую наименьшую энергию нужно затратить, чтобы разделить на отдельные нуклоны ядро 3Li7?

5.27. Какую наименьшую энергию нужно затратить, чтобы оторвать от ядра азота 7N14 один нейтрон?

5.28. Найти минимальную энергию, необходимую для удаления одного протона из ядра углерода 6С12.

5.29. Определить удельную энергию связи Eуд ядра бериллия

4Ве7.

5.30. Какую наименьшую энергию нужно затратить, чтобы разделить ядро углерода 6С12 на три одинаковые части?

5.31. Удельная энергия связи ядра гелия 2He4 равна Eуд. = 7,1 Мэв/нуклон. Определить энергию связи и дефект массы 2He4 .

133

5.32. Найти удельную энергию связи нуклонов в ядре алюминия

13Аl27

5.33.Какая часть δ начального количества атомов актиния 89Ac235 останется через 5 суток? Период полураспада Т1/2 = 10 суток.

5.34.Некоторый радиоактивный препарат имеет постоянную

распада λ = 1,44 10-3 с-1. Через какое время t распадется 75% первоначального количества атомов?

5.35. Определить активность А фосфора Р32 массой m = 10-3 г. Молярная масса фосфора М = 32 10-3 кг/моль, период полураспада Т1/2

=14,3 суток.

5.36.За какое время t распадется 1/4 начального количества ядер радиоактивного изотопа, период полураспада которого равен

Т1/2 = 24 часа?

5.37. Какая часть начального количества атомов распадется за один год в радиоактивном изотопе тория Тh229? Период полураспада

Т1/2 = 7 103 лет.

5.38.Определить число N атомов, распадающихся в

радиоактивном изотопе за время t = 10 с, если его активность A = 0,1 МБк. Считать активность постоянной в течение указанного времени.

5.39. В урановой руде отношение числа ядер 238U к числу ядер 206Pb составляет 2,8. Оценить возраст руды, считая, что весь свинец является конечным продуктом распада уранового ряда. Период полураспада урана 4,5 109 лет.

5.40.Чему равна удельная активность изотопа урана 92U238, если период его полураспада Т1/2 =4,5 109 лет.

5.41.Найти массу m1 урана U238, имеющего такую же активность, как стронций Sr90 массой mSr = 10-3 мг.

5.42.За время t = 1 сутки активность изотопа уменьшилась от

А1 = 118 ГБк до А2 = 7,4 ГБк. Определить период полураспада этого изотопа.

5.43.Сколько α– и β–распадов испытает уран 92U238, превращаясь

вконечном счете в стабильный изотоп 82Pb206?

5.44.Радиоизотоп Х1 с постоянной распада λ1 превращается в радиоизотоп Х2 с постоянной распада λ2. Считая, что в начальный момент препарат содержал только Х1, найти промежуток времени, через который активность радиоизотопа Х2 достигла максимума.

5.45.Определить возраст древних деревянных изделий, если удельная активность изотопа 14С у них составляет 3/5 удельной

активности этого же изотопа в только что срубленных деревьях. Период полураспада 14С равен 5570 лет.

134

5.46.Радиоизотоп испытывает превращения по схеме Х1 → Х2 → Х3 (стабилен) с соответствующими постоянными распада λ1 и λ2. Считая, что в начальный момент препарат содержал только ядра

изотопа Х1 в количестве N10, найти закон накопления стабильного изотопа Х3.

5.47.Активность некоторого препарата уменьшается в 2,5 раза за 7,0 дней. Определить период его полураспада.

5.48. Период полураспада изотопа полония 84Ро210 равен Т = 140 суток. Определите массу свинца 82Рb207, который образуется из m = 1 мг полония за t = 70 суток.

5.49.Первоначально покоившееся ядро полония 84Ро210

испустило α-частицу с кинетической энергией Тα = 5,3 МэВ. Найти скорость отдачи дочернего ядра.

5.50. Определить количество тепла, которое выделяет m = 1 мг препарата 84Ро210 за период, равный среднему времени жизни этих ядер, если известно, что испускаемые α-частицы имеют энергию E=6,3 МэВ и практически все дочерние ядра образуются непосредственно в основном состоянии.

5.51. α-распад ядер 84Ро210 (основное состояние) сопровождается испусканием двух групп α-частиц с кинетическими энергиями 5,30 и 4,50 МэВ. В результате испускания этих α-частиц дочерние ядра оказываются соответственно в основном и в возбужденном состояниях. Найти энергию γ-квантов, испускаемых возбужденными ядрами.

5.52.Вычислить с помощью табличных значений масс атомов энергии позитрона и нейтрона, испускаемых ядром 6С11 в случае, если дочернее ядро не испытывает отдачи.

5.53.Период полураспада радиоактивного нуклида Т1/2 = 1 ч.

Определить среднюю продолжительность жизни τ этого нуклида.

5.54.За один год начальное количество радиоактивного изотопа уменьшилось в три раза. Во сколько раз оно уменьшится за два года?

5.55.Определить начальную активность А0 радиоактивного магния Мg27 массой m = 0,2 мг, а также его активность по истечении времени один час. Период полураспада Т1/2 = 9,5 мин., молярная масса

М= 27 10-3 кг/моль, число Авогадро NА = 6,02 1023 моль-1.

5.56.Атомное ядро, поглотившее γ-фотон (λ = 0,47 пм), пришло в возбужденное состояние и распалось на отдельные нуклоны, разлетевшиеся в разные стороны. Суммарная кинетическая энергия нуклонов Т = 0,4 МэВ. Определитьэнергию связи ядра.

5.57.Ядро бериллия 4Ве7 захватило электрон из К-оболочки атома. Какое ядро образовалось в результате K — захвата?

135

86Rn220

5.58. Ядро плутония 94Pu238 испытало шесть последовательных α-распадов. Написать цепочку ядерных превращений с указанием химических символов, массовых, зарядовых чисел, промежуточных ядер и конечного ядра.

5.59. Покоившееся ядро радона выбросило α-частицу

со скоростью v = 1,6 107 м/с. В какое ядро превратилось ядро радона? Какую скорость v1 получило оно в результате отдачи?

5.60. Какая доля начального количества радиоактивного вещества останется не распавшейся через 1,5 периода полураспада?

5.61. При нормальных условиях один грамм радия образует

V = 0,043 см3 гелия в год. Определить период полураспада радия. 5.62. 1 г урана 92U238 в равновесии с продуктами его распада

выделяет мощность 1,07 10-7 Вт. Найти полное количество тепла, выделяемое одним грамм-атомом урана за среднюю продолжительность жизни атома урана.

5.63. Освобождается или поглощается энергия при ядерной реакции 4Ве9 + 1р1 → 5В9 + 0n1?

5.64. При бомбардировке ядра 13Al27 α-частицами получается радиоактивный изотоп фосфора 15Р30, который распадается с выделением позитрона. Написать уравнения обеих реакций.

5.65.При делении одного ядра урана U235 выделяется энергия 200 МэВ. Какую долю энергии покоя составляет выделившаяся энергия?

5.66.Освобождается или поглощается энергия при ядерной

реакции 3Li7 + 1H1 → 22Hе4? Найти величину этой энергии.

5.67. Электрон и позитрон, имевшие одинаковые кинетические энергии, равные 0,24 МэВ, при соударении превратились в два одинаковых фотона. Определить энергию фотона и соответствующую ему длину волны λ.

5.68.α-частица с кинетической энергией Т возбуждает реакцию 9Ве(α, n)12С. Найти кинетическую энергию нейтрона, вылетевшего под прямым углом к направлению движения α-частицы. Массы покоя частиц считать известными.

5.69.Радиоактивное ядро магния Мg23 выбросило позитрон и нейтрино. Записать реакцию распада ядра Мg23 и определить энергию распада.

5.70.Какую энергию необходимо сообщить, чтобы при реакции

13Al27(α, p) 14Si30 подверглись превращению все ядра, находящиеся в 1 г алюминия?

5.71. При бомбардировке изотопа 3Li6 дейтронами образуются две α-частицы. При этом выделяется энергия, равная 22,3 МэВ. Зная массы дейтрона и α-частицы, найти массу изотопа 3Li6.

136

5.72. При бомбардировке изотопа 3Li6 дейтронами образуются две α-частицы, разлетающиеся симметрично под углом ϕ к направлению скорости бомбардирующих дейтронов. Найти: 1) угол разлета ϕ; 2) энергию образующихся α-частиц, если известно, что энергия бомбардирующих дейтронов равна 0,2 МэВ.

5.73.Изотоп 2Не3 получается бомбардировкой ядер трития 1Н3 протонами. Написать уравнение реакции, найти энергию этой реакции.

5.74.Найти наименьшее значение энергии γ-кванта, достаточное

для осуществления реакции 12Мg24 (γ, n)Y.

5.75.Какое количество воды можно нагреть от 0° С до кипения,

если использовать все тепло, выделяющееся при реакции 3Li7(p, α) при полном разложении одного грамма лития?

5.76.Какое количество энергии в кВт-часах можно получить от деления 1 г урана 92U235, если при каждом делении выделяется энергия, равная приблизительно 200 МэВ?

5.77.Определить энергию Q ядерной реакции Ве9(n, γ)Ве10, если известно, что энергия связи ядра Ве9 равна Есв = 58,16 МэВ, а ядра Ве10

Есв = 64,98 МэВ.

5.78. При реакции Li6 (р, β+) Li7 освобождается энергия Q = 5,028 МэВ. Определить массу Li6. Массы остальных атомов взять из таблицы.

5.79.При ядерной реакции 9Ве (α, n) 12С освобождается энергия Q = 5,70 МэВ. Пренебрегая кинетическими энергиями ядер бериллия и гелия и принимая их суммарный импульс равным нулю, определить кинетические энергии ТС и Тn продуктов реакции.

5.80.Определить суммарную кинетическую энергию Тядер,

образовавшихся в результате реакции 13C (D,α) 11B, если кинетическая энергия ТD дейтрона равна 1,5 МэВ. Ядро-мишень 13C считать неподвижным.

5.81.Определить энергию Q распада ядер углерода 6С10, выбросившего позитрон и нейтрино.

5.82.Вычислить энергию, необходимую для разделения ядра

Nе20 на две α-частицы и ядро С12, если энергия связи на один нуклон в ядрах Nе20, Не4 и С12 равны 8,03; 7,07 и 7,68 МэВ.

5.83.Вычислить в а.е.м. массу ядра С10 с энергией связи на один нуклон 6,04 МэВ.

5.84.Найти энергию реакции 14N (α, р) 17O, если кинетическая

энергия налетающей α-частицы Тα = 4,0 МэВ, а протон, вылетевший под углом ϕ = 60° к направлению движения α-частицы, имеет кинетическую энергию Тр = 2,09 МэВ.

137

5.85.Протоны, налетающие на неподвижную литиевую мишень, возбуждают реакцию 7Li(р, n) 7Ве. При какой кинетической энергии протона возникший нейтрон может оказаться покоящимся?

5.86.Литиевую мишень бомбардируют протоны с кинетической

энергией Т = 1,0 МэВ. Происходит ядерная реакция р + 7Li → 24Hе. Найти кинетическую энергию каждой α-частицы и угол между направлениями их разлета, если разлет произошел симметрично к направлению набегающих протонов.

5.87.Какую кинетическую энергию необходимо сообщить протону, чтобы он смог расщепить покоящееся ядро 2H, энергия связи которого Есв =2,2 МэВ?

5.88.Определить массу атома, ядро которого, испуская α— частицу с энергией 5,46 МэВ, превращается в 84Ро218. Масса полония

МРо = 218,07676 а.е.м.

5.89. Определить энергию, освобождаемую при синтезе 1 кг гелия в термоядерной реакции 1H2 + 1H3 → 2He4 + 0n1.

5.90. Определить энергию быстрых нейтронов, возникающих в результате реакции 4Ве9 + 2He4 → 6C12 + 0n1.

5.91.Найти пороговую кинетическую энергию α-частицы для возбуждения реакции 7Li(α, n) 10В.

5.92.Нейтроны с кинетической энергией Т = 10 МэВ возбуждают

реакцию 12С(n, α) 9B, порог которой Епор = 6,17 МэВ. Найти кинетическую энергию α-частиц, вылетающих под прямым углом к направлению падающих нейтронов.

5.93. Искусственный изотоп азота 7N13 получается
бомбардировкой ядер углерода 6С12 дейтронами. Найти порог	этой
реакции. Найти суммарную кинетическую энергию продуктов	этой

реакции при пороговом значении кинетической энергии дейтронов. Ядра углерода считать неподвижными.

138

Ответы

Ответы к главе 1

1.25.T = 648 K.

1.26.T = 1 кК.

1.27.W = 5,64 кДж.

1.28.Фе = 5,67·1014 Вт.

1.29.Ме/Ме = 0,04.

1.30.в 1,19 раза.

1.31.Ме = 64,2 МВт/м2; Т = 5,8 кК.

1.32.Т = 396 К.

1.33.Ме = aT · σ · T4 = 5,88 кВт/м2; W = Ме · S · t = 1,76 кДж.

1.34.aT = 0,953.

1.35.η = 1 – σ·T4·S/Р = 0,71.

1.36.aT = Ме / σ · T4 = 0,26.

1.37.T = P = 866K.

4π aT R2 σ

1.38. λmax = 10,6 мкм.
1.39. λmax = 547 нм.
1.40.	3,8 кК; 7,6 кК.
1.41.	4,98 кК.
1.42. Увеличилась в 243 раза.
1.43. Т1 = 3,62 кК; Т2 = 7,24 кК.
1.44. λmax = 1,45 мкм.
1.45. (МλТ ) max = 10,44·1012 Вт/м2 · м.	λT +b)=300K .
1.46. Уменьшилась на T = λT 2	(
	1	1

1.47.CV = 16 σcT 3 V = 3 10−9 Дж/(К м3 ).

1.48.4,1 млн. т/с. Около 1011 лет.

−1

1.49.T 18στ − 1 3 =103K.

Cудρd T03=


1.50. N1	= 6,2 · 1018	c-1;	N2 = 1,2 · 1019 c-1;	N3 = 1,1 ·	1019 c-1;
N4	= 5,9 · 1018	c-1;	N5 = 4,6 · 1018 c-1;	N6 = 5,1	· 1018 c-1.
1.51. а) 2,07 эВ;		1,1·10-27 кг · м/с; 3,68·10-36 кг; б) 12,4 кэВ;
	6,62·10-24 кг · м/с; 2,21·10-32 кг; в) 1,24 МэВ;	6,62·10—

22 кг · м/с; 2,21·10-30 кг.

1.52.а) 960 К; б) 1,6·104 К;в) 1,6·1010 К.

1.53.а) 5·1019; б) 1013.

139


1.54.	n =	λ	8m k T	= 7,6 103	, m – масса атома гелия,
		h	π
k –постоянная Больцмана.
				π h2
1.55.	T =				= 745 K, m – масса нейтрона,
		2
			8m k λ

k – постоянная Больцмана.

1.56.ν = 4,53 · 1017 с-1.

1.57.E = b hsinc ϕ = 2,36 10−3 эВ, p =1,26 10−30 кг м/ с.

1.58.E = ( h c )= 2,07 эВ. d sin ϕ2 −sin ϕ1

1.59.F = 4 нН, NФ = 1019 фотонов.

1.60. nΦ =	p λ	13	м	−3		21 -2 -1
	= 2,52 10		, n1Φ = n · c = 7,56 · 10	м с	.
(1+ρ) h c

1.61.P = 4,67 мкПа.

1.62.I = 1,5 кВт /м2.

1.63.F = 2,5·10-11 H.

1.64.р = 10-7 кг · м / с.

1.65.F = 2N/c = 4·10-7 H.

1.66.N = 9 · 1015.

1.67.N1 = 3,77 · 1018.

1.68.n = 1011 м-3.

1.69.р = 11 мкПа.

1.70. р1 = 0,7 мкПа;

р2 = 0,35 мкПа.

1.71.λ = 197 нм; λ0 = 175 нм.

1.72.pmax = 3,45 · 10-25 кг · м / с.

1.73. λ0 Li = 893 нм; λ0 Cs = 657 нм.

1.74.εmin = 4,5 эВ.

1.75.AВ = 4,5 эВ; vmax = 9,1 · 105 м/с; Tmax = 3,8 · 10-19 Дж.

1.76.а) для Cs: vmax = 1,3 · 106 м/с; для Pt: vmax = 7,05 · 105 м/с. б) для Cs: vmax = 6,05 · 105 м/с; из Pt фотоэлектроны не вырываются.

1.77.εmin = 2,15 эВ.

1.78.U = 1,73 В.

1.79.x = 1,37 · 10-4 м.

1.80.λ = 24,2 пм.

1.81.ε′Φ = 0,26 МэВ; pΦ′ = 9,3 10−12 кг м/ с.

1.82.ε′e = 0,1МэВ.

1.83.λ′ = 57 пм.

1.84.θ = 120º или 240º.

140

1.85.ε′Φ = 0,224 МэВ;T = 0,176 МэВ.

1.86.pe′ = 2,8 10−22 кг м/ с.

1.87.0,5.

1.88.θ = 60º40΄.

1.89.εΦ = 0,37 МэВ.

1.90.70%.

1.91.	Δλe = 0,048 Å и Δλp = 2,6 · 10-5 Å.
1.92.	θ = 90°, Т′е = 24,0 кэВ.

1.93.	ε′e =	h c		2 λc sin 2 θ 2	, λc =	h	,	ε′e = 118,184кэВ; 255 кэВ
λ		λ + 2λc sin 2 θ 2	me c

и 0 кэВ.

1.94.θ = 50°.

1.95.pе′ =1,6 10−22кг м/с.

1.96.Δλ = 0,0135 Å , θ = 63º40΄.

ctg

1.97. tgϕ =

m cλ

1.98. θ + φ = 109º30΄.

1.99. λ =

= 0,012A.

e V

1.100. ε′e =

− E = 31кэВ.

2 e V

sin2 θ

ε = 0,939 ГэВ; p = 5,01·10-19 кг·м/с.

1.101.λf = 1,32 фм;

1.102.а) λ = 73,22 пм; б) λ = 75,6 пм.

1.103. λ = 2,42 пм; T = 6,6 кэВ; p′Е = 4,4 10−23 кг м/с.

1.104. εΦ =

ε′

=1,85 МэВ.

ε′

1−

Ф sin2

εν

1.105.1)

λ1 = 4,84 пм, 2) λ2 = 2,64 фм.

141

Ответы к главе 2

2.18. λ = 2πh mev =1,0A .

2.19.

λe =

= 43.

2.20. m = 2π2h2

eU0λ2 =1,67 10−27 кг.

2.21. λ1 =123 пм, λ2 = 2,86 пм, λ3 = 0,186 пм.

2.22.

E =

2π

λ2

− λ2

= 0,45кэВ.

2.23. v =

= 2 106 м/с.

m λ

2d sin θ

2.24. λ = πh

2(η2 −1)

Em = 0,15нм.

2.25. λ = 2πh

2mkT =180 пм, где m — масса молекулы водорода.

2.26. λ1 = λ

(n +1) (n −1)= 2,2 пм.

2.27. v = 4πhl bm

x =106 м/с.

πhl

2.28. T =

= 24эВ.

d x

=π2h2 2med 2 =150 B .

2.30.d = πhk 2mT cosα 2 = 0,21 нм, (k = 4).

2.31.λ = heBR = 0,1 нм.

2.32.λ = 6,6 10−10 м.

2.33.T = ( 2 −1)mc2 = 0,21 МэВ.

2.34.λ = 2πh 2mT (1+T2mc2 ).( η −1)2 sin2 θ2.29. U0

2.35.	λ = λк 1+ mcλкπh = 3,3 пм.
2.36.	T ≤ 4m c2	λ λ = 20,4 кэВ для электрона,
	e
	T ≤ 4mpc2	λ λ =37,5 МэВ для протона,

2.37.U Ag= π2h2k 2 −U0 sin2 θ =15 В, k = 3 .

2med 2

2.38.E = 0,02 эВ, T1 = 2E3k =158 K .

2.39.1) T = h2 2mλ2 =150 эВ;2) T =1,2 ГэВ.

2.40. d =λ 2sinθ=3,1A, sin2θ = D D2 +l2 , θ — угол скольжения.

142

2.41. R ≈ nλl d, где λ = 2πh p = 2πh 2mT .

R1 = 2πhl a 2mT = 0,3 см R2 = R1 2 = 0,42 см.

2.42. v	x	= h m x	v =104	см/с,	v =10см/с,	v =10−20	см/с.
		1		2	3

2.43.v =106 м/с, v1 = 2,2 106 м/с.

2.44.x = htm x0 ≈104 м.

2.45.x λ =100 2π =16 .

2.46.( p p) 100% =16% .

2.47.v v = h m xv ≈10−3 . Траектория имеет смысл.

2.48. T				≈ 2h2	ml2 =15 эВ, x = l 2, p = p .
	min
2.49.		v v = 2h	2ml2T =1,2 10−4 , x = l 2.
2.50. T = h2	2mr2 = 0,2MэВ.
2.51. T ≈8 104 h2 ml2 ,		x = l 2.
2.52. Emin ≈ 2h2	ml2 =15 эВ.
2.53. l = 2h	2mE = 2,9 10−15 м.
2.54.		x = сτ = 3м,	λ λ ≈ λ 2πсτ ≈ 3 10−8 .
2.55.		E ≈ h τ ≈ 6,6 10−8 МэВ.
2.56.		x λ ≈T π T = 2 10−3 .
2.57.		ω ω= 3 10−8 .
	d	2	ψ		2m		bx	2
2.58.		+	E	−		ψ = 0 .
			2		2
	dx		h		2

2.59.ih∂ψ = − h2 ∂2ψ .

∂t 2m ∂x2

2.60.w(r)= max приr = r1 .

2.61.A = 4 α π .

2.62.A = 2 (b − a).

2.63.W = 0,238.

2.64.	A =	2 a .
2.65.	A =	2 a3 .

2.66. r = 2r1 и r = 4r1. 2.67. E = h2k 2 2m .

2.68. 1) m = 5π2h2 2l2 E , 2) n = (η +1)2(η −1)= 3 .

143

2.69. W = 2 x∫2 sin 2 (πx l)dx = 1 +	3	≈ 0,61.
		l	x			3	2π
			1	E = (πhwmax )2
2.70. l = 2 wmax ,	8m .
2.71. En = π2h2n2 2ml2 .
2.72.	En+1,n En	= (2n +1) n2 , 1) 0,78, 2) 0,21,3) 0 . При малых
	дискретность проявляется отчетливо, при больших – нет.
2.73.	Emin	= 4,48 эВ.
2.74. С =		2 l .
2.75.								(x)= 2 l sin(nπx l).
1) С = −C	2	=1	2l , 2)E	n	= π2h2n2	2ml2 , 3)ψ	n
1

2.76.W = 0,475.

2.77.W1 W 2 = 5,22 .

= 2

(nπx l)dx =1

2.78. x

∫xsin 2

∫x{1 − cos(2nπx l)}dx =

2.79. В1

А1 = (k1 − k2 ) (k1 + k2 ), A2 А1 = 2k1

(k1 + k2 ).

2.80. R

− k

4k k

+ k2

D = (k1

+ k2 )2 .

2.81. λ2

= λ1

1 − mU0 λ21

2π2h2

= 218 пм.

2.82.W = 0,0625.

2.83.n = 1+U E =1,25 .

2.84.(U0 T ) 100% = 2% .

2.85.R = 11+− nn 2 .

2.86.U0 = 9,13 эВ.

2.87.R = 0,0295, D = 0,97.

2.88.TU0 =1,03 .

2.89.D = ( 4n )2 .

1+ n

2.90.n12 = 0,384, n21 = 2,61.

2.91.D = 0,2.

2.92.A2 А1 = 2k1 (k1 + k ).

2.93. 1) D = 0,2, 2) D = 6,5 10−3 .

2.94.W1 W 2 = 79 .

2.95.d = 0,143 нм.

144

2.97.W = 0,2.

2.98.U0 − E =10−4 эВ.

Ответы к главе 3

3.18. R = 2215 λ = 1,097 107 м-1.

3.19.U1 = 40,8 В, U2 = 91,8 В.

3.20.n = 3.

3.21.λд = 4 3Rλ =1,22 10−7 м, λк =1 Rλ = 0,91 10−7 м

3.22.ϕион =122В

3.23.λ32 = 36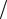5Rλ = 6,55 10−7 м , λ21 = 43Rλ =1,21 10−7 м. Замечание:

правило отбора разрешает переходы, где l = ±1.

3.24.а) λ = 30,4 нм; б) λ = 13,5 нм.

3.25.n = 3; λ1 = 1026 Å; λ2 = 1215 Å и λ3 = 6560 Å.

3.26.λ1 = 656,3 нм; λ2 = 121,6 нм и λ3 = 102,6 нм.

3.27.ϕион = 54,4В

3.28.Три линии, принадлежащие серии Лаймана.

3.29.n = 4.

3.30.Е = -0,544 эВ, n = 5.

3.31.3970 Å; 7,55 1014 с-1.

3.32.Еион = 3hc4λ1 =13,6 эВ.

3.33.Первые две — серии Бальмера (7→2 и 3→2),

последняя — серии Пашена (10→3).

		15	λ		m e	4	1/ 3		−34
3.34.							Дж с.
h =								≈1,05	10
5632	3	2
			π	ε0	c
3.35. n = 2	R d sin ϕ		= 4.
			R d sin ϕ− 4к

3.36.v = 7 105 м/с относительно ядра.

3.37.Скорость отдачи атома v = 3h R/4M = 3,26 м/с. М — масса атома.

3.38.Те = Евозб Не – Е ион Н = 40,8 – 13,6 = 27,2 эВ.

3.39. λ43 =1447Rλ =1,87 10−7 м, λ32 = 365Rλ = 6,55 10−7 м,

λ21 = 43Rλ =1,21 10−7 м. Замечание: правило отбора разрешает переходы, где l = ±1.

145

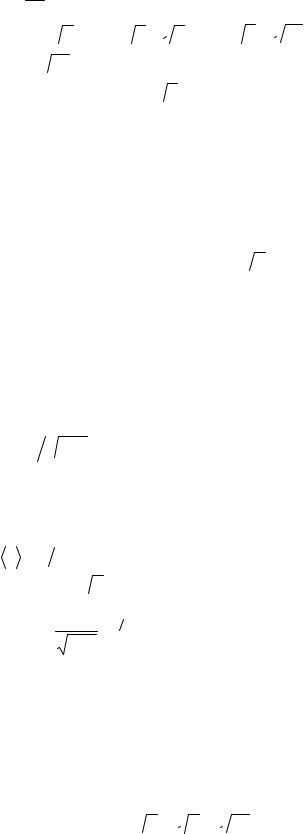
3.40.v = 3,26 м/с

3.41.v = 8,18 105 м/с

3.42.ν = Rν + mv2 =1,07 1015 Гц 4 2h

3.43.L = ± 2h, ±h( 2 − 6), ±h( 6 − 12).

3.44.L = h 12; LZ max = 3h.

3.45.E2p = -3,38 эВ; L = h 2 =1,48 10−34 Дж с.

LZ = h =1,054 10−34 Дж с.

3.46.0,91 10-34Дж с; 2,05 10-34Дж с.

3.47.ϕ = 28,12°.

3.48.2р.

3.49. 32; 2,04 10-34 Дж с; 0,91 10-34 Дж с.

3.50.Во всех nS — состояниях L = 0.

3.51.Во всех – nР состояниях L = h 2 =1,5 10−34 Дж с.

3.52.0; ±1,55 10−34 Дж с, ±2,11 10−34 Дж с.

3.53.L =1,49 10−34 Дж с.

3.54.pm =1,61 10−23 Дж/ Тл.

3.55.Е = –3,4 эВ.

3.56.L =1,5 10−34 Дж с

3.57.pm =1,31 10−23 Дж/ Тл

3.58.C =1 πa3 .

3.59.r = πε0h2 me2 .

3.60.W1 W2 = 0,825

3.61.W1 = 0,324, W2 = 0,676, W2 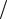W1 = 2,09

3.62.r = 3 2a .

3.63.pm = −μÁ 2 = −1,31 10−23 Äæ / Òë

0,1a	1	e−r a	2

3.64 W = ∫		4πr2dr =1,13 10−3
0	πa3

3.65. а) 9, б) 2, в) 3, г) 5.

3.66. 1s2 2s2 2p6 3s2 3p3, N = 15. 3.67. N = 46.

3.68. а) 7, б) 3

3.69. 2S1/2, 3P1/2,3/2, 2D3/2,5/2.

3 70. 2 s –электрона; 2 s –электрона, 6 p –электронов;

2s –электрона, 6 p –электронов, 10 d-электронов.

3.71.1) j =1, 2, 3; Lj = h 2, h 6, h 12 ,

146

2) j =2, 3,4; Lj = h 6, h 12,h 20 .

3.72. 1) 9; 2) 4; 3) 2; 4) 3; 5) 5.

3.73. 1) 1s2 2s2 2p1 ; 2) 1s2 2s2 2p2 ; 3) 1s2 2s2 2p6 3s1 .

3.74. 1) 3/2, 5/2, 7/2, 9/2; 2) 1,2,3,4,5; 3) 1/2, 3/2,…, 11/2; 4) 1,2,…,7. 3.75. 1) 2S1/2; 2) 1S0; 3) 2S1/2; 4) 1S0; 5) 2P1/2.

3.76. 1) 2S1/2; 2) 2P1/2, 2P3/2; 3) 4P1/2,4P3/2 ,4P3/2 ,4P5/2; 4) 5D0,5D1,5D2,5D3,5D3,5D4.

3.77.1) 4; 2) 7; 3) 7.

3.78.1) 2; 2) 1,3; 3) 2,4; 4) 1,3,6; 5) 2,4,6.

3.79.3P3 , 5D3 , 5F3 , 5G3 , 5H3 .

3.80.3P1/2,3/2 ; 2D5/2,3/2 ; 2F7/2,5/2.

3.81.10.

3.82.Eсв = 5,75 кэВ.

3.83.Li, Na.

o	= 3 10−16	o	=12 10−16 Дж;
3.84. Al: λ = 6,7A; εf	Дж; Co: λ =1,56A; εf

3.85. U = 54,4 кВ. 3.86. Те=2,45 кэВ.

Ответы к главе 4

4.15	1) λe =	h	= 8.	2) нужно
m vd
		d
			e
			2d sin α		o
4.16	λ =			2		cos α =1,74 A.
k 2	+ k 2	− 2k k	2
		1	2	1	2

4.17θ = 60,5°

4.18	v =	3kT	≈105 м/с
		m
		e

4.19Еmax = 5,49 эВ; vmax = 1,39 106 м/c.

4.20ЕF = 11,55 эВ; vmax = 2 106 м/c.

4.21n1/n2 = 1,8.

4.22Число свободных электронов, приходящихся на один атом натрия, 0,995.

4.23n = 1,66 1025 м-3.

4.24Еmax = 4,68 эВ; Тθ = 5,43 104 К.

4.25Т = 2,51 104 К.

147

4.26f(E,T) = 0,6.

4.27Уменьшится в 1,08 раза.

4.28Т = 1491 К.

4.29При Т1=300 К; f1(E,T1) = 0,128; f2(E,T1) = 0,87; при Т2=60 К;

f1(E,T2) = 6,8 10-5; f2(E,T2) = 1.

4.30	Е1 = 2,2 kT; Е2 = -2,2 kT.

4.311) Т = 572 К, 2) При любой температуре.

4.32< Е > = 4,8 эВ.

4.33Еmax = 2,029 эВ; < Е > = 1,217 эВ.

4.34Еmax = 7 эВ.

4.35Т = 394 К.

4.36Не зависит. < Е > = 3 эВ.

4.37Т = 3,3 104 К.

4.38N=3 1023 электронов.

4.39		N	3 / 2
η =		= (1−0,5	) = 0,65.
Nmax
4.40	< Е1 > = 2 10-23 эВ, < Е2 > уменьшается в η раз.
4.41	η =	Ni		= (1− 0,63	/ 2 ) = 0,54.

		Nmax

4.42E = EF(1-0,54)2/3 = 2,8 эВ.

4.43E = EF(1-0,5)2/3 = 3,44 эВ.

4.44N1/ N2 = 0,65.

4.45		n	=	1− (1− 0,02)2 / 3	= 0,086.
	1
n	(0,5)3 / 2

		2			[1− (1− 0,04)3/ 2 ]
4.46		n	=		= 7,424.
	1	(0,04)3/ 2
	n

		2

4.47nn =1−(1−η)3/ 2 = 0,03.

4.48T = 25EkF = 25434 K.

4.49< v > = 1,18 106 м/с.

4.50< v > = 1,05 106 м/с.

4.51< vкв > = 1,14 106 м/с.

4.52< vкв > = 9,9 105 м/с, vмах = 1,27 106 м/с.

148

4.54n1 = 7. n2

4.55Vn =1,423 1029 м−3.

4.56N/N=0,56.

4.57σ = 2,26 См/м.

4.58ρ 208 Ом м.

4.59n = 2,5 1019 м-3.

4.60μp = 0,52 м2/(B c) при n = 4 1019 м-3.

4.61	1) nр = 1,47 1016 м-3; 2)		jn	= 0,74.
	j

							n+ p
4.62	R0	=			R	= 360Ом.
1	−qe	n(μn +μp )lR

4.63R = 1330 Oм.

					1	1	−5
4.64		= ρ1 exp	EF		=1,07 10	Oм м.
ρ2	k			−
T	T
					2	1

4.65σ2/σ1 = ехр(4,83) = 125,7.

3/ 2

4.66

E3 T

= 3,315.

= T

exp

2kT T

1 2

4.67

2kT1T2

T −T

4.68

T2 =

EЗT1

= 308K.

EЗ − 2kT1 ln 2

4.69νкр = 2,6 1014 с-1.

4.70n = 1,36 1021 м-3; μn = 0,306 м2/(B c).

4.71μn = 0,37 м2/(B c).

4.72σ = 6,98 102 См/м.

4.73Ux = 1,2 B.

4.741) nр = 3,69 1021 м-3; 2) μp = 0,85 м2/(B c).

4.751) ne = qelBUρ аϕX = 5 1015 см−3

	2) μе =	qe	ϕX	= 0,05м2 /(В с).
	BUа

	n =	3πBja	17	м	−3
4.76			= 4,2 10		.
8q	ϕ	X
		e

149

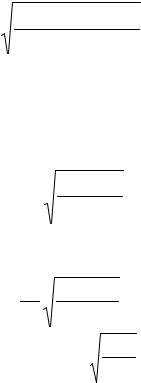
4.77cуд.железа =2,7 Дж/(кг К).

4.78cуд2/ cуд1 = 62,6.

4.79cуд = 1,08 Дж/(кг К).

4.80M = 0,107 кг/моль, материал – серебро.

4.81T = 66,43 K.

4.82Да. Так как при этих температурах с ~ T3. θ = 409,46 K.

4.831) Emax = 6,45 10-21 Дж; 2) pmax = 3,57 10-24 (кг м)/с. 3) λ фотона = 3,08 10-5 м.

4.84

(T )

T = 411,6Дж.

4.85

8π2

3π2

(30

−T

)

= 0,0124,

9θ

4EF

5θ

4.86νmax = 4,1 1013 Гц.

4.871) ωmax = 1,05 1014 рад/с; 2) v = 3,6 103 м/с.

4.88θ = 164 K.

4.89		U =			m	C		(T )	T = 586,57 Дж.

							M	v		1
4.90	θ = 3	3mπ4 R(T 4 −T 4 )	= 331,27K.
								2		1
										5MQ
4.91		Q	=						5kT	2θ3				=1,26 10	−	2.
		1								2
	Q	2	12E	F	π2 (T 4	−T	4 )
											4		3
4.92		Q	= 9,99	10	−2	;		Q	=		π4 (T 4	−T	4 )	.
1			1			2		1
		Q	5	T θ	3
		Q
	2												2
4.93	1) ωma[ = 3		18π2 n						13	рад/ с.
	v−3	+v−3 = 6,13 10
											\|\|

	466,41 K.
4.94	1) Emax = 2,86 10-21 Дж; 2) θ = 207 К; 3) λ = 6,95 10-5 м.
		v =	kθ		M
4.95	1)	h	3	6π2ρN A = 2622 м/ с.
	2)	λmin	= 2d = 23 M	= 0,46 нм.
					ρNA

150

Ответы к главе 5

5.12.m = 7,014 а.е.м. = 6533,88 МэВ.

5.13.m e / m a = 2 10-2%.

5.14.1H3; 3Li7; 7N15.

5.15.5,2 Фм; 7,8 Фм; 10,4 Фм; 13 Фм; 15,6 Фм.

5.16.dК = 8,7 10-15 м, dZn = 1,03 10-14 м, σ1/σ2 0,71.

5.17.VЯ /Va = 2,49 10-14.

5.18.<ρЯ> 0,18 1018 кг/м3.

5.19.	F1 = 0,59 10-33 H, F2 = 0,18 103 H, F2 / F1 = 0,312 1036.
5.20.	m = 4 10-30 кг; EСВ = 2,24 МэВ.
5.21.	Eуд = 7,42 МэВ/нуклон.
5.22.	σ1 /σ2 = 3,36.
5.23.	EУД.1 = 2,839 МэВ/нуклон, EУД.2 = 2,584 МэВ/нуклон;
	1H3 более устойчиво.

5.24.Ma = 3,0141 а.е.м.

5.25.Ma = 5,0113 а.е.м.

5.26.Emin= 39,27 МэВ.

5.27.Emin= 10,55 МэВ.

5.28.Emin= 15,45 МэВ.

5.29.Eуд. = 5,376 МэВ/нуклон.

5.30.Emin= 7,3 МэВ.


5.31.	Eсв = 28,4 МэВ,	m = 0,03 а.е.м.
5.32.	Eуд.= 8,2 МэВ/нуклон.
5.33.	δ = 0,71.
5.34.	t = 963с.
5.35. А(0) = 1,1 1013 Бк.
5.36.	t 9,96 час.
5.37.	N/N = 10-4.
5.38.	106	атомов.
5.39. Возраст руды 2 109 лет.
5.40.	A	=	NA ln 2	= 3,38 мк Ки.

	уд.		MT1/ 2	кг

5.41.	m	= mSr MUTU	= 425 кг.
	U		MSrTSr

5.42.T1/2 = 6 час.

5.43.Nα = 8, Nβ = 6.

5.44.t = λ1 −2 λ2 ln(λ1 / λ2 ).

151

5.45.t = 4104,9 года.

			λ1λ2		1	− e	−λ1t	1− e	−λ2
5.46.	N3	(t) = N10
						−		.
λ2	− λ1		λ1	λ2

5.47.T1/2 = 5,3 дней.

5.48.m = 2,9 10 -7 кг.

5.49.vα = 3 105 м/с.

5.50.Q = 1,862 МДж.

5.51.Eγ = 0,0155 МэВ.

5.52.En = 930,9 МэВ; Ee+ = -7,6 МэВ.

5.53.τ = 86,5 мин.

5.54.η = 9.

5.55. А(0) = 3 1014 Бк/мин, А ( t) = 0,4 1013 Бк/мин.

5.56.Eсв. = 2,24 МэВ.

5.57.3Li7.

5.58.Самостоятельно.

5.59.84Po216; vPo = 2,96 105 м/с.

5.60.N/N = 0,35.

5.61.T1/2 = 1579,36 лет.

5.62.Q = 3,296 1012 Дж.

5.63.Поглощается. Q = 933,49 МэВ.

5.64.Самостоятельно.

5.65.E/E0 = 10-3.

5.66.Выделяется. Q = 17,35 МэВ.

5.67.Eγ = 0,75 МэВ, λ = 1,65 пм.

5.68. Тn = T (1 − mα / mC ) ++(mBe + mα − mC − mn )c2 . 1 mn / mC

5.69.E = 3,55 МэВ.

5.70.E = Q mμ N A =1,35 1023 МэВ.

5.71.mLi6 = 6,0134 а.е.м.

5.72. cos ϕ =	mdTd	= 0,045;ϕ =87,4°. Tα = Td +Q	=11,29МэВ.
	4mαTα	2

5.73.С поглощением. Q = — 1,28 МэВ.

5.74.Eγ = 9,45 МэВ.

5.75.mH2O = 5,53 105 кг.

5.76.Q = 2,3 104 кВт час.

5.77.Q = 6,82 МэВ.

5.78.m = 6,01514 а.е.м.

5.79.TС = 5,26 МэВ; Tn = 0,44 МэВ.

152

5.80.TЯ = 6,7 МэВ.

5.81.Q = -11 МэВ.

5.82.E = 11,9 МэВ.

5.83.mC = 10,0135 а.е.м.

5.84.Q = 1+ mp Tp − 1− mα Tα −2

m0 m0

5.85. Tp = -2,15 МэВ.

5.86. Tα = 9,1 МэВ; ϕ = 170,5°.

5.87. Tp ≥ EСВ (mp + mH 2 ) = 3,3МэВ. mH 2

						T
5.88.	m	= (m	p0	+ m ) 1	+		=

	a		α		931,5 mp0

mpmα TpTα cos θ = −1,2МэВ.

m02

222,0842а.е.м.

5.89.

Q = mHe N Q = 4,23 1014 Дж.

μHe

5.90.

T = mC (mα + mBe − mn − mC ) 931,5МэВ = 5,28МэВ.

mα + mC

5.91.

= mα + mLi

= 4,39МэВ.

ПОР,α

mLi

5.92.

T =

T (m

− m ) −

mC mBe

= 2,2 МэВ.

m + m

ПОР

n C

5.93. Eпор = 0,93 МэВ, Есум = Q + Eпор = 0,13 МэВ.

153

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник