Как найти кинетическую энергию зная напряжение

Как найти кинетическую энергию без скорости Кинетическую энергию можно найти, если у нас есть масса и высота, приравняв ее к потенциальной энергии. Сохранение механической энергии. Кинетическая энергия и потенциальная энергия. KE = PE = mgh.

Как найти кинетическую энергию, имея только массу и высоту

Содержание

  1. Как вычислить кинетическую энергию GCSE
  2. Как найти скорость по массе
  3. Нужна ли вам скорость, чтобы найти кинетическую энергию
  4. Как найти кинетическую энергию по высоте
  5. Как найти кинетическую энергию, если не известна скорость
  6. Как найти скорость, имея только массу и высоту
  7. Какова формула, если скорость неизвестна
  8. Как найти кинетическую энергию, имея только массу
  9. Какова кинетическая энергия, если скорость равна нулю
  10. Как найти V в кинетической энергии

Рекомендую! Смотрите в обзоре: Можно ли соединять кабели VGA в цепочку в 2023.

Как вычислить кинетическую энергию GCSE

Как найти кинетическую энергию, имея только массу и высоту Ek = ½ × m × v2 Ek = кинетическая энергия в джоулях (Дж) m = масса объекта в килограммах (кг) v = скорость объекта в метрах в секунду (м/с).

Рекомендую! Смотрите в обзоре: Как сделать мягкий сброс настроек телевизора в 2023.

Как найти скорость по массе

Нужна ли вам скорость для нахождения кинетической энергии «Чтобы вычислить скорость по массе, вы должны знать значение импульса, поскольку импульс — это то, что относится к скорости и массе вместе. Как только вы узнаете импульс, просто разделите его на массу, чтобы получить скорость.

Рекомендую! Подробнее в посту: Как готовить на пару без холодной пароварки в 2023.

Нужна ли вам скорость, чтобы найти кинетическую энергию

Как найти кинетическую энергию без скорости Количество кинетической энергии в движущемся объекте напрямую зависит от его массы и скорости. Ее можно рассчитать с помощью уравнения: KE = 1 2 масса × скорость 2.

Рекомендую! Подробнее в обзоре: Как скопировать ссылку Google Scholar в 2023.

Как найти кинетическую энергию по высоте

Как найти кинетическую энергию, используя только массу и высоту.

Рекомендую! Подробнее здесь: Можно ли принимать душ с JLab GO Air в 2023?.

Как найти кинетическую энергию, если не известна скорость

Как найти кинетическую энергию без скорости.

Как найти скорость, имея только массу и высоту

Как найти кинетическую энергию, имея только массу и высоту «Здесь ускорение, вызванное силой тяжести, равно g. Из принципа преобразования потенциальная энергия становится равной кинетической энергии, когда объект достигает максимальной высоты. Таким образом, скорость объекта равна √2gh 2 g h, если масса и высота уже даны. «.

Какова формула, если скорость неизвестна

Как найти кинетическую энергию, если не известна скорость «Подставьте ускорение смещение и начальную скорость в это уравнение: (конечная скорость)^2 = (начальная скорость)^2 + 2_(ускорение)_(смещение).

Как найти кинетическую энергию, имея только массу

Как найти кинетическую энергию, если вы не знаете скорость «Кинетическая энергия прямо пропорциональна массе объекта и квадрату его скорости: K. E. = 1/2 m v2. Если масса имеет единицы килограмм, а скорость метр в секунду, то кинетическая энергия имеет единицы килограмм-метр в квадрате в секунду в квадрате. «.

Какова кинетическая энергия, если скорость равна нулю

Нужна ли вам скорость, чтобы найти кинетическую энергию «Поэтому, если скорость становится равной нулю, кинетическая энергия также уменьшается до нуля. «.

Как найти V в кинетической энергии

Нужна ли скорость для нахождения кинетической энергии Руководство пользователя Формула. Формула, используемая данным калькулятором для определения скорости движущегося объекта из кинетической энергии и скорости, следующая: v = (2 — KE / m)½ Символы. V = Скорость объекта. KE = Кинетическая энергия. M = масса объекта. Кинетическая энергия (KE) Масса (m) Скорость (v).

Все права защищены. Несанкционированное копирование, полностью или частично, строго запрещено.

Источник


Загрузить PDF


Загрузить PDF

Существует два вида энергии: потенциальная и кинетическая. Потенциальная энергия — это энергия одного объекта по отношению к другому, которая зависит от их взаимного расположения.[1]
 Например, если вы стоите на вершине холма, то ваша потенциальная энергия будет отличаться от той, которой вы обладали бы у подножия этого холма. Кинетическая энергия — это энергия движущегося объекта.[2]
 Кинетическая энергия возникает при колебаниях, вращении и поступательном движении (перемещении тела из одного места в другое).[3]
 Кинетическую энергию любого объекта легко вычислить, если известны его масса и скорость.[4]

  1. Изображение с названием Calculate Kinetic Energy Step 1

    1

    Запомните формулу для вычисления кинетической энергии. Формула для нахождения кинетической энергии (КЕ) имеет следующий вид: KE = 0,5 x mv2. Здесь m — масса, которая показывает, как много в данном объекте материи, а v — скорость, то есть мера того, насколько быстро объект меняет свое положение в пространстве.[5]

    • Ответ должен быть выражен в стандартных единицах измерения кинетической энергии, джоулях (Дж). Один джоуль эквивалентен 1 кг * м2/с2.

  2. Изображение с названием Calculate Kinetic Energy Step 2

    2

    Определите массу объекта. Если в исходном условии не дана масса, ее придется определить самостоятельно. Для этого можно взвесить предмет и найти массу в килограммах (кг).

    • Настройте весы. Прежде чем взвешивать предмет, необходимо выставить на весах ноль. Это называется тарировкой весов.[6]
    • Положите объект на весы. Осторожно положите предмет на весы и запишите его массу в килограммах.
    • При необходимости переведите граммы в килограммы. В конечную формулу необходимо подставить значение массы в килограммах.

  3. Изображение с названием Calculate Kinetic Energy Step 3

    3

    Найдите скорость объекта. Часто в условии задачи дается скорость объекта. Если скорость не дана, ее можно найти по пройденному расстоянию и затраченному для этого времени.[7]
     Скорость измеряется в метрах в секунду (м/с).

    • Чтобы определить скорость, необходимо расстояние поделить на время: V = d/t. Скорость является векторной величиной, то есть имеет абсолютное значение и направление. Абсолютное значение соответствует величине скорости, а направление указывает на то, куда движется объект.
    • Например, скорость объекта может составлять 80 м/с или –80 м/с, в зависимости от направления движения.
    • Чтобы вычислить скорость, просто поделите пройденное расстояние на затраченное время.

    Реклама

  1. Изображение с названием Calculate Kinetic Energy Step 4

    1

    Запишите формулу. Кинетическая энергия (KE) вычисляется по следующей формуле: KE = 0,5 x mv2. Здесь m — масса, которая показывает, как много в данном объекте материи, а v — скорость, то есть мера того, насколько быстро объект меняет свое положение в пространстве.[8]

    • Ответ записывается в джоулях (Дж). Это стандартная единица измерения кинетической энергии. Один джоуль эквивалентен 1 кг * м2/с2.

  2. Изображение с названием Calculate Kinetic Energy Step 5

    2

    Подставьте в формулу массу и скорость. Если в условии задачи не дана масса или скорость, необходимо найти их. Предположим, что заданы обе эти величины, и необходимо решить следующую задачу: Найдите кинетическую энергию женщины массой 55 кг, которая бежит со скоростью 3,87 м/с. В условии даны масса и скорость, поэтому их можно сразу подставить в формулу:[9]

    • KE = 0,5 x mv2
    • KE = 0,5 x 55 x (3,87)2

  3. Изображение с названием Calculate Kinetic Energy Step 6

    3

    Проведите вычисления. После подстановки массы и скорости можно рассчитать кинетическую энергию (KE). Возведите скорость в квадрат и умножьте полученное значение на массу и на 0,5. Помните, что ответ должен получиться в джоулях (Дж).[10]

    • KE = 0,5 x 55 x (3,87)2
    • KE = 0,5 x 55 x 14,97
    • KE = 411,675 Дж

    Реклама

  1. Изображение с названием Calculate Kinetic Energy Step 7

    1

    Запишите формулу. Кинетическая энергия (KE) вычисляется по следующей формуле: KE = 0,5 x mv2. Здесь m — масса, которая показывает, как много в данном объекте материи, а v — скорость, то есть мера того, насколько быстро объект меняет свое положение в пространстве.[11]

    • Ответ записывается в джоулях (Дж). Это стандартная единица измерения кинетической энергии. Один джоуль эквивалентен 1 кг * м2/с2.

  2. Изображение с названием Calculate Kinetic Energy Step 8

    2

    Подставьте в формулу известные значения. В некоторых задачах дается кинетическая энергия и масса, или кинетическая энергия и скорость. Сначала необходимо подставить в формулу все известные величины.

    • Пример 1: чему равна скорость предмета, если его масса составляет 30 кг и он имеет кинетическую энергию 500 Дж?
      • KE = 0,5 x mv2
      • 500 Дж = 0,5 x 30 x v2
    • Пример 2: чему равна масса предмета, если его кинетическая энергия составляет 100 Дж, и он движется со скоростью 5 м/с?
      • KE = 0,5 x mv2
      • 100 Дж = 0,5 x m x 52

  3. Изображение с названием Calculate Kinetic Energy Step 9

    3

    Преобразуйте уравнение, чтобы найти неизвестную величину. Путем алгебраических преобразований перенесите искомую величину по одну, а все известные величины — по другую сторону знака равенства.

    • Пример 1: чему равна скорость предмета, если его масса составляет 30 кг и он имеет кинетическую энергию 500 Дж?
      • KE = 0,5 x mv2
      • 500 Дж = 0,5 x 30 x v2
      • Умножим массу на 0,5: 0,5 x 30 = 15
      • Поделим кинетическую энергию на получившееся значение: 500/15 = 33,33
      • Извлечем квадратный корень, чтобы найти скорость: 5,77 м/с
    • Пример 2: чему равна масса предмета, если его кинетическая энергия составляет 100 Дж, и он движется со скоростью 5 м/с?
      • KE = 0,5 x mv2
      • 100 Дж = 0,5 x m x 52
      • Возведем скорость в квадрат: 52 = 25
      • Умножим полученное значение на 0,5: 0,5 x 25 = 12,5
      • Поделим кинетическую энергию на эту величину: 100/12,5 = 8 кг

    Реклама

Об этой статье

Эту страницу просматривали 29 568 раз.

Была ли эта статья полезной?

Источник

Содержание:

  • Определение и формула кинетической энергии
  • Кинетическая энергия материальной точки и тела
  • Единицы измерения кинетической энергии
  • Теорема Кенига
  • Примеры решения задач

Определение и формула кинетической энергии

Определение

Кинетическую энергию тела определяют при помощи работы, которая совершается телом при его торможении от начальной скорости, до скорости, равной нулю.

Кинетическая энергия тела – мера механического движения тела. Она зависит от относительной скорости тел.

Встречаются следующие обозначения кинетической энергии: Ek,Wk,T.

Работу, которую производят над телом (A’) можно связать с изменением его кинетической энергии:

$$A^{prime}=E_{k 2}-E_{k 1}(1)$$

Кинетическая энергия материальной точки и тела

Кинетическая энергия материальной точки равна:

$$E_{k}=frac{m v^{2}}{2}=frac{p^{2}}{2 m}=frac{p v}{2}(2)$$

где m – масса материальной точки, p – импульс материальной точки, v – скорость ее движения. Кинетическая энергия является скалярной физической величиной.

Если тело нельзя принять за материальную точку, то его кинетическая энергия рассчитывается как сумма кинетических энергий всех материальных точек, которые составляют исследуемое тело:

$$E_{k}=frac{1}{2} int_{m} v^{2} d m=frac{1}{2} int_{m} rho v^{2} d V(3)$$

где dm – элементарный участок тела, который можно считать материальной точкой, dV – объем выделенного элементарного участка тела,
v – скорость перемещения рассматриваемого элемента, $rho$ — плотность участка, m–масса всего рассматриваемого тела, V – объем тела.

В том случае, если тело (отличное от материальной точки) движется поступательно, то его кинетическую энергию можно рассчитать, применяя формулу (2), в которой все параметры отнесены к телу в целом.

При вращении тело вокруг неподвижной оси его кинетическую энергию можно вычислить, применяя формулу:

$$E_{k}=frac{J omega^{2}}{2}=frac{omega^{2}}{2} int_{m} r^{2} d m=frac{L^{2}}{2 J}=frac{L omega}{2}(4)$$

где J – момент инерции тела по отношению к оси вращения, ?–модуль угловой скорости вращения тела,
r – расстояние от элементарного участка тела до оси вращения,
L – проекция момента импульса вращающегося тела на ось во круг которой идет вращение.

Если твердое тело совершает вращение относительно неподвижной точки (например, точки O), то его кинетическую энергию находят как:

$$E_{k}=frac{bar{L} bar{omega}}{2}(5)$$

$bar{L}$ – момент импульса рассматриваемого тела относительно точки О.

Единицы измерения кинетической энергии

Основной единицей измерения кинетической энергии (как и любого другого вида энергии) в системе СИ служит:

[Ek]=Дж (джоуль),

в системе СГС –[Ek]= эрг.

При этом: 1 дж= 107 эрг.

Теорема Кенига

Для самого общего случая при расчете кинетической энергии применяют теорему Кенига. В соответствии с которой,
кинетическая энергия совокупности материальных точек есть сумма кинетической энергии поступательного перемещения
системы со скоростью центра масс (vc) и кинетической энергии
(E’k) системы при ее относительном движении к поступательному перемещению системы отсчета.
При этом начало системы отсчета связывают с центром масс системы. Математически данную теорему можно записать как:

$$E_{k}=sum_{i=1}^{n} frac{m_{i} v_{i}^{2}}{2}=frac{m v_{c}^{2}}{2}+E_{k}^{prime}$$

где $mathrm{E}_{k}^{prime}=sum_{i=1}^{n} frac{m_{i} v_{i}^{prime 2}}{2}, v_{i}^{prime}=v_{i}-v_{c}, m=sum_{i=1}^{n} m_{i}$ –суммарная масса системы материальных точек.

Так, если рассматривать твердое тело, то его кинетическую энергию можно представить как:

$$E_{k}=frac{m v_{c}^{2}}{2}+frac{J_{c} omega^{2}}{2}(7)$$

где Jc — момент инерции тела по отношению к оси вращения, проходящей через центр масс. В частности, при плоском движении
Jc=const.В общем случае, ось (она называется мгновенной) перемещается в теле, тогда момент инерции является переменным во времени.

Примеры решения задач

Пример

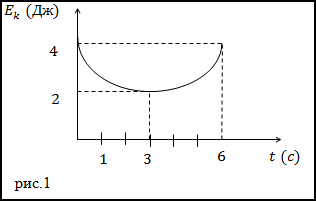
Задание. Какова работа, которая производится над телом за t=3 c (с начала отсчета времени),
при силовом взаимодействии, если изменение кинетической энергии исследуемого тела задано графиком (рис.1)?

Решение. По определению изменение кинетической энергии равно работе (A’),
которая производится над телом при силовом взаимодействии, то есть можно записать, что:

$$A^{prime}=Delta E_{k}(1.1)$$

Исследуя график, приведенный на рис.1 мы видим, что за время t=3 c кинетическая энергия тела изменяется от 4 Дж до 2 Дж, следовательно:

$A^{prime}=2-4=-2$ (Дж)

Ответ. A’=-2 Дж.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Материальная точка движется по окружности, радиус которой равен R. Кинетическая
энергия частицы связана c величиной пути (s), пройденного ей в соответствии с формулой:
$E_{k}=alpha s^{2}(alpha=$const$)$. Какое уравнение связывает силу (F), действующую на точку и путь s?

Решение. В качестве основы для решения задачи используем формулу, определяющую кинетическую энергию материальной точки:

$$E_{k}=frac{m v^{2}}{2}(2.1)$$

Но по условию задачи:

$$E_{k}=alpha s^{2}(2.2)$$

Следовательно, можно приравнять правые части выражений (2.1) и (2.2), и получить:

$$frac{m v^{2}}{2}=alpha s^{2} rightarrow v^{2}=frac{2 alpha s^{2}}{m} rightarrow v=s sqrt{frac{2 alpha}{m}}(2.3)$$

Из второго закона Ньютона нам известно, что сила, действующая на частицу, будет равна:

$$bar{F}=m bar{a}(2.4)$$

где

$$a=sqrt{a_{n}^{2}+a_{tau}^{2}}(2.5)$$

При этом нормальное ускорение частицы (an), перемещающейся по окружности найдем как:

$$a_{n}=frac{v^{2}}{R}=frac{2 alpha s^{2}}{R m}(2.6)$$

Тангенциальную составляющую ускорения (aт)используя определение тангенциального ускорения, определение скорости
($v=frac{d s}{d t}$) и выражение v(s) (2.3) вычислим как:

$$a_{tau}=frac{d v}{d t}=frac{d v}{d s} cdot frac{d s}{d t}=sqrt{frac{2 a}{m}} cdot v=s frac{2 a}{m}(2.7)$$

Используем выражения: (2.5), (2.6), (2.7), окончательно получаем для модуля силы:

$$F=m a=m sqrt{frac{4 alpha^{2} s^{4}}{R^{2} m^{2}}+s^{2} frac{4 alpha^{2}}{m^{2}}}=2 alpha s sqrt{frac{s^{2}}{R^{2}}+1}$$

Ответ. $F=2 alpha s sqrt{frac{s^{2}}{R^{2}}+1}$

Читать дальше: Формула массы тела.

Источник

Расчет кинетической энергии материальной точки массой m и со скоростью v в классической механике.

T=frac{Mv^{2}}{2}

PLANETCALC, Кинетическая энергия материальной точки в классической механике

Кинетическая энергия материальной точки в классической механике

Точность вычисления

Знаков после запятой: 4

Расчет кинетической энергии материальной точки массой m и со скоростью v в релятивистской механике.

Здесь скорость материальной точки не может превышать скорость света (299792458 м/сек.)

T=frac{Mv^{2}}{1-frac{v^{2}}{c^{2}}+sqrt[2]{1-frac{v^{2}}{c^{2}}}}

PLANETCALC, Кинетическая энергия материальной точки в релятивистской механике

Кинетическая энергия материальной точки в релятивистской механике

Точность вычисления

Знаков после запятой: 4

На малых скоростях результаты обоих формул совпадают, но чем ближе к скорости света, тем отличие больше.

Источник

Понравилась статья? Поделить с друзьями:
  • Как исправить все тройки в вузе
  • Как правильно составить силлогизм
  • Как найти хорошего гастроэнтеролога в воронеже
  • Bad module info windows 10 как исправить dayz
  • Как найти площадь фигуры заданной функцией