С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.
Как же рассчитать скорость?
На самом деле, рассчитать ее можно несколькими способами:
- через формулу нахождения мощности;
- через дифференциальные исчисления;
- по угловым параметрам и так далее.
В этой статье рассматривается самый простой способ с самой простой формулой — нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:
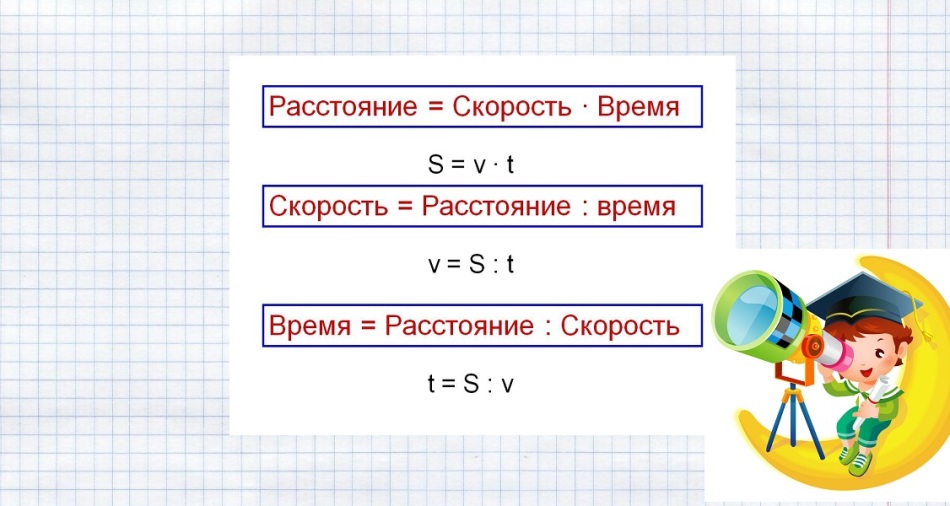
v=S/t, где
- v — скорость объекта,
- S — расстояние, которое пройдено или должно быть пройдено объектом,
- t — время, за которое пройдено или должно быть пройдено расстояние.
Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.
Теперь нужно подставить имеющиеся значения вместо буквенных символов:
v=100 км/1,5 ч=66,66 км/ч
Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.
Таким нехитрым способом можно найти скорость через время и расстояние.
А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:
vср=(v1+v2+v3+…+vn)/n, где v1, v2, v3, vn — значения скоростей объекта на отдельных участках пути S, n — количество этих участков, vср — средняя скорость объекта на всем протяжении всего пути.
Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:
- vср=(S1+S2+…+Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
- S1, S2, Sn — отдельные неравномерные участки всего пути,
- t — общее время, за которое объект прошел все участки.
Можно записать использовать и такой вид вычислений:
- vср=S/(t1+t2+…+tn), где S — общее пройденное расстояние,
- t1, t2, tn — время прохождения отдельных участков расстояния S.
Но можно записать эту же формулу и в более точном варианте:
vср=S1/t1+S2/t2+…+Sn/tn, где S1/t1, S2/t2, Sn/tn — формулы вычисления скорости на каждом отдельном участке всего пути S.
Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.
Другие способы вычисления
Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:
N=F*v*cos α , где N — механическая мощность,
F — сила,
v — скорость,
cos α — косинус угла между векторами силы и скорости.
Способы вычисления расстояния и времени
Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:
S=v*t, где v — понятно что такое,
S — расстояние, которое требуется найти,
t — время, за которое объект прошел это расстояние.
Таким образом вычисляется значение расстояния.
Или вычисляем значение времени, за которое пройдено расстояние:
t=S/v, где v — все та же скорость,
S — расстояние, пройденный путь,
t — время, значение которого в данном случае нужно найти.
Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.
Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.
И это еще не предел!
Видео
В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.
Математика, 4 класс
Урок № 35. Понятие скорости. Единицы скорости
Перечень вопросов, рассматриваемых в теме:
— что такое «скорость»?
— какими единицами измеряется скорость?
— как вычислить скорость?
Глоссарий по теме:
Скорость – это расстояние, пройденное объектом за единицу времени.
Скорость – это величина, её можно измерять и сравнивать.
Чтобы узнать скорость движения, нужно расстояние разделить на время.
Основная и дополнительная литература по теме урока:
1. Моро М.И., Бантова М.А. и др. Математика 4 класс. Учебник для общеобразовательных организаций. Ч.2 — М.; Просвещение, 2017. – с.5-7
2. Моро М.И., Волкова С.И. Математика. Рабочая тетрадь 4 класс. Часть 2. М.; Просвещение, 2016. – с.3
3. Волкова С.И. Математика. Проверочные работы 4 класс. М.; Просвещение, 2017. – с.54
Теоретический материал для самостоятельного изучения
Наверняка вы замечали, что в окружающем нас мире постоянно что-то движется. Что-то движется быстрее, а что-то медленнее. Например, по дороге идёт человек, едет автомобиль, в воздухе летит самолёт. Все они движутся, но автомобиль движется быстрее человека, а самолёт быстрее автомобиля. В математике величиной характеризующей быстроту движения объектов, является скорость.
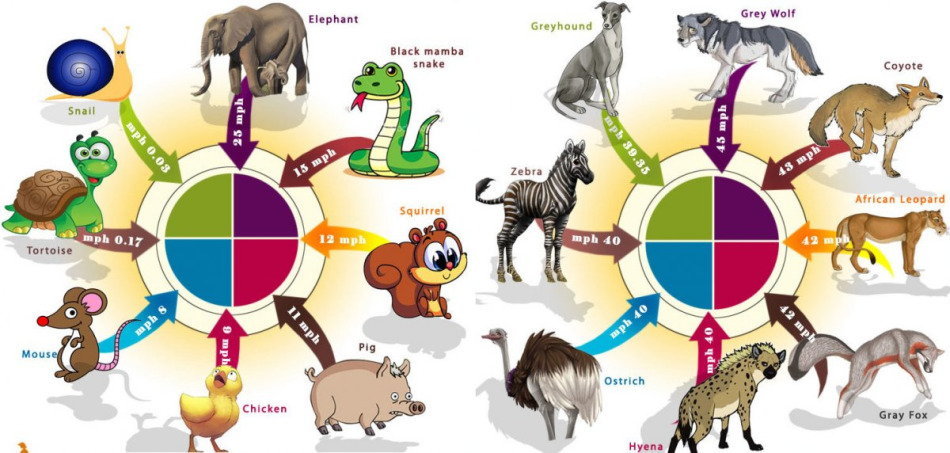
Кто бежит быстрее, зебра или страус, если зебра бежит со скоростью 60 км/ч, а страус за минуту пробегает 500м?
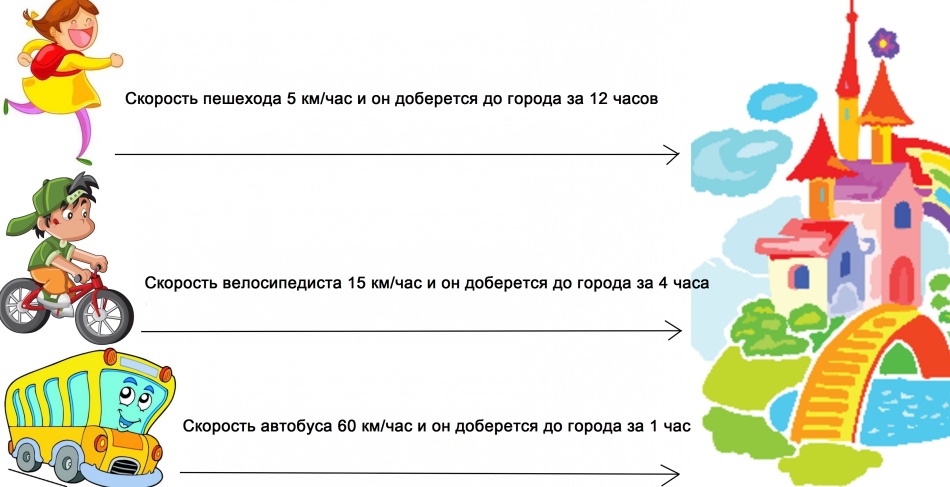
Легковая машина прошла 160 км за 2 часа. В течение каждого часа она проходила одинаковое расстояние. Сколько километров проходила эта машина за один час?
Чтобы найти, какое расстояние машина проехала за один час, нужно все пройденное расстояние, 160 км, разделить на время, 2 часа. Таким образом, скорость движения машины – 80 километров в час. Иначе можно сказать, что за один час машина проходила 80 километров.
Сокращенно записывается так: 80 км/ч.
160 : 2 = 80 км/ч
Космический корабль пролетает 8 тысяч метров в секунду. Его скорость можно записать так: 8000 м/с.
Вы знаете, что 1000 м = 1 км. Значит, скорость космического корабля можно записать иначе: 8000 м/с = 8 км/с.
Например, черепаха за минуту проползает пять метров, это значит, что скорость движения черепахи – пять метров в минуту. Улитка за одну секунду может проползти один сантиметр, то есть скорость улитки – один сантиметр в секунду.
Скорость движения – это расстояние, пройденное за единицу времени.
Единицей времени может быть одна секунда, одна минута или один час.
Чтобы узнать скорость движения, нужно расстояние разделить на время.
Скорость = Расстояние : Время
Задания тренировочного модуля:
1. Соотнесите значение скорости с объектом.
|
Объект |
Значение скорости |
|
черепаха |
90 км/ч |
|
человек |
700 км/ч |
|
автомобиль |
5 м/мин |
|
самолёт |
8 км/с |
|
ракета |
5 км/ч |
Правильный вариант:
|
Объект |
Значение скорости |
|
черепаха |
5 м/мин |
|
человек |
5 км/ч |
|
автомобиль |
90 км/ч |
|
самолёт |
700 км/ч |
|
ракета |
8 км/с |
2. Дед Мороз послал погоню за злым Волшебником, похитившим Снегурочку. Подчеркните имена посланников Деда Мороза, которые смогут догнать похитителя.
Правильный вариант: волк, медведь, олень
3. Выберите один правильный вариант ответа.
Скорость – это величина, которая показывает:
1. пройденный объектом путь;
2. как быстро движется объект;
3. какой путь проходит объект за единицу времени.
Правильный вариант: какой путь проходит объект за единицу времени.
А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:
vср=(v1+v2+v3+…+vn)/n
где v1, v2, v3, vn – значения скоростей объекта на отдельных участках пути S,
n – количество этих участков,
vср – средняя скорость объекта на всем протяжении всего пути.
Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:
vср=(S1+S2+…+Sn)/t,
где vср – средняя скорость объекта на всем протяжении пути,
S1, S2, Sn – отдельные неравномерные участки всего пути,
t – общее время, за которое объект прошел все участки.
Можно записать использовать и такой вид вычислений:
vср=S/(t1+t2+…+tn),
где S – общее пройденное расстояние,
t1, t2, tn – время прохождения отдельных участков расстояния S.
Но можно записать эту же формулу и в более точном варианте:
vср=S1/t1+S2/t2+…+Sn/tn,
где S1/t1, S2/t2, Sn/tn – формулы вычисления скорости на каждом отдельном участке всего пути S.
Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.
Как найти время с помощью скорости и расстояния?
Чтобы узнать расстояние, нужно скорость умножить на время. Чтобы найти время, нужно расстояние разделить на скорость.
Как найти расстояние за минуту?
Чтобы найти расстояние, если известно время и скорость нужно время умножить на скорость. Пример такой задачи: Заяц убегал от Волка со скоростью 1 километр за 1 минуту.
Как найти км в час?
Чтобы найти скорость, нужно расстояние разделить на время движения. Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
Как в математике обозначается скорость время и расстояние?
Скорость принято обозначать маленькой латинской буквой v, время движения – маленькой буквой t, пройденное расстояние – маленькой буквой s. Скорость, время и расстояние связаны между собой. Например, мы вышли из дома и направились в магазин. Мы дошли до магазина за 10 минут.
Как найти расстояние между двумя точками?
Вычисление расстояния между взятыми на плоскости двумя точками А(х А; у А) и В(х В; у В), выполняется по формуле d = √((х А – х В) 2 + (у А – у В) 2) , где d – длина отрезка, который соединяет эти точки на плоскости.
Сколько в среднем человек ходит км в час?
Средняя – 90 – 120 шагов в минуту, что составляет 4 – 5,5 км/ч; Быстрая – 120 – 140 шагов в минуту, что составляет 5,6 – 6,5 км/ч; Очень быстрая – более 140 шагов минуту, что составляет более 6,5 км/ч. Если человек старше 35 лет и никогда ранее не занимался спортом, то ему следует начинать с очень медленной ходьбы.
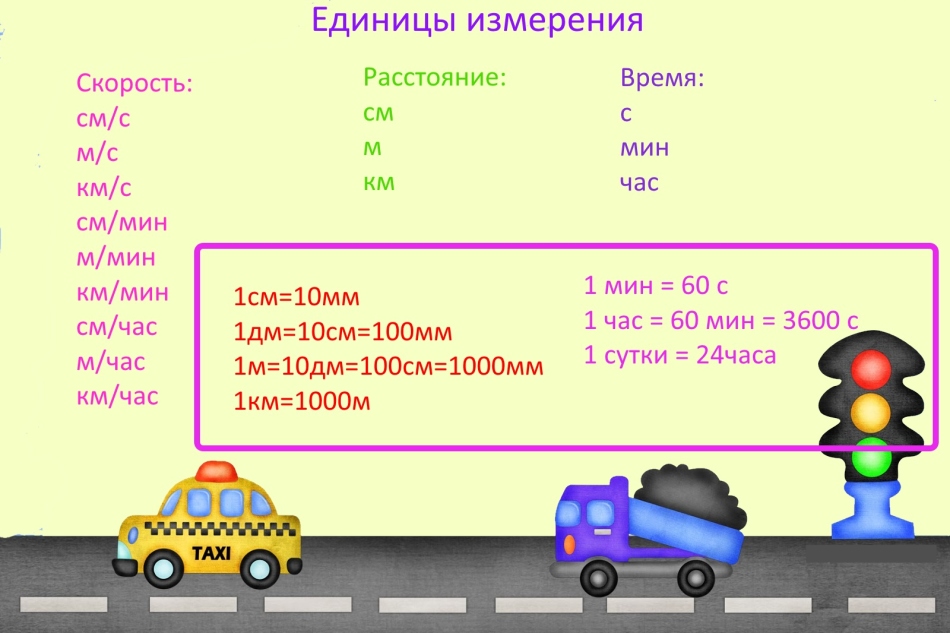
Сколько метр в одном км?
В 1 метре (м) содержится 100 сантиметров (см), 1 м = 100 см. В 1 километре(км) содержится 1000 метров, 1 км = 1000 м.
Что означает формула S V * t?
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t. Задачка 1.
Как записывается расстояние в математике?
Расстояние – это длина от одного пункта до другого. Большие расстояния, в основном, измеряются в метрах и километрах. Расстояние обозначается латинской буквой S.
Как найти расстояние между точками 7 класс?
Как найти расстояние между двумя заданными точками? Для того чтобы найти длину отрезка на координатной прямой надо из координаты ее конца вычесть координату начала по модулю.
Как узнать сколько километров?
Примечание.
- Откройте Google Карты на компьютере.
- Нажмите правой кнопкой мыши на пункт отправления.
- Нажмите Измерить расстояние.
- Чтобы создать путь для измерения, коснитесь любого места на карте. Точно так же можно добавить ещё несколько точек. …
- Когда закончите, на карточке внизу страницы нажмите «Закрыть» .
Сколько километров в 10000 шагов?
8 километров
В 10 000 шагов помещается от 7 до 8 километров в зависимости от длины шага. Они, конечно, не гарантируют полного здоровья, но могут повысить выносливость организма и его устойчивость перед инфекциями.
Какая скорость у человека в час?
30 км/ч — средняя скорость бега тренированного человека на короткой дистанции (100м — 400м). 20 км/ч — средняя скорость бега тренированного человека на средней дистанции (800м — 3км). 16 км/ч — средняя скорость бега тренированного человека на длинной дистанции (10км — 42км).
Как выглядит 1 километр?
Киломе́тр (сокращённо км, km) — широко распространённая кратная метру единица измерения расстояния. 1 км = 1000 м = 0,621 миль = 0,9374 версты = 1094 ярдов = 3281 футов = 1,057⋅10−13 световых лет = 6,67⋅10−9 а.
Сколько см в метре таблица?
Таблица мер измерения
| 1 т | тонна | 1 т = 10 ц = 1 000 кг = 106 г |
|---|---|---|
| 1 м | метр | 1 м = 10 дм |
| 1 дм | дециметр | 1 дм = 10 см = 0,1 м |
| 1 см | сантиметр | 1 см = 10 мм = 0,01 м |
| 1 мм | миллиметр | 1 мм = 1 000мк = 10-3 м |
•3 авг. 2020 г.
Что значит формула S VT?
S=v*t, где v — понятно что такое, S — расстояние, которое требуется найти, t — время, за которое объект прошел это расстояние. Таким образом вычисляется значение расстояния.
Как отмечается расстояние в геометрии?
Расстояние между двумя точками на координатной оси и замечание о его обозначении. Замечание . В геометрии и в школьной геометрии, в частности, принято обозначать одинаково и сам отрезок и его длину. Если имеется отрезок прямой, ограниченный точками А и В, то этот отрезок как геометрический объект обозначается АВ.
Математика
5 класс
Урок № 35
Задачи на движение
Перечень вопросов, рассматриваемых в теме:
- Понятия скорости, времени, расстояния.
- Формулы нахождения скорости, времени, расстояния.
- Понятия скорости сближения, скорости удаления.
Глоссарий по теме
Расстояние – это длина от одного пункта до другого.
Большие расстояния, в основном, измеряются в метрах и километрах.
Расстояние обозначается латинской буквой S.
Чтобы найти расстояние, надо скорость умножить на время движения:
S = v ∙ t
Скорость – это расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Скорость обозначается латинской буквой v.
Чтобы найти скорость, нужно расстояние разделить на время движения:
v = S : t
Время – это продолжительность каких-то действий, событий.
Время движения обозначается маленькой латинской буквой t.
Чтобы найти время, нужно расстояние разделить на скорость движения:
t = S : v
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Основная литература
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К., Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
2. Потапов М. К., Шевкин А. В. Математика. Книга для учителя. 5 – 6 классы — М.: Просвещение, 2010
Дополнительная литература
1. Чесноков А. С., Нешков К. И. Дидактические материалы по математике 5 кл. – М.: Академика учебник, 2014
2. Бурмистрова Т. А. Математика. Сборник рабочих программ. 5–6 классы // Составитель Бурмистрова Т. А.
3. Потапов М. К. Математика: дидактические материалы. 6 кл. // Потапов М. К., Шевкин А. В. — М.: Просвещение, 2010
Теоретический материал для самостоятельного изучения
Очень часто нам встречаются задачи на нахождение скорости, времени и расстояния. Что же всё это такое? Сейчас нам предстоит в этом разобраться.
Расстояние – это длина от одного пункта до другого. (Например, расстояние от дома до школы 2 километра). В основном большие расстояния измеряются в метрах и километрах. Общепринятое обозначение расстояния – заглавная латинская буква S.
Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда. Скорость обозначается маленькой латинской буквой v.
Рассмотрим задачу:
Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 200 метров. Первый школьник добежал за 50 секунд. Второй за 100 секунд. Кто из ребят бежал быстрее?
Решение:
Быстрее бежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. Чтобы найти скорость, нужно расстояние разделить на время движения.
Давайте найдём скорость первого школьника. Для этого разделим 200 метров на время движения первого школьника, то есть на 50 секунд:
200 м : 50 с = 4
Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
У нас расстояние дано в метрах, а время в секундах. Значит, скорость измеряется в метрах в секунду:
200 м : 50 с = 4 (м/с)
Скорость движения первого школьника составляет 4 метра в секунду.
Теперь найдём скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника:
200 м : 100 c = 2 (м/с)
Скорость движения первого школьника – 4 (м/с).
Скорость движения второго школьника – 2 (м/с).
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит, он бежал до спортплощадки быстрее.
Иногда возникает ситуация, когда требуется узнать, за какое время тело преодолеет то или иное расстояние. Время движения обозначается маленькой латинской буквой t.
Рассмотрим задачу:
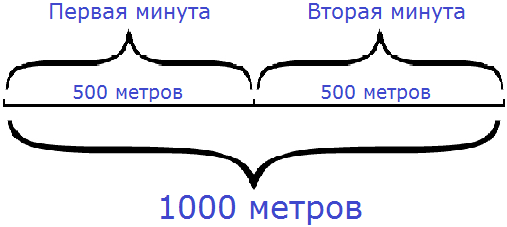
От дома до спортивной секции 1200 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 600 метров в минуту. За какое время мы доедем до спортивной секции?
Решение:
Если за одну минуту мы будем проезжать 600 метров, то сколько таких минут нам понадобится для преодоления тысячи двухсот метров? Очевидно, что надо разделить 1200 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 600 метров. Тогда мы получим время, за которое мы доедем до спортивной секции:
1200 : 600 = 2 (мин)
Ответ: мы доедем до спортивной секции за 2 минуты.
Скорость, время и расстояние связаны между собой.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:
S = v ∙ t
Рассмотрим задачу:
Мы вышли из дома и направились в магазин. Мы дошли до магазина за 15 минут. Наша скорость была 60 метров в минуту. Какое расстояние мы прошли?
Решение:
Если за одну минуту мы прошли 60 метров, то сколько таких отрезков по шестьдесят метров мы пройдём за 15 минут? Очевидно, что умножив 60 метров на 15 минут, мы определим расстояние от дома до магазина:
v = 60 (м/мин)
t = 15 (минут)
S = v ∙ t = 60 ∙ 15 = 900 (метров)
Ответ: мы прошли 900 метров.
Если известно время и расстояние, то можно найти скорость:
v = S : t
Рассмотрим задачу:
Расстояние от дома до школы 800 метров. Школьник дошёл до этой школы за 8 минут. Какова была его скорость?
Скорость движения школьника – это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 800 метров, то какое расстояние он преодолевал за одну минуту?
Чтобы ответить на этот вопрос, нужно разделить расстояние на время движения школьника:
S = 800 метров
t = 8 минут
v = S : t = 800 : 8 = 100 (м/мин)
Ответ: скорость школьника была 100 м/мин.
Если известна скорость и расстояние, то можно найти время:
t = S : v
Рассмотрим задачу:
От дома до спортивной секции 600 метров. Мы должны дойти до неё пешком. Наша скорость будет 120 метров в минуту (120 м/мин). За какое время мы дойдём до спортивной секции?
Если за одну минуту мы будем проходить 120 метров, то сколько таких минут со ста двадцатью метрами будет в шестистах метрах?
Чтобы ответить на этот вопрос, нужно 600 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 120. Тогда мы получим время, за которое мы дойдём до спортивной секции:
S = 600 метров
v = 120 (м/мин)
t = S : v = 600 : 120 = 5 (минут).
Ответ: мы дойдём до спортивной секции за 5 минут.
Итак, все рассмотренные нами формулы мы можем представить в виде треугольника для лучшего запоминания:
Теперь рассмотрим типы задач на движение.
Задачи на сближение.
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причём скорость первого будет 100 метров в минуту, а второго – 105 метров в минуту, то скорость сближения будет составлять 100 плюс 105, то есть 205 метров в минуту. Значит, каждую минуту расстояние между пешеходами будет уменьшаться на 205 метров.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Задача.
Из двух пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 13 км/ч, а скорость второго – 15 км/ч. Через 3 часа они встретились. Определите расстояние между населёнными пунктами.
Решение:
- Найдём скорость сближения велосипедистов:
13 км/ч + 15 км/ч = 28 км/ч
- Определим расстояние между населёнными пунктами. Для этого скорость сближения умножим на время движения:
28 ∙ 3 = 84 км
Ответ: расстояние между населёнными пунктами 84 км.
Задачи на скорость удаления.
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причём скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4 плюс 6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиваться на 10 километров.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Рассмотрим задачу:
С причала одновременно в противоположных направлениях отправились теплоход и катер. Скорость теплохода составляла 60 км/ч, скорость катера 130 км/ч. Какое расстояние будет между ними через 2 часа?
Решение:
- Определим скорость удаления. Для этого сложим их скорости:
60 + 130 = 190 км/ч.
Получили скорость удаления равную 190 км/ч. Данная скорость показывает, что за час расстояние между теплоходом и катером будет увеличиваться на 190 километров.
- Чтобы узнать какое расстояние будет между ними через два часа, нужно 190 умножить на 2:
190 ∙ 2 = 380 км.
Ответ: через 2 часа расстояние между теплоходом и катером будет составлять 380 километров.
Задачи на движение объектов в одном направлении.
В предыдущих пунктах мы рассматривали задачи, в которых объекты (люди, машины, лодки) двигались либо навстречу друг другу, либо в противоположных направлениях. В первом случае мы находили скорость сближения – в ситуации, когда два объекта двигались навстречу друг другу. Во втором случае мы находили скорость удаления – в ситуации, когда два объекта двигались в противоположных направлениях. Но объекты также могут двигаться в одном направлении, причём с различной скоростью.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Рассмотрим задачу:
Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 130 км/ч, а скорость автобуса 90 км/ч. Какое расстояние будет между ними через 1 час? Через 3 часа?
Решение:
- Найдём скорость удаления. Для этого из большей скорости вычтем меньшую:
130 км/ч − 90 км/ч = 40 км/ч
- Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 3 часа в три раза больше:
40 ∙ 3 = 120 км
Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через три часа – 120 км.
Рассмотрим ситуацию, в которой объекты начали своё движение из разных пунктов, но в одном направлении.
Задача.
Пусть на одной улице имеется дом, школа и аттракцион. Дом находится на одном конце улицы, аттракцион на другом, школа между ними. От дома до школы 900 метров. Два пешехода отправились в аттракцион в одно и то же время. Причём первый пешеход отправился в аттракцион от дома со скоростью 90 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 85 метров в минуту. Какое расстояние будет между пешеходами через 3 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Решение:
- Определим расстояние, пройденное первым пешеходом за 3 минуты. Он двигался со скоростью 90 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 270 метров:
90 ∙ 3 = 270 метров
- Определим расстояние, пройденное вторым пешеходом за 3 минуты. Он двигался со скоростью 85 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 255 метров:
85 ∙ 3 = 255 метров
- Теперь найдём расстояние между пешеходами. Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (900м) прибавить расстояние, пройденное вторым пешеходом (255м), и из полученного результата вычесть расстояние, пройденное первым пешеходом (270м):
900 + 255 = 1155 м
1155 – 270 = 885 м
Либо из расстояния от дома до школы (900 м) вычесть расстояние, пройденное первым пешеходом (270 м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (255 м):
900 – 270 = 630 м
630 + 255 = 885 м
Таким образом, через три минуты расстояние между пешеходами будет составлять 885 метров.
- Теперь давайте ответим на вопрос: через сколько минут после начала движения первый пешеход догонит второго?
В самом начале пути между пешеходами было расстояние 900 м. Через минуту после начала движения расстояние между ними будет составлять 895 метров, поскольку первый пешеход двигается на 5 метров в минуту быстрее второго:
90 ∙ 1 = 90 м
85 ∙ 1 = 85 м
900 + 85 – 90 = 985 – 90 = 895 м
Через три минуты после начала движения расстояние уменьшится на 15 метров и будет составлять 885 метров. Это был наш ответ на первый вопрос задачи:
90 ∙ 3 = 270 м
85 ∙ 3 = 255 м
900 + 255 – 270 = 1155 – 270 = 885 м
Можно сделать вывод, что каждую минуту расстояние между пешеходами будет уменьшаться на 5 метров.
А раз изначальные 900 метров с каждой минутой уменьшаются на одинаковые 5 метров, то мы можем узнать сколько раз 900 метров содержат по 5 метров, тем самым определяя через сколько минут первый пешеход догонит второго:
900 : 5 = 180 минут.
Ответ: через три минуты расстояние между пешеходами будет составлять 885 метров, первый пешеход догонит второго через 180 минут = 3 часа.
Разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Заполните таблицу:
|
S |
v |
t |
|
|
1. |
135 км |
9 км/ч |
____ ч |
|
2. |
____ м |
12 м/с |
4 с |
|
3. |
132 м |
____ м/мин |
11 мин |
Для заполнения пропусков воспользуемся формулами нахождения скорости, времени, расстояния:
- Надо найти время: t = S : v
135 : 9 = 15 часов.
- Надо найти расстояние: S = v ∙ t
12 ∙ 4 = 48 м.
- Надо найти скорость: v = S : t
132 : 11 = 12 м/мин.
Верный ответ:
|
S |
v |
t |
|
|
1. |
135 км |
9 км/ч |
15 часов |
|
2. |
48 м |
12 м/с |
4 с |
|
3. |
132 м |
12 м/мин |
11 мин |
№2. Тип задания: единичный / множественный выбор
Выберите верный ответ к задаче:
Из пунктов А и В, расстояние между которыми 300 км, отправились одновременно навстречу друг другу мотоциклист и автомобилист. Скорость автомобиля 60 км/ч, а мотоцикла 30 км/ч. Какое расстояние будет между ними через 3 часа?
Варианты ответов:
- 70
- 30
- 270
- 240
Эта задача относится к типу задач на сближение, т.е. нам надо:
- сложить скорости мотоциклиста и автомобилиста:
60 + 30 = 90 км/ч – скорость сближения;
- узнать, сколько километров они пройдут за 3 часа вместе. Для этого:
90 ∙ 3 = 270 км;
- из общего расстояния нам осталось вычесть пройденное:
300 – 270 = 30 км
Верный ответ: 2. 30 км.
Среди прочих обозначений наиболее часто школьников интересует вопрос о том, как в математике обозначается скорость, время, расстояние
. Связано это с тем, что обозначения этих величин (особенно — скорости) в учебниках по математике и физике можно увидеть различные: с чертой над буквой
v
(читается: [вэ]), со стрелкой над буквой
v
, а также буквы
v
, выделенные курсивом или жирным шрифтом.
Скорость в математике
обозначается буквой
v
, но её написание принято различным для рукописного и печатного текста.
В рукописном тексте скорость движения обычно обозначается строчной (т.е. маленькой) прописной (т.е. не печатной, как в тексте из газеты, а написанной от руки так, как если бы писали письмо) буквой v. В учебниках по математике (т.е. в печатном тексте) обычно скорость движения обозначается печатной буквой v, прямой или выделенной курсивом. Такое обозначение принимается практически во всех задачах по математике, исключение составляют лишь задачи, иллюстрирующие тему «Векторы» (в этом случае обозначение принимается таким же, как и в физике).
В физике
(а точнее — в её разделе «механика») обозначение скорости зависит от того, нужно ли в данной задаче учитывать тот факт, что скорость — величина векторная. Там, где учитывать это не нужно, скорость обозначается строчной буквой v (печатной или прописной, так же, как и в математике). Если же необходимо учитывать то, что скорость характеризуется не только модулем (т.е. величиной), но и направлением, скорость изображается либо прописной буквой
v
с направленной слева направо стрелкой над этой буквой, либо той же прописной буквой v с горизонтальной чертой над этой буквой. В печатном тексте в этом случае обычно скорость обозначают либо печатной строчной буквой
v
со стрелкой или чертой над буквой, либо печатной буквой
v
, выделенной жирным шрифтом (т.е. так:
v
).
Буквой v обозначают скорость движения тел. Для обозначения скорости света и скорости звука принята другая, отличная от обозначения скорости движения тел, буква. Скорость света
обозначается буквой «с» (скорость света в вакууме составляет с = 2,9979х10 8 м/с = 2,9979х10 5 км/с). Скорость звука
так же обозначается буквой с (читается: [цэ]).
Ускорение обозначается
буквой а (исключение составляет лишь ускорение свободного падения, эта величина обозначается буквой g (читается [жэ]), g = 9,81 м/с 2). Если необходимо подчеркнуть, что эта величина — векторная (например, это часто требуется в физике), то над буквой «а» изображается либо горизонтальная черта, либо горизонтальная стрелка (так же, как и при обозначении скорости). В печатном тексте для обозначения ускорения как векторной величины может использоваться и буква «а», выделенная жирным шрифтом.
Если при решении задачи по физике или математике необходимо обозначить время
, то это пишется буквой
так: t (читается: [тэ]), а если расстояние
— пишется буквой
так: s (читается: [эс]). Для обозначения пути
обычно используется строчная (маленькая) буква [эль], т.е.
l
, реже — заглавная (большая) буква [эль], т.е.
L
. Чтобы обозначение пути «
l
» не было похоже на «единицу», эту букву пишут курсивом, т.е. с наклоном.
Вообще, вопросы «как в математике пишется скорость», «как в математике пишется время», «как в математике пишется расстояние» некорректны. Лучше формулировать такой вопрос, употребляя не слово «пишется», а слово «обозначается».
Источники:
- Яворский Б.М., Детлаф А.А., Лебедев А.К. Справочник по физике для инженеров и студентов вузов
- Справочник по элементарной математике. Геометрия, тригонометрия, векторная алгебра/ Под ред. П.Ф. Фильчакова
- Каплан И.А. Практические занятия по высшей математике
Среди прочих обозначений наиболее часто школьников интересует вопрос о том, как в математике обозначается скорость, время, расстояние
. Связано это с тем, что обозначения этих величин (особенно — скорости) в учебниках по математике и физике можно увидеть различные: с чертой над буквой
v
(читается: [вэ]), со стрелкой над буквой
v
, а также буквы
v
, выделенные курсивом или жирным шрифтом.
Скорость в математике
обозначается буквой
v
, но её написание принято различным для рукописного и печатного текста.
В рукописном тексте скорость движения обычно обозначается строчной (т.е. маленькой) прописной (т.е. не печатной, как в тексте из газеты, а написанной от руки так, как если бы писали письмо) буквой v. В учебниках по математике (т.е. в печатном тексте) обычно скорость движения обозначается печатной буквой v, прямой или выделенной курсивом. Такое обозначение принимается практически во всех задачах по математике, исключение составляют лишь задачи, иллюстрирующие тему «Векторы» (в этом случае обозначение принимается таким же, как и в физике).
В физике
(а точнее — в её разделе «механика») обозначение скорости зависит от того, нужно ли в данной задаче учитывать тот факт, что скорость — величина векторная. Там, где учитывать это не нужно, скорость обозначается строчной буквой v (печатной или прописной, так же, как и в математике). Если же необходимо учитывать то, что скорость характеризуется не только модулем (т.е. величиной), но и направлением, скорость изображается либо прописной буквой
v
с направленной слева направо стрелкой над этой буквой, либо той же прописной буквой v с горизонтальной чертой над этой буквой. В печатном тексте в этом случае обычно скорость обозначают либо печатной строчной буквой
v
со стрелкой или чертой над буквой, либо печатной буквой
v
, выделенной жирным шрифтом (т.е. так:
v
).
Буквой v обозначают скорость движения тел. Для обозначения скорости света и скорости звука принята другая, отличная от обозначения скорости движения тел, буква. Скорость света
обозначается буквой «с» (скорость света в вакууме составляет с = 2,9979х10 8 м/с = 2,9979х10 5 км/с). Скорость звука
так же обозначается буквой с (читается: [цэ]).
Ускорение обозначается
буквой а (исключение составляет лишь ускорение свободного падения, эта величина обозначается буквой g (читается [жэ]), g = 9,81 м/с 2). Если необходимо подчеркнуть, что эта величина — векторная (например, это часто требуется в физике), то над буквой «а» изображается либо горизонтальная черта, либо горизонтальная стрелка (так же, как и при обозначении скорости). В печатном тексте для обозначения ускорения как векторной величины может использоваться и буква «а», выделенная жирным шрифтом.
Если при решении задачи по физике или математике необходимо обозначить время
, то это пишется буквой
так: t (читается: [тэ]), а если расстояние
— пишется буквой
так: s (читается: [эс]). Для обозначения пути
обычно используется строчная (маленькая) буква [эль], т.е.
l
, реже — заглавная (большая) буква [эль], т.е.
L
. Чтобы обозначение пути «
l
» не было похоже на «единицу», эту букву пишут курсивом, т.е. с наклоном.
Вообще, вопросы «как в математике пишется скорость», «как в математике пишется время», «как в математике пишется расстояние» некорректны. Лучше формулировать такой вопрос, употребляя не слово «пишется», а слово «обозначается».
Источники:
- Яворский Б.М., Детлаф А.А., Лебедев А.К. Справочник по физике для инженеров и студентов вузов
- Справочник по элементарной математике. Геометрия, тригонометрия, векторная алгебра/ Под ред. П.Ф. Фильчакова
- Каплан И.А. Практические занятия по высшей математике
Как решать задачи на движение? Формула зависимости между скоростью, временем и расстоянием. Задачи и решения.
Формула зависимости времени, скорости и расстояния за 4 класс: как обозначается скорость, время, расстояние?
Люди, животные или машины могут двигаться с определенной скоростью. За определенное время они могут пройти определенный путь. Например: сегодня вы можете дойти до своей школы за полчаса. Вы идете с определенной скоростью и преодолеваете 1000 метров за 30 минут. Путь, который преодолевается, в математике обозначают буквой S
. Скорость обозначается буквой v
. А время, за которое пройден путь, обозначается буквой t
.
- Путь — S
- Скорость — v
- Время — t
Если вы опаздываете в школу, вы можете этот же путь пройти за 20 минут, увеличив свою скорость. А значит, один и тот же путь может быть пройден за разное время и с различной скоростью.
Как зависит время прохождения пути от скорости?
Чем больше скорость, тем быстрее будет пройдено расстояние. И чем меньше скорость, тем больше времени понадобится для прохождения пути.
Как найти время, зная скорость и расстояние?
Для того, чтобы найти время, понадобившееся для прохождения пути, нужно знать расстояние и скорость. Если расстояние разделить на скорость — вы узнаете время. Пример такой задачи:
Задача про Зайца.
Заяц убегал от Волка со скоростью 1 километр за минуту. Он пробежал до своей норы 3 километра. За какое время Заяц добежал до норы?
Как легко решать задачи на движение, где нужно найти расстояние, время или скорость?
- Внимательно прочитайте задачу и определите, что известно из условия задачи.
- Напишите на черновике эти данные.
- Также напишите, что неизвестно и что нужно найти
- Воспользуйтесь формулой для задач про расстояние, время и скорость
- Введите в формулу известные данные и решите задачу
Решение для задачи про Зайца и Волка.
- Из условия задачи определяем, что нам известно скорость и расстояние.
- Также из условия задачи определяем, что нам нужно найти время, которое нужно было зайцу, чтобы добежать до норы.
Пишем в черновик эти данные например так:
Время — неизвестно
Теперь запишем то же самое математическими знаками:
S
— 3 километра
V — 1 км/мин
t
— ?
Вспоминаем и записываем в тетрадь формулу для нахождения времени:
t = S: v
t = 3: 1 = 3 минуты
Как найти скорость, если известно время и расстояние?
Для то, чтобы найти скорость, если известно время и расстояние, нужно расстояние разделить на время. Пример такой задачи:
Заяц убегал от Волка и пробежал до своей норы 3 километра. Он преодолел это расстояние за 3 минуты. С какой скоростью бежал Заяц?
Решение задачи на движение:
- В черновик записываем, что нам известно расстояние и время.
- Из условия задачи определяем, что нужно найти скорость
- Вспоминаем формулу для нахождения скорости.
Формулы для решения таких задач показаны на картинке ниже.
Подставляем известные данные и решаем задачу:
Расстояние до норы — 3 километра
Время, за которое Заяц добежал до норы — 3 минуты
Скорость — неизвестна
Запишем эти известные данные математическими знаками
S
— 3 километра
t
— 3 минуты
v — ?
Записываем формулу для нахождения скорости
v = S: t
Теперь запишем решение задачи цифрами:
v = 3: 3 = 1 км/мин
Как найти расстояние, если известно время и скорость?
Чтобы найти расстояние, если известно время и скорость нужно время умножить на скорость. Пример такой задачи:
Заяц убегал от Волка со скоростью 1 километр за 1 минуту. Чтобы добежать до норы ему понадобилось три минуты. Какое расстояние пробежал Заяц?
Решение задачи: Записываем в черновик, что нам известно из условия задачи:
Скорость Зайца — 1 километр за 1 минуту
Время, которое Заяц бежал до норы — 3 минуты
Расстояние — неизвестно
Теперь, то же самое запишем математическими знаками:
v — 1 км/мин
t
— 3 минуты
S — ?
Вспоминаем формулу для нахождения расстояния:
S = v ⋅ t
Теперь запишем решение задачи цифрами:
S = 3 ⋅ 1 = 3 км
Как научиться решать более сложные задачи?
Чтобы научиться решать более сложные задачи нужно понять как решаются простые, запомнить какими знаками обозначаются расстояние, скорость и время. Если не получается запомнить математические формулы их нужно выписать на лист бумаги и всегда держать под рукой во время решения задач. Решайте с ребенком несложные задачи, которые можно придумать на ходу, например во время прогулки.

Когда решают задачи про скорость, время и расстояние, очень часто делают ошибку, из-за того, что забыли перевести единицы измерения.
ВАЖНО: Единицы измерения могут быть любыми, но, если в одной задаче есть разные единицы измерения, переведите их одинаковые. Например, если скорость измерена в километрах за минуту, то расстояние обязательно должно быть представлено в километрах, а время в минутах.
Для любознательных
: Общепринятая сейчас система мер называется метрической, но так было не всегда, и в старину на Руси использовали другие единицы измерения.
Задача про удава
: Слоненок и мартышка мерили длину удава шагами. Они двигались навстречу друг другу. Скорость мартышка была 60 см за одну секунду, а скорость слоненка 20 см за одну секунду. На измерение они потратили 5 секунд. Какова длина удава? (решение под картинкой)
Решение:
Из условия задачи определяем, что нам известно скорость мартышки и слоненка и время, которое им понадобилось для измерения длины удава.
Запишем эти данные:
Скорость мартышки — 60 см/сек
Скорость слоненка — 20 см/сек
Время — 5 секунд
Расстояние неизвестно
Запишем эти данные математическими знаками:
v1 — 60 см/сек
v2 — 20 см/сек
t — 5 секунд
S — ?
Запишем формулу для расстояние, если известна скорость и время:
S = v ⋅ t
Посчитаем, какое расстояние прошла мартышка:
S1 = 60 ⋅ 5 = 300 см
Теперь посчитаем, сколько прошел слоненок:
S2 = 20 ⋅ 5 = 100 см
Суммируем расстояние, которое прошла мартышка и расстояние, которое прошел слоненок:
S = S1 + S2 = 300 + 100 = 400 см
График зависимости скорости тела от времени: фото
Расстояние, преодолеваемое с разной скорость преодолевается за разное время. Чем больше скорость — тем меньше потребуется времени для передвижения.
Таблица 4 класс: скорость, время, расстояние
В таблице ниже приведены данные для которых нужно придумать задачи, а потом их решить.
| № | Скорость (км/час) | Время (час) | Расстояние (км) |
| 1 | 5 | 2 | ? |
| 2 | 12 | ? | 12 |
| 3 | 60 | 4 | ? |
| 4 | ? | 3 | 300 |
| 5 | 220 | ? | 440 |
Вы можете пофантазировать и придумать задачи к таблице сами. Ниже наши варианты условия задач:
- Мама отправила Красную Шапочку к бабушке. Девочка постоянно отвлекалась и шла по лесу медленно, со скоростью 5 км/час. На путь она потратила 2 часа. Какое расстояние за это время прошла Красная Шапочка?
- Почтальон Печкин вез на велосипеде посылку со скоростью 12 км/час. Он знает, что расстояние между его домом и домом Дяди Федора 12 км. Помогите Печкину рассчитать, сколько времени понадобится на дорогу?
- Папа Ксюши купил автомобиль и решил отвезти семью на море. Машина ехала со скоростью 60 км/час и на дорогу было потрачено 4 часа. Какое расстояние между домом Ксюши и морским побережьем?
- Утки собрались в клин и полетели в теплые края. Птицы махали крыльями без устали 3 часа и преодолели за это время 300 км. Какой была скорость птиц?
- Самолет АН-2 летит со скоростью 220 км/час. Он вылетел из Москвы и летит в Нижний Новгород, расстояние между этими двумя городами 440 км. Сколько времени самолет будет в пути?
Ответы на приведенные задачи можно найти в таблице ниже:
| № | Скорость (км/час) | Время (час) | Расстояние (км) |
| 1 | 5 | 2 | 10 |
| 2 | 12 | 1 | 12 |
| 3 | 60 | 4 | 240 |
| 4 | 100 | 3 | 300 |
| 5 | 220 | 2 | 440 |
Примеры решения задач на скорость, время, расстояние за 4 класс
Если в одной задаче есть несколько объектов движения, нужно научить ребенка рассматривать движение этих объектов отдельно и только потом вместе. Пример такой задачи:
Двое друзей Вадик и Тема решили прогуляться и вышли из своих домов навстречу друг другу. Вадик ехал на велосипеде, а Тема шел пешком. Вадик ехал со скоростью 10 км/час, а Тема шел со скоростью 5 км в час. Через час они встретились. Какое расстояние между домами Вадика и Темы?
Эту задачу можно решить используя формулу зависимости расстояния от скорости и времени.
S = v ⋅ t
Расстояние, которое проехал Вадик на велосипеде будет равно его скорости умноженной на время в пути.
S = 10 ⋅ 1 = 10 километров
Расстояние, которое прошел Тема считают аналогично:
S = v ⋅ t
Подставляем в формулу цифровые значения его скорости и времени
S = 5 ⋅ 1 = 5 километров
Расстояние, которое проехал Вадик нужно прибавить к расстоянию, которое прошел Тема.
10 + 5 = 15 километров
Как научиться решать сложные задачи, для решения которых требуется логически мыслить?
Развивать логическое мышление ребенка, нужно решая с ним простые, а затем и сложные логические задачи. Эти задачи могут состоять из нескольких этапов. Перейти с одного этапа на другой можно только в том случае, если решен предыдущий. Пример такой задачи:
Антон ехал на велосипеде со скоростью 12 км/час, а Лиза ехала на самокате со скоростью в 2 раза меньше, чем у Антона, а Денис шел пешком со скоростью в 2 раза меньше, чем у Лизы. Какова скорость Дениса?
Чтобы решить эту задачу нужно сначала узнать скорость Лизы и только после этого скорость Дениса.

Иногда в учебниках для 4 класса попадаются непростые задачи. Пример такой задачи:
Два велосипедиста выехали из разных городов навстречу друг другу. Один из них спешил и мчался со скоростью 12 км/час, а второй ехал не спеша со скоростью 8 км/час. Расстояние между городами из которых выехали велосипедисты 60 км. Какое расстояние проедет каждый велосипедист, перед тем как они встретятся? (решение под фото)
Решение:
- 12+8 = 20 (км/час) — это общая скорость двух велосипедистов, или скорость с которой они приближались друг к другу
- 60 :
20 = 3 (часа) — это время через которое велосипедисты встретились
- 3 ⋅
8 = 24 (км) — это расстояние, которое проехал первый велосипедист
- 12 ⋅ 3
= 36 (км) — это расстояние, которое проехал второй велосипедист
- Проверка: 36+24=60 (км) — это расстояние, которое проехали два велосипедиста.
- Ответ: 24 км, 36 км.
Предлагайте детям в форме игры решать такие задачи. Возможно, они сами захотят составить свою задачу про друзей, животных или птиц.
На чтение 10 мин. Просмотров 1k. Опубликовано 19 декабря 2022
Вычислить скорость, время и расстояние часто бывает необходимо в повседневной жизни, когда мы рассчитываем время на дорогу. Все эти величины (время, расстояние и скорость) связаны между собой математической формулой и зная две из них всегда можно найти третью. Мы с вами рассмотрим, что понимается под этими величинами, как их найти, решим несколько задач.
Скорость, время и расстояние — это ключевые параметры при решении задач на движение. Эти задачи есть и в ЕГЭ и в ОГЭ по математике. Сегодня мы подробнее остановимся на этих величинах.
Расстояние
Расстояние — это физическая величина, означающая длину между двумя объектами. Расстояние обозначается буквой S и измеряется в единицах длины: метрах. Метр — это международно-принятая единица измерения длины. Однако встречаются и другие единицы длины — километр, сантиметр, миллиметр. В этом случае целесообразно перевести единицы длины в международную систему единиц (СИ).
Например: расстояние от Земли до Солнца равно 149 597 870 700 метров.
Расстояние связано со скоростью и временем:
S=v cdot t
Вот тут таблица длин и их перевода в международную систему единиц — то есть в метры.
| Единицы длины | СИ |
| 1 сантиметр | 0,01 м |
| 1 километр | 1000 м |
| 1 дециметр | 0,1 м |
| 1 миллиметр | 0,001 м |
| 1 микрометр | 1·10-6 м |
| 1 миля | 1609,34 м |
| 1 фут | 0,3048 м |
| 1 ярд | 0,9144 м |
| 1 дюйм | 0,0254 м |
| 1 морская миля | 1852 м |
Время
Время — это физическая величина, которая обозначает непрерывное и необратимое (возможно) движение от прошлого к будущему через настоящее. Это фундаментальная физическая величина, единица измерения времени — секунда. Однако, в задачах могут использоваться и другие единицы времени — часы, минуты, дни.
Время можно найти по формуле:
t=frac{S}{v}
Ученые о времени
По словам греческого философа Парменида (ок. 450 г. до н.э.), время и движение были иллюзиями. Его ученик Зенон Элейский разработал два знаменитых парадокса: «Ахиллес и черепаха» и «Парадокс летящей стрелы», чтобы доказать его утверждения. Платон, живший на пару поколений позже, считал, что время создано вместе со вселенной и существует независимо. Он рассматривал время как пустой контейнер, который можно заполнить движущимися вещами и событиями. Его ученик Аристотель считал, что время не существует независимо от событий, но время есть изменение и движение.
Аристотель пришел к выводу, что время не состоит из последовательных неделимых моментов «сейчас», как пытался сказать Зенон с помощью своего парадокса стрелы. Согласно Аристотелю, не существует серии моментов «сейчас», потому что такие моменты не могли бы исчезнуть в течение их собственной длительности или в следующий момент «сейчас». Исааку Ньютону (1642–1726) время понадобилось в качестве переменной в его уравнениях, и он начал думать о времени с научной точки зрения. Ньютон поддерживал идею Платона о независимости времени. Он разделил время на абсолютное (математическое) время и относительное (обычное) время.
Абсолютное время, или продолжительность, является реальным и математическим, и оно течет неуклонно, независимо от чего-либо внешнего. Относительное время кажущееся и является внешней мерой длительности, которая может быть обнаружена органами чувств с помощью движения, которое может быть точным или неточным.
Готфрид Лейбниц (1646–1716) был согласен с Аристотелем и думал, что без событий и перемен не было бы времени. Физик- теоретик Ли Смолин писал в 2010 году, что исследования квантовой гравитации подтверждают, что четырехмерное пространство-время имеет смысл только в том случае, если время реально, фундаментально и даже является единственным аспектом реальности, который мы непосредственно ощущаем.
Скорость
Скорость обозначается буквой — это физическая величина, которая обозначает какое расстояние проходит объект в единицу времени. Единица измерения скорости — м/с. Однако, встречаются также и км/ч и см/с (эти измерения не входят в международную систему единиц измерения). Скорость показывает как быстро изменяется расстояние во времени.
Например, выражение 9 м/с означает, что тело за 1 секунду проходит 9 метров. То есть за 1 секунду 9 метров, за 2 секунду еще 9 метров, итого за 2 секунду — 18 метров. В курсе школьной математики мы считаем, что скорость равномерная во времени. То есть тело за равные промежутки времени проходит равные расстояния. То есть 9 м/с означает 9 метров в любую из секунд движения тела. Однако, в реальности движение бывает равномерное и неравномерное. Мы не рассматриваем неравномерное движение в курсе математики (1-6 класс), однако в курсе алгебры элементы кинематики с неравномерным движением рассматриваются.
Еще примеры: скорость 100 км/ч — это прохождение расстояния в 100 километров за 1 час.
Формула скорости
Скорость можно найти через расстояние и время по формуле:
v=frac{S}{t}
Средняя скорость
Если движение тела можно разбить на несколько участков и в пределах каждого участка скорость тела не меняется, то целесообразно говорить о средней скорости.
Формула средней скорости:
v=frac{S_{весь ; путь}}{t_{всё ; время}}=frac{S_1+S_2+…+ S_n}{t_1+t_2+…+ t_n}
То есть средняя скорость это отношение всего пути, ко всему времени.
Скорости сближения и удаления
Понятие скорости ученики изучают еще в 4 классе, а далее это понятие расширяется и уточняется. Вводятся такие понятия как скорость сближения и скорость удаления. Не все педагоги используют эти понятия в своей работе, поскольку эти понятия можно использовать только при решении небольшого класса задач на движение и они ограничивают решение задач и другими условиями (например, если тела удаляются или сближаются не по одной прямой, а по перпендикулярным прямым). И все же, давайте мы уточним, о чем вообще идет речь.
Скорость удаления
Если два тела удаляются друг от друга, двигаясь по одной прямой, то в таких случаях говорят о скорости удаления. То есть скорость удаления характеризует расстояние, которое увеличивается по мере удаления двух тел в единицу времени.
Допустим есть два пешехода, которые удаляются друг от друга, первый пешеход удаляется со скоростью 3 км/ч, а второй пешеход со скоростью 4 км/ч. Тогда скорость удаления будет:
3+4=7 км/ч.
Действительно, расстояние, пройденное первым пешеходом за один час будет 3 километра, а расстояние, пройденное вторым пешеходом за то же время будет 4 километра. Тогда при удалении пешеходов друг от друга расстояние между ними увеличивается на 7 километров в каждый час или наши пешеходы удаляются со скоростью 7 км/ч. Мы должны сложить скорости объектов.
Формула скорости удаления:
v_{удаления}=v_1+v_2
где
— скорость одного тела,
— скорость другого тела.
Напомним, что это понятие можно использовать только если тела двигаются в разных направлениях, располагаемых на одной прямой.
Скорость сближения двух тел
Аналогично, рассмотрим ситуацию, если два пешехода двигаются навстречу друг к другу. Один пешеход за один час проходит расстояние 2 км, а второй пешеход за то же время проходит 5 км.
Значит, расстояние между ними будем уменьшаться со скоростью 5+2 = 7 км/ч.
Формула скорости сближения:
v_{сближения}=v_1+v_2
где
— скорость одного тела,
— скорость другого тела.
Если один пешеход догоняет другого. То скорость сближения при движении в одном направлении можно определить, если вычесть из большей скорости меньшую.
То есть, если у нас второго пешехода (=3км/ч) догоняет первый пешеход (
=5 км/ч), то скорость их сближения будет 2 км/ч:
Формула скорости сближения при движении вдогонку:
v_{сближения}=v_1-v_2
где
— скорость одного тела,
— скорость другого тела. При этом
Таблица «скорость, время, расстояние» при решении задач на движение
При решении задач на движение очень удобно пользоваться такой таблицей, в которой три столбца с данными по скорости, времени движения тел и расстоянию, которое они проходят. Эта таблица, кстати помогает легко запомнить формулы скорости, времени и расстояния, если представить что первый столбец — это первый множитель, второй столбец — второй множитель, а третий столбец — произведение.
| Скорость, v, м/с | Время, t, с | Расстояние, S, м |
Простой пример, найти скорость велосипедиста, если за 5 часов он прошел 45 километров.
Составляем таблицу и записываем в нее данные:
| Скорость, v, км/ч | Время, t, ч | Расстояние, S, км |
| ? | 5 | 45 |
Теперь видно, что неизвестна скорость в первом столбце, значит, неизвестен первый множитель. Чтобы определить неизвестный множитель надо произведение разделить на известный множитель: = 45/5 = 9 км/ч.
Важно! В задачах все единицы измерения должны быть приведены либо к международной системе единиц (метр, секунда, м/с) либо к одним единицам измерения (то есть если в задаче есть и м/с и км/ч можно привести всё либо к м/с (тогда и время в секундах и расстояние в метрах), либо к км/ч (тогда и время в часах будет и расстояние в километрах))
Рассмотрим теперь некоторые примеры решения задач
Примеры задач на движение
Задача 1
Школьник идет домой со скоростью 2 км/ч. Расстояние от школы до дома 1 км. За какое время школьник дойдет до дома?
Решение:
Найдем время по формуле: displaystyle t=frac{S}{v}=frac{1}{2}ч.
Школьник дойдет до дома за полчаса.
Ответ: 0,5 ч.
Задача 2
Автомобилист и велосипедист выехали в город из деревни одновременно. Скорость автомобилиста 50 км/ч. Расстояние до города 100 км. Какова скорость велосипедиста, если известно, что он прибыл в город на 8 часов позже автомобилиста?
Решение: Составим таблицу
| Скорость, v, км/ч | Время, t, ч | Расстояние, S, км | |
| Автомобилист | 50 | 100/50 | 100 |
| Велосипедист | x | 100/x | 100 |
Пусть скорость велосипедиста x. В таблице мы сразу смогли написать соотношения для времени движения. По условию задачи дано, что велосипедист прибыл в город на 8 часов позже автомобилиста. Запишем это:
displaystyle frac{100}{x}-frac{100}{50}=8
Мы отнимаем от времени, которое потратил велосипедист (он же потратил больше времени) время, которое потратил автомобилист и получаем 8 часов.
Решим полученное уравнение.
displaystyle frac{100}{x}-2=8
displaystyle frac{100}{x}=10
x=10
Ответ: 10 км/ч
Задача 3
Стрела пролетает 180 метров за 0,05 минуты. Найдите ее скорость.
Решение: прежде чем решать задачу, переведем все единицы в одну систему единиц. Минуты переведем в секунды.
В одной минуте 60 секунд. Значит, чтобы узнать сколько секунд в 0,05 минутах, умножим 0,05 на 60, получим:
0,05 cdot 60=3 c.
Тогда displaystyle v= frac{180}{3}=60 м/с.
Ответ: 60 м/с
Задача 4
Турист прошел лесной участок длиной 10 км со скоростью 5 км/ч, а затем шел по полю 20 км, со скоростью 4 км/ч. Какова средняя скорость туриста?
Решение:
Определим весь путь который прошел турист:
displaystyle S_{весь ; путь}=S_1+S_2=10+20=30 км.
Для прохождения лесного участка турист потратил: displaystyle t_1= frac{S_1}{v_1}=frac{10}{5}=2ч, а на второй участок времени ушло: displaystyle t_2= frac{S_2}{v_2}=frac{20}{4}=5ч
Все время: displaystyle t_{всё ; время}=t_1+t_2=2+5=7ч
Тогда найдем среднюю скорость:
displaystyle v_{ср}= frac{S_{весь ; путь}}{t_{всё ; время}}=frac{30}{7}=4 frac{2}{7} км/ч.
Ответ: displaystyle v_{ср}=4 frac{2}{7}
Задача 5
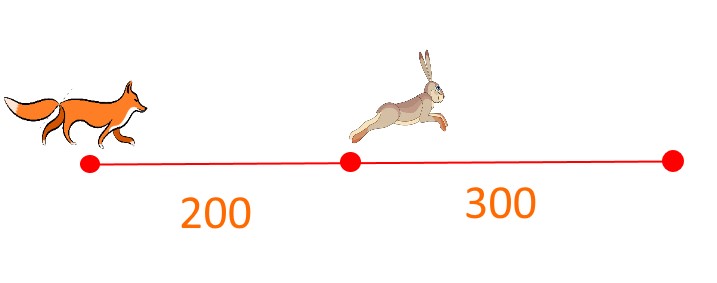
Лиса гонится за зайцем. Скорость лисы 20 м/с, а скорость зайца 15 м/с. Догонит ли лиса зайца, если заяц находится на расстоянии 300 метров от безопасного места, а лиса находится на расстоянии 200 метров от зайца?
Решение:
Заяц добежит до норы за displaystyle t= frac{300}{15}=20 секунд.
Лиса же за 20 секунд пробежит расстояние displaystyle S= 20 cdot 20=400 метров.
Лиса не догонит зайца.
Действительно, скорость сближения лисы и зайца:
displaystyle v=v_{лисы}-v_{зайца}=20-15=5 м/с
То есть, чтобы преодолеть расстояние 200 метров, которое изначально существует между лисой и зайцем, лисе понадобиться displaystyle t=frac{200}{5}=40 с
Заяц же уже 20 секунд будет в безопасном месте.
Ответ: лиса зайца не догонит.
Содержание
- Расстояние, скорость, время
- Расстояние
- Скорость
- Время
- Взаимосвязь скорости, времени, расстояния
- 28 thoughts on “Расстояние, скорость, время”
- Формула нахождения значений скорости, времени и расстояния
- Как же рассчитать скорость?
- Другие способы вычисления
- Способы вычисления расстояния и времени
- Видео
- Математика
- Среднее значение
- Скорость. Время. Расстояние
- Взаимосвязь между скоростью, временем и расстоянием
- Задачи на движение
- Понятие о времени
- Расстояние и скорость
- Общая формула
- Решение задач
- Математика. 5 класс
Расстояние, скорость, время
В этом уроке мы рассмотрим три физические величины, а именно расстояние, скорость и время.
Расстояние
Расстояние мы уже изучали в уроке единицы измерения. Говоря простым языком, расстояние это длина от одного пункта до другого. (Пример: расстояние от дома до школы 2 километра).
Имея дело с большими расстояниями, в основном они будут измеряться в метрах и километрах. Расстояние обозначается латинской буквой S. Можно обозначить и другой буквой, но буква S общепринята.
Скорость
Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Предположим, что двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 100 метров. Первый школьник добежал за 25 секунд. Второй за 50 секунд. Кто добежал быстрее?
Быстрее добежал тот, кто за 1 секунду пробежал бóльшее расстояние. Говорят, что у него скорость движения больше. В данном случае скорость школьников это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Давайте найдём скорость первого школьника. Для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
У нас расстояние дано в метрах, а время в секундах. Значит скорость измеряется в метрах в секунду (м/с)
Итак, скорость движения первого школьника составляет 4 метра в секунду (м/с).
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
Значит скорость движения второго школьника составляет 2 метра в секунду (м/с).
Скорость движения первого школьника — 4 (м/с)
Скорость движения второго школьника — 2 (м/с)
Скорость первого школьника больше. Значит он добежал до спортплощадки быстрее. Скорость обозначается латинской буквой v.
Время
Иногда возникает ситуация, когда требуется узнать за какое время тело преодолеет то или иное расстояние.
Например, от дома до спортивной секции 1000 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 500 метров в минуту (500м/мин). За какое время мы доедем до спортивной секции?
Если за одну минуту мы будем проезжать 500 метров, то сколько таких минут с пятью ста метрами будет в 1000 метрах?
Очевидно, что надо разделить 1000 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 500 метров. Тогда мы получим время, за которое доедем до спортивной секции:
Время движения обозначается маленькой латинской буквой t.
Взаимосвязь скорости, времени, расстояния
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:
s = v × t
Например, мы вышли из дома и направились в магазин. Мы дошли до магазина за 10 минут. Наша скорость была 50 метров в минуту. Зная свою скорость и время, мы можем найти расстояние.
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Очевидно, что умножив 50 метров на 10, мы определим расстояние от дома до магазина:
s = v × t = 50 × 10 = 500 (метров до магазина)
Если известно время и расстояние, то можно найти скорость:
v = s : t
Например, расстояние от дома до школы 900 метров. Школьник дошел до этой школы за 10 минут. Какова была его скорость?
Скорость движения школьника это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 900 метров, то какое расстояние он преодолевал за одну минуту?
Чтобы ответить на этот, нужно разделить расстояние на время движения школьника:
v = s : t = 900 : 10 = 90 (м/мин)
Если известна скорость и расстояние, то можно найти время:
t = s : v
Например, от дома до спортивной секции 500 метров. Мы должны дойти до неё пешком. Наша скорость будет 100 метров в минуту (100 м/мин). За какое время мы дойдем до спортивной секции?
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое мы дойдем до спортивной секции:
t = s : v = 500 : 100 = 5 (минут до спортивной секции)
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
28 thoughts on “Расстояние, скорость, время”
ОЧЕНЬ суперский сайт! Давно добавила его в Избранное! Спасибо за Ваши труды! они очень-очень полезны!
На самом деле незнание математики — это колоссально масштабная проблема. Миллионы людей ее НЕ понимают. И МАЛО кто может ее хорошо объяснить. Благодаря ВАМ — у людей есть шанс исправиться 🙂
тут имеет место неверная трактовка в самих учебниках на подобные задачи. Не указывается, двигались ли школьники с постоянной скоростью или она менялась. Ответом в итоге получается средняя скорость движения школьника по ходу всей дистанции…
Источник
Формула нахождения значений скорости, времени и расстояния
С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.
Как же рассчитать скорость?
На самом деле, рассчитать ее можно несколькими способами:
Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.
Теперь нужно подставить имеющиеся значения вместо буквенных символов:
v=100 км/1,5 ч=66,66 км/ч
Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.
Таким нехитрым способом можно найти скорость через время и расстояние.
А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:
Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:
Можно записать использовать и такой вид вычислений:
Но можно записать эту же формулу и в более точном варианте:
Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.
Другие способы вычисления
Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:
Способы вычисления расстояния и времени
Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:
Таким образом вычисляется значение расстояния.
Или вычисляем значение времени, за которое пройдено расстояние:
Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.
Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.
И это еще не предел!
Видео
В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.
Источник
Математика
Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет
С этой картой можно накопить на мечту, жми ⇒
План урока:
На уроке узнаем, что означает «среднее арифметическое» и как его находят, будем решать задачи с величинами «скорость», «время», «расстояние».
Начнем урок с небольшой тренировки ума! Игра называется «Тройка». Вам нужно собрать в левой части три слагаемых так, чтобы получилось число за красной чертой. Считайте устно. Образец дан в первой строке: 18 + 34 + 16 = 68
Среднее значение
Каждый из нас в жизни встречается с выражениями «в среднем», «средняя температура», «средний заработок». Что это значит?
Рассмотрим на конкретной задаче.
Три друга Иван, Костя и Владимир каждую среду идут вместе от школы до музыкальной студии, где учатся игре на гитаре. Иван от школы до студии насчитал 251 шаг. Костя – 248 шагов, а Владимир насчитал 254 шага. Сколько в среднем шагов от школы до музыкальной студии?
В математике существует понятие «среднее арифметическое». Чтобы найти среднее арифметическое в этой задаче, нужно сложить количество шагов трех друзей, а затем полученную сумму разделить на 3 (по количеству слагаемых).
251 + 248 + 254 = 753 шага.
Можно сказать, что от школы до музыкальной студии в среднем 251 шаг.
Например, найти среднее арифметическое чисел: 5, 8, 7, 4.
Находим сумму чисел 5 + 8 + 7 + 4 = 24
Количество слагаемых – 4, значит, полученную сумму разделим на 4.
Среднее арифметическое – 6.
Пользуясь алгоритмом, найдите среднее арифметическое чисел: 12, 10, 8.
Среднее арифметическое – 10.
Рассмотрим более сложную задачу на нахождение среднего арифметического.
Задача
В столовой детского сада для приготовления завтраков малышам расходовали молоко три дня по 20 л и два дня по 25 л. Сколько в среднем расходовали молока в день?
Решим задачу вместе.
Сначала узнаем, сколько всего молока израсходовали.
20 ∙ 3 + 25 ∙ 2 = 110 (л) – израсходовали всего.
Затем узнаем, сколько дней расходовали молоко на завтрак.
3 + 2 = 5(дн.) – расходовали молоко.
Осталось количество израсходованного молока разделить на число дней.
110 : 5 = 22 (л) – расходовали в среднем за день.
Попробуйте самостоятельно решить подобную задачу.
Задача
Для игрового уголка в классе родители закупили 3 настольные игры: «Пазлы», «Домино», «Математический тренажер». Игра «Пазлы» стоила 160 р., «Домино» – 210 р., а «Математический тренажер» – 230 р.. Найди среднюю стоимость настольной игры.
Скорость. Время. Расстояние
Вы наблюдали, что вокруг нас постоянно что-то или кто-то движется. Некоторые объекты – быстро, а некоторые – совсем медленно. Например, по лесной тропе прогуливается человек, по шоссе едет автомобиль, по воздуху летит вертолет. Все они движутся. Но автомобиль движется быстрее, чем человек, а вертолет – быстрее автомобиля.
В математике, величиной характеризующей быстроту движения объектов называют скоростью.
Скорость движения – это расстояние, пройденное за единицу времени. Единицей времени может быть: 1 секунда, 1 минута, 1 час.
Давайте вместе разберем две простые задачи.
Легковая машина прошла 120 км за 2 часа. В течение каждого часа она проходила одинаковое расстояние. Сколько км прошла машина за 1 час?
120 : 2 = 60 (км) – пройдет машина за 1 час.
Таким образом, скорость движения машины 60 км в час. Сокращенно запишем так:
60 км/ч.
Космический корабль пролетает 8 000 м за 1 секунду. Как по-другому записать его скорость?
Его скорость можно записать так: 8 000 м/с. Мы знаем, что 1 км = 1000 м, поэтому скорость корабля можно записать по-другому: 8 км/с.
Посмотрите скорость движения некоторых животных. Какое животное самое медленное, самое быстрое? Обратите внимание, что скорость можно записать по-разному: в зависимости от того, сколько сантиметров, метров, километров кто-то пролетает, проползает или пробегает за секунду, минуту, час.
С единицами времени вы уже знакомы. Это: секунда, минута, час, сутки, неделя, месяц, год, век.
Расстояние – это длина дороги, соединяющая начало и конец пути.
Расстояние измеряется в следующих единицах:
Миллиметр
Сантиметр
Дециметр
Километр
Взаимосвязь между скоростью, временем и расстоянием
Как же связаны между собой эти величины?
Давайте запомним условные обозначения, принятые в математике:
Скорость – v,
Время – t,
Расстояние – S.
Ребята, это три ключевых формулы для решения задач на движение, которые нужно знать назубок!
Задачи на движение
С задачами на движение мы встречаемся каждый день в обычной жизни.
Расстояние – самое большое из трех величин в задачах на движение. То есть, скорость и время всегда меньше расстояния.
Запомнили формулы, которые являются ключами к правильному решению задач?
Заполните пустые окошки в формулах:
Решим задачи на движение.
Плот двигался по реке со скоростью 5 км/ч, а катер – со скоростью 20 км/ч. Какое расстояние преодолеет плот, и какое катер за 3 часа?
Выделяем величины, чертим таблицу. Читаем задачу по частям и записываем каждую величину в нужную ячейку таблицы.
Какую из трех величин нужно найти? Верно, расстояние. Вспомним формулу: S = v ∙ t
5 ∙ 3 + 15 (км) – пройдет плот.
20 ∙ 3 = 60 (км) – пройдет катер.
Ребята участвовали в соревнованиях по бегу. Максим пробежал 200 м за 40 с, а Артем это же расстояние пробежал за 50 с. С какой скоростью бежал каждый из мальчиков?
Начертите таблицу, как в предыдущей задаче. Запишите величины в нужные ячейки. Поставьте знак вопроса. Пользуясь формулой, решите задачу самостоятельно.
v = S : t
200 : 40 = 5 (м/с) – скорость движения Максима.
200 : 5 = 4 (м/с) – скорость движения Артема.
Решим еще одну задачу.
Два всадника отправились на прогулку на лошадях Рада и Снежка. Лошади преодолели одинаковое расстояние 30 км. Но двигались с разной скоростью. Рада бежала со скоростью 10 км/ч, а Снежка – 15 км/ч. Сколько времени длилась прогулка на Раде, и сколько времени – на Снежке?
Начертите таблицу, заполните ее ячейки. Пользуясь формулой, запишите решение.
30 : 10 = 3 (ч) – прогулка на Раде.
30 : 15 = 2 (ч) – прогулка на Снежке.
Сегодня на уроке мы запомнили формулы-ключи для решения задач на движение, узнали о скорости самых медленных и самых быстрых животных, научились находить среднее арифметическое. До скорых встреч, ребята!
Источник
Понятие о времени
Существует характеристика, с которой приходится сталкиваться каждый день вне зависимости от возраста, социального статуса, различных способностей и умений. С её помощью определяют будущее, прошедшее и настоящее. По сути, это маркер, определяющий событие. Называют его временем. Рассматривая движение, всегда учитывают эту характеристику, как и её прогрессию.
Время является частью пространственной координаты. Но если относительно других осей можно перемещаться в различных направлениях, относительно него движение определяется только вперёд или назад. Неотъемлемой частью, связанной со временем, является пространство, благодаря которому и возможно понять суть параметра.
Исследованием характеристики занимались философы и учёные в различные периоды существования человечества. Видеть и слышать время невозможно, в отличие от осязаемого пространства, которое возможно наблюдать сразу и везде. Причём в нём можно перемещаться.
Сегодня так и нет ответов на следующие вопросы о времени:
В классической физике для определения временного изменения используется специальная координата пространство-время. Принято будущие события обозначать знаком плюс, а прошедшие минусом. Единица измерения времени связана с вращением планеты вокруг своей оси и Солнца. Этот выбор был сделан условно и привязан к удобству жизнедеятельности человечества.
В Международной системе единиц принято за секунду принимать интервал, равный 9 192 631 770 периодам излучения атома цезия-133 в покое при нуле градусов по Кельвину. Обозначают параметр латинской буквой t. Таким образом, время — физическая величина, связанная с перемещением какого-либо тела относительно выбранной системы координат.
Расстояние и скорость
Положение каждой физической точки можно описать с помощью координатных осей. Другими словами, системой, которая по отношению к исследуемому телу остаётся неизменной. Изменение положения относительно другого объекта можно представить пройденным расстоянием. Фактически это путь, для которого известно начало и конец. С физической точки зрения, расстояние — величина, являющаяся размерностью длины, и выражающаяся в её единицах.
В математике мера пройденного пути тесно связана с метрическим пространством, то есть положением, где существует пара (x, d), определённая в декартовом произведении. Соответственно, если координату принять за x, y, можно сказать следующее:
В физике расстояние измеряют единицами длины. В соответствии с СИ за размерность берут метр. Расстояние — мера пройденного пути, то есть длина. Если необходимо просто определить изменение положения без учёта, когда и как оно произошло, используют координатные оси. Но при нахождении пройденного пути за время в формуле для расстояния должна учитываться ещё одна величина — скорость.
Обозначают эту характеристику символом V. Характеризует она быстроту перемещения в выбранной системе отсчёта. По определению скорость равняется производной радиус-вектора точки по времени. Иными словами, это значение, задающееся положением в пространстве относительно неизменной координаты, за которую чаще всего принимается начало.
Одно и то же расстояние можно преодолеть за разное время. Например, чтобы пройти 7 километров человеку понадобится затратить порядка одного часа, на автомобиле же этот путь можно преодолеть за 10 минут, а то и меньше. Вот как раз эти отличия и зависят от скорости движения.
Но на самом деле не всё так однозначно. Скорость необязательно должна быть одинаковой на всём пути. На определённых промежутках она может увеличиваться или уменьшаться, поэтому в математике под её значением понимают среднюю величину. Считается, что тело движется равномерно при прохождении установленного расстояния.
Общая формула
Скорость, время, расстояние — это 3 фундаментальных величины, связанные друг с другом. Исследуя одну характеристику, обязательно нужно учитывать две других. Фактически скорость — это физическая величина, определяющая, какую длину преодолеет физическое тело за единицу времени. Например, значение 120 км/ч показывает, что объект сможет преодолеть 120 километров за один час. В математическом виде связь между тремя характеристиками может быть записана в виде следующей формулы:
Зная это равенство и любых 2 параметра, можно выполнить расчёт третьего, так для времени она будет иметь вид t = S / V, а скорости V = S / t. Проверить правильность формулы для скорости времени и расстояния можно путём анализа размерности. Если в выражение подставить единицы измерения, то после сокращения должна получиться величина, соответствующая определяемой. S = V * t = (м / с) * с = м (метр). Что и требовалось получить. Аналогично можно проверить и 2 оставшиеся формулы: t = s / v = м / (м/с) = м * с / м = с (секунда) и V = S / t = м / с (метр на секунду).
Действительно, пусть имеется физическое тело, находящееся в каком-то месте. Через некоторое время, неважно по каким причинам, оно переместилось в другую точку, при этом не выходя за пределы установленного пространства. Если тело представить в декартовой плоскости, причём за начало принять координату (0, 0), через время объект изменит своё положение, определяющееся значением (x1, y2). В двухмерном же пространстве это изменение можно описать как переход из точки A в Б.
Значит, чтобы тело достигло второй координаты, ему необходимо затратить время. При этом пройденный путь будет находиться в прямой зависимости от него. Расстояние и время должны связываться третьей величиной, которой как раз и является скорость. То есть параметр, определяющий, за сколько тело сможет преодолеть определённую длину.
Как видно, выражение, связывающее 3 величины, довольно простое. Но оно не учитывает, что скорость может быть непостоянной, поэтому если объект проходит свой путь неравномерно, в выражение подставляют среднее значение. Находится оно как сумма всех отдельных скоростей на неравномерных участках: Vср = ΔS / Δt.
Решение задач
Чтобы уметь решать простые задания в средних классах по математике, связанных с движением, нужно знать всего одну формулу. При этом необходимо пристальное внимание уделять размерности. Все вычисления осуществляются в СИ. Вот некоторые из типовых заданий, используемые при обучении школьников в четвёртом классе средней школы:
Все задачи на движение можно разделить на несколько типов: перемещение навстречу, движение вдогонку, нахождение параметров относительно неподвижного объекта. Но, несмотря на их виды, все они решаются по одинаковому алгоритму, поэтому для удобства можно сделать памятку, указав в ней формулы и размерность величин.
Источник
Математика. 5 класс
Конспект урока
Задачи на движение
Перечень вопросов, рассматриваемых в теме:
Расстояние – это длина от одного пункта до другого.
Большие расстояния, в основном, измеряются в метрах и километрах.
Расстояние обозначается латинской буквой S.
Чтобы найти расстояние, надо скорость умножить на время движения:
Скорость – это расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Скорость обозначается латинской буквой v.
Чтобы найти скорость, нужно расстояние разделить на время движения:
Время – это продолжительность каких-то действий, событий.
Время движения обозначается маленькой латинской буквой t.
Чтобы найти время, нужно расстояние разделить на скорость движения:
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К., Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
2. Потапов М. К., Шевкин А. В. Математика. Книга для учителя. 5 – 6 классы — М.: Просвещение, 2010
1. Чесноков А. С., Нешков К. И. Дидактические материалы по математике 5 кл. – М.: Академика учебник, 2014
2. Бурмистрова Т. А. Математика. Сборник рабочих программ. 5–6 классы // Составитель Бурмистрова Т. А.
3. Потапов М. К. Математика: дидактические материалы. 6 кл. // Потапов М. К., Шевкин А. В. — М.: Просвещение, 2010
Теоретический материал для самостоятельного изучения
Очень часто нам встречаются задачи на нахождение скорости, времени и расстояния. Что же всё это такое? Сейчас нам предстоит в этом разобраться.
Расстояние – это длина от одного пункта до другого. (Например, расстояние от дома до школы 2 километра). В основном большие расстояния измеряются в метрах и километрах. Общепринятое обозначение расстояния – заглавная латинская буква S.
Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда. Скорость обозначается маленькой латинской буквой v.
Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 200 метров. Первый школьник добежал за 50 секунд. Второй за 100 секунд. Кто из ребят бежал быстрее?
Быстрее бежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. Чтобы найти скорость, нужно расстояние разделить на время движения.
Давайте найдём скорость первого школьника. Для этого разделим 200 метров на время движения первого школьника, то есть на 50 секунд:
Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
У нас расстояние дано в метрах, а время в секундах. Значит, скорость измеряется в метрах в секунду:
Скорость движения первого школьника составляет 4 метра в секунду.
Теперь найдём скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника:
200 м : 100 c = 2 (м/с)
Скорость движения первого школьника – 4 (м/с).
Скорость движения второго школьника – 2 (м/с).
Скорость первого школьника больше. Значит, он бежал до спортплощадки быстрее.
Иногда возникает ситуация, когда требуется узнать, за какое время тело преодолеет то или иное расстояние. Время движения обозначается маленькой латинской буквой t.
От дома до спортивной секции 1200 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 600 метров в минуту. За какое время мы доедем до спортивной секции?
Если за одну минуту мы будем проезжать 600 метров, то сколько таких минут нам понадобится для преодоления тысячи двухсот метров? Очевидно, что надо разделить 1200 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 600 метров. Тогда мы получим время, за которое мы доедем до спортивной секции:
Ответ: мы доедем до спортивной секции за 2 минуты.
Скорость, время и расстояние связаны между собой.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:
Мы вышли из дома и направились в магазин. Мы дошли до магазина за 15 минут. Наша скорость была 60 метров в минуту. Какое расстояние мы прошли?
Если за одну минуту мы прошли 60 метров, то сколько таких отрезков по шестьдесят метров мы пройдём за 15 минут? Очевидно, что умножив 60 метров на 15 минут, мы определим расстояние от дома до магазина:
S = v ∙ t = 60 ∙ 15 = 900 (метров)
Ответ: мы прошли 900 метров.
Если известно время и расстояние, то можно найти скорость:
Расстояние от дома до школы 800 метров. Школьник дошёл до этой школы за 8 минут. Какова была его скорость?
Скорость движения школьника – это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 800 метров, то какое расстояние он преодолевал за одну минуту?
Чтобы ответить на этот вопрос, нужно разделить расстояние на время движения школьника:
v = S : t = 800 : 8 = 100 (м/мин)
Ответ: скорость школьника была 100 м/мин.
Если известна скорость и расстояние, то можно найти время:
От дома до спортивной секции 600 метров. Мы должны дойти до неё пешком. Наша скорость будет 120 метров в минуту (120 м/мин). За какое время мы дойдём до спортивной секции?
Если за одну минуту мы будем проходить 120 метров, то сколько таких минут со ста двадцатью метрами будет в шестистах метрах?
Чтобы ответить на этот вопрос, нужно 600 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 120. Тогда мы получим время, за которое мы дойдём до спортивной секции:
t = S : v = 600 : 120 = 5 (минут).
Ответ: мы дойдём до спортивной секции за 5 минут.
Итак, все рассмотренные нами формулы мы можем представить в виде треугольника для лучшего запоминания:
Теперь рассмотрим типы задач на движение.
Задачи на сближение.
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причём скорость первого будет 100 метров в минуту, а второго – 105 метров в минуту, то скорость сближения будет составлять 100 плюс 105, то есть 205 метров в минуту. Значит, каждую минуту расстояние между пешеходами будет уменьшаться на 205 метров.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Из двух пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 13 км/ч, а скорость второго – 15 км/ч. Через 3 часа они встретились. Определите расстояние между населёнными пунктами.
13 км/ч + 15 км/ч = 28 км/ч
Ответ: расстояние между населёнными пунктами 84 км.
Задачи на скорость удаления.
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причём скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4 плюс 6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиваться на 10 километров.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
С причала одновременно в противоположных направлениях отправились теплоход и катер. Скорость теплохода составляла 60 км/ч, скорость катера 130 км/ч. Какое расстояние будет между ними через 2 часа?
Получили скорость удаления равную 190 км/ч. Данная скорость показывает, что за час расстояние между теплоходом и катером будет увеличиваться на 190 километров.
Ответ: через 2 часа расстояние между теплоходом и катером будет составлять 380 километров.
Задачи на движение объектов в одном направлении.
В предыдущих пунктах мы рассматривали задачи, в которых объекты (люди, машины, лодки) двигались либо навстречу друг другу, либо в противоположных направлениях. В первом случае мы находили скорость сближения – в ситуации, когда два объекта двигались навстречу друг другу. Во втором случае мы находили скорость удаления – в ситуации, когда два объекта двигались в противоположных направлениях. Но объекты также могут двигаться в одном направлении, причём с различной скоростью.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 130 км/ч, а скорость автобуса 90 км/ч. Какое расстояние будет между ними через 1 час? Через 3 часа?
130 км/ч − 90 км/ч = 40 км/ч
Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через три часа – 120 км.
Рассмотрим ситуацию, в которой объекты начали своё движение из разных пунктов, но в одном направлении.
Пусть на одной улице имеется дом, школа и аттракцион. Дом находится на одном конце улицы, аттракцион на другом, школа между ними. От дома до школы 900 метров. Два пешехода отправились в аттракцион в одно и то же время. Причём первый пешеход отправился в аттракцион от дома со скоростью 90 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 85 метров в минуту. Какое расстояние будет между пешеходами через 3 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Либо из расстояния от дома до школы (900 м) вычесть расстояние, пройденное первым пешеходом (270 м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (255 м):
Таким образом, через три минуты расстояние между пешеходами будет составлять 885 метров.
В самом начале пути между пешеходами было расстояние 900 м. Через минуту после начала движения расстояние между ними будет составлять 895 метров, поскольку первый пешеход двигается на 5 метров в минуту быстрее второго:
900 + 85 – 90 = 985 – 90 = 895 м
Через три минуты после начала движения расстояние уменьшится на 15 метров и будет составлять 885 метров. Это был наш ответ на первый вопрос задачи:
900 + 255 – 270 = 1155 – 270 = 885 м
Можно сделать вывод, что каждую минуту расстояние между пешеходами будет уменьшаться на 5 метров.
А раз изначальные 900 метров с каждой минутой уменьшаются на одинаковые 5 метров, то мы можем узнать сколько раз 900 метров содержат по 5 метров, тем самым определяя через сколько минут первый пешеход догонит второго:
Ответ: через три минуты расстояние между пешеходами будет составлять 885 метров, первый пешеход догонит второго через 180 минут = 3 часа.
Разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Источник