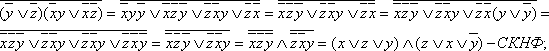Как найти кнф для формулы

Базис
=наиболее изучен и имеет самое широкое
применение на практике.

Определение.
Элементарной
конъюнкцией (дизъюнкцией) называется
конъюнкция (дизъюнкция) переменных или
их отрицаний.

Пример
2.3.1
–

а)
иэлементарные
дизъюнкции;

б)
иэлементарные
конъюнкции;

в)одновременно
является и элементарной дизъюнкцией и
элементарной конъюнкцией.

Определение.
Дизъюнктивной
нормальной формой (ДНФ) называется
дизъюнкция элементарных конъюнкций.
Конъюнктивной нормальной формой (КНФ)
называется конъюнкция элементарных
дизъюнкций.

Пример
2.3.2
–

а)ДНФ;

б)
КНФ.

Теорема.
Любая
формула может быть приведена к ДНФ (КНФ)
(т.е. любая формула эквивалентна некоторой
ДНФ (КНФ)).

Правило
приведения формулы к ДНФ:

а)
все логические операции, присутствующие
в формуле, выразить через
,
используя эквивалентности:

1);

2);

3);

4);

5);

б)
перенести все отрицания к переменным
по закону де Моргана:

;

в)
используя закон дистрибутивности,
преобразовать формулы так, чтобы все
конъюнкции выполнялись раньше дизъюнкций:
.

Пример
2.3.3
— Приведём к ДНФ формулу
.
Для этого

заменим
на,
затем применим закон де Моргана и закон
двойного отрицания:=.

Заметим,
что последняя формула в примере в
некоторых учебниках уже считается ДНФ,
в других же считают, что в элементарных
конъюнкциях и дизъюнкциях каждая
переменная должна встречаться не более
одного раза. Для удаления лишних
переменных применяют следующие
эквивалентности:

а)
(закон
идемпотентности);

б)
(закон
исключённого третьего),(закон
противоречия); в),—
( свойства констант).

Поэтому,
используя закон идемпотентности, в
последнем примере получим ДНФ:
.

Приведение
формулы к КНФ производится так же как
к ДНФ, только вместо пункта в) применяется
пункт в:

в)
используя закон дистрибутивности,
преобразовать формулы так, чтобы все
дизъюнкции выполнялись раньше конъюнкций,
т.е..

Пример
2.3.4
— Приведём к КНФ формулу
.

Заменим
операцию
,
используя формулу:

[закон
де Моргана, двойное

отрицание]
—
КНФ.

ДНФ
и КНФ имеют тот недостаток, что они не
обладают свойством единственности,
т.е. одна и та же формула имеет несколько
ДНФ и КНФ. Этим недостатком не обладают
совершенные нормальные формы.

Определение.
Совершенной
дизъюнктивной нормальной формой
(СДНФ)
называется ДНФ, в которой в каждую
элементарную конъюнкцию каждая переменная
входит ровно один раз, причём, входит
либо сама переменная, либо её отрицание,
и среди элементарных конъюнкций не
должно быть одинаковых; совершенной
конъюнктивной нормальной формой
(СКНФ)
называется КНФ, в которой в каждую
элементарную дизъюнкцию каждая переменная
входит ровно один раз, причём, входит
либо сама переменная, либо её отрицание,
и среди элементарных дизъюнкций не
должно быть одинаковых.

Пример
2.3.5
–

а)
—
СДНФ;

б)
—
СКНФ;

в)
—
не СДНФ, т.к. содержит две одинаковых
элементарных конъюнкции;

г)
—
не СДНФ, т.к. в одной элементарной
конъюнкции содержится и переменная и
её отрицание:.

Теорема.
(Существование
и единственность СДНФ и СКНФ). Всякая
логическая формула единственным образом
(с точностью до порядка следования
элементарных конъюнкций (дизъюнкций))
может быть представлена в СДНФ (СКНФ).

Для
приведения формулы к СДНФ можно
использовать один из двух методов:

І
метод: приводим формулу к ДНФ; если
какая-то элементарная конъюнкция не
содержит некоторой переменной у, то
добавляем её, используя закон расщепления:
;
убираем одинаковые элементарные
конъюнкции, используя закон идемпотентности
.

Пример
2.3.6
— Получим СДНФ функции
,
заданной в ДНФ:

—
СДНФ.

ІІ
метод:
для
данной формулы строим таблицу истинности,
потом применяем правило, основанное на
теореме Шеннона: СДНФ функции
содержит
столько элементарных конъюнкций, сколько
единиц в столбце значений;
каждому единичному набору нулей и единицсоответствует
элементарная конъюнкция всех переменных,
в которойвзято
с отрицанием, еслии
без отрицания, если.

Пример
2.3.7
— Для функции
,
заданной в ДНФ, найти СДНФ. Построим
таблицу истинности:

Т
а б л и ц а 2.3.1

0

0

0

1

1

0

1

0

0

0

0

0

1

1

1

0

1

1

0

1

0

1

0

1

0

0

0

0

0

0

0

1

1

1

0

1

0

0

1

1

1

0

0

0

1

0

0

0

1

1

1

0

1

0

1

0

0

0

1

1

1

1

0

0

0

0

0

0

1

1

1

1

1

0

0

1

0

0

1

1

Функция
принимает значение 1 при следующих
значениях аргументов:
—
это её единичные наборы. По выше
приведённому правилу,—
СДНФ.

Приведение
формулы к СКНФ аналогично приведению
к СДНФ. Также существует два метода:

а)
метод элементарных преобразований;

б)
СКНФ находят по таблице истинности:
СКНФ функции
содержит
столько элементарных дизъюнкций, сколько
нулей в столбце значений;
каждому нулевому набору нулей и единицсоответствует
элементарная дизъюнкция всех переменных,
в которойвзято
с отрицанием, еслии
без отрицания, если.

Пример
2.3.8
— Рассмотрим функцию из предыдущего
примера
.
Приведём её к СКНФ двумя способами:

а)

б)
из таблицы истинности выпишем нулевые
наборы:,
значит, по выше приведённому правилу,—
СКНФ.

Минимизация
булевых функций в классе ДНФ. Карты
Карно

При
решении практических задач часто
возникает проблема минимизации логических
формул, в смысле, например, найти формулу,
содержащую наименьшее число переменных,
или наименьшее число операций, или
наименьшее количество подформул
определённого вида и т.д. К настоящему
времени наиболее изучена задача отыскания
дизъюнктивных форм, минимальных по
числу вхождений переменных. Под вхождением
переменной понимается место, которое
переменная занимает в формуле.

Определение.
Минимальной
ДНФ (МДНФ) называется ДНФ с наименьшим
числом вхождений переменных.

Существует
много способов отыскания МДНФ (метод
Квайна, неопределённых коэффициентов,
с помощью гиперкубов и т.д.). Остановимся
на наиболее простом – с использованием
карт (диаграмм) Карно.

Карта
Карно
–
это таблица, каждая клетка (ячейка)
которой соответствует некоторой
элементарной конъюнкции всех переменных.
Для функции n переменных
существуетвозможных
комбинаций их значений, состоящих из 0
и 1. То есть, например, для n=2 имеемэлементарные
конъюнкции,
которым соответствуют следующие наборы
0 и 1: (1,1), (1,0), (0,1), (0,0); для n=3 ———
(1,1,1), (1,1,0),…,(0,0,0) и т.д. Карты Карно строятся
в виде таблицы размеромтак,
что её столбцы соответствуют значениям
переменных,
строки
—
(или
наоборот); вообще, для одной и той же
функции может быть построено несколько
карт, важно, чтобы соседние ячейки (как
по вертикали, так и по горизонтали)
отличались только значением одной
переменной.

Мы
будем рассматривать в основном функции
двух, трёх и четырёх переменных. Для них
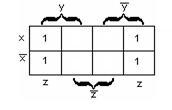
карты Карно имеют следующий вид:

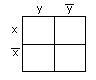
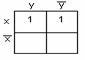
а)
для функции двух переменных х,
у
— рисунок 2.3.1;

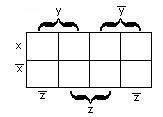
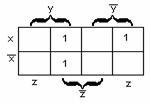
б)для
функции трёх переменных
—
рисунок 2.3.2;

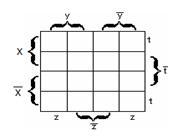
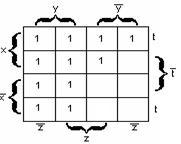
в)
для функции четырёх переменных
—
рисунок 2.3.3.

Рисунок
2.3.1 Рисунок 2.3.2 Рисунок 2.3.3

Для
определения МДНФ булевой функции,
сначала надо найти её СДНФ, затем каждую
элементарную конъюнкцию СДНФ отметить
единицей в соответствующей ячейке карты
Карно.

Пример
2.3.9
— Функции
изаданы
в форме СДНФ. Карта Карно дляна
рисунке 2.3.4; для—
на рисунке 2.3.5.

Рисунок
2.3.4 Рисунок 2.3.5

Заметим,
что, если в картах Карно две, четыре,
восемь (для функции четырёх переменных)
соседних ячеек по вертикали или по
горизонтали содержат 1, то эти ячейки
объединяют в блоки (на картах их отмечают
овалами) и соответствующие этим блокам
дизъюнкции элементарных конъюнкций
можно упростить. Так, в примере 2.3.9 для
функции
имеем
блок из двух ячеек, на рисунке он отмечен
овалом. Этому блоку соответствует
дизъюнкция,
упрощая которую, получим:.
Таким образом, блоку из двух ячеек
функции двух переменных отвечает одна
переменнаях,
а
именно та переменная, которая полностью
«покрывает» этот блок. Формула упростилась
.

Для
функции
также
имеем один блок из двух ячеек, ему
соответствует дизъюнкция элементарных
конъюнкций,
упрощая которую получим,
т.е. блоку из двух ячеек функции трёх
переменных соответствует конъюнкция
двух переменных, «покрывающих» этот
блок. Формула упростилась.

Рассмотрим
ещё несколько примеров.

Пример
2.3.10
—
—
СДНФ функции. Её карта Карно на рисунке
2.3.6. Так какz
находится на обоих концах карты, то её
(карту) можно «скрутить» и считать, что
1 в углах карты образуют блок из четырёх
ячеек. Эти четыре ячейки полностью
«покрывает» переменная z, т.о., МДНФ
функции будет
.

Рисунок
2.3.6 Рисунок 2.3.7 Рисунок 2.3.8

Пример
2.3.11
—
—
СДНФ функции. Её карта Карно на рисунке
2.3.7. На карте есть блок из четырёх ячеек,
который покрывают переменныеи,
поэтому МДНФ функции будет:.

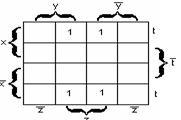
Пример
2.3.12
— Карта Карно для функции

заданной
в СДНФ на рисунке 2.3.8.

На
карте имеем: блок из 8 ячеек покрывает
переменная y;
двум блокам из 4 ячеек соответствуют
элементарные конъюнкции
и,
поэтому МДНФ будет:.

Соседние файлы в предмете Математика

  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Ранее в курсе мы научились определять истинность формул двумя способами:

  • Через таблицу истинности

  • Через доказательство с помощью modus ponens

Эти способы помогают нам доказать общезначимые формулы. Попробуем усложнить задачу и проверить, можно ли доказать общезначимую формулу из аксиом. Чтобы это сделать, нам нужно обратиться к нормальной форме.

В математической логике формулы могут иметь нормальную форму — это значит, что их можно приводить к простейшему виду с помощью эквивалентных преобразований. Другими словами, каждую формулу можно привести к нормальной форме — и тогда нам будет проще доказывать.

В этом уроке мы изучим четыре типа нормальных форм:

  • Дизъюнктивная нормальная форма (ДНФ)

  • Полная дизъюнктивная нормальная форма (ПДНФ)

  • Конъюнктивная нормальная форма (КНФ)

  • Полная конъюнктивная нормальная форма (ПКНФ)

В разных источниках полные формы иногда называют совершенными: тогда используются сокращения СДНФ и СКНФ. Между полными и совершенными формами нет никакой разницы — это один и тот же термин.

Дизъюнктивная нормальная форма (ДНФ)

Дизъюнктивная нормальная форма (ДНФ) — это нормализация логической формулы в булевой математике. Любую логическую формулу можно преобразовать в ДНФ. При этом изначальная формула и ее ДНФ будут эквивалентны.

Другими словами, дизъюнктивная нормальная форма — это дизъюнкция нескольких элементарных конъюнкций. В дизъюнктивной нормальной форме используются операторы AND, OR и NOT.

Дизъюнктивной нормальной формой называется формула, которая эквивалентна данной формуле и состоит из суммы элементарных произведений. Например:

Логическая формула находится в дизъюнктивной нормальной форме только при таких условиях: если существует чередование одной или нескольких конъюнкций одного или нескольких литералов.

Есть еще несколько способов получить дизъюнктивную нормальную форму для логических формул:

  • Метод таблицы истинности

  • Метод деревьев истинности

  • Таблица логических эквивалентностей

Дизъюнктивная нормальная форма помогает автоматически доказывать теоремы. Это один из важных процессов в разработке и верификации интегральных схем, а еще в теории искусственного интеллекта.

Полная дизъюнктивная нормальная форма (ПДНФ)

У ДНФ есть еще и полная версия. Полная дизъюнктивная нормальная форма — это формула ДНФ, в которой все задействованные переменные представлены только один раз в каждом предложении.

Обратите внимание, что у функции может быть только одна ПДНФ. Это упрощает доказательство и снижает вероятность ошибок. Если есть всего один верный ответ, его намного легче проверить.

ПДНФ относится к сумме произведений. Например:

  • — переменные

  • — пример выражения в ПДНФ

  • — основной оператор (сумма)

Чтобы не запутаться, рассмотрим основное отличие между ДНФ и ПДНФ:

  • ДНФ — длина всех переменных в выражении может быть разной

  • ПДНФ — длина всех переменных в выражении должна быть одинаковой

Посмотрим на еще двух примерах:

  • Выражение в ДНФ, которое не считается ПДНФ из-за разной длины переменных:

  • Выражение в ДНФ и ПДНФ одновременно:

Конъюнктивная нормальная форма (КНФ)

В логике есть термин клауза (или клаузула) — это формальная запись доказываемого предложения. Введем это понятие, чтобы отличать объектные высказывания от субъектных.

Для начала вспомним, что в булевой алгебре сложение и умножение — это симметричные операции. Это значит, что всегда можно интерпретировать сложение как умножение, а умножение как сложение. Потому и существует КНФ — форма, симметричная для ДНФ. Как и ДНФ, КНФ полезна для автоматизированного доказательства теорем.

Конъюнктивная нормальная форма (КНФ) — это подход к булевой логике, который выражает формулы в виде конъюнкции клаузул с оператором AND или OR. Каждая клауза соединена конъюнкцией (оператором AND) и при этом должна либо быть литералом, либо содержать дизъюнкцию (оператор OR).

Другими словами, конъюнктивной нормальной формой называется формула, которая эквивалентна данной формуле и состоит из произведения элементарных произведений. Например:

В конъюнктивной нормальной форме высказывания в булевой логике представляют собой конъюнкцию клаузул с клаузулами дизъюнкции. Проще говоря, высказывание — это серия OR, соединенных AND, как в примере ниже:

Полная конъюнктивная нормальная форма (ПКНФ)

ПКНФ относится к продукту сумм. Например:

  • — переменные

  • — пример выражения в ПКНФ

  • — это основной оператор (произведение)

Снова рассмотрим основные отличия между формами:

  • КНФ — длина всех переменных в выражении может быть разной

  • ПКНФ — длина всех переменных в выражении должна быть одинаковой

Например:

  • Выражение в КНФ, но не в ПКНФ:

  • Выражение в КНФ и ПКНФ одновременно:

Источник

Содержание

  • 1 КНФ
  • 2 СКНФ
  • 3 Алгоритм построения СКНФ по таблице истинности
  • 4 Пример построения СКНФ для медианы
    • 4.1 Построение СКНФ для медианы от трех аргументов
    • 4.2 Построение СКНФ для медианы от пяти аргументов
  • 5 Примеры СКНФ для некоторых функций
  • 6 См. также
  • 7 Источники информации

КНФ

Определение:
Простой дизъюнкцией (англ. inclusive disjunction) или дизъюнктом (англ. disjunct) называется дизъюнкция одной или нескольких переменных или их отрицаний, причём каждая переменная встречается не более одного раза.

Простая дизъюнкция

  • полная, если в неё каждая переменная (или её отрицание) входит ровно один раз;
  • монотонная, если она не содержит отрицаний переменных.
Определение:
Конъюнктивная нормальная форма, КНФ (англ. conjunctive normal form, CNF) — нормальная форма, в которой булева функция имеет вид конъюнкции нескольких простых дизъюнктов.

Пример КНФ:

СКНФ

Определение:
Совершенная конъюнктивная нормальная форма, СКНФ (англ. perfect conjunctive normal form, PCNF) — это такая КНФ, которая удовлетворяет условиям:

  • в ней нет одинаковых простых дизъюнкций
  • каждая простая дизъюнкция полная

Пример СКНФ:

Теорема:

Для любой булевой функции , не равной тождественной единице, существует СКНФ, ее задающая.
Доказательство:

Поскольку инверсия функции равна единице на тех наборах, на которых равна нулю, то СДНФ для можно записать следующим образом:
, где обозначает наличие или отсутствие отрицание при

Найдём инверсию левой и правой части выражения:

Применяя дважды к полученному в правой части выражению правило де Моргана, получаем:

Последнее выражение и является СКНФ. Так как СКНФ получена из СДНФ, которая может быть посторена для любой функции, не равной тождественному нулю, то теорема доказана.

Алгоритм построения СКНФ по таблице истинности

  1. В таблице истинности отмечаем те наборы переменных, на которых значение функции равно .
  2. Для каждого отмеченного набора записываем дизъюнкцию всех переменных по следующему правилу: если значение некоторой переменной есть , то в дизъюнкцию включаем саму переменную, иначе ее отрицание.
  3. Все полученные дизъюнкции связываем операциями конъюнкции.

Пример построения СКНФ для медианы

Построение СКНФ для медианы от трех аргументов

1. В таблице истинности отмечаем те наборы переменных, на которых значение функции равно .

x y z
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 1

2. Для каждого отмеченного набора записываем конъюнкцию всех переменных по следующему правилу : если значение некоторой переменной есть , то в дизъюнкцию включаем саму переменную, иначе ее отрицание.

x y z
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 1

3. Все полученные дизъюнкции связываем операциями конъюнкции.

Построение СКНФ для медианы от пяти аргументов

0 0 0 0 0 0
0 0 0 0 1 0
0 0 0 1 0 0
0 0 0 1 1 0
0 0 1 0 0 0
0 0 1 0 1 0
0 0 1 1 0 0
0 0 1 1 1 1
0 1 0 0 0 0
0 1 0 0 1 0
0 1 0 1 0 0
0 1 0 1 1 1
0 1 1 0 0 0
0 1 1 0 1 1
0 1 1 1 0 1
0 1 1 1 1 1
1 0 0 0 0 0
1 0 0 0 1 0
1 0 0 1 0 0
1 0 0 1 1 1
1 0 1 0 0 0
1 0 1 0 1 1
1 0 1 1 0 1
1 0 1 1 1 1
1 1 0 0 0 0
1 1 0 0 1 1
1 1 0 1 0 1
1 1 0 1 1 1
1 1 1 0 0 1
1 1 1 0 1 1
1 1 1 1 0 1
1 1 1 1 1 1

Примеры СКНФ для некоторых функций

Стрелка Пирса:

Исключающее или:

См. также

  • Специальные формы КНФ
  • ДНФ

Источники информации

  • Википедия — СКНФ
  • Е.Л Рабкин, Ю.Б. Фарфоровская — Дискретная математика
Источник

Шаблон:Чистить
Конъюнкти́вная норма́льная фо́рма (КНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид конъюнкции нескольких дизъюнктов.

Например, следующие формулы записаны в КНФ:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {displaystyle A and B}
Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {displaystyle A!}
Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {displaystyle (A or B) and neg A}
Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {displaystyle (A or B or neg C) and (neg D or E or F) and (C or D) and B}

Конъюнктивная нормальная форма удобна для автоматического доказывания теорем.

Приведение булевой формулы к КНФ

Любая булева формула может быть приведена к КНФ. Впрочем, при этом размер булевой формулы может возрасти экспоненциально. Так, например, 2n дизъюнктов потребуется, чтобы записать следующую формулу:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {displaystyle (X_1 and Y_1) or (X_2 and Y_2) or dots or (X_n and Y_n)}

Формальная грамматика, описывающая КНФ

Следующая формальная грамматика описывает все формулы, приведенные к КНФ:

<КНФ> → <дизъюнкт>
<КНФ> → <КНФ> ∧ <дизъюнкт>
<дизъюнкт> → <литерал>
<дизъюнкт> → (<дизъюнкт> ∨ <литерал>)
<литерал> → <терм>
<литерал> → ¬<терм>

где <терм> обозначает произвольную булеву переменную.

Задача выполнимости формулы в КНФ

В теории вычислительной сложности важную роль играет задача выполнимости булевых формул в конъюнктивной нормальной форме. Эта задача NP-полна, и она сводится к задаче 3-SAT, которая в свою очередь сводится ко многим другим NP-полным задачам.

См. также

  • Дизъюнктивная нормальная форма
  • k-конъюнктивная нормальная форма

Шаблон:Нет источников
he:CNF
hu:Konjunktív normálforma
nl:Conjunctieve normaalvorm
pl:Koniunkcyjna postać normalna

Источник

Понравилась статья? Поделить с друзьями:
  • Как исправить кривой гриф на гитаре
  • Как найти тарифы в приложении мегафон
  • Как проволокой найти воду под землей
  • По карте широте точку как найдем
  • Как составить описание герба семьи