Как найти код вещественных чисел

Вещественные числа обычно представляются в виде чисел с плавающей запятой. Числа с плавающей запятой — один из возможных способов представления действительных чисел, который является компромиссом между точностью и диапазоном принимаемых значений, его можно считать аналогом экспоненциальной записи чисел, но только в памяти компьютера.

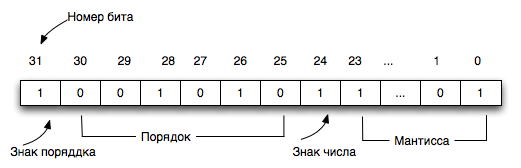
Число с плавающей запятой состоит из набора отдельных двоичных разрядов, условно разделенных на так называемые знак (англ. sign), порядок (англ. exponent) и мантиссу (англ. mantis). В наиболее распространённом формате (стандарт IEEE 754) число с плавающей запятой представляется в виде набора битов, часть из которых кодирует собой мантиссу числа, другая часть — показатель степени, и ещё один бит используется для указания знака числа ( — если число положительное, — если число отрицательное). При этом порядок записывается как целое число в коде со сдвигом, а мантисса — в нормализованном виде, своей дробной частью в двоичной системе счисления. Вот пример такого числа из двоичных разрядов:

Знак
	Порядок	Мантисса
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	14	10	9	0

Знак — один бит, указывающий знак всего числа с плавающей точкой. Порядок и мантисса — целые числа, которые вместе со знаком дают представление числа с плавающей запятой в следующем виде:

, где — знак, — основание, — порядок, а — мантисса.
Десятичное число, записываемое как , где — число в полуинтервале , — степень, в которой стоит множитель ; в нормализированной форме модуль будет являться мантиссой, а — порядком, а будет равно тогда и только тогда, когда принимает отрицательное значение.
Например, в числе

Порядок также иногда называют экспонентой или просто показателем степени.

При этом лишь некоторые из вещественных чисел могут быть представлены в памяти компьютера точным значением, в то время как остальные числа представляются приближёнными значениями.

Более простым вариантом представления вещественных чисел является вариант с фиксированной точкой, когда целая и вещественная части хранятся отдельно. Например, на целую часть отводится всегда бит и на дробную отводится всегда бит. Такой способ в архитектурах процессоров не присутствует. Отдаётся предпочтение числам с плавающей запятой, как компромиссу между диапазоном допустимых значений и точностью.

Нормальная и нормализованная форма

Нормальной формой (англ. normal form) числа с плавающей запятой называется такая форма, в которой мантисса (без учёта знака) в десятичной системе находится на полуинтервале . Такая форма записи имеет недостаток: некоторые числа записываются неоднозначно (например, можно записать в 4 формах — , , , ), поэтому распространена также другая форма записи — нормализованная (англ. normalized), в которой мантисса десятичного числа принимает значения от (включительно) до (не включительно), а мантисса двоичного числа принимает значения от (включительно) до (не включительно). То есть в мантиссе слева от запятой до применения порядка находится ровно один знак. В такой форме любое число (кроме ) записывается единственным образом. Ноль же представить таким образом невозможно, поэтому стандарт предусматривает специальную последовательность битов для задания числа (а заодно и некоторых других полезных чисел, таких как и ).
Так как старший двоичный разряд (целая часть) мантиссы вещественного числа в нормализованном виде всегда равен «», то его можно не записывать, сэкономив таким образом один бит, что и используется в стандарте IEEE 754. В позиционных системах счисления с основанием большим, чем (в троичной, четверичной и др.), этого замечательного свойства нет (ведь целая часть там может быть не только единицей).

Типы чисел с плавающей точкой (по IEEE 754)

Число половинной точности (Binary16, Half precision)

Число́ полови́нной то́чности  — компьютерный формат представления чисел, занимающий в памяти половину машинного слова (в случае 32-битного компьютера — бит или байта). В силу невысокой точности этот формат представления чисел с плавающей запятой обычно используется в видеокартах, где небольшой размер и высокая скорость работы важнее точности вычислений.

Знак
	Порядок	Мантисса
0	0	0	0	0	0	1,	0	0	0	0	0	0	0	0	0	0
	14	10		9	0

Порядок записан со сдвигом . То есть чтобы получить актуально значение порядка нужно вычесть из него сдвиг. Сдвиг можно получить по формуле , где — число бит, отведенное на хранение порядка (в случае числа половинной точности ).

Ограничения точности

• Целые от нуля до передаются как есть.
• Целые от до округляются к ближайшему чётному целому.
• Целые от до округляются до ближайшего целого, делящегося нацело на четыре.
• Целые от до округляются до ближайшего целого, делящегося на восемь.
• Целые от до округляются до ближайшего целого, делящегося на шестнадцать.
• Целые от до округляются до ближайшего целого, делящегося на тридцать два.

Число одинарной точности (Binary32, Single precision, float)

Число́ одина́рной то́чности — компьютерный формат представления чисел, занимающий в памяти одно машинное слово (в случае 32-битного компьютера — бита или байта). Используется для работы с вещественными числами везде, где не нужна очень высокая точность.

Знак
	Порядок (8 бит)	Мантисса (23+1 бита)
0	0	0	0	0	0	0	0	0	1,	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	30	23		22	0

Порядок записан со сдвигом .

Число двойной точности (Binary64, Double precision, double)

Число́ двойно́й то́чности —
компьютерный формат представления чисел, занимающий в памяти два машинных слова (в случае 32-битного компьютера — бита или байт). Часто используется благодаря своей неплохой точности, даже несмотря на двойной расход памяти и сетевого трафика относительно чисел одинарной точности.

Знак
	Порядок (11 бит)	Мантисса (52+1 бит)
0	0	0	0	0	0	0	0	0	0	0	0	1,	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	62	52		51	0

Порядок записан со сдвигом .

Число четверной точности (Binary128, Quadruple precision)

Число́ четверно́й то́чности —
компьютерный формат представления чисел, занимающий в памяти четыре машинных слова (в случае 32-битного компьютера — бит или байт). Используется в случае необходимости крайне высокой точности.

Знак
	Порядок (15 бит)	Мантисса (112+1 бит)
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1,	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	126	112		111

Мантисса (112+1 бит)
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
0

Порядок записан со сдвигом .

Обычно этот формат реализуется программно, случаи аппаратной реализации крайне редки. Также не гарантируется поддержка этого типа в языках программирования, хотя кое-где она и реализована (например, компилятор gcc для архитектуры x86 позволяет использовать тип __float128, являющийся программной реализацией числа с четверной точностью).
В совокупности эти факторы делают Quadruple весьма экзотичным и редко встречающимся форматом чисел с плавающей запятой.

Диапазон значений чисел с плавающей запятой

Диапазон чисел, которые можно записать данным способом, зависит от количества бит, отведённых для представления мантиссы и показателя. Пара значений показателя (когда все разряды нули и когда все разряды единицы) зарезервирована для обеспечения возможности представления специальных чисел. К ним относятся ноль, значения NaN (Not a Number, «не число», получается как результат операций типа деления нуля на ноль) и .

Данная таблица только лишь примерно указывает границы допустимых значений, без учета возрастающей погрешности с ростом абсолютного значения и существования денормализованных чисел.

Название в IEEE 754	Название типа переменной в Си	Диапазон значений	Бит в мантиссе	Бит на переменную
Half precision	—	6,10×10-5..65504	11	16
Single presicion	float	-3,4×1038..3,4×1038	23	32
Double precision	double	-1,7×10308..1,7×10308	53	64
Extended precision	На некоторых архитектурах (например в сопроцессоре Intel) long double	-3,4×104932..3,4×104932	65	80

Особые значения чисел с плавающей точкой

Ноль (со знаком)

Как уже было оговорено выше, в нормализованной форме числа с плавающей точкой невозможно представить ноль. Поэтому для его представления зарезервированы специальные значения мантиссы и порядка — число считается нулём, если все его биты, кроме знакового, равны нулю. При этом в зависимости от значения бита знака ноль может быть как положительным, так и отрицательным.

Знак
	Порядок	Мантисса
0/1	0	0	0	0	0	1,	0	0	0	0	0	0	0	0	0	0	=
	14	10		9	0

Арифметика нуля со знаком

Арифметика отрицательного нуля аналогична таковой для любого отрицательного числа и понятна интуитивно. Вот несколько примеров:

• (если )

• (если )

Неопределенность (NaN)

NaN — это аббревиатура от фразы «not a number«. NaN является результатом арифметических операций, если во время их выполнения произошла ошибка (примеры см. ниже). В IEEE 754 NaN представлен как число, в котором все двоичные разряды порядка — единицы, а мантисса не нулевая.

Знак
	Порядок	Мантисса
0/1	1	1	1	1	1	1,	0/1	0/1	0/1	0/1	0/1	0/1	0/1	0/1	0/1	0/1	=
	14	10		9	0

Любая операция с NaN возвращает NaN. При желании в мантиссу можно записывать информацию, которую программа сможет интерпретировать. Стандартом это не оговорено и мантисса чаще всего игнорируется.

Как можно получить NaN?

• , где

Есть и другие способы получения NaN, подробности можно найти по ссылкам в соответствующем разделе.

По определению NaN ≠ NaN, поэтому, для проверки значения переменной нужно просто сравнить ее с собой.

Бесконечности

В число с плавающей запятой можно записать значение или . Как и нули со знаком, бесконечности позволяют получить хотя бы близкий к правильному результат вычисления в случае переполнения. Согласно стандарту IEEE 754 число с плавающей запятой считается равным бесконечности, если все двоичные разряды его порядка — единицы, а мантисса равна нулю. Знак бесконечности определяется знаковым битом числа.

Знак
	Порядок	Мантисса
0/1	1	1	1	1	1	1,	0	0	0	0	0	0	0	0	0	0	=
	14	10		9	0

Получить бесконечность можно при переполнении и при делении ненулевого числа на ноль. При этом

Денормализованные числа

Денормализованные числа (англ. denormalized/subnormal numbers) — это способ увеличить количество представимых числом с плавающей запятой значений около нуля, дабы повысить точность вычислений. Каждое значение денормализованного числа меньше самого маленького нормализованного («обычного») значения числа с плавающей запятой.
Согласно стандарту, если порядок равен своему минимальному значению (все его биты — нули, а истинное значение порядка равно его сдвигу) и все биты мантиссы равны нулю, то это . Если же мантисса не равна нулю, то это число с порядком, на единицу большим минимального (все биты порядка, кроме младшего — нули) и данной мантиссой, целая часть которой считается равной нулю, а не единице.

То есть число с плавающей запятой, при учете вышесказанного, можно задать следующим образом:

• , если (нормализованное число)

• , если (денормализованное число)

Где — бит знака, — последовательность битов мантиссы, — значение порядка (с учетом сдвига), — минимальное значение порядка, используемое для записи чисел (1 — сдвиг) , — минимальное значение порядка, которое он в принципе может принять (все биты нули, 0 — сдвиг).

Хоть денормализованные числа и позволяют бороться с погрешностями и обрабатывать очень маленькие значения, за эти возможности приходится дорого платить. Ввиду сложности денормализованные числа крайне редко реализуют на аппаратном уровне — вместо этого используются программные реализации, работающие значительно медленнее.

В современных процессорах обработка денормализованных чисел происходит в десятки раз медленнее, чем обработка нормализованных чисел. Ниже приведена часть таблицы из статьи Isaac Dooley, Laxmikant Kale «Quantifying the Interference Caused by Subnormal Floating-Point Values»^[1]

Производитель	Процессор	Замедление (разы)
IBM	PowerPC 970	2,4
AMD	Athlon	6,0
Intel	Pentium 3	15,8
AMD	Athlon 64	21,4
AMD	Opteron64	23,8
Intel	Core Duo	44,2
Intel	P4 Xeon	97,9
Intel	Pentium 4	131,0
Intel	Itanium 2	183,2
Sun	UltraSPARC IV	520,0

В таблице приведены наихудшие результаты тестирования среди всех использованных компиляторов (gcc, icc, xlc) со всеми доступными флагами оптимизации. Исследователи утверждают, что различие среднего случая с худшим незначительно.

Поскольку в стандартных форматах (одинарной и двойной точности) денормализованные числа получаются действительно очень маленькими и практически никак не влияют на результат некоторых вычислений (при этом заметно замедляя их скорость), то иногда они просто игнорируются. При этом используются два простых механизма, получивших называние Flush-to-zero (FTZ) и Denormals-are-zero (DAZ). Первый механизм заставляет операции возвращать ноль, как только становится ясно, что результат будет денормализованным. Второй механизм заставляет операции рассматривать поступающие на вход денормализованные числа как нули.
Ярким примером подобного «отсечения» денормализованных чисел могут послужить видеокарты, в которых резкое падение скорости вычислений в сотню раз недопустимо. Так же, например, в областях, связанных с обработкой звука, нет нужды в очень маленьких числах, поскольку они представляют столь тихий звук, что его не способно воспринять человеческое ухо.

В версии стандарта IEEE 754-2008 денормализованные числа (denormal или denormalized numbers) были переименованы в subnormal numbers, то есть в числа, меньшие «нормальных». Поэтому их иногда еще называют «субнормальными«.

Действия с числами с плавающей запятой

Умножение и деление

Самыми простыми для восприятия арифметическими операциями над числами с плавающей запятой являются умножение и деление. Для того, чтобы умножить два вещественных числа в нормализованной форме необходимо перемножить их мантиссы, сложить порядки, округлить и нормализовать полученное число.

Соответственно, чтобы произвести деление нужно разделить мантиссу делимого на мантиссу делителя и вычесть из порядка делимого порядок делителя. Затем точно так же округлить мантиссу результата и привести его к нормализованной форме.

Сложение и вычитание

Идея метода сложения и вычитания чисел с плавающей точкой заключается в приведении их к одному порядку. Сначала выбирается оптимальный порядок, затем мантиссы обоих чисел представляются в соответствии с новым порядком, затем над ними производится сложение/вычитание, мантисса результата округляется и, если нужно, результат приводится к нормализированной форме. Пример:

Выполним сложение чисел с плавающей точкой и смещенным порядком в 32-х разрядном формате   и .
Переведем   в машинный вид. Для этого сначала переведем его в двоичную систему счисления.
   
  

Нормализуем полученное двоичное число по правилам машинной арифметики.
   

Найдем смещенный порядок. Так как в условии говорится о 32-разрядном представлении, то смещение порядка равно .
          

Число отрицательное, следовательно, в бите знака будет стоять единица.

Итак, первое число в машинном 32-разрядном представлении с плавающей точкой будет иметь вид:
10000111 (жирным шрифтом выделен порядок числа, длина мантиссы — 23 бита).

Переведем второе число в машинный вид, совершая те же действия.

 = ,...  ...  
В качестве мантиссы будут сохранены первые  бита после запятой т.е. .
Очевидно, что порядок со смещением у второго числа будет таким же, как и у первого.

Второе число положительное, следовательно, бит знака будет содержать ноль.

Итак в машинном 32-разрядном представлении второе число будет иметь вид:

10000111
Далее в арифметических операциях будет использоваться число ,=, а не = видимо для упрощения(хотя это не совсем корректно).

Порядки у слагаемых равны, поэтому пропускаем шаг выравнивания порядков и проводим вычитание мантисс по правилам двоичной арифметики. В 
компьютере этим занимается арифметический сопроцессор, встроенный в центральный процессор машины.

,    

Приводим полученный результат к машинному виду. Для этого мы должны внести поправку в порядок — уменьшить его на единицу.
Знак результата —  положительный, следовательно, бит знака содержит ноль.

10000110

Проверим правильность наших вычислений. Переведем результат в десятичное представление.

Найдем реальный порядок результата, вычтя из него значение смещения .

Следовательно, число результата будет иметь вид:
      ,  

Результат наших вычислений верен, так как  -   .

Алгоритм получения представления вещественного числа в памяти ЭВМ

Покажем преобразование действительного числа для представления его в

памяти ЭВМ на примере величины типа Double.

Как видно из таблицы, величина этого типа занимает в памяти байт. На

рисунке ниже показано, как здесь представлены поля мантиссы и порядка (нумерация битов осуществляется справа налево):

Знак	Смещённый порядок	Мантисса
63	62..52	51..0

Можно заметить, что старший бит, отведенный под мантиссу, имеет номер

, т.е. мантисса занимает младшие бита. Черта указывает здесь на

положение двоичной запятой. Перед запятой должен стоять бит целой части

мантиссы, но поскольку она всегда равна , здесь данный бит не требуется и

соответствующий разряд отсутствует в памяти (но он подразумевается).

Значение порядка хранится здесь не как целое число, представленное в

дополнительном коде. Для упрощения вычислений и сравнения действительных

чисел значение порядка в ЭВМ хранится в виде смещенного числа, т.е. к

настоящему значению порядка перед записью его в память прибавляется

смещение. Смещение выбирается так, чтобы минимальному значению порядка

соответствовал нуль. Например, для типа Double порядок занимает бит и

имеет диапазон от до , поэтому смещение равно ₍₎

₍₎. Наконец, бит с номером указывает на знак числа.

Таким образом, из вышесказанного вытекает следующий алгоритм для

получения представления действительного числа в памяти ЭВМ:

1. перевести модуль данного числа в двоичную систему счисления;
2. нормализовать двоичное число, т.е. записать в виде M 2^p, где M —

   мантисса (ее целая часть равна ₍₎) и p — порядок, записанный в

   десятичной системе счисления;

3. прибавить к порядку смещение и перевести смещенный порядок в двоичную

   систему счисления;

4. учитывая знак заданного числа (0 — положительное; 1 — отрицательное),

   выписать его представление в памяти ЭВМ.

Пример. Запишем код числа ,.

1. Двоичная запись модуля этого числа имеет вид .
2. Имеем

   .

3. Получаем смещенный порядок . Далее имеем

   _{() ()}.

4. Окончательно
   

   1	10000000111	0011100001010000000000000000000000000000000000000000
   63	62..52	51..0

Очевидно, что более компактно полученный код стоит записать следующим

образом: C073850000000000₍₁₆₎.

Другой пример иллюстрирует обратный переход от кода действительного

числа к самому числу.

Пример. Пусть дан код 3FEC600000000000₍₁₆₎ или

0	01111111110	1100011000000000000000000000000000000000000000000000
63	62..52	51..0

1. Прежде всего замечаем, что это код положительного числа, поскольку в

   разряде с номером записан нуль. Получим порядок этого числа:

   _{() ()}; .

2. Число имеет вид , или

   ,.

3. Переводом в десятичную систему счисления получаем ,.

См. также

• Представление символов, таблицы кодировок
• Представление целых чисел: прямой код, код со сдвигом, дополнительный код

Примечания

Ссылки

Использованные материалы

На русском

• Википедия — Экспоненциальная запись
• Википедия — Число с плавающей запятой
• Википедия — Отрицательный и положительный ноль
• Хабрахабр — статья пользователя Yruslan «Что нужно знать про арифметику с плавающей запятой»
• Статья Лапшевой Е.Е. «Машинная арифметика с вещественными числами» Статья удалена

На английском

• Wikipedia — NaN
• Wikipedia — Floating point
• Wikipedia — IEEE 754-2008

Что стоит прочесть

• Материалы по стандарту IEEE 754 (англ.)
• Русский перевод стандарта IEEE 754

Кодирование вещественных чисел

Несколько иной
способ применяется для представления
в памяти персонального компьютера
действительных чисел. Рассмотрим
представление величин с плавающей
точкой.

Любое
действительное число можно записать в
стандартном виде M × 10^p,
где 1  M < 10, p —
целое. Например, 120100000 = 1,201 × 10⁸.
Поскольку каждая позиция десятичного
числа отличается от соседней на степень
числа 10, умножение на 10 эквивалентно
сдвигу десятичной запятой на одну
позицию вправо. Аналогично деление на
10 сдвигает десятичную запятую на позицию
влево. Поэтому приведенный выше пример
можно продолжить: 120100000 = 1,201 × 10⁸ =
0,1201 × 10⁹ =
12,01 × 10⁷.
Десятичная запятая «плавает» в
числе и больше не помечает абсолютное
место между целой и дробной частями.

В
приведенной выше записи M называют
мантиссой числа, а p —
его порядком. Для того чтобы сохранить
максимальную точность, вычислительные
машины почти всегда хранят мантиссу в
нормализованном виде, что означает, что
мантисса в данном случае есть число,
лежащее между 1₍₁₀₎ и
2₍₁₀₎ (1  M < 2).
Основание системы счисления здесь, как
уже отмечалось выше, — число 2. Способ
хранения мантиссы с плавающей точкой
подразумевает, что двоичная запятая
находится на фиксированном месте.
Фактически подразумевается, что двоичная
запятая следует после первой двоичной
цифры, т.е. нормализация мантиссы делает
единичным первый бит, помещая тем самым
значение между единицей и двойкой.
Место, отводимое для числа с плавающей
точкой, делится на два поля. Одно поле
содержит знак и значение мантиссы, а
другое содержит знак и значение порядка.

Современный персональный компьютер
позволяет работать со следующими
действительными типами (диапазон
значений указан по абсолютной величине;
в некоторых случаях перечень типов
данных может быть расширен):

Тип	Диапазон	Мантисса	Байты
Real	2,9×10-39..1,7×1038	11-12	6
Single	1,5×10-45..3,4×1038	7-8	4
Double	5,0×10-324..1,7×10308	15-16	8
Extended	3,4×10-4932..1,1×104932	19-20	10

Покажем преобразование
действительного числа для представления
его в памяти ЭВМ на примере величины
типа Double.

Как видно из таблицы, величина это типа
занимает в памяти 8 байт. На рисунке ниже
показано, как здесь представлены поля
мантиссы и порядка (нумерация битов
осуществляется справа налево):

S	Смещенный порядок	Мантисса
63	62..52	51..0

Можно
заметить, что старший бит, отведенный
под мантиссу, имеет номер 51, т.е. мантисса
занимает младшие 52 бита. Черта указывает
здесь на положение двоичной запятой.
Перед запятой должен стоять бит целой
части мантиссы, но поскольку она всегда
равна 1, здесь данный бит не требуется
и соответствующий разряд отсутствует
в памяти (но он подразумевается). Значение
порядка хранится здесь не как целое
число, представленное в дополнительном
коде. Для упрощения вычислений и сравнения
действительных чисел значение порядка
в ЭВМ хранится в виде смещенного
числа,
т.е. к настоящему значению порядка перед
записью его в память прибавляется
смещение. Смещение выбирается так, чтобы
минимальному значению порядка
соответствовал нуль. Например, для типа
Double порядок занимает 11 бит и имеет
диапазон от 2^-1023 до
2¹⁰²³,
поэтому смещение равно 1023₍₁₀₎ =
1111111111₍₂₎.
Наконец, бит с номером 63 указывает на
знак числа.

Таким
образом, из вышесказанного вытекает
следующий алгоритм для
получения представления действительного
числа в памяти ЭВМ:

1. перевести модуль
   данного числа в двоичную систему
   счисления;

2. нормализовать
   двоичное число, т.е. записать в виде M × 2^p,
   где M —
   мантисса (ее целая часть равна 1₍₂₎)
   и p —
   порядок, записанный в десятичной системе
   счисления;

3. прибавить к порядку
   смещение и перевести смещенный порядок
   в двоичную систему счисления;

4. учитывая знак
   заданного числа (0 — положительное;
   1 — отрицательное), выписать его
   представление в памяти ЭВМ.

Пример. Запишем
код числа -312,3125.

1. Двоичная запись
   модуля этого числа имеет вид 100111000,0101.

2. Имеем
   100111000,0101 = 1,001110000101 × 2⁸.

3. Получаем
   смещенный порядок 8 + 1023 = 1031. Далее имеем
   1031₍₁₀₎ =
   10000000111₍₂₎.

4. Окончательно

1	10000000111	0011100001010000000000000000000000000000000000000000
63	62..52	51..0

Очевидно,
что более компактно полученный код
стоит записать следующим образом:
C073850000000000₍₁₆₎.

Другой пример
иллюстрирует обратный переход от кода
действительного числа к самому числу.

Пример. Пусть
дан код 3FEC600000000000₍₁₆₎ или

0	01111111110	1100011000000000000000000000000000000000000000000000
63	62..52	51..0

1. Прежде
   всего замечаем, что это код положительного
   числа, поскольку в разряде с номером
   63 записан нуль. Получим порядок этого
   числа: 01111111110₍₂₎ =
   1022₍₁₀₎;
   1022 — 1023 = -1.

2. Число
   имеет вид 1,1100011 × 2^-1 или
   0,11100011.

3. Переводом в
   десятичную систему счисления получаем
   0,88671875.

2.

В настоящее время
объемы информации удваиваются каждые
три года. Общество переживает информационный
бум. Любая организация, так же как и
каждый человек в отдельности, может
существовать, только обмениваясь
информацией. В нынешних экономических
условиях, когда очень быстро меняются
и ситуация, и законодательство, предприятия
могут выжить только в том случае, если
они вовремя узнают, что, где, когда и
почем. Другими словами, кто владеет
информацией, тот владеет ситуацией.

Носителем информации
выступает документ.

При создании
документов используют различные способы
документирования в зависимости от
содержания информации: звукозапись
(фонодокумент), фотографию (фотодокумент),
запись изображений и звуков (аудиовизуальный
документ) и т. д. Документ, созданный
юридическим или физическим лицом,
оформленный и удостоверенный в
установленном порядке, называется
официальным документом. Документы
выполняют ряд важных функций:

информационную:
являются носителем и источником
информации;

управленческую:
позволяют организовывать, регулировать,
контролировать, анализировать
производственные процессы;

правовую: служат
юридической основой производственной
деятельности, подтверждают факты,
удостоверяют сведения и показатели;

коммуникативную:
помогают организовывать обмен информацией
и общение между различными объектами;

учетную: накапливают
сведения за определенные периоды времени
и позволяют их анализировать, выявляя
тенденции и закономерности;

социальную: отражают
социально-экономическую, политическую,
общественную и другие сферы жизни
государства и его граждан;

культурную: являются
памятником культуры данной эпохи,
показывают ее специфику, колорит, нравы,
обычаи, традиции;

историческую:
являются источником знаний о событиях
и деятелях различных эпох, полнее и
конкретнее других исторических памятников
раскрывают исторические события,
подтверждают и дополняют факты, помогают
восстанавливать историческое прошлое
стран и народов.

Система документации
– это совокупность документов,
взаимосвязанных по признакам происхождения,
назначения, вида, сферы деятельности,
единых требований к их оформлению.[4, с.
7] Все создаваемые управленческие
документы “обслуживают” определенные
управленческие функции, например:
планирование, бухгалтерский учет,
финансирование, отчетность, оперативное
управление, обеспечение кадрами и т. п.
Реквизит документа — обязательный
элемент оформления официального
документа.[4, с. 8] Различные документы
состоят из разного набора реквизитов.
Число реквизитов определяется целями
создания документа, его назначением,
требованиями к содержанию и форме
данного документа. Для многих документов
число реквизитов строго ограничено.
Для ряда документов число и состав
реквизитов установлены законодательными
и нормативными актами. Но в любом случае,
как следует из определения, информация,
зафиксированная на материальном
носителе, должна быть обязательно
оформлена путем проставления необходимых
реквизитов. Только тогда она становится
документом.

В документоведении
документ рассматривается как результат
закрепления (отображения) фактов,
событий, явлений объективной
действительности и мыслительной
деятельности человека любым удобным
способом на специальном материале.

Документы,
зафиксировав (отобразив) информацию,
тем самым обеспечивают ее сохранение
и накопление, возможность передачи
другому лицу, многократное использование,
повторное и неоднократное возвращение
к ней во времени. Они затрагивают
различные сферы деятельности человека
и разделяются на:

текстовые

графические

традиционные
(рукописные, машинописные) и на машинных
носителях

научные

технические

личные и официальные
и др.

Вместе с тем
определение понятия «документ» в
различных науках имеет существенные
отличия. Это зависит, во-первых, от более
или, напротив, менее широкого толкования
понятия информации и, во-вторых, от
выдвижения на первый план какой-либо
одной составляющей документа, от
акцентирования внимания на каком-либо
отдельном его функциональном аспекте.
В информатике, например, документ нередко
определяется как «материальный
объект, содержащий информацию в
закреплённом виде». В результате под
это определение подпадает необъятное
множество объектов, так как в природе
нет материальных объектов, которые не
содержали бы какую-либо информацию. В
документалистике — одной из наук об
информации — под документом понимается
«любая семантическая информация,
выраженная на любом языке и зафиксированная
любым способом на любом носителе с целью
её обращения в динамической информационной
системе». Это определение значительно
сужает понятие документа, но, тем не
менее, включает в него одновременно и
книги, и журналы, и газеты, и служебные
документы и т.п.

Для общественных
наук, в зависимости от их предмета, целей
и задач, в определении понятия документа
характерно выделение каких-то отдельных
его сторон. Так, в юридических науках
акцентируется внимание на правовом
аспекте. В результате документ фигурирует
преимущественно как средство
документирования и доказательства
правовых отношений. В сфере управления
документ исследуется главным образом
как средство фиксации и передачи
управленческих решений. В исторической
науке документы рассматриваются, прежде
всего, как исторические источники, т.е.
носители ретроспективной информации.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Кодирование и обработка в компьютере вещественных чисел

Вернемся к обсуждению того обстоятельства, что в компьютере для записи числа в любой форме представления отводится конечное число разрядов. Для целых чисел это обстоятельство привело к появлению понятий наибольшего целого числа. Однако для каждого целого числа, не превышающего по модулю наибольшего, имеется ровно одно представление в машинном коде и, если не происходит переполнения, результат выполнения операции над целыми числами будет точным, поскольку дискретные множества исходных чисел однозначно отображаются на дискретное множество результатов.

Ситуация радикальным образом меняется при представлении и обработке вещественных чисел. На математической числовой оси вещественные числа образуют непрерывное множество (континуум), т.е. два числа могут находиться сколь угодно близко друг к другу, и на любом отрезке содержится бесконечно много значений чисел. В машинном представлении количество возможных значений чисел конечно; для двоичной системы счисления оно определяется как %%2^k%%, где %%k%% — количество двоичных разрядов в представлении мантиссы. Т.е. вещественные числа в компьютере заменяются их кодами, которые образуют конечное дискретное множество; каждый код оказывается представителем целого интервала значений континуума.

Из данного обстоятельства вытекают ряд следствий:

Следствие 1 состоит в том, что строгие отношения между числами континуума превращаются в нестрогие для их компьютерных представителей, т.е.

• Если %%x^{(1)}>x^{(2)}%%, то %%X^{(1)}geqslant X^{(2)}%%
• Если %%x^{(1)}=x^{(2)}%%, то %%X^{(1)}= X^{(2)}%%
• Если %%x^{(1)}<x^{(2)}%%, то %%X^{(1)}leqslant X^{(2)}%%

Следствие 2. Поскольку код вещественного числа в компьютере является приблизительным представителем многих чисел из интервала, то и результаты вычислений также будут заведомо неточными, содержащими неизбежную погрешность. В этом состоит главная особенность обработки вещественных чисел в компьютере — она всегда ведется с погрешностью (кстати, оценка этой погрешности — самостоятельная и непростая задача).

Следствие 3. Наряду с понятием наибольшего вещественного числа (из-за ограниченности разрядной сетки) появляется понятие наименьшего числа или машинного нуля. Например, в типе Real любое десятичное число, по модулю меньшее 2,3∙10-39 оказывается машинным нулем, т.е. считается равным 0 при сохранении и в операциях с ним. Таким образом, математическое понятие «0» как точное значение числа в компьютерном представлении заменяется понятием «машинный нуль» как значение числа меньшее некоторой определенной величины.

Как уже было сказано, основной формой представления кодов вещественных чисел в компьютере является двоичная нормализованная. При этом записываться и храниться в памяти компьютера должны все составляющие нормализованной формы (знак числа, мантисса, знак порядка и порядок), что требует нескольких ячеек памяти. Например, числа типа Real («вещественный») из языка java размещаются в 6 байтах, т.е. 48 двоичных разрядах. Непосредственное распределение компонентов нормализованного числа по разрядам определяется конструктивными особенностями компьютера и программным обеспечением. Ниже приведен пример размещения числа в двух ячейках памяти (32 разряда):

Поскольку значение мантиссы лежит в интервале %%0,12 ≤ М_2 < 1%%, ноль в разряде целых и разделитель десятичных разрядов в представление не включается, т.е. мантисса содержит только цифры дробной части. Более того, можно не сохранять и первую значащую цифру мантиссы, поскольку она всегда 1 (но, естественно, восстанавливать ее при вычислениях) — это дает возможность хранить дополнительный «скрытый» разряд, т.е. несколько повысить точность обработки. В ходе выполнения арифметических операций, как указывалось ранее, производится нормализация промежуточных и конечного значений, состоящая в сдвиге мантиссы вправо или влево с одновременным изменением порядка, что эквивалентно смещению разделителя десятичных разрядов — именно по этой причине такая форма представления числа получила название «с плавающей запятой». Как и в случае целых чисел, для кодов вещественных чисел существует понятие переполнение, однако возникает оно не после заполнения разрядной сетки мантиссы — это приводит лишь к нормализации числа, а при заполнении всех разрядов порядка. Для представленного выше примера размещения числа в 32-х битах, очевидно,

%%|x_2|^{max}=0,111111 111111 111111 111111_2 cdot 2^{11111} approx 2.147_{10}cdot 10^9%%

При этом точность обработки составит 7 десятичных разрядов. При %%|Х_2| > |X_2|^{max}%% возникнет переполнение, т.е. операция станет некорректной.

Пример. Установить распределение разрядов двоичного представления числа типа Real, если для его записи отводится 48 бит, а максимальное значение десятичного порядка 38. Какова точность обработки таких чисел?

• 2 бита расходуется на запись знака числа и порядка;
• %%k_2 = 3.322cdot k_{10}%%; поскольку %%k_{10} = 38%%, очевидно, максимальный показатель порядка двоичного числа %%k_2 = 3.322 cdot 38 = 126_{10}%%, что требует в двоичном представлении, согласно формуле Хартли, 7 бит;
• под запись мантиссы отводится %%48 — 2 — 7 = 39%% бит;
• с учетом скрытого разряда точность обработки составит %%(39 + 1)/3,322 ≈ 12%% десятичных разрядов.

Изначальной причиной возникновения погрешности обработки кодов вещественных чисел является ограниченность разрядной сетки при их представлении и, следовательно, наличие погрешности неизбежно. Однако ее величина зависит от количества имеющихся разрядов и, в частности, уменьшить погрешность можно за счет расширения разрядной сетки, т.е. выделения большего количества ячеек памяти для записи числа.

Несколько вариантов представления вещественных чисел в языках программирования высокого уровня используется как одно из средств оптимизации программы. Повышение точности вычислений требует больших ресурсов памяти компьютера; одновременно с этим возрастает и время вычислений. Таким образом, при составлении программы для практической задачи решается проблема нахождения компромисса между точностью результата и временем обработки.

В процессе выполнения арифметических действий с нормализованными числами отдельно обрабатываются мантиссы и порядки. Поскольку операции над кодами вещественных чисел в компьютере обладают некоторой спецификой по сравнению с обычными арифметическими, будем обозначать их следующим образом: %%⊕%% — сложение (вычитание), %%⊗%% — умножение, %%Ø%% — деление.

Сложение нормализованных чисел.

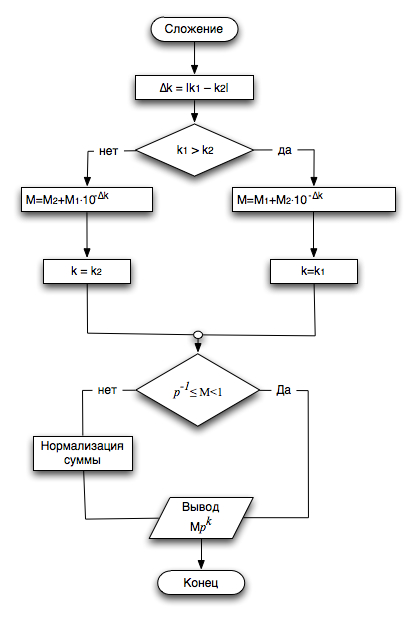
Пусть имеются два числа %%Х_1 = М_1 cdot p^{k_1}%% и %%Х_2 = М_2 cdot р^{k_2}%% (здесь индексы у мантиссы и порядка означают не систему счисления, а служат номерами чисел). Сложение должно начинаться с выявления большего из %%k_1%% и %%k_2%%, нахождения модуля их разности %%∆k = |k_1 – k_2|%% и сдвига вправо на %%∆k%% разрядов мантиссы того числа, у которого k оказался меньше. После этого выполняется сложение мантисс, порядку результата присваивается значение большего из имеющихся и при необходимости производится нормализация результата. Алгоритм сложения нормализованных чисел представлен в виде блок-схемы на рисунке ниже. При сдвиге вправо мантиссы меньшего числа происходит потеря %%∆k%% младших значащих цифр, что приводит к появлению погрешности сложения.

Рассмотрим действие алгоритма на примере сложения десятичных чисел в ограниченной разрядной сетке.

Пример. Найти сумму %%X_1 = 0,87654cdot 10^1%%, а %%Х_2 = 0,94567 cdot 10^2%%, если для записи мантиссы отводится 5 разрядов.

Согласно алгоритму %%∆k = 1%% и %%k_1 < k_2%%. Следовательно, %%k = k_2 = 2%%, а мантисса числа %%X_1%% должна быть сдвинута на 1 разряд вправо (при этом из-за ограниченности разрядной сетки пропадет цифра 4). Новая мантисса получается суммированием %%М = 0,94567 + 0,08765 = 1,03332%%; поскольку она выходит за допустимый интервал представления мантисс, необходимо его нормализовать %%М’ = 0,10333%% (при этом теряется цифра 2 в младшем разряде); %%k’ = k + 1 = 3%%. Окончательно получаем: %%X = — 0,10333 cdot 10^3%%. Точный результат суммирования оказался бы 103,3324.

Следствием существования погрешности сложения (и, в равной мере, вычитания) кодов вещественных чисел оказывается то, что такое суммирование не обладает ассоциативностью, т.е. в общем случае

%%(x_1oplus x_2)oplus x_3 not = x_1oplus (x_2oplus x_3) %%

Вычитание нормализованных чисел, как и чисел целых, не является самостоятельной операцией и сводится к сложению с дополнительным кодом числа.

Умножение нормализованных чисел %%Х_1⊗Х_2%% производится в соответствии с правилами: если по-прежнему %%X_1 = M_1 cdot р^{k_1}%% и %%Х_2 = m_2 cdot p^{k_2}%%, то, очевидно, мантисса произведения %%m = m_1 cdot m_2%%, а порядок %%k = k_1 + k_2%%; при необходимости полученное число нормализуется.

Операция деления, проводимая как над целыми, так и вещественными числами, приводит в общем случае к появлению вещественного числа, поэтому целые числа предварительно преобразуются в вещественный тип, т.е. переводятся в нормализованную форму. Очевидно, при делении %%Х_1∅Х_2%% мантисса частного %%m = frac{М_1}{М_2}%%, а порядок %%k = k_1 — k_2%%. При этом непосредственно операция деления сводится к сдвигу делителя вправо и последовательному вычитанию его из делителя (т.е. сложения с дополнительным кодом вычитаемого). Как и в предыдущих операциях, результат деления при необходимости нормализуется.

В операциях умножения нормализованных чисел в компьютере возможны ситуации, когда не будут в точности выполняться сочетательный и распределительный законы, т.е.

%%(x_1oplus x_2)oplus x_3 not = x_1oplus (x_2oplus x_3) %% и %%(x_1oplus x_2)oplus x_3 not = x_1oplus x_2oplus x_3 %%

Время выполнения операций с кодами вещественных чисел в форме с плавающей запятой гораздо больше, нежели с числами целыми или с фиксированной запятой. По этой причине для ускорения обработки на компьютерах IBM с процессорами Intel 80286 и 80386 ставились так называемые «математические сопроцессоры»; в современных компьютерах команды (точнее, микропрограммы, поскольку они содержат последовательность действий) обработки вещественных чисел включены в перечень команд центрального процессора.

Заканчивая рассмотрение порядка обработки чисел в компьютере, хотелось бы сделать ряд общих замечаний:

1. В компьютерах арифметические устройства выполняют действия не с самими двоичными числами по правилам двоичной арифметики, а с их двоичными кодами (представлениями) по правилам арифметики двоичных кодов.
2. Причиной отличий правил арифметики двоичных кодов от правил обычной арифметики является ограниченность разрядной сетки, применяемой для записи чисел в компьютере. По этой же причине отличаются понятия «ноль» и «машинный ноль», «бесконечность» — «максимальное число», а также становится возможной ситуация переполнения, что требует ее постоянного отслеживания.
3. Применение при вычислениях формы представления чисел с плавающей запятой обеспечивает единообразие при их записи и обработке, и, что важно, в результате автоматического масштабирования числа на каждом этапе его обработки сокращается погрешность вычислений.
4. Различие правил обработки целых и нормализованных чисел приводит к необходимости точного описания типов переменных перед их использованием в программах. Вторая причина описания типов состоит в оптимизации расходования памяти компьютера, поскольку числа разных типов требуют для хранения различных ресурсов памяти.

Кодирование вещественных чисел. Нормализованное представление числа

В компьютерной технике вещественными называются числа, имеющие дробную часть.

Дробные числа могут содержать большой набор цифр. Например: 0.0000345 или 10900000 (т.е очень большие или очень маленькие числа). Для удобства вещественные числа приводят к виду так называемого нормализованного представления числа. Заключается такое представление в том, что число записывается в виде произведения на основание системы счисления, возведенное в ту или иную степень. Например, предыдущие два числа в нормализованном виде будут выглядеть так: 0.345 * 10^-4 и 0.109 * 10⁸. Здесь числа 0.345 и 0.109 – мантиссы вещественных чисел, 10 – основание системы счисления, а -4 и 8 – порядки. При этом запятая (точка), разделяющая дробную и целую части ставится перед первой значащей цифрой (отличной от 0).

Нормализованная форма числа является наиболее удобной для представления дробных чисел в компьютере.

Понятно, что нормализированное представление используется не только для десятичной системы счисления. Вот примеры нормализованных записей дробных чисел в двоичной системе счисления:

101.11 = 0.10111 * 2¹¹
0.001 = 0.1 * 2^-10

Здесь степени 11 и 10 – это двоичная форма десятичных чисел 3 и 2.

Нормализованная форма представления числа – это одна из форм множества вариантов экспоненциальной формы записи числа.

Пусть слово состоит из 2 байт, два слова – это 4 байта или 32 бита.

Нормализированное число одинарной точности, представленное в формате с плавающей точкой, записывается в память следующим образом: знак числа – в бите 15 первого слова (0 – для положительных и 1 – для отрицательных чисел); порядок размещается в битах 7-14 первого слова, а мантисса занимает остальные 23 бита в двух словах (с 0 по 6 бит первого слова и все биты второго слова). Нормализированное число двойной точности записывается в четыре слова памяти и отличается от представления чисел с одинарной точностью только тем, что продолжение мантиссы размещается в следующих за первым словом трех последовательных словах памяти, а всего под мантиссу в этом случае отводится 55 бит.

Порядок числа, представленного в формате с плавающей точкой, изменяется в диапазоне от -128 до +127 и запоминается увеличенным на 128. Такой способ представления порядка называется смещенным.

Следует иметь в виду, что, хотя для мантиссы отведено 23 разряда для чисел одинарной точности и 55 разрядов – для чисел двойной точности, в операциях участвует 24 и 56 разрядов соответственно, т.к. старший разряд мантиссы нормализированного числа не хранится, т.е. имеет место так называемый скрытый разряд. Однако при аппаратном выполнении операций этот разряд автоматически восстанавливается и учитывается. Порядок числа также учитывает скрытый старший разряд мантиссы.

Нормализованная мантисса в двоичной системе счисления всегда представляется десятичным числом m, лежащим в диапазоне 0,5 <= m < 1.

Пример представления числа в формате с плавающей точкой:

0.1₁₀ = 0.000(1100)₂ = 0.(1100)₂*2^-3
-3₁₀ = (-3 + 128)₁₀ = 01111101_2.

Если мантисса представлена бесконечной периодической дробью, то последний учитываемый разряд мантиссы округляется.

-49.5₁₀ = -110001.100₂ = -0.1100011₂*2⁶
6₁₀ = (6 + 128)₁₀ = 10000110₂.

При выполнении арифметических операций над числами, представленными в формате с плавающей точкой, надо отдельно выполнять их для порядков и мантисс. При алгебраическом сложении чисел надо сначала уравнять порядки слагаемых. При умножении порядки надо складывать, а мантиссы — перемножать. При делении из порядка делимого вычитают порядок делителя, а над мантиссами совершают обычную операцию деления. После выполнения операций, если это необходимо, проводят нормализацию результата, что влечет изменение порядков, т.к. каждый сдвиг на один разряд влево соответствует уменьшению порядка на единицу, а сдвиг вправо увеличению на единицу. Введение термина «плавающая точка» как раз и объясняется тем, что двоичный порядок, определяющий фактическое положение точки в изображении числа, корректируется после выполнения каждой арифметической операции, т.е. точка в изображении числа «плавает» (изменяется ее положение) по мере изменения данной величины. А в изображении чисел, представленных в формате с фиксированной точкой, она жестко зафиксирована в определенном месте.

Арифметические операции с числами, представленными в формате с плавающей точкой, намного сложнее таких же операций для чисел, представленных в формате с фиксированной точкой. Но зато плавающая точка позволяет производить операции масштабирования автоматически в самой машине и избавляет от накопления абсолютной погрешности при вычислениях (хотя не избавляет от накопления относительной погрешности).

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Кодирование вещественных чисел
  Составила Соколова Е.В.
  Учитель информатики МБОУ СОШ № 1
  г.Зубцов Тверская обл.

• 

  2 слайд

  Для представления вещественных чисел (конечных и бесконечных десятичных дробей) используют формат с плавающей точкой (запятой).
  Форма с плавающей точкой использует представление вещественного числа R в виде произведения мантиссы m на основание системы счисления р в некоторой целой степени n, которую называют порядком:

  R = m * рn

  m – мантисса,
  n – порядок,
  p – основание системы
  26.12.2020
  2
  Кодирование вещественных чисел

• 

  3 слайд

  Например, число 35,324 можно записать в таком виде: 0.35324х102
  Здесь m=0.35324 — мантисса,
  n=2 — порядок
  Порядок указывает, на какое количество позиций и в каком направлении должна «переплыть», т.е. сместиться десятичная точка в мантиссе. Отсюда название «плавающая точка».
  Однако справедливы и следующие равенства:
  35,324 = 3,5324*101 = 0,0035324*104 = 3532,4*102 и т.п.
  26.12.2020
  3
  Кодирование вещественных чисел

• 

  4 слайд

  Получается, что представление числа в форме с плавающей точкой неоднозначно?
  Чтобы не было неоднозначности, в ЭВМ используют
  нормализованное представление числа в форме с плавающей точкой

  26.12.2020
  4
  Кодирование вещественных чисел

• 

  5 слайд

  Мантисса в нормализованном представлении должна удовлетворять условию:
  0,1p ≤ m < 1p

  Иначе говоря, мантисса меньше единицы и первая значащая цифра — не ноль. Значит для рассмотренного числа нормализованным представлением будет:

  35,324=0.35324 * 102
  26.12.2020
  5
  Кодирование вещественных чисел

• 

  6 слайд

  Машинный
  порядок
  Пусть в памяти компьютера вещественное число представляется в форме с плавающей точкой в двоичной системе счисления (р=2) и занимает ячейку размером 4 байта. В ячейке должна содержаться следующая информация о числе: знак числа, порядок и значащие цифры мантиссы. Вот как эта информация располагается в ячейке:
  26.12.2020
  6
  Кодирование вещественных чисел

• 

  7 слайд

  Машинный
  порядок

  В старшем бите 1-го байта хранится знак числа. В этом разряде 0 обозначает плюс, 1 — минус
  Оставшиеся 7 бит первого байта содержат машинный порядок
  В следующих трех байтах хранятся значащие цифры мантиссы
  26.12.2020
  7
  Кодирование вещественных чисел

• 

  8 слайд

  Что такое машинный порядок?
  В семи двоичных разрядах помещаются двоичные числа в диапазоне от 0000000 до 1111111. В десятичной системе это соответствует диапазону от 0 до 127. Всего 128 значений. Знак порядка в ячейке не хранится. Но порядок, очевидно, может быть как положительным так и отрицательным. Разумно эти 128 значений разделить поровну между положительными и отрицательными значениями порядка.
  26.12.2020
  8
  Кодирование вещественных чисел

• 

  9 слайд

  В таком случае между машинным порядком и истинным (назовем его математическим) устанавливается следующее соответствие:
  Если обозначить машинный порядок Мр, а математический — р, то связь между ними выразится такой формулой:

  Мр = р + 64
  26.12.2020
  9
  Кодирование вещественных чисел

• 

  10 слайд

  Итак, машинный порядок смещён относительно математического на 64 единицы и имеет только положительные значения. При выполнении вычислений с плавающей точкой процессор это смещение учитывает
  В двоичной системе счисления смещение:
  Мр2 = р2+100 00002
  26.12.2020
  10
  Кодирование вещественных чисел

• 

  11 слайд

  Теперь мы можем записать внутреннее представление числа 35,324 в форме с плавающей точкой

  1) Переведем его в двоичную систему счисления с 24 значащими цифрами

  35,324= 100011,0101001011110001102
  26.12.2020
  11
  Кодирование вещественных чисел

• 

  12 слайд

  2) Запишем в форме нормализованного двоичного числа с плавающей точкой:

  0,100011010100101111000110*10110
  Здесь мантисса, основание системы счисления (210=102) и порядок (610=1102)записаны в двоичной системе
  26.12.2020
  12
  Кодирование вещественных чисел

• 

  13 слайд

  3) Вычислим машинный порядок

  Мр2 = 110 + 100 0000 = 100 0110
  4) Запишем представление числа в ячейке памяти
  0
  1
  0
  0
  0
  1
  1
  0
  1
  0
  0
  0
  1
  1
  0
  1
  0
  1
  0
  0
  1
  1
  0
  1
  1
  1
  0
  0
  0
  1
  1
  0
  порядок
  мантисса
  Знак числа
  26.12.2020
  13
  Кодирование вещественных чисел

• 

  14 слайд

  Число в форме с плавающей точкой занимает в памяти компьютера 4 байта (число обычной точности) или 8 байт (число двойной точности).
  Мы рассмотрели пример представления числа 35,324 обычной точности

  26.12.2020
  14
  Кодирование вещественных чисел

• 

  15 слайд

  Для того, чтобы получить внутреннее представление отрицательного числа
  -35,324, достаточно в полученном выше коде заменить в разряде знака числа 0 на 1
  1
  1
  0
  0
  0
  1
  1
  0
  1
  0
  0
  0
  1
  1
  0
  1
  0
  1
  0
  0
  1
  1
  0
  1
  1
  1
  0
  0
  0
  1
  1
  0
  26.12.2020
  15
  Кодирование вещественных чисел

• 

  16 слайд

  Представьте двоичное число -100,12 в четырёхбайтовом формате. Представьте число сначала в форме с плавающей запятой.
  Задание:
  26.12.2020
  16
  Кодирование вещественных чисел

• 

  17 слайд

  -100,12= -0,1001*211
  Мантисса -0,1001
  Порядок 11
  Машинный порядок 11+100 0000=1000011

  Решение:
  1
  1
  0
  0
  0
  1
  0
  1
  1
  0
  0
  1
  0
  0
  0
  0
  0
  0
  0
  0
  0
  0
  0
  0
  0
  0
  0
  0
  0
  0
  0
  0
  26.12.2020
  17
  Кодирование вещественных чисел

• 

  18 слайд

  Задания для самостоятельного выполнения

  Сравните числа:
  а) 318,4785∙109 и 3,184785∙1011
  б) 218,4785∙10-3 и 1847,85∙10-4

  2. Запишите числа в естественной форме:
  а) 0,1100000∙2100
  б) 0,1001111∙2111
  26.12.2020
  18
  Кодирование вещественных чисел

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 263 582 материала в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Вам будут интересны эти курсы:

• Курс профессиональной переподготовки «Клиническая психология: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Введение в сетевые технологии»

• Курс повышения квалификации «Специфика преподавания конституционного права с учетом реализации ФГОС»

• Курс повышения квалификации «История и философия науки в условиях реализации ФГОС ВО»

• Курс повышения квалификации «Управление финансами: как уйти от банкротства»

• Курс повышения квалификации «Страхование и актуарные расчеты»

• Курс повышения квалификации «Основы менеджмента в туризме»

• Курс профессиональной переподготовки «Деятельность по хранению музейных предметов и музейных коллекций в музеях всех видов»

• Курс профессиональной переподготовки «Политология: взаимодействие с органами государственной власти и управления, негосударственными и международными организациями»

• Курс профессиональной переподготовки «Методика организации, руководства и координации музейной деятельности»

• Курс профессиональной переподготовки «Организация деятельности по водоотведению и очистке сточных вод»

• Курс профессиональной переподготовки «Осуществление и координация продаж»

• Курс профессиональной переподготовки «Управление качеством»