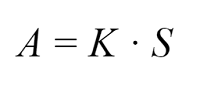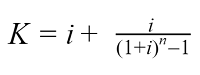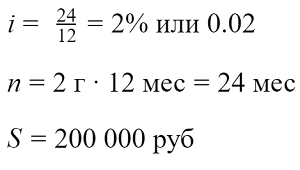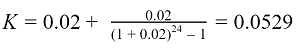Тенденции развития современного общества привели к тому, что те понятия, которые не так давно использовались главным образом в учебниках по экономической теории, стали все чаще встречаться в повседневной жизни. Одним из таких терминов является аннуитет, который все более активно стали использовать в сфере кредитования. Данный инструмент является достаточно выгодным, поэтому есть смысл познакомиться с его отличительными особенностями и способами расчета более подробно. Об этом и пойдет речь в данной статье.
Что такое аннуитет?
Аннуитет это — схема платежей, в соответствие с которой они производятся в одинаковом размере в соответствие с конкретным графиком выплат (а именно на постоянной основе через равные промежутки времени). Таким образом, можно представить аннуитет как поток одинаковых платежей, которые осуществляются через равные временные интервалы.
По аннуитетному виду платежа предполагается что выплаты осуществляются равными суммами через равные промежутки времени. Сумма аннуитетного платежа состоит из двух частей:
- Процентная часть, которая идет на оплату процентов пользования заемными средствами.
- Остаточная часть, которая направляется на оплату основного долга по кредиту.
Аннуитет позволяет сделать величину платежа, который включает в себя не только проценты за период, но и часть основного долга, постоянной. Это дает возможность плательщику заранее оценить свои силы и запланировать выплаты определенной суммы денежных средств в течение оговоренного срока.
Основным отличием от так называемого дифференцированного платежа является то, что при использовании последнего в первую очередь выплачивается полная сумма начисленных за использование кредитных средств процентов, а потом уже основной долг.
Отметим, что принцип аннуитета используется не только в кредитовании, но и для лизинговых платежей.
Какие выделяют виды аннуитета?
Для лучшего понимания использования аннуитета следует рассмотреть, какие его виды существуют. Так, можно отметить наличие следующей классификации:
- отложенный – в данном случае первая выплата производится в конце начального периода;
- немедленный – платеж осуществляется в начале нулевого периода.
Если говорить об аннуитете, используемом в сфере кредитования, то здесь имеет место отложенный аннуитет.
Кроме этого, распространенно выделение различных видов стоимости аннуитета, а именно:
- приведенная;
- будущая стоимость аннуитета.
Такое деление обусловлено стремлением определить максимально объективную ценность денежных средств, которые направлены на кредитование. Как будущая, так и текущая стоимость аннуитета рассчитывается определенным образом с использованием конкретных формул. Проводимый расчет текущей стоимости аннуитета зависит от ряда факторов.
Стоит отметить, что в силу теории о том, что с течением времени денежные средства могут обесцениваться в силу инфляции, имеет место такое понятие, как настоящая стоимость аннуитета. Также здесь играет роль упущенная выгода, ведь если бы кредитор оставил выданные денежные средства у себя, то он имел бы возможность получать доход в виде процентов по вкладу.
Формула расчета аннуитетного платежа
Формула аннуитетного платежа:
где:
- A – ежемесячный аннуитетный платеж;
- K – коэффициент аннуитета;
- S – сумма кредита.
Расчет коэффициента аннуитета:
где:
- K – коэффициент аннуитета;
- i – месячная процентная ставка по кредиту (годовая ставка деленная на 12 месяцев);
- n – количество периодов (месяцев), в течение которых выплачивается кредит.
Знание рассмотренной формулы позволяет провести требуемые расчеты, которые при наличии полных исходных данных не представляют собой особых сложностей. Очевидно, что для применения ее на практике необходимо учитывать некоторые принципиальные моменты. В их числе можно отметить, в первую очередь, принцип, по которому определяются доли основного долга и начисленных процентов в итоговом размере платежа. Для этого применяется определенная методика, которая предполагает прохождение несколько этапов расчета. Мы не будем на ней подробно останавливаться, отметим лишь общий принцип, в соответствии с которым производится расчет размера процентов и аннуитетного платежа, так же как и основного долга в виде разницы между этими двумя величинами для каждого месяца периода. При этом учитывается, что размер основного долга от месяца к месяцу снижается. Последний платеж требует отдельной корректировки в силу применения в процессе расчетов округлений.
Несмотря на равную величину платежей, соотношение суммы основного долга и начисленных процентов в их составе меняется. Если в начале основная доля приходится на проценты, то ближе к концу выплат остается погасить главным образом основную сумму долга.
Пример расчета аннуитетного платежа
Рассчитаем ежемесячный платеж по кредиту с аннуитетным графиком погашения под процентную ставку 24% годовых сроком на 2 года и на сумму 200 000 рублей.
Воспользуемся приведенными выше формулами:
Рассчитаем коэффициент аннуитета:
Теперь мы можем приступить к расчеты самого ежемесячного платежа. Подставим полученное значение коэффициента аннуитета:
Сумма ежемесячного платежа составила 10574.22 рублей.
Переплата по кредиту
Всего за 2 года банку будет выплачено 253 781.3 руб (10574.22 руб умноженные на 24 мес), а переплата составит 53781.3 руб.
Рассчитать кредит можно с помощью калькулятора кредита на нашем сайте.
Обнаружили ошибку? Выделите ее и нажмите Ctrl + Enter.
Оцените страницу:
Уточните, почему:
не нашёл то, что искал
содержание не соответствует заголовку
информация сложно подана
другая причина
Расскажите, что вам не понравилось на странице:
Спасибо за отзыв, вы помогаете нам развиваться!
- Для чего нужно уметь рассчитывать аннуитетный платеж
- Чем аннуитетный платеж отличается от других
- Формула расчета аннуитетных платежей по кредиту
- Другие способы рассчитать аннуитетный платеж
- Воспользоваться специальной функцией в ПО Excel
- Воспользоваться кредитным онлайн-калькулятором
Для чего нужно уметь рассчитывать аннуитетный платеж
Взять кредит в наше время – не проблема. Интернет пестрит банковскими предложениями на любой «вкус и цвет». Но как разобраться во всем этом многообразии и рассмотреть в мутной воде айсберг целиком, а не только его верхушку?
Сайты-агрегаторы кредитных предложений, как правило, предоставляют лишь общие условия:
- размер процентной ставки;
- срок займа;
- максимальную сумму;
- способ погашения – аннуитетный или дифференцированный.
Если последний пункт не указан, то будьте уверены, что речь идет об аннуитетном графике. Этот тип погашения наиболее распространен и предлагается по умолчанию.
Однако из этой информации не очевидно, насколько обременительным будет ежемесячный платеж. Еще сложнее понять, каков будет итоговый размер переплаты.
Сразу предупредим, что банальное умножение процентной ставки на сумму и срок займа в годах даст неверный и сильно завышенный ответ.
Представим, что банк предлагает вам оформить потребительский кредит на сумму 50 000 рублей по ставке 18% годовых на 18 месяцев. Если посчитать способом, указанным выше, то получим ежемесячный платеж – 3527 рублей, а общую переплату – 13 500 рублей.
То есть за полтора года заемщик заплатит «сверху» 27% от суммы займа? Это очень много, и логика подсказывает, что в подсчете скрывается грубая ошибка.
Причина довольно очевидна. Расчет не учитывает, что с каждым месяцем долг уменьшается, а при погашении кредита процент всегда начисляется на остаток долга. Соответственно, с каждым разом размер переплаты будет уменьшаться.
Отсюда вывод – умение правильно рассчитать аннуитетный платеж позволит грамотно спланировать бюджет. А снизить нагрузку на него поможет правильный выбор кредитного предложения.
Для этого не нужно долго искать в интернете, просто ознакомьтесь с тарифами Совкомбанка. Среди них вы обязательно найдете подходящее предложение. Знали ли вы, к примеру, что владельцы универсальной Халвы могут вернуть на свой счет сумму переплаты?
Зачем откладывать деньги долгие месяцы, если можно получить желаемое прямо сейчас? Возьмите кредит в Совкомбанке, оформите услугу «Гарантия минимальной ставки» и получите шанс вернуть проценты по истечении срока кредитования. Для этого расплачивайтесь Халвой каждый месяц и не допускайте просрочек по кредиту. Оставить заявку вы можете в два клика, а деньги мы зачислим на карту и доставим курьером.
Чем аннуитетный платеж отличается от других
Главная особенность аннуитетного графика погашения – одинаковые платежи в течение всего срока кредита при неизменной процентной ставке. Но это не значит, что с каждой выплатой тело кредита сокращается на одну и ту же величину. Это характерно как раз для дифференцированной схемы.
При аннуитетном погашении кредита с каждой выплатой изменяется соотношение между суммой погашения долга и суммой начисленных процентов. Первый показатель постоянно растет, а второй сокращается.
Аннуитетные и дифференцированные платежи: в чем разница
Формула расчета аннуитетных платежей по кредиту
Любая программа и любой кредитный калькулятор опираются на одну и ту же формулу. Она довольно проста, хотя и сложнее, чем для дифференцированной схемы погашения кредита.
ЕП = С × ПС × (1 + ПС)ⁿ / ((1 + ПС)ⁿ – 1), где
ЕП – размер ежемесячного платежа,
С – сумма займа,
ПС – месячная ставка по займу в долях от единицы, которая вычисляется по формуле: годовая ставка / 12 мес. / 100%,
n – срок кредита (в месяцах).
Чтобы воспользоваться этой формулой, потребуется многофункциональный калькулятор с функцией возведения числа в степень. Если у вас такого нет, можно найти онлайн-версию.
Применим формулу расчета аннуитетных платежей к ранее описанной задаче.
ПС = 18% / 12 / 100% = 0,015
ЕП = 50 000 (руб.) × 0,015 × (1 + 0,015)18 / ((1 + 0,015)18 – 1) = 3191 руб.
Чтобы вычислить переплату, умножаем полученную сумму на число платежей (18) и вычитаем сумму займа. Она составит 7433 рубля.
Таким образом, реальная переплата составит 14,8% от суммы кредита.
Как посчитать переплату по кредиту
Другие способы рассчитать аннуитетный платеж
К счастью, можно обойтись и без «мозгового штурма».
Воспользоваться специальной функцией в ПО Excel
Если у вас есть под рукой компьютер, но нет интернета, на помощь придет старая добрая электронная таблица.
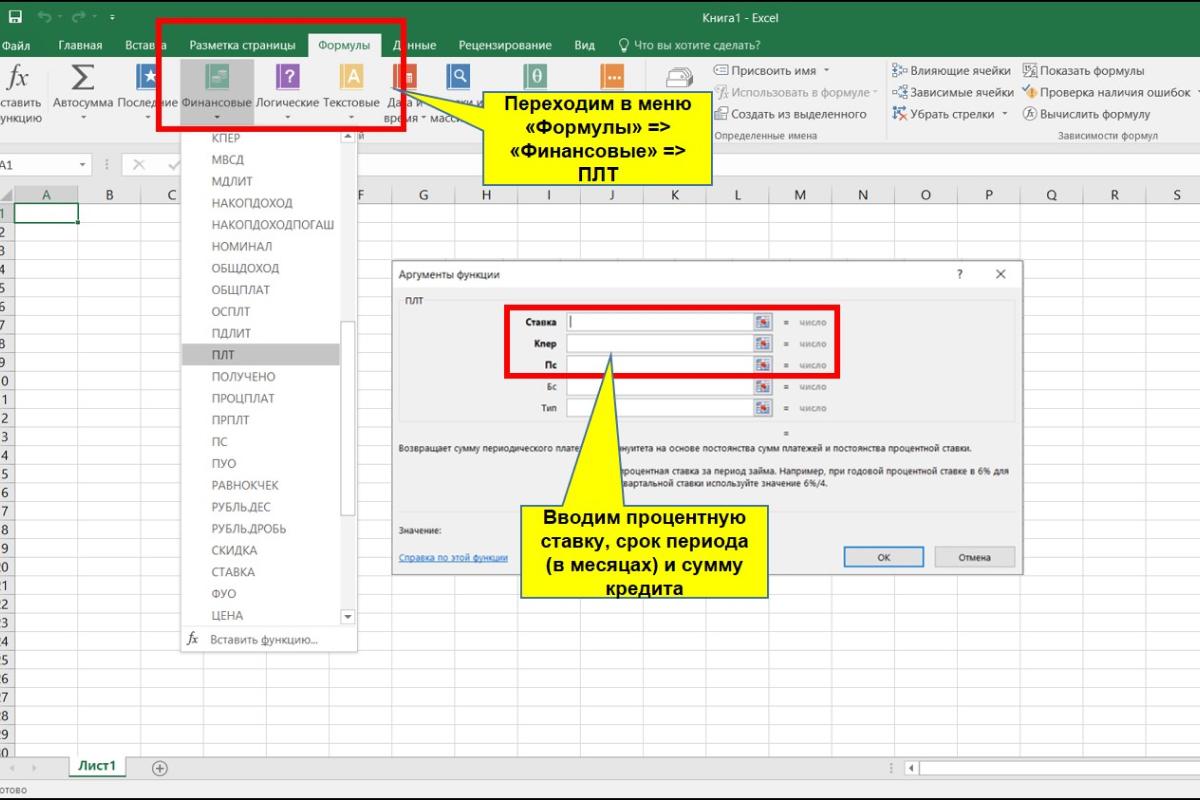
Среди функционала программы есть специальный блок для расчета финансовых задач. Для этого нужно зайти во вкладку «Формулы» в верхней строке основного меню.
Нажмите кнопку «Финансовые», и перед вами откроется полный список всех релевантных функций. Найдите среди них формулу «ПЛТ». Она предназначена как раз для вычисления размера кредитного платежа.
Перед вами откроется небольшое меню, в котором имеется пять полей для ввода исходных данных. Два нижних нас не интересуют, их можно оставить пустыми.
В графе «Ставка» вводим месячную процентную ставку в долях от единицы (формула в предыдущей главе). В поле «Кпер» указываем срок займа в месяцах, в поле «Пс» – сумму кредита.
Важно: если вы введете годовую ПС и срок кредита в годах, то получите неверный ответ. Отталкиваться нужно от периодичности выплат по долгу. Практически всегда речь идет о ежемесячной периодичности.
Далее нажимаем «Ок» и получаем в выбранной ячейке искомое значение. Зная сумму ежемесячного платежа, несложно рассчитать размер переплаты.
Воспользоваться кредитным онлайн-калькулятором
Самый простой способ, если под рукой есть интернет. В глобальной сети таких предложенией – огромное разнообразие.
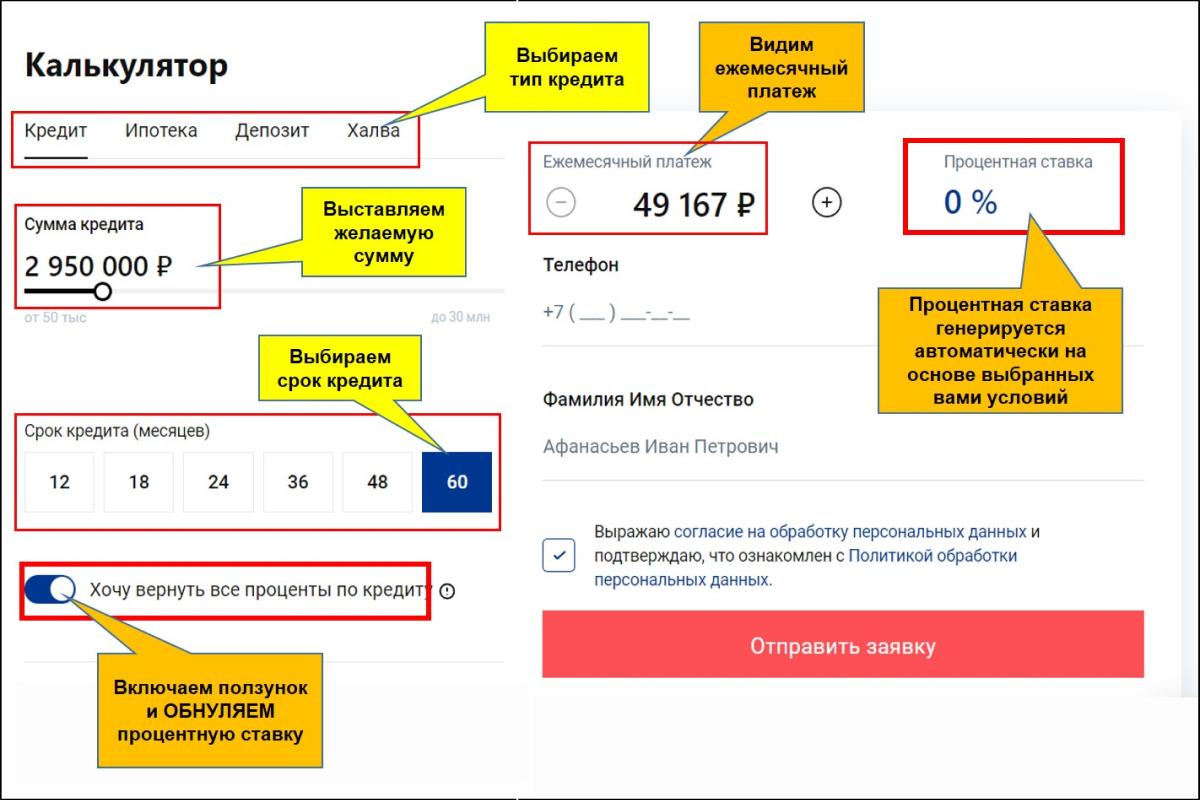
Однако калькулятор калькулятору рознь. Не все они интуитивно понятны. Чтобы не тратить время, можно воспользоваться кредитным калькулятором Совкомбанка. Он один из самых простых в использовании.
Нужно лишь задать срок и желаемую сумму. Кредитный калькулятор автоматически сгенерирует годовую ставку и размер месячного платежа. Обратите внимание, что владельцы Халвы могут в один клик обнулить переплату по займу.
Карта «Халва» — универсальный финансовый инструмент. Используйте свои средства, получайте кешбэк с покупок до 10% и доход на остаток собственных средств по карте до 12%, а также открывайте вклады под выгодный процент. Вы можете взять заемные средства и потратить их на покупки в рассрочку 10 месяцев или больше, если оформите подписку «Халва.Десятка». Оформите Халву в пару кликов, и курьер привезет ее вам!
Таким образом, аннуитетный платеж – это не сложно. Его расчет займет не более 5 минут любым способом.
Эта короткая процедура может уберечь вас от навязанных и необоснованных расходов. Воспитывайте в себе финансовую дисциплину и получайте реальную выгоду от взаимодействия с кредитными организациями.
Содержание материала
- Почему важно считать кредит самому?
- Видео
- Как рассчитать годовые проценты по кредиту?
- Как самостоятельно рассчитать аннуитетный платеж
- Какие данные нужны для расчета платежа по кредиту
- Воспользуемся банковскими калькуляторами
- Виды ежемесячных выплат по кредитам
- Самостоятельный подсчет при аннуитетных платежах
- Из чего состоит ежемесячный платеж
- Формула расчета процентов по кредиту
- Какие данные нужны для расчета
- Пример расчета процентов по кредиту
- Погашать долг можно по-разному
- Как составить график платежей
- График выплаты кредита с аннуитетными платежами
- График выплаты кредита с дифференцированными платежами
Почему важно считать кредит самому?
Кредитами сейчас сложно кого-то удивить. Каждый среднестатистический россиянин имеет или имел как минимум один-два кредита в своей жизни или собирается его взять. Если вы идете в банк для получения кредита и вам дают несколько предложений, то нужно выбрать самое дешевое и выгодное для вас. Для этого нужно рассчитать кредит самому, например в Excel. Нужно также знать размер ежемесячного платежа, чтоб понять нагрузку займа на ваш бюджет. Это тоже можно сделать самостоятельно.
Видео
Как рассчитать годовые проценты по кредиту?
Для аннуитетного платежа достаточно умножить сумму всего взятого кредита на процентную ставку. Наглядно это выглядит так:
10000 * 12% = 1200 рублей составит сумма, которую необходимо выплатить за пользование процентами банку.
При дифференцированном платеже сумма годовых процентов рассчитывается немого сложнее, поскольку необходимо помножить остаток по кредиту на процентную ставку и поделить на 12.
То есть, если из наших 10000 выплачено 5000, то: 5000 * 12%/12 = 50 рублей ежемесячно придется отдавать банку за пользование кредитом. При этом, помножив это же число на 12, получим среднюю сумму для оплаты процентов за весь год.
При обращении в банк для получения кредита следует уточнить, какая система кредитования работает в данной организации. Если предлагается сделать выбор самостоятельно, то есть смысл остановиться на дифференцированном платеже. По такому платежу меньше переплата, да и само осознание того, что платить приходится за свои деньги, является немаловажным фактором при выборе способа кредитования.
Ипотечные кредиты также выгодно выплачивать дифференцированно, так как при растущей стоимости недвижимости невыгодно выплачивать кредит с переплатой значительной суммы средств.
Самым оптимальным решением при выборе выплаты по кредиту будет попросить банковского служащего распечатать примерные графики и суммы платежей по обоим кредитам и сравнить, какой из них наиболее выгодный.
Также полезно будет узнать, какой вид платежа предлагается по умолчанию в каком-либо банке.
Как самостоятельно рассчитать аннуитетный платеж
Для самостоятельного расчета понадобится срок кредита, сумма и процентная ставка.
Стандартная формула расчета аннуитетного платежа выглядит так:
Иногда формула может отличаться. Например, если банк предлагает направлять первые платежи только на погашение процентов. Но чаще всего считают по стандартной формуле.
А вот как рассчитывается коэффициент аннуитета:
Для примера возьмем 300 000 рублей, срок 18 месяцев и процентную ставку 15% годовых.
Месячная процентная ставка = 15% / 12 = 1,25%, то есть 0,0125.
Количество платежей равно количеству месяцев — 18.
Подставляем данные в формулу и считаем коэффициент аннуитета:
0,0125 × (1 + 0,0125)18 / ((1 + 0,0125)18 − 1) = 0,062385
Теперь подставляем коэффициент аннуитета в расчет платежа: 300 000 × 0,062385 = 18 715,44 Р — в точности как в кредитном калькуляторе.
Какие данные нужны для расчета платежа по кредиту
Ежемесячный платеж – важная характеристика для многих. Хочется найти золотую середину – платить посильный взнос с наименьшей переплатой.
Рассчитать его можно самостоятельно или через специальные сервисы. Для этого вам понадобятся:
- ставка,
- размер желаемого займа,
- срок, на который вы хотите занять деньги.
Воспользуемся банковскими калькуляторами
Банки побеспокоились о том, чтобы клиенты не морочили себе голову арифметикой, а сразу получали искомые параметры.
Составлено множество программ, которые названы «калькуляторами». Им стоит только задать основные величины, как они тут же произведут расчёт и покажут всё, что интересует заказчика, вплоть до помесячного графика платежей и суммы переплаты за кредит.
Виды ежемесячных выплат по кредитам
Ежемесячные платежи по кредитам, которые списывают в банках, бывают двух видов: аннуитетные и дифференцированные.
Аннуитетные — с должника на протяжении всего периода пользовании кредитом списывают равные суммы. По очередности списания приоритет у начисленных процентов. Проценты к оплате пересчитываются ежемесячно исходя из неоплаченной на текущий момент суммы долга. Остальная сумма, которая остается после удержания процентов, идет на погашения основной задолженности.
В будущем периоде сумма основного долга становится меньше, и на него насчитывается меньше процентов. Значит, из очередного равного платежа сумма распределится по-другому: меньше уйдет на проценты и больше на основной долг. Чем длиннее срок кредитования, тем большая получается итоговая переплата, хотя сумма ежемесячного платежа будет одинаковой для заемщика с начала и до конца периода кредитования.
Дифференцированные выплаты в отличие от аннуитетных не равные. Вначале кредитования суммы выше, а затем они уменьшаются. Снижение ежемесячного платежа происходит постоянно. Пересчет процентов такой же, как и при аннуитетных выплатах. Но итоговая сумма процентов, уплаченных кредитору, получается меньше.
Банки самостоятельно решают, какой тип ежемесячного платежа установлен по кредиту. Хотя некоторые компании предоставляют заемщику право выбора. Но если выбора нет, то клиент может закрыть кредит досрочно, когда для этого появятся деньги. В этом случае, понадобится заранее уведомить банк о своем желании, чтобы задолженность была погашена правильно.
Особенно важно это сделать при полном досрочном погашении. Если это не отследить, можно столкнуться с неприятностями и испортить свою кредитную историю. Чтобы этого не произошло, после завершения выплат всегда запрашивайте документ, где указано, что ваши обязательства перед кредитором исполнены и долгов нет.
Самостоятельный подсчет при аннуитетных платежах
Для удобства и наглядности подсчета обозначим одинаковые входные данные по кредиту:
- Процентная ставка — 18%.
- Период кредитования — 24 месяца.
- Сумма кредита — 500000 рублей.
Классическая формула для расчета аннуитетного платежа выглядит так:
Разовый аннуитетный платеж = Сумма кредита * Ка
где Ка — это коэффициент аннуитета.
Ка = ((ЕПС* (1 + ЕПС)n)/( (1 + ЕПС)n -1)
где ЕПС — ежемесячная процентная ставка.
Подставляя данные из примера, ЕПС будет выглядеть как 18%/12 = 1,5% = 0,015.
Итоговый расчет примет вид:
500 000 * (0,015 * (1 + 0,015)24)/((1 + 0,015)24 -1) = 24 962,05 рублей в месяц.
Данные полностью совпадают с примером, приведенным выше, где описан подсчет с помощью функции в Excel.
Итоговая сумма, которую выплатит заемщик за весь период пользования кредитом при точном соблюдении графика выплат:
24 962,05 * 24 = 599 089,24 рублей.
Общая сумма переплаты при аннуитетных платежах с приведенными в примере данными составит 99 089,24 рублей.
Из чего состоит ежемесячный платеж
Расплачиваться за взятые в долг деньги придется ежемесячно. Этот взнос складывается из основного долга и процентов, взятых в разном соотношении. В каком именно – зависит от типа платежей.
Вы можете заплатить меньше или больше установленной выплаты. Если заплатите меньше, вас накажут за просрочку штрафами и пени. Они могут прибавиться к следующей выплате. А если заплатите больше – поможете себе и снизите размер общей переплаты.
Формула расчета процентов по кредиту
S = (s3 x i x Kk / Kr) / 100
- S = вычисляемые проценты;
- S3 = общая сумма кредита;
- i = процентная ставка по кредиту;
- Kk = кол-во дней по платежам;
- Kr = кол-во дней на календарный год.
Какие данные нужны для расчета
- Сумма, выданная в кредит;
- Процентная ставка за год;
- Кол-во календарных дней в текущем году.
Пример расчета процентов по кредиту
65000 рублей – сумма переплаты в год. Для того чтобы посчитать сумму переплаты в месяц нужно 65000 рублей разделить на 12.
Погашать долг можно по-разному
Видов платежей два. Они бывают аннуитетными или дифференцированными, и от того, какой вы изберёте, зависит картина выплат.
С точки зрения банка, ежемесячный платёж распадается на несколько частей. Главными в них является тело долга и проценты, но есть и прочие составляющие.
Банк в первую очередь заботится о выплатах процентов, поскольку это его доход. Поэтому в первых платежах, какой бы вид вы ни выбрали, основная часть отводится именно им. По мере продвижения к концу срока доля процентной части уменьшается, а доля основного долга, соответственно, увеличивается.
Если платёж аннуитетный, то его величина остаётся постоянной на всём протяжении погашения долга.
Дифференцированный платёж имеет переменный размер, но в нём тоже есть постоянная часть: это доля основного долга. Процентная часть плавающая, она от максимума в первом платеже постепенно уменьшается до нуля в последнем, поскольку рассчитывается от величины оставшейся части долга (ОстДолга).
, поскольку в этом случае переплата меньше. Банку, соответственно, интереснее аннуитетные, и в последнее время они решительно преобладают. Делается это, якобы, во благо заёмщика, ведь с постоянным платежом ему удобнее обращаться.
Если срок небольшой и проценты невелики, то и разница некритична. А вот на многолетних ипотеках, да ещё с высокими процентами, расхождение весьма ощутимо.
Как составить график платежей
Самый простой способ — воспользоваться кредитным калькулятором: график платежей составляется автоматически.
Еще мы написали калькулятор в экселе, в котором можно прикинуть график платежей и ежемесячные платежи при обоих способах погашения.
Если вы хотите рассчитать график платежей самостоятельно, давайте разберемся на примере ранее рассчитанного платежа: кредит на 300 000 рублей, 18 месяцев под 15% годовых.
При аннуитетном способе ежемесячный платеж неизменный из месяца в месяц. Как мы посчитали выше, в нашем случае он составит 18 715,44 Р.
В целом график платежей уже понятен, но мы дополнительно можем посчитать, каким будет соотношение основного долга и процентов в каждом месяце.
Сначала считаем проценты:
Остаток долга × Процентная ставка × Количество дней в месяце / Количество дней в году
Если год не високосный, а в месяце 30 дней, получится 3698,63 Р — это сумма процентов, которые мы заплатим в первом месяце. На погашение основного долга пойдет остаток от нашего ежемесячного платежа: 18 715,44 Р − 3698,63 Р = 15 016,81 Р.
Во втором месяце сумма процентов начислится на сумму кредита минус платеж по основному долгу в первом месяце: 300 000 Р − 15 015,81 Р = 284 983,19 Р.
Считаем проценты во втором месяце. Предположим, что во втором месяце 31 день: 284 983,19 × 15% × 31 / 365 = 3630,61 Р.
На погашение основного долга во втором месяце пойдет 15 084,83 Р (18 715,44 − 3630,61).
Таким образом можно посчитать соотношение процентов и основного долга в каждом месяце кредита.
График выплаты кредита с аннуитетными платежами
| Номер платежа | Сумма платежа | Сумма в погашение тела кредита | Сумма платежа в погашение процентов | Остаток долга |
|---|---|---|---|---|
| 1 | 18 715,44 | 15 016,81 | 3698,63 | 284 983,19 |
| 2 | 18 715,44 | 15 084,83 | 3630,61 | 269 898,37 |
| 3 | 18 715,44 | 15 387,92 | 3327,51 | 254 510,44 |
| 4 | 18 715,44 | 15 473,04 | 3242,39 | 239 037,40 |
| 5 | 18 715,44 | 15 670,17 | 3045,27 | 223 367,24 |
| 6 | 18 715,44 | 16 053,39 | 2662,05 | 207 313,85 |
| 7 | 18 715,44 | 16 074,31 | 2641,12 | 191 239,53 |
| 8 | 18 715,44 | 16 357,69 | 2357,75 | 174 881,84 |
| 9 | 18 715,44 | 16 487,49 | 2227,95 | 158 394,35 |
| 10 | 18 715,44 | 16 762,63 | 1952,81 | 141 631,73 |
| 11 | 18 715,44 | 16 911,09 | 1804,35 | 124 720,64 |
| 12 | 18 715,44 | 17 126,53 | 1588,91 | 107 594,11 |
| 13 | 18 715,44 | 17 388,93 | 1326,50 | 90 205,18 |
| 14 | 18 715,44 | 17 566,25 | 1149,19 | 72 638,93 |
| 15 | 18 715,44 | 17 819,89 | 895,55 | 54 819,04 |
| 16 | 18 715,44 | 18 017,06 | 698,38 | 36 801,98 |
| 17 | 18 715,44 | 18 246,59 | 468,85 | 18 555,40 |
| 18 | 18 768,91 | 18 555,39 | 213,51 |
Первый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
15 016,81
Сумма платежа в погашение процентов
3698,63
Остаток долга 284 983,19
Второй платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
15 084,83
Сумма платежа в погашение процентов
3630,61
Остаток долга 269 898,37
Третий платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
15 387,92
Сумма платежа в погашение процентов
3327,51
Остаток долга 254 510,44
Четвертый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
15 473,04
Сумма платежа в погашение процентов
3242,39
Остаток долга 239 037,40
Пятый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
15 670,17
Сумма платежа в погашение процентов
3045,27
Остаток долга 223 367,24
Шестой платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
16 053,39
Сумма платежа в погашение процентов
2662,05
Остаток долга 207 313,85
Седьмой платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
16 074,31
Сумма платежа в погашение процентов
2641,12
Остаток долга 191 239,53
Восьмой платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
16 357,69
Сумма платежа в погашение процентов
2357,75
Остаток долга 174 881,84
Девятый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
16 487,49
Сумма платежа в погашение процентов
2227,95
Остаток долга 158 394,35
Десятый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
16 762,63
Сумма платежа в погашение процентов
1952,81
Остаток долга 141 631,73
Одиннадцатый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
16 911,09
Сумма платежа в погашение процентов
1804,35
Остаток долга 124 720,64
Двенадцатый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
17 126,53
Сумма платежа в погашение процентов
1588,91
Остаток долга 107 594,11
Тринадцатый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
17 388,93
Сумма платежа в погашение процентов
1326,50
Остаток долга 90 205,18
Четырнадцатый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
17 566,25
Сумма платежа в погашение процентов
1149,19
Остаток долга 72 638,93
Пятнадцатый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
17 819,89
Сумма платежа в погашение процентов
895,55
Остаток долга 54 819,04
Шестнадцатый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
18 017,06
Сумма платежа в погашение процентов
698,38
Остаток долга 36 801,98
Семнадцатый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
18 246,59
Сумма платежа в погашение процентов
468,85
Остаток долга 18 555,40
Восемнадцатый платеж Сумма платежа 18 768,91 Сумма в погашение тела кредита 18 555,39 Сумма платежа в погашение процентов 213,51 Остаток долга
При дифференцированном платеже проценты в первом месяце будут такими же — 3698,63 Р. Дальше же принцип расчета процентов аналогичен, а сумма основного долга будет каждый месяц уменьшаться равномерно — на 16 666,67 Р (300 000 / 18). Ежемесячный платеж будет складываться из этих двух сумм.
В результате в первые месяцы платеж будет больше, чем при аннуитетном способе, а итоговая переплата будет меньше.
График выплаты кредита с дифференцированными платежами
| Номер платежа | Сумма платежа | Сумма в погашение тела кредита | Сумма платежа в погашение процентов | Остаток долга |
|---|---|---|---|---|
| 1 | 20 365,30 | 16 666,67 | 3698,63 | 283 333,33 |
| 2 | 20 276,26 | 16 666,67 | 3609,59 | 266 666,67 |
| 3 | 19 954,34 | 16 666,67 | 3287,67 | 250 000,00 |
| 4 | 19 851,60 | 16 666,67 | 3184,93 | 233 333,33 |
| 5 | 19 639,27 | 16 666,67 | 2972,60 | 216 666,67 |
| 6 | 19 248,86 | 16 666,67 | 2582,19 | 200 000,00 |
| 7 | 19 214,61 | 16 666,67 | 2547,95 | 183 333,33 |
| 8 | 18 926,94 | 16 666,67 | 2260,27 | 166 666,67 |
| 9 | 18 789,95 | 16 666,67 | 2123,29 | 150 000,00 |
| 10 | 18 515,98 | 16 666,67 | 1849,32 | 133 333,33 |
| 11 | 18 365,30 | 16 666,67 | 1698,63 | 116 666,67 |
| 12 | 18 152,97 | 16 666,67 | 1486,30 | 100 000,00 |
| 13 | 17 899,54 | 16 666,67 | 1232,88 | 83 333,33 |
| 14 | 17 728,31 | 16 666,67 | 1061,64 | 66 666,67 |
| 15 | 17 488,58 | 16 666,67 | 821,92 | 50 000,00 |
| 16 | 17 303,65 | 16 666,67 | 636,99 | 33 333,33 |
| 17 | 17 091,32 | 16 666,67 | 424,66 | 16 666,67 |
| 18 | 16 858,45 | 16 666,67 | 191,78 |
Первый платеж
Сумма платежа
20 365,30
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
3698,63
Остаток долга 283 333,33
Второй платеж
Сумма платежа
20 276,26
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
3609,59
Остаток долга 266 666,67
Третий платеж
Сумма платежа
19 954,34
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
3287,67
Остаток долга 250 000,00
Четвертый платеж
Сумма платежа
19 851,60
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
3184,93
Остаток долга 233 333,33
Пятый платеж
Сумма платежа
19 639,27
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
2972,60
Остаток долга 216 666,67
Шестой платеж
Сумма платежа
19 248,86
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
2582,19
Остаток долга 200 000,00
Седьмой платеж
Сумма платежа
19 214,61
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
2547,95
Остаток долга 183 333,33
Восьмой платеж
Сумма платежа
18 926,94
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
2260,27
Остаток долга 166 666,67
Девятый платеж
Сумма платежа
18 789,95
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
2123,29
Остаток долга 150 000,00
Десятый платеж
Сумма платежа
18 515,98
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
1849,32
Остаток долга 133 333,33
Одиннадцатый платеж
Сумма платежа
18 365,30
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
1698,63
Остаток долга 116 666,67
Двенадцатый платеж
Сумма платежа
18 152,97
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
1486,30
Остаток долга 100 000,00
Тринадцатый платеж
Сумма платежа
17 899,54
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
1232,88
Остаток долга 83 333,33
Четырнадцатый платеж
Сумма платежа
17 728,31
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
1061,64
Остаток долга 66 666,67
Пятнадцатый платеж
Сумма платежа
17 488,58
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
821,92
Остаток долга 50 000,00
Шестнадцатый платеж
Сумма платежа
17 303,65
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
636,99
Остаток долга 33 333,33
Семнадцатый платеж
Сумма платежа
17 091,32
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
424,66
Остаток долга 16 666,67
Восемнадцатый платеж Сумма платежа 16 858,45 Сумма в погашение тела кредита 16 666,67 Сумма платежа в погашение процентов 191,78 Остаток долга
Теги
Аннуитетный платёж
Фото: pixabay.com
Аннуитетный платёж – это платёж, который устанавливается в равной сумме через равные промежутки времени. Так, при аннуитетном графике погашения кредита вы ежемесячно платите одну и ту же сумму, независимо от остатка задолженности. Другим способом внесения ежемесячных платежей является дифференцированный способ погашения.
Для сравнения, при дифференцированной схеме погашения кредита сумма основного долга выплачивается ежемесячно равными долями, а проценты рассчитываются от остатка задолженности. В таком случае сумма ежемесячного платежа уменьшается в процессе погашения кредита.
Например, сумма процентов за первый месяц пользования кредитом равна:
S%1 = S * i,
где S%1 – сумма процентов за первый месяц,
S — сумма кредита.
i — процентная ставка по кредиту в месяц (рассчитывается как годовая, делённая на 12 месяцев).
За второй и следующие месяцы:
S%n = (S — ∆S) * i,
где ∆S – сумма погашенного основного долга.
Как рассчитать ежемесячный платёж?
Формула расчёта суммы ежемесячного платежа при аннуитетной схеме погашения следующая:
A = K * S
где А – сумма ежемесячного аннуитетного платежа,
К — коэффициент аннуитета,
S — сумма кредита.
Сумма кредита известна. А для расчёта К – коэффициента аннуитета, используется следующая формула:
где i — процентная ставка по кредиту в месяц (рассчитывается как годовая, делённая на 12 месяцев),
n — количество периодов (месяцев) погашения кредита.
Применив вышеописанную схему расчёта, вы сможете узнать сумму, которую необходимо будет погашать ежемесячно.
Пример расчёта аннуитетного платежа
Предположим, что нужно провести расчёт ежемесячного платежа по кредиту с аннуитетным графиком погашения под процентную ставку 48% годовых сроком на 4 года на сумму 2 000 рублей. Используя приведённую выше формулу расчёта ежемесячного платежа (A = K • S) и коэффициента К, рассчитаем аннуитетный платёж.
Имеем:
i= 48%/12 месяцев = 4% или 0,04
n = 4 года* 12 месяцев = 48 (месяцев)
S = 2 000
Рассчитываем К:
К=(0,04*〖(1+0,04)〗^48)/(〖(1+0,04)〗^48-1) = 0,0472
А теперь подставим полученное значение в формулу ежемесячного платежа:
А = 0,0472 * 2 000 = 94,4 рублей.
Таким образом, в течение 4 лет (или 48 месяцев) необходимо будет вносить в банк платёж в сумме 94,4 рублей. Переплата по кредиту за 4 года составит 2 531,2 ( = 94,4 * 48 – 2 000).
Кому выгоден аннуитет?
В первую очередь аннуитетный способ погашения выгоден банку. Объясняется это тем, что в течение всего срока погашения кредита проценты начисляются на первоначальную сумму кредита. При дифференцированной графике уплата процентов за 100% суммы кредита происходит только в первом месяце (в случае отсутствия отсрочки уплаты основного долга), далее проценты начисляются на остаток, из-за чего итоговая переплата по кредиту окажется меньше. Иными словами, среди двух кредитов с одинаковыми процентными ставками, сроком погашения и дополнительными комиссиями, кредит с аннуитетной схемой погашения всегда будет дороже.
Для примера, рассчитаем переплату по кредиту, рассмотренному выше, но теперь с дифференцированным графиком погашения. Она составит 1 960 рублей. Это на 571,2 рубля меньше, чем при аннуитетной схеме.
С другой стороны, погашение задолженности и процентов равными долями удобно кредитополучателю, так как ежемесячный платёж является постоянным и не требует уточнения в банке необходимой суммы взноса, в то время как при дифференцированном графике каждый месяц сумма платежа окажется разной.
Применение аннуитетного способа погашения, таким образом, обойдётся дороже, но при этом гораздо удобнее.
Если вы заметили ошибку в тексте новости, пожалуйста, выделите
её и нажмите Ctrl+Enter
Аннуитетный фактор Значение
Коэффициент аннуитета — это математическая концепция, которая помогает найти текущую стоимость будущего депозита или снятия средств. Он используется в финансах и помогает рассчитать максимальную сумму денег, которую можно снять с пенсионного счета без штрафных санкций. Эта концепция также применима к составлению бюджета капиталовложений.
Как следует из названия, его использование может быть распространено на любую ренту. Аннуитет относится к любому финансовому инструменту, который имеет устойчивый отток денежных средств. В таких случаях он помогает определить временную стоимость денег. Еще одним приложением является расчет равных платежей по кредиту. Таким образом, фактор аннуитета помогает в принятии решений.
Оглавление
- Что такое Аннуитетный фактор?
- Объяснение фактора аннуитета
- Формула
- Пример расчета
- Часто задаваемые вопросы (FAQ)
- Рекомендуемые статьи
- фактор аннуитета относится к математической фигуре, которая помогает определить текущую экономическую стоимость любого будущего финансового инструмента.
- Это помогает сделать оценки, например, сколько денег можно снять с пенсионного счета, чтобы можно было возместить стоимость в будущем без штрафных санкций.
- Расчет максимальной суммы снятия с индивидуальных пенсионных счетов осуществляется в соответствии с рекомендациями и спецификациями Службы внутренних доходов (IRS).
- Фактор оценки зависит в основном от срока депозита/инвестиции и процентных ставок. Кроме того, приведенная стоимость также зависит от оттока денежных средств или дохода от инструмента.
Объяснение фактора аннуитета
Фактор аннуитета требует глубокого понимания некоторых других предварительных понятий. Итак, давайте начнем с понимания термина «аннуитет». Аннуитет – это финансовый инструмент, приносящий регулярный доход. Это могут быть процентные выплаты, пенсии или регулярные страховые выплаты.
Фактор — это конкретное математическое значение, которое можно использовать для определения текущей стоимости платежей. Например, какова будет текущая стоимость 12-процентной облигации со сроком погашения через три года? Аннуитетный фактор помогает ответить на этот вопрос. Другие методы, такие как фиксированная амортизация, дисконтированная окупаемость, чистая приведенная стоимость и т. д., могут помочь в аналогичных расчетах.
Но использование фактора чаще можно увидеть в ИРА. Индивидуальные пенсионные счета (IRA) помогают людям делать ранние сбережения после выхода на пенсию. Поскольку он в первую очередь предназначен для сбережений, снятие средств со счета может быть не очень хорошей идеей. Однако для этого есть некоторые ограничения. Например, если человек снимает средства до достижения 59,5 лет, он подвергается штрафу в размере 10%.
Тем не менее, существуют некоторые исключения – расходы на образование, покупка жилья впервые и т. д. Кроме того, IRA Roth может иметь преимущество в этом случае. Однако дело здесь в том, что человек не может продолжать выходить из своей IRA. При превышении лимита на них будет наложен штраф. Этот предел можно определить с помощью метода коэффициента аннуитета.
IRS рекомендует набор таблиц коэффициентов аннуитета для оценки снятия средств, платежей, депозитов и т. д. Для определения оценки используются данные об ожидаемой продолжительности жизни. Используя это, человек может сделать максимальное количество рисунков в зависимости от их текущей стоимости. актуарная таблица опубликованные IRS, предоставляют коэффициенты оценки для аннуитетов, пожизненного имущества и т. д. Коэффициенты оценки для различных спецификаций (аннуитеты, выплачиваемые в конце/начале года) различаются и четко упоминаются IRS.
Формула
Существует два метода расчета коэффициента аннуитета. Методы похожи, но имеют небольшие отличия.
Способ 1
Коэффициент аннуитета, AF =
Здесь «n» — количество лет, а «r» — процентная ставка.
Способ 2
Коэффициент аннуитета также может быть рассчитан как сумма отдельных коэффициентов дисконтирования.
Коэффициент дисконтирования для года 1: (1 + r)-1
Коэффициент дисконтирования для года 2: (1 + r)-2
И так далее.
Чистая приведенная стоимость аннуитета может быть рассчитана как произведение оттока в течение года/периода и коэффициента аннуитета.
Пример расчета
Давайте выполним расчет, чтобы понять чистую приведенную стоимость аннуитета.
Отток денежных средств с 1 года = 100 000 долларов США.
Отток денежных средств со 2-го года = 120 000 долларов США.
Инвестиционный период = 2 года
Процентная ставка = 6%
Следующие шаги помогут в более простом расчете:
Шаг 1: Сначала рассчитайте коэффициент, используя приведенную выше формулу.
Шаг 2: Более простым методом было бы вычислить (1 + r). Здесь значение будет 1,06.
Шаг 3: Теперь возведите в квадрат значение (1 + r), поскольку n=2.
(1 + г)2 = 1,1236
Шаг 4: Затем возьмите обратную величину этого значения, поскольку (1 + r) возводится в отрицательную степень.
1/(1 + г) = 0,8899
Шаг 5: вычтите это значение из 1.
1 – 0,8899 = 0,11
Шаг 6: Разделите 0,11 на процентную ставку, т.е. 0,06.
Аннуитетный коэффициент составит 1,8333.
Шаг 7: Текущая стоимость может быть рассчитана как произведение денежного потока и фактора.
Итак, текущая стоимость 1-го года = (1,8333 x 100 000) = 183 330 долларов США.
Приведенная стоимость года 2 = (1,8333 x 120 000) = 219 996 долларов США.
Альтернативный метод нахождения коэффициента аннуитета как суммы коэффициентов дисконтирования:
AF = DF1 + DF2 + … + DFn
Здесь n = 2 и r = 6%
DF1 = (1 + 0,6)-1
DF2 = (1 + 0,6)-2
AF = 0,9434 + 0,8900
= 1,8333
Часто задаваемые вопросы (FAQ)
1. Как рассчитать аннуитетный коэффициент?
Формула для нахождения коэффициента выглядит следующим образом:
Здесь «r» — процентная ставка, а «n» — количество лет.
Таблица коэффициентов аннуитета IRS может использоваться для определения стоимости аннуитета для различных сценариев. Это значение можно использовать непосредственно для целей оценки, поскольку оно учитывает данные о продолжительности жизни для оценки. 2. Что такое аннуитетный фактор приведенной стоимости?
Фактор текущей стоимости аннуитета помогает найти текущую стоимость будущих инвестиций или депозитов. Из-за этого он играет важную роль в трейдинге и составлении бюджета капитала, а также помогает определить максимальную сумму, которую можно снять с пенсионного счета.
3. В чем разница между коэффициентом аннуитета и коэффициентом дисконта?
Коэффициент аннуитета представляет собой сумму всех коэффициентов дисконтирования за каждый год. Коэффициент дисконтирования можно рассчитать как (1+r)-n, где n = 1, 2, 3, …
Рекомендуемые статьи
Эта статья была руководством к тому, что Annuity Factor. Здесь мы подробно объясним это с помощью формулы, расчета и примера. Вы также можете найти несколько полезных статей здесь —
- Ежегодный взнос
- Формула будущей стоимости аннуитета
- Аннуитет против бессрочного