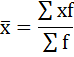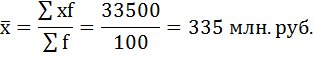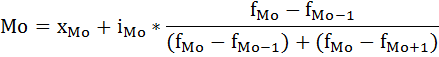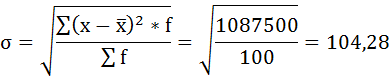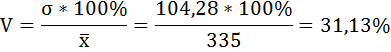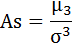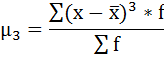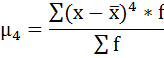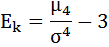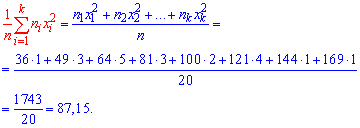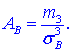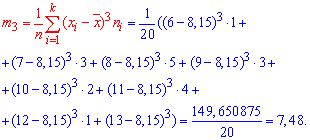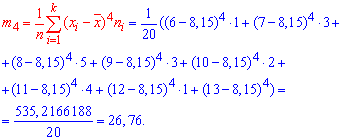Как найти коэффициент асимметрии выборки

Центральный
выборочный момент второго порядка
обозначается S²
и находится по следующей формуле:
    
.

10.Как вычисляется и что характеризует коэффициент асимметрии выборки? Коэффициент эксцесса?

Выборочный
коэффициент асимметрии:

Определяется
по формуле :

,

где
– центральный момент -го порядка()

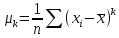
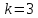
Выборочный
коэффициент эксцесса:

Определяется
по формуле :

Выборочный
коэффициент асимметрии
служит для характеристики смещения
вариационного ряда относительно среднего
значения по величине и направлению.
Если полигон асимметричен, то одна из
его ветвей, начиная с вершины, имеет
более пологий «спуск», чем другая. В
случае отрицательного коэффициента
асимметрии более пологий «спуск» полигон
наблюдается слева. В противном случае
– справа. В первом случае асимметрию
называют левосторонней, а во втором –
правосторонней. Асимметрия менее 0,5
считается малой.

Выборочный
эксцесс
служит для сравнения на «крутость»
выборочного распределения с нормальным
распределением. Эксцесс нормального
распределения равен нулю. Если выборочному
распределению соответствует отрицательный
эксцесс, то полигон имеет более пологую
вершину по сравнению с нормальной
кривой. В случае положительного эксцесса
– более крутой. Отрицательным пределом
величины эксцесса является число –2,
положительный предел – не существует.

11.Какие
оценки параметров называют точечными?
Перечислите основные свойства точечных
оценок.

Точечной
оценкой
неизвестного
параметра распределения θ
называется
приближенное значение этого параметра,
полученное по данным выборки
.

Основные
свойства точечных оценок: состоятельность,
несмещенность, эффективность.

12.Каковы точечные оценки математического ожидания и дисперсии?

Точечная
оценка математического ожидания
определяется по формуле

Точечная
оценка дисперсии
определяется по формуле

13.В чем состоит метод максимального правдоподобия?

Пусть
Х
– дискретная случайная величина, которая
в результате п
испытаний приняла значения х₁,
х₂,
…, х_п.
Предположим, что нам известен закон
распределения этой величины, определяемый
параметром Θ, но неизвестно численное
значение этого параметра. Найдем его
точечную оценку.

Пусть
р(х_i,
Θ)
– вероятность того, что в результате
испытания величина Х
примет значение х_i.
Назовем функцией правдоподобия дискретной
случайной величины Х
функцию аргумента Θ, определяемую по
формуле:

L
(х₁,
х₂,
…, х_п;
Θ)
= p(x₁,Θ)p(x₂,Θ)…p(x_n,Θ).

Тогда
в качестве точечной оценки параметра
Θ принимают такое его значение Θ* = Θ(х₁,
х₂,
…, х_п),
при котором функция правдоподобия
достигает максимума. Оценку Θ* называют
оценкой наибольшего правдоподобия.

Поскольку
функции L
и lnL
достигают максимума при одном и том же
значении Θ, удобнее искать максимум ln
L
– логарифмической функции правдоподобия.
Для этого нужно:

1. найти
   производную
   ;

2. приравнять
   ее нулю (получим так называемое уравнение
   правдоподобия)
   и найти критическую точку;

3. найти
   вторую производную
   ;
   если она отрицательна в критической
   точке, то это – точка максимума.

Достоинства
метода наибольшего правдоподобия:
полученные оценки состоятельны (хотя
могут быть смещенными), распределены
асимптотически нормально при больших
значениях п
и имеют наименьшую дисперсию по сравнению
с другими асимптотически нормальными
оценками; если для оцениваемого параметра
Θ существует эффективная оценка Θ*, то
уравнение правдоподобия имеет единственное
решение Θ*; метод наиболее полно использует
данные выборки и поэтому особенно
полезен в случае малых выборок.

Недостаток
метода наибольшего правдоподобия:
сложность вычислений.

Для
непрерывной случайной величины с
известным видом плотности распределения
f(x)
и неизвестным параметром Θ функция
правдоподобия имеет вид:

L
(х₁,
х₂,
…, х_п;
Θ)
= f(x₁,Θ)f(x₂,Θ)…f(x_n,Θ).

Оценка
наибольшего правдоподобия неизвестного
параметра проводится так же, как для
дискретной случайной величины.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Распределение коммерческих банков по размеру активов характеризуется следующими данными:

Определите характеристики распределения:

а) среднюю;

б) моду;

в) среднее квадратическое отклонение;

г) коэффициент вариации;

д) коэффициент асимметрии и эксцесс.

Решение:

Данный интервальный вариационный ряд содержит открытые интервалы, которые предварительно необходимо закрыть. Для этого из величины верхней границы первого интервала надо вычесть величину второго интервала. Получим нижнюю границу первого интервала.

200 — 100 = 100.

Первый интервал: 100 — 200.

Теперь к нижней границе последнего интервала прибавляем величину предшествующего интервала:

600 + 100 = 700

Последний интервал: 600 — 700.

а) Определение средней по сгруппированным данным производится по формуле средней арифметической взвешенной:

Чтобы применить эту формулу, необходимо варианты признака выразить одним числом (дискретным). За такое дискретное число принимается средняя арифметическая простая из верхнего и нижнего значения каждого интервала.

Так, например, дискретная величина х для первого интервала будет равна: (100 + 200) / 2 = 150.

Построим таблицу рассчётных данных:

 Дальнейший расчёт производится обычным методом определения средней арифметической взвешенной.

б) Определим моду.

Мода — это величина признака наиболее часто встречающегося в совокупности.

В интервальных рядах распределения с равными интервалами мода определяется по формуле:

где

х_Мо – начальное значение интервала, содержащего моду;

i_Мо – величина модального интервала,

f_Мо – частота модального интервала,

f_Мо-1 – частота интервала, предшествующего модальному,

f_Мо+1 – частота интервала, следующего за модальным.

Мода содержится в интервале от 300 до 400, так как у этого интервала наибоьшая частота

f = 52.

  млн. руб.

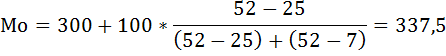
в) Найдём среднее квадратическое отклонение:

Значения размера активов в ряду распределения могут отличаться от среднего значения на 104,28 млн. руб.

Дисперсия будет равна:

σ² = 10 875

г) Коэффициент вариации рассчитаем по формуле:

Совокупность однородна, так как коэффициент вариации не превышает 33%.

д) Рассчитаем показатель асимметрии через отношение центрального момента третьего порядка к среднему квадратическому отклонению данного ряда в кубе, то есть

где μ₃ — центральный момент третьего порядка, рассчитываемый по формуле:

μ₃ = 88 275 000 / 100 = 882 750

As = 882 750 / 104,28³ = 0,78

Так как величина показателя асимметрии положительна, следовательно, речь идёт о правосторонней асимметрии.

Полученный результат свидетельствует о наличии несущественной по величине и положительной по своему характеру асимметрии.

Далее рассчитаем показатель эксцесса (Е_k). Наиболее точно он определяется по формуле с использованием центрального момента четвёртого порядка:

μ₄ = 52 123 312 500 / 100 = 521 233 125

σ⁴ = 118 265 625

E_k = 521 233 125 / 118 265 625 – 3 = 4,41 — 3 = 1,41

Так как Ek > 0 распределение является островершинным.

1. выборочное среднее;
2. выборочную дисперсию;;
3. подправленную дисперсию;
4. выборочное среднее квадратичное отклонение;
5. подправленное среднее квадратичное отклонение;
6. размах выборки;
7. медиану;
8. моду;
9. квантильное отклонение;
10. коэффициент вариации;
11. коэффициент асимметрии;
12. эксцесс для выборки:

Выборка задана рядом 11, 9, 8, 7, 8, 11, 10, 9, 12, 7, 6, 11, 8, 7, 10, 9, 11, 8, 13, 8.

Решение:
Запишем выборку в виде вариационного ряда (в порядке возрастания):
6; 7; 7; 7; 8; 8; 8; 8; 8; 9; 9; 9; 10; 10; 11; 11; 11; 11; 12; 13.
Далее записываем статистическое распределение выборки в виде дискретного статистического распределения частот:

Эмпирическую функцию распределения определим по формуле

Здесь n_x – количество элементов выборки которые меньше х. Используя таблицу и учитывая что объем выборки равен n = 20, запишем эмпирическую функцию распределения:

Далее вычислим числовые характеристики статистического распределения выборки.
Выборочное среднее вычисляем по формуле

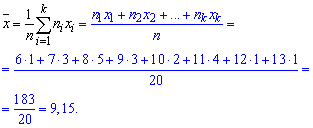
Выборочную дисперсию находим по формуле


Выборочное среднее, что фигурирует в формуле дисперсии в квадрате найдено выше. Остается все подставить в формулу

Подправленную дисперсию вычисляем согласно формулы

Выборочное среднее квадратичное отклонение вычисляем по формуле

Подправленное среднее квадратичное отклонение вычисляем как корень из подправленной дисперсии

Размах выборки вычисляем как разность между наибольшим и наименьшим значениями вариант, то есть:

Медиану находим по 2 формулам:
если число n — четное;
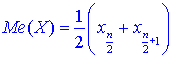
если число n — нечетное.
Здесь берем индексы в x_i согласно нумерации варианта в вариационном ряду.
В нашем случае n = 20, поэтому

Мода – это варианта которая в вариационном ряду случается чаще всего, то есть

Квантильное отклонение находят по формуле

где – первый квантиль, – третий квантиль.
Квантили получаем при разбивке вариационного ряда на 4 равные части.
Для заданного статистического распределения квантильное отклонения примет значение

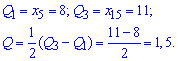
Коэффициент вариации равный процентному отношению подправленного среднего квадратичного к выборочному среднему

Коэффициент асимметрии находим по формуле

Здесь 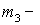центральный эмпирический момент 3-го порядка,

Подставляем в формулу коэффициента асимметрии

Эксцессом статистического распределения выборки называется число, которое вычисляют по формуле:

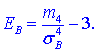
Здесь m₄ центральный эмпирический момент 4-го порядка. Находим момент

а далее эксцесс
Теперь Вы имеете все необходимые формулы чтобы найти числовые характеристики статистического распределения. Как найти моду, медиану и дисперсию должен знать каждый студент, который изучает теорию вероятностей.

Готовые решения по теории вероятностей

• Следующая статья — Построение уравнения прямой регрессии Y на X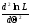