День добрый, дорогой друг!
В предыдущей статье мы с вами разбирали коэффициент Бухгольца. Что это за штука, когда и где он применяется. Сегодня под нашим пристальным взором коэффициент Бергера, — в своем роде «сводный брат» Бухгольца.
Что это такое?
Коэффициент Бергера представляет собой дополнительный числовой показатель и используется для ранжирования участников в турнирной таблице. Принимается во внимание только в случае равенства очков участников.
Автором идеи является чех Оскар Гельбфус, предложивший подобный способ ранжирования в 1873г. В турнирную практику коэффициент Бергера вошел начиная с турнира в Ливерпуле в 1882 году благодаря усилиям Уильяма Зоннеборна и Иоганна Бергера.
Как видите, история распределения мест с помощью «Бергера» прошла более чем солидную проверку временем.
Коэффициент Бергера применяется в турнирах по круговой системе. Когда все участники играют между собой по очереди.
Как считать?
Спешу вас успокоить, никакой высшей математики здесь нет. При желании можно посчитать все в уме.
Формула для посчета коэффициента Бергера выглядит следующим образом:
КБ = СуммаВ + ½ суммыН, где
СуммаВ — Сумма очков соперников у которых участник выиграл
СуммаН — Сумма очков соперников, с которыми участник сыграл вничью.
Очки соперников, которым участник проиграл, — не учитывается. Вернее сумма считается равной нулю.
Например:
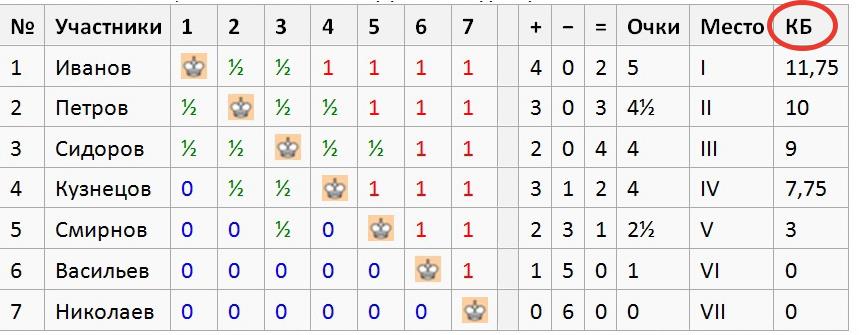
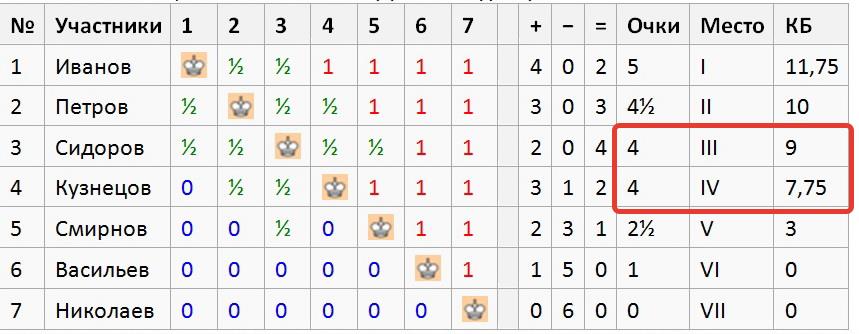
В таблице, приведенной выше, Сидоров и Кузнецов набрали по 4 очка. Для ранжирования в иоговой таблице турнира посчитаем «Бергер» этих участников:
Сидоров: 1 + ½* (5 +4.5 +4 +2.5) = 9
Кузнецов: (2.5 +1) + ½* (4.5 +4) = 7.75
Таким образом, Сидоров опережает Кузнецова в турнирной таблице при равенстве очков по дополнительному показателю – коэффициенту Бергера.
Логика «Бергера»
Любой дополнительный показатель, влияющий на итоговое распределение мест в таблице должен иметь определенную логику. Как бы нести в себе «зерно справедливости».
Логика «Бергера» определяется формулой расчета коэффициента: преимущество имеет игрок, набирающий больше очков против более сильных соперников.
Не скажу, что такая логика безоговорочно справедлива и не может вызывать вопросов.
Возможно поэтому, в последние годы для определения призовых мест, часто вместо дополнительных показателей практикуются дополнительные партии с укороченным контролем. Что не говори, результат за доской всегда в приоритете.
Однако и без дополнительных показателей, особенно при распределении не призовых мест, вряд ли можно обойтись. В почти полутора-вековой истории шахмат ничего более адекватного, чем КБ никто не придумал.
Коэффициент Бергера по-прежнему живет и здравствует также как в 1882г. в Ливерпуле.
Упрощенный подсчет
Примерно с восьмидесятых годов вошел в практику и упрощенный подсчет.
Считается еще проще: Очки поверженных соперников плюсуются, очки тех, кому уступил, — минусуются (берутся со знаком минус). Сумма считается простым арифметическим сложением.
Такой способ упрощает расчеты.
Типичная ошибка
Для турнирной борьбы обычной является такая ситуация: перед последним туром участники прикидывают коэффициенты. Для того, чтобы выбрать тактику на последнюю партию. Например, шахматист Петров думает:
«Мне достаточно сделать ничью, ибо если Иванов обыграет Пупкина и догонит меня по очкам, Бергер у меня лучше»
И Петров соглашается на ничью в позиции с отличными шансами на победу, предвкушая процедуру награждения.
Однако при подсчете коэффициентов вдруг оказывается, что его Бергер хуже, чем у Иванова!
Секрет прост. В последнем туре игрались партии и начислялись очки. Петров же при своих прикидках ориентировался на «очковую массу», которая была актуальна до последнего тура.
Хорошо, когда вы играете в команде, есть тренер или другой человек, который «считает» все эти нюансы. Часто в режиме «онлайн» по ходу последнего тура. Также не составляет труда сделать какой-нибудь калькулятор.
Однако отвлекаться на подобные вещи во время партии весьма рискованно. Полагаю, излишне объяснять, что лучшая математика – победа за доской.
Благодарю за интерес к статье.
Если вы нашли ее полезной, сделайте следующее:
- Поделитесь с друзьями, нажав на кнопки социальных сетей.
- Напишите комментарий (внизу страницы)
- Подпишитесь на обновления блога (форма под кнопками соцсетей) и получайте статьи к себе на почту.
Раньше мы разбирались, что собой представляет коэффициент Бухгольца, где и в каких случаях он используется. Сейчас рассмотрим коэффициент Бергера, который можно считать «сводным братом» Бухгольца.
Что такое коэффициент Бергера
Коэффициент Бергера – это дополнительный числовой показатель, который необходим для ранжирования участников в турнирной таблице. Используется только в том случае, когда наблюдается равенство очков. Реализовал данную идею чех Оскар Гельбфус в далеком 1873 году. Ввели коэффициент в турнирную практику Уильям Зоннеборн и Иоганн Бергер в 1882 году на одном из турниров в Ливерпуле.
Как считать коэффициент Бергера
Для выполнения подсчетов не нужно знаний высшей математики – все можно выполнить в уме. Формула коэффициента Бергера следующая:
КБ = СуммаВ + ½ суммыН
- СуммаВ – суммарные очки соперников, с которыми зафиксирован выигрыш.
- СуммаН – суммарное количество очков противников, с которыми была сделана ничья.
Набранные очки тех противников, с которыми зафиксирован проигрыш, в счет не берутся – их сумма равняется нулю.
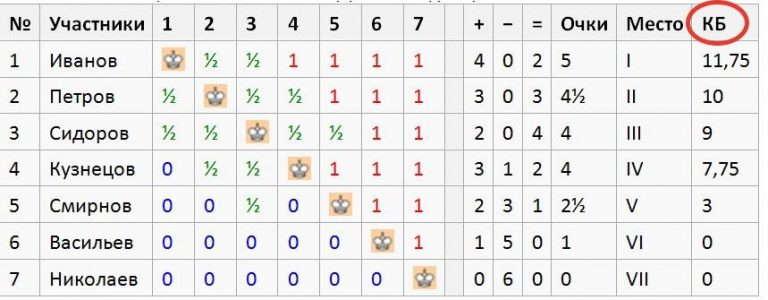
Приведем простой пример на основании вышеприведенной таблицы. Игроки Сидоров и Кузнецов имеют в своем зачете по 4 очка. Чтобы выяснить, кто из них ранжируется выше в итоговой таблице, произведем подсчет коэффициента Бергера:
Сидоров: 1 + ½*(5 +4.5 +4 +2.5) = 9
Кузнецов: (2.5 +1) + ½*(4.5 +4) = 7.75
Как можно наблюдать, Сидоров занимает более высокую позицию в финальном зачете при одинаковом количестве очков именно по Бергеру.
Когда применяется Бергер
Каждый показатель дополнительного плана, который влияет на итоговое распределение мест в турнирной таблице, должен иметь под собой логическое обоснование. «Справедливость» коэффициента Бергера заложена в формуле расчета рейтинга – преимуществом обладает тот игрок, который набрал больше очков в играх с более сильными соперниками.
Нужно отметить, что данная логика иногда вызывает ряд вопросов среди игроков. Именно из-за этого при распределении призовых позиций вошли в практику дополнительные партии, имеющие укороченный контроль. Результат за игровой доской всегда будет приоритетным. Но и без дополнительных показателей обойтись не получится (особенно во время распределения не призовых мест). За полторы сотни лет шахматисты ничего лучше коэффициента Бергера еще не придумали.
В 80-х годах стал популярным упрощенный подсчет, который заключается в том, что очки поверженных игроков идут со знаком плюс, а очки тех, кому игрок проиграл, идут со знаком минус. Конечный показатель вычисляется путем арифметического сложения.
Ошибки при подсчете
При турнирной борьбе часто возникает ситуация, когда перед заключительным туром игроки занимаются анализом коэффициентов, после чего выстраивают тактику на завершающую партию. К примеру, шахматист Иванов думает, что ему можно в последней партии сыграть вничью: «Если Петров обыграет Сидорова (с большой вероятностью) и наберет одинаковое со мной количество очков, по Бергеру я займу более высокую позицию». Иванов делает ничью в партии с прекрасными шансами и с радостью ждет награждение участников. Но при конечном просчете коэффициентов Бергера выясняется, что Петров по данному показателю его опередил.
Почему так происходит? Все элементарно. Иванов при подсчете ориентировался на коэффициенты перед последним туром, в котором проводилось множество поединков. «Очковая» масса изменилась, что и повлекло за собой проигрыш Иванова. Хорошо, когда в команде есть помощник, который ведет подсчет коэффициентов Бергера во время последнего тура в режиме онлайн и передает результаты игроку. Но отвлекаться на данные вещи во время партии не стоит, ведь гораздо надежнее все решать за шахматной доской.
Коэффициент Бергера используется для распределения мест в шахматных турнирах среди участников, набравших равное количество очков. Коэффициент Бергера участника равен сумме всех очков противников, у которых он выиграл, плюс половина суммы очков противников, с которыми он сыграл вничью.
Константин Яковлев — один из участников шахматного турнира, состоящего из 8 туров. В таблице показано количество очков, набранных в турнире соперника Константина, и результат игры с Константином.
1 — выиграл Константин,
0,5 — ничья,
0 — проиграл Константин.
| Тур | Соперник | Очки | Результат |
|---|---|---|---|
| 1 | Васильев Тимур | 5,0 | 0 |
| 2 | Новикова Евгения | 4,0 | 1 |
| 3 | Тарасов Валентин | 6,0 | 0,5 |
| 4 | Павлова Анастасия | 3,0 | 1 |
| 5 | Борисов Степан | 5,5 | 0 |
| 6 | Веселов Дмитрий | 5,0 | 0,5 |
| 7 | Афанасьев Тимур | 8,0 | 0 |
| 8 | Григорьев Павел | 6,0 | 1 |
Вычислите коэффициент Бергера шахматиста Константина Яковлева.
Коэффицие́нт Бе́ргера — способ определения мест в соревнованиях среди участников, набравших равное количество очков. Способ определения места по коэффициенту Бергера был первоначально разработан для круговых (каждый играет с каждым) шахматных турниров. Позже этот метод стали применять и для других соревнований, например, в сёги и го.
Порядок вычисления
В круговых турнирах, где за победу, ничью и поражение присуждается определённое постоянное число очков (например, в шахматах за победу даётся 1 очко, за ничью — 0,5 очка, за поражение — 0 очков), часто случается так, что два или несколько участников набирают одинаковое количество очков. Чтобы определить, кто из этих участников занял более высокое место, подсчитывают коэффициенты Бергера участников.
Коэффициент Бергера определённого участника складывается из суммы всех очков противников, у которых данный участник выиграл, плюс половина суммы очков противников, с которыми данный участник сыграл вничью. Идея, на которой базируется коэффициент: из двух участников, равных по числу очков, сильнее тот, кто выиграл у более сильных противников, то есть у тех, кто набрал больше очков. Поэтому участнику, имеющему больший коэффициент Бергера, присуждается более высокое итоговое место в турнире.
Коэффициент Бергера придуман для круговых турниров, но может, при необходимости, применяться и в других схемах розыгрыша, где игроками, места которых надо распределять, играется равное число партий. Можно его использовать и в турнирах по швейцарской системе, хотя традиционно там применяется коэффициент Бухгольца. В круговых турнирах с 1985 года применяется и «упрощённый Бергер» (предложен М.Дворецким): очки всех соперников, у кого шахматист выиграл, берутся со знаком «плюс», а всех, кому он проиграл — со знаком «минус», по сумме и считается лучший результат. Это позволяет сократить расчёты и не делить предварительно пополам большинство результатов.
Пример
Итоговая таблица гипотетического кругового турнира:
| № | Участники | 1 | 2 | 3 | 4 | 5 | 6 | 7 | + | − | = | Очки | Место | КБ | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Иванов | ½ | ½ | 1 | 1 | 1 | 1 | 4 | 0 | 2 | 5 | I | 11,75 | ||
| 2 | Петров | ½ | ½ | ½ | 1 | 1 | 1 | 3 | 0 | 3 | 4½ | II | 10 | ||
| 3 | Сидоров | ½ | ½ | ½ | ½ | 1 | 1 | 2 | 0 | 4 | 4 | III | 9 | ||
| 4 | Кузнецов | 0 | ½ | ½ | 1 | 1 | 1 | 3 | 1 | 2 | 4 | IV | 7,75 | ||
| 5 | Смирнов | 0 | 0 | ½ | 0 | 1 | 1 | 2 | 3 | 1 | 2½ | V | 3 | ||
| 6 | Васильев | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 5 | 0 | 1 | VI | 0 | ||
| 7 | Николаев | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6 | 0 | 0 | VII | 0 |
Обозначения: 1 — победа, ½ — ничья, 0 — поражение, КБ — коэффициент Бергера.
Участники Сидоров и Кузнецов набрали одинаковое количество очков, по 4 очка. Кто из них займет третье место, решается по коэффициенту Бергера.
Коэффициент Бергера участника Сидорова складывается так: 2,5 (половина очков Иванова) + 2,25 (половина очков Петрова) + 2 (половина очков Кузнецова) + 1,25 (половина очков Смирнова) + 1 (все очки Васильева) + 0 (все очки Николаева) = 9.
Коэффициент Бергера участника Кузнецова так: 0 (за поражение от Иванова) + 2,25 (половина очков Петрова) + 2 (половина очков Сидорова) + 2,5 (все очки Смирнова) + 1 (все очки Васильева) + 0 (все очки Николаева) = 7,75.
Таким образов участник Сидоров имеет более высокий коэффициент Бергера чем участник Кузнецов (9 против 7,75), поэтому третье место присуждается Сидорову. Коэффициент Бергера более высок у того, кто выигрывает или добивается ничьей с более сильными игроками (игроками набирающими большее количество очков). В приведённом примере выигрыш у участника, имеющего ноль очков, не даёт вклада в коэффициент Бергера.
История
Первым такую систему подсчета очков предложил чехословацкий шахматный мастер Оскар Гелбфус (Oskar Gelbfuhs) (9 ноября 1852, Штернберг (Sternberg), Чехословакия — 27 сентября 1877, Тезин (Tesin), Чехословакия) в августе 1873 года. Впервые, на практике, такую систему распределения мест применили Уильям Зоннеборн (William Sonneborn) (1843—1906) и Иоганн Бергер на турнире в Ливерпуле в 1882 году. В 1886 году подсчёт очков по коэффициенту Бергера был введён в практику.
Литература
- Шахматы. Энциклопедический словарь / гл. ред. А. Е. Карпов. — М.: Советская энциклопедия, 1990. — С. 357—358. — 100 000 экз. — ISBN 5-85270-005-3
См. также
- Круговая система
- Швейцарская система
- Коэффициент Бухгольца
| |
|
|---|---|
| Система соревнований | Круговая · Матч · Матч-турнир · Олимпийская · Система Силли · Схевенингенская · Швейцарская · Мак-Магона |
| Система коэффициентов | Коэффициент Бергера · Коэффициент Бухгольца |
Виктор набрал пять очков. Как и Денисова Ольга, с которой он сыграл вничью. Но, возможно, у Ольги просто были более слабые (или более сильные) соперники. Для того, чтобы понять, кто все же сильнее в этом турнире, подсчитаем коэффициент Бергера для Виктора:
1) Щербаков Степан — у него Виктор выиграл +3 балла.
2) Константинов Павел — сыграли вничью — 4,5/2=2,25 то есть +2,25
3) Денисова Ольга сыграли вничью — 5/2=2,5 то есть плюс 2,5
4) Андреев Игорь, тут Виктор выиграл +3 балла
5) Волков Тимофей, сыграли вничью 3,5/2=1,75
6) Петров Иван — тут Виктор проиграл, 0
7) Полякова Юлия, Виктор выиграл, +3

Суммируем полученные очки
3+2,25+2,5+3+1,75+3+2,5 = 18