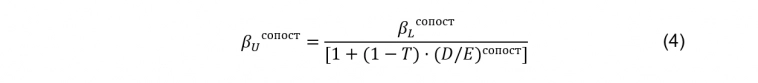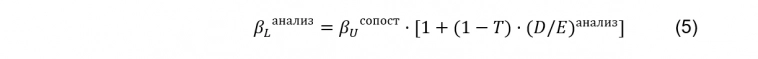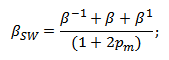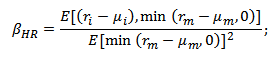Любой инвестор, когда начинает более глубоко погружаться в тему инвестирования в акции, обязательно сталкивается с таким понятием, как коэффициент бета. В данной статье мы рассмотрим следующие ключевые моменты для понимания того, что такое коэффициент бета, и как с ним стоит работать:
-
Что такое бета коэффиент акции.
-
Формула коэффициента бета.
-
Значения коэффициента бета.
-
Расчет коэффициента бета.
-
Пример расчета коэффициента бета.
-
Бета коэффициент портфеля.
Бета коэффициент акции
Коэффициент бета – это статистический коэффициент, который характеризует движение отдельной акции относительно всего рынка в целом.
Изначально бета коэффициент своими создателями задумывался как коэффициент меры риска для отдельной акции относительно всего рынка в целом, при этом для сравнения, как правило, берется динамика основного рыночного фондового индекса. Это определяется путем сравнения поведения цены акции и рыночного фондового индекса. Сравнивая различные периоды роста и падения фондового индекса и те же периоды у акции, мы можем понять, как акция вела себя в той или иной момент. Реагировала на внешние факторы так же сильно, как и рынок в целом или наоборот, акции проявляли большую устойчивость.
Формула коэффициента бета
Формула расчета коэффициента бета достаточно сложна и с чисто математической точки зрения её можно представить следующим образом:
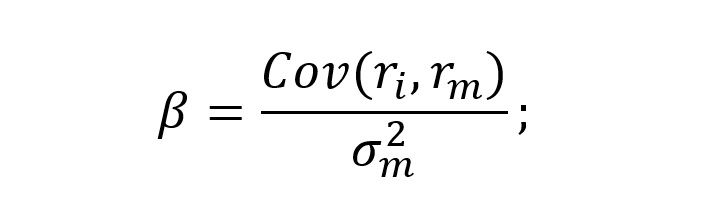
Где:
ri – доходность отдельно взятой (i-й) акции в инвестиционном портфеле за определенный период времени;
rm – доходность рынка (как правило, доходность основного фондового индекса) за определенный период времени;
σ2m – дисперсия доходности рынка (как правило, доходности основного фондового индекса) за определенный период времени.
Если же говорить по смыслу данной формулы, то в числителе находится значения зависимости (корреляции) доходности акции от доходности фондового индекса за определенный период, а в знаменателе разброс доходностей фондового индекса относительно средней доходности за определенный период.
Поэтому, исходя из данной формулы, сразу можно определить, что коэффициент бета будет давать нам представление о степени зависимости доходности акции от доходности фондового индекса, а также о том, насколько доходность отдельной акции в среднем превышает или наоборот, оказывается ниже доходности индекса.
Значения коэффициента бета
Теперь давайте разберемся в показателях коэффициента бета и как их стоит интерпретировать инвестору. Для коэффициента бета характерны несколько пороговых уровней:
-
Коэффициент бета больше 1. Это свидетельствует о том, что динамика акции коррелирует с динамикой фондового индекса, но при этом акция более чувствительно реагирует на любое движение индекса. Например, фондовый индекс растет на 1%, а акция при этом будет расти на 2% и точно так же наоборот, фондовый индекс снижается на 1%, а акция при этом снижается еще большими темпами, например, на 2%.
-
Коэффициент беты равен 1. Это говорит о том, что движения акции полностью повторяют движение фондового индекса, то есть корреляция движений акции и индекса 100%.
-
Коэффициент бета находится в диапазоне больше 0, но меньше 1. Это свидетельствует о том, что в-первую очередь динамика акции коррелирует с динамикой фондового индекса. То есть, акция движется в целом в одном направлении со всем рынком, если фондовый индекс растет, то растет и акция. Но также это говорит о том, что акция менее чувствительно реагирует на движения рынка в целом.
-
Коэффициент бета равен нулю. В данном случае такое значение коэффициента означает, что движение акции вообще никак не связано с движением фондового индекса или по-другому можно сказать, что никак не коррелируют.
-
Коэффициент бета отрицательный и находится в диапазоне от 0 до -1. В данном случае акция имеем обратную корреляцию с фондовым индексом. При этом чувствительность реакции акции более низкая, чем у фондового индекса. Например, фондовый индекс растет на 2%, при этом акция с такими показателями коэффициента бета будет снижаться, но более низкими темпами, нежели растет индекс, то есть, например, на 1%. Точно такая же ситуация справедлива и наоборот, если фондовый индекс будет снижаться на 2%, такая акция будет расти на 1%.
-
Коэффициент бета отрицательный и меньше -1. Такие акции имеют обратную корреляцию с фондовым индексом, то есть в целом движутся в противоположном направлении, при этом такие акции более волатильны и двигаются с большей амплитудой нежели сам индекс. То есть в данном случае акция будет двигаться в противоположную сторону рынку и более сильно реагировать на любые движения фондового индекса. Например, индекс растет на 1%, а акция при этом будет снижаться на 2%, и точно так же наоборот, при снижении рынка на 1%, акция с таким значением коэффициента бета будет расти на 2%.
Таким образом коэффициент бета несет для инвесторов различную ценную информацию: насколько более чувствительно реагирует акция на основные рыночные тенденции и есть ли в данной бумаге внутренняя идея, способная игнорировать общерыночные тенденции, которые охватывают своим движением большинство бумаг на рынке.
Расчет коэффициента бета
Перед большинством инвесторов тут же встает вопрос, как и где взять расчета коэффициента бета, так как формула расчета его достаточно сложна и ручной расчет его просто не представляется возможным.
Здесь стоит прежде всего сказать, что на самом деле расчет коэффициента бета на российском рынке регламентирован и стандартизирован, причем регламентирован он положением Центрального Банка «Положение о деятельности по проведению организованных торгов» (утв. Банком России 17.10.2014 N 437-П). В приложении №2 идет подробное описание расчета коэффициента бета.

Так же расчет коэффициента бета проводится непосредственно самой московской биржей по принципу, описанному в положении Центрального Банка. Коэффициент бета рассчитывается на конец каждой торговой сессии, и его расчет можно скачать на сайте Московской биржи https://www.moex.com/ru/forts/coefficients-values.aspx
При этом, как мы видим из формулы расчета коэффициента, что он рассчитывается за период последних 30-и торговых сессий.
Расчет коэффициента бета происходит точно так же, как и расчет многих технических индикаторов рынка, то есть по принципу скользящего окна, когда в расчетный диапазон коэффициента попадают лишь только 30 последних ценовых значений, и данный диапазон постоянно сдвигается, как только в расчет попадет котировка новой торговой сессии.
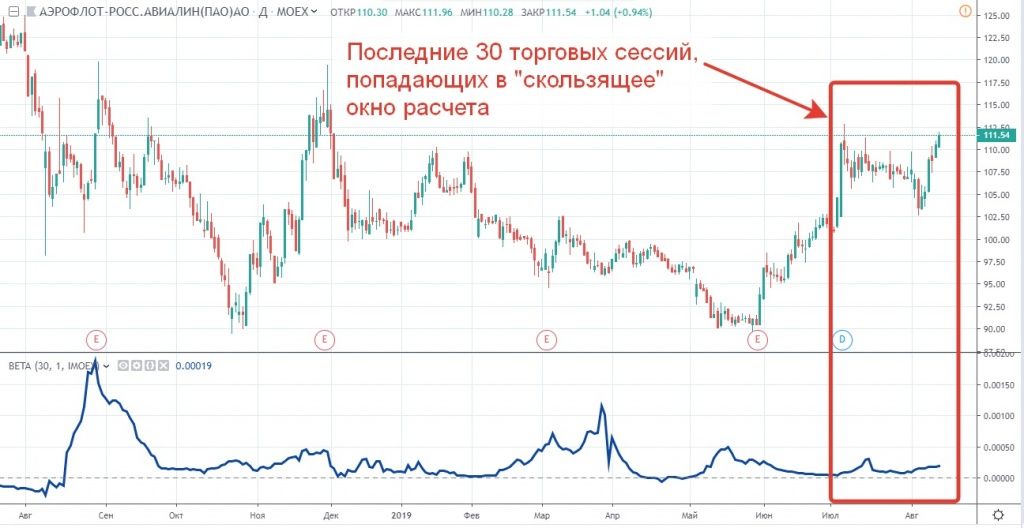
За счет того, что период расчета коэффициента бета сравнительно мал, с инвестиционной точки зрения, это приводит к тому, что значения коэффициента очень волатильны и сильно изменяются во времени. Иногда значение коэффициента от одного месяца к другому может изменяться кардинально, как с точки зрения характеризующей корреляцию акции и индекса, так и с точки зрения степени чувствительности реакции акции на движения индекса. Это можно заметить даже просто по скользящему графику расчета коэффициента, так как во времени он изменяется очень активно и очень резко.
Иными словами, рассчитанные подобным образом значения коэффициента бета, отражают лишь локальные и очень краткосрочные рыночные тенденции, которые не отражают в полной мере заложенных фундаментальных принципов в данный коэффициент.
Изначально коэффициент бета разрабатывался и применялся исключительно в инвестиционных целях и активно использовался для формирования инвестиционных портфелей, в том числе портфелей по модели «Марковица». С этой точки зрения, расчет коэффициента за такой короткий промежуток времени полностью некорректен и не может применяться с инвестиционными целями.
Однако, корректный расчет показателя бета можно сделать даже с помощью инструментов MS Excel, именно такой калькулятор для расчета коэффициента бета мы и реализовали в рамках нашего курса обучения «Школа разумного инвестирования».
Для того чтобы коэффициент бета отражал именно долгосрочные инвестиционные тенденции в акциях, мы должны прибегать к его расчету за более длительные горизонты от 3-х лет.
Пример расчета бета коэффициента
Проведем расчет коэффициента бета на различных бумагах за более длительный промежуток времени с помощью калькулятора для расчета бета коэффициента.
Для расчета мы выберем акции с потенциально бОльшим и потенциально меньшим коэффициентом бета. В качестве примера более агрессивно движущейся акции, которая имеет положительную корреляцию с рынком, мы возьмем обыкновенные акции Сбербанка, а в качестве примера бумаги, которая не зависит от колебаний рынка в целом и демонстрирует самостоятельную динамику, мы возьмем привилегированные акции компании Ленэнерго.
В калькуляторе заполняются поля с датами торговых периодов за последние 3 года, значения дневных цен закрытия по акции за последние 3 года, а также значения фондового индекса на конец торговой сессии за последние 3 года.
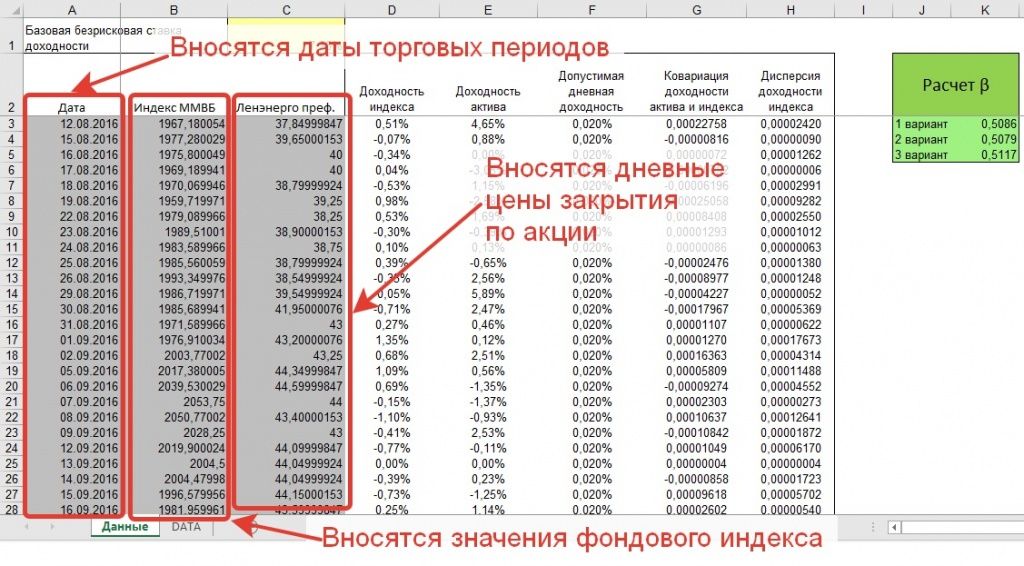
Расчет коэффициента бета в калькуляторе проводится тремя различными способами для подтверждения статистической достоверности расчета коэффициента.
После заполнения данных по котировкам акций Сбербанка и индекса московкой биржи за последние 3 года, мы видим, что значение коэффициента бета по бумаге оказывается большим чем 1.
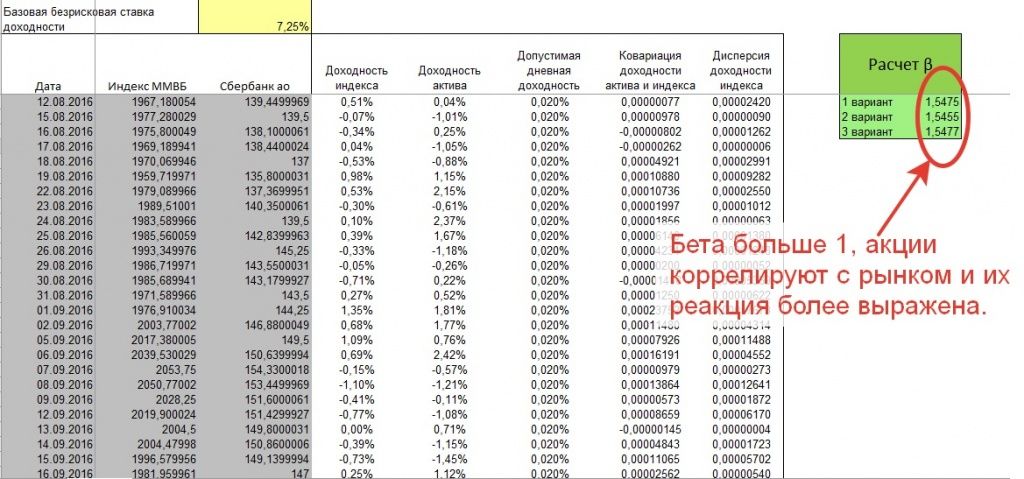
Положительное значение коэффициента бета по акциям Сбербанка говорит нам о том, что акции преимущественно движутся в том же направлении, что и рынок в целом, а значение коэффициента больше 1 свидетельствуют о том, что акции намного более сильно реагируют на рыночные движения.
Во втором случае мы так же проводили расчет коэффициента бета за последние 3 года по привилегированным акциям Ленэнерго.
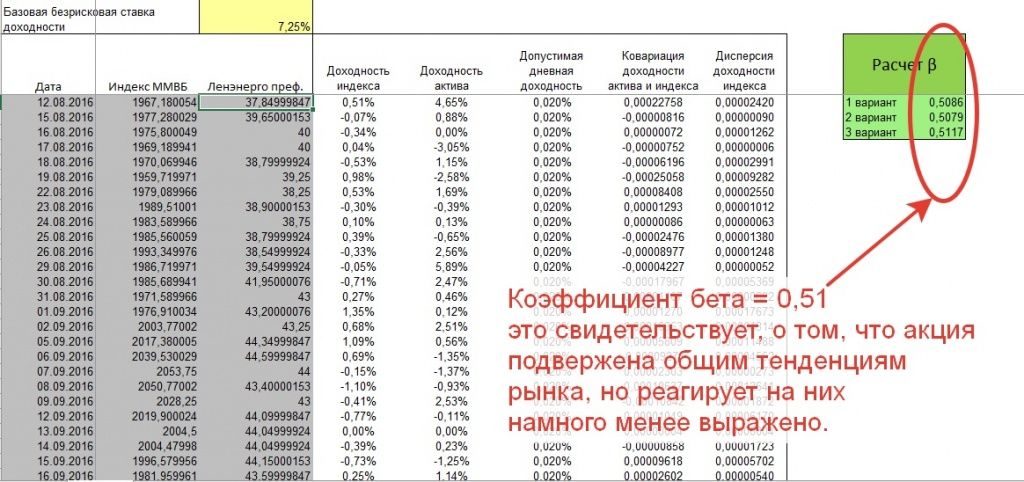
В данном случае значение коэффициента бета оказывается равным 0,51, что свидетельствует о том, что в целом акция не движется в противофазе рынку и лишь частично подвержена влияниям основных общерыночных тенденций.
Бета коэффициент портфеля (практика применения)
Использование коэффициента бета при формировании портфеля и в процессе управление инвестиционным портфелем – это одна из основных, базовых практик портфельного инвестирования, так как значение корректно рассчитанного коэффициента отражает то, как бумага за счет своих внутренних фундаментальных свойств «отрабатывает» движения общерыночных тенденций. Особенно в этом ключе важно понимание того, что под общерыночными тенденциями мы в первую очередь, как правило, подразумеваем общие негативные движения рынка, или проявление кризисных моментов на рынке, которые влияют на все акции. Когда большинство акций на рынке снижается, те бумаги, которые способны противостоять общерыночному снижению, представляют особенную ценность для инвестиционного портфеля.
Поэтому коэффициент бета в инвестиционных портфелях, как правило, в первую очередь может применяться, как весовой коэффициент, который распределяет средства портфеля в акции в зависимости от степени чувствительности к риску той или иной акции.
При этом, в случае, если основная концепция инвестиционного портфеля требует максимальной минимизации риска, то за счет бета коэффициента придается больший вес бумагам с малым значением коэффициента бета, или даже с его отрицательным значением. А в случае, если формируется агрессивный инвестиционный портфель, то веса распределяются наоборот. Акции с большим значением коэффициента бета получают больший вес в инвестиционном портфеле. Это позволяет добиться того, что на фазе роста фондового рынка, акции, включенные в инвестиционный портфель, реагируют более выражено и растут большими темпами, в итоге, это позволяет такому портфелю обгонять фондовый индекс по показателям доходности.
Как работает коэффициент бета мы можем увидеть даже визуально, наложив котировки акции, на значения фондового индекса.
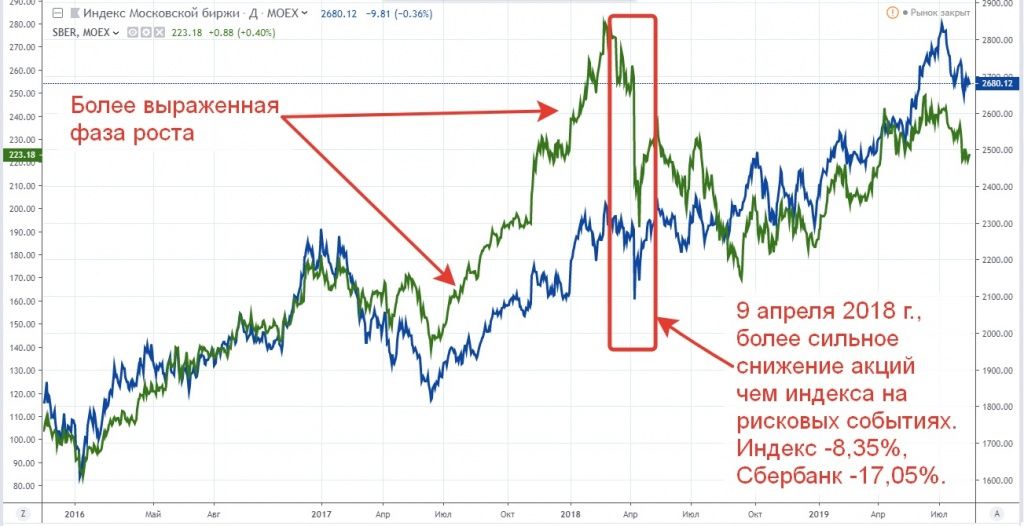
В случае с акцией Сбербанка, где коэффициент бета больше 1, мы можем наблюдать, что поведение бумаги более агрессивное, и если рынок растет, то бумаги растут еще большими темпами, а на коррекционных фазах мы видим, что просадки по акциям случаются более значительные чем по рынку в целом.
И практически противоположную картину мы можем увидеть в акциях с коэффициентом бета меньше 1.
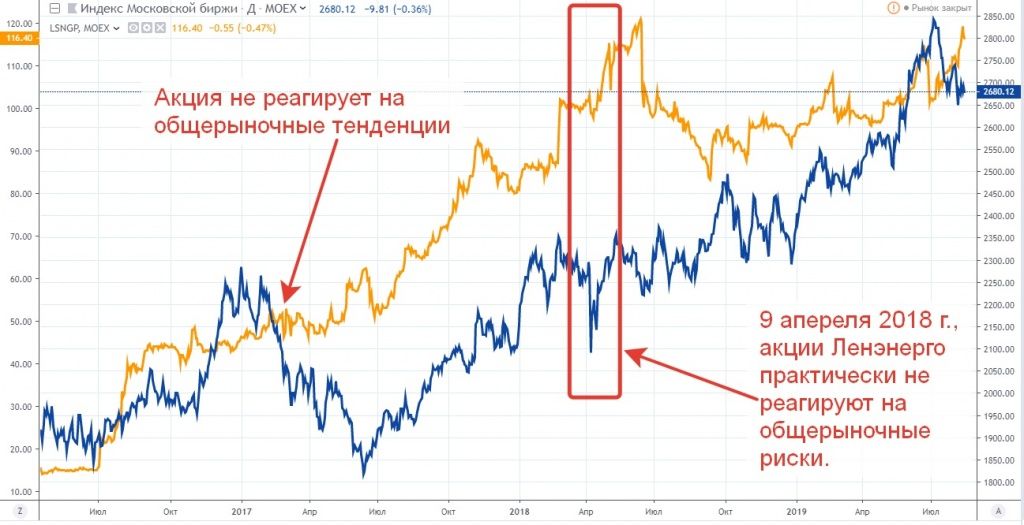
В нашем примере акции Ленэнерго преф. в момент острейшего проявления кризисных моментов на рынке демонстрировали высокую степень устойчивости и практически никак не реагировали на общерыночные тенденции. Поэтому акции, значение коэффициента бета которых меньше 1, так же еще причисляют к категории защитных бумаг, которые способны эффективно противостоять общерыночным негативным тенденциям.
Выводы
Как мы видим, коэффициент бета может быть очень эффективным и полезным инструментом при формировании инвестиционного портфеля, но только с учетом того, что инвесторы корректно определяют его значение и грамотно его используют.
Всему этому мы учим на нашем полном цикле курсов обучения «Школа разумного инвестирования». Начать обучение можно с посещения вводных бесплатных занятий. Записаться на ближайший бесплатный вебинар можно по ссылке — http://finplan.expert
Удачных Вам инвестиций!
Добрый день, друзья!Продолжаем наше исследование о ставках дисконтирования на российском фондовом рынке.
Часть 1 – smart-lab.ru/blog/903001.php
Часть 2 – https://smart-lab.ru/blog/905219.phpКраткое содержание предыдущих частей.Наша исследовательская группа поставила задачу рассчитать параметры моделей CAPM, WACC и ставку дисконтирования, базируясь исключительно на российской финансовой статистике.
Д
ля этого мы определили доходность безрискового актива и премию за рыночный (корпоративный) риск для российского фондового рынка и подошли к расчёту коэффициента бета.____________
Коэффициент β (бета)характеризует меру отраслевого и финансового риска, свойственного для анализируемой компании (отрасли) и отражает амплитуду колебаний её доходности относительно рынка в целом. Можно утверждать, что коэффициент βпоказывает, на сколько процентов изменятся котировки акций анализируемой компании при изменении рынка акций в целом на 1%.Математически бета представляет собой коэффициент регрессии в корреляционном уравнении зависимости доходности анализируемых акций от доходности фондового индекса за исследуемый период.
Расчёт беты для публичной компании выполняется путём регрессионного анализа доходности её акций относительно фондового индекса. Для непубличной компании (акции которой не торгуются на фондовом рынке), бета определяется как средневзвешенная величина коэффициентов β сопоставимых компаний той же отрасли (вида деятельности).
Выбор расчётного периода для определения беты зависит от горизонта планирования: чем он больше, тем больше должна быть глубина ретроспективной статистики для проведения регрессионного анализа. Большинство исследователей сходится в том, что для долгосрочного планирования оптимальным является анализ данных за пять лет. При краткосрочном прогнозировании достаточно проанализировать статистику за 1-2 года.
При этом у различных компаний отрасли может существенно отличаться долговая нагрузка (финансовый рычаг), что обуславливает различные финансовые риски компаний. Полученное в ходе регрессионного анализа значение коэффициента β учитывает фактические показатели финансового рычага сопоставимых компаний (так называемая «рычаговая» бета). Его необходимо «очистить» от фактора долговой нагрузки через формулу Р. Хамады и получить «безрычаговую» бету:
где βU сопост – безрычаговый коэффициент бета сопоставимых компаний;
βL сопост – рычаговый коэффициент бета сопоставимых компаний;
Т – ставка налога на прибыль, доля;
(D/E) сопост – отношение долга к собственному капиталу сопоставимых компаний.
Отношение долга к собственному капиталу (D/E) характеризует долговую нагрузку компании. В случае, когда бета определяется по нескольким сопоставимым компаниями, величина (D/E) сопост принимается как средняя величина.
При этом, в состав долга (D) следует включать только «платную» часть задолженности компании, по которой выплачиваются процентные платежи. В балансовом отчёте долг, как правило, отражается в составе кредитов и займов (краткосрочных и долгосрочных). И наоборот, в состав долга в данном случае не следует включать текущую кредиторскую задолженность и иные беспроцентные обязательства.
После расчёта безрычаговой беты необходимо оценить отношение долга к собственному капиталу анализируемой компании (D/E) анализ, после чего обратно пересчитать бету в рычаговую, используя новое значение долговой нагрузки:
где βLанализ– рычаговый коэффициент бета анализируемой компании;
βUсопост – безрычаговый коэффициент бета сопоставимых компаний;
Т – ставка налога на прибыль, доля;
(D/E) анализ – отношение долга к собственному капиталу анализируемой компании.
Отметим, что при расчёте беты отношение долга к собственному капиталу (D/E) анализопределяется в целом для компании (по её балансовому отчёту) и поэтому может не совпадать со структурой финансирования отдельного инвестиционного проекта (см. выражение (1)).Продолжая наш пример, определим коэффициент β для некоторой непубличной российской компании чёрной металлургии. В силу того, что акции компании не обращаются на бирже, мы будет определять бету по сопоставимым публичным компаниям.
В качестве сопоставимых компаний принимаем Новолипецкий металлургический комбинат (НЛМК), Северсталь и Магнитогорский металлургический комбинат (ММК). Поскольку котировки акций, которые мы будем использовать для определения доходности указанных компаний, не отражают дивиденды, то для оценки доходности рынка в целом выбираем индекс Московской Биржи без учёта дивидендных выплат IMOEX (не путать с ранее использовавшимся индексом MCFTR, который учитывает дивидендные выплаты).
В нашем примере принят длительный горизонт планирования (10 лет), поэтому регрессионный анализ по сопоставимым компаниям проводим за 5 лет (с 2018 по 2022 гг.) с месячным шагом расчёта. Задача по расчёту коэффициентов β легко решается в любой статистической программе, а также при помощи стандартных электронных таблиц (функция «НАКЛОН»).
В результате проведённых расчётов получаем следующие значения коэффициентов для сопоставимых компаний (округлённо): НЛМК – 0,57; Северсталь – 0,49; ММК – 0,88. Среднее значение коэффициента β (при равных весах сопоставимых компаний) составляет 0,64.
Далее определяем долговую нагрузку сопоставимых компаний. Источником информации для этого является финансовая отчётность, размещённая на сайтах эмитентов. Рекомендуется использовать отчётность по стандартам МСФО, хотя при её отсутствии допустимо использовать и отчётность по РСБУ.
Среднее отношение долга к собственному капиталу на начало каждого календарного года из пяти отчётных лет составляет (округлённо): НЛМК – 0,48; Северсталь – 0,66; ММК – 0,15. Средняя долговая нагрузка по сопоставимым компаниям составляет 0,43.
Находим безрычаговую бету сопоставимых компаний: 0,48.
Предположим, что отношение долга к собственному капиталу (D/E) анализируемой компании составляет 0,74. Тогда рычаговая бета анализируемой компании составит 0,76. Полученное значение коэффициента β может быть использовано для расчёта стоимости собственного капитала.👉 В практике инвестиционного анализа возможны ситуации, когда структура пассивов компании неизвестна, в силу чего оценка её долговой нагрузки (D/E) становится затруднительной. Это происходит в том случае, если компания не раскрывает свою финансовую отчётность, либо для реализации инвестиционного проекта создаётся новое предприятие, будущая структура капитала которого пока не определена.
В этом случае можно принять долговую нагрузку на уровне сопоставимых компаний. Тогда рычаговая бета анализируемой компании будет равна рычаговой бете сопоставимых компаний. Следовательно, в этом случае пересчёт рычаговой беты в безрычаговую и обратно не потребуется.
Расчёт коэффициента β сопоставимых компаний может осуществляться на базе отраслевых индексов Московской Биржи, которые отражают динамику котировок акций ведущих российских компаний, экономическая деятельность которых относится к соответствующим секторам народного хозяйства.
С одной стороны, такой подход (назовём его «отраслевой») имеет следствием некоторое снижение точности получаемых результатов. С другой стороны, существенно сокращается трудоёмкость проведения расчётов и сбора исходных данных (ведь тогда не требуется сбор информации о структуре капитала и расчёт долговой нагрузки каждой из сопоставимых компаний).
Отраслевой подход приобретает особую актуальность в настоящее время, когда многие публичные компании в силу геополитической напряжённости перестали публиковать свою финансовую отчётность. В этих условиях получение информации о структуре капитала сопоставимых компаний и пересчёт беты с учётом долговой нагрузки становится принципиально невозможным.
Отсюда следует, что в период моратория на публикацию финансовых отчётов единственно возможным вариантом определения коэффициента β становится регрессионный анализ соответствующего отраслевого индекса Московской Биржи.В настоящее время Московская биржа ведёт статистику по 10 отраслевым индексам, которые охватывают основные сектора отечественной экономики (от транспорта до информационных технологий).
Так, в индекс металлов и добычи в настоящее время входит 13 крупнейших российских компаний черной и цветной металлургии, золотодобычи и др. Следовательно, отраслевые индексы обеспечивают бо́льшую репрезентативность выборки, что повышает точность статистики.
Отраслевые индексы Московской Биржи обладают ещё одним неоспоримым преимуществом: их расчёт ведётся с учётом дивидендных выплат, что позволяет проводить регрессионный анализ относительно индекса Московской Биржи полной доходности с учётом дивидендных выплат (MCFTR), который мы взяли за базу при оценке спрэда доходностей акций и гособлигаций. Это значительно увеличивает методическую согласованность элементов модели CAPM.👉 Таким образом, если перед аналитиком не стоит задача формирования уникальной выборки сопоставимых компаний, либо анализируемая компания не характеризуется аномальной структурой пассивов, то определение коэффициента β вполне допустимо на базе регрессионного анализа соответствующего отраслевого индекса Московской Биржи.
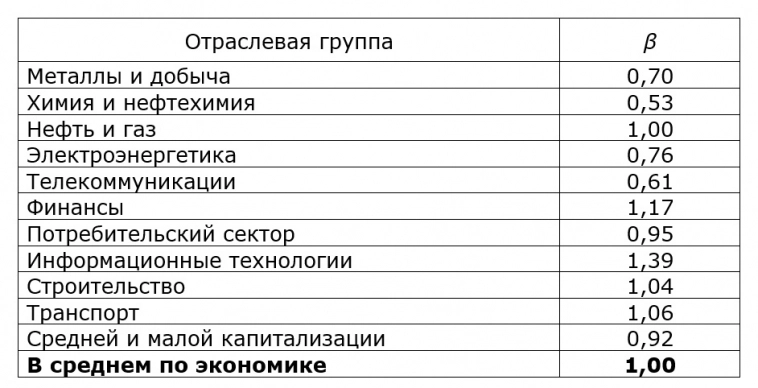
Результаты наших расчётов коэффициентов бета для отраслевых индексов Московской биржи за 2018-2022 гг. (за 5 лет с месячным шагом расчёта) представлены в нижеследующей таблице.
Наименьшее значение беты наблюдается у сектора «Химия и нефтехимия» (0,53), а наибольшее – у сектора «Информационные технологии» (1,39). У сектора «Нефть и газ» бета равна 1,00, что обусловлено высокой долей указанного сектора в российской экономике.Значение коэффициента β отраслевого индекса при «отраслевом» подходе принимается в качестве рычаговой беты анализируемой компании.
В том случае, если по каким-либо причинам модель CAPM рассчитывается без отраслевой привязки (для российского рынка в целом), то следует принимать бету полного индекса Московской Биржи (MCFTR), которая по определению равна 1,00.
Теперь вернёмся к нашему примеру и рассчитаем по «отраслевой» схеме бету для металлургического предприятия. Находим в таблице сектор «Металлы и добыча» и определяем, что для него значение коэффициента β составляет 0,70.
✅ Никаких дополнительных расчётов не требуется. Быстро и эффективно! При этом «отраслевые» коэффициенты бета, рассчитанные нами, останутся актуальными как минимум до 2024 года.Отметим, что полученное «отраслевое» значение беты очень близко к значению, рассчитанному по классическому алгоритму относительно сопоставимых компаний с учётом долговой нагрузки (0,76), что свидетельствует о корректности «отраслевого» подхода.
____________
Итак, нам удалось предложить и апробировать два способа расчёта коэффициентов β на основе отечественных активов.В следующей части нашего исследования мы обсудим как на базе российской финансовой статистики рассчитать премии за страновой риск (С), за размер компании (S1) и за специфические риски (S2).P. S. Я буду рад ответить на Ваши вопросы, конструктивную критику и комментарии.
Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+
АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 (без ограничения срока действия).
ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.
На чтение 9 мин Просмотров 100к.
Разберем такой инвестиционный показатель как – коэффициент бета, рассчитаем его на реальном пример с помощью Excel и рассмотрим различные современные модификации.
Содержание
- Инфографика: Коэффициент бета
- Коэффициент бета. Определение
- Формула расчета коэффициента бета
- Анализ уровня риска по значению коэффициента бета (β)
- Данные для построения коэффициента бета информационными компаниями
- Коэффициент бета в модели оценки капитальных активов –CAPM
- Пример расчета коэффициента бета вExcel
- Недостатки использования коэффициента бета в модели CAPM
- Модификация коэффициента бета
- Коэффициент бета для акций США
- Где посмотреть коэффициент бета для российских акций
Инфографика: Коэффициент бета
Коэффициент бета. Определение
Коэффициент бета (англ. Beta, β, beta coefficient) – определяет меру риска акции (актива) по отношению к рынку и показывает чувствительность изменения доходности акции по отношению к изменению доходности рынка. Коэффициент бета может быть рассчитан не только для отдельной акции, но также и для инвестиционного портфеля. Коэффициент используется как мера систематического риска, и применяется в модели У.Шарпа – оценки капитальных активов CAPM (Capital Assets Price Model). В первые, коэффициент бета рассмотрел Г. Марковиц для оценки систематического риска акций, который получил называние индекс недиверсифицируемого риска. Коэффициент бета позволяет сравнивать между собой акции различных компаний по степени их риска.
Формула расчета коэффициента бета
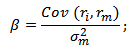
β – коэффициент бета, мера систематического риска (рыночного риска);
ri – доходность i-й акации (инвестиционного портфеля);
rm – рыночная доходность;
σ2m – дисперсия рыночной доходности.
Анализ уровня риска по значению коэффициента бета (β)
Коэффициент бета показывает рыночный риск акции и отражает чувствительность изменения акции по отношению к изменению доходности рынка. В таблице ниже показана оценка уровня риска по коэффициенту бета. Коэффициент бета может иметь как положительный, так и отрицательный знак, который показывает положительную или отрицательную корреляцию между акцией и рынком. Положительный знак отражает, что доходность акций и рынка изменяются в одном направлении, отрицательный – разнонаправленное движение.
|
Значение показателя |
Уровень риска акции |
Направление изменения доходности акции |
|
β > 1 |
Высокий |
Однонаправленное |
|
β = 1 |
Умеренный |
Однонаправленное |
|
0 < β < 1 |
Низкий |
Однонаправленное |
| -1 < β < 0 |
Низкий |
Разнонаправленное |
| β = -1 |
Умеренный |
Разнонаправленное |
|
β < -1 |
Высокий |
Разнонаправленное |
Данные для построения коэффициента бета информационными компаниями
Коэффициент бета используется многими информационно-инвестиционными компаниями для оценки систематического риска: Bloomberg, Barra, Value Line и др . Для построения коэффициента бета используются месячные/недельные данные за несколько лет. В таблице показаны основные параметры оценки показателя различными информационными компаниями.
★ Инвестиционная оценка в Excel. Расчет NPV, IRR, DPP, PI за 5 минут
|
Информационные компании |
Исторический период наблюдения | Частота |
|
Bloomberg |
2 года |
Неделя |
| Barra | 5 лет |
Месяц |
| Value Line | 5 лет |
Месяц |
Можно заметить, что Bloomberg проводит краткосрочную оценку показателя, тогда как Barra и Value Line используют месячные данные доходностей акций и рынка за последние пять лет. Долгосрочная оценка может сильно быть искажена вследствие влияния на акции компании различных кризисов и негативных факторов.
Коэффициент бета в модели оценки капитальных активов – CAPM
Формула расчета доходности акций по модели капитальных активов CAPM (Capital Assets Price Model, модель У.Шарпа) имеет следующий вид:
где:
r – будущая ожидаемая доходность акций компании;
rf – доходность по безрисковому активу;
rm – доходность рынка;
β – коэффициент бета (мера рыночного риска), отражает чувствительность изменения стоимости акций компании в зависимости от изменения доходности рынка (индекса);
Модель CAPM была создана У.Шарпом (1964) и Дж. Линтером (1965) и позволяет спрогнозировать будущее значение доходности акции (актива) на основании линейной регрессии. Модель отражает линейную взаимосвязь планируемой доходности с уровнем рыночного риска, выраженного коэффициентом бета.
Доходность по безрисковому активу, на практике, берется как доходность по государственным ценным бумагам ГКО, ОФЗ. Доходность по ним в России составляет около 12%. Доходность можно посмотреть на сайте ЦБ в разделе «Ставки рынка ГКО-ОФЗ».
Для расчета рыночной доходности используют доходность индекса или фьючерса на индекс (индекс ММВБ, РТС – для России, S&P500 – США).
Пример расчета коэффициента бета в Excel
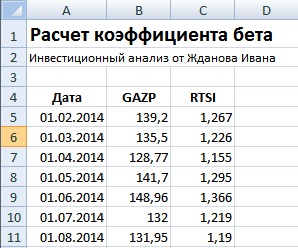
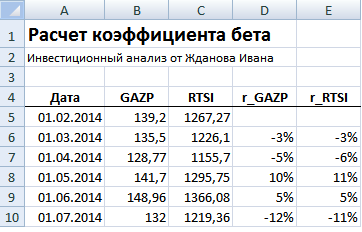
Рассчитаем коэффициент бета в Excel для отечественной компании ОАО «Газпром». Данная компания имеет обыкновенные акции, котировки которых можно посмотреть на сайте finam.ru в разделе «Экспорт данных». Для расчета были взяты месячные котировки акции ОАО «Газпром» (GAZP) и индекса РТС (RTSI) за период с 31.01.2014 по 31.01.2015 г.
Далее необходимо рассчитать доходности по акции и индексу, для этого воспользуемся формулами:
D6=LN(B6/B5)
E6=LN(C6/C5)
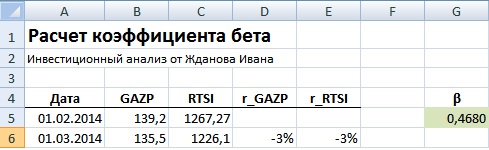
Для расчета коэффициента бета необходимо рассчитать коэффициент линейной регрессии между доходностью акций ОАО «Газпром» и индекса РТС. Рассмотрим два варианта расчета коэффициента бета средствами Excel.
Вариант №1. Расчет через формулу Excel
Расчет через формулы Excel выглядит следующим образом:
=ИНДЕКС(ЛИНЕЙН(D6:D17;E6:E17);1)
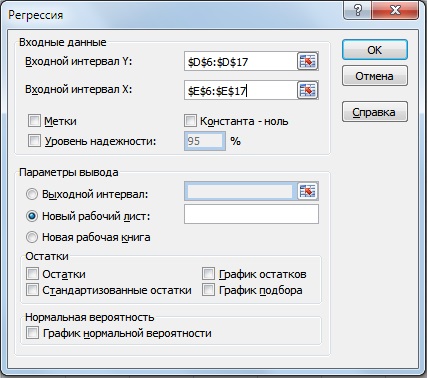
Вариант №2. Расчет через надстройку «Анализ данных»
Второй вариант расчета коэффициента бета использует надстройку Excel «Анализ данных». Для этого необходимо перейти в главном меню программы в раздел «Данные», выбрать опцию «Анализ данных» (если данная надстройка включена) и в инструментах анализа выделить «Регрессия». В поле «Входной интервал Y» выбрать доходности акции ОАО «Газпром», а в поле «Выходные интервал X» выбрать доходности индекса РТС.
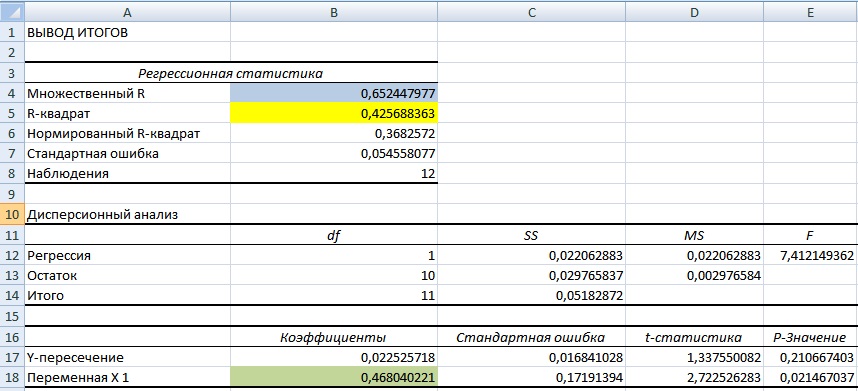
Далее мы получим отчет по регрессии на отдельном листе. В ячейке В18 показано значение коэффициента линейной регрессии, который равен коэффициенту бета = 0,46. Также проанализируем другие параметры модели, так показатель R-квадрат (коэффициент детерминированности) показывает силу взаимосвязи между доходностью акции ОАО «Газпром» и индекса РТС. Коэффициент детерминированности равен 0,4, что является довольно мало для точного прогнозирования будущей доходности по модели CAPM. Множественный R – коэффициент корреляции (0,6), который показывает наличие зависимости между акцией и рынком.
Значение 0,46 коэффициента бета для акции свидетельствует о умеренном риске и в тоже время сонаправленность изменения доходностей.
Недостатки использования коэффициента бета в модели CAPM
Рассмотрим ряд недостатков присущих данному коэффициенту:
- Сложность использования коэффициента бета для оценки низколиквидных акций. Данная ситуация характерна для развивающихся рынков капитала, в частности: России, Индии, Бразилии и т.д.
- Не возможность оценки малых компаний, не имеющих эмиссий обыкновенных акций. Большинство отечественных компаний не проходили процедуры IPO.
- Неустойчивость прогноза коэффициента бета. Использование линейной регрессии для оценки рыночного риска по ретроспективным данным не позволяет получать точные прогнозы риска. Как правило, трудно прогнозировать коэффициент бета более 1 года.
- Не возможность учета несистематических рисков компании: рыночной капитализации, исторической доходности, отраслевой принадлежности, критериев P/E и т.д., которые оказывает влияние на величину ожидаемой доходности.
Модификация коэффициента бета
Так как коэффициент, предложенный У. Шарпов не имел должной устойчивости и не мог использоваться для прогнозирования будущей доходности в модели CAPM, различными учеными были предложены модификации и корректировки данного показателя (англ. adjusted beta, modified beta).Рассмотрим скорректированные коэффициенты бета:
Модификация коэффициента бета от М.Блюма (1971)
Маршал Блюм показал, что со временем коэффициенты бета компаний стремятся к 1. Формула расчета скорректированного показателя следующая:
Использование данных весовых значений позволяет более точно спрогнозировать будущий систематический риск. Так данную модификацию используют многие информационные агентства, такие как: Bloomberg, Value Line и Merrill Lynch.
Модификация коэффициента бета от Бава-Линдсберга (1977)
В своей корректировке Линдсберг предложил рассчитывать односторонний коэффициент бета. Главный постулат заключался в том, что изменение доходности выше определенного уровня большинство инвесторов не рассматривают как риск, а риском считается только то, что ниже уровня. За минимальный уровень риска в данной модели был доходность безрискового актива.
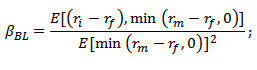
ri – доходность акции; rm – доходность рынка; rf – доходность безрискового актива.
Модификация коэффициента бета от Шоулза-Виллимса
β-1, β, β1 – коэффициенты беты для предыдущего (-1) текущего и следующего (1) периода;
ρm – коэффициент автокорреляции рыночной доходности.
Модификация коэффициента бета от Харлоу-Рао (1989)
Формула отражает одностороннюю бету, с предположением, что инвесторы рассматривают риск только как отклонение от среднерыночной доходности вниз. В отличие от модели Бава-Линдсберга за минимальный уровень риска брался уровень среднерыночной доходности.
где: μi – средняя доходность акции; μm – средняя доходность рынка;
Помимо коэффициента бета на практике используют другие показатели риска-доходности инвестиционного портфеля, ПИФа, более подробно узнать про современные показатели оценки инвестиций вы можете в моей статье: «Оценка эффективности инвестиций, инвестиционного портфеля, акций на примере в Excel«. О практике оценке риска инвестиции читайте в статье: «Методы оценки риска VaR (Value at Risk). Рыночный риск. Пример расчета в Excel «.
Коэффициент бета для акций США
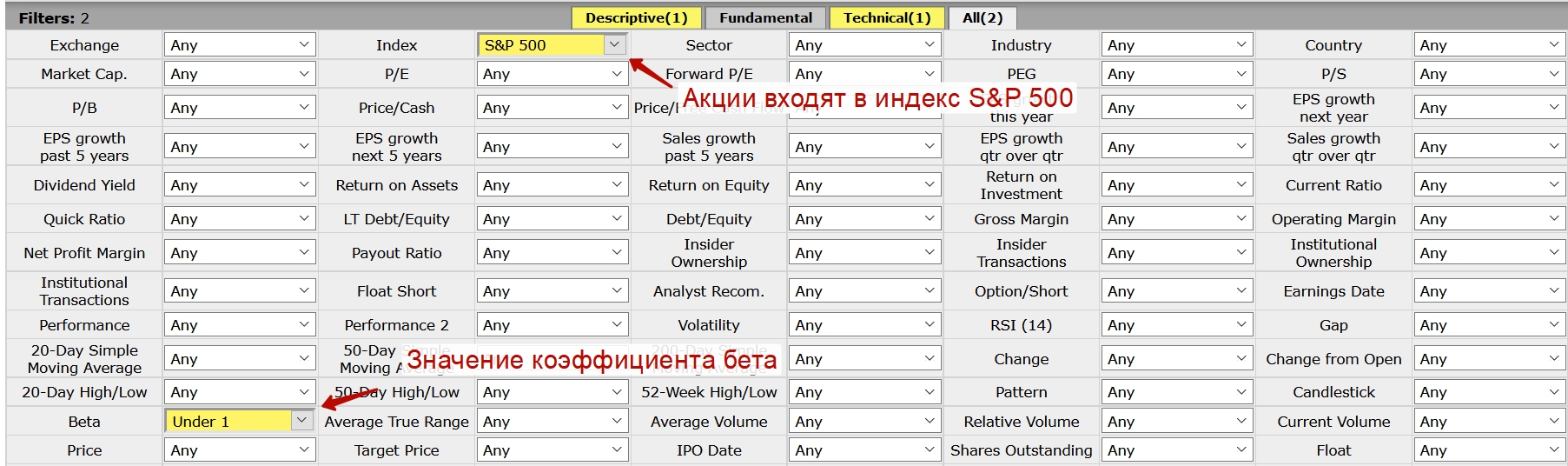
Существуют сервисы позволяющие оценить коэффициент бета для множества компаний и выделить наиболее интересные. Будем применять сервис Finviz. Чтобы найти акции менее чувствительные чем колебания фондового рынка необходимо установить коэффициент бета меньше 1.
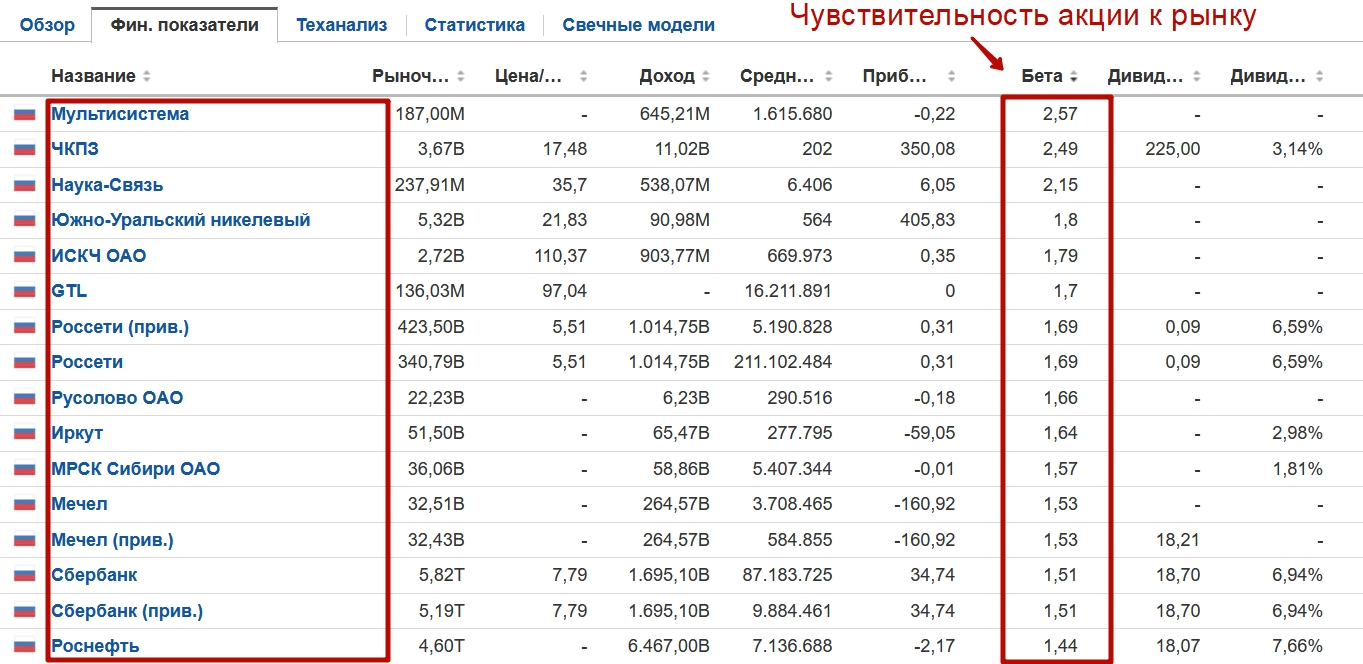
Где посмотреть коэффициент бета для российских акций
Если цель узнать коэффициент бета для российских акций, то для этого можно воспользоваться сервисом investing.com. Помимо отечественных компаний коэффициент бета можно определить для иностранных. Как мы видим для акции Мультисистемы коэффициент равен 2,57 – это значит, что она в 2,5 раза более изменчивая по отношению к рыночному изменению (индексу ММВБ).
Проанализировать акции на бета можно по ссылке.
Высокие значения коэффициента бета при растущем рынке будут обеспечивать дополнительную прибыль, при коррекциях такие акции как правило имеют больше убытков.
Резюме
Коэффициент бета является одним из классических мер рыночного риска для оценки доходности акций, инвестиционных портфелей и ПИФов. Несмотря на сложность использования данного инструмента для оценки отечественных низколиквидных акций и неустойчивость его изменения во времени, коэффициент бета является ключевым показателем оценки инвестиционных рисков. Рассмотренные модификации коэффициента позволяют скорректировать и дать более оценку систематическому риску. С вами был Иван Жданов, спасибо за внимание.
Автор: к.э.н. Жданов Иван Юрьевич
ПРОБЛЕМАТИКА ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА «БЕТА» ПРИ ОЦЕНКЕ БИЗНЕСА
О.Ю. ОРЕХОВА
Кафедра «Бухгалтерский учет, анализ, аудит» Московского инженерно-физического института (государственного университета)
Сегодня особенно остро стоит потребность в оценке бизнеса — новом явлении для современной российской экономики. Это связано с тем, что оценка бизнеса, во-первых, становится неотъемлемым элементом государственного регулирования деятельности компаний, а во-вторых, она становится неотъемлемым элементом финансового менеджмента компаний.
В практике оценки бизнеса сложились три основных подхода определения стоимости компании: доходный, сравнительный и затратный. Несмотря на все достоинства и недостатки данных подходов, наиболее часто (в 90 % случаях) используется доходный подход.
Ключевым моментом при использовании доходного подхода к оценке бизнеса является определение ставки дисконтирования, так как даже при очень тщательном построении денежного потока изменение значения ставки на ± 1 % может привести к значительным колебаниям окончательной стоимости.
Существуют различные методики расчета ставки дисконтирования, среди которых в России наиболее распространенными считаются: модель оценки капитальных активов, метод кумулятивного построения и др.
Каждый оценщик самостоятельно определяет для себя наиболее приемлемую методику расчета ставки дисконтирования с учетом всех достоинств и недостатков тех или иных моделей, а также своей квалификации. Однако на сегодняшний день метод оценки капитальных активов является наиболее часто применяемым, так как он является наиболее математически обоснованным и менее подвержен субъективному мнению оценщиков.
Повышение требований к качеству выполняемых работ за счет ужесточения законодательства РФ по оценочной деятельности с 01.01.2008, а так-
же постоянный рост требований к выполняемым процедурам со стороны заказчиков и менеджмента компаний являются причиной постановки вопроса о наиболее обоснованном проведении всех расчетов, в том числе и ставки дисконтирования.
Несмотря на тот факт, что существует небольшое количество общих методик расчета тех или иных коэффициентов ставки дисконтирования, при их адаптации к современным российским условиям возникает значительное количество рекомендаций по их практическому применению, не всегда приводящих к одинаковым результатам.
В рамках настоящей работы рассмотрена проблема расчета одной из составляющих ставки дисконтирования, при определении ее методом оценки капитальных активов, а именно коэффициента «бета». При этом дается определение коэффициента «бета», приводятся методики его расчета, источники информации о значениях данного коэффициента, а также проведен расчет коэффициента.
В общем случае модель оценки капитальных активов CAPM (Capital Asset Pricing Model) выглядит следующим образом
Г = f + в • (Гт —
где r — доходность оцениваемой компании; f — безрисковая доходность; в — коэффициент, учитывающий чувствительность доходности оцениваемых акций к изменению среднерыночной доходности;
(rm — f)— рыночная премия за риск. Согласно данной модели требуемую доходность в конкретную акцию можно определить, сравнивая риск вложения в данную акцию с риском вложений в диверсифицированный портфель акций. Данное сравнение осуществляется через ряд факторов, в том числе и через коэффициенты систематического риска («бета»).
На практике расчет ставки дисконтирования по модели оценки капитальных активов может производиться как на основе данных российского рынка, так и на основании данных рынка США с последующим переводом полученного значения в ставку дисконтирования для рублевого денежного потока.
В первом случае возникают трудности с определением актива, доходность по которому могла бы быть использована в качестве безрисковой, кроме того, нет статистической информации о рыночной премии за риск.
Поэтому все последующие расчеты будут вестись с позиции, согласно которой расчет ставки дисконтирования по модели оценки капитальных активов первоначально необходимо производить на основании данных рынка США, а затем адаптировать для конкретной российском компании.
Коэффициент «бета» отражает взаимосвязь между риском (доходностью) акции конкретной компании и рынком акций в целом. Он характеризует изменчивость курса конкретных акций относительно состояния рынка и представляет собой показатель, определяющий уровень риска.
При проведении расчетов значение коэффициента доходности рынка в целом приравнивается к единице. В том случае, если значение коэффициента «бета» компании больше 1, то колебания доходности акций выше рыночной амплитуды (в том же направлении). Если значение коэффициента «бета» компании меньше единицы, то колебания доходности акций ниже рыночной амплитуды (в том же направлении). Если значение коэффициента «бета» меньше нуля, то колебания доходности акций происходят в противоположную от общего тренда сторону.
В практике оценки выделяют следующие методики расчета коэффициента «бета»:
• оценка на основе бухгалтерских показателей прибыли;
• метод регрессионного анализа;
• оценка на основе фундаментального исследования.
При оценке коэффициента «бета» на основе фундаментального исследования его значение определяется тремя переменными: видом деятельности, уровнем финансового и операционного рычагов. Однако данный метод субъективен и применяется достаточно редко. Оценка коэффициента «бета» на основе бухгалтерских показателей прибыли практически не применяется вследствие того, что прибыль определяется с периодичностью
раз в квартал (недостаточное количество данных для анализа). Кроме того, на данный показатель влияют внеоперационные факторы.
Общепринятый подход оценке коэффициента «бета» основывается на регрессионном анализе доходности инвестиции относительно доходности рыночного индекса.
Для фирмы, акции которой на протяжении длительного периода торгуются на открытом рынке, не представляет большого затруднения оценить доходы, которые получил бы инвестор от своей инвестиции в собственный капитал. В теории, для оценки коэффициента «бета» активов эти показатели доходности вложений в акции должны быть соотнесены с доходностью рыночного портфеля (т. е. портфеля, который включает в себя все торгуемые активы). На практике обычно в качестве приблизительной оценки рыночного портфеля используется какой-либо фондовый индекс и оценивается коэффициент «бета» для акций относительно индекса.
В качестве индикаторов, характеризующих рынок, наиболее часто используют:
1) индекс акций Нью-Йоркской фондовой биржи (NYSE Composite Index);
2) индекс S&P;
3) индекс Wilshire.
При расчете коэффициента «бета» доходность может исчисляться по разным периодам владения: за день, неделю, месяц, квартал, год. При этом оценщики сталкиваются с определенными трудностями: с одной стороны, чем больше количество наблюдений, тем более достоверные результаты могут быть получены, с другой стороны, чем короче период владения, тем более вероятно то, что данные будут подвержены случайному «шуму».
Анализ проводят на основе информации за различные периоды времени: обычно 2, 3 или 5 лет, поскольку возникает трудность иного свойства: чем большее количество лет принимается во внимание, тем вероятнее, что значение основного риска компании за столь продолжительный период времени изменится.
Стандартная процедура для оценки коэффициентов «бета» предусматривает выяснение регрессии доходности акции (r) относительно рыночной доходности (rm).
rj=a + Р • m
где — доходность акции;
a — точка пересечения на оси абсцисс;
в — наклон линии регрессии;
rm — рыночная доходность.
Р =
cov(r,.; гт)
ст
где ^ — доходность акции;
в — наклон линии регрессии; гт — рыночная доходность. Кроме того, применительно к компаниям, чьи акции котируются на фондовой бирже, легче всего пользоваться публикуемыми оценками коэффициента «бета». Однако при этом следует обращаться к нескольким источникам информации, и коэффициент «бета» компании необходимо сопоставлять с отраслевым значением коэффициента. Если различные источники расходятся в оценке коэффициента «бета» больше чем на 0,2 или коэффициент «бета» компании больше чем на 0,3 отличается от среднеотраслевого значения, то необходимо использовать среднеотраслевое значение показателя.
Однако наиболее часто перед оценщиками встает вопрос об оценке акций компаний, не котирующихся на фондовой бирже, либо оценке долей в уставных капиталах компаний. В этом случае единственным способом расчета коэффициента «бета» является определение среднеотраслевого значения коэффициента «бета» по аналогам, с последующей корректировкой для оцениваемой компании.
Расчет коэффициента «бета» тогда осуществляется в следующей последовательности:
• формируется группа компаний-аналогов;
• определяется «бета» по каждой компании;
• находится среднее значение (средневзвешенное по капитализации, среднеарифметическое, медианное).
На базе значения коэффициента «бета» в целом для отрасли с учетом долговой нагрузки и структуры финансирования рассчитывается значение коэффициента «бета» без учета долговой нагрузки и структуры активов. Далее определяется значение коэффициента «бета» для предприятия с учетом предельной ставки налога на прибыль и соотношения долга и собственного капитала по компании:
в =_в_,
» 1 + D /Е • (1 -1 )
а I а V а’
где ви — коэффициент «бета» без учета финансового рычага (unlevered «бета»); ва — «бета» отрасли;
Ба / Еа — соотношение долга и собственного капитала в среднем по отрасли;
ta — средняя ставка налога на прибыль по компаниям — аналогам отрасли.
Р; = Р« • d + D / E • (1 — t)),
где ви — unlevered «бета»;
Р;. — «бета» оцениваемой компании с учетом финансового рычага;
D¡ / Et — соотношение долга и собственного капитала оцениваемой компании;
t i — ставка налога на прибыль оцениваемой компании.
Так как расчет коэффициента «бета» — достаточно сложная процедура, требующая значительных затрат времени, а также наличия высококвалифицированного персонала, то не все компании, особенно в регионах, могут самостоятельно определять значение данного коэффициента при осуществлении расчетов. В этой связи существует достаточно большое количество информационных агентств, публикующих информацию о значениях данного коэффициента в разрезе отраслей с определенной периодичностью:
1. Standard & Poor’s stock reports проводит исследование по всем акциям американских компаний, котируемым в течение последних 5 лет, при этом расчеты проводятся относительно S&P 500 на конец месяца за последние 60 мес.;
2. Value line NYSE Composite Series — расчеты проводятся относительно NYSE на конец каждой недели за последние 60 мес.;
3. Media General Financial Services проводит исследование по 7 000 акциям Industry Scope, при этом расчеты проводятся относительно S&P 500 на конец месяца по данным за последние 36 мес.;
4. Ibbotson’s Beta Book — расчеты проводятся относительно S&P 500 на конец месяца по данным за последние 5 лет.;
5. New York University’s Stern School of Management и т. д.
При использовании данных информационных агентств оценщики должны хорошо знать, на основании каких данных были проведены вычисления коэффициента «бета» в каждом случае, чтобы объяснить возможные отклонения: на основании S&P или NYSE, по данным на конец недели или месяца, по данным за 2, 3 или 5 лет и т. д.
Кроме того, расчет значений коэффициента «бета» необходимо проводить на основании самых последних данных, ближайших к дате оценки, так как значение коэффициента зависит от структуры активов, источников финансирования, а также изменяется под воздействием таких рыночных факторов, как возросшая конкуренция в отрасли, истечение срока действия основных процентов и т. д.
Таким образом, при проведении работы у оценщиков существует большое количество возможностей для расчета всего одной составляющей ставки дисконтирования — коэффициента «бета». Во-первых, коэффициент «бета» может быть рассчитан самостоятельно либо его значение может быть взято из аналитических исследований информационных агентств. Во-вторых, существуют как минимум три возможных варианта расчета коэффициента. В-третьих, при использовании модели регрессионного анализа оценщики сталкиваются с выбором возможного индикатора, характеризующего рынок (S&P, NYSE и т. д.), периода времени, за который будет анализироваться информация (2, 3, 5 лет и т. д.), периодичности расчета показателей (недельные данные, месячные и т. д.). Кроме того, при определении коэффициента «бета» по компаниям-аналогам существуют различные варианты расчета среднего значения: среднеарифметическое, средневзвешенное, медианное и т. д.
В результате с учетом описанных вариантов расчетов возможно получение абсолютно различных значений коэффициента «бета».
В рамках данной статьи для подтверждения вышеизложенных выводов было проведено исследование по расчету коэффициента «бета» в разрезе отраслей методом регрессионного анализа, результаты которого представлены ниже.
При проведении исследования использовались данные информационно-аналитической системы Bloomberg Professional по состоянию на 01.01.2008.
Так как в работе рассматривается вариант расчета ставки дисконтирования, при котором в начале определяется ее значение на основании данных американского рынка, то для целей исследования были отобраны только компании США, торгующиеся на бирже.
Кроме того, поскольку таких компаний на бирже представлено достаточно много, то критерием отбора было также условие, что их выручка и рыночная капитализация должны составлять не менее 0,1 млн долл. США.
Таким образом, были отобраны 5 000 компаний. Далее компании были сгруппированы по отраслям классификатора информационно-аналитической системы Bloomberg Professional (всего 70 отраслей).
После группировки компаний оказалось, что по отраслям «Venture Capital», «Storage», «Shipbuilding» и «REITS» были отобраны всего одна или две компании (всего семь компаний). В этой связи
результаты расчетов по данным предприятиям в дальнейших расчетах не использовались ввиду нерепрезентативности выборки.
Далее из выборки были исключены компании, по которым не было информации о величине собственного или заемного капитала, так как без этих данных невозможно было бы рассчитать unlevered «бета». Таким образом, для целей анализа осталось 4 348 компаний.
По каждой компании была собрана информация о рыночной капитализации, о величине заемного капитала и о величине собственного капитала за последнюю отчетную дату.
Далее были проведены расчеты значения коэффициента «бета»:
• по значениям доходности на конец недели за последние 5 лет;
• по значениям доходности на конец месяца за последние 5 лет;
• по значениям доходности на конец недели за последние 2 года;
• по значениям доходности на конец месяца за последние 2 года.
Значение коэффициента «бета» определялось на основании индекса S&P.
Полученные значения коэффициента «бета» по четырем вышеобозначенным группам были проанализированы на выполнение условий правила трех сигм (разброс 3 %) с целью исключения из выборки случайных величин. Таким образом, в окончательную выборку вошли 4 189 компаний по 64 отраслям экономики.
По каждой отрасли было найдено среднеарифметическое, средневзвешенное по капитализации и медианное значения коэффициентов «бета», рассчитанных на основании данных о доходности на конец недели или месяца за последние 2 года или 5 лет.
Далее по каждой компании в выборке было найдено значение unlevered «бета» путем перевода значения коэффициента «бета» с учетом финансового рычага (average «бета») через соотношения долга и собственного капитала и ставки налога на прибыль. В качестве ставки по налогу на прибыль использовалось предельное значение ставки по налогу на прибыль в США в размере 35 %.
Затем также были найдены среднеарифметическое, средневзвешенное по капитализации и медианное значения коэффициентов «бета», рассчитанных на основании данных о доходности на конец недели или месяца за последние 2 года или 5 лет.
Результаты расчета коэффициента «бета»
№ п/п Количес- Average beta Unlevered beta
Отрасль тво ком- Данные за 5 лет Данные за 2 года Данные за 5 лет Данные за 2 года
паний* недельные месячные недельные месячные недельные месячные недельные месячные
1 Банки 507
Вариант 1** 0,421 0,614 0,510 0,506 0,237 0,354 0,285 0,290
Вариант 2 *** 0,877 0,840 1,013 0,820 0,357 0,342 0,407 0,326
Вариант 3**** 0,261 0,654 0,334 0,519 0,149 0,349 0,181 0,280
2 Биотехнология 117
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
Вариант 1 1,300 2,025 1,208 1,621 1,075 1,663 1,043 1,281
Вариант 2 0,917 1,255 0,797 0,914 0,694 0,952 0,607 0,688
Вариант 3 1,254 1,848 1,076 1,635 0,979 1,476 0,944 1,107
3 Коммерческие услуги 201
Вариант 1 0,957 1,242 0,939 1,091 0,834 1,084 0,706 0,840
Вариант 2 1,082 1,098 1,094 1,154 0,717 0,742 0,712 0,712
Вариант 3 0,926 1,218 0,965 1,039 0,760 0,941 0,676 0,685
4 Компьютеры 138
Вариант 1 1,040 1,658 0,846 1,039 0,934 1,579 0,717 0,902
Вариант 2 1,250 1,481 1,147 1,515 1,101 1,306 1,015 1,334
Вариант 3 1,085 1,572 0,929 1,116 0,956 1,407 0,771 0,895
5 Электроника 133
Вариант 1 1,001 1,555 0,902 0,909 0,869 1,416 0,783 0,806
Вариант 2 1,287 1,651 1,143 1,160 1,090 1,381 0,966 0,969
Вариант 3 1,044 1,487 0,938 0,991 0,929 1,242 0,829 0,742
6 Продукты здравоохранения 186
Вариант 1 0,767 1,328 0,759 1,009 0,959 1,700 0,841 1,061
Вариант 2 0,688 0,559 0,691 0,604 0,603 0,489 0,601 0,524
Вариант 3 0,768 1,278 0,744 0,879 0,713 1,081 0,673 0,762
7 Страхование 110
Вариант 1 0,806 0,968 0,848 0,827 0,679 0,810 0,713 0,681
Вариант 2 0,860 0,967 0,793 0,810 0,601 0,679 0,558 0,547
Вариант 3 0,828 0,946 0,878 0,878 0,698 0,748 0,712 0,740
8 Интернет 141
Вариант 1 1,247 2,180 1,073 1,580 1,116 1,975 0,945 1,386
Вариант 2 1,286 1,670 1,194 1,803 1,164 1,458 1,091 1,624
Вариант 3 1,293 2,041 1,090 1,628 1,145 1,718 0,952 1,378
9 Нефть и газ 133
Вариант 1 0,838 1,280 0,968 1,336 0,612 0,915 0,705 0,988
Вариант 2 0,865 0,799 1,087 1,025 0,705 0,640 0,888 0,827
Вариант 3 0,893 1,129 1,038 1,288 0,657 0,820 0,782 0,944
10 Фармацевтические препараты 175
Вариант 1 1,056 1,824 1,016 1,405 0,807 1,459 0,837 1,086
Вариант 2 0,915 0,837 0,959 0,990 0,717 0,651 0,759 0,787
вариант 3 1,074 1,573 0,929 1,317 0,806 1,228 0,786 0,960
11 Розничная продажа 217
Вариант 1 1,129 1,338 1,156 1,196 0,919 1,061 0,944 0,874
Вариант 2 1,047 0,964 1,069 0,818 0,840 0,776 0,854 0,640
Вариант 3 1,202 1,303 1,227 1,220 0,956 0,997 1,006 0,912
12 Сбережения и кредиты 163
Вариант 1 0,342 0,706 0,387 0,595 0,170 0,363 0,186 0,309
Вариант 2 0,831 1,048 1,001 1,067 0,363 0,436 0,422 0,453
Вариант 3 0,221 0,745 0,255 0,596 0,127 0,317 0,109 0,259
* Окончательное количество компаний, принявших участие в выборке. ** Среднеарифметическое значение. *** Средневзвешенное по капитализации значение. **** Медианное значение.
Окончание таблицы
№ п/п Количес- Average beta Unlevered beta
Отрасль тво ком- Данные за 5 лет Данные за 2 года Данные за 5 лет Данные за 2 года
паний* недельные месячные недельные месячные недельные месячные недельные месячные
13 Полупроводники 125
Вариант 1 1,614 2,265 1,258 1,070 1,388 1,784 1,088 0 , 930
Вариант 2 1,646 1,968 1,320 1,147 1,564 1,860 1,257 1,083
Вариант 3 1,649 2,208 1,300 1,106 1,454 1,995 1,101 1,006
14 Программное обеспечение 169
Вариант 1 1,028 1,665 0,858 1,073 1,003 1,686 0,827 1,120
Вариант 2 1,104 1,139 1,023 1,549 1,042 1,054 0,965 1,482
Вариант 3 1,075 1,529 0,936 1,067 0,995 1,392 0,802 0,972
15 Телекоммуникации 159
Вариант 1 1,225 1,883 1,012 1,310 0,833 1,324 0,665 0,786
Вариант 2 1,129 1,327 1,003 1,164 0,815 0,953 0,723 0,846
Вариант 3 1,206 1,730 0,991 1,280 0,948 1,372 0,790 0,696
При проведении исследования в определенных отраслях было отобрано недостаточное количество компаний, что могло привести к искажению результатов. Однако по 15 отраслям было отобрано более 100 компаний в разрезе каждой группы, в связи с чем говорить об искажении полученных значений ввиду нерепрезентативности выборки нельзя.
Результаты расчета коэффициента «бета» по данным отраслям представлены в таблице.
Таким образом, значения коэффициента «бета» в значительной степени зависят от применяемой методики расчета. При этом каждый из полученных результатов может быть использован для определения ставки дисконтирования с одинаковой вероятностью и без каких-либо ограничений.
Кроме того, хотелось бы отметить, что в таблице приведены результаты только по небольшому количеству возможных методик расчета.
Поэтому перед оценщиками при выполнении работ встает непростая задача по выбору того или иного значения коэффициента «бета» при расчете ставки дисконтирования. Несмотря на то, что все значения математически верны, выбор той или иной величины может привести к значительным расхождениям в окончательной стоимости.
Наиболее часто на практике стараются использовать значение коэффициента «бета», определенное на основании еженедельных данных о доходности за последние 5 лет. При этом, если акции компании котируются на бирже, то в качестве индикатора используют индекс данной биржи.
Если оцениваются акции, которые не котируются на бирже, или оценивается доля в уставном капитале, расчет коэффициента «бета» проводят на основании среднеотраслевых данных по компаниям-аналогам (определяют среднеарифметическое значение относительно индекса S&P).
В заключение хотелось бы отметить, что оценщики имеют право любым способом определять значение коэффициента «бета», как описанными в данной работе, так и в других. При этом главным требованием остается четкое обоснование выбора того или иного значения.
Литература
1. Дамодаран А. Инвестиционная оценка. Инструменты и техника оценки любых активов. М.: Альпина Бизнес Букс, 2004.
2. Фишмен Д., Пратт Ш. , Гриффит К, Уилсон К. Руководство по оценке стоимости бизнеса. М.: КВИНТО-КОНСАЛТИНГ, 2000.
3. Коупленд Т., Колер Т., Мурин Дж. Стоимость компаний: оценка и управление. М.: Олимп-Бизнес, 2005.
4. БрейлиР., Майерс С. Принципы корпоративных финансов. М.: Олимп-Бизнес, 1997.
5. ГрязноваА. Г., ФедотоваМ. А, ЭскиндаровМ. А., Тазихина Т. В., Иванова Е. Н, Щербакова О. Н. Оценка стоимости предприятия (бизнеса). М.: ИНТЕРРЕКЛАМА, 2003.
6. !П;ете^ресурсы.