Как найти коэффициент безопасности

Коэффициентом
безопасности называют
отношение предельных напряжений
к максимальным напряжениям, возникающим
при ра­боте детали.

1.
Коэффициент безопасности при статических
нагрузках можно определять по формулам:

для
пластичных материалов

(1.10)

для
хрупких материалов

(1.11)

2.
Коэффициент безопасности при переменных
(циклических) нагрузках с учетом основных
факторов, влияющих на предел вы­носливости,
для любого материала определяют [15; 35;
5] по фор­мулам:

при
симметричном цикле

(1.12)

при
асимметричном цикле, когда с возрастанием
нагрузки цикл остается подобным рабочему
[14; 5], т. е. возрастание напряжений
происходит по направлению ОМN
(рис.
1.3):

Рис.
1.7.
Диаграмма
предельных напряжений

(1.13)

при
асимметричном цикле, ког­да
среднее напряжение не меняет­ся, а
амплитуда растет, т. е. по линии МР
(рис.
1.3):

(1.14)

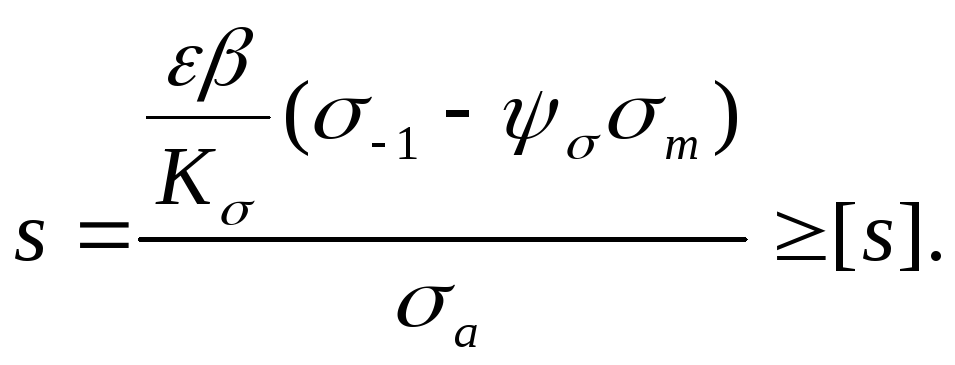
При
совместном действии нор­мального
σ_а
и касательного τ_а
на­пряжений (изгиб, кручение),
из­меняющихся синфазно,

(1.15)

где
s_σ;
s_τ
–
коэффициент безопасности по нормальным
и касатель­ным
напряжениям (1.24. . .1.26) с заменой σ
на
τ.

Допустимое
значение коэффициента безопасности
[s]
назначают на основании опыта проектирования
и эксплуатации машин или рассчитывают
с учетом требуемой надежности деталей.
При отсут­ствии необходимых данных
допустимый коэффициент безопасности
приближенно можно определить на основе
так называемого диф­ференциального
метода как произведение частных
коэффициен­тов [14; 38]:

(1.16)

где
s₁
– коэффициент, учитывающий степень
точности расчета. Рас­чет приводить
к завышенным напряжениям и степень
завышения определить
трудно: s₁
=
1,
расчет приводит к заведомо заниженным
напряжениям;
s₁
=
1,2…1,3; s₂
– коэффициент, учитывающий одно­родность
механических свойств материала. Для
деталей, изготов­ленных из углеродистых
и легированных сталей при высокой
темпе­ратуре отпуска, s₂
=
1,2…1,3; для деталей, изготовленных из
высоко­прочных сталей с пониженными
пластическими свойствами (с низ­кой
температурой отпуска) и высокопрочных
чугунов, s₂
=
1,3…1,5; для деталей из стального литья
s₂
=
1,5…2; для чугунных деталей s₂
=
2…2,5; для деталей из цветных сплавов
(кованых и катаных) s₂
=
1,5…2; s₃
– коэффициент, учитывающий степень
ответственно­сти детали. Поломка
детали не вызывает остановки машины:
s₃
=
1; поломка детали вызывает остановку
машины: s₃
=
1,1…1,2; по­ломка детали вызывает аварию:
s₃
=
1,2…1,3.

Коэффициент
безопасности по пределу прочности
выбирается довольно большим. Например,
для высокопрочных сталей – около
2…2,5, для серого чугуна 3…3,5, для стального
и цветного литья 2,5…3, для особо хрупких
материалов 4…6.

Коэффициент
безопасности по пределу текучести для
пластич­ных материалов (сталей) при
достаточно точных расчетах выбира­ют
1,2…1,5 и выше. Коэффициент безопасности
при контактных нагружениях можно принять
1,1…1,2. Коэффициент безопасности по
пределу выносливости – 1,3…2,5. Например,
при недостаточно пол­ном объеме
экспериментальных данных о нагрузках
и характери­стиках материала или
ограниченном числе натурных испытаний
[s]
= 1,5…2; при малом объеме или отсутствии
экспериментальных испытаний и пониженной
однородности материала (литые и свар­ные
детали) [s]
= 2…3.

Пример.
Определить коэффициент безопасности
для вала d
=
60 мм с од­ной шпоночной канавкой,
который нагружен в опасном сечении
изгибающим мо­ментом М
= 1,5
· 10⁶
Н · мм и крутящим моментом Т
=
4 · 10⁶
Н · мм. Материал вала – сталь 40ХН (табл.
1.2, σ_b
=
1000 Н/мм²;
σ_-1F
=
530 Н/мм²).
Поверх­ность вала шлифованная.
Напряжение изгиба изменяется по
симметричному цик­лу, кручения – по
пульсирующему. Срок службы N_LE
>
N₀

Решение.

1. При
   сложном напряженном состоянии (изгиб
   и кручение) ко­эффициент безопасности
   определяется по выражению (1.15)

где
s_σ,
s_τ–
коэффициент безопасности по изгибу и
кручению.

2.
По формуле определяем коэффициент
безопасности по нормальным напряжениям
при симметричном цикле изгиба:

Здесь
амплитудное и наибольшее напряжения
цикла равны и определяются по формуле:

где
W
= 18 760 мм³
– момент сопротивления изгибу вала d
=
60 мм, ослабленно­го шпоночным пазом.

3. Находим
эффективный коэффициент концентрации
напряжений для валов с одной шпоночной
канавкой при изгибе (σ_b
=
1000 Н/мм ) К_σ
=
2,3; масштабный фактор ε = 0,77; коэффициент
состояния по­верхности β = 0,88.

Тогда

4. Коэффициент
безопасности по касательным напряжениям
при пульсиру­ющем цикле нагружения
по формуле:

5. По
выражению определим амплитудное и
среднее напряжения:

где
W_р
=
4 · 10⁴
мм³
— момент сопротивления кручению вала
ослабленного шпо­ночным пазом.

6. Находим
масштабный фактор ε = 0,77; коэффициент
состояния поверхно­сти β = 0,88; коэффициент
чувствительности материала к асимметрии
ψ_τ
=
0,09.

Эффективный
коэффициент концентрации напряжений
при кручении K_τ
=
2,2.

7. Используя
приближенное соотношение

Определяем
τ_-1
= 0,55 · 530 = 290 Н/мм².

Тогда

8. Определяем
коэффициент безопасности

Для
выяснения прочности вала установим
минимально допустимый коэффи­циент
безопасности по выражению (1.16):

где
s₁
=
1; s
₂ =
1,2; s₃
=
1,2 (с. 16).

Таким
образом,s<[s]
и, следовательно, прочность вала
недостаточна. Необхо­димо принять
решение к повышению s.

Рис.
1.8.
Эскиз
к примеру 1

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Фактор, на который мощность инженерной системы превышает ожидаемую нагрузку, чтобы гарантировать безопасность в случае ошибки или неопределенности

В технике коэффициент безопасности (FoS ), также известный как (и взаимозаменяемый) коэффициент безопасности (SF), выражает, насколько надежнее система больше, чем необходимо для предполагаемой нагрузки. Коэффициенты безопасности часто рассчитываются с использованием подробного анализа, поскольку всестороннее тестирование нецелесообразно для многих проектов, таких как мосты и здания, но способность конструкции выдерживать нагрузку должна быть определена с разумной точностью.

Многие системы намеренно построены намного сильнее, чем требуется для нормального использования, чтобы учесть чрезвычайные ситуации, неожиданные нагрузки, неправильное использование или ухудшение (надежность ).

Содержание

• 1 Определение
• 2 Расчет
  • 2.1 Расчетный коэффициент и коэффициент безопасности
  • 2.2 Запас прочности
  • 2.3 Резервный коэффициент
• 3 Расчет выхода и конечных результатов
• 4 Выбор конструкции коэффициенты
• 5 См. также
• 6 Примечания
• 7 Дополнительная литература

Определение

Есть два определения коэффициента безопасности (FoS):

1. Отношение абсолютного прочность (конструктивная способность) к фактической приложенной нагрузке; это мера надежности конкретной конструкции. Это расчетное значение, которое иногда для ясности называют реализованным коэффициентом безопасности.
2. Постоянное требуемое значение, установленное законом, стандартом., спецификация, контракт или custom, которым структура должна соответствовать или превосходить. Это может быть указано как проектный коэффициент, проектный коэффициент безопасности или требуемый коэффициент безопасности.

Реализованный коэффициент безопасности должен быть больше, чем требуемый проектный коэффициент безопасности. Однако использование между различными отраслями и инженерными группами непоследовательно и сбивает с толку; важно знать, какие определения используются. Причина большой путаницы состоит в том, что различные справочники и агентства по стандартизации по-разному используют определения и термины фактора безопасности. В нормах проектирования и в учебниках по конструкции и машиностроению часто используется термин «коэффициент безопасности» для обозначения доли общих структурных возможностей над необходимыми и реализованными факторами безопасности (первое использование). Во многих учебниках «Прочность материалов» для студентов бакалавриата «Фактор безопасности» используется как постоянное значение, предназначенное в качестве минимального целевого значения для проектирования (повторное использование).

Расчет

Есть несколько способов сравнить коэффициент безопасности конструкций. Все различные расчеты в основном измеряют одно и то же: какую дополнительную нагрузку сверх ожидаемой конструкция действительно выдержит (или должна выдержать). Разница между методами заключается в способе вычисления и сравнения значений. Значения коэффициента безопасности можно рассматривать как стандартизованный способ сравнения прочности и надежности между системами.

Использование запаса прочности не означает, что объект, конструкция или конструкция являются «безопасными». Многие факторы обеспечения качества, инженерное проектирование, производство, установка и конечное использование могут влиять на безопасность чего-либо в той или иной конкретной ситуации.

Расчетный коэффициент и коэффициент безопасности

Разница между коэффициентом безопасности и расчетным коэффициентом безопасности (расчетный коэффициент безопасности) заключается в следующем: коэффициент безопасности или предел текучести — это то, насколько фактически спроектированная деталь выдержать сможет (первое «использование» сверху). Расчетный фактор или рабочее напряжение — это то, что требуется для того, чтобы изделие могло выдержать (второе «использование»). Расчетный коэффициент определяется для приложения (обычно предоставляется заранее и часто устанавливается нормативными строительными нормами или политикой) и не является фактическим расчетом, коэффициент безопасности — это отношение максимальной прочности к предполагаемой нагрузке для фактический предмет, который был разработан.

Фактор безопасности = предел текучести, рабочее напряжение { displaystyle { text {Factor of Safety}} = { frac { text {предел текучести}} { text {рабочее напряжение}}}}

• Расчетная нагрузка это максимальная нагрузка, которую деталь должна когда-либо испытывать при эксплуатации.

Согласно этому определению конструкция с FOS ровно 1 будет поддерживать только расчетную нагрузку и не более. Любая дополнительная нагрузка приведет к разрушению конструкции. Конструкция с FOS 2 выйдет из строя при двойной расчетной нагрузке.

Запас прочности

Многие правительственные учреждения и отрасли (например, аэрокосмическая) требуют использования запаса прочности (MoS или MS ) для описания соотношения прочности конструкции к требованиям. Есть два разных определения запаса прочности, поэтому необходимо внимательно определить, какое из них используется для данного приложения. Одно использование M.S. как мера возможностей, как FoS. Другое использование M.S. является мерой удовлетворения проектных требований (проверка требований). Можно концептуально представить запас прочности (наряду с коэффициентом резерва, поясняемый ниже), чтобы показать, какая часть общей способности конструкции удерживается «в резерве» во время загрузки.

М.С. как мера структурной способности: это определение запаса прочности, обычно встречающееся в учебниках, описывает, какую дополнительную нагрузку сверх расчетной нагрузки может выдержать деталь до выхода из строя. По сути, это мера избыточных возможностей. Если запас равен 0, деталь не будет принимать никаких дополнительных нагрузок до того, как выйдет из строя, если значение отрицательное, деталь выйдет из строя до достижения расчетной нагрузки при эксплуатации. Если запас равен 1, он может выдержать одну дополнительную нагрузку, равную максимальной нагрузке, на которую он был рассчитан (т. Е. Удвоенной расчетной нагрузке).

Запас прочности = Расчетная нагрузка при отказе — 1 { displaystyle { text {Запас прочности}} = { frac { text {Нагрузка при отказе}} { text {Расчетная нагрузка}}} — 1}

Запас прочности = Фактор безопасности — 1 { displaystyle { text {Запас прочности}} = { text {Фактор безопасности}} — 1}

MS в качестве меры проверки требований: многие агентства и организации, такие как NASA и AIAA, определяют запас прочности, включая расчетный коэффициент, другими словами, запас прочности рассчитывается после применения расчетный фактор. В случае запаса, равного 0, деталь имеет точно требуемую прочность (коэффициент безопасности будет равен расчетному коэффициенту). Если имеется деталь с требуемым расчетным коэффициентом 3 и запасом 1, то эта деталь будет иметь коэффициент безопасности 6 (способна выдерживать две нагрузки, равные ее расчетному коэффициенту 3, выдерживая шестикратную расчетную нагрузку до разрушения). Запас, равный 0, будет означать, что деталь будет проходить с коэффициентом безопасности 3. Если запас меньше 0 в этом определении, хотя деталь не обязательно выйдет из строя, требования к конструкции не были выполнены. Удобство этого использования заключается в том, что для всех приложений проходит маржа 0 или выше, не нужно знать детали приложения или сравнивать с требованиями, просто взглянув на расчет маржи, можно узнать, прошел ли проект или нет. Это полезно для надзора и проверки проектов с различными интегрированными компонентами, так как разные компоненты могут иметь различные факторы проектирования, а расчет маржи помогает предотвратить путаницу.

. Расчетный коэффициент безопасности = [Предоставляется в качестве требования].

Запас прочности = Расчетная нагрузка при отказе × Расчетный коэффициент безопасности — 1 { displaystyle { text {Запас прочности}} = { frac { text {Отказ Нагрузка}} { text {Расчетная нагрузка × Расчетный коэффициент безопасности}}} — 1}

Запас прочности = реализованный коэффициент безопасности Расчетный коэффициент безопасности — 1 { displaystyle { text {Запас прочности}} = { frac { text {Реализованный коэффициент безопасности}} { text {Расчетный коэффициент безопасности}}} — 1}

Для успешного проектирования реализованный коэффициент безопасности всегда должен быть равен или превышать проектный коэффициент безопасности, поэтому запас прочности больше или равно нулю. Иногда, но нечасто, запас прочности используется в процентах, например, 0,50 M.S. эквивалентно 50% M.S. Когда дизайн удовлетворяет этому тесту, говорят, что он имеет «положительный запас», и, наоборот, «отрицательный запас», когда это не так.

В области ядерной безопасности (как это реализовано на объектах, принадлежащих правительству США) запас прочности был определен как величина, которая не может быть уменьшена без проверки контролирующим государственным учреждением. Министерство энергетики США издает DOE G 424.1-1 «Руководство по применению при рассмотрении требований к непроверенным вопросам безопасности» в качестве руководства для определения того, как определить и определить, будет ли снижен запас прочности в результате предлагаемого изменения. В руководстве разрабатывается и применяется концепция качественного запаса прочности, который может не быть явным или поддающимся количественной оценке, но может быть оценен концептуально, чтобы определить, произойдет ли увеличение или уменьшение при предлагаемом изменении. Этот подход становится важным при изучении проектов с большими или неопределенными (историческими) полями и тех, которые зависят от «мягких» элементов управления, таких как программные ограничения или требования. Коммерческая ядерная промышленность США использовала аналогичную концепцию при оценке запланированных изменений до 2001 года, когда 10 CFR 50.59 был пересмотрен для сбора и применения информации, доступной в анализе рисков для конкретных объектов и других инструментах количественного управления рисками.

Коэффициент резерва

Часто используемый в Европе показатель силы — это «коэффициент резерва (RF)». При выражении прочности и приложенных нагрузок в одних и тех же единицах запасной коэффициент определяется одним из двух способов в зависимости от отрасли:

RF = испытательная прочность / испытательная нагрузка. RF = предельная прочность / предельная нагрузка

Применяемые нагрузки зависят от многих факторов, в том числе применяемых факторов безопасности.

Расчет предела текучести и предела

Для пластичных материалов (например, большинства металлов) часто требуется, чтобы коэффициент запаса прочности сравнивался как с yield, так и с пределом сильные стороны. Расчет текучести определяет коэффициент безопасности до тех пор, пока деталь не начнет пластически деформироваться. Окончательный расчет определит коэффициент безопасности до отказа. Для хрупких материалов эти значения часто настолько близки, что их невозможно различить, поэтому обычно приемлемо рассчитывать только предельный коэффициент безопасности.

Выбор проектных факторов

Соответствующие проектные коэффициенты основаны на нескольких соображениях, таких как точность прогнозов приложенных нагрузок, прочности, оценки износа и воздействия окружающей среды, которому продукт будет подвергаться в процессе эксплуатации; последствия инженерного сбоя; и стоимость чрезмерной инженерии компонента для достижения этого коэффициента безопасности. Например, для компонентов, отказ которых может привести к значительным финансовым потерям, серьезным травмам или смерти, может использоваться коэффициент безопасности четыре или выше (часто десять). Расчетный коэффициент некритических компонентов обычно может быть равен двум. Анализ рисков, анализ видов и последствий отказов и другие инструменты обычно используются. Факторы проектирования для конкретных приложений часто устанавливаются законом, политикой или отраслевыми стандартами.

В зданиях обычно используется коэффициент запаса прочности 2,0 для каждого элемента конструкции. Значение для зданий относительно низкое, потому что нагрузки хорошо понятны, и большинство конструкций избыточны. Сосуды под давлением используют от 3,5 до 4,0, автомобили используют 3,0, а самолеты и космические корабли используют от 1,2 до 3,0 в зависимости от области применения и материалов. Пластичные, металлические материалы имеют тенденцию использовать более низкое значение, а хрупкие материалы используют более высокие значения. В области аэрокосмической техники обычно используются более низкие коэффициенты проектирования, поскольку затраты, связанные с весом конструкции, высоки (то есть самолет с общим коэффициентом безопасности 5, вероятно, будет слишком тяжелым, чтобы оторваться от земли). Этот низкий коэффициент проектирования является причиной того, что детали и материалы для аэрокосмической промышленности подлежат очень строгому контролю качества и строгим графикам профилактического обслуживания, чтобы обеспечить надежность. Обычно применяемый коэффициент безопасности составляет 1,5, но для герметичного фюзеляжа он равен 2,0, а для конструкций основных стоек шасси он часто составляет 1,25.

В некоторых случаях непрактично или невозможно, чтобы деталь соответствовала «стандарту» расчетный коэффициент. Штрафы (массовые или иные) за выполнение требования помешали бы системе быть жизнеспособной (например, в случае самолета или космического корабля). В этих случаях иногда определяется, чтобы компонент соответствовал более низкому, чем обычно, коэффициенту безопасности, что часто называется «отказом» от требования. Это часто сопровождается дополнительным подробным анализом или проверкой контроля качества, чтобы гарантировать, что деталь будет работать так, как нужно, поскольку она будет загружена ближе к своим пределам.

Для циклических, повторяющихся или непостоянных нагрузок важно учитывать возможность усталости металла при выборе запаса прочности. Циклическая нагрузка значительно ниже предела текучести материала может вызвать отказ, если она повторяется через достаточное количество циклов.

Согласно Элишакову понятие фактора безопасности в инженерном контексте, по-видимому, впервые было введено в 1729 году Бернаром Форестом де Белидором (1698-1761), который был французом инженер, работающий в области гидравлики, математики, гражданского и военного строительства. Философские аспекты факторов безопасности исследовали Доорн и Ханссон

См. Также

• Инженерный допуск
• Расчет по предельным состояниям
• Вероятностный дизайн
• Избыточность (полное управление качеством)
• Жертвенный часть — Компонент, спроектированный так, чтобы в первую очередь выйти из строя для защиты остальной части устройства
• Статистические помехи
• Проверка и проверка

Примечания

Дополнительная литература

• Лаланн, К., Разработка спецификаций — 2-е изд., ISTE-Wiley, 2009

Лениво пока фотографии из командировки выкладывать. Потому — продолжу «умничать».

Расчет любой конструкции на прочность, необязательно самолёта, начинается с определения собственно нагрузки на эту конструкцию. Необходимо определить, что мы в итоге хотим получить от изделия, какие нагрузки оно должно выдерживать. Понятное дело, я буду говорить об нагрузках на самолет.

Очевидно, что при полете крыло самолета нагружено распределенной нагрузкой — подъемной силой. На заглавном рисунке эта эпюра нагрузки показана на правой консоли и обозначена буквой q.

Интенсивность этой распределенной нагрузки должна быть такой, чтобы общая результирующая подъемной силы была равна:
Y = f*Ny*m, где:
f — коэффициент безопасности (не путать с запасом прочности)
Ny — максимальная эксплуатационная перегрузка (та, которая записана в РЛЭ в разделе ограничения)
m — масса летательного аппарата.

По порядку об этих трех параметрах.
Коэффициент безопасности f показывает во сколько раз разрушающая нагрузка (перегрузка в общем случае) больше максимальной эксплуатационной. Авиационные конструкции расчитываются не по допускаемым напряжениям, как в общем машиностроении, а по разрушающим. Потому что, понятно — культура веса, минимизация массы — основное направление деятельности инженеров при проектировании самолетов. Относительная близость к разрушающим нагрузкам компенсируется высокой точностью определения нагрузок на самолет и применением различных методов расчета, для получения уверенного результата расчета.

Диапазон величин коэффициента безопасности для многоразового летательного аппарата лежит в пределах f = 1.5….2.5 в зависимости от режима полета и типа конструктивного элемента. Максимальные коэффициенты безопасности применяют к герметичным конструкциям, которые нагружены избыточным давлением — баллоны высокого давления, гермокабины, пассажирские салоны. Почему минимальное значение коэффициента безопасности равно 1.5 для самолетов? Одним из требований к авиационной конструкции гласит, что в самолете должны отстутствовать необратимые пластические деформации материала. То есть при достижении предельных эксплуатационных перегрузок самолет не должен, грубо говоря, потерять форму безвозвратно. Это уже завязано на параметр материала — предел текучести. Т.е. такие напряжения, при которых материал возвращается к своим первоначальным размерам полностью и деформируется упруго после снятия нагрузки. А разрушающие напряжения для большинства металлов примерно в 1.5 раза больше предела текучести.

Максимальная эксплуатационная перегрузка Ny зависит от типа проектируемого летательного аппарата. Различают несколько групп самолетов, разделенных по величине максимальной эксплуатационной перегрузки:

1. Неманевренные самолеты. Это самолеты с максимальной Ny не более 2.5 ед.
Это все пассажирские и транспортные самолеты.

2. Ограниченно маневренные самолеты с максимальной экслуатационной Ny лежащей в интервале от 2.5 до 6 единиц. Сюда относятся фронтовые бомбардировщики, штурмовики, тяжелые перехватчики (Су-24, Су-25, МиГ-25, МиГ-31)

3. Маневренные самолеты. Самолеты с максимальной эксплуатационной перегрузкой от 6 до 9 единиц. Это — все современные истребители.

4. Спортивно-пилотажные самолеты. Этот те экстремальные самолеты, которые могут выходить на перегрузки до Ny=+12 единиц — Су-29, Су-31, Як-55, наверное зарубежные аналоги — всякие Extra 300.

Исходя из класса самолета определяется и природа возникновения максимальных эксплуатационных перегрузок. Для неманевренных самолетов выход на максимальные перегрузки связан с полетом в неспокойном воздухе, для остальных — максимальные перегрузки достигаются в следствии, естессна, криволинейного полета — маневрирования.

Масса самолета. Было бы просто сказать, что мол самолет должен без проблем выходить на максимальную перегрузку при максимальной взлетной массе. И на значительном числе самолетов такое условие выполняется. Правда порой такие жертвы ни к чему и дабы не перетяжелять конструкцию вводятся некоторые ограничения на максимальные массы и максимальные перегрузки.

Вернусь обратно к заглавному рисунку. Если на правой консоли я нарисовал распределение подъемной силы по размаху крыла, то на левой консоли я нарисова эпюру изгибающего момента. Наугад, примерно. Но общую картину она отражает. Следует также заметить, что крыло, помимо изгиба нагружается еще и крутящим моментом, так как линия действия резуьтирующей аэродинамической силы и линия жесткости крыла не совпадают.

Распределение подъемной силы по размаху и по хорде крыла зависит от режима полета самолета. В некоторых случаях максимальным будет изгибающий момент, в некоторых — крутящий, а могут быть и такие случаи, когда вроде и изгибающий момент не максимален, и крутящий тоже. Однако совместное их действие вызывает максимальные напряжения в элементах конструкции. Такие предельные режимы полета называются расчетными случаями (loadcase). Предствляют они собой крайние точки эксплуатационных ограничений самолета (flight envelope). Расчетных случаев — великое множество, к отдельным элементам конструкции и агрегатам могут применяться дополнительные комбинации нагрузок и для них количество расчетных случаев может исчисляться десятками, а то и сотнями.

В таблице ниже приведены несколько основных полетных случаев:

В шапке таблицы названия расчетных случаев — А, А-штрих, B, C, D и D-штрих, слева — параметры полета самолета:
Су — коэффициент подъемной силы крыла
ny — перегрузка
q — скоростной напор.
f — коэффициент безопасности принимаемый для данного расчетного случая.

Случай А — полет самолета при максимальной эксплуатационной перегрузке на углах атаки соответствующих максимальному коэффициенту подъемной силы (близких к критическому углу атаки для самолета). Скоростной напор при этом не будет максимальным, а будет зависить от описаного в таблице соотношения. Этот расчетный случай возможен при энергичном вводе самолета в вертикальный маневр, действие на самолет вертикального порыва воздуха.

Случай А-штрих — криволинейный полет самолета при предельном скоростном напоре и максимальной эксплуатационное перегрузке. Подъемная сила одинакова в двух этих случаях, она равна весу самолета умноженому на ny. Другое дело, что в расчетном случае А перегрузка реализуется за счет максимального угла атаки, путем быстрого выхода самолета на него и интенсивным торможением, а в случае А-штрих перегрузка реализуется на малых углах атаки при максимальном скоростном напоре. Реализация расчетного случая А-штрих возможна, например при выводе самолета из пикирования. Коэффициент безопасности равен тоже 1.5.

Основная разница — в распределении подъемной силы по размаху и хорде крыла. В случае А распределение будет таким, каким я его нарисовал на заглавной картинке — плавно увеличивающимся от законцовок к фюзеляжу. В случае А-штрих, который характеризуется меньшими углами атаки на диаграмме распределения подъемной силы будут наблюдаться провалы в местах крепления двигателей, внешних подвесок и фюзеляжа. Эти элементы не столь совершенны аэродинамически как профиль крыла, а потому вклад в формирование подъемной силы заметен только на больших углах атаки, коих не наблюдается в случае А-штрих.

Различным будет и распределение нагрузки по хорде крыла. Проще рисунок показать:

Расчетный случай В — полет при перегрузке, примерно в половину от максимальной эксплуатационной, но с отклоненными элеронами. На максимальном скоростном напоре. Это комбинация совместного действия на крыло изгибающего и крутящих моментов умереной величины. f=2

Расчетный случай С — полет на углах атаки соответсвущих нулевой подъемной силе с отклоенными элеронами. Случай характеризуется практически нулевыми изгибающими моментами и максимальным крутящим. Пример — восходящая или нисходящая вертикальная бочка. f=2

Помимо полетных случаев есть еще и различные варианты расчетных случаев при посадке — посадки на основные опоры, посадки на переднюю опору, посадки с боковой перегрузкой, посадки на воду, посадки с убраным шасси. Помимо всего прочего есть уж совсем специальные расчетные случаи. К примеру при расчете нервюр на передней кромке 787 есть такой сучай — заклинивание привода выпуска предкрылка. А привод предкрылка — это такой вал, который идет через переднюю кромку и выпускает секции предкрылка посредством зубчатой передачи. Так вот в этом расчетном случае предполагается, что этот вал заклинивает и весь крутящий момент дожен быть уравновешен узлами крепления двигателя, который и вращает вал. То есть болты должны выдержать перерезывающую силу, да и нервюра сама, будучи довольно ажурной не должна потечь или сломаться. Но это — уже дебри.

Вернемся к картинке, которая была выложена в предыдущем лекционном рассказе. С деформацией крыла 787. Я нашел более красивый вариант:

На этой картинке показана зависимость прогиба крыла в зависимости от величины нагружения.

Neutral — понятное дело, крыло не нагружено.

10 feet In Flight — это положение крыла при полете с перегрузкой Ny = 1G, то есть — равномерный прямолинейный полет.

Limit Load — Этого пункта на картинке нет. А зря. Limit (Maximal) load — это как раз прогиб крыла при действии максимальной эксплуационной перегрузки, Ny = 2.5G Предельная, максимальная нагрузка (перегрузка) — так ее правильно называть.

150% Max Load — это ни что иное как разрушающая нагрузка. Она — это предельная перегрузка умноженая на коэффициент безопасности — те самые 150%. Корректные названия — расчетная нагрузка, разрушающая. По нерусски — ultimate load.

Когда в репортажах или статьях про статиспытания нового самолета говорят, что самолет выдержа 150% расчетной нагрузки — это неверно. 150% максимальной нагрузки — это верно.

Таким образом сравнительно легко можно прикинуть разрушающую перегрузку для любого самолета — достаточно открыть РЛЭ, найти там максимально допустимую перегрузку и умножить ее на 1.5. Для неманевренных самолетов с Ny = 2.5G разрушающая перегрузка будет равна не менее чем 3.75G. Сознательно написал не менее, потому что идеально точно спроектировать самолет не получается, прочнисты всегда перестраховываются и чуть добавляют материала в запас.

В диапазоне от нулевой нагрузки до предельной дожно выполняться требование отсутствия необратимых пластических деформаций в планере самолета. (1G < Ny < 2.5G)

В диапазоне от предельной нагрузки до разрушающей гарантируется неразрушение самолета, но допускается наличие пластических деформаций.(2.5G < Ny < 3.75G)

В диапазоне от расчетной нагрузки и выше не гарантируется по результатам расчета практически ничего. Не, вру. Конструкция должна на статических испытаниях выдержать расчетную нагрузку в течении не менее трех секунд. (Ny >= 3.75G)

Вот известная уже картинка. На ней как раз планер 787 нагружен расчетной нагрузкой:

Часто, да почти всегда, коэффициент безопасности ошибочно называют запасом прочности. Это не так. О различии этих параметров — в следующий раз.

В инженерии коэффициент безопасности ( FoS ), также известный как (и взаимозаменяемый) коэффициент безопасности ( SF ), выражает, насколько сильнее система, чем она должна быть для предполагаемой нагрузки. Коэффициенты безопасности часто рассчитываются с использованием подробного анализа, поскольку всестороннее тестирование нецелесообразно для многих проектов, таких как мосты и здания, но способность конструкции выдерживать нагрузку должна быть определена с разумной точностью.

Многие системы намеренно построены намного сильнее, чем необходимо для нормального использования, чтобы учесть аварийные ситуации, неожиданные нагрузки, неправильное использование или ухудшение ( надежность ).

Определение

Есть два определения коэффициента безопасности (FoS):

• Отношение абсолютной прочности конструкции (структурной способности) к фактической приложенной нагрузке; это показатель надежности конкретной конструкции. Это расчетное значение, которое иногда для ясности называют реализованным фактором безопасности .
• Постоянное требуемое значение, установленное законом, стандартом , спецификацией , контрактом или обычаем , которому конструкция должна соответствовать или превосходить. Это может называться расчетным коэффициентом , расчетным коэффициентом безопасности или требуемым коэффициентом безопасности .

Реализованный коэффициент безопасности должен быть больше требуемого расчетного коэффициента безопасности. Однако использование между различными отраслями и инженерными группами непоследовательно и сбивает с толку; используется несколько определений. Причина большой путаницы заключается в том, что различные справочники и агентства по стандартизации по-разному используют определения и термины фактора безопасности. Дизайн кода, структурные и машиностроительные учебники часто ссылаются на «фактор безопасности» , как часть общей структурной способности над тем, что нужно. Это реализованные факторы безопасности (первое использование). Во многих учебниках по прочности материалов для бакалавриата «Фактор безопасности» используется как постоянное значение, предназначенное как минимальная цель для проектирования (повторное использование).

Расчет

Есть несколько способов сравнить коэффициент надежности конструкций. Все различные расчеты в основном измеряют одно и то же: какую дополнительную нагрузку сверх ожидаемой конструкция фактически выдержит (или должна выдержать). Разница между методами заключается в способе вычисления и сравнения значений. Значения коэффициента безопасности можно рассматривать как стандартизованный способ сравнения прочности и надежности между системами.

Использование запаса прочности не означает, что элемент, конструкция или конструкция являются «безопасными». Многие факторы обеспечения качества , инженерного проектирования , производства , установки и конечного использования могут влиять на безопасность чего-либо в той или иной конкретной ситуации.

Расчетный коэффициент и запас прочности

Разница между коэффициентом безопасности и расчетным коэффициентом (расчетный коэффициент безопасности) заключается в следующем: коэффициент безопасности или предел текучести — это то, сколько разработанная деталь фактически сможет выдержать (первое «использование» сверху). Расчетный коэффициент, или рабочее напряжение, — это то, что должен выдерживать элемент (второе «применение»). Расчетный коэффициент определяется для приложения (обычно предоставляется заранее и часто устанавливается регулирующими строительными нормами или политикой) и не является фактическим расчетом, коэффициент запаса прочности — это отношение максимальной прочности к предполагаемой нагрузке для фактического спроектированного объекта.

• Расчетная нагрузка максимальная нагрузка часть должна когда — нибудь в обслуживании.

Согласно этому определению, конструкция с FOS ровно 1 будет поддерживать только расчетную нагрузку и не более. Любая дополнительная нагрузка приведет к разрушению конструкции. Конструкция с FOS 2 выйдет из строя при удвоенной расчетной нагрузке.

Запас прочности

Многие государственные учреждения и отрасли (например, аэрокосмическая промышленность) требуют использования запаса прочности ( MoS или MS ) для описания соотношения прочности конструкции и требований. Есть два разных определения запаса прочности, поэтому необходимо внимательно определить, какое из них используется для данного приложения. Одно использование MS — это как мера возможностей, например, FoS. Другое использование MS — это мера удовлетворения проектных требований (проверка требований). Можно концептуально представить запас прочности (вместе с коэффициентом резерва, поясняемый ниже), чтобы показать, какая часть общей способности конструкции удерживается «в резерве» во время загрузки.

MS как мера структурной способности: это определение запаса прочности, обычно встречающееся в учебниках, описывает, какую дополнительную нагрузку сверх расчетной нагрузки может выдержать деталь до выхода из строя. По сути, это мера избыточных возможностей. Если запас равен 0, деталь не будет принимать дополнительную нагрузку до того, как выйдет из строя, если значение отрицательное, деталь выйдет из строя до достижения расчетной нагрузки при эксплуатации. Если запас равен 1, он может выдержать одну дополнительную нагрузку, равную максимальной нагрузке, на которую он был рассчитан (т. Е. Удвоенной расчетной нагрузке).

MS как мера проверки требований: многие агентства и организации, такие как NASA и AIAA, определяют запас прочности, включая проектный коэффициент, другими словами, запас прочности рассчитывается после применения проектного коэффициента. В случае запаса, равного 0, деталь имеет точно требуемую прочность (коэффициент запаса прочности будет равен расчетному коэффициенту). Если имеется деталь с требуемым расчетным коэффициентом 3 и запасом 1, эта деталь будет иметь коэффициент безопасности 6 (способна выдерживать две нагрузки, равные ее расчетному коэффициенту 3, выдерживая шестикратную расчетную нагрузку до разрушения ). . Запас 0 означал бы, что деталь будет проходить с коэффициентом безопасности 3. Если запас меньше 0 в этом определении, хотя деталь не обязательно выйдет из строя, требования к конструкции не были выполнены. Удобство этого использования заключается в том, что для всех приложений проходит маржа 0 или выше, не нужно знать детали приложения или сравнивать с требованиями, просто взглянув на расчет маржи, можно узнать, прошел ли проект или нет. Это полезно для надзора и проверки проектов с различными интегрированными компонентами, поскольку разные компоненты могут иметь различные факторы проектирования, а расчет маржи помогает предотвратить путаницу.

• Фактор безопасности конструкции обеспечиваются как требование.

Для успешного проектирования реализованный коэффициент безопасности всегда должен быть равен или превышать проектный коэффициент безопасности, чтобы запас прочности был больше или равен нулю. Иногда, но нечасто, запас прочности используется в процентах, например, 0,50 MS эквивалентно 50% MS. Когда конструкция удовлетворяет этому тесту, говорят, что она имеет «положительный запас», и, наоборот, « отрицательная маржа », когда это не так.

В области ядерной безопасности (как это реализовано на государственных объектах США) запас прочности был определен как величина, которая не может быть уменьшена без проверки контролирующим государственным учреждением. Министерство энергетики США издает DOE G 424.1-1 «Руководство по применению при рассмотрении требований к непроверенным вопросам безопасности» в качестве руководства для определения того, как определить и определить, будет ли снижен запас прочности в результате предлагаемого изменения. В руководстве разрабатывается и применяется концепция качественного запаса прочности, который может не быть явным или поддающимся количественной оценке, но может быть оценен концептуально, чтобы определить, произойдет ли увеличение или уменьшение при предлагаемом изменении. Этот подход становится важным при изучении проектов с большими или неопределенными (историческими) полями, а также тех, которые зависят от «мягких» элементов управления, таких как программные ограничения или требования. Коммерческая ядерная промышленность США использовала аналогичную концепцию при оценке запланированных изменений до 2001 года, когда 10 CFR 50.59 был пересмотрен с целью сбора и применения информации, доступной в анализе рисков для конкретных объектов и других инструментах количественного управления рисками.

Резервный фактор

Мерилом силы, часто используемым в Европе, является фактор резерва (RF). Поскольку прочность и прилагаемые нагрузки выражены в одних и тех же единицах, коэффициент запаса определяется одним из двух способов в зависимости от отрасли:

Прикладываемые нагрузки имеют множество факторов, в том числе применяемые факторы безопасности.

Расчет доходности и предела

Для пластичных материалов (например , большинство металлов), часто требуется, чтобы коэффициент безопасности сверяется как выход и конечной прочности. Расчет текучести определит коэффициент запаса прочности до тех пор, пока деталь не начнет пластически деформироваться . Окончательный расчет определит коэффициент безопасности до отказа. Для хрупких материалов эти значения часто настолько близки, что их невозможно различить, поэтому обычно приемлемо рассчитывать только предельный коэффициент безопасности.

Выбор факторов дизайна

Соответствующие проектные факторы основаны на нескольких соображениях, таких как точность прогнозов приложенных нагрузок , прочности, оценок износа и воздействия окружающей среды, которому продукт будет подвергаться в процессе эксплуатации; последствия инженерного сбоя; и стоимость чрезмерной инженерии компонента для достижения этого коэффициента безопасности. Например, для компонентов, отказ которых может привести к значительным финансовым потерям, серьезным травмам или смерти, может использоваться коэффициент безопасности четыре или выше (часто десять). Расчетный коэффициент некритических компонентов обычно может составлять два. Анализ рисков , неспособность режима и анализ эффектов , а также другие инструменты , которые обычно используются. Факторы проектирования для конкретных приложений часто устанавливаются законом, политикой или отраслевыми стандартами.

Здания обычно используют коэффициент безопасности 2,0 для каждого элемента конструкции. Стоимость зданий относительно невысока, поскольку нагрузки хорошо известны, а большинство конструкций избыточны . Сосуды под давлением используют от 3,5 до 4,0, автомобили используют 3,0, а самолеты и космические корабли используют от 1,2 до 3,0 в зависимости от применения и материалов. Для пластичных металлических материалов обычно используется более низкое значение, а для хрупких материалов — более высокие значения. В области аэрокосмической техники обычно используются более низкие конструктивные коэффициенты, поскольку затраты, связанные с весом конструкции, высоки (т. Е. Самолет с общим коэффициентом безопасности 5, вероятно, будет слишком тяжелым, чтобы оторваться от земли). Этот низкий коэффициент проектирования является причиной того, что детали и материалы для аэрокосмической отрасли подлежат очень строгому контролю качества и строгим графикам профилактического обслуживания, чтобы обеспечить надежность. Обычно применяемый коэффициент безопасности составляет 1,5, но для герметичного фюзеляжа он равен 2,0, а для конструкций основных стоек шасси он часто составляет 1,25.

В некоторых случаях соответствие детали «стандартному» расчетному коэффициенту непрактично или невозможно. Штрафы (массовые или иные) за выполнение требования могут помешать жизнеспособности системы (например, в случае самолета или космического корабля). В этих случаях иногда определяется, чтобы компонент соответствовал более низкому, чем обычно, коэффициенту безопасности, что часто называют «отказом» от требования. Это часто сопровождается дополнительным подробным анализом или проверкой контроля качества, чтобы гарантировать, что деталь будет работать должным образом, поскольку она будет загружена ближе к предельным значениям.

Для циклических, повторяющихся или непостоянных нагрузок важно учитывать возможность усталости металла при выборе запаса прочности. Циклическая нагрузка значительно ниже предела текучести материала может вызвать отказ, если она повторяется через достаточное количество циклов.

Согласно Элишакову, понятие фактора безопасности в инженерном контексте, по-видимому, впервые было введено в 1729 году Бернаром Форестом де Белидором (1698-1761), французским инженером, работавшим в области гидравлики, математики, гражданского и военного строительства. Философские аспекты факторов безопасности исследовали Доорн и Ханссон.

Смотрите также

• Инженерная толерантность
• Расчет предельного состояния
• Вероятностный дизайн
• Избыточность (полное управление качеством)
• Жертвенная часть  — Компонент, спроектированный таким образом, чтобы в первую очередь выйти из строя, чтобы защитить остальную часть устройства.
• Статистическая интерференция
• Верификация и валидация

Примечания

дальнейшее чтение

• Лаланн, К., Разработка спецификации — 2-е изд. , ISTE-Wiley, 2009 г.