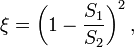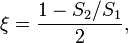Лабораторная
работа.
ОПРЕДЕЛЕНИЕ
КОЭФФИЦИЕНТА ГИДРАВЛИЧЕСКОГО ТРЕНИЯ
(КОЭФФИЦИЕНТА ДАРСИ).
1. Цель работы:
— Изучение способов
определения коэффициента гидравлического
трения;
— Изучение методики
экспериментального определения
коэффициента гидравлического трения;
— Установление
зависимости коэффициента гидравлического
трения от числа Рейнольдса.
2. Основные
теоретические положения.
В
реальных потоках жидкости присутствуют
силы вязкого трения. В результате слои
жидкости трутся друг об друга в процессе
движения. На это трение затрачивается
часть энергии потока, по этой причине
в процессе движения неизбежны потери
энергии. Эта энергия, как и при любом
трении, преобразуется в тепловую энергию.
Из-за этих потерь энергия потока жидкости
по длине потока, и в его направлении
постоянно уменьшается, то есть напор
потока
H
в
направлении движения потока становится
меньше. Если рассмотреть два соседних
сечения потока
1-1
и
2-2,
то
потери гидродинамического напора h
составят:
,
где
H1-1—
напор в первом сечении потока жидкости,
H2-2—
напор во втором сечении потока,
h
—
потерянный напор — энергия, потерянная
каждой единицей веса движущейся жидкости
на преодоление сопротивлений на пути
потока от сечения
1-1
до
сечения
2-2.
С
учётом потерь энергии
уравнение
Бернулли для потока реальной жидкости
будет
выглядеть
. (1)
Индексами
1 и 2 обозначены характеристики потока
в сечениях
1-1
и
2-2.
Если
учесть, что характеристики потока –
средняя скорость течения
и
коэффициент Кориолиса
зависят
от геометрии потока, которая для напорных
потоков определяется геометрией
трубопровода, понятно, что потери энергии
(напора) в разных трубопроводах будут
изменяться неодинаково.
Выделяют два вида
потерь напора – потери на трение по
длине трубопровода и местные потери.
Потери на трение
по длине.
При течении реальных
(вязких) жидкостей по трубам и каналам
возникают потери напора, обусловленные
внутренним трением. Эти потери
пропорциональны длине участка русла,
на котором они имеют место, и поэтому
они называются потерями
на трение по длине.
Гидравлические
потери в напорных потоках происходят
за счет уменьшения вдоль потока удельной
потенциальной энергии жидкости. Удельная
кинетическая энергия жидкости в этом
случае если и меняется вдоль потока при
заданном расходе, то не за счет потерь
энергии, а вследствие изменения размеров
поперечного сечения русла, так как она
зависит только от скорости, а скорость
определяется расходом и площадью сечения
В общем случае
величина потери на трение по длине
определяется по формуле Дарси-Вейсбаха:
, (2)
где
— средняя скорость потока, L
– длина участка трубопровода, d
– диаметр трубопровода,
— коэффициент гидравлического трения
(коэффициент Дарси).
Значение коэффициента
зависит от режима течения жидкости.
При ламинарном
режиме течения
зависит только от числа Рейнольдса
и может быть найден по формуле:
. (3)
При турбулентном
режиме
в общем случае является функцией как
числа Re,
так и шероховатости поверхности
трубопровода (эквивалентная высота
выступов шероховатости ).
Конкретный вид зависимости
зависит
от соотношения величин шероховатости
и числа Re.
Наиболее универсальной для турбулентных
течений является формула Альтшуля:
. (4)
3. Описание
лабораторной установки.
Гидравлическая
принципиальная схема стенда приведена
на рисунке 1.
В состав стенда
входят гидробак Б, шестеренный насос
Н, фильтр Ф, предохранительный клапан
КП, регулятор расхода РР, два
гидрораспределителя Р1 и Р2, пружинный
аккумулятор А, два гидродросселя ДР1 и
ДР2, трубопроводы. Привод насоса
осуществляется от электродвигателя.
Информационно-измерительная система
стенда включает 6 манометров (МН1 – МН6,
манометр МН5 – электроконтактный с
двумя управляемыми контактами), расходомер
скоростного типа РА, термометр Т и
электронный секундомер.
Управление
гидрораспределителями осуществляется
тумблерами Р1 и Р2.
При установке
тумблера в положение “РУЧН.” электронный
секундомер используется для определения
времени прохождения через расходомер
РА заданного объема жидкости (с тем,
чтобы в дальнейшем определять расход
жидкости в трубопроводе).
Рис. 1 Схема
гидравлическая принципиальная стенда
Питание секундомера
включается тумблером “Вкл.”, начало
отсчета времени – тумблером “Счет.”,
сброс показаний электронного табло –
кнопкой “Сброс”. При нажатии кнопки
“Сброс” секундомер не должен производить
отсчет времени, то есть тумблер “Счет”
необходимо переключить в нижнее
положение.
Исследуемым в
данной работе участком является участок
ab.
4. Порядок выполнения:
4.1. Включить питание
стенда;
4.2. Включить питание
электродвигателя;
4.3. Включить тумблер
Р1 в положение “Вкл.”.
4.4. Дать возможность
поработать установке в течение 5 – 6
минут.
4.5. При различных
значениях расхода зарегистрировать по
манометрам МН1 и МН2 давления Pa
и Pb,
а также время прохождения через расходомер
заданного объема рабочей жидкости и
температуру жидкости. Результаты
измерений занести в таблицу в протоколе
испытаний.
4.6. После выполнения
всех опытов отключить питание электронного
секундомера, электродвигателя и стенда.
5. Обработка
результатов измерений:
5.1. Для каждого
отсчёта с помощью уравнения Бернулли
(1) вычислить потерю напора на трение
hтр.
5.2. Рассчитать для
каждого опыта значения скорости течения
и числа Рейнольдса:
, (5)
, (6)
где S
– площадь поперечного сечения
трубопровода.
. (7),
где d
– внутренний диаметр трубопровода,
— коэффициент кинематической вязкости
жидкости, который находится в зависимости
от температуры по таблице 1.
Таблица 1. Коэффициент
кинематической вязкости масла при
различных температурах
|
t °C |
10 |
15 |
20 |
25 |
30 |
35 |
|
ν, |
400·10-6 |
250·10-6 |
160·10-6 |
120·10-6 |
90·10-6 |
70·10-6 |
5.3. С помощью формулы
Дарси-Вейсбаха (2), зная величину потерь
напора hтр,
выразить для каждого опыта коэффициент
гидравлического трения .
5.4. С помощью формулы
(3) или (4) – в зависимости от наблюдаемого
режима течения – вычислить теоретические
значения коэффициента гидравлического
трения .
5.5. Результаты
расчётов занести в таблицу 2.
|
№ |
, |
, |
Re |
|
|
|
|
1 |
||||||
|
2 |
||||||
|
3 |
||||||
|
4 |
||||||
|
5 |
||||||
|
6 |
||||||
|
7 |
5.6. Построить в
одной координатной плоскости графики
зависимости
и
.
5.7. Рассчитать
погрешности измерений, результаты
занести в таблицу 2.
6. Содержание
отчёта.
Отчёт по лабораторной
работе должен содержать:
-
краткие теоретические
положения; -
схему экспериментальной
установки; -
протокол испытаний;
-
обработку
результатов опыта; -
график зависимости
и
;
-
анализ полученных
результатов.
Протокол испытаний
Лабораторная
работа №
Определение коэффициента
гидравлического трения.
Группа:
Дата испытаний:
Исполнители:
Исходные данные:
Внутренний диаметр
трубопроводов d
= м
Длина исследуемого
участка l
= м
Плотность масла
= кг/м3
Результаты
испытаний:
|
№ |
V, |
t, |
T, |
Pa, |
Pb, |
|
1 |
|||||
|
2 |
|||||
|
3 |
|||||
|
4 |
|||||
|
5 |
|||||
|
6 |
|||||
|
7 |
Подпись
исполнителей
Подпись
преподавателя
Соседние файлы в папке Гидравлика лабы
- #
- #
- #
- #
- #
- #
- #
В этой статье будет обсуждаться тема под названием «Коэффициент трения Дарси» и факты, связанные с коэффициентом трения Дарси. В гидромеханике уравнение коэффициента трения Дарси играет очень важную роль.
Коэффициент трения Дарси представляет собой физический параметр, который связан с потерей напора или потери давления из-за трения на определенном участке длины змеевика или трубы со средней скоростью несжимаемой жидкости. Коэффициент трения Дарси является безразмерной физической величиной.
Что такое коэффициент трения Дарси?
Коэффициент трения Дарси — это физический параметр, который используется для описания потерь на змеевике или трубе из-за трения. Коэффициент трения Дарси применим как для потока в открытом, так и в закрытом канале.
Кредит изображения — Wikimedia Commons
Коэффициент трения Дарси — это физический параметр, описываемый как физическая величина, используемая для расчета потерь энергии на трение. Коэффициент трения Дарси относится к сопротивлению из-за трения и скорости несжимаемой жидкости внутри змеевика или трубы.
Коэффициент трения Дарси широко используется в турбулентных потоках для расчета величины потери напора при трении в трубе.
Формула коэффициента трения Дарси:
Уравнение для коэффициента трения Дарси приведено ниже:
Hf = 4fLv2/2gD
Где,
Hf = Потеря давления или потеря напора
f = коэффициент коэффициента трения или коэффициент коэффициента трения
L = длина змеевика или трубы
v = скорость несжимаемой жидкости
g = ускорение свободного падения (значение g равно 9.8 метра в секунду в квадрате)
D = диаметр змеевика или трубы
Уравнение потери давления: —
В цилиндрическом змеевике или трубе, по которой движется несжимаемая жидкость, в цилиндрическом змеевике или трубе, имеющих постоянный диаметр D, потери давления возникают при вязком эффекте, который выражается как Δp, прямо пропорциональный длине цилиндрического катушка или труба могут быть выражены как с помощью уравнения Дарси – Вейсбаха,
Где,
Δp/L = потеря давления на единицу длины, выраженная в Пакалях на метр.
fD = Коэффициент коэффициента трения или Коэффициент коэффициента трения
v = скорость несжимаемая жидкость который выражается как метр в секунду
DH= Гидравлический диаметр, который выражается в метрах
ρ = плотность жидкости, выраженная в кг на кубический метр.
Форма потери головы: —
Термин потери напора, который выражается как Δh, представляет собой потерю давления, возникающую из-за трения при одинаковой длине столба несжимаемой жидкости.
Математическая форма потери напора:
Δp =ρgΔh
Δh= Потеря напора возникает из-за трения при одинаковой длине змеевика или трубы и единицей измерения является метр.
g = ускорение свободного падения (значение g равно 9.8 метра в секунду в квадрате)
Выгодно, если потеря напора возникает из-за трения при одинаковой длине змеевика или трубы,
Где,
L = длина змеевика или трубы, единица измерения – метр
Уравнение Дарси – Вейсбаха может быть записано для потери напора,
В виде объемного потока:-
Соотношение между объемным расходом и средней скоростью потока:
Q = А *
Где,
Q = Единица объемного расхода — кубический метр в секунду.
A = площадь поперечного сечения змеевика или трубы, единица измерения – квадратный метр.
v = скорость несжимаемой жидкости, выраженная в метрах в секунду.
В змеевике или трубе течет жидкость с диаметром трубы D_c,
Уравнение Дарси – Вейсбаха можно записать в виде
Форма напряжения сдвига: —
Уравнение Дарси – Вейсбаха может быть представлено в виде касательного напряжения,
Как рассчитать коэффициент трения Дарси?
Процесс расчета коэффициент трения для турбулентного потока приведен ниже,
- Сначала нам нужно определить значение Число Рейнольдса для турбулентного потока по этой формуле
- ρ х В х Д х мк
- На следующем шаге относительная шероховатость должна быть рассчитана по формуле frac{k}{D}, значение которой должно быть меньше 0.01.
- На последнем шаге используйте формулу Муди для шероховатости с помощью числа Рейнольдса,
- f = 0.0055 x [1 + (2 x 10^4 xk/D +106/Повторно)1/3
Коэффициент трения Дарси для ламинарного потока:
Коэффициент трения Дарси для ламинарного потока можно записать как
Коэффициент трения Дарси для ламинарного течения в круглых трубах: —
fD = 64/Re
Где,
Re = число Рейнольдса
Где,
μ = вязкость несжимаемой жидкости
v = мк/р
Коэффициент трения Дарси для ламинарного течения в некруглых трубах: —
f = К/Re
Диапазон трения Дарси коэффициент ламинарного течения в некруглых трубах является,
Ламинарный поток:-
- При значении числа Рейнольдса менее 2000 такой тип течения называется ламинарным течением.
- Математический анализ турбулентного течения прост.
- Скорость турбулентного потока слишком мала.
- Регулярное движение возникает в жидкостях, которые текут в движении ламинарным потоком.
- Ламинарное течение вообще очень редкий тип течения.
- Профиль скоростей ламинарного течения у стенки трубы или стержня максимален.
- Профиль скорости ламинарного течения в центральном сечении стержня или трубы минимален.
- Возникает среднее движение, в котором течет боковая жидкость.
Кредит изображения — Википедия
Коэффициент трения Дарси для турбулентного потока:
Максимальной системой жидкости в ядерных установках является работающая с проточным типом турбулентного течения. Сопротивление этого потока подчиняется уравнению Дарси – Вейсбаха.
Трение турбулентного потока – это измерение напряжения сдвига, которое прикладывается к стенке стержня или трубы во время турбулентного течения. Турбулентное течение подчиняется уравнению Дарси – Вейсбаха, которое прямо пропорционально квадрату средней скорости текущей жидкости в определенной области..
Турбулентный поток:-
- Число Рейнольдса больше 3500.
- Скорость слишком высока.
- Появляется неравномерное движение
- Возникает среднее движение, в котором течет боковая жидкость.
- Профиль скорости турбулентного потока в определенной области быстро падает, когда речь идет о стенке трубы или стержня.
- Профиль скорости турбулентного потока в определенной области явно плоский, если речь идет о центральном сечении стержня или трубы.
Формула коэффициента трения для турбулентного потока:
Уравнение Коулбрука – Уайта определяется как f для коэффициента трения Дарси, функция числа Рейнольдса как Re, относительная шероховатость трубы выражается как ε / Dh как для гладких, так и для шероховатых труб.
Формула коэффициента трения для турбулентного потока:
или,
Где,
Dh (м, фут) = гидравлический диаметр для заполнения жидкостью круглых трубопроводов.
Dh = D = Внутренний диаметр области, откуда течет турбулентный поток
Rh (м, фут) = гидравлический радиус для заполнения жидкостью круглых трубопроводов.
Rh = D/4= Внутренний диаметр области, откуда течет турбулентный поток/4
Уравнение Коулбрука решается численно из-за его неявного характера. В настоящее время W-функцию Ламберта также используют для получения откровенной переформулировки уравнения Коулбрука.
а = 2.51/Re
или,
10-1/2 = топор + б
p = 10-1/2
Мы получим,
px = топор + б
Расширенные формы: —
Дополнительная математическая форма уравнения Коулбрука:
Где,
1.7384…. = 2 log (2 * 3.7) = 2 log (7.4)
18.574 = 2.51*3.7*2
И
Или,
Где,
1.1364…. = 1.7384… = – 2 log (2) = 2 log
(7.4) – 2 log (2) = 2 log (3.7)
9.287 = 18.574/2 = 2.51 * 3.7
Диаграмма коэффициента трения Дарси:
Диаграмма коэффициента трения Дарси представляет собой комбинацию четырех физических параметров, таких как коэффициент потери давления, число Рейнольдса и относительная шероховатость змеевика или трубы и соотношение диаметров змеевика или трубы.
Диаграмма коэффициента трения Дарси представляет собой безразмерный физический фактор с помощью уравнения Дарси – Вейсбаха, который можно записать как
Падение давления можно рассчитать как,
Или,
Выражение для коэффициента трения Дарси для ламинарного потока:
В турбулентном потоке соотношение между числом Рейнольдса выражается как Re, коэффициент трения выражается как fD, а относительную шероховатость представить в виде ∈/D сложно.
Выражение для коэффициента трения Дарси для турбулентного потока:
Коэффициент трения Дарси для различных материалов:
Коэффициент трения Дарси для различных материалов приведен ниже.
| Трубный материал | Абсолютная шероховатость | |
| Футов | микроны | |
| Медь или тянутая латунь | 0.000005 | 1.5 |
| Коммерческая сталь | 0.000150 | 45 |
| Бетон | 0.001 — 01 | 300 – 3000 |
| Деревянный посох | 0.0006 – 0.003 | 200 – 900 |
| Кованое железо | 0.000150 | 45 |
| Клепаная сталь | 0.003 – 0.03 | 900 – 9000 |
Коэффициент трения Дарси для трубы:
Диаграмма настроения или коэффициент трения для трубы представляет собой относительную шероховатость змеевика или трубы, которая выражается как ∈ / D. и число Рейнольдса.
Коэффициент трения Дарси для воды:
Капризная диаграмма или коэффициент трения для воды определяется как потеря давления воды на змеевике или трубе из-за трения между трубой и потоком воды внутри нее.
From Wikipedia, the free encyclopedia
In fluid dynamics, the Darcy friction factor formulae are equations that allow the calculation of the Darcy friction factor, a dimensionless quantity used in the Darcy–Weisbach equation, for the description of friction losses in pipe flow as well as open-channel flow.
The Darcy friction factor is also known as the Darcy–Weisbach friction factor, resistance coefficient or simply friction factor; by definition it is four times larger than the Fanning friction factor.[1]
Notation[edit]
In this article, the following conventions and definitions are to be understood:
- The Reynolds number Re is taken to be Re = V D / ν, where V is the mean velocity of fluid flow, D is the pipe diameter, and where ν is the kinematic viscosity μ / ρ, with μ the fluid’s Dynamic viscosity, and ρ the fluid’s density.
- The pipe’s relative roughness ε / D, where ε is the pipe’s effective roughness height and D the pipe (inside) diameter.
- f stands for the Darcy friction factor. Its value depends on the flow’s Reynolds number Re and on the pipe’s relative roughness ε / D.
- The log function is understood to be base-10 (as is customary in engineering fields): if x = log(y), then y = 10x.
- The ln function is understood to be base-e: if x = ln(y), then y = ex.
Flow regime[edit]
Which friction factor formula may be applicable depends upon the type of flow that exists:
- Laminar flow
- Transition between laminar and turbulent flow
- Fully turbulent flow in smooth conduits
- Fully turbulent flow in rough conduits
- Free surface flow.
Transition flow[edit]
Transition (neither fully laminar nor fully turbulent) flow occurs in the range of Reynolds numbers between 2300 and 4000. The value of the Darcy friction factor is subject to large uncertainties in this flow regime.
Turbulent flow in smooth conduits[edit]
The Blasius correlation is the simplest equation for computing the Darcy friction
factor. Because the Blasius correlation has no term for pipe roughness, it
is valid only to smooth pipes. However, the Blasius correlation is sometimes
used in rough pipes because of its simplicity. The Blasius correlation is valid
up to the Reynolds number 100000.
Turbulent flow in rough conduits[edit]
The Darcy friction factor for fully turbulent flow (Reynolds number greater than 4000) in rough conduits can be modeled by the Colebrook–White equation.
Free surface flow[edit]
The last formula in the Colebrook equation section of this article is for free surface flow. The approximations elsewhere in this article are not applicable for this type of flow.
Choosing a formula[edit]
Before choosing a formula it is worth knowing that in the paper on the Moody chart, Moody stated the accuracy is about ±5% for smooth pipes and ±10% for rough pipes. If more than one formula is applicable in the flow regime under consideration, the choice of formula may be influenced by one or more of the following:
- Required accuracy
- Speed of computation required
- Available computational technology:
- calculator (minimize keystrokes)
- spreadsheet (single-cell formula)
- programming/scripting language (subroutine).
Colebrook–White equation[edit]
The phenomenological Colebrook–White equation (or Colebrook equation) expresses the Darcy friction factor f as a function of Reynolds number Re and pipe relative roughness ε / Dh, fitting the data of experimental studies of turbulent flow in smooth and rough pipes.[2][3]
The equation can be used to (iteratively) solve for the Darcy–Weisbach friction factor f.
For a conduit flowing completely full of fluid at Reynolds numbers greater than 4000, it is expressed as:
or
where:
Note: Some sources use a constant of 3.71 in the denominator for the roughness term in the first equation above.[4]
Solving[edit]
The Colebrook equation is usually solved numerically due to its implicit nature. Recently, the Lambert W function has been employed to obtain explicit reformulation of the Colebrook equation.[5][6][7]


or


will get:
then:
Expanded forms[edit]
Additional, mathematically equivalent forms of the Colebrook equation are:
- where:
- 1.7384… = 2 log (2 × 3.7) = 2 log (7.4)
- 18.574 = 2.51 × 3.7 × 2
- where:
and
- or
- where:
- 1.1364… = 1.7384… − 2 log (2) = 2 log (7.4) − 2 log (2) = 2 log (3.7)
- 9.287 = 18.574 / 2 = 2.51 × 3.7.
- where:
The additional equivalent forms above assume that the constants 3.7 and 2.51 in the formula at the top of this section are exact. The constants are probably values which were rounded by Colebrook during his curve fitting; but they are effectively treated as exact when comparing (to several decimal places) results from explicit formulae (such as those found elsewhere in this article) to the friction factor computed via Colebrook’s implicit equation.
Equations similar to the additional forms above (with the constants rounded to fewer decimal places, or perhaps shifted slightly to minimize overall rounding errors) may be found in various references. It may be helpful to note that they are essentially the same equation.
Free surface flow[edit]
Another form of the Colebrook-White equation exists for free surfaces. Such a condition may exist in a pipe that is flowing partially full of fluid. For free surface flow:
The above equation is valid only for turbulent flow. Another approach for estimating f in free surface flows, which is valid under all the flow regimes (laminar, transition and turbulent) is the following:[8]
![{displaystyle f=left({frac {24}{Re_{h}}}right)left[{frac {0.86e^{W(1.35Re_{h})}}{Re_{h}}}right]^{2(1-a)b}left{{frac {1.34}{left[ln {12.21left({frac {R_{h}}{epsilon }}right)}right]^{2}}}right}^{(1-a)(1-b)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7de3c487b30f641f798cde297f6569f86328b370)
where a is:

and b is:

where Reh is Reynolds number where h is the characteristic hydraulic length (hydraulic radius for 1D flows or water depth for 2D flows) and Rh is the hydraulic radius (for 1D flows) or the water depth (for 2D flows). The Lambert W function can be calculated as follows:
![{displaystyle W(1.35Re_{h})=ln {1.35Re_{h}}-ln {ln {1.35Re_{h}}}+left({frac {ln {ln {1.35Re_{h}}}}{ln {1.35Re_{h}}}}right)+left({frac {ln {[ln {1.35Re_{h}}]^{2}-2ln {ln {1.35Re_{h}}}}}{2[ln {1.35Re_{h}}]^{2}}}right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec5b97d997675072f66f9f560ada492a970d9321)
Approximations of the Colebrook equation[edit]
Haaland equation[edit]
The Haaland equation was proposed in 1983 by Professor S.E. Haaland of the Norwegian Institute of Technology.[9] It is used to solve directly for the Darcy–Weisbach friction factor f for a full-flowing circular pipe. It is an approximation of the implicit Colebrook–White equation, but the discrepancy from experimental data is well within the accuracy of the data.
The Haaland equation[10] is expressed:
Swamee–Jain equation[edit]
The Swamee–Jain equation is used to solve directly for the Darcy–Weisbach friction factor f for a full-flowing circular pipe. It is an approximation of the implicit Colebrook–White equation.[11]
Serghides’s solution[edit]
Serghides’s solution is used to solve directly for the Darcy–Weisbach friction factor f for a full-flowing circular pipe. It is an approximation of the implicit Colebrook–White equation. It was derived using Steffensen’s method.[12]
The solution involves calculating three intermediate values and then substituting those values into a final equation.
The equation was found to match the Colebrook–White equation within 0.0023% for a test set with a 70-point matrix consisting of ten relative roughness values (in the range 0.00004 to 0.05) by seven Reynolds numbers (2500 to 108).
Goudar–Sonnad equation[edit]
Goudar equation is the most accurate approximation to solve directly for the Darcy–Weisbach friction factor f for a full-flowing circular pipe. It is an approximation of the implicit Colebrook–White equation. Equation has the following form[13]
Brkić solution[edit]
Brkić shows one approximation of the Colebrook equation based on the Lambert W-function[14]
The equation was found to match the Colebrook–White equation within 3.15%.
Brkić-Praks solution[edit]
Brkić and Praks show one approximation of the Colebrook equation based on the Wright 
,
,
, and
The equation was found to match the Colebrook–White equation within 0.0497%.
Praks-Brkić solution[edit]
Praks and Brkić show one approximation of the Colebrook equation based on the Wright 
,
,
, and
The equation was found to match the Colebrook–White equation within 0.0012%.
Niazkar’s solution[edit]
Since Serghides’s solution was found to be one of the most accurate approximation of the implicit Colebrook–White equation, Niazkar modified the Serghides’s solution to solve directly for the Darcy–Weisbach friction factor f for a full-flowing circular pipe.[17]
Niazkar’s solution is shown in the following:
Niazkar’s solution was found to be the most accurate correlation based on a comparative analysis conducted in the literature among 42 different explicit equations for estimating Colebrook friction factor.[17]
Blasius correlations[edit]
Early approximations for smooth pipes[18] by Paul Richard Heinrich Blasius in terms of the Darcy–Weisbach friction factor are given in one article of 1913:[19]
.
Johann Nikuradse in 1932 proposed that this corresponds to a power law correlation for the fluid velocity profile.[20]
Mishra and Gupta in 1979 proposed a correction for curved or helically coiled tubes, taking into account the equivalent curve radius, Rc:[21]
,
with,
where f is a function of:
- Pipe diameter, D (m, ft)
- Curve radius, R (m, ft)
- Helicoidal pitch, H (m, ft)
- Reynolds number, Re (dimensionless)
valid for:
- Retr < Re < 105
- 6.7 < 2Rc/D < 346.0
- 0 < H/D < 25.4
Table of Approximations[edit]
The following table lists historical approximations to the Colebrook–White relation[22] for pressure-driven flow. Churchill equation[23] (1977) is the only equation that can be evaluated for very slow flow (Reynolds number < 1), but the Cheng (2008),[24] and Bellos et al. (2018)[8] equations also return an approximately correct value for friction factor in the laminar flow region (Reynolds number < 2300). All of the others are for transitional and turbulent flow only.
| Equation | Author | Year | Range | Ref |
|---|---|---|---|---|
|
|
Moody | 1947 | 
|
|
|
|
Wood | 1966 | 
|
|
|
|
Eck | 1973 | ||
|
|
Swamee and Jain | 1976 | 
|
|
|
|
Churchill | 1973 | ||
|
|
Jain | 1976 | ||
|
|
Churchill | 1977 | ||
|
|
Chen | 1979 | 
|
|
|
|
Round | 1980 | ||
|
|
Barr | 1981 | ||
|
|
Zigrang and Sylvester | 1982 | ||
|
|
Haaland[10] | 1983 | ||
|
|
Serghides | 1984 | ||
|
if |
Tsal | 1989 | [25] | |
|
|
Manadilli | 1997 | 
|
|
|
|
Romeo, Royo, Monzon | 2002 | ||
|
|
Goudar, Sonnad | 2006 | ||
|
|
Vatankhah, Kouchakzadeh | 2008 | ||
|
|
Buzzelli | 2008 | ||

where
|
Cheng | 2008 | All flow regimes | [24] |
|
|
Avci, Kargoz | 2009 | ||
|
|
Evangelides, Papaevangelou, Tzimopoulos | 2010 | ||
|
|
Fang | 2011 | ||
|
|
Brkić | 2011 | ||
|
|
S.Alashkar | 2012 | ||
![{displaystyle f=left({frac {64}{mathrm {Re} }}right)^{a}left[0.75ln {frac {mathrm {Re} }{5.37}}right]^{2(a-1)b}left[0.88ln 3.41{frac {D}{epsilon }}right]^{2(a-1)(1-b)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5e8a7d8a434e99b5cce7f5478cb5f61cc462ca6)
where
|
Bellos, Nalbantis, Tsakiris | 2018 | All flow regimes | [8][26] |

where
|
Niazkar | 2019 | [17] | |

|
Tkachenko, Mileikovskyi | 2020 | Deviation 5.36 %,
|
[27] |

where
|
Tkachenko, Mileikovskyi | 2020 | Deviation 0.00072 %,
|
[27] |
References[edit]
- ^ Manning, Francis S.; Thompson, Richard E. (1991). Oilfield Processing of Petroleum. Vol. 1: Natural Gas. PennWell Books. ISBN 978-0-87814-343-6., 420 pages. See page 293.
- ^ Colebrook, C. F.; White, C. M. (1937). «Experiments with Fluid Friction in Roughened Pipes». Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. 161 (906): 367–381. Bibcode:1937RSPSA.161..367C. doi:10.1098/rspa.1937.0150.
Often erroneously cited as the source of the Colebrook-White equation. This is partly because Colebrook (in a footnote in his 1939 paper) acknowledges his debt to White for suggesting the mathematical method by which the smooth and rough pipe correlations could be combined.
- ^ Colebrook, C F (1939). «Turbulent Flow in Pipes, with Particular Reference to the Transition Region Between the Smooth and Rough Pipe Laws». Journal of the Institution of Civil Engineers. 11 (4): 133–156. doi:10.1680/ijoti.1939.13150. ISSN 0368-2455.
- ^ VDI Gesellschaft (2010). VDI Heat Atlas. Springer. ISBN 978-3-540-77876-9.
- ^ More, A. A. (2006). «Analytical solutions for the Colebrook and White equation and for pressure drop in ideal gas flow in pipes». Chemical Engineering Science. 61 (16): 5515–5519. Bibcode:2006ChEnS..61.5515M. doi:10.1016/j.ces.2006.04.003.
- ^ Brkić, D. (2012). «Lambert W Function in Hydraulic Problems» (PDF). Mathematica Balkanica. 26 (3–4): 285–292.
- ^ Keady, G. (1998). «Colebrook-White Formula for Pipe Flows». Journal of Hydraulic Engineering. 124 (1): 96–97. CiteSeerX 10.1.1.1027.8918. doi:10.1061/(ASCE)0733-9429(1998)124:1(96).
- ^ a b c Bellos, Vasilis; Nalbantis, Ioannis; Tsakiris, George (December 2018). «Friction Modeling of Flood Flow Simulations». Journal of Hydraulic Engineering. 144 (12): 04018073. doi:10.1061/(asce)hy.1943-7900.0001540. ISSN 0733-9429.
- ^ Haaland, SE (1983). «Simple and Explicit Formulas for the Friction Factor in Turbulent Flow». Journal of Fluids Engineering. 105 (1): 89–90. doi:10.1115/1.3240948.
- ^ a b Massey, Bernard Stanford (1989). Mechanics of fluids. Chapman & Hall. ISBN 978-0-412-34280-6.
- ^ Swamee, P.K.; Jain, A.K. (1976). «Explicit equations for pipe-flow problems». Journal of the Hydraulics Division. 102 (5): 657–664. doi:10.1061/JYCEAJ.0004542.
- ^ T.K, Serghides (1984). «Estimate friction factor accurately». Chemical Engineering Journal. 91 (5): 63–64. ISSN 0009-2460.
- ^ Goudar, C. T; Sonnad, J. R. (2008). «Comparison of the iterative approximations of the Colebrook-White equation: Here’s a review of other formulas and a mathematically exact formulation that is valid over the entire range of Re values». Hydrocarbon Processing. 87 (8).
- ^
Brkić, Dejan (2011). «An Explicit Approximation of Colebrook’s equation for fluid flow friction factor» (PDF). Petroleum Science and Technology. 29 (15): 1596–1602. doi:10.1080/10916461003620453. S2CID 97080106. - ^
Brkić, Dejan; Praks, Pavel (2019). «Accurate and Efficient Explicit Approximations of the Colebrook Flow Friction Equation Based on the Wright ω-Function». Mathematics. 7 (1): 34. doi:10.3390/math7010034. - ^
Praks, Pavel; Brkić, Dejan (2020). «Review of new flow friction equations: Constructing Colebrook’s explicit correlations accurately». Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería. 36 (3). arXiv:2005.07021. doi:10.23967/j.rimni.2020.09.001. - ^ a b c Majid, Niazkar (2019). «Revisiting the Estimation of Colebrook Friction Factor: A Comparison between Artificial Intelligence Models and C-W based Explicit Equations». KSCE Journal of Civil Engineering. 23 (10): 4311–4326. doi:10.1007/s12205-019-2217-1. S2CID 203040860.
- ^ Massey, B. S. (2006). Mechanics of Fluids (8th ed.). Taylor & Francis. p. 254 eq 7.5. ISBN 978-0-415-36205-4.
- ^ Trinh, Khanh Tuoc (2010), On the Blasius correlation for friction factors, arXiv:1007.2466, Bibcode:2010arXiv1007.2466T
- ^ Nikuradse, Johann (1932). «Gesetzmässigkeiten der Turbulenten Stromung in Glatten Rohren». VDI Forschungsheft. Verein Deutscher Ingenieure. 359 B (3): 1–36.
- ^ Bejan, Adrian; Kraus, Allan D. (2003). Heat Transfer Handbook. John Wiley & Sons. ISBN 978-0-471-39015-2.
- ^ Brkić, Dejan (March 2012). «Determining Friction Factors in Turbulent Pipe Flow». Chemical Engineering. Beograd: 34–39.(subscription required)
- ^ Churchill, S.W. (November 7, 1977). «Friction-factor equation spans all fluid-flow regimes». Chemical Engineering: 91–92.
- ^ a b Cheng, Nian-Sheng (September 2008). «Formulas for Friction Factor in Transitional Regimes». Journal of Hydraulic Engineering. 134 (9): 1357–1362. doi:10.1061/(asce)0733-9429(2008)134:9(1357). hdl:10220/7647. ISSN 0733-9429.
- ^ Zeyu, Zhang; Junrui, Chai; Zhanbin, Li; Zengguang, Xu; Peng, Li (2020-06-01). «Approximations of the Darcy–Weisbach friction factor in a vertical pipe with full flow regime». Water Supply. 20 (4): 1321–1333. doi:10.2166/ws.2020.048. ISSN 1606-9749.
- ^ Bellos, Vasilis; Nalbantis, Ioannis; Tsakiris, George (2020-10-01). «Erratum for «Friction Modeling of Flood Flow Simulations» by Vasilis Bellos, Ioannis Nalbantis, and George Tsakiris». Journal of Hydraulic Engineering. 146 (10): 08220005. doi:10.1061/(ASCE)HY.1943-7900.0001802. ISSN 1943-7900.
- ^ a b Mileikovskyi, Viktor; Tkachenko, Tetiana (2020-08-17). «Precise Explicit Approximations of the Colebrook-White Equation for Engineering Systems». Lecture Notes in Civil Engineering. 100: 303–310. doi:10.1007/978-3-030-57340-9_37. ISBN 978-3-030-57339-3. ISSN 2366-2557. S2CID 224859478.(subscription required)
Further reading[edit]
- Moody, L.F. (1944). «Friction Factors for Pipe Flow». Transactions of the ASME. 66 (8): 671–684.
- Brkić, Dejan (2011). «Review of explicit approximations to the Colebrook relation for flow friction» (PDF). Journal of Petroleum Science and Engineering. 77 (1): 34–48. Bibcode:2011JPSE…77…34B. doi:10.1016/j.petrol.2011.02.006.
- Brkić, Dejan (2011). «W solutions of the CW equation for flow friction» (PDF). Applied Mathematics Letters. 24 (8): 1379–1383. doi:10.1016/j.aml.2011.03.014.
- Brkić, Dejan; Ćojbašić, Žarko (2017). «Evolutionary Optimization of Colebrook’s Turbulent Flow Friction Approximations». Fluids. 2 (2): 15. Bibcode:2017Fluid…2…15B. doi:10.3390/fluids2020015. ISSN 2311-5521.
- Brkić, Dejan; Praks, Pavel (2019). «Accurate and efficient explicit approximations of the Colebrook flow friction equation based on the Wright ω-function». Mathematics 7 (1): article 34. https://doi.org/10.3390/math7010034. ISSN 2227-7390
- Praks, Pavel; Brkić, Dejan (2020). «Review of new flow friction equations: Constructing Colebrook’s explicit correlations accurately». Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería 36 (3): article 41. https://doi.org/10.23967/j.rimni.2020.09.001. ISSN 1886-158X (online version) — ISSN 0213-1315 (printed version)
- Niazkar, Majid (2019). «Revisiting the Estimation of Colebrook Friction Factor: A Comparison between Artificial Intelligence Models and C-W based Explicit Equations». KSCE Journal of Civil Engineering. 23 (10): 4311–4326. doi:10.1007/s12205-019-2217-1. S2CID 203040860.
External links[edit]
- Web-based calculator of Darcy friction factors by Serghides’ solution.
- Open source pipe friction calculator.
Страница 1 из 2
В 1856 году французский гидравлик Анри Дарси экспериментально получил уравнение баланса импульса для медленного стационарного течения несжимаемой жидкости в пористой среде:
Сегодня это уравнение так и называется — «закон Дарси» — и активно применяется в гидравлике малых скоростей при моделировании течений в трубопроводах и пористых средах.
Область применения модели движения Дарси
Модель Дарси определяет линейную зависимость между градиентом давления и скоростью фильтрации. Но такое допущение возможно только для медленных течений с числом Рейнольдса Re < 2000. Однако не только скорость определяет область применения модели.
При моделировании неньютоновских жидкостей (например, нефти) связь между градиентом давления и скоростью фильтрации вероятнее всего будет описана нелинейным или дифференциальным законом. В этом случае применимость модели Дарси ставится под вопрос.
Успешный опыт применения модели Дарси продемонстрирован не только на трубопроводных задачах, но и при моделировании течения в теплообменниках, пропитки пористых композитных материалов, а также в задачах термо- гравитационной конвекции, оценки водопроницаемости грунтов и др.
Математическая основа закона Дарси
Рассмотрим более детально уравнение Дарси:
p [Па], ρ [кг/м3], V [м/с] – давление, плотности и скорость жидкости;
μ [Па⋅c] – динамическая вязкость жидкости;
g [м/с2] – ускорение свободного падения;
k [м2] , φ [ — ] – коэффициент проницаемости и пористость среды.
Можно заметить, что по своей структуре уравнение Дарси очень похоже на другое популярное и более каноническое уравнение движения – уравнение в форме Навье — Стокса:
Преобразуем уравнение в форме Навье-Стокса к уравнению Дарси
В итоге уравнение Н-С для несжимаемой жидкости принимает вид:
Уравнение Дарси — это частный случай уравнения движения в форме Навье-Стокса, полученное для медленных течений вязкой несжимаемой среды
От теории — к практике
Как говорилось ранее, модель Дарси хорошо зарекомендовала себя при моделировании течения в трубопроводах. Вычислим по формуле Дарси перепад давления в трубе (L = 2 м, d = 0.1 м) при течении воды со скоростью V = 0.001м/с.
Для такой постановки задачи (g = 0 м/с2, φ = 1) формула Дарси принимает вид: 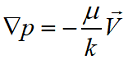
Вычисление коэффициента сопротивления (D)
Выведем формулу для расчёта коэффициента сопротивления D. Эта величина потребуется не только для аналитической оценки, а также и далее при создании расчётного проекта FlowVision.
Выразим коэффициент сопротивления через сопоставление уравнения Дарси с эмпирической формулой Вейсбаха для течения в круглой трубе.
Выражение для коэффициента сопротивления принимает вид:
Здесь 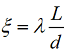
Коэффициент потерь на трение вычислим по формуле Пуазейля: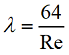
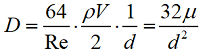
Вычисление перепада давления (Δp)
Воспользуемся выведенным ранее уравнением движения в форме Дарси:Подставим известные числовые значения: D = 3.2 кг/с·м3, L = 2 м, V = 0.001м/с. Отсюда потери давления между входом и выходом трубы Δp = 0.0064 [Па].
Моделирование во FlowVision
В качестве основы воспользуемся проектом обучающего примера Lam_tube. Клиентская часть проекта находится в папке с обучающими примерами в инсталляционной директории /TutorialSamplesRussProjectsLam_tube.
Проведём расчёты проекта Lam_tube с использованием двух моделей движения: Навье-Стокса и Дарси.
Модель Навье-Стокса
Запустим проект на расчёт без изменений. Через 1000 секунд расчётного времени будет достигнуто стационарное значение величины давления на входе – зафиксируем его: Δp = 0.0071 [Па].
Модель Дарси
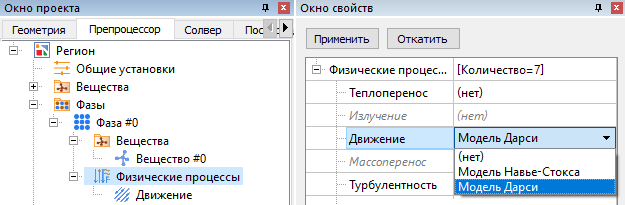
Преобразуем проект для моделирования с помощью модели Дарси.
Шаг 1. В физических процессах фазы выбираем Движение = Модель Дарси.
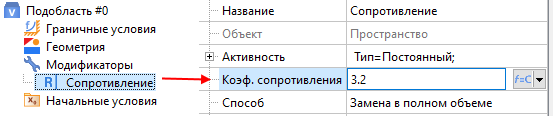
Шаг 2. Во всём расчётном пространстве задаём гидравлическое сопротивление (коэффициент D) с помощью модификатора Сопротивление.
Обязательное условие использования модели Дарси — задание дополнительного гидравлического сопротивления среды с помощью модификатора «Сопротивление» (или «Анизотропное сопротивление» — для случая пористой среды).
Если коэффициент сопротивления не задан, то для расчёта автоматически принимается, что D=1e-6. Безусловно, это обеспечивает некорректный результат перепада давления.
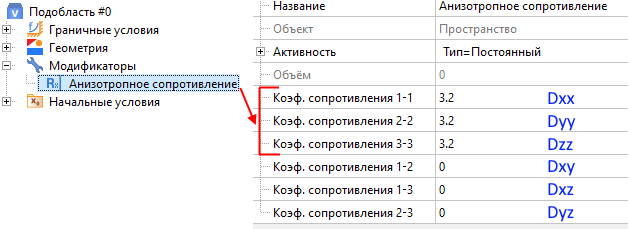
В случае использования модификатора Анизотропное сопротивление, гидравлическое сопротивление определяется симметричной матрицей проекций сопротивления по направлениям на координатные оси:
Шаг 3. Запускаем расчёт и контролируем перепад давления на графике окна мониторинга: Δp = 0.00636 [Па]. Установившееся решение достигается за 20 с расчётного времени.
Модель Дарси FlowVision согласуется с аналитикой с точностью 1%. При сравнении модели Дарси и модели Навье-Стокса разница в величине перепада давления = 10%*.
*Для уточнения расчёта по модели Дарси используйте трубу большей длины (примерно в 3 раза). В обучающем примере малая длина трубы не позволяет достигнуть установившегося ламинарного профиля скорости на выходе. Однако при увеличении длины модель Дарси максимально близко согласуется с моделью Навье-Стокса.
Основное преимущество модели Дарси заключается в быстром достижении установившегося решения: стационарное решение модель Дарси в 50 раз быстрее, чем модель Навье-Стокса.
модель Дарси для разных геометрических моделей труб
Аналитический расчёт по формуле Дарси имеет место быть только для прямолинейного участка трубы. Определение перепада давления для труб сложной формы возможно только с помощью проведения численного моделирования.
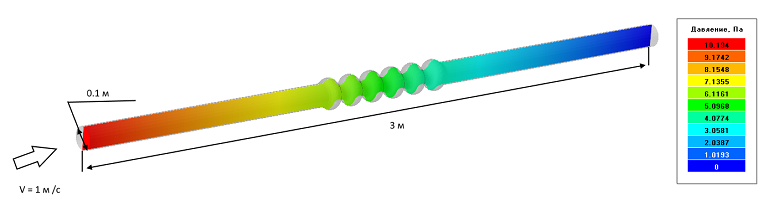
Гофрированная труба с течением воды
Сильфоны обычно применяются для компенсации температурного расширения трубопроводов, а также для предотвращения разрушения труб при их деформации.
Исходные данные задачи: L = 3 м., d = 0.1 м., V = 1 м/с.
Вычисляем коэффициент сопротивления для закона Дарси: D = 32μ / d2 = 3.2 кг/с·м3 , указываем это значение в модификаторе Сопротивление, запускаем расчёт и наблюдаем результаты.
Течение воды в изогнутой трубе
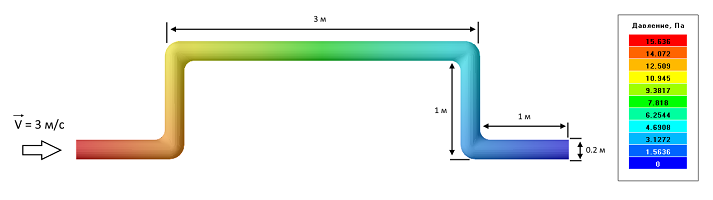
Изгибы труб — это обычное дело при прокладывании трубопровода в черте города. Посмотрим какой перепад давления образуется в изолированном изогнутом участке.
Исходные данные задачи: L = 7 м., d = 0.2 м., V = 3 м/с.
Вычисляем коэффициент сопротивления для закона Дарси: D = 32μ / d2 = 0.8 кг/с·м3
Течение воды в изогнутой в трубе с изгибами в двух плоскостях
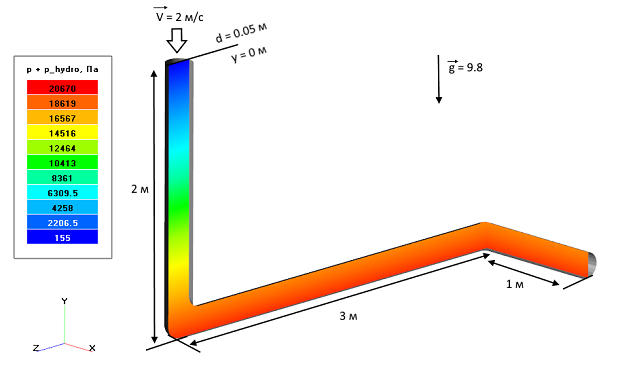
Данный пример демонстрирует более сложную пространственную конфигурацию трубопровода. Здесь уже необходимо учитывать влияние сил гравитации.
Исходные данные задачи: L = 6 м., d = 0.05 м., V = 2 м/с.
Вычисляем коэффициент сопротивления для закона Дарси: D = 32μ / d2 = 12.8 кг/с·м3
Распределение давления (с учётом гидростатики) в изогнутой трубе
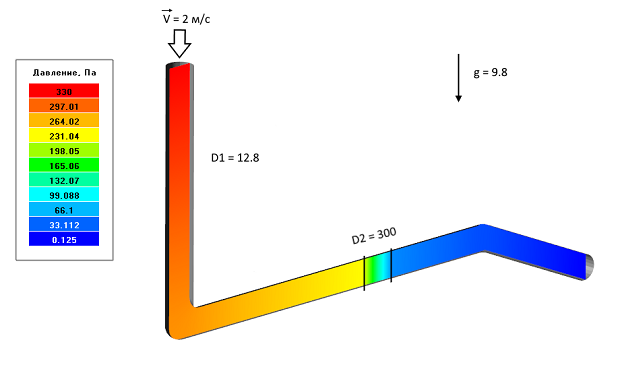
Течение воды в изогнутой в трубе с фильтром
Пористая среда фильтра создаёт дополнительное гидравлическое сопротивление, которое учитывается при задании модификатора Сопротивление или Анизотропное сопротивление.
Исходные данные задачи: L = 6 м., d = 0.05 м., V = 2 м/с.
Вычисляем коэффициент сопротивления для закона Дарси: D1 = 32μ / d2 = 12.8 кг/с·м3
Коэффициент сопротивления фильтра примем D2 = 300 кг/с·м3
Распределение давления в изогнутой трубе с фильтром
Формула Дарси — формула, определяющая потери напора или потери давления на гидравлических сопротивлениях:
где
- Δh — потери напора на гидравлическом сопротивлении;
- ξ — коэффициент потерь (коэффициент Дарси;
- V — средняя скорость течения жидкости;
- g — ускорение свободного падения;
- величина
называется скоростным напором.
Формула Дарси, определяющая потери давления на гидравлических сопротивлениях, имеет вид:
где
- ΔP — потери давления на гидравлическом сопротивлении;
- ρ — плотность жидкости.
Содержание
- 1 Формула Дарси-Вейсбаха
- 2 Определение коэффициента потерь на трение по длине
- 3 Определение коэффициента Дарси для местных сопротивлений
- 4 См. также
- 5 Литература
Формула Дарси-Вейсбаха
Если гидравлическое сопротивление представляет собой участок трубы длиной L и диаметром D, то коэффициент Дарси определяется следующим образом:
где λ — коэффициент потерь на трение по длине.
Тогда формула Дарси приобретает вид:
или для потери давления:
Последние две зависимости получили название формулы Дарси-Вейсбаха.
Если определяются потери на трение по длине для трубы некруглого поперечного сечения, то D представляет собой гидравлический диаметр.
Следует отметить, что потери напора на гидравлических сопротивлениях не всегда пропорциональны скоростному напору.
Определение коэффициента потерь на трение по длине
Коэффициент λ определяется по разному для разных случаев.
Для ламинарного течения в гладких трубах с жёсткими стенками, коэффициент потерь на трение по длине определяется по формуле:
где Re — число Рейнольдса.
Иногда для гибких труб в расчётах приниают
Для турбулентного течения существуют более сложные зависимости. Одна из наиболее часто используемых формул — это формула Блазиуса:
Эта формула даёт хорошие результаты при числах Рейнольдса, изменяющихся в пределах от критического числа Рейнольдса Reкр до значений Re = 105. Формула Блазиуса применяется для гидравлически гладких труб.
Для гидравлически шероховатых труб коэффициент потерь на трение по длине определяется графически по эмпирическим зависимостям. Графики для определения коэффициента потерь на трение по длине для шероховатых труб можно посмотреть здесь (k — размер шероховатости, d — диаметр трубы).
Определение коэффициента Дарси для местных сопротивлений
Рис. 1. Гидравлический конфузор: Q1 — поток жидкости в широком сечении трубы; Q2 — поток жидкости в узком сечении трубы
Для каждого вида местных сопротивлений существуют свои зависимости для определения коэффициента ξ.
К числу наиболее распространённых местных сопротивлений относятся внезапное расширение трубы, внезапное сужение трубы и поворот трубы.
1. При внезапном расширении трубы:
где S1 и S2 — площади поперечного сечения трубы, соответственно перед расширением и после него.
2. При внезапном сужении трубы коэффициент Дарси определяется по формуле:
Рис. 2. Зависимость коэффициента Дарси от угла δ поворота трубы
где S1 и S2 — площади поперечного сечения трубы, соответственно, перед сужением и после него.
3. При постепенном сужении трубы (конфузор):
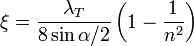
где 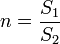
4. При резком (без закругления) повороте трубы (колено) коэффициент Дарси определяется по графическим зависимостям (рис. 2).
См. также
- Гидравлические потери
Литература
- Гидравлика, гидромашины и гидроприводы: Учебник для машиностроительных вузов/ Т.М. Башта, С.С. Руднев, Б.Б. Некрасов и др. — 2-е изд., перераб. – М.: Машиностроение, 1982.
- Гейер В.Г., Дулин В.С., Заря А.Н. Гидравлика и гидропривод: Учеб для вузов. — 3-е изд., перераб. и доп. — М.: Недра, 1991.














![{displaystyle {frac {1}{sqrt {f}}}=-1.8log left[left({frac {varepsilon /D}{3.7}}right)^{1.11}+{frac {6.9}{mathrm {Re} }}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa8b1135412b36f1187e9aa4a0d62fe4ef242a40)
![{displaystyle f={frac {0.25}{left[log left({frac {varepsilon /D}{3.7}}+{frac {5.74}{mathrm {Re} ^{0.9}}}right)right]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c3ac58cccef05823ac222f6b1b60785be55e99c)












![{displaystyle {frac {1}{sqrt {f}}}={aleft[ln left(d/qright)+D_{CFA}right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/345e6d0e3c43c4469e6427b95266ca616839bcaf)


![{textstyle displaystyle {frac {1}{sqrt {f}}}approx 0.8686cdot left[B-C+displaystyle {frac {1.038cdot C}{mathrm {0.332+} ,x}}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/570f28ab9e725323d57f6781f5942d8d57224da7)





![{textstyle displaystyle {frac {1}{sqrt {f}}}approx 0.8685972cdot left[B-C+displaystyle {frac {C}{x-0.5588cdot C+1.2079}},right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/906a42727fa511a6a7cf70b5c36fb06fe853ac23)





![R_{c}=Rleft[1+left({frac {H}{2pi R}}right)^{2}right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/08b33dd271026b50bfeafca0247f634c2a7718cf)
![{displaystyle f=0.0055left[1+left(2times 10^{4}cdot {frac {varepsilon }{D}}+{frac {10^{6}}{mathrm {Re} }}right)^{frac {1}{3}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f11333c539c7f6dd44466220c70a89dc9a53aabc)








![{displaystyle f/8=left[left({frac {8}{mathrm {Re} }}right)^{12}+{frac {1}{(Theta _{1}+Theta _{2})^{1.5}}}right]^{frac {1}{12}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9df10838ab570f62a16fa65a775875af9dcb232)
![{displaystyle Theta _{1}=left[-2.457ln left(left({frac {7}{mathrm {Re} }}right)^{0.9}+0.27{frac {varepsilon }{D}}right)right]^{16}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/def15520f2899b9f241aa05e0d089b9a2f225090)

![{displaystyle {frac {1}{sqrt {f}}}=-2log left[{frac {varepsilon /D}{3.7065}}-{frac {5.0452}{mathrm {Re} }}log left({frac {1}{2.8257}}left({frac {varepsilon }{D}}right)^{1.1098}+{frac {5.8506}{mathrm {Re} ^{0.8981}}}right)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f606b0eb472a1f5cc127d10cf6fcd0e4d20e32ab)
![{displaystyle {frac {1}{sqrt {f}}}=1.8log left[{frac {mathrm {Re} }{0.135mathrm {Re} (varepsilon /D)+6.5}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c7c861ac3fb007965c187f79bb24793fc1e6b15)

![{displaystyle {frac {1}{sqrt {f}}}=-2log left[{frac {varepsilon /D}{3.7}}-{frac {5.02}{mathrm {Re} }}log left({frac {varepsilon /D}{3.7}}-{frac {5.02}{mathrm {Re} }}log left({frac {varepsilon /D}{3.7}}+{frac {13}{mathrm {Re} }}right)right)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/773cf597c19b079337975c21b4f0ca1baceda4c1)
![{displaystyle {frac {1}{sqrt {f}}}=-2log left[{frac {varepsilon /D}{3.7}}-{frac {5.02}{mathrm {Re} }}log left({frac {varepsilon /D}{3.7}}+{frac {13}{mathrm {Re} }}right)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe42c74ed67b54b7da652afb7cdee93b00e3cb3d)












![{displaystyle {frac {1}{sqrt {f}}}=-2log leftlbrace {frac {varepsilon /D}{3.7065}}-{frac {5.0272}{mathrm {Re} }}log left[{frac {varepsilon /D}{3.827}}-{frac {4.657}{mathrm {Re} }}log left(left({frac {varepsilon /D}{7.7918}}right)^{0.9924}+left({frac {5.3326}{208.815+mathrm {Re} }}right)^{0.9345}right)right]rightrbrace }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e05f2a38ad68fb3ed4e3a72dcbc7b01ea240b1f0)
![{displaystyle {frac {1}{sqrt {f}}}=0.8686ln left[{frac {0.4587mathrm {Re} }{(S-0.31)^{frac {S}{(S+1)}}}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d690d249d66e7cdfa6081a57f580789d06b96542)

![{displaystyle {frac {1}{sqrt {f}}}=0.8686ln left[{frac {0.4587mathrm {Re} }{(S-0.31)^{frac {S}{(S+0.9633)}}}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca9e6fef62402105334a778a0b2cf3390cdcba88)







![{displaystyle f=1.613left[ln left(0.234left({frac {varepsilon }{D}}right)^{1.1007}-{frac {60.525}{mathrm {Re} ^{1.1105}}}+{frac {56.291}{mathrm {Re} ^{1.0712}}}right)right]^{-2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51dcf74ea95184f05051d1fb7258bb20b28a4965)
![{displaystyle f=left[-2log left({frac {2.18beta }{mathrm {Re} }}+{frac {varepsilon /D}{3.71}}right)right]^{-2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46fd6bc15ddb12f5098b8e3beced65061bdd32e1)











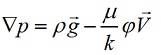
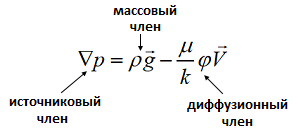
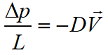
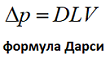
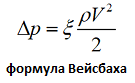
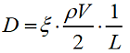
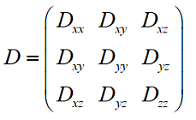
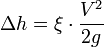
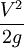 называется скоростным напором.
называется скоростным напором.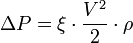
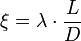
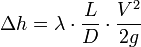
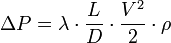
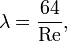
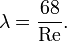
![lambda = frac{0,316}{sqrt[4]{mathrm{Re}}}.](http://dic.academic.ru/pictures/wiki/files/49/17f64e27c31fa4ba18d72540bdf11185.png)