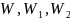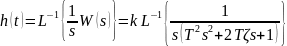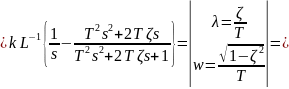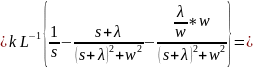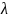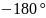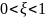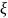Ударный спектр и добротность колебательной системы
Ударный спектр — это график значений максимального отклика на внешнее воздействие системы резонаторов с одной степенью свободы, упорядоченный по собственным частотам резонаторов.
Определение краткое и достаточно точное, но почему-то у людей возникают дополнительные вопросы. Дополнительные вопросы возникают оттого, что людям трудно представить себе образ даже одного резонатора с одной степенью свободы, то что говорить о целой системе.
Если объяснять этот термин на пальцах, то надо подходить к этому вопросу аккуратно и последовательно, чтобы постепенно сложить в голове человека образ описываемого явления. С материальными объектами проще — их достаточно показать, чтобы человеку всё стало ясно. С информационными явлениями гораздо сложнее, но мы эту проблему решим.
Резонатор с одной степень свободы
Представим себе объект, который может совершать колебания в пространстве только в направлении одной оси. Это и будет резонатор с одной степенью свободы. Пружины и маятники — это всё примеры резонаторов с одной степенью свободы. Хотя природа их колебаний различна в теории они описываются аналогичными уравнениями. У них есть одна собственная частота и одна резонансная частота. Для удобства практического использования эти частоты объединяют в одну, но это две разные частоты. Резонансная частота — это частота действия внешней силы, на которой достигается максимальная амплитуда колебаний. Собственная частота — это частота затухающих колебаний, когда внешняя сила исчезла и система теряет энергию, возвращаясь в положение равновесия (останавливается).
Представим себе знакомый нам всем с детства маятник — качели.
Резонансная частота маятника не зависит от массы груза (то есть не разницы кто сидит на качелях хрупкая маленькая девочка или её большой тяжёлый папа), а зависит только от длины подвеса. Чем длиннее этот подвес, тем меньше резонансная частота. Чем выше качели, тем дольше период одного качания.
Ребёнок, впервые попавший на качели, поначалу прилагает много самых разных усилий с произвольной частотой, но качели почти не двигаются. Достаточно быстро он понимает темп, в котором надо делать усилия, чтобы раскачивать качели и понимает, что делать их надо в момент, когда качели замирают на одном из пиков.
Говоря сухим научным языком, когда частота действия внешней силы совпадает с частотой резонанса система начинает в этот самый резонанс входить, увеличивая амплитуду колебаний.
Сил у ребёнка немного и раскачать качели он сильно не может. В определённый момент все силы его начинают уходит не на увеличение амплитуды колебаний, а на поддержание колебаний на том же уровне. В этот момент вся энергия, которую прикладывает ребёнок, будет тратиться за один период колебаний на преодоление трения подвеса и сопротивление воздуха. Если предположить, что в каждый период колебаний качелей ребёнок прикладывает одинаковое усилие совершая работу A, то достигнув максимальных колебаний за n раз, он затратит количество энергии:
W=n×A,
которая перейдёт в энергию качания качелей (часть этой энергии будет рассеяна, но пока это не существенно).
После этого вся его энергия будет полностью рассеиваться за один такт качения:
A=E×d
После понимания этого момента можно переходит к понятию добротности.
Добротность
Добротность — параметр колебательной системы, определяющий ширину резонанса и характеризующий, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний. В общем виде для любой колебательной системы добротность вычисляется по следующей формуле:
f0 — резонансная частота;
W — запасённая энергия системы;
Pd — рассеиваемая мощность;
Ed — рассеиваемая энергия за один период колебаний;
A — работа, совершаемая внешней силой за один период колебаний;
n — количество колебаний, которое сделал система, прежде чем достигла максимальной амплитуды колебаний.
Из этой формулы можно сделать один очень важный вывод, который нам пригодится:
Чем выше добротность колебательной системы, тем больше колебаний сделает система под действием внешний силы, прежде чем достигнет максимальной амплитуды.
То есть, чем выше качели (чем длиннее маятник — тем выше его добротность) тем больше нужно сделать колебаний, чтобы их раскачать. От величины внешней силы зависит только амплитуда колебаний, которые может совершать система. Если ребёнок не сам качается на качелях, а его качает папа (а у папы силы больше и энергии он даёт больше), качели будут подниматься гораздо выше, но максимальной амплитуды качели достигнут примерно за то же число колебаний, если папа будет качать с одинаковым усилием. В качании на качелях самое главное не переусердствовать иначе ребёнка может укачать или качели сломаются.
Собственная частота
Когда дети становятся старше, им надоедает просто качаться на качелях и они раскачавшись прыгают с них, стараясь подлететь повыше и подальше приземлиться (хорошо что детские площадки посыпают песком). После такого прыжка на качелях не остаётся источника внешней толкающей силы, да и отцу становится «не очень интересно » толкать пустые качели. Постепенно амплитуда качения уменьшается и качели останавливаются. Интервал времени между двумя ближайшими моментами отклонения качелей (маятника, резонатора, сигнала и т.д.) называется периодом собственных колебаний, а обратная ему величина — частотой собственных колебаний.
Одни колебательные системы останавливаются быстро, всего за пару тройку колебаний (большинство качелей во дворе останавливаются не более чем за 7 колебаний), а колебания других могут затухать очень долго (колокола — это тоже колебательные системы). Скорость, с которой колебания затухают, очень важный параметр. Он называется декремент затухания.
Декремент затухания
Декремент затухания или логарифмический декремент колебаний — это безразмерная физическая величина, описывающая уменьшение амплитуды колебательного процесса и равная натуральному логарифму отношения двух последовательных (или через некоторое целое количество периодов) амплитуд колеблющейся величины в одну и ту же сторону:
Декремент затухания равен показателю экспоненты в законе затухающих колебаний:
Из декремента затухания можно рассчитать другую величину — коэффициент демпфирования по следующей формуле:
Коэффициент демпфирования (затухания)
Декремент затухания величина расчётная и рассчитывается по графику затухающих колебаний. Для колебательных систем с вязким трением (сила сопротивления пропорциональная скорости движения) физической величиной определяющей характер колебаний является коэффициент демпфирования.
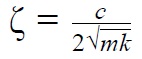
c — коэффициент силы сопротивления движению;
k — коэффициент упругости;
m — масса подвижного груза.
При коэффициенте демпфирования меньшем единицы колебательная система будет плавно затухать. Чем меньше будет коэффициент, тем дольше будут длиться колебания. При коэффициенте равном единице или большем никаких колебаний система испытывать не будет, а просто плавно будет стремиться к нулевому положению. Так, например, дверные доводчики настраивают на коэффициент демпфирования 1 и более, чтобы дверь автоматически закрылась через некоторое время без удара о створку. Демпферы для входных дверей в метро наоборот настроены на коэффициент демпфирования меньше 1. После того как человек толкнёт такую дверь она сделает два три колебания и остановится.
Коэффициент демпфирования связан с добротностью следующей формулой:
Из формулы следует, что чем больше добротность колебательной системы, тем меньше декремент затухания. Чем меньше декремент затухания, тем меньше теряется энергии с каждым колебанием и тем больше колебаний совершит система перед остановкой. Этот простой вывод нам пригодится для дальнейшей работы.
Если рассматривать качели, маятники и прочие системы с низкой собственной частотой (и большим периодом колебаний соответственно), то считать количество колебаний достаточно легко. Но когда мы рассматриваем колокола, балки и прочие системы с высокой собственной частотой, то «на глаз» подсчитать количество колебаний при затухании становится невозможно.
Система резонаторов
Если собрать несколько резонаторов с разными собственными частотами, но одинаковыми значениями декремента затухания, то получится та самая система резонаторов, о которой шла речь в самом начале статьи. Представьте себе площадку в парке отдыха, на которой установлены качели разных размеров, но похожие по конструкции. От размеров качелей будет зависеть собственная частота, а от конструкции и материалов декремент затухания. Таким образом, у них будут разные собственные частоты и одинаковый декремент затухания.
Если представить себе, что все качели одновременно испытывают воздействие внешней возбуждающей силы, от которой они начинают раскачиваться, то максимальная амплитуда колебаний, которую в какой-то момент достигнут качели, будет тем самым максимальным откликом. Подобным внешним воздействием может быть землетрясение. Если упорядочить значения максимальных ответов по возрастанию собственных частот соответствующих резонаторов, то полученный график называется ударным спектром. Если мы имеем дело с землетрясением, то в этом случае ударный спектр называют спектром ответа.
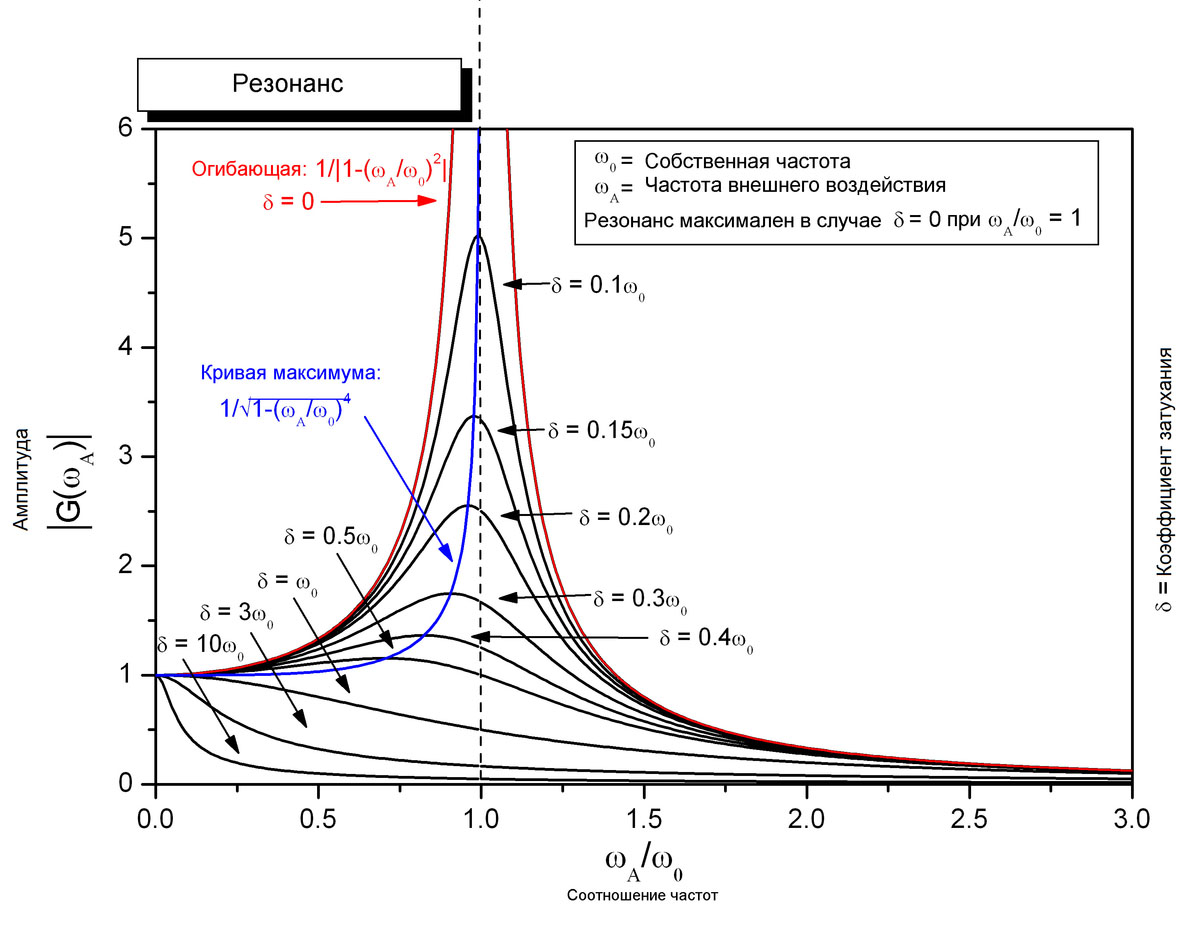
Как мы уже выяснили выше, максимальный отклик некоторых резонаторов может быть достигнут не тогда, когда мгновенное значение силы максимально, а в какой-нибудь другой момент. Этот момент зависит от гармоник, которые присутствуют в сигнале, и от их длительности. Даже если на систему действует гармонический сигнал с одной частотой, то раскачиваться под его воздействием будут все резонаторы. Максимального по амплитуде колебаний отклика достигнет резонатор с собственной частотой наиболее близкой к частоте колебаний, остальные будут колебаться меньше. Наглядно это демонстрирует график резонанса.
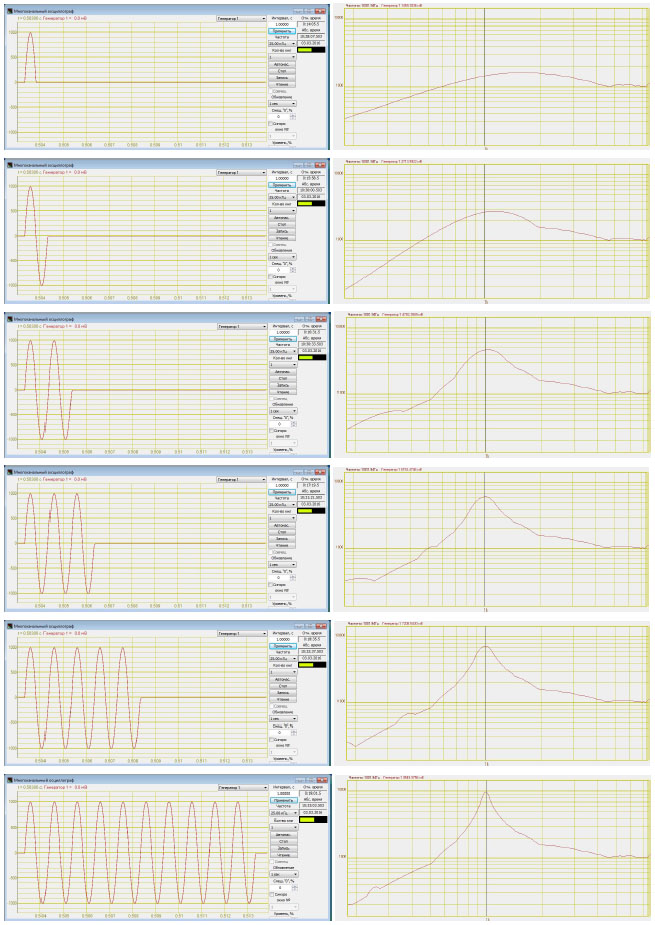
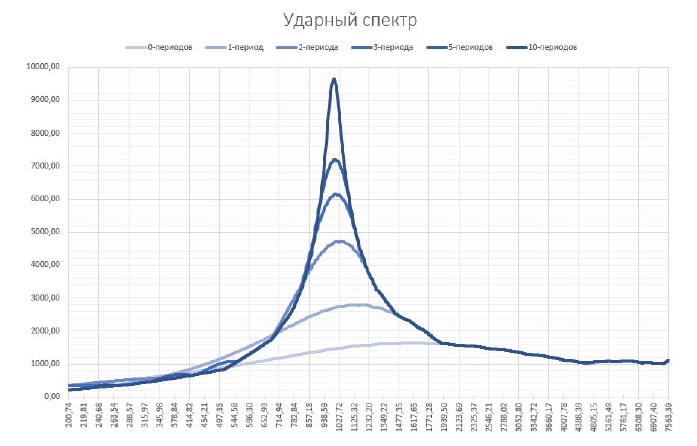
Если мы имеем дело, не с установившимися колебаниями, а с коротким воздействием, то картина будет иной. Будем на систему резонаторов действовать импульсом, состоящем из нескольких периодов синусоидального сигнала с частотой 1000 Гц от полу-периода до 10 периодов. Скажем заранее, что коэффициент демпфирования всех резонаторов равен 0,05, а добротность соответственно равна 10.
Как мы видим на графиках ударного спектра с ростом длительности воздействия увеличивается максимальный отклик системы резонаторов, причём частота, соответствующая максимальному отклику приближается к частоте сигнала генератора. На этом месте возникает уместный вопрос: «Почему от импульсов с малым числом периодов сильнее откликаются (то есть имеют большее значение) резонаторы с частотами большими частоты действующего импульса?». Для ответа на этот вопрос нужно внимательно рассмотреть график резонанса, приведённый выше.
На графике резонанса изображена зависимость ответной реакции резонатора на входное воздействие постоянной амплитуды при изменяющейся частоте входного сигнала. На графике хорошо видно, что у резонаторов с низкой добротностью резонанс наступает на частоте заметно меньшей чем собственная частота резонатора. По мере роста добротности резонатора пик резонанса становится острее и выше, а частота приближается к собственной частоте резонатора.
В ударном спектре всё наоборот. Частота входного сигнала остаётся неизменной, а варьируются собственные частоты резонаторов. Добротность каждого резонатора ограничена сверху, но длительность входного воздействия позволяет раскачать все резонаторы. Поэтому добротность каждого резонатора будет определяться количеством периодов в сигнале (но не более 10).
Если частота резонатора выше частоты входного сигнала, то соотношение wa/w0 < 1 и отклик не опускается ниже амплитуды входного сигнала. То есть маятники с коротким подвесом от низкочастотного воздействия не раскачиваются, а просто ходят за ним. Соответственно, небольшие строения (телефонные будки, ларьки и прочие) при землетрясении не испытывают внутренних напряжений и не ломаются, а двигаются все целиком за волной.
Если частота резонатора ниже, то соотношение wa/w0 > 1 и амплитуда отклика быстро падает с уменьшением частоты резонатора. То есть маятники с длинным подвесом от высокочастотных воздействия даже не трогаются с места. Соответственно, большие строения (точнее сказать, строения из крупных блоков) никак не реагируют на работу отбойного молотка на улице, будь их там даже тысячи работающих одновременно.
Если взять график резонанса соответствующий δ=0.5w0, то он будет примерно соответствовать спектру ударного отклика на полу-период синуса с той лишь разницей, что он будет отражён в другую сторону. Сигналам с большим числом периодов соответствуют графики с большей добротностью. Если совместить несколько графиков ударных спектров в одних осях, то мы увидим график напоминающий график резонанса, приведённый выше, но развёрнутый в обратном направлении.
Вывод
Подводя итог статьи необходимо сделать вывод, что ударный спектр это прекрасный показатель внутреннего состояния объекта. Так для небольших объектов при построение ударного спектра по выходному сигналу можно выяснить состояние «внутренней системы резонаторов». Усталость материи, внутренние трещины и прочие неприятности вносят изменения в эту «внутреннюю систему резонаторов». Обычно это выражается в том, что происходит изменение собственных и резонансных частот, реже происходит падение добротности колебательных контуров.
Так, например, церковные колокола со временем «понижают» свои голоса, то есть у них происходит уменьшение собственной частоты (унтертона) и высота их звука падает. Таким образом проявляется эффект «старения» бронзы [1]. Если же колокол треснет (например, в сильный мороз), то он резко потеряет чистоту звука, то есть упадёт его добротность.
Можно представить себе испытуемый объект как систему резонаторов в виде набора струн (можно представить себе рояль), определить и запомнить какие «струны» в нём звучат и как сильно. А после эксплуатации по изменению этого набора откликов можно судить об внутренних изменениях. Так, например, ГОСТы на механические испытания рекомендую измерять и сравнивать АЧХ до и после испытаний. Ещё пример, при изменении основного тона собственных колебаний здания более чем в два раза в меньшую либо в большую сторону (одна из методик контроля), МЧС делает заключение, что здание находится в аварийном состоянии.
При землетрясениях наоборот измеряют ударный спектр самого землетрясения. Таким образом учёные оценивают степень разрушения зданий и сооружений [2]. Для каждого типа сооружений вычисляется диапазон наиболее разрушительных частот. Чем выше рассчитанный спектр в определённой полосе, тем больше повреждений получит здание.
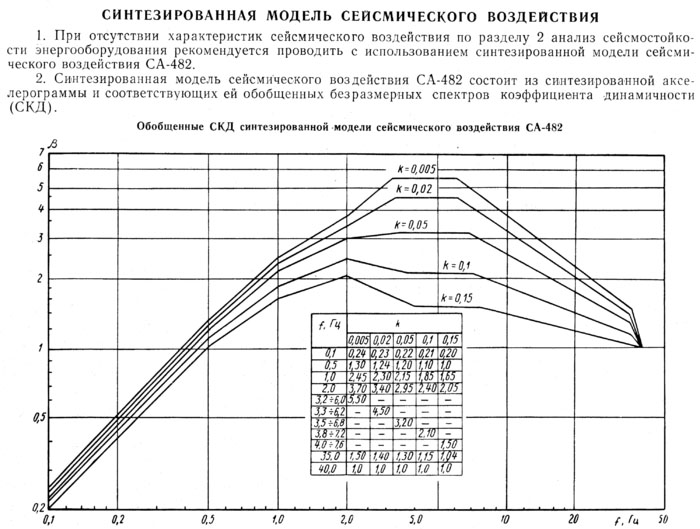
При проектировании зданий в сейсмоопасных районах в конструкцию здания закладывают системы демпфирования колебаний. Системы демпфирования рассчитывают на гашение наиболее опасных частот. Такие частоты определяются исходя из анализа сейсмограмм в данной области за всё время наблюдений. И в конце проектных работы модель здания подвергают испытаниям на модельные землетрясения [3].
Ссылки
- https://www.muszone.ru/articles/23.html
- https://ru.wikipedia.org/wiki/%D0%9C%D0%BE%D0%B4%D0%B5%D0%BB%D1%8C_%D1%81%D0%B5%D0%B9%D1%81%D0%BC%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B3%D0%BE_%D0%B2%D0%BE%D0%B7%D0%B4%D0%B5%D0%B9%D1%81%D1%82%D0%B2%D0%B8%D1%8F_%C2%AB%D0%A1%D0%90-482%C2%BB
- https://ru.wikipedia.org/wiki/Сейсмостойкое_строительство
- https://www.iris.edu/hq/inclass/video/building_resonance__boss_model_construction__use
P.S.
В конце можно позволить отступить от области механики и сейсмики в область социальную. В обществе имеют место аналогичные явления, называемые «общественным резонансом». Если какое-то событие овладевает умами многих людей (говорят «нашло отклик в сердцах людей»), и о нём долго вспоминают и обсуждают (говорят «событие долго будоражит умы»), то налицо общественный резонанс. Такие события могут побудить людей к действиям, например, написать письмо на телевидение, в редакцию газеты или в руководящие органы. Руководство телеканала или администрация отсортируют письма, получат весь спектр ответов, проанализируют ситуацию и примут какие-то действия.
Подобная аналогия из жизни общества может быть не абсолютно точно повторяет свойства резонанса и ударного спектра в механике, но позволяет приблизить к пониманию механического резонанса большое число людей, не имеющих технического образования.
From Wikipedia, the free encyclopedia
This article is about damping in oscillatory systems. For other uses, see Damping (disambiguation).
Damping is an influence within or upon an oscillatory system that has the effect of reducing or preventing its oscillation. In physical systems, damping is produced by processes that dissipate the energy stored in the oscillation.[1] Examples include viscous drag (a liquid’s viscosity can hinder an oscillatory system, causing it to slow down; see viscous damping) in mechanical systems, resistance in electronic oscillators, and absorption and scattering of light in optical oscillators. Damping not based on energy loss can be important in other oscillating systems such as those that occur in biological systems and bikes[2] (ex. Suspension (mechanics)). Not to be confused with friction, which is a dissipative force acting on a system. Friction can cause or be a factor of damping.
The damping ratio is a dimensionless measure describing how oscillations in a system decay after a disturbance. Many systems exhibit oscillatory behavior when they are disturbed from their position of static equilibrium. A mass suspended from a spring, for example, might, if pulled and released, bounce up and down. On each bounce, the system tends to return to its equilibrium position, but overshoots it. Sometimes losses (e.g. frictional) damp the system and can cause the oscillations to gradually decay in amplitude towards zero or attenuate. The damping ratio is a measure describing how rapidly the oscillations decay from one bounce to the next.
The damping ratio is a system parameter, denoted by ζ (zeta), that can vary from undamped (ζ = 0), underdamped (ζ < 1) through critically damped (ζ = 1) to overdamped (ζ > 1).
The behaviour of oscillating systems is often of interest in a diverse range of disciplines that include control engineering, chemical engineering, mechanical engineering, structural engineering, and electrical engineering. The physical quantity that is oscillating varies greatly, and could be the swaying of a tall building in the wind, or the speed of an electric motor, but a normalised, or non-dimensionalised approach can be convenient in describing common aspects of behavior.
Oscillation cases[edit]
Depending on the amount of damping present, a system exhibits different oscillatory behaviors and speeds.
- Where the spring–mass system is completely lossless, the mass would oscillate indefinitely, with each bounce of equal height to the last. This hypothetical case is called undamped.
- If the system contained high losses, for example if the spring–mass experiment were conducted in a viscous fluid, the mass could slowly return to its rest position without ever overshooting. This case is called overdamped.
- Commonly, the mass tends to overshoot its starting position, and then return, overshooting again. With each overshoot, some energy in the system is dissipated, and the oscillations die towards zero. This case is called underdamped.
- Between the overdamped and underdamped cases, there exists a certain level of damping at which the system will just fail to overshoot and will not make a single oscillation. This case is called critical damping. The key difference between critical damping and overdamping is that, in critical damping, the system returns to equilibrium in the minimum amount of time.[citation needed]
Damped sine wave[edit]
Plot of a damped sinusoidal wave represented as the function
A damped sine wave or damped sinusoid is a sinusoidal function whose amplitude approaches zero as time increases. It corresponds to the underdamped case of damped second-order systems, or underdamped second-order differential equations.[3]
Damped sine waves are commonly seen in science and engineering, wherever a harmonic oscillator is losing energy faster than it is being supplied.
A true sine wave starting at time = 0 begins at the origin (amplitude = 0). A cosine wave begins at its maximum value due to its phase difference from the sine wave. A given sinusoidal waveform may be of intermediate phase, having both sine and cosine components. The term «damped sine wave» describes all such damped waveforms, whatever their initial phase.
The most common form of damping, which is usually assumed, is the form found in linear systems. This form is exponential damping, in which the outer envelope of the successive peaks is an exponential decay curve. That is, when you connect the maximum point of each successive curve, the result resembles an exponential decay function. The general equation for an exponentially damped sinusoid may be represented as:
where:
Other important parameters include:
Damping ratio definition[edit]
The effect of varying damping ratio on a second-order system.
The damping ratio is a parameter, usually denoted by ζ (Greek letter zeta),[4] that characterizes the frequency response of a second-order ordinary differential equation. It is particularly important in the study of control theory. It is also important in the harmonic oscillator. In general, systems with higher damping ratios (one or greater) will demonstrate more of a damping effect. Underdamped systems have a value of less than one. Critically damped systems have a damping ratio of exactly 1, or at least very close to it.
The damping ratio provides a mathematical means of expressing the level of damping in a system relative to critical damping. For a damped harmonic oscillator with mass m, damping coefficient c, and spring constant k, it can be defined as the ratio of the damping coefficient in the system’s differential equation to the critical damping coefficient:
where the system’s equation of motion is
and the corresponding critical damping coefficient is
or
where
is the natural frequency of the system.
The damping ratio is dimensionless, being the ratio of two coefficients of identical units.
Derivation[edit]
Using the natural frequency of a harmonic oscillator 
This equation is more general than just the mass–spring system, and also applies to electrical circuits and to other domains. It can be solved with the approach
where C and s are both complex constants, with s satisfying
Two such solutions, for the two values of s satisfying the equation, can be combined to make the general real solutions, with oscillatory and decaying properties in several regimes:
Phase portrait of damped oscillator, with increasing damping strength. It starts at undamped, proceeds to underdamped, then critically damped, then overdamped.
- Undamped
- Is the case where
corresponds to the undamped simple harmonic oscillator, and in that case the solution looks like
, as expected. This case is extremely rare in the natural world with the closest examples being cases where friction was purposefully reduced to minimal values.
- Underdamped
- If s is a pair of complex values, then each complex solution term is a decaying exponential combined with an oscillatory portion that looks like
. This case occurs for
, and is referred to as underdamped (e.g., bungee cable).
- Overdamped
- If s is a pair of real values, then the solution is simply a sum of two decaying exponentials with no oscillation. This case occurs for
, and is referred to as overdamped. Situations where overdamping is practical tend to have tragic outcomes if overshooting occurs, usually electrical rather than mechanical. For example, landing a plane in autopilot: if the system overshoots and releases landing gear too late, the outcome would be a disaster.
- Critically damped
- The case where
is the border between the overdamped and underdamped cases, and is referred to as critically damped. This turns out to be a desirable outcome in many cases where engineering design of a damped oscillator is required (e.g., a door closing mechanism).
Q factor and decay rate[edit]
The Q factor, damping ratio ζ, and exponential decay rate α are related such that[5]
When a second-order system has 


Logarithmic decrement[edit]
For underdamped vibrations, the damping ratio is also related to the logarithmic decrement 
where
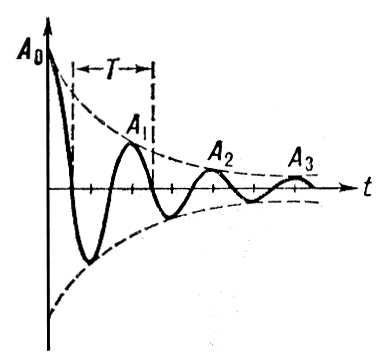
where x0 and x1 are amplitudes of any two successive peaks.
As shown in the right figure:
where 



Percentage overshoot[edit]
In control theory, overshoot refers to an output exceeding its final, steady-state value.[9] For a step input, the percentage overshoot (PO) is the maximum value minus the step value divided by the step value. In the case of the unit step, the overshoot is just the maximum value of the step response minus one.
The percentage overshoot (PO) is related to damping ratio (ζ) by:
Conversely, the damping ratio (ζ) that yields a given percentage overshoot is given by:
Examples and applications[edit]
Viscous drag[edit]
When an object is falling through the air, the only force opposing its freefall is air resistance. An object falling through water or oil would slow down at a greater rate, until eventually reaching a steady-state velocity as the drag force comes into equilibrium with the force from gravity. This is the concept of viscous drag, which for example is applied in automatic doors or anti-slam doors.[10]
Damping in electrical systems / resistance[edit]
Electrical systems that operate with alternating current (AC) use resistors to damp the electrical current, since they are periodic. Dimmer switches or volume knobs are examples of damping in an electrical system. [10]
Magnetic damping[edit]
Kinetic energy that causes oscillations is dissipated as heat by electric eddy currents which are induced by passing through a magnet’s poles, either by a coil or aluminum plate. In other words, the resistance caused by magnetic forces slows a system down. An example of this concept being applied is the brakes on roller coasters. [11]
References[edit]
- ^ Steidel (1971). An Introduction to Mechanical Vibrations. John Wiley & Sons. p. 37.
damped, which is the term used in the study of vibration to denote a dissipation of energy
- ^ J. P. Meijaard; J. M. Papadopoulos; A. Ruina & A. L. Schwab (2007). «Linearized dynamics equations for the balance and steer of a bicycle: a benchmark and review». Proceedings of the Royal Society A. 463 (2084): 1955–1982. Bibcode:2007RSPSA.463.1955M. doi:10.1098/rspa.2007.1857. S2CID 18309860.
lean and steer perturbations die away in a seemingly damped fashion. However, the system has no true damping and conserves energy. The energy in the lean and steer oscillations is transferred to the forward speed rather than being dissipated.
- ^ Douglas C. Giancoli (2000). [Physics for Scientists and Engineers with Modern Physics (3rd Edition)]. Prentice Hall. p. 387 ISBN 0-13-021517-1
- ^ Alciatore, David G. (2007). Introduction to Mechatronics and Measurement (3rd ed.). McGraw Hill. ISBN 978-0-07-296305-2.
- ^ William McC. Siebert. Circuits, Signals, and Systems. MIT Press.
- ^
Ming Rao and Haiming Qiu (1993). Process control engineering: a textbook for chemical, mechanical and electrical engineers. CRC Press. p. 96. ISBN 978-2-88124-628-9. - ^ «Dynamics and Vibrations: Notes: Free Damped Vibrations».
- ^ «Damping Evaluation». 19 October 2015.
- ^ Kuo, Benjamin C & Golnaraghi M F (2003). Automatic control systems (Eighth ed.). NY: Wiley. p. §7.3 p. 236–237. ISBN 0-471-13476-7.
- ^ a b «damping | Definition, Types, & Examples». Encyclopedia Britannica. Retrieved 2021-06-09.
- ^ «Eddy Currents and Magnetic Damping | Physics». courses.lumenlearning.com. Retrieved 2021-06-09.
11. Britannica, Encyclopædia. “Damping.” Encyclopædia Britannica, Encyclopædia Britannica, Inc., www.britannica.com/science/damping.
12. OpenStax, College. “Physics.” Lumen, courses.lumenlearning.com/physics/chapter/23-4-eddy-currents-and-magnetic-damping/.

Демпфирование — это влияние внутри или на колебательная система, которая уменьшает, ограничивает или предотвращает ее колебания. В физических системах затухание создается процессами, которые рассеивают энергию, запасенную в колебаниях. Примеры включают вязкое сопротивление в механических системах, сопротивление в электронных генераторах, а также поглощение и рассеяние света в оптических генераторах. Демпфирование, не основанное на потерях энергии, может быть важным в других колебательных системах, таких как те, которые встречаются в биологических системах и велосипедах.
Коэффициент демпфирования является безразмерным мера, описывающая, как колебания в системе затухают после возмущения. Многие системы демонстрируют колебательное поведение, когда они выходят из положения статического равновесия. Например, масса, подвешенная на пружине, может, если ее потянуть и отпустить, подпрыгнет вверх и вниз. При каждом отскоке система стремится вернуться в свое положение равновесия, но проскакивает его. Иногда потери (например, фрикционные ) демпфируют систему и могут вызывать постепенное затухание амплитуды колебаний до нуля или ослабление. Коэффициент затухания — это мера, описывающая, насколько быстро колебания затухают от одного отскока к другому.
Коэффициент демпфирования — это системный параметр, обозначаемый ζ (дзета), который может варьироваться от без демпфирования (ζ = 0), с недостаточным демпфированием (ζ < 1) through от критического демпфирования (ζ = 1) до сверхдемпфирования (ζ>1).
Поведение колебательных систем часто представляет интерес в самых разных дисциплинах, включая техника управления, химическая инженерия, машиностроение, структурная инженерия и электротехника. Осциллирующая физическая величина варьируется в значительной степени, и это может быть раскачивание высокого здания на ветру или скорость электродвигателя, но нормализованный или безразмерный подход может быть удобным для описания общих аспектов поведения.
Содержание
- 1 Случаи колебаний
- 2 Определение
- 3 Выведение
- 4 Коэффициент добротности и скорость затухания
- 5 Логарифмический декремент
- 6 Процентное превышение
- 7 Ссылки
Случаи колебаний
В зависимости от величины демпфирования, система стержень демонстрирует различное колебательное поведение.
- Там, где система пружина-масса полностью без потерь, масса будет колебаться бесконечно, причем каждый отскок будет иметь одинаковую высоту с последним. Этот гипотетический случай называется незатухающим.
- Если система содержит большие потери, например, если эксперимент с пружиной и массой проводился в вязкой жидкости, масса могла бы медленно вернуться в свое положение покоя. без превышения. Этот случай называется чрезмерным демпфированием.
- Обычно масса имеет тенденцию выходить за пределы своего начального положения, а затем возвращается, снова превышая ее. При каждом перерегулировании часть энергии в системе рассеивается, и колебания затухают до нуля. Этот случай называется недостаточным демпфированием.
- Между случаями избыточного демпфирования и недостаточного демпфирования существует определенный уровень демпфирования, при котором система просто не сможет выйти за пределы допустимого диапазона и не совершит ни одного колебания. Этот случай называется критическим демпфированием. Ключевое различие между критическим демпфированием и избыточным демпфированием заключается в том, что при критическом демпфировании система возвращается в состояние равновесия за минимальное время.
Определение

Коэффициент демпфирования — это параметр, обычно обозначаемый ζ (дзета), который характеризует частотную характеристику обыкновенного дифференциального уравнения второго порядка. Это особенно важно при изучении теории управления. Это также важно в гармоническом осцилляторе .
. Коэффициент демпфирования представляет собой математическое средство выражения уровня демпфирования в системе относительно критического демпфирования. Для демпфированного гармонического осциллятора с массой m, коэффициентом демпфирования c и жесткостью пружины k его можно определить как отношение коэффициента демпфирования в дифференциальном уравнении системы к критическому коэффициенту демпфирования:
- ζ = ccc, { displaystyle zeta = { frac {c} {c_ {c}}},}
- ζ = фактическое демпфирование, критическое демпфирование, { displaystyle zeta = { frac { text {фактическое демпфирование}} { text {critical демпфирование}}},}
где уравнение движения системы равно
- md 2 xdt 2 + cdxdt + kx = 0 { displaystyle m { frac {d ^ {2} x} {dt ^ {2} }} + c { frac {dx} {dt}} + kx = 0}
и соответствующий критический коэффициент демпфирования равен
- cc = 2 км { displaystyle c_ {c} = 2 { sqrt {km }}}
или
- cc = 2 мкм = 2 м ω n { displaystyle c_ {c} = 2m { sqrt { frac {k} {m}}} = 2m omega _ {n} }
где
- ω n = km { displaystyle omega _ {n} = { sqrt { frac {k} {m}}}}
— собственная частота системы.
Коэффициент демпфирования безразмерен и представляет собой отношение двух коэффициентов одинаковых единиц.
Выведение
Использование собственной частоты гармонического осциллятора ω n = km { displaystyle omega _ {n} = { sqrt { frac {k} {m}}}}
- d 2 xdt 2 + 2 ζ ω ndxdt + ω n 2 x = 0. { displaystyle { frac {d ^ {2} x} {dt ^ {2}}} + 2 zeta omega _ {n} { frac {dx} {dt}} + omega _ {n} ^ {2} x = 0.}
Это уравнение можно решить с помощью подхода.
- x (t) = C est, { displaystyle x (t) = Ce ^ {st}, ,}
где C и s оба являются комплексными константами, где s удовлетворяет
- s = — ω n (ζ ± i 1 — ζ 2). { displaystyle s = — omega _ {n} left ( zeta pm i { sqrt {1- zeta ^ {2}}} right).}
Два таких решения для двух значений из s, удовлетворяющих уравнению, можно объединить, чтобы получить общие реальные решения с колебательными и затухающими свойствами в нескольких режимах:
- Незатухающий
- Это случай, когда ζ = 0 { displaystyle zeta = 0}
соответствует незатухающему простому гармоническому осциллятору, и в этом случае решение выглядит как exp (i ω nt) { displaystyle exp (i omega _ {n} t) }
, как и ожидалось.
- Недостаточное демпфирование
- Если s — пара комплексных значений, то каждый член комплексного решения представляет собой убывающую экспоненту в сочетании с колеблющейся частью, которая выглядит как ехр (я ω N 1 — ζ 2 T) { Displaystyle ехр влево (я omega _ {n} { sqrt {1- zeta ^ {2}}} т справа)}
. Этот случай имеет место для 0 ≤ ζ < 1 {displaystyle 0leq zeta <1}
и называется недостаточным демпфированием.
- Сверхдемпфирование
- Если s — пара действительных значений, то решение просто сумма двух убывающих экспонент без колебаний. Этот случай имеет место для ζ>1 { displaystyle zeta>1}
, и называется чрезмерным демпфированием.
- Критически демпфировано
- Случай, когда displaystyle = zeta = 1}
— это граница между случаями сверхдемпфирования и недостаточного демпфирования, и называется критическим демпфированием. Это оказывается желательным результатом во многих случаях, когда требуется инженерное проектирование демпфированного осциллятора ( например, механизм закрытия двери).
Q-фактор и скорость затухания
Q-фактор, коэффициент демпфирования ζ и экспоненциальная скорость затухания α связаны таким образом, что
- ζ = 1 2 Q = α ω n. { Displaystyle zeta = { frac {1} {2Q}} = { alpha over omega _ {n}}.}
Когда система второго порядка имеет ζ < 1 {displaystyle zeta <1}


Логарифмический декремент
Для недостаточно демпфированных колебаний коэффициент демпфирования также связан с логарифмическим декрементом δ { displaystyle delta}
- ζ = 1 1 + (2 π δ) 2, где δ ≜ ln x 1 x 2 { displaystyle zeta = { frac {1} { sqrt {1+ left ({ frac {2 pi} { delta}} right) ^ {2}}}} qquad { text {where}} qquad delta triangleq ln { frac {x_ {1}} {x_ {2 }}}}
где x 1 { displaystyle x_ {1}}

Процентное превышение
В теории управления, превышение относится к выходному сигналу, превышающему его конечное установившееся значение. Для ступенчатого входа , процентное превышение (PO) — это максимальное значение минус значение шага, деленное на значение шага. В случае единичного шага перерегулирование — это просто максимальное значение реакции на скачок минус один.
Процентное превышение (PO) связано с коэффициентом демпфирования (ζ) следующим образом:
- PO = 100 e — (ζ π 1 — ζ 2) { displaystyle PO = 100e ^ {- left ( { frac { zeta pi} { sqrt {1- zeta ^ {2}}}} right)}}
И наоборот, коэффициент демпфирования (ζ), который дает определенный процент превышения (PO), равен задается по формуле:
- ζ = — ln (PO 100) π 2 + ln 2 (PO 100) { displaystyle zeta = { frac {- ln left ({ frac {PO} {100} } right)} { sqrt { pi ^ {2} + ln ^ {2} left ({ frac {PO} {100}} right)}}}}
Ссылки
Эта статья о затухании в колебательных системах. Для использования в других целях, см Демпфирование (значения).

Демпфирование — это влияние внутри колебательной системы или на нее, которое снижает или предотвращает ее колебания. В физических системах затухание вызывается процессами, которые рассеивают энергию, запасенную в колебаниях. Примеры включают вязкое сопротивление (вязкость жидкости может препятствовать колебательной системе, вызывая ее замедление) в механических системах, сопротивление в электронных генераторах, а также поглощение и рассеяние света в оптических генераторах. Демпфирование, не основанное на потерях энергии, может быть важным в других колебательных системах, например, в биологических системах и велосипедах (например, подвеска (механика) ). Не следует путать с трением, которое представляет собой диссипативную силу, действующую на систему. Трение может быть причиной или быть фактором демпфирования.
Коэффициент демпфирования — это безразмерная мера, описывающая, как колебания в системе затухают после возмущения. Многие системы демонстрируют колебательное поведение, когда они выходят из положения статического равновесия. Например, масса, подвешенная на пружине, может, если ее потянуть и отпустить, подпрыгнуть вверх и вниз. При каждом отскоке система стремится вернуться в свое положение равновесия, но проскакивает его. Иногда потери (например, фрикционные ) демпфируют систему и могут вызывать постепенное затухание амплитуды колебаний до нуля или ослабление. Коэффициент затухания — это мера, описывающая, насколько быстро колебания затухают от одного отскока к другому.
Коэффициент демпфирования — это системный параметр, обозначаемый ζ (дзета), который может варьироваться от незатухающего ( ζ = 0), слабозатухающего ( ζ lt;1) до критически затухающего ( ζ = 1) до чрезмерного демпфирования ( ζ gt; 1).
Поведение колебательных систем часто представляет интерес в самых разных дисциплинах, включая технику управления, химическую инженерию, машиностроение, структурную инженерию и электротехнику. Физическая величина, которая колеблется, сильно варьируется и может быть колебанием высокого здания на ветру или скоростью электродвигателя, но нормализованный или безразмерный подход может быть удобным для описания общих аспектов поведения.
СОДЕРЖАНИЕ
- 1 Колебательные корпуса
- 2 Затухающая синусоида
- 3 Определение коэффициента демпфирования
- 4 Вывод
- 5 Q- фактор и скорость затухания
- 6 Логарифмический декремент
- 7 Процент превышения
- 8 примеров и приложений
- 8.1 Вязкое сопротивление
- 8.2 Демпфирование в электрических системах
- 8.3 Магнитное демпфирование
- 9 ссылки
Колебательные случаи
В зависимости от степени демпфирования система демонстрирует различные колебательные режимы и скорости.
- Там, где система пружина-масса полностью без потерь, масса будет колебаться бесконечно, причем каждый отскок будет иметь одинаковую высоту с последним. Этот гипотетический случай называется незатухающим.
- Если бы система имела большие потери, например, если бы эксперимент с пружиной и массой проводился в вязкой жидкости, масса могла бы медленно возвращаться в исходное положение, никогда не превышая ее. Этот случай называется сверхдемпфированием.
- Обычно масса имеет тенденцию выходить за пределы своего начального положения, а затем возвращаться, снова выскакивая за пределы. При каждом выбросе некоторая энергия в системе рассеивается, и колебания затухают до нуля. Этот случай называется недемпфированным.
- Между случаями с избыточным и недостаточным демпфированием существует определенный уровень демпфирования, при котором система просто не сможет перескочить и не совершит ни одного колебания. Этот случай называется критическим демпфированием. Ключевое различие между критическим демпфированием и избыточным демпфированием состоит в том, что при критическом демпфировании система возвращается в состояние равновесия за минимальное время.
Затухающая синусоида
Не путать с затухающей волной (радиопередача).
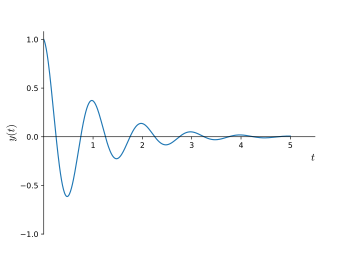
у ( т ) знак равно е — т ⋅ потому что ( 2 π т ) { Displaystyle у (т) = е ^ {- т} cdot соз (2 пи т)}
Затухать синусоидой или затухающая синусоида является синусоидальной функцией, амплитуда которого приближается к нулю при возрастании времени, соответствующем underdamped случае затухающих систем второго порядка, или underdamped дифференциальных уравнений второго порядка. Затухающие синусоидальные волны обычно встречаются в науке и технике, где гармонический осциллятор теряет энергию быстрее, чем подается. Истинная синусоида, начинающаяся в момент времени = 0, начинается в начале координат (амплитуда = 0). Косинусоидальная волна начинается с максимального значения из-за разницы фаз от синусоидальной волны. Данная синусоидальная форма волны может иметь промежуточную фазу, имеющую как синусоидальную, так и косинусоидальную составляющие. Термин «затухающая синусоида» описывает все такие затухающие формы волны, независимо от их начальной фазы.
Наиболее распространенная форма демпфирования, которая обычно принимается, — это форма, встречающаяся в линейных системах. Эта форма представляет собой экспоненциальное затухание, при котором внешняя огибающая последовательных пиков представляет собой кривую экспоненциального затухания. То есть, когда вы соединяете максимальную точку каждой последующей кривой, результат напоминает функцию экспоненциального затухания. Общее уравнение для экспоненциально затухающей синусоиды может быть представлено как:
- у ( т ) знак равно А ⋅ е — λ т ⋅ потому что ( ω т — ϕ ) { Displaystyle у (T) = A CDOT е ^ {- лямбда т} CDOT соз ( омега т- фи)}
куда:
- у ( т ) { Displaystyle у (т)}
— мгновенная амплитуда в момент времени t ;
- А { displaystyle A}
— начальная амплитуда огибающей;
- λ { displaystyle lambda}
— скорость убывания, обратная единицам времени независимой переменной t ;
- ϕ { displaystyle phi}
— фазовый угол при t = 0;
- ω { displaystyle omega}
— угловая частота.
К другим важным параметрам относятся:
Определение коэффициента демпфирования
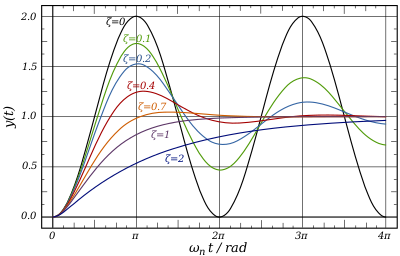
Коэффициент затухания является параметром, обычно обозначается z, (греческой буквы дзета), который характеризует частотный отклик в виде обыкновенного дифференциального уравнения второго порядка. Это особенно важно при изучении теории управления. Это также важно в гармоническом осцилляторе. В общем, системы с более высокими коэффициентами демпфирования (один или больше) будут демонстрировать больший эффект демпфирования. Системы с недостаточным демпфированием имеют значение меньше единицы. Системы с критическим демпфированием имеют коэффициент демпфирования ровно 1 или, по крайней мере, очень близок к нему.
Коэффициент демпфирования представляет собой математическое средство выражения уровня демпфирования в системе относительно критического демпфирования. Для затухающего гармонического осциллятора с массой m, коэффициентом демпфирования c и жесткостью пружины k его можно определить как отношение коэффициента демпфирования в дифференциальном уравнении системы к критическому коэффициенту демпфирования:
- ζ знак равно c c c знак равно фактическое демпфирование критическое затухание , { displaystyle zeta = { frac {c} {c_ {c}}} = { frac { text {фактическое демпфирование}} { text {критическое демпфирование}}},}
где уравнение движения системы
- м d 2 Икс d т 2 + c d Икс d т + k Икс знак равно 0 { displaystyle m { frac {d ^ {2} x} {dt ^ {2}}} + c { frac {dx} {dt}} + kx = 0}
а соответствующий критический коэффициент демпфирования равен
- c c знак равно 2 k м { displaystyle c_ {c} = 2 { sqrt {км}}}
или
- c c знак равно 2 м k м знак равно 2 м ω п { displaystyle c_ {c} = 2m { sqrt { frac {k} {m}}} = 2m omega _ {n}}
куда
- ω п знак равно k м { displaystyle omega _ {n} = { sqrt { frac {k} {m}}}}
— собственная частота системы.
Коэффициент демпфирования безразмерен и представляет собой отношение двух коэффициентов одинаковых единиц.
Вывод
Используя собственную частоту гармонического осциллятора и определение коэффициента демпфирования выше, мы можем переписать это как: ω п знак равно k / м { textstyle omega _ {n} = { sqrt {{k} / {m}}}}
- d 2 Икс d т 2 + 2 ζ ω п d Икс d т + ω п 2 Икс знак равно 0. { displaystyle { frac {d ^ {2} x} {dt ^ {2}}} + 2 zeta omega _ {n} { frac {dx} {dt}} + omega _ {n} ^ {2} x = 0.}
Это уравнение является более общим, чем просто система масса-пружина, а также применимо к электрическим цепям и другим областям. Это можно решить с помощью подхода.
- Икс ( т ) знак равно C е s т , { displaystyle x (t) = Ce ^ {st},}
где C и s — комплексные константы, причем s удовлетворяет
- s знак равно — ω п ( ζ ± я 1 — ζ 2 ) . { displaystyle s = — omega _ {n} left ( zeta pm i { sqrt {1- zeta ^ {2}}} right).}
Два таких решения для двух значений s, удовлетворяющих уравнению, могут быть объединены для получения общих реальных решений с колебательными и затухающими свойствами в нескольких режимах:
- Незатухающий
- Это случай, когда соответствует незатухающему простому гармоническому осциллятору, и в этом случае решение выглядит так, как ожидалось. Этот случай чрезвычайно редок в мире природы, и наиболее близкими примерами являются случаи, когда трение было целенаправленно снижено до минимальных значений. ζ знак равно 0 { displaystyle zeta = 0}
exp ( я ω п т ) { Displaystyle ехр (я омега _ {п} т)}
- Недостаточно демпфированный
- Если s — это пара комплексных значений, то каждый член комплексного решения представляет собой убывающую экспоненту в сочетании с колеблющейся частью, которая выглядит так. Этот случай имеет место и называется недостаточным демпфированием (например, эластичный кабель). exp ( я ω п 1 — ζ 2 т ) { textstyle exp left (я omega _ {n} { sqrt {1- zeta ^ {2}}} t right)}
0 ≤ ζ lt; 1 { Displaystyle 0 Leq zeta lt;1}
- Сверхдемпфированный
- Если s — пара действительных значений, то решение представляет собой просто сумму двух убывающих экспонент без колебаний. Этот случай имеет место и называется сверхдемпфированием. Ситуации, в которых чрезмерное демпфирование практично, имеют тенденцию к трагическим последствиям, если происходит перенапряжение, обычно электрическое, а не механическое. Например, посадка самолета на автопилоте: если система пролетит мимо и выпустит шасси слишком поздно, это приведет к катастрофе. ζ gt; 1 { displaystyle zetagt; 1}
- Критически затухающий
- Случай, когда является границей между случаями сверхдемпфирования и недостаточного демпфирования, называется критически демпфированным. Это оказывается желательным результатом во многих случаях, когда требуется инженерное проектирование демпфирующего генератора (например, механизма закрытия двери). ζ знак равно 1 { displaystyle zeta = 1}
Q — фактор и скорость распада
Q — фактор, коэффициент демпфирования ζ, и экспоненциальной скорости распада α связаны таким образом, что
- ζ знак равно 1 2 Q знак равно α ω п . { displaystyle zeta = { frac {1} {2Q}} = { alpha over omega _ {n}}.}
Когда система второго порядка имеет (то есть, когда система underdamped), она имеет два комплексно — сопряженных полюсов, каждый из которых имеет действительную часть из ; то есть параметр скорости затухания представляет собой скорость экспоненциального затухания колебаний. Более низкий коэффициент демпфирования подразумевает меньшую скорость затухания, и поэтому системы с очень слабым демпфированием колеблются в течение длительного времени. Например, высококачественный камертон с очень низким коэффициентом демпфирования имеет длительные колебания, которые очень медленно затухают после удара молотком. ζ lt; 1 { displaystyle zeta lt;1}


Логарифмический декремент
Для недостаточно затухающих колебаний коэффициент демпфирования также связан с логарифмическим декрементом. Коэффициент затухания может быть найден для любых двух пиков, даже если они не являются смежными. Для соседних пиков: δ { displaystyle delta}
- ζ знак равно δ δ 2 + ( 2 π ) 2 { displaystyle zeta = { frac { delta} { sqrt { delta ^ {2} + left (2 pi right) ^ {2}}}}}
куда δ знак равно пер Икс 0 Икс 1 { displaystyle delta = ln { frac {x_ {0}} {x_ {1}}}}
где x 0 и x 1 — амплитуды любых двух последовательных пиков.
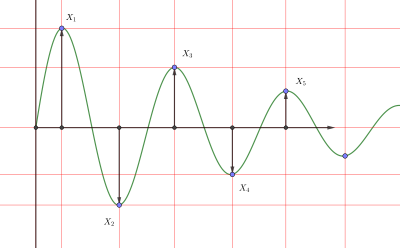
Как показано на правом рисунке:
- δ знак равно пер Икс 1 Икс 3 знак равно пер Икс 2 Икс 4 знак равно пер Икс 1 — Икс 2 Икс 3 — Икс 4 { displaystyle delta = ln { frac {x_ {1}} {x_ {3}}} = ln { frac {x_ {2}} {x_ {4}}} = ln { frac { x_ {1} -x_ {2}} {x_ {3} -x_ {4}}}}
где, — амплитуды двух последовательных положительных пиков и, — амплитуды двух последовательных отрицательных пиков. Икс 1 { displaystyle x_ {1}}


Процент превышения
В теории управления, перерегулирование относится к выходу превышает его окончательное, стационарное значение. Для пошагового ввода, то процент перерегулирование (РО) представляет собой максимальное значение минус значение шага, деленное на значение шага. В случае единичного шага перерегулирование — это просто максимальное значение реакции на скачок минус один.
Процент превышения (PO) связан с коэффициентом демпфирования ( ζ) следующим образом:
- п О знак равно 100 exp ( — ζ π 1 — ζ 2 ) { displaystyle mathrm {PO} = 100 exp left ({- { frac { zeta pi} { sqrt {1- zeta ^ {2}}}}} right)}
И наоборот, коэффициент демпфирования ( ζ), который приводит к заданному процентному превышению, определяется как:
- ζ знак равно — пер ( п О 100 ) π 2 + пер 2 ( п О 100 ) { displaystyle zeta = { frac {- ln left ({ frac { rm {PO}} {100}} right)} { sqrt { pi ^ {2} + ln ^ {2 } left ({ frac { rm {PO}} {100}} right)}}}}
Примеры и приложения
Вязкое сопротивление
Представьте, что вы роняете предмет. Пока этот объект падает в воздухе, единственная сила, препятствующая его свободному падению, — это сопротивление воздуха. Если вы уроните объект в воду или масло, он начнет замедляться с большей скоростью, пока в конечном итоге не достигнет установившейся скорости, поскольку сила сопротивления уравновесится с силой тяжести. Это концепция вязкого сопротивления. Применение этой концепции в повседневной жизни объясняет физику автоматических дверей или дверей с защитой от захлопывания.
Демпфирование в электрических системах
Электрические системы, работающие с переменным током (AC), используют резисторы для гашения электрического тока, поскольку они являются периодическими. Диммерные переключатели или ручки регулировки громкости являются примерами демпфирования в электрической системе.
Магнитное демпфирование
Кинетическая энергия, вызывающая колебания, рассеивается в виде тепла электрическими вихревыми токами, которые индуцируются при прохождении через полюса магнита катушкой или алюминиевой пластиной. Другими словами, сопротивление, вызванное магнитными силами, замедляет работу системы. Примером применения этой концепции в реальном мире являются тормоза на американских горках.
использованная литература
11. Британника, Энциклопедия. «Демпфирование». Британская энциклопедия, Британская энциклопедия, Inc., www.britannica.com/science/damping.
12. OpenStax, Колледж. «Физика». Lumen, course.lumenlearning.com/physics/chapter/23-4-eddy-currents-and-mintage-damping/.
Исходя из условия
минимума времени
затухания процесса (
время, начиная с которого переходная
характеристика остается в пределах
5% от установившегося значения),
экспериментально был определен
коэффициент демпфирования
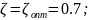
Ниже
на графике (рис. 18) приведены ПХ для ПФ:
у которых коэффициент демпфирования
0.7, 0.69, 0.71 соответственно. Можно заметить,
что именно
является искомой величиной, поскольку
дальнейший рост/уменьшение ζ приводит
к увеличению
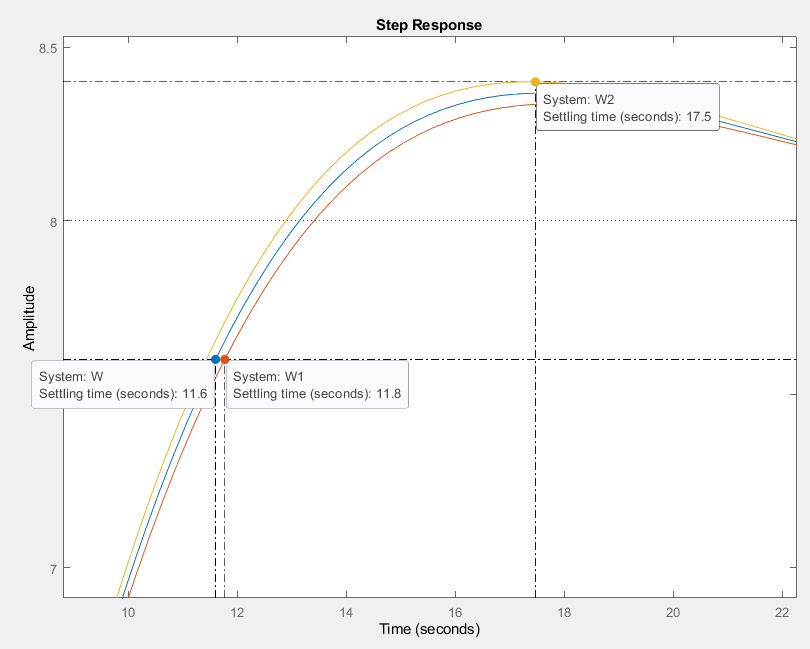
Рис.
18. ПХ для разных
Расположение
на комплексной плоскости корней ХП при
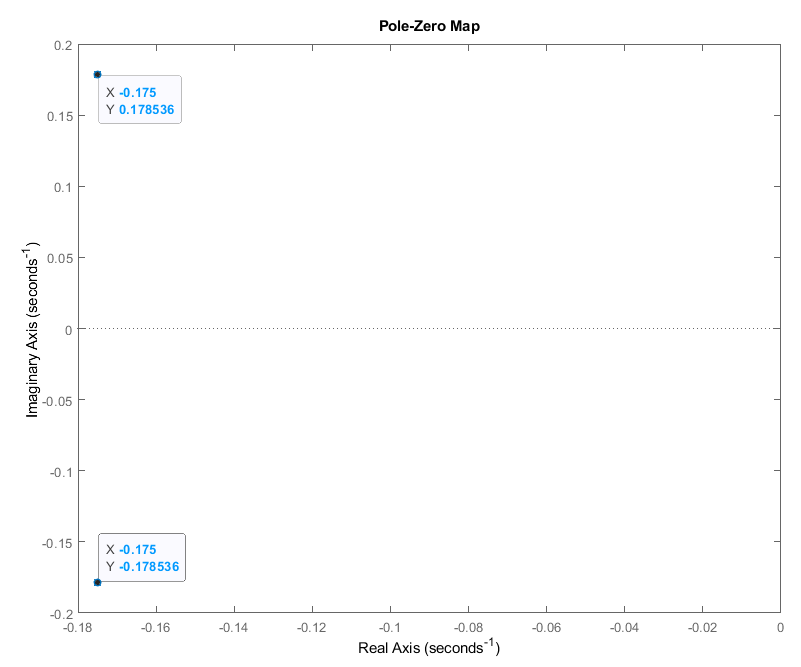
Рис.
19. Расположение корней ХП на комплексной
плоскости.
Высота
резонансного пика ЛАЧХ и частота
резонанса при
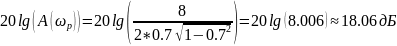
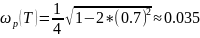
3.5. Переходная и частотные характеристики (афх и лчх) при изменении знака коэффициента демпфирования на .
Найдем характеристики
ПФ при отрицательном коэффициенте и
сравним с характеристиками ПФ при
положительном коэффициенте.
Передаточная
функция примет следующий вид:
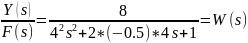
Найдем переходную
характеристику:
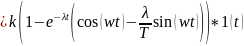
где
– показатель затухания; w
– угловая частота колебаний;
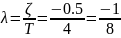

Амплитуда переходной
характеристики будет неограниченно
расти, так как имеют место положительные
комплексно-сопряженные полюсы (рис.
20):
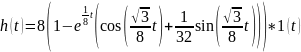
Найдем логарифмические
частотные характеристики:
ЛАЧХ не изменится
(рис. 21):
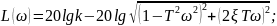
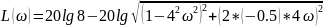
ЛФЧХ зеркально
отразится относительно
(рис. 21):

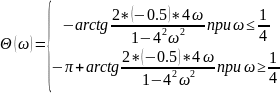
Найдем
амплитудно-фазовую характеристику:
АФХ зеркально
отразится относительно действительной
оси (рис. 22):
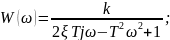
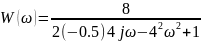
Построим
соответствующий график с помощью
программного средства MATLAB/Simulink.
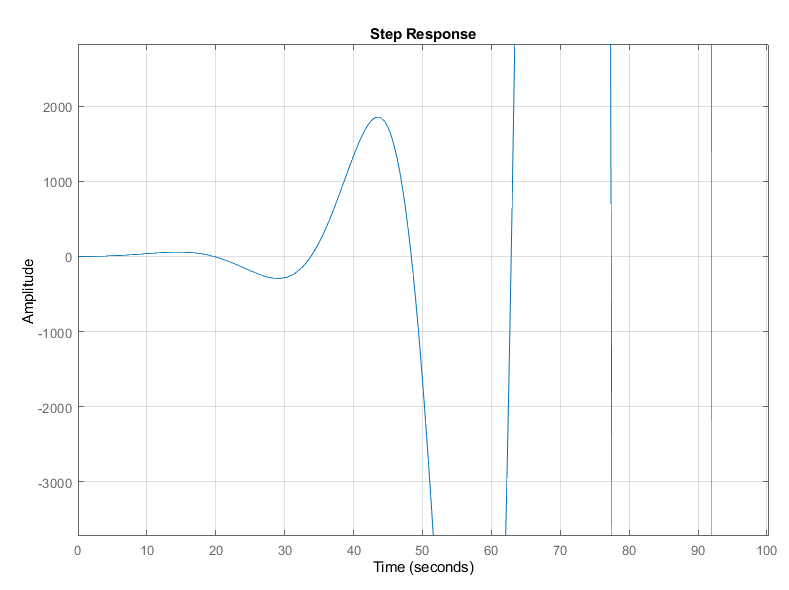
Рис. 20. Переходная
характеристика для
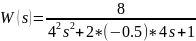
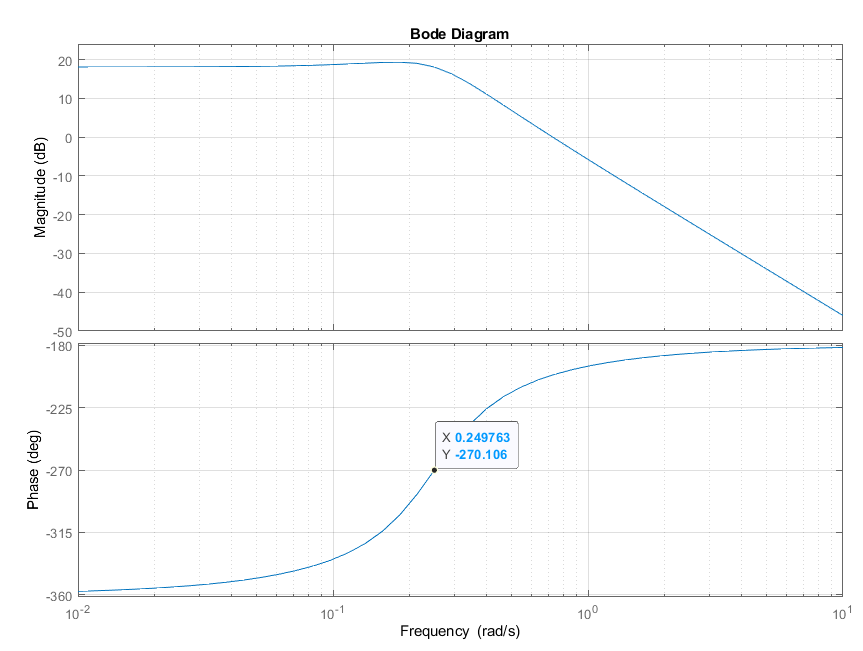
Рис. 21. Логарифмические
частотные характеристики для
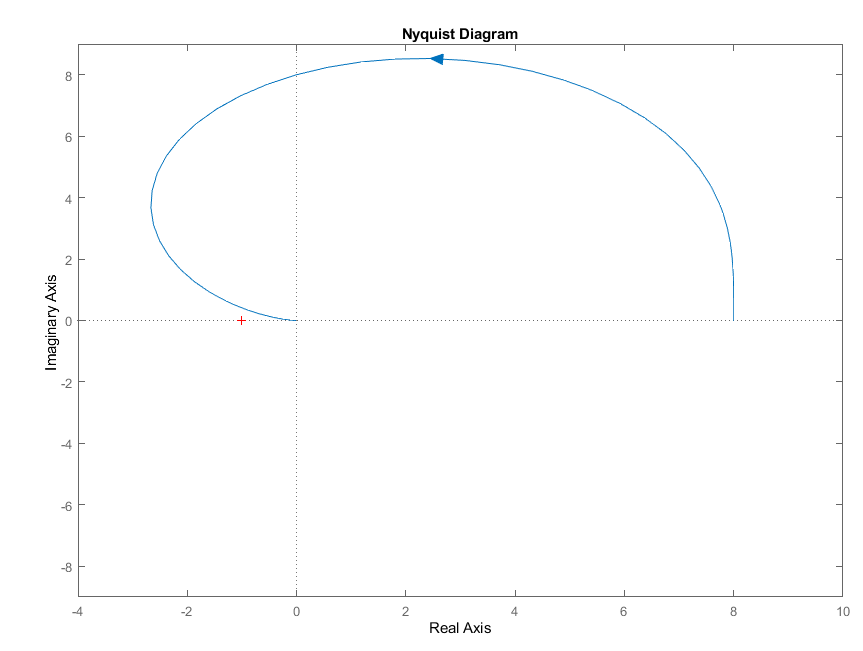
Рис. 22. АФХ для
4. Вывод.
В
результате выполнения задания были
получены ПФ, ПХ, АФХ, ЛАЧХ, ЛФЧХ, а также
изучены свойства апериодического звена
2-го порядка с коэффициентом демпфирования
;
При
звено описывает колебательно-затухающей
переходный процесс.
Было установлено,
что движение полюсов при изменении
параметра от 0 до 1, начинается с мнимой
оси при ξ = 0, и заканчивается отрицательным
действительным числом при ξ = 1. Была
получена зависимость резонансного пика
АЧХ от коэффициента демпфирования, а
также приведены советующие графики.
Экспериментально
было определено оптимальное значение
коэффициента демпфирования ξ
= ξ
опт. = 0.7 из условия минимума времени tр
затухания процесса.
Были рассмотрены переходная и частотные
характеристики при изменении знака
коэффициента демпфирования ξ на — ξ:
амплитуда переходной характеристики
будет неограниченно расти, так как имеют
место положительные комплексно-сопряженные
полюсы.
Заключение
В
результате выполнения данной лабораторной
работа мы изучили ПХ, ПФ, АФХ, ЛАЧХ и ЛФЧХ
апериодического звена второго порядка,
а также изучили его свойства. Были
разобраны два случаи, когда коэффициент
демпфирования
= 0 и
= 0,5: при
апериодическое
звено 2-го порядка вырождается в
консервативное
звено,
которое дает незатухающие колебания
на выходе, а при
звено описывается колебательно-затухающим
переходным процессом. Причем уменьшение
повышает колебательность переходных
процессов, кроме того при
ЛАЧХ имеет так называемый «горб» на
сопрягающей частоте, что говорит о
наличии резонанса в системе.
Также
был получен опыт моделирования
передаточных функций и дифференциальных
уравнений в
среде MATLAB/Simulink
и MATLAB
(Command
Window).
Стоит отметить, что параметр
позволяет судить о многих свойствах
системы таких, как колебательность,
резонанс, устойчивость и т.д.
Для передаточной функции, имеющей
коэффициент демпфирования
= 0, частоту резонанса можно было найти
исходя из физических параметров
предоставленной LC-цепи.
Таким образом, знание физических свойств
объекта помогло при исследовании типовых
звеньев.
Соседние файлы в папке УТС 5 семестр
- #
- #
- #
- #
- #
- #



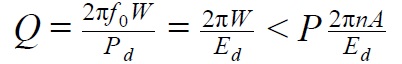
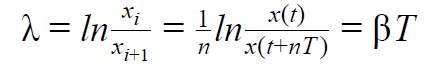
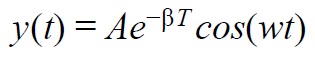
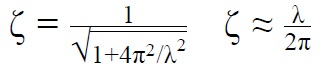
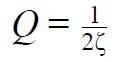





























 . Этот случай имеет место для 0 ≤ ζ < 1 {displaystyle 0leq zeta <1}
. Этот случай имеет место для 0 ≤ ζ < 1 {displaystyle 0leq zeta <1}





 — мгновенная амплитуда в момент времени t ;
— мгновенная амплитуда в момент времени t ; — начальная амплитуда огибающей;
— начальная амплитуда огибающей; — скорость убывания, обратная единицам времени независимой переменной t ;
— скорость убывания, обратная единицам времени независимой переменной t ; — фазовый угол при t = 0;
— фазовый угол при t = 0; — угловая частота.
— угловая частота.