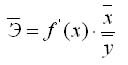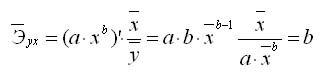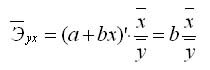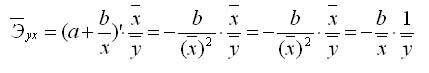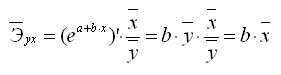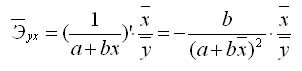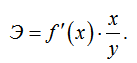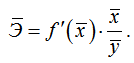Коэффициент эластичности
Как и в экономической теории и ряде других дисциплинах в эконометрике есть понятие среднего коэффициента эластичности Э – который показывает, на сколько процентов в среднем изменится показатель у от своего среднего значения при изменении фактора х на 1% от своей средней величины:
Для более подробного изучения вопроса об эластичности советуем посмотреть это видео
Коэффициент эластичности для степенной модели
В эконометрических исследованиях и экономической теории при изучении эластичности спроса от цен широко используется степенная функция
Коэффициент эластичности, можно определить и при наличии других форм связи, но только для степенной функции он представляет постоянную величину, равную параметру b. В других функциях коэффициент зависит от значений фактора х, поэтому интерпретировать модель сразу для прочих моделей невозможно, требуются дополнительные расчеты
Коэффициент эластичности для линейной модели
В силу того что k-эластичности для линейной регрессии не является постоянной, а зависит от соответствующего значения Х, то рассчитывается средний показатель эластичности по формуле
k-эластичности гиперболической модели:
k-эластичности для экспоненциальной модели:
k-эластичности для обратной модели:
Несмотря на обширное использование в эконометрике коэффициентов эластичности, иногда бывает, когда их расчет не имеет экономического смысла. Это происходит в тех случаях, когда для рассматриваемых признаков бессмысленно определение изменения значений в процентах. Например, вряд ли стоит определять, на сколько процентов может измениться заработная плата с ростом стажа работы на 1 %. В таких случаях степенная функция, даже если она оказывается оптимальной по формальным соображениям (исходя из минимального значения остаточной вариации), не может быть экономически интерпретирована.
Например, изучая соотношение ставок межбанковского кредита у (в % годовых) и срока его предоставления (в днях) было получено степенное уравнение регрессии с очень высоким коэффициентом корреляции (0,98). k-эластичности 0,4% лишен смысла, так как срок предоставления кредита не измеряется в процентах.
В множественной регрессии k-эластичности показывает, на сколько процентов изменяется в среднем результат с изменением соответствующего фактора на 1 % при неизменности действия других факторов. Степенные модели множественной регрессии получили широкое распространение в производственных функциях, при анализе спроса и потребления.
Таблица коэффициентов эластичности
Коэффициент
эластичности представляет собой
показатель силы связи фактора x
с результатом
у,
показывающий,
на сколько процентов изменится
значение у
при
изменении значения фактора на 1 %.
Коэффициент
эластичности (Э)
рассчитывается
как относительное
изменение у
на
единицу относительного изменения x:
. (24)
Различают
обобщающие (средние) и точечные
коэффициенты
эластичности.
Обобщающий
коэффициент эластичности рассчитывается
для среднего значения
:
и
показывает, на сколько процентов
изменится у
относительно
своего среднего
уровня при росте х
на
1 %
относительно
своего среднего
уровня.
Точечный
коэффициент эластичности рассчитывается
для
конкретного значения х
= х0:
и показывает,
на сколько процентов изменится у
относительно
уровня
у(х0)
при
увеличении х
на
1% от уровня х0.
В
зависимости от вида зависимости между
х
и
у
формулы
расчета коэффициентов эластичности
будут меняться. Основные
формулы приведены в табл. 2.
Таблица 2
|
Вид |
Точечный коэффициент эластичности |
Средний |
|
Линейная |
|
|
|
Парабола |
|
|
|
Равносторонняя |
|
|
|
Степенная |
|
|
|
Показательная |
|
|
|
Полулогарифмическая у |
|
|
Только
для степенных функций
коэффициент
эластичности
представляет собой постоянную независящую
от
х
величину
(равную в данном случае параметру b).
Именно
поэтому степенные функции широко
используются в эконометрических
исследованиях. Параметр b
в
таких функциях
имеет четкую экономическую интерпретацию
– он показывает
процентное изменение результата при
увеличении фактора на 1 %. Так, если
зависимость спроса у
от
цен p
характеризуется
уравнением вида:
,
то, следовательно,
с увеличением цен на 1 % спрос снижается
в среднем
на 1,5 %.
Несмотря
на широкое использование в эконометрике
коэффициентов эластичности, возможны
случаи, когда их расчет экономического
смысла не имеет. Это происходит тогда,
когда для рассматриваемых признаков
бессмысленно
определение изменения значений в
процентах. Например,
бессмысленно определять, на сколько
процентов изменится
заработная плата с ростом возраста
рабочего на 1%.
В
такой ситуации степенная функция, даже
если она оказывается
наилучшей по формальным соображениям
(исходя из
наибольшего значения R2),
не может быть экономически интерпретирована.
1.4. Анализ гетероскедастичности
В
соответствии с третьей предпосылкой
метода наименьших квадратов требуется,
чтобы дисперсия остатков была
гомоскедастичной.
Это значит, что для каждого значения
фактора хi
остатки имеют одинаковую дисперсию.
Если это условие применения МНК не
соблюдается, то имеет место
гетероскедастичность
(рис. 1).
Гомоскедастичность остатков
означает, что дисперсия остатков i
одинакова для каждого значения х.
Гетероскедастичность будет
сказываться на уменьшении эффективности
оценок bi.
В частности, становится затруднительным
использование формулы стандартной
ошибки коэффициента регрессии
,
предполагающей единую дисперсию остатков
для любых значений фактора.
Рассмотрим тесты,
которые позволяют провести анализ
модели на гомоскедастичность.
При малом объеме выборки,
что наиболее характерно для эконометрических
исследований, для оценки гетероскедастичности
может использоваться метод
ГольдфельдаКвандта,
разработанный в 1965 г. Гольдфельд и Квандт
рассмотрели однофакторную линейную
модель, для которой дисперсия остатков
возрастает пропорционально квадрату
фактора. Для того чтобы оценить нарушение
гомоскедастичности, они предложили
параметрический тест,
который включает в себя следующие шаги:
-
Упорядочение п
наблюдений по мере возрастания переменной
х. -
Исключение из рассмотрения
С
центральных наблюдений; при этом (п
С)/2 > р,
где р
число оцениваемых параметров.
Из экспериментальных
расчетов, проведенных авторами метода
для случая одного фактора, рекомендовано
при п
= 30 принимать С
= 8, а при п
= 60 – соответственно С
= 16.
-
Разделение совокупности
из (п
С)
наблюдений на две группы (соответственно
с малыми и большими значениями фактора
х)
и определение по каждой из групп
уравнений регрессии. -
Определение остаточной
суммы квадратов для первой (S1)
и второй (S2)
групп и нахождение их отношения: R
= S1/S2,
где
S1
> S2.
При
выполнении нулевой гипотезы о
гомоскедастичности отношение R
будет удовлетворять F-критерию
с (пС2р)/2
степенями свободы для каждой остаточной
суммы квадратов. Чем больше величина R
превышает табличное значение F-критерия,
тем более нарушена предпосылка о
равенстве дисперсий остаточных величин.
Критерий ГольдфельдаКвандта
используется и при проверке остатков
множественной регрессии на
гетероскедастичность.
Наличие гетероскедастичности
в остатках регрессии можно проверить
и с помощью ранговой
корреляции Спирмэна.
Суть проверки заключается в том, что в
случае гетероскедастичности абсолютные
остатки i
коррелированы со значениями фактора
хi.
Эту корреляцию можно измерять с помощью
коэффициента ранговой корреляции
Спирмэна:
, (25)
где d
абсолютная разность между рангами
значений хi
и |i|.
Статистическую значимость
можно оценить с помощью
t-критерия:
. (26)
Сравнив эту величину с
табличной величиной при
= 0,05 и числе степеней свободы (п
m).
Принято считать, что если t
> t,
то корреляция между i
и хi
статистически значима, т. е. имеет место
гетероскедастичность остатков. В
противном случае принимается гипотеза
об отсутствии гeтероскедастичности
остатков.
Рассмотренные критерии не
дают количественной оценки зависимости
дисперсии ошибок регрессии от
соответствующих значений факторов,
включенных в регрессию. Они позволяют
лишь определить наличие или отсутствие
гетероскедастичности остатков. Поэтому
если гетероскедастичность остатков
установлена, можно количественно оценить
зависимость дисперсии ошибок регрессии
от значений факторов. С этой целью могут
быть использованы тесты Уайта, Парка,
Глейзера и др.
Тест Уайта
предполагает, что
дисперсия ошибок регрессии представляет
собой квадратичную функцию от значений
факторов, т.е. при наличии одного фактора
2
= а+
bx
+ cx2
+ u,
или при наличии факторов:
2
= a
+ b1x1
+ b11+b2x2
+ b22+b12x1x2
+ … + bpxp
+ bpp
+
+ b1px1xp
+ b2px2xp
+ … + u.
Так что модель включает в
себя не только значения факторов, но и
их квадраты, а также попарные произведения.
Поскольку каждый параметр модели
=f(хi)
должен быть рассчитан на основе
достаточного числа степеней свободы,
то чем меньше объем исследуемой
совокупности, тем в меньшей мере
квадратичная функция сможет содержать
попарные произведения факторов. Например,
если регрессия строится по 30 наблюдениям
как yi
= a
+ b1x
+ i,
то последующая квадратичная функция
для остатков может быть представлена
лишь как
2
= а
+ b1x
+ b11х2
+ u,
поскольку
на каждый параметр при х
должно приходиться не менее 67
наблюдений. В настоящее время тест Уайта
включен в стандартную программу
регрессионного анализа в пакете
Econometric Views. О наличии или отсутствии
гетероскедастичности остатков судят
по величине F-критерия
Фишера для квадратичной функции регрессии
остатков. Если фактическое значение
F-критерия
выше табличного, то, следовательно,
существует четкая корреляционная связь
дисперсии ошибок от значений факторов,
включенных в регрессию, и имеет место
гетероскедастичность остатков. В
противном случае (Fфакт
< Fтабл)
делается вывод об отсутствии
гeтероскедастичности остатков регрессии.
Тест
Парка
также относится к формализованным
тестам гетероскедастичности.
Предполагается, что дисперсия остатков
связана со значениями факторов функций
ln
2
= а
+ b
ln
х
+ и.
Данная регрессия строится для каждого
фактора в условиях многофакторной
модели. Проверяется значимость
коэффициента регрессии b
по t-критерию
Стьюдента. Если коэффициент регрессии
для уравнения ln2
окажется статистически значимым, то,
следовательно, существует зависимость
ln2
от lnх,
т.е. имеет место гетероскедастичность
остатков.
Если
тесты Уайта и Парка предназначены для
оценки гетероскедастичности для квадрата
остатков 2,
то тест
Глейзера
основывается на регрессии абсолютных
значений остатков ||,
т.е. рассматривается функция |i|
= а
+ b
+ иi.
Регрессия |i|
от хi
строится при разных значениях параметра
с,
и далее отбирается та функция, для
которой коэффициент регрессии b
оказывается наиболее значимым, т.е.
имеет место наибольшее значение
t-критерия
Стьюдента или F-критерия
Фишера и R2.
При
обнаружении гетероскедастичности
остатков регрессии ставится цель ее
устранения, чему служит применение
обобщенного метода наименьших квадратов
(см. ниже).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
анастасия александровна янченко
Эксперт по предмету «Эконометрика»
Задать вопрос автору статьи
Сущность коэффициента эластичности
Коэффициент эластичности, как и индексы детерминации и корреляции для нелинейных форм связи, используются для характеристики зависимостей результативной и факторных переменных. Коэффициент эластичности позволяет дать оценку степени зависимости переменных.
Определение 1
Коэффициент эластичности – это показатель силы связи фактора с результатом, который показывает, как изменится значение результата в случае изменения на 1 процент значения фактора.
Замечание 1
Цель расчета коэффициента эластичности в эконометрике — показать относительное изменение анализируемого показателя при единичном относительном изменении экономического фактора, который на него влияет при неизменности остальных факторов.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Средние и точечные коэффициенты
Коэффициент эластичности может быть рассчитан как средний и точечный коэффициент.
Средний коэффициент эластичности показывает, на сколько процентов будет меняться результативная переменная относительно ее среднего уровня при изменении факторной переменной на 1 % относительно своего среднего значения.
Замечание 2
Средние показатели эластичности можно сопоставлять друг с другом, а, значит, ранжировать факторы в зависимости от силы их воздействия на результаты.
Точечный коэффициент эластичности характеризуется тем, что на эластичность функции влияет заданное значение факторной переменной.
Точечный коэффициент эластичности показывает, как изменится результативная переменная (в процентном выражении) относительно ее значения в определенной точке при изменении факторной переменной на 1 % относительно установленного уровня.
Применение коэффициента эластичности
«Эластичность в эконометрике» 👇
Зачастую коэффициент эластичности используется при проведении анализа производственных функций. Вместе с тем, расчет коэффициентов эластичности не всегда будет иметь смысл, поскольку в ряде случаев невозможно или даже бессмысленно интерпретировать факторные переменные в процентном отношении.
Приведем примеры ситуаций, когда нет смысла рассчитывать коэффициент эластичности:
- Ситуация, для анализируемых признаков нецелесообразно определять их изменение в процентном выражении. Примером может выступать задача по расчету относительного изменения заработной платы в случае увеличения стажа работы на определенной должности на 1%. В подобной ситуации определение правильной степенной функции не дает возможности ее экономически интерпретировать.
- Еще один пример — изучение соотношения ставок межбанковского кредитования (в процентах годовых) и периода его предоставления в днях. В данном случае будет получено уравнение регрессии, которое характеризуется довольно высоким показателем корреляции. Расчет коэффициента эластичности не имеет смысла, поскольку срок межбанковского кредитования не может быть измерен в процентном выражении. Для подобной зависимости больший интерес для анализа представляет линейная функция, которая имеет более низкое значение показателя корреляции. Коэффициент регрессии позволяет дать оценку процентному изменению кредитных ставок при увеличении периода его предоставления на один день.
Для линейных моделей множественной регрессии, в которых факторные признаки различаются по своей сути или характеризуются различными единицами измерения, коэффициенты регрессии — несопоставимы. Исходя из этого, уравнение регрессии может быть дополнено соизмеримыми параметрами близости связи фактора и результата, которые позволяют проранжировать факторы в зависимости от силы влияния на результат.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Коэффициент эластичности для разных типов регрессий
При решении задач некоторых разделов статистики и эконометрики вычисляется коэффициент эластичности. Это характерно для задач, в которых определяется наличие связи между двумя некоторыми экономическими факторами. Коэффициент эластичности показывает, на сколько процентом изменится в среднем результатирующий фактор, при изменении зависимого фактора на 1% .
Формула для расчета коэффициента эластичности:
Так как для некоторых функций коэффициент эластичности не является постоянной величиной, а зависит от соответствующего значения фактора x, то обычно рассчитывается средний коэффициент эластичности:
Приведем формулы для расчета средних коэффициентов эластичности для наиболее часто используемых типов уравнений регрессии
Коэффициент эластичности
Как и в экономической теории и ряде других дисциплинах в эконометрике есть понятие среднего коэффициента эластичности Э – который показывает, на сколько процентов в среднем изменится показатель у от своего среднего значения при изменении фактора х на 1% от своей средней величины:
Для более подробного изучения вопроса об эластичности советуем посмотреть это видео
Коэффициент эластичности для степенной модели
В эконометрических исследованиях и экономической теории при изучении эластичности спроса от цен широко используется степенная функция
Коэффициент эластичности, можно определить и при наличии других форм связи, но только для степенной функции он представляет постоянную величину, равную параметру b. В других функциях коэффициент зависит от значений фактора х, поэтому интерпретировать модель сразу для прочих моделей невозможно, требуются дополнительные расчеты
Коэффициент эластичности для линейной модели
В силу того что k-эластичности для линейной регрессии не является постоянной, а зависит от соответствующего значения Х, то рассчитывается средний показатель эластичности по формуле
k-эластичности гиперболической модели:
k-эластичности для экспоненциальной модели:
k-эластичности для обратной модели:
Несмотря на обширное использование в эконометрике коэффициентов эластичности, иногда бывает, когда их расчет не имеет экономического смысла. Это происходит в тех случаях, когда для рассматриваемых признаков бессмысленно определение изменения значений в процентах. Например, вряд ли стоит определять, на сколько процентов может измениться заработная плата с ростом стажа работы на 1 %. В таких случаях степенная функция, даже если она оказывается оптимальной по формальным соображениям (исходя из минимального значения остаточной вариации), не может быть экономически интерпретирована.
Например, изучая соотношение ставок межбанковского кредита у (в % годовых) и срока его предоставления (в днях) было получено степенное уравнение регрессии с очень высоким коэффициентом корреляции (0,98). k-эластичности 0,4% лишен смысла, так как срок предоставления кредита не измеряется в процентах.
В множественной регрессии k-эластичности показывает, на сколько процентов изменяется в среднем результат с изменением соответствующего фактора на 1 % при неизменности действия других факторов. Степенные модели множественной регрессии получили широкое распространение в производственных функциях, при анализе спроса и потребления.
Парная линейная регрессия. Задачи регрессионного анализа
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Понятие линейной регрессии. Парная линейная регрессия
Линейная регрессия — выраженная в виде прямой зависимость среднего значения какой-либо величины от некоторой другой величины. В отличие от функциональной зависимости y = f(x) , когда каждому значению независимой переменной x соответствует одно определённое значение величины y, при линейной регрессии одному и тому же значению x могут соответствовать в зависимости от случая различные значения величины y.
Если в результате наблюдения установлено, что при каждом определённом значении x существует сколько-то (n) значений переменной y, то зависимость средних арифметических значений y от x и является регрессией в статистическом понимании.
Если установленная зависимость может быть записана в виде уравнения прямой
то эта регрессионная зависимость называется линейной регрессией.
О парной линейной регрессии говорят, когда установлена зависимость между двумя переменными величинами (x и y). Парная линейная регрессия называется также однофакторной линейной регрессией, так как один фактор (независимая переменная x) влияет на результирующую переменную (зависимую переменную y).
В уроке о корреляционной зависимости были разобраны примеры того, как цена на квартиры зависит от общей площади квартиры и от площади кухни (две различные независимые переменные) и о том, что результаты наблюдений расположены в некотором приближении к прямой, хотя и не на самой прямой. Если точки корреляционной диаграммы соединить ломанной линией, то будет получена линия эмпирической регрессии. А если эта линия будет выровнена в прямую, то полученная прямая будет прямой теоретической регрессии. На рисунке ниже она красного цвета (для увеличения рисунка щёлкнуть по нему левой кнопкой мыши).
По этой прямой теоретической регрессии может быть сделан прогноз или восстановление неизвестных значений зависимой переменной по заданным значениям независимой переменной.
В случае парной линейной регрессии для данных генеральной совокупности связь между независимой переменной (факториальным признаком) X и зависимой переменной (результативным признаком) Y описывает модель
,
— свободный член прямой парной линейной регрессии,
— коэффициент направления прямой парной линейной регрессии,
— случайная погрешность,
N — число элементов генеральной совокупности.
Уравнение парной линейной регрессии для генеральной совокупности можно построить, если доступны данные обо всех элементах генеральной совокупности. На практике данные всей генеральной совокупности недоступны, но доступны данные об элементах некоторой выборки.
Поэтому параметры генеральной совокупности оценивают при помощи соответствующих параметров соответствующей выборки: свободный член прямой парной линейной регрессии генеральной совокупности заменяют на свободный член прямой парной линейной регрессии выборки , а коэффициент направления прямой парной линейной регрессии генеральной совокупности — на коэффициент направления прямой парной линейной регрессии выборки .
В результате получаем уравнение парной линейной регрессии выборки
— оценка полученной с помощью модели линейной регрессии зависимой переменной Y,
— погрешность,
n — размер выборки.
Чтобы уравнение парной линейной регрессии было более похоже на привычное уравнение прямой, его часто также записывают в виде
.
Уравнение парной линейной регрессии и метод наименьших квадратов
Определение коэффициентов уравнения парной линейной регрессии
Если заранее известно, что зависимость между факториальным признаком x и результативным признаком y должна быть линейной, выражающейся в виде уравнения типа , задача сводится к нахождению по некоторой группе точек наилучшей прямой, называемой прямой парной линейной регрессии. Следует найти такие значения коэффициентов a и b , чтобы сумма квадратов отклонений была наименьшей:
.
Если через и обозначить средние значения признаков X и Y,то полученная с помощью метода наименьших квадратов функция регрессии удовлетворяет следующим условиям:
- прямая парной линейной регрессии проходит через точку ;
- среднее значение отклонений равна нулю: ;
- значения и не связаны: .
Условие метода наименьших квадратов выполняется, если значения коэффициентов равны:
,
.
Пример 1. Найти уравнение парной линейной регрессии зависимости между валовым внутренним продуктом (ВВП) и частным потреблением на основе данных примера урока о корреляционной зависимости (эта ссылка, которая откроется в новом окне, потребуется и при разборе следующих примеров).
Решение. Используем рассчитанные в решении названного выше примера суммы:
Используя эти суммы, вычислим коэффициенты:
Таким образом получили уравнение прямой парной линейной регрессии:
Составить уравнение парной линейной регрессии самостоятельно, а затем посмотреть решение
Пример 2. Найти уравнение парной линейной регрессии для выборки из 6 наблюдений, если уже вычислены следующие промежуточные результаты:
;
;
;
;
Анализ качества модели линейной регрессии
Метод наименьших квадратов имеет по меньшей мере один существенный недостаток: с его помощью можно найти уравнение линейной регрессии и в тех случаях, когда данные наблюдений значительно рассеяны вокруг прямой регрессии, то есть находятся на значительном расстоянии от этой прямой. В таких случаях за точность прогноза значений зависимой переменной ручаться нельзя. Существуют показатели, которые позволяют оценить качество уравнения линейной регрессии прежде чем использовать модели линейной регрессии для практических целей. Разберём важнейшие из этих показателей.
Коэффициент детерминации
Коэффициент детерминации принимает значения от 0 до 1 и в случае качественной модели линейной регрессии стремится к единице. Коэффициент детерминации показывает, какую часть общего рассеяния зависимой переменной объясняет независимая переменная:
,
— сумма квадратов отклонений, объясняемых моделью линейной регрессии, которая характеризует рассеяние точек прямой регрессии относительно арифметического среднего,
— общая сумма квадратов отклонений, которая характеризует рассеяние зависимой переменной Y относительно арифметического среднего,
— сумма квадратов отклонений ошибки (не объясняемых моделью линейной регрессии), которая характеризует рассеяние зависимой переменной Y относительно прямой регресии.
Пример 3. Даны сумма квадратов отклонений, объясняемых моделью линейной регрессии (3500), общая сумма квадратов отклонений (5000) и сумма квадратов отклонений ошибки (1500). Найти коэффициент детерминации двумя способами.
F-статистика (статистика Фишера) для проверки качества модели линейной регрессии
Минимальное возможное значение F-статистики — 0. Чем выше значение статистики Фишера, тем качественнее модель линейной регрессии. Этот показатель представляет собой отношение объясненной суммы квадратов (в расчете на одну независимую переменную) к остаточной сумме квадратов (в расчете на одну степень свободы):
где m — число объясняющих переменных.
Сумма квадратов остатков
Сумма квадратов остатков (RSS) измеряет необъясненную часть дисперсии зависимой переменной:
—
остатки — разности между реальными значениями зависимой переменной и значениями, оценёнными уравнением линейной регрессии.
В случае качественной модели линейной регрессии сумма квадратов остатков стремится к нулю.
Стандартная ошибка регрессии
Стандартная ошибка регрессии (SEE) измеряет величину квадрата ошибки, приходящейся на одну степень свободы модели:
Чем меньше значение SEE, тем качественнее модель.
Пример 4. Рассчитать коэффициент детерминации для данных из примера 1.
Решение. На основании данных таблицы (она была приведена в примере урока о корреляционной зависимости) получаем, что SST = 63 770,593 , SSE = 10 459,587 , SSR = 53 311,007 .
Можем убедиться, что выполняется закономерность SSR = SST — SSE :
Получаем коэффициент детерминации:
.
Таким образом, 83,6% изменений частного потребления можно объяснить моделью линейной регресии.
Интерпретация коэффициентов уравнения парной линейной регрессии и прогноз значений зависимой переменной
Итак, уравнение парной линейной регрессии:
.
В этом уравнении a — свободный член, b — коэффициент при независимой переменной.
Интерпретация свободного члена: a показывает, на сколько единиц график регрессии смещён вверх при x=0, то есть значение переменной y при нулевом значении переменной x.
Интерпретация коэффициента при независимой переменной: b показывает, на сколько единиц изменится значение зависимой переменной y при изменении x на одну единицу.
Пример 5. Зависимость частного потребления граждан от ВВП (истолкуем это просто: от дохода) описывается уравнением парной линейной регрессии . Сделать прогноз потребления при доходе в 20 000 у.е. Выяснить, на сколько увеливается потребление при увеличении дохода на 5000 у.е. Меняется ли потребление, если доход не меняется?
Решение. Подставляем в уравнение парной линейной регрессии x i = 20000 и получаем прогноз потребления при доходе в 20 000 у.е. y i = 17036,4662 .
Подставляем в уравнение парной линейной регрессии x i = 5000 и получаем прогноз увеличения потребления при увеличении дохода на 5000 у.е. y i = 4161,9662 .
Если доход не меняется, то x i = 0 и получаем, что потребление уменьшается на 129,5338 у.е.
Задачи регрессионного анализа
Регрессионный анализ — раздел математической статистики, объединяющий практические методы исследования регрессионной зависимости между величинами по статистическим данным.
Наиболее частые задачи регрессионного анализа:
- установление факта наличия или отсутствия статистических зависимостей между переменными величинами;
- выявление причинных связей между переменными величинами;
- прогноз или восстановление неизвестных значений зависимых переменных по заданным значениям независимых переменных.
Также делаются проверки статистических гипотез о регрессии. Кроме того, при изучении связи между двумя величинами по результатам наблюдений в соответствии с теорией регрессии предполагается, что зависимая переменная имеет некоторое распределение вероятностей при фиксированном значении независимой переменной.
В исследованиях поведения человека, чтобы они претендовали на объективность, важно не только установить зависимость между факторами, но и получить все необходимые статистические показатели для результата проверки соответствующей гипотезы.
Проверка гипотезы о равенстве нулю коэффициента направления прямой парной линейной регрессии
Одна из важнейших гипотез в регрессионном анализе — гипотеза о том, что коэффициент направления прямой регрессии генеральной совокупности равен нулю.
Если это предположение верно, то изменения независимой переменной X не влияют на изменения зависимой переменной Y: переменные X и Y не коррелированы, то есть линейной зависимости Y от X нет.
рассматривают во взаимосвязи с альтернативной гипотезой
.
Статистика коэффициента направления
соответствует распределению Стьюдента с числом степеней свободы v = n — 2 ,
где — стандартная погрешность коэффициента направления прямой линейной регресии b 1 .
Доверительный интервал коэффициента направления прямой линейной регрессии:
.
Критическая область, в которой с вероятностью P = 1 — α отвергают нулевую гипотезу и принимают альтернативную гипотезу:
Пример 6. На основе данных из предыдущих примеров (о ВВП и частном потреблении) определить доверительный интервал коэффициента направления прямой линейной регресии 95% и проверить гипотезу о равенстве нулю коэффициента направления прямой парной линейной регрессии.
Можем рассчитать, что , а стандартная погрешность регрессии .
Таким образом, стандартная погрешность коэффициента направления прямой линейной регресии b 1 :
.
Так как и (находим по таблице в приложениях к учебникам по статистике), то доверительный интервал 95% коэффициента направления прямой парной линейной регрессии:
.
Так как гипотетическое значение коэффициента — нуль — не принадлежит доверительному интервалу, с вероятностью 95% можем отвергнуть основную гипотезу и принять альтернативную гипотезу, то есть считать, что зависимая переменная Y линейно зависит от независимой переменной X.
http://function-x.ru/statistics_regression1.html
Коэффициент эластичности
Понятие коэффициент эластичности широко используется в эконометрике.
Коэффициент эластичности показывает, на сколько процентов (в моменте) измениться результат, если фактор (входной параметр) изменится на 1%.
Формула расчета коэффициента эластичности
Э = 100% * dy/dx * x/y
Примечательно, что для показательной функции коэффициент эластичности в точности равен показателю степени, то есть
Если результат описывается функцией y=a * xb, то коэффициент эластичности: Э=b.
Каков же будет результат для других функций?
Рассмотрим следующие функции:
- y = a + b * x — линейная функция.
- y = a + b * x + c * x2 — парабола.
- y = a + b / x — гипербола.
- y = a * bx — показательная функция.
- y = a + b * ln(x) — линейная-логарифмическая функция.
- y = 1 / (1 + b * e-(c*x) — логистическая функция.
- y = 1 / (a + b * x) — обратная функция.
Допустим, данные функции описывают рост доходов.
Формулы коэффициентов эластичности:
- Э1 = b * x / (a + b * x) — коэффициент эластичности линейной функции.
- y = (b * x + 2 * c * x2) / (a + b * x + c * x2)— коэффициент эластичности параболы.
- y = — b / (a * x + b) — коэффициент эластичности гиперболы.
- y = x * ln(x) — коэффициент эластичности показательной функции.
- y = b / (a + b * ln(x)) — коэффициент эластичности линейная-логарифмической функции.
- y = c * x / (1 + ec*x / b) — коэффициент эластичности логистической функции.
- y = — b * x / (a + b * x) — коэффициент эластичности обратной функции.
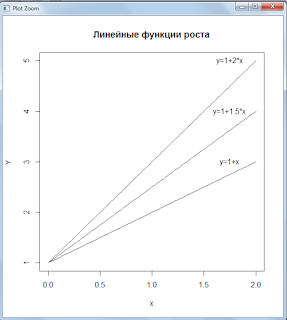
Линейная функция
Рассмотрим линейную функцию. Для этого построим графики трех различных линейных функций:
Скрипт R:
dy <- c(1,5)
a <- 1
b1 <- 1
curve(a + b1 * x, 0, 2, 100, ylim = dy, ylab = ‘Y’)
title(‘Линейные функции роста’)
text(1.75,3,»y=1+x»)
b2 <- 1.5
curve(a + b2*x, 0, 2, 100, ylim= dy, ylab = ‘Y’, add=TRUE)
text(1.75,4,»y=1+1.5*x»)
b3 <- 2
curve(a + b3*x, 0, 2, 100, ylim= dy, ylab = ‘Y’, add=TRUE)
text(1.75,5,»y=1+2*x»)
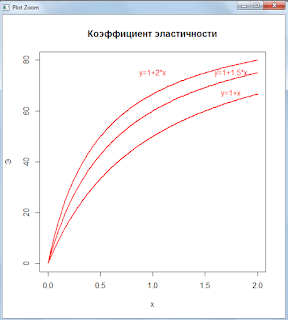
Им отвечают следующие коэффициенты эластичности:
Скрипт R:
dy1 <- c(0,80)
curve(100 * b1*x / (a+b1*x), 0, 2, 100, col=’red’, lwd =2,
ylim = dy1, ylab = ‘Э’ )
title(‘Коэффициент эластичности’)
text(1.75,67,»y=1+x»,col=’red’)
curve(100 * b2*x / (a+b2*x), 0, 2, 100, col=’red’, lwd =2,
add= TRUE, ylim = dy1 )
text(1.75,75,»y=1+1.5*x»,col=’red’)
curve(100 * b3*x / (a+b3*x), 0, 2, 100, col=’red’, lwd =2,
add= TRUE, ylim = dy1 )
text(1,75,»y=1+2*x»,col=’red’)
Заметим, что эластичность линейной функции по мере роста убывает. Это может служить источником «обратной манипуляции» — хотя доходы в абсолютной величине растут, тем не менее в процентном отношении они падают. Что могут вменить успешным, чтобы скрыть или умалить заслуги менеджеров.
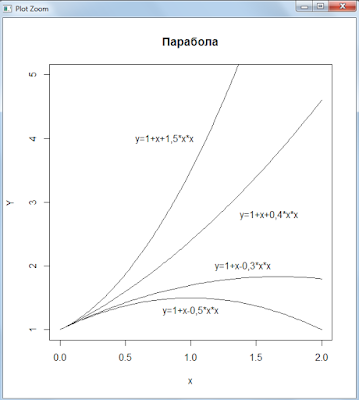
Парабола
Графики «параболических» доходов:
Скрипт R:
a <- 1
b1 <- 1
c1 <- -0.5
curve(a + b1*x + c1 * x * x, 0, 2, 100, ylim= dy, ylab = ‘Y’)
title(‘Парабола’)
text(1,1.3,»y=1+x-0,5*x*x»)
c2 <- 0.4
curve(a + b1*x + c2 * x * x, 0, 2, 100, ylim=dy,add= TRUE)
text(1.6,2.8,»y=1+x+0,4*x*x»)
c3 <- 1.5
curve(a + b1*x + c3 * x * x, 0, 2, 100, ylim=dy,add= TRUE)
text(0.8,4,»y=1+x+1,5*x*x»)
c4 <- -0.3
curve(a + b1*x + c4 * x * x, 0, 2, 100, ylim=dy,add= TRUE)
text(1.4,2,»y=1+x-0,3*x*x»)
Коэффициенты эластичности парабол:
Скрипт R:
dy1 <- c(-100,150)
a <- 1
b1 <- 1
c1 <- -0.5
curve( 100 * (b1 + 2 * c1 * x) / (a+b1*x+c1*x*x), 0, 2, 100,
col=’red’, lwd =2, ylim = dy1, ylab = ‘Y’)
title(‘Коэффициент эластичности’)
text(1.6,-91,»y=1+x-0,5*x*x»)
curve( 100 * (b1 + 2 * c2 * x) / (a+b1*x+c2*x*x), 0, 2, 100,
add = TRUE, col=’red’, lwd =2, ylim = dy1)
text(1.6,50,»y=1+x+0,4*x*x»)
curve( 100 * (b1 + 2 * c3 * x) / (a+b1*x+c3*x*x), 0, 2, 100,
add = TRUE, col=’red’, lwd =2, ylim = dy1)
text(1.6,110,»y=1+x+1,5*x*x»)
c4 <- -0.3
curve( 100 * (b1 + 2 * c4 * x) / (a+b1*x+c4*x*x), 0, 2, 100,
add = TRUE, col=’red’, lwd =2, ylim = dy1)
text(1.6,20,»y=1+x-0,3*x*x»)
Гипербола
Графики гиперболических доходов могут применяться для аппроксимации тенденций с насыщением:
Скрипт R:
dy <- c(2,6)
a <- 6
b1 <- -2
curve(a + b1 / x, 0.5, 2.5, 100, ylab = ‘Y’, ylim = dy)
title(‘Гипербола’)
text(1.5,4.5,»y=6-2/x»)
b2 <- -1.5
curve(a + b2 / x, 0.5, 2.5, 100, ylab = ‘Y’, ylim = dy, add = TRUE)
text(1,4.5,»y=6-1.5/x»)
b3 <- -1
curve(a + b3 / x, 0.5, 2.5, 100, ylab = ‘Y’, ylim = dy, add = TRUE)
text(1,5.25,»y=6-1/x»)
Коэффициенты эластичности гипербол:
Скрипт R:
dy <- c(0,100)
b1 <- -2
curve(-b1 *100 / (a*x+b1), 0.4, 2, 100, col=’red’, lwd =2, ylim = dy)
title(‘Коэффициент эластичности’)
text(1.6,35,»y=6-2/x»)
b2 <- -1.5
curve(-b2 *100 / (a*x+b2), 0.4, 2, 100, col=’red’, lwd =2,
ylim = dy, add = TRUE)
text(1.1,35,»y=6-1.5/x»)
b3 <- -1
curve(-b3 *100 / (a*x+b3), 0.4, 2, 100, col=’red’, lwd =2,
ylim = dy, add = TRUE)
text(0.5,35,»y=6-1/x»)
Показательная функция доходов
Графики функций:
Скрипт R:
dy <- c(1,4)
a <- 1
b1 <- 2
curve(a * b1 ^ x, 0, 2, 100, ylab = ‘Y’, ylim = dy)
title(‘Показательная функция’)
text(1.5,1.1,»y=2^x»)
b2 <- 1.5
curve(a * b2 ^ x, 0, 2, 100, ylab = ‘Y’, ylim = dy, add = TRUE)
text(1.5,1.57,»y=1.5^x»)
b3 <- 1.2
curve(a * b3 ^ x, 0, 2, 100, ylab = ‘Y’, ylim = dy, add = TRUE)
text(1.5,2.4,»y=1.2^x»)
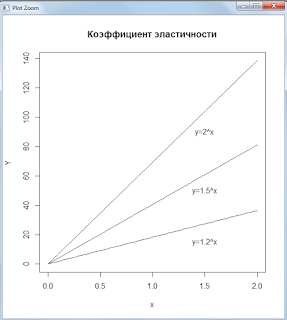
Коэффициенты эластичности показательной функции:
Скрипт R:
a <- 1
b1 <- 2
curve(100 * x * log(b1), 0, 2, 100, ylab = ‘Y’)
title(‘Коэффициент эластичности’)
text(1.5,90,»y=2^x»)
b2 <- 1.5
curve(100 * x * log(b2), 0, 2, 100, ylab = ‘Y’, add = TRUE)
text(1.5,50,»y=1.5^x»)
b3 <- 1.2
curve(100 * x * log(b3), 0, 2, 100, ylab = ‘Y’, add = TRUE)
text(1.5,15,»y=1.2^x»)
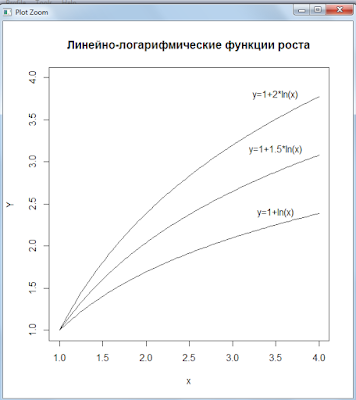
Линейная-логарифмическая функция
Графики функций:
Скрипт R:
dy <- c(1,4)
a <- 1
b1 <- 1
curve(a + b1 * log(x), 1, 4, 100, ylab = ‘Y’, ylim= dy)
title(‘Линейно-логарифмические функции роста’)
text(3.5,2.4,»y=1+ln(x)»)
b2 <- 1.5
curve(a + b2*log(x), 1, 4, 100, ylim= dy, ylab = ‘Y’, add=TRUE)
text(3.5,3.15,»y=1+1.5*ln(x)»)
b3 <- 2
curve(a + b3*log(x), 1, 4, 100, ylim= dy, ylab = ‘Y’, add=TRUE)
text(3.5,3.8,»y=1+2*ln(x)»)
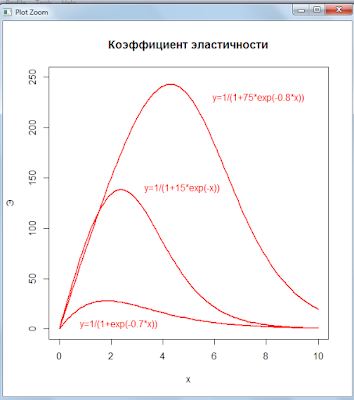
Коэффициенты эластичности линейно-логарифмической функции:
Скрипт R:
dy1 <- c(40,150)
curve(100 * b1 / (a+b1*log(x)), 1, 4, 100, col=’red’, lwd =2,
ylab = ‘Э’, ylim = dy1 )
title(‘Коэффициент эластичности’)
text(1.75,55,»y=1+ln(x)»,col=’red’)
b2 <- 1.5
curve(100 * b2 / (a+b2*log(x)), 1, 4, 100, col=’red’, lwd =2,
add= TRUE, ylim = dy1 )
text(3,55,»y=1+1.5*ln(x)»,col=’red’)
b3 <- 2
curve(100 * b3 / (a+b3*log(x)), 1, 4, 100, col=’red’, lwd =2,
add= TRUE, ylim = dy1 )
text(2.7,80,»y=1+2*ln(x)»,col=’red’)
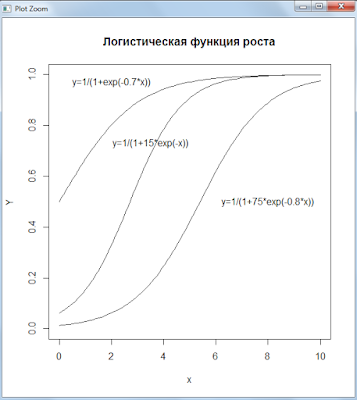
Логистическая функция роста
Графики функций:
Скрипт R:
c1 <- 0.7
curve(1 / (1 + b1 * exp(- c1 * x)), 0, 10, 100, ylab = ‘Y’,ylim= dy)
title(‘Логистическая функция роста’)
text(2,0.97,»y=1/(1+exp(-0.7*x))»)
b2 <- 15
c2 <- 1
curve(1 / (1 + b2 * exp(- c2 * x)), 0, 10, 100, ylim= dy, ylab = ‘Y’, add=TRUE)
text(3.5,0.73,»y=1/(1+15*exp(-x))»)
b3 <- 75
c3 <- 0.8
curve(1 / (1 + b3 * exp(- c3 * x)), 0, 10, 100, ylim= dy, ylab = ‘Y’, add=TRUE)
text(8,0.5,»y=1/(1+75*exp(-0.8*x))»)
Графики функций:
Скрипт R:
b1 <- 1
c1 <- 0.7
curve(100 * c1 * x / (exp(c1 * x) / b1 + 1), 0, 10, 100,
col=’red’, lwd =2, ylab = ‘Э’, ylim = dy1 )
title(‘Коэффициент эластичности’)
text(2.3,5,»y=1/(1+exp(-0.7*x))»,col=’red’)
b2 <- 15
c2 <- 1
curve(100 * c2 * x / (exp(c2 * x) / b2 + 1), 0, 10, 100,
col=’red’, lwd =2,
add= TRUE, ylim = dy1 )
text(4.75,140,»y=1/(1+15*exp(-x))»,col=’red’)
b3 <- 75
c3 <- 0.8
curve(100 * c3 * x / (exp(c3 * x) / b3 + 1), 0, 10, 100,
col=’red’, lwd =2,
add= TRUE, ylim = dy1 )
text(7.7,230,»y=1/(1+75*exp(-0.8*x))»,col=’red’)
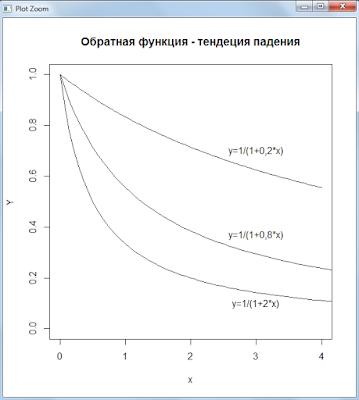
Обратная функция — тенденция падения
Графики функций:
Скрипт R:
dy <- c(0,1)
a <- 1
b1 <- 0.2
curve(1 / (a + b1 * x), 0, 4, 100, ylab = ‘Y’,ylim= dy)
title(‘Обратная функция — тенденция падения’)
text(3,0.7,»y=1/(1+0,2*x)»)
b2 <- 0.8
curve(1 / (a + b2 * x), 0, 7, 100, ylim= dy, ylab = ‘Y’, add=TRUE)
text(3,0.37,»y=1/(1+0,8*x)»)
b3 <- 2
curve(1 / (a + b3 * x), 0, 7, 100, ylim= dy, ylab = ‘Y’, add=TRUE)
text(3,0.1,»y=1/(1+2*x)»)
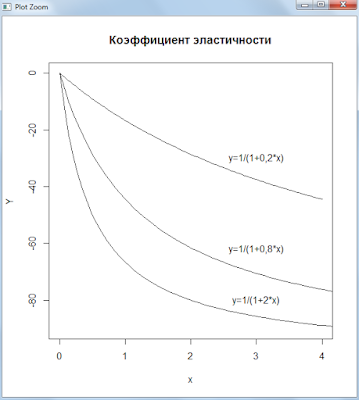
Графики функций:
Скрипт R:
dy <- c(-90,0)
a <- 1
b1 <- 0.2
curve(100 * (-b1 * x) / (a + b1 * x), 0, 4, 100, ylab = ‘Y’, ylim= dy)
title(‘Коэффициент эластичности’)
text(3,-30,»y=1/(1+0,2*x)»)
b2 <- 0.8
curve(100 * (-b2 * x) / (a + b2 * x), 0, 7, 100, ylab = ‘Y’, add=TRUE, ylim= dy)
text(3,-62,»y=1/(1+0,8*x)»)
b3 <- 2
curve(100 * (-b3 * x) / (a + b3 * x), 0, 7, 100, ylab = ‘Y’, add=TRUE, ylim= dy)
text(3,-80,»y=1/(1+2*x)»)
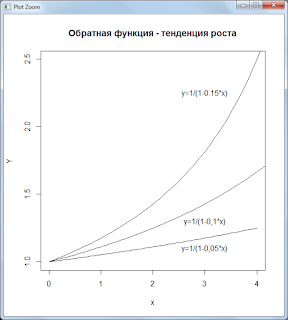
Обратная функция — тенденция роста
Графики функций:
Скрипт R:
dy <- c(1,2.5)
a <- 1
b1 <- -0.05
curve(1 / (a + b1 * x), 0, 4, 100, ylab = ‘Y’,ylim= dy)
title(‘Обратная функция — тенденция роста’)
text(3,1.1,»y=1/(1-0,05*x)»)
b2 <- -0.1
curve(1 / (a + b2 * x), 0, 7, 100, ylim= dy, ylab = ‘Y’, add=TRUE)
text(3,1.3,»y=1/(1-0,1*x)»)
b3 <- -0.15
curve(1 / (a + b3 * x), 0, 7, 100, ylim= dy, ylab = ‘Y’, add=TRUE)
text(3,2.25,»y=1/(1-0.15*x)»)
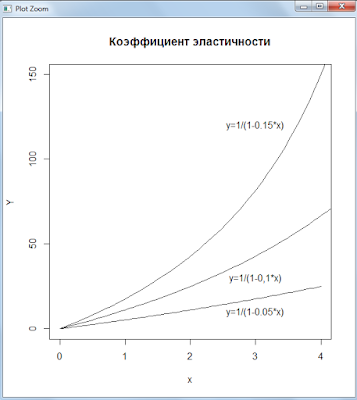
Графики коэффициента эластичности:
Скрипт R:
dy <- c(0,150)
a <- 1
b1 <- -0.05
curve(100 * (-b1 * x) / (a + b1 * x), 0, 4, 100, ylab = ‘Y’, ylim= dy)
title(‘Коэффициент эластичности’)
text(3,10,»y=1/(1-0.05*x)»)
b2 <- -0.1
curve(100 * (-b2 * x) / (a + b2 * x), 0, 7, 100, ylab = ‘Y’, ylim= dy, add=TRUE)
text(3,30,»y=1/(1-0,1*x)»)
b3 <- -0.15
curve(100 * (-b3 * x) / (a + b3 * x), 0, 7, 100, ylab = ‘Y’, ylim= dy, add=TRUE)
text(3,120,»y=1/(1-0.15*x)»)