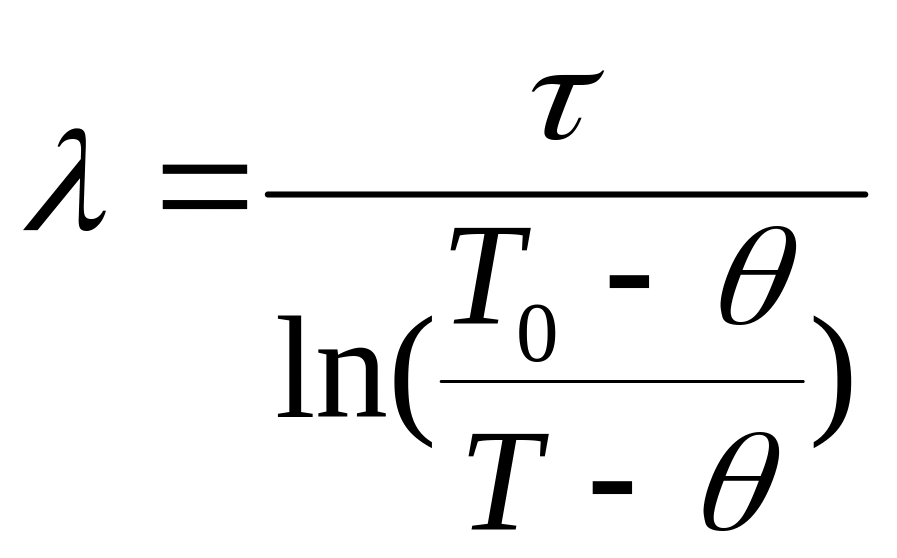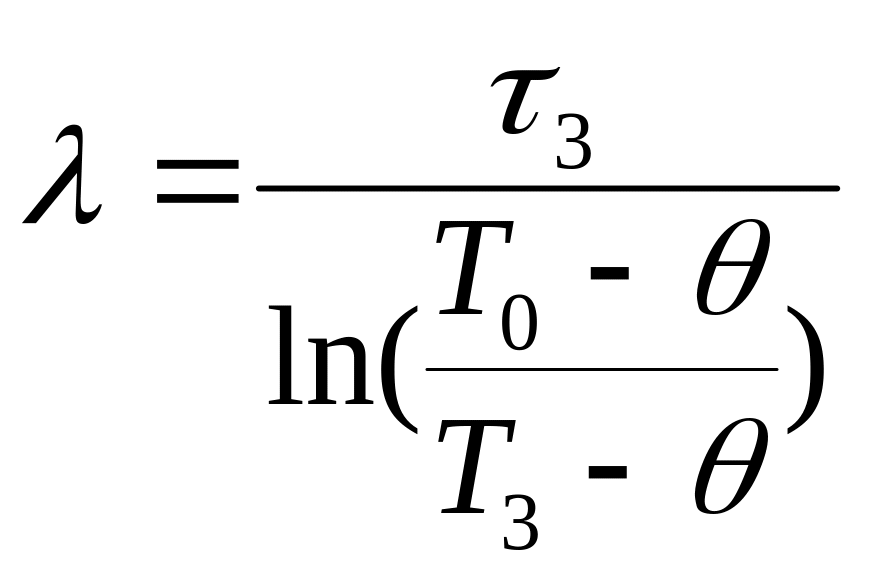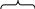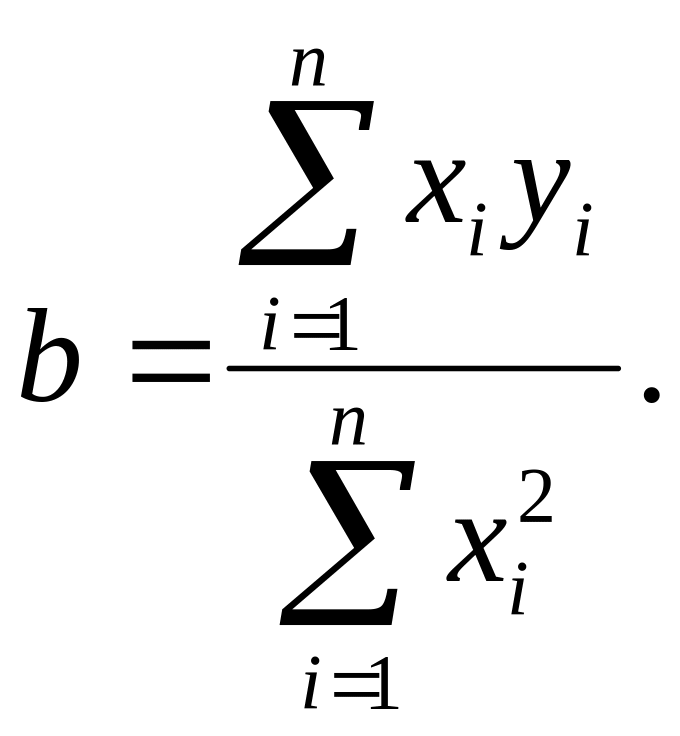Как найти коэффициент инерции

Коэффициент — инерция

Cтраница 1

Коэффициент инерции а характеризует инертность механической системы, а коэффициент жесткости с — упругие свойства системы.
 [1]

Коэффициенты инерции, определяемые по формулам ( 9), назовем эквивалентными моментами инерции основных звеньев планетарного ряда с безынерционным водилом.
 [2]

Коэффициент инерции А — величина постоянная; ею может быть, например, масса точки, момент инерции, приведенная масса системы двух точек.
 [3]

Коэффициент инерции т I является моментом инерции балансира относительно оси вращения.
 [4]

Коэффициент инерции массы 3 полного графа численно равен массовому моменту инерции У3 конструктивного водила передачи относительно оси вращения.
 [6]

Коэффициент инерции массы 3 представляет собой массовый момент инерции конструктивного водила цилиндрического дифференциала относительно оси вращения.
 [8]

Коэффициент инерции вращающихся частей 1 V У различных типов подвижного состава имеет разные величины: от 1 03 до 1 12 у различных вагонов, от 1 11 до 1 12 у тепловозов, от 1 15 до 1 30 у электровозов. Величину 1 у для всего состава определяют как средневзвешенное значение из коэффициентов инерции отдельных единиц подвижного состава.
 [9]

Коэффициентом инерции называется отношение суммы приведенного к валу двигателя момента инерции приводимого механизма и момента инерции ротора к моменту инерции ротора двигателя.
 [10]

Коэффициентом инерции называется отношение суммы приведенного к валу двигателя момента инерции приводимого механизма и момента инерции ротора ( якоря) двигателя к моменту инерции ротора ( якоря) двигателя.
 [11]

Коэффициентом инерции называется отношение суммы приведенного к валу двигателя момента инерции приводимого механизма и момента инерции ротора к моменту инерции ротора двигателя.
 [12]

Чему равен коэффициент инерции и коэффициент квазиупругости.
 [13]

Как вычисляют коэффициенты инерции системы и от каких параметров они зависят.
 [14]

Для поезда коэффициент инерции вращающихся частей определяют как средневзвешенную величину.
 [15]

Страницы:  

   1

   2

   3

Здесь Oij — коэффициенты инерции  [c.327]

Это уравнение выражает малые колебания системы. Разделив коэффициент жесткости с на коэффициент инерции гп, найдем квадрат частоты колебаний системы, и для получения ответа остается только извлечь квадратный корень.  [c.440]

Примем за обобщенную координату q угол поворота маятника. Определим параметры колебаний. Обобщенная скорость q = ш, коэффициент инерции а = У = 1,  [c.277]

Решение. Возмущающую силу считаем гармонической. Жесткость рессор с= mg/5 выражает обобщенный коэффициент жесткости. Обобщенный коэффициент инерции а = т-,  [c.280]

Разделив и помножив это равенство на коэффициент инерции а и приняв во внимание (248), выразим так статическое отклонение  [c.281]

Следовательно, коэффициент инерции а = т (см. с. 267).  [c.285]

Следовательно, обобщенный коэффициент инерции а = тР/3.  [c.287]

Дифференцируя это равенство по обобщенной координате, найдем восстанавливающую силу дифференцируя дважды, найдем и обобщенный коэффициент жесткости с = mgl, поделив который на коэффициент инерции, определим квадрат круговой частоты колебаний  [c.287]

Положительная постоянная а называется коэффициентом инерции. Обычно по размерности коэффициент инерции является или массой, или моментом инерции.  [c.393]

Величина периода определяется только свойствами колеблющейся системы, т. е. коэффициентом инерции а и жесткостью с. Независимость периода колебаний от амплитуды называется изохронностью колебаний. Собственные линейные колебания, если нет возмущающих сил, могут возникнуть только при начальных условиях, неравных нулю, т. е. когда в начальный момент система имеет не равные нулю начальную обобщенную координату <7о или начальную обобщенную скорость ро.  [c.397]

Постоянные величины Оц, Оха, 22 называются коэффициентами инерции системы. С точностью до членов третьего и более высокого порядка по отношению к д , д , Qi, д , получаем следующее выражение для кинетической энергии  [c.431]

Условия определенной положительности сведутся к условиям для коэффициентов жесткости, полностью аналогичным условиям для коэффициентов инерции.  [c.433]

Приведенные коэффициенты сопротивления удовлетворяют условиям, которые полностью аналогичны условиям для коэффициентов инерции.  [c.435]

Отбрасывая отрицательные значения частот, как не дающие новых решений и не имеющих физического значения, получаем две частоты. Меньшую из частот обозначают 1, большую — п. Частоты 1 и а являются частотами собственных колебаний системы. Они не зависят от начальных условий и полностью определяются значениями коэффициентов инерции и жесткости.  [c.436]

Так как квадратичные формы для кинетической и потенциальной энергий определенно положительны, то коэффициенты инерции и жесткости удовлетворяют условиям (59) и (61), т. е.  [c.437]

Сравнивая (4) и (5), видим, что эти уравнения полностью аналогичны. Только в уравнение для системы вместо координаты х входит обобщенная координата д, вместо массы — коэффициент инерции о, а вместо жесткости Со следует взять коэффициент жесткости с.  [c.416]

Постоянные величины <2ц, 12, а 2 называются коэффициентами инерции системы. Отбрасывая члены третьего и более высокого порядка по отношению к <7,, 92, получаем следующее выражение  [c.454]

Сравнивая ее с разложением кинетической энергии (57), получаем значения коэффициентов инерции  [c.470]

Если рассмотреть случай стационарных связей и сравнить выражение Т = То с выражениями кинетической энергии неизменяемой системы при поступательном движении, при движении твердого тела вокруг неподвижной точки и т. д., то становится ясным, что в одних случаях коэффициенты Про можно рассматривать как величины, аналогичные массе, в других — как величины, аналогичные моментам инерции, и т. д. Поэтому коэффициенты Про иногда называют коэффициентами инерции.  [c.130]

Коэффициенты этой положительно определенной квадратичной формы являются функциями координат точек системы qj и не зависят явно от времени. Они называются иногда коэффициентами инерции . Происхождение этого названия объясняется физическим смыслом этих коэффициентов в частных случаях, как было показано выше.  [c.228]

Механическая система состоит из двух одинаковых блоков, подвижного и неподвижного, массы т каждый, невесомой нерастял<имой нити, переброшенной через эти блоки, и горизонтальной пружины жесткости с. Считая массу каждого из блоков равномерно распределенной по ободу и пренебрегая массой пружины, опре-дсл1ггь коэффициенты инерции и жесткости системы, со-  [c.160]

Выражение в квадратных скобках есть обобщенный коэффициент инерции, а rriigl — обобщенный коэффициент жесткости. Частоту собственных колебаний системы можем получить непосредственно по формуле (257). Но можно составить дифференциальное уравнение (253)  [c.284]

Сравииаая еес разложением кинетической энергии (57), получаем коэффициенты инерции  [c.446]

---

Курс теоретической механики 1973 (1973) — [
c.440
]

Курс теоретической механики 1981 (1981) — [
c.267
]

Теоретическая механика (1986) — [
c.31
,
c.333
]

Прикладная механика твердого деформируемого тела Том 3 (1981) — [
c.84
]

Теплоэнергетика и теплотехника Общие вопросы Книга1 (2000) — [
c.158
]

Динамическая теория звука (1960) — [
c.28
,
c.62
]

Курс теоретической механики Том2 Изд2 (1979) — [
c.448
]

Проектирование и конструирование горных машин и комплексов (1982) — [
c.227
]

---

Обработка результатов

1. По имеющимся у
   Вас данным п.1, постройте график
   зависимости t(τ)
   для ртутного термометра (аналогично
   графику рис.1) и определите его коэффициент
   инерции λ, как время, в течение которого
   разность температур между термометром
   и средой уменьшается в е раз.

2. По тем же данным
   рассчитайте коэффициент инерции
   термометра по методу наименьших
   квадратов, изложенному в приложении.
   Рассчитайте средний квадрат ошибки
   определения λ.

3. Сравните результаты
   вычислений со значением λ, полученным
   по методике п.2 раздела «Выполнение
   работы». Совпадают ли они? Находится
   ли разность между ними в пределах
   вычисленной ошибки?

4. Составьте таблицу
   λ(V)
   и постройте график, пользуясь результатами
   п.3 раздела «Выполнение работы».

5. Определите значение
   коэффициента инерции ртутного термометра
   в воде по результатам, полученным в п.
   4 раздела «Выполнение работы».
   Сравните его значение со значением
   коэффициента инерции в воздухе. Объясните
   разницу. Определите, выполняется ли
   формула (3), для чего узнайте по справочным
   таблицам значение плотности воды и
   воздуха.

6. По графикам,
   полученным при выполнении п.п.5.1 — 5.7,
   определите значение λ для каждого опыта
   и постройте график λ(V)
   для резисторного датчика температуры.
   Укажите также значение коэффициента
   инерции датчика в воде. Объясните ход
   кривой λ(V)
   и различие в значениях коэффициента
   инерции датчика в воздухе и в воде.

Требования к отчету

Отчет
должен содержать:

1. Краткое изложение
   сведений из теории.

2. Описание процедуры
   выполнения работы и таблицы всех
   исходных данных — как полученных в
   работе, так и рассчитанных в процессе
   обработки. В качестве отчетного документа
   должен быть приложен лист миллиметровой
   бумаги с графиками, полученными при
   работе с двухкоординатным самописцем.
   Лист должен быть подписан лаборантом
   или преподавателем сразу же после
   выполнения работы.

3. Рабочие формулы
   для вычисления коэффициента инерции
   и среднего квадрата ошибки для всех
   случаев. Формулы должны быть написаны
   как в буквенном выражении, так и с
   применением конкретных величин,
   полученных в работе.

4. Вычисленные
   значения всех коэффициентов инерции
   и среднего квадрата ошибки.

5. Графическую
   зависимость λ(V)
   для ртутного и резисторного термометров.

6. Результаты
   сравнения зависимости λ(V)
   с теоретической зависимостью (формула
   3).

7. Анализ и обсуждение
   результатов.

Приложение Использование метода наименьших квадратов для расчета коэффициента тепловой инерции термометра

Для определения
величины коэффициента тепловой инерции
термометр, имеющий температуру T₀,
вносится в среду с постоянной температурой
θ. Фиксируется изменение температуры
термометра T
в различные моменты времени τ . Результатом
эксперимента является набор табличных
данных, представленный в табл. 1. Задачей
экспериментатора является определение
по этому набору данных при известных
значениях T₀
и θ коэффициента тепловой инерции
термометра λ.

Таблица 1

Результаты
измерений:

Время τ, с.	τ 1	τ 2	τ 3	……	τ n-1	τ n
Темпера- тура T, К	T1	T2	T3	……	Tn-1	Tn

В
том случае, если бы сделанные при выводе
уравнения (1) допущения выполнялись
точно, а результаты опыта не содержали
бы погрешностей, то для определения λ
можно было бы воспользоваться решением
уравнения (1) относительно λ, то есть:

подставив в качестве
значений τ и Т любые их значения из
таблицы (1). Так, например, если в качестве
τ взять из таблицы (1) момент времени τ₃,
то:

Подобный подход,
хотя и привлекает внимание своей
простотой, не является корректным, так
как далеко не оптимальным образом
учитывает весь накопленный в ходе
проведения эксперимента материал. Ведь
понятно, что в каждом измерении, в том
числе выполненным в момент времени τ₃,
имеются погрешности, для уменьшения
влияния которых на погрешность расчета
λ целесообразно учесть все имеющиеся
в табл.1 данные. На практике это обычно
достигается тем, что до выполнения
расчетов по имеющемуся в табл.1 набору
данных строится график (рис.2). В ходе
его построения, то есть при представлении
характера изменения разности Т-θ во
времени плавной линией происходит
отбраковка (контроль) результатов
измерений (например, на рис.1 не учитываются
результаты измерений для τ = τ₅),
уменьшается (сглаживается) влияние
погрешностей каждого измерения на общий
ход зависимости Т-θ от времени и т.д. И
только уже после такого контроля и
сглаживания, по графику, а не по данным
табл. 1, определяется значение входящей
в формулу (5) разности Т-θ.

T-θ

T^*—
θ

τ*

τ₇

τ₆

τ₅

τ₄

τ₃

τ₂

τ₁

τ

Рис.2 Графическая
форма представления результатов
измерений

(Т₀
— θ)/(Т^*
— θ) = 2.

Например,
это может быть значение, отличающееся
от начального отклонения (Т₀
— θ) в 2 раза.
Тогда, подставив соответствующий такому
изменению (Т
— θ) момент
времени τ* в соотношение (5), получим:

Этот второй из
рассмотренных подходов к обработке
данных наблюдений из табл. 1 хотя и
позволяет учесть весь имеющийся
экспериментальный материал, однако,
также не свободен от недостатков. Прежде
всего, это наличие субъективного фактора:
разные экспериментаторы по одному и
тому же набору данных могут по-разному
провести сглаживающую кривую. Кроме
того, точность определения λ в этом
случае будет зависеть от масштаба
графика, от того, в какой момент времени
с этого графика снимается значение (Т
— θ)
(уменьшенное в 2,5, в 3 или иное число раз
по сравнению с начальной разностью (Т₀
— θ) ) и т.д.
Наконец, этот подход требует значительных
затрат времени на обработку одного
цикла наблюдений из-за необходимости
нанесения вручную всех точек на график.

От всех этих
недостатков в значительной степени
свободен третий из рассматриваемых
здесь подходов к обработке данных
наблюдений. Он основан на использовании
метода наименьших квадратов. Рассмотрим
реализацию этого подхода.

Для
получения расчетных формул преобразуем
соотношение (5), введя следующие
обозначения:

Т

огда,
с учетом сделанных обозначений уравнение
(5) будет иметь следующий вид:

При
наличии n
пар табличных данных X_i
и Y_i
(i
= 1,2,…n)
оценка параметра b
по методу наименьших квадратов может
быть получена по формуле:

Поскольку искомым
параметром является не коэффициент b,
а параметр λ, то для его расчета с учетом
обозначений (6) получает вместо соотношения
(8) следующее уравнение:

Таким образом,
задача сводится к расчету λ по формуле
(9) с учетом обозначений (6). При ручном
расчете студенту предлагается построить
таблицу значений y,
b
и x
для всех значений времени τ_i,
в эту же таблицу внести строки, в которых
будет рассчитано значение x_i²
и произведения x_iy_i,
а затем по формуле (9) рассчитать значения
сумм, входящих в числитель и знаменатель
и, соответственно, значение коэффициента
тепловой инерции термометра λ. Примерный
вид такой таблицы, служащей основой для
расчета, показан в табл.2.

Табл. 2.

Время τ, с.	τ 1	……	τ n-1	τ n
Темпера- тура T,(по Кельвину!!!)	T1	……	Tn-1	Tn
	Y1	……	Yn-1	Yn
		……
	X12	……	Xn-12	Xn2
		……

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Что такое инерция

Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.

Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».

Определение момента инерции

Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.

По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.

Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.

Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.

Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:

Теорема Штейнера

От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.

Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Теорема Гюйгенса-Штейнера гласит:

Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.

Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:

Пример решения задачи на нахождение момента инерции

Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.

Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.

Решение:

Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:

Массу кольца можно представить в виде:

Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:

В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.

Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.

Решение:

Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:

Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.

Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.

Коэффициент инерции неподвижного тела в колебательном потоке Калькулятор

Search
Дом	Инженерное дело ↺
Инженерное дело	Гражданская ↺
Гражданская	Прибрежная и океаническая инженерия ↺
Прибрежная и океаническая инженерия	Расчет сил на структуры океана ↺
Расчет сил на структуры океана	Уравнение Морисона (MOJS) ↺

Коэффициент инерции неподвижного тела в колебательном потоке Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Добавлен массовый коэффициент: 4.5 —> Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

5.5 —> Конверсия не требуется

6 Уравнение Морисона (MOJS) Калькуляторы

Коэффициент инерции неподвижного тела в колебательном потоке формула

Коэффициент инерции = 1+Добавлен массовый коэффициент

C_m = 1+C_a

Что такое уравнение Морисона?

Уравнение Морисона представляет собой сумму двух составляющих силы: силы инерции в фазе с местным ускорением потока и силы сопротивления, пропорциональной квадрату (со знаком) мгновенной скорости потока. Сила инерции имеет функциональную форму, найденную в теории потенциального потока, в то время как сила сопротивления имеет форму, найденную для тела, помещенного в установившийся поток. В эвристическом подходе Морисона, О’Брайена, Джонсона и Шаафа эти две составляющие силы, инерция и сопротивление, просто складываются для описания действующей силы в колебательном потоке. Поперечная сила — перпендикулярная направлению потока из-за образования вихрей — должна рассматриваться отдельно.