In statistics, the Pearson correlation coefficient (PCC, pronounced ) ― also known as Pearson’s r, the Pearson product-moment correlation coefficient (PPMCC), the bivariate correlation,[1] or colloquially simply as the correlation coefficient[2] ― is a measure of linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of teenagers from a high school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation).
Examples of scatter diagrams with different values of correlation coefficient (ρ)
Several sets of (x, y) points, with the correlation coefficient of x and y for each set. The correlation reflects the strength and direction of a linear relationship (top row), but not the slope of that relationship (middle), nor many aspects of nonlinear relationships (bottom). N.B.: the figure in the center has a slope of 0 but in that case the correlation coefficient is undefined because the variance of Y is zero.
Naming and history[edit]
It was developed by Karl Pearson from a related idea introduced by Francis Galton in the 1880s, and for which the mathematical formula was derived and published by Auguste Bravais in 1844.[a][6][7][8][9] The naming of the coefficient is thus an example of Stigler’s Law.
Definition[edit]
Pearson’s correlation coefficient is the covariance of the two variables divided by the product of their standard deviations. The form of the definition involves a «product moment», that is, the mean (the first moment about the origin) of the product of the mean-adjusted random variables; hence the modifier product-moment in the name.
For a population[edit]
Pearson’s correlation coefficient, when applied to a population, is commonly represented by the Greek letter ρ (rho) and may be referred to as the population correlation coefficient or the population Pearson correlation coefficient. Given a pair of random variables 
where
The formula for 
the formula for 
where
The formula for 
the formula for 
Pearson’s correlation coefficient does not exist when either 

For a sample[edit]
Pearson’s correlation coefficient, when applied to a sample, is commonly represented by 




where
Rearranging gives us this formula for 
where 
This formula suggests a convenient single-pass algorithm for calculating sample correlations, though depending on the numbers involved, it can sometimes be numerically unstable.
Rearranging again gives us this[10] formula for 
where 
An equivalent expression gives the formula for 
where
Alternative formulae for 

where
Practical issues[edit]
Under heavy noise conditions, extracting the correlation coefficient between two sets of stochastic variables is nontrivial, in particular where Canonical Correlation Analysis reports degraded correlation values due to the heavy noise contributions. A generalization of the approach is given elsewhere.[12]
In case of missing data, Garren derived the maximum likelihood estimator.[13]
Some distributions (e.g., stable distributions other than a normal distribution) do not have a defined variance.
Mathematical properties[edit]
The values of both the sample and population Pearson correlation coefficients are on or between −1 and 1. Correlations equal to +1 or −1 correspond to data points lying exactly on a line (in the case of the sample correlation), or to a bivariate distribution entirely supported on a line (in the case of the population correlation). The Pearson correlation coefficient is symmetric: corr(X,Y) = corr(Y,X).
A key mathematical property of the Pearson correlation coefficient is that it is invariant under separate changes in location and scale in the two variables. That is, we may transform X to a + bX and transform Y to c + dY, where a, b, c, and d are constants with b, d > 0, without changing the correlation coefficient. (This holds for both the population and sample Pearson correlation coefficients.) More general linear transformations do change the correlation: see § Decorrelation of n random variables for an application of this.
Interpretation[edit]
The correlation coefficient ranges from −1 to 1. An absolute value of exactly 1 implies that a linear equation describes the relationship between X and Y perfectly, with all data points lying on a line. The correlation sign is determined by the regression slope: a value of +1 implies that all data points lie on a line for which Y increases as X increases, and vice versa for −1.[14] A value of 0 implies that there is no linear dependency between the variables.[15]
More generally, (Xi − X)(Yi − Y) is positive if and only if Xi and Yi lie on the same side of their respective means. Thus the correlation coefficient is positive if Xi and Yi tend to be simultaneously greater than, or simultaneously less than, their respective means. The correlation coefficient is negative (anti-correlation) if Xi and Yi tend to lie on opposite sides of their respective means. Moreover, the stronger either tendency is, the larger is the absolute value of the correlation coefficient.
Rodgers and Nicewander[16] cataloged thirteen ways of interpreting correlation or simple functions of it:
- Function of raw scores and means
- Standardized covariance
- Standardized slope of the regression line
- Geometric mean of the two regression slopes
- Square root of the ratio of two variances
- Mean cross-product of standardized variables
- Function of the angle between two standardized regression lines
- Function of the angle between two variable vectors
- Rescaled variance of the difference between standardized scores
- Estimated from the balloon rule
- Related to the bivariate ellipses of isoconcentration
- Function of test statistics from designed experiments
- Ratio of two means
Geometric interpretation[edit]
Regression lines for y = gX(x) [red] and x = gY(y) [blue]
For uncentered data, there is a relation between the correlation coefficient and the angle φ between the two regression lines, y = gX(x) and x = gY(y), obtained by regressing y on x and x on y respectively. (Here, φ is measured counterclockwise within the first quadrant formed around the lines’ intersection point if r > 0, or counterclockwise from the fourth to the second quadrant if r < 0.) One can show[17] that if the standard deviations are equal, then r = sec φ − tan φ, where sec and tan are trigonometric functions.
For centered data (i.e., data which have been shifted by the sample means of their respective variables so as to have an average of zero for each variable), the correlation coefficient can also be viewed as the cosine of the angle θ between the two observed vectors in N-dimensional space (for N observations of each variable)[18]
Both the uncentered (non-Pearson-compliant) and centered correlation coefficients can be determined for a dataset. As an example, suppose five countries are found to have gross national products of 1, 2, 3, 5, and 8 billion dollars, respectively. Suppose these same five countries (in the same order) are found to have 11%, 12%, 13%, 15%, and 18% poverty. Then let x and y be ordered 5-element vectors containing the above data: x = (1, 2, 3, 5, 
By the usual procedure for finding the angle θ between two vectors (see dot product), the uncentered correlation coefficient is
This uncentered correlation coefficient is identical with the cosine similarity.
The above data were deliberately chosen to be perfectly correlated: y = 0.10 + 0.01 x. The Pearson correlation coefficient must therefore be exactly one. Centering the data (shifting x by ℰ(x) = 3.8 and y by ℰ(y) = 0.138) yields x = (−2.8, −1.8, −0.8, 1.2, 4.2) and y = (−0.028, −0.018, −0.008, 0.012, 0.042), from which
as expected.
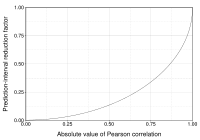
Interpretation of the size of a correlation[edit]
This figure gives a sense of how the usefulness of a Pearson correlation for predicting values varies with its magnitude. Given jointly normal X, Y with correlation ρ, 
Several authors have offered guidelines for the interpretation of a correlation coefficient.[19][20] However, all such criteria are in some ways arbitrary.[20] The interpretation of a correlation coefficient depends on the context and purposes. A correlation of 0.8 may be very low if one is verifying a physical law using high-quality instruments, but may be regarded as very high in the social sciences, where there may be a greater contribution from complicating factors.
Inference[edit]
Statistical inference based on Pearson’s correlation coefficient often focuses on one of the following two aims:
- One aim is to test the null hypothesis that the true correlation coefficient ρ is equal to 0, based on the value of the sample correlation coefficient r.
- The other aim is to derive a confidence interval that, on repeated sampling, has a given probability of containing ρ.
We discuss methods of achieving one or both of these aims below.
Using a permutation test[edit]
Permutation tests provide a direct approach to performing hypothesis tests and constructing confidence intervals. A permutation test for Pearson’s correlation coefficient involves the following two steps:
- Using the original paired data (xi, yi), randomly redefine the pairs to create a new data set (xi, yi′), where the i′ are a permutation of the set {1,…,n}. The permutation i′ is selected randomly, with equal probabilities placed on all n! possible permutations. This is equivalent to drawing the i′ randomly without replacement from the set {1, …, n}. In bootstrapping, a closely related approach, the i and the i′ are equal and drawn with replacement from {1, …, n};
- Construct a correlation coefficient r from the randomized data.
To perform the permutation test, repeat steps (1) and (2) a large number of times. The p-value for the permutation test is the proportion of the r values generated in step (2) that are larger than the Pearson correlation coefficient that was calculated from the original data. Here «larger» can mean either that the value is larger in magnitude, or larger in signed value, depending on whether a two-sided or one-sided test is desired.
Using a bootstrap[edit]
The bootstrap can be used to construct confidence intervals for Pearson’s correlation coefficient. In the «non-parametric» bootstrap, n pairs (xi, yi) are resampled «with replacement» from the observed set of n pairs, and the correlation coefficient r is calculated based on the resampled data. This process is repeated a large number of times, and the empirical distribution of the resampled r values are used to approximate the sampling distribution of the statistic. A 95% confidence interval for ρ can be defined as the interval spanning from the 2.5th to the 97.5th percentile of the resampled r values.
Standard error[edit]
If 

where 

Testing using Student’s t-distribution[edit]
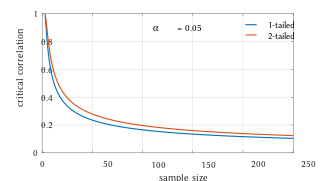
Critical values of Pearson’s correlation coefficient that must be exceeded to be considered significantly nonzero at the 0.05 level.
For pairs from an uncorrelated bivariate normal distribution, the sampling distribution of the studentized Pearson’s correlation coefficient follows Student’s t-distribution with degrees of freedom n − 2. Specifically, if the underlying variables have a bivariate normal distribution, the variable
has a student’s t-distribution in the null case (zero correlation).[23] This holds approximately in case of non-normal observed values if sample sizes are large enough.[24] For determining the critical values for r the inverse function is needed:
Alternatively, large sample, asymptotic approaches can be used.
Another early paper[25] provides graphs and tables for general values of ρ, for small sample sizes, and discusses computational approaches.
In the case where the underlying variables are not normal, the sampling distribution of Pearson’s correlation coefficient follows a Student’s t-distribution, but the degrees of freedom are reduced.[26]
Using the exact distribution[edit]
For data that follow a bivariate normal distribution, the exact density function f(r) for the sample correlation coefficient r of a normal bivariate is[27][28][29]
where 

In the special case when 
where 
Using the exact confidence distribution[edit]
Confidence intervals and tests can be calculated from a confidence distribution. An exact confidence density for ρ is[30]
where 

Using the Fisher transformation[edit]
In practice, confidence intervals and hypothesis tests relating to ρ are usually carried out using the Fisher transformation, 
F(r) approximately follows a normal distribution with
and standard error
where n is the sample size. The approximation error is lowest for a large sample size 


Using the approximation, a z-score is
under the null hypothesis that 

To obtain a confidence interval for ρ, we first compute a confidence interval for F(
The inverse Fisher transformation brings the interval back to the correlation scale.
For example, suppose we observe r = 0.7 with a sample size of n=50, and we wish to obtain a 95% confidence interval for ρ. The transformed value is arctanh(r) = 0.8673, so the confidence interval on the transformed scale is 0.8673 ± 1.96/√47, or (0.5814, 1.1532). Converting back to the correlation scale yields (0.5237, 0.8188).
In least squares regression analysis[edit]
The square of the sample correlation coefficient is typically denoted r2 and is a special case of the coefficient of determination. In this case, it estimates the fraction of the variance in Y that is explained by X in a simple linear regression. So if we have the observed dataset 

where the 
The two summands above are the fraction of variance in Y that is explained by X (right) and that is unexplained by X (left).
Next, we apply a property of least square regression models, that the sample covariance between 

Thus
where 
In the derivation above, the fact that
can be proved by noticing that the partial derivatives of the residual sum of squares (RSS) over β0 and β1 are equal to 0 in the least squares model, where
.
In the end, the equation can be written as
where
The symbol 

Sensitivity to the data distribution[edit]
Existence[edit]
The population Pearson correlation coefficient is defined in terms of moments, and therefore exists for any bivariate probability distribution for which the population covariance is defined and the marginal population variances are defined and are non-zero. Some probability distributions, such as the Cauchy distribution, have undefined variance and hence ρ is not defined if X or Y follows such a distribution. In some practical applications, such as those involving data suspected to follow a heavy-tailed distribution, this is an important consideration. However, the existence of the correlation coefficient is usually not a concern; for instance, if the range of the distribution is bounded, ρ is always defined.
Sample size[edit]
- If the sample size is moderate or large and the population is normal, then, in the case of the bivariate normal distribution, the sample correlation coefficient is the maximum likelihood estimate of the population correlation coefficient, and is asymptotically unbiased and efficient, which roughly means that it is impossible to construct a more accurate estimate than the sample correlation coefficient.
- If the sample size is large and the population is not normal, then the sample correlation coefficient remains approximately unbiased, but may not be efficient.
- If the sample size is large, then the sample correlation coefficient is a consistent estimator of the population correlation coefficient as long as the sample means, variances, and covariance are consistent (which is guaranteed when the law of large numbers can be applied).
- If the sample size is small, then the sample correlation coefficient r is not an unbiased estimate of ρ.[10] The adjusted correlation coefficient must be used instead: see elsewhere in this article for the definition.
- Correlations can be different for imbalanced dichotomous data when there is variance error in sample.[31]
Robustness[edit]
Like many commonly used statistics, the sample statistic r is not robust,[32] so its value can be misleading if outliers are present.[33][34] Specifically, the PMCC is neither distributionally robust,[citation needed] nor outlier resistant[32] (see Robust statistics § Definition). Inspection of the scatterplot between X and Y will typically reveal a situation where lack of robustness might be an issue, and in such cases it may be advisable to use a robust measure of association. Note however that while most robust estimators of association measure statistical dependence in some way, they are generally not interpretable on the same scale as the Pearson correlation coefficient.
Statistical inference for Pearson’s correlation coefficient is sensitive to the data distribution. Exact tests, and asymptotic tests based on the Fisher transformation can be applied if the data are approximately normally distributed, but may be misleading otherwise. In some situations, the bootstrap can be applied to construct confidence intervals, and permutation tests can be applied to carry out hypothesis tests. These non-parametric approaches may give more meaningful results in some situations where bivariate normality does not hold. However the standard versions of these approaches rely on exchangeability of the data, meaning that there is no ordering or grouping of the data pairs being analyzed that might affect the behavior of the correlation estimate.
A stratified analysis is one way to either accommodate a lack of bivariate normality, or to isolate the correlation resulting from one factor while controlling for another. If W represents cluster membership or another factor that it is desirable to control, we can stratify the data based on the value of W, then calculate a correlation coefficient within each stratum. The stratum-level estimates can then be combined to estimate the overall correlation while controlling for W.[35]
Variants[edit]
Variations of the correlation coefficient can be calculated for different purposes. Here are some examples.
Adjusted correlation coefficient[edit]
The sample correlation coefficient r is not an unbiased estimate of ρ. For data that follows a bivariate normal distribution, the expectation E[r] for the sample correlation coefficient r of a normal bivariate is[36]
therefore r is a biased estimator of
The unique minimum variance unbiased estimator radj is given by[37]
-
(1)
where:
An approximately unbiased estimator radj can be obtained[citation needed] by truncating E[r] and solving this truncated equation:
-
(2)
An approximate solution[citation needed] to equation (2) is
-
(3)
where in (3)
are defined as above,
- radj is a suboptimal estimator,[citation needed][clarification needed]
- radj can also be obtained by maximizing log(f(r)),
- radj has minimum variance for large values of n,
- radj has a bias of order 1⁄(n − 1).
Another proposed[10] adjusted correlation coefficient is[citation needed]
radj ≈ r for large values of n.
Weighted correlation coefficient[edit]
Suppose observations to be correlated have differing degrees of importance that can be expressed with a weight vector w. To calculate the correlation between vectors x and y with the weight vector w (all of length n),[38][39]
- Weighted mean:
- Weighted covariance
- Weighted correlation
Reflective correlation coefficient[edit]
The reflective correlation is a variant of Pearson’s correlation in which the data are not centered around their mean values.[citation needed] The population reflective correlation is
The reflective correlation is symmetric, but it is not invariant under translation:
The sample reflective correlation is equivalent to cosine similarity:
The weighted version of the sample reflective correlation is
Scaled correlation coefficient[edit]
Scaled correlation is a variant of Pearson’s correlation in which the range of the data is restricted intentionally and in a controlled manner to reveal correlations between fast components in time series.[40] Scaled correlation is defined as average correlation across short segments of data.
Let 


The scaled correlation across the entire signals 
where 

By choosing the parameter 
Pearson’s distance[edit]
A distance metric for two variables X and Y known as Pearson’s distance can be defined from their correlation coefficient as[41]
Considering that the Pearson correlation coefficient falls between [−1, +1], the Pearson distance lies in [0, 2]. The Pearson distance has been used in cluster analysis and data detection for communications and storage with unknown gain and offset.[42]
The Pearson «distance» defined this way assigns distance greater than 1 to negative correlations. In reality, both strong positive correlation and negative correlations are meaningful, so care must be taken when Pearson «distance» is used for nearest neighbor algorithm as such algorithm will only include neighbors with positive correlation and exclude neighbors with negative correlation. Alternatively, an absolute valued distance, 
Circular correlation coefficient[edit]
For variables X = {x1,…,xn} and Y = {y1,…,yn} that are defined on the unit circle [0, 2π), it is possible to define a circular analog of Pearson’s coefficient.[43] This is done by transforming data points in X and Y with a sine function such that the correlation coefficient is given as:
where 

Partial correlation[edit]
If a population or data-set is characterized by more than two variables, a partial correlation coefficient measures the strength of dependence between a pair of variables that is not accounted for by the way in which they both change in response to variations in a selected subset of the other variables.
Decorrelation of n random variables[edit]
It is always possible to remove the correlations between all pairs of an arbitrary number of random variables by using a data transformation, even if the relationship between the variables is nonlinear. A presentation of this result for population distributions is given by Cox & Hinkley.[44]
A corresponding result exists for reducing the sample correlations to zero. Suppose a vector of n random variables is observed m times. Let X be a matrix where 

where an exponent of −+1⁄2 represents the matrix square root of the inverse of a matrix. The correlation matrix of T will be the identity matrix. If a new data observation x is a row vector of n elements, then the same transform can be applied to x to get the transformed vectors d and t:
This decorrelation is related to principal components analysis for multivariate data.
Software implementations[edit]
- R’s statistics base-package implements the correlation coefficient with
cor(x, y), or (with the P value also) withcor.test(x, y). - The SciPy Python library via
pearsonr(x, y). - The Pandas Python library implements Pearson correlation coefficient calculation as the default option for the method
pandas.DataFrame.corr - Wolfram Mathematica via the
Correlationfunction, or (with the P value) withCorrelationTest. - The Boost C++ library via the
correlation_coefficientfunction. - Excel has an in-built
correl(array1, array2)function for calculationg the pearson’s correlation coefficient.
See also[edit]
- Anscombe’s quartet
- Association (statistics)
- Coefficient of colligation
- Yule’s Q
- Yule’s Y
- Concordance correlation coefficient
- Correlation and dependence
- Correlation ratio
- Disattenuation
- Distance correlation
- Maximal information coefficient
- Multiple correlation
- Normally distributed and uncorrelated does not imply independent
- Odds ratio
- Partial correlation
- Polychoric correlation
- Quadrant count ratio
- RV coefficient
- Spearman’s rank correlation coefficient
Footnotes[edit]
- ^ As early as 1877, Galton was using the term «reversion» and the symbol «r» for what would become «regression».[3][4][5]
References[edit]
- ^ «SPSS Tutorials: Pearson Correlation».
- ^ «Correlation Coefficient: Simple Definition, Formula, Easy Steps». Statistics How To.
- ^ Galton, F. (5–19 April 1877). «Typical laws of heredity». Nature. 15 (388, 389, 390): 492–495, 512–514, 532–533. Bibcode:1877Natur..15..492.. doi:10.1038/015492a0. S2CID 4136393. In the «Appendix» on page 532, Galton uses the term «reversion» and the symbol r.
- ^ Galton, F. (24 September 1885). «The British Association: Section II, Anthropology: Opening address by Francis Galton, F.R.S., etc., President of the Anthropological Institute, President of the Section». Nature. 32 (830): 507–510.
- ^ Galton, F. (1886). «Regression towards mediocrity in hereditary stature». Journal of the Anthropological Institute of Great Britain and Ireland. 15: 246–263. doi:10.2307/2841583. JSTOR 2841583.
- ^ Pearson, Karl (20 June 1895). «Notes on regression and inheritance in the case of two parents». Proceedings of the Royal Society of London. 58: 240–242. Bibcode:1895RSPS…58..240P.
- ^ Stigler, Stephen M. (1989). «Francis Galton’s account of the invention of correlation». Statistical Science. 4 (2): 73–79. doi:10.1214/ss/1177012580. JSTOR 2245329.
- ^ «Analyse mathematique sur les probabilités des erreurs de situation d’un point». Mem. Acad. Roy. Sci. Inst. France. Sci. Math, et Phys. (in French). 9: 255–332. 1844 – via Google Books.
- ^ Wright, S. (1921). «Correlation and causation». Journal of Agricultural Research. 20 (7): 557–585.
- ^ a b c d e Real Statistics Using Excel: Correlation: Basic Concepts, retrieved 22 February 2015
- ^ Weisstein, Eric W. «Statistical Correlation». mathworld.wolfram.com. Retrieved 22 August 2020.
- ^ Moriya, N. (2008). «Noise-related multivariate optimal joint-analysis in longitudinal stochastic processes». In Yang, Fengshan (ed.). Progress in Applied Mathematical Modeling. Nova Science Publishers, Inc. pp. 223–260. ISBN 978-1-60021-976-4.
- ^ Garren, Steven T. (15 June 1998). «Maximum likelihood estimation of the correlation coefficient in a bivariate normal model, with missing data». Statistics & Probability Letters. 38 (3): 281–288. doi:10.1016/S0167-7152(98)00035-2.
- ^ «2.6 — (Pearson) Correlation Coefficient r». STAT 462. Retrieved 10 July 2021.
- ^ «Introductory Business Statistics: The Correlation Coefficient r». opentextbc.ca. Retrieved 21 August 2020.
- ^ Rodgers; Nicewander (1988). «Thirteen ways to look at the correlation coefficient» (PDF). The American Statistician. 42 (1): 59–66. doi:10.2307/2685263. JSTOR 2685263.
- ^ Schmid, John Jr. (December 1947). «The relationship between the coefficient of correlation and the angle included between regression lines». The Journal of Educational Research. 41 (4): 311–313. doi:10.1080/00220671.1947.10881608. JSTOR 27528906.
- ^ Rummel, R.J. (1976). «Understanding Correlation». ch. 5 (as illustrated for a special case in the next paragraph).
- ^ Buda, Andrzej; Jarynowski, Andrzej (December 2010). Life Time of Correlations and its Applications. Wydawnictwo Niezależne. pp. 5–21. ISBN 9788391527290.
- ^ a b Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences (2nd ed.).
- ^ Bowley, A. L. (1928). «The Standard Deviation of the Correlation Coefficient». Journal of the American Statistical Association. 23 (161): 31–34. doi:10.2307/2277400. ISSN 0162-1459. JSTOR 2277400.
- ^ «Derivation of the standard error for Pearson’s correlation coefficient». Cross Validated. Retrieved 30 July 2021.
- ^ Rahman, N. A. (1968) A Course in Theoretical Statistics, Charles Griffin and Company, 1968
- ^ Kendall, M. G., Stuart, A. (1973) The Advanced Theory of Statistics, Volume 2: Inference and Relationship, Griffin. ISBN 0-85264-215-6 (Section 31.19)
- ^ Soper, H.E.; Young, A.W.; Cave, B.M.; Lee, A.; Pearson, K. (1917). «On the distribution of the correlation coefficient in small samples. Appendix II to the papers of «Student» and R.A. Fisher. A co-operative study». Biometrika. 11 (4): 328–413. doi:10.1093/biomet/11.4.328.
- ^ Davey, Catherine E.; Grayden, David B.; Egan, Gary F.; Johnston, Leigh A. (January 2013). «Filtering induces correlation in fMRI resting state data». NeuroImage. 64: 728–740. doi:10.1016/j.neuroimage.2012.08.022. hdl:11343/44035. PMID 22939874. S2CID 207184701.
- ^ Hotelling, Harold (1953). «New Light on the Correlation Coefficient and its Transforms». Journal of the Royal Statistical Society. Series B (Methodological). 15 (2): 193–232. doi:10.1111/j.2517-6161.1953.tb00135.x. JSTOR 2983768.
- ^ Kenney, J.F.; Keeping, E.S. (1951). Mathematics of Statistics. Vol. Part 2 (2nd ed.). Princeton, NJ: Van Nostrand.
- ^ Weisstein, Eric W. «Correlation Coefficient—Bivariate Normal Distribution». mathworld.wolfram.com.
- ^ Taraldsen, Gunnar (2020). «Confidence in Correlation». doi:10.13140/RG.2.2.23673.49769.
- ^ Lai, Chun Sing; Tao, Yingshan; Xu, Fangyuan; Ng, Wing W.Y.; Jia, Youwei; Yuan, Haoliang; Huang, Chao; Lai, Loi Lei; Xu, Zhao; Locatelli, Giorgio (January 2019). «A robust correlation analysis framework for imbalanced and dichotomous data with uncertainty» (PDF). Information Sciences. 470: 58–77. doi:10.1016/j.ins.2018.08.017. S2CID 52878443.
- ^ a b Wilcox, Rand R. (2005). Introduction to robust estimation and hypothesis testing. Academic Press.
- ^ Devlin, Susan J.; Gnanadesikan, R.; Kettenring J.R. (1975). «Robust estimation and outlier detection with correlation coefficients». Biometrika. 62 (3): 531–545. doi:10.1093/biomet/62.3.531. JSTOR 2335508.
- ^ Huber, Peter. J. (2004). Robust Statistics. Wiley.[page needed]
- ^ Katz., Mitchell H. (2006) Multivariable Analysis – A Practical Guide for Clinicians. 2nd Edition. Cambridge University Press. ISBN 978-0-521-54985-1. ISBN 0-521-54985-X
- ^ Hotelling, H. (1953). «New Light on the Correlation Coefficient and its Transforms». Journal of the Royal Statistical Society. Series B (Methodological). 15 (2): 193–232. doi:10.1111/j.2517-6161.1953.tb00135.x. JSTOR 2983768.
- ^ Olkin, Ingram; Pratt,John W. (March 1958). «Unbiased Estimation of Certain Correlation Coefficients». The Annals of Mathematical Statistics. 29 (1): 201–211. doi:10.1214/aoms/1177706717. JSTOR 2237306..
- ^ «Re: Compute a weighted correlation». sci.tech-archive.net.
- ^ «Weighted Correlation Matrix – File Exchange – MATLAB Central».
- ^ Nikolić, D; Muresan, RC; Feng, W; Singer, W (2012). «Scaled correlation analysis: a better way to compute a cross-correlogram» (PDF). European Journal of Neuroscience. 35 (5): 1–21. doi:10.1111/j.1460-9568.2011.07987.x. PMID 22324876. S2CID 4694570.
- ^ Fulekar (Ed.), M.H. (2009) Bioinformatics: Applications in Life and Environmental Sciences, Springer (pp. 110) ISBN 1-4020-8879-5
- ^ Immink, K. Schouhamer; Weber, J. (October 2010). «Minimum Pearson distance detection for multilevel channels with gain and / or offset mismatch». IEEE Transactions on Information Theory. 60 (10): 5966–5974. CiteSeerX 10.1.1.642.9971. doi:10.1109/tit.2014.2342744. S2CID 1027502. Retrieved 11 February 2018.
- ^ Jammalamadaka, S. Rao; SenGupta, A. (2001). Topics in circular statistics. New Jersey: World Scientific. p. 176. ISBN 978-981-02-3778-3. Retrieved 21 September 2016.
- ^ Cox, D.R.; Hinkley, D.V. (1974). Theoretical Statistics. Chapman & Hall. Appendix 3. ISBN 0-412-12420-3.
External links[edit]
- «cocor». comparingcorrelations.org. – A free web interface and R package for the statistical comparison of two dependent or independent correlations with overlapping or non-overlapping variables.
- «Correlation». nagysandor.eu. – an interactive Flash simulation on the correlation of two normally distributed variables.
- «Correlation coefficient calculator». hackmath.net. Linear regression. –
- «Critical values for Pearson’s correlation coefficient» (PDF). frank.mtsu.edu/~dkfuller. – large table.
- «Guess the Correlation». – A game where players guess how correlated two variables in a scatter plot are, in order to gain a better understanding of the concept of correlation.
Коэффициент корреляции Пирсона (также известный как «коэффициент корреляции продукта и момента») является мерой линейной связи между двумя переменными X и Y. Он имеет значение от -1 до 1, где:
- -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными
- 0 указывает на отсутствие линейной корреляции между двумя переменными
- 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.
Формула для нахождения коэффициента корреляции Пирсона
Формула для нахождения коэффициента корреляции Пирсона, обозначаемого как r , для выборки данных ( из Википедии ):
Скорее всего, вам никогда не придется вычислять эту формулу вручную, так как вы можете использовать программное обеспечение, чтобы сделать это за вас, но полезно иметь представление о том, что именно делает эта формула, на примере.
Предположим, у нас есть следующий набор данных:
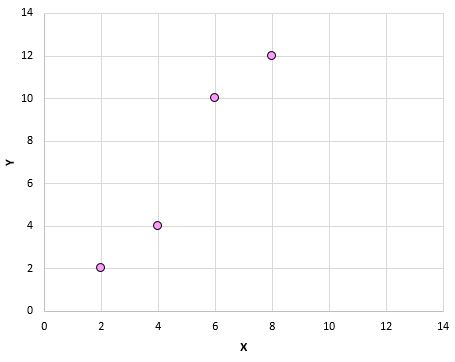
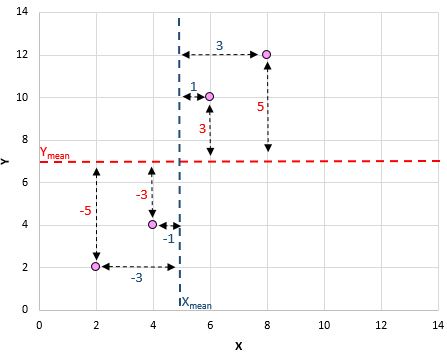
Если мы нанесем эти пары (X, Y) на диаграмму рассеяния, это будет выглядеть так:
Просто взглянув на эту диаграмму рассеяния, мы можем сказать, что существует положительная связь между переменными X и Y: когда X увеличивается, Y также имеет тенденцию к увеличению. Но чтобы точно определить, насколько положительно связаны эти две переменные, нам нужно найти коэффициент корреляции Пирсона.
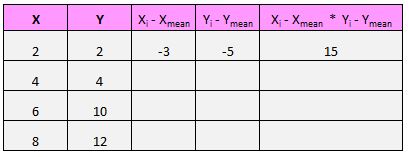
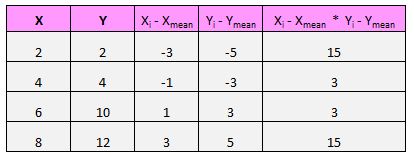
Давайте сосредоточимся только на числителе формулы:
Для каждой пары (X, Y) в нашем наборе данных нам нужно найти разницу между значением x и средним значением x, разницей между значением y и средним значением y, а затем умножить эти два числа вместе.
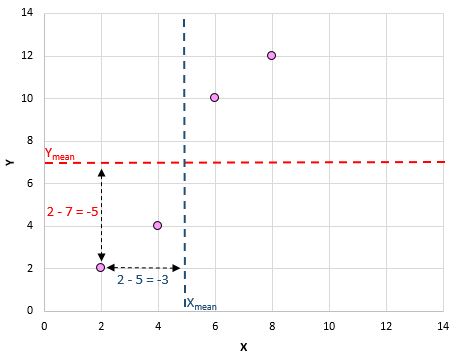
Например, наша первая пара (X, Y) — это (2, 2). Среднее значение x в этом наборе данных равно 5, а среднее значение y в этом наборе данных равно 7. Таким образом, разница между значением x в этой паре и средним значением x составляет 2 – 5 = -3. Разница между значением y в этой паре и средним значением y составляет 2 – 7 = -5. Затем, когда мы перемножаем эти два числа вместе, мы получаем -3 * -5 = 15.
Вот визуальный взгляд на то, что мы только что сделали:
Далее нам просто нужно сделать это для каждой отдельной пары:
Последний шаг для получения числителя формулы — просто сложить все эти значения:
15 + 3 + 3 + 15 = 36
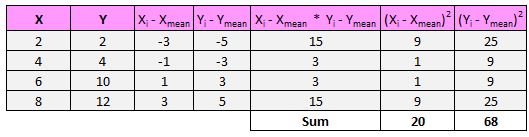
Затем знаменатель формулы говорит нам найти сумму всех квадратов разностей для x и y, затем умножить эти два числа вместе, а затем извлечь квадратный корень:
Итак, сначала мы найдем сумму квадратов разностей для x и y:
Затем мы перемножим эти два числа вместе: 20 * 68 = 1360.
Наконец, мы возьмем квадратный корень: √ 1360 = 36,88 .
Итак, мы нашли, что числитель формулы равен 36, а знаменатель равен 36,88. Это означает, что наш коэффициент корреляции Пирсона равен r = 36/36,88 = 0,976.
Это число близко к 1, что указывает на сильную положительную линейную связь между нашими переменными X и Y. Это подтверждает взаимосвязь, которую мы видели на диаграмме рассеяния.
Визуализация корреляций
Напомним, что коэффициент корреляции Пирсона говорит нам о типе линейной связи (положительная, отрицательная, отсутствие) между двумя переменными, а также о силе этой связи (слабая, умеренная, сильная).
Когда мы строим диаграмму рассеяния двух переменных, мы можем видеть реальную связь между двумя переменными. Вот множество различных типов линейных отношений, которые мы можем увидеть:
Сильная, положительная связь: по мере увеличения переменной по оси X переменная по оси Y также увеличивается. Точки расположены плотно друг к другу, что указывает на прочную связь.
Коэффициент корреляции Пирсона: 0,94
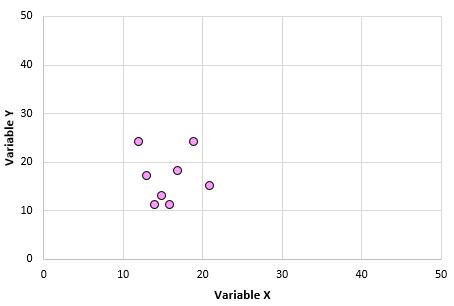
Слабая, положительная связь: по мере увеличения переменной по оси X переменная по оси Y также увеличивается. Точки довольно разбросаны, что указывает на слабую связь.
Коэффициент корреляции Пирсона: 0,44
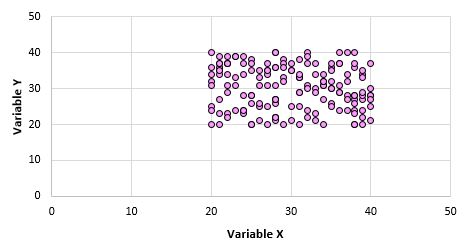
Нет взаимосвязи: нет четкой взаимосвязи (положительной или отрицательной) между переменными.
Коэффициент корреляции Пирсона: 0,03
Сильная, отрицательная связь: по мере увеличения переменной по оси X переменная по оси Y уменьшается. Точки расположены плотно друг к другу, что указывает на сильную связь.
Коэффициент корреляции Пирсона: -0,87
Слабая, отрицательная связь: по мере увеличения переменной по оси X переменная по оси Y уменьшается. Точки довольно разбросаны, что указывает на слабую связь.
Коэффициент корреляции Пирсона: – 0,46
Проверка значимости коэффициента корреляции Пирсона
Когда мы находим коэффициент корреляции Пирсона для набора данных, мы часто работаем с выборкой данных, полученной из большей совокупности.Это означает, что можно найти ненулевую корреляцию для двух переменных, даже если они фактически не коррелированы в генеральной совокупности.
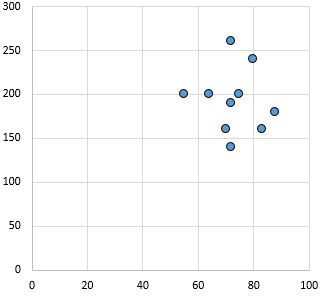
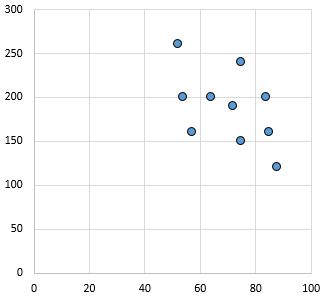
Например, предположим, что мы делаем диаграмму рассеяния для переменных X и Y для каждой точки данных во всей совокупности, и она выглядит следующим образом:
Ясно, что эти две переменные не коррелированы. Однако возможно, что когда мы берем выборку из 10 точек из генеральной совокупности, мы выбираем следующие точки:
Мы можем обнаружить, что коэффициент корреляции Пирсона для этой выборки точек равен 0,93, что указывает на сильную положительную корреляцию, несмотря на то, что корреляция населения равна нулю.
Чтобы проверить, является ли корреляция между двумя переменными статистически значимой, мы можем найти следующую тестовую статистику:
Тестовая статистика T = r * √ (n-2) / (1-r 2 )
где n — количество пар в нашей выборке, r — коэффициент корреляции Пирсона, а тестовая статистика T следует за распределением с n-2 степенями свободы.
Давайте рассмотрим пример того, как проверить значимость коэффициента корреляции Пирсона.
Пример
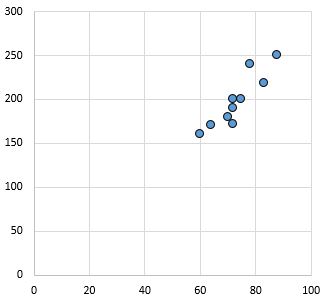
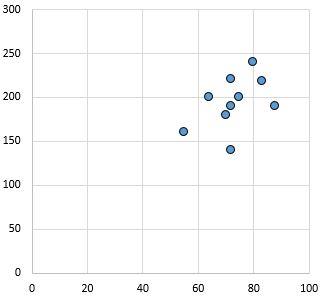
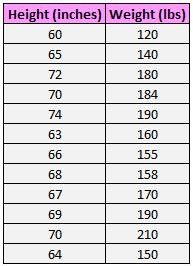
Следующий набор данных показывает рост и вес 12 человек:
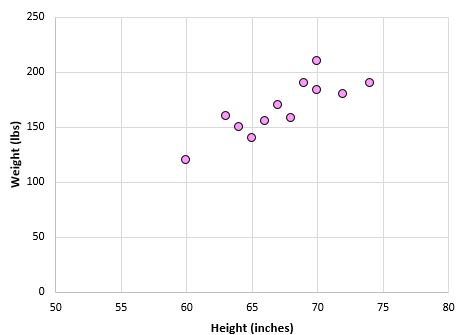
Диаграмма рассеяния ниже показывает значение этих двух переменных:
Коэффициент корреляции Пирсона для этих двух переменных составляет r = 0,836.
Статистика теста T = 0,836 * √ (12 -2) / (1-0,836 2 ) = 4,804.
Согласно нашему калькулятору распределения t , при оценке 4,804 с 10 степенями свободы p-значение равно 0,0007. Поскольку 0,0007 < 0,05, мы можем заключить, что корреляция между весом и ростом в этом примере является статистически значимой при альфа = 0,05.
Предостережения
Хотя коэффициент корреляции Пирсона может быть полезен для определения того, имеют ли две переменные линейную связь, мы должны помнить о трех вещах при интерпретации коэффициента корреляции Пирсона:
1. Корреляция не подразумевает причинно-следственной связи. Тот факт, что две переменные коррелированы, не означает, что одна из них обязательно вызывает более или менее частое появление другой. Классическим примером этого является положительная корреляция между продажами мороженого и нападениями акул. Когда продажи мороженого увеличиваются в определенное время года, количество нападений акул также увеличивается.
Означает ли это, что потребление мороженого вызывает нападения акул? Конечно нет! Это просто означает, что летом как потребление мороженого, так и нападения акул, как правило, увеличиваются, поскольку летом мороженое более популярно, а летом больше людей ходят в океан.
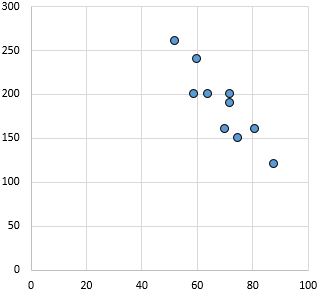
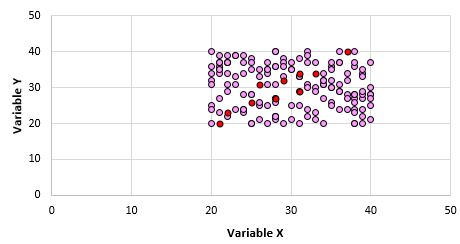
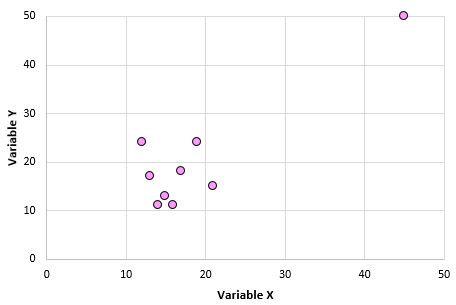
2. Корреляции чувствительны к выбросам. Один экстремальный выброс может резко изменить коэффициент корреляции Пирсона. Рассмотрим пример ниже:
Переменные X и Y имеют коэффициент корреляции Пирсона 0,00.Но представьте, что у нас есть один выброс в наборе данных:
Теперь коэффициент корреляции Пирсона для этих двух переменных равен 0,878.Один этот выброс меняет все. Вот почему, когда вы вычисляете корреляцию для двух переменных, рекомендуется визуализировать переменные с помощью диаграммы рассеяния для проверки выбросов.
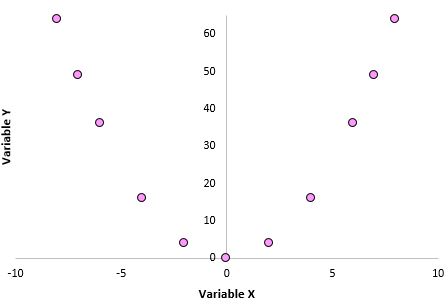
3. Коэффициент корреляции Пирсона не фиксирует нелинейные отношения между двумя переменными. Представьте, что у нас есть две переменные со следующими отношениями:
Коэффициент корреляции Пирсона для этих двух переменных равен 0,00, поскольку между ними нет линейной зависимости. Однако эти две переменные имеют нелинейную связь: значения y — это просто квадрат значений x.
При использовании коэффициента корреляции Пирсона помните, что вы просто проверяете, связаны ли две переменные линейно.Даже если коэффициент корреляции Пирсона говорит нам, что две переменные не коррелированы, они все равно могут иметь некоторую нелинейную связь. Это еще одна причина, по которой полезно создавать диаграмму рассеяния при анализе взаимосвязи между двумя переменными — это может помочь вам обнаружить нелинейную взаимосвязь.
Термин
«корреляция» был введен в науку выдающимся
английским естествоиспытателем Френсисом
Гальтоном в 1886 г. Однако точную формулу
для подсчета коэффициента корреляции
разработал его ученик Карл Пирсон.
Знакомство с корреляционным анализом
мы начнем с изучения этого коэффициента.
Сам коэффициент характеризует наличие
только линейной связи между признаками,
обозначаемыми, как правило, символами
X
и
Y.
Формула
расчета коэффициента корреляции
построена таким образом, что, если связь
между признаками имеет линейный характер,
коэффициент Пирсона точно устанавливает
тесноту этой связи. Поэтому он называется
также коэффициентом линейной корреляции
Пирсона.
Величина
коэффициента линейной корреляции
Пирсона не может превышать +1 и быть
меньше чем -1. Эти два числа +1 и -1 –
являются границами для коэффициента
корреляции. Когда при расчете получается
величина большая +1 или меньшая -1 –
следовательно, произошла ошибка в
вычислениях.
Если
коэффициент корреляции по модулю
оказывается близким к 1, то это соответствует
высокому уровню связи между переменными.
Так, в частности, при корреляции переменной
величины с самой собой величина
коэффициента корреляции будет равна
+1. Подобная связь характеризует прямо
пропорциональную зависимость. Если же
значения переменной X
будут
распложены в порядке возрастания, а те
же значения (обозначенные теперь уже
как переменная Y)
будут
располагаться в порядке убывания,
то в этом случае корреляция между
переменными X
и Y
будет равна точно –1. Такая величина
коэффициента корреляции характеризует
обратно пропорциональную зависимость.
Знак
коэффициента корреляции очень важен
для интерпретации полученной связи.
Подчеркнем еще раз, что если знак
коэффициента линейной корреляции –
плюс, то связь между коррелирующими
признаками такова, что большей величине
одного признака (переменной) соответствует
большая величина другого признака
(другой переменной). Иными словами, если
один показатель (переменная) увеличивается,
то соответственно увеличивается и
другой показатель (переменная). Такая
зависимость носит название прямо
пропорциональной зависимости.
Если
же получен знак минус, то большей величине
одного признака соответствует меньшая
величина другого. Иначе говоря, при
наличии знака минус, увеличению одной
переменной (признака, значения)
соответствует уменьшение другой
переменной. Такая зависимость носит
название обратно пропорциональной
зависимости. При этом выбор переменной,
которой приписывается характер
(тенденция) возрастания – произволен.
Это может быть как переменная X,
так
и переменная Y.
Однако
если психолог будет считать, что
увеличивается переменная X,
то
переменная Y
будет
соответственно уменьшаться, и наоборот.
Эти положения очень важно четко усвоить
для правильной интерпретации полученной
корреляционной зависимости.
В
общем виде формула для подсчета
коэффициента корреляции такова:
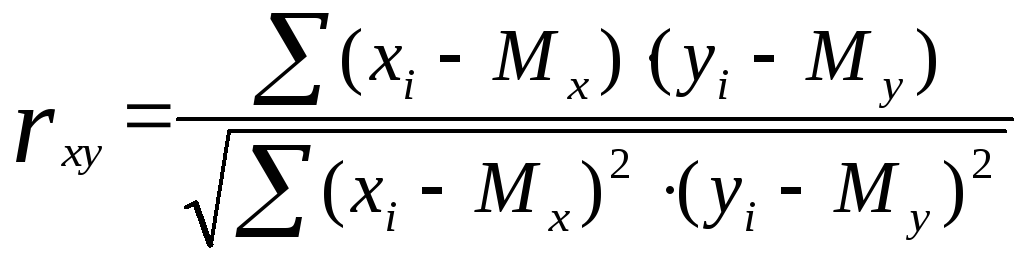
где
xi
– значения, принимаемые переменной X;
yi
–
значения, принимаемые переменной Y;
Мх
–
средняя по X;
Му
–
средняя по Y.
Расчет
коэффициента корреляции Пирсона
предполагает, что переменные X
и Y
распределены
нормально.
Формула
(9.1) предполагает, что из каждого значения
xi
переменной X,
должно
вычитаться ее среднее значение Мх.
Это
неудобно. Поэтому для расчета коэффициента
корреляции используют не эту формулу,
а ее аналог, получаемый простыми
преобразованиями:
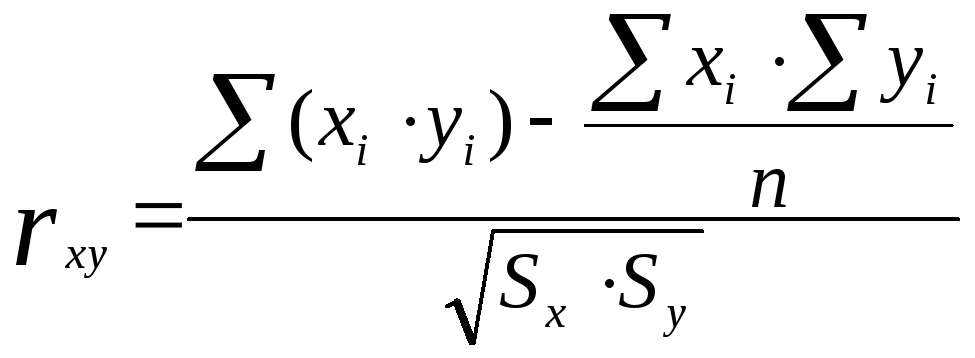
(9.2)
где и
,
или
модификацию этой формулы:
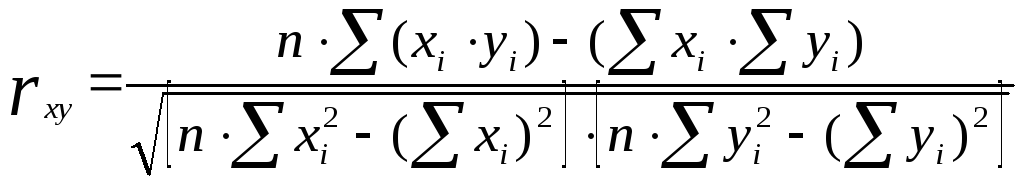
(9.3)
Согласно
формулам (9.2) и (9.3) необходимо подсчитать
сумму каждой переменной, сумму квадратов
каждой переменной и сумму последовательных
произведений переменных друг на друга.
Подчеркнем, что сумма квадратов – не
равняется квадрату суммы!
Обратим
внимание еще вот на какое обстоятельство.
В формуле (9.1) встречается величины
.
(9.4)
При
делении на n
(число
значений переменной X
или Y)
она
называется ковариацией. Выражение (9.4)
может быть подсчитано только в тех
случаях, когда число значений переменной
X
равно
числу значений переменной Y
и равно n.
Формула
(9.4) предполагает также, что при расчете
коэффициентов корреляции нельзя
произвольно переставлять элементы в
коррелируемых столбцах, как это делается,
например, в случае расчета по критерию
S
Джонкира.
Используя
формулу (9.3), решим следующую задачу.
Пример
9.1.
20
школьникам были даны тесты на
наглядно-образное и вербальное мышление.
Измерялось среднее время решения заданий
теста в секундах. Психолога интересует
вопрос: существует ли взаимосвязь между
временем решения этих задач? Переменная
X
обозначает
среднее время решения наглядно-образных,
а переменная Y
– среднее
время решения вербальных заданий тестов.
Решение.
Прежде всего, сформулируем
гипотезы.
Н0:
связь
между временем решения наглядно-образных
и вербальных задач отсутствует.
Н1:
связь
между временем решения наглядно-образных
и вербальных задач присутствует.
Представим
исходные данные в виде таблицы, в которой
введены дополнительные столбцы,
необходимые для расчета по формуле
(9.3). В таблице 9.1 даны индивидуальные
значения переменных X
и
Y,
построчные
произведения переменных Х
и Y,
квадраты
переменных всех индивидуальных значений
переменных X
и
Y,
а
также суммы всех вышеперечисленных
величин.
Таблица
9.1
|
№ испытуемых |
X |
Y |
X∙Y |
X∙X |
Y∙Y |
|
Среднее
наглядно-образных заданий |
Среднее
вербальных заданий |
||||
|
1 |
19 |
17 |
323 |
361 |
289 |
|
2 |
32 |
7 |
224 |
1024 |
49 |
|
3 |
33 |
17 |
561 |
1089 |
289 |
|
4 |
44 |
28 |
1232 |
1936 |
784 |
|
5 |
28 |
27 |
756 |
784 |
729 |
|
6 |
35 |
31 |
1085 |
1225 |
961 |
|
7 |
39 |
20 |
780 |
1521 |
400 |
|
8 |
39 |
17 |
663 |
1521 |
289 |
|
9 |
44 |
35 |
1540 |
1936 |
1225 |
|
10 |
44 |
43 |
1892 |
1936 |
1849 |
|
11 |
24 |
10 |
240 |
576 |
100 |
|
12 |
37 |
28 |
1036 |
1369 |
784 |
|
13 |
29 |
13 |
377 |
841 |
169 |
|
14 |
40 |
43 |
1720 |
1600 |
1849 |
|
15 |
42 |
45 |
1890 |
1764 |
2025 |
|
16 |
32 |
24 |
768 |
1024 |
5760 |
|
17 |
48 |
45 |
2160 |
2304 |
2025 |
|
18 |
42 |
26 |
1092 |
1764 |
679 |
|
19 |
33 |
16 |
528 |
1089 |
256 |
|
20 |
47 |
26 |
1222 |
2209 |
676 |
|
Сумма |
731 |
518 |
20089 |
27873 |
16000 |
Рассчитываем
эмпирическую величину коэффициента
корреляции по формуле (9.3).
.
Определяем
критические значения для полученного
коэффициента корреляции по таблице
критических значений коэффициента
корреляции Пирсона (таблица 1 приложения
1). Особо отметим, что в этой таблице
величины критических значений
коэффициентов линейной корреляции
Пирсона даны по абсолютной величине.
Следовательно, при получении как
положительного, так и отрицательного
коэффициента корреляции по формуле
(9.3) оценка уровня значимости этого
коэффициента проводится по той же
таблице без учета знака, а знак добавляется
для дальнейшей интерпретации характера
связи между переменными X
и
Y.
При
нахождении критических значений для
вычисленного коэффициента линейной
корреляции Пирсона гэмп
число
степеней свободы рассчитывается как k
=
n
–
2. В нашем случае к
=
20, поэтому n
– 2
= 20 – 2 = 18. В первом столбце таблицы 1
приложения 1 в строке, обозначенной
числом 18, находим:
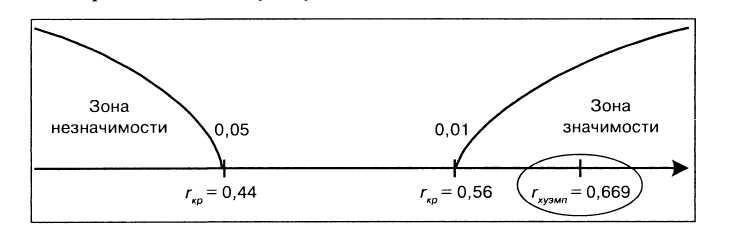
Строим
соответствующую ось значимости.
Ввиду
того, что величина расчетного коэффициента
корреляции попала в зону значимости –
гипотеза Н0
отвергается
и принимается гипотеза Н1.
Иными словами, связь между временем
решения наглядно-образных и вербальных
задач статистически значима на 1% уровне
и положительна. Полученная прямо
пропорциональная зависимость говорит
о том, что чем выше среднее время решения
наглядно-образных задач, тем выше среднее
время решения вербальных, и наоборот.
Для
применения коэффициента корреляции
Пирсона необходимо соблюдать следующие
условия:
-
Сравниваемые
переменные должны быть получены в
интервальной шкале или шкале отношений. -
Распределения
переменных Х
и Y
должны быть близки к нормальному. -
Число
варьирующих признаков в сравниваемых
переменных X
и
Y
должно быть одинаковым. -
Таблицы
уровней значимости для коэффициента
корреляции Пирсона рассчитаны от n
=
5 до n
= 1000.
Оценка уровня значимости по таблицам
осуществляется при числе степеней
свободы k
=
n
– 2.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Обычно принято количественно оценивать линейные связи с помощью коэффициента корреляции Пирсона. Чтобы указать силу и направление связи между двумя переменными, он принимает значение от -1 до 1.
Это может помочь инвесторам в диверсификации. Расчеты по диаграммам рассеяния исторических доходностей между парами активов, такими как акции-облигации, акции-товары, облигации-недвижимость и т.д., помогут инвесторам строить портфели риск-доходность.
Теперь мы познакомимся с коэффициентом корреляции Пирсона и узнаем, как с его помощью измерить связь между двумя связанными переменными.
Индекс содержания
- Что такое коэффициент корреляции Пирсона?
- Что делает тест коэффициента корреляции Пирсона?
- Формула и расчет коэффициента корреляции Пирсона
- Определение силы коэффициента корреляции Пирсона по продуктивному моменту
- Примеры коэффициента корреляции Пирсона
- Вывод
Что такое коэффициент корреляции Пирсона?
Коэффициент корреляции Пирсона или коэффициент корреляции Пирсона или r Пирсона определяется в статистике как измерение силы связи между двумя переменными и их ассоциации друг с другом.
Проще говоря, коэффициент корреляции Пирсона рассчитывает эффект изменения одной переменной при изменении другой переменной.
Например: До определенного возраста (в большинстве случаев) рост ребенка будет увеличиваться по мере увеличения его возраста. Конечно, его рост зависит от различных факторов, таких как гены, местоположение, диета, образ жизни и т.д.
Этот подход основан на ковариации и, таким образом, является лучшим методом для измерения взаимосвязи между двумя переменными.
Что делает тест коэффициента корреляции Пирсона?
Коэффициент корреляции Пирсона имеет высокую статистическую значимость. Он рассматривает взаимосвязь между двумя переменными. Он стремится провести линию через данные двух переменных, чтобы показать их взаимосвязь. Связь между переменными измеряется с помощью калькулятора коэффициента корреляции Пирсона. Эта линейная связь может быть положительной или отрицательной.
Например:
- Положительная линейная связь: В большинстве случаев, универсально, доход человека увеличивается по мере увеличения его возраста.
- Отрицательная линейная зависимость: Если автомобиль увеличивает скорость, время, затраченное на поездку, уменьшается, и наоборот.
Из приведенного выше примера видно, что коэффициент корреляции Пирсона, r, пытается выяснить две вещи — силу и направление связи при заданных объемах выборки.
Коэффициент корреляции Пирсона формула и расчет
Формула коэффициента корреляции выявляет связь между переменными. Она возвращает значения от -1 до 1. Используйте приведенный ниже калькулятор корреляции коэффициента Пирсона для измерения силы связи между двумя переменными.
Формула коэффициента корреляции Пирсона:
Где:
N = количество пар оценок
?xy = сумма произведений парных оценок
?x = сумма оценок x
?y = сумма оценок y
?x2 = сумма квадратов оценок x
?y2 = сумма квадратов оценок y
Расчет
Здесь представлено пошаговое руководство по расчету коэффициента корреляции Пирсона:
Шаг первый:Создайте таблицу коэффициентов корреляции.
Постройте график данных, включив в него обе переменные. Пометьте эти переменные ‘x’ и ‘y’. Добавьте три дополнительных столбца — (xy), (x^2) и (y^2). Обратитесь к этой простой диаграмме данных.
Шаг второй: Используйте базовое умножение для завершения таблицы.
Шаг третий: Сложите все колонки снизу вверх.
Шаг четвертый: Подставьте значения в формулу корреляции.
Если результат отрицательный, то между двумя переменными существует отрицательная корреляционная связь. Если результат положительный, между переменными существует положительная корреляционная связь. Результаты также могут определять силу линейной связи, т.е, сильная положительная связь, сильная отрицательная связь, средняя положительная связь и так далее.
Определение силы коэффициента продукционно-моментной корреляции Пирсона
.
Коэффициент продукционно-моментной корреляции Пирсона, или просто коэффициент корреляции Пирсона или коэффициент корреляции r, определяет силу линейной связи между двумя переменными.
Чем сильнее связь между двумя переменными, тем ближе ваш ответ будет склоняться к 1 или -1. Значения 1 или -1 означают, что все точки данных расположены на прямой линии «наилучшего соответствия». Это означает, что изменение факторов какой-либо переменной не ослабляет корреляцию с другой переменной. Чем ближе ваш ответ лежит к 0, тем больше разброс в переменных.
Как интерпретировать коэффициент корреляции Пирсона
Ниже приведены предлагаемые рекомендации по интерпретации корреляции коэффициента Пирсона:
Обратите внимание, что сила связи переменных зависит от того, что вы измеряете, и от объема выборки.
На графике можно заметить связь между переменными и сделать предположения еще до их расчета. Графики рассеяния, если они расположены близко к линии, показывают сильную связь между переменными.
Чем ближе графики рассеяния лежат к линии, тем сильнее связь между переменными. Чем дальше они удаляются от линии, тем слабее взаимосвязь. Если линия почти параллельна оси x из-за беспорядочного расположения точек разброса на графике, можно предположить, что корреляция между двумя переменными отсутствует.
Что означают термины сила и направление?
Термины «сила» и «направление» имеют статистическое значение. Вот прямое объяснение этих двух слов:
- Сила: Сила означает корреляцию отношений между двумя переменными. Она означает, насколько последовательно будет изменяться одна переменная в результате изменения другой. Значения, близкие к +1 или -1, указывают на сильную взаимосвязь. Эти значения достигаются, если точки данных лежат на линии или очень близко к ней.
Чем дальше удаляются точки данных, тем слабее сила линейной зависимости. Когда нет практического способа провести прямую линию, потому что точки данных разбросаны, сила линейной зависимости самая слабая.
- Направление: Направление линии указывает на положительную линейную или отрицательную линейную связь между переменными. Если линия имеет восходящий наклон, переменные имеют положительную связь.
Это означает, что увеличение значения одной переменной приведет к увеличению значения другой переменной. Отрицательная корреляция показывает нисходящий наклон. Это означает, что увеличение значения одной переменной приводит к уменьшению значения другой переменной.
.Примеры коэффициента корреляции Пирсона
Рассмотрим несколько наглядных примеров, которые помогут вам интерпретировать таблицу коэффициента корреляции:
Большая положительная корреляция
- На рисунке выше показана корреляция почти +1.
- Трассы рассеяния почти выстроены в прямую линию.
- Наклон положительный, что означает, что если одна переменная увеличивается, другая переменная также увеличивается, показывая положительную линейную линию.
- Это означает, что изменение одной переменной прямо пропорционально изменению другой переменной.
- Примером большой положительной корреляции может быть: «По мере роста детей увеличиваются размеры их одежды и обуви».
Средняя положительная корреляция
- На рисунке выше изображена положительная корреляция.
- Корреляция выше +0,8, но ниже 1+.
- Она показывает довольно сильный линейный восходящий паттерн.
- Примером средней положительной корреляции может быть — По мере увеличения количества автомобилей увеличивается спрос на топливо.
Малая отрицательная корреляция
- На рисунке выше графики рассеяния не так близки к прямой линии по сравнению с предыдущими примерами
- Она показывает отрицательную линейную корреляцию приблизительно -0.5
- Изменение одной переменной обратно пропорционально изменению другой переменной, так как наклон отрицательный.
- Примером небольшой отрицательной корреляции может быть — Чем больше кто-то ест, тем меньше он голоден.
Слабая корреляция / отсутствие корреляции
- Площадки рассеяния находятся далеко от линии.
- Трудно провести линию практически.
- Корреляция приблизительно равна +0.15
- Невозможно утверждать, что изменение одной переменной прямо пропорционально или обратно пропорционально другой переменной.
- Примером слабой/отсутствующей корреляции может быть — Повышение цен на топливо приводит к тому, что меньше людей заводят домашних животных.
Conclusion
Коэффициент корреляции Пирсона можно определить, собрав данные о двух интересующих вас переменных с помощью опроса. С его помощью можно узнать, является ли корреляция между двумя переменными положительной или отрицательной и насколько она сильна.
Research Suite — это набор инструментов для проведения исследований и преобразования информации, которые можно использовать для сбора данных для анализа коэффициента корреляции Пирсона. После экспорта данных опроса из и импорта их в электронную таблицу или статистическое приложение вы можете провести корреляционный анализ.
предлагает полезные инструменты анализа данных, такие как перекрестная табуляция, визуализация данных и статистическое тестирование, в дополнение к расчету коэффициента корреляции. Эти качества могут помочь вам в исследовании и понимании взаимосвязи ваших переменных.
Готовы обнаружить взаимосвязь между вашими переменными и продвинуться в анализе данных? Начните бесплатную пробную версию сегодня, чтобы узнать, как наше программное обеспечение для проведения опросов может помочь вам легко определить коэффициент корреляции Пирсона. Не упустите этот шанс улучшить анализ данных и исследования.
Обнаружение взаимосвязей между явлениями – одна из главных задач статистического анализа. На то есть две причины. Первая. Если известно, что один процесс зависит от другого, то на первый можно оказывать влияние через второй. Вторая. Даже если причинно-следственная связь отсутствует, то по изменению одного показателя можно предсказать изменение другого.
Взаимосвязь двух переменных проявляется в совместной вариации: при изменении одного показателя имеет место тенденция изменения другого. Такая взаимосвязь называется корреляцией, а раздел статистики, который занимается взаимосвязями – корреляционный анализ.
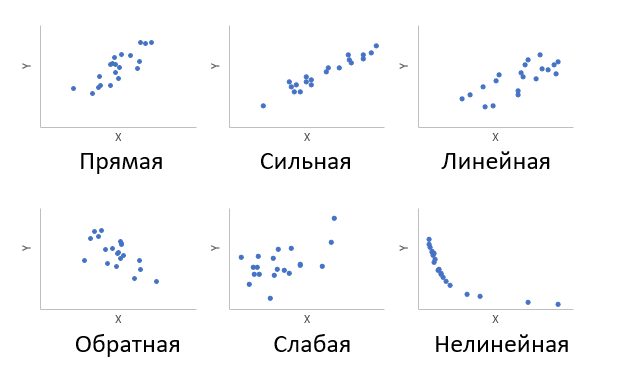
Корреляция – это, простыми словами, взаимосвязанное изменение показателей. Она характеризуется направлением, формой и теснотой. Ниже представлены примеры корреляционной связи.
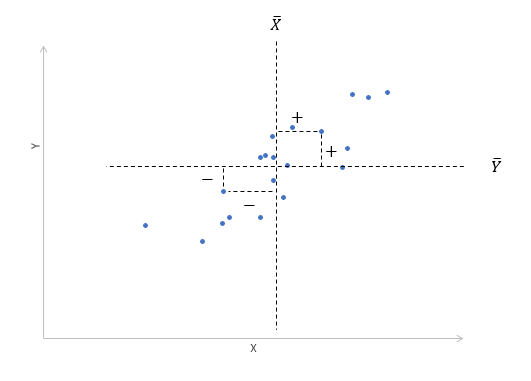
Далее будет рассматриваться только линейная корреляция. На диаграмме рассеяния (график корреляции) изображена взаимосвязь двух переменных X и Y. Пунктиром показаны средние.
При положительном отклонении X от своей средней, Y также в большинстве случаев отклоняется в положительную сторону от своей средней. Для X меньше среднего, Y, как правило, тоже ниже среднего. Это прямая или положительная корреляция. Бывает обратная или отрицательная корреляция, когда положительное отклонение от средней X ассоциируется с отрицательным отклонением от средней Y или наоборот.
Линейность корреляции проявляется в том, что точки расположены вдоль прямой линии. Положительный или отрицательный наклон такой линии определяется направлением взаимосвязи.
Крайне важная характеристика корреляции – теснота. Чем теснее взаимосвязь, тем ближе к прямой точки на диаграмме. Как же ее измерить?
Складывать отклонения каждого показателя от своей средней нет смысла, получим нуль. Похожая проблема встречалась при измерении вариации, а точнее дисперсии. Там эту проблему обходят через возведение каждого отклонения в квадрат.
Квадрат отклонения от средней измеряет вариацию показателя как бы относительно самого себя. Если второй множитель в числителе заменить на отклонение от средней второго показателя, то получится совместная вариация двух переменных, которая называется ковариацией.
Чем больше пар имеют одинаковый знак отклонения от средней, тем больше сумма в числителе (произведение двух отрицательных чисел также дает положительное число). Большая положительная ковариация говорит о прямой взаимосвязи между переменными. Обратная взаимосвязь дает отрицательную ковариацию. Если количество совпадающих по знаку отклонений примерно равно количеству не совпадающих, то ковариация стремится к нулю, что говорит об отсутствии линейной взаимосвязи.
Таким образом, чем больше по модулю ковариация, тем теснее линейная взаимосвязь. Однако значение ковариации зависит от масштаба данных, поэтому невозможно сравнивать корреляцию для разных переменных. Можно определить только направление по знаку. Для получения стандартизованной величины тесноты взаимосвязи нужно избавиться от единиц измерения путем деления ковариации на произведение стандартных отклонений обеих переменных. В итоге получится формула коэффициента корреляции Пирсона.
Показатель имеет полное название линейный коэффициент корреляции Пирсона или просто коэффициент корреляции.
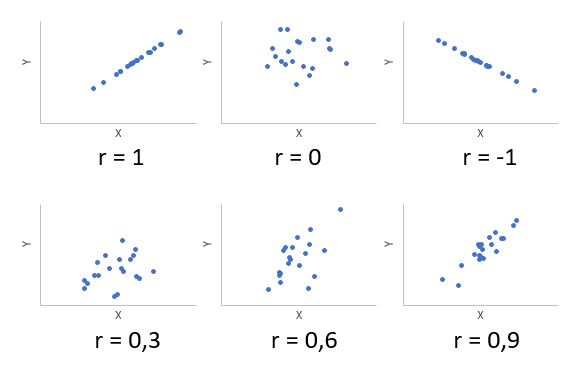
Коэффициент корреляции показывает тесноту линейной взаимосвязи и изменяется в диапазоне от -1 до 1. -1 (минус один) означает полную (функциональную) линейную обратную взаимосвязь. 1 (один) – полную (функциональную) линейную положительную взаимосвязь. 0 – отсутствие линейной корреляции (но не обязательно взаимосвязи). На практике всегда получаются промежуточные значения. Для наглядности ниже представлены несколько примеров с разными значениями коэффициента корреляции.
Таким образом, ковариация и корреляция отражают тесноту линейной взаимосвязи. Последняя используется намного чаще, т.к. является относительным показателем и не имеет единиц измерения.
Диаграммы рассеяния дают наглядное представление, что измеряет коэффициент корреляции. Однако нужна более формальная интерпретация. Эту роль выполняет квадрат коэффициента корреляции r2, который называется коэффициентом детерминации, и обычно применяется при оценке качества регрессионных моделей. Снова представьте линию, вокруг которой расположены точки.
Линейная функция является моделью взаимосвязи между X иY и показывает ожидаемое значение Y при заданном X. Коэффициент детерминации – это соотношение дисперсии ожидаемых Y (точек на прямой линии) к общей дисперсии Y, или доля объясненной вариации Y. При r = 0,1 r2 = 0,01 или 1%, при r = 0,5 r2 = 0,25 или 25%.
Выборочный коэффициент корреляции
Коэффициент корреляции обычно рассчитывают по выборке. Значит, у аналитика в распоряжении не истинное значение, а оценка, которая всегда ошибочна. Если выборка была репрезентативной, то истинное значение коэффициента корреляции находится где-то относительно недалеко от оценки. Насколько далеко, можно определить через доверительные интервалы.
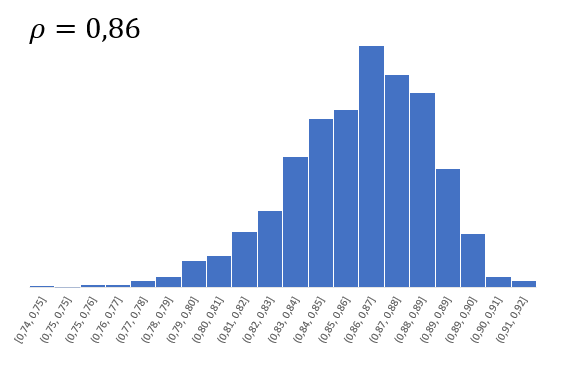
Согласно Центральное Предельной Теореме распределение оценки любого показателя стремится к нормальному с ростом выборки. Но есть проблемка. Распределение коэффициента корреляции вблизи придельных значений не является симметричным. Ниже пример распределения при истинном коэффициенте корреляции ρ = 0,86.
Предельное значение не дает выйти за 1 и, как бы «поджимает» распределение справа. Симметричная ситуация наблюдается, если коэффициент корреляции близок к -1.
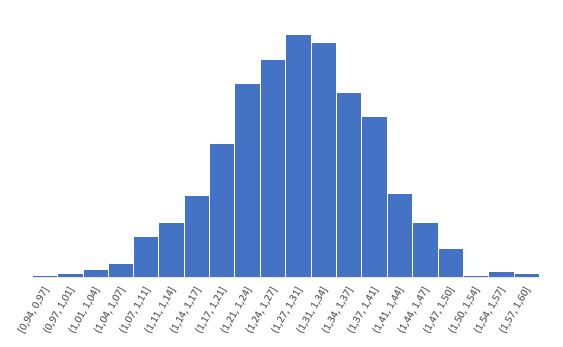
В общем рассчитывать на свойства нормального распределения нельзя. Поэтому Фишер предложил провести преобразование выборочного коэффициента корреляции по формуле:
Распределение z для тех же r имеет следующий вид.
Намного ближе к нормальному. Стандартная ошибка z равна:
Далее исходя из свойств нормального распределения несложно найти верхнюю и нижнюю границы доверительного интервала для z. Определим квантиль стандартного нормального распределения для заданной доверительной вероятности, т.е. количество стандартных отклонений от центра распределения.
cγ – квантиль стандартного нормального распределения;
N-1 – функция обратного стандартного распределения;
γ – доверительная вероятность (часто 95%).
Затем рассчитаем границы доверительного интервала.
Нижняя граница z:
Верхняя граница z:
Теперь обратным преобразованием Фишера из z вернемся к r.
Нижняя граница r:
Верхняя граница r:
Это была теоретическая часть. Переходим к практике расчетов.
Как посчитать коэффициент корреляции в Excel
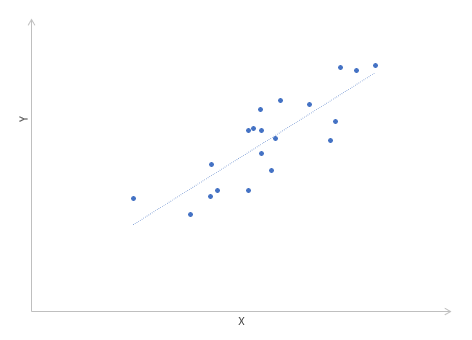
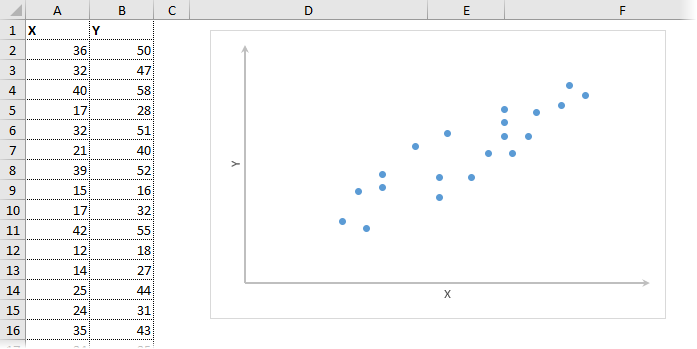
Корреляционный анализ в Excel лучше начинать с визуализации.
На диаграмме видна взаимосвязь двух переменных. Рассчитаем коэффициент парной корреляции с помощью функции Excel КОРРЕЛ. В аргументах нужно указать два диапазона.
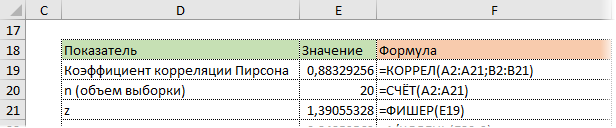
Коэффициент корреляции 0,88 показывает довольно тесную взаимосвязь между двумя показателями. Но это лишь оценка, поэтому переходим к интервальному оцениванию.
Расчет доверительного интервала для коэффициента корреляции в Excel
В Эксель нет готовых функций для расчета доверительного интервала коэффициента корреляции, как для средней арифметической. Поэтому план такой:
— Делаем преобразование Фишера для r.
— На основе нормальной модели рассчитываем доверительный интервал для z.
— Делаем обратное преобразование Фишера из z в r.
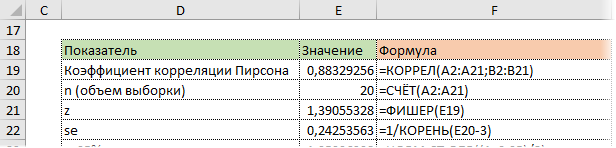
Удивительно, но для преобразования Фишера в Excel есть специальная функция ФИШЕР.
Стандартная ошибка z легко подсчитывается с помощью формулы.
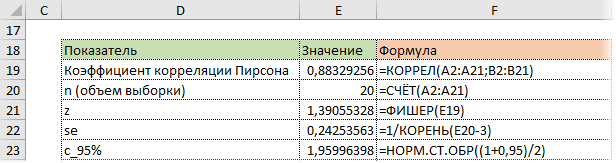
Используя функцию НОРМ.СТ.ОБР, определим квантиль нормального распределения. Доверительную вероятность возьмем 95%.
Значение 1,96 хорошо известно любому опытному аналитику. В пределах ±1,96σ от средней находится 95% нормально распределенных величин.
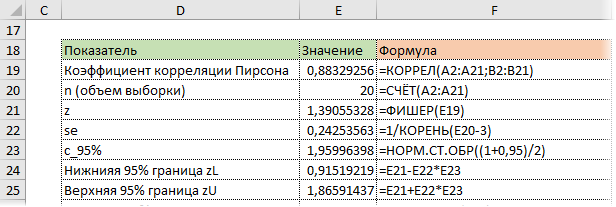
Используя z, стандартную ошибку и квантиль, легко определим доверительные границы z.
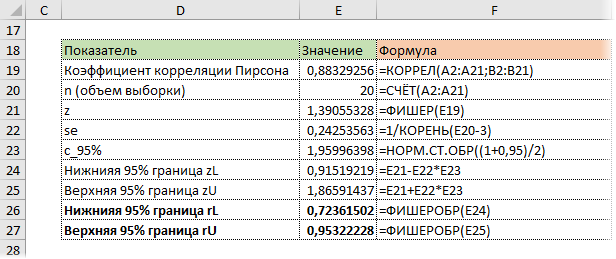
Последний шаг – обратное преобразование Фишера из z назад в r с помощью функции Excel ФИШЕРОБР. Получим доверительный интервал коэффициента корреляции.
Нижняя граница 95%-го доверительного интервала коэффициента корреляции – 0,724, верхняя граница – 0,953.
Надо пояснить, что значит значимая корреляция. Коэффициент корреляции статистически значим, если его доверительный интервал не включает 0, то есть истинное значение по генеральной совокупности наверняка имеет тот же знак, что и выборочная оценка.
Несколько важных замечаний
1. Коэффициент корреляции Пирсона чувствителен к выбросам. Одно аномальное значение может существенно исказить коэффициент. Поэтому перед проведением анализа следует проверить и при необходимости удалить выбросы. Другой вариант – перейти к ранговому коэффициенту корреляции Спирмена. Рассчитывается также, только не по исходным значениям, а по их рангам (пример показан в ролике под статьей).
2. Синоним корреляции – это взаимосвязь или совместная вариация. Поэтому наличие корреляции (r ≠ 0) еще не означает причинно-следственную связь между переменными. Вполне возможно, что совместная вариация обусловлена влиянием третьей переменной. Совместное изменение переменных без причинно-следственной связи называется ложная корреляция.
3. Отсутствие линейной корреляции (r = 0) не означает отсутствие взаимосвязи. Она может быть нелинейной. Частично эту проблему решает ранговая корреляция Спирмена, которая показывает совместный рост или снижение рангов, независимо от формы взаимосвязи.
В видео показан расчет коэффициента корреляции Пирсона с доверительными интервалами, ранговый коэффициент корреляции Спирмена.
↓ Скачать файл с примером ↓
Поделиться в социальных сетях:




![{displaystyle operatorname {cov} (X,Y)=operatorname {mathbb {E} } [(X-mu _{X})(Y-mu _{Y})],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e88bc4ba085b98d5cca09b958ad378d50127308)
![{displaystyle rho _{X,Y}={frac {operatorname {mathbb {E} } [(X-mu _{X})(Y-mu _{Y})]}{sigma _{X}sigma _{Y}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/042c646e848d2dc6e15d7b5c7a5b891941b2eab6)
![{displaystyle {begin{aligned}mu _{X}={}&operatorname {mathbb {E} } [,X,]\mu _{Y}={}&operatorname {mathbb {E} } [,Y,]\sigma _{X}^{2}={}&operatorname {mathbb {E} } left[,left(X-operatorname {mathbb {E} } [X]right)^{2},right]=operatorname {mathbb {E} } left[,X^{2},right]-left(operatorname {mathbb {E} } [,X,]right)^{2}\sigma _{Y}^{2}={}&operatorname {mathbb {E} } left[,left(Y-operatorname {mathbb {E} } [Y]right)^{2},right]=operatorname {mathbb {E} } left[,Y^{2},right]-left(,operatorname {mathbb {E} } [,Y,]right)^{2}\&operatorname {mathbb {E} } [,left(X-mu _{X}right)left(Y-mu _{Y}right),]=operatorname {mathbb {E} } [,left(X-operatorname {mathbb {E} } [,X,]right)left(Y-operatorname {mathbb {E} } [,Y,]right),]=operatorname {mathbb {E} } [,X,Y,]-operatorname {mathbb {E} } [,X,]operatorname {mathbb {E} } [,Y,],,end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2469cdb397ef7d50c200b03c9e9f7311f0ab2b1)
![{displaystyle rho _{X,Y}={frac {operatorname {mathbb {E} } [,X,Y,]-operatorname {mathbb {E} } [,X,]operatorname {mathbb {E} } [,Y,]}{{sqrt {operatorname {mathbb {E} } left[,X^{2},right]-left(operatorname {mathbb {E} } [,X,]right)^{2}}}~{sqrt {operatorname {mathbb {E} } left[,Y^{2},right]-left(operatorname {mathbb {E} } [,Y,]right)^{2}}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5984dfb290912b0e0b92a984bf49cdd628c38b2c)

















![z={frac {x-{text{mean}}}{text{SE}}}=[F(r)-F(rho _{0})]{sqrt {n-3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da7a3d54a70f9005e3bf9a2accf62cbf0fa0ea71)
![{displaystyle 100(1-alpha )%{text{CI}}:operatorname {artanh} (rho )in [operatorname {artanh} (r)pm z_{alpha /2}{text{SE}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/affc3f0ee39499c97bb851229113f49d83100bf2)
![{displaystyle 100(1-alpha )%{text{CI}}:rho in [tanh(operatorname {artanh} (r)-z_{alpha /2}{text{SE}}),tanh(operatorname {artanh} (r)+z_{alpha /2}{text{SE}})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf658969d39ea848505750b5cd76db21da78dd5c)


![{displaystyle {begin{aligned}r(Y,{hat {Y}})&={frac {sum _{i}(Y_{i}-{bar {Y}})({hat {Y}}_{i}-{bar {Y}})}{sqrt {sum _{i}(Y_{i}-{bar {Y}})^{2}cdot sum _{i}({hat {Y}}_{i}-{bar {Y}})^{2}}}}\[6pt]&={frac {sum _{i}(Y_{i}-{hat {Y}}_{i}+{hat {Y}}_{i}-{bar {Y}})({hat {Y}}_{i}-{bar {Y}})}{sqrt {sum _{i}(Y_{i}-{bar {Y}})^{2}cdot sum _{i}({hat {Y}}_{i}-{bar {Y}})^{2}}}}\[6pt]&={frac {sum _{i}[(Y_{i}-{hat {Y}}_{i})({hat {Y}}_{i}-{bar {Y}})+({hat {Y}}_{i}-{bar {Y}})^{2}]}{sqrt {sum _{i}(Y_{i}-{bar {Y}})^{2}cdot sum _{i}({hat {Y}}_{i}-{bar {Y}})^{2}}}}\[6pt]&={frac {sum _{i}({hat {Y}}_{i}-{bar {Y}})^{2}}{sqrt {sum _{i}(Y_{i}-{bar {Y}})^{2}cdot sum _{i}({hat {Y}}_{i}-{bar {Y}})^{2}}}}\[6pt]&={sqrt {frac {sum _{i}({hat {Y}}_{i}-{bar {Y}})^{2}}{sum _{i}(Y_{i}-{bar {Y}})^{2}}}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d86595f3f77e8ee96952760d9176a5fa140cc562)




![{displaystyle operatorname {mathbb {E} } left[rright]=rho -{frac {rho left(1-rho ^{2}right)}{2n}}+cdots ,quad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/683b838e709e3b32a3c22dfec4fa665a593f42ad)


![{displaystyle r=operatorname {mathbb {E} } [r]approx r_{text{adj}}-{frac {r_{text{adj}}left(1-r_{text{adj}}^{2}right)}{2n}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e094c3fdfcb0bfd127f4be74e582f22a407201c4)
![{displaystyle r_{text{adj}}approx rleft[1+{frac {1-r^{2}}{2n}}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbf3f71f2cfe17f8f0d422d5ac0d482cc429a925)





![{displaystyle operatorname {corr} _{r}(X,Y)={frac {operatorname {mathbb {E} } [,X,Y,]}{sqrt {operatorname {mathbb {E} } [,X^{2},]cdot operatorname {mathbb {E} } [,Y^{2},]}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6d897e4b303a062ed14cc9f88f35f5c8ffc91f7)