17 авг. 2022 г.
читать 2 мин
V Крамера — это мера силы связи между двумя номинальными переменными .
Он находится в диапазоне от 0 до 1, где:
- 0 указывает на отсутствие связи между двумя переменными.
- 1 указывает на идеальную связь между двумя переменными.
Он рассчитывается как:
V Крамера = √ (X 2 /n) / мин (c-1, r-1)
куда:
- X 2 : Статистика хи-квадрат
- n: общий размер выборки
- р: количество рядов
- c: количество столбцов
Как интерпретировать V Крамера
В следующей таблице показано, как интерпретировать V Крамера на основе степеней свободы:
| Степени свободы | Маленький | Середина | Большой | | — | — | — | — | | 1 | 0,10 | 0,30 | 0,50 | | 2 | 0,07 | 0,21 | 0,35 | | 3 | 0,06 | 0,17 | 0,29 | | 4 | 0,05 | 0,15 | 0,25 | | 5 | 0,04 | 0,13 | 0,22 |
Следующие примеры показывают, как интерпретировать V Крамера в различных ситуациях.
Пример 1: Интерпретация V Крамера для таблицы 2×3
Предположим, мы хотим узнать, есть ли связь между цветом глаз и полом, поэтому мы опрашиваем 50 человек и получаем следующие результаты:
Мы можем использовать следующий код в R для вычисления V Крамера для этих двух переменных:
library (rcompanion)
#create table
data = matrix(c(6, 9, 8, 5, 12, 10), nrow= 2 )
#view table
data
[,1] [,2] [,3]
[1,] 6 8 12
[2,] 9 5 10
#calculate Cramer's V
cramerV(data)
Cramer V
0.1671
V Крамера оказывается равным 0,1671 .
Степени свободы будут рассчитываться как:
- df = мин (# строк-1, # столбцов-1)
- дф = мин (1, 2)
- дф = 1
Ссылаясь на приведенную выше таблицу, мы видим, что Крамеровский V, равный 0,1671, и степени свободы = 1 указывают на небольшую (или «слабую») связь между цветом глаз и полом.
Пример 2: Интерпретация V Крамера для таблицы 3×3
Предположим, мы хотим узнать, существует ли связь между цветом глаз и предпочтениями политических партий, поэтому мы опрашиваем 50 человек и получаем следующие результаты:
Мы можем использовать следующий код в R для вычисления V Крамера для этих двух переменных:
library (rcompanion)
#create table
data = matrix(c(8, 2, 4, 5, 8, 6, 6, 3, 8), nrow= 3 )
#view table
data
[,1] [,2] [,3]
[1,] 8 5 6
[2,] 2 8 3
[3,] 4 6 8
#calculate Cramer's V
cramerV(data)
Cramer V
0.246
V Крамера оказывается равным 0,246 .
Степени свободы будут рассчитываться как:
- df = мин (# строк-1, # столбцов-1)
- дф = мин (2, 2)
- дф = 2
Ссылаясь на приведенную выше таблицу, мы видим, что коэффициент Крамера V, равный 0,246 , и степени свободы = 2 указывают на среднюю (или «умеренную») связь между цветом глаз и предпочтениями политической партии.
Дополнительные ресурсы
В следующих руководствах объясняется, как рассчитать V Крамера в различных статистических программах:
Как рассчитать V Крамера в Excel
Как рассчитать V Крамера в R
Как рассчитать V Крамера в Python
Коэффициент
Чупрова измеряет взаимосвязь качественных
неальтернативных признаков, измеренных
по номинальной шкале. Подсчитывается
по формуле:
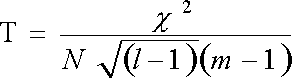
хи
– квадрат, коэффициент квадратической
сопряженности
l,
m
— число граф и строк в составленной
таблице сопряженности признаков
N
— общее число объектов в изучаемой
совокупности
Коэффициент
Крамера подсчитывается для неальтернативных
признаков, измеренных по номинальной
шкале, по формуле:
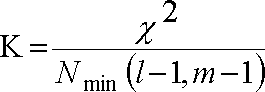
—
хи – квадрат, коэффициент квадратический
сопряженности
¯минимальное
из чисел в таблице ( l-1,
m
– 1)
χ-квадрат
– коэффициент квадратической сопряженности
используется для установления факта
существования взаимосвязи признаков,
измеренных по номинальной шкале, и при
подсчете коэффициентов Чупрова и
Крамера. Его
формула:
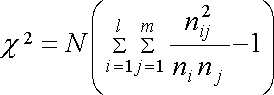
N
— итоговая сумма всех значений признаков
в таблице сопряженности
—
значение признаков в одной из клеток
таблицы
—
сумма значений признаков в одной из
строк таблицы (например, первой)
—
сумма значений признака в первой графе
таблицы.
21. Среднее арифметическое простое и взвешенное, особенности применения
Наиболее
распространенным видом средних величин
является средняя арифметическая, которая
в зависимости от характера имеющихся
данных может быть простой или взвешенной.
Средняя
арифметическая простая применяется,
когда значение вариантов встречается
по одному числу раз.
Средняя
арифметическая взбешенная применяется,
когда отдельное значение признака
повторяется неодинаковое количество
раз, т.е. она используется в расчетах
средней по 2 сгруппированным данным или
вариационным рядам, которые могут быть
дискретными и интервальными.
При
расчете средней по интервальному
вариационному ряду для выполнения
необходимых вычислений переходят о
интервалов к их серединам.
22. Коэффициенты связи для дихотомических таблиц
При
сравнении двух переменных, измеренных
в дихотомической шкале, мерой корреляционной
связи служит так называемый коэффициент
φ. Коэффициент фи представляет собой
коэффициент корреляции для дихотомических
данных.
Величина
коэффициента φ лежит в интервале между
+1 и -1и его знак для интерпретации
результатов не имеет значения.
Он
может быть как положительным и
отрицательным, характеризуя направление
связи двух дихотомически измеренных
признаков. Коэффициент φ можно вычислить
методом кодирования, а также используя
так называемую четырехпольную таблицу,
или таблицу сопряженности.
Для
применения коэффициента корреляции φ
необходимо соблюдать следующие условия:
1.
Сравниваемые признаки должны быть
измерены в дихотомической шкале.
2.
Число варьирующих признаков в сравниваемых
переменных X
и
Y должно быть одинаковым.
необходимо
соблюдать следующие условия:
1.
Сравниваемые признаки должны быть
измерены в разных шкалах: одна X – в
дихотомической шкале; другая Y – в шкале
интервалов или отношений.
2.
Переменная Y имеет нормальный закон
распределения.
3.
Число варьирующих признаков в
сравниваемых переменных X
и
Y должно быть одинаковым.
Основное
назначение корреляционного анализа
это выявление связи между переменными.
Мерой
связи являются коэффициенты корреляции.
Выбор
коэффициента корреляции напрямую
зависит от типа шкалы, в которой измерены
переменные, числа варьирующих признаков
в сравниваемых переменных и распределения
переменных.
Наличие
корреляции двух переменных еще не
означает что между ними существует
причинная связь.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
5.2 Индуктивная статистика
5.2.2 Сила связи между переменными в перекрёстных таблицах
Меры силы связи между переменными
Тест χ2 показывает только значимость взаимосвязи между переменными, но он никак не характеризует силу этой взаимосвязи.
Простое доказательство: если удвоить все числа в таблице, то и значение χ2 удвоится.
Меры силы взаимосвязи:
— Фи-коэффициент (φ)
— Коэффициент сопряженности признаков (C)
— Коэффициент Крамера (V)
— Коэффициент лямбда (λ)
Фи-коэффициент
Чем выше φ, тем сильнее взаимосвязь между переменными.
Значения больше 0,30 считаются существенными.
Проблемы:
— φ не стандартизовано, то есть оно зависит от количества строк и столбцов таблицы; верхний предел = 1 существует только в таблицах 2х2
— значения φ разных исследований нельзя сравнивать
Взаимосвязь не очень сильна
Коэффициент сопряженности признаков
Чем выше C, тем сильнее взаимосвязь между переменными.
Значения больше 0,30 считаются существенными.
Верхний предел C=1, но он не может быть достигнут.
Проблемы:
— C не стандартизован, то есть зависит от количества размерности таблицы
— значения C разных исследований нельзя сравнивать
Взаимосвязь не очень сильна
Коэффициент Крамера
r – количество строк в таблице
c – количество столбцов в таблице
Чем выше V, тем сильнее взаимосвязь между переменными.
Значения больше 0,30 считаются существенными.
Верхний предел V=1, но он может быть достигнут только на таблицах размерности 2х2.
Проблемы:
— V не стандартизован, то есть зависит от количества размерности таблицы
— значения V разных исследований нельзя сравнивать
Взаимосвязь не очень сильна
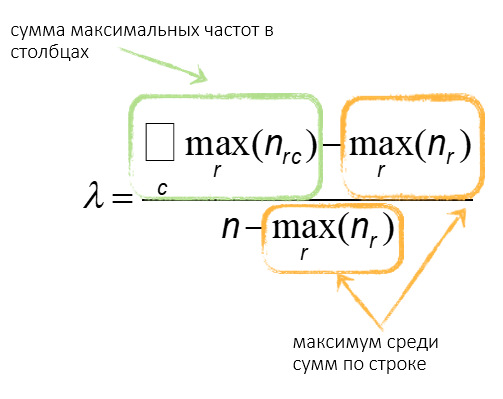
Коэффициент лямбда
r – индекс строк
c – индекс столбцов
Показывает выраженное в процентах улучшение возможности прогнозирования значения зависимой переменной при заданном значении независимой переменной.
Значения стандартизированы и лежат в пределах от 0 до 1
(1 – прогноз может быть сделан без ошибки, 0 – улучшения в прогнозировании нет).
Значения λ разных исследований можно сравнивать.
Знание пола увеличивает нашу способность прогнозирования на коэффициент 0,333, т.е. улучшает ее на 33,3%
| Пол | |||
|
Пользование интернетом |
Мужской |
Женский |
Сумма по строке |
|
редко |
5 |
10 |
15 |
|
часто |
10 |
5 |
15 |
|
Сумма по столбцу |
15 |
15 |
n=30 |
редко = r = 1
часто = r = 2
мужской = с = 1
женский = с = 2
В начало раздела
Информация о файлах Cookie
Мы используем файлы cookie, чтобы пользоваться нашим сайтом было удобно. В этих файлах сохраняются ваши предпочтения и информация о ваших посещениях. Нажимая кнопку «Принять все», вы соглашаетесь на использование всех файлов cookie. Однако вы можете отказаться от отдельных категорий файлов cookie в разделе «Настройки».
Меры связанности для переменных с номинальной шкалой
Коэффициент корреляции нельзя применять в качестве характеристики зависимости между переменными, если эти переменные принадлежат к номинальной шкале и имеют более двух категорий, потому что между их кодировками невозможно установить порядкового отношения и, следовательно, они не могут быть расположены в определенном, рационально объяснимом порядке.
Наилучшим средством для анализа таких зависимостей считается представленный в разделе 11.3.1 тест хи-квадрат, после которого при необходимости можно провести анализ наблюдаемых и ожидаемых частот, а также нормированных остатков. Этот анализ был описан в разделе 8.7.2.
Тем не менее и в этом случае также производились попытки разработать критерии количественной оценки степени связанности двух переменных, поставленных во взаимное соответствие. Эти критерии показывают степень взаимной зависимости или независимости двух переменных, принадлежащих к с номинальной шкале, причем значение
0 соответствует полной независимости переменных, а 1 — их максимальной зависимости. Меры связанности не могут иметь отрицательных значений, так как при отсутствии порядкового отношения нельзя дать ответа на вопрос о направлении зависимости.
В опросе членов городской организации одной из политических партий среди прочего выяснялось их занятие и определялось, выполняет ли респондент какую-либо партийную функцию. Выдержка из ответов респондентов-мужчин содержится в файле partei.sav.
-
Загрузите файл partei.sav и создайте таблицу сопряженности с переменной funk в
строках и переменной beruf в столбцах. -
Задайте вывод ожидаемых частот, стандартизованных остатков, процентов по столбцам и критерия хи-квадрат.
Занятие * Партийная работа Crosstabulation (Таблица сопряженности)
|
|
|
|||||
| Наемный работник |
|
Предпри-ниматель |
||||
|
|
|
|
13 |
|
|
|
|
|
12,4 |
|
|
|
||
|
|
59,1% |
|
|
|
||
|
|
,2 |
|
|
|||
|
|
|
9 |
|
|
|
|
|
|
9,6 |
|
|
|
||
|
|
40,9% |
|
|
|
||
|
|
-,2 |
|
|
|||
|
|
|
22 |
|
|
|
|
|
|
22,0 |
|
|
|
||
|
|
100,0% |
|
|
|
Chi-Square Tests
|
Value |
df |
Asymp. Sig. (2-sided) |
|
|
Pearson Chi-Square (Критерий хи-квадрат по Пирсону) |
15,01 7 (a) |
2 |
,001 |
|
Likelihood Ratio (Отношение правдоподобия) |
16,421 |
2 |
,000 |
|
Li near-by-Li near Association (Зависимость линейный-линейный) |
4,420 |
1 |
,036 |
|
N of Valid Cases |
64 |
а. и cells (,0%) have expected count less than 5. The minimum expected count is 11,50. (0 ячеек (,0%) имеют ожидаемую частоту менее 5. Минимальная ожидаемая частота 7,88.)
Результат получился максимально значимым: участие в партийной работе весьма характерно для государственных служащих, а для предпринимателей — совсем не характерно, тогда как наемные работники находятся посредине. Теперь зададим (кнопкой Statistics…) вывод всех мер связанности для переменных, принадлежащих к номинальной шкале (флажки в группе Nominal).
Directional Measures (Направленные меры)
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
a. Not assuming the null hypothesis (Нулевая гипотеза не принимается).
b. Using the asymptotic standard error assuming the null hypothesis (Используется асимптотическая
стандартная ошибка с принятием нулевой гипотезы).
с. Based on chi-square approximation (На основе аппроксимации по распределению хи-квадрат).
d. Likelihood ratio chi-square probability (Степень правдоподобия при распределении вероятности
по закону хи-квадрат).
Symmetric Measures (Симметричные меры)
|
Value |
Approx. Sig. |
||
|
Nominal by Nominal (Номинальный-номинальный) |
Phi (Фи) |
,484 |
,001 |
|
Cramer’s V (V Крамера) |
,484 |
,001 |
|
|
Contingency Coefficient (Коэффициент сопряженности признаков) |
,436 |
,001 |
|
|
N of Valid Cases |
64 |
a. Not assuming the null hypothesis (Нулевая гипотеза не принимается).
b. Using the asymptotic standard error assuming the null hypothesis (Используется асимптотическая
стандартная ошибка с принятием нулевой гипотезы).
Коэффициент сопряженности признаков (Пирсона)
Его величина всегда находится в пределах от 0 до 1 и вычисляется (как и значения критериев Фишера (<р) и Крамера (V)) с использованием значения критерия хи-квадрат:
Здесь N — общая сумма частот в таблице сопряженности. Так как
N всегда больше нуля, коэффициент сопряженности признаков никогда не достигает единицы. Максимальное значение зависит от количества строк и столбцов таблицы сопряженности и в таблице размером 3*2 составляет (как в данном примере) 0,762. По этой причине коэффициенты сопряженности признаков для двух таблиц с разным количеством полей несопоставимы.
Критерий Фишера (<р)
Этот коэффициент можно использовать только для таблиц 2*2, так как в других случаях он может превысить значение 1:
Критерий Крамера (V)
Этот критерий представляет собой модификацию критерия Фишера и для любых таблиц сопряженности он дает значение в пределах от 0 до 1, включая 1:
Здесь k — наименьшее из количеств строк и столбцов.
Три названных критерия основаны на использовании критерия хи-квадрат. Они различными способами нормируют его значение по отношению к размеру выборки. Так, если формуле для V Крамера положить k = 2, то значения (р и V Крамера совпадут. Определение значимости основано на значении критерия хи-квадрат.
При оценке полученных значений мер связанности, находящихся в нашем примере в промежутке между 0,4 и 0,5, следует учесть, что значение 1 достигается очень редко или вообще никогда. Другие меры связанности (Я, т Гудмена-Крускала и коэффициент неопределенности) определяются на основе так называемой концепции пропорционального сокращения ошибки. При определении этих критериев одна переменная рассматривается как зависимая; по этой причине данные критерии называются «направленными мерами».
Лямбда
В данном примере вопрос о партийной работе можно рассматривать как зависимую переменную, определяемую родом занятий. Если для какого-то отдельно взятого человека надо сделать предположение о том, выполняет ли он партийную работу или нет, то, естественно, делается наиболее вероятное предположение, соответствующее наиболее часто даваемому ответу — в данном случае, предположение о том, что опрашиваемый занимается партийной работой. Такой ответ дают 56,3% респондентов; однако в 43,7% наблюдений наше предположение будет неверным.
Вероятность предположения можно повысить, если учитывать другую переменную — род занятий. Для наемных работников, как и для государственных служащих, можно достаточно уверенно прогнозировать участие в партийной работе, причем этот прогноз окажется неверным для 9 наемных работников и для 2 государственных служащих. В то же время для предпринимателей можно с большими основаниями предположить, что они не занимаются партийной работой, и ошибиться в 7 наблюдениях. Таким образом, для общего числа 64 опрашиваемых мы получаем 9 + 2 + 7=18 наблюдений, или 28,1 %, в которых прогноз будет неверен. Легко видеть, что первоначальная вероятность ошибки 43,7% значительно сократилась.
На основе этих двух вероятностей можно вычислить относительное сокращение
ошибки, которое и называется лямбда:
Лямбда=(Ошибка при первом прогнозе — Ошибка при втором прогнозе)/Ошибка при первом
В нашем примере:
Лямбда =( 43,7% — 28.1%)/43,7% = ,357
Если ошибка при втором прогнозе сокращается до 0, лямбда будет равна 1. Если ошибки при первом и при втором прогнозе одинаковы, лямбда = 0. В этом случае вторая переменная никак не помогает в уточнении предсказания значения первой (зависимой переменной); то есть выбранные две переменные совершенно не зависят друг от
друга.
Так как ваш быстрый, но совершенно не умеющий соображать компьютер не знает, какую переменную следует считать зависимой, SPSS вычисляет оба значения Я, поочередно рассматривая каждую из переменных как зависимую. В случае, если выясняется, что ни одну из выбранных переменных нельзя объявить зависимой, выводится среднее двух этих значений с обозначением «лямбда
-симметричная».
Тау (т) Гудмена-Крускала
Это вариант меры связанности , который SPSS всегда вычисляет совместно с ней. При определении этой меры количество правильных предсказаний определяется по-иному: наблюдаемые частоты взвешиваются с учетом своих процентов и складываются. Для первого прогноза это дает:
36 * 56,3% + 28 * 43,8% =32,53
Согласно этому выражению, из 64 респондентов неверное предположение сделано для 31,47, что составляет 49,17%.
С учетом второй переменной количество верных предположений (второй прогноз)
составляет:
13 * 59,1 % + 16 * 88,9 % + 7 * 29,2 % + 9 * 40,9 % + 2 * 11,1 % + 17 * 70,8 % =
39,89
Итак, при втором прогнозе сделано 24,11 неверных прогнозов из 64, что составляет 37,67%. Тогда сокращение ошибки равно
(49.17 %-37.67%)/49,17 %=0,235
Это значение выводится под названием «тау Гудмена-Крускала». И в этом случае SPSS выдает второе значение т, рассматривая вторую переменную, как зависимую.
Коэффициент неопределенности
Это еще один вариант критерия лямбда, при определении которого имеется в виду не ошибочное предсказание, а «неопределенность», то есть степень неточности предсказаний. Эта неопределенность вычисляется по достаточно сложным формулам, которые мы опускаем. Коэффициент неопределенности также принимает значения в диапазоне от 0 до 1. Значение 1 говорит о том, что одну переменную можно точно предсказать по значениям другой.
В статистике , V Крамера (иногда упоминаются как фи Крамер и обозначаются как φ с ) является мерой ассоциации между двумя номинальными переменными , что дает значение от 0 до +1 (включительно). Он основан на статистике хи-квадрат Пирсона и был опубликован Харальдом Крамером в 1946 году.
Использование и интерпретация
φ c — это взаимная корреляция двух дискретных переменных, которая может использоваться с переменными, имеющими два или более уровней. φ c — это симметричная мера: не имеет значения, какую переменную мы помещаем в столбцы, а какую — в строки. Кроме того, порядок строк / столбцов не имеет значения, поэтому φ c может использоваться с номинальными типами данных или выше (в частности, упорядоченными или числовыми).
V Крамера также может применяться к качеству соответствия моделей хи-квадрат, когда существует таблица 1 × k (в данном случае r = 1). В этом случае k принимается как количество необязательных результатов, и оно функционирует как мера тенденции к единственному результату.
V Крамера варьируется от 0 (что соответствует отсутствию ассоциации между переменными) до 1 (полная ассоциация) и может достигать 1 только тогда, когда каждая переменная полностью определяется другой.
φ c 2 — среднеквадратичная каноническая корреляция между переменными.
В случае таблицы непредвиденных обстоятельств 2 × 2 V Крамера равно коэффициенту Phi .
Обратите внимание, что, поскольку значения хи-квадрат имеют тенденцию увеличиваться с увеличением количества ячеек, чем больше разница между r (строки) и c (столбцы), тем более вероятно, что φ c будет стремиться к 1 без убедительных доказательств значимой корреляции.
V можно рассматривать как связь между двумя переменными как процент от их максимально возможного изменения. V 2 — среднеквадратичная каноническая корреляция между переменными.
Расчет
Пусть выборка размера n одновременно распределенных переменных и для задается частотами
-
количество раз, когда значения наблюдались.
Тогда статистика хи-квадрат будет:
V Крамера вычисляется путем деления квадратного корня из статистики хи-квадрат на размер выборки и минимальное измерение минус 1:
куда:
Р-значение для значения из V является той же, что вычисляется с помощью критерия хи-квадрат тест Пирсона .
Формула дисперсии V = φ c известна.
В R функция cramerV() из пакета rcompanion вычисляет V с помощью функции chisq.test из пакета stats. В отличие от функции cramersV() из lsr пакета, cramerV() также предлагает возможность исправления смещения. Применяется исправление, описанное в следующем разделе.
Коррекция смещения
V Крамера может быть сильно предвзятой оценкой его аналога по населению и будет иметь тенденцию переоценивать силу ассоциации. Поправка смещения, используя приведенные выше обозначения, дается выражением
куда
и
Затем оценивает ту же численность населения, что и V Крамера, но обычно с гораздо меньшей среднеквадратичной ошибкой . Причина исправления заключается в том, что в условиях независимости
.
Смотрите также
Другие меры корреляции для номинальных данных:
- Коэффициент фи
- Т. Чупрова
- Коэффициент неопределенности
- Коэффициент лямбда
- Индекс Рэнда
- Индекс Дэвиса – Боулдина
- Индекс Данна
- Индекс Жаккара
- Индекс Фаулкса – Маллоуса
Другие статьи по теме:
- Таблица сопряженности
- Размер эффекта
- Кластерный анализ § Внешняя оценка
Рекомендации
внешняя ссылка
- Мера ассоциации для непараметрической статистики (Алан К. Акок и Гордон Р. Ставиг, стр. 1381, 1381–1386)
- Номинальная ассоциация: Phi and Cramer’s Vl с домашней страницы Пэта Даттало.




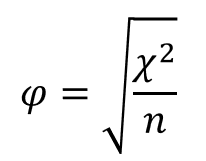
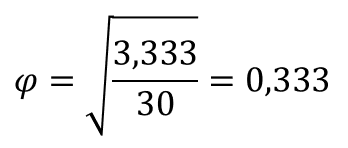
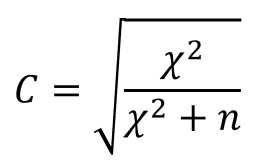
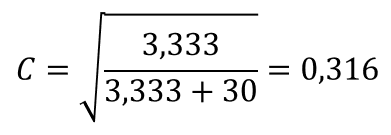
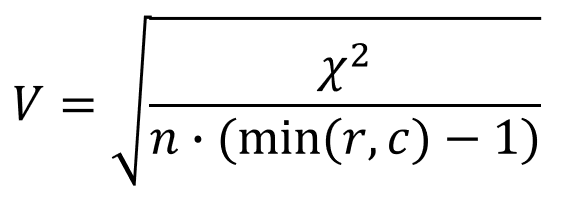
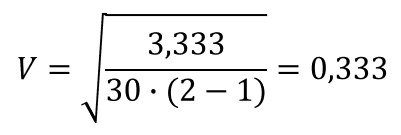
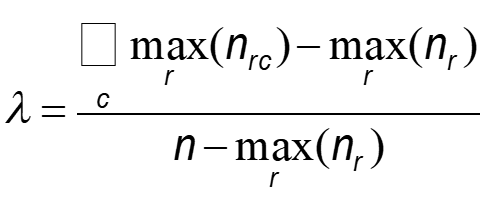
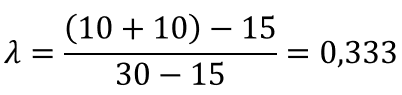
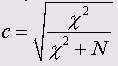
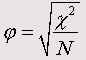
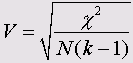












![{ Displaystyle Е [ varphi ^ {2}] = { гидроразрыва {(к-1) (г-1)} {п-1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/935b9625bc543ee6d3e8efd2f5623773c88fe0c7)