17 авг. 2022 г.
читать 2 мин
Коэффициент вариации , часто обозначаемый аббревиатурой CV , представляет собой способ измерения степени разброса значений в наборе данных по отношению к среднему значению. Он рассчитывается как:
CV = σ / μ
куда:
- σ: стандартное отклонение набора данных
- μ: среднее значение набора данных
Проще говоря, коэффициент вариации — это отношение между стандартным отклонением и средним значением.
Он часто используется для сравнения вариаций между двумя разными наборами данных. Например, в финансах он используется для сравнения среднего ожидаемого дохода от инвестиций с ожидаемым стандартным отклонением инвестиций.
Например, предположим, что инвестор рассматривает возможность инвестирования в следующие два взаимных фонда:
Взаимный фонд A: среднее = 9%, стандартное отклонение = 12,4%
Взаимный фонд B: среднее = 5%, стандартное отклонение = 8,2%
Инвестор может рассчитать коэффициент вариации для каждого фонда:
- CV для взаимного фонда A = 12,4% / 9% = 1,38
- CV для взаимного фонда B = 8,2% / 5% = 1,64
Поскольку взаимный фонд А имеет более низкий коэффициент вариации, он предлагает лучшую среднюю доходность по сравнению со стандартным отклонением.
В следующем пошаговом примере объясняется, как рассчитать коэффициент вариации для следующего набора данных на калькуляторе TI-84:
Набор данных: 3, 8, 8, 13, 16, 11
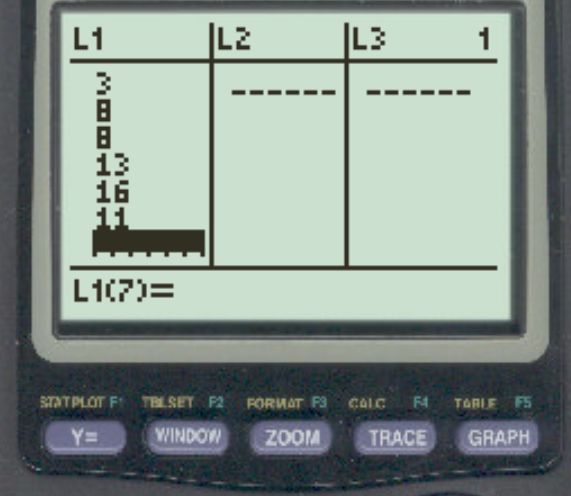
Шаг 1: введите данные
Сначала мы введем значения данных.
Нажмите Stat , затем нажмите EDIT.Затем введите значения набора данных в столбец L1:
Шаг 2: Найдите коэффициент вариации
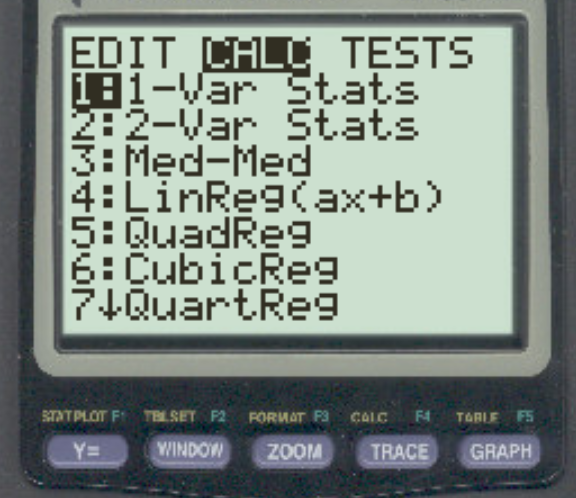
Затем нажмите Stat , а затем прокрутите вправо и нажмите CALC .
Затем нажмите 1-Var Stats .
В появившемся новом экране нажмите Enter .
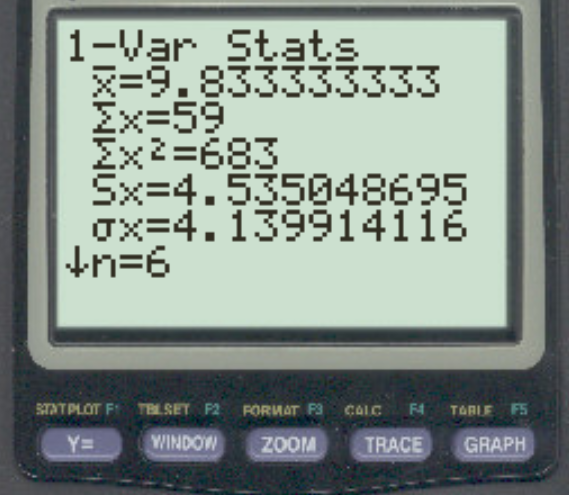
После того, как вы нажмете Enter , появится список сводной статистики:
На этом экране мы можем наблюдать значения среднего и стандартного отклонения выборки:
- Среднее ( х ): 9,8333
- Стандартное отклонение выборки (Sx): 4,535
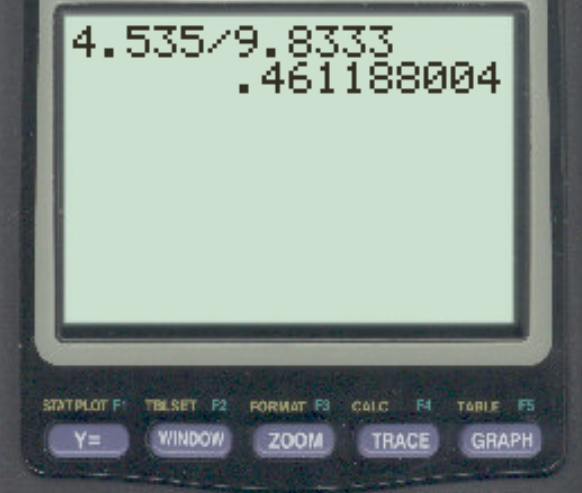
Затем мы можем рассчитать коэффициент вариации как:
Коэффициент вариации для этого набора данных оказывается равным 0,4611.В процентном отношении это равно 46,11% .
Дополнительные ресурсы
Как найти сводку из пяти чисел на калькуляторе TI-84
Как найти межквартильный диапазон на калькуляторе TI-84
Коэффициент корреляции Пирсона используется для измерения силы линейной связи между двумя переменными.
Символ для коэффициента корреляции — r, а r всегда находится в диапазоне от -1 до 1.
Ограничения r:
- Его можно рассчитать только для линейных отношений.
- На него влияют выбросы. Останец это число значительно отличается от всех других результатов. Если вы пытаетесь вычислить среднее (среднее) чисел, сильно отличающееся число означает, что результаты будут искажены и не обязательно являются истинным представлением данных. То же самое и для коэффициентов корреляции. Если есть выброс, коэффициент корреляции ненадежен.
Что означает значение r
|
1 |
|
|
сильная положительная линейная ассоциация |
|
|
0,75 |
|
|
умеренная положительная линейная ассоциация |
|
|
0,5 |
|
|
слабая положительная линейная ассоциация |
|
|
0,25 |
|
|
нет ассоциации |
|
|
0 |
|
|
нет ассоциации |
|
|
— 0,25 |
|
|
слабая отрицательная линейная ассоциация |
|
|
— 0,5 |
|
|
умеренная отрицательная линейная ассоциация |
|
|
— 0,75 |
|
|
сильная отрицательная линейная ассоциация |
|
|
-1 |
Abacus: «Конечно, в мои дни все было проще!»
Как рассчитать коэффициент корреляции на калькуляторе Ti-89
- Нажмите кнопку APPS
- Выберите редактор статистики / списка
- Введите данные независимой переменной в list1. Независимая переменная вызывает изменение зависимой переменной. Например, если вы выяснить, влияет ли чей — то возраст, как они счастливы, вы бы возраст человека независимой переменной, потому что вы пытаетесь выяснить, если возраст человека меняет свой уровень счастья.
- Введите данные зависимой переменной в list2.
- Выберите F4: Calc.
- Выберите 3: Регрессии
- Выберите 2: Лин Рег (ax + b)
- Там, где написано «X list», введите list1 (без пробелов). Вы делаете это, потому что вы сохранили независимую переменную в списке 1, а по оси X (нижняя горизонтальная линия графика) всегда отображается независимая переменная.
- Там, где написано «Y список», введите list2 (без пробелов).
- Там, где написано «Сохранить RegEan в:», выберите любой из раскрывающихся вариантов. Это не имеет значения, есть просто параметры, чтобы вы могли повторно получить доступ к данным позже, если они вам понадобятся, вместо сохранения поверх ранее сохраненных данных, которые могут вам все еще понадобиться.
- Нажмите ввод ТОЛЬКО ОДИН РАЗ.
- Через несколько секунд на экране калькулятора должно появиться окно. Значение r — это ваш коэффициент корреляции.
Как найти коэффициент детерминации на калькуляторе TI 89
Коэффициент детерминации (r ^ 2) просто вычисляется возведением в квадрат коэффициента корреляции. Просто введите свой коэффициент корреляции и нажмите ^ 2.
Онлайн калькулятор для расчета коэффициента вариации, коэффициент вариации – это величина равная отношению стандартного (среднеквадратичного) отклонения случайной величины к ее математическому ожиданию, выражается в процентах.
В статистике принято, что:
— при коэффициенте вариации меньше 10%, степень рассеивания данных считается незначительной;
— если коэффициент от 10% до 20% — средней;
— больше 20% и меньше или равно 33% — значительной.
Совокупность считается однородной если коэффициент не превышает 33%, а если больше 33%, то – неоднородной.
Одно из основных применений коэффициента вариации — оценка инвестиционных рисков, например для расчет начальной максимальной цены контракта (НМЦК).
Коэффициенты корреляции — это индикаторы силы линейной связи между двумя разными переменными x и y. Коэффициент линейной корреляции больше нуля указывает на положительную взаимосвязь. Значение меньше нуля означает отрицательную связь. Наконец, нулевое значение указывает на отсутствие связи между двумя переменными x и y. В этой статье объясняется значение коэффициента линейной корреляции для инвесторов, как рассчитать ковариацию для акций и как инвесторы могут использовать корреляцию для прогнозирования рынка.
Ключевые выводы:
- Коэффициенты корреляции используются для измерения силы линейной связи между двумя переменными.
- Коэффициент корреляции больше нуля указывает на положительную взаимосвязь, а значение меньше нуля означает отрицательную взаимосвязь.
- Нулевое значение указывает на отсутствие связи между двумя сравниваемыми переменными.
- Отрицательная корреляция или обратная корреляция — ключевая концепция при создании диверсифицированных портфелей, которые могут лучше противостоять волатильности портфеля.
- Расчет коэффициента корреляции занимает много времени, поэтому данные часто загружаются в калькулятор, компьютер или статистическую программу, чтобы найти коэффициент.
Понимание корреляции
Коэффициент корреляции ( ρ ) — это мера, которая определяет степень, в которой связано движение двух разных переменных. Наиболее распространенный коэффициент корреляции, генерируемый корреляцией произведения-момента Пирсона, используется для измерения линейной связи между двумя переменными. Однако в нелинейной зависимости этот коэффициент корреляции не всегда может быть подходящей мерой зависимости.
Возможный диапазон значений коэффициента корреляции от -1,0 до 1,0. Другими словами, значения не могут превышать 1,0 или быть меньше -1,0. Корреляция -1,0 указывает на абсолютную отрицательную корреляцию, а корреляция 1,0 указывает на идеальную положительную корреляцию. Если коэффициент корреляции больше нуля, это положительная связь. И наоборот, если значение меньше нуля, это отрицательная связь. Нулевое значение указывает на отсутствие связи между двумя переменными.
Краткий обзор
При интерпретации корреляции важно помнить, что наличие корреляции между двумя переменными не означает, что одна вызывает другую.
Корреляция и финансовые рынки
На финансовых рынках коэффициент корреляции используется для измерения акции движутся в противоположных направлениях, коэффициент корреляции отрицательный.
Если коэффициент корреляции двух переменных равен нулю, между переменными нет линейной зависимости. Однако это только для линейной зависимости. Возможно, что переменные имеют сильную криволинейную связь. Когда значение ρ близко к нулю, обычно между -0,1 и +0,1, считается, что переменные не имеют линейной зависимости (или очень слабой линейной зависимости).
Например, предположим, что цены на кофе и компьютеры наблюдаются и обнаруживают корреляцию +,0008. Это означает, что между двумя переменными нет корреляции или взаимосвязи.
Расчет ρ
Ковариация двух переменных в вопросе должны быть рассчитаны, прежде чем корреляция может быть определена. Затем требуется стандартное отклонение каждой переменной . Коэффициент корреляции определяется делением ковариации на произведение стандартных отклонений двух переменных.
Стандартное отклонение — это мера разброса данных от среднего значения. Ковариация — это мера того, как две переменные изменяются вместе. Однако его масштабы безграничны, поэтому его трудно интерпретировать. Нормализованная версия статистики вычисляется путем деления ковариации на произведение двух стандартных отклонений. Это коэффициент корреляции.
Положительное соотношение
Положительная корреляция — когда коэффициент корреляции больше 0 — означает, что обе переменные движутся в одном направлении. Когда ρ равно +1, это означает, что две сравниваемые переменные имеют идеальную положительную взаимосвязь; когда одна переменная движется выше или ниже, другая переменная движется в том же направлении с той же величиной.
Чем ближе значение ρ к +1, тем сильнее линейная зависимость. Например, предположим, что стоимость цен на нефть напрямую связана с ценами на авиабилеты с коэффициентом корреляции +0,95. Взаимосвязь между ценами на нефть и стоимостью авиабилетов имеет очень сильную положительную корреляцию, так как значение близко к +1. Таким образом, если цена на нефть снижается, цены на авиабилеты также уменьшаются, а если цена на нефть растет, то же самое происходит и с ценами на авиабилеты.
На приведенной ниже диаграмме мы сравниваем один из крупнейших банков США, JPMorgan Chase & Co. ( биржевым фондом Financial Select SPDR Exchange Traded Fund (ETF) (XLF ).1 Как вы понимаете, компания JPMorgan Chase & Co. должна иметь положительную корреляцию с банковской отраслью в целом. Мы видим, что коэффициент корреляции в настоящее время составляет 0,98, что свидетельствует о сильной положительной корреляции. Значение выше 0,50 обычно свидетельствует о положительной корреляции.
Понимание корреляции между двумя акциями (или одной акцией) и отраслью может помочь инвесторам оценить, как акции торгуются по сравнению с аналогами. Все типы ценных бумаг, включая облигации, сектора и ETF, можно сравнить с помощью коэффициента корреляции.
Отрицательная корреляция
Отрицательная (обратная) корреляция возникает, когда коэффициент корреляции меньше 0. Это указывает на то, что обе переменные движутся в противоположном направлении. Короче говоря, любое значение от 0 до -1 означает, что две ценные бумаги движутся в противоположных направлениях. Когда ρ равно -1, связь считается полностью отрицательно коррелированной. Короче говоря, если одна переменная увеличивается, другая уменьшается с той же величиной (и наоборот). Однако степень отрицательной корреляции двух ценных бумаг может меняться со временем (и они почти никогда не коррелируют точно все время).
Примеры отрицательной корреляции
Например, предположим, что проводится исследование для оценки взаимосвязи между наружной температурой и счетами за отопление. В исследовании делается вывод об отрицательной корреляции между ценами на отопление и температурой наружного воздуха. Коэффициент корреляции равен -0,96. Эта сильная отрицательная корреляция означает, что по мере снижения температуры на улице цены на отопление увеличиваются (и наоборот).
Когда дело доходит до инвестирования, отрицательная корреляция не обязательно означает, что следует избегать ценных бумаг. Коэффициент корреляции может помочь инвесторам диверсифицировать свой портфель, включив в него набор инвестиций, имеющих отрицательную или низкую корреляцию с фондовым рынком. Короче говоря, при снижении риска волатильности в портфеле иногда все же привлекаются противоположности.
Например, предположим, что у вас есть сбалансированный портфель на 100 000 долларов, который инвестируется на 60% в акции и 40% в облигации. В год высоких экономических показателей доходность акционерного капитала вашего портфеля может составить 12%, а доходность облигационного компонента — -2%, поскольку процентные ставки растут (что означает, что цены на облигации падают). Таким образом, общая доходность вашего портфеля составит 6,4% ((12% x 0,6) + (-2% x 0,4). В следующем году, когда экономика заметно замедлится и процентные ставки будут снижены, ваш портфель акций может принести -5 %, в то время как ваш портфель облигаций может приносить 8%, что дает вам общую доходность портфеля 0,2%.
Что, если бы вместо сбалансированного портфеля ваш портфель состоял на 100% из акций? Используя те же предположения о доходности, ваш портфель, полностью состоящий из акций, будет иметь доходность 12% в первый год и -5% во второй год. Эти цифры явно более волатильны, чем доходность сбалансированного портфеля, составляющая 6,4% и 0,2%.
Коэффициент линейной корреляции
Коэффициент линейной корреляции — это число, вычисленное на основе заданных данных, которое измеряет силу линейной связи между двумя переменными, x и y. Знак коэффициента линейной корреляции указывает направление линейной зависимости между x и y. Когда r (коэффициент корреляции) близок к 1 или -1, линейная зависимость сильная; когда он близок к 0, линейная зависимость слабая.
Даже для небольших наборов данных вычисления коэффициента линейной корреляции могут оказаться слишком длинными, чтобы их можно было выполнять вручную. Таким образом, данные часто загружаются в калькулятор или, что более вероятно, в компьютер или статистическую программу, чтобы найти коэффициент.
Коэффициент Пирсона
Как расчет коэффициента Пирсона, так и базовая линейная регрессия — это способы определить, как статистические переменные связаны линейно. Однако эти два метода различаются. Коэффициент Пирсона — это мера силы и направления линейной связи между двумя переменными без предположения о причинно-следственной связи. Коэффициент Пирсона показывает корреляцию, а не причинно-следственную связь. Коэффициенты Пирсона варьируются от +1 до -1, где +1 представляет положительную корреляцию, -1 представляет отрицательную корреляцию, а 0 означает отсутствие взаимосвязи.
Простая линейная регрессия описывает линейную связь между переменной ответа (обозначенной y) и независимой переменной (обозначенной x) с использованием статистической модели. Статистические модели используются для прогнозов.
Краткий обзор
Упростите линейную регрессию, вычислив корреляцию с помощью такого программного обеспечения, как Excel.
В финансах, например, корреляция используется в нескольких анализах, включая расчет стандартного отклонения портфеля. Поскольку это требует много времени, корреляцию лучше всего рассчитать с помощью такого программного обеспечения, как Excel. Корреляция объединяет статистические концепции, а именно дисперсию и стандартное отклонение. Дисперсия — это дисперсия переменной вокруг среднего значения, а стандартное отклонение — это квадратный корень из дисперсии.
Поиск корреляции с помощью Excel
В Excel есть несколько методов расчета корреляции. Самый простой — получить два набора данных рядом и использовать встроенную формулу корреляции:
Если вы хотите создать корреляционную матрицу для ряда наборов данных, в Excel есть подключаемый модуль анализа данных, который находится на вкладке «Данные» в разделе «Анализ».
Выберите таблицу доходов. В этом случае наши столбцы имеют заголовки, поэтому мы хотим установить флажок «Ярлыки в первой строке», чтобы Excel обрабатывал их как заголовки. Затем вы можете выбрать вывод на том же листе или на новом листе.
Как только вы нажмете Enter, данные будут созданы автоматически. Вы можете добавить текст и условное форматирование, чтобы очистить результат.
Часто задаваемые вопросы о коэффициенте линейной корреляции
Что такое коэффициент линейной корреляции?
Коэффициент линейной корреляции — это число, вычисленное на основе заданных данных, которое измеряет силу линейной связи между двумя переменными, x и y.
Как найти коэффициент линейной корреляции?
Корреляция объединяет несколько важных и связанных статистических концепций, а именно дисперсию и стандартное отклонение. Дисперсия — это дисперсия переменной вокруг среднего значения, а стандартное отклонение — это квадратный корень из дисперсии.
Формула:
Вычисления слишком длинные, чтобы их можно было выполнять вручную, и программное обеспечение, такое как Excel или статистическая программа, является инструментами, используемыми для вычисления коэффициента.
Что подразумевается под линейной корреляцией?
Коэффициент корреляции — это значение от -1 до +1. Коэффициент корреляции +1 указывает на идеальную положительную корреляцию. Когда переменная x увеличивается, переменная y увеличивается. Когда переменная x уменьшается, переменная y уменьшается. Коэффициент корреляции -1 указывает на абсолютную отрицательную корреляцию. По мере увеличения переменной x переменная z уменьшается. Когда переменная x уменьшается, переменная z увеличивается.
Как найти коэффициент линейной корреляции на калькуляторе?
Графический калькулятор необходим для расчета коэффициента корреляции.Следующие инструкции предоставлены Statology.
Шаг 1. Включите диагностику
Вам нужно будет сделать этот шаг на калькуляторе только один раз. После этого вы всегда можете начать с шага 2 ниже. Если вы этого не сделаете, r (коэффициент корреляции) не будет отображаться при запуске функции линейной регрессии.
Нажмите [2nd], а затем [0], чтобы войти в каталог вашего калькулятора. Прокрутите, пока не увидите «DiagnosticsOn».
Нажимайте Enter, пока на экране калькулятора не появится надпись «Готово».
Это важно повторить: вам никогда не придется делать это снова, если вы не перезагрузите калькулятор.
Шаг 2: введите данные
Введите свои данные в калькулятор, нажав [STAT], а затем выбрав 1: Edit. Чтобы упростить задачу, вы должны ввести все свои «данные x» в L1 и все «данные y» в L2.
Шаг 3: Рассчитайте!
После того, как вы введете свои данные, вы перейдете к [STAT], а затем к меню CALC вверху. Наконец, выберите 4: LinReg и нажмите Enter.
Это оно! Готово! Теперь вы можете просто считать коэффициент корреляции прямо с экрана (его r). Помните, что если r не отображается на вашем калькуляторе, необходимо включить диагностику. Это то же самое место на калькуляторе, где вы найдете уравнение линейной регрессии и коэффициент детерминации.
Суть
Коэффициент линейной корреляции может быть полезен при определении взаимосвязи между инвестициями и рынком в целом или другими ценными бумагами. Его часто используют для прогнозирования доходности фондового рынка. Это статистическое измерение полезно во многих отношениях, особенно в финансовой отрасли. Например, это может быть полезно для определения того, насколько хорошо взаимный фонд ведет себя по сравнению с его эталонным индексом, или его можно использовать для определения того, как взаимный фонд ведет себя по отношению к другому фонду или классу активов. Добавляя взаимный фонд с низкой или отрицательной корреляцией к существующему портфелю, можно получить преимущества диверсификации.
Онлайн-калькулятор соотношений поможет вам определить одинаковые коэффициенты, указав три из четырех частей двух соотношений. Кроме того, этот калькулятор соотношений лучше всего подходит для нахождения пятой и шестой частей из трех соотношений, давая любые четыре части. Наш решатель соотношений выполняет следующие семь операций как с двумя, так и с тремя отношениями.
- Найдите эквивалент отношения
- Сделайте соотношение больше
- Сделайте соотношение меньше
- Упростить соотношение
- Упростите соотношение до формы “1: n: m”
- Упростите соотношение до формы “n: 1: m”
- Упростите соотношение до формы “n: m: 1”
Прежде чем мы собираемся использовать этот калькулятор соотношений, мы должны знать основное определение, формулу соотношения и то, как найти соотношение вручную. Продолжайте читать, чтобы получить краткие сведения о том, как делать соотношения.
Кроме того, вы можете попробовать наш онлайн-калькулятор пропорций, который поможет вам легко решить проблему пропорций разными методами.
Читать дальше!
Что такое коэффициент?
Его можно определить как «сравнение двух конкретных чисел, очень часто представленных в виде дробей». Просто он показывает, сколько одной части отношения содержится в другой части. Наш искатель соотношений разработан для вычисления этого контраста и определения взаимосвязи между числами.
как посчитать соотношение чисел (шаг за шагом):
Отношение состоит из двух частей: числитель и знаменатель, как и дробь. Если у нас есть два отношения, и мы хотим вычислить соотношение для недостающего значения в соотношении, просто выполните следующие действия:
- Запишите отношения в виде дроби и вставьте любую переменную (x или y) в пропущенное значение
- Установите дроби равными друг другу
- Используя перекрестное умножение, сгенерируйте уравнение
- Найдите недостающую переменную
- Наконец, попробуйте калькулятор соотношений, чтобы проверить свой ответ.
Вы можете воспользоваться нашим онлайн-калькулятором дробей, чтобы сложить, вычесть, умножить или разделить две или три дроби. Здесь у нас есть ручной пример, чтобы прояснить понимание:
Пример:
У нас есть 6 кусочков пиццы, из которых съедаются 2. Теперь мы хотим знать, сколько кусочков можно съесть из 54 кусочков пиццы?
Решение:
Шаг 1:
Запишите соотношение в виде дроби как:
Съеденный ломтик / всего ломтик = 2/6
Съеденный ломтик / всего ломтик = x / 54
Шаг 2:
Приравняйте дроби друг к другу:
2/6 = х / 54
Шаг 3:
Крестным умножением:
6х = 54 * 2
х = 54 * 2/6
х = 108/6
х = 18
Мы рекомендуем вам использовать наш калькулятор соотношений, если вы собираетесь решать комплексные отношения больших чисел.
Как использовать онлайн-калькулятор соотношений:
Наш калькулятор – точный инструмент для упрощения и поиска неизвестного значения в соотношении. Вам просто нужно придерживаться следующих пунктов для расчета соотношений:
Проведите по!
Входы:
- Прежде всего, нажмите вкладку, чтобы выбрать, сколько соотношений вы хотите выполнить
- вычисления. Это может быть A: B или A: B: C
- Затем выберите метод расчета из раскрывающегося списка этого калькулятора.
- Затем введите в поля в соответствии с выбранными входными параметрами.
- Как только вы закончите, нажмите кнопку расчета
Выходы:
Калькулятор показывает:
- Отсутствующие значения
- Упрощение соотношения
- Визуальное представление отношения (круговая диаграмма)
Заметка:
Этот калькулятор соотношений не даст вам значений, которые вам не нужны; он даст вам результат в соответствии с входными параметрами.
Что такое золотое сечение?
Когда две величины имеют то же отношение, что и отношение их суммы к большей из двух величин, то это соотношение называется золотым сечением. Например, если величины выражены в x и y, то золотое сечение между x и y равно (x + y) / x = x / y.
Конечное примечание:
К счастью, вы узнали о том, как рассчитать соотношение соотношения вручную и с помощью калькулятора. Соотношение используется везде, от приготовления пищи до строительства дома. Это очень полезно для образования K-12 и во многих других областях науки, таких как механика, бизнес и бухгалтеры, еда и многие другие. Когда дело доходит до решения отношений для комплексных чисел, просто используйте онлайн-калькулятор соотношений, который поможет вам найти недостающее значение в соотношении и выполнить упрощение отношения по вашему желанию.
Other Langauges: Ratio Calculator, Oran Hesaplama, Kalkulator Rasio, Kalkulator Współczynnika, Verhältnis Berechnen, 比率 計算, 비율계산기, Výpočet Poměru, Calculadora Razão, Calcul Ratio, Calcolo Rapporto, حساب النسبة, Suhde Laskuri, Forhold Lommeregner.