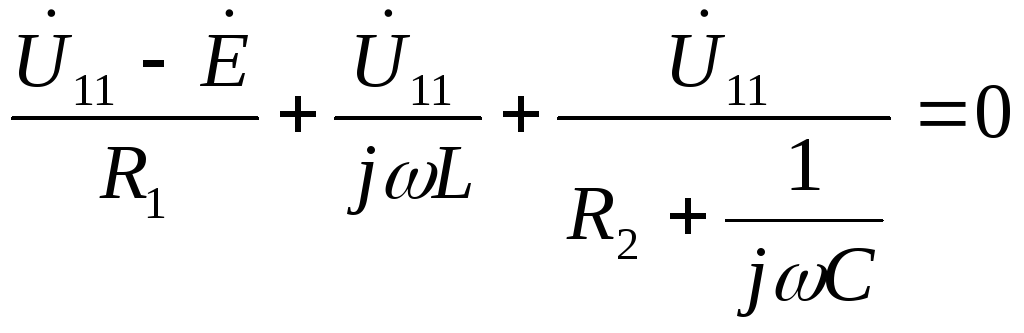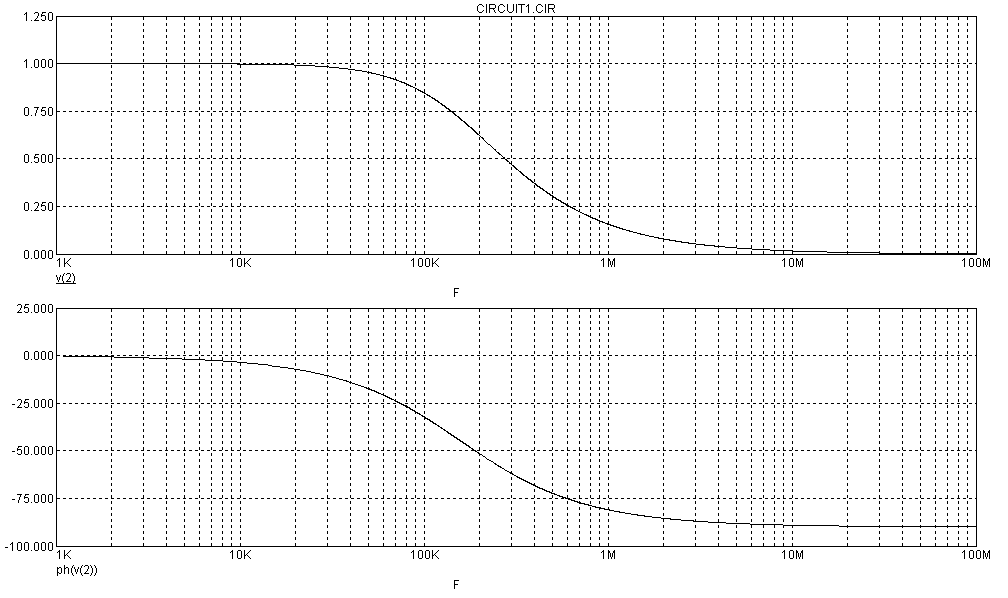Как найти коэффициент передачи по напряжению
1.5 Определение внешних частотных характеристик
четырехполюсников через A параметры
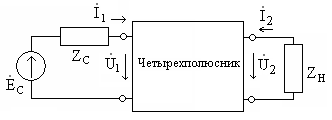
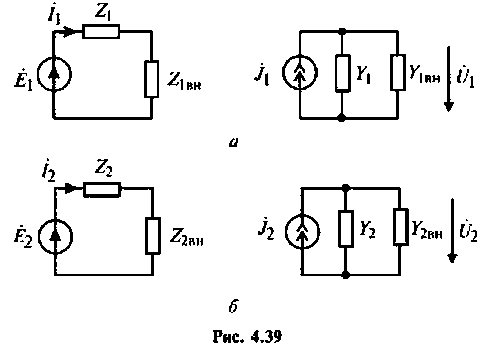
Частотные характеристики четырехполюсника определены выражениями (1.11) — (1.17) в самой общей форме. Однако если взять за основу уравнения четырехполюсника (1.20) и добавить к ним соотношение, связывающее ток и напряжение в нагрузке: 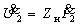
1. Входное сопротивление со стороны первичных зажимов:
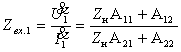
2. Входная проводимость со стороны первичных зажимов:
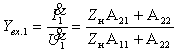
3. Коэффициент передачи по напряжению:
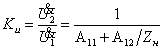
В частном случае, когда Zн = 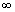
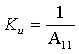
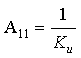
4. Коэффициент передачи по току:
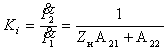
В частном случае, когда Zн = 0, т.е. имеет место режим короткого замыкания в нагрузке, получим
5. Передаточное сопротивление:
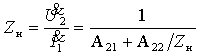
6. Передаточная проводимость:
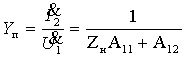
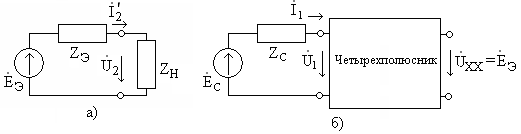
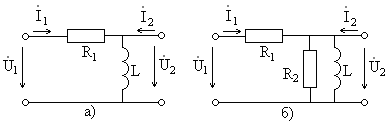
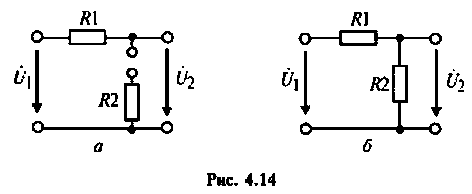
Пример 1.11. Найти коэффициент передачи по напряжению для цепи, представленной на рис. 1.16а.
Четырехполюсник представляет собой «продольное» звено (рис. 1.16(б)) с эквивалентным сопротивлением:
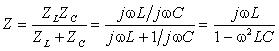
Используя результат ранее рассмотренного примера 1.7, получим набор А- параметров
Рис.1.16. Схема продольного реактивного звена, нагруженного на резистивное сопротивление: а)исходная цепь; б)комплексная схема
Тогда по формуле (1.27) с учетом равенства Z н = r найдем коэффициент передачи по напряжению
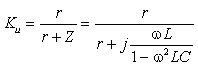
Запишем полученное выражение в показательной форме, выделяя АЧХ и ФЧХ искомой частотной характеристики
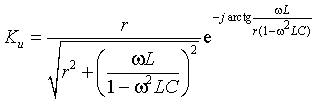
где 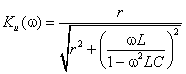
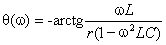
В цепях при наличии полного набора элементов r, L, C целесообразно также ввести в рассмотрение относительную частоту, определив ее в долях резонансной частоты колебательного контура. Для данного примера имеем:
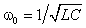
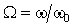
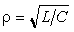
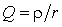
С учетом введенных обозначений выражения (1.31) и (1.32) принимают вид:
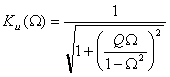
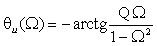
Пример1.12. Найти А — параметры цепочечной схемы RC фильтра нижних частот (рис. 1.17а). По найденным параметрам определить коэффициенты передачи 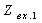
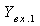
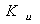
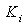
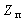
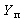
Рис. 1.17. Схема RC фильтра нижних частот:а)исходная цепь;
Решение задачи начинаем с изображения комплексной расчетной схемы замещения расчетной цепи (рис. 1.17б), где 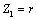
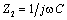
На основании (1.24) найдем А — параметры исследуемой схемы, перемножив две одинаковые матрицы. 
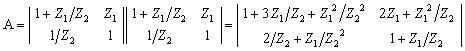
Для определения коэффициентов передачи воспользуемся полученными ранее выражениями (1.25) — (1.30), и после подстановки в них комплексных параметров 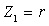
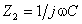
1. Входное сопротивление четырехполюсника:
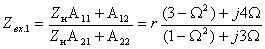
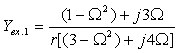
3. Коэффициент передачи по напряжению:
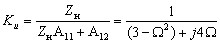
4. Коэффициент передачи по току:
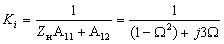
5. Передаточное сопротивление:
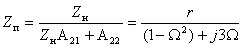
6. Передаточную проводимость:
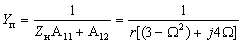
Каждое из полученных выражений следует записать в показательной форме, чтобы выделить АЧХ и ФЧХ. Например, для коэффициента 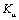
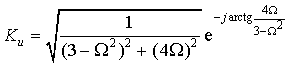
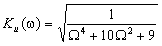
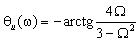
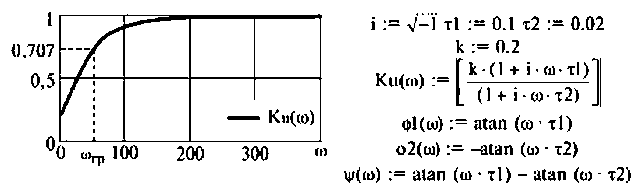
На рис. 1.18а,б показано поведение АЧХ и ФЧХ функции 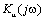
Рис. 1.18. Частотные зависимости коэффициента передачи напряжения К u
Анализ показывает, что RC фильтр нижних частот обеспечивает плавное уменьшение амплитуд гармонических сигналов с ростом частоты. При этом даже для очень низких частот, близких к нулю, имеет место трехкратное уменьшение сигнала на выходе. Фазовая характеристика указывает на увеличение модуля угла сдвига фаз с ростом частоты. Для частот Ω > 1.73 этот угол превосходит по величине 90˚.
Изучение материала первого раздела пособия рекомендуется завершить решением задач приложения 1. Вариант указывается преподавателем или выбирается самостоятельно.
Источник
Коэффициент передачи
Определение и формула коэффициента передачи
Форма представления коэффициента передачи зависит от формы математического представления сигналов входа и выхода. Это могут быть, например, операторы Лапласа или Фурье, тогда коэффициенты передачи называют операторными.
Коэффициент передачи и коэффициент усиления
В частности, если величины входного и выходного сигналов однородны, тогда коэффициент передачи называют коэффициентом усиления. Так, коэффициентом усиления по напряжению (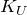
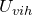
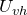
В выражении для коэффициента усиления можно использовать не только амплитуды, но и действующие значения напряжения.
Если коэффициенты усиления выражают в децибелах, то определением коэффициента преобразования (усиления) по напряжению будет выражение:
Коэффициенты усиления по току и мощности в децибелах выражают как:
Коэффициент усиления каскада равен произведению отдельных элементов каскада, если он выражен в относительных единицах:
Общий коэффициент усиления каскада равен сумме отдельных элементов каскада, если он выражен в децибелах.
K(дб)=
Если в усилителе коэффициент передачи больше единицы для безразмерного коэффициента или больше нуля для коэффициента, представленного в децибелах, то коэффициент называют коэффициентом усиления.
Коэффициент передачи может быть представлен в комплексном виде. Он используется для анализа устройств, которые зависят от частоты сигналов.
Комплексный коэффициент передачи линейного звена находят как отношение комплексной амплитуды выходного сигнала к комплексной амплитуде входного сигнала:
где 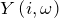

Единицы измерения
Коэффициент усиления — может быть величиной безразмерной. При решении задач следует обратить внимание на то, чтобы величины входных и выходных сигналов были выражены в одних единицах.
Или коэффициент усиления может выражаться в логарифмических единицах — децибелах.
Примеры решения задач
| Задание | Что такое частотный годограф? |
| Решение | Комплексный коэффициент передачи применяют для графического изображения свойств звена. С этой целью строят частотный годограф. Частотным годографом называют геометрическое место точек, которое создает конец вектора комплексного коэффициента передачи, если частота сигнала изменяется от 0 до  . Форма диаграммы сложная и только в простейших случаях это может быть окружность или прямая. Годограф строят как параметрическую кривую на комплексной плоскости, где параметром является частота. Данную характеристику можно построить в декартовой и полярной системах координат. Для построения годографа в декартовой системе координат комплексный коэффициент передачи представляют в алгебраической форме. При этом по оси абсцисс откладывают вещественную часть, по оси ординат мнимую. Для каждой частоты наносят точку на комплексной плоскости. Полученные точки соединяют плавной кривой. Около каждой точки выставляют соответствующие ей частоты. Фактически частотный годограф представляет собой кривую зависимости модуля комплексного коэффициента передачи от угловой частоты. Она показывает, как система преобразует сигналы разной частоты. . Форма диаграммы сложная и только в простейших случаях это может быть окружность или прямая. Годограф строят как параметрическую кривую на комплексной плоскости, где параметром является частота. Данную характеристику можно построить в декартовой и полярной системах координат. Для построения годографа в декартовой системе координат комплексный коэффициент передачи представляют в алгебраической форме. При этом по оси абсцисс откладывают вещественную часть, по оси ординат мнимую. Для каждой частоты наносят точку на комплексной плоскости. Полученные точки соединяют плавной кривой. Около каждой точки выставляют соответствующие ей частоты. Фактически частотный годограф представляет собой кривую зависимости модуля комплексного коэффициента передачи от угловой частоты. Она показывает, как система преобразует сигналы разной частоты. |
Для узла, к которому подключен инвертирующий выход, запишем закон Кирхгофа для токов:
Рассмотрим контур, который включает источник напряжения, вход усилителя, и сопротивление 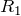
Рассмотрим контур, который включает вход усилителя, сопротивление 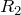
Выразим из (2.3) выходное напряжение и учтем, что: если усилитель работает в линейном режиме, то входные токи в рассматриваемый усилитель равны нулю (в нашем случае 
Источник
Содержание:
Частотные методы анализа электрических цепей:
Частотные характеристики являются компонентами комплексных функций цепи.
Комплексная функция цепи (КФЦ)
Амплитудно-частотная характеристика (АЧХ)
Фазочастотная характеристика (ФЧХ)
Амплитудно-фазовая частотная характеристика (АФЧХ) (комплексная функция цепи)
где 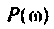
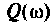
Комплексные функции простых цепей можно рассчитать непосредственно по закону Ома.
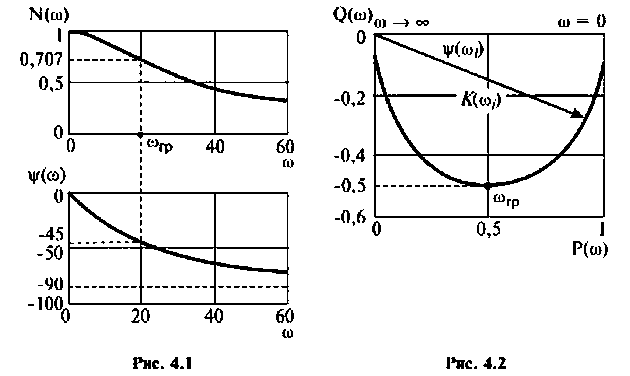
На рис.4.1 показаны АЧХ и ФЧХ, а на рис.4.2 — АФЧХ простейшей интегрирующей цепи (апериодического звена). По АЧХ определяют полосу пропускания
Полосой пропускания П называется диапазон частот, на границах которого мощность сигнала уменьшается в 2 раза, а амплитуда (действующее значение) напряжения (тока) — в 
Полоса пропускания может измеряться в радианах в секунду 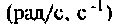
Например, для простой интегрирующей цепи полоса пропускания (см. рис. 4.1)
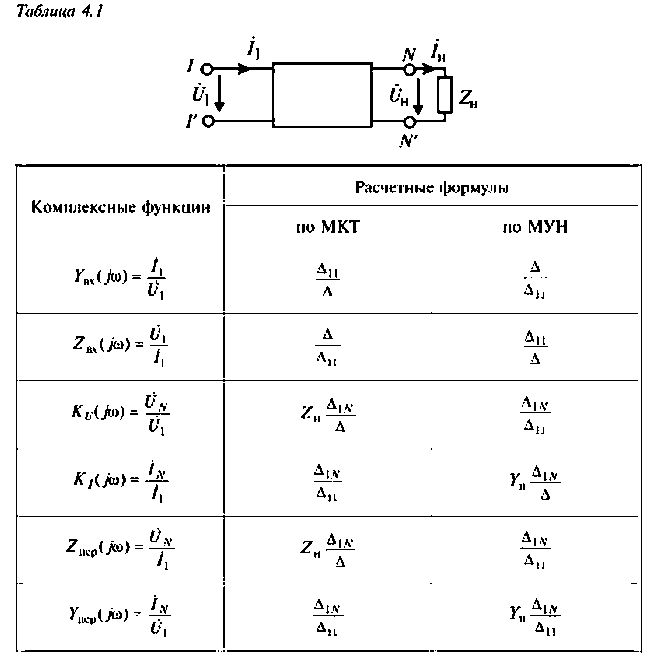
Для сложных цепей КФЦ рассчитывают по MKT или МУН. В табл. 4.1 приведены соотношения для расчета КФЦ, выраженные через определитель и алгебраические дополнения матрицы контурных сопротивлений и узловых проводимостей.
Частотные характеристики цепей с одним реактивным элементом
Примеры решения типовых задач:
Пример 4.2.1.
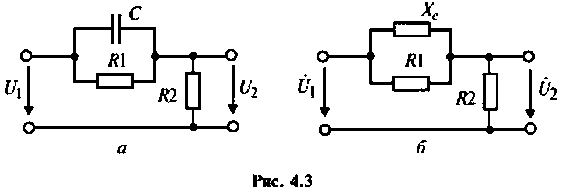
Определить комплексный коэффициент передачи по напряжению для дифференцирующего RC-контура (рис.4.3, а), рассчитать и построить графики АЧХ и ФЧХ.
Решение
1. Изобразим комплексную схему замещения цепи (рис. 4.3, б).
2. Определим комплексное напряжение на выходе цепи в виде
Преобразуем полученное выражение, вынеся зa скобки в числителе и знаменателе члены, не содержащие 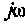
Следовательно.
Введем обозначения:
Величина 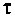
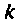
С учетом принятых обозначений
Для получения аналитических выражений АЧХ и ФЧХ запишем комплексную функцию в показательной форме.
Так как выражение (4.2) есть отношение двух полиномов, то удобно числитель и знаменатель записать отдельно в показательной форме, а затем разделить:
3. Из (4.3) запишем АЧХ и ФЧХ соответственно:
4. Построим график АЧХ и ФЧХ качественно по двум точкам. Для этого рассчитаем значения 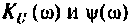
График АЧХ 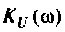
График функции ФЧХ 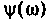
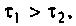
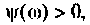
Исследуя функцию (4.5) на экстремум, можно показать, что она имеет максимум на частоте
где
Подставляя 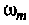
Графики АЧХ и ФЧХ изображены на рис. 4.4.
Пример 4.2.2.
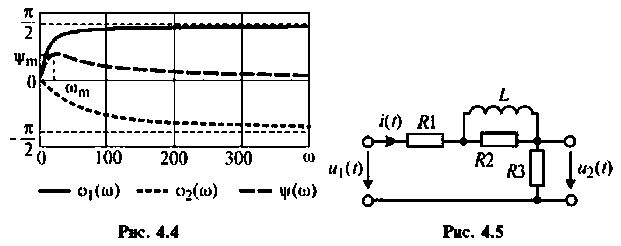
Для электрической цепи, изображенной на рис. 4.5, определить АЧХ 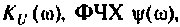
Решение
1. Найдем комплексную функцию К(; (/ш) но формуле делителя напряжения
Преобразуем полученное выражение к виду
Обозначим:
Следовательно,
Отсюда: АЧХ
ФЧХ
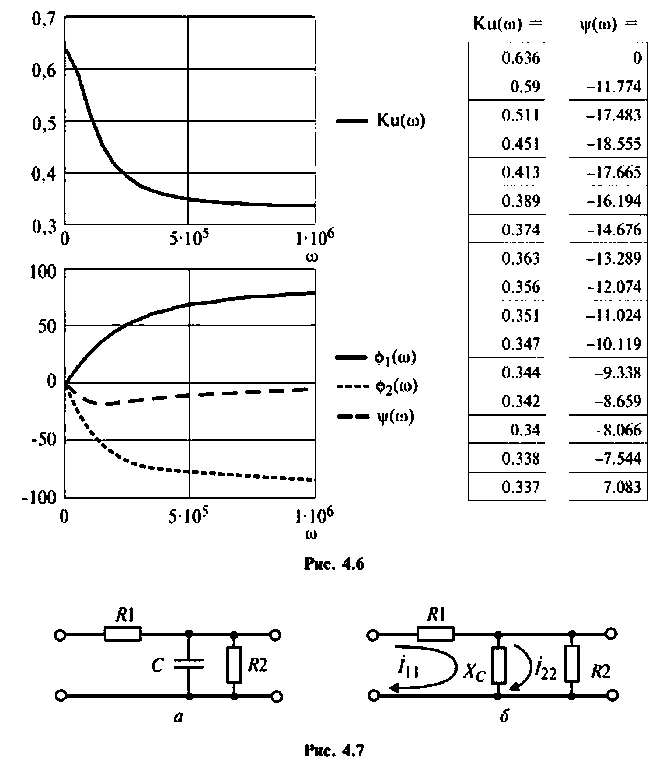
2. Рассчитаем граничную частоту. По определению
Из (4.7) найдем
Следовательно,
Из уравнения (4.9) получаем, что
Отсюда
3. Построим график функций.
Вычислим значения (4.7) и (4.8) для частот с дискретностью
Графики и таблицы выполним в среде Mathcad (рис. 4.6).
Пример 4.2.3.
Определить комплексный коэффициент передачи интегрирующей цепи (рис. 4.7, а), используя метод контурных токов. Построить в среде Mathcad график АЧХ, определить полосу пропускания.
Параметры цепи:
Решение
1. Представим цепь комплексной схемой замещения (рис. 4.7, б). Данная цепь имеет два независимых контура. Ток 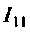
2.Составим матрицы контурных сопротивлений для двух независимых контуров
3.Определим комплексный коэффициент передачи, используя соотношение, приведенное в табл. 4.1.
где сопротивление нагрузки равно
Подставляя найденные выражения, получаем
или
где
4. Рассчитаем 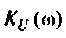
Объяснить полученные результаты можно, рассуждая так: на нулевой частоте (режим постоянного тока) сопротивление емкости бесконечно велико, ток в ней равен нулю, что эквивалентно разрыву этой ветви. При этом цепь становится резистивным делителем напряжения с передаточной функцией 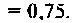
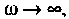
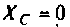
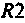
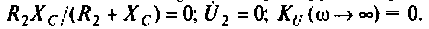
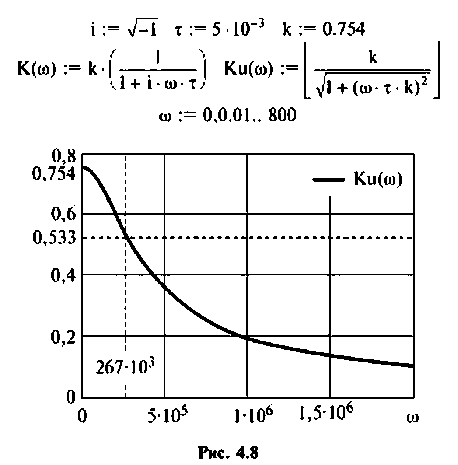
По полученным выражениям строим график АЧХ (рис. 4.8) и среде Mathcad.
5. Определяем полосу пропускания. По определению
Поэтому из (4.11) имеем
После преобразований уравнения (4.12) получаем
откуда
или
Следовательно, цепь имеет полосу пропускания
На рис. 4.8 указана граничная частота
Данная цепь представляет собой фильтр нижних частот с полосой пропускания 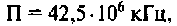

Пример 4.2.4.
Найти комплексную передаточную проводимость 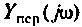
Параметры цепи: 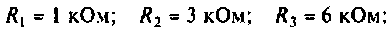
Определить АЧХ и ФЧХ, построить их графики в среде Mathcad.
Решение
1. Изобразим комплексную схему замещения цепи (рис. 4.9, б). Схема имеет два независимых узла. В данном случае
2. Составим матрицу узловых проводимостей. При определении собственной проводимости узлов необходимо помнить, что собственная проводимость ветви, состоящей из последовательно включенных пассивных элементов, находится из соотношения 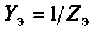
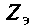
В начале рассчитывают комплексное сопротивление этой ветви, 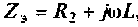
Составим матрицу проводимостей цепи 1 2
Как видим, общие проводимости узлов взяты со знаком минус, так как узловые напряжения 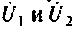
3.Определим комплексную передаточную проводимость по соотношению, приведенному в табл. 4.1
где 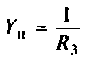
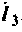
Найдем алгебраические дополнения:
После подстановки найденных значений получим
Для определении АЧХ и ФЧХ запишем выражения для модуля и аргумента
4. Рассчитаем значения 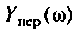
Примечание. Эти значения можно найти без вывода аналитического выражения для 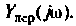
Учитывая, что 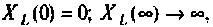
Для первой схемы:
Следовательно,
Аналогично для второй схемы получим
При расчете сложных схем такой прием можно применять для проверки правильности полученного аналитического выражения КФЦ.
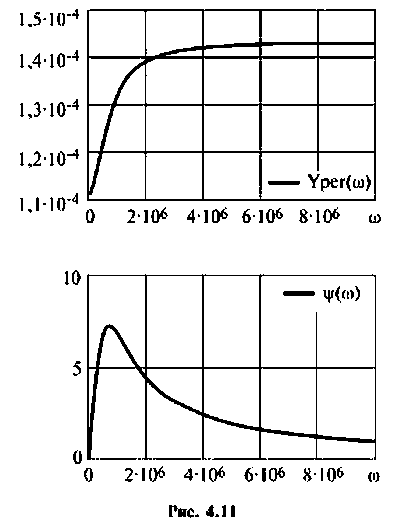
Из (4.13) видно, что функция наметен монотонной, но для качественного построения графика АЧХ (рис. 4.11) необходимо воспользоваться ПЭВМ, например построить функцию в среде Mathcad.
Пример 4.2.5.
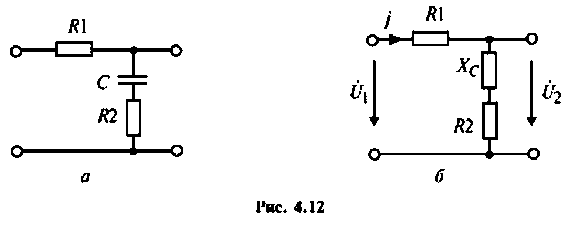
Для интегрирующего RС-контура (рис.4.12,а) определить комплексный коэффициент передачи по напряжению, рассчитать АЧХ, ФЧХ, ВЧХ, МЧХ. Построить графики АЧХ, ФЧХ. АФЧХ, если
Решение
1. Составим комплексную схему замещения цепи (рис. 4.12, б).
2. Определим 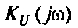
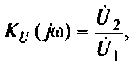
Следовательно.
3. Для нахождения АЧХ и ФЧХ комплексную функцию 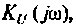
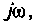
Найдем модуль (АЧХ) и аргумент (ФЧХ) комплексной функции;
Для определения вещественной и мнимой частотных характеристик запишем КФЦ в алгебраической форме. Для этого умножим и разделим (4.14) на комплексно-сопряженный знаменатель:
4. Для приближенного построения графиков АЧХ, ФЧХ. АФХ найдем значения 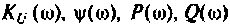
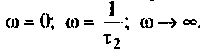
Для более точного и наглядного представления графиков воспользуемся ПЭВМ и математической средой Mathcad.
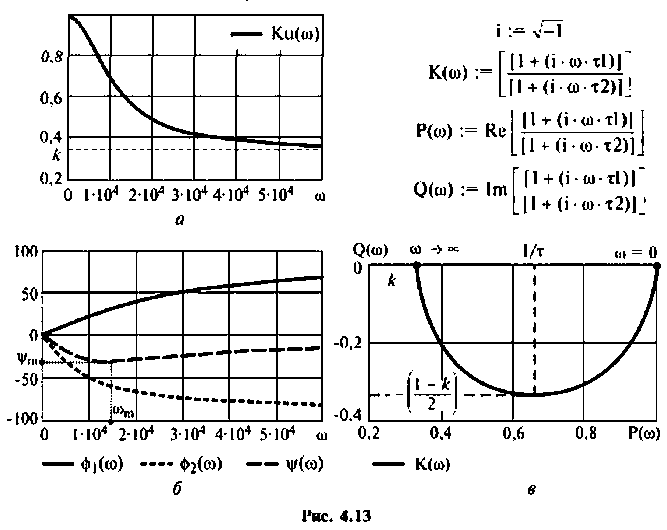
Графики характеристик приведены на рис. 4.13.
АЧХ представляет монотонно убывающую функцию (рис. 4.13, а).
ФЧХ принимает отрицательные значения, т.е. контур вносит фазовое отставание, а на частоте 
Взяв производную, получим
Решая полученное уравнение относительно 
Подставляя 
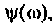
АФХ (рис. 4.13, в) представляет собой полуокружность, расположенную в 4-м квадрате. Центр окружности находится на оси 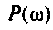
Радиус окружности нетрудно определить из соотношения:
МЧХ:
Отрицательное значение 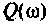
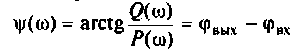
5. Проверка расчетов АЧХ. Воспользуемся эквивалентными схемами цепи для частот 
На частоте 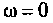
При 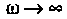
Подставляя эти значения частот в аналитическое выражение (4.14) для 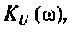
Следовательно, расчет АЧХ выполнен верно.
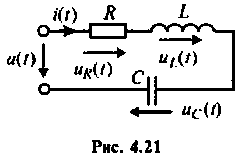
Частотные характеристики последовательного колебательного контура
Основные теоретические сведения:
В последовательном колебательном контуре (рис. 4.21) возникает резонанс напряжений, если выполняется условие
т. е. 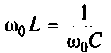
Резонансная частота
Волновое сопротивление контура
Сопротивление контура при резонансе
Собственная добротность контура
Добротность нагруженного контура
Затухание контура
Абсолютная расстройка
Относительная расстройка
Обобщенная расстройка
Фактор расстройки:
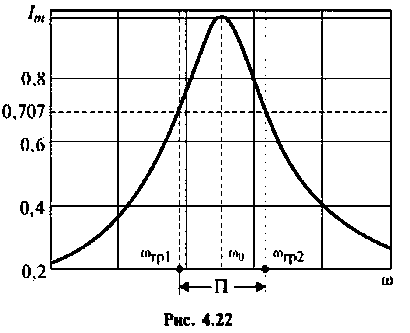
Абсолютная полоса пропускания (рис. 4.22)
Относительная полоса пропускания
Для нагруженного контура:
Комплексные коэффициенты передачи по напряжению:
на активном сопротивлении
на индуктивности
на емкости
Примеры решения типовых задач:
Пример 4.3.1.
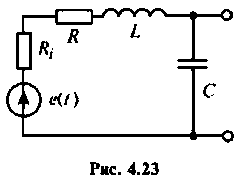
Последовательный колебательный контур (рис. 4.23) подключен к источнику напряжению. Контур настроен в резонанс.
Параметры цепи:
Определить резонансную частоту, волновое сопротивление. добротность и полосу пропускания, ток и напряжения на элементах контура.
Построить АЧХ и ФЧХ по напряжению на конденсаторе в среде Mathcad.
Решение
1. Определяем резонансную частоту контура
2. Находим волновое сопротивление контура
3. Вычисляем добротность нагруженного контура
4. Определяем полосу пропускания
5. Рассчитываем ток и напряжения на элементах контура при резонансе
Напряжение на R равно
Напряжения на реактивных элементах
6. Рассчитаем АЧХ и ФЧХ комплексного коэффициента передачи напряжения с емкости.
Учитывая (4.22), из (4.29) получим:
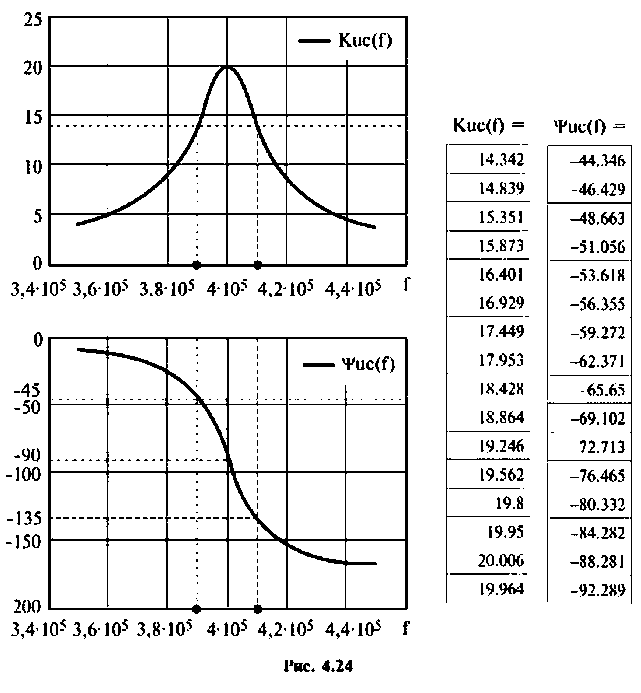
Для построения графиков АЧХ и ФЧХ, выполнения расчетов используем среду Mathcad. АЧХ, ФЧХ в виде графиков и таблиц приведены на рис. 4.24.
Следует заметить, что максимум А11Х достигается на частоте
т.е. при 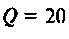
Задача 4.3.2.
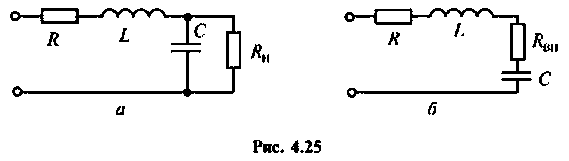
К последовательному колебательному контуру (рис. 4.25) с параметрами 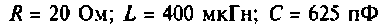
Определить собственную добротность и добротность нагруженного контура, полосу пропускания нагруженного и ненагруженного контура.
Решение
1. Рассчитаем вторичные параметры ненагруженного контура:
2.Определим вторичные параметры наруженного контура. Так как сопротивление нагрузки активное, причем 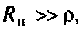
Для определения добротности рассчитаем сопротивление 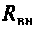
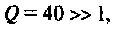
Следовательно,
Вывод. Подключение нагрузки ухудшает добротность контура, что приводит к расширению полосы пропускания.
Пример 4.3.3.
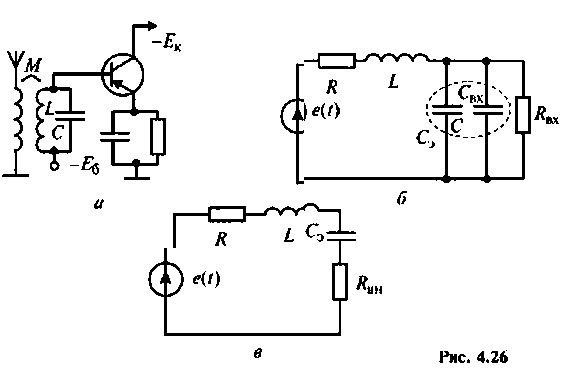
На рис. 4.26, а изображена входная цепь приемника, а на рис. 4.26, б — ее эквивалентная схема. Известны входное сопротивление и входная емкость транзистора входного каскада УВЧ: 
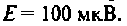
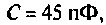
Определить абсолютную полосу пропускания и ток в контуре на резонансной частоте.
Решение
1. Определяем эквивалентную емкость контура
2. Рассчитываем резонансную частоту контура
3. Находим волновое сопротивление и сопротивление, вносимое в контур за счет транзистора усилителя (рис. 4.26, в):
4. Определяем добротность нагруженного контура
5. Рассчитаем абсолютную полосу пропускания нагруженного контура
6. Находим ток в контуре
Пример 4.3.4.
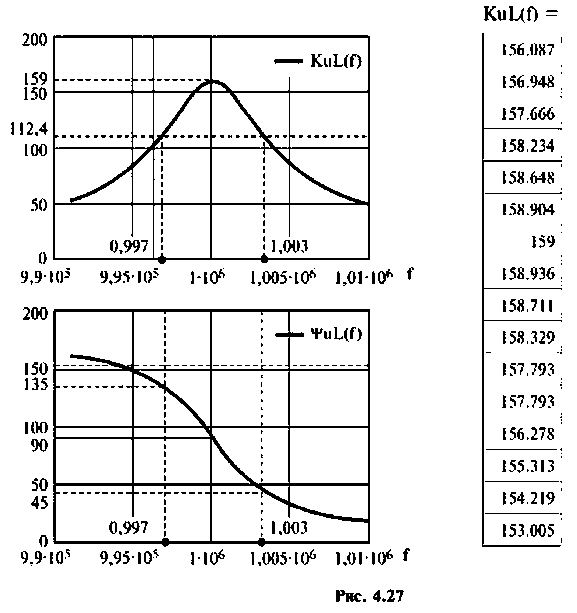
Рассчитать емкость последовательного колебательного контура, если резонансная частота контура 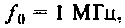
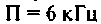
Построить АЧХ и ФЧХ комплексного коэффициента передачи напряжения с индуктивности в среде Mаthcad.
Решение
1. Определим требуемую добротность контура
2. Рассчитаем емкость конденсатора. Из формулы 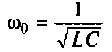
3. Рассчитаем АЧХ и ФЧХ.
Воспользуемся комплексным коэффициентом передачи напряжения с индуктивности по формуле (4.28). Учитывая 4.22), запишем:
Вычислим значения функций на частотах:
Определим частоту, при которой АЧХ имеет максимум
Смещением частоты 
Результаты расчетов АЧХ и ФЧХ б графическом и табличном видах приведены на рис. 4.27.
Частотные характеристики параллельного колебательного контура
Основные теоретические сведения:
Параллельный колебательный контур образуется путем параллельного соединения катушки индуктивности и конденсатора. Оба элемента, кроме основного эффекта (запасания энергии), имеют потери энергии. В расчетной схеме (рис. 4.29, а) тепловые потери в элементах учтены включением условных сопротивлений
где резонансная частота колебаний
Для реального контура 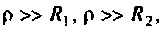
При резонансе сопротивление контура является активным, поэтому ток 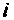
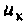
Сопротивление параллельного колебательного контура при резонансе максимально и равно (без учета внешней цепи)
где
Добротность 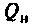
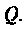
или через их проводимости
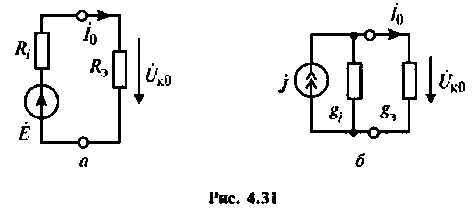
Важными параметрами цепи при резонансе являются токи в ветвях и напряжение на контуре. Ток в обшей ветви (ток источника) при резонансе минимален и равен (см. рис. 4.31)
При этом напряжение на контуре максимально и равно
Токи в индуктивности и в емкости при резонансе равны по значению и противоположны по направлению. Они образуют замкнутый ток в контуре, равный
Частотные свойства параллельного колебательного контура обычно оценивают по нормированной АЧХ
где 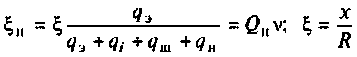
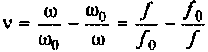
Параллельный контур, показанный на рис. 4.29, имеет по одной реактивности в ветвях. Такой контур называется простым или контуром I вида. Для уменьшения шунтирующего действия внешних цепей часто применяют сложные параллельные контуры.
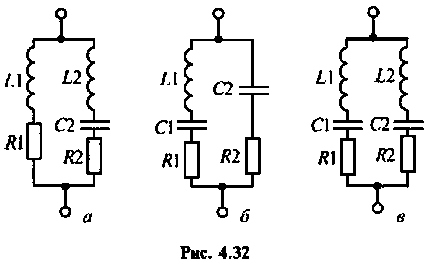
На рис. 4.32, а, б, в показаны контуры II, (III и IV) видов, соответственно.
Главной особенностью этих контуров является то, что их резонансное сопротивление меньше резонансного сопротивления простого контура с такими же параметрами.
Сопротивление контуров (рис.4.32) при резонансе рассчитывается по формулам, соответственно:
где 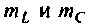
Примеры решения типовых задач:
Пример 4.4.1.
Параллельный контур (см. рис. 4.29, а) подключен к источнику с параметрами 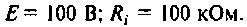
Параметры катушки индуктивности:
Определить действующие значения тока в контуре, тока на входе цепи и напряжения на контуре при резонансе, абсолютную и относительную полосы пропускания контура, добавочное сопротивление необходимое для расширения полосы пропускания в 2 раза.
Решение
1. Определим резонансную частоту колебания
2. Рассчитаем волновое сопротивление
3. Определим сопротивление контура при резонансе
4. Найдем действующее значение тока на входе контура (см. рис. 4.31, а) при резонансе
5. Определим соответственную добротность контура
6. Найдем ток в контуре и напряжение на нем:
7. Определим добротность нагруженного контура
8. Рассчитаем абсолютную и относительную полосы пропускания:
9. Определяем добавочное cопротивление 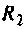
Пример 4.4.2.
Рассчитать полосу пропускания колебательного контура (см. рис. 4.30, а).
Дано:
Определить сопротивление 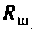
Решение
1. Рассчитаем волновое сопротивление и резонансную частоту контура:
2.Рассчитаем добротность цепи без шунта. Воспользуемся трехветвевой эквивалентной схемой цепи и соотношением (4.32). Найдем проводимость элементов схемы:
Тогда
3. Определим полосу пропускания
4. Найдем сопротивление шунта, необходимою для расширения полосы до 10 кГц,
В этом случае добротность цепи должна быть равна
Тогда из (4.32) получаем
Следовательно, сопротивление шунта должно быть равно
Пример 4.4.3.
Параллельный колебательный контур с параметрами: 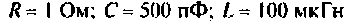
Определить собственную добротность контура, добротность нагруженного контура, абсолютную полосу пропускания и граничные частоты полосы пропускания. Построить резонансную кривую по напряжению на ЭВМ.
Решение
1. Определим волновое сопротивление контура
2. Рассчитаем собственную добротность контура
3. Найдем сопротивление контура при резонансе
4. Определим добротность нагруженного контура по формуле (4.31)
5. Рассчитаем резонансную частоту
6. Найдем полосу пропускания
7. Определим граничные частоты полосы пропускания:
8. Построим резонансную характеристику контура но напряжению. Из выражения (4.33) запишем
Напряжение па контуре при резонансе
Для построения резонансной характеристики задаемся характерными значениями частот: 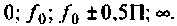
Пример 4.4.4.
Определить резонансную частоту, эквивалентное сопротивление при резонансе и добротность сложного контура (рис. 4.32, а), подключенного к источнику напряжения.
Дано:
Решение
1. Определим резонансную частоту и сопротивление параллельного контура при резонансе:
Сопротивление контура при резонансе
2. Рассчитаем эквивалентное сопротивление сложного контура II вида
3. Найдем добротность нагруженного контура II вида
Сравним значения 
Вывод. За счет неполного включения индуктивности 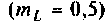
Частотные характеристики связанных колебательных контуров
Основные теоретические сведения:
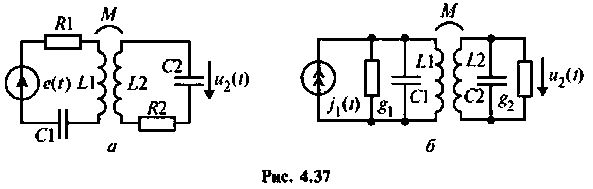
С целью повышения коэффициента прямоугольности АЧХ контуров применяют связанные контуры последовательного и параллельного питания (рис. 4.37, а, б).
Частотные характеристики связанных контуров рассмотрим на примере системы из двух контуров.
Эквивалентные схемы связанных контуров
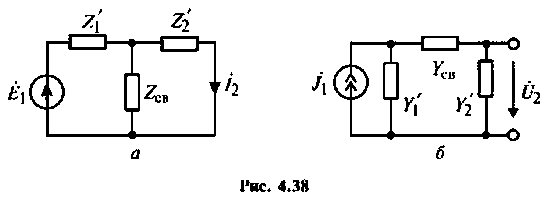
Во всех случаях систему связанных контуров можно представить в виде Т- или П-образной эквивалентной схемы (рис. 4.38).
Количественной характеристикой связи является сопротивление связи 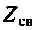
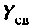
Удобным параметром для оценки связи является коэффициент связи
В случае реактивной связи для Т-образной схемы
Для П-образной схемы
где — сопротивление (проводимость) связи;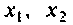
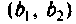
Для этого используют понятия вносимого сопротивления 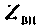
Резонансы в связанных контурах:
При настройке контуров в резонанс добиваются максимального тока (напряжения) во вторичном контуре.
Настройка связанных контуров может производиться различными способами, поэтому различают шесть резонансов. В табл. 4.3, 4.4 приведены виды и условия резонансов, способы настройки и соотношения для токов (напряжений) в связанных контурах последовательного (параллельного) питания.
Резонансные характеристики связанных контуров:
Для двух неидентичных связанных контуров: последовательного питания
где
параллельного питания:
где 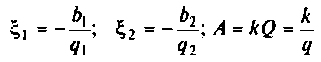
Если контуры идентичны, то обобщенная расстройка
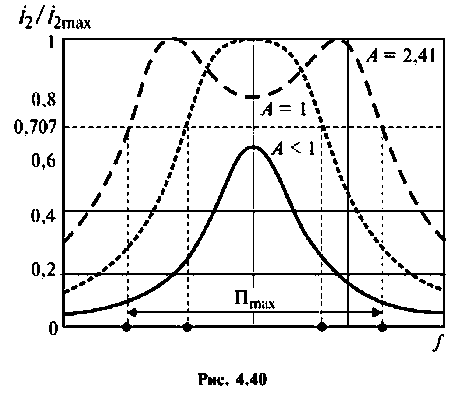
На рис. 4.40 приведены резонансные характеристики при различных факторах связи.
Относительная полоса пропускания:
а) связь слабая
б) связь критическая
в) связь сильная
При 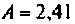
Примеры решения типовых задач:
Пример 4.5.1.
В системе двух индуктивно связанных контуров (см. рис.4.37,а) известны следующие параметры: коэффициент связи
Определить емкость 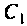
Решение
Емкость конденсатора 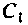
отсюда
Определим реактивное сопротивление 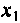
Peaктивное сопротивление второго контура
Рассчитаем полное сопротивление второго контура
Определим сопротивление связи контуров
Следовательно
Находим емкость первого контура
Пример 4.5.2.
Рассчитать емкости связанных контуров (см. рис. 4.37,а) и оптимальное сопротивление связи, если система настроена и полный резонанс. Определить токи, мощности в контурах при этом режиме, а также КПД системы.
Дано:
Решение
1. Определим емкость конденсатора 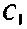
Отсюда
2. Сопротивление оптимальной связи при полном резонансе
3. Рассчитаем токи в первом и втором контурах при полном резонансе
4. Определим активные мощности в первом и втором контурах и КПД связанных контуров:
Пример 4.5.3.
На рис. 4.37, а показана система из двух идентичных связанных контуров с параметрами: 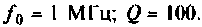
Решение
1. Определим полосу пропускания одиночного контура
2. Рассчитаем полосу пропускания системы связанных контуров:
1) определим параметр связи для
Таким образом при 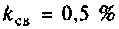
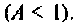
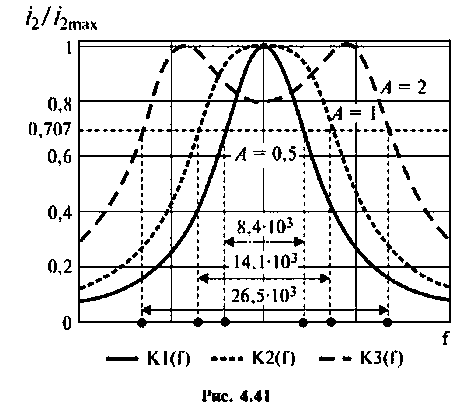
Абсолютная полоса пропускания (рис. 4.41, резонансная кривая А = 0,5)
2) при 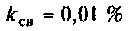
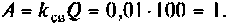
3) если 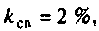
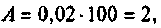
Рассчитаем полосу пропускания для этого случая.
Вид резонансных кривых по току и полоса пропускания для критической и сильной связи показаны на рис. 4.41, кривые А = 1 и А = 2.
Пример 4.5.4.
Антенный контур (см. рис. 4.37,б) индуктивно связан с входным контуром усилителя высокой частоты. Оба контура настроены в резонанс на частоту 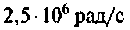
Дано:
Входное сопротивление УВЧ считать бесконечно большим.
Определить емкости и добротности контуров, их взаимную индуктивность, а также ток и напряжение на емкости во вторичном контуре.
Решение
1.Емкости контуров определим из формулы резонансной частоты. Емкость конденсатора первого контура
Емкость конденсатора второго контура
2. Рассчитаем волновое сопротивление контуров:
3. Рассчитаем добротности контуров и параметр связи:
4. Определим взаимную индуктивность двух связанных контуров
5. Рассчитаем ток во вторичном контуре. Известно (см. табл. 4.3), что при полном резонансе
Тогда, учитывая, что контуры настроены в резонанс, то из (4.34) получаем
Оба контура по условию настроены в резонанс, поэтому расстройки равны нулю:
С учетом этого рассчитаем ток во втором контуре
6. Найдем напряжение на конденсаторе вторичного контура
Пример 4.5.5.
На рис. 4.42 приведена схема одного каскада УПЧ радиоприемника, в котором избирательность обеспечивается двумя связанными контурами с емкостной связью. Оба контура настроены в резонанс на промежуточную частоту
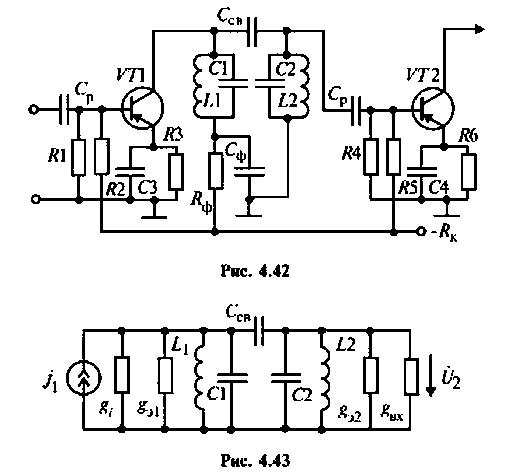
Эквивалентная схема этого каскада (рис. 4.43) имеет следующие параметры: 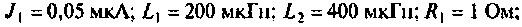
Определить емкости и добротности контуров, емкость связи, напряжение на емкости во вторичном контуре, а также полосу пропускания каскада УПЧ.
Решение
1. Из формулы резонансной частоты найдем емкость первого контура. С учетом влияния выходной емкости транзистора 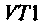
Емкость второго контура с учетом влияния входной емкости транзистора 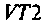
2. Определим емкость связи
3. Рассчитаем добротности нагруженных контуров при отсутствии связи между ними. Для расчета воспользуемся формулой (4.31)
где
где
4. Рассчитаем параметр связи
5. Рассчитаем напряжение на втором контуре. Известно (см. табл. 4.4), что при полном резонансе
Тогда, учитывая, что контуры настроены в резонанс 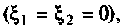
Найдем проводимость контуров
Тогда
6. Рассчитаем полосу пропускания каскадов УПЧ. учитывая, что А = 1,2.
Частотные методы расчета и построения переходных и установившихся процессов в электрических цепях
Основные теоретические сведения:
Зная частотную характеристику электрической цепи 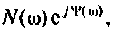
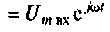
где 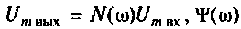
С помощью частотной характеристики электрической цели можно не только определить выходную величину цепи в установившемся режиме при гармоническом входном воздействии, но и найти реакцию цепи в переходном процессе на произвольное воздействие 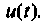
Найдем реакцию цепи на единичную ступенчатую функцию (т.е. найдем переходную функцию цепи), используя ее частотную характеристику. Как известно, интеграл Фурье для единичной ступенчатой функции имеет вид
т.е. единичная ступенчатая функция может быть представлена как бесконечная сумма элементарных колебаний вида
Каждому из этих колебаний соответствует выходное колебание 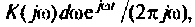
Представляя 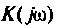
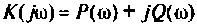
где 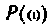
Построение переходной функции с помощью вещественной частотной характеристики методами численного интегрирования:
Выражение (4.38) позволяет вычислить переходную функцию ЭЦ и определить качество переходного процесса. Однако интегрирование этого выражения аналитическими методами — задача весьма трудоемкая, а чаще всего просто практически невыполнимая. С применением современных ЭВМ и методов численного интегрирования (метод прямоугольников, трапеций, метод Симпсона и др.) эта задача существенно упрощается, ее решение сводится к составлению программы для ПЭВМ. В инженерной практике интегрирование достаточно осуществлять в области существенных частот от 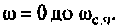

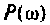
В результате интегрирования получают совокупность значений 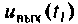
В качестве примера построения алгоритма численного интегрирования рассмотрим интегрирование с точки зрения простоты вычислений и точности результата. Сущность метода заключается в следующем. Пусть необходимо вычислить определенный интеграл
Вид подынтегральной функции, соответствующей выражению
при фиксированном времени 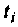
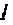
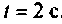
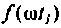
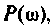
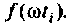
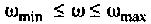
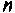
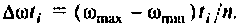
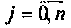

Очевидно, что погрешность численного интегрирования зависит и от выбора числа интервалов 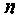
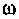
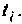
При этом одно полное колебание подынтегральной функции представляется не менее чем шестнадцатью трапециями.
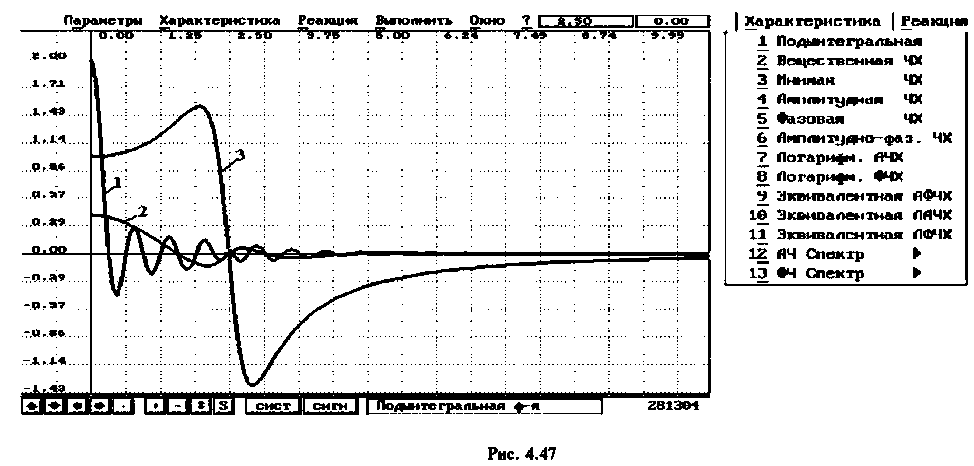
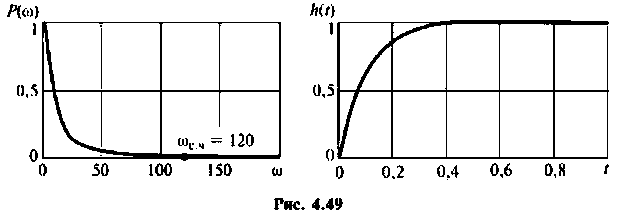
В качестве примера для построения переходной функции возьмем электрическую цепь, ВЧХ которой была построена и приведена на рис. 4.47 (кривая 3). На рис. 4.48 приведена переходная функция этой сложной электрической цепи.
Переходная функция на рис. 4.48 получена с помощью пакета ПП «Сигнал» [5].
Для вычисления интеграла (4.39) необходимо определить значение частоты для верхнего предела интегрирования 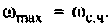
Алгебраическая форма КФ
где 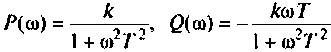
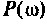
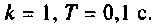
Из графика ВЧХ видно, что при 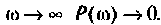
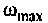
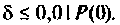
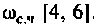
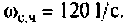
Для случая электрических цепей с дифференцирующими свойствами может оказаться, что при 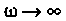
Приведенный пример наглядно показывает, что использование частотных характеристик для построения временных характеристик с помощью ЭВМ существенно расширяет возможности частотных методов анализа электрических цепей.
Спектральный метод расчета и построения выходных величин электрических цепей при сложных входных воздействиях:
Применение частотных методов при анализе и синтезе электрических цепей с требуемыми динамическими характеристиками и использованием ЭВМ позволяет не только строить переходные характеристики, но и строить реакцию цепи на любые детерминированные воздействия, оценивать их в установившихся режимах.
Математической основой частотных методов анализа электрических цепей и систем автоматического управления является обратное преобразование Фурье, позволяющее получать изображение выходного сигнала системы y(t) с помощью вещественной и мнимой частотных характеристик систем. В свою очередь, по вещественной или мнимой частотным характеристикам можно построить переходный процесс выходной величины и оценить реакцию цепи в переходном и установившемся режимах.
Как известно, реакция системы определяется по формуле обратного преобразования Фурье [4]
где
После соответствующих преобразований выражение (4.46) примет вид:
I) для ступенчатой входной функции 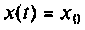
2) для линейной входной функции 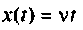
y{t) = vP(0)t+±l
2 r0(
Л» И
(4.48)
О)
3) для параболической входной функции 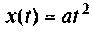
4) для полиномиального воздействия вида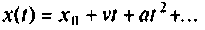
Применение ЭВМ и численных методов интегрирования позволяет отказаться от графических и табличных методов построения переходных и других необходимых функций в электрических цепях.
Примеры решения типовых задач:
Пример 4.6.1.
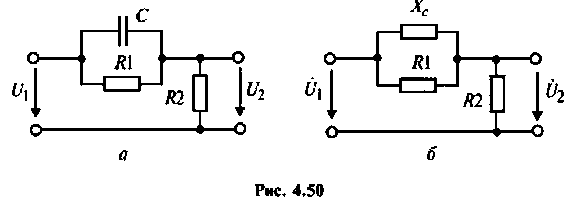
Определить комплексный коэффициент передачи по напряжению для дифференцирующего 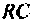
Решение
1. Изобразим комплексную схему замещения цепи (рис. 4.50, б).
2. Определим комплексное напряжение на выходе цепи в виде
Преобразуем полученное выражение, вынеся за скобки в числителе и знаменателе члены, не содержащие 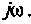
Следовательно
Введем обозначения:
Величина 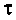
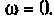
Для получения аналитических выражений ВЧХ и МЧХ запишем комплексную функцию и алгебраической форме
где
Примем:
Для определения частоты 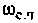
Из частотных характеристик КПФ принимаем 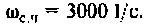
Переходная функция, показанная на рис.4.52, соответствует дифференцирую щему фазоопережающему контуру, который широко применяется в электронных и радиотехнических устройствах, системах автоматического управления.
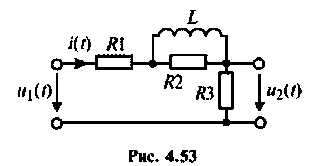
Пример 4.6.2.
Для электрической цепи, изображенной на рис, 4.53, определить КПФ 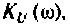
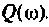
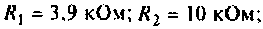
Решение
1. Найдем комплексную функцию 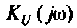
Преобразуем полученное выражение к виду
Обозначим:
Следовательно,
Для получения аналитических выражений ВЧХ и МЧХ запишем комплексную функцию и алгебраической форме
где
Для определения частоты 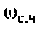
По виду ВЧХ и МЧХ определяем, что для построения переходной функции необходимо применить МЧХ. Примем из графика МЧХ 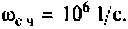
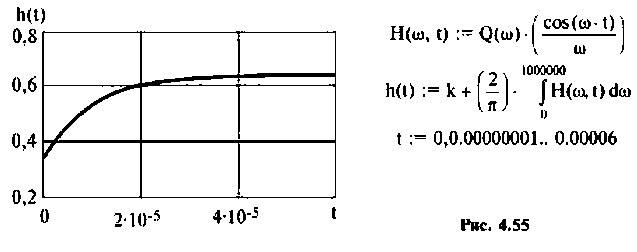
Из рис. 4.55 видно, что переходная функция соответствует интегрирующему контуру.
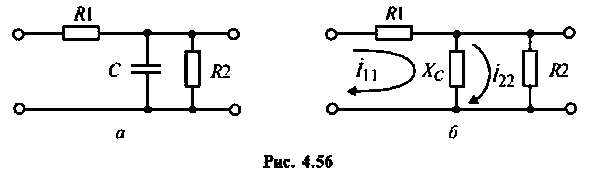
Пример 4.6.3.
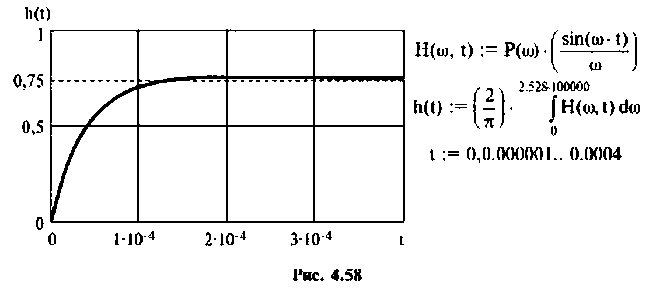
Определить комплексный коэффициент передачи интегрирующей цепи (рис. 4.56, а), используя метод контурных токов. Построить в среде Mathcad графики АЧХ, ВЧХ, МЧХ. Рассчитать и построить эпюру входного и выходного напряжения, если на вход цепи поступает напряжение вида 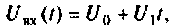
Параметры цепи:
Решение
1.Представим цепь комплексной схемой замещения (рис. 4.56, б). Данная цепь имеет два независимых контура. Ток 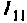
2.Составим матрицы контурных сопротивлений для двух независимых контуров
3.Определим комплексный коэффициент передачи, используя соотношение, приведенное в табл. 4.1.
где сопротивление нагрузки
Подставляя найденные выражения, получаем
т.е.
где
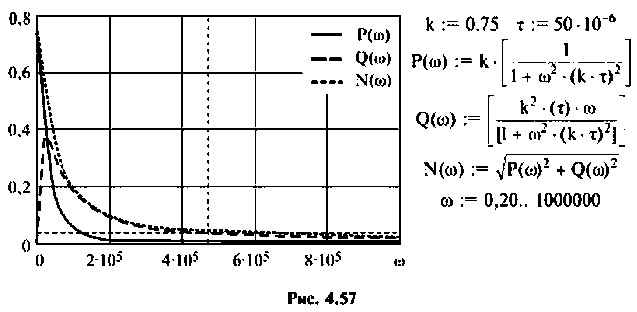
4. Рассчитаем 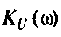
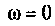
Объяснить полученные результаты можно, рассуждая так: на нулевой частоте (режим постоянного тока) сопротивление емкости бесконечно велико, ток в ней равен нулю, что эквивалентно разрыву этой ветви. При этом цепь становится резистивным делителем напряжения с передаточной функцией 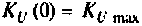
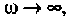
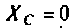
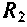
5.Определим выражения для АЧХ, ВЧХ, МЧХ. Представим КГ1Ф (4.55) в алгебраической форме
где 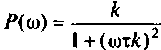
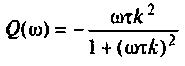
Амплитудно-частотную характеристику запишем в виде
6. В среде Mathcad построим частотные характеристики и определим
По ВЧХ на рис. 4.57 определяем, что существенная частота
7. Построим переходную функцию электрической цепи, которая представлена на рис. 4.58.
Переходная функция электрической цепи соответствует апериодическому звену.
8. Построим реакцию электрической цепи на напряжение, изменяющееся но линейному закону (рис. 4.59).
- Операторные передаточные функции
- Свободные колебания в пассивных электрических цепях
- Цепи с распределёнными параметрами
- Волновые параметры длинной линии
- Энергетические характеристики двухполюсников
- Комплексные функции электрических цепей
- Гармонические колебания в колебательном контуре
- Частотные характеристики линейных электрических цепей
|
24 / 24 / 0 Регистрация: 26.01.2013 Сообщений: 300 |
|
|
1 |
|
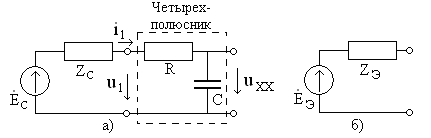
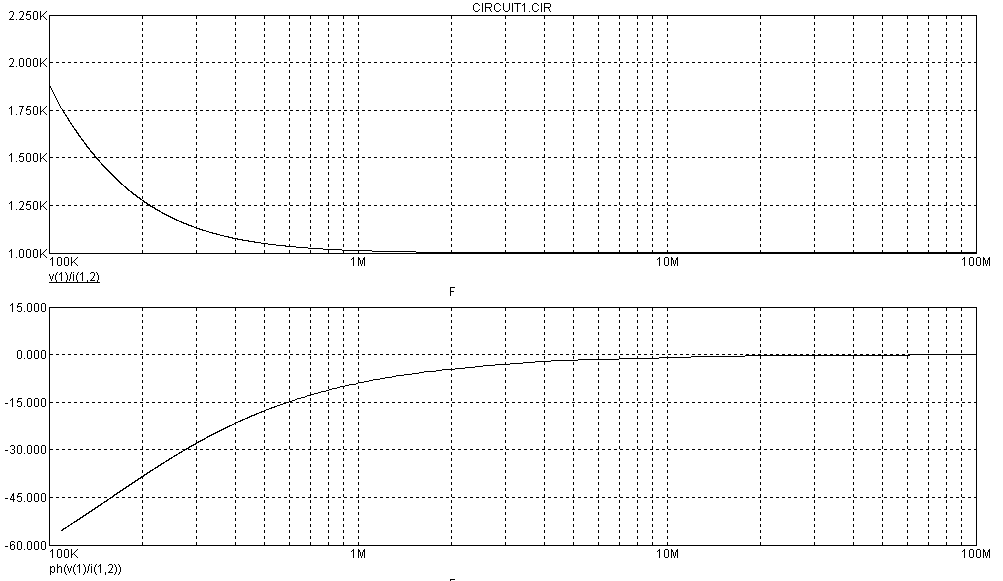
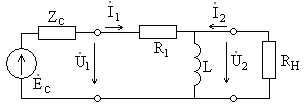
Рассчитать коэффициент передачи для схемы22.04.2013, 22:51. Показов 6408. Ответов 16
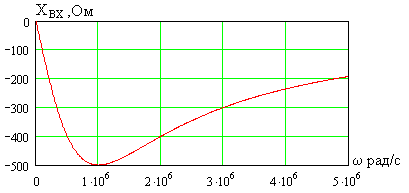
Помогите, пожалуйста, выразить коэффициент передачи для данной схемы:
Uг — генератор Тоесть получается Вольт*Ом / Ом+Ом*А*ОМ. «Спасибы» гарантирую!
0 |
|
7483 / 4147 / 474 Регистрация: 25.08.2012 Сообщений: 11,529 Записей в блоге: 11 |
|
|
22.04.2013, 22:58 |
2 |
|
Uг=I1*[Ri+(z1*(z2+z3))] Не верно.
1 |
|
24 / 24 / 0 Регистрация: 26.01.2013 Сообщений: 300 |
|
|
22.04.2013, 23:37 [ТС] |
3 |
|
OldFedor,Помогите написать правильно. я запутался.
0 |
|
7483 / 4147 / 474 Регистрация: 25.08.2012 Сообщений: 11,529 Записей в блоге: 11 |
|
|
23.04.2013, 08:32 |
4 |
|
OldFedor,Помогите написать правильно. я запутался. 0. z0 = Rвн Далее — подставляйте, умножайте на сопряженные, сокращайте и получите K(w)= Ка + jКр По сути у Вас делитель. Удачи.
2 |
|
24 / 24 / 0 Регистрация: 26.01.2013 Сообщений: 300 |
|
|
20.05.2013, 23:10 [ТС] |
5 |
|
Актуально!!! Помогите кто-нибудь на маткаде
0 |
|
24 / 24 / 0 Регистрация: 26.01.2013 Сообщений: 300 |
|||||
|
26.05.2013, 01:02 [ТС] |
6 |
||||
|
можно тему удалить.никто не видит(
0 |
|
24 / 24 / 0 Регистрация: 26.01.2013 Сообщений: 300 |
|||||
|
26.05.2013, 01:06 [ТС] |
7 |
||||
|
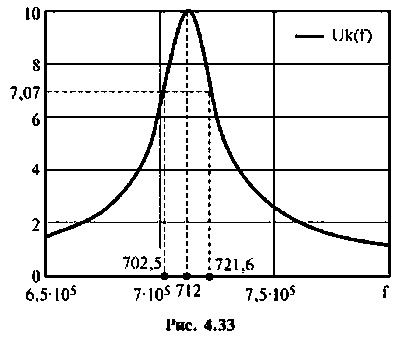
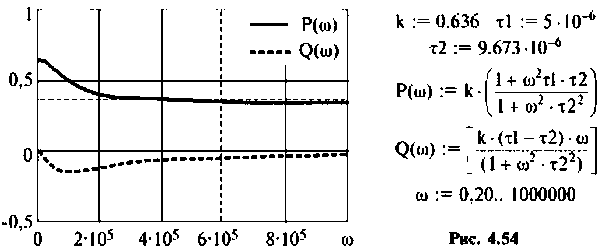
Привет,ребята! В Маткаде нужно рассчитать коэффициент передачи для данного 4х-полюсника. Я уже замучился, график не получается.
Исходные:
0 |
|
24 / 24 / 0 Регистрация: 26.01.2013 Сообщений: 300 |
|
|
26.05.2013, 18:53 [ТС] |
8 |
|
если не трудно, допишите,пожалуйста, до конца. так как мы всей группой застряли. старый препод неправильную формулу даёт.
0 |
|
7483 / 4147 / 474 Регистрация: 25.08.2012 Сообщений: 11,529 Записей в блоге: 11 |
|
|
26.05.2013, 19:28 |
9 |
|
допишите,пожалуйста, до конца Что?
1 |
|
24 / 24 / 0 Регистрация: 26.01.2013 Сообщений: 300 |
|
|
26.05.2013, 19:43 [ТС] |
10 |
|
Далее — подставляйте, умножайте на сопряженные, сокращайте и получите K(w)= Ка + jКр Вот дальше, прошу!
0 |
|
7483 / 4147 / 474 Регистрация: 25.08.2012 Сообщений: 11,529 Записей в блоге: 11 |
|
|
26.05.2013, 19:51 |
11 |
|
Вот дальше, прошу! Сожалею, но необходимо выполнить требования raxp, пост №7
1 |
|
24 / 24 / 0 Регистрация: 26.01.2013 Сообщений: 300 |
|
|
26.05.2013, 20:05 [ТС] |
12 |
|
я извинился,тема та удалена, наказание снято.
0 |
|
7483 / 4147 / 474 Регистрация: 25.08.2012 Сообщений: 11,529 Записей в блоге: 11 |
|
|
26.05.2013, 20:50 |
13 |
|
я извинился,тема та удалена, наказание снято. Завтра постараюсь выкроить полчаса.
1 |
|
24 / 24 / 0 Регистрация: 26.01.2013 Сообщений: 300 |
|
|
26.05.2013, 21:32 [ТС] |
14 |
|
не круто завтра
0 |
|
7483 / 4147 / 474 Регистрация: 25.08.2012 Сообщений: 11,529 Записей в блоге: 11 |
|
|
27.05.2013, 11:54 |
15 |
|
не круто завтра ну ладно Вообще то, после слов «ну ладно» — просто бросят Вам помогать. Я начну, а Вы закончите.
z23=R-jxC
2 |
|
24 / 24 / 0 Регистрация: 26.01.2013 Сообщений: 300 |
|
|
27.05.2013, 14:10 [ТС] |
16 |
|
благодарю! Вы-принципиальный
0 |
|
OldFedor |
|
27.05.2013, 14:12
|
|
Не по теме:
Вы-принципиальный Так воспитали…
1 |
Коэффициент передачи
Коэффициент передачи (также коэффициент преобразования) — отношение напряжения на выходе той или иной системы, предназначенной для передачи электрических сигналов, к напряжению на входе. В частном случае, когда значения выходного и входного сигнала являются однородными, коэффициент передачи называют коэффициентом усиления. KП = UВЫХ / UВХ. Коэффициент передачи часто выражают в логарифмическом виде, как 20 lg (UВЫХ / UВХ), дБ.
Содержание
Коэффициент усиления и ослабления сигнала
- В усилительных устройствах коэффициент передачи больше единицы (больше нуля в логарифмическом масштабе) называют коэффициентом усиления (не путать с коэффициентом усиления антенны).
- При рассмотрении пассивных устройств, а также линий передачи, когда выходное напряжение меньше входного, употребляют понятие ослабление сигнала.
Комплексный коэффициент передачи
При анализе частотнозависимых устройств часто возникает необходимость в векторном представлении коэффициента передачи
- Комплексный коэффициент передачи K(jω) — отношение комплексной амплитуды (КА)Y выходной величины системы к комплексной амплитуде X входной величины синусоидальной формы при заданном значении её частоты ω.
Также ещё используется (в основном на практике в теории передачи сигналов по каналу связи) обратный комплексный коэффициент передачи (1/K(jω)). Так как ККП в этом случае меньше единицы и имеет дробный вид, что усложняет расчёты, комплексную амплитуду выходного сигнала Y можно вычислить умножением КА входного сигнала X на K(jω), если комплексный коэффициент передачи априори известен. Комплексный коэффициент передачи является комплексной величиной, а его компоненты зависят от частоты входного сигнала. Может быть представлен вектором на комплексной плоскости (построенная таким образом кривая называется годографом коэффициента передачи).
Измерения
- Прямое измерение — производится с помощью установок для измерения ослаблений или измерителей коэффициента передачи, в том числе панорамных.
- Совокупное измерение — производится с помощью измерения мощности или напряжения сигнала на выходе и на входе, и последующего расчета.
- Измерение методом сравнения — производится с помощью аттенюатора, являющегося мерой ослабления. В качестве меры коэффициента усиления, в принципе, можно применить откалиброванный измерительный усилитель, однако на практике это, как правило, не используется.
- Для измерения комплексных коэффициентов передачи применяются измерители импеданса и комплексных коэффициентов передачи, или, на сверхвысоких частотах, измерители комплексных коэффициентов и КСВ.
Литература
- Хлытчиев С. М. Основы автоматики и автоматизации производственных процессов. — 1985
- Словарь радиолюбителя — Л.: Энергия, 1979
- Гусев В. Г. Электроника. — 1991
Ссылки
- Добавить иллюстрации.
- Радиотехнические величины и параметры
Wikimedia Foundation . 2010 .
Полезное
Смотреть что такое «Коэффициент передачи» в других словарях:
коэффициент передачи — Отношение комплексной амплитуды сигнала на выходе системы (усилителя, фильтра и т.п) к комплексной амплитуде сигнала на ее входе. Часто используют модуль коэффициента передачи, являющийся действительной величиной. [Система неразрушающего контроля … Справочник технического переводчика
коэффициент передачи — perdavimo koeficientas statusas T sritis automatika atitikmenys: angl. transfer coefficient; transfer gain; transmission gain vok. Übertragungskoeffizient, m; Übertragungsmaß, n rus. коэффициент передачи, m pranc. coefficient de transfert, m;… … Automatikos terminų žodynas
коэффициент передачи — perdavimo faktorius statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, lygus elektrinės grandinės išėjimo ir įėjimo signalų įtampų, srovių arba galių dalmeniui. atitikmenys: angl. transfer coefficient; transfer factor;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
коэффициент передачи — perdavimo faktorius statusas T sritis fizika atitikmenys: angl. transfer factor; transfer ratio vok. Übertragungsfaktor, m; Übertragungsverhältnis, n rus. коэффициент передачи, m pranc. facteur de transmission, m; rapport de transfert, m … Fizikos terminų žodynas
коэффициент передачи при виброизоляции — коэффициент передачи Ндп коэффициент амортизации Отношение амплитуды виброперемещения (виброскорости, виброускорения защищаемого объекта или действующей на него силы) к амплитуде той же величины источника возбуждения при гармонической вибрации.… … Справочник технического переводчика
коэффициент передачи между оптическими полюсами — коэффициент передачи между полюсами Отношение мощности оптического излучения на одном из оптических полюсов компонента ВОСП к мощности оптического излучения на другом из его оптических полюсов, выраженное в децибелах. [ГОСТ 26599 85] Тематики… … Справочник технического переводчика
коэффициент передачи интегральной микросхемы — коэффициент передачи Отношение абсолютного значения изменения выходного напряжения усилителя рассогласования интегральной микросхемы к абсолютному изменению входного напряжения. Обозначение KUP [ГОСТ 19480 89] Тематики микросхемы Синонимы… … Справочник технического переводчика
коэффициент передачи модуля СВЧ — коэффициент передачи Кпер Отношение мощности на выходе модуля СВЧ к мощности на его входе при согласовании входа и выхода по заданному коэффициенту стоячей волны. [ГОСТ 23221 78] Тематики компоненты техники связи Обобщающие термины модули СВЧ,… … Справочник технического переводчика
коэффициент передачи мощности преобразовательного прибора СВЧ — коэффициент передачи мощности Кпер Отношение мощности преобразованного сигнала прибора СВЧ к мощности входного сигнала. [ГОСТ 23769 79] Тематики приборы и устройства защитные СВЧ Синонимы коэффициент передачи мощности … Справочник технического переводчика
коэффициент передачи по напряжению интегральной микросхемы — коэффициент передачи по напряжению Отношение напряжения на выходе интегральной микросхемы к заданному значению коммутируемого напряжения при включенном канале. Обозначение Кп KU [ГОСТ 19480 89] Тематики микросхемы Синонимы коэффициент передачи по … Справочник технического переводчика
Коэффициент передачи
Форма представления коэффициента передачи зависит от формы математического представления сигналов входа и выхода. Это могут быть, например, операторы Лапласа или Фурье, тогда коэффициенты передачи называют операторными.
Коэффициент передачи и коэффициент усиления
В частности, если величины входного и выходного сигналов однородны, тогда коэффициент передачи называют коэффициентом усиления. Так, коэффициентом усиления по напряжению () называют физическую величину, равную отношению амплитуды переменной компоненты выходного напряжения (
) к амплитуде входного напряжения (
):
В выражении для коэффициента усиления можно использовать не только амплитуды, но и действующие значения напряжения.
Если коэффициенты усиления выражают в децибелах, то определением коэффициента преобразования (усиления) по напряжению будет выражение:
Коэффициенты усиления по току и мощности в децибелах выражают как:
Коэффициент усиления каскада равен произведению отдельных элементов каскада, если он выражен в относительных единицах:
Общий коэффициент усиления каскада равен сумме отдельных элементов каскада, если он выражен в децибелах.
K(дб)=
Если в усилителе коэффициент передачи больше единицы для безразмерного коэффициента или больше нуля для коэффициента, представленного в децибелах, то коэффициент называют коэффициентом усиления.
Коэффициент передачи может быть представлен в комплексном виде. Он используется для анализа устройств, которые зависят от частоты сигналов.
Комплексный коэффициент передачи линейного звена находят как отношение комплексной амплитуды выходного сигнала к комплексной амплитуде входного сигнала:
где — комплексная амплитуда выходного сигнала,
— комплексная амплитуда сигнала на входе,
— частота.
Единицы измерения
Коэффициент усиления — может быть величиной безразмерной. При решении задач следует обратить внимание на то, чтобы величины входных и выходных сигналов были выражены в одних единицах.
Или коэффициент усиления может выражаться в логарифмических единицах — децибелах.
Примеры решения задач
| Задание | Что такое частотный годограф? |
| Решение | Комплексный коэффициент передачи применяют для графического изображения свойств звена. С этой целью строят частотный годограф. Частотным годографом называют геометрическое место точек, которое создает конец вектора комплексного коэффициента передачи, если частота сигнала изменяется от 0 до |
Для узла, к которому подключен инвертирующий выход, запишем закон Кирхгофа для токов:
Рассмотрим контур, который включает источник напряжения, вход усилителя, и сопротивление , запишем второй закон Кирхгофа для этого контура:
Рассмотрим контур, который включает вход усилителя, сопротивление и выход схемы, получаем:
Выразим из (2.3) выходное напряжение и учтем, что: если усилитель работает в линейном режиме, то входные токи в рассматриваемый усилитель равны нулю (в нашем случае ); напряжение на входе в такой усилитель равно нулю
=0. Тогда:
Коэффициент передачи
- Коэффициент передачи (также коэффициент преобразования) — отношение мощности, напряжения или тока на выходе той или иной системы, предназначенной для передачи электрических сигналов, соответственно, к мощности, напряжению или току на входе системы. Например, выражение для коэффициента передачи по напряжению: KV = V2 / V1.
Коэффициент передачи часто выражают в децибелах (дБ, dB), в основе которых лежит десятичный логарифм отношения величин. Например: KV (дБ) = 20 lg (V2 / V1). В случае, когда значения рассматриваемых величин уже представлены в децибелах: KV (дБ) = V2 (дБ) − V1 (дБ). Коэффициент передачи, выраженный в децибелах, может иметь знак плюс или минус в зависимости от соотношения величин на выходе и на входе.
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
В статье описаны некоторые типовые применения операцио́нных усили́телей (ОУ) в аналоговой схемотехнике.
При включении биполярного транзистора по схеме с общим эмиттером (ОЭ) входной сигнал подаётся на базу относительно эмиттера, а выходной сигнал снимается с коллектора относительно эмиттера. При этом выходной сигнал инвертируется относительно входного (для гармонического сигнала фаза выходного сигнала отличается от входного на 180°). Данное включение транзистора позволяет получить наибольшее усиление по мощности, потому что усиливается и ток, и напряжение.
СВОЙСТВА
1.1. Четырехполюсник
Полюсом называют вывод (контакт,
клемму, зажим) электрической цепи, к
которому что-либо подключается (источник
сигнала, нагрузка, другая цепь).
Электрические цепи классифицируют по
числу полюсов на:
— двухполюсники (сопротивление,
индуктивность, емкость, идеальные и
реальные источники сигнала, полупроводниковый
диод);
— трехполюсники (например, трехфазный
источник напряжения без нейтрали,
трехфазная нагрузка при соединении
«треугольником» на рис. 1.1, биполярный
транзистор);
— четырехполюсники (усилители сигналов,
фильтры).
Значительно реже возникают цепи с
большим числом полюсов.
Рис. 1.1
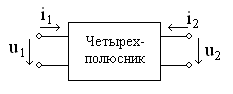
называют электрическую цепь с четырьмя
полюсами, разделенными на пару входных
и пару выходных полюсов, как показано
на рис. 1.2. Входные полюсы обычно
изображаются сле-
Рис. 1.2 ва и имеют
индекс 1, а вы-
4
ходные – справа с индексом 2. Входной и
выходной токи чаще всего обозначают
втекающимив четырехполюсник.
Различают линейные (содержащие только
линейные элементы) и нелинейные (в состав
которых входит хотя бы один нелинейный
элемент) четырехполюсники (рис.1.3).
Рис. 1.3
Свойства линейных четырехполюсников
рассматривают при гармонических
воздействиях (это простые сигналы,
расчет которых удобно проводить методом
комплексных амплитуд).
В линейном четырехполюснике при
гармоническом воздействии все токи и
напряжения являются также гармоническими
с той же частотой, а их амплитуды и
начальные фазы зависят от частоты
воздействия. В этом случае свойства
цепи описывают частотными характеристиками– зависимостями от частоты входного
сигнала различных характеристик,
например:
— входного и выходного сопротивлений
или проводимостей;
— коэффициентов передачи или обратной
связи по току или напряжению;
— коэффициента передачи мощности;
— сопротивлений (проводимостей) прямой
передачи или обратной связи.
5
1.2 Входное и выходное сопротивления
четырехполюсника
В качестве частотных характеристик
рассматриваются входное
и выходное
сопротивления как функция частоты
сигнала. По определению при заданном
сопротивлении нагрузки четырехполюсника,
подключенной к его выходу,
.
(1.1)
Выходное сопротивление определяется
при известном внутреннем сопротивлении
источника входного сигнала
,
.
(1.2)
Знание этих характеристик необходимо
при анализе возможностей подключения
к четырехполюснику реального источника
сигнала и нагрузки.
Рассмотрим четырехполюсник с подключенными
к нему реальным источником напряжения
с внутренним сопротивлением
и нагрузкой
,
как показано на рис. 1.4.
Рис.1.4
6
Э
схема вход-ной цепи четырехполюсника
показана на рис. 1.5, где— входное сопротивление четырехполюсника.
Если необходимо обеспечитьмаксимум
амплитудывходного напряже-
Рис. 1.5
ния
, то по закону Ома полу-
чим
.
(1.3)
Представляя
и
,
можно записать
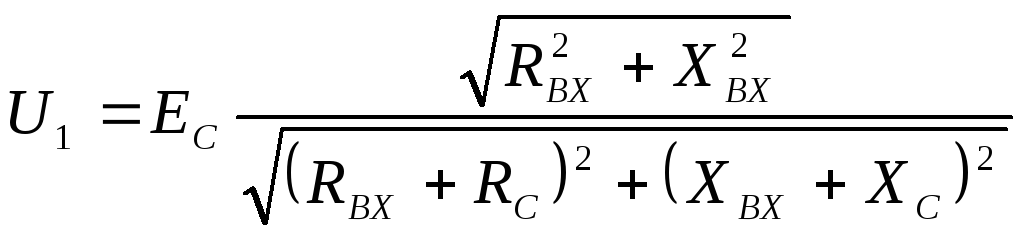
(1.4)
Для идеального источника напряжения
и входное напряжение равно ЭДС источника.
Если обеспечить условие максимумапо
,
,
(1.5)
то из (1.4) следует
.
(1.6)
и при условии
входное напряжение
четырехполюсника станет больше ЭДС
источника сигнала.
7
Это обусловлено резонансными явлениями
во входной цепи, которые будут
рассматриваться в дальнейшем.
Для обеспечения максимума мощности,
потребляемой четырехполюсником от
источника сигнала, из общего выражения
,
(1.7)
где
—комплексно сопряженнаяамплитуда
входного тока, получим

(1.8)
где
— комплексно-сопряженная ЭДС источника,
а— оператор вычисления реальной части
числа. С учетом того, что произведение
комплексно-сопряженных чисел равно
квадрату их модуля,
,
(1.9)
в результате получим
.
(1.10)
Из полученного выражения нетрудно
получить условие максимума потребляемой
четырехполюсником (рис. 3.6) мощности
(условие согласования источника
сигнала с четырехполюсником),
8

Аналогичный анализ можно провести и
для выходной цепи четырехполюсника. В
соответствии с теоремой об эквивалентном
источнике напряжения (повторите этот
материал) эквивалентная схема выходной
цепи схемы рис. 1.4 имеет вид, показанный
на рис. 1.6а, гдеи
— эквивалентные ЭДС и внутреннее
сопротивление активного двухполюсника,
показанного на рис. 1.6б, а.
Рис. 1.6
Мощность в нагрузке аналогично (1.10)
равна
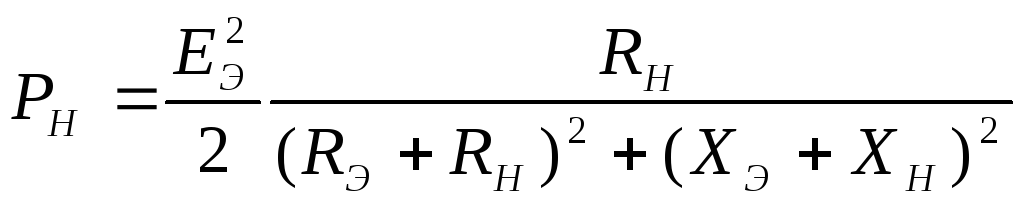
(1.12)
где
и
.
В результате нетрудно получить условие
передачи максимума мощности от источника
сигнала через четырехполюсник в нагрузку
(условие согласования четырехполюсника
с нагрузкой),

9
В качестве примера рассмотрим цепь на
рис. 1.7, в состав которой входят источник
входного сигнала (реальный источник
гармонического напряжения с комплексной
амплитудой
,
внутренним сопротивлениеми частотой
),RC- четырехполюсник и
нагрузка.
Рис. 1.7
Схема цепи для определения входного
сопротивления нагруженного четырехполюсника
показана на рис. 1.8. Величина
определяется выражением

Рис. 1.8
При активной нагрузке
,
умножая числитель и знаменатель дроби
на комплексно-сопряженный множитель,
получим
10

модуль входного сопротивления равен

а активную
и реактивную
составляющие можно записать в виде
,

На рис. 1.9 приведены зависимости от
частоты модуля
и активной составляющей
входного сопротивления четырехполюсника
прикОм
инФ.
Рис. 1.9
11
На рис. 1.10 показана зависимость от
частоты реактивной составляющей входного
сопротивления четырехполюсника.
Рис. 1.10
Как видно, входное сопротивление
четырехполюсника существенно изменяется
в выбранном диапазоне частот и имеет
емкостный характер. Модуль и активная
составляющая сопротивления уменьшаются
с ростом частоты от значения
при
до
на бесконечной частоте (на высоких
частотах емкость шунтирует нагрузку).
Рассмотрим, каким должно быть внутреннее
сопротивление источника сигнала, чтобы
обеспечить передачу максимума мощность
в четырехполюсник на частоте
рад/с.
В этом случае входное сопротивление
четырехполюсника равно
Ом.
Тогда в соответствии с (1.11) источник
сигнала должен иметь внутреннее
сопротивление равнымОм.
Характер трехмерной зависимости мощностиот активной
и реактивной
составляющих входного сопротивления
четырехполюсника в соответствии с
(1.10) приВ
показан на рис. 1.11. Максимумимеет место при условии (1.11).
12
Рис. 1.11
Подставляя в (1.10) выражения для активной
и реактивной
составляющих для цепи рис. 1.7, получим
зависимость потребляемой четырехполюсником
мощностиот частоты сигнала. Она показана на рис.
1.12 приВ
иОм.
Рис. 1.12
13
Как видно, на частоте
рад/с, когда
Ом
и выполняется условие согласования
(1.11), имеет место максимум потребляемой
четырехполюсником мощности.
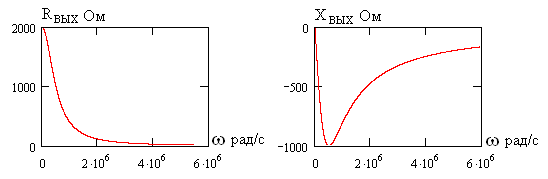
Рассмотрим выходное сопротивление
четырехполюсника рис. 1.7, для этого
рассмотрим цепь на рис. 1.13а. В соответствии
с теоремой об эквивалентном источнике
ее можно заменить эквивалентным реальным
источником напряжения, показанным на
рис. 1.13б. Эквивалентная ЭДС
равна напряжению холостого хода цепи
рис. 1.13а,,
а эквивалентное сопротивлениеравно сопротивлению цепи рис. 1.13а при
выключенном источнике, как показано на
рис. 1.14. Сопротивлениеи есть внутреннее сопротивление
четырехполюсника.
Рис. 1.13
Для цепей на рис. 1.13а и рис. 1.14 нетрудно
получить параметры эквивалентного
источника рис. 1.13б. Его ЭДС и внутреннее
сопротивление
равны
,
.
14
Рис. 1.14
На рис. 1.15 показана программа MathCADдля расчета значений выходного
сопротивления,
на рис. 1.16 приведены зависимости от
частоты модуля и аргумента,
а на рис. 1.17 – его активнойи реактивной
составляющих при
кОм,
кОм
инФ.
Рис. 1.15
Рис. 1.16
15
Рис. 1.17
Как видно, модуль выходного сопротивления
максимален на постоянном токе и быстро
падает с ростом частоты. Выходное
сопротивление всегда имеет емкостный
характер. На частоте
рад/с
Ом и
Ом.
Для обеспечения максимальной мощности
в нагрузке ее сопротивление должно
удовлетворять условию (1.13). Проведите
самостоятельно анализ, аналогичный
показанному на рис. 1.11.
1.3. Комплексный коэффициент передачи
Комплексный коэффициент передачи по
напряжениюопределяется выражением
,
(1.14)
аналогично вводятся в рассмотрение
комплексный коэффициент передачи
тока
16
(1.15)
и коэффициент (не комплексный)
передачи мощности
,
(1.16)
где
— мощность, потребляемая четырехполюсником,
а— мощность, передаваемая в нагрузку. Для
расчета коэффициентов передачи необходимо
при заданном источнике входного сигнала
определить комплексные амплитуды
входного и выходного напряжений, токов
или мощностей.
В
схема которого показана на рис. 1.12, и
определим его комплексный коэффициент
передачи напряжения вида (1.14).
Подключим на вход четырехполюс-
Рис. 1.18
полюсника идеальный
источник напряжения с ЭДС
,
как показано на рис. 1.13, и воспользуемся
методом узловых напряжений. В цепи
имеется два узла и необходимо определить
единственное узловое напряжение.
Выражая черезтоки ветвей и используя первый закон
Кирхгофа, получим уравнение метода
узловых напряжений:
17
Рис. 1.19
После алгебраических преобразований
получим
.
Тогда по Закону Ома можно определить
выходное напряжение

Подставляя выражение для
,
с учетомполучим
.
Тогда комплексный коэффициент передачи
четырехполюсника по напряжению равен
.
Как видно,
— комплексная функция частоты сигнала,
18
ее называют комплексной частотной
характеристикой (КЧХ). Графически она
отображается линией в трехмерном
пространстве (осьи две оси для отображения комплексного
числа), что неудобно практически.
На плоскости КЧХ изображается в виде
годографа. Для его построения
заданный интервал частот разбивается
с равномерным шагом, для каждого значения
частоты вычисляются и отображаются на
комплексной плоскости по осям абсцисс
и ординат соответственно действительнаяи мнимая
составляющие комплексного коэффициента
передачи.
П
годографа КЧХ цепи на рис. 1.18 прикОм,
мГн
инФ
показан на рис. 1.20. Стрелка показывает
направление увеличения частоты входного
сигнала. На частоте
величина
действительна, а точка годографа
расположена на оси абсцисс.
Рис.
1.20
1.4. Амплитудно-частотная и фазочастотная
характеристики четырехполюсника
Комплексный коэффициент передачи
четырехполюсника можно представить в
показательной форме,
,
(1.17)
19
где
—
его модуль, а— аргумент.
Амплитудно-частотная характеристика(АЧХ)представляет собой зависимостьмодулякомплексного коэффициента передачи от
частоты. Она представляет собой отношениеамплитудилидействующих значений
выходного сигнала к входному.
Фазочастотная характеристика(ФЧХ)– это зависимость от частотыаргументакомплексного коэффициента передачи.
Она представляет собойсдвиг фаз между
выходным и входным сигналами.
Обычно выражение для
представляет собой дробь с комплексными
числителем и знаменателем, которую
необходимо представить в виде
.
(1.18)
Тогда модуль частного (дроби) равен
частному модулейчислителя и
знаменателя,
,
(1.19)
а ее аргумент – разности аргументов
числителя и знаменателя,
.
(1.20)
Аргумент комплексного числа
определяется выражением
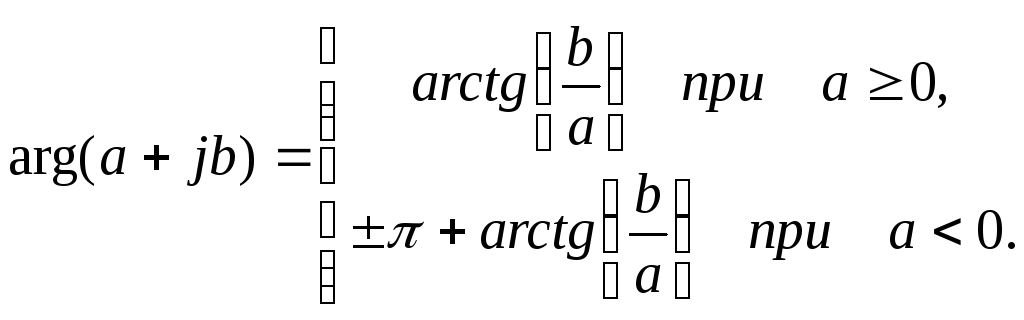
20
Численные значения АЧХ безразмерны,
а ФЧХ измеряется вугловых единицах(радианах или градусах).
В инженерной практике широко используется
измерение АЧХ в децибелах (дБ). Если
рассматриваются модули коэффициентовпередачи напряжения или тока, то их
значение в децибелах равно
.
(1.22)
Если же речь идет о коэффициенте передачи
мощности
,
то
.
(1.23)
Логарифмическая мера АЧХ весьма удобна
при анализе четырехполюсников. Если
,
то получим, чтодБ
и амплитуда сигнала не меняется при
прохождении через четырехполюсник.
Если,
тои происходитусилениесигнала, а
если наоборот, тои наблюдаетсяослабление (затухание)сигнала. Основным достоинством
логарифмической меры является возможность
отображать графически широкий диапазон
изменения АЧХ от маленьких величинили
дБ
до больших значенийили
дБ.
Измерение коэффициентов передачи в
децибелах удобно при их перемножении,
например, при каскадном соединении
согласованно нагруженных четырехполюсников
(эти вопросы рассматриваются в дальнейшем),
при этом значения в децибелах будут
складываться.
Определим АЧХ и ФЧХ цепи, показанной на
рис. 1.12. Для найденного комплексного
коэффициента передачи по напряжению
модуль (АЧХ) и аргумент (ФЧХ) соответственно
равны
21
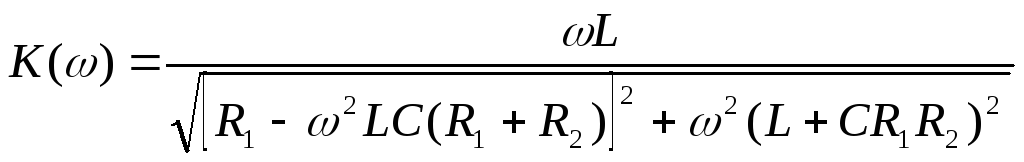
где
.
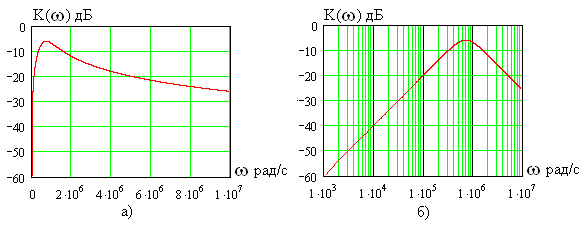
На рис. 1.21 показан график АЧХ
четырехполюсника, показанного на рис.
1.18 при
кОм,
мГн
инФ.
Максимум АЧХ имеет место на частоте,
в чем нетрудно убедиться, взяв производнуюи приравняв ее нулю. На рис. 1.22приведен график ФЧХ четырехполюсника.
Рис. 1.21
На частотах
ФЧХ
,
то есть выходное
22
напряжение опережает по фазе входное,
а если
,
то наоборот. На частотесдвиг фаз между этими напряжениями
равен нулю (они синфазны).
Рис. 1.22
На рис. 1.23а показана та же АЧХ, что и на
рис. 1.15, но в децибелах, а на рис. 1.23б –
еще и в логарифмическом масштабе по оси
частот. Как видно, переход к логарифмическим
масштабам по оси ординат (дБ) и оси частот
позволяет разборчиво представить АЧХ
в широком диапазоне значений. Недостатком
подобных графиков является искажение
формы кривых по сравнению с равномерным
масштабом на рис. 1.21.
Рис. 1.23
23
1.5. Схемотехническое моделирование
Рассмотрим применение пакета программ
схемотехнического моделирования
MicroCAP7для анализа частотных характеристик
четырехполюсников.
Пример моделируемой цепи показан на
рис. 1.24. Проведите расчет ее частотных
характеристик при
кОм
инФ.
На рис. 1.25 представлены
зависимости от частоты модуля и
аргумента входного сопротив-
Рис. 1.24 ления, модуль
сопротивления за-
дается выражением
,
а аргумент – функцией.
Вычислите значения этих характеристик
на частоте 200кГц и сравните с результатами
моделирования.
Рис. 1.25
24
На рис. 1.26 показаны зависимости от
частоты модуля (АЧХ) и аргумента (ФЧХ)
комплексного коэффициента передачи
цепи рис. 1.24.
Рис. 1.26
Схемотехническое моделирование в режиме
«ACAnalysis»
позволяет получить различные частотные
характеристики исследуемой цепи.
Рассмотрим модель той же цепи, но с
подключенной нагрузкой
кОм
(рис. 1.27). На рис. 1.28 показаны результаты
моделирования АЧХ (в децибелах) и
ФЧХ в режиме «Stepping» при
измененииот 1 кОм (верхняя кривая) до 200 Ом (нижняя
кривая) с одинаковым шагом 200 Ом.
Рис. 1.27
25
Рис. 1.28
Как видно, моделирование позволяет
исследовать влияние параметра цепи на
частотные характеристики с целью,
например, выбора его оптимального
значения.
1.6. Задания для самостоятельного решения
З
1.1. Определите входное сопротивление
четырехполюсника, показанного на рис.
1.29. Получите формулы для его модуля и
аргумента, активной и реактивной
составляющих. С помощью пакета программMathCADпостройте графики
длякОм
имГн
приотсутствии
нагрузки()и при ее наличии (
кОм).
Рис. 1.29
Задание 1.2. Для цепи рис. 1.30
прикОм,
26
мГн
икОм на частоте
рад/с определите, при каком комплексном
сопротивленииреального источника сигнала в нагруженный
четырехполюсник будет передана
максимальная мощность. Вычислите
величину этой мощности при ЭДС источника
напряженияВ.
Рис. 1.30
Задание 1.3. Для четырехполюсника с
подключенным источником напряжения с
ЭДСВ
иОм, показанного на рис. 1.31, определите
выходное сопротивление, используя
теорему об эквивалентном источнике.
Получите формулы для его модуля и
аргумента, активной и реактивной
составляющих. С помощью пакета программMathCADпостройте соответствующие
графики длякОм
имГн.
Н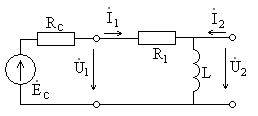
частотерад/с определите, при каком комплексном
сопротивлении нагрузки,
подключенной к четырехполюснику рис.
1.31, в нее будет передана максимальная
мощность.
Рис.
1.31
27
Задание 1.4. Рассчитайте входную и
выходную проводимости показанного на
рис. 1.32 четырехполюсника, рассмотрите
ее в диапазоне частот прикОм,
нФ,
мА,
Ом
икОм.
Постройте соответствующие графики.
Рис. 1.32
Задание 1.5. Рассчитайте комплексный
коэффициент передачи и постройте
годографы КЧХ четырехполюсников, схемы
которых показаны на рис. 1.33. Определите
их АЧХ и ФЧХ, постройте их графики.
Рис. 1.33
Задание 1.6. Выполните задания 1.1-1.5
методом схемотехнического моделирования.
Сравните полученные результаты с
расчетными. Сравните АЧХ в линейном
масштабе и в децибелах, оцените их
преимущества и недостатки.
28

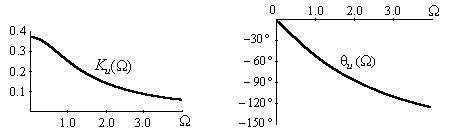
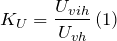
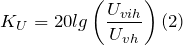

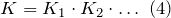
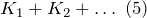
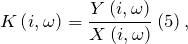

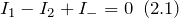
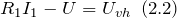
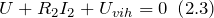
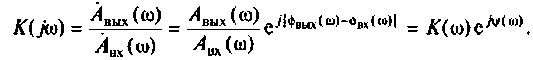
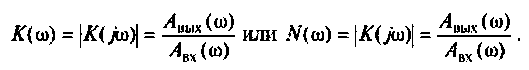
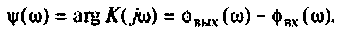
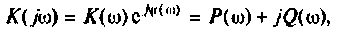
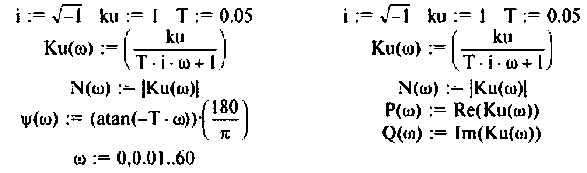
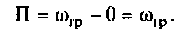
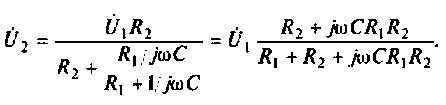
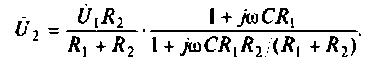
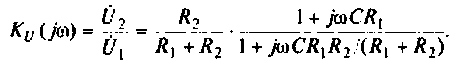
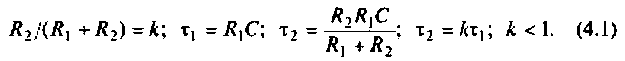
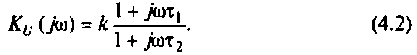
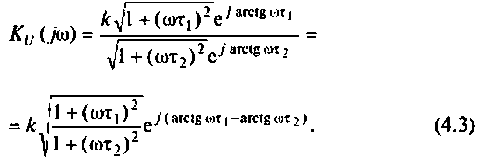
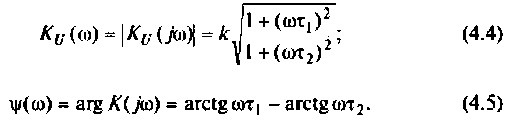
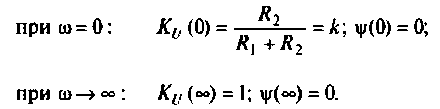
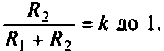
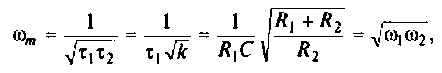
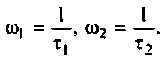
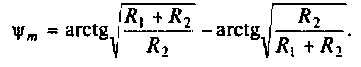
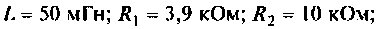
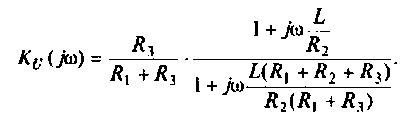
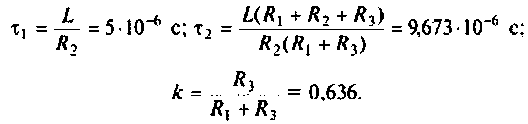
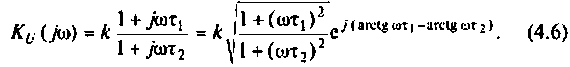
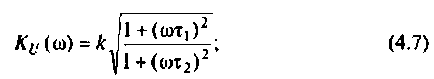
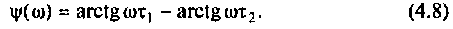
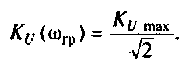
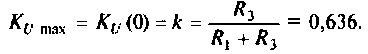
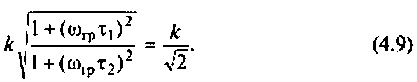
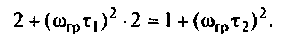
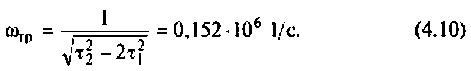
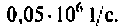
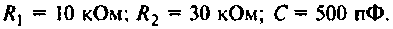
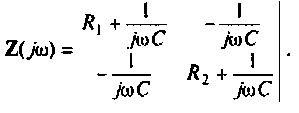
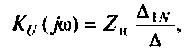
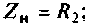
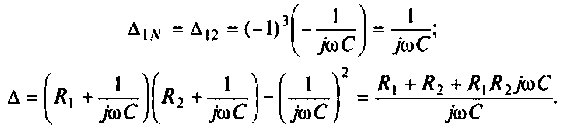
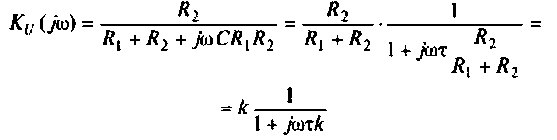
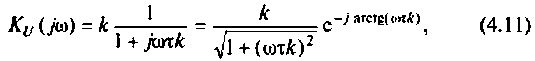
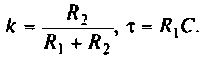
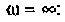
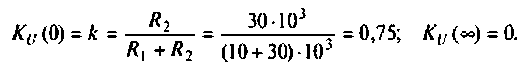
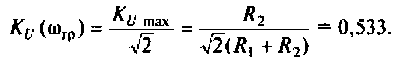
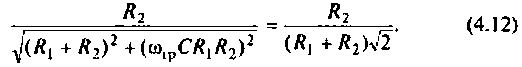
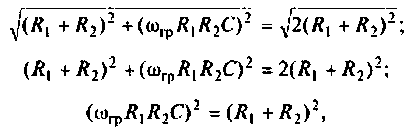
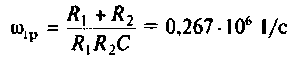
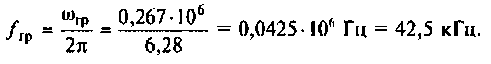
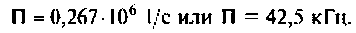
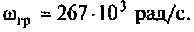
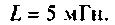
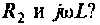
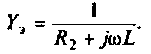
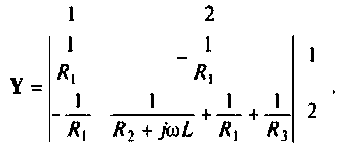
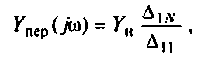
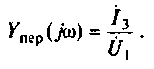
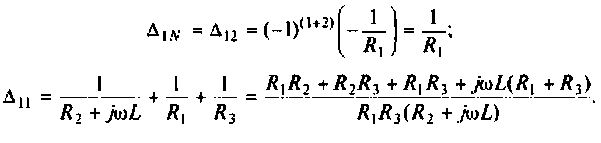
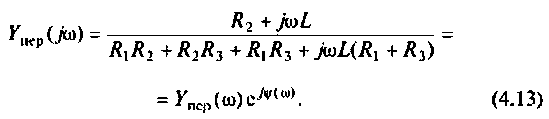
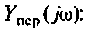
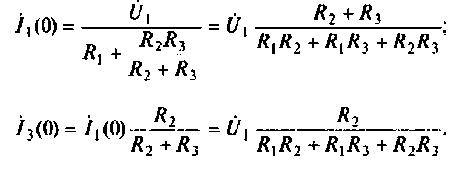
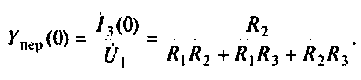
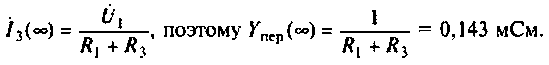
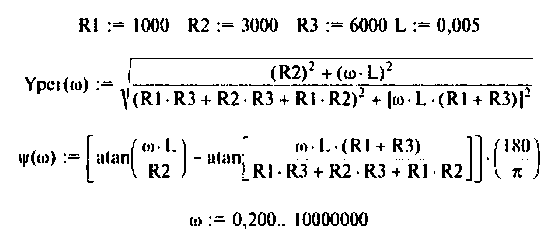
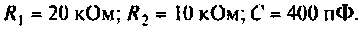
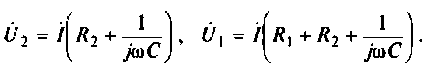
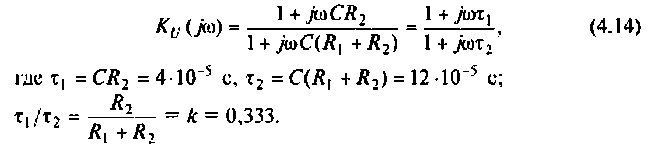
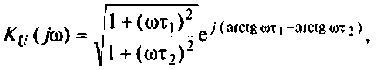
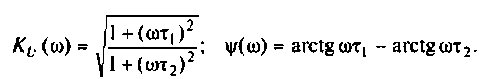
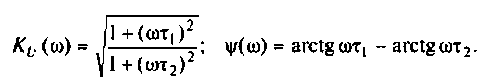

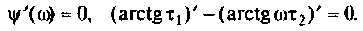
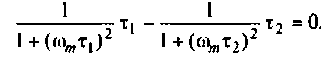
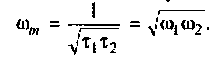
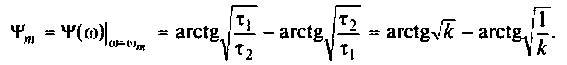
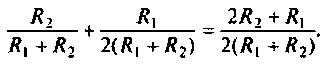
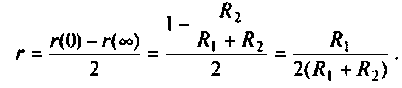
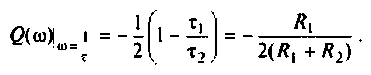
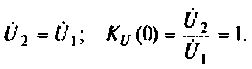
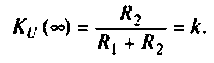
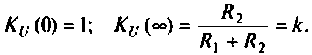
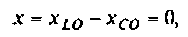
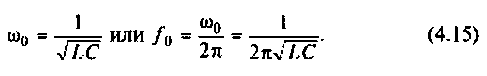
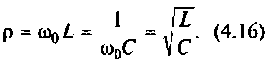
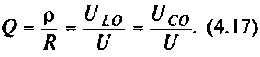
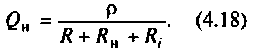

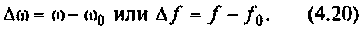

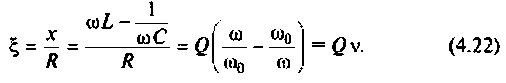
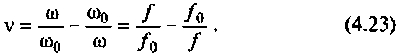
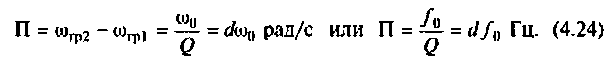

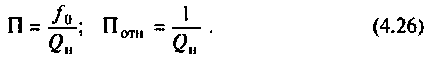
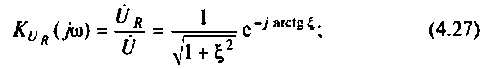
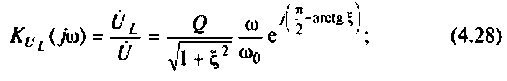
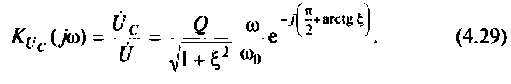
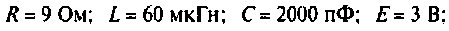
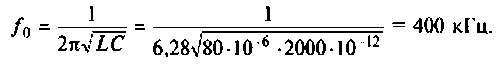
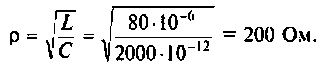
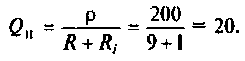
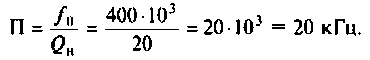
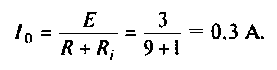
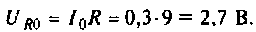
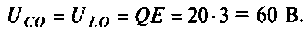
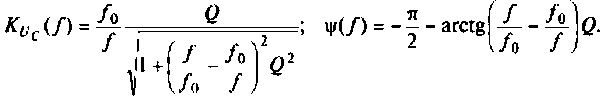
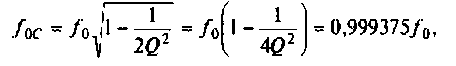
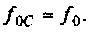
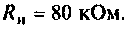
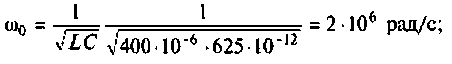
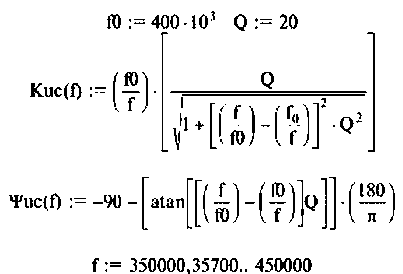
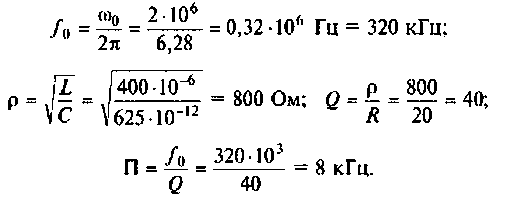
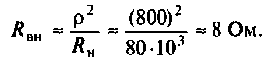
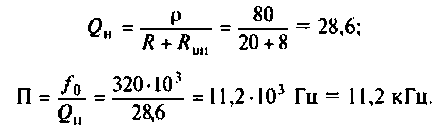
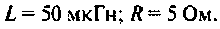
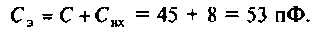
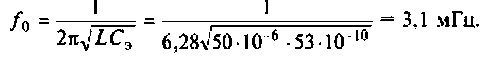
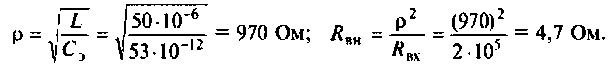
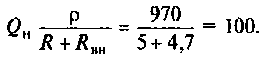
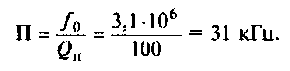
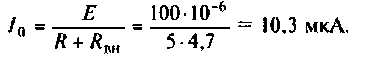
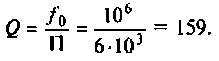
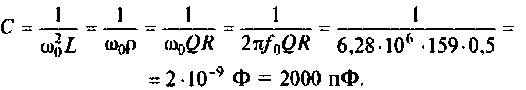
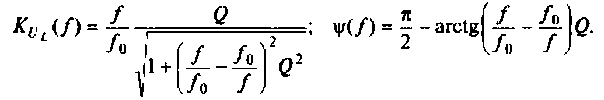
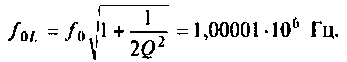
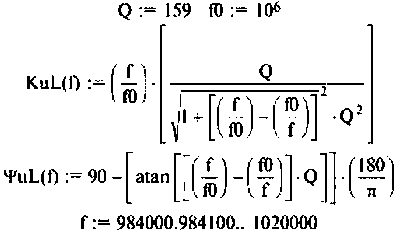
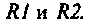
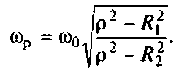
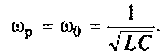
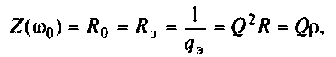
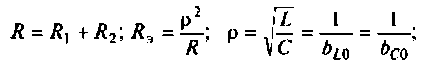
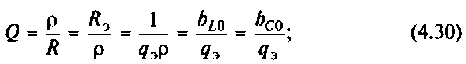
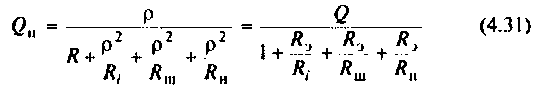
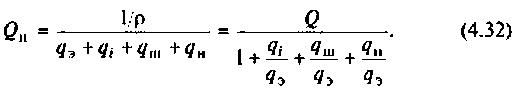
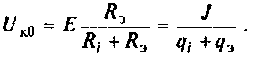
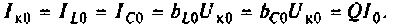
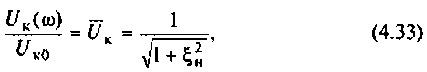
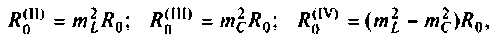
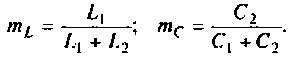
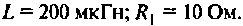
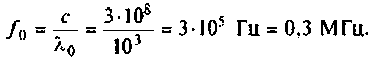
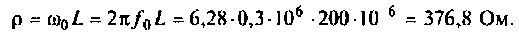
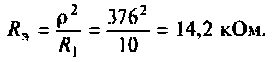
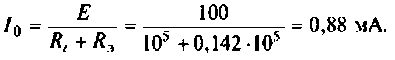
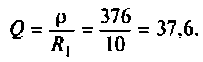
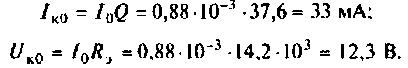
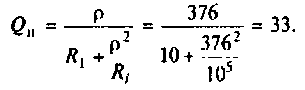
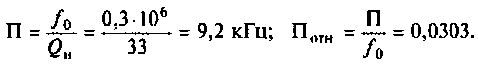
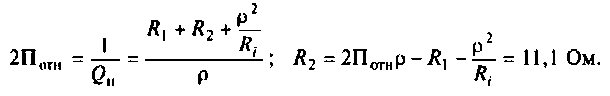
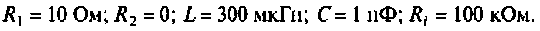
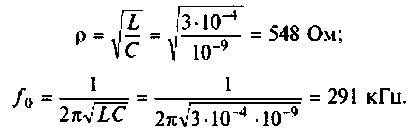
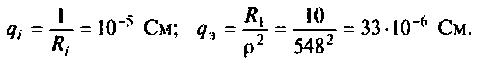
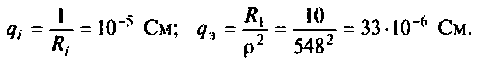
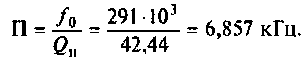
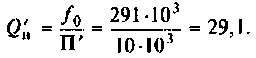
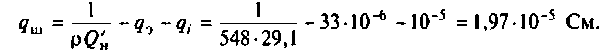
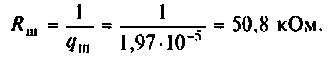
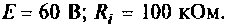
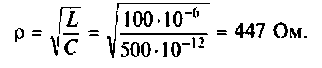
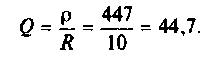
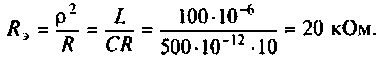
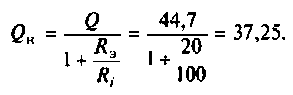
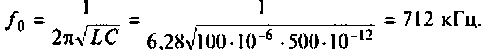
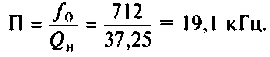
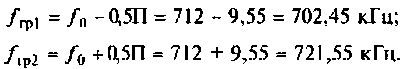
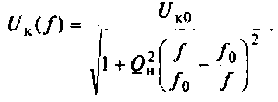
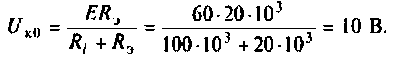
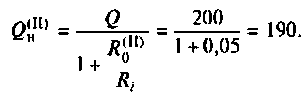
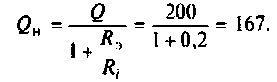


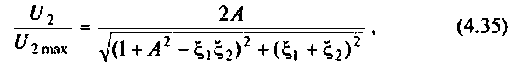
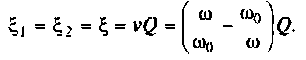
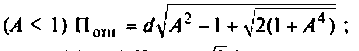
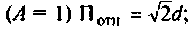
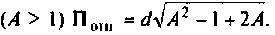
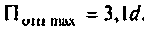
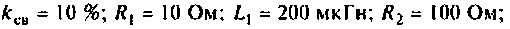
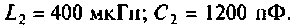
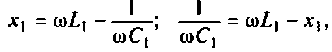
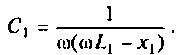
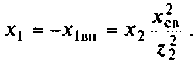
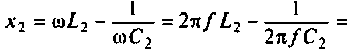
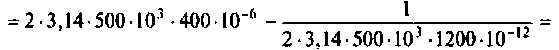
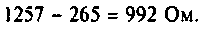
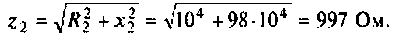
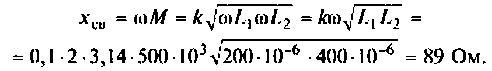
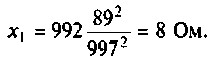
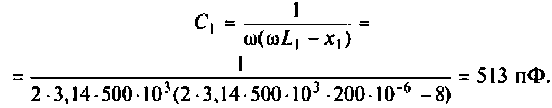
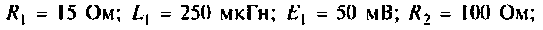
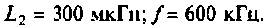
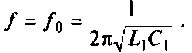
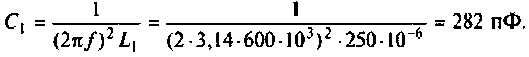
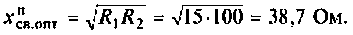
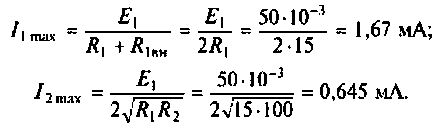
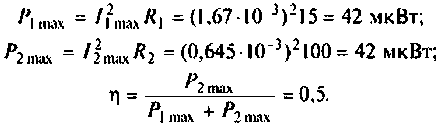
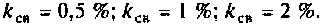
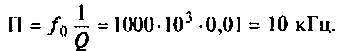
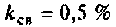
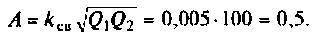
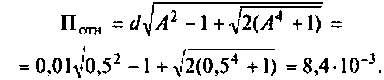
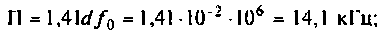
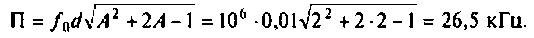

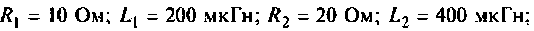
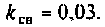
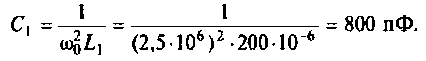
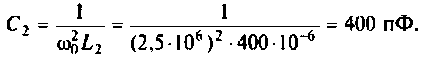
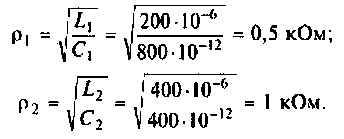
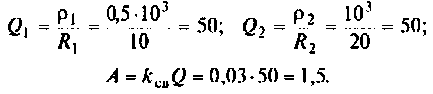
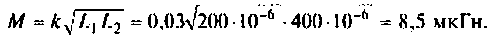
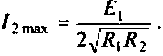
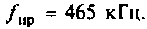
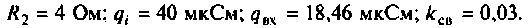
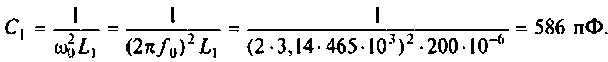
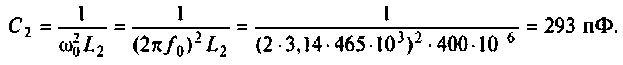
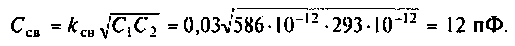
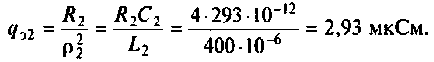
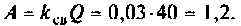
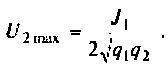
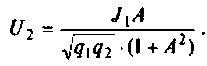
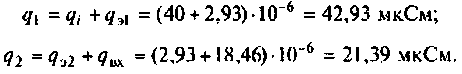
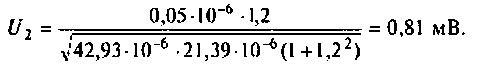
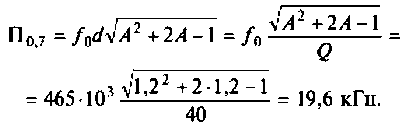
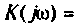
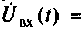
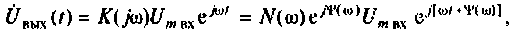
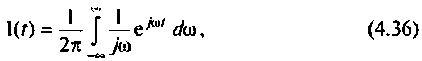
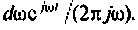
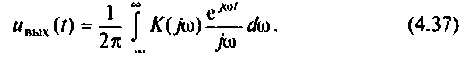
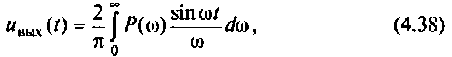
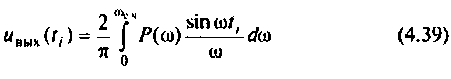
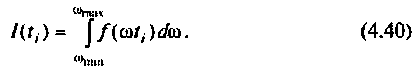
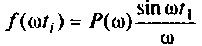
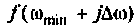
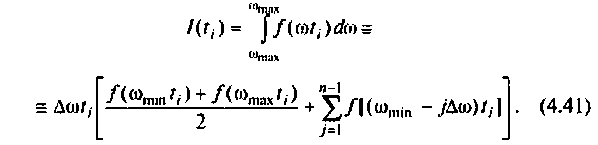

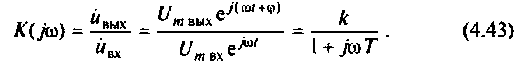
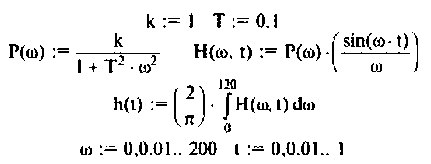
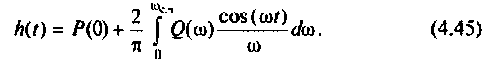
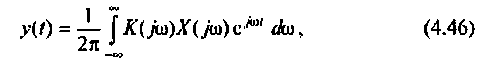
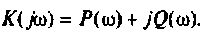
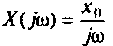
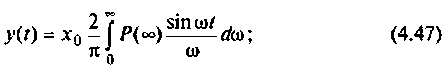
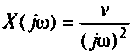
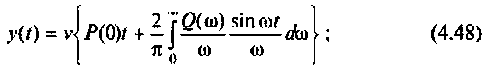
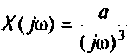
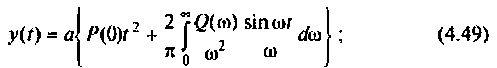
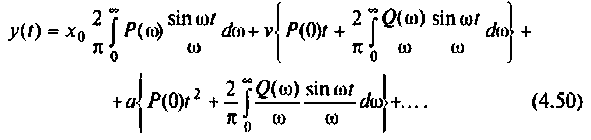
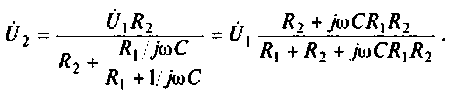
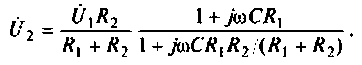
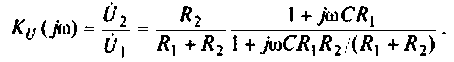
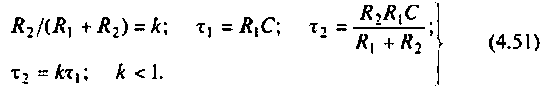
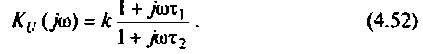
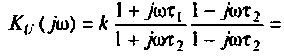
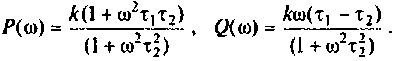
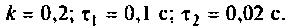
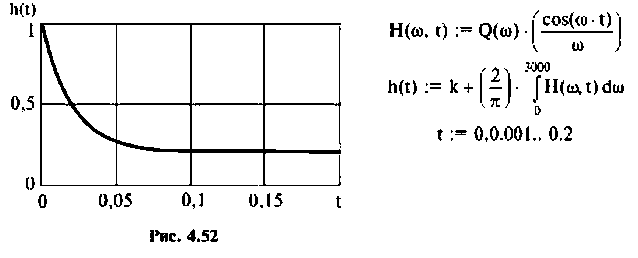
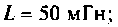
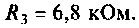
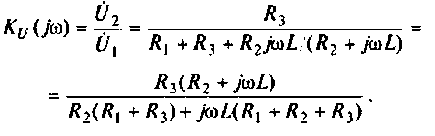
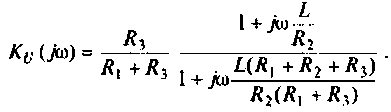
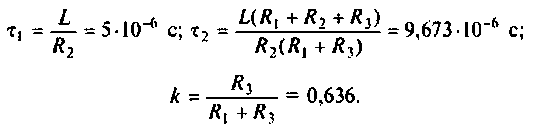
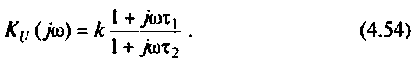
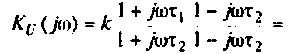
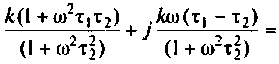
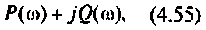
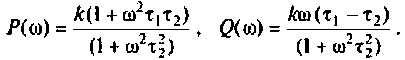
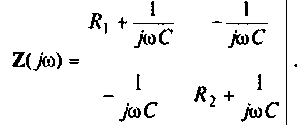
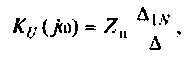
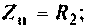
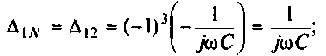
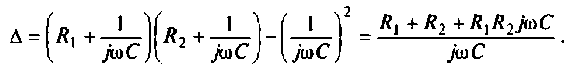
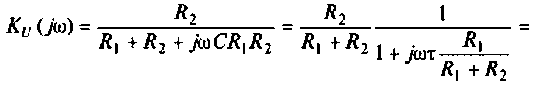
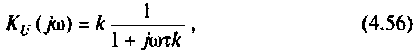
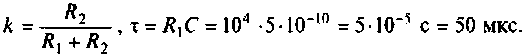
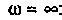
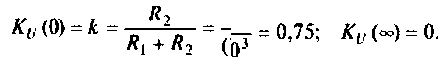
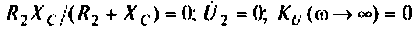
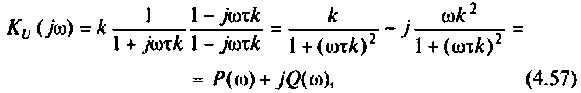
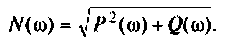
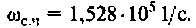
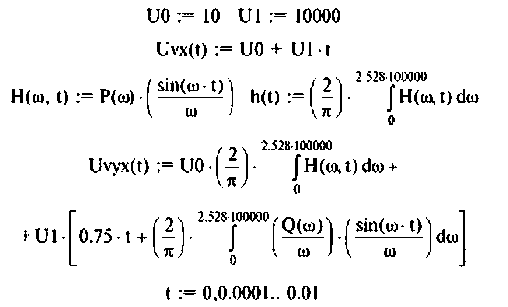


 Пожалуйста.
Пожалуйста.
 ну ладно
ну ладно