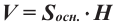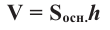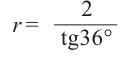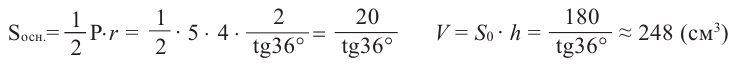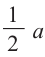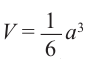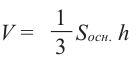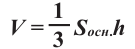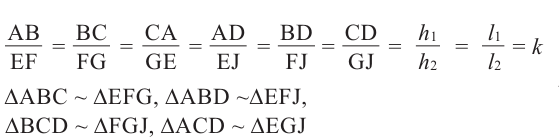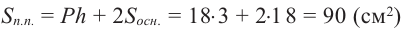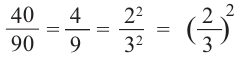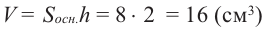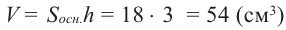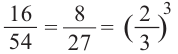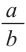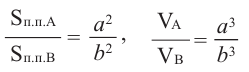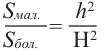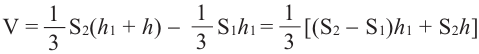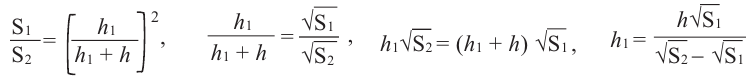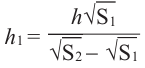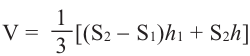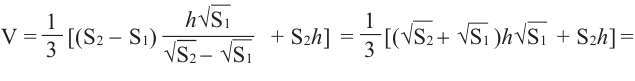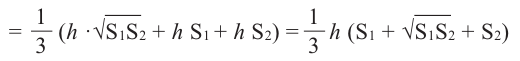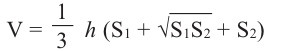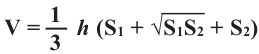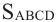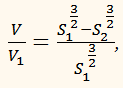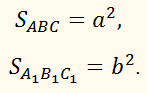Объем пространственных фигур — определение и вычисление с примерами решения
Содержание:
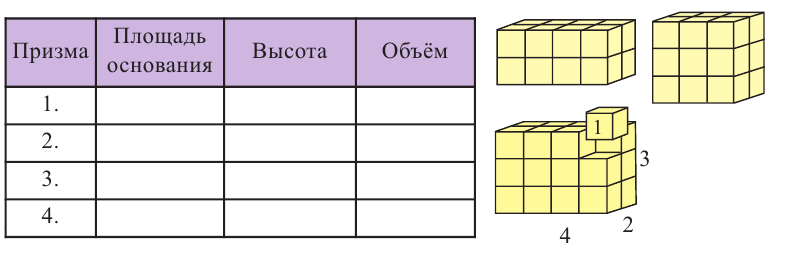
Исследование. Соберите не менее 4 призм различных размеров из кубиков и изобразите полученные призмы.
- Предположим, что ребро каждого кубика, из которых состоит призма, равна 1 единице, площадь грани равна 1 квадратной единице, а объём равен 1 кубической единице.
- Данные для каждой призмы запишите в таблицу.
- Какая связь существует между площадью основания призмы и высотой?
- Вытащите один кубик из угла конструкции и изобразите вид впереди, сверху и сбоку каждого кубоида.
Если тело можно разделить на конченое число треугольных пирамид, то оно называется простым телом. Для простых тел объём — положительная величина, численное значение которой удовлетворяет следующим свойствам.
- Объёмы конгруэнтных тел равны.
- Объём куба, ребро которого равно единице, равен кубической единице.
- Если тело можно разделить на простые части, то его объём равен сумме объёмов полученных частей.
Тела, имеющие одинаковые объёмы называются равновеликими. Объём прямоугольного параллелепипеда, размеры которого являются натуральными числами, равен
количеству кубических единиц, из которых он состоит. Можно также показать, что объём прямоугольного параллелепипеда, размеры которого заданы любыми действительными числами равен произведению трёх измерений: 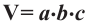
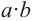
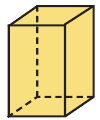
Следствие: Объём куба с ребром а равен:
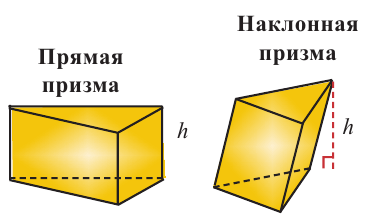
Объём любой прямой призмы равен произведению площади основания и высоты. Справедливость данного утверждения проверим на прямой призме, в основании которой лежит прямоугольный треугольник.
Достроим основание призмы до прямоугольника, получим призму, достроенную до прямоугольного параллелепипеда. Объём полученной призмы равен 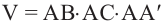
Плоскость 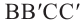
В треугольнике ABC, являющимся основанием прямой призмы, проведём высоту так, чтобы она пересекала противоположную сторону во внутренней области: 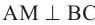
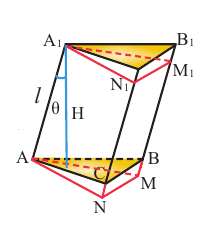
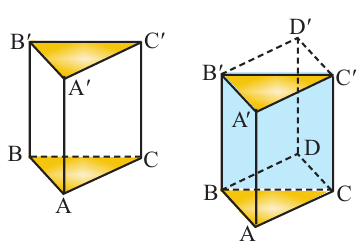
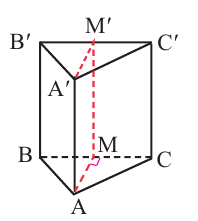
Если основанием прямой призмы является произвольный многоугольник, то её также можно разделить на треугольные призмы и найти её объём как сумму объёмов данных призм. Наклонную призму АВСА’В’С’ преобразуем в прямую призму равного объёма. Для этого:
- проведём плоскость перпендикулярную боковым рёбрам;
- отделим оставшуюся при сечении верхнюю часть призмы;
- переместим и соединим её с оставшейся внизу частью;
- высота полученной прямой призмы является боковым ребром наклонной призмы, т.е.
, основание же является перпендикулярным сечением наклонной призмы. Объём данной прямой призмы является также объёмом наклонной призмы.
Следствие. Объём наклонной призмы равен произведению перпендикулярного сечения и ребра призмы: 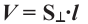
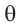
Поэтому, 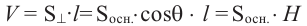
Таким образом объём призмы равен произведению площади основания и высоты.
Принцип Кавальери для нахождении объёмов
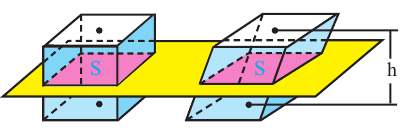
Если площади сечений параллельных основаниям двух тел равны, то равны и их объёмы, при условии, что основания лежат в одной плоскости, а высоты равны. Этот принцип открыл итальянский математик Бонавентура Кавальери (1598 — 1647).
Объем призмы
Объем призмы равен произведению площади основания и высоты.
Пример №1
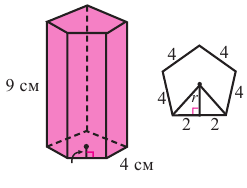
Найдём объём правильной пятиугольной призмы, стороны основания которой равны 4 см, а длина бокового ребра 9 см. Центральный угол правильного пятиугольника равен 360 : 5 = 72° значит апофема равна:
Площадь правильного многоугольника равна полупроизведению периметра и апофемы.
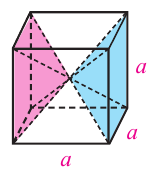
Исследование. 1. Диагонали куба деляг его на 6 конгруэнтных пирамид. Основание каждой пирамиды — грань куба, а высота
каждой пирамиды равна
а)Докажите, что объём каждой пирамиды равен
б)Докажите, что объём каждой пирамиды равен
Объём пирамиды
Объем пирамиды равен одной третьей произведения площади основанию на высоту.
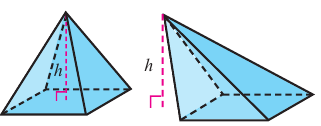
1)заданной пирамиды ТАВС;
Основания 2-ой и 3-ей пирамид конгруэнтны: 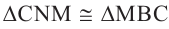
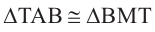
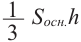
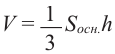
Подобие фигур в пространстве
Подобные фигуры имеют одинаковую форму и пропорциональные размеры.
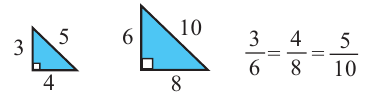
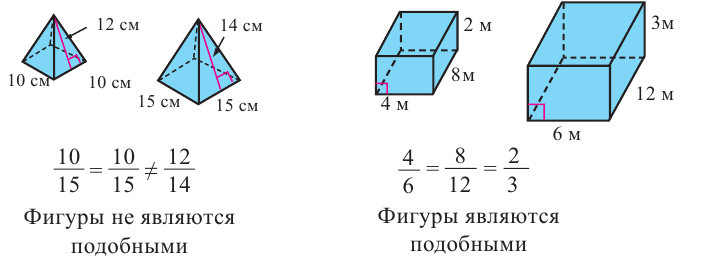
Например, прямоугольные треугольники на рисунке подобны, так как отношения соответствующих сторон равны.
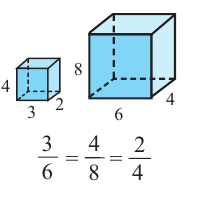
Прямоугольные параллелепипеды на рисунке подобны, так как отношения соответствующих линейных размеров равны и соответствующие грани являются подобными четырёхугольниками. Правильные многогранники подобны. В частном случае подобными являются все кубы, правильные тетраэдры и т.д.
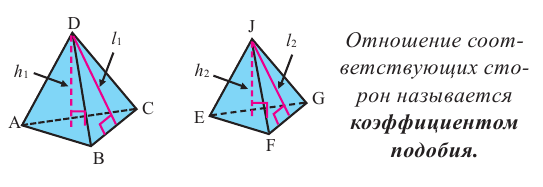
Подобные фигуры
Если при преобразовании расстояние между любыми двумя точками, меняется в одинаковое число раз, то такое преобразование называется подобием. Одна и другая, полученная при преобразовании подобием, фигура называются подобными фигурами. Коэффициент подобия равен отношению расстояний между парой любых двух соответсвующих точек.
Пример №2
Определим подобны или нет фигуры на рисунке.
Площади поверхностей и объёмы подобных фигур
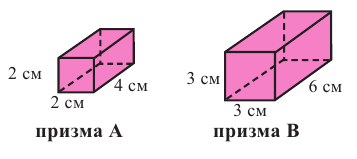
Исследование. Покажите подобны или нет следующие фигуры.
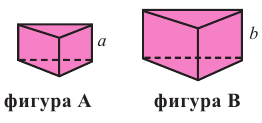
Призмы А и В (прямоугольные параллелепипеды) подобные призмы
с коэффициентом подобия равным 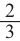
Для данных призм найдите:
а)отношение площадей полных поверхностей;
а)площадь полной поверхности призмы А
площадь полной поверхности призмы В
Отношение полной поверхности призмы А к полной поверхности призмы В
б)объём призмы А
объём призмы В
Отношение объёма призмы А к объёму призмы В
Если коэффициент подобия двух пространственных фигур равен 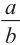
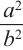
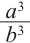
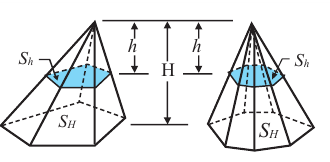
Пирамида, полученная сечением плоскости параллельной основанию, подобна данной. Коэффициент подобия можно найти из отношения соответствующих линейных размеров.
Например, на рисунке даны высоты. Тогда, отношения их боковых поверхностей, основании и полных поверхностей равно квадрату отношения высот.
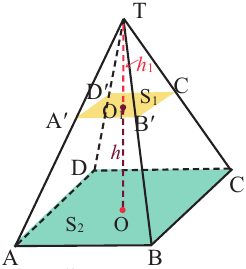
Объём усечённой пирамиды
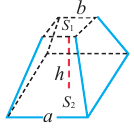
Исследование. В древнем Египте объём правильной усечённой четырёхугольной пирамиды вычисляли по формуле 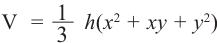
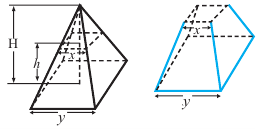
Объём усечённой пирамиды можно также найти как разность объёмов пирамид, при сечении плоскостью параллельной основанию.
Здесь V — объём усечённой пирамиды, S2 и S1 площади нижнего и верхнего оснований. h — высота усечённой пирамиды, h1 — высота меньшей пирамиды.
Так как эти пирамиды подобны, то отношение площадей равно квадрату отношений высот. Запишем это равенство и найдём высоту меньшей пирамиды.
Учитывая выражение
в равенстве
Объём усечённой призмы
Объём усечённой пирамиды с площадями оснований 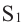
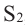
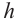
Задачи на сечение плоскостью
Пример:
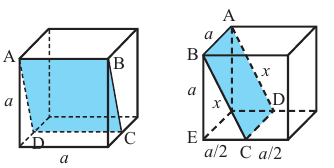
На рисунке показано сечение куба, с ребром а, плоскостью АВDО. Точки D и С являются серединами рёбер. Найдём площадь сечения.
Решение:
Дано: куб, длина ребра которого равна а точки D и С середины рёбер.
Найдите:
Для удобства повернём куб и отметим данные задачи на рисунке. Из 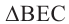
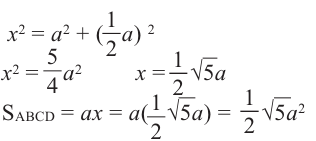
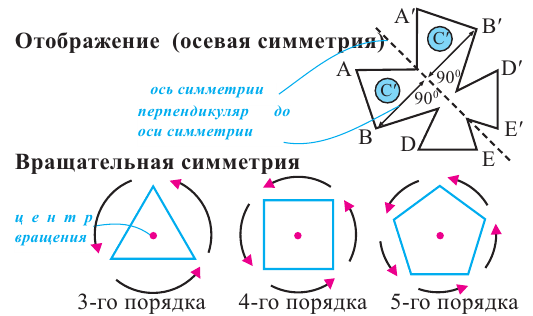
Симметрия в пространстве
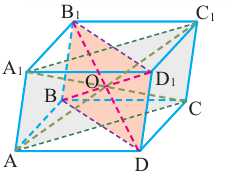
В пространственных фигурах также можно наблюдать различную симметрию. Известно, что в параллелепипеде диагональные сечения являются параллелограммами и диагонали ВD1 и DВ1 пересекаясь в точке О делятся пополам.
Можно показать, что другие диагонали также пересекаются в точке О и делятся пополам. Значит, точка пересечения диагоналей параллелепипеда является центром его симметрии.
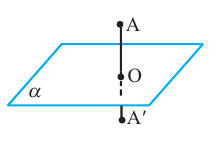
В пространстве, помимо симметрии относительно точки и прямой, рассматривается симметрия относительно плоскости.
Если отрезок АА’ пересекает плоскость а посередине, и перпендикулярен плоскости, то говорят, что точки А и А’ симметричны относительно плоскости а.
Если точки фигуры, симметричные некоторой плоскости, также принадлежат этой фигуре,то эту плоскость называют плоскостью симметрии, а фигуру называют симметричной относительно плоскости.
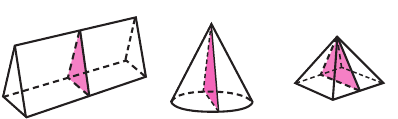
Прямоугольный параллелепипед, у которого все линейные размеры разные, кроме центра симметрии имеет ещё три оси и три плоскости симметрии. Прямая, проходящая через точку пересечения диагоналей противоположных граней, называется осью симметрии,а плоскость, проходящая перпендикулярно через середину рёбер называется плоскостью симметрии. Параллелепипед, у которого два линейных размера равны, имеет 5 плоскостей симметрии. Данные изображения нарисуйте в тетрадь.
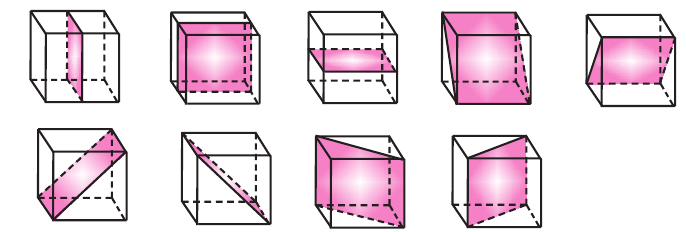
Точка пересечения диагоналей куба является его центром симметрии. Прямые, проходящие через середину параллельных рёбер, не принадлежащих одной грани (их всего 6) и прямые, проходящие через центры противоположных граней(их всего три), являются осями симметрии куба. У куба 9 плоскостей симметрии. Они изображены на следующих рисунках.
Вращательная симметрии
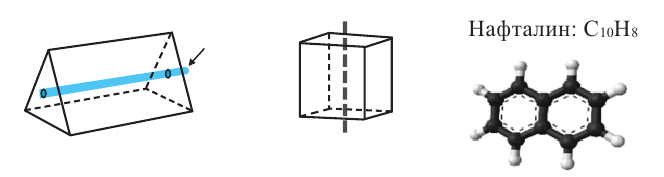
Вращательная симметрия пространственных фигур похожа на вращательную симметрию плоских фигур. Однако, для объёмных фигур она определяется при помощи оси вращения.
Вращательная и осевая симметрия широко применяется при изучении строения молекул веществ.
Пример №3
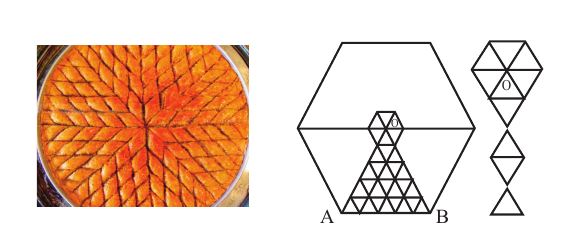
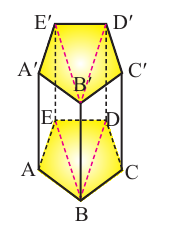
На рисунке показан вид сверху деталей, в виде правильных треугольных призм. Из них сконструирована правильная шестиугольная призма с центром основания О. Сколько деталей понадобилось для этого?
Основанием призмы является правильный шестиугольник, состоящий их 6 конгруэнтных треугольников. Каждый треугольник заполнен призмами. По изображению видно, что в один треугольник помещено 1+3 + 5 + 7 + 9 = 25 призм . Для правильной шестиугольной призмы таких призм нужно будет 6 • 25 = 150.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Объёмы поверхностей геометрических тел
- Фигуры вращения: цилиндр, конус, шар
- Объем фигур вращения
- Длина дуги кривой
- Площадь многоугольника
- Правильные многоугольники
- Вписанные и описанные многоугольники
- Площадь прямоугольника
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Подобные треугольники
Определение
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.
Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.
Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.
Признаки подобия треугольников
I признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
II признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Свойства подобных треугольников
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
- Отношение периметров подобных треугольников равно коэффициенту подобия.
- Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.
Примеры наиболее часто встречающихся подобных треугольников
1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.
2. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –
3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.
Здесь вы найдете подборку задач по теме «Подобные треугольники» .
Подобные треугольники
Подобные треугольники — это треугольники, у которых все три угла равны, а все стороны одного треугольника в одно и то же число раз длиннее (или короче) сторон другого треугольника, то есть треугольники подобны если их углы равны, а сходственные стороны пропорциональны.
Сходственные стороны — это стороны двух треугольников, лежащие против равных углов.
Рассмотрим два треугольника ABC и A1B1C1, у которых ∠A = ∠A1, ∠B = ∠B1, ∠C = ∠C1:
Стороны AB и A1B1, BC и B1C1, CA и C1A1, лежащие напротив равных углов, называются сходственными сторонами. Следовательно, отношения сходственных сторон равны:
| AB | = | BC | = | AC | = k, |
| A1B1 | B1C1 | A1C1 |
k — это коэффициент подобия ( число, равное отношению сходственных сторон подобных треугольников). Если k = 1, то треугольники равны, то есть равенство треугольников – это частный случай подобия.
Подобие треугольников обозначается знаком
: ABC
A1B1C1.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия. Если обозначить площади двух подобных треугольников буквами S и S1, то:
Первый признак подобия треугольников
Если два угла одного треугольника равны двум углам другого, то треугольники подобны.
то ABC
A1B1C1.
Второй признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то треугольники подобны.
| Если | AB | = | AC | , ∠A = ∠A1, |
| A1B1 | A1C1 | |||
| то ABC
A1B1C1. |
Третий признак подобия треугольников
Если три стороны одного треугольника пропорциональны трём сходственным сторонам другого, то треугольники подобны.
http://izamorfix.ru/matematika/planimetriya/podob_treug.html
Подобность многогранников.
Два многогранника называются подобными, если они имеют соответственно
равные многогранные углы и соответственно подобные грани.
Соответственные элементы подобных многогранников называются сходственными. У подобных многогранников
двугранные углы равны и одинаково расположены; сходственные рёбра пропорциональны.
Если в пирамиде проведём секущую площадь параллельно
основанию, то она отсечёт от неё другую пирамиду, подобную данной.
Поверхности подобных многогранников относятся, как
квадраты сходственных линейных элементов многогранников.
Объёмы подобных многогранников относятся как кубы
сходственных линейных элементов этих многогранников.
Квадраты объёмов подобных многогранников относятся как
кубы площадей сходственных граней.
Подобные цилиндры и конусы.
Два цилиндра, конуса
или усечённых конуса называются подобными, если подобны их осевые сечения.
Боковые и полные поверхности подобных цилиндров, конусов и
усечённых конусов относятся, как квадраты их сходственных линейных элементов. (радиусов оснований, высот, образующих).
Объёмы подобных тел.
Пусть Т и Т‘ – два простых подобных тела. Это означает, что существует
преобразования подобия, при котором тело
Т переходить в тело Т‘. Обозначим через k коэффициент
подобия.
Разобьём тело Т на треугольные пирамиды
Р1, Р2,
…, Рn …
Преобразования подобия, которое переводит тело Т в тело Т‘ переводит пирамиды
Р1, Р2,
…, Рn в пирамиды Р1‘, Р2‘, …, Рn‘.
Эти пирамиды составляют тело Т‘ и поэтому объём тела Т‘ равен сумме объёмов пирамид
Р1‘, Р2‘, …, Рn‘.
Так как пирамиды Р1‘ и Р1 подобны и коэффициент подобия равен k,
то и отношение их высот равно k, а отношение площадей их оснований равно k2. Поэтому, отношение объёмов пирамид равно k3. Так как тело Т состоит из пирамид Р1, а тело Т‘ состоит из пирамид Р1‘,
то отношение объёмов тел Т‘ и Т тоже равно
k3.
Число k – коэффициент подобия – равен отношению расстояний
между любыми двумя соответствующими парами точек при преобразования подобия. Поэтому,
это число равно отношению любых двух соответствующих линейных размеров тел Т‘ и
Т.
Таким образом, мы приходим к следующему выводу:
Объёмы двух подобных
тел относятся как кубы их соответствующих линейных размеров.
Квадраты объёмов
подобных тел относятся, как кубы площадей соответствующих граней.
Объёмы подобных цилиндров, конусов и усечённых конусов относятся,
как кубы их соответствующих линейных элементов (радиусов оснований,
высот, образующих).
Объёмы шаров относятся, как кубы их радиусов или диаметров.
ЗАДАЧА:
Площади оснований усечённой пирамиды S1 и S2, а её объём равен
V. Определить объём полной пирамиды.
РЕШЕНИЕ:
Пусть S1 > S2. Обозначим
объём полной пирамиды через V1, а объём пирамиды, дополняющей данную усечённую пирамиду
до полной, через V2
Тогда:
или
Составляя производную пропорцию, получим:
С учётом V1 –
V2 = V, находим:
откуда:
ОТВЕТ:
ЗАДАЧА:
Площади оснований усечённой пирамиды
равны а2 и b2. Найти площадь сечения, которое параллельно площадям
оснований усечённой пирамиды и делящего её объём пополам.
РЕШЕНИЕ:
В усечённой пирамиде АС1 (для простоты
рисунка рассматривается треугольная пирамида) дано:
Необходимо найти площадь сечения А‘‘ё (пл. АВС ∥ пл. А‘‘ё), которое делит усечённую
пирамиду на равновеликие по объёму части.
Дополним усечённую пирамиду до полной. Пирамиды
SАВС, SА‘‘ё, SA1B1C1 –
подобные.
Обозначим площадь искомого сечения А‘‘ё через х2, а объёмы пирамид
SАВС, SА‘‘ё и SA1B1C1
соответственно
Va, Vx, Vb.
Тогда:
или
где t –
некоторое число, которое обозначает величину этих отношений. Тогда:
Va = a3t, Vx
= x3t, Vb = b3t.
По условию задачи:
Va – Vx =
Vx – Vb,
или
a3t – x3t = x3t – b3t,
откуда:
2x3 = a3 + b3.
поэтому,
ОТВЕТ:
Задания к уроку 19
Движение в пространстве
Начнем с понятия отображения пространства на себя.
Оно идентично отображению плоскости на себя, с которым мы уже знакомы.
Итак, пусть каждой точке пространства поставлена в соответствие точка
. Точку
мы будем называть образом точки
, а саму точку
прообразом точки
(рис. 1).
Рис. 1 Образ и прообраз
Если каждой точке пространства соответствует образ, и кроме того, каждая точка имеет прообраз, то говорят, что задано отображение пространства на себя. Исходя из определения понятно, что отображение пространства – это функция.
Что будет происходить с геометрическими телами при отображении пространства?
Произвольное отображение скорее всего отправит точки одного тела в совершенно разные места пространства. То есть тело при отображении скорее всего разорвется и будет размазано по большой, может быть даже бесконечной области (рис. 2).
Рис. 2 Произвольное отображение
Но мы хотим рассмотреть такой математический инструмент, который будет описывать процессы, происходящие в реальной жизни, и который окажется полезным для расчетов.
Понятно, что движение предмета в обычном понимании не подразумевает его разрывание на множество частей и разлету их в разные места. Если мы передвинем какой-то объект, то все его точки должны располагаться относительно друг друга точно так же, как и до перемещения (рис. 3).
Рис. 3 Движение в обычном понимании
Это достаточно сложное требование. На самом деле достаточно потребовать, чтобы сохранились расстояния между точками (рис. 4). Для математического движения это и будет основным его свойством.
Рис. 4 Сохранение расстояния между точками объекта
Дадим определение движения. Отображение пространства на себя называется движением, если оно сохраняет расстояние между точками. Т.е. расстояние между любыми двумя точками должно быть равно расстоянию между их образами (рис. 5).
Рис. 5 Определение движения
Если проводить аналогию с числовыми функциями, то таким свойством обладают только очень простые из известных нам функций. Например, сохраняет расстояние. То есть, если мы возьмем два любых числа
и
, то функция увеличит каждое из этих чисел на
, но расстояние между образами останется тем же (рис. 6).
Рис. 6 Функция, сохраняющая расстояние
Функция уже изменяет расстояния, увеличивает их в три раза (рис. 7).
Рис. 7 Функция, изменяющая расстояние
Покажем, что движение, определенное таким образом, в самом деле сохраняет форму объекта, т.е. описывает движение в привычном нам бытовом смысле.
Теорема. Движение сохраняет форму объекта.
Покажем, что при движении отрезок переходит в отрезок.
Рис. 8 Образ отрезка
Посмотрим на образ отрезка (рис.8). Его концы перейдут в точки
причем, расстояние между ними будет тоже самое.
Рис. 9 Образ произвольной точки отрезка
Рассмотрим произвольную точку отрезка
. Ее образ
(рис. 9).
Т.е. .
Но это возможно только если лежит на отрезке
. В самом деле, если предположить, что
не лежит на
, то по неравенству треугольника
(рис.10)
Рис. 10 Неравенство треугольника
Теперь легко показать, что прямая переходит в прямую.
Рис. 11 Образ прямой
Отметим на прямой точки
и
. Они перейдут в точки
и
. Проведем через них прямую
. Покажем, что
и есть образ прямой
(рис. 11).
Рис. 12 принадлежит отрезку
Для этого отметим на прямой точку
(рис.12). Если она лежит между
и
, то есть на отрезке
, то
лежит на отрезке
, а значит и на прямой
.
Рис. 13 лежит между
и
Если лежит между
и
, то
лежит на отрезке
(рис.13). В любом случае
лежит на прямой
.
Все эти рассуждения мы уже проводили в планиметрии. Новым будет утверждение, что плоскость переходит в плоскость.
Рис. 14 Образ плоскости
Отметим на плоскости три точки
,
и
, не лежащие на одной прямой. Пусть их образы
. Проведем через эти три точки плоскость
. Покажем, что она и будет образом плоскости
(рис.14).
Рис. 15 Образ произвольной точки плоскости
Возьмем произвольную точку на плоскости
. Проведем через нее прямую так, чтобы она пересекала две стороны треугольника
в точках
и
(рис. 15). Так как отрезки переходят в отрезки, то образы этих двух точек
и
будут лежать на образах соответствующих сторон треугольника, т.е. в плоскости
. Точка
(образ
) лежит на прямой
, а, следовательно, и в плоскости
. Таким образом, все точки плоскости
переходят при движении на плоскость
.
Рис. 16 Многогранник
Так как выпуклый многогранник однозначно задается своими гранями и ребрами (то есть отрезками и плоскостями) (рис. 16), то многогранник при движении переходит в многогранник (рис. 17).
Рис. 17 Образ многогранника
Так как трехмерное тело можно сколь угодно приблизить набором таких многогранников, то мы делаем общий вывод: при движении любое трехмерное тело или плоская фигура переходят в им равные.
Рис. 18 Приближение трехмерного тела многогранником
Таким образом, математическое движение в самом деле описывает привычное нам движение в быту.
Параллельный перенос
Теперь рассмотрим виды движений. Всего их будет пять – три мы знаем из планиметрии (параллельный перенос, центральная и осевая симметрия), ещё один мы определим с учётом появления третьего измерения (поворот не вокруг точки, а вокруг оси), а ещё один будет специфическим, то есть не имеющим аналога на плоскости (третий вид симметрии – зеркальная симметрия).
Начнём с параллельного переноса, который нам знаком уже по планиметрии.
Каждую точку пространства передвинем на вектор (рис. 19).
Рис. 19 Параллельный перенос на вектор
То есть, рассмотрим такое отображение, что для любой точки и ее образа
:
.
Сначала попробуйте самостоятельно доказать, что такое отображение является движением, т.е. сохраняет расстояния между точками.
Доказательство:
Итак, возьмем две точки и
. Построим их образы
и
(рис. 20).
Рис. 20 Иллюстрация к доказательству
Так как векторы и
равны, то две противоположные стороны четырехугольника
равны и параллельны, а значит, он является параллелограммом. Следовательно
.
Таким образом, параллельный перенос сохраняет расстояния между точками, а, следовательно, является движением. (Параллельный перенос – движение, при котором все точки пространства перемещаются в одном и том же направлении на одно и то же расстояние).
Если рассмотреть модель координат в пространстве, то параллельный перенос на вектор означает добавление к координатам точки координат вектора переноса.
Виды симметрии в пространстве
В планиметрии мы рассматривали два вида симметрии – центральную (относительно точки) и осевую (относительно прямой). Интуитивно мы не очень склонны считать симметрию движением. Но любая симметрия соответствует определяющему свойству движения – сохраняет расстояние между точками. Поэтому как математический инструмент, мы ее, конечно, относим к движению.
Понятие центральной симметрии в пространстве практически не отличается от такого же понятие на плоскости. Выберем точку , которая будет являться центром симметрии. Точки
и
называются симметричными относительно точки
, если точка
– середина отрезка
(рис. 21).
Рис. 21 Центральная симметрия
Центральной симметрией назовем такое отображение пространства на себя, при котором любая точка переходит в точку, симметричную ей относительно центра . Точка
называется центром симметрии.
Покажем, что центральная симметрия является движением, то есть сохраняет расстояния.
Теорема. Центральная симметрия является движением, то есть сохраняет расстояние.
Доказательство:
Рис. 22 Иллюстрация к доказательству
Пусть точки и
имеют образы
и
(рис. 22). Тогда треугольники
и
равны по первому признаку, следовательно
(рис. 23).
Рис. 23 Иллюстрация к доказательству
Таким образом, центральная симметрия сохраняет расстояние, т.е. является движением.
Выведем формулы преобразования координат при центральной симметрии.
Пусть центр симметрии имеет координаты: . Рассмотрим точку
и ее образ
(рис. 24). Так как
– середина отрезка
, то ее координаты равны среднему арифметическому координат точек
и
:
Рис. 24 Центральная симметрия
Выразим координаты образа, т.е. :
Конечно, удобно в качестве центра симметрии брать начало координат. Тогда точка имеет нулевые координаты и формулы преобразования координат принимают очень простой вид:
То есть, чтобы точку отобразить симметрично началу координат, нужно поменять знак у всех ее координат (рис. 25).
Рис. 25 Центральная симметрия относительно начала координат
Осевая симметрия в пространстве определяется так же, как и в планиметрии. Точки и
называются симметричными относительно прямой
, если отрезок
пересекает прямую а под прямым углом и точкой пересечения делится пополам (рис. 26).
Рис. 26 Осевая симметрия относительно прямой
Отображение пространства на себя, при котором любая точка переходит в точку
, симметричную ей относительно прямой
, называется осевой симметрией. Прямая
называется осью симметрии.
Теорема. Осевая симметрия является движением.
Зададим прямоугольную систему координат, приняв ось симметрии за ось (ось аппликат).
Рис. 27 Осевая симметрия относительно оси аппликат
Рассмотрим точку и ее образ
(рис. 27). Так как отрезок
перпендикулярен оси
, то он параллелен плоскости
. Следовательно точки
и
имеют одинаковые аппликаты (координаты
).
Рис. 28 Проекции на плоскость
Проекции точек и
на ось
имеют те же самые абсциссы и ординаты, что и сами точки и нулевые аппликаты (рис. 28). Но эти точки симметричны относительно начала координат. Следовательно, их абсциссы и ординаты отличаются только знаками. Таким образом, мы получили формулы преобразования координат:
Если бы координата тоже меняла свой знак, то мы получили бы не осевую, а центральную симметрию.
Теперь посмотрим, что происходит с расстоянием между точками при осевой симметрии. Пусть точки имеют образы
(рис. 29).
Рис. 29 Точки и их образы
Найдем координаты векторов и
:
Воспользуемся формулами преобразования координат () для второго вектора:
Таким образом, первые две координаты у этих векторов отличаются знаком, а третьи совпадают. Так как длина вектора равна квадратному корню из суммы квадратов его координат, то длины этих векторов равны, а значит равны расстояния между прообразами и образами. Итак, осевая симметрия является движением.
Новым для нас видом симметрии является симметрия относительно плоскости. Ее еще называют зеркальной симметрией. Название связано с тем, что именно зеркально симметричное отображение мы видим в зеркале.
Рис. 30 Отражение в зеркале
По понятным причинам ее не могло быть в планиметрии.
Две точки называются симметричными относительно некоторой плоскости, если отрезок, их соединяющий, пересекает плоскость под прямым углом и делится точкой пересечения пополам (рис.31).
Рис. 31 Симметрия относительно плоскости
Теорема. Зеркальная симметрия является движением.
Используем снова координатный метод. Пусть плоскостью симметрии будет плоскость . Тогда у образа и прообраза отличаются только аппликаты своим знаком, а абсциссы и ординаты совпадают (рис.32).
Рис. 32 — плоскость симметрии
Рассмотрим расстояния между точкам и
и их образами при зеркальной симметрии
и
. Пусть точки
и
имеют координаты:
и
. Тогда их образы:
и
.
У векторов и
тоже отличаются только аппликаты и только знаком:
Понятно, что длины таких векторов равны. Следовательно, зеркальная симметрия является движением, так как сохраняет расстояния.
Поворот вокруг оси
Последним типом движения, который мы рассмотрим, будет поворот вокруг прямой. Он очень напоминает поворот вокруг точки на плоскости.
Чтобы повернуть точку вокруг прямой
на угол
проведем плоскость через точку
перпендикулярно прямой
. В этой плоскости уже и осуществим поворот. То есть построим точку
таким образом, чтобы
, а угол
был равен углу поворота
(рис. 33).
Рис. 33 Поворот относительно прямой
Рассмотрим поворот двух точек и изучим, что происходит с расстоянием между ними. Проведем через точки и
плоскости, перпендикулярные оси поворота. Повернем каждую точку на угол
в своей плоскости.
перейдет в
, а
в
(рис. 34).
Рис. 34 Поворот двух точек вокруг прямой
Построим проекции точек и
на верхнюю плоскость. Обозначим их
и
. Очевидно,
переходит
при повороте на угол
(рис.35).
Рис. 35 Проекции точек и
Треугольники и
равны по первому признаку (рис. 36). Следовательно
.
Рис. 36 Равные треугольники и
Тогда прямоугольные треугольники и
равны по двум катетам.
Рис. 37 Равные треугольники и
Следовательно . То есть расстояние между прообразами и образами равны. Таким образом поворот вокруг оси сохраняет расстояние и является движением.
Легко заметить, что поворот на является осевой симметрией (рис. 38). То есть осевая симметрия – это частный случай поворота.
Рис. 38 Поворот на
Вспомним для сравнения, что в планиметрии центральная симметрия являлась поворотом вокруг точки на .
Подобие в пространстве
Подобие в пространстве определяется так же, как и на плоскости. Вспомним, что две основные характеристики тела – размер и форма. Подобные тела имеют одинаковую форму, но могут иметь совершенно разные размеры. Например, любые два круга подобны. Очевидно, что любые два шара также подобны (рис. 39).
Рис. 39 Подобные шары
Итак, два тела подобны, если одно из них может быть получено из другого путём увеличения (или уменьшения) всех его линейных размеров в одном и том же отношении. Автомобиль и его модель – подобные тела (рис. 40).
Рис. 40 Автомобиль и его модель
Отношение линейных размеров подобных тел называется коэффициентом подобия (рис. 41).
Рис. 41 Коэффициент подобия
В подобных телах все соответственные углы (линейные и двугранные) равны (рис. 42).
Рис. 42 Равенство углов в подобных фигурах
Объяснение этого факта сводится к подобию треугольников, на которые можно разбить любую грань многогранника и к подобию сечений плоскостями, перпендикулярным ребрам, т.е., содержащим линейные углы двугранных углов.
Мы знаем, что площади подобных треугольников относятся как квадрат коэффициента подобия (рис. 43): .
Рис. 43 Подобные треугольники
Опять разбивая все грани на треугольники, мы приходим к выводу, что все площади поверхностей или сечений подобных тел относятся как квадрат коэффициента подобия (рис. 44).
Рис. 44 Разбиение граней на треугольники
Отношение объемов кубов равно кубу коэффициента подобия (так как объём куба равен , соответственно, увеличение или уменьшение длины ребра в
раз приведёт к изменению объёма куба в
раз):
.
Рис. 45 Отношение объемов кубов
Так как любой многогранник можно приблизить кубами разных размеров, то приходим к выводу, что это справедливо и для любых тел.
Рис. 46 Приближение многогранника кубами
Объемы подобных тел относятся как куб коэффициента подобия.
Все наверное видели фантастические фильмы про увеличенных в силу мутации насекомых или пауков (рис. 47).
Рис. 47 Мутировавшие насекомые
Если все линейные размеры насекомого увеличить в 100 раз, то коэффициент подобия между исходным насекомым и увеличенным будет 100. Если изначально насекомое было 0,5 см в высоту, то теперь оно будет иметь рост полметра
То же самое с длиной, 2-х сантиметровый таракан превратится в гиганта двух метров длиной. Площадь поверхности тела такого насекомого увеличится не в 100 раз, а в 100 в квадрате, то есть в 10 000 раз. А объем, следовательно и масса, — уже в миллион раз. Таким образом, если исходный таракан весил 1 грамм, то увеличенный “всего лишь в 100 раз” будет весить уже 1 тонну.
Кстати, непропорциональное увеличение поверхности тела и массы является одним из утешительных объяснений, почему такие монстры не могут существовать. Насекомое дышит через поверхность тела. Чтобы обеспечивать массу, увеличившуюся в миллион раз, нужно в миллион раз больше воздуха. Но площадь поверхности тела такого гиганта увеличится только в 10 тысяч раз. Так что, если не изменится биологическая структура мутанта, он просто задохнётся.
Преобразование подобия. Гомотетия
Свойства подобия тел удобно описывать с помощью преобразования подобия. Преобразованием подобия с коэффициентом называют такое отображение пространства на себя, при котором любые две точки пространства
и
переходят в такие точки
и
, что
(рис. 48).
Рис. 48 Преобразование подобия
Из самого определения понятно, что подобие в общем случае не является движением.
Движением оно будет только тогда, когда .
Используя преобразование подобия легко дать определения подобных тел. Тела называются подобными, если существует такое преобразование подобия, переводящее одно тело в другое.
Рассмотрим частный случай преобразования подобия. Оно называется центральным подобием или гомотетией. Гомотетией с центром и коэффициентом гомотетии
называется такое отображение пространства на себя, при котором каждая точка
переходит в точку
, такую что:
Рис. 49 Гомотетия с центром
Легко видеть, что гомотетия с тем же центром и обратным коэффициентом , переводит точку
в точку
. То есть является обратным преобразованием.
Понятно, что не любое преобразование подобия является гомотетией. Но не сложно убедиться, что любое преобразование подобия можно представить как результат последовательного выполнения движения и гомотетии.
Теорема. Любое преобразование подобия представимо в виде движения и гомотетии.
Доказательство:
Рис. 50 Иллюстрация к доказательству
Рассмотрим преобразование подобия с коэффициентом . Тогда две точки
и
перейдут при его выполнении в точки
и
такие, что
(переход от фигуры 1 к фигуре 2) (рис. 50).
Рассмотрим теперь гомотетию с коэффициентом . Применим ее к точками
и
(рис. 51).
Рис. 51 Иллюстрация к доказательству
Получим точки и
такие что:
(переход от 2 к 3). Это означает, что результатом последовательного применения этих преобразований является движение (переход от 1 к 3) (рис. 52).
Рис. 52 Иллюстрация к доказательству
Применим теперь к точкам и
гомотетию с тем же центром и обратным коэффициентом, т.е.
. Тогда мы вернемся к точка
и
(рис.53).
Рис. 53 Иллюстрация к доказательству
Мы взяли произвольные точки и
, применили к ним движение (состоящее из преобразования подобия с коэффициентом
и гомотетии c коэффициентом
) а потом гомотетию с коэффициентом
. И получили опять тоже самое преобразование подобия с коэффициентом
. То есть прошли от 1 фигуры к 3, а потом к фигуре 2. Получается, что произвольное преобразование подобия представимо в виде комбинации движения и гомотетии.
Список рекомендованной литературы.
- Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10-11класс. Учебник. – АО «Издательство “Просвещение”».
- Мордкович А. Г., Смирнова И. М. Математика. Базовый уровень. 11 класс. Учебник. – ООО «ИОЦ МНЕМОЗИНА».
- Погорелов А. В. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10-11 класс. Базовый и углубленный уровни. Учебник. – АО «Издательство “Просвещение”».
Рекомендованные ссылки на ресурсы интернет.
- Интернет-портал «yaklass.ru»
- Интернет-портал «webmath.ru»
- Интернет-портал «math24.ru»
Рекомендованное домашнее задание
- Найдите координаты образов точек
при:
а) центральной симметрии относительно начала координат
б) осевой симметрии относительно координатных осей
в) зеркальной симметрии относительно координатных плоскостей - Какие координаты имеет точка
, если при центральной симметрии с центром
точка
переходит в точку
.
- Найдите объем многогранника
, если известен объем подобного многогранника
), а коэффициент подобия
.
- При движении прямая
отображается на прямую
, плоскость
на
. Докажите, что если
, то
.
Гипермаркет знаний>>Математика>>Математика 11 класс>>Математика:Объемы подобных тел
Объемы подобных тел
Пусть Т и Т’ — два простых подобных тела. Это значит, что существует преобразование подобия, при котором тело Т переходит в тело Т’. Обозначим через k коэффициент подобия.
Разобьем тело Т на треугольные пирамиды Р1, Р2, ….., Рn-Преобразование подобия, которое переводит тело Т в тело Т’, переводит пирамиды Р1, Р2, ….., Рn в пирамиды Р’1, Р’2, ….., Р’n. Эти пирамиды составляют тело Т’, и поэтому объем тела Т’ равен сумме объемов пирамид Р’1, Р’2, ….., Р’n.
Так как пирамиды Р1‘ и Р, подобны и коэффициент подобия равен k, то отношение их высот равно k, а отношение площадей их оснований равно k3.
Следовательно, отношение объемов пирамид равно k3. Так как тело Т составлено из пирамид Рi а тело Т’ составлено из пирамид Р’i то отношение объемов тел Т’ и Т тоже равно k3.
Число k — коэффициент подобия — равно отношению расстояний между любыми двумя соответствующими парами точек при преобразовании подобия.
Следовательно, это число равно отношению любых двух соответствующих линейных размеров тел Т’ и Т. Таким образом, мы приходим к следующему выводу:
Объемы двух подобных тел относятся как кубы их соответствующих линейных размеров.
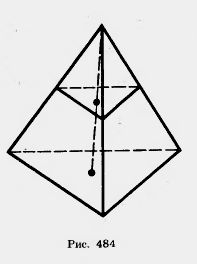
Задача (48). Через середину высоты пирамиды проведена плоскость, параллельная основанию. В каком отношении она делит объем пирамиды?
Решение. Как мы знаем, проведенная плоскость отсекает подобную пирамиду (рис. 484). Коэффициент подобия равен отношению высот, т. е.
Поэтому объемы пирамид относятся как . Следовательно, плоскость делит нашу пирамиду на части, объемы которых относятся как
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн
Содержание урокаконспект урока
опорный каркас
презентация урока
акселеративные методы
интерактивные технологии Практика
задачи и упражнения
самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников Иллюстрации
аудио-, видеоклипы и мультимедиа
фотографии, картинки
графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты Дополнения
рефераты
статьи
фишки для любознательных
шпаргалки
учебники основные и дополнительные
словарь терминов
прочие Совершенствование учебников и уроков
исправление ошибок в учебнике
обновление фрагмента в учебнике
элементы новаторства на уроке
замена устаревших знаний новыми Только для учителей
идеальные уроки
календарный план на год
методические рекомендации
программы
обсуждения Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний — Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов —
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других «взрослых» тем.
Разработка — Гипермаркет знаний 2008-
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: 
Задание 2 Профильного ЕГЭ по математике – это основы стереометрии. Это задачи на вычисление объемов и площадей поверхности многогранников и тел вращения.
Ничего сложного здесь нет. Все эти задачи доступны даже десятикласснику. И даже гуманитарию.
Как решать задания по стереометрии из первой части Профильного ЕГЭ?
Повторим формулы для вычисления объемов и площадей поверхности многогранников (призмы, пирамиды… ) и тел вращения (цилиндра, конуса и шара)
Проверим себя – умеем ли мы рисовать чертежи?
Посмотрим, как решаются простые задачи по стереометрии и задачи с секретами.
Запоминаем один из главных лайфхаков решения задач по стереометрии:
Отношение объемов подобных тел равно кубу коэффициента подобия.
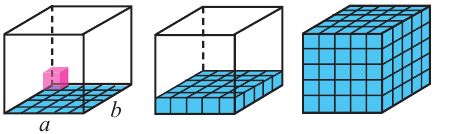
Если все линейные размеры объемного тела увеличить в k раз, то его площадь увеличится в раз, а объем в
раз.
И решаем задачи. У нас все получится!
1. Во сколько раз увеличится площадь поверхности и объем куба, если его ребро увеличить в два раза?
Отношение площадей поверхности подобных тел равно квадрату коэффициента подобия, а отношение объемов – кубу коэффициента подобия. При увеличении ребра в 2 раза площадь поверхности увеличится в 4 раза, а объем – в 8 раз.
2. Площадь основания конуса равна 18. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью.
Плоскость, параллельная основанию, отсекает от конуса меньший конус, все линейные размеры которого в 3 раза меньше, чем у большого. Поэтому площадь сечения в 9 раз меньше площади основания. Она равна 2.
3. Объем пирамиды равен 10. Через середину высоты параллельно основанию пирамиды проведено сечение, которое является основанием меньшей пирамиды с той же вершиной. Найдите объем меньшей пирамиды.
Меньшая пирамида подобна большой, коэффициент подобия Отношение объемов подобных тел равно кубу коэффициента подобия. Поэтому объем меньшей пирамиды в 8 раз меньше объема исходной пирамиды. Он равен
4. Объём правильной четырёхугольной пирамиды SABCD равен 116. Точка E — середина ребра SB. Найдите объём треугольной пирамиды EABC.
Площадь основания пирамиды ЕАВС в 2 раза меньше, чем у пирамиды ABCDS. Высота пирамиды ЕАВС равна половине высоты пирамиды ABCDS. Значит, объем пирамиды ЕАВС в 4 раза меньше объема пирамиды ABCDS. Он равен
5. В правильной четырехугольной пирамиде SABCD точка E – середина ребра AB, боковое ребро SC равно 4, длина отрезка SE равна Найти объем пирамиды SABCD .
Найдем сторону основания пирамиды. По теореме Пифагора, для треугольника SAE получаем, что Соответственно, сторона основания пирамиды равна
Если обозначить центр основания за H, то высоту пирамиды найдем по теореме Пифагора, для треугольника SHE – она равна 2.
Применяя формулу для объема пирамиды , получаем ответ: 16.
Многие задания №2 Профильного ЕГЭ по математике можно считать подготовительными – для того, чтобы научиться решать задачу 14 из второй части ЕГЭ.
Для решения некоторых из них стоит выучить основные определения и теоремы стереометрии. В общем, то, что входит в программу по стереометрии.
6. Стороны основания треугольной пирамиды равны 15, 16 и 17. Боковые ребра наклонены к плоскости основания под углами 45°. Найдите объем пирамиды.
Пусть точка О – проекция точки S на плоскость основания пирамиды. Прямоугольные треугольники АОS, ВОS, СОS равны (по общему катету ОS и острому углу). Значит, АО = ВО = СО. Точка О, равноудаленная от вершин основания, – это центр окружности, описанной вокруг треугольника АВС. Тогда АО = ВО = СО = OS = R, где R – радиус этой окружности.
Радиус описанной окружности найдем по формуле
Площадь найдем по формуле Герона:
, где
– полупериметр.
Заметим, что если боковые ребра пирамиды наклонены к плоскости основания под одинаковым углом, то вершина проецируется в центр основания.
7. В правильной треугольной призме , все ребра которой равны 3, найдите угол между прямыми
и
. Ответ дайте в градусах.
Угол между скрещивающимися прямыми равен углу между параллельными им прямыми, лежащими в одной плоскости. Поскольку и
параллельны, найдем угол между
и
. Он равен 45 градусов, так как грань – квадрат.
Ответ: 45.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Профильный ЕГЭ по математике. Задание №2. Стереометрия» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023

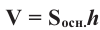
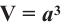
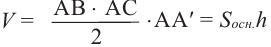
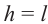 , основание же является перпендикулярным сечением наклонной призмы. Объём данной прямой призмы является также объёмом наклонной призмы.
, основание же является перпендикулярным сечением наклонной призмы. Объём данной прямой призмы является также объёмом наклонной призмы.