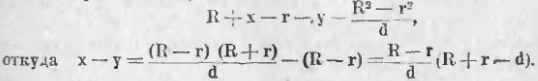Как найти коэффициент подобия радиусов

Математика

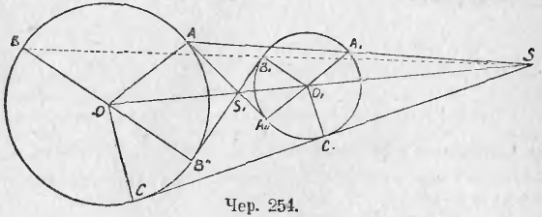
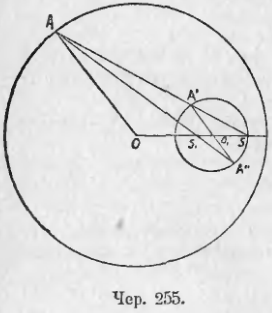
260. Возьмем два круга O и O1 (чер. 254 и 255). Построим радиус OA и параллельный ему радиус другого круга O1A1, который имеет одинаковое направление с OA, или O1A11 тоже параллельный OA, но имеющий обратное с ним направление. Построим затем прямые AA1 и AA11, проходящие чрез концы этих радиусов. Тогда представляется следующая задача:

По данным радиусам R и r кругов и по расстоянию их центров OO1 = d найти расстояние от одного из центров (напр., от O) точек пересечения линий центров с прямою AA1 и с прямою AA11.

Назовем OS чрез x; тогда O1S = x – d. ∆OAS

∆O1A1S, следовательно, OS/O1S = OA/O1A1 или x/(x – d) = R/r, откуда rx = Rx – dR.
Определяя отсюда x, получим

Отсюда мы видим, что положение точки пересечения S прямых OO1 и AA1 не зависит от того, в каком направлении от центра мы построили параллельные радиусы OA и O1A1, так что прямая BB1, соединяющая концы другой пары параллельных радиусов OB и O1B1, должна пройти чрез точку S и, кроме того, имеем (∆O1SB1

∆OSB): SB1/SB = r/R. Таким образом точка S обладает всеми свойствами внешнего центра подобия двух подобно расположенных фигур.

Также, называя OS1 чрез y, получим S1O1 = d – y и из подобия ∆OAS1 и ∆O1A11S1: y(d – y) = R/r. Отсюда находим yr = dR – yR и

Отсюда видим, что положение точки S1 также не зависит от того, какую именно пару параллельных, но идущих в обратных направлениях, радиусов мы взяли. Чрез эти же точку S1 должна пройти прямая B1B11, соединяющая концы радиусов OB11 и O1B1 параллельных, но имеющих обратные направления. Кроме того, имеем (∆O1B1S1

Таким образом точка S1 обладает всеми свойствами внутреннего центра подобия двух кругов.

Если один круг лежит внутри другого (чер. 255), то оба центра подобия расположены внутри меньшего круга: внешний лежит вне отрезка OO1, а внутренний — внутри его.

Центры O и O1 также соответствуют друг другу, так как SO1/SO = r/R (из подобия ∆OAS и ∆O1A1S) и S1O1/S1O = r/R (из подобия ∆S1O1A11 и ∆S1OA).

Итак, всякие два круга подобно расположены и имеют два центра подобия — внутренний и внешний; центру одного круга соответствует центр другого и любой точке одного соответствует та точка другого, которая расположена на радиусе, параллельном радиусу первого круга, идущему чрез взятую точку, и имеющем то же или обратное направление. Обратно: если чрез S построить любую прямую A и соответствующие точки пересечения соединить с центрами, то полученные радиусы должны быть параллельны между собою.

261. Если окажется, что радиус, напр., O1C1 (чер. 254), перпендикулярен к прямой SC1, то и радиус OC, соединяющий центр O другого круга с его точкою C, соответствующей точке C1, должен быть также перпендикулярен к SC. Отсюда следует, что касательная из точки S к одному из наших кругов должна касаться и другого круга. Точно так же, если построим касательную к одному кругу чрез точку S1, то она должна касаться и другого круга.

Этим пользуются для решения задачи: построить общую касательную к двум данным кругам .

Надо найти сначала их центры подобия, для чего надо построить радиус OA и параллельный ему диаметр A1A11 второго круга (чер. 254). Соединив концы A и A1, найдем внешний центр подобия S и соединив A и A11, найдем внутренний центр подобия S1. Затем чрез найденные центры подобия S и S1 построим касательные к одному кругу — они и должны быть общими касательными. Всего общих касательных у двух кругов может быть 4. Если два круга имеют внешнее касание, то точка касания служит их внутренним центром подобия, и общих касательных тогда будем иметь 3; если два круга пересекаются, то внутренний ценр подобия лежит внутри обоих кругов, и из него нельзя построить касательных, — тогда получим только две общих касательных чрез внешний центр подобия; если 2 круга имеют равные радиусы, то внешний центр подобия удаляется в бесконечность и тогда две внешних касательных параллельны линии центров; если два круга имеют внутреннее касание, то точка касания служит их внешним центром подобия, — тогда возможна лишь одна общая касательная; если, наконец, один круг внутри другого, то оба центра подобия расположены внутри обоих кругов, и общих касательных вовсе не существует.

262. Можно применить понятие о центре подобия кругов к решению задачи, которую раньше мы решили другим способом (п. 227 зад. 3): построить круг, касающийся двух пересекающихся прямых и проходящий чрез данную точку .

Точка пересечения данных прямых является внешним центром подобия искомого круга и какого-либо еще касающегося данных прямых и расположенного внутри того же угла, где лежит данная точка, но не проходящего чрез эту точку. Последний круг легко построить. Затем найдем на нем точку, соответствующую данной, построим чрез найденную точку радиус построенного круга, а чрез данную точку построим прямую, параллельную этому радиусу, — точка пересечения ее с биссектором угла и должна быть центром искомого круга. Задача имеет 2 решения, так как у построенного сначала круга можно найти 2 точки, любую из которых можно принять за соответствующую данной.

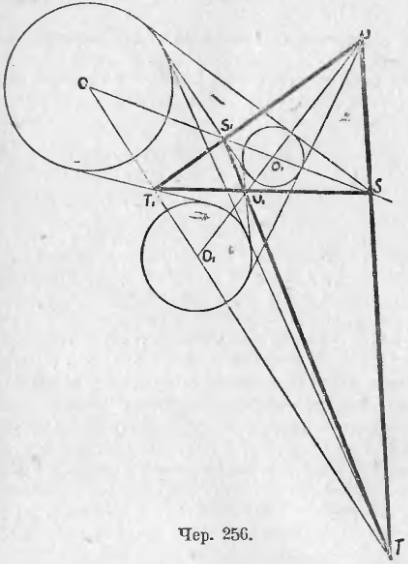
263. Если возьмем три каких-либо круга O, O1 и O2 (чер. 256), то они попарно подобно расположены и к ним применимо свойство п. 256. У этих трех кругов всего 6 центров подобия и они располагаются на четырех прямых: UST, US1T1, SU1T1 и TS1U1. Чрез каждый центр подобия проходят 2 из этих четырех прямых.

264. Степень точки относительно круга . В п. 222 мы познакомились с понятием о степени точки относительно круга. Этим именем называется, как мы знаем, произведение отрезков какой-либо прямой, проходящей чрез эту точку и пересекающей круг, от этой точки до точек пересечения прямой с кругом. Если точка вне круга, то это произведение равно квадрату касательной из нашей точки к ругу; если точка внутри круга, то это произведение равно квадрату половины хорды, делящейся в этой точке пополам. Чтобы отличить первый случай от второго, считают степень точки во втором случае отрицательною и перед указанным квадратом половины хорды ставят знак минус.

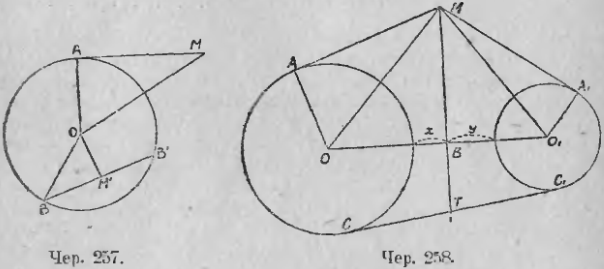
Пусть имеем круг O (чер. 257) и точку M вне его. Построив касательную MA и прямые MO и OA, найдем из прямоугольного треугольника AOM, что степень точки M = MA 2 = OM 2 – OA 2 = OM 2 – R 2 , где OA обозначаем чрез R.

Возьмем теперь точку M1 внутри круга. Степень этой точки равна произведению отрезков хорды M1B и M1B’, взятому со знаком минус. Если эта хорда перпендикулярна к прямой OM1, соединяющей точку M1 с центром, то хорда делится в точке M1 пополам и M1B1 = M1B и, следовательно, степень точки M1 = –M1B 2 . Из прямоугольного треугольника OM1B найдем: M1B 2 = OB 2 – OM1 2 = R 2 – OM1 2 , а, следовательно, степень точки M1 = – M1B 2 = –(R 2 – OM1 2 ) = OM1 2 – R 2 .

В обоих случаях степень точки выражается одинаково: она равна квадрату расстояния точки от центра минус квадрат радиуса.

Если точка лежит на круге, то легко увидим, что ее степень равна нулю.

265. Пусть теперь имеем 2 круга O и O1 (чер. 258). Возникает вопрос, не существует ли таких точек, степени которых относительно обоих кругов равны между собой. Если такие точки существуют, то где они расположены? Допустим, что M такая точка. Называя радиус OA чрез R и радиус O1A1 чрез r, имеем для этой точки M

Из этого равенства и их равенства OB + O1B = d мы можем определить отрезки OB и O1B, — получим для каждого одно решение (уравнения первой степени), откуда заключаем, что точка B вполне определена. Отсюда выводим: если бы мы нашли другую точку M1, степени которой относительно наших кругов равны, и на нее опустим перпендикуляр на линию центров, то он должен пройти чрез ту же точку B и, следовательно, слиться с MB. Следовательно, все точки, степени которых относительно двух кругов равны, расположены на перпендикуляре к линии центров. Этот перпендикуляр носит название — радикальная ось двух кругов. Обратно, легко показать, что всякая точка перпендикуляра MB имеет равные степени относительно наших кругов.

Из равенства (2) видим: 1) если R = r, то OB – O1B = 0 и OB = O1B, т. е. радикальная ось двух равных кругов делит расстояние между их центрами пополам; 2) если R > r, то OB > O1B, т. е. радикальная ось расположена ближе к центру меньшего круга.

Но, если мы назовем чрез x и y расстояния точки B от круга O и от круга O1 (мы применяемся к случаю данному на чертеже: круги расположены один вне другого), то OB = R + x, O1B = r + y и, подставив в равенство (2), найдем:
f48

У нас R + r 0 (ибо считаем, что R > r). Тогда из последнего равенства вытекает x 2 = TC1 2 , или TC = TC1, т. е. общая касательная двух кругов делится радикальною осью пополам.

Если два круга пересекаются, то радикальная ось должна пройти чрез точки пересечения, так как степень каждой из этих точек одинакова относительно каждого круга (она равна нулю); для построения радикальной оси в этом случае следует лишь построить прямую, определяемую этими точками пересечения.

Если два круга касаются, то радикальная ось есть перпендикуляр к линии центров чрез точку касания.

266. Пусть имеем 3 круга O, O1 и O2 (чер. 259). Построив радикальные ости mn и m1n1 двух пар кругов, мы найдем, что они пересекаются в какой-либо точке C, если только центры всех трех кругов не расположены на одной прямой. Так как точка C лежит на оси m1n1, то степени ее относительно кругов O1 и O2 одинаковы. Отсюда следует, что точка C имеет одинаковые степени и относительно кругов O и O2, т. е. она должна лежать на радикальной оси последней пары кругов. Итак,

Радикальные оси трех кругов, взятых попарно, пересекаются в одной точке, которая называется радикальным центром трех рассматриваемых кругов.

Если из радикального центра построить касательные ко всем трем кругам, то они равны между собою.

Если три круга попарно пересекаются, то их общие хорды проходят чрез одну точку (общая хорда двух пересекающихся кругов есть их радикальная ось).

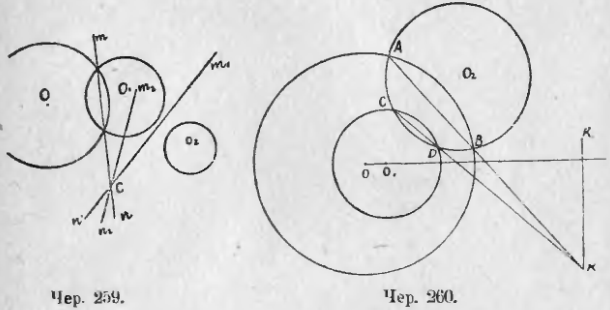
267. Свойством предыдущего п. можно воспользоваться для построения радикальной оси для двух непересекающихся кругов . Пусть даны круги O и O1 (чер. 260). Построим третий круг O2 чтобы его центр не лежал на линии центров OO1 и чтобы он пересекался с каждым из данных кругов: с кругом O и точках A и B и с кругом O1 в точках C и D. Тогда AB есть радикальная ось кругов O и O2, CD — радикальная ось кругов O1 и O2, точка пересечения K прямых AB и CD есть радикальный центр наших трех кругов. Построив прямую KK1 ⊥ OO1, получим радикальную ось кругов O и O1.

268. Построить круг, касающийся данного круга и проходящий чрез две данных точки .

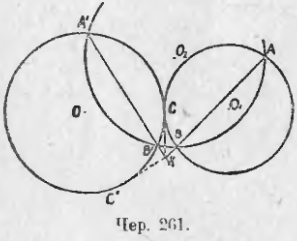
Пусть дан круг O и точки A и B (чер. 261). Воспользуемся предыдущею задачею. Искомый круг должен касаться данного; следовательно, радикальною осью этой пары кругов должна служить их общая касательная. Если бы ее удалось построить, то легко было бы построить и искомый круг. Для построения этой радикальной оси воспользуемся, как в предыдущем п., третьим кругом O2, пересекающим и данный и искомый круг. Но у искомого круга мы знаем пока только 2 точки A и B; следовательно, и этот третий круг O2 мы можем построить лишь так, чтобы он проходил чрез точки A и B. Итак, построим любой круг O2, проходящий чрез точки A и B и пересекающий круг O, напри., в точках A’ и B’. Тогда прямая AB есть радикальная ось искомого круга и круга O2, прямая A’B’ есть радикальная ось кругов O и O2, а точка их пересечения K есть радикальный центр всех трех кругов. Теперь нетрудно построить радикальную ось круга O и искомого, так как она должна касаться круга O: надо чрез точку K построить касательную к кругу O, а их можно построить две KC и KC’ (C и C’ точки касания). Тогда получим два решения: 1) искомый круг определяется точками A, B и C и 2) искомый круг определяется точками A, B и C’.

269. Мы имеем в виду решить еще две задачи на построение кругов: 1) построить круг, касающий двух данных кругов и проходящий чрез данную точку; и 2) построить круг, касающийся трех данных кругов (задача Аполлонин). Для этого надо познакомиться еще с некоторыми свойствами центра подобия и радикальной оси двух кругов.

Чрез центр подобия S кругов O и O1 (чер. 262) построена общая касательная SCC1 к этим кругам и секущая SB, соответственные точки которой суть A и A1, B и B1.

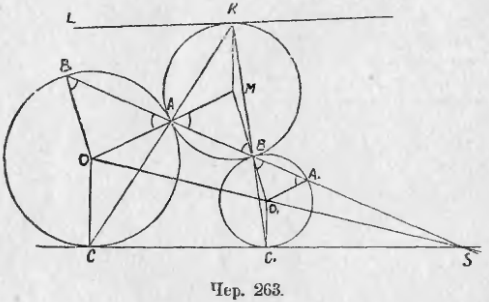
270. Пусть круг M касается кругов O и O1 (чер. 263), обоих внешним образом в точках A и B. Построим прямую AB и пусть эта прямая пересекает еще круг O в точке B1 и круг O1 в A1. Тогда OAM есть прямая, — следовательно, углы при основаниях в равнобедренных треугольниках OAB1 и MAB равны; также O1BM есть прямая и, следовательно, углы при основании в равнобедренном треугольнике O1A1B равны углам в ∆MAB (на чертеже равные углы отмечены). Отсюда заключаем, что O1A1 || OA и O1B || OB1, откуда следует, что прямая B1ABA1 проходит чрез внешний центр подобия кругов O и O1. Итак, если круг касается двух других, то точки касания расположены на прямой, проходящей чрез центр подобия, но не суть соответственные точки .

Мы разобрали случай, когда M с O и с O1 имеет внешнее касание; также будет и для случая, когда M с O и с O1 имеет внутреннее касание; но если M имеет с одним из кругов внешнее касание, а с другим внутреннее, то вместо внешнего центра подобия надо взять внутренний. Поэтому в предыдущем заключении мы и не указали, чрез какой именно центр подобия проходит прямая, соединяющая точки касания.

Если построить еще общую касательную SC1C, то прямые CA и C1B, как мы знаем, пересекаются в точке K, лежащей на радикальной оси кругов O и O1. Но можно выяснить еще, что точка K лежит на круге M.

Точка A есть внутренний центр подобия кругов O и M, причем точке O соответствует точка M, радиус OC (который ⊥ SC) соответствует некоторый радиус MX круга M, который параллелен OC, но имеет обратное с ним направление. Точка B есть внутренний центр подобия кругов O1 и M, причем точке O1 соответствует точка M и радиус O1C1 круга O1 соответствует некоторый радиус MY круга M, который параллелен радиусу O1C1, но имеет обратное с ним направление. Отсюда следует, что радиусы MX и MY параллельны друг другу (ибо O1C1 || OC) и одинаково направлены, но они имеют общую точку M, — следовательно, они совпадают. С другой стороны, точка X должна лежать на прямой CA и точка Y на прямой C1B. Поэтому совпадение радиусов MX и MY требует, чтобы точка X и точка Y совпали с точкою K, где пересекаются прямые CA и C1B. Следовательно, точка K есть конец радиуса MK круга, и M, и K лежит на круге M.

Далее прямой SC относительно центра подобия A должна соответствовать прямая KL, проходящая чрез K (ибо SC проходит чрез C) и параллельная SC. Кроме того, прямая KL ⊥ MK, ибо SC ⊥ OC (радиусы OC и MK соответствуют друг другу). Поэтому прямая KL касается круга M в точке K. К тому же результату придем, рассматривая соответствие относительно центра подобия B.

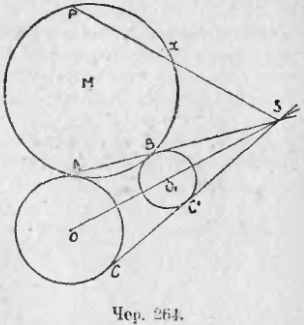
271. Теперь мы можем приступить к решению первой из намеченных задач: даны круги O и O1 и точка P (чер. 264). Требуется построить круг, касающийся кругов O и O1 и проходящий чрез P.

Пусть M искомый круг и точки A и B суть точки касания. Тогда легко найти точку X, где луч SP (S центр подобия кругов O и O1) пересекает круг M. Мы имеем:

SP · SX = SA · SB = SC · SC1 (п. 269)

Отсюда SX/SC = SC1/SP, т. е. отрезок SX есть четвертый пропорциональный к трем известным отрезкам SC, SC1 и SP, — построить его мы умеем. Тогда задача сведется к задаче п. 268.

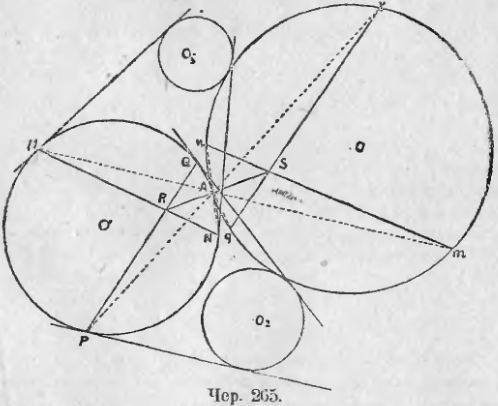
272. Задача Апполония . Даны три круга O1, O2 и O3 (чер. 265). Построить круг, касающийся трех данных.

Мы будем рассуждать лишь в предположении, что мы ищем круг, касающийся каждого из данных внешним образом. Применить к другим случаям не представит затруднений (всего задача имеет 8 решений).

Пусть круг O есть искомый и A есть точка касания кругов O и O1; тогда прямой MN, соединяющей точки касания M и N общих касательных для кругов O1 и O3, соответствует относительно центра подобия A (точка A есть внутренний центр подобия кругов O1 и O) радикальная ось mn кругов O1 и O3: точке M соответствует точка m, лежащая на круге O и на радикальной оси кругов O1 и O3 (п. 270) и также точке N соответствует точка n, лежащая на радикальной оси кругов O1 и O. Точно так же прямой PQ, соединяющей точки касания круга O1 с общими касательными для кругов O1 и O2, соответствует радикальная ось pq кругов O1 и O2.

Точке R, где MN и PQ пересекаются, соответствует точка S, где mn и pq пересекаются, т. е. радикальный центр кругов O1, O2 и O3. Поэтому точки R и S лежат на одной прямой с A.

Точки R и S мы можем построить; соединив их, получим (между ними) точку касания искомого круга с кругом O1, после чего задача легко решается.

Преобразование подобия

Преобразование подобия — это преобразование евклидова пространства, при котором для любых двух точек A, B и их образов A’, B’ имеет место соотношение | A’B’ | = k | AB | , где k — положительное число, называемое коэффициентом подобия.

Содержание:

Гомотетия и ее свойства

Пусть дан многоугольник ABCD (рис. 2.439).

1. Возьмем произвольную точку О.

2. Построим векторы и т. д.

3. Многоугольник будет подобным многоугольнику (рис. 2.439).

В этом построении использовалось требование, при котором точка X переходит в такую точку , что а точка о переходит в себя.

Таким образом, задача построения фигуры, подобной данной фигуре, приводит к новому виду преобразований, которое называют гомотетией.

Определение. Гомотетией с центром O и коэффициентом называют преобразование, при котором каждая точка X переходит в точку , такую, что

Если при гомотетии фигура переходит в фигуру , то эти фигуры называют гомотетичными.

Если k = 1, то каждая точка X перейдет сама в себя.

Если k > 0, то гомотетичные фигуры располагаются по одну сторону от центра гомотетии (рис. 2.440, 2.441).

Если k 0 (рис. 2.440), то точки X и лежат на прямой ОХ по одну сторону от центра гомотетии (так, векторы сонаправлены).

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Планиметрия. Страница 9

  • Главная
  • Репетиторы
  • Учебные материалы
  • Контакты

1.Преобразование подобия и его свойства

Преобразованием подобия называется преобразование фигуры G в фигуру G’, у которой расстояние между точками изменяется в одно и тоже число раз. Т.е. ОA’ = k OA. Это означает, что для любых двух точек геометрической фигуры выполняется равенство A’B’ = k AB. (Рис.1) Число k называется коэффициентом подобия.

Если взять произвольную точку, например точку О. И отложить отрезок OB’ = k OB, то такое преобразование фигуры G в фигуру G’ называется гомотетией. А число k называется коэффициентом гомотетии. Таким образом, гомотетия есть преобразование подобия.

Свойства преобразования подобия

Преобразование подобия переводит прямые в прямые, полупрямые в полупрямые, отрезки в отрезки и при этом углы между прямыми сохраняются.

Рис.2 Подобие фигур.

Подобие треугольников по двум углам

Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. (Рис.3)

Докажем это утверждение. Пусть даны два треугольника ABC и A’B’C’.

Преобразованием подобия преобразуем треугольник A’B’C’ в треугольник A»B»C» с коэффициентом k, т.е. подвергнем гомотетии. Полученный треугольник A»B»C» равен треугольнику ABC по стороне и прилегающим к ней углам. Т.к. преобразование подобия сохраняет углы, а расстояние между двумя точками изменяется в k раз. Следовательно треугольники A’B’C’ и A»B»C» подобны. А т.к. треугольники ABC и A»B»C» равны, то треугольник ABC подобен треугольнику A’B’C’.

Рис.3 Подобие треугольников по двум углам.

3.Подобие треугольников по двум сторонам и углу между ними

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны, то такие треугольники подобны.

Докажем это утверждение. (Доказательство аналогично доказательству подобия по двум углам) Пусть даны два треугольника ABC и A’B’C’.

Преобразованием подобия преобразуем треугольник A’B’C’ в треугольник A»B»C» с коэффициентом k, т.е. подвергнем гомотетии. Полученный треугольник A»B»C» равен треугольнику ABC по двум сторонам и углу между ними со сторонами kA’B’=A»B» и kA’C’=A»C». Т.к. преобразование подобия сохраняет углы, а расстояние между двумя точками изменяется в k раз. Следовательно треугольники A’B’C’ и A»B»C» подобны. А т.к. треугольники ABC и A»B»C» равны, то треугольник ABC подобен треугольнику A’B’C’, т.е. kA’B’=AB, kB’C’=BC и kA’C’=AC.

6.Пример 1

Докажите, что фигура подобная окружности, есть окружность.

Доказательство:

Пусть даны две окружности F и F’ с радиусами R1 и R2 . Подберем коэффициент k так, чтобы kR1 = R2. Необходимо доказать, что окружности подобны.

Зададим на плоскости систему координат с осями Оx и Oy таким образом, чтобы центр первой окружности F совпал с началом координат. Параллельным переносом переместим вторую окружность F’ так, чтобы ее центр также совпал с началом координат. На окружности F возьмем две произвольные точки А и В. И проведем между ними хорду. Также проведем к этим точкам радиусы ОА и ОВ, которые продлим до окружности F’, т.е. ОA’ и OB’. Оси Оx и Оy повернем так, чтобы ось Oy пересекала хорду под прямым углом (Рис.7). Тогда k OA = OA’.

Теперь рассмотрим треугольник ОАС.

Рис.7 Задача. Докажите, что фигура подобная окружности, есть окружность.

Таким образом, мы пришли к выводу, что A’B’ = k AB. А это означает, что расстояние между любыми двумя точками окружности F’ в k раз больше, чем расстояние между подобными точками в окружности F, т.е фигуру F’ можно получить преобразованием подобия или гомотетией относительно точки О. А это значит, что окружности F и F’ подобны.

Пример 2

У треугольников АВС и А1В1С1 ∠A = ∠A1, ∠B = ∠B1. AB = 6, AC = 9, A1B1 = 10, B1C1 = 10. Найдите остальные стороны треугольников.

Решение:

Пусть даны два треугольника АВС и А1В1С1 ∠A = ∠A1, ∠B = ∠B1 (Рис.8). Данные треугольники подобны по двум углам: ∠A = ∠A1 и ∠В = ∠B1. Отсюда следует, что все стороны второго треугольника отличаются от сторон первого треугольника в k число раз, т.е. коэффициент подобия. Найдем число k:

k = AB / А1В1 = 6 / 10 = 3 / 5

Отсюда следует, что

ВС = k * В1С1 = (3 / 5) * 10 = 6 см

А1С1 = АС / k = 9 / (3 / 5) = 15 см

Рис.8 Задача. У треугольников АВС и А1В1С1.

Пример 3

В трапеции ABCD основание АD = 32 см, а основание ВС = 8 см. Угол между диагональю АС и стороной СD равен углу ∠АВС, т.е. ∠АВС = ∠АСD. Найдите диагональ АС.

Решение:

В трапеции два основания лежат на параллельных прямых (Рис.9). Отсюда следует, что угол ∠CAD = ∠BCA, как внутренние накрест лежащие углы. Следовательно, треугольники АВС и АСD подобны по двум углам: ∠AВС = ∠АCD по условию задачи, ∠CAD = ∠BCA, как внутренние накрест лежащие углы.

Тогда можно составить следующие соотношение:

k = АС / ВС = AD / AC . Следовательно,

AC 2 = 8 * 32 = 256

Отсюда, АС = 16 см.

Рис.9 Задача. В трапеции ABCD основание АD = 32 см.

Пример 4

В остроугольном треугольнике АВС проведены высоты AD, BE, CF. Найдите углы треугольника DEF, если в треугольнике АВС ∠А = α, ∠В = β, ∠С = γ.

Решение:

Рассмотрим два прямоугольных треугольника AFC и ABE. Они подобны по одному острому углу, так как угол при вершине А у них общий. Следовательно, угол ∠FCE = ∠ABE. Обозначим его как ϕ3. Аналогичным образом обозначим:

Рассмотрим два прямоугольных треугольника AFO и DOC. Они подобны по одному острому углу: углы при вершине О равны как вертикальные (Рис.10). Отсюда следует, что треугольники FOD и AOC также подобны по двум пропорциональным сторонам и углу между ними.

Так как OD / OF = OC / AO

Следовательно, OD / OС = OF / AO

Отсюда следует равенство углов:

Треугольники BFO и EOC подобны. У них углы при вершине О равны как вертикальные, а углы при вершинах F и E прямые. Отсюда следует подобие треугольников FOE и BOC. Следовательно,

Рис.10 Задача. В остроугольном треугольнике АВС.

Так как ϕ1 + ϕ2 + ϕ3 = 90° (из прямоугольного треугольника BFC), то в треугольнике FDE угол при вершине F равен:

Аналогичным образом выводится, что:

Пример 5

В треугольник ABC вписан ромб ADEF, таким образом, что угол А у них общий, а вершина Е находится на стороне ВС. АВ = 12 см, АС = 4 см. Найдите сторону ромба.

Решение:

Так как у ромба противоположные стороны параллельны, то треугольники АВС и DBE подобны по двум углам: ∠А = ∠D, ∠C = ∠E как соответственные (Рис.11).

Тогда можно составить следующие соотношение:

AC / DE = AB / (AB — AD)

так как AD = DE, то

AC / DE = AB / (AB — DE)

4 / DE = 12 / (12 — DE)

48 — 4 DE = 12 DE

Отсюда, DE = 3 см.

Рис.11 Задача. В треугольник ABC вписан ромб ADEF.

источники:

http://natalibrilenova.ru/preobrazovanie-podobiya/

http://www.mathtask.ru/0057-planimetry.php

Главная > Учебные материалы > Математика: Планиметрия. Страница 9
1 2 3 4 5 6 7 8 9 10 11 12

Рис.1 Преобразование подобия и его свойства.

2.Подобие фигур. Подобие треугольников по двум углам

Две фигуры называются подобными, если преобразованием подобия они переходят друг в друга. (Рис.2)

Если две фигуры подобны третьей, то они подобны друг другу.

Из свойств преобразования подобия следует, что у подобных фигур, соответсвующие стороны пропорциональны и соответствующие углы равны.

Рис.3 Подобие треугольников.

4.Подобие треугольников по трем сторонам

Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.

Доказательство. (Доказательство аналогично доказательству подобия по двум углам) Пусть даны два треугольника ABC и A’B’C’.

Преобразованием подобия преобразуем треугольник A’B’C’ в треугольник A»B»C» с коэффициентом k, т.е. подвергнем гомотетии. В результате получим треугольник A»B»C», который равен треугольнику ABC по трем сторонам kA’B’=A»B», kВ’C’=В»C» и kA’C’=A»C». Т.к. преобразование подобия сохраняет углы, а расстояние между двумя точками изменяется в k раз. Следовательно треугольники A’B’C’ и A»B»C» подобны. И т.к. треугольники ABC и A»B»C» равны, то треугольник ABC подобен треугольнику A’B’C’.

Рис.4 Подобие треугольников по трем сторонам.

5.Подобие прямоугольных треугольников

Если два прямоугольных треугольника имеют по одному равному острому углу, то такие треугольники подобны.

Пусть дан прямоугольный треугольник ABC. Проведем высоту CD. Треугольники ABC и ADC подобны, т.к. угол А у них общий. Так же как и треугольники ADC и BDC. Следовательно:

Т.е. катет прямоугольного треугольника равен средней геометрической гипотенузы и проекции этого катета на гипотенузу. А высота в прямоугольном треугольнике равна средней геометрической между проекциями катетов на гипотенузу.

Отсюда можно сделать вывод, что в любом треугольнике биссектриса делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам. (Свойство биссектрисы треугольника).

Рис.5 Подобие прямоугольных треугольников.

Докажем это утверждение. Пусть дан треугольник ABC. (Рис.6) BE — биссектриса. Треугольники ABE и BCD подобны. Углы В у них равны. Треугольники ADE и DCF также подобны. Углы D у них равны, как вертикальные. Отсюда можно записать следующие соотношения для двух пар треугольников.

Т.е. отрезки AD и DC пропорциональны сторонам AB и BC.

Рис.6 Подобие прямоугольных треугольников.
Источник

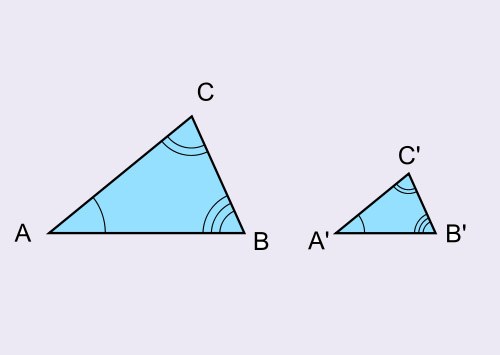
Коэффициент подобия треугольников — что это?

Как его найти?

Коэффициент подобия треугольников, определение.

Подобные треугольники имеют равные углы и пропорциональные сходственные стороны.

Сходственные стороны (другое название — соответственные) — это стороны, которые лежат напротив равных углов.

На рисунке представлены подобные треугольники ABC и A1B1C1.

Для их сторон выполняется следующее равенство:

Величина, которая равна отношению сходственные сторон треугольников, называется коэффициентом подобия.

Коэффициент подобия треугольников обозначается буквой k, k > 0.

Таким образом, приведённое выше равенство можно записать в виде:

коэффициент подобия треугольников

Найти коэффициент подобия треугольников можно несколькими способами.

1) Через отношение сходственных сторон (например, AB / A1B1).

2) Этот коэффициент также равен отношению периметров подобных треугольников.

P(ABC) = A + B + C, P(A1B1C1) = A1 + B1 + C1.

k = P(ABC) / P(A1B1C1).

3) Через площади подобных треугольников.

k² = S(ABC) / S(A1B1C1).

4) Отношение длин высот, медиан, биссектрис подобных треугольников также равно коэффициенту подобия.

Пример.

Даны подобные треугольники DEC и AON.

Коэффициент подобия = 1,5, а сторона DE = 12 см.

Требуется найти сторону AO.

_

По определению коэффициента подобия k = DE / AO = 1,5.

Так как DE = 12 см, то можно записать:

12 / AO = 1,5.

AO = 12 / 1,5 = 8 см.

Значит, длина стороны AO составляет 8 см.

модератор выбрал этот ответ лучшим

smile­6008
[28.5K]

3 года назад 

Для того чтобы найти коэффициент подобия треугольников необходимо сначала определиться что же это понятие значит.

Итак, подобный треугольник, это треугольник, геометрическая фигура, у которой одинаковые углы и одинаковые стороны, которые находятся напротив друг друга. То есть называются подобными.

Для того чтобы найти коэффициент подобия треугольников обратимся к формуле.

Для вычисления коэффициент используют разные способы расчёта.

Проще всего найти коэффициент, если вычислить площади треугольников.

Другой способ расчёта коэффициента примениние расчёта через отношение сходственных сторон подобных треугольников.

Дубло­н
[177K]

2 месяца назад 

Говоря о коэффициенте подобия треугольников, необходимо знать, что есть подобные фигуры, а точнее подобные треугольники. Под таковыми являются треугольники, чьи углы равные, а сходственные стороны этих треугольников пропорциональны. Так вот, отношение этих сходственных сторон и есть коэффициент подобия.

Коэффициент подобия можно определить, зная величину как сходственных сторон, так и величину периметров подобных треугольников, так и величину площади подобных треугольников.

Бутаф­ога
[31.1K]

3 месяца назад 

Говоря простым языком, подобные треугольники называют такие геометрические фигуры, у которых углы одинаковые, а стороны пропорциональные.

Стоит отметить как понятие соответственных сторон, лежащих напротив одинаковых углов. Отсюда вытекает коэффициент подобия, равный отношению соответственных сторон подобных треугольников.

Корне­тОбол­енски­й
[162K]

3 месяца назад 

Подобными называются фигуры, одинаковые по форме, но разные по размеру. Треугольники считаются подобными, если у них углы равны, а их соответственные стороны пропорциональны друг другу.

Рассмотрим рисунок:

Изображённые на нем треугольники подобны, поскольку у них соответствующие углы равны между собой, а соответственные (второе название сходственные) стороны пропорциональны.

Коэффициент подобия равняется отношению сходственных сторон имеющихся подобных треугольников, т.е. сторон, лежащих напротив равных углов.

Простыми словами, Коэффициент подобия показывает, в какое количество раз один треугольник больше другого, обозначается буквой k, при этом k>0. Т.е. коэффициент подобия всегда является положительной величиной.

Коэффициент подобия можно найти несколькими способами:

  • поделить одну сходственную сторону на другую. Это правило работает, если известны длины сторон треугольников.
  • Можно вычислить также коэффициент подобия треугольников в случае, если по условию задачи известны их площади. Существует свойство подобных треугольников, говорящее, что отношение их площадей равняется коэффициента подобия, умноженному на себя, т.е. собственному квадрату. Тогда, разделив значения площадей у подобных треугольников и, извлекши квадратный корень из результата, получим коэффициент подобия.
  • Также k находится через отношение длин медиан, биссектрис или серединных перпендикуляров, проведенных к соответственным сторонам, если длины этих медиан, серединных перпендикуляров или биссектрис известны по условию задачи.
  • Если известны периметры подобных треугольников, то их отношение будет давать всё тот же коэффициент подобия.
  • Если в подобные треугольники вписаны окружности, то отношение их радиусов или диаметров также даст коэффициент подобия. У подобных треугольников отношение диаметров или радиусов описанных вокруг них окружностей равно коэффициенту подобия.
  • Если по условиям задачи известны диаметры или радиусы этих окружностей, либо есть возможность каким-либо способом вычислить из площадей окружностей, то коэффициент подобия ищется и таким способом.

Krust­all
[125K]

8 месяцев назад 

Подобными фигурами называются фигуры, одинаковые по форме, но разные по величине. Треугольники подобны, если их углы равны, а стороны пропорциональны друг другу. Также есть три признака, которые позволяют определить сходство без выполнения всех условий. Первый признак состоит в том, что в подобных треугольниках два угла одного равны двум углам другого. Второй признак подобия треугольников состоит в том, что две стороны одного пропорциональны двум сторонам другого и углы между этими сторонами равны. Третий признак сходства — пропорциональность трех сторон одного по отношению к трем сторонам другого.

Треугольники называются подобными, если они имеют равные углы и соответствующие стороны пропорциональны. Число k, равное отношению соответствующих сторон треугольников, называется коэффициентом подобия.

Давайте вспомним, какие треугольники называются подобными.

Треугольники считаются подобными, если у них:

  • равны углы,
  • пропорциональны соответственные стороны.

Выделяют три признаки по добия треугольников:

  • по трем сторонам,
  • по двум сторонам и углу между ними,
  • по двум углам.

Коэффициент подобия треугольников равен отношению соответственных ( сходственных ) сторон этих треугольников.

Вычислить этот коэффициент можно несколькими путями, в основе которых, по сути, лежит пропорциональность их сходственных сторон:

1.) Непосредственно как отношение сторон.

2.) Через периметры этих треугольников ( то есть через суммы длин их сторон ).

3.) Через площади этих фигур.

4.) Как отношение их биссектрис, высот или медиан.

Серге­й Гории­нов
[5.5K]

5 лет назад 

Коэффициент подобия треугольников — это безразмерная величина, равная отношению соответствующих сторон подобных треугольников:

К=a1/a2=b1/b2=c1/c2, где a1,b1,c1 — стороны первого подобного треугольника, а a2,b2,c2 — стороны второго подобного треугольника.

Также существует коэффициент подобия площадей подобных треугольников, равный квадрату коэффициента подобия треугольника.

Лара Изюми­нка
[59.9K]

2 года назад 

При изучении темы «Подобие треугольников» очень важно понимание , что такое коэффициент подобия траугольников.

Итак, коэффициент подобия — это отношение сходственных сторон в подобных треугольниках.

Сходственные стороны, это стороны, которые лежат против равных углов.

Коэффициент подобия помогает найти площадь подобного треугольника, если известна площадь другого.

Здесь пользуемся тем , что отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Также можно найти стороны одного подобного треугольника, если есть стороны другого и известен коэффициент подобия. Ьема изучается в 8 классе в курсе геометрии.

Nasty­a Chuk
[6.8K]

3 года назад 

Актуальный вопрос на самом деле, поскольку он необходим для понимания различий между видами треугольников и их пропорциями.Предназн­ачение коэффициента подобия : показывает во сколько раз стороны нашего треугольника соответственно больше сторон другого треугольника и какую же часть составляют они от сходственных стороны.Коэффициент подобия обозначается как «к» и выражается всегда через некое соотношение 2-х или 3-х треугольников.

Знаете ответ?
Источник

Как найти коэффициент подобия треугольников

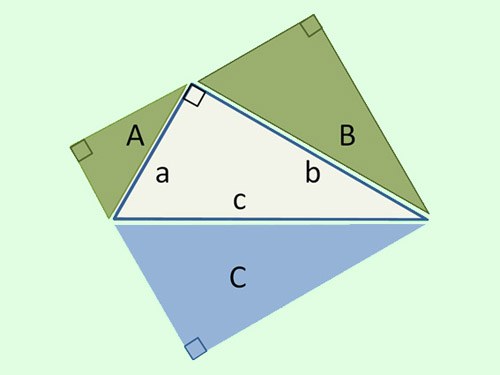
Подобные фигуры – это фигуры, одинаковые по форме, но разные по размеру.Треугольники являются подобными, если их углы равны, а стороны пропорциональны друг другу. Существуют также три признака, позволяющих определить подобие без соблюдения всех условий. Признак первый – у подобных треугольников два угла одного равны двум углам другого. Второй признак подобия треугольников -две стороны одного пропорциональны двум сторонам другого, а углы между этими сторонами у них равны. Третий признак подобия – это пропорциональность трех сторон одного трем сторонам другого.Как найти коэффициент подобия треугольниковВам понадобится

Коэффициент подобия выражает пропорциональность, это отношение длин сторон одного треугольника к сходственным сторонам другого: k = AB/A’B’= BC/B’C’ = AC/A’C’. Сходственные стороны в треугольниках находятся напротив равных углов. Коэффициент подобия можно найти разными способами.Как найти коэффициент подобия треугольников

Например, в задании даны подобные треугольники и приведены длины их сторон. Требуется найти коэффициент подобия. Поскольку треугольники подобны по условию, найдите их сходственные стороны. Для этого запишите длины сторон одного и другого по возрастанию. Найдите отношение сходственных сторон, которое будет коэффициентом подобия.

Вы можете вычислить коэффициент подобия треугольников, если вам известны их площади. Одно из свойств подобных треугольников гласит, что отношение их площадей равняется квадрату коэффициента подобия. Разделите значения площадей подобных треугольников одно на другое и извлеките квадратный корень из результата.

Отношения периметров, длин медиан, медиатрис, построенных к сходственным сторонам, равны коэффициенту подобия. Если разделить длину биссектрис или высот, проведенных из одинаковых углов, вы также получите коэффициент подобия. Воспользуйтесь этим свойством для нахождения коэффициента, если в условии задачи даны эти величины.

По теореме синусов для любого треугольника отношения сторон к синусам противолежащих углов равны диаметру описанной вокруг него окружности. Из этого вытекает, что у подобных треугольников отношение радиусов или диаметров описанных окружностей равно коэффициенту подобия. Если в задаче известны радиусы этих окружностей, или их можно вычислить из площадей кругов, найдите коэффициент подобия этим путем.

Используйте аналогичный путь для нахождения коэффициента, если у вас имеются вписанные в подобные треугольники окружностис известными радиусами.

Источник

Говорят, что треугольник FGH
 подобен треугольнику АВС с
коэффициентом k ,
когда
F =
A ,
G =
B,
H =
C, а также FG
/ AB = FH
/ AC = GH
/ BC = k.
Если в ходе решения задания не важен
коэффициент подобия k
, то просто говорят, что треугольники
FGH и АВС
подобны и пишут 
АВС
FGH . Необходимо знать
три признака подобия треугольников: по
двум пропорциональным соответствующим
сторонам и равным углам между ними; по
двум равным соответствующим углам; по
трем пропорциональным соответствующим
сторонам. Так же необходимо помнить,
что коэффициент подобия треугольников
может быть найден как отношение их
соответствующих компонент, имеющих
линейные размеры (например, как отношение
соответствующих высот, медиан или
биссектрис, а также как отношение
периметров, радиусов вписанных или
радиусов описанных окружностей и т.
п.). Квадрат коэффициента подобия
треугольников равен отношению площадей
соответствующих фигур, связанных с
этими треугольниками (например, отношению
площадей самих треугольников, отношению
площадей, вписанных в них кругов, и
т.п.). Часто встречаются ситуации, когда
подобные треугольники расположены как
на рис. 6 при
ABC =
ADE или на рис.
7 при
GKL =
FGK . В этих ситуациях
имеем
ABC

ADE и
HKL

HGF соответственно.

А
F
G

D
H

E

B
K
L

Рис. 6 C
Рис. 7

П

одобные
треугольники встречаются и при решении
заданий, связанных с окружностью. На
рис. 8 – 11 приведены такие ситуации.

В
A B

С
F


F A

D B
(касательная) C

А B

F C

D
Рис. 10
D

Рис. 8 C

D
A

Рис. 9
Рис. 11

На каждом из рисунков 8 – 10 подобие
треугольников AFD и
CFB является
необходимым и достаточным условием для
того, чтобы точки A,
B, C
и D лежали на
одной окружности.

Из подобия этих треугольников следуют
полезные соотношения: AFFC
= BFFD
на рисунке 8, CB
: AD = FB
: FD на рисунке 9, а
если к тому же на этом рисунке угол DBF
прямой, то есть FB
: FD = Cos
 ВFD,
 то получаем равенство СВ : АD
= Cos
AFD. На рисунке 10 из
подобия треугольников AFD
и CFB следует,
что FBFA
= FDFC
. На рисунке 11 подобными являются
треугольники АВС и BDC
(величины углов BAD и
CBD равны половине
угловой величины одной дуги BD
, а угол С общий). Откуда получается
полезное равенство для отрезка касательной
ВС, имеющее вид ВС =

.

Теперь можно переходить к решению
заданий 2.1 – 2.5.

7.1. Стороны АВ и ВС треугольника
АВС пересекает прямая, параллельная
АС, соответственно в точках D
и E . Периметр и
площадь треугольника АВС равны 12
(ед. и ед.2).

Найдите радиус окружности, вписанной
в треугольник BDE, если
DA + AC
+ CE = 6+ DE.

7.2. Около треугольника АВС описана
окружность. Продолжение медианы АD
пересекает окружность в точке Е
. Найдите длину отрезка СЕ, если
AB = 8, AD
= 12, AE = 15.

7.3. В треугольнике АВС точка
D лежит на стороне
АС, причем АD
= 2, DС = 7 и 
А = 450. Найдите площадь
треугольника АВD,
если АВD
= АСВ .

7.4. В треугольнике АВС проведены
высоты ВD и
СЕ. Найдите DЕ,
если AB / AD
= 3 и ВС = 15.

7.5. На стороне АС треугольника
АВС как на диаметре построена
окружность, пересекающая прямые АВ
и ВС в двух точках D
и E соответственно.
Найдите сторону ВС, если известно,
что АВ = 1 и АС = 2DE
=

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #

    06.09.2019647.68 Кб2ПЗ.doc

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Совет 1: Как обнаружить показатель подобия треугольников

Сходственные фигуры – это фигуры, идентичные по форме, но различные по размеру.Треугольники являются сходственными, если их углы равны, а стороны пропорциональны друг другу. Существуют также три знака, разрешающих определить подобие без соблюдения всех условий. Знак 1-й – у сходственных треугольников два угла одного равны двум углам иного. 2-й знак подобия треугольников – две стороны одного пропорциональны двум сторонам иного, а углы между этими сторонами у них равны. 3-й знак подобия – это пропорциональность 3 сторон одного трем сторонам иного.

Как обнаружить показатель подобия треугольников

Вам понадобится

  • – ручка;
  • – бумага для записей.

Инструкция

1. Показатель подобия выражает пропорциональность, это отношение длин сторон одного треугольника к подобным сторонам иного: k = AB/A’B’= BC/B’C’ = AC/A’C’. Подобные стороны в треугольниках находятся наоборот равных углов. Показатель подобия дозволено обнаружить различными методами.

Сходственные треугольники

2. Скажем, в задании даны сходственные треугольники и приведены длины их сторон. Требуется обнаружить показатель подобия . От того что треугольники подобны по условию, обнаружьте их подобные стороны. Для этого запишите длины сторон одного и иного по возрастанию. Обнаружьте отношение подобных сторон, которое будет показателем подобия .

3. Вы можете вычислить показатель подобия треугольников , если вам знамениты их площади. Одно из свойств сходственных треугольников гласит, что отношение их площадей равняется квадрату показателя подобия . Поделите значения площадей сходственных треугольников одно на другое и извлеките квадратный корень из итога.

4. Отношения периметров, длин медиан, медиатрис, построенных к подобным сторонам, равны показателю подобия . Если поделить длину биссектрис либо высот, проведенных из идентичных углов, вы также получите показатель подобия . Воспользуйтесь этим свойством для нахождения показателя, если в условии задачи даны эти величины.

5. По теореме синусов для всякого треугольника отношения сторон к синусам противолежащих углов равны диаметру описанной вокруг него окружности. Из этого вытекает, что у сходственных треугольников отношение радиусов либо диаметров описанных окружностей равно показателю подобия . Если в задаче знамениты радиусы этих окружностей, либо их дозволено вычислить из площадей кругов, обнаружьте показатель подобия этим путем.

6. Используйте подобный путь для нахождения показателя, если у вас имеются вписанные в сходственные треугольники окружности с знаменитыми радиусами.

Совет 2: Как обнаружить показатель прироста

Для того дабы рассчитать показатель прихода для всякого финансового показателя, довольно знать его числовое выражение в различные моменты времени и уметь использовать примитивную формулу.

Как обнаружить показатель прихода

Инструкция

1. Выберите финансовый показатель, показатель прихода которого вам нужно посчитать. Помните, что показатель прихода показывает, в какую сторону изменился показатель во времени, следственно вам необходимо знать два значения, скажем, размер валовой выручки 2010 и 2011.

2. Рассчитайте показатель прихода. Для этого поделите показатель нового периода на показатель прошлого периода. Из полученного значения вычтите 1, умножьте на 100%. Для валовой выручки формула выглядит дальнейшим образом:(Валовая выручка 2011/Валовая выручка 2010-1)*100%.

3. Не путайте показатель прихода с показателем роста, конечный рассчитывается по формуле:(Валовая выручка 2011/Валовая выручка 2010)*100%.Показатель роста неизменно имеет правильный знак, даже в тех случаях, если, скажем, валовая выручка (либо всякий иной финансовый показатель) упала со 100 условных рублей в 2010 году до 50 в 2011. Рассчитанный показатель роста составляет 50%, а прихода -50%.

4. Проверьте себя. До подсчета показателя прихода сравните между собой финансовые показатели 2-х периодов. Если данные больше раннего периода огромнее, чем больше позднего, значит, случилось настоящее сокращение исследуемой величины, и показатель прихода будет негативным. Напротив, если показатель со временем подрос, значит, показатель прихода будет иметь позитивный знак.

5. Обратите внимание, что дозволено применять показатель прихода не только в тех случаях, когда имеются два последовательных во времени значения одного финансового показателя. Расчет показателей роста и прихода также ведется для сопоставления данных определенного периода одного года, скажем, месяца либо квартала, с данными аналогичного периода предыдущего года. То есть дозволено посмотреть, увеличилась ли валовая выручка октября 2011 года по сопоставлению с размером валовой выручки октября 2010 года.

Совет 3: Как обнаружить показатель вариации

Математическая статистика невероятна без постижения вариации и, в том числе, расчета коэффициента вариации . Он получил самое огромное использование на практике вследствие несложному расчету и наглядности итога.

Как обнаружить показатель вариации

Вам понадобится

  • – вариация из нескольких числовых значений;
  • – калькулятор.

Инструкция

1. Вначале обнаружьте выборочную среднюю. Для этого сложите все значения вариационного ряда и поделите их на число постигаемых единиц. Скажем, если требуется обнаружить показатель вариации 3 показателей 85, 88 и 90 для расчета выборочной средней нужно прибавить эти значения и поделить на 3: х(ср)=(85+88+90)/3=87,67.

2. После этого рассчитайте ошибку репрезентативности выборочной средней (среднее квадратическое отклонение). Для этого из всего значения выборки вычтите среднее значение, обнаруженное в первом шаге. Возведите все разности в квадрат и сложите полученные итоги между собой. Вы получили числитель дроби. В примере расчет будет выглядеть так: (85-87,67)^2+(88-87,67)^2+(90-87,67)^2=(-2,67)^2+0,33^2+2,33^2=7,13+0,11+5,43=12,67.

3. Дабы получить знаменатель дроби умножьте число элементов выборки n на (n-1). В примере это будет выглядеть как 3х(3-1)=3х2=6.

4. Поделите числитель на знаменатель и из полученного числа выразите дробь, дабы получить ошибку репрезентативности Sх. У вас получится 12,67/6=2,11. Корень из 2,11 равен 1,45.

5. Приступайте к самому основному: обнаружьте показатель вариации . Для этого поделите полученную ошибку репрезентативности на выборочную среднюю, обнаруженную в первом шаге. В примере 2,11/87,67=0,024. Дабы получить итог в процентах, умножьте полученное число на 100% (0,024х100%=2,4%). Вы обнаружили показатель вариации , и он равен 2,4%.

6. Обратите внимание, полученный показатель вариации достаточно неважный, следственно вариация знака считается слабой и постигаемую общность абсолютно дозволено считать однородной. Если бы показатель превышал 0,33 (33%), то среднюю величину невозможно было считать нормальной, и постигать по ней общность было бы неверно.

Полезный совет
Вы можете проверить итог «на глаз», дабы убедится в его верности. Оцените приблизительно элементы выборки, если они примерно не отличаются, у вас должен получиться неважный процент отклонения. Чем мощней разброс значений показателя, тем огромнее будет показатель вариации.

Совет 4: Как обнаружить показатель распределения

Основным показателем производительности экстракции является коэффициент распределения . Он считается по формуле: Со/Св, где Со – насыщенность извлекаемого вещества в органическом растворителе (экстракторе), а Св – насыщенность этого же вещества в воде, позже наступления баланса. Как дозволено опытным путем обнаружить показатель разделения?

Как обнаружить показатель разделения

Вам понадобится

  • – лабораторная емкость;
  • – раствор уксусной кислоты;
  • – диэтиловый фир;
  • – вода;
  • – пробка;
  • – раствор гидроксида натрия;
  • – делительная воронка.

Инструкция

1. Перед вами поставлена такая задача. Дан раствор уксусной кислоты знаменитой концентрации, диэтиловый эфир, проверочный (титровальный) раствор щелочи – гидроксида натрия, а также раствор индикатора – фенолфталеина. Следует рассчитать показатель разделения вещества – уксусной кислоты – между диэтиловым эфиром и водой. Как это сделать?

2. В лабораторную емкость (скажем, плоскодонную колбу со шлифом) налейте определенный объем раствора уксусной кислоты –50 мл. Потом в эту же колбу добавьте такой же объем диэтилового эфира, плотно закройте «пришлифованной» пробкой и несколько минут встряхивайте смесь (вручную либо с подмогой качалки).

3. Позже встряхивания сделайте перерыв на 15 – 20 минут (четко увидите, как смесь расслоится). Повторите встряхивание. Эту процедуру следует проделать минимум двукратно, для больше полной экстракции уксусной кислоты и, соответственно, больше точного итога.

4. Во время первого «отстаивания», проведите контрольное титрование некоторого числа раствора кислоты раствором гидроксида натрия в присутствии индикатора фенолфталеина. Запишите, сколько миллилитров щелочи ушло на нейтрализацию, обозначив эту величину С1.

5. Позже последнего «отстаивания» смеси, когда проявится отчетливая граница раздела фаз, осмотрительно перелейте в делительную воронку. Отвергнув нижний краник, отберите больше весомый водный слой. В нем по-бывшему содержится уксусная кислота, но, разумеется, в меньшей концентрации – чай часть ее была экстрагирована эфиром.

6. Отберите верно такое же число раствора кислоты, как и при контрольном титровании, и вновь оттитруйте его резким натром в присутствии фенолфталеина. Число миллилитров щелочи, затраченное на нейтрализацию, обозначьте С2. Показатель разделения рассчитайте по формуле: С1/С2. Задача решена.

Обратите внимание!
Диэтиловый эфир – дюже летучее и пожароопасное вещество! При работе с ним будьте весьма осмотрительны.

Совет 5: Как обнаружить показатель ритмичности

Ритмичность производства – один из основополагающих показателей ведения удачного бизнеса. Он обозначает, что все заказы и взятые на себя обязательства по производству продукции будут исполнены в срок и в надлежащем качестве. А это ведет к своевременному поступлению средств за отгруженную продукцию, которые пойдут и на становление производства, и на выплату заработной платы работникам, и на закупку сырья и др. нужды. Бывалый хозяйственник знает, что все процессы производства связаны между собой, и следственно отчетливо отслеживает ритмичность выпуска продукции.

Как обнаружить показатель ритмичности

Инструкция

1. Для оценки ритмичности производства обыкновенно проводится обзор выпуска продукции по месяцам, неделям либо дням. Высчитываются плановые объемы, исполненные объемы, недовыполненные объемы производства и время, соответствующее их выполнению. Дальше составляется таблица, в которой определенному периоду времени соответствует определенный показатель выпуска товара. Обзор охватывает тот интервал времени, тот, что нужен для отчетливой организации труда.

2. Всеобщий показатель ритмичности (Рд) высчитывайте на основе обзора выпуска продукции и определяется по формуле:Рд =Ад*100/ Ам, где:Чистилище – фактический выпуск продукции за декаду;Ам – фактический выпуск продукции за месяц.Впрочем данный показатель является довольно всеобщим, от того что не рассматривает число рабочих дней в периоде, а также выполнение планового графика производства.

3. Для больше подлинного определения ритмичности применяют коэффициент ритмичности (Кр). Эта величина показывает долю выпущенной продукции без нарушения графика. Воспользуйтесь формулой:Кр=Аф/Ап, где:Аф – фактический выпуск продукции за определенный период времени;Ап – плановое задание по выпуску продукции за тот же период времени.

4. Помимо этого, показатель ритмичности дозволено вычислить и по формуле:Кр=1-Ан/Ап, где: Ан – недовыполнение плана по выпуску продукции за определенный период;Ап – плановое задание по выпуску за тот же период.

5. Во втором случае расчет базируется на плановом графике выпуска товаров. Провести обзор производства и рассчитать показатель ритмичности дозволено за всякий необходимый отрезок времени: смену, день, неделю, декаду и т.д.

Обратите внимание!
Определение показателя ритмичности – значимый этап оперативного планирования производства, что является предпосылкой для отчетливой работы каждого предприятия.

Совет 6: Как обнаружить показатель эластичности

Упругость потребности либо предложения является главной колляцией, которая дает точную количественную оценку могущества определенных факторов на объемы продаж. Дабы определить степень восприимчивости рынка к сходственным воздействиям, надобно обнаружить коэффициент эластичности .

Как обнаружить показатель гибкости

Инструкция

1. Различные товары на рынке продаются по-различному, и этому есть уйма причин, которые в финальном выводе сводятся к определенному соотношению между спросом и предложением. Это соотношение является базовым законом рынка и зависит от многих факторов: цена самого товара, его аналога, тот, что может выбрать покупатель, ярус прибылей возможного клиента и т.д.

2. В всеобщем виде упругость – это метаморфоза некоторой функции в итоге метаморфозы ее довода. Иными словами, математически эту колляцию дозволено представить в виде дроби: отношения относительного приращения функции к приходу само­стоятельной переменной.

3. Показатель эластичности показывает степень увеличения либо уменьшения объема спроса/предложения при изменении некоторого фактора на 1 %. Таким образом, дозволено предварительно рассчитать реакцию покупателя и выработать необходимую тактику, скажем, провести стимулирующую рекламную акцию, организовать скидки некоторым категориям клиентов на ограниченное время и т.д.

4. Дабы обнаружить коэффициент эластичности , дозволено воспользоваться двумя способами: вычисление по дуге и в точке. Выбор метода зависит от того, какими начальными данными вы располагаете. Скажем, дуговая упругость полагает расчет между двумя определенными точками на графике (косой) потребности либо предложения. При этом нужно знать цены и объемы продукции в начале и конце получившейся дуги.

5. Если все указанные данные у вас есть, то воспользуйтесь дальнейшей формулой:Ke = (Q2 – Q1)/((Q2 + Q1)/2) : (P2 – P1)/((P2 + P1)/2), где:Ke – коэффициент эластичности ;Q1 и Q2 – объемы продукции в первой и 2-й точке дуги;P1 и P2 – соответствующие этим точкам цены.

6. Точечную упругость легко определить, если вам знаменит только первоначальный ярус цен и функция потребности (предложения) при этой величине. Для расчета обнаружьте ее производную и умножьте на соотношение между доводом и функцией:Ke = Q’(P)•P/Q(P), где:Р – цена;Q(P) – функция спроса/предложения по данной цене;Q’(P) – ее первая производная.

Совет 7: Как обнаружить показатель жесткости

Жесткость – это способность детали либо конструкции противодействовать приложенной к нему внешней силе, по вероятности сберегая свои геометрические параметры. Основная колляция жесткости – коэффициент жесткости .

Как обнаружить показатель жесткости

Вам понадобится

  • – рессорная пружина;
  • – грузы с определенной массой;
  • – линейка;
  • – тетрадь для записей;
  • – калькулятор.

Инструкция

1. Представьте, что вы решили своими руками соорудить грузовую тележку для мотоцикла либо автомобиля, дабы вывозить мусор со двора, привозить с поля урожай и так дальше. Желанно, дабы тележка была на рессорах. Если у вас есть пружинные рессоры, и вы знаете их коэффициент жесткости , вы можете вычислить, какой массы груз они способны нести. Показатель жесткости также дозволено вычислить опытным путем.

2. Разные пружины предуготовлены для работы на сжатие, растяжение, кручение либо изгиб. В школе на уроках физики детей учат определять коэффициент жесткости пружины, работающей на растяжение. Для этого на штативе вертикально подвешивается пружина в свободном состоянии. Один из учеников с поддержкой линейки замеряет ее длину. И итог записывается в тетрадь как L 1 = …

3. После этого к нижнему концу подвешивается груз определенной массы, скажем, 0.1 кг. Он воздействует на пружину, растягивая ее, с силой 1Ньютон (1Н). Напарник измеряет получившуюся длину растянутой пружины. Показание L 2, которое, безусловно, будет огромным, также записывается в тетрадь как L 2 = … Простым арифметическим действием L 2 – L 1 = находится величина растяжения L.

Как обнаружить <b>коэффициент</b> <strong>жесткости</strong>

4. По закону Гука: F упр. = kL. Следственно, дабы обнаружить коэффициент упругости (k), нужно силу растяжения пружины (F) поделить на величину удлинения (L). k = F/L.

5. Дабы опытным путем определить коэффициент упругости заготовленной вами для тележки пружины, ее нужно будет сжимать. Эта работа гораздо труднее исполняемой в школьной лаборатории. Во-первых, замерьте длину пружины в свободном состоянии и запишите итог(L 1).

6. Установите пружину вертикально в какую-либо гильзу, оставив свободной небольшую верхнюю часть. Возьмите определенный груз, скажем, гимнастическую гирю 16, 24 либо 32 кг. Установите ее на верхний торец пружины и подметьте на гильзе либо непринужденно измерьте линейкой длину сжатой пружины (L 2). Осмотрительно снимите гирю.

7. Вычислите значение L как разницу: L 1 – L 2. Подставьте значения в теснее знаменитую формулу k = F/L. Подбирайте по формуле F = kL возможную массу перевозимого груза, исходя из величины сжатия пружины.

Видео по теме

Обратите внимание!
Проявляйте максимальную осторожность при работе с пружиной. Она, тяготясь распрямиться, в всякий момент может «выстрелить» в непредсказуемом направлении и нанести увечье.

Источник

Понравилась статья? Поделить с друзьями:
  • Path python как найти
  • Как найти девушка в кунгуре
  • Как исправить запавшую клавишу на клавиатуре
  • Как правильно составить резюме с примером
  • Как найти спонсора для волейбольной команды