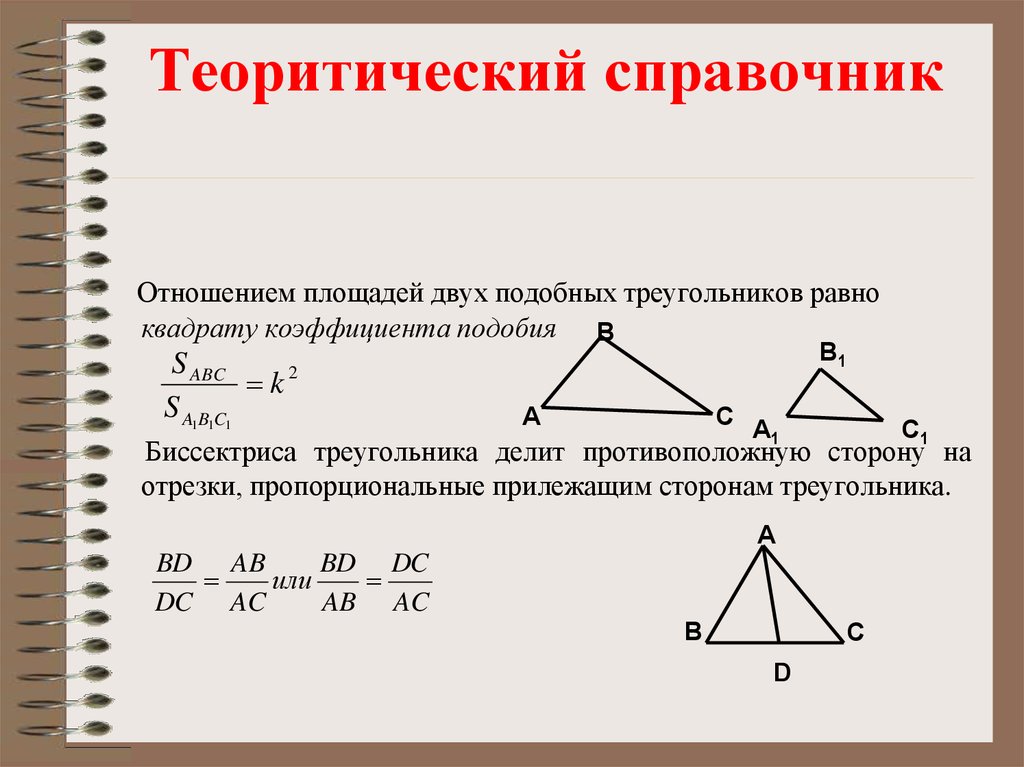
Как найти коэффициент подобия равносторонних треугольников - Исправление недочетов и поиск решений вместе с Examum.ru

A₁B₁C₁.

Отношение площадей подобных треугольников равно квадрату коэффициента подобия. Если обозначить площади двух подобных треугольников буквами S и S₁, то:

Если два угла одного треугольника равны двум углам другого, то треугольники подобны.

A₁B₁C₁.

Второй признак подобия треугольников

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то треугольники подобны.

Если	AB	=	AC	, ∠A = ∠A₁,
A₁B₁	A₁C₁
то ABC A₁B₁C₁.

Третий признак подобия треугольников

Если три стороны одного треугольника пропорциональны трём сходственным сторонам другого, то треугольники подобны.

Подобные треугольники

Определение

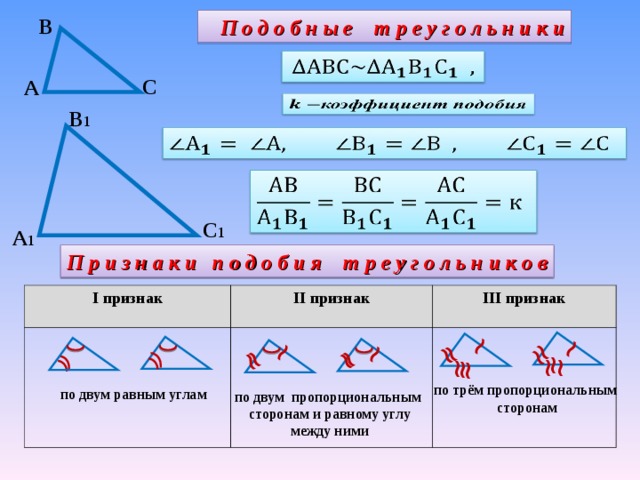
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.

Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.

Признаки подобия треугольников

I признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

II признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Свойства подобных треугольников

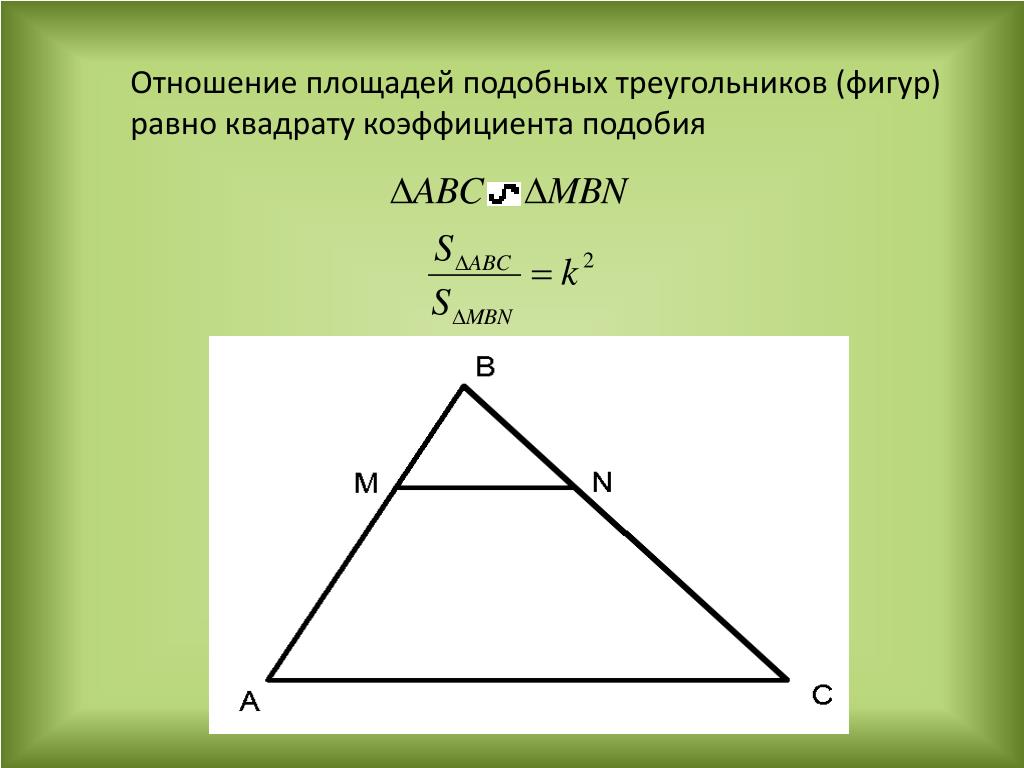
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Отношение периметров подобных треугольников равно коэффициенту подобия.
Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.

Примеры наиболее часто встречающихся подобных треугольников

1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.

2. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –

3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.

Здесь вы найдете подборку задач по теме «Подобные треугольники» .

Геометрия

План урока:

Пропорциональные отрезки

Если известна длина двух отрезков, то можно узнать, во сколько раз один из них больше другого. Например, если некоторый отрезок NM = 24 см, а другой отрезок KP = 4 см, то можно утверждать, что NM в 6 раз длиннее, так как

Величину NM/KP именуют отношением отрезков NM и KP. Надо заметить, что в ряде случаев отношение отрезков можно найти, не зная их длины. Пусть в ∆МКР проведена медиана МН. Очевидно, что отрезок КР будет вдвое длиннее КН, ведь Н – середина КР:

Другой пример – это отношение между диагональю квадрата и его стороной.

Используя теорему Пифагора, несложно показать, что в любом квадрате АВСD

Наконец, в прямоугольном треуг-ке, один из углов которого равен 30°, гипотенуза всегда вдвое длиннее меньшего из катетов:

Если отношение отрезка AB к А₁В₁ равно отношению отрезка СD к С₁D₁, то говорят, что отрезки AB и CD пропорциональны отрезкам А₁В₁ и С₁D₁. Например, пусть

Получается, AВ и CD пропорциональны А₁В₁ и С₁D₁. Важно отметить, что пропорциональны могут быть также сразу три и более отрезка.

Определение подобных треугольников

В жизни нередко можно наблюдать объекты, у которых совпадает форма, но отличаются размеры. В качестве примера можно привести мяч для настольного тенниса и баскетбольный мяч. Оба этих предмета имеют форму шара, на баскетбольный мяч значительно больше. Другой пример – настоящий танк и игрушка, изображающая его. Часто подобны друг другу матрешки, которые вкладываются друг в друга – все они выглядят одинаково, а отличаются только общим размером. Наконец, подобны и знаменитые египетские пирамиды:

Такие объекты в геометрии именуют подобными. Подобны друг другу любые две окружности и любые два квадрата. Но особо важную роль в геометрии играют подобные треугольники. Рассмотрим это понятие подробнее.

Пусть есть два треуг-ка, ∆AВС и ∆А₁В₁С₁, у которых соответственно равны углы:

Стороны, которые лежат против одинаковых углов в таких треуг-ках, именуют сходственными. Ими являются стороны AВ и А₁В₁, ВС и В₁С₁, АС и А₁С₁.

Можно дать такое определение подобных треугольников:

Таким образом, подобие треугольников (оно обозначается символом ∾) обозначает выполнение сразу нескольких равенств:

Отношение между сходственными сторонами подобных треуг-ков именуется коэффициентом подобия и обозначается буквой k:

Грубо говоря, подобие треуг-ков означает, что их форма одинакова, но один из них в несколько раз больше или меньше другого. Чтобы получить, из одного треуг-ка другой, равный ему по размерам, его надо просто «масштабировать». Например, на этом рисунке все стороны исходного треуг-ка просто увеличили в три раза:

Это значит, что коэффициент подобия в данном случае равен 3. Однако важно понимать, что в различных геометрических задачах подобные треуг-ки также могут быть повернуты друг относительно друга:

Задание. ∆AВС подобен ∆DEF. Известно, что

Найдите длину ЕF.

Решение. Как только в задаче появляются подобные треуг-ки, стоит сразу же определить их коэффициент подобия, а для этого надо разобраться, какие стороны будут сходственными. Так как∠А = ∠Е, то лежащие против них стороны DF и ВС– сходственные. Их отношение и будет равно коэффициенту подобия:

Получили, что стороны ∆DEF вдвое длиннее сходственных им сторон ∆AВС. У подобных треуг-ков углы одинаковы, поэтому∠С = ∠D. Отсюда следует, что стороны AВ и ЕF сходственны, а потому ЕF вдвое больше:

Задание. ∆AВС и∆DEF – подобные. Известно, что

Найдите длину ЕF.

Решение. По сравнению с предыдущей задачей изменилось только одно условие, теперь∠А = ∠D. Однако это меняет сходственные стороны. Из подобия треуг-ков следует, что∠С = ∠Е. Тогда сходственными оказываются уже стороны AВ и DF. Найдем коэффициент подобия треугольников:

Сходственными являются также стороны ВС и ЕF (ведь∠А = ∠D), поэтому ЕF в 1,25 раза длиннее:

Эти две задачи показывают, как важно правильно определять сходственные стороны подобных треугольников.

Естественно, что все равные друг другу треуг-ки являются одновременно и подобными, причем их коэффициент подобия равен единице.

Задание. Докажите, что у подобных треуг-ков отношение их периметров равно коэффициенту подобия.

Решение. Пусть подобны ∆ AВС и ∆А₁В₁С₁, причем

Периметр ∆AВС можно вычислить так:

Мы доказали утверждение, сформулированное в условии.

Первый признак подобия треугольников

Оказывается, для того, чтобы доказать подобие треуг-ков, не требуется сравнивать все их углы и находить соотношение всех сторон. Существуют три простых признака подобия треугольников.

Однако прежде, чем сформулировать их, нам придется доказать отдельное утверждение, которое известно как обобщенная теорема Фалеса («обычную», не обобщенную теорему мы уже изучали ранее).

Если прямые ВВ₁ и СС₁ (показаны красным цветом)параллельны, то отрезки AВ и АС пропорциональны отрезкам AВ₁ и АС₁, то есть справедливо соотношение:

Доказывать будем от противного. Пусть отрезки AВ и АС непропорциональны AВ₁ и АС₁. Тогда отметим наАС такую точку Н, которая разобьет АС на пропорциональные отрезки, то есть

Естественно, эта точка не будет совпадать с С₁. Рассмотрим случай, когда она окажется правее, чем С₁:

Теперь поступим следующим образом. Проведем через стороны угла большое число прямых, параллельных ВС, которые будут разбивать АС на одинаковые отрезки. По теореме Фалеса эти же прямые отсекут одинаковые отрезки и на AВ. При этом мы проведем настолько много параллельных прямых, что хотя бы одна из них пересечет отрезок С₁Н:

Пусть эта прямая пересечет отрезок С₁Н в некоторой точке С₂, а сторону AВ в точке В₂. Ясно, что отрезки AВ и АВ₂ пропорциональны отрезкам АС и АС₂, так как они состоят из одинакового количества одинаковых отрезков. Например, на построенном рисунке отношение AB₂ к AB равно 5/8, так как AB₂ состоит из 5 отрезков, отсеченных зелеными параллельными прямыми, а AB состоит из 8 таких отрезков. Аналогично и отношение АС₂ к АС также равно 5 к 8. Таким образом, можно записать:

Здесь мы рассмотрели случай, когда точка Н лежит правее С₁, то есть АН >C₁. Случай, когда АН 2 раз. Докажем это.

Пусть ∆AВС и ∆А₁В₁С₁ подобны с коэффициентом подобия k. Снова проведем в них высоты СН и СН₁:

Запишем очевидные равенства:

В итоге получили, что площади подобных треугольников отличаются в k 2 раз.

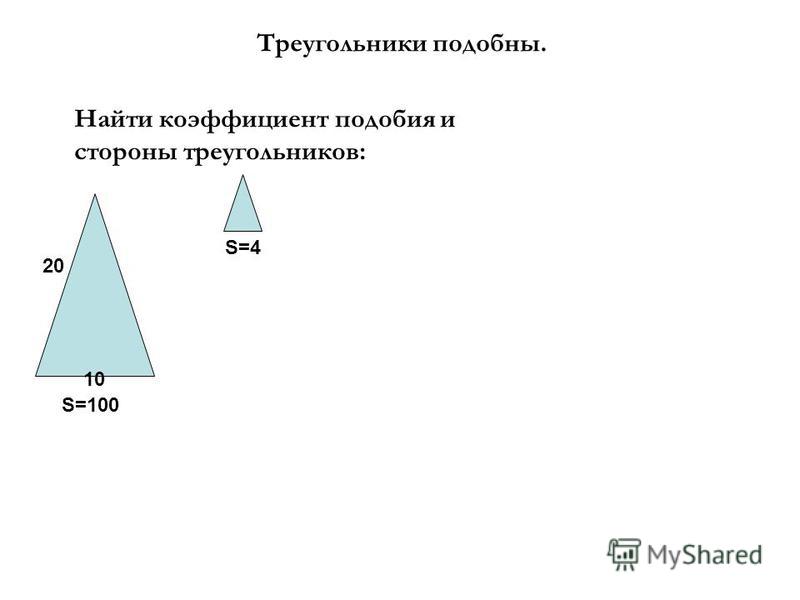
Задание. Известно, у ∆AВС площадь составляет 10, а отрезок AВ имеет длину 5. ∆DEF подобен ∆AВС, причем сторона DE, сходственная AВ, равна 15. Вычислите площадь ∆DEF.

Решение. По условию задачи легко найти коэффициент подобия ∆AВС и ∆DEF, надо лишь поделить одну сходственную сторону на другую:

Задание. Площади двух подобных треуг-ков составляют 75 м 2 и 300 м 2 . Одна из сторон второго треуг-ка равна 9 м. Вычислите сходственную ей сторону первого треуг-ка.

Решение. Зная площади треуг-ков, легко найдем коэффициент их подобия:

Если коэффициент равен 2, то стороны первого многоугольника вдвое меньше сторон второго, поэтому интересующая нас сторона равна

источники:

Подобные треугольники

http://100urokov.ru/predmety/urok-6-podobnye-treugolniki

Источник

Подобные треугольники. Признаки подобия треугольников

Содержание

Определение подобных треугольников
Коэффициент подобия треугольников
Перый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Отношение площадей подобных треугольников

Определение подобных треугольников

Определение 1. Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.

Определение 2. Сходственными называются стороны подобных треугольников, лежащих напротив равных углов.

На рисунке 1 углы треугольников ( small ABC ) и ( small A_1B_1C_1 ) соответственно равны:

Тогда стороны ( small AB ) и ( small A_1B_1 ), ( small BC ) и ( small B_1C_1 ), ( small AC ) и ( small A_1C_1 ) называются сходственными.

Определение 1 можно понимать так: два треугольника подобны, если для них можно ввести обозначения и (Рис.1) так, что

Если два треугольника и подобны, то это обозначают так:

Коэффициент подобия треугольников

Коэффициентом подобия треугольников k − это число, равное отношению сходственных сторон (см. формулу (2)).

Перый признак подобия треугольников

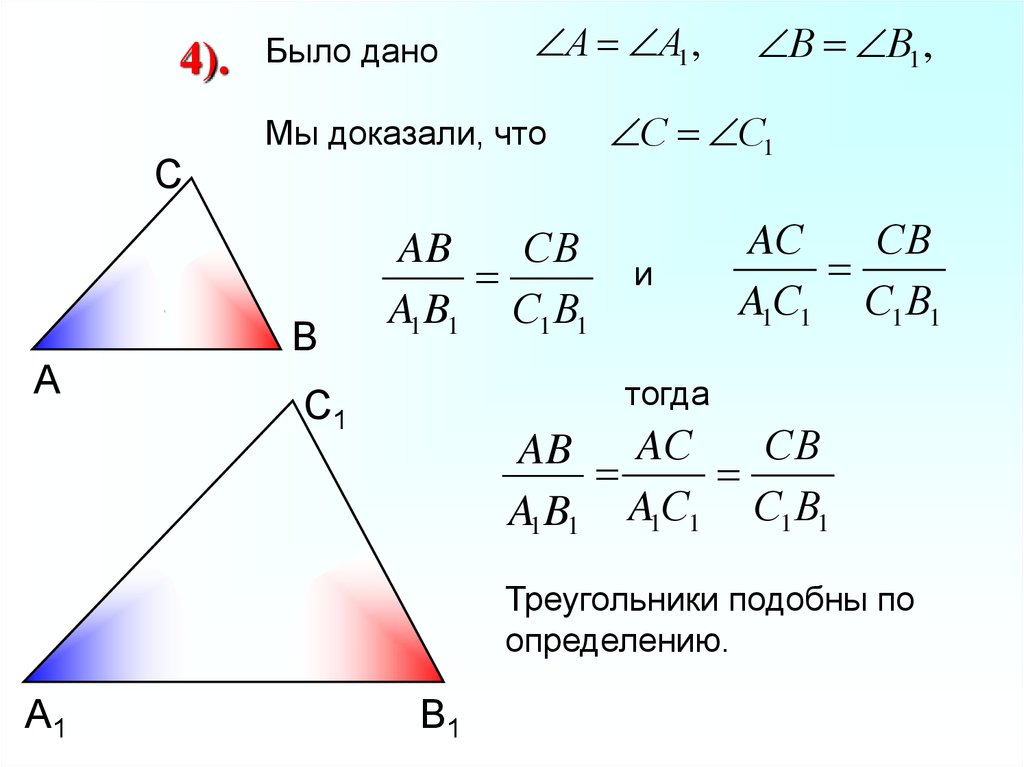
Теорема 1. Если два угла одного треугольника соответсвенно равны двум углам другого треугольника, то такие треугольники подобны.

Доказательство. Пусть заданы два треугольника и и пусть , . Докажем, что (Рис.2).

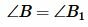
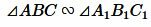
Поскольку сумма углов треугольника равна 180°, то можно записать:

и, так как , , получим:

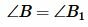
Таким образом углы треугольника соответственно равны углам треугольника . Покажем, теперь, что стороны одного треугольника пропорциональны сходственным сторонам другого треугольника, т. е. выполнено равенство (2).

Площади треугольников и по двум сторонам и углу между ними можно вычислить формулами:

Из (3) и (4), и из следует:

С другой стороны:

Из (6) и (7), и из 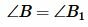следует:

Левые части уравнения (5) и (8) равны. Следовательно равны и правые части:

Умножая левую и правую части уравнения (9) на 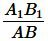, получим:

Продолжая аналогичные рассуждения, получим:

Сравнивая (8) и (11), получим:

Умножая левую и правую части уравнения (12) на 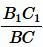, получим:

Из (10) и (13), получим:

То есть стороны треугольника пропорциональны сходственным сторонам треугольника . Что и требовалось доказать.

Второй признак подобия треугольников

Теорема 2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны, то такие треугольники подобны.

Доказательство. Пусть заданы два треугольника и и пусть , . Докажем, что (Рис.3).

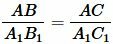
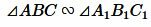
Рассмотрим треугольник 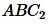у которого

Из условия (15) следует, что треугольники 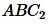и подобны (по первому признаку подобия треугольников). Следовательно:

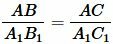
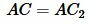
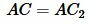
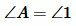
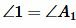
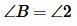
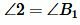
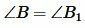
Но по условию теоремы . Поэтому . Треугольники и равны по двум сторонам и углу между ними (сторона AB общая, , (поскольку и )). Следовательно и поскольку , то .

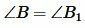
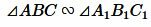
Получили, что и . Тогда по первому признаку подобия треугольников .

Третий признак подобия треугольников

Теорема 3. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Доказательство. Пусть стороны треугольников пропорциональны:

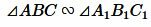
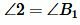
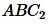
Докажем, что . Рассотрим треугольник у которого , (Рис.3). Треугольники и подобны по первому признаку подобия треугольников. Тогда выполнено следующее равенство:

Сравнивая равенства (16) и (17) получаем: , .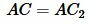

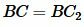
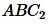
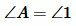
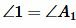
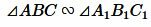
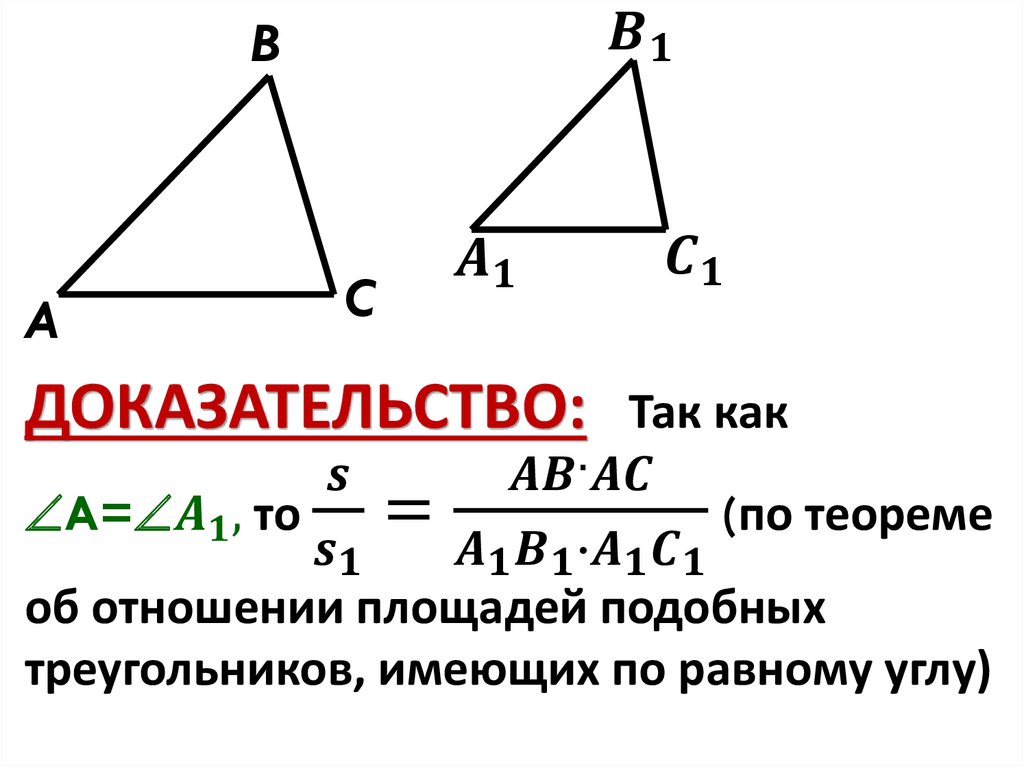
Из этих рассуждений следует, что треугольники и равны по трем сторонам (см. статью Треугольники. Признаки равенства треугольников). Тогда , а поскольку , то . Следовательно, по второму признаку подобия треугольников, треугольники и подобны: .

Отношение площадей подобных треугольников

Теорема 4. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Доказательство. Пусть треугольники и подобны. Тогда

где -коэффициент подобия.

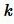
Площади треугольников 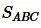и по двум сторонам и углу между ними равны:

Тогда

Источник

Подобные треугольники

3 октября 2022

Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны соответственным сторонам другого.

Подобные треугольники — ключевая тема геометрии 8 класса. Они будут преследовать нас до самого конца школы. И сегодня мы разберём всё, что нужно знать о них.

План такой:

Основное определение
Лемма о подобных треугольниках
Свойства подобных треугольников
Разбор задач

1. Основное определение

Определение. Треугольники называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны соответственным сторонам другого.

Рассмотрим треугольники $ABC$ и $MNK$:

У них есть равные углы: $angle A=angle M$, $angle B=angle N$, $angle C=angle K$. И пропорциональные стороны:

[frac{AB}{MN}=frac{BC}{NK}= frac{AC}{MK}= frac{color{red}{3}}{color{red}{2}}]

Следовательно, треугольники $ABC$ и $MNK$ подобны. Записывается это так:

[Delta ABCsim Delta MNK]

Число $k={color{red}{3}}/{color{red}{2}};$ называется коэффициентом подобия. К нему мы ещё вернёмся.

Пропорциональные стороны подобных треугольников (например, $AB$ и $MN$, либо $BC$ и $NK$) в некоторых учебниках называют сходственными. На практике этот термин применяется редко. Мы будем говорить просто «соответственные стороны».

Дальше идёт очень важное замечание.

1.1. Обозначение подобных треугольников

В геометрии один и тот же треугольник можно называть по-разному. Например, $Delta ABC$, $Delta BCA$ или $Delta CAB$ — это всё один и тот же треугольник. То же самое касается и углов.

Но в подобных треугольниках есть негласное правило:

При обозначении подобных треугольников порядок букв выбирают так, чтобы равные углы перечислялись в одной и той же последовательности.

Вернёмся к нашим треугольникам $ABC$ и $MNK$:

Поскольку $anglecolor{red}{A}=anglecolor{red}{M}$ и $anglecolor{blue}{B}=anglecolor{blue}{N}$, можно записать $Deltacolor{red}{A}color{blue}{B}Csim Deltacolor{red}{M}color{blue}{N}K$. Или $Delta Ccolor{red}{A}color{blue}{B}sim Delta Kcolor{red}{M}color{blue}{N}$. Но никак не $Deltacolor{red}{A}color{blue}{B}Csim Delta Kcolor{red}{M}color{blue}{N}$.

Да, это негласное правило. И если вы нарушите последовательность букв, это не ошибка. Никто не снизит вам за это баллы. А если снизит — добро пожаловать на апелляцию.

Правильная запись позволяет быстро и безошибочно выписывать пропорциональные стороны треугольников. Рассмотрим два подобных треугольника:

[Delta ABCsim Delta MNK]

Берём две первые буквы из каждого треугольника: ${AB}/{MN};$. Затем две последние буквы: ${BC}/{NK};$. Наконец, вычёркиваем «центральную» букву: ${AC}/{MK};$.

Приравниваем полученные три дроби:

[frac{AB}{MN}=frac{BC}{NK}=frac{AC}{MK}]

Вот и всё! Даже рисунок не нужен! Этот приём настолько прост и эффективен, что его в обязательном порядке изучают на моих занятиях, курсах и вебинарах.

В будущем мы увидим, что подобные треугольники чаще всего ищут как раз для составления таких пропорций.

2. Лемма о подобных треугольниках

Подобные треугольники появляются всякий раз, когда прямая, параллельная стороне треугольника, пересекает его стороны.

Теорема 1. Прямая, пересекающая две стороны треугольника и параллельная третьей стороне, отсекает треугольник, подобный исходному.

Доказательство. Рассмотрим треугольник $ABC$. Пусть прямая $MNparallel AB$ отсекает треугольник $MNC$:

Докажем, что $Delta ABCsim Delta MNC$. Рассмотрим треугольники $ABC$ и $MNC$. У них есть общий угол $ACB$.

Углы $ABC$ и $MNC$ — соответственными при $MNparallel AB$ и секущей $BC$. Следовательно, они равны: $angle ABC=angle MNC$.

Аналогично равны углы $BAC$ и $NMC$. Следовательно, треугольники $ABC$ и $MNC$ имеют три соответственно равных угла.

Докажем теперь, что соответственные стороны пропорциональны. Т.е. докажем пропорцию

[frac{AB}{MN}=frac{BC}{NC}=frac{AC}{MC}]

Рассмотрим угол $ACB$. Параллельные прямые $AB$ и $MN$ пересекают стороны этого угла. По теореме о пропорциональных отрезках:

[frac{AC}{MC}=frac{BC}{NC}]

Это равенство — второе в искомом:

[frac{AB}{MN}= color{red}{frac{BC}{NC}=frac{AC}{MC}}]

Осталось доказать первое равенство. Дополнительное построение: прямая $KNparallel AC$:

Поскольку $AMparallel KN$ (по построению) и $AKparallel MN$ (по условию), четырёхугольник $AKNM$ — параллелограмм. Поэтому $AK=MN$.

Рассмотрим угол $ABC$. Параллельные прямые $AC$ и $KN$ пересекают стороны этого угла. По теореме о пропорциональных отрезках:

[frac{AB}{AK}=frac{BC}{NC}]

Учитывая, что $AK=MN$, получаем

[frac{AB}{MN}=frac{BC}{NC}=frac{AC}{MC}]

Итак, соответственные углы треугольников $ABC$ и $MNC$ равны, а их стороны пропорциональны. Следовательно, по определению подобных треугольников

[Delta ABCsim Delta MNC]

Что и требовалось доказать.

Эта лемма — не признак подобия. Это самостоятельная теорема, которая ускоряет решение многих задач.

Признаки подобия разобраны в отдельном уроке — см. «Признаки подобия треугольников».

Частный случай этой леммы — средняя линия. Она отсекает треугольник со сторонами в два раза меньше, чем у исходного:

Оформляется это так. Поскольку $AM=MC$ и $BN=NC$, то $MN$ — средняя линия треугольника $ABC$. Следовательно, прямые $AB$ и $MN$ параллельны, откуда

[Delta ABCsim Delta MNC]

3. Свойства подобных треугольников

Два важнейших свойства: связь периметров и связь площадей.

3.1. Периметры подобных треугольников

Теорема 2. Отношение периметров подобных треугольников равно коэффициенту подобия.

Доказательство. Рассмотрим подобные треугольники $ABC$ и $MNK$:

Запишем равенство из определения подобия. Поскольку $Delta ABCsimDelta MNK$, стороны этих треугольников пропорциональны:

[frac{AB}{MN}=frac{BC}{NK}=frac{AC}{MK}=color{red}{k}]

Здесь число $color{red}{k}$ — коэффициент подобия. Полученное тройное равенство можно переписать так:

[frac{AB}{MN}=color{red}{k}; frac{BC}{NK}=color{red}{k}; frac{AC}{MK}=color{red}{k}]

Или, что то же самое:

[begin{align}AB&=color{red}{k}cdot MN \ BC &=color{red}{k}cdot NK \ AC &=color{red}{k}cdot MK \ end{align}]

Периметр треугольника $MNK$:

[{{P}_{Delta MNK}}=MN+NK+MK]

Периметр треугольника $ABC$:

[begin{align}{{P}_{Delta ABC}} &=AB+BC+CD= \ &=color{red}{k}cdot MN+color{red}{k}cdot NK+color{red}{k}cdot MK= \ &=color{red}{k}cdot left( MN+NK+MK right)= \ &=color{red}{k}cdot {{P}_{Delta MNK}} end{align}]

Итого получаем равенство

[{{P}_{Delta ABC}}=color{red}{k}cdot {{P}_{Delta MNK}}]

Обычно именно в таком виде это равенство и применяют. Но можно записать его и как отношение:

[frac{{{P}_{Delta ABC}}}{{{P}_{Delta MNK}}}=color{red}{k}]

В любом случае, мы получили отношение, которое и требовалось доказать.

3.2. Площади подобных треугольников

Теорема 3. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Доказательство. Первые шаги очень похожи на доказательство предыдущей теоремы. Вновь рассмотрим подобные треугольники $ABC$ и $MNK$:

Поскольку $Delta ABCsimDelta MNK$, углы $ABC$ и $MNK$ равны. Следовательно, равны синусы этих углов:

[begin{align}angle ABC &=angle MNK=color{blue}{alpha} \ sin angle ABC &=sin angle MNK=sin color{blue}{alpha} end{align}]

Кроме того, стороны подобных треугольников пропорциональны:

[frac{AB}{MN}=frac{BC}{NK}=frac{AC}{MK}=color{red}{k}]

В частности, из этого равенства следует, что

[frac{AB}{MN}=color{red}{k}; frac{BC}{NK}=color{red}{k}]

Или, что то же самое:

[begin{align}AB &= color{red}{k}cdot MN \ BC &= color{red}{k}cdot NK \ end{align}]

Площадь треугольника $MNK$:

[{{S}_{Delta MNK}}=frac{1}{2}cdot MNcdot NKcdot sin color{blue}{alpha} ]

Площадь треугольника $ABC$:

[begin{align}{{S}_{Delta ABC}} &=frac{1}{2}cdot ABcdot BCcdot sincolor{blue}{alpha} = \ &=frac{1}{2}cdotcolor{red}{k}cdot MNcdotcolor{red}{k}cdot NKcdot sincolor{blue}{alpha} = \ &={color{red}{k}^{2}}cdot frac{1}{2}cdot MNcdot NKcdot sin alpha = \ &={color{red}{k}^{2}}cdot {{S}_{Delta MNK}} end{align}]

Получаем равенство

[{{S}_{Delta ABC}}={color{red}{k}^{2}}cdot {{S}_{Delta MNK}}]

Перепишем в виде отношения:

[frac{{{S}_{Delta ABC}}}{{{S}_{Delta MNK}}}={color{red}{k}^{2}}]

Что и требовалось доказать.

Для доказательства теоремы мы использовали формулу площади треугольника:

[{{S}_{Delta }}=frac{1}{2}absin alpha ]

Тригонометрию проходят после подобия, поэтому мы опираемся на ещё не изученный материал.

Впрочем, ничто не мешает взять уже известную формулу:

[{{S}_{Delta }}=frac{1}{2}ah]

Здесь $a$ — сторона треугольника, $h$ — высота, проведённая к этой стороне. Дело в том, что высоты в подобных треугольниках тоже пропорциональны. И не только высоты. Назовём это Свойством 3.3.:)

3.3. Элементы подобных треугольников

Теорема 4. Отношение высот, биссектрис и медиан, проведённых к соответствующим сторонам подобных треугольников, равно коэффициенту подобия.

Проиллюстрируем это на высотах. Пусть треугольники $ABC$ и $MNK$ подобны:

В этом случае высоты $CDbot AB$ и $KLbot MN$ относятся как

[frac{CD}{KL}=frac{AB}{MN}= color{red}{k}]

Для доказательства этой теоремы нужно знать признаки подобия. Поэтому оставим его до следующего урока. А сейчас переходим к задачам.

4. Задачи на подобие

Здесь разобрано пять задач на подобие треугольников. Все они довольно простые. За сложными задачами добро пожаловать в задачник.:)

Задача 1. Готовые треугольники

Известно, что треугольники $ABC$ и $MNK$ подобны, причём $angle A=angle M$, $angle B=angle N$, $angle C=angle K$. Кроме того, стороны $AB=6$, $BC=7$, $AC=10$ и $MN=9$. Найдите стороны $NK$ и $MK$.

Решение. Построим треугольники $ABC$ и $MNK$, отметим известные стороны:

Из условия $Delta ABCsim Delta MNK$ следует, что верно равенство

[frac{AB}{MN}=frac{BC}{NK}=frac{AC}{MK}]

Подставим в это равенство всё, что нам известно:

[frac{color{red}{6}}{color{red}{9}}=frac{color{red}{7}}{NK}=frac{color{red}{10}}{MK}]

Опустим последнюю дробь и получим пропорцию

[frac{color{red}{6}}{color{red}{9}}=frac{color{red}{7}}{NK}]

Найдём сторону $NK$:

[NK=frac{color{red}{9}cdot color{red}{7}}{color{red}{6}}=10,5]

Аналогично, убирая среднюю дробь, получим пропорцию

[frac{color{red}{6}}{color{red}{9}}=frac{color{red}{10}}{MK}]

Найдём сторону $MK$:

[NK=frac{color{red}{9}cdot color{red}{10}}{color{red}{6}}=15]

Ответ: $NK=10,5$, $MK=15$.

Задача 2. Прямая, параллельная стороне

Прямая, параллельная стороне $AC$ треугольника $ABC$, пересекает сторону $AB$ в точке $D$, а сторону $BC$ — в точке $E$. Найдите:

а) Отрезок $BD$, если $AB=16$, $AC=20$, $DE=15$.

б) Отрезок $AD$, если $AB=28$, $BC=63$, $BE=27$.

Решение. Для начала построим рисунок. Он будет общий для обоих пунктов.

Из условия следует, что прямая $DE$ пересекает стороны треугольника $ABC$:

Поскольку $DEparallel AC$, по лемме о подобных треугольниках прямая $DE$ отсекает от треугольника $ABC$ новый треугольник, подобный исходному:

[Delta ABCsim Delta DBE]

Из подобия треугольников $ABC$ и $DBE$ следует равенство

[frac{AB}{DB}=frac{BC}{BE}=frac{AC}{DE}]

Решаем пункт а). Подставляем в это равенство всё, что нам известно:

[frac{color{red}{16}}{DB}=frac{BC}{BE}=frac{color{red}{20}}{color{red}{15}}]

Вычёркиваем среднюю дробь и получаем пропорцию

[frac{color{red}{16}}{DB}=frac{color{red}{20}}{color{red}{15}}]

Отсюда легко найти $DB$ (или, что то же самое, $BD$):

[DB=frac{color{red}{16}cdotcolor{red}{15}}{color{red}{20}}=12]

Аналогично решаем пункт б). Подставляем в исходное равенство известные величины:

[frac{color{red}{28}}{DB}=frac{color{red}{63}}{color{red}{27}}=frac{AC}{DE}]

Первые две дроби образуют пропорцию, из которой вновь легко найти $DB$:

[DB=frac{color{red}{28}cdotcolor{red}{27}}{color{red}{63}}=12]

Осталось найти $AD$:

[begin{align}AD &=AB-BD= \ &=color{red}{28}-color{red}{12}=16 end{align}]

Ответ: а) $BD=12$; б) $AD=16$.

Важное замечание по работе с пропорциями. Ни в коем случае не нужно перемножать числа в числителе.

Напротив: нужно разложить их на множители и сократить!

Взгляните:

[DB=frac{color{red}{28}cdotcolor{red}{27}}{color{red}{63}}=frac{4cdotcolor{blue}{7}cdot 3cdotcolor{green}{9}}{color{blue}{7}cdotcolor{green}{9}}=12]

Так вы сэкономите время, избежите умножения столбиком и защитите себя от множества ошибок. Никогда не умножайте большие числа, если дальше их нужно будет сокращать.

Задача 3. Доказательство подобия

Точки $M$ и $K$ — середины сторон $CD$ и $AD$ квадрата $ABCD$ соответственно. Докажите, что треугольники $MDK$ и $BCD$ подобны.

Решение. Сделаем первоначальный рисунок по условию задачи:

Здесь нет прямых, параллельных сторонам треугольника, поэтому лемма о подобных треугольниках не поможет. Докажем подобие по определению.

Сначала разберёмся с углами. Поскольку $ABCD$ — квадрат, и $KD=MD$ — половина стороны квадрата, треугольники $MDK$ и $BCD$ — прямоугольные и равнобедренные.

Все острые углы треугольников $MDK$ и $BCD$ равны 45°. Можем записать это так:

[begin{align}angle BCD &=angle MDK={90}^circ \ angle CBD &=angle DMK={45}^circ \ angle CDB &=angle DKM={45}^circ \ end{align}]

Дополнительное построение: диагональ квадрата $color{red}{AC}$:

Рассмотрим треугольник $ACD$. Отрезок $KM$ — средняя линия, поэтому $KM={color{red}{AC}}/{2};$. С другой стороны, $AC=BD$ как диагонали квадрата. Поэтому верно равенство

[frac{KM}{BD}=frac{KM}{color{red}{AC}}=frac{1}{2}]

Но тогда выполняется следующее равенство:

[frac{MD}{BC}=frac{DK}{CD}=frac{MK}{BD}=frac{1}{2}]

А это вместе с равенством углов как раз и означает, что треугольники $MDK$ и $BCD$ подобны:

[Delta MDKsim Delta BCD]

Доказательство завершено.

Мы доказали подобие треугольников по определению. Если пользоваться признаками подобия, всё будет намного быстрее. Но пока мы не вправе пользоваться этими признаками.

Задача 4. Вписанный ромб

В треугольник $ABC$ вписан ромб $BDEK$ так, как показано на рисунке. Найдите сторону ромба, если $AB=10$, $BC=15$.

Решение. Пусть искомая сторона ромба равна $color{red}{x}$. Из условия задачи получим такой рисунок:

Зная, что $AB=10$ и $BC=15$, выразим $AK$ и $CD$:

[begin{align}AK &=10-color{red}{x} \ CD &=15-color{red}{x} \ end{align}]

Далее рассмотрим треугольник $ABC$. Поскольку $BDEK$ — ромб, то $KEparallel BC$. По лемме о подобных треугольниках имеем:

[Delta ABCsim Delta AKE]

В подобных треугольниках подобные стороны пропорциональны, поэтому

[frac{AB}{AK}=frac{BC}{KE}=frac{AC}{AE}]

Подставим в это равенство всё, что нам известно или выражено через $color{red}{x}$:

[frac{10}{10-color{red}{x}}=frac{15}{color{red}{x}}=frac{AC}{AE}]

Последняя дробь оказалась бесполезной. Вычеркнем её и получим пропорцию:

[frac{10}{10-color{red}{x}}=frac{15}{color{red}{x}}]

Применяем основное свойство пропорции и уравнение:

[begin{align}10cdotcolor{red}{x} &=15cdot left( 10- color{red}{x} right) \ 2cdotcolor{red}{x} &=3cdot left( 10- color{red}{x} right) \ &cdots\ color{red}{x} &=6 end{align}]

Это и есть искомая сторона ромба. Она равна $color{red}{x}=6$.

Ответ: $BD=6$.

Задача 5. Свойства биссектрисы

В треугольнике $ABC$ стороны $AB=8$, $BC=12$, угол $ABC={120}^circ $. Отрезок $BD$ — биссектриса. Найдите длину $BD$.

Решение. Из условия задачи можно сделать вот такой рисунок:

Поскольку $BD$ — биссектриса угла в треугольнике, точка $D$ делит сторону $AC$ на отрезки, пропорциональные сторонам $AB$ и $BC$. Это можно записать так:

[frac{AD}{CD}=frac{AB}{CB}=frac{color{red}{8}}{color{red}{12}}=frac{color{red}{2}}{color{red}{3}}]

Обозначим пропорциональные отрезки переменными. Пусть $AD=color{blue}{2x}$, $CD=color{blue}{3x}$.

Дополнительное построение: прямая $DMparallel AB$:

Рассмотрим угол $ACB$. Поскольку $DMparallel AB$, по теореме о пропорциональных отрезках получаем, что

[frac{BM}{CM}=frac{AD}{CD}=frac{color{red}{2}}{color{red}{3}}]

Вновь обозначим пропорциональные отрезки переменными. Пусть $BM=color{blue}{2y}$, $CM=color{blue}{3y}$. Но тогда

[BC=BM+MC=color{blue}{5y}=color{red}{12}]

Получаем, что $color{blue}{y}=color{red}{2,4}$. Отсюда легко найти длину $BM$:

[BM=color{blue}{2y}=2cdotcolor{red}{2,4}= color{red}{4,8}]

Далее заметим, что если угол $ABC$ равен 120°, то

[angle ABD=angle CBD={60}^circ ]

С другой стороны, прямые $AB$ и $MD$ параллельны по построению. Прямая $BD$ — секущая для этих параллельных прямых.

Следовательно, углы $ABD$ и $BDM$ — внутренние накрест лежащие, поэтому

[angle BDM=angle ABD={60}^circ ]

Рассмотрим треугольник $BDM$. В нём есть два угла по 60°. Следовательно, это равносторонний треугольник:

[BD=BM=color{red}{4,8}]

Мы нашли длину отрезка $BD$. Задача решена.

Ответ: $BD=4,8$.

Итак, с определением разобрались. В следующем уроке разберём признаки подобия.:)

Смотрите также:

Как применяется теорема косинусов и подобие треугольников для решения широкого класса задач в планиметрии.
Теорема менелая
Комбинаторика в задаче B6: легкий тест
Введение системы координат
Четырехугольная пирамида: как найти координаты вершин
Нестандартная задача B5 на площадь круга

Источник

Коэффициент подобия треугольников — интернет энциклопедия для студентов
Определение подобных треугольников
- - Свойство прямой, параллельной какой-либо стороне треугольника.
  - Отношение площадей двух подобных треугольников
  - Построение подобных треугольников
Математическая задача: Коэффициент подобия — вопрос № 977, геометрия
- - Правильный ответ:
  - Пошаговое объяснение:
    - You need to know the following knowledge to solve this word math problem:
    - Единицы физических величин:
    - Уровень задачи:
коэффициент подобия треугольников, формула и примеры. Похожие термины, их приведение, примеры
- - Понятие монома
  - Стандартная форма монома
  - Приведение одночлена к стандартному виду
  - Подобные мономы
  - Сложение одночленов
  - Вычитание одночленов
  - Умножение одночленов
- Определение и примеры подобных терминов.
- Приведение подобных терминов, правило, примеры
- Найдите отношение подобных сторон, которое и будет коэффициентом подобия
- Законы подобия — в аэродинамике
- Используйте это свойство для нахождения коэффициента, если эти значения приведены в условии задачи

Коэффициент подобия треугольников — интернет энциклопедия для студентов

Определение и формула коэффициента подобия треугольников

ОПРЕДЕЛЕНИЕ

Треугольники называются подобными, если они имеют равные углы, а соответствующие стороны пропорциональны.

Рис.1

На рисунке 1 показаны аналогичные треугольники ABC и (
A_{1} B_{1} C_{1}
) , в которых

(
frac{A B}{A_{1} B_{1}}=frac{B C}{B_{1} C_{1}}=frac{C A}{C_{1} A_{1}}=k, quad angle A=angle A_{1}, angle B=angle B_{1}, angle C=angle C_{1}
)

Число k, равное отношению соответствующих сторон треугольников, называется коэффициентом подобия.

Примеры решения проблем

ПРИМЕР 1

Задача

В треугольнике ABC со сторонами AB = 3 см, BC = 6 см на стороне переменного тока, точка K была отмечена, так что треугольники ABC и AKB аналогичны коэффициенту подобия k = 3. Найдите AC и KB.

Решение

Поскольку треугольники ABC и AKB аналогичны, их соответствующие стороны пропорциональны, т. е.

(

frac{A B}{A K}=frac{B C}{K B}=frac{A C}{A B}=3
)

затем

(
frac{B C}{K B}=frac{6}{K B}=3 Rightarrow K B=2 mathrm{cm}
)

а также

(
frac{A C}{A B}=frac{A C}{3}=3 Rightarrow A C=9 mathrm{cm}
)

Ответ: AC = 9 см, КБ = 2 см

ПРИМЕР 2

Задание

Стороны MK и DE, KT и EF являются соответствующими сторонами одинаковых треугольников MKT и DEF, MK = 18 см, KT = 16 см, MT = 28 см, MK: DE = 4: 5. Найдите стороны треугольника отсроченный

Решение

Сделайте снимок.

Треугольники MKT и DEF аналогичны, а отношение их сторон равно MK: DE = 4: 5. Следовательно, коэффициент подобия этих треугольников (
k=frac{4}{5}
).Как следствие,

(
M K=frac{4}{5} cdot D E Rightarrow D E=22,5 mathrm{cm}, K T=frac{4}{5} cdot E F Rightarrow E F=20 mathrm{cm}
)

а также

(
M T=frac{4}{5} cdot D F Rightarrow D F=35 mathrm{cm}
)

Ответ

DE = 22,5 см, EF = 20 см, DF = 35 см

Физика

166

Реклама и PR

Педагогика

Психология

Социология

Астрономия

Биология

Культурология

Экология

Право и юриспруденция

Политология

Экономика

Финансы

История

Философия

Информатика

Право

Информационные технологии

Экономическая теория

Менеджент

719

Математика

338

Химия

Микро- и макроэкономика

Медицина

Государственное и муниципальное управление

География

542

Информационная безопасность

Аудит

Безопасность жизнедеятельности

Архитектура и строительство

Банковское дело

Рынок ценных бумаг

Менеджмент организации

Маркетинг

238

Кредит

Инвестиции

Журналистика

Конфликтология

Этика

Формулы дифференцирования Признаки равенства треугольников Катет прямоугольного треугольника Гипотенуза прямоугольного треугольника Признаки подобия треугольников и свойства

Узнать цену работы

Узнай цену

своей работы

Имя

Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое

Принимаю Политику
конфиденциальности

Подпишись на рассылку,
чтобы не пропустить информацию об акциях

Определение подобных треугольников

Рассмотрим два прямоугольных треугольника с острыми углами в 60° и 30° (рис. 364).

Стороны второго треугольника по сравнению с первым уменьшены в два раза:

(frac{AB}{A’B’}) = 2; (frac{AC}{A’C’}) = 2; (frac{BC}{B’C’}) = 2.

У этих треугольников углы попарно равны. Стороны, лежащие против равных углов, пропорциональны:

(frac{AB}{A’B’}) = (frac{AC}{A’C’} = frac{BC}{B’C’}) = 2.

Такие треугольники называют подобными. Стороны, лежащие против равных углов, называются сходственными.

Таким образом, подобными называются треугольники, у которых yглы попарно равны, а сходственные стороны пропорциональны.

Подобие треугольников записывается так: (Delta)ABС (sim) (Delta)А’В’С’.

Отношение сходственных сторон подобных фигур называется коэффициентом подобия. В данном случае коэффициентом подобия треугольников АBС и А’В’С’ будет число 2.

Если же взять отношения ^A’B’/_AB = ^A’C’/_AC = ^B’C’/_BC , то коэффициент подобия будет равен ¹/₂.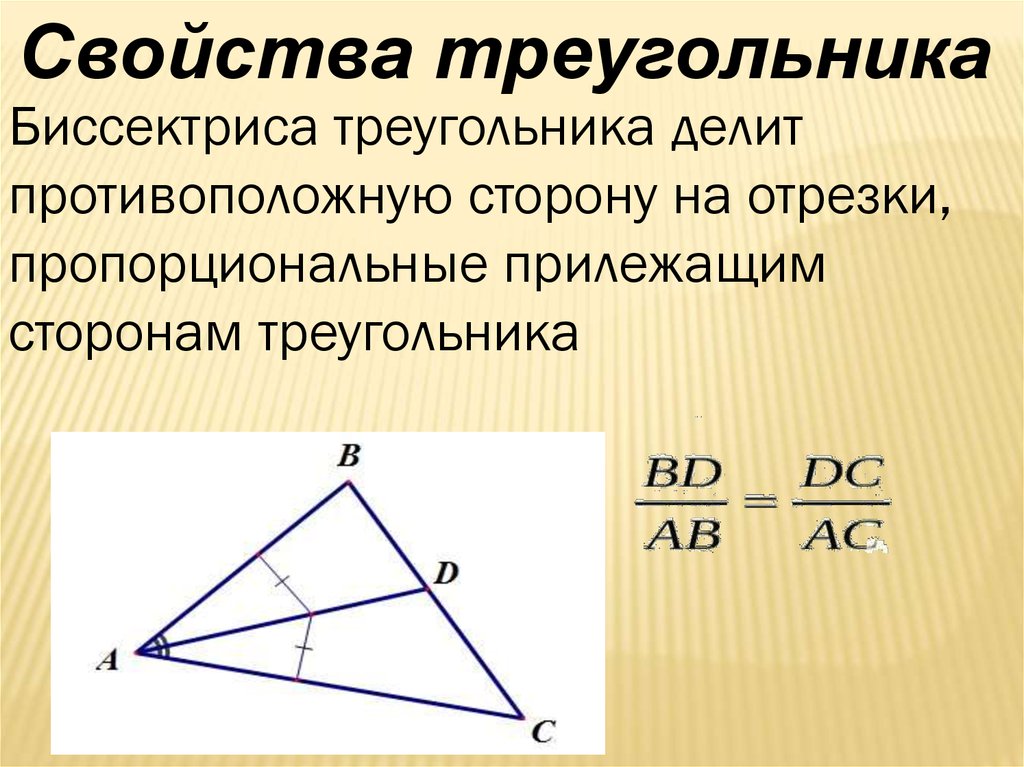

Свойство прямой, параллельной какой-либо стороне треугольника.

Проведём в треугольнике АBС прямую DЕ параллельно стороне АС (рис. 365).

Получим треугольник DВЕ. Докажем, что (Delta)ABС (sim) (Delta)DВЕ.

Вследствие параллельности сторон DЕ и АС ∠1 = ∠2 и ∠3 = ∠4.

Угол В является общим для этих треугольников. Следовательно, углы этих треугольников попарно равны.

Так как DЕ || АС, то (frac{AB}{DB} = frac{BC}{BE}).

Проведём через точку Е прямую, параллельную стороне AB (рис. 366).

Получим: (frac{BC}{BE} = frac{AC}{AK}), но АК = DЕ.

Поэтому

(frac{BC}{BE} = frac{AC}{DE})

Сопоставляя полученную пропорцию с пропорцией (frac{AB}{DB} = frac{BC}{BE}) получим:

(frac{AB}{DB} = frac{BC}{BE} = frac{AC}{DE}), т.е.

сходственные стороны треугольников AВС и DВЕ пропорциональны.

Раньше было доказано, что углы этих треугольников попарно равны.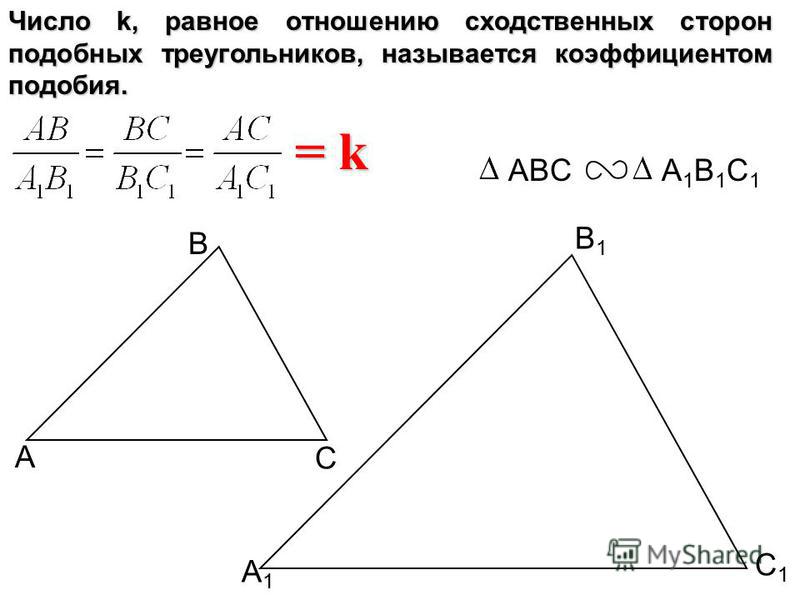

Значит, (Delta)ABС (sim) (Delta)DВЕ.

Следовательно, прямая, проведённая параллельно какой-либо стороне треугольника, отсекает от него треугольник, подобный данному.

Отношение площадей двух подобных треугольников

Пусть (triangle AВС sim triangle AВС)(черт. 380). Из подобия треугольников следует, что

∠A = ∠A, ∠B = ∠B и ∠С = ∠С. Кроме того, ^AB/_AB = ^BC/_BC = ^AC/_AC.

В этих треугольниках из вершин В и В проведём высоты и обозначим их через h и h. Площадь первого треугольника будет равна ^AC•h/₂, а площадь второго треугольника ^AC•h/₂.

Обозначив площадь первого треугольника через S, а площадь второго — через S получим: ^S/_S= ^AC•h/_AC•hили ^S/_S = ^AC/_AC• ^h/_h

Из подобия треугольников АВО и АВО (они подобны, потому что прямоугольные, и, кроме того, имеют по равному острому углу, а именно ∠A = ∠A) следует:

h/_h= ^AB/_AB .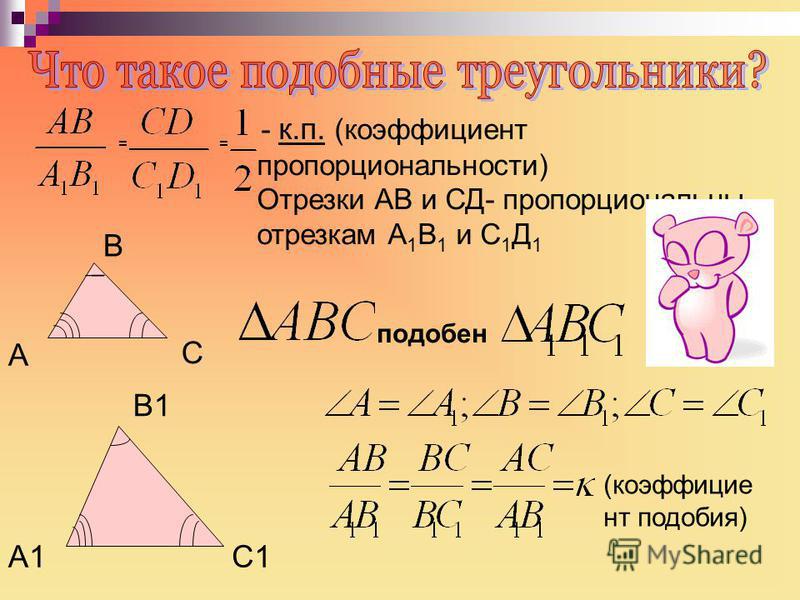 2} $$

Итак, площади подобных треугольников относятся как квадраты сходственных сторон.

Полученную формулу можно преобразовать так: ^S/_S= (^AC/_AC)².

Значит, можно сказать, что отношение площадей двух подобных треугольников равно квадрату отношения их сходственных сторон.

Построение подобных треугольников

Мы уже знаем, что для построения треугольника, подобного данному, достаточно из какой-нибудь точки, взятой на стороне треугольника, провести прямую, параллельную стороне треугольника. Получим треугольник, подобный данному (черт. 382):

$$ triangle AСВ sim triangle AСB $$

Математическая задача: Коэффициент подобия — вопрос № 977, геометрия

Коэффициент подобия двух равносторонних треугольников равен 3,5 (т.е. 7:2). Длина стороны меньшего треугольника равна 2,4 см. Вычислите периметр и площадь большего треугольника.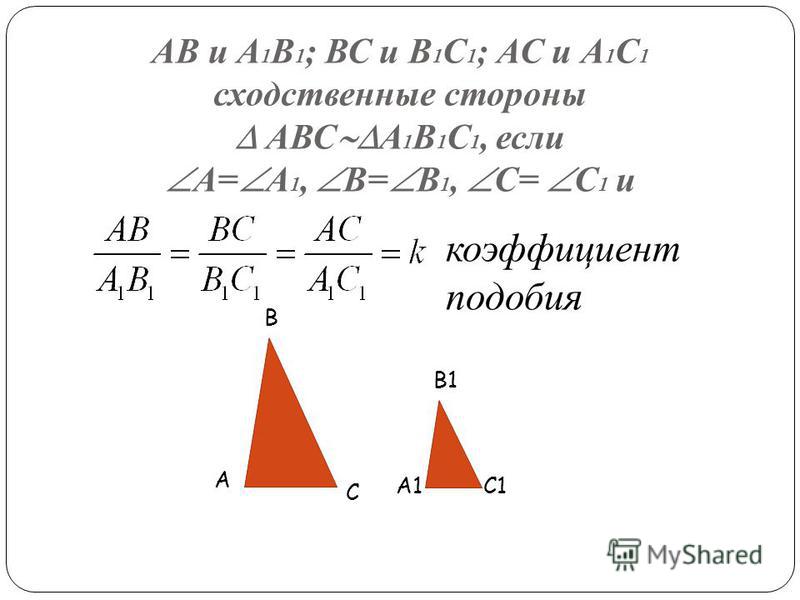

Правильный ответ:

p = 25,2 см
S = 30,55 см ²

Пошаговое объяснение:

p1=3a=2a2−S2=7,2 (а/2)2

=43

а2=2,494 см2 p=3,5⋅p1=3,5⋅7,2=25,2 см

S=3,52⋅S1=3,52⋅2,494=30,55 см2

Попробуйте рассчитать с помощью нашего калькулятора треугольников.

Нашли ошибку или неточность? Не стесняйтесь

пишите нам

. Спасибо!

Советы для связанных онлайн-калькуляторов

Вы хотите преобразовать единицы длины?
Теорема Пифагора является основой для калькулятора прямоугольного треугольника.
Расчет равностороннего треугольника.
См. также наш калькулятор тригонометрического треугольника.

You need to know the following knowledge to solve this word math problem:

geometry
similarity of triangles
arithmetic
square root
multiplication
planimetrics
Pythagorean theorem
площадь фигуры
периметр
треугольник

Единицы физических величин:

длина

Уровень задачи:

практика для 13-летних
практика для 14-летних
старшая школа

Мы рекомендуем вам посмотреть этот видеоурок по этой математической задаче 2 13 900 4 9102: видео Окружность 64104
Треугольник ABC имеет длину окружности 11 см. Треугольник A’B’C’, как и треугольник ABC, имеет длины сторон на 6 см, 120 мм и на 1,5 дм больше, чем у треугольника ABC. Вычислите площадь треугольника A’B’C’.

Длина окружности 42471
Длины сторон треугольника ABC относятся как 4:2:5. Вычислите размер наибольшей стороны подобного треугольника KLM, длина окружности которого равна 66 см.

Равносторонний 6306
Мы составили ромб из четырех равносторонних треугольников со стороной 7 см. Какая у него схема?

Равносторонний 37341
Вычислите периметр и площадь равностороннего треугольника со стороной 20 дм.

Прямоугольная трапеция
Прямоугольная трапеция ABCD с основаниями AB и CD разделена диагональю AC на два равносторонних прямоугольных треугольника. Длина диагонали АС равна 62 см. Вычислите площадь трапеции в квадратных см и подсчитайте, сколько различных периметров

Прямоугольный 40961
Прямоугольный треугольник ABC имеет стороны a = 5 см, b = 8 см. Подобный треугольник A’B’C’ в 2,5 раза меньше.

Вычислите, какой процент от площади треугольника ABC составляет площадь треугольника A’B’C’.

Сечение окружности
Равносторонний треугольник со стороной 33 представляет собой сечение вписанной окружности, центр которого находится в одной из вершин треугольника, а дуга касается противоположной стороны. Вычислить: а) длину дуги б) отношение длины окружности к сектору окружности а

Треугольники
Равносторонний треугольник со стороной 16 см имеет такой же периметр, как и равнобедренный треугольник со стороной 23 см. Вычислите основание x равнобедренного треугольника.

Прямоугольные треугольники
Длины соответствующих сторон двух прямоугольных треугольников относятся как 2:5. При каком отношении медианы относятся к гипотенузе этих прямоугольных треугольников? В каком отношении находятся площади этих треугольников? Меньший прямоугольный треугольник имеет стороны 6 и 8 c

Определить 80754
Периметр треугольника MAK равен 216 мм, сторона a = 81 мм и сторона k = 62 мм.

Определить длину стороны треугольника OSA, если треугольник MAK равен треугольнику OSA.

Подобие 80742
Вычислите периметр треугольника ABC, если известно, что он подобен треугольнику EFG, в котором e=144 мм, f=164 мм, g=92 мм, а коэффициент подобия равен 4. Выразите результат в см.

Подобие 30821
Дан квадрат ABCD со стороной а = 5,3см. Определите размер стороны подобного квадрата, если коэффициент подобия k = 3 см. Вычислите площадь и периметр увеличенного квадрата

Стороны треугольника
Стороны треугольника ABC имеют длину 4 см, 5 см и 7 см. Постройте треугольник A’B’C’, подобный треугольнику ABC, длина окружности которого равна 12 см.

Коэффициент подобия
В треугольнике ТМА длины сторон t = 5 см, m = 3,5 см, а = 6,2 см. Другой подобный треугольник имеет длины сторон 6,65 см, 11,78 см и 9,5 см. Определить коэффициент подобия этих треугольников и приписать друг другу подобные стороны.

Треугольник eq
Рассчитать с точностью до сотых см высоту равностороннего треугольника со стороной 12 см.

Вычислите также его периметр и площадь.

Рассчитать 64444
Длина тени липы 429см. Длина теневого метра 78см. Рассчитайте высоту липы.

Подобные треугольники
Треугольники ABC и XYZ подобны. Найдите недостающие длины сторон треугольников. a) a = 5 см b = 8 см x = 7,5 см z = 9 см b) a = 9 см c = 12 см y = 10 см z = 8 см c) b = 4 см c = 8 см x = 4,5 см z = 6 см

коэффициент подобия треугольников, формула и примеры. Похожие термины, их приведение, примеры

Понятие монома

Определение монома: моном — это алгебраическое выражение, в котором используется только умножение.

Стандартная форма монома

Что такое стандартная форма монома? Одночлен записывается в стандартной форме, если у него на первом месте стоит числовой множитель и этот множитель, он называется коэффициентом одночлена, в одночлене он только один, буквы одночлена расположены в алфавитном порядке и каждая буква встречается только один раз.

Пример монома в стандартной форме:

здесь на первом месте стоит число, коэффициент одночлена, а это число всего одно в нашем одночлене, каждая буква встречается только один раз и буквы расположены в алфавитном порядке, в данном случае это латиница.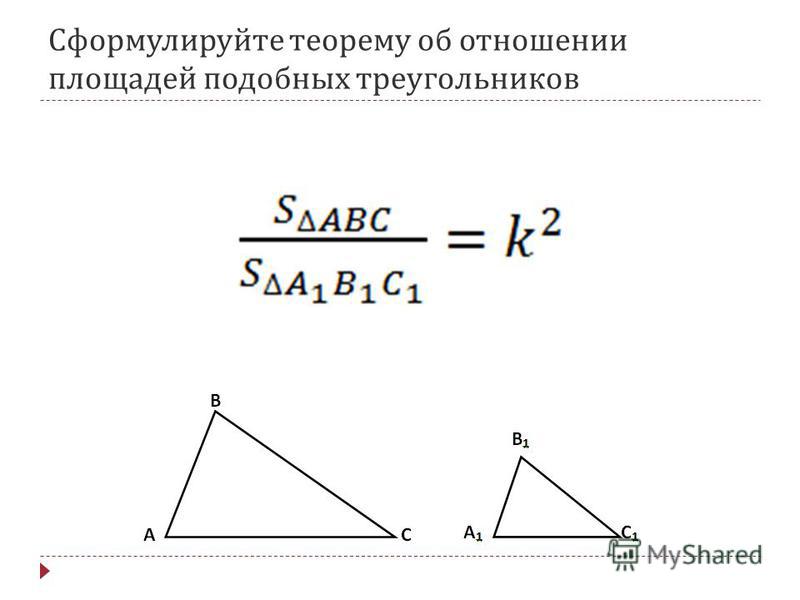

Еще один пример одночлена стандартной формы:

каждая буква встречается только один раз, они расположены в латинском алфавитном порядке, но где коэффициент у монома, т.е. числовой множитель, который должен стоять первым? Здесь он равен единице: 1адм.

Может ли мономиальный коэффициент быть отрицательным? Да, может быть, пример: -5а.

Может ли мономиальный коэффициент быть дробным? Да, может быть, пример: 5.2а.

Если моном состоит только из цифры, т.е. не имеет букв, как привести его к стандартному виду? Любой моном, который является числом, уже находится в стандартной форме, например: число 5 является мономом стандартной формы.

Приведение одночлена к стандартному виду

Как привести одночлен к стандартному виду? Рассмотрим примеры.

Пусть задан моном 2a4b, нам нужно привести его к стандартному виду. Умножаем два его числовых множителя и получаем 8ab. Теперь моном записывается в стандартной форме, т.е. имеет только один числовой множитель, пишется первым, каждая буква в мономе встречается только один раз, и эти буквы расположены в алфавитном порядке. Итак, 2a4b = 8ab.

Дано: одночлен 2a4a, приведите одночлен к стандартному виду. Перемножаем числа 2 и 4, произведение аа заменяем на вторую степень а 2 . Получаем: 8а 2 . Это стандартная форма этого монома. Итак, 2а4а = 8а 2 .

Подобные мономы

Что такое подобные мономы? Если одночлены различаются только коэффициентами или равны, то они называются подобными.

Пример подобных мономов: 5а и 2а. Эти мономы различаются только коэффициентами, значит, они подобны.

Одночлены 5abc и 10cba подобны? Приводим второй одночлен к стандартному виду, получаем 10abc. Теперь ясно, что мономы 5abc и 10abc отличаются только своими коэффициентами, а значит, они подобны.

Сложение одночленов

Какова сумма одночленов? Мы можем только суммировать подобные одночлены. Рассмотрим пример сложения мономов. Чему равна сумма мономов 5а и 2а? Суммой этих мономов будет аналогичный им моном, коэффициент которого равен сумме коэффициентов при слагаемых. Итак, сумма мономов равна 5а + 2а = 7а.

Еще примеры сложения мономов:

2а 2 + 3а 2 = 5а 2
2а 2 b 3 с 4 + 3а 2 b 3 с 4 = 5а 2 b 3 с 4

Снова. Вы можете добавлять только похожие мономы; сложение сводится к сложению их коэффициентов.

Вычитание одночленов

Чем отличаются одночлены? Мы можем вычитать только одинаковые одночлены. Рассмотрим пример вычитания одночленов. В чем разница между мономами 5а и 2а? Разностью этих мономов будет аналогичный им моном, коэффициент которого равен разности коэффициентов этих мономов. Итак, разность мономов равна 5а — 2а = 3а.

Другие примеры вычитания одночленов:

10a2 — 3a2 = 7a2
5a 2 b 3 c 4 — 3a 2 b 3 c 4 = 2a 2 b 3 c 4

Умножение одночленов

Что такое произведение одночленов? Рассмотрим пример:

т.е. произведение мономов равно моному, множители которого составлены из множителей исходных мономов.

Другой пример:

2a 2 b 3 * a 5 b 9 = 2a 7 b 12 .

Как появился этот результат? Каждый фактор имеет «а» в степени: в первом – «а» в степени 2, а во втором – «а» в степени 5. Это означает, что произведение будет иметь «а» в степени из 7, потому что при умножении одинаковых букв их степени складываются:

А 2 * а 5 = а 7 .

То же самое относится к фактору «b».

Коэффициент первого множителя равен двум, а второго — единице, поэтому в результате получаем 2 * 1 = 2.

Вот как был рассчитан результат 2a 7 b 12.

Из этих примеров видно, что коэффициенты одночленов перемножаются, а одинаковые буквы заменяются суммами их степеней в произведении.

Есть. В этой статье мы дадим определение однородным слагаемым, разберемся, что называется приведением однородных слагаемых, рассмотрим правила, по которым выполняется это действие, и приведем примеры сокращения однородных слагаемых с подробным описанием решения.

Навигация по страницам.

Определение и примеры подобных терминов.

Разговор о таких терминах возникает после знакомства с буквенными выражениями, когда возникает необходимость проводить с ними преобразования. Согласно учебникам математики Н.Я. Виленкин определение подобных терминов дается в 6 классе и имеет следующую редакцию:

Определение.

Похожие термины — термины, имеющие одинаковую буквенную часть.

Следует внимательно рассмотреть это определение. Во-первых, речь идет о терминах, а, как известно, термины являются составными элементами сумм. Это означает, что такие термины могут присутствовать только в выражениях, являющихся суммами. Во-вторых, в озвученном определении таких терминов присутствует незнакомое понятие «буквальная часть». Что понимается под буквенной частью? Когда это определение дается в шестом классе, буквенная часть относится к одной букве (переменной) или произведению нескольких букв. В-третьих, остается вопрос: «Что это за термины с буквенной частью»? Это слагаемые, являющиеся произведением определенного числа, так называемого числового коэффициента, и буквенной части.

Теперь можно привести примеров похожих терминов .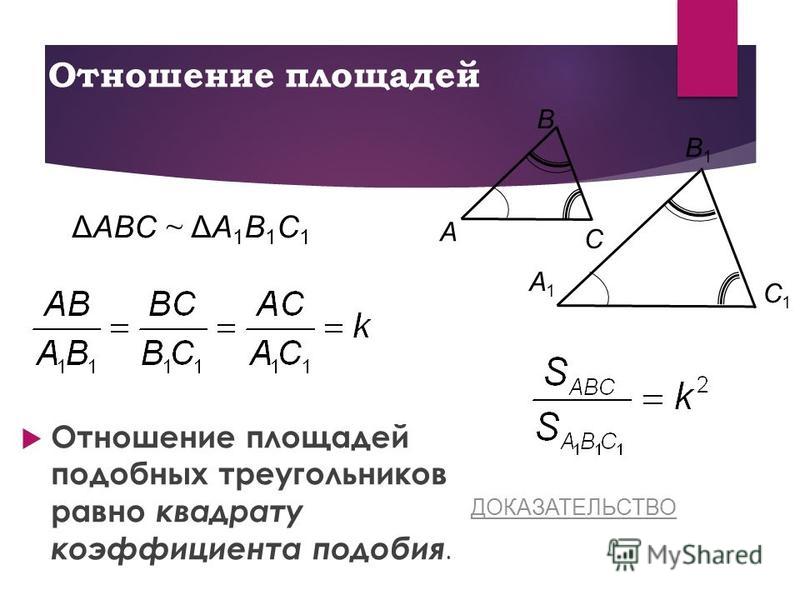 Рассмотрим сумму двух термов 3·a и 2·a вида 3·a+2·a . Слагаемые в этой сумме имеют одинаковую буквенную часть, которая обозначается буквой а, поэтому по определению эти слагаемые подобны. Числовыми коэффициентами этих подобных членов являются числа 3 и 2 .

Другой пример: в сумме 5 x y 3 z+12 x y 3 z+1 члены 5·x·y 3 ·z и 12·x·y 3 ·z с одной и той же буквенной частью x·y 3 ·z подобны. Заметим, что y 3 присутствует в буквальной части, его наличие не нарушает данного выше определения буквальной части, так как оно, по сути, является произведением y·y·y .

Отдельно отметим, что числовые коэффициенты 1 и −1 для таких термов часто явно не выписываются. Например, в сумме 3 z 5 +z 5 −z 5 все три члена 3 z 5 , z 5 и −z 5 подобны, имеют одинаковую буквенную часть z 5 и коэффициенты 3 , 1 и −1 соответственно при которые 1 и -1 не видны отчетливо.

Исходя из этого, в сумме 5+7 x−4+2 x+y подобными членами являются не только 7 x и 2 x, но и члены без буквенной части 5 и −4 .

В дальнейшем расширяется и понятие буквальной части — буквенной частью я начинаю считать не просто произведение букв, а произвольное буквальное выражение.

Например, в учебнике алгебры для 8 класса авторов Ю. Н. Макарычева, Н. Г. Миндюка, К. И. Нешкова, С. Б. Суворова, под редакцией С. А. Теляковского, приводится сумма формы, и говорится, что ее составляющие члены подобны. Общая литеральная часть этих подобных терминов – это выражение с корнем вида .

Аналогично подобными членами в выражении 4 (x 2 +x−1/x)−0,5 (x 2 +x−1/x)−1 можно считать члены 4 (x 2 +x−1/x) и −0,5 (x 2 +x−1/x) , так как они имеют одинаковую буквенную часть (x 2 +x−1/x) .

Обобщая всю изложенную выше информацию, можно дать следующее определение подобных терминов.

Определение.

Подобными терминами называются термины в буквальном выражении, имеющие одинаковую буквенную часть, а также термины, не имеющие буквенной части, где под буквенной частью понимается любое буквальное выражение.

Отдельно скажем, что подобные термины могут быть одинаковыми (когда их числовые коэффициенты равны), а могут быть разными (когда их числовые коэффициенты различны).

В заключение этого абзаца обсудим один очень тонкий момент. Рассмотрим выражение 2 x y+3 y x . Похожи ли члены 2 x y и 3 y x? Этот вопрос можно сформулировать и так: «Один и тот же литеральный элемент x y и y x указанных терминов»? Порядок буквенных множителей в них разный, так что на самом деле они не совпадают, поэтому термы 2·x·y и 3·y·x в свете введенного выше определения не подобны.

Однако довольно часто такие термины называют похожими терминами (но для строгости лучше этого не делать). В этом случае они руководствуются следующим: согласно перестановке множителей в произведении она не влияет на результат, поэтому исходное выражение 2 x y+3 y x можно переписать как 2 x y+3 x y , условия которых аналогичны. То есть, когда говорят о подобных термах 2 x y и 3 y x в выражении 2 x y+3 y x , то имеют в виду термы 2 x y и 3 x y в преобразованном выражении вида 2 x y+3 x y .

Приведение подобных терминов, правило, примеры

Преобразование выражений, содержащих похожие термины, подразумевает добавление этих терминов. Это действие имеет специальное название — приведение подобных терминов .

Приведение однотипных терминов осуществляется в три этапа:

сначала переставляются термины так, чтобы похожие термины находились рядом друг с другом;
после этого буквенная часть подобных терминов выносится за скобки;
, наконец, вычисляется значение числового выражения, заключенного в скобки.

Разберем записанные шаги на примере. Приведем аналогичные члены в выражении 3 x y+1+5 x y . Во-первых, мы переставляем члены так, чтобы одинаковые члены 3 x y и 5 x y находились рядом друг с другом: 3 x y+1+5 x y=3 x y+5 x y+1. Во-вторых, выносим буквальную часть скобок, получаем выражение x·y·(3+5)+1 . В-третьих, вычисляем значение выражения, которое образовалось в скобках: x·y·(3+5)+1=x·y·8+1 . Поскольку числовой коэффициент принято писать перед буквенной частью, перенесем его на это место: x·y·8+1=8·x·y+1. На этом приведение подобных членов закончено.

Для удобства три вышеописанных шага объединены в правило приведения подобных терминов : чтобы привести похожие термины, нужно сложить их коэффициенты и умножить результат на буквенную часть (если есть).

Решение предыдущего примера по правилу приведения однородных членов будет короче. Приведем его. Коэффициентами подобных членов 3 x y и 5 x y в выражении 3 x y+1+5 x y являются числа 3 и 5, их сумма равна 8, умножив ее на буквенную часть x y , получим результат сокращения этих членов 8·х·у . Осталось не забыть про член 1 в исходном выражении, в итоге имеем 3 x y+1+5 x y=8 x y+1 .

Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. Теорема (второй критерий равенства треугольников). Если два угла одного треугольника соответственно равны двум углам другого, то эти треугольники подобны. Подобными треугольниками называются, у которых углы равны, а подобные стороны пропорциональны: , где — коэффициент подобия.

Примеры применения этого следствия см.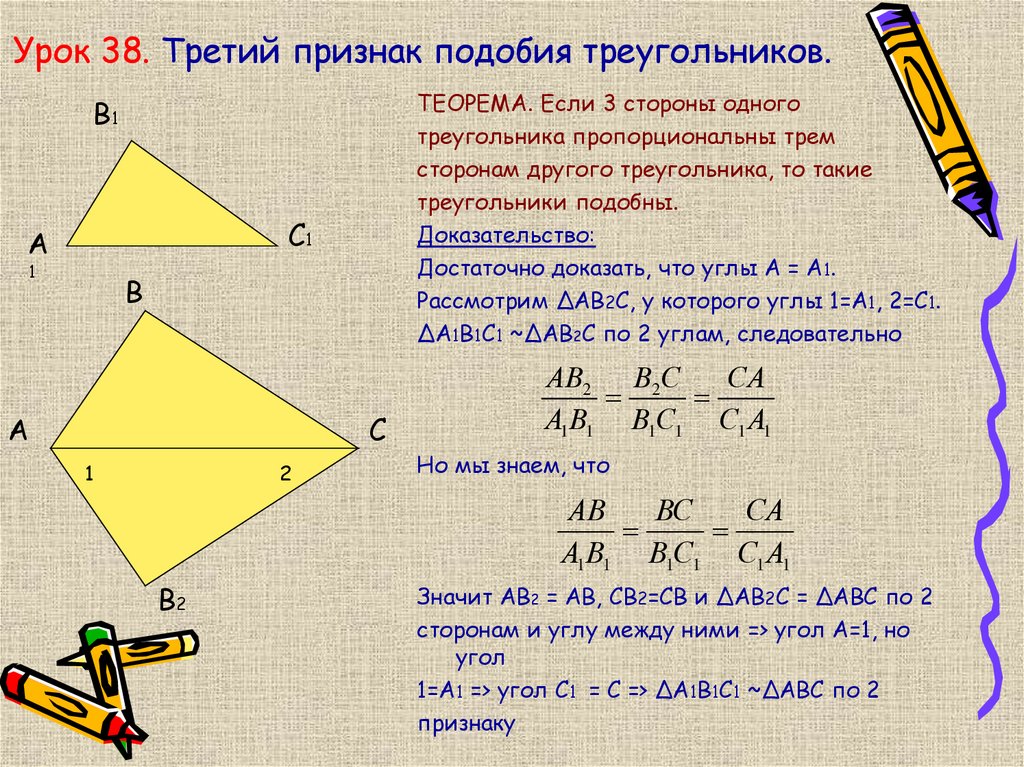 ниже в разделах: «Примеры подобных треугольников» и «Свойства параллельности (антипараллельности) сторон связанных треугольников». Поэтому, например, ортотреугольник ортотреугольника и исходный треугольник подобны, как треугольники с параллельными сторонами. Точки, не лежащие на одной прямой, при любом сходстве переходят в точки, не лежащие на одной прямой. Подобие называется правильным (неправильным), если движение D(displaystyle D) является правильным (неправильным).

В таких треугольниках важное место занимает понятие соотношения отрезков. Треугольники в чем-то похожи. Для установления подобия треугольников необходимо установить справедливость шести равенств (углов и отношений сторон), но сделать это не всегда удается. Всего сходства три. Объяснение: площадь треугольника — это произведение двух линейных элементов — стороны и высоты.

Нам дан периметр треугольника, мы можем найти периметр треугольника, так как нам даны длины его сторон, значит мы найдем коэффициент подобия и определим искомые длины сторон.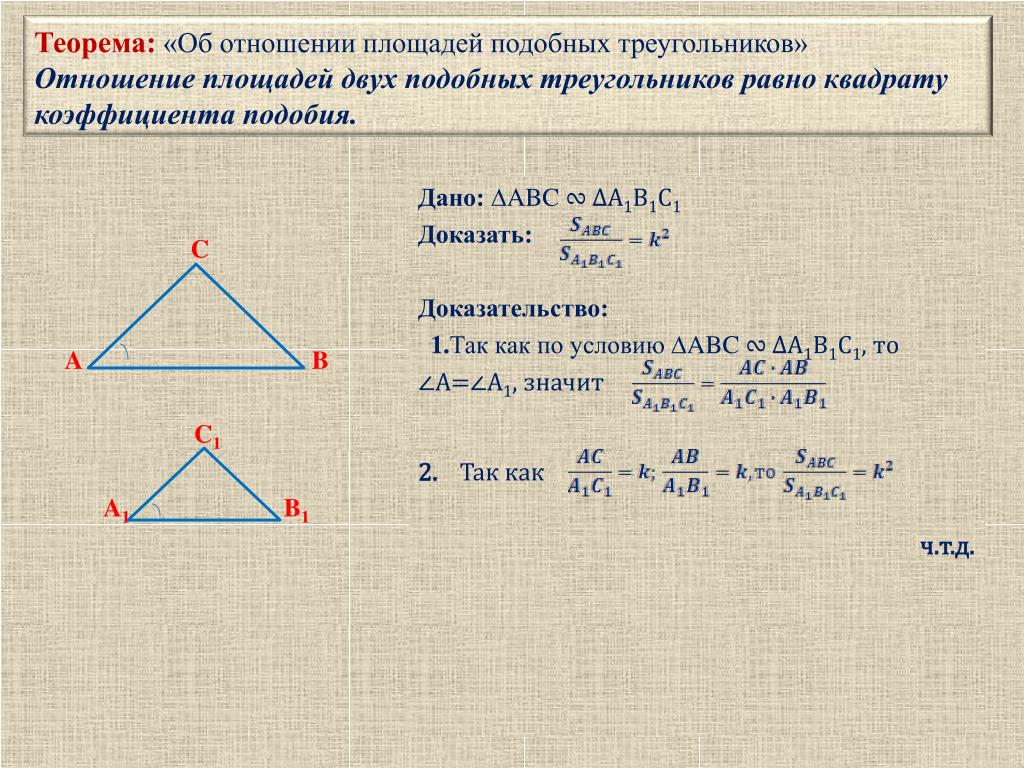 Коэффициент подобия выражает пропорциональность, это отношение длин сторон одного треугольника к таким же сторонам другого: k = AB/A’B’= BC/B’C’ = AC/A’C’.

Найдите отношение подобных сторон, которое и будет коэффициентом подобия

Например, в задаче даны подобные треугольники и даны длины их сторон. Так как треугольники подобны по условию, найдите их равные стороны. Разделите значения площадей подобных треугольников один на один и из полученного результата извлеките квадратный корень. Отношения периметров, длин медиан, медиатрис, построенных на подобных сторонах, равны коэффициенту подобия.

Законы подобия — в аэродинамике

Согласно теореме синусов для любого треугольника отношения сторон к синусам противоположных углов равны диаметру описанной вокруг него окружности. Используйте аналогичный способ, чтобы найти коэффициент, если у вас есть окружности, вписанные в подобные треугольники с известными радиусами.

Собственное подобие сохраняет ориентацию фигур, а несобственное — меняет ориентацию на противоположную.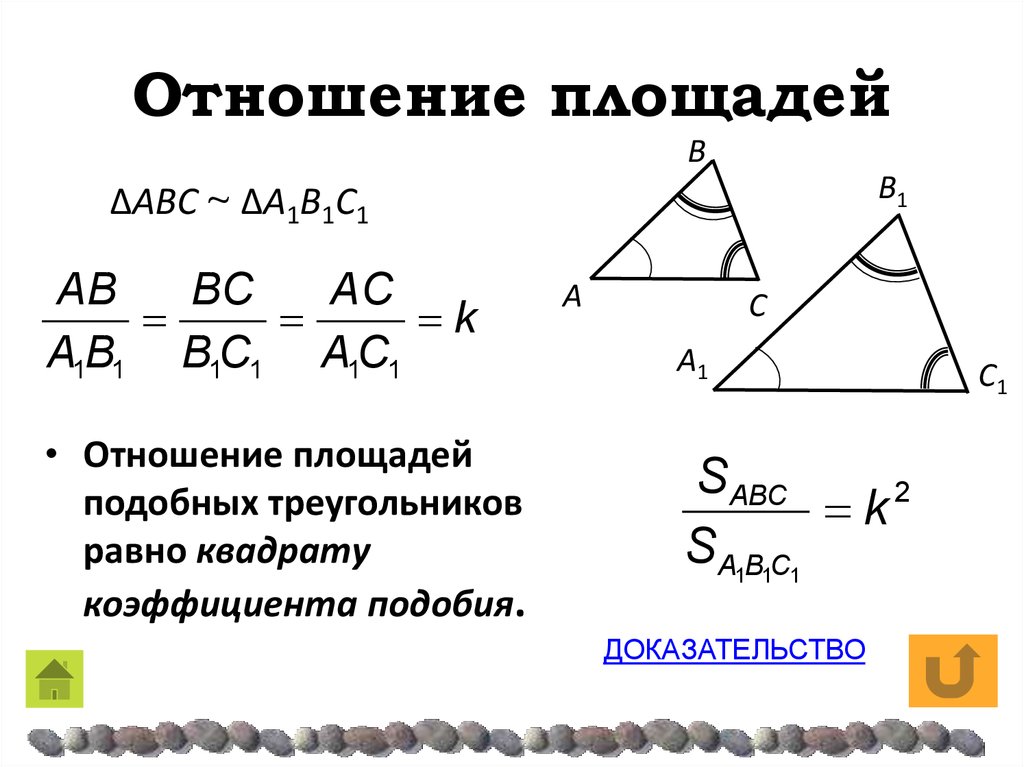 Подобие определяется аналогично (с сохранением указанных выше свойств) в 3-мерном евклидовом пространстве, а также в n-мерном евклидовом и псевдоевклидовом пространствах. Подобные стороны в треугольниках противолежащие равным углам. Коэффициент подобия можно найти разными способами. Для этого запишите длины сторон одной и другой в порядке возрастания.

Вы можете рассчитать коэффициент подобия треугольников, если знаете их площади. Если вы разделите длину биссектрисы или высоты, проведенной из одних и тех же углов, вы также получите коэффициент подобия.

Используйте это свойство для нахождения коэффициента, если эти значения приведены в условии задачи

Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. Коэффициент подобия k равен отношению соответствующих линейных размеров фигур F и Следовательно, площади подобных фигур связаны как квадраты их соответствующих линейных размеров. Мы выяснили, что равенство треугольников является частным случаем подобия.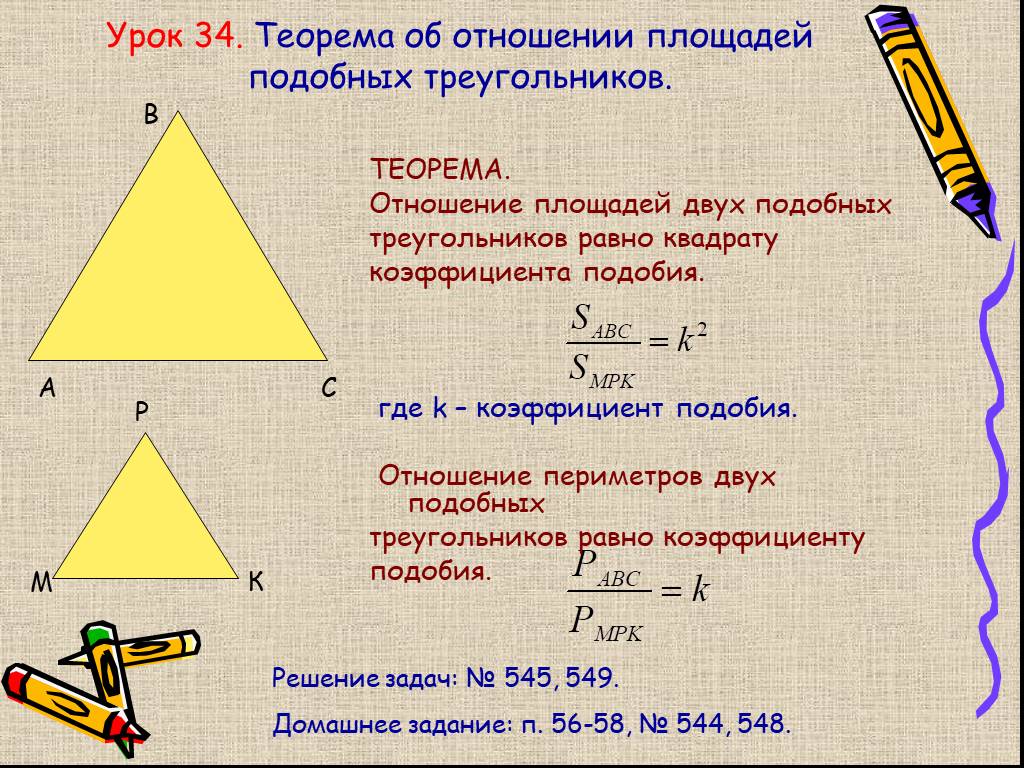

Под множителем понимают любое число, на которое данное делится без остатка. То есть это число, которое точно показывает, сколько раз повторять другое число, которое называется множителем, как член. Результат таких математических расчетов называется произведением. Если множителей в примере несколько, то они нумеруются и называются, соответственно, «первый множитель», «второй множитель» и т. д.

Существует также понятие «множитель», где он используется как неотъемлемая часть сложные формулы. Итак, множитель Ланде является составной частью формулы расщепления энергетических уровней в магнитном поле.

Высшее использует понятие «интегрирующий множитель», т. е. , после умножения на которое часть дифференциального уравнения превращается в полный дифференциал некоторой функции.

В экономической теории существует понятие коэффициента дисконтирования, введенного (мультипликатор дисконтирования) как расчетный показатель для долгосрочных денежных операций. В частности, он используется для определения суммы, вложенной для получения желаемого дохода через определенный период времени.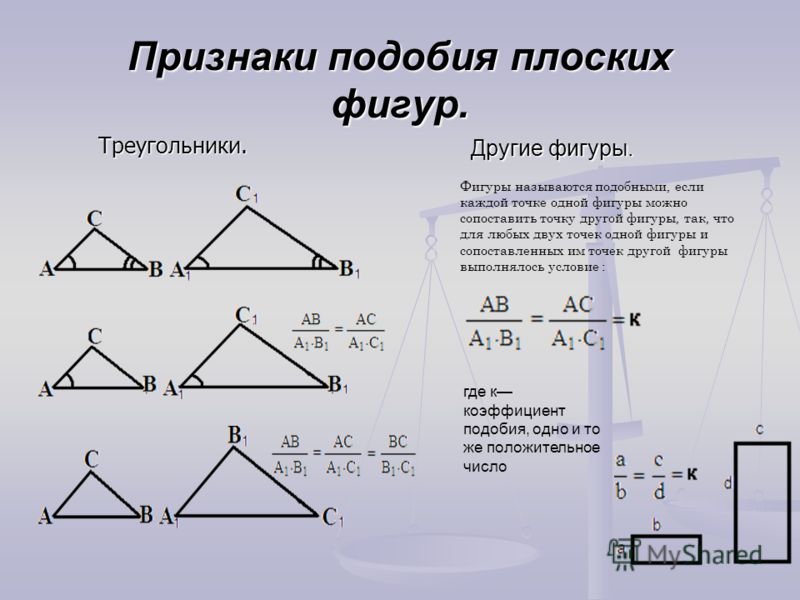 Одна и та же концепция используется как страховыми компаниями, так и аудиторами в перспективных оценках, анализе затрат и инвестиционных рисков.

Из математики «множитель» также заимствован специалистами в области линейного программирования, которые используют множители Лагранжа (множители Лагранжа) для проверки оптимальности допустимого решения целевой функции. Обозначается греческой буквой «» и используется при решении теоретических задач на условный экстремум.

«Работа» — еще один пример слова, имеющего несколько значений или, с научной точки зрения, омонимов. Его используют в разных областях — от математики до юриспруденции.

Инструкция

В m называют результат умножения двух или более чисел или переменных вместе. Одни и те же числа, которые перемножаются, называются множителями или факторами. Многие физические величины с точки зрения являются произведениями других физических величин. Например, мощность есть произведение напряжения и тока или времени и энергии, а напряжение, в свою очередь, может быть рассчитано как произведение тока и сопротивления.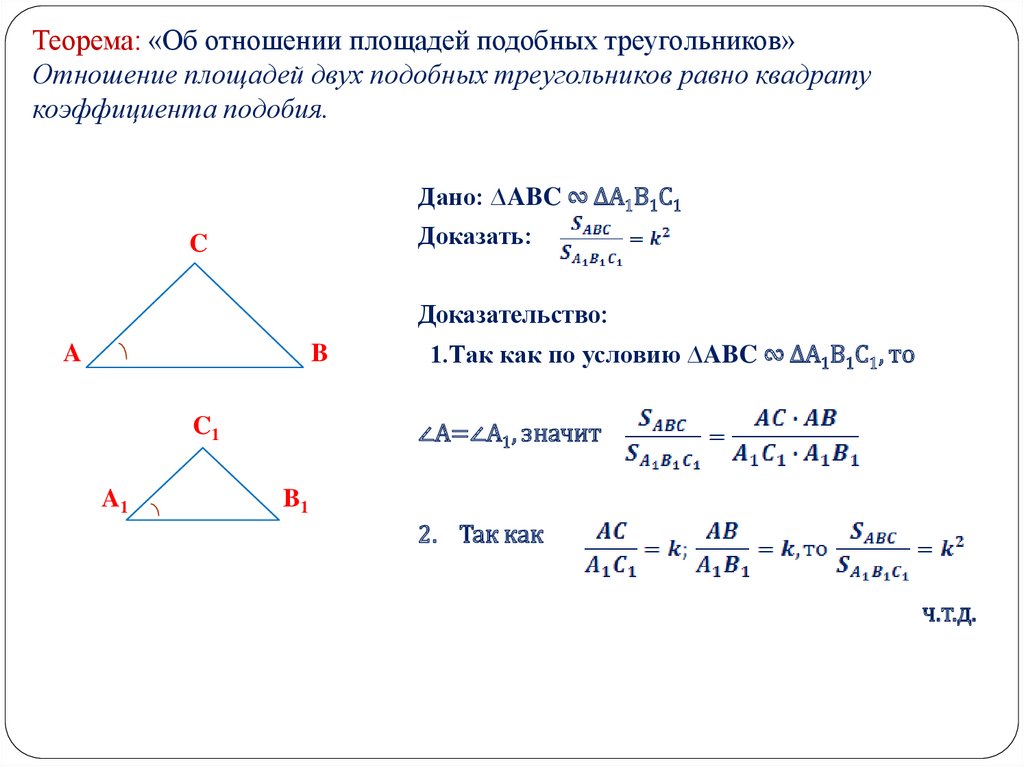 Обратной операцией умножения является деление. Если произведение разделить на один из коэффициентов, получится другой.

Иногда термин «работа» используется как синоним термина «реализация». Например, в военном деле иногда встречается оборот «производство выстрела». Но все равно говорят и пишут очень редко. А вот «производить» как синоним «осуществлять» употребляется гораздо чаще.

Произведение относится к одному из видов объектов интеллектуальной собственности. Работы защищены так называемым авторским правом. Они делятся на три типа: произведения науки, литературы и искусства. Все они охраняются на один и тот же срок: в течение всей жизни автора и через семьдесят лет после его смерти. Право на произведение может передаваться по наследству, и тогда наследники становятся правообладателями. Если произведение содержит описание каких-либо практических действий, то реализация этого описания на практике не считается использованием произведения (этим авторское право отличается от патентного права). Но его использованием считаются такие действия, как воспроизведение (в юридическом смысле слова так называется только копирование), публичный показ и исполнение в эфире и по кабелю, создание производных произведений, перевод на другой язык, как а также так называемое доведение до всеобщего сведения, то есть, говоря простым языком, выкладывание в Интернет или иную телекоммуникационную сеть. В для обозначения произведения в юридическом смысле слова используется термин произведение — буквально «произведение».

Видео по теме

Источники:

математические работы

— вложение денег в бизнес с целью получения дополнительной прибыли. Как правило, инвестор стремится получить как можно больше информации о проекте. Именно для этого вложение марки .

Инвестиции класс представляет собой изучение и анализ проекта, стоимости и экономической эффективности. Данная процедура проводится при поиске новых инвесторов, при страховании рисков, а также анализ проводится в случае развития какого-либо инвестиционного проекта.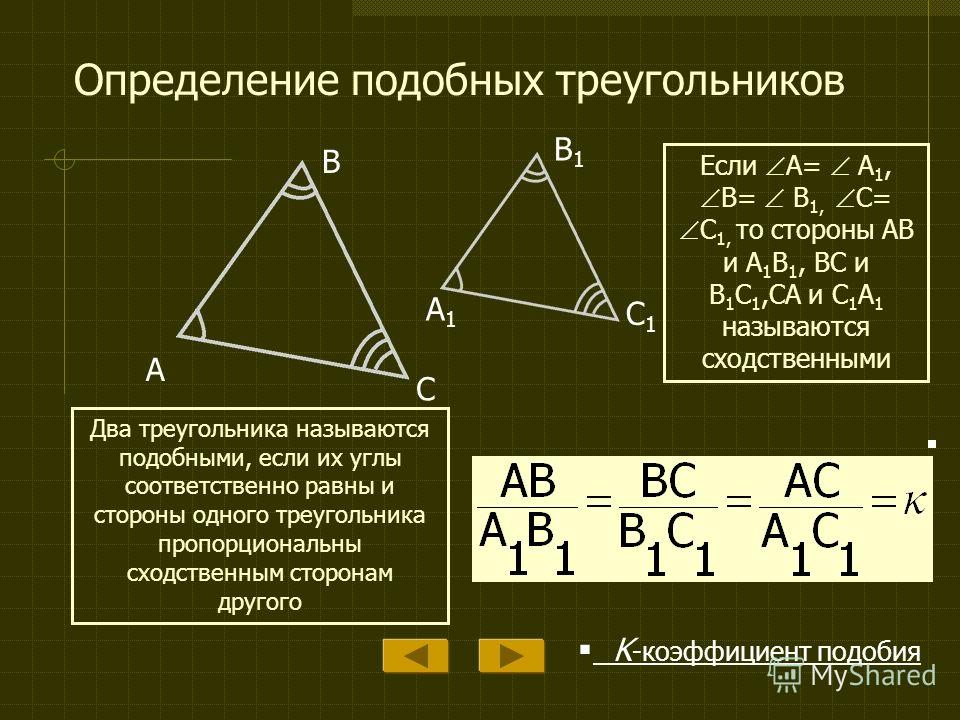 Оценка может осуществляться по нескольким факторам, например, оценивается на рынке, то есть по рыночной стоимости. Оценить проект может новый акционер, а также лизинговая компания или банк, например, в случае кредита. В некоторых случаях государство прибегает к оценке инвестиций частных предприятий, например, когда планируется финансовая поддержка. Часто государство финансирует сельскохозяйственные предприятия. Кто проводит анализ инвестиционного проекта? Для этого существуют специальные компании, в штате которых есть оценщики. В некоторых крупных организациях работает профессионал, который постоянно оценивает и анализирует финансовый рынок, следит за стоимостью и прибыльностью проекта. Все данные фиксируются и предоставляются управляющему, который впоследствии привлекает инвесторов. Есть показатели, что класс инвестиции: — показатель рентабельности — показывает эффективность проекта. Для его расчета нужно разделить реальную величину денежных потоков на сумму всех вложенных инвестиций; — время — показывает минимальное время, через которое вложения принесут желаемый доход; — внутренняя норма доходности — показывает ставку дисконтирования (норма доходности), при которой величина дохода от инвестиций равна сумме средств, вложенных в проект; — чистый дисконтированный доход — показывает сумму ожидаемого дохода от проекта, которая приведена к начальному моменту времени.

В математической науке существует множество разновидностей чисел: натуральные, простые, положительные, отрицательные, составные и ряд других, которые постепенно усваиваются при усвоении школьного курса математики. Особое внимание следует уделить составным числам.

Составное число — это число, которое делится не только на единицу и само на себя, но и на ряд других делителей и. Примеры составных чисел: 4, 8, 24, 39 и т. д. Этот ряд можно продолжать до бесконечности. Составные числа являются разновидностью натуральных чисел.

Натуральные числа — это все без исключения числа после единицы, которые появляются сами по себе при перечислении различных предметов (например, на улице 14 домов, в 149000 и т. д.). Все натуральные числа являются целыми числами (т. е. такими числами, которые не содержат дробей).

Другими словами, все натуральные числа делятся на простые и . Существует базовая арифметика простых чисел, смысл которой в том, что любое составное число можно вычислить с помощью произведения двух простых чисел, причем единственно возможным способом. Например, число 21 натуральное и составное. Оно получается путем умножения трех и семи. 3 и 7 — простые числа.

Простые и составные числа имеют взаимосвязанные свойства:
— Пусть а будет составным числом. Тогда оно обязательно имеет хотя бы один простой делитель n, который при возведении во вторую степень был бы меньше или равен составному числу. Например, число 48 делится на 3. Три во второй степени становится девятью, а 9 меньше 48.
— Пусть числа а и b простые. Тогда, если они имеют наибольший общий делитель, который не будет превышать 1, то такие числа будем называть взаимно простыми. Это, например, 3 и 7, 11 и 19и т. д.
— Произведение наибольшего общего делителя и наименьшего общего кратного двух простых чисел всегда является произведением этих двух чисел.

0 и 1 стоят особняком в ряду всех простых чисел. Единицу можно назвать простым числом только потому, что она получается нулевым произведением количества простых чисел.

Видео по теме

Разблокировка множителя используется при разгоне процессоров.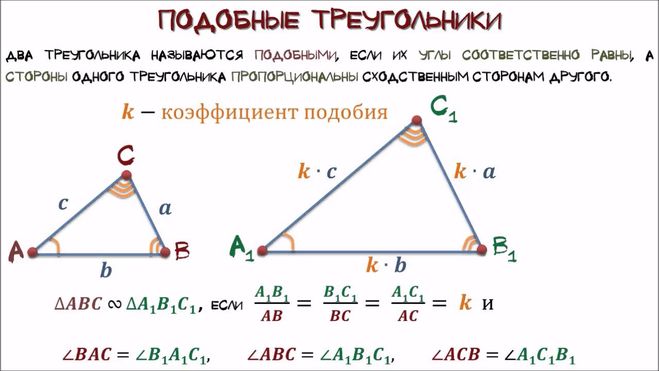 Все платы поддерживают выбираемые множители, поэтому вам нужно закоротить определенные контакты на процессоре, чтобы изменить этот параметр.

Вам понадобится

— компьютер;
— Навыки работы с электроникой.

Инструкция

Разобрать системный блок и вытащить процессор для разблокировки множителя. Найдите на нем мосты. Посмотрите на них внимательно. Между двумя точками, которые необходимо соединить, чтобы замкнуть контакты, имеется паз. В нем можно увидеть тонкий медный налет.

Если замкнуть перемычки карандашом или припоем, то вы так же замкнёте медную подложку, и в результате процессор будет очень сложно вернуть к жизни. Поэтому самое главное в замыкании умножителя — замкнуть перемычки так, чтобы не задеть медное покрытие.

Заполните канавки диэлектриком, в качестве него можно использовать суперклей. Будьте очень осторожны при этом, потому что клей не должен попасть на контактную площадку моста, а канавка должна быть полностью заполнена, чтобы обеспечить лучшую изоляцию.

Источник

Как найти коэффициент подобия треугольников

Подобные фигуры – это фигуры, одинаковые по форме, но разные по размеру.Треугольники являются подобными, если их углы равны, а стороны пропорциональны друг другу. Существуют также три признака, позволяющих определить подобие без соблюдения всех условий. Признак первый – у подобных треугольников два угла одного равны двум углам другого. Второй признак подобия треугольников — две стороны одного пропорциональны двум сторонам другого, а углы между этими сторонами у них равны. Третий признак подобия – это пропорциональность трех сторон одного трем сторонам другого.

Вам понадобится

— ручка;
— бумага для записей.

Инструкция

Коэффициент подобия выражает пропорциональность, это отношение длин сторон одного треугольника к сходственным сторонам другого: k = AB/A’B’= BC/B’C’ = AC/A’C’. Сходственные стороны в треугольниках находятся напротив равных углов. Коэффициент подобия можно найти разными способами.

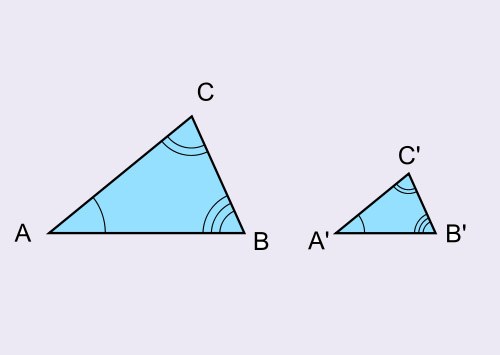
Например, в задании даны подобные треугольники и приведены длины их сторон. Требуется найти коэффициент подобия. Поскольку треугольники подобны по условию, найдите их сходственные стороны. Для этого запишите длины сторон одного и другого по возрастанию. Найдите отношение сходственных сторон, которое будет коэффициентом подобия.

Вы можете вычислить коэффициент подобия треугольников, если вам известны их площади. Одно из свойств подобных треугольников гласит, что отношение их площадей равняется квадрату коэффициента подобия. Разделите значения площадей подобных треугольников одно на другое и извлеките квадратный корень из результата.

Отношения периметров, длин медиан, медиатрис, построенных к сходственным сторонам, равны коэффициенту подобия. Если разделить длину биссектрис или высот, проведенных из одинаковых углов, вы также получите коэффициент подобия. Воспользуйтесь этим свойством для нахождения коэффициента, если в условии задачи даны эти величины.

По теореме синусов для любого треугольника отношения сторон к синусам противолежащих углов равны диаметру описанной вокруг него окружности. Из этого вытекает, что у подобных треугольников отношение радиусов или диаметров описанных окружностей равно коэффициенту подобия. Если в задаче известны радиусы этих окружностей, или их можно вычислить из площадей кругов, найдите коэффициент подобия этим путем.

Используйте аналогичный путь для нахождения коэффициента, если у вас имеются вписанные в подобные треугольники окружности с известными радиусами.

Источники:

как найти отношение сторон
Ритмичность работы предприятия

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник