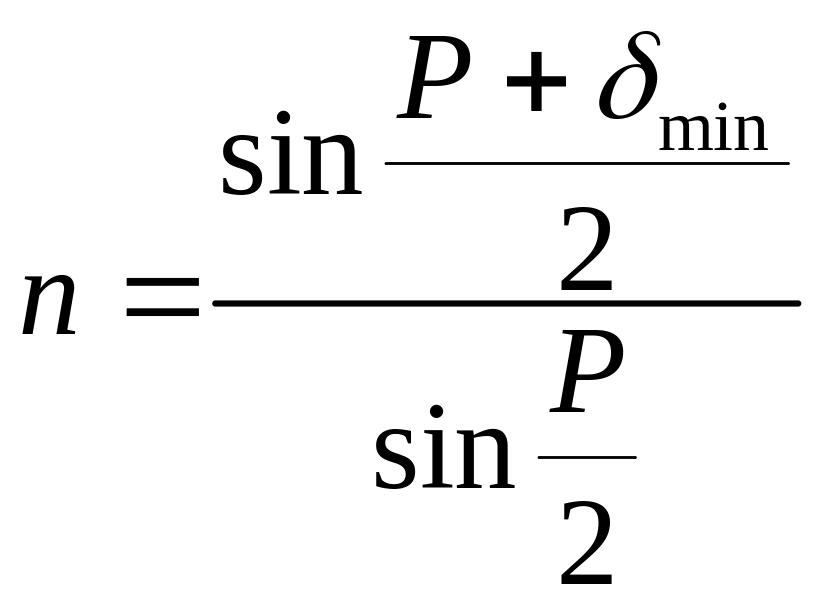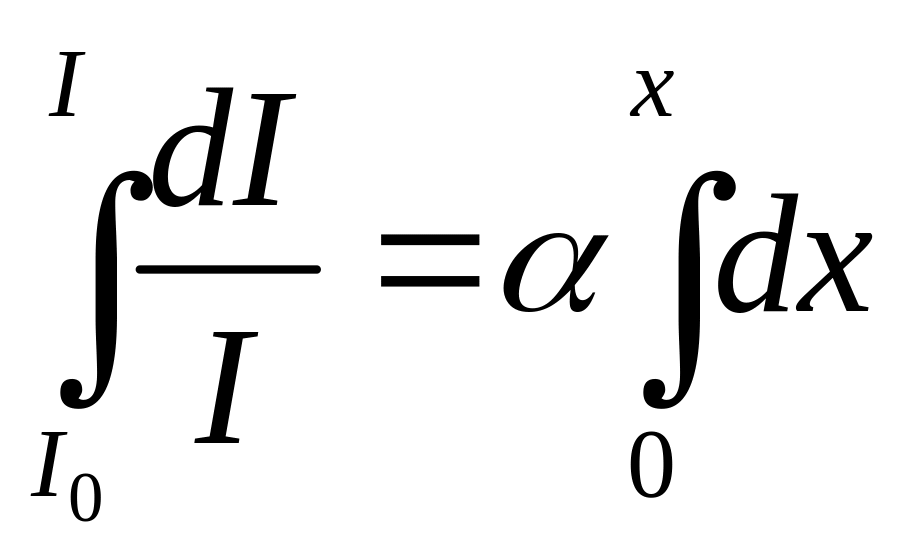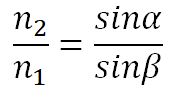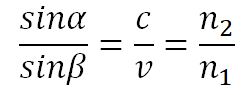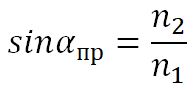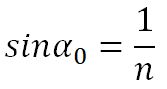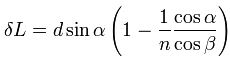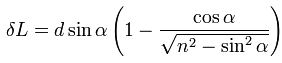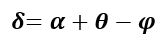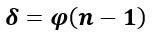Показатель преломления призмы.
Если
луч света переходит из одной среды в
другую, то на границе радела этих сред
он претерпевает преломление. При
преломлении
света выполняются следующие законы:
1. Падающий
и преломленный лучи, и перпендикуляр,
восстановленный
к границе раздела двух сред в точке
падения луча, лежат в одной
плоскости.
2
.
Отношение синуса угла падения к синусу
угла преломления для данных
двух сред есть величина постоянная, и
называется относительным
показателем преломления второй среды
относительно первой (рис.4).
(7)
Если
луч падает из вакуума в данную
среду, то показатель преломления
данной среды относительно
вакуума называется абсолютным
показателем преломления.
Показатель преломления зависит
от длины волны падающего света.
Законы
преломления света дают возможность
построить ход луча через
призму.
Пусть
ABC
есть сечение трехгранной призмы
плоскостью, перпендикулярной
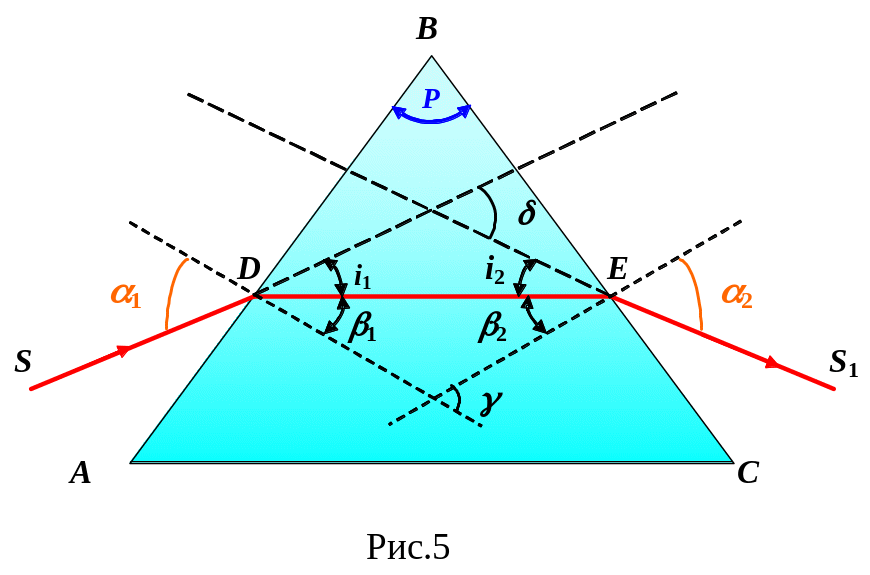
к обеим преломляющим поверхностям (рис.
5). На рис. 5 изображен ход монохроматического
луча через призму. Для этого луча угол
Р
является преломляющим углом призмы.
Луч S
падает на грань АВ
призмы под углом α1.
В точке D
он преломляется в сторону
основания АС
и пойдет внутри призмы по направление
DE,
образуя угол преломления β1.
В
стретив
грань ВС
под углом падения β2,
луч вторично преломится в сторону
основания и выйдет из призмы под углом
преломления
α2
в направлении ES1.
Угол между
направлениями падающего и выходящего
лучей называется углом отклонения δ.
Из построения видно, что:
|
; ; ; |
(8) |
Из соотношения
(8) для угла δ
имеем
|
|
(9) |
Величина угла
отклонения δ
зависит от преломляющего угла призмы
Р
и показателя преломления призмы.
При заданном угле
преломления Р
и показателя преломления n
угол
δ
зависит от угла падения α1
на первую преломляющую
грань.
Если угол падения α1
таков, что преломляющийся луч DE
проходит
внутри призмы перпендикулярно биссектрисе
преломляющего угла
Р,
то угол δ
будет
иметь наименьшее значение. При AB
= BC
луч
DE
проходит через призму параллельно
основанию AC
призмы.
Тогда,
очевидно, α1
=
α2
и β1
=
β2.
Следовательно, из (9) для угла δ
имеем:
|
|
(10) |
а
преломляющий угол Р
из соотношения (8) будет равен:
|
|
(11) |
Если
значение α1
из (10) и β1
из (11) подставить в формулу (7), выражающую
закон преломления, то окончательно
будем иметь:
|
|
(12) |
Формула
(12) является расчетной. Она дает возможность
определить показатель
преломления n
призмы, зная величину преломляющего
угла
Р
(угол Р
обычно равен 450
либо 60°) и измерив с помощью гониометра
наименьший угол отклонения луча
для
любого из семи
основных цветов в сплошном спектре.
Поглощение света.
При прохождении
электромагнитной волны (света) через
вещество
часть энергии волны затрачивается на
возбуждение колебаний электронов,
находящихся внутри атомов вещества.
Частично эта энергия вновь возвращается
излучения в виде вторичных волн,
возбуждаемых электронами; частично же
она переходит в другие виды энергии
(например, во внутреннюю энергию
вещества). Таким образом, интенсивность
света при прохождении через вещество
уменьшается –
свет поглощается
в веществе. Вынужденные колебания
электронов, а, следовательно,
и поглощение света, становятся особенно
интенсивными при
резонансной частоте.
Пусть
через однородное вещество распространяется
пучок параллельных
лучей (рис. 6).
Выделим
в этом веществе бесконечно тонкий слой
толщины dx,
ограниченный
параллельными поверхностями,
перпендикулярными к направлению
распространения света. Опыт показывает,
что изменение интенсивности
света на пути dx
пропорционально величине этого пути
и величине самой интенсивности:
|
|
(13) |
где α
–
коэффициент поглощения, зависящий от
рода вещества.
Пусть
на входе в поглощающий слой (на границе
или в каком-то месте
внутри вещества) интенсивность света
равна I0.
Найдем интенсивность
света I,
прошедшего слой вещества толщины х.
Для этого
проинтегрируем выражение (13), предварительно
разделив переменные:
|
|
Взяв интегралы,
получим:
|
|
откуда
|
|
(14) |
Выражение (14)
называется законом Бугера. Согласно
этому закону интенсивность
света убывает в поглощающем веществе
экспоненциально.
При
интенсивность
оказывается в «
»
раз
меньше,
чем
.
Таким образом, коэффициент поглощения
есть величина, обратная толщине слоя,
при прохождении которого интенсивность
света убывает в «
»
раз.
Коэффициент поглощения зависит от рода
вещества и длины волны (частоты) света.
Так как длина волны
(частота)
определяет цвет света, следовательно,
лучи различных цветов
поглощаются данным веществом по-разному.
Например, оконное стекло
хорошо пропускает видимый свет и почти
полностью поглощает ультрафиолетовые
лучи. Для газов при низком давлении
коэффициент поглощения
для большинства длин волн близок к нулю,
металлы практически
непрозрачны для света.
Как
уже отмечалось, коэффициент поглощения
α
зависит от длины волны λ.
Поэтому выражение (14) можно записать в
виде:
|
|
(15) |
При поглощении
света веществами, растворенными в
практически не поглощающем растворителе
(например, в чистой воде), коэффициент
поглощения пропорционален концентрации
растворенного вещества c.
|
αλ |
(16) |
где
α1λ
коэффициент пропорциональности, также
зависящий от длины волны λ.
Соотношение (16) называют законом Бера.
Для таких растворов закон Бугера
примет вид:
|
|
(17) |
Преобразуем
выражение (17)
|
или |
Переходя к десятичным логарифмам, имеем:
|
|
(18) |
Величина
называется оптической плотностью
раствора. Введя оптическую плотность,
соотношение (18) можно записать:
откуда
,
где
.
Оптическая
плотность D
пропорциональна концентрации раствора
«с»
и
толщине слоя вещества x,
через
который проходит
свет. Коэффициент пропорциональности
ε,
зависящий
от длины
волны λ
и природы растворенного вещества,
называется молекулярной
оптической плотностью (молекулярной
экстинкцией).
Отношение
называется прозрачностью или
светопропуcканием
раствора.
Между
оптической плотностью и светопропусканием
имеется следующая зависимость:
|
|
Следует
отметить, что ослабление света может
происходить за счет
рассеяния световой энергии в стороны
также по экспоненциальному
закону. Однако, в случае прозрачных тел,
рассеянием можно пренебречь.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Индивидуальный проект на
тему: «Показатель преломления призмы»
Учебная дисциплина:
Математика
Введение
Дисперсия света. Мы
всегда сталкиваемся с этим явлением в жизни, но не всегда замечаем этого. Но
если быть внимательным, то явление дисперсии всегда нас окружает. Одно из таких
явлений — это обычная радуга. Наверное, нет человека, который не любовался бы
радугой. На первый взгляд радуга это что-то простое, на самом деле при
возникновении радуги происходят сложные физические процессы.Дисперсия света —
это совокупность явлений, зависимых от показателя преломления <https://ru.wikipedia.org/wiki/%D0%9F%D0%BE%D0%BA%D0%B0%D0%B7%D0%B0%D1%82%D0%B5%D0%BB%D1%8C_%D0%BF%D1%80%D0%B5%D0%BB%D0%BE%D0%BC%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F> вещества. Именно эта величина (показатель преломления), а в
частности показатель преломления <https://ru.wikipedia.org/wiki/%D0%9F%D0%BE%D0%BA%D0%B0%D0%B7%D0%B0%D1%82%D0%B5%D0%BB%D1%8C_%D0%BF%D1%80%D0%B5%D0%BB%D0%BE%D0%BC%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F> призмы стала темой моей работы, цель которой — её изучение,
более глубокое понимание.
Применение призмы и
показателя её преломления
Оптические приборы,
такие как оптические призмы являются одним из основных элементов при создании
оптических систем и оптических приборов.Призмы широко используются в оптических
приборах различного назначения, таких как наблюдательные оптические приборы
(телескопы, бинокли, микроскопы и другие), оптические приборы для регистрации
изображений на электронных приёмниках, сложные многофункциональные оптические
приборы. Причём, чем сложнее оптический прибор, тем большее количество и
номенклатура оптических призм может в нём использоваться.
Оптические призмы в
зависимости от их оптической конструкции функционально позволяют изменять ход
лучей в оптических приборах и направление оптической оси системы; оборачивать
оптические изображения; уменьшать габариты оптических систем; разделять пучки
лучей в оптическихсистемах; объединять поля в оптических системах; вращать в
оптических системах изображения; компенсировать в оптических системах поворот
изображения; разлагать белый свет в спектр; получать поляризованный свет и т.д.
Явление преломления
света также играет важную роль в нашей жизни, преломление имеет важнейшее
практическое значение при определении свойств данных прозрачных сред.Показатель
преломления является одной из очень важных характеристик прозрачной среды, по
которой можно различать сорта стекла, различные драгоценные камни.
Призма (оптика)
Виды призм
Призма — оптический
элемент из прозрачного материала (например, оптического стекла) в форме
геометрического тела — призмы
<https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_(%D0%B3%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F)>,
имеющий плоские полированные грани, через которые входит и выходит свет. Свет
<https://ru.wikipedia.org/wiki/%D0%A1%D0%B2%D0%B5%D1%82> в призме
преломляется
<https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B5%D0%BB%D0%BE%D0%BC%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5>.
Важнейшей характеристикой призмы является показатель преломления
<https://ru.wikipedia.org/wiki/%D0%9F%D0%BE%D0%BA%D0%B0%D0%B7%D0%B0%D1%82%D0%B5%D0%BB%D1%8C_%D0%BF%D1%80%D0%B5%D0%BB%D0%BE%D0%BC%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F>
материала, из которого она изготовлена.
Дисперсионные
призмы
Дисперсионные
призмы используют в спектральных приборах для пространственного разделения
излучений различных длин волн.
Простая трёхгранная
призма
Призма
Броунинга-Резерфорда
<https://ru.wikipedia.org/w/index.php?title=%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_%D0%91%D1%80%D0%BE%D1%83%D0%BD%D0%B8%D0%BD%D0%B3%D0%B0-%D0%A0%D0%B5%D0%B7%D0%B5%D1%80%D1%84%D0%BE%D1%80%D0%B4%D0%B0&action=edit&redlink=1>
Дисперсионная
призма Аббе
<https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_%D0%90%D0%B1%D0%B1%D0%B5>
Призма Амичи
<https://ru.wikipedia.org/w/index.php?title=%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_%D0%90%D0%BC%D0%B8%D1%87%D0%B8&action=edit&redlink=1>
(призма прямого зрения)
Призма Литтрова
<https://ru.wikipedia.org/w/index.php?title=%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_%D0%9B%D0%B8%D1%82%D1%82%D1%80%D0%BE%D0%B2%D0%B0&action=edit&redlink=1>
Призма Корню
<https://ru.wikipedia.org/w/index.php?title=%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_%D0%9A%D0%BE%D1%80%D0%BD%D1%8E&action=edit&redlink=1>
Призма Пеллин-Брока
<https://ru.wikipedia.org/w/index.php?title=%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_%D0%9F%D0%B5%D0%BB%D0%BB%D0%B8%D0%BD-%D0%91%D1%80%D0%BE%D0%BA%D0%B0&action=edit&redlink=1>
Поляризационные
призмы
Призма Аренса
<https://ru.wikipedia.org/w/index.php?title=%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_%D0%90%D1%80%D0%B5%D0%BD%D1%81%D0%B0&action=edit&redlink=1>
Призма Волластона
<https://ru.wikipedia.org/w/index.php?title=%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_%D0%92%D0%BE%D0%BB%D0%BB%D0%B0%D1%81%D1%82%D0%BE%D0%BD%D0%B0&action=edit&redlink=1>
Призма Глазебрука
<https://ru.wikipedia.org/w/index.php?title=%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_%D0%93%D0%BB%D0%B0%D0%B7%D0%B5%D0%B1%D1%80%D1%83%D0%BA%D0%B0&action=edit&redlink=1>
Призма
Глана-Тейлора <https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_%D0%93%D0%BB%D0%B0%D0%BD%D0%B0-%D0%A2%D0%B5%D0%B9%D0%BB%D0%BE%D1%80%D0%B0>
Призма
Глана-Томпсона
<https://ru.wikipedia.org/w/index.php?title=%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_%D0%93%D0%BB%D0%B0%D0%BD%D0%B0-%D0%A2%D0%BE%D0%BC%D0%BF%D1%81%D0%BE%D0%BD%D0%B0&action=edit&redlink=1>
Призма Глана-Фуко
<https://ru.wikipedia.org/w/index.php?title=%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_%D0%93%D0%BB%D0%B0%D0%BD%D0%B0-%D0%A4%D1%83%D0%BA%D0%BE&action=edit&redlink=1>
Призма Николя
<https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_%D0%9D%D0%B8%D0%BA%D0%BE%D0%BB%D1%8F>
Призма Номарски
<https://ru.wikipedia.org/w/index.php?title=%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_%D0%9D%D0%BE%D0%BC%D0%B0%D1%80%D1%81%D0%BA%D0%B8&action=edit&redlink=1>
Призма Рошона
<https://ru.wikipedia.org/w/index.php?title=%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_%D0%A0%D0%BE%D1%88%D0%BE%D0%BD%D0%B0&action=edit&redlink=1>
Призма Сенармонта
<https://ru.wikipedia.org/w/index.php?title=%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_%D0%A1%D0%B5%D0%BD%D0%B0%D1%80%D0%BC%D0%BE%D0%BD%D1%82%D0%B0&action=edit&redlink=1>
Призма Фуко
<https://ru.wikipedia.org/w/index.php?title=%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_%D0%A4%D1%83%D0%BA%D0%BE&action=edit&redlink=1>
Параллелепипед
Френеля <https://ru.wikipedia.org/wiki/%D0%9F%D0%B0%D1%80%D0%B0%D0%BB%D0%BB%D0%B5%D0%BB%D0%B5%D0%BF%D0%B8%D0%BF%D0%B5%D0%B4_%D0%A4%D1%80%D0%B5%D0%BD%D0%B5%D0%BB%D1%8F>
Отражательные
призмы
Отражательные
призмы используют для изменения хода лучей, изменения направления оптической оси,
изменения направления линии визирования, для уменьшения габаритных размеров
приборов.
Призма Аббе
<https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_%D0%90%D0%B1%D0%B1%D0%B5>
Призма Аббе-Порро
<https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_%D0%90%D0%B1%D0%B1%D0%B5-%D0%9F%D0%BE%D1%80%D1%80%D0%BE>
Призма Аббе-Кёнига
<https://ru.wikipedia.org/w/index.php?title=%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_%D0%90%D0%B1%D0%B1%D0%B5-%D0%9A%D1%91%D0%BD%D0%B8%D0%B3%D0%B0&action=edit&redlink=1>
Призма дихроидная
<https://ru.wikipedia.org/w/index.php?title=%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_%D0%B4%D0%B8%D1%85%D1%80%D0%BE%D0%B8%D0%B4%D0%BD%D0%B0%D1%8F&action=edit&redlink=1>
Призма Дове
<https://ru.wikipedia.org/w/index.php?title=%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_%D0%94%D0%BE%D0%B2%D0%B5&action=edit&redlink=1>
Призма
Пехана-Шмидта
<https://ru.wikipedia.org/w/index.php?title=%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_%D0%9F%D0%B5%D1%85%D0%B0%D0%BD%D0%B0-%D0%A8%D0%BC%D0%B8%D0%B4%D1%82%D0%B0&action=edit&redlink=1>
Призма Лемана
<https://ru.wikipedia.org/w/index.php?title=%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_%D0%9B%D0%B5%D0%BC%D0%B0%D0%BD%D0%B0&action=edit&redlink=1>
Пентапризма
<https://ru.wikipedia.org/wiki/%D0%9F%D0%B5%D0%BD%D1%82%D0%B0%D0%BF%D1%80%D0%B8%D0%B7%D0%BC%D0%B0>
Призма Порро
<https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_%D0%9F%D0%BE%D1%80%D1%80%D0%BE>
Призма
Шмидта-Пехана
<https://ru.wikipedia.org/w/index.php?title=%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_%D0%A8%D0%BC%D0%B8%D0%B4%D1%82%D0%B0-%D0%9F%D0%B5%D1%85%D0%B0%D0%BD%D0%B0&action=edit&redlink=1>
Призмы с «крышей»
<https://ru.wikipedia.org/w/index.php?title=%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D1%8B_%D1%81_%C2%AB%D0%BA%D1%80%D1%8B%D1%88%D0%B5%D0%B9%C2%BB&action=edit&redlink=1>
Название призмы
обозначается двумя или тремя буквами и числом, записанным через дефис. Первая
буква означает количество отражательных граней (отражений) в призме. («А» —
одна, «Б» — две, «В» — три и т. д.). «Крыша», условно, считается одной гранью и
для её обозначения ставят индекс «к» после первой буквы. (например, Ак, Бк)
Оставшаяся буква указывает характер конструкции. («Р» — равнобедренная, «П» —
пентапризма, «У» — полупентапризма, «С» — ромбическая, «М» — дальномерного
типа, «Л» — призма Лемана). Цифры, записанные через дефис, указывают угол
излома оптической оси. (0°,90°,180°). Например, «ВкР-45°» — равнобедренная
призма с тремя отражательными гранями и крышей, с изломом оси на 45°.
Составные призмы
указываются по их собственным именам и углам излома оси. Например, «А-0°» —
Призма Аббе, «Бк-90°» — башмачная призма с крышей, «К-0°» — призма-куб.
Показатель
преломления
Показатель
преломления вещества — величина, равная отношению фазовых скоростей
<https://ru.wikipedia.org/wiki/%D0%A4%D0%B0%D0%B7%D0%BE%D0%B2%D0%B0%D1%8F_%D1%81%D0%BA%D0%BE%D1%80%D0%BE%D1%81%D1%82%D1%8C>
света <https://ru.wikipedia.org/wiki/%D0%A1%D0%B2%D0%B5%D1%82>
(электромагнитных волн
<https://ru.wikipedia.org/wiki/%D0%AD%D0%BB%D0%B5%D0%BA%D1%82%D1%80%D0%BE%D0%BC%D0%B0%D0%B3%D0%BD%D0%B8%D1%82%D0%BD%D0%BE%D0%B5_%D0%B8%D0%B7%D0%BB%D1%83%D1%87%D0%B5%D0%BD%D0%B8%D0%B5>)
ввакууме и в данной среде
.
Показатель
преломления, как абсолютный, так и относительный, равен отношению синуса угла
падения к синусу угла преломления (Закон преломления света
<https://ru.wikipedia.org/wiki/%D0%97%D0%B0%D0%BA%D0%BE%D0%BD_%D0%BF%D1%80%D0%B5%D0%BB%D0%BE%D0%BC%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F_%D1%81%D0%B2%D0%B5%D1%82%D0%B0>),
и зависит от природы вещества и длины волны излучения <https://ru.wikipedia.org/wiki/%D0%94%D0%BB%D0%B8%D0%BD%D0%B0_%D0%B2%D0%BE%D0%BB%D0%BD%D1%8B>;
для некоторых веществ показатель преломления достаточно сильно меняется при
изменении частоты электромагнитных волн от низких частот до оптических и далее,
а также может ещё более резко меняться в определённых областях частотной шкалы.
По умолчанию обычно имеется в виду оптический диапазон или диапазон,
определяемый контекстом.
Существуют
оптически анизотропные <https://ru.wikipedia.org/wiki/%D0%90%D0%BD%D0%B8%D0%B7%D0%BE%D1%82%D1%80%D0%BE%D0%BF%D0%B8%D1%8F>
вещества, в которых показатель преломления зависит от направления и поляризации
<https://ru.wikipedia.org/wiki/%D0%9F%D0%BE%D0%BB%D1%8F%D1%80%D0%B8%D0%B7%D0%B0%D1%86%D0%B8%D1%8F_%D1%81%D0%B2%D0%B5%D1%82%D0%B0>
света. Такие вещества достаточно распространены, в частности, это все кристаллы
с достаточно низкой симметрией кристаллической решётки, а также вещества,
подвергнутые механической деформации.
Показатель преломления
можно выразить как корень из произведения магнитной и диэлектрической
проницаемостей среды .
В поглощающих
средах диэлектрическая проницаемость содержит мнимую компоненту, поэтому показатель преломления
становится комплексным:
. В области оптических частот,
где , действительная
часть показателя преломления 
часть — поглощение.

Рис. 1. Падение и
преломление лучей (волн) света
По закону
преломления
<https://ru.wikipedia.org/wiki/%D0%97%D0%B0%D0%BA%D0%BE%D0%BD_%D0%A1%D0%BD%D0%B5%D0%BB%D0%BB%D0%B8%D1%83%D1%81%D0%B0>
волн преломлённый луч BC (rayon réfracté
на рис.1.) содержится в одной плоскости с лучом AB(rayon incidentна рис.1.),
каковой падает на поверхность раздела сред, и нормалью N в точке падения B, а
отношение синуса
<https://ru.wikipedia.org/wiki/%D0%A1%D0%B8%D0%BD%D1%83%D1%81> угла
падения к синусу угла
преломления равно
отношениюскоростей <https://ru.wikipedia.org/wiki/%D0%A4%D0%B0%D0%B7%D0%BE%D0%B2%D0%B0%D1%8F_%D1%81%D0%BA%D0%BE%D1%80%D0%BE%D1%81%D1%82%D1%8C>
распространения и
волн в этих средах. Это
отношение является постоянным для данных сред и называется относительным
показателем преломления второй
среды относительно первой.
Для выполняется:
, где
и
— фазовые скорости света в первой и второй
средах соответственно.
Очевидно, что
относительным показателем преломления второй среды по отношению к первой является
величина, равная .
Эта величина, при
прочих равных условиях, обычно меньше единицы при переходе луча из среды более
плотной в среду менее плотную, и больше единицы при переходе луча из среды
менее плотной в среду более плотную (например, из газа или из вакуума в
жидкость или твердое тело). Есть исключения из этого правила, и потому принято
называть среду оптически более или менее плотной, чем другая (не путать с
оптической плотностью
<https://ru.wikipedia.org/wiki/%D0%9E%D0%BF%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D0%BF%D0%BB%D0%BE%D1%82%D0%BD%D0%BE%D1%81%D1%82%D1%8C>
как мерой непрозрачности среды).
Луч, падающий из
вакуума на поверхность какой-нибудь среды, преломляется сильнее, чем при
падении на неё из другой среды; показатель преломления среды, соответствующий
лучу, падающему на неё из вакуума, называется абсолютным показателем
преломления или просто показателем преломления; это и есть показатель
преломления, определение которого дано в начале статьи. Показатель преломления
любого газа, в том числе воздуха, при обычных условиях много меньше, чем
показатели преломления жидкостей или твердых тел, поэтому приближенно (и со
сравнительно неплохой точностью) об абсолютном показателе преломления можно
судить по показателю преломления относительно воздуха.
Показатель
преломления призмы
Пусть луч AB падает
на одну из гранен призмы <http://edu.alnam.ru/book_dmath.php?id=278>.
Преломившись в точке B, луч пойдет по направлению BC и, вторично преломившись в
точке C, выйдет из призмы <http://edu.alnam.ru/book_dmath.php?id=278> в
воздух (рис. 2). Найдем угол , на который луч, пройдя через призму, отклонится
от первоначального направления. Этот угол мы будем называть углом отклонения.
Угол между преломляющими гранями, называемый преломляющим углом призмы,
обозначим .
Рис. 2. Преломление
в призме
Из четырехугольника
BOCN, в котором углы приB и C прямые, найдем, что угол BNC равен . Пользуясь этим, из четырехугольника
BMCN находим.
Отсюда.
Угол , как внешний угол в треугольнике BCN,
равен
где r — угол
преломления в точке B, а —
угол падения в точке C луча, выходящего из призмы
<http://edu.alnam.ru/book_dmath.php?id=278>. Далее, пользуясь законом
преломления, имеем
.
С помощью
полученных уравнений, зная преломляющий угол призмы
<http://edu.alnam.ru/book_dmath.php?id=278> и показатель преломления
<http://sernam.ru/book_phis_t3.php?id=84> n, мы можем при любом угле
падения i вычислить угол отклонения .
Особенно простую
форму получает выражение для угла отклонения в том случае, когда преломляющий
угол призмы мал, т. е.
призма <http://edu.alnam.ru/book_dmath.php?id=278> тонкая, а угол падения
i невелик; тогда угол также
мал. Заменяя приближенно в формулах и
синусы углов самими углами (в радианах), имеем
Подставляя эти
выражения в формулу и
пользуясь , находим
Этой формулой, справедливой
для тонкой призмы при падении на нее лучей под небольшим углом, мы
воспользуемся в дальнейшем.
Обратим внимание,
что угол отклонения луча в призме зависит от показателя преломления вещества,
из которого сделана призма <http://edu.alnam.ru/book_dmath.php?id=278>.
Как мы указывали выше, показатель преломления для разных цветов света различен
(дисперсия <http://sernam.ru/book_tp.php?id=22>). Для прозрачных тел
показатель преломления <http://sernam.ru/book_phis_t3.php?id=84>
фиолетовых лучей наибольший, затем следуют лучи синие, голубые, зеленые,
желтые, оранжевые, и, наконец, красные, которые имеют наименьший показатель
преломления. В соответствии с этим угол отклонения для фиолетовых лучей наибольший, для красных —
наименьший, и луч белого цвета, падающий на призму, по выходе из нее окажется
разложенным на ряд цветных лучей (рис. 3. и рис. 4.), т. е. образуется спектр
лучей.
Рис. 3. Разложение
белого света при преломлении в призме
Падающий пучок
белого света изображен в виде фронта с перпендикулярным к нему направлением
распространения волны. Для преломленных пучков показана только направления
распространения волн.
Рис. 4.
Заключение
В заключении я хочу сказать, что в целом поставленная цель об
изучении, более глубоком понимании такой величины как показатель преломления
призмы в итоге достигнута. Теперь, увидев радугу или гало, мы можем не только
любоваться этим красивым явлением, но и больше понимаем причину их
возникновения на «физическом» языке, а не просто — поверхностным пониманием. Таким
образом, посредством теоретического изучения данной темы и была достигнута
основная цель.
Список литературы
Башмаков М. И., Математика. Сборник задач профильной
направленности, «Академия», 2012. — 208 с.
Кабардин О. Ф., Физика: справочник для школьников и поступающих в
вузы, «АСТ-ПРЕСС КНИГА», 2015. ―528
с.://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_(%D0%BE%D0%BF%D1%82%D0%B8%D0%BA%D0%B0)://ru.wikipedia.org/wiki/%D0%9F%D0%BE%D0%BA%D0%B0%D0%B7%D0%B0%D1%82%D0%B5%D0%BB%D1%8C_%D0%BF%D1%80%D0%B5%D0%BB%D0%BE%D0%BC%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F://ru.wikipedia.org/wiki/%D0%94%D0%B8%D1%81%D0%BF%D0%B5%D1%80%D1%81%D0%B8%D1%8F_%D1%81%D0%B2%D0%B5%D1%82%D0%B0://www.studmed.ru/docs/document23113/content://sernam.ru/book_phis_t3.php?id=87
Приложение
Таблица №1 Показатели преломления для длины волны 589,3 нм
|
Тип |
Среда |
Температура, |
Значение |
|
Кристаллы |
|||
|
NaCl |
|||
|
KCl |
|||
|
KBr |
|||
|
Оптические |
|||
|
К8 |
20 |
1,5163 |
|
|
ТК4 |
20 |
1,6111 |
|
|
СТК9 |
20 |
1,7424 |
|
|
Ф1 |
20 |
1,6128 |
|
|
ТФ10 |
20 |
1,8060 |
|
|
СТФ3 |
20 |
2,1862[4] |
|
|
Драгоценные |
|||
|
Берилл |
|||
|
Изумруд |
|||
|
Сапфир |
|||
|
Сапфир |
— |
1,770 |
|
|
Жидкости |
|||
|
Бензол |
20-25 |
1,5014 |
|
|
Глицерин |
20-25 |
1,4730 |
|
|
Кислота |
20-25 |
1,4290 |
|
|
Кислота |
20-25 |
1,2540 |
|
|
Масло |
20-25 |
1,560 |
|
|
Масло |
20-25 |
1,470 |
Принцип Гюйгенса:
Каждая точка, до которой доходит световое возбуждение, является, в свою очередь, центром вторичных волн; поверхность, огибающая в некоторый момент времени эти вторичные волны, указывает положение к этому моменту фронта действительно распространяющейся волны.
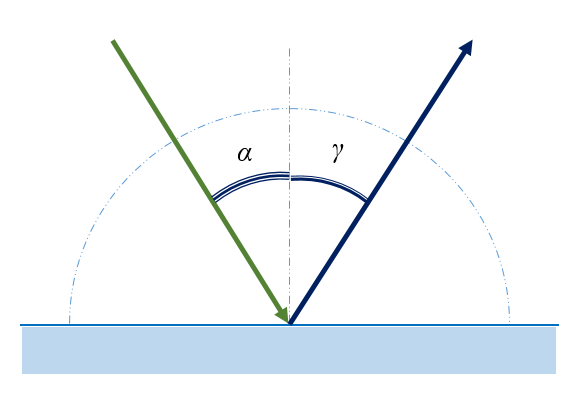
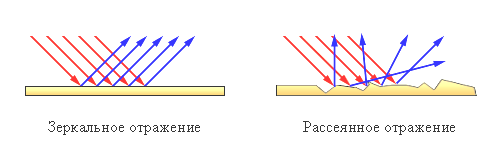
Закон отражения:
- отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенным к границе раздела двух сред в точке падения;
- угол падения α равен углу отражения γ:
α = γ
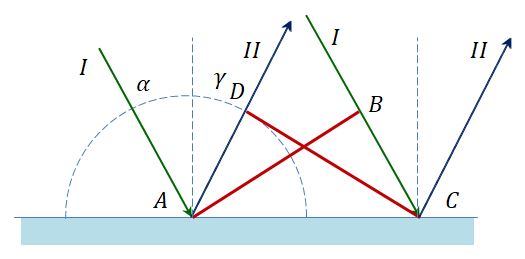
Вывод на основе принципа Гюйгенса:
Предположим, что плоская волна (фронт волны АВ), распространяющаяся в вакууме вдоль направления I со скоростью с, падает на границу раздела двух сред. Когда фронт волны АВ достигнет отражающей поверхности в точке А, эта точка начнет излучать вторичную волну.
Для прохождения волной расстояния ВС требуется время Δt = BC/υ. За это же время фронт вторичной волны достигнет точек полусферы, радиус AD которой равен: υΔt = ВС. Положение фронта отраженной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление распространения этой волны – лучом II. Из равенства треугольников ABC и ADC вытекает закон отражения: угол падения α равен углу отражения γ.
Закон преломления (закон Снелиуса):
- луч падающий, луч преломленный и перпендикуляр, проведенный к границе раздела в точке падения, лежат в одной плоскости;
- отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред.
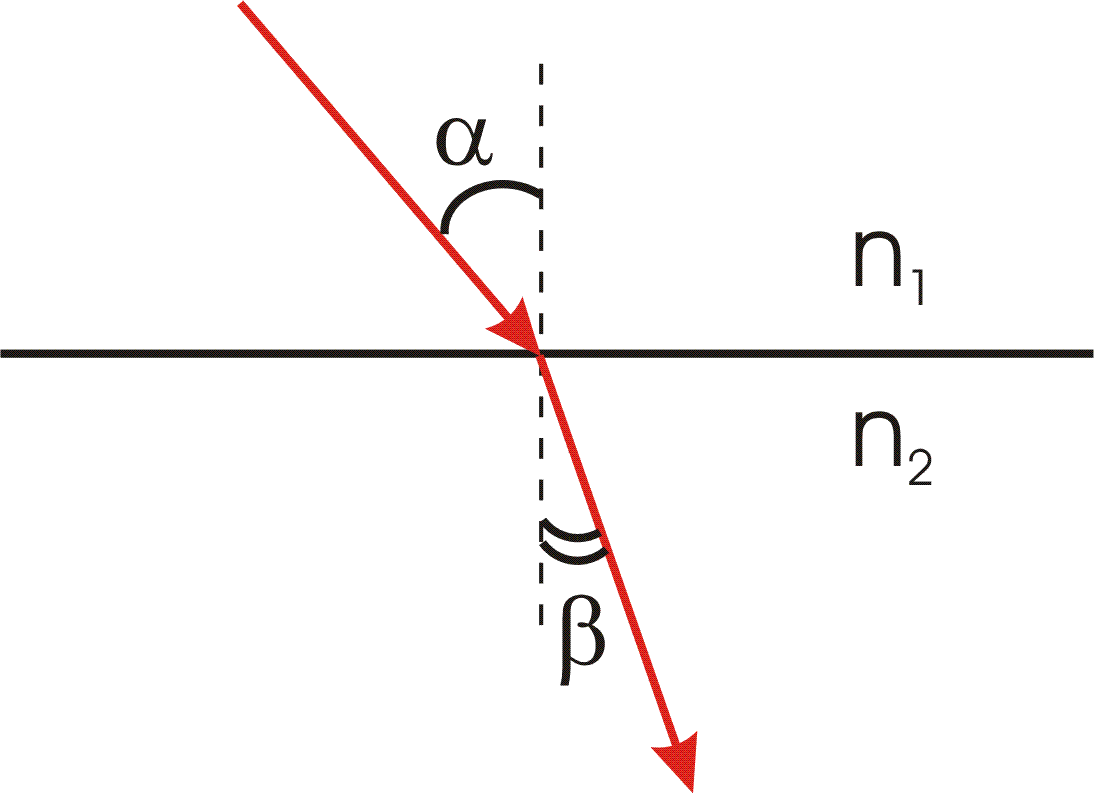

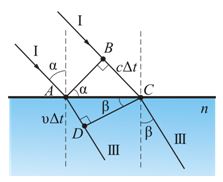
Вывод закона преломления. Предположим, что плоская волна (фронт волны АВ), распространяющаяся в вакууме вдоль направления I со скоростью с, падает на границу раздела со средой, в которой скорость ее распространения равна v.
Пусть время, затрачиваемое волной для прохождения пути ВС, равно Δt. Тогда ВС = сΔt. За это же время фронт волны, возбуждаемой точкой А в среде со скоростью u, достигнет точек полусферы, радиус которой AD = vΔt. Положение фронта преломленной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление ее распространения – лучом III. Из рис. видно, что


Отсюда следует закон Снелиуса:
Принцип Ферма: свет распространяется между двумя точками по пути, для прохождения которого необходимо наименьшее время.
Покажем применение этого принципа к решению той же задачи о преломлении света.
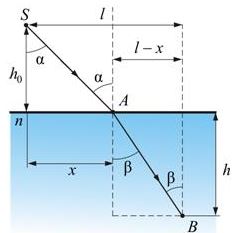
Луч от источника света S, расположенного в вакууме идет до точки В, расположенной в некоторой среде за границей раздела
В каждой среде кратчайшим путем будут прямые SA и AB. Точку A охарактеризуем расстоянием x от перпендикуляра, опущенного из источника на границу раздела. Определим время, затраченное на прохождение пути SAB:

Для нахождения минимума найдем первую производную от τ по х и приравняем ее к нулю:

отсюда приходим к тому же выражению, что получено исходя из принципа Гюйгенса: 
Следствия из принципа Ферма:
1. Обратимость световых лучей: если обратить луч III, заставив его падать на границу раздела под углом β, то преломленный луч в первой среде будет распространяться под углом α, т. е. пойдет в обратном направлении вдоль луча I.
2. Если свет распространяется из среды с большим показателем преломления n1 (оптически более плотной) в среду с меньшим показателем преломления n2 (оптически менее плотной) ( n1 > n2 ), например из стекла в воздух, то, согласно закону преломления, преломленный луч удаляется от нормали и угол преломления β больше, чем угол падения α:
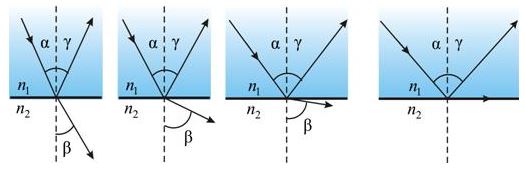
3. С увеличением угла падения увеличивается угол преломления, до тех пор, пока при некотором угле падения (α = αпр) угол преломления не окажется равным π/2.
Полное отражение
Угол αпр называется предельным углом полного отражения. При углах падения α > αпр весь падающий свет полностью отражается.
По мере приближения угла падения к предельному, интенсивность преломленного луча уменьшается, а отраженного – растет.
Если α = αпр , то интенсивность преломленного луча обращается в нуль, а интенсивность отраженного равна интенсивности падающего.
Таким образом, при углах падения в пределах от αпр до π/2, луч не преломляется, а полностью отражается в первую среду, причем интенсивности отраженного и падающего лучей одинаковы. Это явление называется полным отражением.
В случае, если вторая среда — воздух
Преломление света в плоскопараллельной пластине
Плоскопараллельная пластина — это оптический прибор, представляющий собой ограниченный параллельными поверхностями слой однородной среды, прозрачной в некотором интервале длин волн λ оптического излучения.
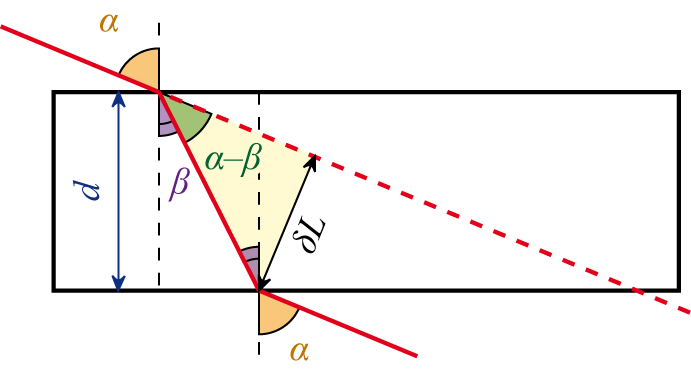
Основным оптическим свойством пластины является то, что луч, падающий на пластину, в результате двукратного преломления на поверхностях пластины параллельно смещается на некоторую величинуδL относительно исходного луча
Величина смещения в плоскопараллельной пластине
Величина сдвига луча света δL зависит:
- от угла падения света α,
- от толщины пластины d,
- от показателя преломления вещества, из которого изготовлена плоскопараллельная пластина n.
C увеличением любого из этих параметров смещение луча света увеличивается.
Смещение луча можно выразить через угол падения
Из этого выражения видно, что величина смещения луча в пластине зависит от угла падения, толщины пластины и показателя преломления. Из формулы видно, что отклонения луча не происходит, если:
- угол падения равен нулю: α = 0,
- относительный показатель преломления равен единице (преломления не происходит): n = 1 ,
- толщина пластины равна нулю: d = 0
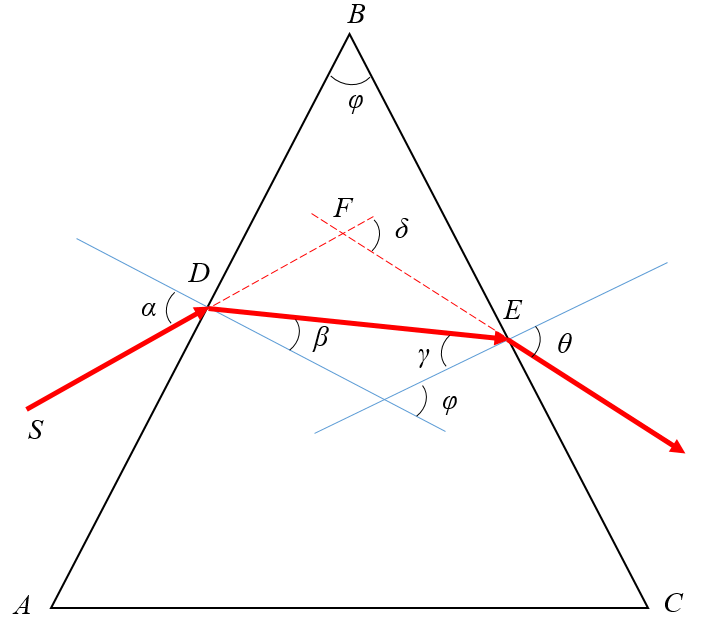
Ход луча через треугольную призму
Призма — оптический элемент из прозрачного материала (например, оптического стекла) в форме геометрического тела — призмы, имеющий плоские полированные грани, через которые входит и выходит свет. Свет в призме преломляется. Важнейшей характеристикой призмы является показатель преломления материала, из которого она изготовлена.
На призму из точки S падает луч света. Испытав 2 преломления, он выходит с отклонением на угол δ, который называется угол отклонения луча. Угол при вершине призмы АВС – φ называется преломляющим углом.
Если световой луч падает на преломляющую грань призмы под произвольным углом, то угол отклонения луча призмой определяется формулой
Если световой луч падает на преломляющую грань призмы под малым углом (практически перпендикулярнопреломляющей грани призмы), то угол отклонения луча призмой определяется формулой
Если призма сделана из материала, показатель преломления которого больше, чем у среды, в которой находится призма, отклонение лучей происходит к основанию призмы.
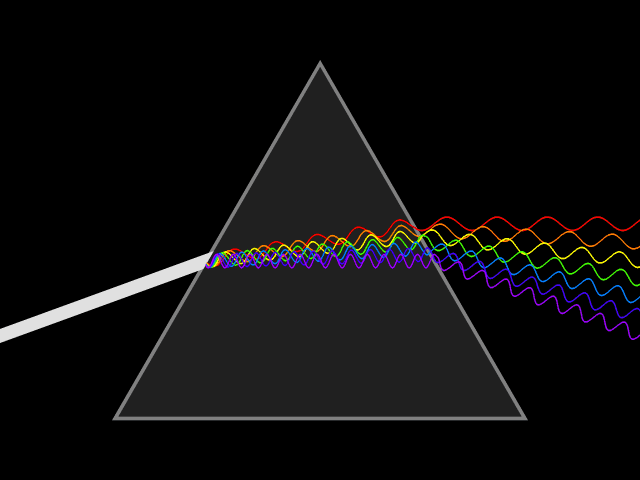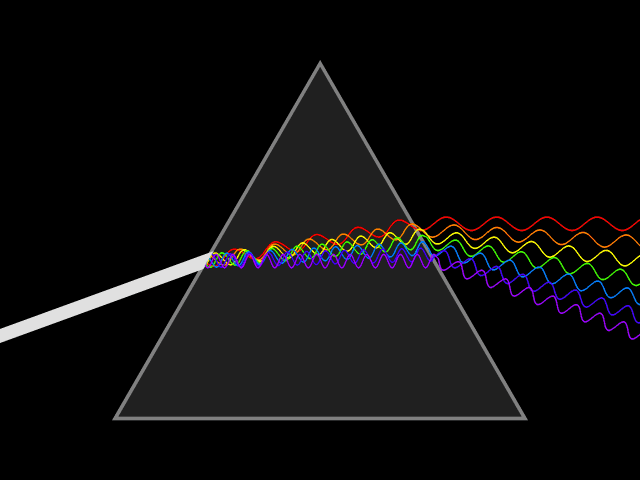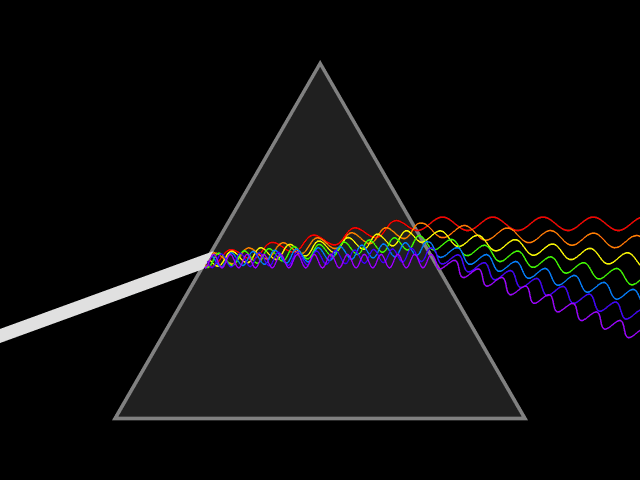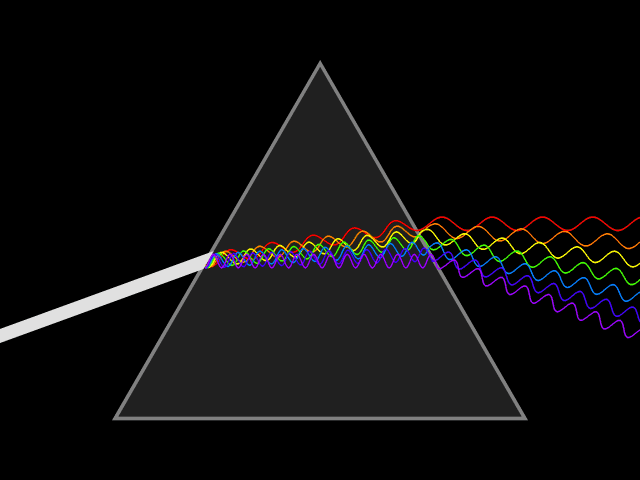
Лучи различного цвета (различной частоты или длины волны) отклоняются призмой по-разному. В случае нормальной дисперсии (показатель преломления материала тем выше, чем больше частота светового излучения) призма наиболее сильно отклоняет фиолетовые лучи; наименее — красные.