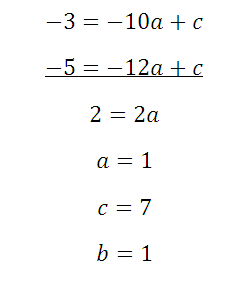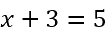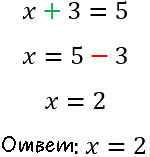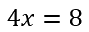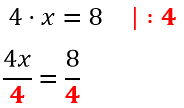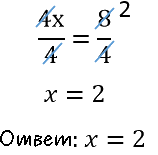Как найти коэффициент при х в уравнении

Числовой коэффициент выражения: определение, примеры

В математических описаниях часто фигурирует термин «числовой коэффициент», например, в работе с буквенными выражениями и выражениями с переменными. Материал статьи ниже раскрывает понятие этого термина, в том числе, на примере решения задач на нахождение числового коэффициента.

Определение числового коэффициента. Примеры

Учебник Н.Я. Виленкина (учебный материал для учащихся 6 классов) задает такое определение числового коэффициента выражения:

Если буквенное выражение является произведением одной или нескольких букв и одного числа, то это число называется числовым коэффициентом выражения.

Числовой коэффициент зачастую называют просто коэффициентом.

Данное определение дает возможность указать примеры числовых коэффициентов выражений.

Рассмотрим произведение числа 5 и буквы a , которое будет иметь следующий вид: 5 · a . Число 5 является числовым коэффициентом выражения согласно определению выше.

В заданном произведении x · y · 1 , 3 · x · x · z десятичная дробь 1 , 3 – единственным числовой множитель, который и будет служить числовым коэффициентом выражения.

Также разберем такое выражение:

7 · x + y . Число 7 в данном случае не служит числовым коэффициентом выражения, поскольку заданное выражение не является произведением. Но при этом число 7 – числовой коэффициент первого слагаемого в заданном выражении.

Пусть дано произведение 2 · a · 6 · b · 9 · c .

Мы видим, что запись выражения содержит три числа, и, чтобы найти числовой коэффициент исходного выражения, его следует переписать в виде выражения с единственным числовым множителем. Собственно, это и является процессом нахождения числового коэффициента.

Отметим, что произведения одинаковых букв могут быть представлены как степени с натуральным показателем, поэтому определение числового коэффициента верно и для выражений со степенями.

Выражение 3 · x 3 · y · z 2 – по сути оптимизированная версия выражения 3 · x · x · x · y · z · z , где коэффициент выражения – число 3 .

Отдельно поговорим о числовых коэффициентах 1 и — 1 . Они очень редко записаны в явном виде, и в этом их особенность. Когда произведение состоит из нескольких букв (без явного числового множителя), и перед ним обозначен знак плюс или вовсе нет никакого знака, мы можем говорить, что числовым коэффициентом такого выражения является число 1 . Когда перед произведением букв обозначен знак минус, можно утверждать, что в этом случае числовой коэффициент – число — 1 .

Далее определение числового коэффициента расширяется с произведения нескольких букв и числа до произведения числа и нескольких буквенных выражений.

К примеру, в произведении — 5 · x + 1 число — 5 будет служить числовым коэффициентом.

По аналогии, в выражении 8 · 1 + 1 x · x число 8 – коэффициент выражения; а в выражении π + 1 4 · sin x + π 6 · cos — π 3 + 2 · x числовой коэффициент — π + 1 4 .

Нахождение числового коэффициента выражения

Выше мы говорили о том, что если выражение представляет собой произведение с единственным числовым множителем, то этот множитель и будет являться числовым коэффициентом выражения. В случае, когда выражение записано в ином виде, предстоит совершить ряд тождественных преобразований, который приведет заданное выражение к виду произведения с единственным числовым множителем.

Задано выражение − 3 · x · ( − 6 ) . Необходимо определить его числовой коэффициент.

Решение

Осуществим тождественное преобразование, а именно произведем группировку множителей, являющихся числами, и перемножим их. Тогда получим: − 3 · x · ( − 6 ) = ( ( − 3 ) · ( − 6 ) ) · x = 18 · x .

В полученном выражении мы видим явный числовой коэффициент, равный 18 .

Ответ: 18

Задано выражение a — 1 2 · 2 · a — 6 — 2 · a 2 — 3 · a — 3 . Необходимо определить его числовой коэффициент.

Решение

С целью определения числового коэффициента преобразуем в многочлен заданное целое выражение. Раскроем скобки и приведем подобные слагаемые, получим:

a — 1 2 · 2 · a — 6 — 2 · a 2 — 3 · a — 3 = = 2 · a 2 — 6 · a — a + 3 — 2 · a 2 + 6 · a — 3 = — a

Числовым коэффициентом полученного выражения будет являться число — 1 .

График линейной функции, его свойства и формулы

О чем эта статья:

Понятие функции

Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, следуя которому по значениям независимой переменной можно найти соответствующие значения функции. Вот какими способами ее можно задать:

Табличный способ помогает быстро определить конкретные значения без дополнительных измерений или вычислений.

Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.

Словесный способ.

Графический способ — наглядно. Его мы и разберем в этой статье.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Понятие линейной функции

Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.

Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.

Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.

Если известно конкретное значение х, можно вычислить соответствующее значение у.

Нам дана функция: у = 0,5х — 2. Значит:

если х = 0, то у = -2;

если х = 2, то у = -1;

если х = 4, то у = 0 и т. д.

Для удобства результаты можно оформлять в виде таблицы:

Графиком линейной функции является прямая. Для ее построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.

Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.

k и b — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.

Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты k и b.

Функция	Коэффициент k	Коэффициент b
y = 2x + 8	k = 2	b = 8
y = −x + 3	k = −1	b = 3
y = 1/8x − 1	k = 1/8	b = −1
y = 0,2x	k = 0,2	b = 0

Может показаться, что в функции y = 0,2x нет числового коэффициента b, но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа y = kx + b есть коэффициенты k и b.

Свойства линейной функции

Область определения функции — множество всех действительных чисел.

Множеством значений функции является множество всех действительных чисел.

График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.

Функция не имеет ни наибольшего, ни наименьшего значений.

Четность и нечетность линейной функции зависят от значений коэффициентов k и b:

b ≠ 0, k = 0, значит, y = b — четная;

b = 0, k ≠ 0, значит, y = kx — нечетная;

b ≠ 0, k ≠ 0, значит, y = kx + b — функция общего вида;

b = 0, k = 0, значит, y = 0— как четная, так и нечетная функция.

Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.

График функции пересекает оси координат:

ось абсцисс ОХ — в точке (−b/k; 0);

ось ординат OY — в точке (0; b).

x = −b/k — является нулем функции.

Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.

Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.

Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0 функция принимает отрицательные значения на промежутке (−∞; −b/k) и положительные значения на промежутке (−b/k; +∞).

При k 0, то этот угол острый, если k

Построение линейной функции

В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.

Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:

В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:

если k > 0, то график наклонен вправо;

если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;

если b 0, то график функции y = kx + b выглядит так:

0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>

Если k > 0 и b > 0, то график функции y = kx + b выглядит так:

0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>

Если k > 0 и b

В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.

Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.

Например, график уравнения х = 3:

Условие параллельности двух прямых:

График функции y = k₁x + b₁ параллелен графику функции y = k₂x + b₂, если k₁ = k₂.

Условие перпендикулярности двух прямых:

График функции y = k₁x + b₁ перпендикулярен графику функции y = k₂x + b₂, если k₁k₂ = −1 или k₁ = −1/k₂.

Точки пересечения графика функции y = kx + b с осями координат:

С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.

Координаты точки пересечения с осью OY: (0; b).

С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.

Координаты точки пересечения с осью OX: (−b/k; 0).

Решение задач на линейную функцию

Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!

Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.

В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.

Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.

Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:

Таким образом, нам надо построить график функции y = -4x — 10

Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).

Поставим эти точки в координатной плоскости и соединим прямой:

Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).

Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.

Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.

Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.

Вычтем из второго уравнения системы первое, и получим k = 3.

Подставим значение k в первое уравнение системы, и получим b = -2.

Ответ: уравнение прямой y = 3x — 2.

Метод неопределенных коэффициентов и его универсальность

Разделы: Математика

Применение метода неопределённых коэффициентов основано на следующих двух теоремах.

Теорема №1 (о многочлене, тождественно равном нулю).

Если при произвольных значениях аргумента x значение многочлена f(x) = а₀+ а₁х + а₂х 2 +. + а _nx n , заданного в стандартном виде, равно нулю, то все его коэффициенты а₀, а₁, а₂, . а_n равны нулю.

Теорема №2 (следствие теоремы № 1).

Деление многочлена на многочлен.

Пример 1. Выполнить деление многочлена х 5 – 6х 3 + 2х 2 -4 на многочлен х 2 – х + 1.

Решение: Надо найти такие многочлены Q(x) и R(x), что х 5 – 6х 3 + 2х 2 -4 = (х 2 – х + 1) Q(x) + R(x), причём степень многочлена R(x) меньше степени многочлена (х 2 – х + 1). Из того, что степень произведения многочленов равна сумме их степеней, следует, что степень многочлена Q(x) равна 5 – 2 = 3.

Многочлены Q(x) и R(x) имеют вид:

Раскроем скобки в правой части равенства:

Для отыскания неизвестных коэффициентов получаем систему уравнений:

Ответ: Q(x) = x 3 + x 2 — 6x — 5, R(x) = x + 1.

Пример 2. Выполнить деление многочлена х 7 –1 на многочлен х 3 + х + 1.

Решение: Надо найти такие многочлены Q(x) и R(x), что х 7 –1 = (х 3 + х + 1) Q(x) + R(x), причём степень многочлена R(x) меньше степени многочлена (х 3 + х + 1).

Из того, что степень произведения многочленов равна сумме их степеней, следует, что степень многочлена Q(x) равна 7– 3 = 4.

Многочлены Q(x) и R(x) имеют вид: Q(x) = q ₄x 4 + q ₃x 3 + q ₂x 2 + q ₁x + q₀,
R(x) = r ₂x 2 + r ₁x + r0.

Подставим Q(x) и R(x):

Раскроем скобки в правой части равенства:

Получаем систему уравнений:

Ответ: Q(x) = x 4 — x 2 — x + 1, R(x) = 2x 2 — 2.

Расположение многочлена по степеням.

Возьмем функцию Поставим перед собой задачу «расположить многочлен по степеням f(x) по степеням (х-х₀).

Задача сводится к нахождению неизвестных коэффициентов а₀, а₁, . а_n. В каждом конкретном случае эти числа найти легко. Действительно, расположим многочлены, находящиеся в левой и правой частях равенства, по степеням x. Так как мы имеем тождество, то (по теореме № 2) коэффициенты при одинаковых степенях x должны быть равны между собой. Приравняв коэффициенты правой части соответствующим заданным коэффициентам левой, мы придем к системе n+1 уравнений с n+1 неизвестными а₀, а₁, . а_n , которую нужно решить.

Пример 3. Расположим многочлен по степеням.

Приравниваем коэффициенты при одинаковых степенях и получаем систему:

Решая систему, находим:

Ответ: .

Пример 4. Расположим f(x) = х 4 — 8х 3 + 24х 2 — 50х + 90 по степеням (х-2).

Решение: Полагаем х₄ — 8х 3 + 24х 2 — 50х + 90

Ответ: f(x) =

Представление произведения в виде многочлена стандартного вида.

Пример 5. Не выполняя действий, представим в виде многочлена стандартного вида произведение (х — 1)(х + 3)(х + 5).

Решение: Произведение есть многочлен третьей степени, коэффициент при старшем члене равен 1, а свободный член равен (- 15), тогда запишем:

(х — 1)(х + 3)(х + 5) = х 3 + ах 2 + вх — 15, где а и в — неизвестные коэффициенты.

Для вычисления их положим х = 1 и х = — 3, тогда получим:

откуда а =7, в = 7.

Ответ: х 3 +7х 2 + 7х — 15.

Разложение многочлена на множители

Пример 6. Дан многочлен

Разложим его на множители, если известно, сто все его корни – целые числа.

Решение: Будем искать разложение в виде:

полагая числа a, b, c и d его корнями. Раскроем скобки в правой части и сгруппируем по одинаковым степеням.

Приравниваем коэффициенты при одинаковых степенях.

Так как корни нашего многочлена – целые, то из последнего уравнения системы заключаем, что они должны быть делителями числа 30. Следовательно, их следует искать среди чисел

Проведя испытания, установим, что корни нашего многочлена -2, -5, 1 и 3. Следовательно х 4 + 3х 3 — 15х 2 — 19х + 30 = (х — 1)(х — 3)(х + 2)(х + 5)

Пример 7. Дан многочлен .

Разложим его на множители, если известно, сто все его корни – целые числа.

Решение: Будем искать разложение в виде:

полагая числа a, b, c и d его корнями. Раскроем скобки в правой части и сгруппируем по одинаковым степеням.

Приравниваем коэффициенты при одинаковых степенях.

Так как корни нашего многочлена – целые, то из последнего уравнения системы заключаем, что они должны быть делителями числа 84. Следовательно, их следует искать среди чисел

Проведя испытания, установим, что корни нашего многочлена -7,-2,2,3. Следовательно х 4 + 4х 3 — 25х 2 — 16х + 84 = (х — 2)(х — 3)(х + 2)(х + 7)

Пример 8. Разность является целым числом. Найдем это число.

Решение: Так как,

Тогда

Положим где a и b – неизвестные коэффициенты.

Тогда

Решая данную систему уравнений, получим а = 5, b = -4.

Значит так как

Аналогично устанавливаем, что

Следовательно

Пример 9. Является ли разность целым числом.

Решение: Т.к.

тогда —

Положим где a и b – неизвестные коэффициенты.

Тогда откуда

из второго уравнения тогда первое уравнение принимает вид

b 2 = 12,5 — — не удовлетворяет условию задачи, или b 2 = 9, откуда b = -3 или b = 3 — не удовлетворяет числу Значит, а = 5.

Аналогично,

Окончательно получаем: — иррациональное число.

Уничтожение иррациональности в знаменателе

Пример 10. Избавимся от иррациональности в знаменателе:

Решение:

отсюда

Раскроем скобки, сгруппируем:

Ответ:

Пример 11. Избавимся от иррациональности в знаменателе:

Решение: ,

отсюда

Раскроем скобки, сгруппируем

Отсюда

Итак

Следовательно

Ответ:

Применение метода неопределенных коэффициентов при решении уравнений

Пример 12. Решим уравнение х 4 + х 3 — 4х 2 — 9х — 3 = 0.

Решение: Предположим, что корни уравнения — целые числа, тогда их надо искать среди чисел

Если х = 1, то
если х = -1, то
если х = 3, то
если х = -3, то

Отсюда делаем вывод, что рациональных корней наше уравнение не имеет.

Попробуем разложить многочлен на множители в следующем виде:

, где a, b, c и d – целые. Раскроем скобки:

Приравнивая соответствующие коэффициенты выражений для неизвестных a, b, c и d получаем систему уравнений:

Так как bd = -3, то будем искать решения среди вариантов:

Проверим вариант № 2, когда b = —1; d = 3:

Пример 13. Решить уравнение: х 4 — 15х 2 + 12х + 5= 0.

Решение: Разложим многочлен f(х) = х 4 — 15х 2 + 12х + 5 на множители в следующем виде: , где a, b, c и d -целые. Раскроем скобки:

Приравнивая соответствующие коэффициенты выражений для неизвестных a, b, c и d получаем систему уравнений:

Так как , bd = 5, то будем искать решения среди вариантов:

Системе удовлетворяет вариант №2, т.е. а = 3, b = -1, c = -3, d = 5.

Итак,

D =13
D = 29

Ответ:

О решении одного класса кубических уравнений.

Пусть дано кубическое уравнение: а ₁ х 3 + b ₁х 2 +с ₁х +d₁ = 0, где а ≠ 0.
Приведём его к виду х 3 + ах 2 +bх + с = 0 (1), где а = , в = , с =
Положим в уравнении (1) х = у + m. Тогда получим уравнение:
Раскроем скобки, сгруппируем: y 3 +3у 2 m + 3ym 2 + m 3 + ay 2 + 2aym +am 2 + by +bm + с = 0,
y 3 + y 2 (a +3m) +y(3m 2 +2am +b) + m 3 +am 2 +bm + с = 0.

Для того, чтобы уравнение (1) было двучленным, должно выполняться условие:

Решения этой системы: m = -; a 2 = 3b. Таким образом, при произвольном с и при a 2 = 3b уравнение подстановкой х = у — можно привести к двучленному уравнению третьей степени.

Пример14. Решить уравнение: х 3 + 3х 2 +3х — 9 =0.

Решение: В данном уравнении а = 3, в =3, тогда условие a 2 = 3b выполняется, а m = — = -1. Выполним подстановку х = у -1.

Уравнение принимает вид: (у -1) 3 +3(у -1) 2 +3(у -1) – 9 = 0.
y 3 -3y 2 +3у -1 +3у 2 – 6у +3 +3у –3 – 9 = 0.
y 3 – 10 = 0, откуда у = , а х = — 1.

Ответ: — 1.

Пример15. Решить уравнение: х 3 + 6х 2 + 12х + 5 = 0.

Решение: а = 6, в =12, тогда условие a 2 = 3b (62 = 3×12) выполняется, а m = — = -2.

Выполним подстановку х = у — 2. Уравнение принимает вид: (у -2) 3 +6(у -2) 2 +12(у -2) + 5 = 0.

у 3 – 6у 2 + 12у – 8 + 6у 2 -24у + 24 + 12у – 24 + 5 = 0.
у 3 – 3 = 0, у = , а х = — 2.

Ответ: – 2.

Рассмотренные в работе примеры могут быть решены и другими способами. Но цель работы заключалась в том, чтобы решить их методом неопределённых коэффициентов, показать универсальность этого метода, его оригинальность и рациональность, не отрицая того, что в некоторых случаях он приводит к громоздким, но не сложным преобразованиям.

источники:

http://skysmart.ru/articles/mathematic/grafik-linejnoj-funkcii

http://urok.1sept.ru/articles/550924

Была ли эта статья полезной?

Для решения линейных уравнений используют два основных правила (свойства).

Свойство № 1
или
правило переноса

Давайте разберём правило переноса на примере. Пусть нам требуется решить линейное уравнение.

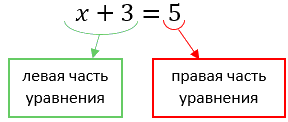
Вспомним, что у любого уравнения есть левая и правая часть.

Перенесем число «3» из левой части уравнения в правую.

Так как
в левой части уравнения у числа «3»
был знак «+», значит в правую часть уравнения
«3» перенесется со знаком «−».

Полученное числовое значение «x = 2» называют корнем уравнения.

Рассмотрим другое уравнение.

5x = 4x + 9

По правилу переноса перенесем «4x» из правой
части уравнения в левую, поменяв знак на противоположный.

Несмотря на то, что перед «4x» не стоит никакого знака,
мы понимаем, что перед «4x» стоит знак «+».

5x = 4x + 9
5x = +4x + 9
5x − 4x = 9

Теперь приведем подобные и решим уравнение до конца.

5x − 4x = 9
x = 9

Ответ: x = 9

Свойство № 2
или
правило деления

Разберемся на примере, как использовать правило деления при решении линейных уравнений.

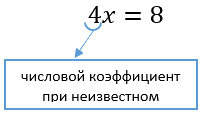
Число «4», которое стоит при «x»,
называют числовым коэффициентом при неизвестном.

Между числовым коэффициентом и неизвестном всегда стоит действие умножение.

Чтобы решить уравнение необходимо сделать так, чтобы при «x» стоял коэффициент
«1».

Давайте зададим себе вопрос: «На что нужно разделить «4», чтобы
получить
«1»?».
Ответ очевиден, нужно разделить на «4».

Используем правило деления и разделим левую и правую части уравнения на «4».
Не забудьте, что делить нужно и левую, и правую части.

Используем сокращение дробей и решим линейное уравнение до конца.

Как решить уравнение, если «x» отрицательное

Часто в уравнениях встречается ситуация, когда при «x» стоит отрицательный коэффициент.
Как, например, в уравнении ниже.

−2x = 10

Чтобы решить такое уравнение, снова зададим себе вопрос:
«На что нужно разделить «−2»,
чтобы получить «1»?». Нужно разделить на «−2».

−2x = 10         |:(−2)

=
                 
x = −5                 

Ответ: x = −5           

Примеры решения линейных уравнений

Рассмотрим другие примеры решения линейных уравнений. Обычно для решения уравнений нужно
применять оба свойства (правило переноса и правило деления).

Также требуется вспомнить правило раскрытия скобок и
правило приведения подобных.

• 
  25x − 1 = 9
  25x = 9 + 1
  25x = 10        |: 25

  =
  
  x =
  
  Ответ: x =

  ---

• 
  11(y − 4) + 10(5 − 3y) − 3(4 − 3y) = −6

  11y − 44 +
  50 −
  30y − 12
  + 9y = −6

  11y − 30y +
  9y −
  44 + 50 − 12 = −6

  20y − 30y + 6 − 12 = −6
  −10y − 6 = −6
  −10y = −6 + 6
  −10y = 0         |:(−10)
  =
  

  y = 0

  
  Ответ: y = 0

---

Ваши комментарии

Оставить комментарий:

---

План урока:

Определение квадратного уравнения

Решение квадратного уравнения

Уравнения, сводящиеся к квадратным

Задачи, решаемые с помощью квадратных уравнений

Теорема Виета

Разложение квадратного трехчлена на множители

Дробно-рациональные уравнения

Определение квадратного уравнения

Изучая понятие многочленов, мы познакомились с квадратными трехчленами. Так называют полином 2-ой степени, содержащий только одну переменную. Если его приравнять к нулю, то получится квадратное уравнение. Дадим определение квадратному уравнению:

Приведем несколько конкретных примеров:

• 5х² + 4х + 7 = 0
• – 3х² + х – 1,5 = 0
• 0,05х² + 99,568х – 47,21 = 0

Числа a, b и с называют коэффициентами квадратного уравнения. Отметим, что числа b и c могут равняться нулю, и в этом случае соответствующее слагаемое просто не записывается:

• 9х² + 5х = 0
• 17х² – 34 = 0

Эти уравнения именуют неполными.

Если же коэффициент а=0, то получается линейное уравнение, которое мы уже умеем решать:

• 6х – 2 = 0
• 67х + 89 = 0

Естественно, что для обозначения переменной может использоваться любая буква, а не только х:

• у² + 3,5х – 93 = 0
• – 32z² + 11z – 78 = 0

Для обозначения коэффициентов могут использоваться специальные термины:

• а – старший коэффициент;
• b– второй коэффициент;
• с – свободный член.

Неполные квадратные уравнения можно очень легко решить. Сначала рассмотрим пример, в котором b = 0:

5х² – 45 = 0

Перенесем вправо свободный коэффициент:

5х² = 45

Далее поделим на старший коэффициент обе части равенства:

х² = 9

Понятно, что х равен квадратному корню из 9. Напомним, что у каждого положительного числа есть два квадратных корня! Один из них является положительным числом и называется арифметическим, а другой противоположен ему по знаку. Поэтому можно записать, что

Иногда используют более короткую запись:

х = ± 3

Не любое квадратное уравнение, у которого нет второго коэффициента b, будет иметь решение. Рассмотрим уравнение

3х² + 75 = 0

Будем решать его таким же путем, перенося свободный коэффициент c вправо и деля уравнение на старший коэффициент a:

3х² + 75 = 0

3х² = – 75

х² = – 25

Квадрат действительного числа не может быть отрицательным. Значит, данное уравнение не будет иметь корней.

Сформулируем общий алгоритм решения неполных квадратных уравнений такого типа:

Теперь изучим неполные уравнения, в которых нет свободного слагаемого с. Рассмотрим их на примере:

7х² + 21х = 0

Слева вынесем переменную х за скобки:

х(7х + 21) = 0

Теперь слева находится произведение двух множителей, а справа – ноль. Очевидно, что произведение может равняться нулю лишь в том случае, когда один из составляющих его множителей (х или 7х + 21) является нулем.

Зная это, запишем:

х = 0 или 7х + 21 = 0

Получили корень х = 0 и ещё одно линейное уравнение, которое легко решить:

7х + 21 = 0

7х = – 21

х = – 3

В результате имеем два корня: 0 и – 3

Опишем общий алгоритм решения этих неполных уравнений:

Решение квадратного уравнения

Найти решение квадратного уравнения, если оно полное, достаточно тяжело. Нам поможет формула квадрата суммы:

(а + b)² = a² + 2ab + b²

Напомним, что с ее помощью можно разложить на множители некоторые квадратные полиномы:

х² + 8х + 16 = х² + 2•4•х + 4² = (х + 4)²

Конечно, здесь нам повезло с квадратным трехчленом – его коэффициенты позволяли воспользоваться формулой квадрата суммы. Однако похожие преобразования можно выполнить и тогда, когда коэффициенты не такие удобные:

х² + 8х + 20 = х² + 8х + 16 + 4 =(х² + 8х + 16) + 4 = (х² + 2•4•х + 4²) + 4 =

= (х + 4)² + 4

Здесь мы разложили число 20 на сумму 16 + 4, чтобы можно было часть выражения «свернуть» формулой квадрата суммы. Такой прием можно применить вообще к любому квадратному трехчлену:

4х² + 10х + 4 = (2х)² + 2•2х•2,5 + 2,5² – 2,5² + 4 = (2х + 2,5)² – 2,5² + 4 =

= (2х + 2,5)² – 6,25 + 4 = (2х + 2,5)² – 2,25

Здесь мы добавили к трехчлену слагаемое 2,5² и тут же его отняли. Оно было необходимо для получения формулы квадрата суммы.

Отметим, что подобное свертывание можно использовать для решения квадратного уравнения. Действительно, пусть дано уравнение

4х² + 10х + 4 = 0

Выше мы уже преобразовали трехчлен, стоящий слева. Произведем замену:

(2х + 2,5)² – 2,25 = 0

Имеем уравнение, очень похожее на неполное, где отсутствует коэффициент b. Попробуем его решить аналогичным путем:

Из этой записи мы получили два линейных уравнения:

2х + 2,5 = – 1,5 или 2х + 2,5 = 1,5

Решая их, находим два корня:

2х = – 1,5 – 2,5 или 2х = 1,5 – 2,5

2х = – 4 или 2х = – 1

х = – 2 или х = – 0,5

Аналогично можно решить и любое другое полное квадратное уравнение. Однако проще пользоваться специальными формулами, в которые надо подставлять значения коэффициентов a, b, с и получать корни квадратного уравнения. Выведем эти формулы.

Пусть есть уравнение

ах² + bх + с = 0

Поделим обе части уравнения на коэффициент а:

Далее надо выделить квадрат суммы, что бы потом свернуть его по формуле сокращенного умножения:

Далее обозначим числитель в правой части (b² – 4ac) буквой D. Эту величину называют дискриминантом квадратного уравнения.

Перепишем уравнение с учетом этой замены:

Далее рассмотрим три случая:

1. D< 0. Если D отрицателен, то и вся дробь справа меньше нуля (так как в знаменателе стоит 4а² – заведомо положительное число). Слева стоит квадрат выражения, а он никак не может оказаться отрицательным. В итоге имеем, что при отрицательном дискриминанте у уравнения отсутствуют корни.
2. D = 0. При таком варианте справа получается ноль:

Квадрат только одного числа равен нулю – самого нуля, поэтому

Итак, при нулевом дискриминанте у уравнения есть только один корень.

1. D> 0. В этом варианте дробь справа оказывается положительным числом, а потому у нее есть два квадратных корня. Решение будет выглядеть так:

Полученное выражение называют основной формулой корней квадратного уравнения.

Если дискриминант – положительное число, то уравнение существует два корня. Для вычисления первого из них надо в формуле квадратного уравнения вместо знака ± поставить минус, а для вычисления второго – знак плюс. Часто 1-ый корень обозначают как х₁, а 2-ой – как х₂. Заметим, что если D = 0, то при подстановке в основную формулу будет получаться один и тот же корень независимо от выбора знака плюс или минус.

Пример. Решите уравнение

2х² – 5х – 3 = 0

Решение. Выпишем коэффициенты уравнения

a = 2

b = – 5

c = – 3

Вычислим значение дискриминанта:

D = b² – 4ас = (– 5)² – 4•2•(– 3) = 25 + 24 = 49

Так как он больше нуля, то должно получиться два корня. Их можно найти по основной формуле квадратного уравнения:

Ответ: – 0,5; 3

Пример. Найдите все корни уравнения

3х² + 6х + 5 = 0

Решение. Найдем дискриминант:

D = b² – 4ас = 6² – 4•3•5 = 36 – 60 = – 24

Дискриминант оказался отрицательным, значит, и корней у уравнения нет.

Ответ: нет корней.

Пример. Найдите значения х, при которых выполняется равенство

4х² – 12х + 9 = 0

Решение. Вычислим дискриминант:

D = (– 12)² – 4•4•9 = 144 – 144 = 0

Так как D = 0, существует лишь один корень:

Ответ: 1,5

Пример. Найдите значения у, при которых справедливо равенство

2у² + 4у + 9 = у² + 11у + 3

Решение. На первый взгляд это уравнение не похоже на изучавшие до этого квадратные уравнения. Однако слагаемые, записанные справа, можно перенести влево, после чего можно будет привести подобные слагаемые:

2у² + 4у + 9 = у² + 11у + 3

2у² + 4у+ 9–у²– 11у– 3 = 0

у² – 7у + 6 = 0

Получили классическое квадратное уравнение, для которого можно рассчитать дискриминант:
D = b² – 4ас = (– 7)² – 4•1•6 = 49 – 24 = 25

Найдем значения двух корней:

Ответ: 1; 6

Уравнения, сводящиеся к квадратным

Так как любое квадратное уравнение решается довольно легко, то другие, более сложные уравнения, часто пытаются свести к квадратным. Сначала рассмотрим так называемые биквадратные уравнения. Пусть надо решить уравнение

2х⁴–26х² + 72 = 0

На первый взгляд в левой части стоит полином четвертой, а не второй степени, то есть это уравнение не является квадратным. Введем переменную t, равную х²:

t = х²

Если это выражение возвести в квадрат, то получим

t² = (х²)² = х⁴

Теперь заменим в исходном уравнении х⁴ на t², а х² на t:

2t²–26t + 72 = 0

Получили квадратное уравнение, из которого можно найти значение t. Посчитаем дискриминант:

D = (– 26)²– 4•2•72 = 676 – 576 = 100

Можно найти два значения t:

Однако нам надо найти значение х, а не t. Вспомним, что мы проводили замену

х² = t

Подставляя вместо t найденные корни 4 и 9, получим ещё два уравнения:

х² = 4

х² = 9

Первое имеет корни (– 2) и 2, а второе (– 3) и 3. Все эти 4 числа являются корнями исходного уравнения

2х⁴ – 26х² + 72 = 0

Уравнения, которые можно свести к квадратному заменой переменных t = x², называют биквадратными уравнениями.

Мы рассмотрели пример, в котором биквадратное уравнение имело 4 корня. Однако порою их может быть и меньше.

Пример. Укажите все корни уравнения

у⁴ + 4у² – 5 = 0

Решение. Данное уравнение подходит под определение биквадратного, а потому произведем замену t = y²:

t² + 4t – 5 = 0

Решаем его:

D = 4²– 4•1•(– 5) = 16 – (– 20) = 36

далее проводим обратную замену и получаем уравнения:

у² = – 5

у² = 1

Первое из них не имеет решения, ведь квадрат числа – это неотрицательное число. Поэтому решать придется только второе уравнение:

у² = 1

у = –1 и у = 1

Ответ –1 и 1.

Подстановка t = x² самая простая и очевидная, однако, порою нужно выполнять более сложные подстановки.

Пример. Найдите все z, для которых выполняется условие

(z – 2)(z – 3)(z – 4)(z – 5) = 24

Решение.Замена неочевидна, и всё же попробуем такой вариант:

t = z– 3,5

Тогда содержимое каждой скобки примет вид:

z– 2 = z– 3,5 + 1,5 = t + 1,5

z– 3 = z– 3,5 + 0,5 = t + 0,5

z– 4 = z– 3,5 – 0,5 = t–0,5

z– 5 = z – 3,5 – 1,5 = t–1,5

Уравнение примет вид:

(t + 1,5)(t + 0,5)(t – 0,5)(t – 1,5) = 24

Поменяем местами скобки:

(t – 0,5)(t + 0,5)(t – 1,5)(t + 1,5) = 24

Можно заметить, что в соседние скобки можно переписать, используя формулу разности квадратов:

(t²– 0,5²)(t²– 1,5²) = 24

Для удобства произведем ещё одну замену s = t²:

(s– 0,5²)(s– 1,5²) = 24

(s– 0,25)(s– 2,25) = 24

Раскроем скобки в левой части:

s²– 2,25s– 0,25s + 0,5625 = 24

s²– 2,5s + 0,5625– 24 = 0

s²– 2,5s– 23,4375 = 0

Получили классическое квадратное уравнение, которое решается через дискриминант:

D = (– 2,5)² – 4•1•(– 23,4375) = 6,25 + 93,75 = 100

Произведем 1-ую обратную замену t² = s:

t² = – 3,75

t² = 6,25

Первое уравнение решений не имеет, а у второго ровно 2 корня:

Пришло время второй замены z– 3,5 = t, из которой получаем два уравнения:

z– 3,5 = – 2,5 или z– 3,5 = 2,5

z= – 2,5 + 3,5 или z= 2,5 + 3,5

z = – 1 или z = 6

Ответ: – 1 и 6.

Задачи, решаемые с помощью квадратных уравнений

При рассмотрении задач, связанных с геометрией, свойствами чисел, движением тел, очень часто возникают квадратные уравнения.

Пример. Площадь прямоугольника составляет 126 см², а одна из его сторон на 5 см длиннее другой. Каковы длины сторон этого прямоугольника?

Решение. Обозначим как k длину той стороны прямоугольника, которая меньше. Тогда протяженность второй стороны будет равна k + 5 см. Площадь прямоугольника – это произведение его сторон, а потому можно записать:

k(k + 5) = 126

Решим это уравнение:

k(k + 5) – 126 = 0

k² + 5k – 126 = 0

D = 5²– 4•1•(– 126) = 25 + 504 = 529

Первый корень равен (– 14). Однако ясно, что длина стороны прямоугольника не может измеряться отрицательным числом, поэтому этот корень надо отбросить. Остается только k = 9. То есть длина первой стороны равна 9 см. Вторая сторона равна k + 5, то есть 9 + 5 = 14 см.

Ответ: 9 и 14 см.

Пример. Сумма квадратов двух последовательных нечетных чисел составляет 290. Что это за числа?

Решение. Обозначим первое число как n. Нечетные числа чередуются с четными, поэтому следующим нечетным числом будет n + 2. Перепишем условие задачи в виде уравнения и найдем его корни:

n² + (n + 2)² = 290

n² + n² + 4n + 4 – 290 = 0

2n² + 4n – 286 = 0

D = 4²– 4•2•(– 286) = 16 + 2288 = 2304

Получили два решения. Если первое число равно – 13, то второе составит n + 2 = – 11. Если же n = 11, то второе число будет равно 13.

Ответ: – 13 и 11, либо 11 и 13.

Теорема Виета

Большое значения имеют уравнения, у которых старшим коэффициентом является единица. Математики называют их приведенными уравнениями.

Дадим несколько примеров приведенных квадратных уравнений:

• х² + 6х + 29 = 0
• у² – 7,54у + 87 = 0
• z² + 21z + 112 = 0

Название «приведенное» возникло из-за того, что каждое квадратное уравнение можно сделать приведенным, если поделить его части на коэффициент перед х². Пусть есть уравнение

4х² + 5х + 6 = 0

Поделим на 4 обе его части:

х² + 1,25х + 1,5 = 0

Для приведенного уравнения сформулирована теорема Виета, которая указывает на взаимосвязь его корней и коэффициентов:

Доказать это очень легко. Если у уравнения

х² + px + q = 0

существует два корня, то они вычисляются по формулам:

Найдем их сумму:

Аналогично можно посчитать и их произведение:

Естественно, если у уравнения не существует корней (D< 0), то теорема к нему неприменима. Если же корень есть ровно один корень, тогда надо считать, что у уравнения два одинаковых корня.

Удостоверимся в верности этой теоремы на примерах.

1. х²– 8х + 15 = 0; корни (х₁ и х₂) равны 3 и 5, в чем можно убедиться подстановкой:

3² – 8•3 + 15 = 0

5² – 8•5 + 15 = 0

Перемножим корни и получим 3•5 = 15 (свободный член), при сложении корней получается 3 + 5 = 8 (второй коэффициент без минуса);

1. у² + 13у + 42= 0, корни (– 6) и (– 7), произведение корней 42, сумма корней – 13;
2. х² + 2х – 8 = 0, корни (– 4) и 2, их сумма равна (– 2), а произведение (– 8).

Справедливо и утверждение, известное как обратная теорема Виета:

Возьмем числа 4 и 9. Их сумма равна 13, а произведение 36, поэтому они являются корнями уравнения:

х² – 13х + 36 = 0

в чем можно убедиться, подставив их вместо х.

Пример. Учитель математики перед уроком составляет квадратные уравнения, причем стремится к тому, чтобы у них были целые корни (чтобы детям было просто считать). Подскажите ему пример уравнения, чьи корни равны 3 и 8.

Решение. Перемножим и сложим числа 3 и 8:

3•8 = 24

3 + 8 = 11

Соответственно, уравнением с корнями 3 и 8 будет

х² – 11х + 24 = 0

Ответ: х² – 11х + 24 = 0

Разложение квадратного трехчлена на множители

При решении уравнения

ах² + bх + с = 0

мы находим его корни. Однако отдельно выделяют и такое понятие, как корень многочлена. Так называют значение переменной, которая обращает полином в ноль.

Понятно, что для нахождения корней полинома второй степени следует решить квадратное уравнение.

Сначала рассмотрим трехчлены, у которых коэффициент при х²а равен 1. Предположим, что нам удалось разложить его на произведение двух линейных полиномов:

х² + bх + с = (х –s)(х –k)

где s и k– какие-то произвольные числа.

Выражение справа является произведением, а потому обращается в ноль только тогда, когда нулю равен один из множителей:

х – s = 0 или х – k = 0

х = s или х = k

Так как при х = s или х = k в ноль обращается правая часть тождества, то также должна обращаться и левая часть. Получается, что числа s и k – это корни трехчлена х² + bх + с.

Убедимся в этом, раскрыв скобки в правой части тождества:

(х –s)(х –k) = х²–kx–sx + sk = х²– (k + s)х + sk

подставим это выражение в исходное равенство:

х² + bх + с = (х – s)(х — k) = х² – (k + s)х + sk

х² + bх + с = х² – (k + s)х + sk

Получается, произведение s и k дает свободный член, а их сумма в точности равна коэффициенту при х, взятому со знаком минус. Значит, по теореме Виета, они являются корнями уравнения!

Обозначим корни уравнения как х₁ и х₂. Если у трехчлена коэффициент а отличен от единицы, то эта формула (ее называют формулой разложения квадратного трехчлена на множители) примет несколько иной вид:

ах² + bx + c = а(х – х₁)(х – х₂)

То есть справедливо утверждение:

А теперь и докажем его.

Пусть есть уравнение ах² + bx + c = 0 с корнями х₁ и х₂. Поделим его на а:

х² + (b/a)х + с/а = 0

по теореме Виета можно записать:

х₁+ х₂ = – b/a

х₁•х₂ = с/а

Умножив первое тождество на (– а), а второе наа, получим

– а(х₁ + х₂) = b

ах₁•х₂ = с

Осталось подставить эти равенства в исходный многочлен:

ах² + bx + c = ах²– а(х₁ + х₂)х + ах₁•х₂= а(х²– хх₁–хх₂ + х₁•х₂) =

= а(х(х – х₁) – х₂(х – х₁)) = а(х – х₁)(х – х₂)

Для чего же мы доказывали эту теорему? С ее помощью можно выполнить разложение квадратного трехчлена на множители. Проиллюстрируем это на примерах.

Пример. Разложите полином

2х² + 12х – 14

на множители.

Решение. Для начала следует решить уравнение 2х² + 12х – 14 = 0:

D = 12²– 4•2•(– 14) = 144 + 112 = 256

Найдя х₁ и х₂, можем выполнить и разложение:

2х² + 12х – 14 = 2(х – 1)(х – (– 7)) = 2(х – 1)(х + 7)

Ответ: 2(х – 1)(х + 7)

Пример. Упростите выражение

Решение. На первый взгляд кажется, что сокращать нечего. Однако и в числителе, и в знаменателе находятся квадратные трехчлены. Разложим их на множители, решив соответствующие уравнения:

h²+ 2h– 15 = 0

D = 2² – 4•1•(– 15) = 4 + 60 = 64

Получаем, что

h²– 2h– 15 = (h+ 5)(h– 3)

Теперь раскладываем второй полином:

h²– 9h +18 = 0

D = (– 9)² – 4•1•18 = 81 – 72 = 9

Соответственно, можно записать:

h²– 9h +18 = (h– 3)(h– 6)

А теперь подставим в исходную дробь полученные выражения:

Отметим, что если у полинома второй степени нет корней, то и разложить его на множители не получится.

Дробно-рациональные уравнения

Периодически приходится сталкиваться с уравнениями, где переменные присутствуют в знаменателе какой-нибудь дроби. Их называют дробно-рациональными уравнениями. Обычно их можно свести к более простому виду, но при этом следует учитывать ту особенность, что корень уравнения не должен обращать знаменатель в ноль.

Пример. Найдите решение дробно-рационального уравнения

Решение. Для начала перенесем дробь из правой части в левую, а потом приведем дроби к общему знаменателю:

Умножим уравнение на величину (х – 2)(х + 3)

(х + 1)(х – 2) + 10х – 4(х + 3) = 0

х² – 2х + х – 2 + 10х – 4х – 12 = 0

х² + 5х – 14 = 0

D = 5²– 4•1•(– 14) = 25 + 56 = 81

Казалось бы, мы нашли два корня: 2 и (– 7). Однако в исходном уравнении в знаменателе стоит выражение (х – 2)(х – 3). При х = 2 оно обращается в нуль, то есть дробь потеряет смысл. Поэтому корень 2 следует отбросить, и остается лишь корень (– 7)

Ответ: – 7

Нахождение коэффициентов квадратичной функции y=ax² + bx +c

I Нахождение коэффициента а :

1. по графику параболы определяем координаты вершины (m,n)

2. по графику параболы определяем координаты любой точки A (x;y)

3. подставляем эти значения в формулу квадратичной функции, заданной в другом виде:

y=а(х-m)²+n

1. решаем полученное уравнение.

II. нахождение коэффициента b: b= — (х₁ + х₂) это для приведённого уравнения

1. Сначала находим значение коэффициента a (шаг I, смотри выше)

В формулу для абсциссы параболы m = 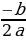подставляем значения m и а

1. Вычисляем значение коэффициента b.

III. нахождение коэффициента с: с = х₁ ∙ х₂ это для приведённого уравнения

1. Находим координату у точки пересечения графика параболы с осью Оу, это значение равно коэффициенту с, т.е. точка (0;C)-точка пересечения графика параболы с осью Оу.

2. Если по графику невозможно найти точку пересечения с осью Оу, то выполняем шаги I, II {находим коэффициенты а,Ь)

3. Подставляем найденные значения а, b ,А(х ; у) в уравнение у=ах² +bх+с и находим с.

I Нахождение коэффициента а :

1. по графику параболы определяем координаты вершины (m,n)

2. по графику параболы определяем координаты любой точки A (x;y)

3. подставляем эти значения в формулу квадратичной функции, заданной в другом виде:

y=а(х-m)²+n

1. решаем полученное уравнение.

II. нахождение коэффициента b:

1. Сначала находим значение коэффициента a (шаг I, смотри выше)

В формулу для абсциссы параболы m = 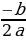подставляем значения m и а

1. Вычисляем значение коэффициента b.

III. нахождение коэффициента с:

1. Находим координату у точки пересечения графика параболы с осью Оу, это значение равно коэффициенту с, т.е. точка (0;C)-точка пересечения графика параболы с осью Оу.

2. Если по графику невозможно найти точку пересечения с осью Оу, то выполняем шаги I, II {находим коэффициенты а,b)

3. Подставляем найденные значения а, b ,А(х ; у) в уравнение у=ах² +bх+с и находим с.

Рассмотрим задачу: где невозможно по графику найти точно m и n необходимо найти все коэффициенты уравнения, задающего график:

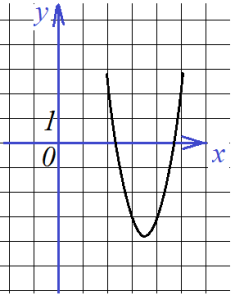
Найти все коэффициенты по графику функции

Подставляем в уравнение: координаты выбранных точек, например, таких: (2;2), (5;2), (4;-3). Получается:

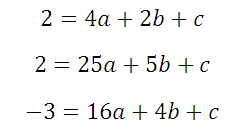
Последние два уравнения вычтем:

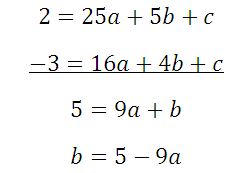
Данное выражение подставим в первое и второе уравнения:

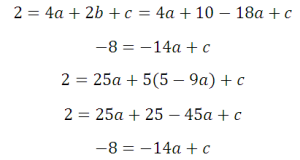
Вычтем два получившихся уравнения:

Зная а, можем найти и остальные коэффициенты:

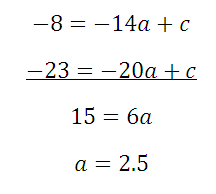
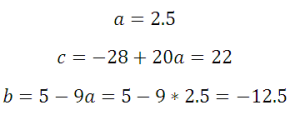
Следующая задача: найти коэффициенты уравнения, задающего график функции, изображенный на рисунке:

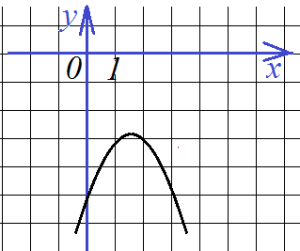
Найти все коэффициенты по графику функции

Здесь будет немного попроще, так как определить коэффициент с можно по рисунку: с=-5. Это значит, что потребуется только две точки, и система будет состоять только из двух уравнений. Возьмем для ее составления точки (1;-3) и (2;-3):

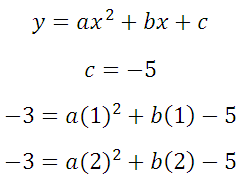
Вычтем получившиеся уравнения (второе – из первого) и определим коэффициенты а и b:

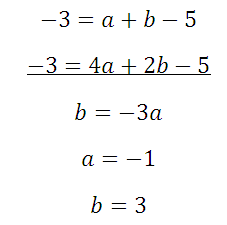
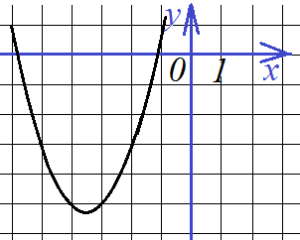
Найти все коэффициенты по графику функции

Наконец, еще одно такое же задание. Снова необходимо определить все коэффициенты функции, график которой представлен на рисунке:

Зададимся точками. Их будет три, уравнений тоже три, так как нам необходимо найти три коэффициента – a, b и c.

Точки будут: (-2; -3),(-5; -3) и  (-3; -5) . Тогда уравнения:

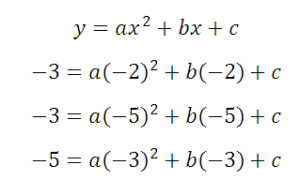
Из первого уравнения вычитаем второе:

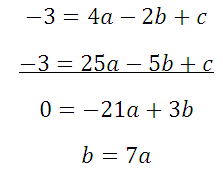
Полученное подставим в первое и третье:

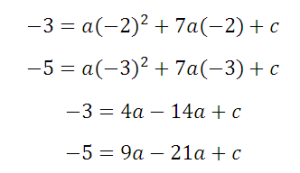
Полученные уравнения вычтем вновь, и найдем искомое: