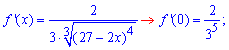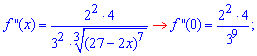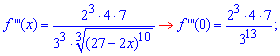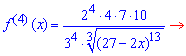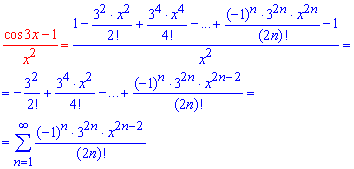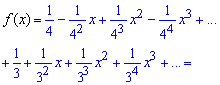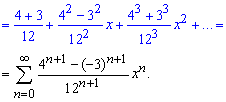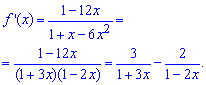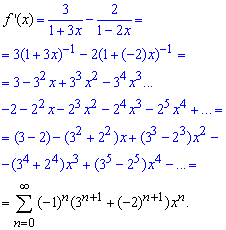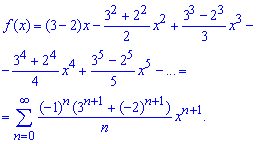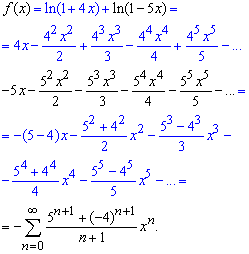Идея представления функции в виде многочлена с остаточным слагаемым основана на разложении функции в степенной ряд.
Ряды Тейлора и Маклорена
Бесконечно дифференцируемую в точке x0x_0 функцию действительной переменной f(x)f(x) можно разложить в ряд по степеням двучлена (x−x0)(x-x_0):
f(x)=f(x0)+f′(x0)1!(x−x0)+f′′(x0)2!(x−x0)2+…+f(n)(x0)n!(x−x0)n+…=f(x)=f(x_0)+dfrac{f{‘}(x_0)}{1!}(x-x_0) +dfrac{f{»}(x_0)}{2!}(x-x_0)^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +ldots =
=∑k=0∞f(k)(x0)k!(x−x0)k=sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k
Этот ряд называют рядом Тейлора.
В случае x0=0x_0=0, полученный степенной ряд:
f(x)=f(0)+f′(0)1!x+f′′(0)2!(x−x0)2+…+f(n)(x0)n!(x−x0)n+…=f(x)=f(0)+dfrac{f{‘}( 0)}{1!} x +dfrac{f{»}(0)}{2!}(x-x_0)^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +ldots =
=∑k=0∞f(k)(x0)k!(x−x0)k=sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k
называют рядом Маклорена.
Запишем разложения основных элементарных функций в ряд Маклорена, укажем соответствующие интервалы сходимости и приведем примеры их определения.
- Показательная функция:
ex=1+x1!+x22!+x33!+…+xnn!+…=∑k=1∞xnn!,∣x∣<∞e^x=1+dfrac{x}{1!} +dfrac{x^2}{2!} +dfrac{x^3}{3!}+ldots+dfrac{x^n}{n!}+ldots=sumlimits_{k=1}^{infty} dfrac{x^n}{n!},quad |x|<infty
- Тригонометрические функции:
sinx=x1!−x33!+x55!−x77!+…+(−1)n+1x2n−1(2n−1)!+…=∑k=1∞(−1)k+1x2k−1(2k−1)!,∣x∣<∞sin x=dfrac{x}{1!} -dfrac{x^3}{3!} +dfrac{x^5}{5!} -dfrac{x^7}{7!} +ldots+dfrac{(-1)^{n+1}x^{2n-1}}{(2n-1)!}+ldots=sumlimits_{ k =1}^{infty} dfrac{(-1)^{ k +1}x^{2 k -1}}{(2 k -1)!},quad |x|<infty
cosx=1−x22!+x44!−x66!+…+(−1)n+1x2n(2n)!+…=∑k=0∞(−1)kx2k(2k)!,∣x∣<∞cos x=1 -dfrac{x^2}{2!} +dfrac{x^4}{4!} -dfrac{x^6}{6!} +ldots+dfrac{(-1)^{n+1}x^{2n}}{(2n)!}+ldots=sumlimits_{ k =0}^{infty} dfrac{(-1)^{k}x^{2 k }}{(2 k)!},quad |x|<infty
arctgx=x−x33+x55−x77+…+(−1)nx2n+12n+1+…=∑k=0∞(−1)kx2k+12k+1,∣x∣≤1arctg x=x-dfrac{x^3}{3} +dfrac{x^5}{5} -dfrac{x^7}{7} +ldots+dfrac{(-1)^{n}x^{2n+1}}{2n+1}+ldots=sumlimits_{ k =0}^{infty} dfrac{(-1)^{ k }x^{2 k +1}}{2 k +1},quad |x|le{1}
- Логарифмическая функции:
ln(1+x)=x1!−x22!+x33!−x44!+…+(−1)n+1xnn!+…=∑k=1∞(−1)k+1xkk!,x∈(−1;1]ln (1+x)=dfrac{x}{1!} -dfrac{x^2}{2!} +dfrac{x^3}{3!} -dfrac{x^4}{4!} +ldots+dfrac{(-1)^{n+1}x^{n}}{n!}+ldots=sumlimits_{ k =1}^{infty} dfrac{(-1)^{ k +1}x^{ k }}{ k!},quad xin (-1;1]
- Степенная функции:
(1+x)α=1+α1!x+α(α−1)2!x2+α(α−1)(α−2)3!x3+…+α(α−1)…(α−n+1)n!xn+…=(1+x)^alpha=1+dfrac{alpha }{1!}x+dfrac{alpha (alpha -1)}{2!}x^2 +dfrac{alpha (alpha -1)( alpha -2)}{3!} x^3 +ldots+dfrac{alpha (alpha -1) ldots ( alpha-n+1)} {n!} {x^n}+ldots=
=∑k=0∞α(α−1)…(α−k+1)k!xk=sumlimits_{ k =0}^{infty} dfrac{alpha (alpha -1) ldots ( alpha-k+1)}{ k!} {x^ k }
11−x=1+x+x2+…+xn+…=∑k=0∞xk,∣x∣<1dfrac{1}{1-x}=1+x+x^2+ldots+x^n+ldots =sumlimits_{ k =0}^{infty}x^{ k },quad |x|<1
Пример 1
Найдем для функции:
f(x)=sinxf(x)=sin x
интервал сходимости ряда:
f(x)=sinx==∑n=1∞(−1)n+1x2n−1(2n−1)!f(x)=sin x==sumlimits_{n=1}^{infty} dfrac{(-1)^{n+1}x^{2n-1}}{(2n-1)!}
Воспользуемся признаком Даламбера:
limn→∞∣an+1an∣=limn→∞∣x2n+1/(2n+1)!x2n−1/(2n−1)!∣=x2limn→∞12n(2n+1)=0limlimits_{n to infty } left | dfrac {a_{n+1}}{a_n} right | = limlimits_{n to infty } left | dfrac {x^{2n+1}/{(2n+1)!}}{ x^{2n-1}/{(2n-1)!}} right | =x^2 limlimits_{n to infty } dfrac {1} {2n(2n+1)}=0
Полученный результат говорит о том, что предел равен нулю для любого xx, и, следовательно, интервалом сходимости ряда является вся числовая ось.
Пример 2
Найдем интервал сходимости ряда для функции
f(x)=arctgx=∑n=0∞(−1)nx2n+12n+1,∣x∣≤1f(x)=arctg x= sumlimits_{n=0}^{infty} dfrac{(-1)^{n}x^{2n+1}}{2n+1}, quad |x|le{1}
Воспользовавшись признаком Даламбера применительно к степенному ряду, получаем:
limn→∞∣an+1an∣=limn→∞∣x2n+1/(2n+1)x2n−1/(2n−1)∣=x2limn→∞2n−12n+1=x2limn→∞2−1n2+1n=x2limlimits_{n to infty } left | dfrac {a_{n+1}}{a_n} right | = limlimits_{n to infty } left | dfrac {x^{2n+1}/(2n+1)}{ x^{2n-1}/(2n-1)} right | =x^2 limlimits_{n to infty } dfrac {2n-1} {2n+1}=x^2 limlimits_{n to infty } dfrac {2-dfrac{1}{n}}{2+dfrac{1}{n}}= x^2
Условие сходимости по этому признаку имеет вид:
x2<1x^2<1
В граничных точках x=±1x=pm1 получаем знакопеременный ряд вида:
∑n=0∞anx2n+1sumlimits_{n=0}^{infty} a_n x^{2n+1},
где ∣an∣=1n+1|a_n|=dfrac {1}{n+1}
Заметим, что
limn→∞∣an∣=0limlimits_{n to infty } |a_n|=0
и, согласно признаку Лейбница, знакопеременный ряд сходится. Таким образом, интервалом сходимости исходного ряда является: ∣x∣≤1|x| le 1.
Применение формулы и рядов Маклорена
Вычисление значений функций
Идея использования рядов для приближенного вычисления примечательна тем, что можно добиться требуемой точности, т.е. фактически найти требуемое значение со сколь угодно высокой точностью.
Пример
Вычислим значение числа ee с точностью до второго знака после запятой. Воспользуемся разложением в ряд Маклорена функции f(x)=exf(x)=e^x при x=1x=1, вычислив сумму до шестого члена в разложении и с остаточным членом в форме Лагранжа:
e1=1+11!+12!+13!+14!+15!+ec6!,0≤c≤1e^1=1+dfrac {1}{1!} +dfrac {1}{2!} +dfrac {1}{3!} +dfrac {1}{4!} +dfrac {1}{5!} +dfrac {e^c}{6!},quad 0le c le 1
Далее:
e1=16360!+ec6!≈2.716+ec6!,0≤c≤1e^1=dfrac {163}{60!} +dfrac {e^c}{6!}approx 2.716+dfrac {e^c}{6!},quad 0le c le 1
Учитывая, что ec6!<0.0014dfrac {e^c}{6!}<0.0014 получаем результат e≈2.72e approx 2.72
Вычисление пределов функций
На практике часто встречаются такие пределы, которые нельзя найти, используя первый и второй замечательные пределы, правило Лопиталя или другие способы вычислений. В этих случаях можно воспользоваться разложением элементарных функций в степенной ряд Маклорена и уже затем найти сам предел.
Пример
Вычислим:
limx→0e2x−1−2x−2x2x−sinxlimlimits_{x to 0 } dfrac {e^{2x}-1-2x-2x^2}{x-sin {x}}
Заменим exe^x и sinxsin{x} их разложениями в степенные ряды, находим:
limx→0e2x−1−2x−2x2x−sinx=limx→0(1+2x+4×22!+8×33!+…)−1−2x−2x2x−(x−x33!+x55!−…)=limlimits_{x to 0 } dfrac {e^{2x}-1-2x-2x^2}{x-sin {x}}=limlimits_{x to 0 } dfrac {left( 1+2x+dfrac{4x^2}{2!}+dfrac{8x^3}{3!}+ldots right)-1-2x-2x^2}{x-left( x-dfrac{x^3}{3!}+dfrac{x^5}{5!}-ldots right)}=
=limx→08×33!+16×44!+…x33!−x55!+…=limx→083!+16×4!+…13!−x25!+…=8=limlimits_{x to 0 } dfrac {dfrac{8x^3}{3!}+dfrac{16x^4}{4!}+ldots} {dfrac{x^3}{3!} -dfrac{x^5}{5!}+ldots} = limlimits_{x to 0 } dfrac {dfrac{8}{3!}+dfrac {16x}{4!} +ldots} {dfrac{1}{3!} -dfrac{x^2}{5!}+ldots}=8
Вычисление определенных интегралов
Конечно, на практике лучше всего вычислять точное значение определенного интеграла. Но очень часто соответствующие неопределенные интегралы является «неберущимися». Поэтому для приближенного вычисления определенного интеграла используется разложение подынтегральной функции в ряд Маклорена.
Пример
Вычислим с точностью до третьего знака после запятой:
∫01x3e−xdxdisplaystyle intlimits_0^1 sqrt[3] x e^{-x} dx
Для приближенного вычисления этого определенного интеграла используется разложение функции f(x)=sqrt[3]xe−xf(x)= sqrt[3] x e^{-x} в ряд Маклорена:
f(x)=sqrt[3]xe−x=x1/3−x4/3+12×7/3−16×10/3+…f(x)= sqrt[3] x e^{-x}=x^{1/3}-x^{4/3}+dfrac{1}{2}x^{7/3}-dfrac{1}{6}x^{10/3}+ldots
Интервал, заданный пределами интегрирования: 0≤x≤10 le x le 1 входит в радиус сходимости полученного ряда (−∞;+∞)(-infty;+infty).
Интегрируя почленно, получаем:
∫01f(x)=∫01×1/3dx−∫01×4/3dx+12∫01×7/3dx−16∫01×10/3dx+…=displaystyleintlimits_0^1 f(x)= intlimits_0^1 x^{1/3}dx-intlimits_0^1 x^{4/3}dx+dfrac{1}{2}intlimits_0^1 x^{7/3}dx-dfrac{1}{6}intlimits_0^1 x^{10/3}dx+ldots=
=34×4/3∣01−37×7/3∣01+32⋅10×10/3∣01−36⋅13×13/3∣01+…= dfrac{3}{4} Biggl. x^{4/3}Biggr |_0^1-dfrac{3}{7} Biggl. x^{7/3}Biggr |_0^1+dfrac{3}{2 cdot 10} Biggl. x^{10/3}Biggr |_0^1-dfrac{3}{6 cdot 13} Biggl. x^{13/3}Biggr|_0^1+ldots
и с учетом требуемой точности:
∫01x3e−xdx≈34−37+32⋅10−36⋅13≈928+29260≈197455≈0,433displaystyleintlimits_0^1 sqrt[3] x e^{-x} dx approx dfrac{3}{4}-dfrac{3}{7}+dfrac{3}{2 cdot 10}-dfrac{3}{6 cdot 13}approx dfrac{9}{28}+dfrac{29}{260} approx dfrac{197}{455} approx 0,433
Лекция 16. Ряды Тейлора и Маклорена
16.1. Разложение элементарных
функций в ряды Тейлора и
Маклорена
Покажем,
что если произвольная функция
задана на множестве
, в окрестности точки
имеет множество производных и является
суммой степенного ряда:
,
то
можно найти коэффициенты этого ряда.
Подставим
в степенной ряд
.
Тогда
.
Найдем
первую производную функции
:
При
:
.
Для
второй производной получим:
При
:
.
Продолжая
эту процедуру n
раз получим:
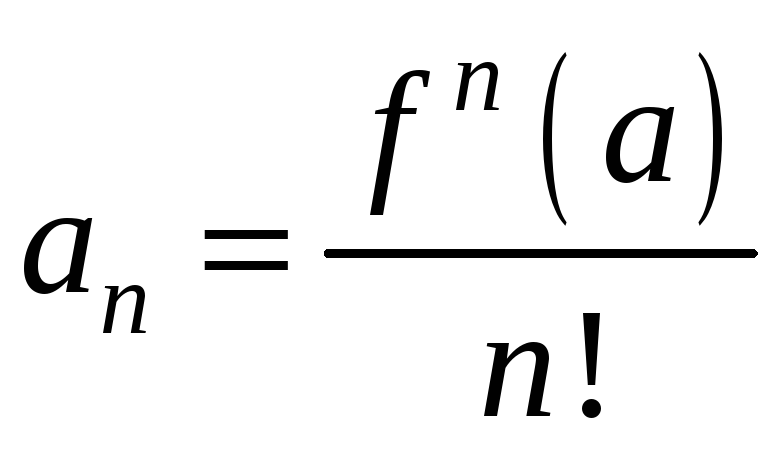
Таким
образом, получили степенной ряд вида:
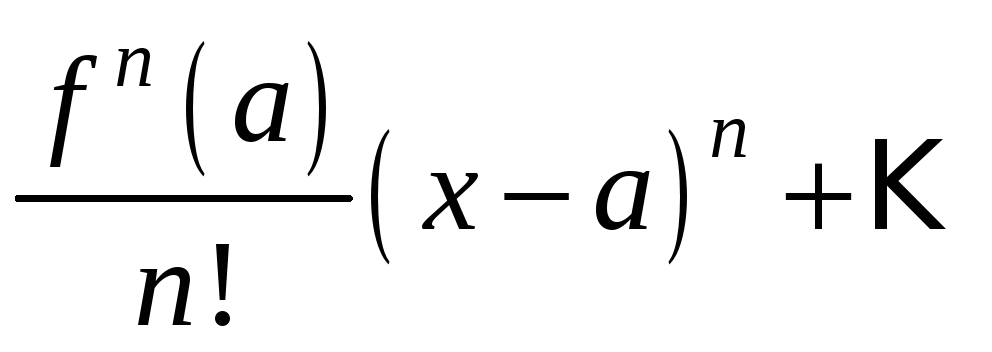
который
называется рядом Тейлора
для функции
в окресности точки
.
Частным
случаем ряда Тейлора является ряд
Маклорена
при
:
Остаток
ряда Тейлора (Маклорена) получается
отбрасыванием от основных рядов n
первых членов и обозначается как
.
Тогда функцию
можно записать как сумму n
первых членов ряда
и остатка
:
,
то
есть
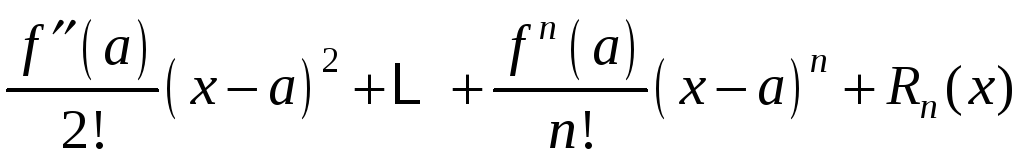
Остаток
обычно
выражают разными формулами.
Одна
из них в форме Лагранжа:
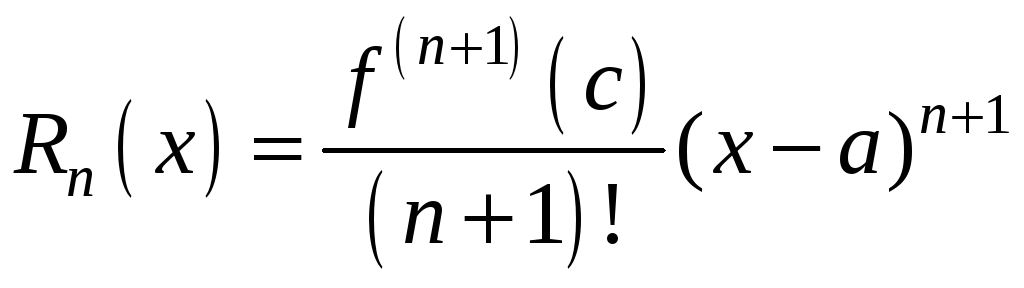
где
.
.
Заметим,
что на практике чаще используется
ряд Маклорена. Таким
образом, для того, чтобы записать функцию
в виде суммы степенного ряда
необходимо:
1)
найти коэффициенты ряда Маклорена
(Тейлора);
2)
найти область сходимости полученного
степенного ряда;
3)
доказать, что данный ряд сходится
к функции
.
Теорема
1
(необходимое и достаточное условие
сходимости ряда Маклорена). Пусть радиус
сходимости ряда
.
Для того, чтобы этот ряд сходился
в интервале
к функции
,
необходимо
и достаточно, чтобы выполнялось условие:
в указанном интервале.
Теорема
2. Если производные любого порядка
функции
в некотором промежутке
ограниченны по абсолютной величине
одним и тем же числом M,
то есть
,
то в этом промежутке функцию
можно разложить в ряд
Маклорена.
Пример
1. Разложить в
ряд Тейлора в окрестности
точки
функцию
.
Решение.
Находим
значение функции и ее производных при
.
,
;
,
;
,
;
,
;
,
………………………………………………………………………………………………………………………
,
;
Подставляем
эти значения в ряд. Получаем:
,
или
.
Область сходимости
.
Пример
2. Разложить
функцию
в ряд Тейлора в окрестности
точки
.
Решение:
Находим
значение функции и ее производных при
.
,
;
,
;
………..……………………………
,
.
Подставляем
эти значения в ряд. Получаем:
или
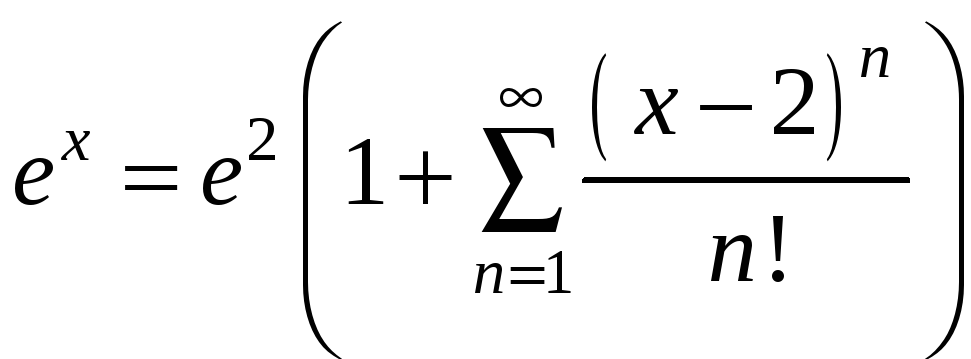
Найдем
область сходимости этого ряда. По
признаку Даламбера ряд сходится,
если
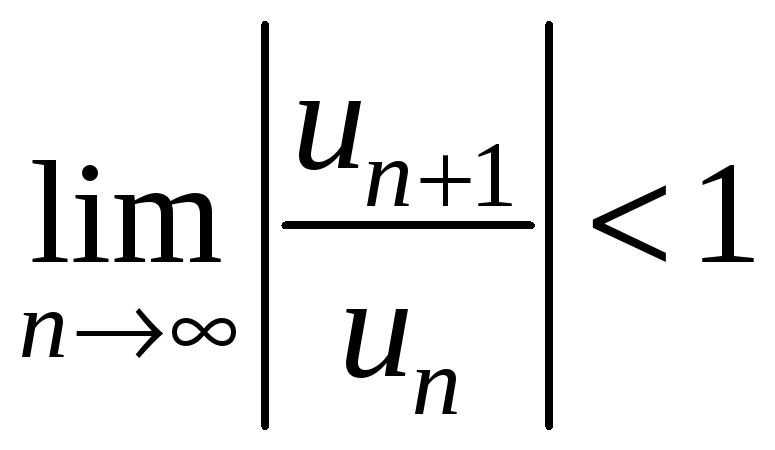
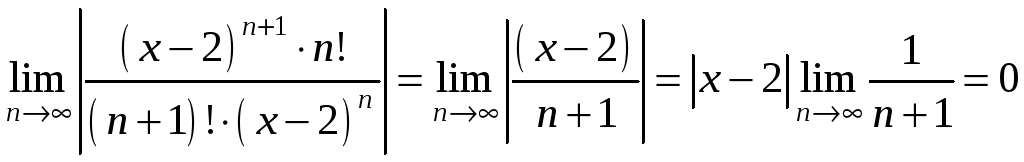
Следовательно,
при любом
этот предел менее 1, а
потому область сходимости ряда будет:
.
Рассмотрим
несколько примеров разложения
в ряд Маклорена основных элементарных
функций. Напомним, что ряд Маклорена:
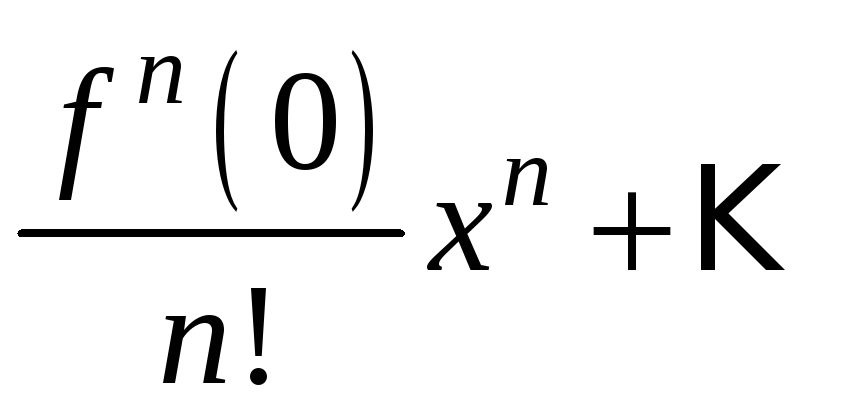
сходится
на интервале
к функции
.
Отметим,
что для разложения функции
в ряд необходимо:
а)
найти коэффициенты ряда Маклорена для
данной функции;
б)
вычислить радиус сходимости
для полученного ряда;
в)
доказать, что полученный ряд сходится
к функции
.
Пример
3. Рассмотрим функцию
.
Решение.
Вычислим
значение функции и ее производных при
.
.
Тогда числовые коэффициенты ряда
имеют вид:
для
любого n. Подставим найденные
коэффициенты в ряд Маклорена и получим:
Найдем
радиус сходимости полученного ряда, а
именно:
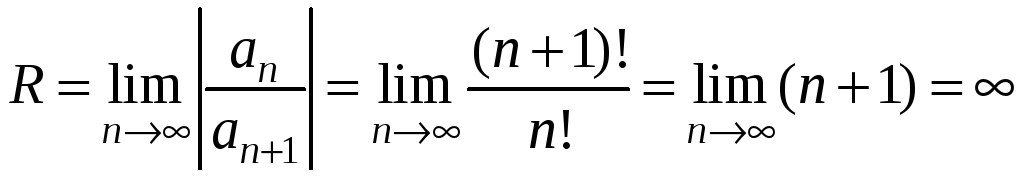
Следовательно,
ряд сходится на
интервале
.
Этот
ряд сходится к функции
при любых значениях
,
потому что на любом
промежутке
функция
и ее производные по
абсолютной величине
ограничены числом
.
Пример
4. Рассмотрим
функцию
.
Решение.
Найдем
значение функции и ее производных при
:
Нетрудно
заметить, что производные четного
порядка,
а производные нечетного
порядка
.
Подставим найденные коэффициенты в ряд
Маклорена и получим
разложение:
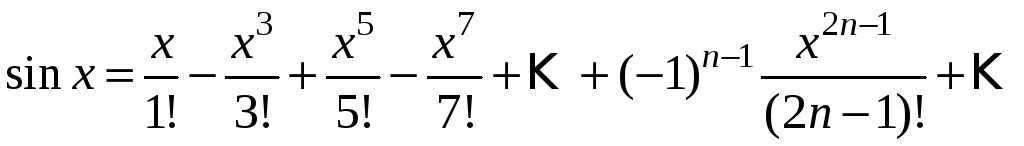
Найдем
интервал сходимости данного ряда. По
признаку Даламбера:
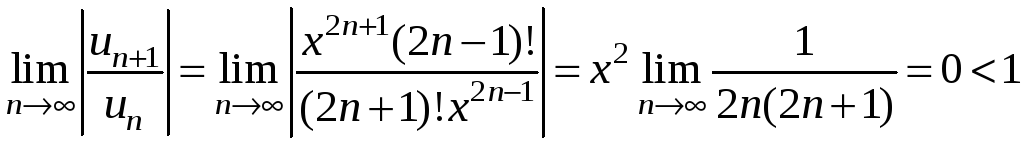
для
любого
.
Следовательно, ряд сходится
на интервале
.
Этот
ряд сходится к функции
,
потому что все ее производные
ограничены единицей.
Пример
5.
.
Решение.
Найдем
значение функции и ее производных при
:
Таким
образом, коэффициенты данного ряда:
и
,
следовательно:
Аналогично
с предыдущим рядом область сходимости
.
Ряд сходится к функции
,
потому что все ее
производные ограничены единицей.
Обратим
внимание, что функция
нечетная и разложение
в ряд по нечетным
степеням, функция
– четная и разложение в ряд по четным
степеням.
Пример
6. Биномиальный
ряд :.
Решение.
Найдем
значение функции и ее производных при
:
Отсюда
видно, что:
Подставим
эти значения коэффициентов в ряд
Маклорена и получим разложение данной
функции в степенной ряд:
Найдем
радиус сходимости этого ряда:
Следовательно,
ряд сходится на интервале
.
В предельных точках при
и
ряд может сходится или нет в зависимости
от показателя степени
.
Исследованный
ряд сходится на интервале
к функции
,
то есть сумма ряда
при
.
Пример
7. Разложим в
ряд Маклорена функцию
.
Решение.
Для
разложения в ряд этой
функции используем биномиальный ряд
при
.
Получим:
На
основе свойства степенных рядов
(степенной ряд можно интегрировать в
области его сходимости) найдем интеграл
от левой и правой частей данного ряда:
Найдем
область сходимости данного ряда:
,
то
есть областью сходимости данного ряда
является интервал
.
Определим сходимость ряда на концах
интервала. При
получим числовой ряд с общим членом
.
Этот ряд является гармоничным рядом,
то есть расходится. При
получим числовой ряд с общим членом
.
Ряд
по признаку Лейбница сходится. Таким
образом, областью сходимости данного
ряда является промежуток
.
16.2. Применение
степенных рядов степеней в приближенных
вычислениях
В
приближенных вычислениях степенные
ряды играют исключительно большую роль.
С их помощью составлены таблицы
тригонометрических функций, таблицы
логарифмов, таблицы значений других
функций, которые используют в разных
областях знаний, например в теории
вероятностей и математической статистике.
Кроме того, разложение
функций в степенной ряд полезно для их
теоретического исследования. Главным
вопросом при использовании степенных
рядов в приближенных вычислениях
является вопрос оценки погрешности при
замене суммы ряда суммой его первых n
членов.
Рассмотрим
два случая:
-
функция
разложена в знакочередующийся ряд; -
функция
разложена в знакопостоянный ряд.
Вычисление с помощью знакочередующихся
рядов
Пусть
функция
разложена в знакочередующийся степенной
ряд. Тогда при вычислении этой функции
для конкретного значения
получаем числовой ряд, к которому можно
применить признак Лейбница. В соответствии
с этим признаком, если сумму ряда заменить
суммой его первых n членов, то
абсолютная погрешность не превышает
первого члена остатка этого ряда, то
есть:.
Пример
8. Вычислить
с точностью до 0,0001.
Решение.
Будем
использовать ряд Маклорена для
,
подставив значение угла в радианах:
Если
сравнить первый и второй члены ряда с
заданной точностью, то:
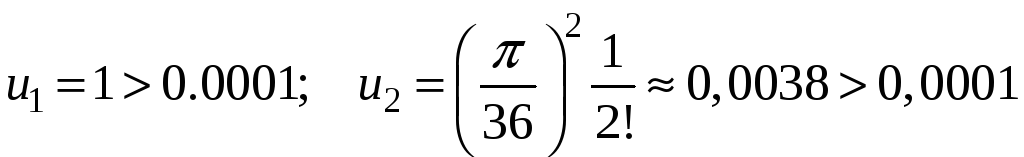
Третий
член разложения:
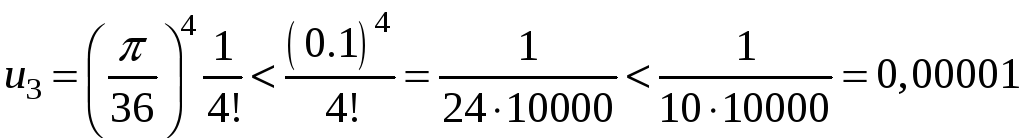
меньше
заданной точности вычисления.
Следовательно, для вычисления
достаточно оставить два члена ряда, то
есть
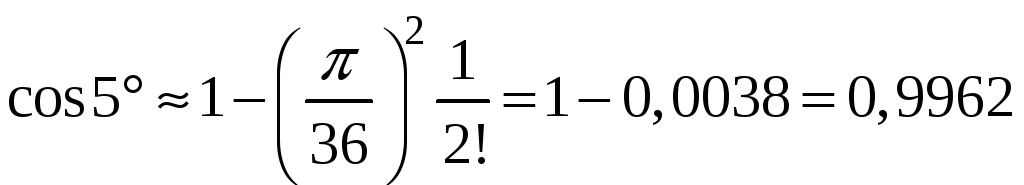
Таким
образом
.
Пример
9. Вычислить
с точностью 0,001.
Решение.
Будем
использовать формулу биномиального
ряда. Для этого запишем
в виде:
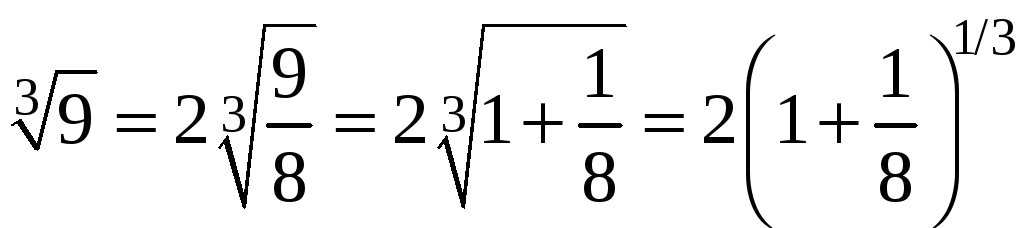
В
этом выражении
,
Сравним
каждый из членов ряда с точностью,
которая задана. Видно, что
.
Следовательно, для вычисления
достаточно оставить три члена ряда.
или
.
Вычисление с помощью
знакоположительных
рядов
Пример
10. Вычислить
число
с точностью до 0,001.
Решение.
В
ряд для функцїї
подставим
.
Получим:
Оценим
погрешность, которая возникает при
замене суммы ряда суммой первых
членов. Запишем очевидное неравенство:
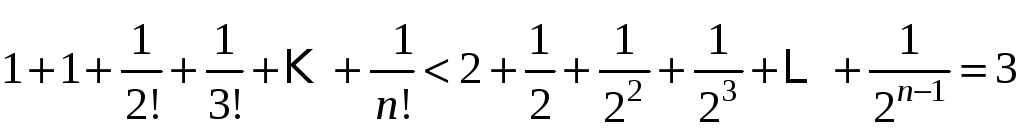
то
есть 2<<3.
Используем формулу остаточного члена
ряда в форме Лагранжа:
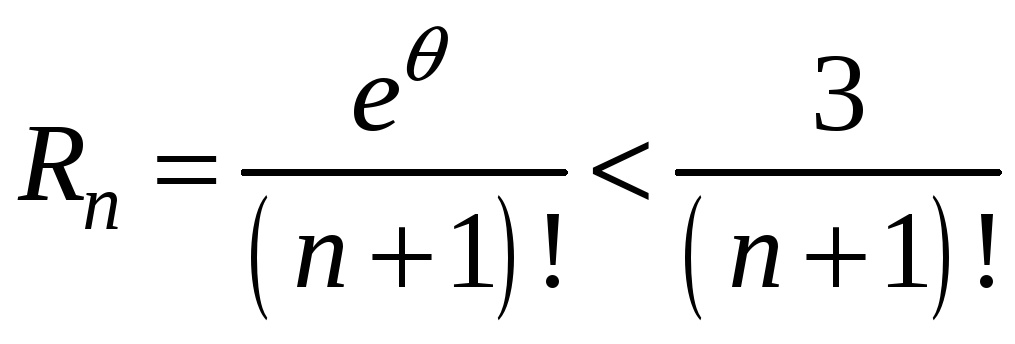
.
По
условию задачи нужно найти n
такое, чтобы выполнялось неравенство:
или
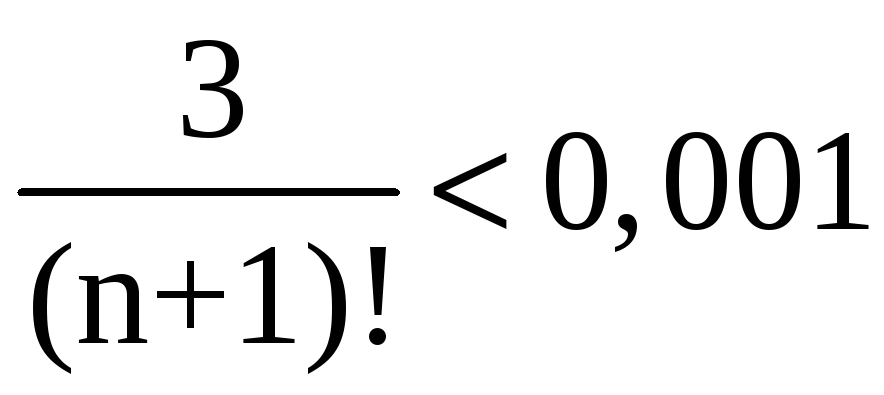
Легко
проверить, что при n
= 6:

Следовательно,
.
Отсюда
Пример
11. Вычислить
с точностью 0,0001.
Решение.
Заметим,
что для вычисления логарифмов можно
было бы применить ряд для функции
,
но этот ряд очень медленно сходится и
для достижения заданной точности нужно
было бы взять 9999 членов! Поэтому для
вычисления логарифмов, как правило,
используется ряд для функции
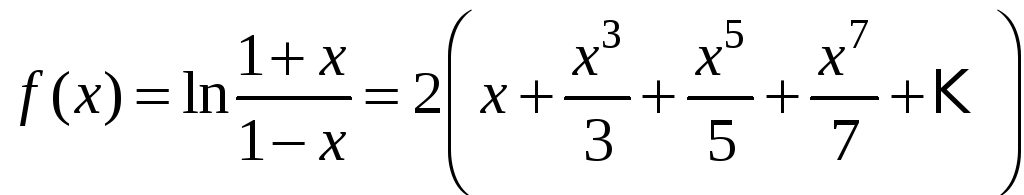
который сходится на интервале
.
Вычислим
с помощью этого ряда. Пусть
,
тогда
.
Следовательно,
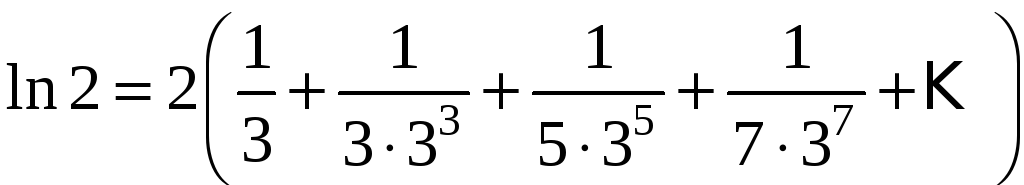
или
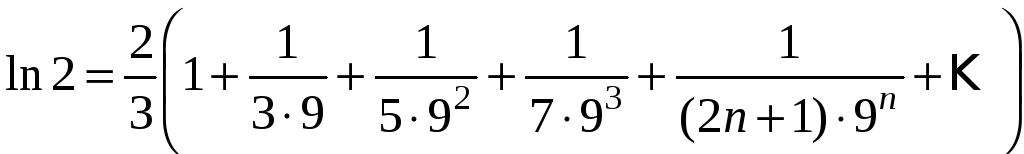
Для
того, чтобы вычислить
с заданной точностью, возьмем сумму
первых четырех членов:
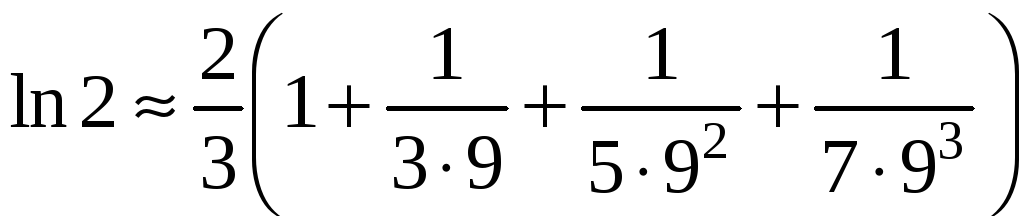
Остаток
ряда
отбросим. Оценим погрешность. Очевидно,
что
или 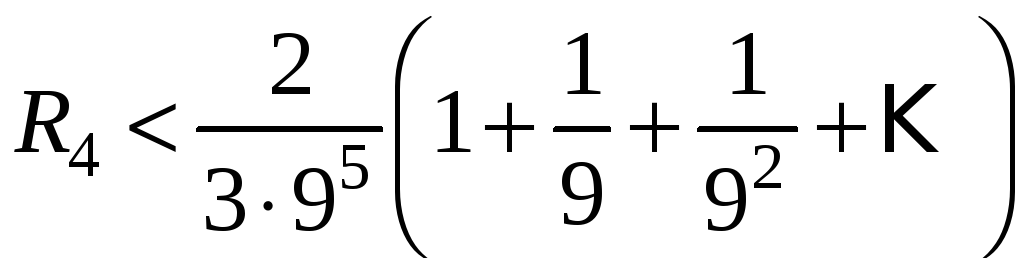
Отсюда
Таким
образом, в ряду, который был использован
для вычисления, достаточно было взять
только четыре первые
слагаемые вместо 9999 в ряду для функции
.
Вопросы для самодиагностики
1.
Что такое ряд Тейлора?
2.
какой вид имеел ряд Маклорена?
3.
Сформулировать теорему о разложении
функции в ряд Тейлора.
4.
Записать разложение в ряд Маклорена
основных функций.
5.
Указать области сходимости рассмотренных
рядов.
6.
Как выполнить оценку погрешности в
приближенных вычислениях с помощью
степенных рядов?
11
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Разложение в ряд Маклорена некоторых функций
- Рассмотрим геометрический ряд
- Пример с решением
Предположим, что функция 


Выразим коэффициенты ряда через 


Полагая в полученных равенствах х=0. получим 
Подставляя значения коэффициентов 

По этой ссылке вы найдёте полный курс лекций по высшей математике:
Следует отметить, что не все функции могут быть разложены в рад Маклорена- Может оказаться, что ряд Маклорена, составленный формально для функции 

Так же как и для числовых рядов, сумму
ряда Маклорена можно представить в виде (13.9)
где 

Тогда на основании свойства 4 сходящихся рядов (см. §13.1) можно сформулировать теорему.
Теорема. Для того чтобы ряд Маклорена сходился к функции 


Возможно вам будут полезны данные страницы:
Можно доказать, что если функция 
Замечание. Ряд Маклорена является частным случаем рядо Тейлора
Ряд Тейлора тесно связан с формулой Тейлора:
где 


Очевидно, что при выполнении условия (14.7) остаток 

Разложение в ряд Маклорена некоторых функций
1.
Имеем
По формуле (13.6)


2.
Имеем 


Очевидно, что производные четного порядка 


3. 

4. 





Рад (14.11) называется биномиальным. Если 

5.
Получить разложение для этой функции можно проще, ие вычисляя непосредственно коэффициенты ряда (14.6) с помощью производных.
Рассмотрим геометрический ряд




Интегрируя почленно равенство (14.12) в интервале (0; х), где



Можно доказать, что рады, приведенные в формулах (14.8) — (14.13), сходятся к функциям, для которых они составлены.
При разложении более сложных функций используют непосредственно формулу (14.6) либо таблицу простейших разложений (14.8) — (14.13).
Пример с решением
Разложить в ряд функции:
Решение:
а) Так как по (14.8)
то, заменяя 






Теперь

Лекции:
- Полное приращение и полный дифференциал функции многих переменных
- Производная косинуса
- Решение задачи Коши
- Дифференциальные уравнения
- Алгебраические комплексные числа
- Логарифмы: примеры и решения
- Производная и дифференциал
- Правило Лопиталя: пример решения
- Ряд тейлора примеры решения
- Каноническое уравнение эллипса
«Найти разложение в ряд Маклорена функци f(x)« — именно так звучит задание по высшей математике, которое одним студентам по силам, а другие не могут справиться с примерами. Есть несколько способов разложения ряда по степенях, здесь будет дана методика разложения функций в ряд Маклорена. При развитии функции в ряд нужно хорошо уметь вычислять производные.
Пример 4.7 Разложить функцию в ряд по степеням x
Вычисления: Выполняем разложение функции согласно формуле Маклорена. Сначала разложим в ряд знаменатель функции
напоследок умножим разложение на числитель.
Первое слагаемое — значение функции в нуле f (0) = 1/3.
Найдем производные функции первого и высших порядков f (x) и значение этих производных в точке x=0
Далее с закономерности изменения значения производных в 0 записываем формулу для n-й производной
Итак, знаменатель представим в виде разложения в ряд Маклорена
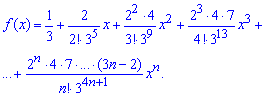
Умножаем на числитель и получаем искомое разложение функции в ряд по степеням х
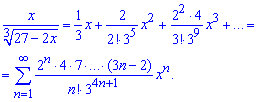
Как видите ничего сложного здесь нет.
Все ключевые моменты базируются на умении вычислять производные и быстрому обобщении значение производной старших порядков в нуле. Следующие примеры помогут Вам научиться быстро раскладывать функцию в ряд.
Пример 4.10 Найти разложение в ряд Маклорена функции
Вычисления: Как Вы возможно догадались раскладывать в ряд будем косинус в числителе. Для этого можете использовать формулы для бесконечно малых величин, или же вывести разложение косинуса через производные. В результате придем к следующему ряду по степеням x
Как видите имеем минимум вычислений и компактную запись разложения в ряд.
Пример 4.16 Разложить функцию в ряд по степеням x:
7/(12-x-x^2)
Вычисления: В подобного рода примерах необходимо дробь разложить через сумму простейших дробей.
Как это делать мы сейчас не будем показывать, но с помощью неопределенных коэффициентов придем к сумме дох дробей.
Далее записываем знаменатели в показательной форме
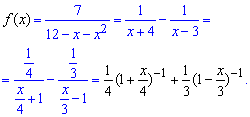
Осталось разложить слагаемые с помощью формулы Маклорена. Подытоживая слагаемые при одинаковых степенях «икс» составляем формулу общего члена разложения функции в ряд
Последнюю часть перехода к ряду в начале трудно реализовать, поскольку сложно объединить формулы для парных и непарных индексов (степеней), но с практикой у Вас это будет получаться все лучше.
Пример 4.18 Найти разложение в ряд Маклорена функции
Вычисления: Найдем производную этой функции:
Разложим функцию в ряд, воспользовавшись одной из формул Макларена:
Ряды почленно суммируем на основе того, что оба абсолютно совпадающие. Проинтегрировав почленно весь ряд получим разложение функции в ряд по степеням x
Между последними двумя строками разложения имеется переход который в начале у Вас будет забирать много времени. Обобщение формулы ряда не всем дается легко, поэтому не переживайте по поводу того что не можете достать красивой и компактной формулы.
Пример 4.28 Найти разложение в ряд Маклорена функции:
Запишем логарифм следующим образом
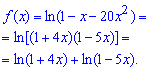
По формуле Маклорена раскладываем в ряд по степеням x логарифм функцию
Конечное свертывания на первый взгляд сложное, однако при чередовании знаков Вы всегда получите нечто подобное. Входной урок по теме расписания функций в ряд завершено. Другие не менее интересные схемы разложения будут подробно рассмотрены в следующих материалах.

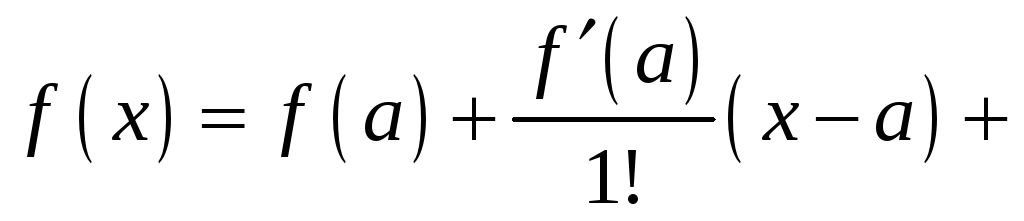
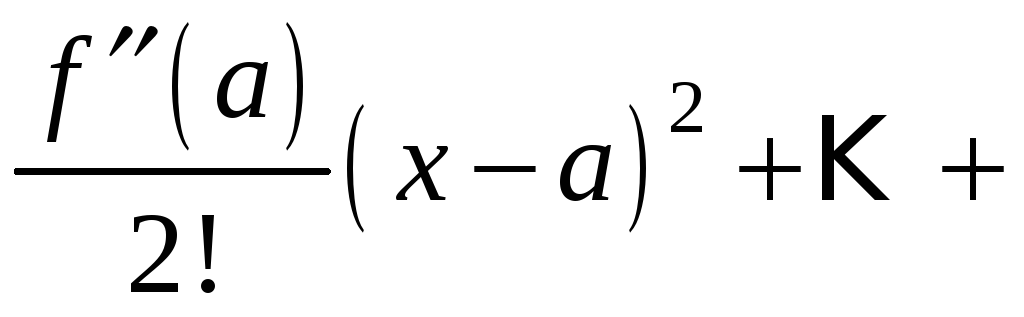
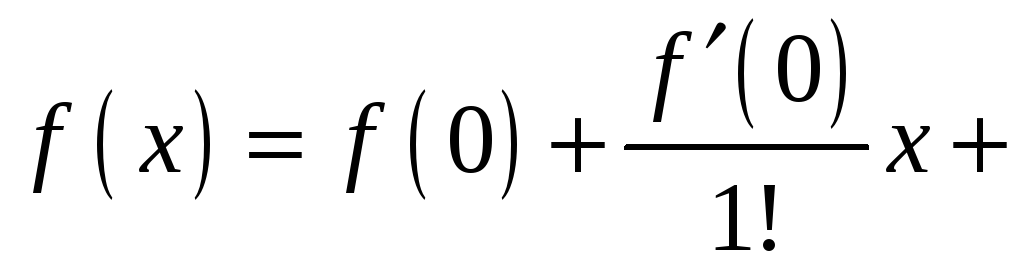
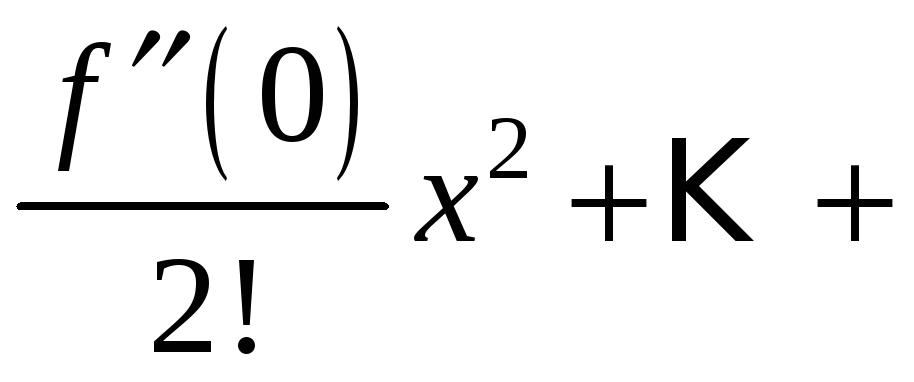
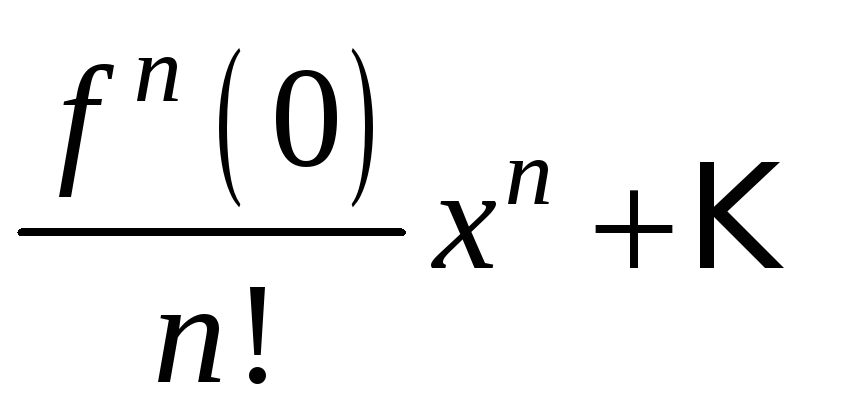
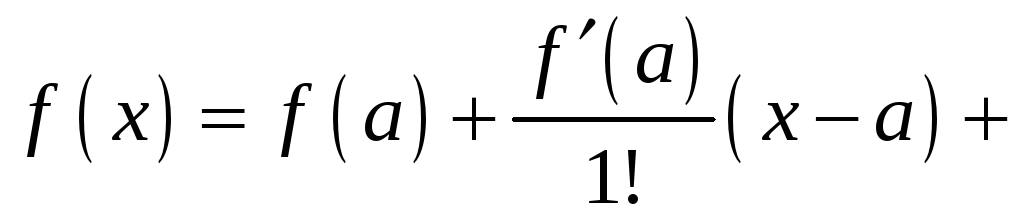
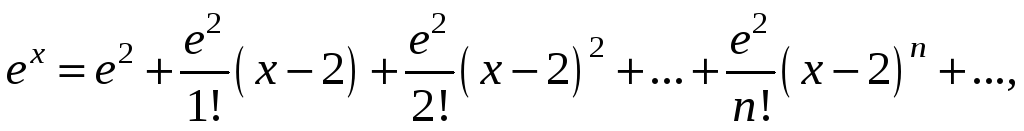
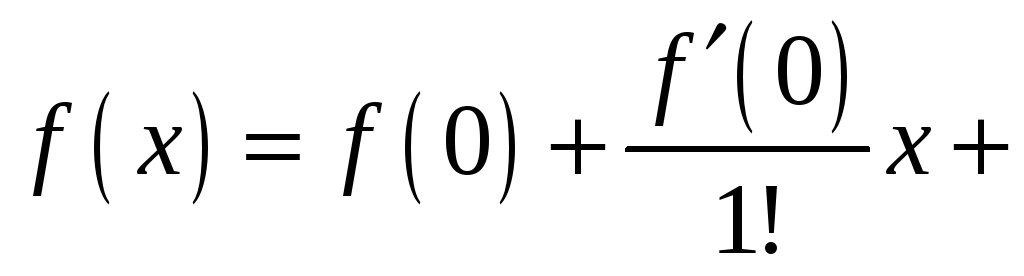
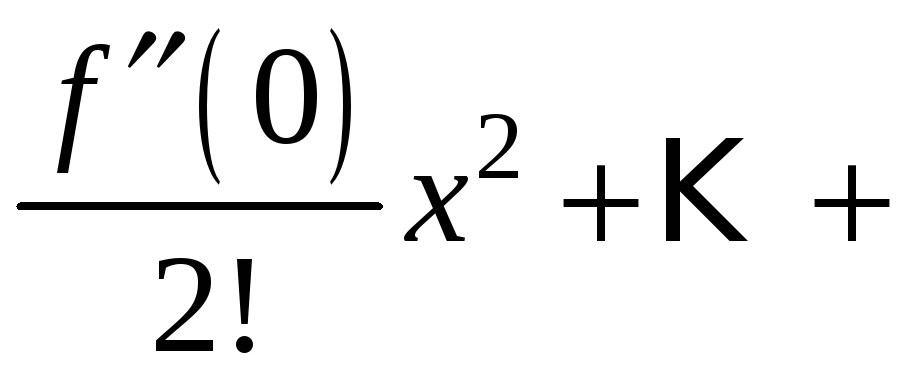
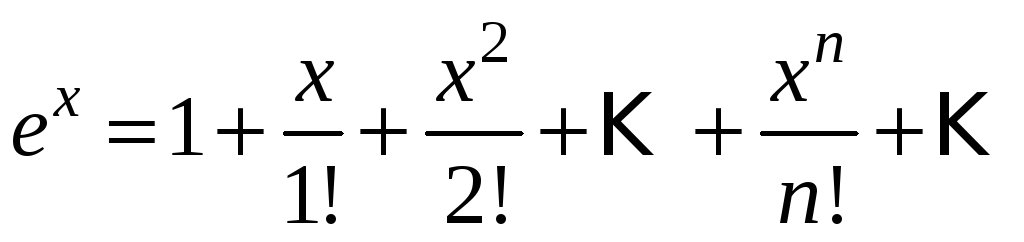
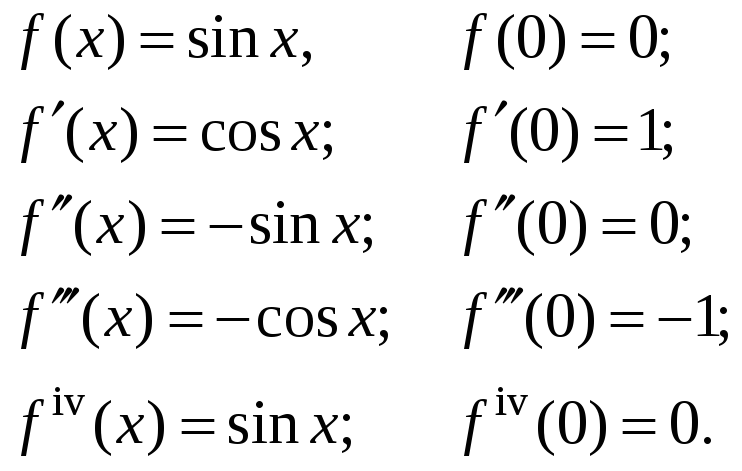
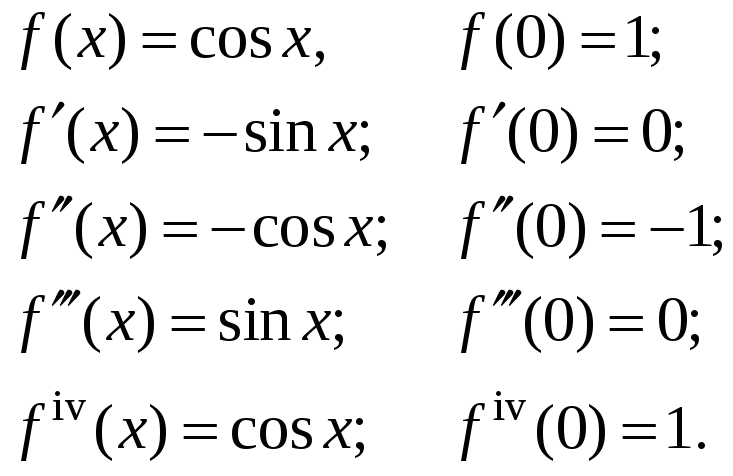
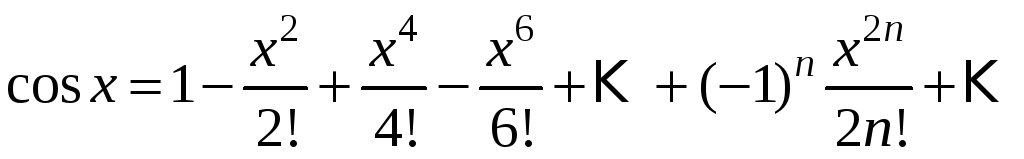
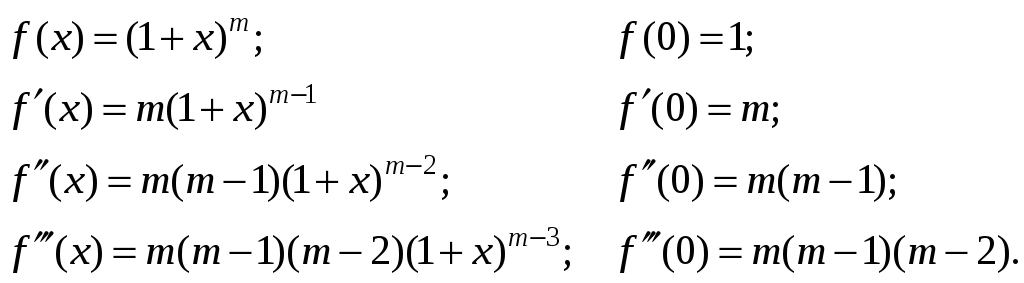

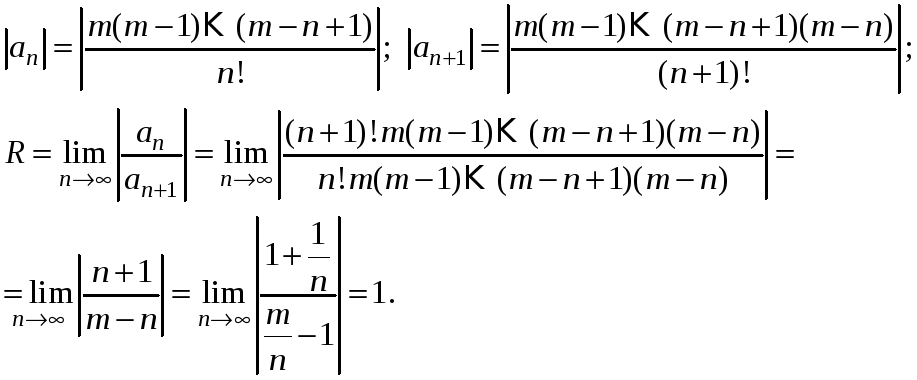
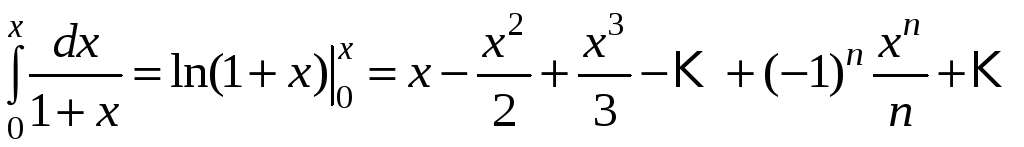
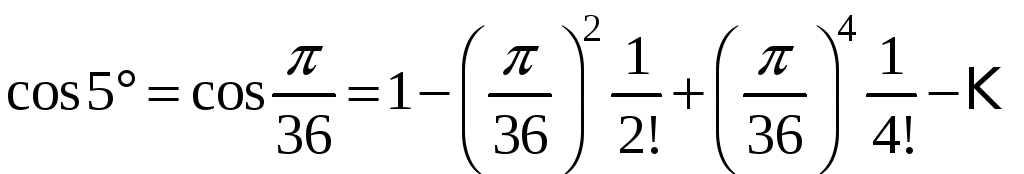
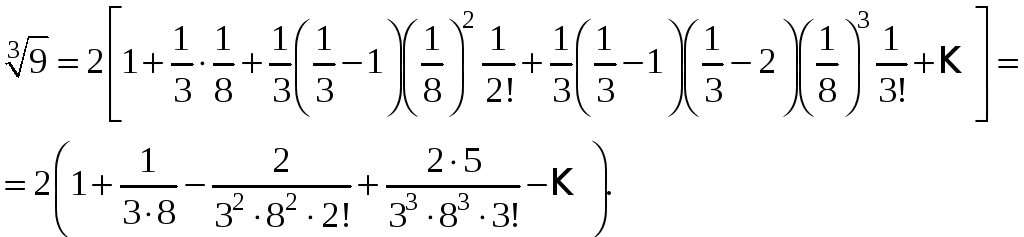
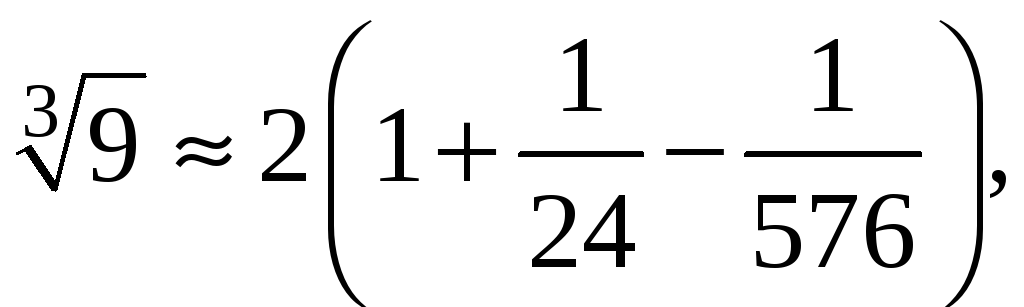
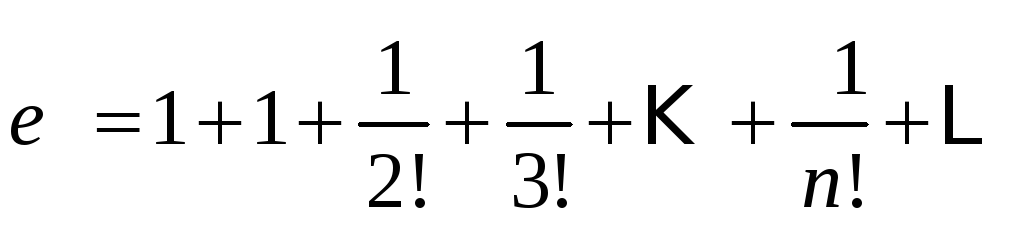
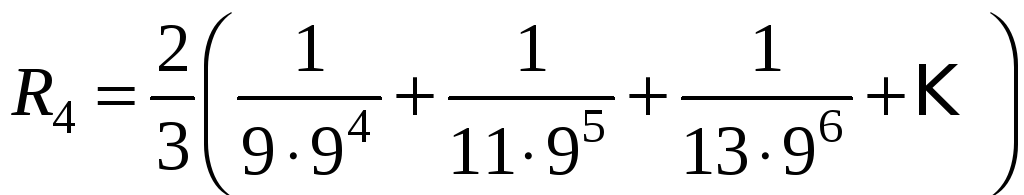
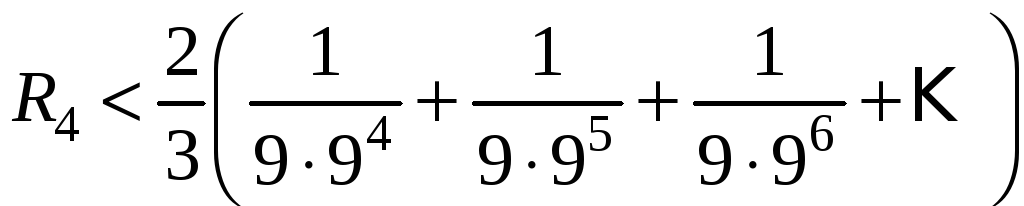
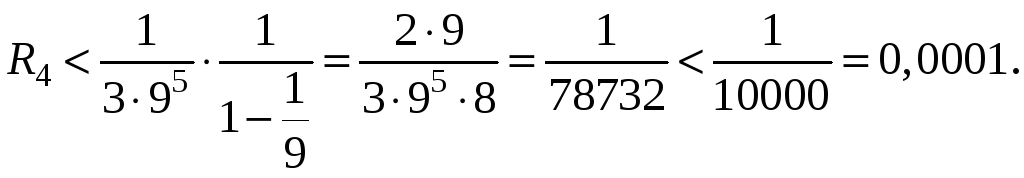



 ряда Маклорена можно представить в виде (13.9)
ряда Маклорена можно представить в виде (13.9)