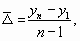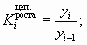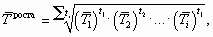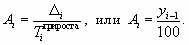Гражданское право — работа с недвижимостью. договорная работа, наследственное право, банкротство.
Важнейшим показателем эффективности производства в анализе финансовой ситуации компании является показатель темпа роста. Поговорим об особенностях его расчета.
Как рассчитать темп роста: формула
Что называют снижением темпа роста цен?
Подробнее
Этот термин показывает изменение значения любого экономического или статистического показателя в текущем периоде к его начальному значению (являющемуся базовым) за определенный временной промежуток. Измеряется он в процентах или коэффициентах.
Например, при сравнении объема выпуска товаров на конец года (допустим, в значении 100000 руб.) к показателю объема на начало года (70000 руб.) темп роста находят отношением конечного значения к начальному: 100000 / 70000 = 1,428. Индекс роста в примере составил 1,429. Это означает, что на конец года объем выпуска составил 142,9%.
Как рассчитать темп роста в процентах — формула:
ТР = Пт / Пб х 100%,
где Пк и Пб – показатели значений текущего и базового периодов.
Узнайте, может ли темп роста быть отрицательной величиной.
Темп роста показывает интенсивность изменений какого-либо процесса по отношению к его начальному (базовому) значению. Результат вычислений – один из трех вариантов:
-
ТР больше 100%, следовательно, конечное значение возросло в сравнении с начальным, т.е. налицо рост показателя;
-
ТР = 100%, т.е. изменений ни в большую, ни в меньшую сторону не произошло – показатель остался на прежнем уровне;
-
ТР меньше 100%, значит, анализируемый показатель снизился к началу периода.
Приведем примеры, как рассчитать темп роста в процентах по каждому варианту расчета, объединив исходные данные в таблицу:
|
Объем выпуска в тыс. руб. |
Расчет (Пт / Пб х 100%) |
|
|
2017 (Пб) |
2018 (Пт) |
|
|
600 |
800 |
133,3% |
|
600 |
600 |
100% |
|
600 |
400 |
66,7% |
Такой темп роста называют базисным, поскольку база сравнения по периодам остается неизменной – показатель на начало периода. Если же сравнительная база изменяется, а темп роста вычисляют отношением текущего значения к предыдущему (а не базисному), то этот показатель будет цепным.
Узнайте, чем отличается темп роста от темпа прироста.
Как рассчитать цепные темпы роста
Рассмотрим пример расчета базисного и цепного темпов роста:
|
Период |
Объем в тыс.руб. |
Темп роста в % |
|
|
базисный |
цепной |
||
|
1 кв. |
300 |
100 |
— |
|
2 кв. |
310 |
103,3 (310 / 300) |
103,3 (310 / 300) |
|
3 кв. |
280 |
93,3 (280 / 300) |
90,3 (280 / 310) |
|
4 кв. |
360 |
120 (360 / 300) |
128,6 (360 / 280) |
Цепные темпы роста характеризуют насыщенность изменения уровней от квартала к кварталу, базисные же отражают ее в целом за весь временной интервал (показатель 1 квартала – база сравнения).
Сравнивая показатели в приведенном примере, можно отметить, что ряд значений, рассчитанных к началу периода, имеет меньшую амплитуду колебаний, чем цепные показатели, вычисления которых привязаны не к началу года, а к каждому предшествующему кварталу.
Как рассчитать темпы прироста
Кроме расчета темпов роста, принято высчитывать и темпы прироста. Эти значения также бывают базисными и цепными. Базисный прирост определяют как отношение разности показателей текущего и базового периодов к значению базового периода по формуле:
∆ ТР = (Птек – Пбаз) / Пбаз х 100%
Цепной прирост рассчитывают как разность между текущим и предыдущим показателями, деленную на темп роста предыдущего периода:
∆ ТР = (Птек – Ппр.п) / Ппр. п х 100%.
Более простым способом расчета является формула: ∆ ТР = ТР – 100%, где расчетные показатели темпа роста уменьшаются на 100%, т. е. исходную величину. Показатель темпа прироста в отличие от значений темпа роста может иметь отрицательное значение, поскольку темп роста (или снижения) показывает динамику изменений показателя, а темп прироста говорит о том, какой характер они носят.
Продолжая пример, рассчитаем приросты объемов в рассматриваемых периодах:
|
Период |
Темпы прироста |
|
|
базисные |
цепные |
|
|
1 кв. |
— |
— |
|
2 кв. |
3,3% (103,3 – 100) или ((310 – 300) / 300 х 100) |
3,3% (103,3 – 100) или ((310 – 300) / 300 х 100) |
|
3 кв. |
— 6,7% (93,3 – 100) или ((280 – 300) / 300 х 100) |
-9,7% (90,3 – 100) или ((280 – 310) / 310 х 100) |
|
4 кв. |
20% (120 – 100) или (( 360 – 300) / 300 х 100) |
28,6% (128,6 – 100) или ((360 – 280) / 280 х 100) |
Анализируя результаты вычислений, экономист может сделать вывод:
-
Прирост объемов наблюдался во 2-м и 4-м кварталах, причем во 2-м он был наименьшим (3,3%). В 3-м квартале объем выпуска сократился на 6,7% в сравнении с показателями начала года;
-
Цепные темпы прироста обнаружили более глубокие колебания: объемы 3-го квартала снизились по отношению к показателям 2-го на 9,7%. Зато выпуск товаров в 4-м квартале вырос почти на треть в сравнении с итогами 3-го квартала. Столь существенные изменения в объемах производства могут свидетельствовать о сезонности выпускаемых продуктов, перебоях в снабжении необходимым сырьем или других причинах, которые исследует аналитик.
Как рассчитать средний темп роста
Средний темп роста – обобщающая характеристика уровня изменений. Расчет средних темпов роста и прироста также разграничивают на базисные и цепные. Для определения среднего темпа роста расчетные показатели по периодам складывают и делят на количество периодов. Таким же образом находят и средние темпы приростов. Вернемся к предыдущему примеру, рассчитав средние значения базисных темпов роста и прироста, а также аналогичных цепных показателей.
|
Показатель |
Значение в % |
Расчет |
|
Средний темп роста (базисный) |
105,5 |
(103,3 + 93,3 + 120) / 3 |
|
Средний темп прироста (базисный) |
5,5 |
(3,3 – 6,7 + 20) / 3 |
|
Средний темп роста (цепной) |
107,4 |
(103,3 + 90,3 + 128,6) / 3 |
|
Средний темп прироста (цепной) |
7,4 |
(3,3 – 9,7 + 28,6) / 3 |
Полученные цифры свидетельствуют о том, что в среднем с начала года объемы выпуска выросли на 5,5%, а в поквартальной привязке рост составил 7,4%.
Читайте также: Экспресс-анализ финансового состояния предприятия

Специализация: Гражданское право — работа с недвижимостью. договорная работа, наследственное право, банкротство.
Окончила в 2005 г. Тверской государственный университет, юридический факультет, специальность-юриспруденция.
Юрист в сфере недвижимости:составление договоров, регистрация в Росреестре прав и сделок,оформление наследственных прав,
сопровождение сделок с недвижимым имуществом,судебный опыт по делам,связанным с признанием прав на недвижимость.
Имеется опыт работы помощником арбитражного управляющего.
Цепные:
Базисные:
2. Определяем цепные и базисные темпы
роста (Т).
Цепные:
Базисные:
3. Определяем цепные и базисные
абсолютные приросты ().
Цепные:
Базисные:
4. Определяем цепные и базисные темпы
прироста ().
Цепные:
Базисные:
Проверим связь между базисными и цепными
абсолютными приростами:
.
Проверим связь между базисными и цепными
коэффициентами роста:
.
1.8.5. Определение
средних показателей динамики
По показателям
изменения уровней ряда динамики
(абсолютные приросты, темпы роста и
прироста), полученным в результате
анализа исходного ряда, могут быть
рассчитаны обобщающие показатели в
виде средних величин — средний абсолютный
прирост, средний темп роста, средний
темп прироста.
Средний абсолютный
прирост
может быть получен по одной из формул:
или
,
гдеn
— число уровней ряда динамики;
— первый уровень
ряда динамики;
—
последний уровень ряда динамики;
— цепные абсолютные
приросты.
Средний коэффициент
роста можно
определить, пользуясь формулами:
;
;
,
где n
— число рассчитанных цепных или базисных
темпов роста;
— уровень ряда,
принятый за базу для сравнения;
— последний уровень
ряда;
— цепные коэффициенты
роста;
— первый базисный
коэффициент роста;
—
последний базисный коэффициент роста.
Средний темп
роста
вычисляется по формуле:
.
Средний темп
прироста:
,
или
.
Средняя величина
абсолютного значения 1% прироста:
1.8.6. Определение в рядах динамики общей тенденции развития (тренд)
Определение уровней
ряда динамики на протяжении длительного
периода времени обусловлено действием
ряда факторов, которые неоднородны по
силе и направлению воздействия,
оказываемого на изучаемое явление.
Рассматривая
динамические ряды, пытаются разделить
эти факторы на постоянно действующие
и оказывающие определяющее воздействие
на уровни ряда, формирующие основную
тенденцию развития, и случайные факторы,
приводящие к кратковременным изменениям
уровней ряда динамики. Наиболее важна
при анализе ряда динамики его основная
тенденция развития (тренд), но часто по
одному лишь внешнему виду ряда динамики
ее установить невозможно, поэтому
используют специальные методы обработки,
позволяющие показать основную тенденцию
ряда. Методы обработки используются
как простые, так и достаточно сложные.
Простейший способ
обработки ряда динамики, применяемый
с целью установления закономерностей
развития — метод
укрупнения интервалов.
Суть метода в том,
чтобы от интервалов, или периодов
времени, для которых определены исходные
уровни ряда динамики, перейти к более
продолжительным периодам времени и
посмотреть, как уровни ряда изменяются
в этом случае.
Пример.
Данные о реализации молочной продукции
в магазинах города по месяцам представлены
таблицей (в тоннах)
|
месяц |
1987 |
1988 |
1989 |
|
январь |
5,3 |
5,3 |
5,4 |
|
февраль |
5,3 |
5,1 |
5,2 |
|
март |
7,9 |
8,3 |
8,2 |
|
апрель |
8,2 |
9,0 |
9,3 |
|
май |
9,8 |
9,5 |
10,1 |
|
июнь |
12,5 |
13,0 |
13,1 |
|
июль |
11,8 |
12,2 |
12,5 |
|
август |
10,3 |
10,4 |
10,8 |
|
сентябрь |
8,2 |
8,0 |
8,3 |
|
октябрь |
6,5 |
6,6 |
6,8 |
|
ноябрь |
5,4 |
5,5 |
5,7 |
|
декабрь |
5,5 |
5,5 |
5,6 |
|
итого за |
96,7 |
98,4 |
101 |
Исходные уровни
ряда динамики подвержены сезонным
изменениям; для определения общей
тенденции развития переходят от
ежемесячных уровней к годовым уровням:
1987г. — 96,7 тонн
1988г. — 98,4 тонн
1989г. — 101 тонна
Эти цифры, полученные
в результате перехода к годовым уровням
ряда динамики, показывают общую тенденцию
роста реализации молочной продукции.
Другой способ
определения тенденции в ряду динамики
— метод
скользящих средних.
Суть метода заключается в том, что
фактические уровни ряда заменяются
средними уровнями, вычисленными по
определённому правилу, например:
—исходные или
фактические уровни ряда динамики
заменяются средними уровнями:
…
…
…
В результате
получается сглаженный ряд, состоящий
из скользящих пятизвенных средних
уровней
.
Между расположением уровнейи
устанавливается соответствие:
— —
— —,
сглаженный ряд
короче исходного на число уровней
,
где k — число уровней, выбранных для
определения средних уровней ряда.
Сглаживание методом
скользящих средних можно производить
по четырём, пяти или другому числу
уровней ряда, используя соответствующие
формулы для усреднения исходных уровней.
Полученные при
этом средние уровни называются
четырёхзвенными скользящими средними,
пятизвенными скользящими средними и
т.д.
При сглаживании
ряда динамики по чётному числу уровней
выполняется дополнительная операция,
называемая центрированием, поскольку,
при вычислении скользящего среднего,
например по четырём уровням,
относится к временной точке между
моментами времени, когда были зафиксированы
фактические уровнии
.
Схема вычислений и расположений уровней
сглаженного ряда становится сложнее:
… — исходные
уровни;
— —
…
— сглаженные уровни;
— —
…
— центрированные сглаженные уровни;
.
Метод скользящих
средних не позволяет получить численные
оценки для выражения основной тенденции
в ряду динамики, давая лишь наглядное
графическое представление (пример 1).
Пример.
Таблица 1.
|
Годы |
Валовый |
Скользящая |
|
1960 |
4,3 |
— |
|
1961 |
4,5 |
— |
|
1962 |
4,3 |
4,72 |
|
1963 |
5,2 |
5,00 |
|
1964 |
5,3 |
5,30 |
|
1965 |
5,7 |
5,64 |
|
1966 |
6,0 |
5,78 |
|
1967 |
6,0 |
5,86 |
|
1968 |
5,9 |
6,10 |
|
1969 |
5,7 |
6,32 |
|
1970 |
6,9 |
6,58 |
|
1971 |
7,1 |
6,94 |
|
1972 |
7,3 |
7,48 |
|
1973 |
7,7 |
7,68 |
|
1974 |
8,4 |
7,92 |
|
1975 |
7,9 |
8,22 |
|
1976 |
8,3 |
8,38 |
|
1977 |
8,8 |
8,54 |
|
1978 |
8,5 |
8,94 |
|
1979 |
9,2 |
9,18 |
|
1980 |
9,9 |
9,30 |
|
1981 |
9,6 |
— |
|
1982 |
9,3 |
— |
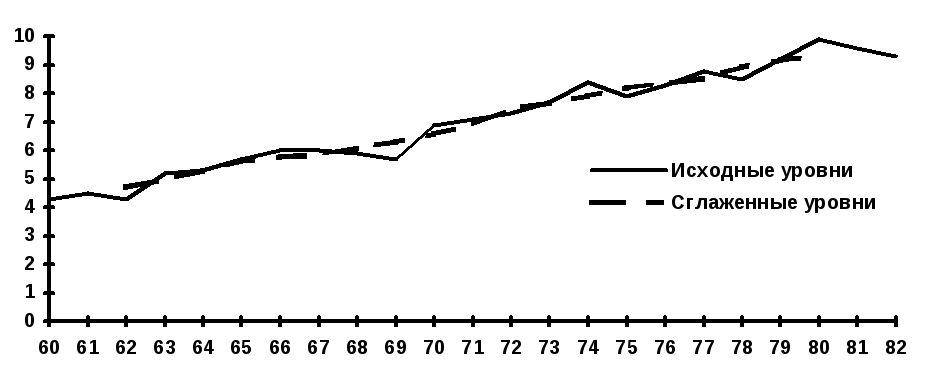
На рис. 1 показан
график, построенный по данным о валовом
сборе хлопка-сырца в стране за ряд лет
наблюдения и по расчетным данным,
представленным в таблице 1.
Рис. 1. Валовый
сбор хлопка — сырца
Наиболее совершенным
способом определения тенденции развития
в ряду динамики является метод
аналитического выравнивания. При этом
методе исходные уровни ряда динамики
заменяются теоретическими или расчетными
,
которые представляют из себя некоторую
достаточно простую математическую
функцию времени, выражающую общую
тенденцию развития ряда динамики. Чаще
всего в качестве такой функции выбирают
прямую, параболу, экспоненту и др.
Например,
,
где
— коэффициенты, определяемые в методе
аналитического выравнивания;
— моменты времени,
для которых были получены исходные и
соответствующие теоретические уровни
ряда динамики, образующие прямую,
определяемую коэффициентами
.
Расчет коэффициентов
ведется на основе метода наименьших
квадратов:
Если вместо
подставить
(или соответствующее выражение для
других математических функций), получим:
Это функция двух
переменных
(все
и
известны), которая при определенных
достигает минимума. Из этого выражения
на основе знаний, полученных в курсе
высшей математики об экстремуме функций
n переменных, получают значения
коэффициентов.
Для прямой:
где n — число
моментов времени, для которых были
получены исходные уровни ряда
.
Если вместо
абсолютного времени
выбрать
условное время таким образом, чтобы,
то записанные выражения для определенияупрощаются:
Пример.
Нечетное число уровня ряда.
|
1981 |
1982 |
1983 |
1984 |
1985 |
1986 |
1987 |
абсолютное |
|
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
условное |
Чётное число уровней ряда.
|
1981 |
1982 |
1983 |
1984 |
1985 |
1986 |
1987 |
1988 |
абсолютное |
|
-7 |
-5 |
-3 |
-1 |
1 |
3 |
5 |
7 |
условное |
В обоих случаях
.
Пример.
Выполняется аналитическое выравнивание
ряда, отражающего производство стали
в стране по годам (млн. т).
|
1985 |
1986 |
1987 |
1988 |
1989 |
|
141,3 |
144,8 |
146,7 |
151,5 |
149,0 |
В качестве математической функции,
отражающей тенденцию развития, выбирается
прямая
,
определениепроизводится для условного времени, в
результате,
.
|
Год |
Производство |
Условное время |
Теоретические уровни |
|
1985 |
141,3 |
-2 |
142,2 |
|
1986 |
144,8 |
-1 |
144,4 |
|
1987 |
146,7 |
0 |
146,7 |
|
1988 |
151,5 |
1 |
148,9 |
|
1989 |
149,0 |
2 |
151,1 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Показатели ряда динамики
Примеры решения задач
Задача 1
По АО
«Керамик» имеются данные о производстве кирпича за год. Рассчитайте все
недостающие в таблице уровни ряда и цепные показатели анализа динамики.
Рассчитайте средний уровень ряда, средние абсолютный прирост и темп роста.
| Месяцы |
Произведено кирпича, тыс.р. |
Цепные показатели | |||
| абсолютный | темп роста, % | темп прироста, % |
абсолютное значение 1% прироста |
||
| Январь | 450 | ||||
| Февраль | 100 | ||||
| Март | 80 | ||||
| Апрель | -30 | ||||
| Май | 250 | ||||
| Июнь | -30 | ||||
| Июль | |||||
| Август | 300 | 5,0 | |||
| Сентябрь | 150 | ||||
| Октябрь | 80 | ||||
| Ноябрь | -60 | ||||
| Декабрь | 300 |
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Формулы цепных показателей динамики
Абсолютный цепной прирост можно
найти по формуле:
-уровень ряда;
-предыдущий
уровень ряда
Цепной темп роста:
Темп прироста:
Абсолютное
содержание 1% прироста:
Расчет недостающих уровней ряда динамики
Исходя из формул, заполним
недостающие показатели:
Февраль:
Март:
Апрель:
Май:
Июнь:
Июль:
Август:
Сентябрь:
Октябрь:
Ноябрь:
Декабрь:
Вычисление цепных показателей динамики
|
Абсолютные приросты цепные: |
Темпы роста цепные: |
|
Темпы прироста цепные: |
Абсолютное содержание 1% прироста: |
Показатели динамики производства кирпича
| Месяцы |
Произведено кирпича, тыс.р. |
Цепные показатели |
|||
| абсолютный |
темп роста, % |
темп прироста, % |
абсолютное значение 1% прироста |
||
| Январь | 450 | —- | 100 | —- | —— |
| Февраль | 900 | 450 | 200 | 100 | 4.5 |
| Март | 720 | -180 | 80.0 | -20.0 | 9,0 |
| Апрель | 690 | -30 | 95.8 | -4.2 | 7.2 |
| Май | 1725 | 1035 | 250.0 | 150.0 | 6.9 |
| Июнь | 1208 | -517 | 70.0 | -30.0 | 17.25 |
| Июль | 500 | -708 | 41.4 | -58.6 | 12.08 |
| Август | 800 | 300 | 160.0 | 60.0 | 5,0 |
| Сентябрь | 1200 | 400 | 150.0 | 50.0 | 8,0 |
| Октябрь | 2160 | 960 | 180.0 | 80.0 | 12,0 |
| Ноябрь | 2100 | -60 | 97.2 | -2.8 | 21.6 |
| Декабрь | 6300 | 4200 | 300 | 200 | 21,0 |
Расчет средних уровней ряда динамики
Средний
уровень исследуемого динамического ряда найдем по формуле средней
арифметической:
Среднегодовой
абсолютный прирост:
Среднегодовой
темп роста:
Среднегодовой
темп прироста:
Вывод к задаче
Среднемесячный
показатель производства составил 1562,8 тыс.р. В среднем за месяц показатель
увеличивался на 531,8 тыс.р. или на 27,1% в относительном выражении.
Задача 2
Для
изучения динамики товаропотока рассчитайте:
- Абсолютные и относительные показатели динамики по годам периода (абсолютные
приросты – базисные и цепные; темпы роста – базисные и цепные). - Динамические средние за период в целом – среднегодовой уровень ряда,
среднегодовой абсолютный прирост, среднегодовой темп роста. Объясните их смысл. - Выполните прогнозы уровня ряда на следующий год, используя среднегодовой
абсолютный прирост и среднегодовой темп роста. Сделайте выводы о развитии
изучаемого процесса. - Постройте график динамики изучаемого процесса.
Динамика
экспорта РФ в Португалию, млрд. долл. США
| Годы | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
| Экспорт | 0.62 | 1.14 | 1.38 | 1.25 | 0.21 | 0.13 | 0.20 |
Решение
1)
|
Абсолютные приросты цепные: |
Абсолютные приросты базисные: |
|
Темпы роста цепные: |
Темпы роста базисные: |
|
Темпы прироста цепные: |
Темпы прироста базисные: |
Показатели динамики экспорта 2004-2010 гг.
| Годы |
Экспорт, млрд.долл |
Абсолютные приросты, млрд.долл |
Темпы роста, % |
Темпы прироста, % |
|||
| цепные | базисные | цепные | базисные | цепные | базисные | ||
| 2004 | 0.62 | —— | —— | 100.0 | 100.0 | —— | —— |
| 2005 | 1.14 | 0.52 | 0.52 | 183.9 | 183.9 | 83.9 | 83.9 |
| 2006 | 1.38 | 0.24 | 0.76 | 121.1 | 222.6 | 21.1 | 122.6 |
| 2007 | 1.25 | -0.13 | 0.63 | 90.6 | 201.6 | -9.4 | 101.6 |
| 2008 | 0.21 | -1.04 | -0.41 | 16.8 | 33.9 | -83.2 | -66.1 |
| 2009 | 0.13 | -0.08 | -0.49 | 61.9 | 21.0 | -38.1 | -79.0 |
| 2010 | 0.20 | 0.07 | -0.42 | 153.8 | 32.3 | 53.8 | -67.7 |
2)
Средний уровень исследуемого динамического ряда найдем по формуле средней
арифметической:
Среднегодовой
абсолютный прирост:
Среднегодовой
темп роста:
Среднегодовой
темп прироста:
Таким
образом в среднем за исследуемый период экспорт
составлял 0,704 млрд. долл. в год. В среднем показатель уменьшался на 0,07 млрд.долл. в год или на 17,2% в
относительном выражении.
3)
Прогноз на 2011 год с помощью среднего абсолютного прироста:
Прогноз
на 2011 год с помощью среднегодового темпа роста:
На
2011 год показатель, прогнозируемый с помощью среднего
абсолютного прироста составил 0,13 млрд. долл., а с помощью
среднегодового темпа роста – 0,166 млрд. долл.
4)
График динамики экспорта 2004-2010 гг.
Пример решения задачи. Ряд динамики
Условие задачи
Определить
вид ряда динамики. Для полученного ряда рассчитать: цепные и базисные
абсолютные приросты, темпы
роста, темпы прироста, средний уровень ряда, средний темп роста, средний
темп прироста. Проверить взаимосвязь абсолютных приростов и темпов роста. По
расчетам сделать выводы. Графически изобразить полученный ряд динамики.
| Годы |
Объем производства, млн.р. |
| 2011 | 12 |
| 2012 | 10 |
| 2013 | 11 |
| 2014 | 10 |
| 2015 | 9 |
Решение задачи
Данный
ряд динамики – интервальный, так как значение показателя заданы за определенный
интервал времени.
Определяем цепные и базисные показатели ряда динамики
|
Абсолютные приросты цепные: |
Абсолютные приросты базисные: |
|
Темпы роста цепные: |
Темпы роста базисные: |
|
Темпы прироста цепные: |
Темпы прироста базисные: |
Показатели динамики объема производства 2011-2015 гг
| Годы |
Объем производства, млн.р. |
Абсолютные приросты, млн.р. | Темпы роста, % | Темпы прироста, % | |||
| цепные | базисные | цепные | базисные | цепные | базисные | ||
| 2011 | 12 | —— | —— | 100.0 | 100.0 | —— | —— |
| 2012 | 10 | -2 | -2 | 83.3 | 83.3 | -16.7 | -16.7 |
| 2013 | 11 | 1 | -1 | 110.0 | 91.7 | 10.0 | -8.3 |
| 2014 | 10 | -1 | -2 | 90.9 | 83.3 | -9.1 | -16.7 |
| 2015 | 9 | -1 | -3 | 90.0 | 75.0 | -10.0 | -25.0 |
Определяем средние показатели ряда динамики
Средний
уровень исследуемого динамического ряда найдем по формуле средней
арифметической:
Среднегодовой
абсолютный прирост:
Среднегодовой
темп роста:
Среднегодовой
темп прироста:
Строим график
График динамики объема производства 2011-2015 гг
Таким образом на протяжении всего исследуемого
периода за исключением 2013 года объем производства продукции на предприятиях
снижался. В среднем предприятия производили продукции на 10,4 млн.р. в год. В
среднем показатель снижался на 0,75 млн.р. в год или на 6,9% в относительном
выражении.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная оплата переводом на карту СберБанка.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
9.2. Показатели ряда динамики
При анализе динамического ряда рассчитываются следующие показатели:
- средний уровень динамического ряда;
- абсолютные приросты: цепные и базисные, средний абсолютный прирост;
- темпы роста: цепные и базисные, средний темп роста;
- темпы прироста: цепные и базисные, средний темп прироста;
- абсолютное значение одного процента прироста.
Цепные и базисные показатели вычисляются для характеристики изменения уровней динамического ряда и различаются между собой базами сравнения: цепные рассчитываются по отношению к предыдущему уровню (переменная база сравнения), базисные — к уровню, принятому за базу сравнения (постоянная база сравнения).
Средние показатели представляют собой обобщенные характеристики ряда динамики. С их помощью сравнивают интенсивность развития явления по отношению к различным объектам, например по странам, отраслям, предприятиям и т.д., или периодам времени.
9.2.1. Средний уровень ряда динамики
Конкретное числовое значение статистического показателя, относящееся к моменту или периоду времени, называется уровнем ряда динамики и обозначается через yi (где i — показатель времени).
Методика расчета среднего уровня зависит от вида динамического ряда, а именно: является ли он моментным или интервальным, с равными или неравными временными промежутками между соседними датами.
Если дан интервальный ряд динамики абсолютных или средних величин с равными периодами времени, то для расчета среднего уровня применяется формула средней арифметической простой:
где y1, y2, yi, …, yn — уровни динамического ряда;
п — число уровней ряда.
Пример 9.2. По данным таблицы определим среднемесячный размер страхового возмещения, выплаченного страховой компанией, в расчете на один пострадавший объект за полугодие:
| Месяц | Январь | Февраль | Март | Апрель | Май | Июнь |
|---|---|---|---|---|---|---|
| Средний размер выплаченного страхового возмещения, тыс. руб | 106 | 108 | 108 | 111 | 110 | 112 |
Если временные промежутки интервального динамического ряда неравны, то значение среднего уровня находят по формуле средней арифметической взвешенной, в которой в качестве весов используют длину временных периодов, соответствующих уровням ряда динамики (ti)
Пример 9.3. По данным, представленным в таблице, определим среднемесячный размер страхового возмещения, выплаченного страховой компанией, в расчете на один пострадавший объект:
| Месяц | Январь | Февраль | Март | II квартал | III квартал | IV квартал |
|---|---|---|---|---|---|---|
| Средний размер выплаченного страхового возмещения, тыс. руб. | 106 | 110 | 138 | 150 | 160 | 140 |
В моментных рядах динамики с одинаковыми временными промежутками между датами средний уровень ряда рассчитывается по формуле средней хронологической простой
где yn — значения показателя на конец рассматриваемого периода.
Пример 9.4. По приведенным ниже данным о размере денежных средств на счете вкладчика на начало каждого месяца определим средний размер вклада в I квартале 2006 г.:
| Дата | 01.01.06 | 01.02.06 | 01.03.06 | 01.04.06 |
|---|---|---|---|---|
| Остаток денежных средств, руб. | 132 000 | 147 289 | 151 870 | 148 500 |
Средний уровень моментного ряда динамики равен:
Хотя I квартал включает три месяца (январь, февраль, март), в расчете должны быть использованы четыре уровня ряда (включая данные на 1 апреля). Это легко доказать. Действительно, если исчислять средние уровни по месяцам, то получим:
в январе
в феврале
в марте
Рассчитанные средние образуют интервальный ряд динамики с равными временными промежутками, в котором средний уровень исчисляется, как мы видели выше, по формуле средней арифметической простой:
Аналогично, если требуется рассчитать средний уровень моментного ряда динамики с равными интервалами между датами за первое полугодие, то в качестве последнего уровня в формуле средней хронологической простой следует взять данные на 1 июля, а если за год — данные на 1 января следующего года.
В моментных рядах динамики с неравными промежутками между датами для определения среднего уровня применяется формула средней хронологической взвешенной:
где ti — длина временного периода между двумя соседними датами.
Пример 9.5. По данным о запасах товаров на начало месяца определим средний размер товарных запасов в 2006 г.
| Дата | 01.01.06 | 01.02.06 | 01.03.06 | 01.07.06 | 01.09.06 | 01.12.06 | 01.01.07 |
|---|---|---|---|---|---|---|---|
| Запасы товаров, тыс. руб. | 1 320 | 1 472 | 1 518 | 1 300 | 1 100 | 1 005 | 920 |
Средний уровень ряда равен:
Расстояние между датами
Если имеется полная информация о значениях моментного статистического показателя на каждую дату, то среднее значение этого показателя за весь период исчисляется по формуле средней арифметической взвешенной:
где yi — значения показателя
ti — длина периода, в течение которого это значение статистического показателя оставалось неизменным.
Если мы дополним пример 9.4 информацией о датах изменения денежных средств на счете вкладчика в I квартале 2006 г., то получим:
- остаток денежных средств на 1 января — 132 000 руб.;
- января выдано — 19 711 руб.;
- 28 января внесено — 35 000 руб.;
- 20 февраля внесено — 2000 руб.;
- 24 февраля внесено — 2581 руб.;
- 3 марта выдано — 3370 руб. (в марте других изменений не происходило).
Итак, с 1 по 4 января (четыре дня) значение показателя оставалось равным 132 000 руб., с 5 по 27 января (23 дня) его значение составило 112 289 руб., с 28 января по 19 февраля (23 дня) — 147 289 руб., с 20 по 23 февраля (четыре дня) — 149 289 руб., с 24 февраля по 2 марта (семь дней) — 151 870 руб., с 3 по 31 марта (29 дней) — 148 500 руб. Для удобства проведения расчетов представим эти данные в таблице:
| Длина периода, дней | 4 | 23 | 23 | 4 | 7 | 29 |
|---|---|---|---|---|---|---|
| Остаток денежных средств, руб. | 132 00 | 112 289 | 147 289 | 149 289 | 151 879 | 148 500 |
По формуле средней арифметической взвешенной находим значение среднего уровня ряда
Как видим, среднее значение отличается от полученного в примере 9.4, оно является более точным, так как в вычислениях использовалась более точная информация. В примере 9.4 были известны лишь данные на начало каждого месяца, при этом не оговаривалось, когда же именно происходили изменения показателя, была применена формула хронологической средней.
В заключение отметим, что расчет среднего уровня ряда теряет свой аналитический смысл в случаях большой изменяемости показателя внутри ряда, а также при резкой смене направления развития явления.
9.2.2. Показатели абсолютного изменения уровней динамического ряда
Абсолютные приросты рассчитываются как разность между двумя значениями соседних уровней динамического ряда (цепные приросты) или как разность между значениями текущего уровня и уровня, принятого за базу сравнения (базисные приросты). Показатели абсолютного прироста имеют те же единицы измерения, что и уровни динамического ряда. Они показывают, на сколько единиц изменился показатель при переходе от одного момента или периода времени к другому.
Базисные абсолютные приросты рассчитывают по формуле
где уi — i-й текущий уровень ряда,
y1 — первый уровень ряда динамики, принятый за базу сравнения.
Формула для определения цепных абсолютных приростов имеет вид
где уi — 1 — уровень, предшествующий i-му уровню динамического ряда.
Средний абсолютный прирост показывает, на сколько единиц в среднем ежемесячно, или ежеквартально, или ежегодно и т.д. изменялось значение показателя в течение рассматриваемого периода времени. В зависимости от того, какими данными мы располагаем, его можно рассчитать следующими способами:
-
— цепные абсолютные приросты показателя;
-
где yn — последний уровень ряда
Пример 9.6. По данным таблицы определим показатели абсолютных приростов размера страхового возмещения, выплаченного страховой компанией.
 |
* Сумма всех рассчитанных цепных абсолютных приростов дает базисный абсолютный прирост последнего периода.
Среднемесячный абсолютный прирост за полугодие равен
Таким образом, в среднем ежемесячно размер выплат страхового возмещения увеличивался на 1,2 тыс. руб.
9.2.3. Показатели относительного изменения уровней динамического ряда
Характеристиками относительного изменения уровней ряда динамики являются коэффициенты и темпы роста значений показателя и темпы их прироста.
Коэффициент роста представляет собой соотношение двух уровней динамического ряда, выраженное в виде простого кратного отношения. Он показывает, во сколько раз изменилось значение показателя в одном периоде (моменте) времени по сравнению с другим. Темп роста — это коэффициент роста, выраженный в процентах. Он показывает, сколько процентов составляет значение показателя в данном периоде, если уровень, с которым проводится сравнение, принять за 100%.
Так же, как и абсолютные приросты, коэффициенты и темпы роста могут быть цепными и базисными.
Цепные коэффициент и темп роста измеряют относительное изменение текущего уровня показателя по сравнению с предшествующим ему уровнем:
коэффициент роста:
темп роста:
Базисные коэффициент и темп роста характеризуют относительное изменение текущего уровня показателя по сравнению с базисным (чаще всего с первым) уровнем:
коэффициент роста
темп роста
Цепные и базисные коэффициенты роста имеют между собой следующую связь:
- произведение всех рассчитанных до текущего периода цепных коэффициентов роста дает базисный коэффициент роста текущего периода:
- деление базисного коэффициента роста текущего периода на базисный коэффициент роста предшествующего периода дает цепной коэффициент роста текущего периода:
Средние темп роста и коэффициент роста в динамических рядах с равноотстоящими уровнями рассчитываются по формуле средней геометрической простой


Эти формулы могут быть приведены к следующему виду:
Для того чтобы определить, на сколько процентов текущий уровень показателя больше или меньше значения предшествующего или базисного уровня, рассчитываются темпы прироста. Они исчисляют путем вычитания 100% из соответствующих темпов роста:
Средний темп прироста рассчитывается аналогичным образом: из среднего темпа роста вычитаются 100%:
Пример 9.7. В таблице приведены рассчитанные коэффициенты роста, темпы роста и прироста показателя, характеризующего среднемесячный размер выплаченного компанией страхового возмещения за период с января по июнь.
| Месяц | Средний размер выплаченного страхового возмещения, тыс. руб., yi | Коэффициент роста | Темпы роста, % | Темпы прироста, % | Абсолютное значение 1% прироста, тыс. руб. | |||
|---|---|---|---|---|---|---|---|---|
| цепные | базисные | цепные | базисные | цепные | базисные | |||
| Январь | 106 | — | 1 | — | 100 | — | — | — |
| Февраль | 108 | 1,019 | 1,019 | 101,9 | 101,9 | 1,9 | 1,9 | 1,06 |
| Март | 108 | 1,000 | 1,000 | 100,0 | 101,9 | 0 | 1,9 | 1,08 |
| Апрель | 111 | 1,028 | 1,047 | 102,8 | 104,7 | 2,8 | 4,7 | 1,08 |
| Май | 110 | 0,991 | 1,038 | 99,1 | 103,8 | -0,9 | 3,8 | 1,11 |
| Июнь | 112 | 1,018 | 1,057 | 101,8 | 105,7 | 1,8 | 5,7 | 1,10 |
По формуле средней геометрической простой определим среднемесячный коэффициент роста показателя за период с февраля по июнь:
или
Средний темп роста, соответственно, равен 101,1%. Следовательно, в среднем ежемесячно размер выплат страхового возмещения увеличивался в 1,011 раза, или на 1,1%.
Если известны средние темпы (или коэффициенты) роста за некоторые неравные отрезки времени, то средний темп роста за весь период исчисляется по формуле средней геометрической взвешенной:
где Тi — средний темп роста за i-й период времени;
ti — длина i-го периода.
Пример 9.8. Среднегодовые коэффициенты роста числа страховых компаний в одной из областей России составили за период 1991-1995 гг. — 1,18; 1995-2000 гг. — 1,24; 2000-2004 — 1,56. Определим среднегодовой коэффициент роста числа страховых компаний за весь период с 1991 по 2004 гг.
Решение:
Таким образом, за период с 1991 по 2004 гг. среднегодовой темп роста числа страховых компаний в одной из областей России составил 131,1%, соответственно, среднегодовой темп прироста — 31,1%.
Для более полного анализа динамики расчет цепных показателей роста и прироста уровней динамического ряда часто сопровождаются указаниями абсолютных значений 1% прироста.
Абсолютное значение 1% прироста (Аi) определяется как отношение значения абсолютного прироста показателя к его темпу прироста в i-й момент времени:
В последней графе таблицы примера 9.7 рассчитаны цепные абсолютные значения 1% прироста.








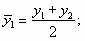






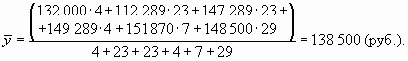

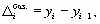

 — цепные абсолютные приросты показателя;
— цепные абсолютные приросты показателя;