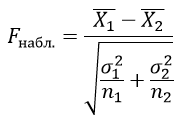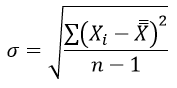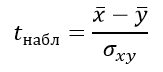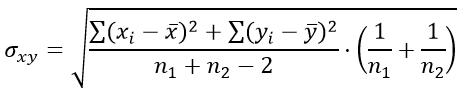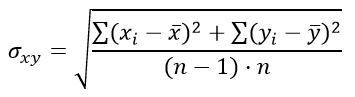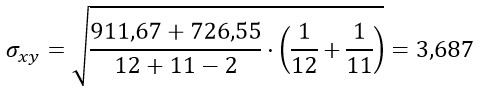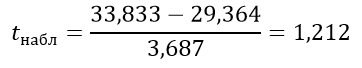Предположим, что надо сравнить между собой результаты выполнения тестов на внимание в двух группах. Чтобы узнать различаются ли группы между собой необходимо вычислить t-критерий Стьюдента для независимых выборок.
1. Внесем данные по группам в таблицу:
| № | Результаты группы №1 (сек.) | Результаты группы №2 (сек.) |
| 1 | 30 | 46 |
| 2 | 45 | 49 |
| 3 | 41 | 52 |
| 4 | 38 | 55 |
| 5 | 34 | 56 |
| 6 | 36 | 40 |
| 7 | 31 | 47 |
| 8 | 30 | 51 |
| 9 | 49 | 58 |
| 10 | 50 | 46 |
| 11 | 51 | 46 |
| 12 | 46 | 56 |
| 13 | 41 | 53 |
| 14 | 37 | 57 |
| 15 | 36 | 44 |
| 16 | 34 | 42 |
| 17 | 33 | 40 |
| 18 | 49 | 58 |
| 19 | 32 | 54 |
| 20 | 46 | 53 |
| 21 | 41 | 51 |
| 22 | 44 | 57 |
| 23 | 38 | 56 |
| 24 | 50 | 44 |
| 25 | 37 | 42 |
| 26 | 39 | 49 |
| 27 | 40 | 50 |
| 28 | 46 | 55 |
| 29 | 42 | 43 |
Шаг 2. Проверить распределения на нормальность.
Шаг 3. Рассчитать среднее арифметическое, стандартное отклонение и количество человек в каждой группе.
| Результаты группы №1 (сек.) | Результаты группы №2 (сек.) |
Шаг 4. Вычисляем эмпирическое значения по формуле t-критерия Стьюдента для независимых выборок
Шаг 5. Вычисляем степени свободы.
Шаг 6. Определяем по таблице критических значений t-Стьюдента уровень значимости.
Значение 6,09 больше чем значение 3,473 следовательно уровень значимости меньше 0,001
Шаг 7. Если уровень значимости меньше 0,05 делается вывод о наличи различий между группами. Таким образом между двумя группами есть различия в скорости выполнения тестов на внимание.
| Расчет критерия Т-Стьюдента для независимых выборок | |
| Расчет критерия Т-Стьюдента для независимых выборок в SPSS | Пример критерия Т-Стьюдента для независимых выборок в SPSS |
| Расчет критерия Т-Стьюдента для независимых выборок в Excell | Пример критерия Т-Стьюдента для независимых выборок в Excell |
| Критерий Т-Стьюдента для независимых выборок |
Пример расчета t-критерия Стьюдента для независимых выборок
Предположим, что надо сравнить между собой результаты выполнения тестов на внимание в двух группах.
1. Внесем данные по группам в таблицу:
| № | Результаты группы №1 (сек.) | Результаты группы №2 (сек.) |
| 1 | 30 | 46 |
| 2 | 45 | 49 |
| 3 | 41 | 52 |
| 4 | 38 | 55 |
| 5 | 34 | 56 |
| 6 | 36 | 40 |
| 7 | 31 | 47 |
| 8 | 30 | 51 |
| 9 | 49 | 58 |
| 10 | 50 | 46 |
| 11 | 51 | 46 |
| 12 | 46 | 56 |
| 13 | 41 | 53 |
| 14 | 37 | 57 |
| 15 | 36 | 44 |
| 16 | 34 | 42 |
| 17 | 33 | 40 |
| 18 | 49 | 58 |
| 19 | 32 | 54 |
| 20 | 46 | 53 |
| 21 | 41 | 51 |
| 22 | 44 | 57 |
| 23 | 38 | 56 |
| 24 | 50 | 44 |
| 25 | 37 | 42 |
| 26 | 39 | 49 |
| 27 | 40 | 50 |
| 28 | 46 | 55 |
| 29 | 42 | 43 |
Шаг 2.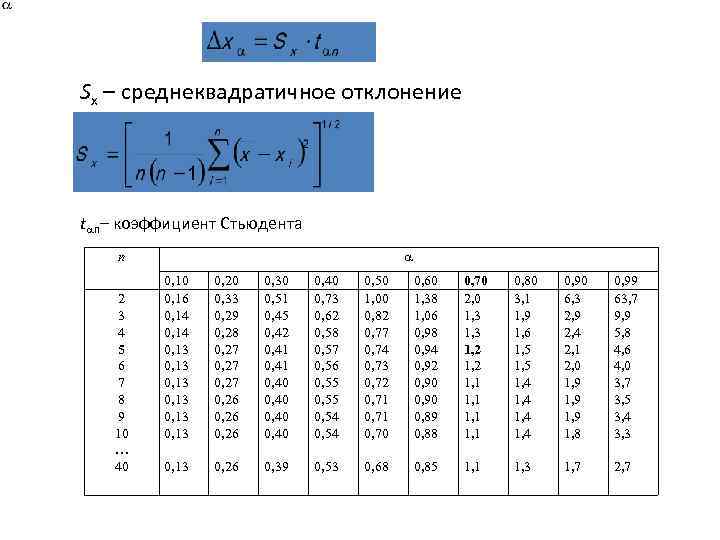
Шаг 3. Рассчитать среднее арифметическое, стандартное отклонение и количество человек в каждой группе.
| Результаты группы №1 (сек.) | Результаты группы №2 (сек.) |
Шаг 4. Вычисляем эмпирическое значения по формуле t-критерия Стьюдента для независимых выборок
Шаг 5. Вычисляем степени свободы.
Шаг 6. Определяем по таблице критических значений t-Стьюдента уровень значимости.
Значение 6,09 больше чем значение 3,473 следовательно уровень значимости меньше 0,001
Шаг 7. Если уровень значимости меньше 0,05 делается вывод о наличи различий между группами. Таким образом между двумя группами есть различия в скорости выполнения тестов на внимание.
| Расчет критерия Т-Стьюдента для независимых выборок | |
| Расчет критерия Т-Стьюдента для независимых выборок в SPSS | Пример критерия Т-Стьюдента для независимых выборок в SPSS |
| Расчет критерия Т-Стьюдента для независимых выборок в Excell | Пример критерия Т-Стьюдента для независимых выборок в Excell |
| Критерий Т-Стьюдента для независимых выборок |
T Формула распределения | Вычислить распределение T студентов
Формула для расчета распределения T (которое также широко известно как распределение T Стьюдента) показана как вычитание среднего значения генеральной совокупности (среднее значение второй выборки) из среднего значения выборки (среднего значения первой выборки), которое составляет [ x̄ – μ ], которое затем делится на стандартное отклонение средних значений, которое изначально делится на квадратный корень из n, который представляет собой количество единиц в этой выборке [s ÷ √(n)].

Т-распределение — это вид распределения, который выглядит почти как кривая нормального распределения или кривая нормального распределения, но с немного более толстым и коротким хвостом. Если размер выборки мал, то это распределение будет использоваться вместо нормального распределения.
t = (x̄ – μ) / (s/√n)
В отличие от критериев
Розенбаума и Манна-Уитни критерий t
Стьюдента является параметрическим,
т. е. основан на определении основных
статистических показателей – средних
значений в каждой выборке (и
)
и их дисперсий (s2x
и s2y),
рассчитываемых по стандартным формулам
(см. раздел 5).
Использование критерия
Стьюдента предполагает соблюдение
следующих условий:
-
Распределения значений
для обеих выборок должны соответствовать
закону нормального распределения (см.
раздел 6). -
Суммарный объем выборок
должен быть не менее 30 (для β1
= 0,95) и не менее 100 (для β2
= 0,99). -
Объемы двух выборок
не должны существенно отличаться друг
от друга (не более чем в 1,5 ÷ 2 раза).
Идея критерия Стьюдента
достаточно проста. Предположим, что
значения переменных в каждой из выборок
распределяются по нормальному закону,
т. е. мы имеем дело с двумя нормальными
распределениями, отличающимися друг
от друга по средним значениям и дисперсии
(соответственно
и
,
и
,
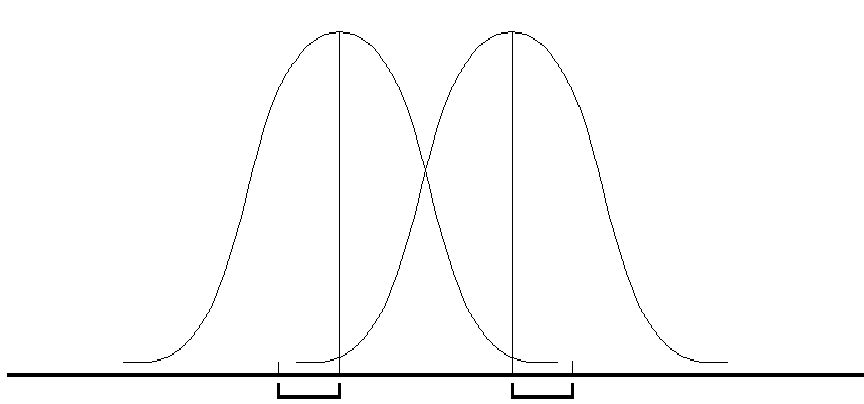
см. рис. 7.1).
sx
sy
Рис.
7.1. Оценка различий между двумя независимыми
выборками:
и
—
средние значения выборок x
и y;
sx
и sy
—
стандартные отклонения
Нетрудно понять, что
различия между двумя выборками будут
тем больше, чем больше разность между
средними значениями и чем меньше их
дисперсии (или стандартные отклонения).
В
случае независимых выборок коэффициент
Стьюдента определяют по формуле:
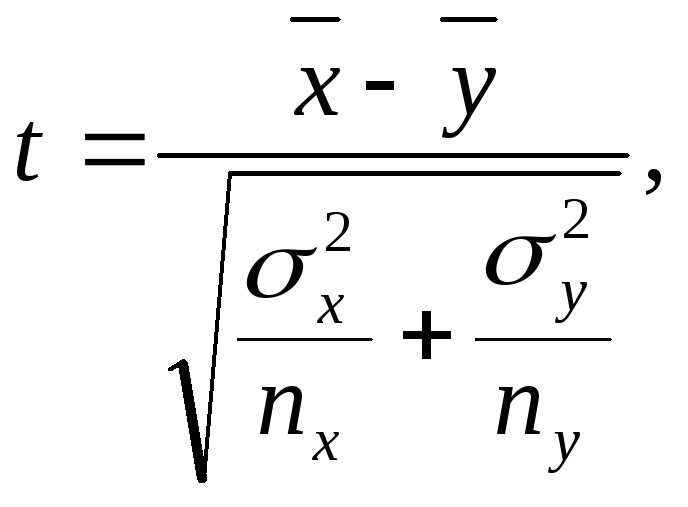
где nx
и ny
– соответственно численность выборок
x
и y.
После вычисления
коэффициента Стьюдента в таблице
стандартных (критических) значений t
(см. Приложение, табл. Х) находят величину,
соответствующую числу степеней свободы
n
= nx
+ ny
– 2, и сравнивают
ее с рассчитанной по формуле. Если tэксп.
£
tкр.,
то гипотезу о достоверности различий
между выборками отвергают, если же
tэксп.
> tкр.,
то ее принимают. Другими словами, выборки
достоверно отличаются друг от друга,
если вычисленный по формуле коэффициент
Стьюдента больше табличного значения
для соответствующего уровня значимости.
В рассмотренной нами
ранее задаче вычисление средних значений
и дисперсий дает следующие значения:
xср.
= 38,5; σх2
= 28,40; уср.
= 36,2; σу2
= 31,72.
Можно видеть, что
среднее значение тревожности в группе
девушек выше, чем в группе юношей. Тем
не менее эти различия настолько
незначительны, что вряд ли они являются
статистически значимыми. Разброс
значений у юношей, напротив, несколько
выше, чем у девушек, но различия между
дисперсиями также невелики.
Подставляем
значения в формулу:
Вывод
tэксп.
= 1,14 < tкр.
= 2,05 (β1
= 0,95). Различия между двумя сравниваемыми
выборками не являются статистически
достоверными. Данный вывод вполне
согласуется с таковым, полученным при
использовании критериев Розенбаума и
Манна-Уитни.
Другой
способ определения различий между двумя
выборками по критерию Стьюдента состоит
в вычислении доверительного интервала
стандартных отклонений. Доверительным
интервалом называется среднеквадратичное
(стандартное) отклонение, деленное на
корень квадратный из объема выборки и
умноженное на стандартное значение
коэффициента Стьюдента для n
– 1 степеней свободы (соответственно,
и
).
Примечание
Величина
=mx
называется
среднеквадратичной ошибкой (см. раздел
5). Следовательно, доверительный интервал
есть среднеквадратичная ошибка,
умноженная на коэффициент Стьюдента
для данного объема выборки, где число
степеней свободы ν = n
– 1, и заданного уровня значимости.
Две
независимые друг от друга выборки
считаются достоверно различающимися,
если доверительные интервалы для этих
выборок не перекрываются друг с другом.
В нашем случае мы имеем для первой
выборки 38,5 ± 2,84, для второй 36,2 ± 3,38.
Следовательно,
случайные вариации xi
лежат в диапазоне 35,66 ¸
41,34, а вариации yi
– в диапазоне 32,82 ¸
39,58. На основании этого можно констатировать,
что различия между выборками x
и y
статистически недостоверны (диапазоны
вариаций перекрываются друг с другом).
При этом следует иметь в виду, что ширина
зоны перекрытия в данном случае не имеет
значения (важен лишь сам факт перекрытия
доверительных интервалов).
Метод
Стьюдента для зависимых друг от друга
выборок (например, для сравнения
результатов, полученных при повторном
тестировании на одной и той же выборке
испытуемых) используют достаточно
редко, поскольку для этих целей существуют
другие, более информативные статистические
приемы (см. раздел 10). Тем не менее, для
данной цели в первом приближении можно
использовать формулу Стьюдента следующего
вида:
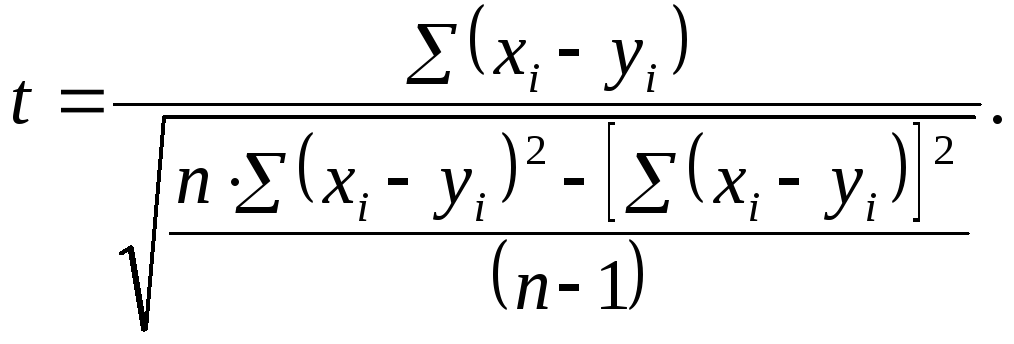
Полученный результат
сравнивают с табличным значением для
n
– 1 степеней свободы, где n
– число пар значений x
и y.
Результаты сравнения интерпретируются
точно так же, как и в случае вычисления
различий между двумя независимыми
выборками.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
23.02.201514.96 Mб37Longman_Advanced_Learners_39_Grammar.pdf
- #
- #
- #
- #
- #
- #
- #
- #
- #
Критерий Стьюдента применяется для проверки равенства средних значений двух выборок, сравнение количественных значений только двух выборок с нормальным распределением случайной величины.
Критерий Стьюдента определяется по формуле:
$bar{X_1}$ – выборочные средние значения первой выборки;
$bar{X_2}$ – выборочные средние значения второй выборки;
n1 – объем первой выборки;
n2 – объем второй выборки;
σ1 и σ2 – среднее квадратическое отклонение в соответствующих выборках и находятся из формулы:
Число степеней свободы определяется по формуле:
k=n1+n2−2
Fкр(α, k) определяется по таблице
При Fнабл<Fкр нулевая гипотеза принимается.
Формула критерия Стьюдента для несвязанных независимых выборок:
Формула для определения стандартной ошибки разности средних арифметических σxy:
Число степеней свободы определяется выражением:
k=n1+n2–2
При n1=n2 число степеней свободы находится по формуле:
k=2n-2
а стандартная ошибка разности средних арифметических σxy задаётся выражением:
Пример
Даны две выборки.
В первой выборки продажа товара со скидкой, а во второй без скидки.
| № п/п | X | Y |
| 1 | 25 | 19 |
| 2 | 34 | 31 |
| 3 | 23 | 17 |
| 4 | 35 | 24 |
| 5 | 33 | 28 |
| 6 | 25 | 31 |
| 7 | 45 | 39 |
| 8 | 41 | 32 |
| 9 | 27 | 38 |
| 10 | 54 | 43 |
| 11 | 32 | 21 |
| 12 | 32 |
По критерию Стьюдента определить зависит ли спрос на товар от скидок на него при p=0.99?
Решение
В соответствии с таблицей n1=12, n2=11
Вычислим дисперсии D(X), D(Y)
| № п/п | X | Y | D(X) | D(Y) |
| 1 | 25 | 19 | 78,028 | 107,4 |
| 2 | 34 | 31 | 0,0278 | 2,6777 |
| 3 | 23 | 17 | 117,36 | 152,86 |
| 4 | 35 | 24 | 1,3611 | 28,769 |
| 5 | 33 | 28 | 0,6944 | 1,8595 |
| 6 | 25 | 31 | 78,028 | 2,6777 |
| 7 | 45 | 39 | 124,69 | 92,86 |
| 8 | 41 | 32 | 51,361 | 6,9504 |
| 9 | 27 | 38 | 46,694 | 74,587 |
| 10 | 54 | 43 | 406,69 | 185,95 |
| 11 | 32 | 21 | 3,3611 | 69,95 |
| 12 | 32 | 3,3611 | ||
| Сумма | 406 | 323 | 911,67 | 726,55 |
| Среднее | 33,833 | 29,364 |
Подставим значения в формулу стандартной ошибки разности средних арифметических σxy:
Вычисляем критерий Стьюдента:
Число степеней свободы равно:
k=12+11–2=21
По таблице Стьюдента находим критическое значение:
tкрит=2,8310
Отсюда tкрит> tнабл, следовательно, зависит.
18274
Предположим, что надо сравнить между собой результаты выполнения тестов на внимание в двух группах. Чтобы узнать различаются ли группы между собой необходимо вычислить t-критерий Стьюдента для независимых выборок.
1. Внесем данные по группам в таблицу:
| № | Результаты группы №1 (сек.) | Результаты группы №2 (сек.) |
| 1 | 30 | 46 |
| 2 | 45 | 49 |
| 3 | 41 | 52 |
| 4 | 38 | 55 |
| 5 | 34 | 56 |
| 6 | 36 | 40 |
| 7 | 31 | 47 |
| 8 | 30 | 51 |
| 9 | 49 | 58 |
| 10 | 50 | 46 |
| 11 | 51 | 46 |
| 12 | 46 | 56 |
| 13 | 41 | 53 |
| 14 | 37 | 57 |
| 15 | 36 | 44 |
| 16 | 34 | 42 |
| 17 | 33 | 40 |
| 18 | 49 | 58 |
| 19 | 32 | 54 |
| 20 | 46 | 53 |
| 21 | 41 | 51 |
| 22 | 44 | 57 |
| 23 | 38 | 56 |
| 24 | 50 | 44 |
| 25 | 37 | 42 |
| 26 | 39 | 49 |
| 27 | 40 | 50 |
| 28 | 46 | 55 |
| 29 | 42 | 43 |
Шаг 2. Проверить распределения на нормальность.
Шаг 3. Рассчитать среднее арифметическое, стандартное отклонение и количество человек в каждой группе.
Шаг 4. Вычисляем эмпирическое значения по формуле t-критерия Стьюдента для независимых выборок
Шаг 5. Вычисляем степени свободы.
Шаг 6. Определяем по таблице критических значений t-Стьюдента уровень значимости.
Значение 6,09 больше чем значение 3,473 следовательно уровень значимости меньше 0,001
Шаг 7. Если уровень значимости меньше 0,05 делается вывод о наличи различий между группами. Таким образом между двумя группами есть различия в скорости выполнения тестов на внимание.
Кванти́ли (проценти́ли) распределе́ния Стью́дента (коэффициенты Стьюдента) — числовые характеристики, широко используемые в задачах математической статистики таких как построение доверительных интервалов и проверка статистических гипотез.
Содержание
- 1 Определение
- 2 Замечания
- 3 Таблица квантилей
- 3.1 Пример
- 4 См. также
Определение
Пусть 


![{displaystyle alpha in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/daf3c62599ea71319c85f715c9e590d2bab2d036)


.
Замечания
- Прямо из определения следует, что случайная величина, имеющая распределение Стьюдента с
степенями свободы, не превышает значение
с вероятностью
и превышает его с вероятностью
.
- Функция
строго возрастает для любого
. Следовательно, определена её обратная функция
, и
.
- Функция
не имеет простого представления. Однако, возможно вычислить её значения численно.
- Распределение
симметрично. Следовательно,
.
Таблица квантилей
Нижеприведённая таблица получена с помощью функции tinv пакета MATLAB. Чтобы получить значение 


Пример
;
.
См. также
- Распределение Стьюдента;
- Доверительный интервал для математического ожидания нормальной выборки.
Квантили
| 0.55 | 0.6 | 0.65 | 0.7 | 0.75 | 0.8 | 0.85 | 0.9 | 0.95 | 0.975 | 0.99 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.1584 | 0.3249 | 0.5095 | 0.7265 | 1.0000 | 1.3764 | 1.9626 | 3.0777 | 6.3138 | 12.7062 | 31.8205 |
| 2 | 0.1421 | 0.2887 | 0.4447 | 0.6172 | 0.8165 | 1.0607 | 1.3862 | 1.8856 | 2.9200 | 4.3027 | 6.9646 |
| 3 | 0.1366 | 0.2767 | 0.4242 | 0.5844 | 0.7649 | 0.9785 | 1.2498 | 1.6377 | 2.3534 | 3.1824 | 4.5407 |
| 4 | 0.1338 | 0.2707 | 0.4142 | 0.5686 | 0.7407 | 0.9410 | 1.1896 | 1.5332 | 2.1318 | 2.7764 | 3.7469 |
| 5 | 0.1322 | 0.2672 | 0.4082 | 0.5594 | 0.7267 | 0.9195 | 1.1558 | 1.4759 | 2.0150 | 2.5706 | 3.3649 |
| 6 | 0.1311 | 0.2648 | 0.4043 | 0.5534 | 0.7176 | 0.9057 | 1.1342 | 1.4398 | 1.9432 | 2.4469 | 3.1427 |
| 7 | 0.1303 | 0.2632 | 0.4015 | 0.5491 | 0.7111 | 0.8960 | 1.1192 | 1.4149 | 1.8946 | 2.3646 | 2.9980 |
| 8 | 0.1297 | 0.2619 | 0.3995 | 0.5459 | 0.7064 | 0.8889 | 1.1081 | 1.3968 | 1.8595 | 2.3060 | 2.8965 |
| 9 | 0.1293 | 0.2610 | 0.3979 | 0.5435 | 0.7027 | 0.8834 | 1.0997 | 1.3830 | 1.8331 | 2.2622 | 2.8214 |
| 10 | 0.1289 | 0.2602 | 0.3966 | 0.5415 | 0.6998 | 0.8791 | 1.0931 | 1.3722 | 1.8125 | 2.2281 | 2.7638 |
| 11 | 0.1286 | 0.2596 | 0.3956 | 0.5399 | 0.6974 | 0.8755 | 1.0877 | 1.3634 | 1.7959 | 2.2010 | 2.7181 |
| 12 | 0.1283 | 0.2590 | 0.3947 | 0.5386 | 0.6955 | 0.8726 | 1.0832 | 1.3562 | 1.7823 | 2.1788 | 2.6810 |
| 13 | 0.1281 | 0.2586 | 0.3940 | 0.5375 | 0.6938 | 0.8702 | 1.0795 | 1.3502 | 1.7709 | 2.1604 | 2.6503 |
| 14 | 0.1280 | 0.2582 | 0.3933 | 0.5366 | 0.6924 | 0.8681 | 1.0763 | 1.3450 | 1.7613 | 2.1448 | 2.6245 |
| 15 | 0.1278 | 0.2579 | 0.3928 | 0.5357 | 0.6912 | 0.8662 | 1.0735 | 1.3406 | 1.7531 | 2.1314 | 2.6025 |
| 16 | 0.1277 | 0.2576 | 0.3923 | 0.5350 | 0.6901 | 0.8647 | 1.0711 | 1.3368 | 1.7459 | 2.1199 | 2.5835 |
| 17 | 0.1276 | 0.2573 | 0.3919 | 0.5344 | 0.6892 | 0.8633 | 1.0690 | 1.3334 | 1.7396 | 2.1098 | 2.5669 |
| 18 | 0.1274 | 0.2571 | 0.3915 | 0.5338 | 0.6884 | 0.8620 | 1.0672 | 1.3304 | 1.7341 | 2.1009 | 2.5524 |
| 19 | 0.1274 | 0.2569 | 0.3912 | 0.5333 | 0.6876 | 0.8610 | 1.0655 | 1.3277 | 1.7291 | 2.0930 | 2.5395 |
| 20 | 0.1273 | 0.2567 | 0.3909 | 0.5329 | 0.6870 | 0.8600 | 1.0640 | 1.3253 | 1.7247 | 2.0860 | 2.5280 |
| 21 | 0.1272 | 0.2566 | 0.3906 | 0.5325 | 0.6864 | 0.8591 | 1.0627 | 1.3232 | 1.7207 | 2.0796 | 2.5176 |
| 22 | 0.1271 | 0.2564 | 0.3904 | 0.5321 | 0.6858 | 0.8583 | 1.0614 | 1.3212 | 1.7171 | 2.0739 | 2.5083 |
| 23 | 0.1271 | 0.2563 | 0.3902 | 0.5317 | 0.6853 | 0.8575 | 1.0603 | 1.3195 | 1.7139 | 2.0687 | 2.4999 |
| 24 | 0.1270 | 0.2562 | 0.3900 | 0.5314 | 0.6848 | 0.8569 | 1.0593 | 1.3178 | 1.7109 | 2.0639 | 2.4922 |
| 25 | 0.1269 | 0.2561 | 0.3898 | 0.5312 | 0.6844 | 0.8562 | 1.0584 | 1.3163 | 1.7081 | 2.0595 | 2.4851 |
| 26 | 0.1269 | 0.2560 | 0.3896 | 0.5309 | 0.6840 | 0.8557 | 1.0575 | 1.3150 | 1.7056 | 2.0555 | 2.4786 |
| 27 | 0.1268 | 0.2559 | 0.3894 | 0.5306 | 0.6837 | 0.8551 | 1.0567 | 1.3137 | 1.7033 | 2.0518 | 2.4727 |
| 28 | 0.1268 | 0.2558 | 0.3893 | 0.5304 | 0.6834 | 0.8546 | 1.0560 | 1.3125 | 1.7011 | 2.0484 | 2.4671 |
| 29 | 0.1268 | 0.2557 | 0.3892 | 0.5302 | 0.6830 | 0.8542 | 1.0553 | 1.3114 | 1.6991 | 2.0452 | 2.4620 |
| 30 | 0.1267 | 0.2556 | 0.3890 | 0.5300 | 0.6828 | 0.8538 | 1.0547 | 1.3104 | 1.6973 | 2.0423 | 2.4573 |
| 31 | 0.1267 | 0.2555 | 0.3889 | 0.5298 | 0.6825 | 0.8534 | 1.0541 | 1.3095 | 1.6955 | 2.0395 | 2.4528 |
| 32 | 0.1267 | 0.2555 | 0.3888 | 0.5297 | 0.6822 | 0.8530 | 1.0535 | 1.3086 | 1.6939 | 2.0369 | 2.4487 |
| 33 | 0.1266 | 0.2554 | 0.3887 | 0.5295 | 0.6820 | 0.8526 | 1.0530 | 1.3077 | 1.6924 | 2.0345 | 2.4448 |
| 34 | 0.1266 | 0.2553 | 0.3886 | 0.5294 | 0.6818 | 0.8523 | 1.0525 | 1.3070 | 1.6909 | 2.0322 | 2.4411 |
| 35 | 0.1266 | 0.2553 | 0.3885 | 0.5292 | 0.6816 | 0.8520 | 1.0520 | 1.3062 | 1.6896 | 2.0301 | 2.4377 |
| 36 | 0.1266 | 0.2552 | 0.3884 | 0.5291 | 0.6814 | 0.8517 | 1.0516 | 1.3055 | 1.6883 | 2.0281 | 2.4345 |
| 37 | 0.1265 | 0.2552 | 0.3883 | 0.5289 | 0.6812 | 0.8514 | 1.0512 | 1.3049 | 1.6871 | 2.0262 | 2.4314 |
| 38 | 0.1265 | 0.2551 | 0.3882 | 0.5288 | 0.6810 | 0.8512 | 1.0508 | 1.3042 | 1.6860 | 2.0244 | 2.4286 |
| 39 | 0.1265 | 0.2551 | 0.3882 | 0.5287 | 0.6808 | 0.8509 | 1.0504 | 1.3036 | 1.6849 | 2.0227 | 2.4258 |
| 40 | 0.1265 | 0.2550 | 0.3881 | 0.5286 | 0.6807 | 0.8507 | 1.0500 | 1.3031 | 1.6839 | 2.0211 | 2.4233 |
| 41 | 0.1264 | 0.2550 | 0.3880 | 0.5285 | 0.6805 | 0.8505 | 1.0497 | 1.3025 | 1.6829 | 2.0195 | 2.4208 |
| 42 | 0.1264 | 0.2550 | 0.3880 | 0.5284 | 0.6804 | 0.8503 | 1.0494 | 1.3020 | 1.6820 | 2.0181 | 2.4185 |
| 43 | 0.1264 | 0.2549 | 0.3879 | 0.5283 | 0.6802 | 0.8501 | 1.0491 | 1.3016 | 1.6811 | 2.0167 | 2.4163 |
| 44 | 0.1264 | 0.2549 | 0.3878 | 0.5282 | 0.6801 | 0.8499 | 1.0488 | 1.3011 | 1.6802 | 2.0154 | 2.4141 |
| 45 | 0.1264 | 0.2549 | 0.3878 | 0.5281 | 0.6800 | 0.8497 | 1.0485 | 1.3006 | 1.6794 | 2.0141 | 2.4121 |
| 46 | 0.1264 | 0.2548 | 0.3877 | 0.5281 | 0.6799 | 0.8495 | 1.0483 | 1.3002 | 1.6787 | 2.0129 | 2.4102 |
| 47 | 0.1263 | 0.2548 | 0.3877 | 0.5280 | 0.6797 | 0.8493 | 1.0480 | 1.2998 | 1.6779 | 2.0117 | 2.4083 |
| 48 | 0.1263 | 0.2548 | 0.3876 | 0.5279 | 0.6796 | 0.8492 | 1.0478 | 1.2994 | 1.6772 | 2.0106 | 2.4066 |
| 49 | 0.1263 | 0.2547 | 0.3876 | 0.5278 | 0.6795 | 0.8490 | 1.0475 | 1.2991 | 1.6766 | 2.0096 | 2.4049 |
| 50 | 0.1263 | 0.2547 | 0.3875 | 0.5278 | 0.6794 | 0.8489 | 1.0473 | 1.2987 | 1.6759 | 2.0086 | 2.4033 |
| 100 | 0.1260 | 0.2540 | 0.3864 | 0.5261 | 0.6770 | 0.8452 | 1.0418 | 1.2901 | 1.6602 | 1.9840 | 2.3642 |
| 1000 | 0.1257 | 0.2534 | 0.3854 | 0.5246 | 0.6747 | 0.8420 | 1.0370 | 1.2824 | 1.6464 | 1.9623 | 2.3301 |