Коэффициент теплопроводности газов
Коэффициент
пропорциональности
в уравнении Фурье для теплопроводности
(15) – это и есть коэффициент теплопроводности.
Он является физическим параметром,
характеризующим интенсивность процесса
теплопроводности в веществе, т.е. скорость
переноса тепла.
Физический
смысл коэффициента теплопроводности
вытекает непосредственно из закона
Фурье (15): коэффициент теплопроводности
численно равен плотности теплового
потока при градиенте температуры, равном
единице. Это означает, что в случае
однородного изотропного тела коэффициент
теплопроводности численно равен
количеству теплоты, проходящему через
единицу поверхности в единицу времени
вследствие теплопроводности при перепаде
температуры на единицу длины нормали,
равном одному градусу. В случае изотропной
среды, когда величина коэффициента
не зависит от направления, векторы
и
лежат на одной прямой, но направлены в
противоположные стороны.
Размерность
коэффициента теплопроводности в системе
СИ – ватт на метр-кельвин:.
Теплопроводность
зависит от агрегатного состояния
вещества, его состава, чистоты, температуры,
давления и других факторов.
Что
касается зависимости от агрегатного
состояния, то теплопроводность газов
при нормальных условиях обычно в
несколько десятков и сотен раз меньше
теплопроводности жидкостей, и в сотни
тысяч и миллионы раз меньше, чем
теплопроводность твердых тел. Численное
значение
для воздуха при нормальных условиях
составляет
.
Из
уравнения (12) видно, что коэффициент
теплопроводности газов
,
(16)
где
– концентрация молекул вещества,
–средняя
скорость молекул вещества,
–средняя
длина свободного пробега молекулы,
–молярная
теплоемкость газа при постоянном объеме,
–число
Авогадро,
–плотность
вещества,
–удельная
теплоемкость газа при постоянном объеме,
–масса
молекулы.
Теперь
рассмотрим, от каких факторов зависит
и, следовательно, от каких не зависит
коэффициент теплопроводности газов.
Поскольку
для всех молекул примерно одинаковы, и
значения
мало отличаются для различных газов,
главное изменение теплопроводности
при фиксированной концентрации
частиц газа происходит из-за различия
в средней скорости теплового движения
молекул:
,
(17)
где
– средняя скорость молекулы;
–постоянная
Больцмана;
–температура
вещества;
–масса
молекулы.
Из
формул (16) и (17) следует, что коэффициент
теплопроводности газов обратно
пропорционален
(у легких газов коэффициент теплопроводности
больше, чем у тяжелых) и прямо пропорционален
.
В действительности же коэффициент
теплопроводности, как показывает опыт,
растет с температурой несколько быстрее,
чем
.
Это объясняется тем, что коэффициент
теплопроводности прямо пропорционален
еще и средней длине свободного пробега,
а эта величина тоже растет с температурой.
Для многоатомных газов необходимо еще
учесть возрастание теплоемкости
с температурой.
Из
входящих в (16) величин только число
молекул в единице объема
и длина свободного пробега
зависят от давления. Но
прямо пропорционально давлению газа
(),
а
обратно пропорциональна давлению газа,
так как средняя длина свободного пробега
молекулы газа
,
(18)
где
– эффективный диаметр молекулы,
–концентрация
молекул.
Следовательно,
коэффициент теплопроводности газов не
зависит от давления (исключение составляет
случай малых давлений).
Установим
связь коэффициента теплопроводности
с другими коэффициентами, характеризующими
процессы переноса.
Известно,
что коэффициент динамической вязкости
равен

(19)
где
– концентрация
молекул вещества,
–средняя
скорость молекул вещества,
–средняя
длина свободного пробега молекулы,
–масса
молекулы,
–плотность
вещества.
А
коэффициент диффузии равен
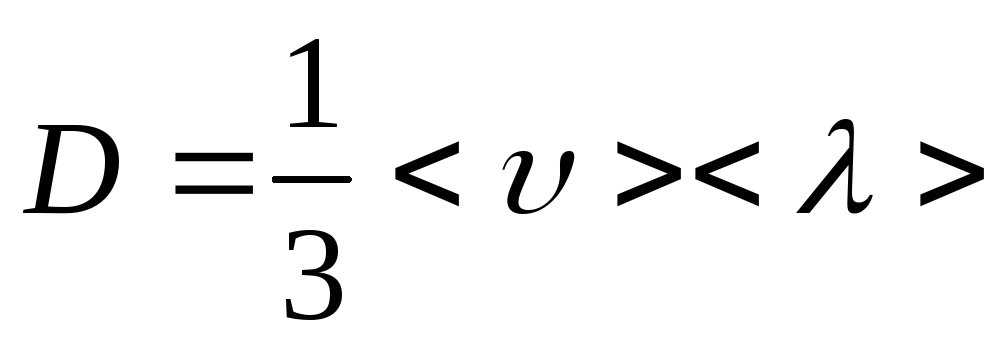
(20)
где
– средняя скорость молекул вещества,
–средняя
длина свободного пробега молекулы.
Тогда
из выражений (16), (19) и (20) следует, что
,
(21)
и
,
(22)
где
– коэффициент теплопроводности,
–коэффициент
динамической вязкости,
–коэффициент
диффузии,
–молярная
теплоемкость газа при постоянном объеме,
–удельная
теплоемкость газа при постоянном объеме,
–число
Авогадро,
–масса
молекулы,
–плотность
вещества.
Наличие
этой связи между коэффициентами процессов
переноса обусловлено одинаковой
физической природой процессов переноса
и тем, что все они описываются одинаковыми
уравнениями вида (8).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Процесс передачи теплоты от слоя с высокой температурой к слою с низкой температурой.
В газах при таких условиях может возникать также явление конвекции – передачи теплоты потоками газа.
Теплопроводность идеального газа
Чтобы продемонстрировать теплопроводность идеального газа, достаточно взять газ в цилиндрическом сосуде с изоляционными стенками, но теплопроводными основами и нагревать газ сверху.
При этом каждый нижний слой газа будет иметь более низкую температуру, но соответственно большую плотность. Поэтому конвекционные потоки не будут возникать.
По закону Фурье количество теплоты ΔQΔQ, которое переносится через некоторую поверхность SS, перпендикулярную оси OzΟz, пропорционально градиенту температуры ΔТ/ΔzΔТ/Δz, площади поверхности SS и времени ΔτΔτ:
ΔQ=−k(ΔTΔz)SΔτDelta Q=-kleft( frac{Delta T}{Delta z} right)SDelta tau
где кк – коэффициент теплопроводности, который зависит от природы и состояния газа. Численно он равен количеству теплоты, которая переносится через единицу площади за единицу времени, когда градиент температуры равен единице. Коэффициент теплопроводности выражают в ваттах на метр, умноженный на кельвин (Вт / (м · К)).
Коэффициент теплопроводности
С точки зрения молекулярно-кинетической теории теплопроводность – это процесс переноса внутренней энергии из одного слоя в другой, который осуществляется вследствие хаотического движения молекул.
Исходя из этого, определим количество перенесенной энергии и коэффициент теплопроводности.
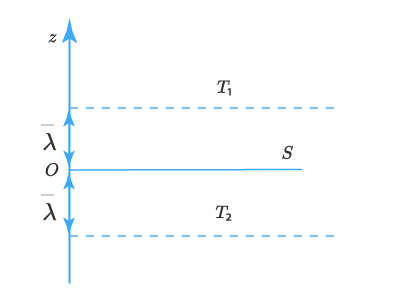
Пусть в среде газа существует спад градиента температуры в направлении оси OzOz. Рассмотрим некоторую поверхность SS внутри газа, перпендикулярную оси OzOz:
Будем считать, что выше этой поверхности температура газа Т1Т_1, а под поверхностью – Т2Т_2, причем Т1Т_1 > Т2Т_2.
В результате хаотического движения молекул газа через поверхность SS за время ΔτΔτ сверху вниз и снизу вверх пройдет одинаковое количество молекул, но перенесут они разное количество теплоты (энергии):
-
Сверху вниз
16n0SvΔτcVmT1frac{1}{6}{{n}_{0}}SvDelta tau {{c}_{V}}m{{T}_{1}}
где cvmT1c_vmT_1 – количество теплоты, что переносится одной молекулой верхнего слоя.
- Снизу вверх
16n0SvΔτcVmT2frac{1}{6}{{n}_{0}}SvDelta tau {{c}_{V}}m{{T}_{2}}
где cvmT2c_vmT_2 – количество теплоты, что переносится одной молекулой нижнего слоя газа.
Найдем результирующее количество теплоты, которое переносится через поверхность SS за время ΔτΔτ:
ΔQ=16n0SvΔτcVm(T1−T2)Delta Q=frac{1}{6}{{n}_{0}}SvDelta tau {{c}_{V}}m({{T}_{1}}-{{T}_{2}})
Т1Т_1 и Т2Т_2 относятся к слоям газа, которые содержатся с разных сторон от поверхности SS на расстоянии λλ от нее. Поэтому (Т1Т_1 — Т2Т_2) является разницей температур слоев газа на расстоянии 2λ2λ. Через градиент температуры ее можно записать так:
T1−T2=(ΔTΔz)2λ{{T}_{1}}-{{T}_{2}}=left( frac{Delta T}{Delta z} right)2lambda
Выполнив в соответствии с этим равенством замену в выражении, получим:
ΔQ=13vλρcV(ΔTΔz)SΔτDelta Q=frac{1}{3}vlambda rho {{c}_{V}}left( frac{Delta T}{Delta z} right)SDelta tau
Сопоставив выражения ΔQΔQ, найдем коэффициент теплопроводности:
k=13vλρcVk=frac{1}{3}vlambda rho {{c}_{V}}
Коэффициент теплопроводности не зависит от давления, поскольку vv, cvc_v и произведение λρλρ не зависят от давления. Коэффициент теплопроводности, как и другие коэффициенты переноса, растет с повышением температуры. Эти результаты согласуются с опытными данными.
Сопоставив выражения коэффициентов вязкости и теплопроводности, получим соотношение:
k=ηcVk=eta {{c}_{V}},
которое легко можно проверить экспериментально.
Проверка показала, что данная зависимость незначительно приближается к исследовательским данным. Это объясняется тем, что при выводе формул делались упрощения, в частности расчеты строились на средних значениях скоростей и длин свободного пробега молекул, а надо было бы учитывать законы распределения этих величин. Точнее это соотношение выражается формулой:
k=AηcVk=Aeta {{c}_{V}}
где АА – множитель, зависящий от природы газа. Для одноатомного газа АА = 2,5, двухатомного – 1,9, трехатомного – 1,6.
Тест по теме «Теплопроводность»
7. Теплопроводность газов
Пусть между двумя параллельными стенками, перпендикулярными оси х и имеющими температуры Т1 и Т2 (Т1>Т2) поддерживается постоянная
разность температур. При этом через газ, находящийся между стенками,
установится постоянный поток тепла с градиентом температуры . Рассмотрим поток тепла через площадку ΔS между стенками, на которой температура
газа равна Т. Для расчета
хаотичное движение молекул по всем направлениям заменяем их движением вдоль
трех осей декартовой системы координат. Считаем, что вдоль оси х движется одна треть общего числа
молекул. Из них одна половина движется слева направо другая половина справа
налево. Очевидно, до площадки ΔS достигают без столкновений, (т.е. без
изменения направления движения) только те молекулы, которые отстоят от нее на
расстоянии не далее длины свободного пробега молекул (рис.6). Через площадку ΔS за единицу времени слева направо
Рис.6
и справа
налево проходит одинаковое число молекул, равное . Температура
на поверхности, расположенной на расстоянии от площадки ΔS равна
и на такой же поверхности, расположенной справа
равна . Энергия, которой обладают молекулы на той же
поверхности, расположенной слева равна , и на
поверхности, расположенной справа .
Количество теплоты, переносимое за
единицу времени молекулами, движущимися слева направо и справа налево, равно
,
.
Количество
тепла, перенесенного через площадку за единицу времени равно
,
(2.35)
где ,
— удельная теплоемкость газа при
постоянном объеме, — плотность газа. Из сравнения (2.35) с
эмпирической Фурье находим коэффициент теплопроводности газа
.
(2.36)
Таким
образом, молекулярно-кинетическая теория дает явное выражение зависимости
коэффициента теплопроводности от микроскопических параметров молекул.
Количество переносимого тепла Q называется тепловым потоком; эту величину обычно относят к единице времени — часу. Тепловой поток, отнесенный к единице поверхности, называется удельным тепловым потоком, плотностью теплового потока, или тепловой нагрузкой поверхности нагрева q.
Величины Q, а также q являются вектором, за положительное направление которого принимают направление по нормали к изотермической поверхности в сторону уменьшения температуры, т. е. противоположно направлению вектора температурного градиента.
Связь между количеством тепла dQ, проходящим через элементарную площадку dF, лежащую на изотермической поверхности, в единицу времени, и температурным градиентом установил Фурье:
 |
(1) |
Удельный тепловой поток определяется соотношением:
 |
(2) |
Знак минус в правой части уравнений (1) и (2) указывает на то, что тепловой поток и температурный градиент, как векторы, имеют противоположные направления. Множитель пропорциональности λ называется коэффициентом теплопроводности. Коэффициент λ является физическим параметром вещества и характеризует способность его проводить тепло.
Из уравнения (2) следует, что коэффициент теплопроводности λ имеет размерность:
 |
(3) |
Следовательно, величина коэффициента теплопроводности определяет собой количество тепла, которое проходит в единицу времени через единицу изотермической поверхности при температурном градиенте, равном единице.
В общем случае коэффициент теплопроводности имеет различные значения для различных веществ. Для данного вещества коэффициент теплопроводности зависит от его физических характеристик, температуры, давления, влажности и структуры. Для веществ, имеющих практическое применение, не удалось установить аналитическую зависимость коэффициента теплопроводности от физических характеристик вещества. При инженерных расчетах значения коэффициента теплопроводности выбираются из справочных таблиц, составленных по опытным данным. На рисунке показаны пределы изменения коэффициента теплопроводности различных веществ.
Порядок величин коэффициента теплопроводности для различных веществ
Опыт показывает, что для материала определенной структуры и влажности, находящегося при атмосферном давлении, коэффициент теплопроводности зависит от температуры. Для многих материалов с достаточной для практики точностью зависимость коэффициента теплопроводности от температуры можно принять линейной:
 |
(4) |
где λо — значение коэффициента теплопроводности при температуре t0;
b — постоянная, определяемая опытным путем.
Значения коэффициента теплопроводности газов находятся в пределах от 0,004 до 0,4 Вт×м-1×K-1. С повышением температуры коэффициент теплопроводности идеальных газов увеличивается, а от изменения давления практически не зависит. Исключение составляют очень низкие (20 мм рт. ст.) и очень высокие (>2000 атм) давления. Наибольшие значения коэффициента теплопроводности у гелия и водорода (в 5 — 10 раз больше, чем у других газов). Это объясняется большой скоростью движения молекул гелия и водорода между очередными соударениями.
Коэффициент теплопроводности водяного пара и других реальных газов, существенно отличающихся от идеальных, заметно зависит от давления.
Для газовых смесей коэффициент теплопроводности необходимо определять опытным путем, так как закон аддитивности для коэффициента λ неприменим.
Коэффициент теплопроводности капельных жидкостей лежит примерно в пределах от 0,07 до 0,5 Вт×м-1×K-1. С повышением температуры для большинства жидкостей коэффициент λ убывает, исключение составляют вода и глицерин. При увеличении давления коэффициент теплопроводности жидкостей возрастает.
Коэффициент теплопроводности металлов лежит в пределах от 1,72 до 310 Вт×м-2. Наиболее теплопроводным металлом является серебро (λ = 310), затем красная медь (λ = 292), золото (λ = 224), алюминий (λ = 155) и т. д. При наличии примесей в металле коэффи-миенттеплопроводности уменьшается. Так, например, красная медь со следами мышьяка имеет λ = 105 Вт×м-1×K-1. Для железа с 0,1% углерода λ = 39 Вт×м-1×K-1, с 1,0% углерода λ = 29, с 1,5% углерода λ = 27 Вт×м-1×K-1. Для закаленной углеродистой стали коэффициент теплопроводности на 10 — 25% ниже, чем для незакаленной. При повышении температуры значения коэффициента теплопроводности чистых металлов уменьшаются. Это объясняется тем, что с повышением температуры появляются тепловые неоднородности в металле, вызывающие усиление рассеивания электронов. В отличие от чистых металлов коэффициент теплопроводности сплавов увеличивается с ростом температуры.
Коэффициент теплопроводности строительных и теплоизоляционных материалов лежит в пределах от 0,02 до 2,1 Вт×м-1×K-1, причем с повышением температуры он возрастает. Как правило, с увеличенном плотности материала коэффициент теплопроводности растет. Он зависит от структуры материала, его пористости и влажности. Наличие пор во многих строительных и теплоизоляционных материалах (кирпич, бетон, асбест, шлак и т. п.) не позволяет рассматривать их кик сплошную среду. Применение к таким телам закона Фурье является условным. Коэффициент теплопроводности порошкообразных и пористых тел в значительной степени зависит от плотности. Например, коэффициент теплопроводности асбеста при возрастании плотности от 400 до 800 кг/м3 увеличивается от 0,08 до 0,18 Вт×м-1×K-1. Такое положение объясняется тем, что с увеличением плотности материала уменьшается количество воздуха в порах, у которого коэффициент теплопроводности значительно меньше, чем у твердой части пористого тела. Для влажного материала коэффициент теплопроводности значительно больше, чем для сухого и для воды в отдельности. Это объясняется конвективным переносом тепла, возникающим вследствие капиллярного движения воды по пористому материалу, а также тем, что абсорбционно связанная влага имеет другие характеристики по сравнению со свободной водой.
Теплопрово́дность — способность материальных тел проводить энергию (теплоту) от более нагретых частей тела к менее нагретым частям тела путём хаотического движения частиц тела (атомов, молекул, электронов и т. п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества.
Теплопроводностью называется также количественная характеристика способности тела проводить тепло. В сравнении тепловых цепей с электрическими это аналог проводимости.
Количественно способность вещества проводить тепло характеризуется коэффициентом теплопроводности. Эта характеристика равна количеству теплоты, проходящему через однородный образец материала единичной длины и единичной площади за единицу времени при единичной разнице температур (1 К). В Международной системе единиц (СИ) единицей измерения коэффициента теплопроводности является Вт/(м·K).
Исторически считалось, что передача тепловой энергии связана с перетеканием гипотетического теплорода от одного тела к другому. Однако с развитием молекулярно-кинетической теории явление теплопроводности получило своё объяснение на основе взаимодействия частиц вещества. Молекулы в более нагретых частях тела движутся быстрее и передают энергию посредством столкновений медленным частицам в более холодных частях тела.
Блок: 1/7 | Кол-во символов: 1365
Источник: https://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BF%D0%BB%D0%BE%D0%BF%D1%80%D0%BE%D0%B2%D0%BE%D0%B4%D0%BD%D0%BE%D1%81%D1%82%D1%8C
Содержание
- 1 Закон теплопроводности Фурье
- 1.1 Связь с электропроводностью
- 1.2 Коэффициент теплопроводности газов
- 1.3 Теплопроводность в сильно разреженных газах
- 2 Коэффициент теплопроводности
- 3 КРАТКИЕ СВЕДЕНИЯ О ТЕПЛОПЕРЕДАЧЕ
-
-
- 3.0.0.1 Рисунок 1. Передача теплоты через плоскую стенку: а — однослойную; б — многослойную
- 3.0.1 ПЕРЕДАЧА ТЕПЛОТЫ КОНВЕКЦИЕЙ
- 3.0.2 ПЕРЕДАЧА ТЕПЛОТЫ ИЗЛУЧЕНИЕМ
- 3.0.3 СЛОЖНЫЙ ТЕПЛООБМЕН
- 3.0.3.1 Рисунок 2. Передача теплоты от греющей жидкости, нагреваемой среде через разделительную стенку: а — однослойную; б — многослойную
-
-
Закон теплопроводности Фурье
В установившемся режиме плотность потока энергии, передающейся посредством теплопроводности, пропорциональна градиенту температуры:
где — вектор плотности теплового потока — количество энергии, проходящей в единицу времени через единицу площади, перпендикулярной каждой оси, — коэффициент теплопроводности (удельная теплопроводность), — температура. Минус в правой части показывает, что тепловой поток направлен противоположно вектору (то есть в сторону скорейшего убывания температуры). Это выражение известно как закон теплопроводности Фурье.
В интегральной форме это же выражение запишется так (если речь идёт о стационарном потоке тепла от одной грани параллелепипеда к другой):
где — полная мощность тепловых потерь, — площадь сечения параллелепипеда, — перепад температур граней, — длина параллелепипеда, то есть расстояние между гранями.
Связь с электропроводностью
Связь коэффициента теплопроводности с удельной электрической проводимостью в металлах устанавливает закон Видемана — Франца:
где — постоянная Больцмана, — заряд электрона, — абсолютная температура.
Коэффициент теплопроводности газов
В газах коэффициент теплопроводности может быть найден по приближённой формуле
где — плотность газа, — удельная теплоёмкость при постоянном объёме, — средняя длина свободного пробега молекул газа, — средняя тепловая скорость. Эта же формула может быть записана как
где — сумма поступательных и вращательных степеней свободы молекул (для двухатомного газа , для одноатомного ), — постоянная Больцмана, — молярная масса, — абсолютная температура, — эффективный (газокинетический) диаметр молекул, — универсальная газовая постоянная. Из формулы видно, что наименьшей теплопроводностью обладают тяжелые одноатомные (инертные) газы, наибольшей — легкие многоатомные (что подтверждается практикой, максимальная теплопроводность из всех газов — у водорода, минимальная — у радона, из нерадиоактивных газов — у ксенона).
Теплопроводность в сильно разреженных газах
Приведённое выше выражение для коэффициента теплопроводности в газах не зависит от давления. Однако если газ сильно разрежен, то длина свободного пробега определяется не столкновениями молекул друг с другом, а их столкновениями со стенками сосуда. Состояние газа, при котором длина свободного пробега молекул ограничивается размерами сосуда называют высоким вакуумом. При высоком вакууме теплопроводность убывает пропорционально плотности вещества (то есть пропорциональна давлению в системе): , где — размер сосуда, — давление.
Таким образом коэффициент теплопроводности вакуума тем ближе к нулю, чем глубже вакуум. Это связано с низкой концентрацией в вакууме материальных частиц, способных переносить тепло. Тем не менее, энергия в вакууме передаётся с помощью излучения. Поэтому, например, для уменьшения теплопотерь стенки термоса делают двойными, серебрят (такая поверхность лучше отражает излучение), а воздух между ними откачивают.
Блок: 2/7 | Кол-во символов: 2963
Источник: https://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BF%D0%BB%D0%BE%D0%BF%D1%80%D0%BE%D0%B2%D0%BE%D0%B4%D0%BD%D0%BE%D1%81%D1%82%D1%8C
Коэффициент теплопроводности
Коэффициент λ , Вт/(м·К), в уравнении закона Фурье численно равен плотности теплового потока при падении температуры на один Кельвин (градус) на единицу длины. Коэффициент теплопроводности различных веществ зависит от их физических свойств. Для определённого тела величина коэффициента теплопроводности зависит от структуры тела, его объёмного веса, влажности, химического состава, давления, температуры. В технических расчётах величину λ берут из справочных таблиц, причём надо следить за тем, чтобы условия, для которых приведено в таблице значение коэффициента теплопроводности, соответствовали условиям рассчитываемой задачи.
Теплопередача всегда происходит от более теплого тела до более холодного, в результате Второго закона термодинамики. Передача тепла происходит до тех пор, пока тела и их окрестности не достигнут теплового равновесия. Тепло передается конвекцией, излучением или проводимостью. Хотя эти три процесса могут происходить одновременно, может случиться, что один механизм преобладает над двумя другими.
Электромагнитное излучение представляет собой комбинацию электрических и магнитных полей, осциллирующих и перпендикулярных друг другу, распространяющихся через пространство, несущее энергию из одного места в другое. В отличие от проводимости и конвекции, или других типов волн, таких как звук, которым необходима материальная среда для распространения, электромагнитное излучение не зависит от материи для ее распространения, на самом деле передача энергии излучением более эффективными в вакууме. Однако на скорость, интенсивность и направление потока энергии влияет присутствие вещества.
Особенно сильно зависит коэффициент теплопроводности от температуры. Для большинства материалов, как показывает опыт, эта зависимость может быть выражена линейной формулой:
(9.7)
где λ o — коэффициент теплопроводности при 0 °С;
β — температурный коэффициент.
Таким образом, эти волны могут проходить межпланетное и межзвездное пространство и достигать Земли от. Вулканизм, сейсмическая активность, явления метаморфизма и орогенеза — это некоторые из явлений, которые контролируются переносом и выделением тепла. Фактически, тепловой баланс Земли контролирует активность в литосфере, в астеносфере, а также во внутренней части планеты.
Тепло, достигающее поверхности Земли, имеет два источника: внутреннее пространство планеты и солнце. Часть этой энергии возвращается в космос. Если принято, что солнце и биосфера поддерживают среднюю температуру на поверхности планеты с небольшими колебаниями, то теплота, исходящая изнутри планеты, обусловливает геологическую эволюцию планеты, то есть она контролирует тектонику плит, магматизма, генерации горных цепей, эволюции внутренней части планеты, в том числе ее магнитного поля.
Коэффициент теплопроводности газов , а в особенности паров сильно зависит от давления. Численное значение коэффициента теплопроводности для различных веществ меняется в очень широких пределах — от 425 Вт/(м·К) у серебра, до величин порядка 0,01 Вт/(м·К) у газов. Это объясняется тем, что механизм передачи теплоты теплопроводностью в различных физических средах различен.
Это физическое свойство материала и является мерой способности материала «проводить» тепло. Если рассматривать одномерный случай, то закон Фурье записывается. Если тепловой поток и температура среды не изменяются со временем, процесс считается стационарным. Если в объеме материала нет тепла, мы будем иметь. Где ρ — плотность материала. Это выражение позволяет вычислять температуру в точках в пределах области при условии наложения граничных условий.
Мы можем применить это уравнение, чтобы попытаться узнать что-то о распределении температуры внутри планеты, используя в качестве граничных условий поток и температуру, известные поверхности. Интегрирование этого уравнения снова дает. Это последнее выражение может быть использовано для определения изменения температуры с глубиной. Рассмотрим, следовательно, случай Земли, полагая, что тепло переносится, главным образом, проводимостью. Кривая температуры-глубины называется «геотермальной». Анализ рисунка показывает, что на глубинах более 100 км мантия должна иметь значительное плавление, а для глубин более 150 км должна плавиться вся мантия.
Металлы имеют наибольшее значение коэффициента теплопроводности. Теплопроводность металлов уменьшается с ростом температуры и резко снижается при наличии в них примесей и легирующих элементов. Так, теплопроводность чистой меди равна 390 Вт/(м·К), а меди со следами мышьяка — 140 Вт/(м·К). Теплопроводность чистого железа 70 Вт/(м·К), стали с 0,5 % углерода — 50 Вт/(м·К), легированной стали с 18 % хрома и 9 % никеля — только 16 Вт/(м·К).
Эти «предсказания» не согласуются с информацией, полученной в результате изучения распространения сейсмических волн, поэтому мы должны сделать вывод о том, что модель теплопроводности не предсказывает правильно профиль температур в мантии. Несмотря на то, вождение модель не в прогнозировании температуры в верхней мантии, она представляет значительный успех при применении к внешней части планеты, т.е. земной коры, где внутреннее тепло главным образом в результате радиоактивного распада и транспортируется на поверхность, путем вождения.
Зависимость теплопроводности некоторых металлов от температуры показана на рис. 9.2.
Газы имеют невысокую теплопроводность (порядка 0,01…1 Вт/(м·К)), которая сильно возрастает с ростом температуры.
Теплопроводность жидкостей ухудшается с ростом температуры. Исключение составляют вода и глицерин . Вообще коэффициент теплопроводности капельных жидкостей (вода, масло, глицерин) выше, чем у газов, но ниже, чем у твердых тел и лежит в пределах от 0,1 до 0,7 Вт/(м·К).
Мы вернемся к этой проблеме при изучении теплового потока на континентах. Рассмотрим слой жидкости, нагретой в нижней части и охлажденный в верхней части. Когда жидкость нагревается, ее плотность уменьшается из-за расширения. В рассматриваемом случае верхняя часть жидкого слоя будет более холодной и, следовательно, плотнее нижней. Эта ситуация является гравитационно неустойчивой, препятствуя охлаждению жидкой жидкости, и чем больше нагревается, тем быстрее возникают конвекционные токи. Движение жидкости обусловлено движущими силами.
Рассмотрим, таким образом, прямоугольный жидкостный элемент, как показано на рисунке. Силами, действующими на элемент жидкости, являются: силы из-за градиента давления, силы тяжести и силы тяги. Для последнего необходимо учитывать плотность жидкости. Вертикальная составляющая полученной силы будет тогда.
Рис. 9.2. Влияние температуры на коэффициент теплопроводности металлов
Инструкция
Теплота является суммарной кинетической энергией молекул тела, переход которой от одних молекул к другим или от одного тела к другому может осуществляться посредством трех типов передачи: теплопроводностью, конвекцией и тепловым излучением.
Хотя радиоактивные изотопы существуют в небольших количествах в земной коре и также менее распространены в мантии, его естественный распад производит значительное количество тепла, как можно видеть из таблицы слева. Наиболее важными элементами этого процесса являются уран, торий и калий; видно, что вклад урана и тория выше, чем у калия.
В следующей таблице представлена концентрация радиоактивных элементов и тепловое образование некоторых пород. Гранит — это камень, который выделяет больше тепла из-за распада радиоактивных материалов, поскольку он имеет самую высокую концентрацию этих элементов. Измерение тепла, генерируемого земной корой, в настоящее время может быть использовано для расчета тепла, выделяемого в прошлом. С другой стороны, концентрация радиоактивных элементов может быть использована в датировке горных пород.
При теплопроводности тепловая энергия переходит от более нагретых частей тела к более холодным. Интенсивность ее передачи зависит от градиента температур , а именно от отношения разности температур, а также площади поперечного сечения и коэффициента теплопроводности . В таком случае формула для определения теплового потока q выглядит так:q = -kS(∆T/∆x), где:k — коэффициент теплопроводности материала;S – площадь поперечного сечения.
Скорость распада радиоактивного изотопа дается формулой. Хотя скорость выработки тепла в земной коре примерно на два порядка выше, чем у мантии, необходимо учитывать скорость производства мантии, поскольку объем мантии намного выше объема коры. Эта реакция была произведена в лаборатории при температурах и давлениях порядка тех, которые находятся на границе сердцевины-мантии.
На рисунке показано распределение теплового потока вдоль Земли. Тепло, потерянное через поверхность планеты, равномерно распределено. В следующей таблице приведены основные вклады: 73% тепла теряется через океаны, которые составляют 60% поверхности Земли. Большая часть тепла теряется при создании и охлаждении океанической литосферы, когда новый материал отходит от средних гребней. Тектоника плит принципиально связана с охлаждением Земли. С другой стороны, представляется, что средняя скорость создания дна океана определяется балансом между темпами выработки тепла и общей скоростью потери той же самой высокой температуры на всей поверхности планеты.
Эта формула называется законом теплопроводности Фурье, а знак минус в формуле указывает направление вектора теплового потока, который противоположен градиенту температуры. Согласно этому закону, понижению теплового потока можно добиться, уменьшив один из его составляющих. Например, можно воспользоваться материалом с другим коэффициентом теплопроводности, меньшим поперечным сечением или разностью температур.
В моделях тектоники плиты восхождение мантийных материалов происходит на океанских хребтах. Эти материалы после охлаждения приводят к появлению новой океанической коры. При удалении от восходящей зоны новая кора остывает до больших глубин, образуя более толстую и толстую жесткую пластину.
На следующем рисунке показаны наблюдаемые значения теплового потока в зависимости от возраста океанической литосферы, а также значения, рассчитанные по теоретической модели. Учитывая сказанное в предыдущем абзаце, этот график можно интерпретировать как представление значений потока как функции расстояния до хребта. Как видно, тепловой поток вблизи океанических хребтов имеет высокие значения, уменьшаясь при удалении от восходящей зоны мантийных материалов. Сравнивая наблюдаемые значения с вычисленными значениями, проверяется, что потоки, полученные из моделей, выше, чем те, которые наблюдаются вблизи хребта.
Конвективный тепловой поток осуществляется в газообразных и жидких веществах. В этом случае говорят о передаче тепловой энергии от нагревателя к среде , которая зависит от совокупности факторов: размера и формы нагревающего элемента, скорости движения молекул, плотности и вязкости среды и пр. В этом случае применима формула Ньютона:q = hS(Tэ — Tср), где:h – коэффициент конвективного переноса, отражающий свойства нагреваемой среды;S – площадь поверхности нагревательного элемента;Tэ – температура нагревательного элемента;Tср – температура окружающей среды.
Тепловое излучение – метод передачи тепла, который являются разновидностью электромагнитного излучения . Величина теплового потока при такой теплопередаче подчиняется закону Стефана-Больцмана:q = σS(Ти^4 – Тср^4), где:σ – постоянная Стефана-Больцмана;S – площадь поверхности излучателя;Tи – температура излучателя;Тср – температура окружающей среды, поглощающей излучение.
Если поперечное сечение объекта имеет сложную форму, для вычисления его площади следует разбить его на участки простых форм. После этого появится возможность рассчитать площади этих участков по соответствующим формулам, а затем их сложить.
Инструкция
Разделите поперечное сечение объекта на области , имеющие формы треугольников, прямоугольников, квадратов, секторов, кругов, полукругов и четвертей кругов. Если в результате разделения будут получаться ромбы, разделите каждый из них на два треугольника, а если параллелограммы — на два треугольника и один прямоугольник . Измерьте размеры каждой из этих областей: стороны, радиусы. Все измерения осуществляйте в одинаковых единицах.
Прямоугольный треугольник можно представить в виде половины прямоугольника , разделенного надвое по диагонали. Для расчета площади такого треугольника умножьте друг на друга длины тех сторон, которые примыкают к прямому углу (они называются катетами), затем результат умножения поделите на два. Если же треугольник прямоугольным не является , для расчета его площади вначале проведите в нем из любого угла высоту. Он окажется разделенным на два разных треугольника, каждый из которых будет прямоугольным. Измерьте длины катетов каждого из них, а затем по результатам измерений вычислите их площади.
Чтобы вычислить площадь прямоугольника, умножьте друг на друга длины двух его примыкающих друг к другу сторон. У квадрата они равны, поэтому можно длину одной стороны умножить саму на себя, то есть, возвести ее в квадрат.
Для определения площади
Блок: 3/3 | Кол-во символов: 12984
Источник: https://ulodshi.ru/the-heat-flux-transferred-by-the-radiation-formula-heat-flow-is.html
КРАТКИЕ СВЕДЕНИЯ О ТЕПЛОПЕРЕДАЧЕ
Вопросы передачи теплоты, или теплового обмена, являются основными вопросами отопительной техники. Необходимым условием теплообмена между телами или веществами является наличие разности температур. Чем больше эта разность, тем интенсивнее происходит теплообмен.
Различают три вида передачи теплоты: а) теплопроводностью, или кондукцией; б) конвекцией, или переносом теплоты движущимися частицами вещества; в) лучеиспусканием, или радиацией.
В большинстве случаев в различных тепловых процессах имеют место одновременно все три вида теплопередачи с преобладанием какого-либо из них.
Передача теплоты теплопроводностью. Такая передача осуществляется при непосредственном соприкосновении каких-либо двух тел или веществ. Теплопередача происходит внутри самого тела или вещества, которое проводит теплоту. В отопительной технике теплопередача теплопроводностью играет большую роль.
Теплопроводность обусловлена различием температур отдельных частей тела, поэтому можно считать, что распространение теплоты неразрывно связано с распределением температуры. Температурное поле, изменяющееся с течением времени, называют неустановившимся, или нестационарным. Если же температурное поле не меняется, его называют установившимся, или стационарным.
Для характеристики процесса распространения теплоты вводят понятие о тепловом потоке. Тепловой поток Q — это количество теплоты W, Дж, проходящей за время т, с, через данную поверхность в направлении нормали к ней:
Тепловой поток измеряют в ваттах (Вт).
Если количество переданной теплоты W отнести к площади поверхности F и времени т, то получим величину
которую называют плотностью теплового потока, или удельным тепловым потоком, и измеряют в Вт/м2.
Рассмотрим стационарный процесс распространения теплоты через однородную плоскую однослойную стенку (рис. 1, а).
Рисунок 1. Передача теплоты через плоскую стенку: а — однослойную; б — многослойную
Из закона распространения теплоты путем теплопроводности (закона Фурье) следует:
где W — количество переданной теплоты, Дж; λ — коэффициент пропорциональности, называемый коэффициентом теплопроводности, Вт/(м·К); tсl — температура одной поверхности стенки, К; tсll — температура другой поверхности стенки, К; δ — толщина стенки, м; F — площадь поверхности стенки, м2; τ — время, с.
Отсюда
т.е. коэффициент теплопроводности численно равен количеству теплоты, которое проходит в единицу времени (1с) в теле через единицу поверхности (1 м2) при падении температуры на 1 К на 1 м пути теплового потока.
Если обе части уравнения (3) разделить на Ft, to получим
или
где δ/λ — термическое сопротивление теплопроводности.
Таким образом, плотность теплового потока q прямо пропорциональна разности температур на поверхностях стенки и обратно пропорциональна термическому сопротивлению теплопроводности.
Коэффициент теплопроводности λ у различных материалов неодинаков и зависит от их свойств, а у газообразных и жидких веществ — от плотности, влажности, давления и температуры этих веществ. При технических расчетах значения λ выбирают по соответствующим справочным таблицам.
Рассмотрим теперь процесс передачи теплоты через многослойную стенку.
На рис. 1, б изображена плоская стенка, состоящая из трех слоев, указаны промежуточные температуры на границах этих слоев, а также толщина слоев и значения коэффициентов теплопроводности для каждого слоя. При стационарном режиме тепловой поток, проходящий через каждый отдельный слой, будет один и тот же. Тогда для каждого слоя в соответствии с формулой (6) можно записать:
Отсюда
Сложив правые и левые части этих уравнений, получим:
Следовательно, плотность теплового потока многослойной стенки
Из записанных уравнений для трех разностей температур можно получить формулы для вычисления промежуточных температур. Например:
и
ПЕРЕДАЧА ТЕПЛОТЫ КОНВЕКЦИЕЙ
Конвекция — это перенос теплоты движущейся массой жидкости или газа из области с одной температурой в область с другой температурой. Конвекция всегда сопровождается теплопроводностью, этот процесс называют конвективным теплообменом.
Теплоотдача конвекцией зависит от большого числа различных факторов:
характера конвекции — конвекции свободной, происходящей под действием внутренних сил, возникающих вследствие разности плотностей нагретых и холодных частиц, или вынужденной, происходящей под действием внешних сил — ветра, насоса, вентилятора;
режима течения жидкости — течения при малых скоростях параллельно-струйчатого характера без перемешивания (ламинарный режим) или течения при больших скоростях (течение неупорядоченное, вихревое), когда в теплоносителе наблюдаются вихри, перемещающие жидкость не только в направлении движения, но и в поперечном направлении (турбулентный режим);
скорости движения теплоносителя;
направления теплового потока (нагревание или охлаждение);
физических свойств теплоносителя — коэффициента теплопроводности, теплоемкости, плотности, вязкости, температурного напора, зависящего от разности температур теплоносителя и поверхности стенок;
площади поверхности стенки F, омываемой теплоносителем;
формы стенки, ее размеров и других факторов.
Расчет процесса конвективного теплообмена производят на основе закона Ньютона, который выражается формулой
где W — количество переданной теплоты, Дж; α — коэффициент пропорциональности, называемый коэффициентом теплоотдачи, Вт/(м2·К); F — площадь поверхности теплообмена, м2; t и tcl — температуры соответственно жидкости и стенки, К; т — время, с.
Коэффициент теплоотдачи а показывает, какое количество теплоты передается от жидкости (греющего тела) к стенке или наоборот в единицу времени через единицу поверхности при разности температур между поверхностью стенки и жидкостью в 1 К.
Разделив обе части уравнения (8) на Ft, получим выражение для плотности теплового потока при теплоотдаче:
или
где 1/α — термическое сопротивление теплоотдачи.
Коэффициент теплоотдачи а определяют опытным или аналитическим методом. Аналитический метод весьма сложен и не обеспечивает нужной точности.
ПЕРЕДАЧА ТЕПЛОТЫ ИЗЛУЧЕНИЕМ
Все тела излучают электромагнитные волны. Излучение, причиной которого является возбуждение атомов и молекул вещества вследствие их теплового движения, называют тепловым. Лучистый поток — это энергия излучения, Дж, проходящая в единицу времени (1 с) через поверхность площадью F, м2, во всех направлениях пространства.
Излучение зависит от температуры тела: чем выше температура тела, тем интенсивнее испускание тепловых лучей.
Тела, полностью поглощающие падающую на них лучистую энергию, называют абсолютно черными. Тела, обладающие свойством полного и правильного отражения всей падающей лучистой энергии, называют зеркальными, а тела, обладающие свойством полного диффузного отражения этой энергии, называют абсолютно белыми. Тела, полностью пропускающие сквозь себя падающую лучистую энергию, называют абсолютно прозрачными, или проницаемыми.
Согласно закону Стефана-Больцмана полное количество энергии, излучаемой единицей поверхности абсолютно черного тела в единицу времени,
где С0 — коэффициент излучения абсолютно черного тела, равный 5,67 Вт/(м2 ·К4); Т — абсолютная температура поверхности тела, К.
Из этого уравнения следует, что энергия излучения пропорциональна абсолютной температуре в четвертой степени.
Поток излучения ?Q, проходящий через единицу поверхности, называют плотностью потока излучения, Вт/м2,
Энергия излучения, падающего на тело Епад, частично поглощается (ЕА), частично отражается (ЕR) и частично проникает сквозь него (ED):
Отношение А = ЕА/Епад называют коэффициентом поглощения, R = ER/ Епад — коэффициентом отражения, D = ЕD/Епад — коэффициентом пропускания. Для абсолютно черного тела А = 1. Тела, для которых А < 1, называют серыми. Для абсолютно белого тела R = 1, для абсолютно прозрачного тела D = 1.
Согласно закону Кирхгофа, учитывающему способность различных тел к лучеиспусканию и лучепоглощению, коэффициент лучеиспускания любого тела при определенной температуре и определенной длине волны излучения пропорционален поглощательной способности данного тела при той же температуре и той же длине волны. При данной температуре тело излучает тем больше теплоты, чем больше оно поглощает лучей, т.е. чем оно чернее. Идеальное абсолютно черное тело поглощает все падающие на него лучи, поэтому абсолютно черное тело и излучает наибольшее количество тепловых лучей.
При термодинамическом равновесии отношение излучательной способности тела к его поглощательной способности не зависит от природы тела, а является одинаковой для всех тел функцией температуры и равно излучательной способности абсолютно черного тела Е0 при той же температуре:
Отношение излучательной способности данного тела к излучательной способности абсолютно черного тела при той же температуре называют степенью черноты тела
Следовательно, излучательную способность тела можно представить как степень его черноты, умноженную на излучательную способность абсолютно черного тела: Е = εЕ0
Степень черноты различных тел меняется от нуля до единицы и зависит от состояния поверхности, материала, температуры и других факторов.
СЛОЖНЫЙ ТЕПЛООБМЕН
Рассмотренные выше явления передачи теплоты протекают обычно одновременно. Например, когда тело (поверхность нагрева) омывается газом, то наряду с конвективным теплообменом имеется теплообмен излучением (радиацией). В системах отопления, вентиляции и кондиционирования наиболее часто встречающийся случай теплообмена — это передача теплоты от греющей жидкости, нагреваемой среде (воздух, жидкость) через разделительную стенку (рис. 2, а). В этом случае вначале происходит теплоотдача от греющей жидкости со средней температурой t1 стенке с температурой tcl. Далее теплота передается в результате теплопроводности стенки ее противоположной поверхности с температурой tcll и, наконец, эта поверхность стенки отдает теплоту нагреваемой среде со средней температурой t2. Тогда плотность теплового потока для однослойной стенки с учетом формул (6) и (10) будет
где α1 — коэффициент теплоотдачи от греющей жидкости левой (см. рис. 2, а) поверхности стенки; δ — толщина стенки; λ — коэффициент теплопроводности разделительной стенки; α2 — коэффициент теплоотдачи от правой поверхности стенки, нагреваемой среде.
Рисунок 2. Передача теплоты от греющей жидкости, нагреваемой среде через разделительную стенку: а — однослойную; б — многослойную
Если дробь
обозначить буквой k, то формула для подсчета количества теплоты, передаваемой через площадь F за время τ, примет следующий вид:
Величину k называют коэффициентом теплопередачи , а обратную ему величину — полным термическим сопротивлением теплопередачи R0 = 1/k = 1/α1 + δ/λ + 1/α2.
Если разделительная стенка состоит из нескольких слоев, например из трех (рис. 2, б), то плотность теплового потока с учетом формул (7) и (10) будет
а коэффициент теплопередачи
В многочисленных теплообменных устройствах, применяемых в любой области промышленности, в том числе в системах отопления, вентиляции и кондиционирования, основным рабочим процессом является теплообмен между теплоносителями. Такой теплообмен называют теплопередачей.
Блок: 2/2 | Кол-во символов: 13403
Источник: https://www.baurum.ru/_library/?cat=supply_warm&id=1531
Кол-во блоков: 7 | Общее кол-во символов: 30715
Количество использованных доноров: 3
Информация по каждому донору:
- https://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BF%D0%BB%D0%BE%D0%BF%D1%80%D0%BE%D0%B2%D0%BE%D0%B4%D0%BD%D0%BE%D1%81%D1%82%D1%8C: использовано 2 блоков из 7, кол-во символов 4328 (14%)
- https://ulodshi.ru/the-heat-flux-transferred-by-the-radiation-formula-heat-flow-is.html: использовано 1 блоков из 3, кол-во символов 12984 (42%)
- https://www.baurum.ru/_library/?cat=supply_warm&id=1531: использовано 1 блоков из 2, кол-во символов 13403 (44%)
|
Поделитесь в соц.сетях: |
Оцените статью:
|