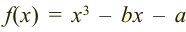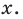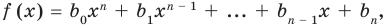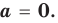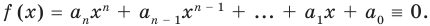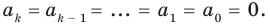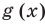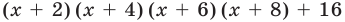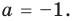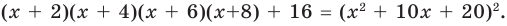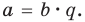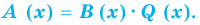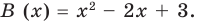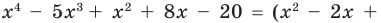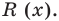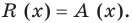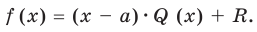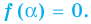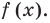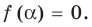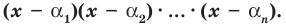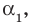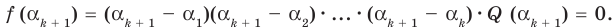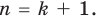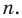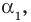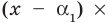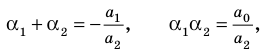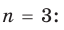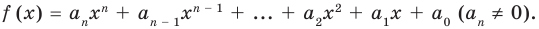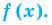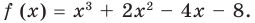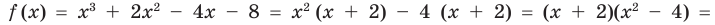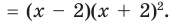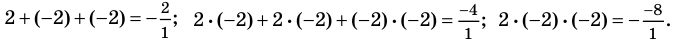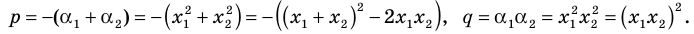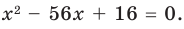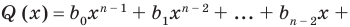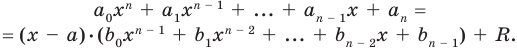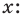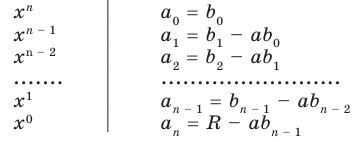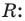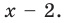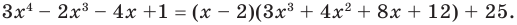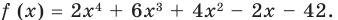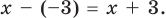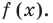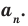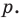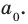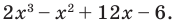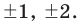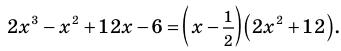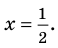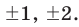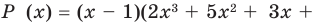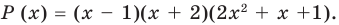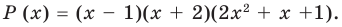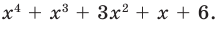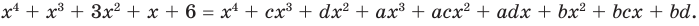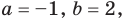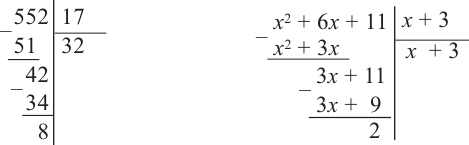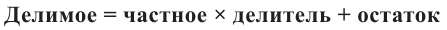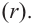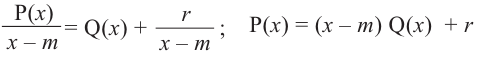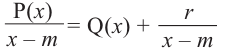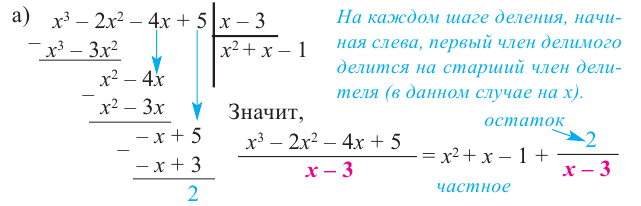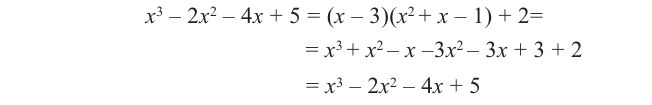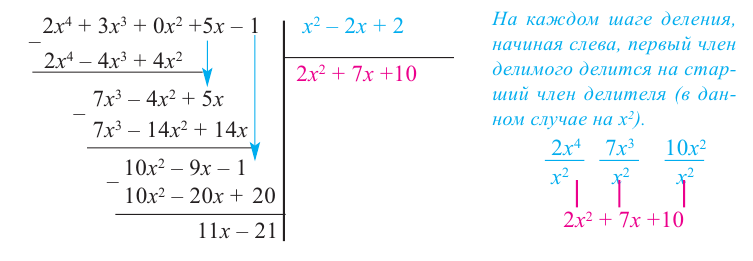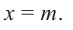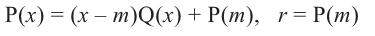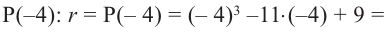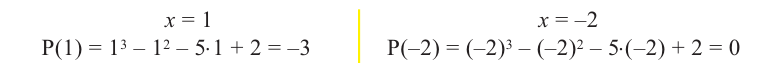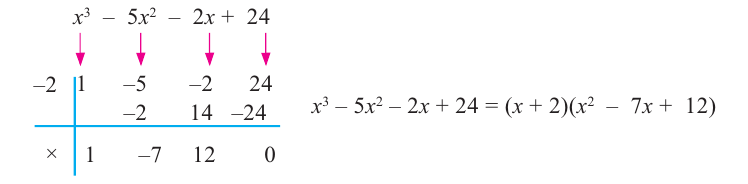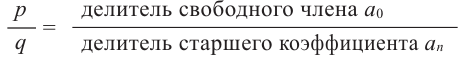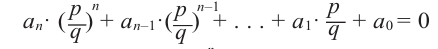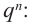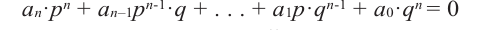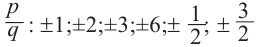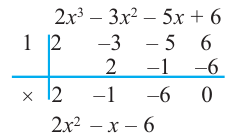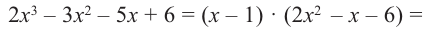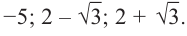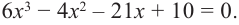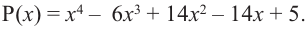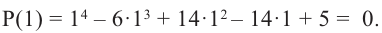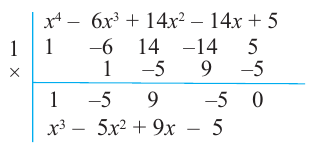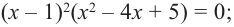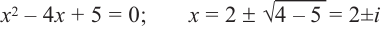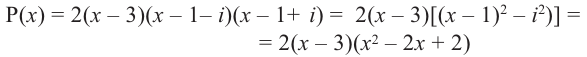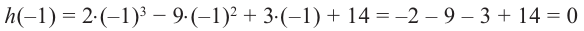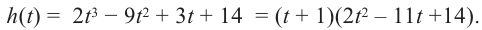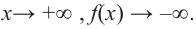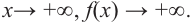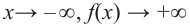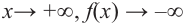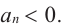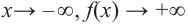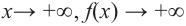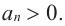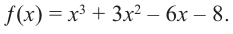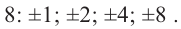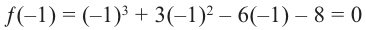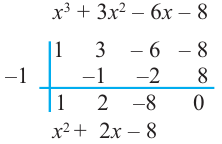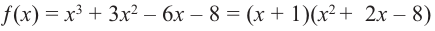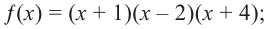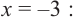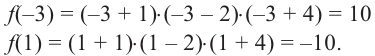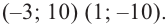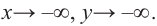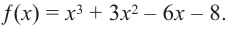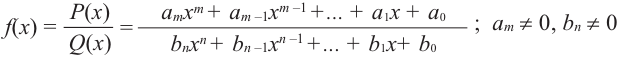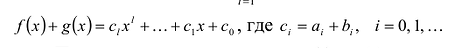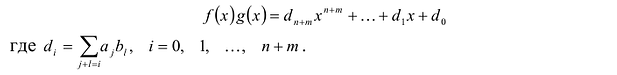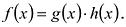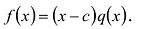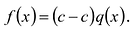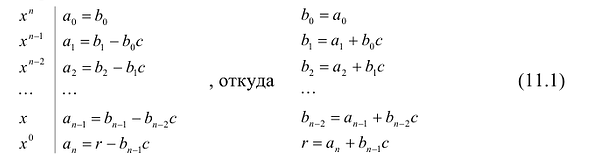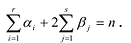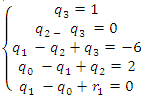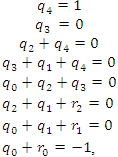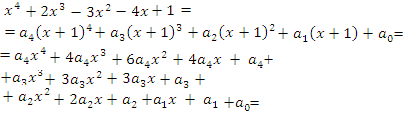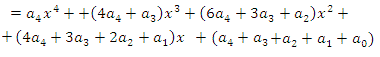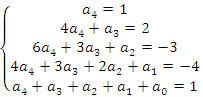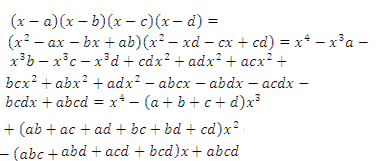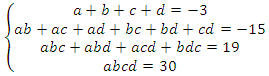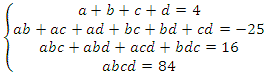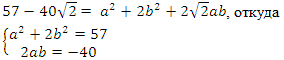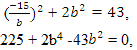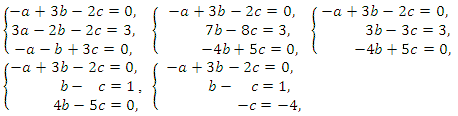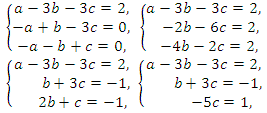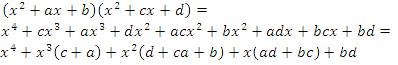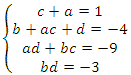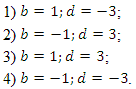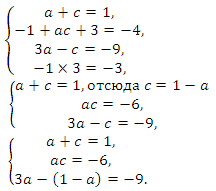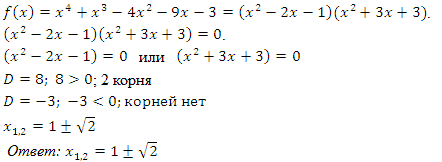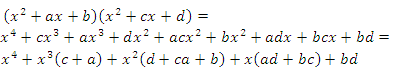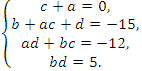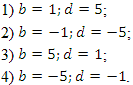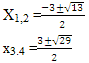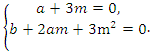Метод неопределённых коэффициентов
26 июля 2022
Метод неопределённых коэффициентов — это «полуолимпиадный» приём, с помощью которого вы сможете раскладывать на множители многочлены, которые не раскладываются, и решать уравнения, которые не решаются.:)
В двух словах этот метод звучит так:
В любой непонятной ситуации вводим новую переменную. А затем думаем, что с этой переменной делать.
Сегодня мы детально изучим метод неопределённых коэффициентов. Мы разберём столько разных задач, что не понять этот приём будет просто невозможно. И да: речь пойдёт не только о многочленах.:)
Содержание
- Основная идея
- Разложение многочлена на множители
- Решение уравнений
- Деление многочлена на многочлен
- Выделение точного квадрата
- Избавление от иррациональности
- Зачем всё это нужно
1. Основная идея
Чтобы понять основную идею метода неопределённых коэффициентов, рассмотрим простую наводящую задачу. Допустим, у нас есть квадратный трёхчлен, разложенный на множители:
[Pleft( x right)=left( x-3 right)left( x+2 right)]
Если раскрыть скобки и привести подобные слагаемые, то получится тот же многочлен, записанный в стандартном виде:
[Pleft( x right)={{x}^{2}}-x-6]
Зная разложение на множители, легко получить стандартный вид многочлена. А вот обратный переход — от стандартного вида к множителям — является вычислительно сложной операцией, но всё ещё возможной: считаем дискриминант, находим корни, вспоминаем теорему Виета и т.д.
Немного усложним задачу. Рассмотрим разложение на множители многочлена четвёртой степени (почему именно четвёртой — см. урок. «Разложение на множители»):
[Pleft( x right)=left( {{x}^{2}}-3x+1 right)left( {{x}^{2}}+x+4 right)]
Раскроем скобки и приведём подобные. Вновь получим многочлен в стандартном виде:
[Pleft( x right)={{x}^{4}}-2{{x}^{3}}+2{{x}^{2}}-11x+4]
Но как выполнить обратную операцию? Как по стандартному виду многочлена определить, на какие множители его можно разложить? Тут на помощь и приходит метод неопределённых коэффициентов.
Проблема разложения на множители
Рассмотрим задачу в общем виде. Допустим, нам нужно разложить на множители многочлен четвёртой степени:
[Pleft( x right)= color{blue}{{a}_{4}}{{x}^{4}}+ color{blue}{{a}_{3}}{{x}^{3}}+ color{blue}{{a}_{2}}{{x}^{2}}+ color{blue}{{a}_{1}}x+ color{blue}{{a}_{0}}]
Из курса алгебры мы знаем, что произвольный многочлен не всегда раскладывается на линейные двучлены вида $x-color{red}{a}$. Однако он совершенно точно раскладывается на квадратные трёхчлены вида $color{red}{a}{{x}^{2}}+color{red}{b}x+color{red}{c}$:
[Pleft( x right)=left(color{blue}{a}{{x}^{2}}+color{blue}{b}x+color{blue}{c} right)left( color{blue}{d}{{x}^{2}}+color{blue}{e}x+color{blue}{f} right)]
Записав такое разложение, мы уже наполовину выполнили задачу. Но нам неизвестны коэффициенты $color{blue}{a}$, $color{blue}{b}$, $color{blue}{c}$ и $color{blue}{d}$, $color{blue}{e}$, $color{blue}{f}$. Отсюда, кстати, и название приёма — «метод неопределённых коэффициентов». И чтобы найти эти самые неопределённые коэффициенты, воспользуемся следующей теоремой.
Теорема о нулевом многочлене
Теорема (критерий многочлена, тождественно равного нулю). Многочлен
[Pleft( x right)= color{blue}{{a}_{n}}{{x}^{n}}+ color{blue}{{a}_{n-1}}{{x}^{n-1}}+ ldots + color{blue}{{a}_{1}}x+ color{blue}{{a}_{0}}]
тождественно равен нулю (т.е. при любом значении переменной $x$) тогда и только тогда, когда все его коэффициенты равны нулю:
[color{blue}{{a}_{n}}= color{blue}{{a}_{n-1}}= ldots = color{blue}{{a}_{1}}= color{blue}{{a}_{0}}= color{red}{0}]
Доказательство я вынесу на отдельную страницу (см. урок «Корни многочлена»). Потому что у этой теоремы много применений, но нас сейчас интересует не сама теорема, а лишь одно-единственное следствие из неё:
Следствие (критерий равенства двух многочленов). Пусть даны два многочлена:
[begin{align}Aleft( x right) &= color{blue}{{a}_{n}}{{x}^{n}}+ color{blue}{{a}_{n-1}}{{x}^{n-1}}+ ldots + color{blue}{{a}_{1}}x+ color{blue}{{a}_{0}}\ Bleft( x right) &= color{blue}{{b}_{n}}{{x}^{n}}+ color{blue}{{b}_{n-1}}{{x}^{n-1}}+ ldots + color{blue}{{b}_{1}}x+ color{blue}{{b}_{0}}\ end{align}]
Эти два многочлена тождественно равны друг другу (т.е. $Aleft( x right)=Bleft( x right)$ при любом $x$) тогда и только тогда, когда равны их коэффициенты при соответствующих степенях:
[color{blue}{{a}_{n}}= color{blue}{{b}_{n}}; color{blue}{{a}_{n-1}}= color{blue}{{b}_{n-1}}; ldots ; color{blue}{{a}_{1}}= color{blue}{{b}_{1}}; color{blue}{{a}_{0}}= color{blue}{{b}_{0}}]
Вот тут всё становится на свои места!
Основной алгоритм
Пусть даны два представления одного и того же многочлена. Например, в стандартном виде и разложение на множители:
[begin{align} Pleft( x right) &= color{blue}{{a}_{4}}{{x}^{4}}+ color{blue}{{a}_{3}}{{x}^{3}}+ color{blue}{{a}_{2}}{{x}^{2}}+ color{blue}{{a}_{1}}x+ color{blue}{{a}_{0}}= \ &=left( color{blue}{a}{{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( color{blue}{d}{{x}^{2}}+ color{blue}{e}x+ color{blue}{f} right) end{align}]
Тогда для нахождения неизвестных коэффициентов в любом из этих разложений необходимо выполнить три шага:
- Раскрыть все скобки и привести подобные, чтобы получить две записи в стандартном виде;
- Приравнять соответствующие коэффициенты, составить систему уравнений;
- Решить эту систему и правильно интерпретировать ответ.
Вот и вся суть метода. Первые два пункта очевидны. Проблемы возникают лишь на третьем шаге, поскольку зачастую системы уравнений получаются нелинейными. И мы детально разберём, как решать подобные системы.
Но для начала — парочка простых задач.:)
Задача 1.1. Основная идея
Задача. Найдите числа $a$, $b$, $c$, при которых многочлены $Pleft( x right)$ и $Qleft( x right)$ равны:
[begin{align}Pleft( x right) &=2{{x}^{4}}+3{{x}^{3}}-5x-2\ Qleft( x right) &=left( ax+3 right)left( {{x}^{3}}-b right)-3x+c\ end{align}]
Решение. Согласно Теореме 1, многочлены $Pleft( x right)$ и $Qleft( x right)$ равны, когда в точности равны их коэффициенты. Поэтому раскроем скобки в многочлене $Qleft( x right)$ и найдём эти коэффициенты:
[begin{align}Qleft( x right) &=a{{x}^{4}}+3{{x}^{3}}-abx-3b-3x+c= \ &=color{blue}{a}{{x}^{4}}+ color{blue}{3}{{x}^{3}}+left( color{blue}{-ab-3} right)x+left( color{blue}{c-3b} right) end{align}]
Для удобства коэффициенты выделены синим цветом. Сравним их с коэффициентами многочлена $Pleft( x right)$:
[begin{align}& color{blue}{a}{{x}^{4}}+ color{blue}{3}{{x}^{3}}+left( color{blue}{-ab-3} right)x+left( color{blue}{c-3b} right)= \ = & color{red}{2}{{x}^{4}}+ color{red}{3}{{x}^{3}}+left( color{red}{-5} right)x+left( color{red}{-2} right) \ end{align}]
Чтобы многочлены были равны, должны выполняться равенства
[color{blue}{a}= color{red}{2};quad color{blue}{-ab-3}= color{red}{-5};quad color{blue}{c-3b}= color{red}{-2}]
Получили систему уравнения, которая легко решается:
[color{blue}{a}= color{red}{2}; color{blue}{b}= color{red}{1}; color{blue}{c}= color{red}{1}]
Ответ: $a=2$, $b=1$, $c=1$.
Задача 1.2. Альтернативный подход
Задача. Найдите числа $a$, $b$, $c$, при которых многочлены $Pleft( x right)$ и $Qleft( x right)$ равны:
[begin{align}Pleft( x right) &=3{{x}^{4}}+7{{x}^{3}}+3{{x}^{2}}+x+2\ Qleft( x right) &=left( x+1 right)left( a{{x}^{3}}+b{{x}^{2}}-x+c right)\ end{align}]
Решение. Решим эту задачу двумя способами: «чистым» методом неопределённых коэффициентов и с привлечением схемы Горнера.
Способ 1. «Чистый» метод неопределённых коэффициентов. Раскрываем скобки в многочлене $Qleft( x right)$:
[begin{align}Qleft( x right) &=a{{x}^{4}}+b{{x}^{3}}-{{x}^{2}}+cx+a{{x}^{3}}+b{{x}^{2}}-x+c= \ &= color{blue}{a}{{x}^{4}}+left( color{blue}{a+b} right){{x}^{3}}+left( color{blue}{b-1} right){{x}^{2}}+left( color{blue}{c-1} right)x+ color{blue}{c} end{align}]
Приравниваем многочлены $Qleft( x right)$ и $Pleft( x right)$:
[begin{align}& color{blue}{a}{{x}^{4}}+left( color{blue}{a+b} right){{x}^{3}}+left( color{blue}{b-1} right){{x}^{2}}+left( color{blue}{c-1} right)x+ color{blue}{c}= \= & color{red}{3}{{x}^{4}}+ color{red}{7}{{x}^{3}}+ color{red}{3}{{x}^{2}}+ color{red}{1}x+ color{red}{2} \ end{align}]
Получим набор из пяти уравнений:
[begin{array}{rrr}color{blue}{a}= color{red}{3}; & color{blue}{b-1}= color{red}{3}; & color{blue}{c}= color{red}{2}.\ color{blue}{a+b}= color{red}{7}; & color{blue}{c-1}= color{red}{1}; & {}\ end{array}]
Решаем систему из этих уравнений и получаем ответ:
[color{blue}{a}=color{red}{3}; color{blue}{b}=color{red}{4}; color{blue}{c}=color{red}{2}]
Способ 2. Привлечение схемы Горнера. Поскольку многочлен $Qleft( x right)$ разложен на множители, сделаем то же самое и с многочленом $Pleft( x right)$ — выделим из него множитель-двучлен $x+1$. Для этого заполним таблицу для $x=color{red}{-1}$:
[begin{array}{r|r|r|r|r|r} {} & color{blue}{3} & color{blue}{7} & color{blue}{3} & color{blue}{1} & color{blue}{2}\ hline color{red}{-1} & 3 & 4 & -1 & 2 & color{green}{0}\ end{array}]
Получили остаток $r=color{green}{0}$, и многочлен $Pleft( x right)$ можно переписать так:
[Pleft( x right)=left( x+1 right)left( 3{{x}^{3}}+4{{x}^{2}}-1x+2 right)]
Приравняем многочлены $Pleft( x right)$ и $Qleft( x right)$:
[begin{align}&left( x+1 right)left( color{red}{3}{{x}^{3}}+ color{red}{4}{{x}^{2}}+left( color{red}{-1} right)x+ color{red}{2} right)= \ = &left( x+1 right)left( color{blue}{a}{{x}^{3}}+ color{blue}{b}{{x}^{2}}+left( color{blue}{-1} right)x+ color{blue}{c} right) \ end{align}]
И сразу получаем ответ:
[color{blue}{a} =color{red}{3}; color{blue}{b} =color{red}{4}; color{blue}{c} =color{red}{2}]
Ответ: $a=3$, $b=4$, $c=2$.
Если вам непонятно, как работает схема Горнера и при чём тут разложение на множители, см. урок «Схема Горнера» — это ещё один универсальный алгоритм. Который, как и метод неопределённых коэффициентов, будет полезен во многих нестандартных задачах.
2. Разложение многочлена на множители
Переходим к серьёзным задачам. Всё, что мы решали выше, сводилось к простым линейным уравнениям, которые решались обычной подстановкой.
Теперь мы разберём многочлены четвёртой степени — те самые, с которых начинали рассуждения. И заодно научимся решать нелинейные системы методом целочисленного перебора.
Задача 2.1. Самая стандартная
Задача. Разложите многочлен на множители методом неопределённых коэффициентов:
[Pleft( x right)={{x}^{4}}+2{{x}^{3}}+2{{x}^{2}}+10x+25]
Этот многочлен вообще не имеет действительных корней, в чём легко убедиться, выделив точные квадраты:
[begin{align}Pleft( x right) &=left( {{x}^{4}}+2{{x}^{3}}+{{x}^{2}} right)+left( {{x}^{2}}+10x+25 right)= \ &={{x}^{2}}{{left( x+1 right)}^{2}}+{{left( x+5 right)}^{2}} end{align}]
Полученная сумма равна нулю только если $x=-5$ и одновременно $x=0$ или $x=-1$. Что, очевидно, невозможно. Следовательно, линейных множителей в разложении не будет.
Зато квадратные множители точно будут, поэтому используем метод неопределённых коэффициентов. Предположим, что многочлен раскладывается на произведение двух квадратных трёхчленов:
[Pleft( x right)=left( {{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( {{x}^{2}}+ color{blue}{d}x+ color{blue}{e} right)]
Раскрываем скобки и приводим подобные:
[begin{align}Pleft( x right)={{x}^{4}}+left( color{blue}{b+d} right){{x}^{3}} &+ left( color{blue}{bd+c+e} right){{x}^{2}}+ \ & +left( color{blue}{be+d} right)x+ color{blue}{ce} \ end{align}]
Сравниваем коэффициенты полученного многочлена с коэффициентами исходного:
[Pleft( x right)={{x}^{4}}+ color{red}{2}{{x}^{3}}+ color{red}{2}{{x}^{2}}+ color{red}{10}x+ color{red}{25}]
Выписываем равенства:
[begin{array}{rr}color{blue}{b+d}= color{red}{2}; & color{blue}{be+dc}= color{red}{10};\ color{blue}{bd+c+e}= color{red}{2}; & color{blue}{ce}= color{red}{25}.\ end{array}]
Получили систему из четырёх нелинейных уравнений. Универсального алгоритма для решения таких систем не существует. Однако здесь хорошо работает метод целочисленного перебора.
Рассмотрим последнее уравнение:
[ color{blue}{c} cdot color{blue}{e}= color{red}{25}]
Какие числа нужно перемножить, чтобы в произведении получилось 25? Вот несколько вариантов:
[begin{align}color{blue}{c} cdotcolor{blue}{e} &= color{red}{1} cdotcolor{red}{25}= color{red}{5} cdotcolor{red}{5} = \ & =left( color{red}{-1} right)cdot left( color{red}{-25} right)= \ & =left( color{red}{-5} right)cdot left( color{red}{-5} right) end{align}]
Рассмотрим вариант, когда $color{blue}{c}= color{red}{5}$ и $color{blue}{e}= color{red}{5}$. Именно он будет правильным ответом, в чём мы сейчас убедимся.
Подставим $color{blue}{c}= color{red}{5}$ и $color{blue}{e}= color{red}{5}$ в оставшиеся три уравнения. Получим систему
[left{ begin{align}b+d &=2 \ bd+5+5 &=2 \ 5b+5d &=10 \ end{align} right.]
Последнее уравнение является следствием первого, поэтому система равносильна двум уравнениям:
[left{ begin{align}b+d &=2 \ bd &=-8 \ end{align} right.]
Эта система имеет два решения, которые легко находятся методом подбора: $color{blue}{b} = color{red}{4}$ и $color{blue}{d}= color{red}{-2}$, либо наоборот $color{blue}{b}= color{red}{-2}$ и $color{blue}{d}= color{red}{4}$. Получаем два варианта разложения:
[begin{align}{{P}_{1}}left( x right) &=left( {{x}^{2}}+ color{red}{4}x+ color{red}{5} right)left( {{x}^{2}}+left( color{red}{-2} right)x+ color{red}{5} right) \ {{P}_{2}}left( x right) &=left( {{x}^{2}}+left( color{red}{-2} right)x+ color{red}{5} right)left( {{x}^{2}}+ color{red}{4}x+ color{red}{5} right) \ end{align}]
Но ведь на самом деле это одно и то же разложение — просто множители поменялись местами. Поэтому мы вправе выбрать любой вариант.
Запишем окончательный ответ:
[Pleft( x right)=left( {{x}^{2}}+4x+5 right)left( {{x}^{2}}-2x+5 right)]
Важное замечание. После приведения подобных и сравнения коэффициентов мы получили систему из нескольких нелинейных уравнений, которые затем начали решать методом целочисленного перебора.
Такие уравнения будут преследовать нас постоянно — это основная трудность метода неопределённых коэффициентов.
Чтобы в процессе перебора не упустить из виду какой-нибудь вариант, целесообразно составлять таблицу всех возможных вариантов. Например, для равенства $color{blue}{c}cdot color{blue}{e}= color{red}{25}$ таблица выглядит так:
[begin{array}{r|r|r|r|r}color{blue}{c} & color{red}{1} & color{red}{-1} & color{red}{5} & color{red}{-5}\ hline color{blue}{e} & color{red}{25} & color{red}{-25} & color{red}{5} & color{red}{-5}\ end{array}]
Обратите внимание: в таблице нет варианта $color{blue}{c}= color{red}{25}$, $color{blue}{e}= color{red}{1}$ и $color{blue}{c}= color{red}{-25}$, $color{blue}{e}= color{red}{-1}$, потому что они получаются из первых двух вариантов перестановкой множителей в итоговом разложении.
Тем не менее, в некоторых примерах придётся рассматривать все возможные варианты. Один из таких примеров мы рассмотрим чуть позже, а пока давайте потренируемся на более адекватных задачах.:)
Задача 2.2. Снова стандартная
Задача. Разложите многочлен на множители методом неопределённых коэффициентов:
[Pleft( x right)={{x}^{4}}+5{{x}^{3}}+5{{x}^{2}}-4x-2]
Решение. Запишем искомое разложение:
[Pleft( x right)=left( {{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( {{x}^{2}}+ color{blue}{d}x+ color{blue}{e} right)]
Нужно найти четыре числа: $color{blue}{b}$, $color{blue}{c}$, $color{blue}{d}$, $color{blue}{e}$. Собственно, это и есть «неопределённые коэффициенты». Раскрываем скобки и приводим подобные:
[begin{align}Pleft( x right)={{x}^{4}}+left( color{blue}{b+d} right){{x}^{3}} &+left( color{blue}{bd+c+e} right){{x}^{2}}+ \ &+left( color{blue}{be+d} right)x+ color{blue}{ce} \ end{align}]
Сравниваем коэффициенты этого многочлена с коэффициентами исходного:
[Pleft( x right)={{x}^{4}}+ color{red}{5}{{x}^{3}}+ color{red}{5}{{x}^{2}}+left( color{red}{-4} right)x+left( color{red}{-2} right)]
Получаем четыре уравнения, которые должны выполняться одновременно:
[begin{array}{rr}color{blue}{b+d}= color{red}{5}; & color{blue}{be+dc}= color{red}{-4};\ color{blue}{bd+c+e}= color{red}{5}; & color{blue}{ce}= color{red}{-2}.\ end{array}]
Произведение коэффициентов $color{blue}{c}cdot color{blue}{e}= color{red}{-2}$ — отрицательное число. Положим для определённости, что $color{blue}{c} gt 0$ и $color{blue}{e} lt 0$. Выпишем все возможные варианты:
[begin{array}{r|r|r}color{blue}{c} & color{red}{1} & color{red}{2}\ hline color{blue}{e} & color{red}{-2} & color{red}{-1}\ end{array}]
Рассмотрим первый вариант: $color{blue}{c}=color{red}{1}$ и $color{blue}{e}=color{red}{-2}$. Получим систему
[left{ begin{align}b+d &=5 \ bd+1-2 &=5 \ -2b+d &=-4 end{align} right.]
Вычтем почленно из последнего уравнения первое и получим
[begin{align}-3b &=-9 \ color{blue}{b} &= color{red}{3}end{align}]
Подставляем $color{blue}{b}= color{red}{3}$ в первое уравнение и получаем $color{blue}{d}= color{red}{2}$. Найденные значения $color{blue}{b}$ и $color{blue}{d}$ удовлетворяют всем трём равенствам. Следовательно, мы нашли решение системы:
[color{blue}{b}= color{red}{3}; color{blue}{c}= color{red}{1}; color{blue}{d}= color{red}{2}; color{blue}{e}= color{red}{-2}]
Откуда получаем искомое разложение на множители:
[Pleft( x right)=left( {{x}^{2}}+3x+1 right)left( {{x}^{2}}+2x-2 right)]
Важное замечание. К сожалению, в процессе целочисленного перебора далеко не всегда верный вариант будет попадаться сразу, на первом же шаге. Когда я собирал материалы для этого урока, иногда верным оказывался лишь четвёртый вариант из четырёх возможных.:)
Поэтому не переживайте, когда видите несовместную систему. Это нормально и даже неизбежно.
И вообще давайте посмотрим, как это выглядит на практике. Например, рассмотрим второй вариант в только что решённой задаче: $color{blue}{c}=color{red}{2}$ и $color{blue}{e}=color{red}{-1}$. Это приведёт нас к системе уравнений:
[left{ begin{align}b+d &=5 \ bd+2-1 &=5 \ -b+2d &=-4 end{align} right.]
Складываем первое уравнение с последним — и тут же получаем проблему:
[begin{align}3d &=1 \ color{blue}{d} &= color{red}{{1}/{3};} \ end{align}]
Получили дробный коэффициент $color{blue}{d}$, откуда следует, что коэффициент $color{blue}{b}$ тоже дробный:
[color{blue}{b}=5- color{blue}{d}=color{red}{{14}/{3};}]
Но тогда не выполняется второе равенство. Следовательно, система несовместна.
Задача 2.3. Упрощённые выкладки
Задача. Разложите многочлен на множители методом неопределённых коэффициентов:
[Pleft( x right)={{x}^{4}}+{{x}^{3}}+3{{x}^{2}}+32x-10]
В этот раз распишу всё кратко — только основные выкладки. Разложим многочлен $Pleft( x right)$ на два квадратных трёхчлена:
[Pleft( x right)=left( {{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( {{x}^{2}}+ color{blue}{d}x+ color{blue}{e} right)]
Раскрываем скобки, приводим подобные:
[begin{align}Pleft( x right)={{x}^{4}}+left( color{blue}{b+d} right){{x}^{3}} &+left( color{blue}{bd+c+e} right){{x}^{2}}+ \ &+left( color{blue}{be+d} right)x+ color{blue}{ce} \ end{align}]
Сравниваем с исходным многочленом:
[Pleft( x right)={{x}^{4}}+ color{red}{1}{{x}^{3}}+ color{red}{3}{{x}^{2}}+ color{red}{32}x+left( color{red}{-10} right)]
Получаем четыре уравнения:
[begin{array}{rr}color{blue}{b+d}= color{red}{1}; & color{blue}{be+dc}= color{red}{32};\ color{blue}{bd+c+e}= color{red}{3}; & color{blue}{ce}= color{red}{-10}.\ end{array}]
Поскольку $color{blue}{ce}= color{red}{-10} lt 0$, положим $color{blue}{c} gt 0$, $color{blue}{e} lt 0$. Возможные варианты:
[begin{array}{r|r|r|r|r}color{blue}{c} & color{red}{1} & color{red}{2} & color{red}{5} & color{red}{10} \ hline color{blue}{e} & color{red}{-10} & color{red}{-5} & color{red}{-2} & color{red}{-1} \ end{array}]
Первые три варианта дают несовместные системы с дробными коэффициентами $color{blue}{b}$ и $color{blue}{d}$ (проверьте это!). Рассмотрим последний вариант: $color{blue}{c}= color{red}{10}$, $color{blue}{e}= color{red}{-1}$. Получим систему
[left{ begin{align}b+d &=1 \ bd+10-1 &=3 \ -b+10d &=32 end{align} right.]
Решение системы: $color{blue}{b}= color{red}{-2}$, $color{blue}{d}= color{red}{3}$. Окончательное разложение на множители:
[Pleft( x right)=left( {{x}^{2}}-2x+10 right)left( {{x}^{2}}+3x-1 right)]
3. Решение уравнений методом неопределённых коэффициентов
Одно из важнейших приложений метода неопределённых коэффициентов — это решение уравнений высших степеней. В самом деле, зачем мы раскладываем многочлен $Pleft( x right)$ на множители? Обычно по одной из двух причин:
- Решить уравнение $Pleft( x right)=0$. Ведь произведение равно нулю, когда хотя бы один из множителей равен нулю;
- Сократить рациональную дробь вида ${Pleft( x right)}/{Qleft( x right)};$. В этом случае многочлен $Qleft( x right)$ также придётся разложить на множители.
Про рациональные дроби мы поговорим в отдельном уроке (см. урок «Разложение на простейшие»). А вот уравнения мы разберём сейчас.
Допустим, нужно решить уравнение вида
[color{blue}{{a}_{n}}{{x}^{n}}+ color{blue}{{a}_{n-1}}{{x}^{n-1}}+ ldots + color{blue}{{a}_{1}}x+ color{blue}{{a}_{0}}=0]
В левой части равенства стоит стандартный многочлен. И если коэффициенты многочлена целые, то мы уже знаем как минимум два способа решения таких уравнений:
- Теорема Безу для отыскания рациональных корней-кандидатов;
- Схема Горнера для быстрой проверки этих кандидатов.
И эта связка отлично работает, когда многочлен имеет рациональные корни вида $x={color{blue}{p}}/{color{red}{q}};$. Вот буквально: мы найдём все такие корни и решим уравнение.
А если корни иррациональны? Безу и Горнер тут бесполезны. Зато полезным оказывается разложение на множители, когда вместо большого и страшного многочлена $Pleft( x right)$ в левой части уравнения появится произведение двух многочленов меньшей степени:
[Hleft( x right)cdot Qleft( x right)=0]
А дальше всё стандартно: произведение равно нулю, когда $Hleft( x right)=0$ или $Qleft( x right)=0$. И вот мы свели исходную задачу к двум уравнениям меньших степеней, которые наверняка легко решаются.:)
Задача 3.1. «Нерешаемое» уравнение
Задача. Решите уравнение методом неопределённых коэффициентов
[{{x}^{4}}+2{{x}^{3}}+3{{x}^{2}}+2x-3=0]
Это приведённое целочисленное уравнение, но его нельзя решить по теореме Безу и схеме Горнера. Ведь целые корни этого уравнения являются делителями свободного члена $color{blue}{{a}_{0}}=-3$. Таких делителей ровно четыре:
[x=pm 1; pm 3]
И все они дают ненулевой остаток в схеме Горнера:
[begin{array}{r|r|r|r|r|r} {} & color{blue}{1} & color{blue}{2} & color{blue}{3} & color{blue}{2} & color{blue}{-3}\ hlinecolor{red}{1} & 1 & 3 & 6 & 8 & color{red}{5}\ hlinecolor{red}{-1} & 1 & 1 & 2 & 0 & color{red}{-3}\ hlinecolor{red}{3} & 1 & 5 & 18 & 56 & color{red}{165}\ hlinecolor{red}{-3} & 1 & -1 & 6 & -16 & color{red}{45}\ end{array}]
Остаётся только метод неопределённых коэффициентов. Разложим уравнение на произведение двух квадратных трёхчленов:
[left( {{x}^{2}}+color{blue}{b}x+color{blue}{c} right)left( {{x}^{2}}+color{blue}{d}x+color{blue}{e} right)=0]
Раскроем скобки и приведём подобные в правой части равенства:
[begin{align}{{x}^{4}}+left( color{blue}{b+d} right){{x}^{3}} &+ left( color{blue}{bd+c+e} right){{x}^{2}}+ \ &+ left( color{blue}{be+dc} right)x+ color{blue}{ce}=0 \ end{align}]
Вспоминаем коэффициенты многочлена в исходном уравнении:
[{{x}^{4}}+ color{red}{2}{{x}^{3}}+ color{red}{3}{{x}^{2}}+ color{red}{2}x+left( color{red}{-3} right)=0]
Получаем уже привычный набор из четырёх уравнений:
[begin{array}{rr} color{blue}{b+d}=color{red}{2}; & color{blue}{be+dc}=color{red}{2};\ color{blue}{bd+c+e}=color{red}{3}; & color{blue}{ce}=color{red}{-3}.\ end{array}]
Рассмотрим последнее уравнение: $color{blue}{ce}=color{red}{-3}$. Произведение отрицательно, значит, множители разных знаков. Без ограничения общности положим $color{blue}{c} gt color{red}{0}$, $color{blue}{e} lt color{red}{0}$. Составим таблицу вариантов:
[begin{array}{r|r|r} color{blue}{c} & color{red}{1} & color{red}{3}\ hlinecolor{blue}{e} & color{red}{-3} & color{red}{-1}\ end{array}]
Итого два варианта. Рассмотрим первый вариант: $color{blue}{c}=color{red}{1}$, $color{blue}{e}=color{red}{-3}$. Получим систему
[left{ begin{align}b+d &=2\ bd+1-3 &=3\ -3b+d &=2 end{align} right.]
Вычитая из первого уравнения последнее, получаем $color{blue}{b}=color{red}{0}$, $color{blue}{d}=color{red}{2}$, что противоречит второму уравнению. Система несовместна.
Второй вариант: $color{blue}{c}=color{red}{3}$, $color{blue}{e}=color{red}{-1}$. Система уравнений:
[left{ begin{align}b+d &=2 \ bd+3-1 &=3 \ -b+3d &=2 end{align} right.]
Складывая первое и последнее уравнение, получаем $color{blue}{b}=color{red}{1}$, $color{blue}{d}=color{red}{1}$. При подстановке во второе уравнение получаем верное числовое равенство. Следовательно, мы нашли решение:
[color{blue}{b}=color{red}{1}; color{blue}{c}=color{red}{3}; color{blue}{d}=color{red}{1}; color{blue}{e}=color{red}{-1}]
Переписываем уравнение:
[left( {{x}^{2}}+x+3 right)left( {{x}^{2}}+x-1 right)=0]
Многочлен в первой скобке не имеет действительных корней, во второй — имеет:
[{{x}^{2}}+x-1=0]
Дискриминант положителен:
[D={{1}^{2}}-4cdot 1cdot left( -1 right)=1+4=5]
Корней будет два:
[x=frac{-1pm sqrt{5}}{2}]
Неудивительно, что эти корни не были обнаружены по теореме Безу. Ведь они являются иррациональными.:)
Ответ: $x=frac{-1pm sqrt{5}}{2}$.
Задача 3.2. «Нерешаемое» уравнение — 2
Задача. Решите уравнение методом неопределённых коэффициентов:
[{{x}^{4}}-4{{x}^{3}}+5{{x}^{2}}-2x-6=0]
Это задание похоже на предыдущее, поэтому распишем всё кратко. Ожидаемое разложение на множители:
[left( {{x}^{2}}+color{blue}{b}x+color{blue}{c} right)left( {{x}^{2}}+color{blue}{d}x+color{blue}{e} right)=0]
Найдём такое разложение методом неопределённых коэффициентов. Раскрываем скобки, приводим подобные:
[begin{align}{{x}^{4}}+left( color{blue}{b+d} right){{x}^{3}} &+ left( color{blue}{bd+c+e} right){{x}^{2}}+ \ &+ left( color{blue}{be+dc} right)x+ color{blue}{ce}=0 \ end{align}]
Сравниваем с коэффициентами исходного многочлена:
[{{x}^{4}}+left( color{red}{-4} right){{x}^{3}}+ color{red}{5}{{x}^{2}}+left( color{red}{-2} right)x+left( color{red}{-6} right)=0]
Выписываем четыре уравнения:
[begin{array}{rr} color{blue}{b+d}=color{red}{-4}; & color{blue}{be+dc}=color{red}{-2};\ color{blue}{bd+c+e}=color{red}{5}; & color{blue}{ce}=color{red}{-6}.\ end{array}]
Поскольку $color{blue}{ce}=color{red}{-6}$, полагаем $color{blue}{c} gt color{red}{0}$, $color{blue}{e} lt color{red}{0}$. Возможные варианты
[begin{array}{r|r|r|r|r} color{blue}{c} & color{red}{1} & color{red}{2} & color{red}{3} & color{red}{6}\ hlinecolor{blue}{e} & color{red}{-6} & color{red}{-3} & color{red}{-2} & color{red}{-1}\ end{array}]
Перебирая варианты, обнаруживаем, что правильная комбинация — это $color{blue}{c}=color{red}{3}$, $color{blue}{e}=color{red}{-2}$:
[left{ begin{align} b+d &=-4 \ bd+3-2 &=5 \ -2b+3d &=-2 end{align} right.]
Дважды прибавим к последнему уравнению первое — получим
[begin{align} 5d&=-10 \ color{blue}{d} &= color{red}{-2} \ color{blue}{b} &= color{red}{-2} end{align}]
Следовательно, исходное уравнение примет вид
[left( {{x}^{2}}-2x+3 right)left( {{x}^{2}}-2x-2 right)=0]
Многочлен в первой скобке корней не имеет (в этом легко убедиться, посчитав дискриминант). Рассмотрим вторую скобку:
[{{x}^{2}}-2x-2=0]
Дискриминант положительный:
[D={{left( -2 right)}^{2}}-4cdot1cdot left( -2 right)=4+8=12]
Уравнение имеет два корня:
[x=frac{2pm sqrt{12}}{2}=frac{2pm 2sqrt{3}}{2}=1pm sqrt{3}]
Ответ: $x=1pm sqrt{3}$.
Задача 3.3. Более сложное уравнение
Задача. Решите уравнение методом неопределённых коэффициентов:
[2{{x}^{4}}-4{{x}^{3}}+{{x}^{2}}-6x-3=0]
Это уравнение принципиально отличается от предыдущих тем, что старший коэффициент $color{blue}{{a}_{4}}=2$. Многочлен не является приведённым, поэтому разложение на множители, вообще говоря, выглядит так:
[left( color{blue}{a}{{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( color{blue}{d}{{x}^{2}}+ color{blue}{e}x+ color{blue}{f} right)=0]
Итого шесть неизвестных коэффициентов. Для сравнения: раньше их было всего четыре.
Однако задачу можно существенно упростить, если сделать два допущения:
- Оба старших коэффициента — $color{blue}{a}$ и $color{blue}{d}$ — являются целыми и положительными.
- Положим для определённости, что $color{blue}{a} gt color{blue}{d}$.
В этом и состоит ключевая идея метода неопределённых коэффициентов: мы вводим дополнительные ограничения, которые в итоге почти наверняка выполняются. Да, есть небольшой риск «промахнуться» в своих допущениях, но это компенсируется многократным упрощением дальнейших выкладок.
В нашем случае из двух допущений немедленно следует, что $color{blue}{a}=color{red}{2}$, $color{blue}{b}=color{red}{1}$, и уравнение примет вид
[left( color{red}{2}{{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( {{x}^{2}}+ color{blue}{e}x+ color{blue}{f} right)=0]
Осталось всего четыре неизвестных коэффициента. Раскроем скобки и приведём подобные:
[begin{align}color{red}{2}{{x}^{4}}+left( color{blue}{b+2e} right){{x}^{3}} &+left( color{blue}{be+c+2f} right){{x}^{2}}+ \ &+left( color{blue}{bf+ce} right)x+ color{blue}{cf}=0 \ end{align}]
Сравним с коэффициентами исходного уравнения:
[color{red}{2}{{x}^{4}}+left( color{red}{-4} right){{x}^{3}}+color{red}{1}{{x}^{2}}+left( color{red}{-6} right)x+left( color{red}{-3} right)=0]
Получим четыре уравнения, но из-за коэффициента $color{blue}{a}=color{red}{2}$ они отличаются от привычных:
[begin{array}{rr} color{blue}{b+2e}= color{red}{-4}; & color{blue}{bf+ce}= color{red}{-6};\ color{blue}{be+c+2f}= color{red}{1}; & color{blue}{cf}= color{red}{-3}.\ end{array}]
Многочлены в первой и второй скобке не являются взаимозаменяемыми (поскольку у них разные коэффициенты при ${{x}^{2}}$), поэтому необходимо рассмотреть все возможные комбинации, дающие $color{blue}{cf}= color{red}{-3}$:
[begin{array}{r|r|r|r|r} color{blue}{c} & color{red}{1} & color{red}{3} & color{red}{-1} & color{red}{-3}\ hlinecolor{blue}{f} & color{red}{-3} & color{red}{-1} & color{red}{3} & color{red}{1}\ end{array}]
Рассмотрим каждую комбинацию. В первом случае быстро обнаружится, что система несовместна. А вот второй случай, когда $color{blue}{c}= color{red}{3}$ и $color{blue}{f}= color{red}{-1}$, представляет интерес:
[left{ begin{align}b+2e &=-4 \ be+3-2 &=1 \ -b+3e &=-6 end{align} right.]
Складываем первое уравнение с последним — получаем
[begin{align}5e &=-10 \ color{blue}{e} &= color{red}{-2} \ color{blue}{b} &= color{red}{0} end{align}]
Итак, система совместна. Получили разложение на множители:
[left( 2{{x}^{2}}+3 right)left( {{x}^{2}}-2x-1 right)=0]
Многочлен в первых скобках принимает только положительные значения, поэтому не имеет корней:
[2{{x}^{2}}+3ge 0+3 gt 0]
Рассмотрим вторые скобки:
[{{x}^{2}}-2x-1=0]
Это квадратное уравнение. Дискриминант положительный:
[D={{2}^{2}}-4cdot 1cdot left( -1 right)=4+4=8]
Следовательно, уравнение имеет два различных корня:
[x=frac{2pm sqrt{8}}{2}=frac{2pm 2sqrt{2}}{2}=1pm sqrt{2}]
Это и есть корни исходного уравнения четвёртой степени.
Ответ: $x=1pm sqrt{2}$.
4. Деление многочлена на многочлен
Ещё одна задача, где работает метод неопределённых коэффициентов — это деление одного многочлена на другой с остатком. Напомню, что разделить многочлен $Pleft( x right)$ на двучлен $Tleft( x right)$ с остатком — это значит представить его в виде
[Pleft( x right)=Qleft( x right)cdot Tleft( x right)+Rleft( x right)]
При этом степень остатка $Rleft( x right)$ должна быть меньше степени делителя $Tleft( x right)$. Кроме того,
[deg Qleft( x right)+deg Tleft( x right)=deg Pleft( x right)]
При соблюдении таких ограничений многочлены $Qleft( x right)$ и $Rleft( x right)$ всегда определяются однозначно. Их коэффициенты мы как раз и будем находить.
Задача 4.1. Деление на двучлен
Задача. Используя метод неопределённых коэффициентов, найдите частное $Qleft( x right)$ и остаток $Rleft( x right)$ при делении многочлена
[Pleft( x right)={{x}^{3}}-5{{x}^{2}}+15x-6]
на двучлен $Tleft( x right)=x-3$.
Итак, мы хотим представить многочлен $Pleft( x right)$ в виде
[Pleft( x right)=Qleft( x right)cdot left( x-3 right)+Rleft( x right)]
где $Qleft( x right)$ — неполное частное. Точнее, $Qleft( x right)$ — квадратный трёхчлен, потому что
[begin{align} deg Qleft( x right) &=deg Pleft( x right)-deg Tleft( x right)= \ &=3-1=2end{align}]
Кроме того, степень делителя $deg Tleft( x right)=1$, поэтому степень остатка $deg Rleft( x right)=0$, т.е. $Rleft( x right)$ — это просто число. С учётом этих фактов многочлен $Pleft( x right)$ примет вид
[Pleft( x right)=left( color{blue}{a}{{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( x-3 right)+ color{blue}{d}]
Раскроем скобки, приведём подобные слагаемые:
[Pleft( x right)= color{blue}{a}{{x}^{3}}+left( color{blue}{b-3a} right){{x}^{2}}+left( color{blue}{c-3b} right)x+left( color{blue}{d-3c} right)]
С другой стороны, изначально тот же многочлен $Pleft( x right)$ имел вид
[Pleft( x right)= color{red}{1}{{x}^{3}}+left( color{red}{-5} right){{x}^{2}}+ color{red}{15}x+left( color{red}{-6} right)]
Приравниваем коэффициенты и получаем четыре равенства:
[begin{array}{rr} color{blue}{a}= color{red}{1}; & color{blue}{c-3b}= color{red}{15};\ color{blue}{b-3a}= color{red}{-5}; & color{blue}{d-3c}= color{red}{-6}.\ end{array}]
Это система из четырёх уравнений с четырьмя неизвестными, которая легко решается:
[color{blue}{a}= color{red}{1}; color{blue}{b}= color{red}{-2}; color{blue}{c}= color{red}{9}; color{blue}{d}= color{red}{21}]
Подставим найденные числа в $Qleft( x right)$ и $Rleft( x right)$:
[begin{align} & Qleft( x right)={{x}^{2}}-2x+9 \ & Rleft( x right)=21 \end{align}]
Ответ: $Qleft( x right)={{x}^{2}}-2x+9$, $Rleft( x right)=21$.
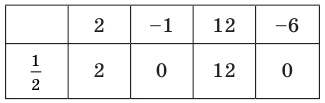
Поскольку мы делим $Pleft( x right)$ на двучлен $x-color{red}{3}$, составим таблицу для $x=color{red}{3}$:
[begin{array}{r|r|r|r|r} {} & color{blue}{1} & color{blue}{-5} & color{blue}{15} & color{blue}{-6}\ hlinecolor{red}{3} & 1 & -2 & 9 & color{green}{21}\ end{array}]
Перепишем многочлен $Pleft( x right)$ согласно этой таблице и сравним с записью для метода неопределённых коэффициентов:
[begin{align}Pleft( x right) &=left( color{red}{1}{{x}^{2}}- color{red}{2}x+ color{red}{9} right)left( x-color{red}{3} right)+ color{green}{21}= \ &=left( color{blue}{a}{{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( x- color{red}{3} right)+ color{blue}{d} end{align}]
Получили те же числа, что и при решении «напролом».
Впрочем, такие рассуждения актуальны лишь при делении на двучлен вида $x-color{red}{a}$. В следующем задании они нам уже не помогут.:)
Задача 4.2. Многочлен с параметром
Задача. При каких значениях параметров $a$ и $b$ многочлен
[Pleft( x right)={{x}^{3}}+a{{x}^{2}}-x+b]
делится без остатка на многочлен
[Tleft( x right)={{x}^{2}}+2x+5]
Решение. Если многочлен $Pleft( x right)$ делится без остатка на многочлен $Tleft( x right)$, то его можно представить в виде
[Pleft( x right)=Qleft( x right)cdot Tleft( x right)]
Здесь многочлен $Qleft( x right)$ — это частное, и его степень равна
[deg Qleft( x right)=deg Pleft( x right)-deg Tleft( x right)=3-2=1]
Итак, $Qleft( x right)$ — линейный двучлен вида $color{blue}{c}x+color{blue}{d}$ (коэффициенты $color{blue}{a}$ и $color{blue}{b}$ уже заняты в условии задачи). Выражение для $Pleft( x right)$ можно переписать так:
[Pleft( x right)=left( color{blue}{c}x+ color{blue}{d} right)left( {{x}^{2}}+2x+5 right)]
Найдём коэффициенты $color{blue}{c}$ и $color{blue}{d}$. Раскрываем скобки (стандартная процедура для метода неопределённых коэффициентов) и приводим подобные:
[Pleft( x right)= color{blue}{c}{{x}^{3}}+left( color{blue}{2c+d} right){{x}^{2}}+left( color{blue}{5c+2d} right)x+ color{blue}{5d}]
Сравниваем с коэффициентами исходного многочлена:
[Pleft( x right)= color{red}{1}{{x}^{3}}+ color{red}{a}{{x}^{2}}+left( color{red}{-1} right)x+ color{red}{b}]
Приравниваем соответствующие «красные» и «синие» коэффициенты и получаем четыре равенства:
[begin{array}{rr}color{blue}{c}= color{red}{1}; & color{blue}{5c+2}d= color{red}{-1};\color{blue}{2c+d}= color{red}{a}; & color{blue}{5d}= color{red}{b}.\end{array}]
Итак, у нас четыре линейных уравнения и четыре переменных. Эта система имеет только одно решение:
[ color{blue}{a}= color{red}{-1}; color{blue}{b}= color{red}{-15}; color{blue}{c}= color{red}{1}; color{blue}{d}= color{red}{-3}]
Впрочем, нас интересуют лишь переменные $color{blue}{a}$ и $color{blue}{b}$.
Ответ: $a=-1$, $b=-15$.
Задача 4.3. Квадратный трёхчлен
Задача. Используя метод неопределённых коэффициентов, найдите частное $Qleft( x right)$ и остаток $Rleft( x right)$ при делении многочлена
[Pleft( x right)=2{{x}^{2}}+3x-3]
на двучлен $Tleft( x right)=2x-1$.
Решение. Частное $Qleft( x right)$ имеет степень
[deg Qleft( x right)=deg Pleft( x right)-deg Tleft( x right)=2-1=1]
Следовательно, $Qleft( x right)$ — линейный двучлен вида $color{blue}{a}x+ color{blue}{b}$, а остаток $Rleft( x right)$ — просто число $color{blue}{c}$. С учётом этого перепишем многочлен $Pleft( x right)$:
[begin{align}Pleft( x right) &=left( ax+b right)left( 2x-1 right)+c= \ &=2a{{x}^{2}}-ax+2bx-b+c= \ &= color{blue}{2a}{{x}^{2}}+left( color{blue}{2b-a} right)x+left( color{blue}{c-b} right) end{align}]
Сравним с исходным видом этого же многочлена:
[Pleft( x right)= color{red}{2}{{x}^{2}}+color{red}{3}x+left( color{red}{-3} right)]
Приравниваем соответствующие коэффициенты — получаем три уравнения:
[color{blue}{2a}=color{red}{2};quadcolor{blue}{2b-a}=color{red}{3};quadcolor{blue}{c-b}=color{red}{-3}]
Эта система легко решается:
[color{blue}{a}=color{red}{1}; color{blue}{b}=color{red}{2}; color{blue}{c}=color{red}{-1}]
Следовательно, неполное частное $Qleft( x right)=x+2$ и остаток $Rleft( x right)=-1$.
Ответ: $Qleft( x right)=x+2$, $Rleft( x right)=-1$.
Задача 4.4. Сложный многочлен
Задача. Используя метод неопределённых коэффициентов, найдите частное $Qleft( x right)$ и остаток $Rleft( x right)$ при делении многочлена
[Pleft( x right)={{x}^{5}}-1]
на квадратный трёхчлен $Tleft( x right)={{x}^{2}}+2x-1$.
Решение. На самом деле это несложная задача, но вычислений будет много. Запишем результат деления с остатком:
[Pleft( x right)=Qleft( x right)cdot left( {{x}^{2}}+2x-1 right)+Rleft( x right)]
Сразу найдём степени неполного частного и остатка:
[begin{align} deg Qleft( x right) &=deg Pleft( x right)-deg Tleft( x right)=5-2=3 \ deg Rleft( x right) & lt deg Tleft( x right)=2Rightarrow deg Rleft( x right)=1 \ end{align}]
Переходим к методу неопределённых коэффициентов. Сначала запишем общий вид многочленов $Qleft( x right)$ и $Rleft( x right)$:
[begin{align}Qleft( x right) &= color{blue}{a}{{x}^{3}}+ color{blue}{b}{{x}^{2}}+ color{blue}{c}x+ color{blue}{d} \ Rleft( x right) &= color{blue}{k}x+ color{blue}{l} \ end{align}]
Пусть вас не пугает большое количество переменных. Это нормально для многочленов высших степеней. Подставим наши выражения в формулу для $Pleft( x right)$:
[begin{align}Pleft( x right) &=left( color{blue}{a}{{x}^{3}}+ color{blue}{b}{{x}^{2}}+ color{blue}{c}x+ color{blue}{d} right)left( {{x}^{2}}+2x-1 right)+ \ &+ color{blue}{k}x+ color{blue}{l} \ end{align}]
Раскрываем скобки. Для удобства запишем одночлены одинаковой степени в одном и том же столбце:
[begin{array}{rrrrrr} color{blue}{a}{{x}^{5}} & + color{blue}{2a}{{x}^{4}} & — color{blue}{a}{{x}^{3}} & {} & {} & {}\ {} & + color{blue}{b}{{x}^{4}} & + color{blue}{2b}{{x}^{3}} & — color{blue}{b}{{x}^{2}} & {} & {}\ {} & {} & + color{blue}{c}{{x}^{3}} & + color{blue}{2c}{{x}^{2}} & — color{blue}{c}x & {}\ {} & {} & {} & + color{blue}{d}{{x}^{2}} & + color{blue}{2d}x & — color{blue}{d}\ {} & {} & {} & {} & + color{blue}{k}x & + color{blue}{l}\ end{array}]
Приводим подобные слагаемые:
[begin{align}Pleft( x right) &=color{blue}{a}{{x}^{5}}+left( color{blue}{2a+b} right){{x}^{4}}+left( color{blue}{-a+2b+c} right){{x}^{3}}+ \ &+left( color{blue}{-b+2c+d} right){{x}^{2}}+left( color{blue}{-c+2d+k} right)x+left( color{blue}{-d+l} right) \ end{align}]
Сравниваем эту запись с исходным многочленом:
[Pleft( x right)= color{red}{1}cdot {{x}^{5}}+ color{red}{0}cdot {{x}^{4}}+ color{red}{0}cdot {{x}^{3}}+ color{red}{0}cdot {{x}^{2}}+ color{red}{0}cdot x+left( color{red}{-1} right)]
Получаем шесть уравнений, которые последовательно решаются:
[begin{array}{ll}color{blue}{a}= color{red}{1} & color{blue}{d}=b-2c= color{red}{-12}\ color{blue}{b}=-2a= color{red}{-2} & color{blue}{k}=c-2d= color{red}{29}\ color{blue}{c}=a-2b= color{red}{5} & color{blue}{l}=d-1= color{red}{-13}\ end{array}]
Подставим найденные коэффициенты в выражения для $Qleft( x right)$ и $Rleft( x right)$:
[begin{align}Qleft( x right) &={{x}^{3}}-2{{x}^{2}}+5x-12 \ Rleft( x right) &=29x-13 \ end{align}]
Мы нашли неполное частное и остаток от деления. Это и есть окончательный ответ.
Ответ: $Qleft( x right)={{x}^{3}}-2{{x}^{2}}+5x-12$, $Rleft( x right)=29x-13$.
5. Выделение точного квадрата
Ещё одно приложение метода неопределённых коэффициентов — это «сворачивание» многочленов по формулам сокращённого умножения:
[begin{align}{{left( apm b right)}^{2}} &={{a}^{2}}pm 2ab+{{b}^{2}} \ {{left( apm b right)}^{3}} &={{a}^{3}}pm 3{{a}^{2}}b+3a{{b}^{2}}pm {{b}^{3}} \ end{align}]
Здесь всё как в разложении на множители: раскрывать скобки и привести подобные легко, а вот обратный переход — по коэффициентам «угадать» формулу сокращённого умножения — операция весьма нетривиальная.
Такие «нетривиальные операции» регулярно встречаются в задачах с параметрами и при работе с корнями. Параметрам посвящён отдельный урок, а вот корни мы рассмотрим прямо сейчас.
Задача 5.1. Избавление от корня
Задача. Упростите выражение
[sqrt{7+4sqrt{3}}]
Решение. Единственное, что здесь можно упростить — это избавиться от внешнего большого корня. Для этого нужно представить подкоренное выражение в виде точного квадрата:
[7+4sqrt{3}={{left( color{blue}{a}+ color{blue}{b}sqrt{3} right)}^{2}}]
Почему именно такая конструкция возводится в квадрат? Всё просто: в исходной сумме мы видим одно слагаемое с корнем и одно слагаемое без него. Для получения такой суммы исходные слагаемые тоже должны быть разными: одно с корнем, а другое — без него.
В этом случае числа $color{blue}{a}$ и $color{blue}{b}$ будут либо рациональными, либо вообще целыми. И в этом вся суть метода неопределённых коэффициентов, потому что найти такие числа не составит особого труда — достаточно раскрыть скобки по формуле квадрата суммы:
[begin{align}{{left( color{blue}{a}+ color{blue}{b}sqrt{3} right)}^{2}} &={color{blue}{a}^{2}}+2color{blue}{ab}sqrt{3}+{{left( color{blue}{b}sqrt{3} right)}^{2}}= \ &=left( {color{blue}{a}^{2}}+3{color{blue}{b}^{2}} right)+2color{blue}{ab}sqrt{3} end{align}]
Сравниваем полученное разложение с исходным выражением:
[color{red}{7}+color{red}{4}sqrt{3}=left( {color{blue}{a}^{2}}+3{color{blue}{b}^{2}} right)+2color{blue}{ab}sqrt{3}]
Чтобы эти выражения были гарантированно равны друг другу, достаточно потребовать, чтобы слагаемые без корня совпадали. Как и слагаемые с корнем:
[left{ begin{align}{color{blue}{a}^{2}}+3{color{blue}{b}^{2}} &=7 \ 2color{blue}{ab} &=4 end{align} right.]
Это нелинейная система с двумя переменными, которая легко решается методом подбора:
[left{ begin{align}{color{blue}{a}^{2}}+3cdot {color{blue}{b}^{2}} &={color{red}{2}^{2}}+3cdot {color{red}{1}^{2}} \ color{blue}{a}cdotcolor{blue}{b} &=color{red}{2}cdotcolor{red}{1} end{align} right.]
Научиться раскладывать целые числа на «правильные» слагаемые и множители — вопрос небольшой практики. Просто попробуйте — и вы поймёте, насколько это быстро и легко.
Нам остаётся лишь записать решение:
[color{blue}{a}=color{red}{2}; color{blue}{b}=color{red}{1}]
Затем подставить найденные числа в исходное выражение:
[begin{align}sqrt{7+4sqrt{3}} &=sqrt{{{left( 2+sqrt{3} right)}^{2}}}= \ &=left| 2+sqrt{3} right|= \ &=2+sqrt{3} end{align}]
Ответ: $2+sqrt{3}$.
Важное замечание. Помните, что корень не просто «сжигает» квадрат вокруг выражения — на их месте появляется модуль:
[sqrt{{{a}^{2}}}=left| a right|]
Потому что арифметический квадратный корень — это по определению всегда неотрицательное число:
[begin{align}sqrt{{{5}^{2}}} &=left| 5 right|=5 \ sqrt{{{left( -8 right)}^{2}}} &=left| -8 right|=8 end{align}]
Когда под модулем стоит иррациональное выражение, его знак следует проверять отдельно. Иначе даже при правильном ответе его можно счесть недостаточно обоснованным.
Если вы забыли, как проверять знаки таких выражений, вернитесь к уроку «Знаки иррациональных выражений». В двух словах: для такой проверки используются либо цепочки неравенств, либо цепочки равносильных преобразований.
В следующем задании мы отработаем оба способа.
Задача 5.2. Предварительные преобразования
Задача. Упростите выражение
[sqrt{37-5sqrt{48}}]
Под корнем мы видим ещё один корень: $sqrt{48}$ — это большое число, с ним сложно работать. Поэтому прежде чем искать точный квадрат, немного упростим выражение:
[begin{align}sqrt{37-5sqrt{48}} &=sqrt{37-5sqrt{color{red}{16}cdot 3}}= \ &=sqrt{37-5cdot color{red}{4}cdot sqrt{3}}= \ &=sqrt{37-20sqrt{3}} end{align}]
Теперь представляем подкоренное выражение в виде точного квадрата
[37-20sqrt{3}={{left( color{blue}{a}- color{blue}{b}sqrt{3} right)}^{2}}]
Обратите внимание: перед нами квадрат разности. Потому что в исходном подкоренном выражении элементы не складывались, а именно вычитались. Этот факт ещё даст о себе знать, когда будем выяснять знак подмодульного выражения.
Ну а пока всё просто. Сравниваем старую запись и новую:
[color{red}{37}-color{red}{20}sqrt{3}=left( {color{blue}{a}^{2}}+3{color{blue}{b}^{2}} right)-2color{blue}{ab}sqrt{3}]
Получаем систему уравнений:
[left{ begin{align}{color{blue}{a}^{2}}+3{color{blue}{b}^{2}} &=37 \ 2color{blue}{ab} &=20 end{align} right.]
Второе уравнение перепишем в виде $color{blue}{ab}=10$, а затем разложим правые части равенств на «правильные» слагаемые и множители:
[left{ begin{align}{color{blue}{a}^{2}}+3cdot {color{blue}{b}^{2}} &={color{red}{5}^{2}}+3cdot {color{red}{2}^{2}} \ color{blue}{a}cdotcolor{blue}{b} &=color{red}{5}cdotcolor{red}{2} end{align} right.]
Получили красивое решение:
[color{blue}{a}=color{red}{5}; color{blue}{b}=color{red}{2}]
Возвращаемся к исходному выражению и извлекаем корень:
[sqrt{37-20sqrt{3}}=sqrt{{{left( 5-2sqrt{3} right)}^{2}}}=left| 5-2sqrt{3} right|]
Чтобы раскрыть модуль, нужно выяснить знак иррационального числа $5-2sqrt{3}$. Для этого можно заметить, что $sqrt{3} lt 2$, поэтому
[5-2sqrt{3} gt 5-2cdot 2=1 gt 0]
Это и есть цепочка неравенств. Также можно напрямую сравнить число $5-2sqrt{3}$ с нулём:
[begin{align}5-2sqrt{3} &vee 0 \ 5 &vee 2sqrt{3} \ 25 &vee 12 end{align}]
Очевидно, что $25 gt 12$, поэтому мы ещё раз убеждаемся, что исходное число положительное, и модуль раскрывается со знаком «плюс»:
[left| 5-2sqrt{3} right|=5-2sqrt{3}]
Ответ: $5-2sqrt{3}$.
Но всё это были довольно простые примеры с квадратным корнем. Как насчёт корней $n$-й степени?
Задача 5.3. Проблема с корнем
Задача. Упростите выражение
[sqrt[3]{sqrt{10}-3}cdot sqrt[6]{19+6sqrt{10}}]
Решение. Для начала вспомним свойства корней $n$-й кратности. Их можно умножать:
[sqrt[n]{a}cdot sqrt[n]{b}=sqrt[n]{acdot b}]
А также извлекать корень из корня:
[sqrt[k]{sqrt[m]{a}}=sqrt[mcdot k]{a}]
В частности, второй корень из задачи можно переписать так:
[sqrt[6]{19+6sqrt{10}}=sqrt[3]{sqrt{19+6sqrt{10}}}]
Чтобы избавиться от внутреннего квадратного корня, представим подкоренное выражение в виде точного квадрата. Но поскольку $sqrt{10}=sqrt{5}cdot sqrt{2}$, возможны два варианта:
[begin{align}19+6sqrt{10} &={{left( color{blue}{a}+ color{blue}{b}sqrt{10} right)}^{2}} \ 19+6sqrt{10} &={{left( color{blue}{a}sqrt{2}+ color{blue}{b}sqrt{5} right)}^{2}} \ end{align}]
Однако в исходном выражении (т.е. прямо в условии задачи) есть ещё один $sqrt{10}$, который пока никак не преобразуется и никуда не денется, поэтому целесообразно рассмотреть лишь первый вариант:
[begin{align} color{red}{19}+ color{red}{6}sqrt{10} &={{left( color{blue}{a}+ color{blue}{b}sqrt{10} right)}^{2}}= \ &=ldots =left( {color{blue}{a}^{2}}+10{color{blue}{b}^{2}} right)+ 2color{blue}{ab}sqrt{10} end{align}]
Получаем стандартную систему:
[left{ begin{align}{color{blue}{a}^{2}}+10{color{blue}{b}^{2}} &=19 \ 2 color{blue}{ab} &=6 end{align} right.]
Второе уравнение равносильно $color{blue}{ab}=3$, и всю систему можно переписать так:
[left{ begin{align}{color{blue}{a}^{2}}+10cdot {color{blue}{b}^{2}} &={color{red}{3}^{2}}+10cdot {color{red}{1}^{2}} \ color{blue}{a} cdotcolor{blue}{b} &= color{red}{3}cdotcolor{red}{1} end{align} right.]
Очевидно, что $color{blue}{a}=color{red}{3}$, $color{blue}{b}=color{red}{1}$, поэтому
[begin{align}sqrt{19+6sqrt{10}} &=sqrt{{{left( 3+sqrt{10} right)}^{2}}}= \ &=left| 3+sqrt{10} right|= \ &=3+sqrt{10} end{align}]
Возвращаемся к исходному заданию:
[sqrt[3]{sqrt{10}-3}cdot sqrt[3]{3+sqrt{10}}=sqrt[3]{{{left( sqrt{10} right)}^{2}}-{{3}^{2}}}=1]
Ответ: 1.
Наконец, рассмотрим задание, где требуется выделить куб суммы и куб разности. Как вы понимаете, это задание совершенно другого уровня сложности.:)
Задача 5.4. Куб суммы и куб разности
Задача. Упростите выражение
[sqrt[3]{10+6sqrt{3}}+sqrt[3]{10-6sqrt{3}}]
Чтобы «красиво» извлечь корень третьей степени, нужно представить подкоренное выражение в виде точного куба. Начнём с суммы:
[begin{align}color{red}{10}+ color{red}{6}sqrt{3} &={{left( color{blue}{a}+ color{blue}{b}sqrt{3} right)}^{3}}= \ &={color{blue}{a}^{3}}+3{color{blue}{a}^{2}} color{blue}{b}sqrt{3}+3color{blue}{a}{color{blue}{b}^{2}}cdot 3+{color{blue}{b}^{3}}cdot 3sqrt{3}= \ &=left( {color{blue}{a}^{3}}+9color{blue}{a}{color{blue}{b}^{2}} right)+left( 3{color{blue}{a}^{2}}color{blue}{b}+3{color{blue}{b}^{3}} right)sqrt{3} end{align}]
Получаем систему с двумя неизвестными:
[left{ begin{align}{color{blue}{a}^{2}}+9color{blue}{a}{color{blue}{b}^{2}} &=10 \ 3{color{blue}{a}^{2}}color{blue}{b}+3{color{blue}{b}^{3}} &=6 end{align} right.]
Методом подбора находим решение: $color{blue}{a}=color{red}{1}$, $color{blue}{b}=color{red}{1}$. Несмотря на грозный внешний вид, такие системы часто легко решаются простым перебором с проверкой:
[{{left( 1+1cdot sqrt{3} right)}^{3}}=1+3sqrt{3}+9+3sqrt{3}=10+6sqrt{3}]
Возвращаемся к исходному выражению:
[begin{align}& sqrt[3]{10+6sqrt{3}}+sqrt[3]{10-6sqrt{3}}= \ = &sqrt[3]{left( 1+sqrt{3} right)}+sqrt[3]{left( 1-sqrt{3} right)}= \ = & 1+sqrt{3}+1-sqrt{3}=2 \ end{align}]
Ответ: 2.
6. Избавление от иррациональности в знаменателе
Последний приём, который мы рассмотрим в этом уроке — избавление от иррациональностей в знаменателе с помощью неопределённых коэффициентов.
Из курса алгебры мы помним, как избавлять от простых иррациональностей. Например, домножение на квадратный корень:
[frac{1}{sqrt{2}}=frac{1cdotcolor{red}{sqrt{2}}}{sqrt{2}cdotcolor{red}{sqrt{2}}}=frac{sqrt{2}}{2}]
Или домножение на сопряжённое:
[frac{1}{sqrt{3}-1}=frac{1cdot left( color{red}{sqrt{3}+1} right)}{left( sqrt{3}-1 right)cdot left( color{red}{sqrt{3}+1} right)}=frac{sqrt{3}+1}{2}]
Но всё это касается лишь самых простых корней — квадратных. Уже в случае с кубическими корнями такой фокус не пройдёт. Тут-то на помощь к нам и приходят коэффициенты-переменные.
Задача 6.1. Корень третьей степени
Задача. Избавьтесь от иррациональности в знаменателе:
[frac{10}{1+sqrt[3]{9}}]
Поскольку это иррациональное число, то никакие преобразования не избавят нас от корней полностью.
Заметим, что $sqrt[3]{9}=sqrt[3]{3}cdot sqrt[3]{3}$. Попробуем возвести число $sqrt[3]{3}$ в разные степени:
[begin{array}{c|c|c|c|c|c|c}n & 1 & 2 & 3 & 4 & 5 & 6\ hline{{left( sqrt[3]{3} right)}^{n}} & sqrt[3]{3} & sqrt[3]{9} & 3 & 3sqrt[3]{3} & 3sqrt[3]{9} & 9\ end{array}]
Итак, все степени числа $sqrt[3]{3}$ можно разделить на три типа:
- Целые числа $color{blue}{a}in mathbb{Z}$;
- Иррациональные выражения вида $color{blue}{b}sqrt[3]{3}$ где $color{blue}{b}in mathbb{Z}$;
- Выражения вида $color{blue}{c}sqrt[3]{9}$, где $color{blue}{c}in mathbb{Z}$.
Логично предположить (и это можно доказать), что результат деления на $1+sqrt[3]{9}$ можно представить в виде комбинации слагаемых этих трёх типов:
[frac{10}{1+sqrt[3]{9}}=color{blue}{a}+ color{blue}{b}sqrt[3]{3}+ color{blue}{c}sqrt[3]{9}]
Однако нам неизвестны коэффициенты $color{blue}{a}$, $color{blue}{b}$ и $color{blue}{c}$. Найти их — в этом и состоит суть задачи.:)
И тут к делу подключается метод неопределённых коэффициентов. Преобразуем уравнение так, чтобы найти эти коэффициенты. Для начала умножим обе части на $1+sqrt[3]{9}$:
[10=left( 1+sqrt[3]{9} right)left( color{blue}{a}+ color{blue}{b}sqrt[3]{3}+ color{blue}{c}sqrt[3]{9} right)]
Раскрываем скобки:
[color{blue}{a}+ color{blue}{b}sqrt[3]{3}+ color{blue}{c}sqrt[3]{9}+ color{blue}{a}sqrt[3]{9}+ 3color{blue}{b}+ 3color{blue}{c}sqrt[3]{3}=10]
Группируем слагаемые относительно одинаковых корней:
[begin{align}& left( color{blue}{a}+ 3color{blue}{b} right)+left( color{blue}{b}+ 3color{blue}{c} right)sqrt[3]{3}+left( color{blue}{a} + color{blue}{c} right)sqrt[3]{9}= \ = &color{red}{10}+ color{red}{0}cdot sqrt[3]{3}+ color{red}{0}cdot sqrt[3]{9} \ end{align}]
Выше мы предположили, что все коэффициенты $color{blue}{a}$, $color{blue}{b}$, $color{blue}{c}$ — целые (в крайнем случае рациональные). Следовательно, множители при корнях $sqrt[3]{3}$ и $sqrt[3]{9}$ должны быть равны нулю (иначе число слева будет иррациональным):
[begin{align}color{blue}{b}+ 3color{blue}{c} &= color{red}{0} \ color{blue}{a}+ color{blue}{c} &= color{red}{0} end{align}]
С учётом этих двух условий само уравнение примет вид
[color{blue}{a}+ 3color{blue}{b}= color{red}{10}]
Получили систему из трёх уравнений с тремя неизвестными:
[left{ begin{align}color{blue}{a}+ 3color{blue}{b} &= color{red}{10} \ color{blue}{b}+ 3color{blue}{c} &= color{red}{0} \ color{blue}{a}+ color{blue}{c} &= color{red}{0} end{align} right.]
Все уравнения линейные, система решается элементарно. Решением будут числа $color{blue}{a}= color{red}{1}$, $color{blue}{b}= color{red}{3}$, $color{blue}{c}= color{red}{-1}$, поэтому исходное выражение можно переписать так:
[frac{10}{1+sqrt[3]{9}}= color{red}{1}+ color{red}{3}cdot sqrt[3]{3}- color{red}{1}cdot sqrt[3]{9}]
Ответ: $1+3sqrt[3]{3}-sqrt[3]{9}$.
Важное замечание. Чтобы избавиться от иррациональности конкретно в этой задаче, достаточно было домножить числитель и знаменатель дроби на недостающую часть куба суммы:
[begin{align} frac{10}{1+sqrt[3]{9}} &=frac{10cdot left( color{red}{1-sqrt[3]{9}+sqrt[3]{{{9}^{2}}}} right)}{left( 1+sqrt[3]{9} right)left( color{red}{1-sqrt[3]{9}+sqrt[3]{{{9}^{2}}}} right)}= \ &=ldots =1+3sqrt[3]{3}-sqrt[3]{9} end{align}]
Однако такой подход не работает, когда в знаменателе стоит конструкция вида $color{blue}{a}+ color{blue}{b}sqrt[3]{3}+ color{blue}{c}sqrt[3]{9}$. А метод неопределённых коэффициентов работает всегда.:)
Попробуем решить ещё одну задачу такого же типа.
Задача 6.2. То же самое, но чуть сложнее
Задача. Избавьтесь от иррациональности в знаменателе:
[frac{46}{2-3sqrt[3]{2}}]
Решение. Найдём несколько степеней числа $sqrt[3]{2}$:
[begin{array}{c|c|c|c|c|c|c}n & 1 & 2 & 3 & 4 & 5 & 6\ hline{{left( sqrt[3]{2} right)}^{n}} & sqrt[3]{2} & sqrt[3]{4} & 2 & 2sqrt[3]{2} & 2sqrt[3]{4} & 4\ end{array}]
На будущее: для корня $n$-й степени достаточно рассмотреть первые $n$ степеней. В нашем случае достаточно было выписать $sqrt[3]{2}$, $sqrt[3]{4}$ и $sqrt[3]{8}=2$ — новых иррациональных чисел мы уже не получим.
Итак, решаем задачу методом неопределённых коэффициентов. Попробуем подобрать целые (или рациональные) числа $color{blue}{a}$, $color{blue}{b}$, $color{blue}{c}$ такие, что
[frac{46}{2-3sqrt[3]{2}}= color{blue}{a}+ color{blue}{b}sqrt[3]{2}+ color{blue}{c}sqrt[3]{4}]
Умножаем обе части уравнения на $2-3sqrt[3]{2}$:
[left( 2-3sqrt[3]{2} right)left( color{blue}{a}+ color{blue}{b}sqrt[3]{2}+ color{blue}{c}sqrt[3]{4} right)=46]
Раскрываем скобки, приводим подобные:
[begin{align}2color{blue}{a}+ 2color{blue}{b}sqrt[3]{2}+ 2color{blue}{c}sqrt[3]{4} -3color{blue}{a}sqrt[3]{2} -3color{blue}{b}sqrt[3]{4} -6color{blue}{c} &= color{red}{46} \ left( 2color{blue}{a}- 6color{blue}{c} right)+left( 2color{blue}{b}- 3color{blue}{a} right)sqrt[3]{2}+left( 2color{blue}{c}- 3color{blue}{b} right)sqrt[3]{4} &= color{red}{46}end{align}]
Это равенство верно при соблюдении трёх условий:
[left{ begin{align}2color{blue}{a}- 6color{blue}{c} &= color{red}{46} \ 2color{blue}{b}- 3color{blue}{a} &=color{red}{0} \ 2color{blue}{c}- 3color{blue}{b} &=color{red}{0} \ end{align} right.]
Это система из трёх линейных уравнений с тремя неизвестными. Её решение:
[color{blue}{a}= color{red}{-4}; color{blue}{b}= color{red}{-6}; color{blue}{c}= color{red}{-9}]
Следовательно, исходное выражение можно переписать так:
[frac{46}{2-3sqrt[3]{2}}= color{red}{-4-6}cdot sqrt[3]{2} color{red}{-9}cdot sqrt[3]{4}]
Ответ: $-4-6sqrt[3]{2}-9sqrt[3]{4}$.
Важное замечание. Здесь тоже можно «составить» куб суммы в знаменателе:
[begin{align}frac{46}{2-3sqrt[3]{2}} &=frac{46cdot left( color{red}{{{2}^{2}}+2cdot 3sqrt[3]{2}+9sqrt[3]{4}} right)}{{{2}^{3}}-{{left( 3sqrt[3]{2} right)}^{3}}} \ &= ldots =-4-6sqrt[3]{2}-9sqrt[3]{4} end{align}]
Почему не использовать этот приём всегда? Потому что в следующей задаче он уже не сработает. Там помогут только неопределённые коэффициенты и решение системы уравнений.
Задача 6.3. Когда кубы уже не помогают
Это задание чуть сложнее, потому что здесь не помогут формулы сокращённого умножения. Да и сами вычисления будут чуть сложнее, чем в предыдущих задачах.
Задача. Избавьтесь от иррациональности в знаменателе:
[frac{2}{1+sqrt[3]{3}-sqrt[3]{9}}]
Мы уже встречались с числами $sqrt[3]{3}$ и $sqrt[3]{9}$, поэтому знаем, что исходное выражение можно представить в виде
[frac{2}{1+sqrt[3]{3}-sqrt[3]{9}}= color{blue}{a}+ color{blue}{b}sqrt[3]{3}+ color{blue}{c}sqrt[3]{9}]
Преобразуем выражение, избавившись от дроби:
[left( color{blue}{a}+ color{blue}{b}sqrt[3]{3}+ color{blue}{c}sqrt[3]{9} right)cdot left( 1+sqrt[3]{3}-sqrt[3]{9} right)= color{red}{2}]
Раскроем скобки, приведём подобные:
[begin{align}left( color{blue}{a}- 3color{blue}{b}+ 3color{blue}{c} right) &+left( color{blue}{a}+ color{blue}{b} -3color{blue}{c} right)sqrt[3]{3}+ \ &+left( -color{blue}{a}+ color{blue}{b}+ color{blue}{c} right)sqrt[3]{9}= color{red}{2} \ end{align}]
Это равенство возможно при соблюдении трёх условий:
[left{ begin{align}color{blue}{a}- 3color{blue}{b}+ 3color{blue}{c} &= color{red}{2} \ color{blue}{a}+ color{blue}{b}- 3color{blue}{c} &= color{red}{0} \ -color{blue}{a}+ color{blue}{b}+ color{blue}{c} &= color{red}{0} end{align} right.]
Три линейных уравнения, три переменных. Всё решается легко:
[color{blue}{a}= color{red}{2}; color{blue}{b}= color{red}{1}; color{blue}{c}= color{red}{1}]
Следовательно, исходное выражение перепишется так:
[frac{2}{1+ sqrt[3]{3}- sqrt[3]{9}}= color{red}{2}+ color{red}{1}cdot sqrt[3]{3}+ color{red}{1}cdot sqrt[3]{9}]
Ответ: $2+sqrt[3]{3}+sqrt[3]{9}$.
Как видите, никакие кубы суммы здесь уже не помогут.:)
7. Зачем всё это нужно
В этом уроке мы рассмотрели пять типов задач, которые можно решить методом неопределённых коэффициентов. У внимательного читателя наверняка возник вопрос: зачем вообще нужен этот метод, когда многие из этих задач можно решить проще и быстрее с помощью отдельных специальных приёмов?
В самом деле:
- Большинство многочленов отлично раскладываются на множители с помощью теоремы Безу и схемы Горнера — об этом мы говорили в отдельном уроке. Но только при условии, что среди корней есть рациональные.
- То же самое можно сказать и про решение уравнений.
- Делить многочлены друг на друга с остатком вообще лучше столбиком. Это самый быстрый и самый надёжный способ — при условии, что среди коэффициентов нет параметров.
- Точные квадраты зачастую можно подобрать, если немного подумать. Как и дополнительные множители для избавления от иррациональности. Если только это не «тяжёлый» случай, где формулы сокращённого умножения не работают.
Так зачем же нужен метод неопределённых коэффициентов? Всё дело в тех самых оговорках: «при условии», «только если не тяжёлый случай» и т.д.
Основная сила этого метода — в его универсальности. Да, считать придётся чуть больше, чем при использовании более специализированных приёмов. И да: целочисленный перебор не всегда приводит нас к успеху.
Но перед нами прежде всего универсальный алгоритм. Который точно работает — всегда, везде, без всяких оговорок. И если задача не решается методом неопределённых коэффициентов, то «специализированные» приёмы тем более не помогут.
Более того: область применения этого метода намного шире. Например, мы не рассмотрели разложение рациональных дробей в простейшие, а это очень важный приём, например, в интегрировании — и ему тоже нет альтернативы.
Поэтому берите на вооружение всё, что вы сегодня узнали, практикуйтесь — и да прибудут с вами решённые задачи, олимпиады и университетские зачёты и экзамены.:)
Смотрите также:
- Бином Ньютона
- Схема Горнера
- Сравнение дробей
- Четырехугольная пирамида в задаче C2
- Задача B5: площадь кольца
- Сечения и двугранные углы
Содержание:
Многочлен – это сумма одночленов, причем сам одночлен — это частный случай многочлена.
История многочелена:
Живший в 1050-1122 гг Омар Хаям известен в мире как мастер рубай. Однако имя Омара Хаяма также упоминается наряду с именами гениальных математиков. Именно Омар Хаям впервые представил общую формулу корней уравнения кубического многочлена
Многочлены от одной переменной и действия над ними
Определение многочленов от одной переменной и их тождественное равенство
Рассмотрим одночлен и многочлен, которые зависят только от одной переменной, например, от переменной
По определению одночлена числа и буквы (в нашем случае одна буква — 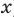
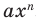
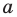
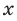
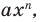
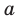
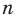
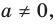
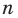
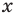
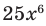
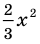
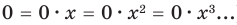
По определению многочлен от одной переменной 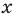
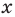
многочленом от одной переменной 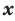
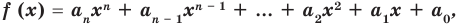
где коэффициенты 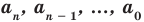
Если 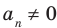
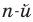
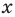
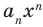
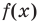
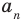
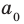
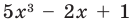
Заметим, что иногда нумерацию коэффициентов многочлена начинают с начала записи выражения (1), и тогда общий вид многочлена 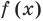
где 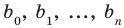
Теорема 1. Одночлены 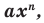
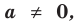
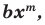
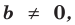
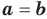
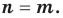
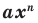
Поскольку равенство одночленов
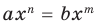
выполняется при всех значениях 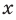
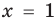
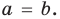
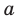
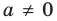
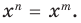
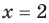
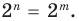
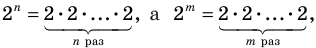
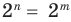
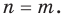
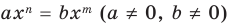
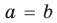
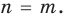
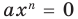
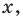
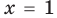
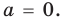
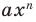
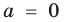
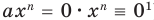
Далее любой одночлен вида 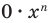
Теорема 2. Если многочлен 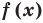
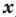
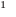
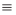
Для доказательства используем метод математической индукции. Пусть
При 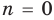
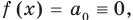
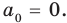
Предположим, что при 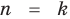
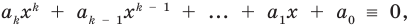
Докажем, что данное утверждение выполняется и при 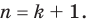
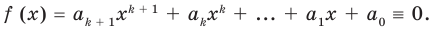
Поскольку равенство (3) выполняется при всех значениях 
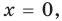
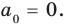
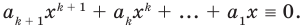

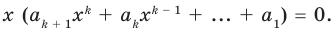
Равенство (4) должно выполняться при всех значениях 
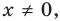
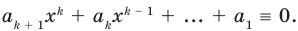
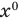
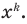
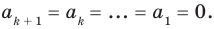
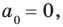
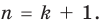
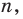
Многочлен, у которого все коэффициенты равны нулю, обычно называют нулевым многочленом, или нуль-многочленом, и обозначают 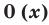
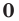
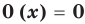
Теорема 3. Если два многочлена 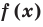
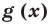
Пусть многочлен 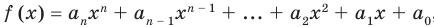
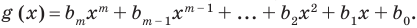
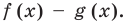
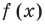
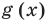
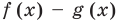
Но 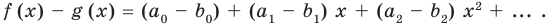
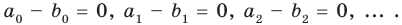
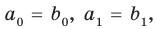
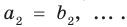
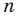
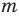
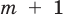
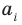
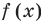
имеют одинаковую степень и соответственно равные коэффициенты при одинаковых степенях.
Теорема 3 является основанием так называемого метода неопределенных коэффициентов. Покажем его применение на следующем примере.
Пример:
Докажите, что выражение
является полным квадратом.
Решение:
► Данное выражение может быть записано в виде многочлена четвертой степени, поэтому оно может быть полным квадратом только многочлена второй степени вида 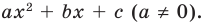
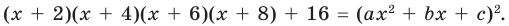
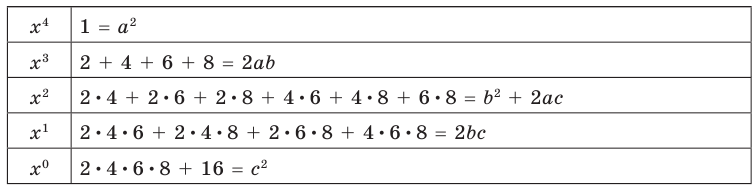
Раскрывая скобки в левой и правой частях этого тождества и приравнивая коэффициенты при одинаковых степенях 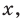
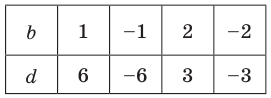
Из первого равенства получаем 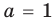
При 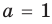
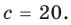
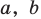
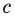
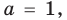
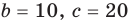
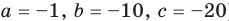
Действия над многочленами. Деление многочлена на многочлен с остатком
Сложение и умножение многочленов от одной переменной выполняется с помощью известных правил сложения и умножения многочленов. В результате выполнения действий сложения или умножения над многочленами от одной переменной всегда получаем многочлен от той же переменной.
Из определения произведения двух многочленов вытекает, что старший член произведения двух многочленов равен произведению старших членов множителей, а свободный член произведения равен произведению свободных членов множителей. Отсюда получаем, что степень произведения двух многочленов равна сумме степеней множителей.
При сложении многочленов одной степени получаем многочлен этой же степени, хотя иногда можно получить многочлен меньшей степени. Например, 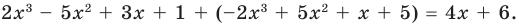
Например, 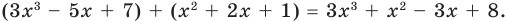
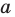
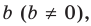
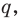
Определение: Многочлен 
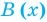
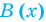

Как и для целых чисел, операция деления многочлена на многочлен выполняется не всегда, поэтому во множестве многочленов вводится операция деления с остатком. Говорят, что
многочлен 








Например, поскольку 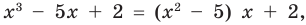
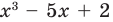
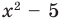
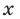
Иногда деление многочлена на многочлен удобно выполнять «уголком», как и деление многозначных чисел, пользуясь следующим алгоритмом.
Пример №1
Разделим многочлен 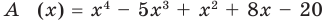
Решение:
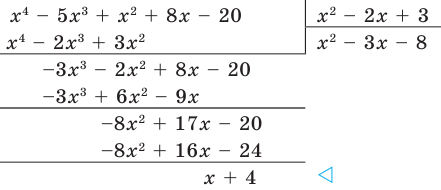
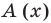
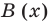
Если обозначить результат выполнения первого шага алгоритма через 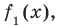
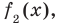
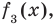
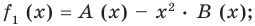
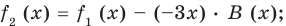
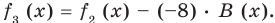
Сложим почленно равенства (1), (2), (3) и получим
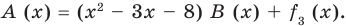
Учитывая, что степень многочлена 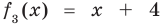
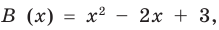
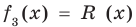
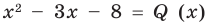
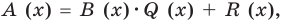
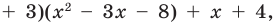
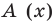
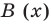
Очевидно, что приведенное обоснование можно провести для любой пары многочленов 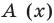
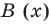
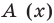
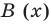
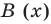
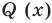
Отметим, что в случае, когда степень делимого 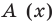
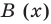
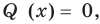
Теорема Безу. Корни многочлена. Формулы Виета
Рассмотрим деление многочлена 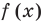
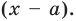
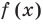
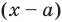
Это равенство выполняется тождественно, то есть при любом значении 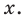
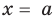
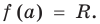
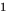
Теорема 1 (теорема Безу). Остаток от деления многочлена 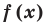
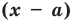
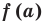
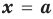
Пример №2
Докажите, что 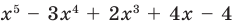
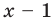
Решение:
► Подставив в 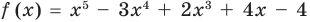
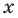
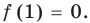
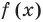

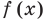

Определение: Число 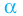
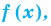
Если многочлен 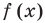

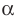
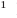
Действительно, если 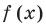
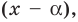

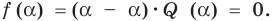
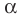
Справедливо и обратное утверждение. Оно является следствием теоремы Безу.
Теорема 2. Если число 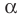
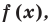
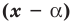
По теореме Безу остаток от деления 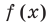

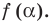
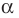
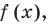
Обобщением теоремы 2 является следующее утверждение.
Теорема 3. Если многочлен 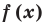
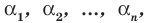
Для доказательства используем метод математической индукции.
При 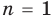
Допустим, что утверждение справедливо при 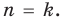
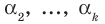
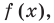
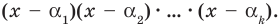
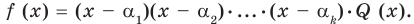
Докажем, что утверждение теоремы справедливо и при 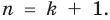
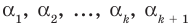
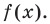
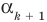
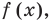
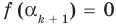
По условию все корни 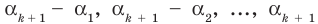
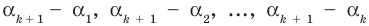
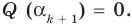
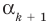
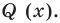
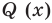
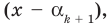
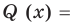
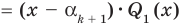
Это означает, что 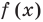
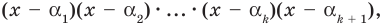
Таким образом, теорема справедлива для любого натурального
Следствие. Многочлен степени 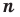
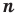
Допустим, что многочлен 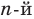
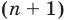
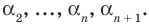
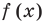
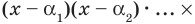
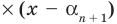
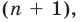
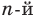
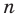
Пусть теперь многочлен 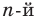
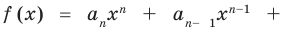
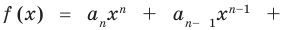
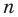
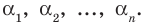
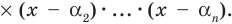
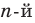
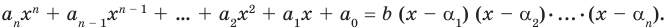
Если раскрыть скобки в правой части равенства (2) и приравнять коэффициенты при старших степенях, то получим, что 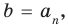
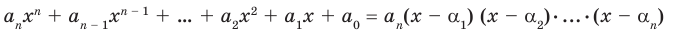
Сравнивая коэффициенты при одинаковых степенях 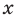
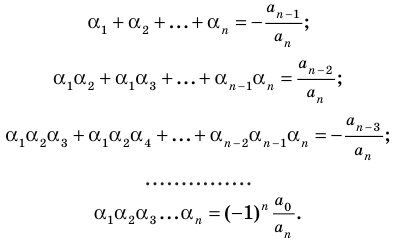
Например, при 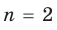
а при
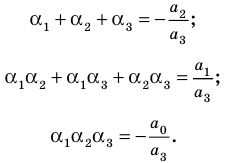
Выполнение таких равенств является необходимым и достаточным
условием того, чтобы числа 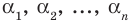
Формулы (3) и (4) справедливы не только для случая, когда все корни многочлена 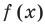
Если многочлен 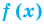
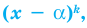
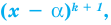


Например, если произведение 
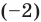
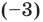
При использовании формул Виета в случае кратных корней необходимо каждый корень записать такое количество раз, которое равно его кратности.
Пример №3
Проверьте справедливость формул Виета для многочлена
Решение:
►
Поэтому 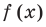
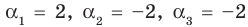
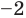
Проверим справедливость формулы (5). В нашем случае: 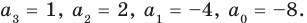
Как видим, все равенства выполняются, поэтому формулы Виета справедливы для данного многочлена.
Пример №4
Составьте квадратное уравнение, корнями которого являются квадраты корней уравнения
Решение:
► Обозначим корни уравнения 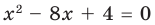
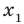
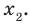
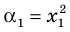
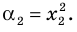
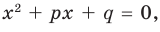
По формулам Виета имеем 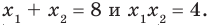
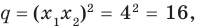
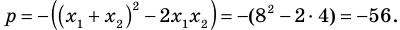
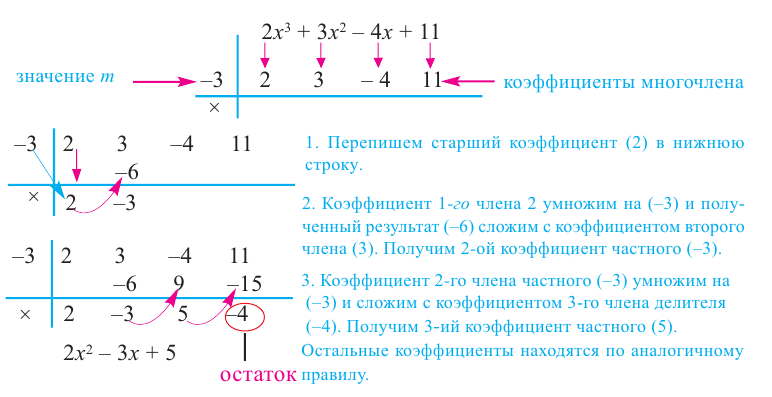
Схема Горнера
Делить многочлен 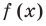
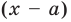
специальной схемы, которую называют схемой Горнера.
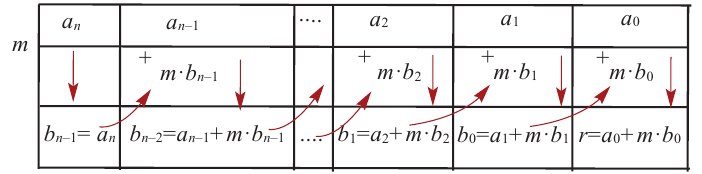
Пусть многочлен 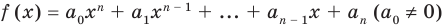
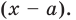
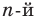
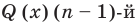
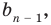
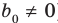
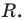
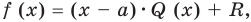
Левая и правая части полученного равенства тождественно равны, поэтому, перемножив многочлены, стоящие в правой части, можем приравнять коэффициенты при соответствующих степенях
Найдем из этих равенств коэффициенты 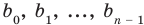
Как видим, первый коэффициент неполного частного равен первому коэффициенту делимого. Остальные коэффициенты неполного частного и остаток находятся одинаково: для того чтобы найти коэффициент 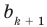
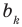
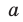
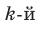
Пример №5
Разделите по схеме Горнера многочлен 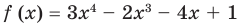
Решение:
► Запишем сначала все коэффициенты многочлена 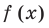
Таким образом,
Пример №6
Проверьте, является ли 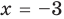
Решение:
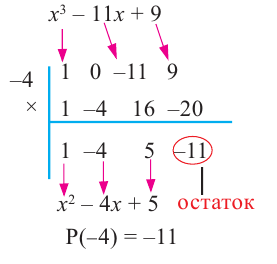
► По теореме Безу остаток от деления многочлена 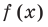
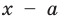
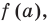
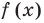
Поскольку 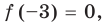
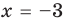
Нахождение рациональных корней многочлена с целыми коэффициентами
Теорема 4. Если многочлен с целыми коэффициентами 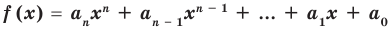
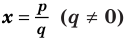
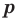
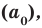
Если 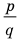
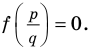
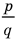
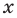
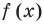
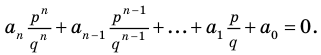
Умножим обе части равенства (1) на 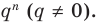
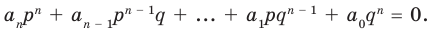
В равенстве (2) все слагаемые, кроме последнего, делятся на 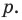
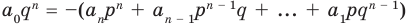
Но когда мы записываем рациональное число в виде 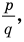
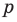
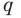
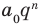
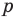
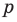
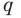
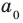
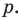
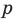
Аналогично все слагаемые равенства (2), кроме первого, делятся на 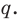
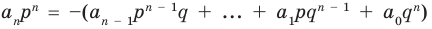
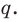
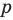
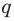
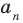
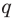
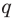
Отметим два следствия из этой теоремы. Если взять 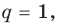
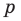
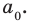
Следствие 1. Любой целый корень многочлена с целыми коэффициентами является делителем его свободного члена.
Если в заданном многочлене 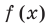
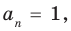
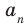
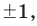
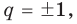
Следствие 2. Если коэффициент при старшем члене уравнения с целыми коэффициентами равен 1, то все рациональные корни этого уравнения (если они существуют) — целые числа.
Пример №7
Найдите рациональные корни многочлена
Решение:
► Пусть несократимая дробь 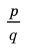
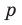
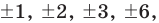
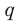
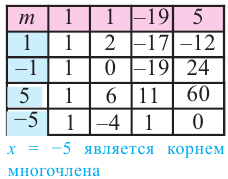
Таким образом, рациональные корни многочлена необходимо искать среди чисел 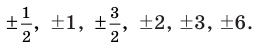
При 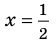
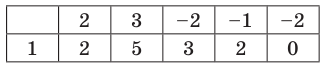
Кроме того, по схеме Горнера можно записать, что
Многочлен 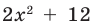
Пример №8
Разложите многочлен 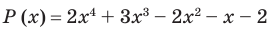
Решение:
► Ищем целые корни многочлена среди делителей свободного члена:
Подходит 1. Делим 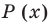

Тогда
Ищем целые корни кубического многочлена 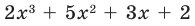
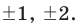
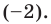
Имеем
Квадратный трехчлен 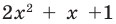
Ответ:
Отметим, что во множестве действительных чисел не всегда можно найти все корни многочлена (например, квадратный трехчлен 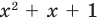
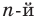
Например, многочлен четвертой степени раскладывается на произведение двух квадратных трехчленов. Для нахождения коэффициентов этого разложения иногда можно применить метод неопределенных коэффициентов.
Пример №9
Разложите на множители многочлен
Решение:
► Попытка найти рациональные корни ничего не дает: многочлен не имеет рациональных (целых) корней.
Попытаемся разложить этот многочлен на произведение двух квадратных трехчленов. Поскольку старший коэффициент многочлена равен 1, то и у квадратных трехчленов возьмем старшие коэффициенты равными 1. То есть будем искать разложение нашего многочлена в виде:
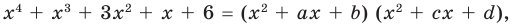
где 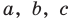
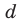
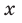
Получаем систему
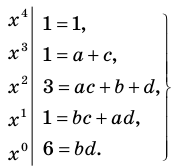
Попытка решить эту систему методом подстановки приводит к уравнению 4-й степени, поэтому попробуем решить систему (4) в целых числах. Из последнего равенства системы (4) получаем, что 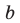
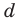
Коэффициенты 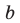
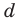
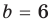
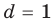
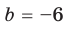
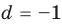
Для каждой пары значений 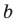
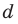
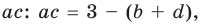
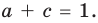
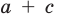
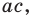
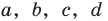
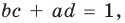
Как видим, системе (4) удовлетворяет набор целых чисел 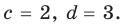
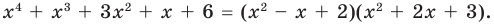
Поскольку квадратные трехчлены 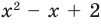
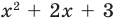
Деление многочлена на многочлен
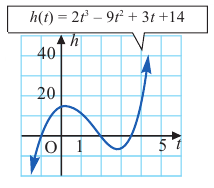
Задача. Объём подарочных коробок, размеры которых даны в сантиметрах, можно смоделировать функцией 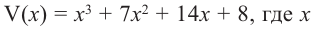
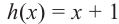
Исследование. Изучите, как правило деления многозначных чисел столбиком можно применить при делении многочлена.
a) Для каждого из двух случаев укажите, какие числа и какие многочлены соответствуют понятиям делимое, делитель и частное.
b) Как был найден первый член при делении многочлена? Каковы сходные и отличительные черты данного деления и деления многозначных чисел?
c) Как вы убедились,что каждое из двух делений выполнено правильно?
Выражение вида 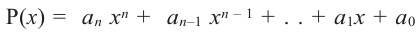
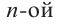
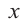
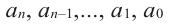
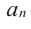
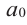
Деление целого числа па целое число можно проверить равенством
Аналогичное правило справедливо и при делении многочлена на многочлен. Если многочлен 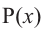
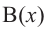
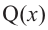
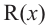
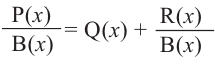
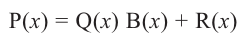
Здесь, степень многочлена 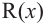
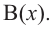
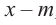
В этом случае:
Пример №10
а) Разделите многочлен 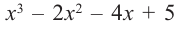
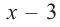
Ответ запишите в виде
b) Определите множество допустимых значений переменной.
c) Выполните проверку.
Решение:
b) При этом 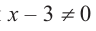
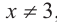
c) Должно выполняться тождество
Пример №11
Разделите 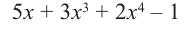
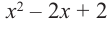
Решение:
запишем делимое в порядке убывания степеней. Введем в запись отсутствующие члены с коэффициентом равным 0.
Пример №12
1) Исследуйте деление столбиком многочлена 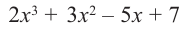
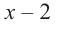
2) На каждом шаге деления делимое делится на старший член делителя, на 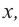
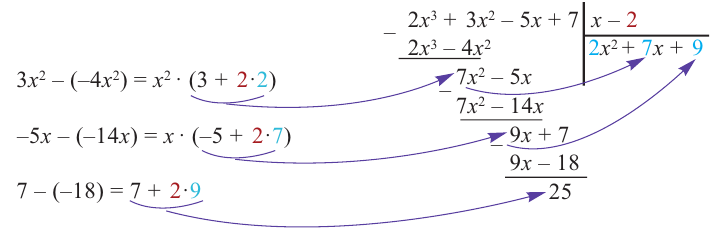
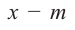
При делении многочлена на двучлен вида 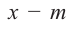
Пример №13
Разделите многочлен 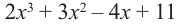
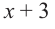
Решение:
коэффициенты делимого записываются в порядке убывания степеней (отсутствующий член записывается с коэффициентом равным нулю). Если двучлен имеет вид 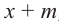
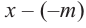
Запишем двучлен 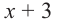
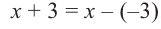
Таким образом, для делимого 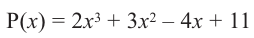
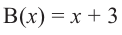
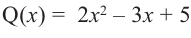
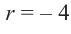
Деление можно записать в виде: 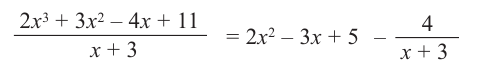
Теорема об остатке
Теорема об остатке (Теорема Безу)
Остаток от деления многочлена 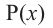
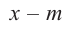
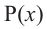
Доказательство: В равенстве 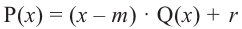
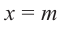
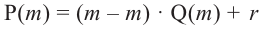
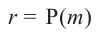
Пример №14
Найдите остаток от деления многочлена 
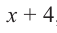
Решение: запишем делитель в виде 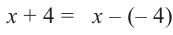
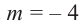
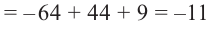
Проверим решение.
Теорема о разложении многочлена на множители
Значения переменной 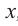
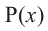
Теорема. Если число 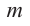
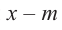
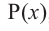
Действительно, если 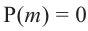
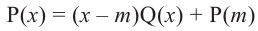
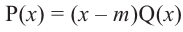
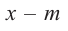
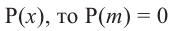
Пример №15
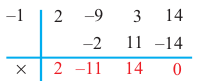
При помощи теоремы о разложении многочлена на множители определите, являются ли двучлены 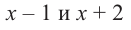
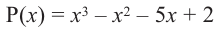
Решение: вычислим значение многочлена 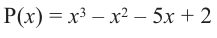
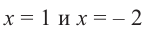
Значит, 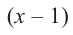
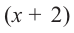
Пример №16
Зная, что 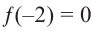
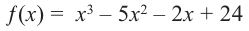
Решение: так как 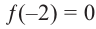
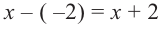
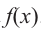
Учитывая, что 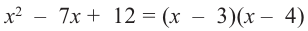
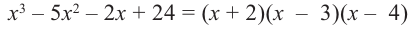
Отсюда получаем, что 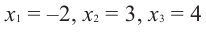
Примечание: Если многочлен задан в виде 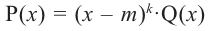
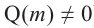
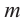
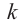
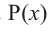
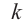
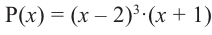
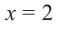
Нахождение рациональных корней
Теорема о рациональных корнях
Если для многочлена 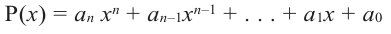
Доказательство. Пусть несократимая дробь 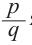
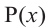
Умножим обе части равенства на
Так как в последнем равенстве каждый член, кроме члена 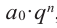
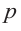
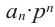
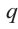
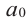
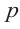
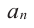
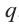
Пример №17
Найдите рациональные корни многочлена 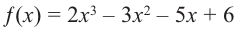
Решение: свободный член 6, старший коэффициент 2.
Для 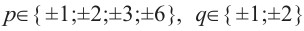
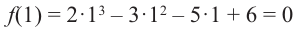
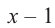
Так как, 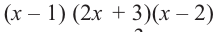
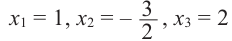
Следствие 1. Если старший коэффициент 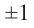
Следствие 2. Целые корни многочлена с целыми коэффициентами (если они имеются) являются делителями свободного члена.
Пример №18
Найдите корни многочлена
Решение: по теореме о рациональных корнях многочлена, целый корень данного многочлена (если он существует) надо искать среди делителей числа 5. Это числа ±5; ±1.
Запишем это короче при помощи синтетического деления и проверим, являются ли эти числа корнями многочлена.
Так как 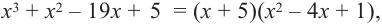
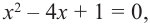
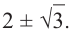
Внимание! Если коэффициенты многочлена являются рациональными числами, то для нахождения рациональных корней уравнения 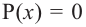
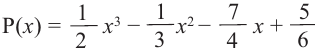
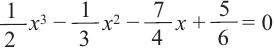
уравнение
Для нахождения рациональных корней выполните следующие действия.
1. Записывается множество всех возможных дробей, числителями которых являются делители свободного члена, а знаменателями являются делители старшего коэффициента.
2. Из этих чисел выбирается число 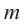
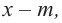
3. Для данного многочлена при помощи синтетического деления на двучлен 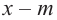
4. Если другой множитель является квадратным трехчленом или его можно разложить при помощи формул сокращенного умножения, находятся другие корни. Иначе все линейные множители находятся синтетическим делением.
5. Возможно, что ни одно число из списка не будет нулем многочлена. В этом случае многочлен не имеет рациональных корней. Например, рациональными корнями многочлена 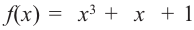
Проверим: 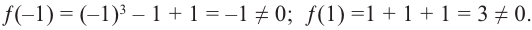
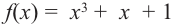
Основная теорема алгебры
Покажем на примере, что многочлен 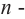
Пример №19
Найдите все корни многочлена
Решение: рациональными корнями данного многочлена (если они существуют), согласно правилу, могут являться числа ±1, ±5. Проверим:
Значит, 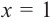
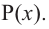
В выражении 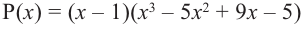
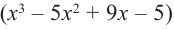
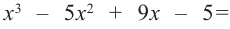
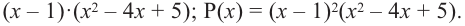
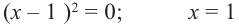
Корни:
Во всех рассмотренных нами примерах уравнение 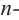
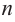
Теорема. Любой многочлен ненулевой степени имеет хотя бы один корень на множестве комплексных чисел.
Если 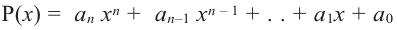
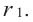
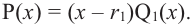
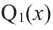
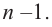
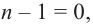
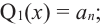
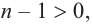
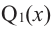
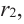
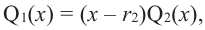
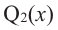
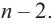
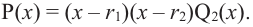
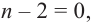
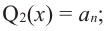
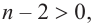
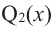
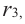
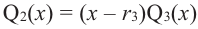
Продолжая процесс 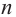
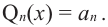
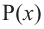
здесь числа 
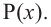
Следствие. Многочлен 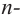
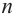
Отметим, что если комплексное число 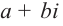
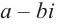
Любой многочлен с действительными коэффициентами можно представить в виде произведения двучленов вида 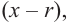
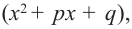
Отсюда можно сделать вывод, что многочлен нечетной степени с действительными коэффициентами всегда имеет действительные корни.
Пример №20
Запишите в виде произведения множителей многочлен наименьшей степени, если коэффициент при старшем члене равен 2, а корни равны 3 и
Решение: так как число 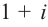
- Заказать решение задач по высшей математике
Пример №21
При движении скоростной карусели в Лунапарке изменение высоты (в метрах) кабины от нулевого уровня за первые 5 секунд можно смоделировать функцией 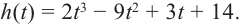
Решение: во всех случаях, кроме значений 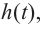
1. Проверим, является ли число 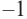
2. Число 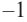
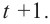
Учитывая, что 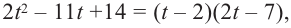
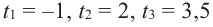
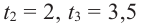
Функция-многочлен
График функции-многочлен
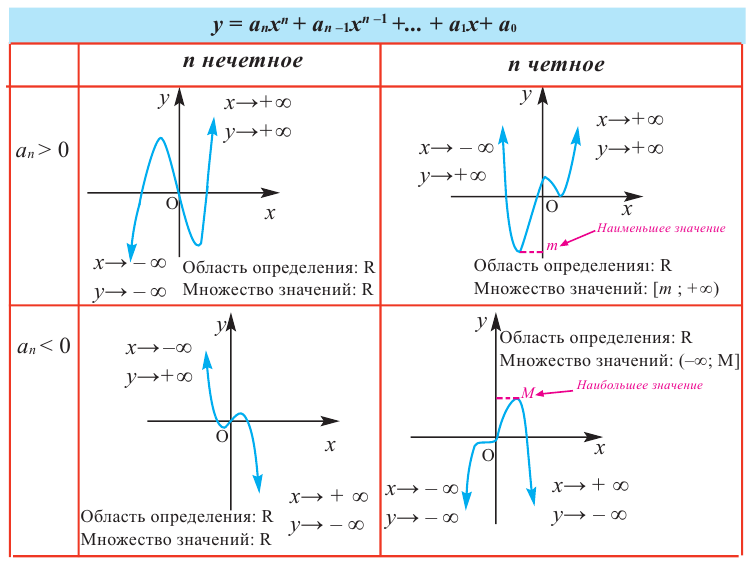
В стандартном виде функция — многочлен записывается как 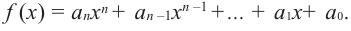
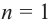
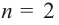
При возрастании значений аргумента по абсолютному значению многочлен ведет себя как функция старшего члена 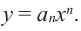
Пример №22
Определите характер поведения функции — многочлен в зависимости от степени и коэффициента при старшем члене при возрастании аргумента по абсолютному значению.
a) 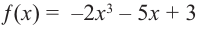
Решение: а) степень многочлена 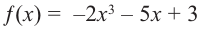
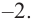
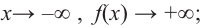
b) степень многочлена 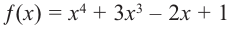
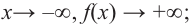
Пример №23
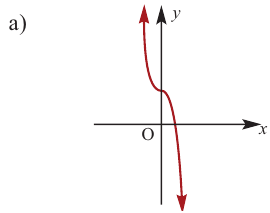
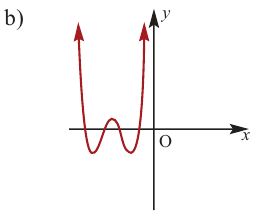
По графику определите как ведет себя функция — многочлен при неограниченном возрастании аргументов но абсолютному значению, четность или нечетность степени многочлена, знак коэффициента старшего члена.
Решение:
при
при
Многочлен нечетной степени
Решение:
при
при
Многочлен четной степени
Отметим, что если 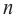
Алгоритм построения эскиза графика функции — многочлен.
1. Находятся точки пересечения графика с осями координат (если они есть). Эти точки отмечаются на координатной плоскости.
2. Вычисляются значения функции в некоторых точках между действительными нулями. Соответствующие точки отмечаются на координатной плоскости.
3. Определяется поведение графика при больших значениях аргумента по абсолютному значению.
4. На основе полученных данных строят схематически график.
Пример №24
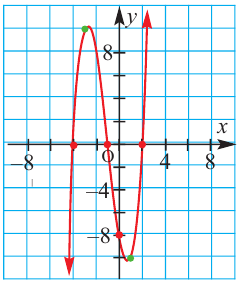
Постройте график функции
Решение:
1. Применим теорему о рациональных корнях. Разложим многочлен на множители и найдем нули функции.
По теореме возможные рациональные нули надо искать среди чисел, которые являются делителями числа
Проверим 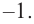
Значит, двучлен 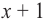
Зная, что 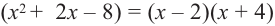
Отсюда находим нули 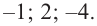
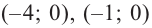
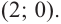
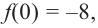
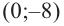
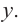
2. Найдем еще несколько значений функции в точках, не требующих сложных вычислений. Например, в точках 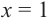
Отметим точки
3. Определим, как меняется график при уменьшении или увеличении значений 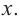
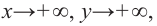
4. Соединим отмеченные точки и получим схематический график функции
Рациональная функция
Рациональной функцией называется функция, которою можно представить в виде отношения двух многочленов:
Самым простым примером рациональной функции является функция
График функции 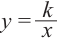
При стремлении значений 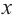
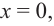
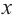
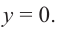
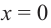
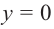
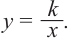
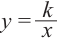
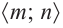
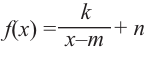
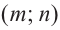
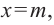
Пример №25
Постройте график функции
Решение: точки пересечения с осью 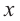
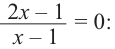
При 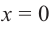
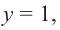
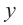
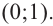
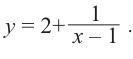
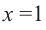
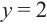
Отметим на координатной плоскости точки, соответствующие парам значений из таблицы и, учитывая горизонтальную и вертикальную асимптоту, изобразим ветви гиперболы, которые пересекают координатные оси в точках 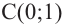
В общем случае, для построения графика рациональной функции надо найти точки пересечения с осями координат (если они есть) и ее асимптоты. Если выражение, которое задает рациональную функцию, имеет вид дроби, знаменатель которой обращается в нуль в точке 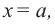
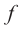
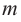
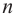
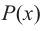
Для 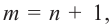
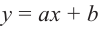
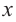
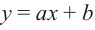
Пример №26
Найдите асимптоты и схематично изобразите график функции
Решение: Точки пересечения с осью 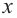
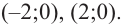
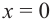
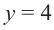
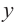
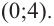
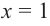
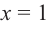
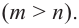
Для больших, но модулю, значений 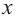
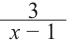
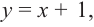
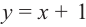
Отметим точки, координаты которых соответствуют парам из таблицы. Учитывая вертикальную и наклонную асимптоту, схематично изобразим график функции.
Многочлены в линейной алгебре
Многочленом от переменной х степени n называется выражение вида:
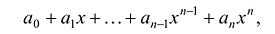
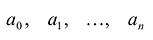
Если коэффициент 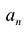
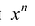
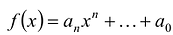
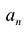
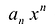
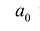
Два многочлена называются равными, если они имеют одинаковую степень и коэффициенты при одинаковых степенях равны.
Суммой многочленов 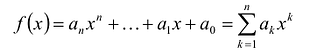
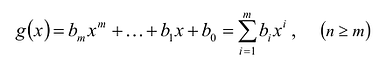
Произведением многочленов 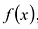
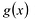
Легко проверить, что сложение и умножение многочленов ассоциативно, коммутативно и связаны между собой законом дистрибутивности.
Многочлен 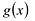
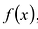
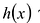
Теорема о делении с остатком
Для любых многочленов 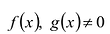
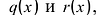
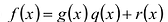
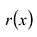
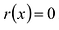
Многочлены g(x) и r(x) называются соответственно частным и остатком. Если g(x) делит 
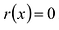
Число с называется корнем многочлена 

Теорема Безу
Число с является корнем многочлена 

Пусть с — корень многочлена 


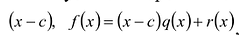
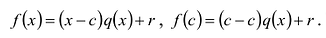

Обратно, пусть (х-с) делит 
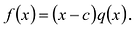
Следствие. Остаток от деления многочлена 
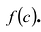
Многочлены первой степени называются линейными многочленами. Теорема Безу показывает, что разыскание корней многочлена 
Многочлен 
Пусть 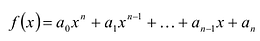
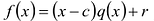
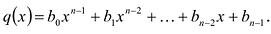
Число с-называется корнем кратности к многочлена 
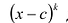

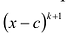

Чтобы поверить, будет ли число с корнем многочлена 

Число различных корней многочлена не превосходит его степени.
Большое значение имеет следующая основная теорема.
Основная теорема. Всякий многочлен с числовыми коэффициентами ненулевой степени имеет хотя бы один корень (может быть комплексный).
Следствие. Всякий многочлен степени 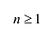
где 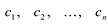

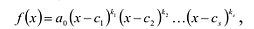
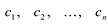

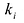
Если многочлен 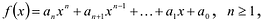
Значит, у многочлена с действительными коэффициентами комплексные корни входят парами.
Следствие. Многочлен с действительными коэффициентами нечетной степени имеет нечетное число действительных корней.
Пусть 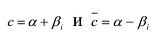


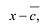
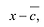

Утверждение 2. Многочлен с действительными коэффициентами степени 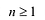
При вычислении интегралов от рациональных функций нам понадобится представление рациональной дроби в виде суммы простейших.
Рациональной дробью называется дробь где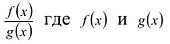
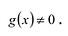

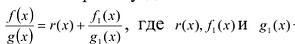
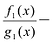
Лемма 1, Если 
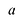
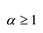
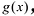
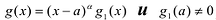
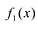
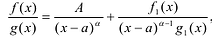
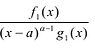
При этом несложно показать, что полученное выражение является рациональной дробью с вещественными коэффициентами.
Лемма 2. Если 
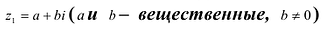
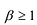
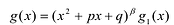
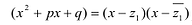
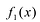
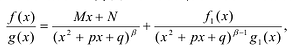
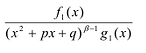
Рациональные дроби вида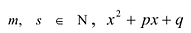
Всякая правильная рациональная дробь представима единственным образом в виде суммы простейших дробей.
При практическом получении такого разложения оказывается удобным так называемый метод неопределенных коэффициентов.
Он состоит в следующем:
При этом если степень многочлена 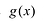
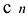
Число неизвестных 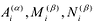
Таким образом, получается система n уравнений с n неизвестными. Существование решения у этой системы следует из приведенной выше теоремы.
- Квадратичные формы — определение и понятие
- Системы линейных уравнений с примерами
- Линейное программирование
- Дифференциальное исчисление функций одной переменной
- Кривые второго порядка
- Евклидово пространство
- Матрица — виды, операции и действия с примерами
- Линейный оператор — свойства и определение
|
0 / 0 / 0 Регистрация: 13.12.2017 Сообщений: 2 |
|
|
1 |
|
|
13.12.2017, 12:27. Показов 6798. Ответов 3
Добрый день, видел уже на форуме тему с этим примером, но там его не решили, буду благодарен за помощь. _
0 |
|
4712 / 3365 / 1074 Регистрация: 01.09.2014 Сообщений: 9,247 |
|
|
13.12.2017, 14:34 |
2 |
|
1 |
|
2644 / 2220 / 239 Регистрация: 03.07.2012 Сообщений: 8,064 Записей в блоге: 1 |
|
|
13.12.2017, 21:59 |
3 |
|
Получите 357
0 |
|
3944 / 2858 / 665 Регистрация: 08.06.2007 Сообщений: 9,668 Записей в блоге: 4 |
|
|
14.12.2017, 10:18 |
4 |
|
Восьмая степень x получается, например, если первый член одночлена взять в степени 3, второй — в степени 2, третий в степени — 2 (третий не дает вклада в степень x, но сумма степеней должна равняться семи). Перемножаем всё с учетом знака, получаем
0 |
оксана николаевна кузнецова
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Рассмотрим основные определения и теоремы о многочленах.
Определение 1
Функция
[f(x)=A_{0} x^{n} +A_{1} x^{n-1} +…+A_{n} ,]
где $nin Z$, называется многочленом, число $n$ — степень многочлена. Коэффициенты $A_{0} ,A_{1} ,…,A_{n} $при переменных являются действительными или комплексными числами.
Определение 2
Корень многочлена — это значение переменной $x$, при котором заданный многочлен обращается в ноль.
Теорема 1
При делении многочлена $f(x)$ на $x-a$ получается остаток, который равен $f(a)$.
Следствие 1
Если $a$ есть корень заданного многочлена, т.е. $f(a)=0$, то заданный многочлен представляется в виде следующего произведения
[f(x)=(x-a)cdot f_{1} (x),]
где $f_{1} (x)$ — многочлен.
Теорема 3
Любой многочлен степени $n$ может быть представлен как разложение многочлена на $n$ линейных сомножителей вида $x-a$ и множитель, который равен коэффициенту при $x^{n} $:
[f(x)=A_{0} cdot (x-a_{1} )cdot (x-a_{2} )cdot …cdot (x-a_{n} ),]
где $a_{1} ,a_{2} ,…,a_{n} $ — корни многочлена.
Пример 1
Записать разложение заданного многочлена $f(x)=x^{3} -6x^{2} +11x-6$ на множители.
«Разложение многочлена на множители» 👇
Решение:
При $x=1$ получаем $f(1)=0$. Следовательно, исходный многочлен делится на $x-1$ без остатка. После деления получаем разложение многочлена следующего вида:
[x^{3} -6x^{2} +11x-6=(x-1)cdot (x^{2} -5x+6).]
Найдем корни второго сомножителя, который является квадратным многочленом:
[x^{2} -5x+6=0][D=(-5)^{2} -4cdot 1cdot 6=25-24=1][x_{1} =frac{5-1}{2} =2,x_{2} =frac{5+1}{2} =3]
Получим разложение многочлена:
[x^{3} -6x^{2} +11x-6=(x-1)cdot (x-2)cdot (x-3).]
Теорема 4
Если заданный многочлен тождественно равен нулю, то все коэффициенты этого многочлена равны нулю.
Теорема 5
Если два заданных многочлена тождественно равны друг другу, то коэффициенты одного из этих многочленов равны соответствующим коэффициентам другого.
Пример 2
Определить коэффициенты многочлена $ax^{3} +bx^{2} +cx+d$ тождественно равного многочлену $2x^{2} +3x$.
Решение:
На основании теоремы 5 получаем, что $a=0,, , b=2,, , c=3,, , d=0$.
Если в разложении многочлена степени $n$ на линейные множители
$f(x)=A_{0} cdot (x-a_{1} )cdot (x-a_{2} )cdot …cdot (x-a_{n} )$, (*)
некоторые линейные сомножители оказываются одинаковыми, то данные множители можно объединить, и тогда разложение данного многочлена на множители будет иметь следующий вид:
$f(x)=A_{0} cdot (x-a_{1} )^{k_{1} } cdot (x-a_{2} )^{k_{2} } cdot …cdot (x-a_{n} )^{k_{m} } $ ($k_{1} +k_{2} +…+k_{m} =n$).
В формуле (*) корни многочлена $a_{1} ,a_{2} ,…,a_{n} $ могут быть не только вещественными, но и комплексными числами.
Пример 3
Записать разложение на множители многочлена, имеющего корень $x=1$ кратности 2, корень $x=-3$ кратности 3.
Решение:
Искомое разложение запишется следующим образом:
[f(x)=(x-1)^{2} cdot (x+3)^{3} .]
Определение 2
Многочленом $n$-ой степени называется функция
[P_{n} (z)=a_{n} z^{n} +a_{n-1} z^{n-1} +a_{n-2} z^{n-2} +…+a_{1} z+a_{0} ,]
где коэффициенты $a_{0} ,a_{1} ,a_{2} ,…,a_{n-1} ,a_{n} $ — постоянные комплексные числа, $a_{n} ne 0$, $zin Z$ — комплексная переменная. Число $z_{0} $, при котором многочлен принимает нулевое значение ($P_{n} (z_{0} )=0$), называется корнем многочлена.
Теорема 6
Любой многочлен, степень которого $nge 1$, имеет комплексный корень.
Пример 4
Найти корни заданного многочлена $P(z)=z^{2} +2z+2$ и разложить на множители.
Решение:
[z^{2} +2z+2=0][D=2^{2} -4cdot 1cdot 2=4-8=-4][begin{array}{l} {z_{1} =frac{-2-sqrt{-4} }{2} =frac{-2-2sqrt{-1} }{2} =frac{-2-2i}{2} =-1-i,} \ {z_{2} =frac{-2+sqrt{-4} }{2} =frac{-2+2sqrt{-1} }{2} =frac{-2+2i}{2} =-1+i} end{array}]
$z_{1} =-1-i,z_{2} =-1+i$ — комплексные корни многочлена
Искомое разложение запишется следующим образом:
[P(z)=z^{2} +2z+2=(z-(-1-i))cdot (z-(-1+i)).]
Многочлен $P_{n} (z)$ комплексной переменной $z$ с действительными коэффициентами $a_{0} ,a_{1} ,a_{2} ,…,a_{n-1} ,a_{n} $ обладает следующими свойствами:
- Если $bar{z}$ — число, комплексно-сопряженное для числа $z$, то имеет место равенство $P_{n} (bar{z})=mathop{P_{n} (z)}limits^{_ _ _ _ _ } $.
- Если некоторое число $z_{1} =a+bcdot i$ является корнем заданного многочлена $P_{n} (z)$, то число $z_{2} =bar{z}_{1} =a-bcdot i$ тоже является корнем заданного многочлена.
- Если некоторое число $z_{1} =a+bcdot i$ является корнем заданного многочлена с действительными коэффициентами $P_{n} (z)$, то $P_{n} (z)$ без остатка делится на квадратный трехчлен $z^{2} +pz+q$, где $p=-2a,; q=a^{2} +b^{2} $.
- Если некоторое число $z_{1} =a+bcdot i$ является корнем заданного многочлена $P_{n} (z)$ кратности $k$, то число $z_{2} =bar{z}_{1} =a-bcdot i$ так же является корнем данного многочлена и той же кратности. В разложение заданного многочлена на множители наряду с линейными множителями $x-(a+bi)$ входит столько же линейных множителей $x-(a-bi)$.
Пример 5
Найти комплексные корни заданного многочлена $P(z)=z^{2} +2z+5$, используя свойства многочленов.
Решение:
[z^{2} +2z+5=0][D=2^{2} -4cdot 1cdot 5=4-20=-16]
$z_{1} =frac{-2-sqrt{-16} }{2} =frac{-2-4sqrt{-1} }{2} =frac{-2-4i}{2} =-1-2i$ — комплексный корень многочлена.
Следовательно, на основании свойств число $z_{2} =-1+2i$ является корнем заданного многочлена.
Пример 6
Проверить выполнимость свойства $P_{n} (bar{z})=mathop{P_{n} (z)}limits^{_ _ _ _ _ } $ для многочлена $P(z)=z^{2} +2z+5$ и комплексного числа $z=1+i$.
Решение:
[P_{2} (z)=P(1+i)=(1+i)^{2} +2cdot (1+i)+5=1+2i+i^{2} +2+2i+5=7+4i][P_{2} (overline{z})=P(1-i)=(1-i)^{2} +2cdot (1-i)+5=1-2i+i^{2} +2-2i+5=7-4i][overline{P_{2} (z)}=7-4i]
Следовательно, равенство $P_{2} (bar{z})=mathop{P_{2} (z)}limits^{_ _ _ _ _ } $ является верным.
Примечание
Для многочленов определены следующие операции: сложение, вычитание, умножение. Операция деления многочленов определена не для любых двух многочленов, однако, как и для целых чисел, имеется возможность выполнить деление с остатком.
Пример 7
Вычислить сумму и разность двух многочленов:
$f_{1} (z)=(1+i)z^{3} +3z^{2} +(1-i)cdot z+5$ и $f_{2} (z)=(1-3i)cdot z^{3} +2z^{2} +(1+2i)cdot z+1$.
Решение:
[begin{array}{l} {f_{1} (z)+f_{2} (z)=left((1+i)cdot z^{3} +3z^{2} +(1-i)cdot z+5right)+left((1-3i)cdot z^{3} +2z^{2} +(1+2i)cdot z+1right)=} \ {=(1+i+1-3i)cdot z^{3} +(3+2)cdot z^{2} +(1-i+1+2i)cdot z+(5+1)=(2-2i)cdot z^{3} +5cdot z^{2} +(2+i)cdot z+6} end{array}][begin{array}{l} {f_{1} (z)-f_{2} (z)=left((1+i)cdot z^{3} +3z^{2} +(1-i)cdot z+5right)-left((1-3i)cdot z^{3} +2z^{2} +(1+2i)cdot z+1right)=} \ {=(1+i-1+3i)cdot z^{3} +(3-2)cdot z^{2} +(1-i-1-2i)cdot z+(5-1)=4icdot z^{3} +z^{2} +(-3i)cdot z+4} end{array}]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Применение метода неопределённых коэффициентов основано на следующих двух теоремах.
Теорема №1 (о многочлене, тождественно равном нулю).
Если при произвольных значениях аргумента x значение многочлена f(x) =
а0+ а1х
+ а2х2 +…+ а
nxn, заданного в стандартном виде, равно нулю, то все его коэффициенты
а0, а1, а2, …, аn
равны нулю.
Теорема №2 (следствие теоремы № 1).
Пусть и f(x) = а0+а1х +…+
а
nxn, и g (x)=
b
0+
b
1х + b
2х2 +…+
bnxn.
Для того чтобы f(x)= g(x)необходимо и достаточно, что бы
а0=
b0,
а1
= b1,
а2
= b
2
,
…, а
n= bn
Рассмотрим примеры, иллюстрирующие использование метода неопределенных коэффициентов.
Деление многочлена на многочлен.
Пример 1. Выполнить деление многочлена х5 – 6х3 + 2х2 -4 на многочлен
х2 – х + 1.
Решение: Надо найти такие многочлены Q(x) и R(x), что х5 – 6х3 + 2х2
-4 = (х2 – х + 1) Q(x) + R(x), причём степень многочлена R(x) меньше степени многочлена (х2 –
х + 1). Из того, что степень произведения многочленов равна сумме их степеней, следует, что степень многочлена Q(x) равна 5 – 2 = 3.
Многочлены Q(x) и R(x) имеют вид:
Q(x) = q 3x3 + q 2x2 + q 1x + q0,
R(x) = r 1x + r0.
Подставим Q(x) и R(x):
х5 – 6х3 + 2х2 -4 = (х2 – х + 1)( q
3x3 + q 2x2 + q 1x + q0) + r
1x + r0.
Раскроем скобки в правой части равенства:
х5 – 6х3 + 2х2 -4 =
= q 3x 5 + q 2x4 + q 1x3 + q
0x2 – q 3x4 — q 2x3 — q
1x2 –q 0 x + q 3x3 + q
2x2 + q 1x + q 0 + r 1x + r0 =
= q 3x 5 + (q2 – q3) x4 + (q1 — q
2 + q3) x3 + (q0 — q 1 + q2) x2 + (q1 – q0 +r1) x + q0 +r0.
Для отыскания неизвестных коэффициентов получаем систему уравнений:
q0 +r0. = — 4, решая которую, получаем q3
=1, q2 =1, q1 =-6, q0 =-5, r1
= 1, r0 = 1.
Ответ: Q(x) = x3 + x2 — 6x — 5, R(x) = x + 1.
Пример 2. Выполнить деление многочлена х7 –1 на многочлен х3 + х + 1.
Решение: Надо найти такие многочлены Q(x) и R(x), что
х7 –1 = (х3 + х + 1) Q(x) + R(x), причём степень многочлена R(x) меньше степени многочлена (х3 + х + 1).
Из того, что степень произведения многочленов равна сумме их степеней, следует, что степень многочлена Q(x) равна 7– 3 = 4.
Многочлены Q(x) и R(x) имеют вид:
Q(x) = q 4x4 + q 3x3 + q 2x2 + q
1x + q0,
R(x) = r 2x2 + r 1x + r0.
Подставим Q(x) и R(x):
х7 –1 = (х3 + х + 1) (q 4x4 + q 3x3 + q
2x2 + q 1x + q0 ) + ( r 2x2 + r
1x + r0 ).
Раскроем скобки в правой части равенства:
х7 –1= q 4x 7 + q 3x6 + q
2x5 + q 1x4 + q 0x 3 + q
4x5 + q 3x4 + q 2x3 + q
1x2 + q 0 x + q 4x4 + q
3x3 + q 2x2 +q
1x + q 0 + r
2x2 +r 1x + r0.
х7 –1= q 4x 7 + q 3x6+(q2 + q4) x5+(q1+ q3) x4+(q0 + q
2 + q3) x3+(q1 + q2 +r2) x2 +(q0 +r1) x+( q0 +r0).
Получаем систему уравнений:
их которой получаем: q4=1, q3 = 0, q2= -1, q1 = -1, q0 =1, r2 = 2, r1 =0 , r0 = -2.
Ответ: Q(x) = x4 — x2 — x + 1, R(x) = 2x2 — 2.
Расположение многочлена по степеням.
Возьмем функцию
Поставим перед собой задачу «расположить многочлен по степеням
f(x) по степеням (х-х0).
Задача сводится к нахождению неизвестных коэффициентов а0, а1,
…, аn.
В каждом конкретном случае эти числа найти легко. Действительно, расположим многочлены, находящиеся в левой и правой частях равенства, по степеням x. Так как мы имеем тождество, то (по теореме № 2) коэффициенты при одинаковых степенях x должны быть равны между собой. Приравняв коэффициенты правой части соответствующим заданным коэффициентам левой, мы придем к системе
n+1 уравнений с n+1 неизвестными а0, а1, …, аn
,
которую нужно решить.
Пример 3. Расположим многочлен
по степеням.
Решение. Полагаем:
Приравниваем коэффициенты при одинаковых степенях и получаем систему:
Решая систему, находим:
Ответ:
.
Пример 4. Расположим f(x) = х4 — 8х3 + 24х2 — 50х + 90 по степеням (х-2).
Решение: Полагаем х4 — 8х3 + 24х2
— 50х + 90
Ответ: f(x) =
Представление произведения в виде многочлена стандартного вида.
Пример 5. Не выполняя действий, представим в виде многочлена стандартного вида
произведение (х — 1)(х + 3)(х + 5).
Решение: Произведение есть многочлен третьей степени, коэффициент при старшем
члене равен 1, а свободный член равен (- 15), тогда запишем:
(х — 1)(х + 3)(х + 5) = х3 + ах2 + вх — 15, где
а и в — неизвестные коэффициенты.
Для вычисления их положим х = 1 и х = — 3, тогда получим:
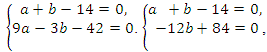
7.
Ответ: х3 +7х2 + 7х — 15.
Разложение многочлена на множители
Пример 6. Дан многочлен
Разложим его на множители, если известно, сто все его
корни – целые числа.
Решение: Будем искать разложение в виде:
полагая числа a, b, c и d его
корнями.
Раскроем скобки в правой части и сгруппируем по одинаковым степеням.
Приравниваем коэффициенты при одинаковых степенях.
Так как корни нашего многочлена – целые, то из последнего уравнения системы
заключаем, что они должны быть делителями числа 30. Следовательно, их следует
искать среди чисел
Проведя испытания, установим, что корни нашего многочлена -2,
-5, 1 и 3.
Следовательно х4+ 3х3 — 15х2 — 19х + 30 = (х —
1)(х — 3)(х + 2)(х + 5)
Ответ: (х — 1)(х — 3)(х + 2)(х + 5)
Пример 7. Дан многочлен
.
Разложим его на множители, если известно, сто все его
корни – целые числа.
Решение: Будем искать разложение в виде:
полагая числа a, b, c и d его
корнями.
Раскроем скобки в правой части и сгруппируем по одинаковым степеням.
Приравниваем коэффициенты при одинаковых степенях.
Так как корни нашего многочлена – целые, то из последнего уравнения системы
заключаем, что они должны быть делителями числа 84. Следовательно, их следует
искать среди чисел
Проведя испытания, установим, что корни нашего многочлена -7,-2,2,3.
Следовательно х4+ 4х3 — 25х2 — 16х + 84 = (х —
2)(х — 3)(х + 2)(х + 7)
Ответ: (х — 2)(х — 3)(х +2)(х + 7)
Упрощение выражений
Пример 8. Разность
является целым числом. Найдем это число.
Решение: Так как,
Тогда
Положим где a и b – неизвестные коэффициенты.
Тогда
Решая данную систему уравнений, получим а = 5,
b = -4.
Значит так как
Аналогично устанавливаем, что
Следовательно
Ответ: -10
Пример 9. Является ли разность
целым числом.
Решение: Т.к.
тогда —
Положим
где a и
b
– неизвестные коэффициенты.
Тогда откуда
из второго уравнения
тогда первое уравнение принимает вид
b2 = 12,5 — — не удовлетворяет
условию задачи, или b2 = 9, откуда
b = -3 или b = 3 — не удовлетворяет числу
Значит, а
= 5.
Аналогично,
Окончательно получаем:
—
иррациональное число.
Ответ: нет.
Уничтожение иррациональности в знаменателе
Пример 10. Избавимся от иррациональности в знаменателе:
Решение:
отсюда
Раскроем скобки, сгруппируем:
с = 4;
b — 4 = 1;
-а + 15 — 8 = 0;
b = 5;
а = 7
Ответ:
Пример 11. Избавимся от иррациональности в знаменателе:
Решение:
,
отсюда
Раскроем скобки, сгруппируем
Отсюда
Итак
Следовательно
Ответ:
Применение метода неопределенных коэффициентов при решении уравнений
Пример 12. Решим уравнение х4 + х3
— 4х2 — 9х — 3 = 0.
Решение: Предположим, что корни уравнения — целые числа, тогда их надо искать
среди чисел
Если х = 1, то
если х = -1, то
если х = 3, то
если х = -3, то
Отсюда делаем вывод, что рациональных корней наше уравнение не имеет.
Попробуем
разложить многочлен
на множители в следующем виде:
, где
a, b, c и d – целые.
Раскроем скобки:
Приравнивая соответствующие коэффициенты выражений для неизвестных a, b, c
и d
получаем систему уравнений:
Так как
bd
= -3, то будем искать решения среди вариантов:
Проверим вариант № 2, когда
b = —1; d = 3:
а = -2, с =3
Пример 13. Решить уравнение: х4 — 15х2
+ 12х + 5= 0.
Решение: Разложим многочлен f(х) =
х4 — 15х2 + 12х + 5 на множители в следующем виде:
, где a, b, c и
d -целые. Раскроем скобки:
Приравнивая соответствующие коэффициенты выражений для неизвестных a, b, c
и d получаем систему уравнений:
Так как , bd = 5, то будем искать решения среди вариантов:
Системе удовлетворяет вариант №2, т.е. а = 3,
b = -1, c = -3, d
= 5.
Итак,
D =13
D = 29
Ответ:
О решении одного класса кубических уравнений.
Пусть дано кубическое уравнение: а 1 х3 + b 1х2 +с
1х +d1 = 0, где а ≠ 0.
Приведём его к виду х3 + ах2 +bх + с = 0 (1), где а =
, в =
, с =
Положим в уравнении (1) х = у + m. Тогда получим уравнение:
Раскроем скобки, сгруппируем: y3+3у2m + 3ym2 + m3 + ay2+ 2aym +am2 + by +bm + с = 0,
y3 + y2(a +3m) +y(3m2 +2am +b) + m3 +am2 +bm + с = 0.
Для того, чтобы уравнение (1) было двучленным, должно выполняться условие:
Решения этой системы: m = —;
a2 = 3b. Таким образом, при произвольном с и при
a2
= 3b уравнение подстановкой х = у —
можно привести к двучленному уравнению
третьей степени.
Пример14. Решить уравнение: х 3 + 3х 2+3х — 9 =0.
Решение: В данном уравнении а = 3, в =3, тогда условие
a2 = 3b выполняется, а m =
— = -1. Выполним подстановку х = у -1.
Уравнение принимает вид: (у -1)3 +3(у -1)2
+3(у -1) – 9 = 0.
y3 -3y2 +3у -1 +3у2 – 6у +3 +3у –3 – 9 = 0.
y3 – 10 = 0, откуда у =
, а х =
— 1.
Ответ:
— 1.
Пример15. Решить уравнение: х 3 + 6х 2+ 12х + 5 = 0.
Решение: а = 6, в =12, тогда условие a2 = 3b (62 = 3×12) выполняется, а
m =
— = -2.
Выполним подстановку х = у — 2. Уравнение принимает вид: (у -2)3 +6(у
-2)2 +12(у -2) + 5 = 0.
у3 – 6у2 + 12у – 8 + 6у2 -24у + 24 + 12у – 24 + 5 = 0.
у3 – 3 = 0, у =
, а х =
— 2.
Ответ:
– 2.
Рассмотренные в работе примеры могут быть решены и другими способами. Но цель
работы заключалась в том, чтобы решить их методом неопределённых коэффициентов,
показать универсальность этого метода, его оригинальность и рациональность, не
отрицая того, что в некоторых случаях он приводит к громоздким, но не сложным
преобразованиям.