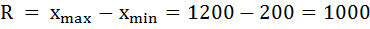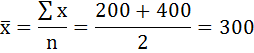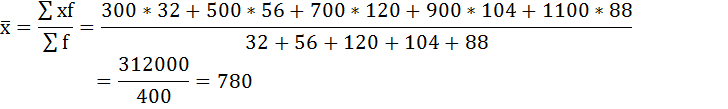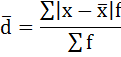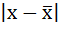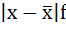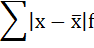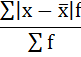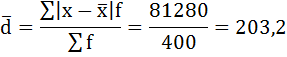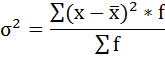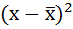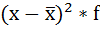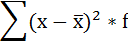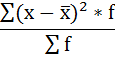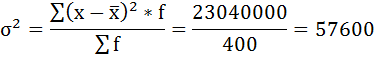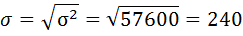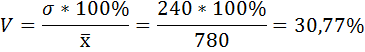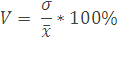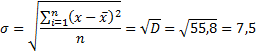По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города:
| Размер вклада, руб. | До 400 | 400 — 600 | 600 — 800 | 800 — 1000 | Свыше 1000 |
|---|---|---|---|---|---|
| Число вкладчиков | 32 | 56 | 120 | 104 | 88 |
Определите:
1) размах вариации;
2) средний размер вклада;
3) среднее линейное отклонение;
4) дисперсию;
5) среднее квадратическое отклонение;
6) коэффициент вариации вкладов.
Решение:
Данный ряд распределения содержит открытые интервалы. В таких рядах условно принимается величина интервала первой группы равна величине интервала последующей, а величина интервала последней группы равна величине интервала предыдущей.
Величина интервала второй группы равна 200, следовательно, и величина первой группы также равна 200. Величина интервала предпоследней группы равна 200, значит и последний интервал будет иметь величину, равную 200.
| Размер вклада, руб. | 200 — 400 | 400 — 600 | 600 — 800 | 800 — 1000 | 1000 — 1200 |
|---|---|---|---|---|---|
| Число вкладчиков | 32 | 56 | 120 | 104 | 88 |
1) Определим размах вариации как разность между наибольшим и наименьшим значением признака:
Размах вариации размера вклада равен 1000 рублей.
2) Средний размер вклада определим по формуле средней арифметической взвешенной.
Предварительно определим дискретную величину признака в каждом интервале. Для этого по формуле средней арифметической простой найдём середины интервалов.
Среднее значение первого интервала будет равно:
второго — 500 и т. д.
Занесём результаты вычислений в таблицу:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х | xf |
|---|---|---|---|
| 200-400 | 32 | 300 | 9600 |
| 400-600 | 56 | 500 | 28000 |
| 600-800 | 120 | 700 | 84000 |
| 800-1000 | 104 | 900 | 93600 |
| 1000-1200 | 88 | 1100 | 96800 |
| Итого | 400 | — | 312000 |
Средний размер вклада в Сбербанке города будет равен 780 рублей:
3) Среднее линейное отклонение есть средняя арифметическая из абсолютных отклонений отдельных значений признака от общей средней:
Порядок расчёта среднего линейонго отклонения в интервальном ряду распределения следующий:
1. Вычисляется средняя арифметическая взвешенная, как показано в п. 2).
2. Определяются абсолютные отклонения вариант от средней:
3. Полученные отклонения умножаются на частоты:
4. Находится сумма взвешенных отклонений без учёта знака:
5. Сумма взвешенных отклонений делится на сумму частот:
Удобно пользоваться таблицей расчётных данных:
Среднее линейное отклонение размера вклада клиентов Сбербанка составляет 203,2 рубля.
4) Дисперсия — это средняя арифметическая квадратов отклонений каждого значения признака от средней арифметической.
Расчёт дисперсии в интервальных рядах распределения производится по формуле:
Порядок расчёта дисперсии в этом случае следующий:
1. Определяют среднюю арифметическую взвешенную, как показано в п. 2).
2. Находят отклонения вариант от средней:
3. Возводят в квадрат отклонения каждой варианты от средней:
4. Умножают квадраты отклонений на веса (частоты):
5. Суммируют полученные произведения:
6. Полученная сумма делится на сумму весов (частот):
Расчёты оформим в таблицу:
5) Среднее квадратическое отклонение размера вклада определяется как корень квадратный из дисперсии:
6) Коэффициент вариации — это отношение среднего квадратического отклонения к средней арифметической:
По величине коэффициента вариации можно судить о степени вариации признаков совокупности. Чем больше его величина, тем больше разброс значений признаков вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя.
Коэффициент вариации — это статистическая метрика, которая может помочь специалистам зарегистрировать изменения в данных с течением времени. Эта метрика также может быть эффективным методом расчета финансового риска и вознаграждения за инвестиционную деятельность. Вы можете рассчитать коэффициент вариации с помощью простой формулы.
В этой статье мы обсудим, что такое коэффициент вариации и как его рассчитать, а также приведем несколько примеров применения этого статистического измерения к различным инвестиционным сценариям.
Основные выводы:
-
Коэффициент вариации — это эффективная метрика для быстрой оценки относительной дисперсии точек данных вокруг среднего значения выборки.
-
Финансовые аналитики и инвесторы могут часто оценивать коэффициент вариации для анализа риска и волатильности в зависимости от ожидаемой доходности инвестиций.
-
Более низкое соотношение между стандартным отклонением и средним значением может указывать на более высокий коэффициент доходности, в то время как более высокое соотношение может указывать на более низкий коэффициент доходности.
Что такое коэффициент вариации?
Коэффициент вариации (CV) измеряет разброс точек данных вокруг среднего значения. Отношение стандартного отклонения к среднему значению делает CV ценным ресурсом при сравнении вариаций одного ряда данных с другим. Он показывает, насколько сильно варьируются данные в выборке по сравнению со средним значением популяции.
Когда вы оцениваете CV, вы можете представить значение в процентах, где более низкий процент может указывать на более низкий CV, а более высокий процент может означать более высокий CV. В финансовом и инвестиционном анализе, где волатильность и риск могут влиять на потенциальную доходность, более низкий CV означает более низкое соотношение риска и доходности, что указывает на лучший компромисс между потенциальной доходностью и риском, присущим конкретному инвестиционному инструменту.
Какова формула для коэффициента вариации?
Формула CV использует стандартное отклонение и среднее значение данных вашей выборки для расчета коэффициента, отражающего дисперсию ваших значений вокруг среднего. В статистическом анализе основной формулой для расчета коэффициента вариации является:
CV = стандартное отклонение выборочного среднего x 100
При применении формулы в бизнесе, например, в финансовых расчетах, многие специалисты упрощают формулу CV, чтобы она соответствовала таким финансовым показателям, как доходность инвестиций, прирост капитала, риск и волатильность инвестиций. Поэтому многие аналитики могут также использовать следующую формулу для расчета CV с точки зрения финансового риска и вознаграждения:
CV = прогнозируемая доходность волатильности x 100
Использование коэффициента вариации
Вы можете использовать КВ для определения соотношения риска и доходности, а также для определения того, превышает ли вознаграждение риск инвестиций. КВ также иногда может привести к неточному или непригодному для использования значению. Например, вычисление отрицательного значения или нуля может указывать на то, что измерение коэффициента неточно отражает ваш коэффициент. Нахождение коэффициента вариации в данных относится не только к сфере бизнеса и финансов.
Например, биологи и исследователи часто используют его в своих наблюдениях для расчета повторяемости результатов данных. Педагоги также могут применять CV для сравнения методик преподавания, выясняя, что приводит к повышению среднего балла. Метеорологи используют его для измерения временной изменчивости осадков. Однако существуют некоторые споры относительно точности CV в этих ситуациях. При широком диапазоне переменных и условий возрастает вероятность неточности.
Как рассчитать коэффициент вариации
Чтобы рассчитать коэффициент вариации, выполните следующие шаги, используя вышеупомянутую формулу:
1. Определите волатильность
Чтобы найти волатильность или стандартное отклонение, вычтите среднюю цену за период из каждой ценовой точки. Чтобы преобразовать разницу в дисперсию, возведите в квадрат, просуммируйте и усредните ответ. Квадратный корень из дисперсии становится приемлемым процентом для волатильности.
2. Определение ожидаемой доходности
Чтобы найти ожидаемую доходность, умножьте потенциальные исходы или доходность на вероятность их наступления. Сумма всех собранных ответов становится ожидаемой доходностью. На данном этапе оба показателя готовы для формулы.
3. Разделить
Рассчитав показатели волатильности и ожидаемой доходности, разделите их друг на друга. Большинство ответов дается в виде десятичных дробей. Вы также можете преобразовать CV в проценты.
4. Умножить на 100
Чтобы перевести в проценты, умножьте десятичные числа на 100. При этом десятичный знак сдвигается на две цифры, создавая либо целое число, либо десятичный процент. Окончательный ответ — коэффициент вариации.
Как рассчитать коэффициент вариации в электронной таблице
Некоторые предприятия и частные лица используют электронные таблицы для записи больших объемов данных за длительные периоды времени. Они выбирают электронные таблицы не только для того, чтобы успевать за огромным количеством собранных данных, но и для того, чтобы легко рассчитать коэффициент вариации в своих данных. Электронные таблицы могут записывать расчеты вместе с данными и продолжать их по мере добавления новых данных. Вы можете рассчитать коэффициент вариации с помощью электронной таблицы, выполнив следующие три шага:
1. Используйте функцию стандартного отклонения для набора данных
Программы для работы с электронными таблицами должны иметь определенную функцию для стандартного отклонения. Для того чтобы расчет работал, набор данных должен содержать эту функцию. Во многих распространенных программах электронных таблиц для вычисления стандартного отклонения можно ввести команду =STDEVP. Введите формулу в пустую ячейку рядом с соответствующим набором данных, который вы оцениваете.
2. Рассчитайте среднее значение
Вычисление среднего значения в электронных таблицах требует специальных формул. Например, в большинстве приложений электронных таблиц вы можете использовать =AVERAGE для применения программной функции. При вводе команды среднего значения поместите его в ячейку рядом с соответствующим набором данных, чтобы легче его увидеть.
3. Разделите стандартное отклонение на среднее значение
Разделите ячейки, содержащие стандартное отклонение и среднее значение. Например, чтобы разделить стандартное отклонение в ячейке A3 и среднее значение в ячейке A5, вы можете использовать функцию =A3A5 в пустой ячейке для вычисления коэффициента и отображения коэффициента вариации.
Некоторые программы обработки электронных таблиц могут вычислять коэффициент вариации с помощью команды =STDEV.P, что устраняет необходимость в нескольких шагах. В зависимости от программы, вы можете просто ввести команду в пустую ячейку и обозначить диапазон данных, которые вы хотите рассчитать. После этого в выбранной ячейке появится значение CV.
Пример расчета
Чтобы принять обоснованное решение между акциями и облигациями, Джамиля применяет формулу коэффициента вариации для определения соотношения риска и доходности для обоих инвестиционных инструментов. Сначала она оценивает инвестиции в акции, волатильность которых составляет 5%, а прогнозируемая доходность — 13%. Используя эти значения в формуле, Джамиля находит:
-
CV = среднее стандартное отклонение выборки x 100 =
-
CV = прогнозируемая доходность волатильности x 100 =
-
CV = (0.05) (0.13) x 100 = 0.38 x 100 = 38%
Чтобы рассчитать коэффициент вариации облигации для сравнения, Джамиля делит волатильность в 3% на прогнозируемую доходность в 15%. Используя формулу, она оценивает:
-
CV = стандартное отклонение выборочного среднего x 100 =
-
CV = прогнозируемая доходность волатильности x 100 =
-
CV = (0.03) (0.15) x 100 = 0.2 = 20%
Джамиля сравнивает инвестиции в облигации и акции и приходит к выводу, что CV инвестиций в облигации в размере 20% указывает на более низкое соотношение риска и доходности, чем CV акций в размере 38%. Теперь, когда Джамиля понимает, какой инвестиционный инструмент представляет наименьшее соотношение риска и доходности, она может выбрать наиболее подходящий вариант для достижения своих финансовых целей.
В статистике под вариацией понимают количественные
изменения величины исследуемого признака в пределах однородной совокупности,
обусловленные взаимодействием различных факторов. Причины, порождающие вариацию социально-экономических
явлений, очень сложны и многообразны. Они лежат в коренных особенностях
исследуемого явления, в его сущности, а также в методологии сбора исходной
информации. Социально-экономические явления, как правило, обладают большой
вариацией. Если исследуются результаты целенаправленной человеческой
деятельности, то вариация будет выражать вмешательство многочисленных факторов,
природу которых не всегда можно установить. Однако, в большинстве теоретических
исследований и практических применений статистики необходимы наряду со средней
показатели вариации, характеризующие группировку значений признака вокруг
средней, т. е. степень упорядоченности
статистической совокупности.
В соответствии с определением вариация измеряется
степенью колеблемости вариантов признака от уровня их
средней величины. Именно на этом и основано большинство показателей,
применяемых в статистике для измерения вариации значений признака в
совокупности. К показателям вариации относятся: размах вариации, среднее
линейное отклонение, дисперсия, среднее квадратическое
отклонение, коэффициент вариации.
Простейшим показателем вариации является размах вариации, определяемый как разность между максимальным и минимальным значениями
признака:
Размах вариации выражается в тех же единицах
измерений, что в варианты ряда. По величине его можно определить, например,
передовое и отстающее в достижении какой-либо цели. Величина вариации служит
также и для характеристики средней. Размах вариации имеет и самостоятельное
значение. Например, в промышленности для измерения точности изделий
устанавливают определенные пределы, соответствующие иногда величине размаха
вариации их признаков.
Однако показатель размаха вариации не может в полной
мере охарактеризовать колеблемость ряда, поскольку он
не учитывает промежуточных значений вариантов внутри этих пределов, а по этому
не отражает колеблемость ряда в целом, кроме того, он
полностью зависит от максимального и минимального значений, которые могут
оказаться не достаточно характерными.
Таким образом, размах вариации отражает иногда
случайную, а не типичную для данного ряда величину колеблемости.
По этому необходимы другие показатели вариации, основанные на всех значениях
признака в данной совокупности, а именно: среднее линейное отклонение,
дисперсия и среднее квадратическое отклонение.
Среднее линейное отклонение представляет среднюю
арифметическую из абсолютных значений отклонений отдельных вариантов от их
среднего значения.
Для данных, где частота каждого варианта равна
единице, среднее линейное отклонение определяется по формуле:
Для вариационных рядов
определяется с учетом частот по формуле:
Среднее линейное отклонение по сравнению с размахом
вариации дает более полную характеристику колеблемости
признака в совокупности.
Средний квадрат отклонений вариантов от их средней
величины называют дисперсией
.
Дисперсия рассчитывается по формуле:
Для негруппированных
данных, где частота каждого варианта равна единице, дисперсия рассчитывается по
формуле простой средней:
Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии:
либо при равенстве весов:
Среднее квадратическое
отклонение является также обобщающим показателем колеблемости
признака и характеризует средний показатель отклонения вариантов ряда от их
общей средней. Выражается s в тех же именованных числах, в которых выражены
варианты совокупности и средняя величина.
Дисперсия и среднее квадратическое отклонение — наиболее широко применяемые
показатели вариации. Объясняется это тем, что они входят в большинство теорем
теории вероятностей, служащих фундаментом математической статистики. Кроме
того, дисперсия может быть разложена на составные элементы, позволяющие оценить
влияние различных факторов, обусловливающих вариацию признака. Порядок расчета
среднего квадратического отклонения следующий:
1) Определяется средняя
величина:
2) Рассчитывается
отклонения вариантов от средней:
3) Отклонение каждого
варианта от средней возводится в квадрат:
4) Квадрат отклонений
взвешивается по частотам:
5) Взвешенные по
частотам квадраты отклонений суммируются:
6) Полученная сумма
делится на сумму частот, и из нее извлекается квадратный корень.
Среднее квадратическое
отклонение можно вычислить, составив следующую расчетную таблицу:
| № п/п |
|
Линейные отклонения от средней
|
Квадрат линейных отклонений
|
Взвешенные квадраты
|
| … | … | … | … | … |
|
Итого |
Среднее квадратическое
отклонение можно вычислить на основании математических преобразований значений
варьирующего признака, применяя способ условных моментов:
где первый условный
момент:
второй условный момент:
Среднее квадратическое
отклонение по способу условных моментов определяется по формуле:
Система условных
моментов различных порядков, в частности, третьего
и
четвертого
используется при расчете различных
статистических характеристик (например, коэффициентов асимметрии и эксцесса).
Чем больше σ, тем разнообразнее состав
совокупности по величине изучаемого признака, и, наоборот, чем меньше σ, тем
состав совокупности по величине изучаемого признака более одинаков. Однако
оценка величины σ
как качественной характеристики ряда в конечном итоге определяется сущностью
изучаемых явлений. Среднее квадратическое отклонение
используется для сопоставления вариации по однородным совокупностям, а также
для одной совокупности за разные годы. Среднее квадратическое
отклонение является критерием надежности средней. Чем меньше оно, тем лучше
средняя арифметическая отражает всю представляемую совокупность.
Коэффициент осцилляции – процентное отношение размаха
вариации к средней
Линейный
коэффициент вариации (относительное линейное отклонение) измеряют через
соотношение среднего линейного отклонения и средней:
Коэффициент вариации представляет собой отношение
среднего квадратического отклонения к средней
арифметической:
Характеризуя степень колеблемости
признака, коэффициент вариации позволяет давать сравнительную характеристику
этой колеблемости одного и того же признака в
различных совокупностях.
Коэффициент вариации используется также, если
сравнивается степень вариации одного и того же признака в двух совокупностях,
имеющих разные по величине средние. Как относительные величины коэффициенты
вариации могут сопоставляться не только для одинаковых одноименных показателей,
но и для различных показателей, выраженных в разных единицах измерения. Таким
образом, коэффициент вариации в отличие от среднего квадратического
отклонения позволяет сопоставить глубину вариации неоднородных совокупностей.
Коэффициент вариации
Из
всех показателей вариации среднеквадратическое
отклонение в наибольшей степени
используется для проведения других
видов статистического анализа. Однако
среднеквадратическое отклонение дает
абсолютную оценку меры разбросанности
значений и чтобы понять, насколько она
велика относительно самих значений,
требуется относительный показатель.
Такой показатель называется он коэффициент
вариации.
Формула
коэффициента вариации:
Данный
показатель измеряется в процентах (если
умножить на 100%).
В
статистике принято, что, если коэффициент
вариации
меньше
10%, то степень рассеивания данных
считается незначительной,
от
10% до 20% — средней,
больше
20% и меньше или равно 33% — значительной,
значение
коэффициента вариации не превышает
33%, то совокупность считается однородной,
если
больше 33%, то – неоднородной.
Средние,
рассчитанные для однородной совокупности
– значимы, т.е. действительно характеризуют
эту совокупность, для неоднородной
совокупности – незначимы, не характеризуют
совокупность из-за значительного
разброса значений признака в совокупности.
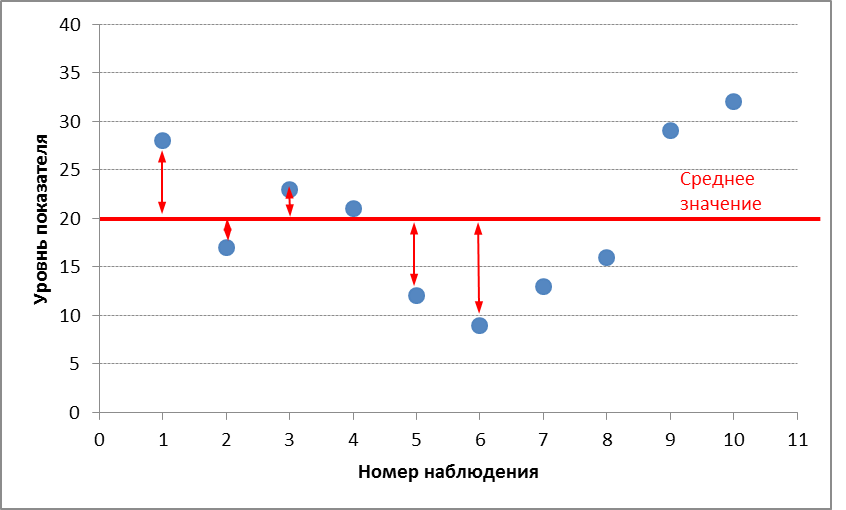
Возьмем
пример с расчетом среднего линейного
отклонения.
И
график для напоминания
По
этим данным рассчитаем: среднее значение,
размах вариации, среднее линейное
отклонение, дисперсию и стандартное
отклонение.
Среднее
значение – это обычная средняя
арифметическая.
Размах
вариации – разница между максимумом и
минимумом:
Среднее
линейное отклонение считается по
формуле:
Дисперсия
считается по формуле:
Среднеквадратическое
отклонение – квадратный корень из
дисперсии:
Расчет
сведем в табличку.
Вариация
показателя отражает изменчивость
процесса или явления. Ее степень может
измеряться с помощью нескольких
показателей.
-
Размах
вариации –
разница между максимумом и минимумом.
Отражает диапазон возможных значений. -
Среднее
линейное отклонение –
отражает среднее из абсолютных (по
модулю) отклонений всех значений
анализируемой совокупности от их
средней величины. -
Дисперсия –
средний квадрат отклонений. -
Среднеквадратическое
отклонение –
корень из дисперсии (среднего квадрата
отклонений). -
Коэффициент
вариации –
наиболее универсальных показатель,
отражающий степень разбросанности
значений независимо от их масштаба и
единиц измерения. Коэффициент вариации
измеряется в процентах и может быть
использован для сравнения вариации
различных процессов и явлений.
Таким
образом, в статистическом анализе
существует система показателей,
отражающих однородность явлений и
устойчивость процессов. Часто показатели
вариации не имеют самостоятельного
смысла и используются для дальнейшего
анализа данных. Исключением является
коэффициент вариации, который характеризует
однородность данных, что является ценной
статистической характеристикой.
7
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #