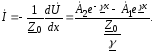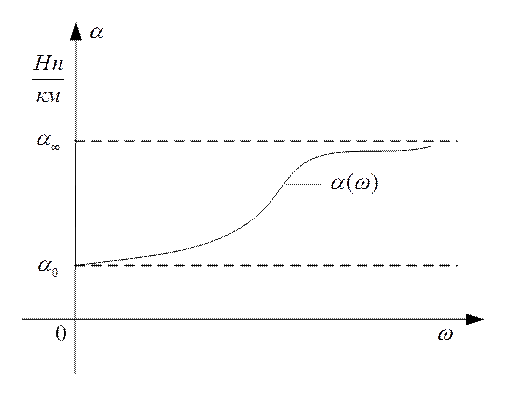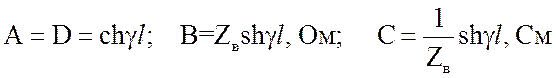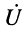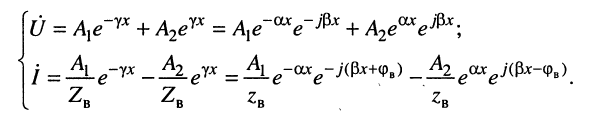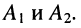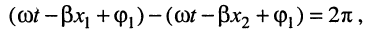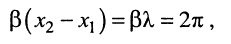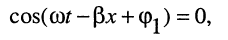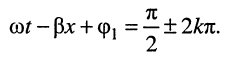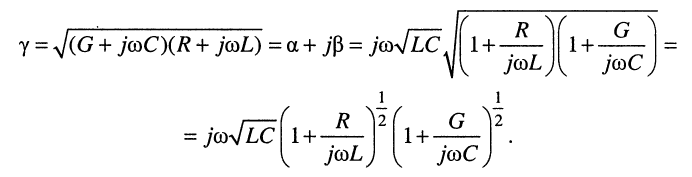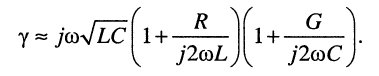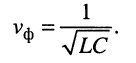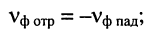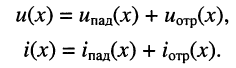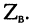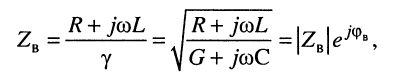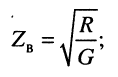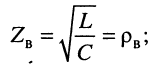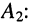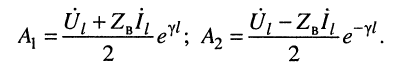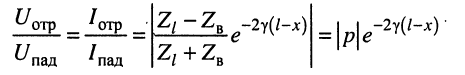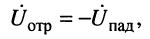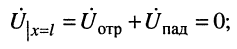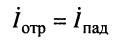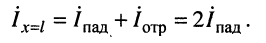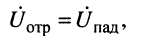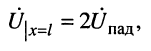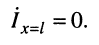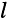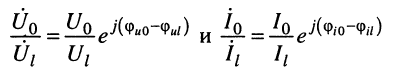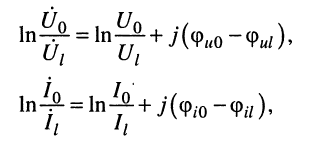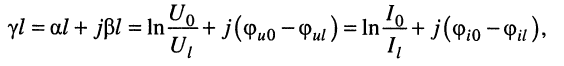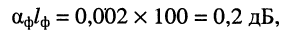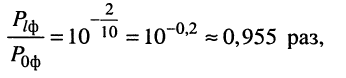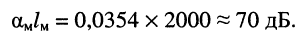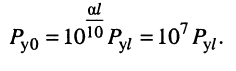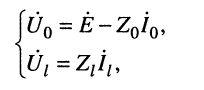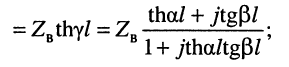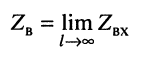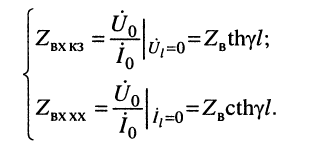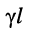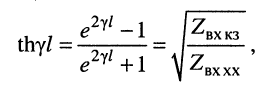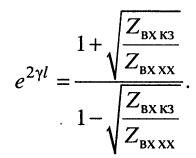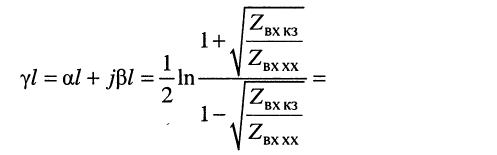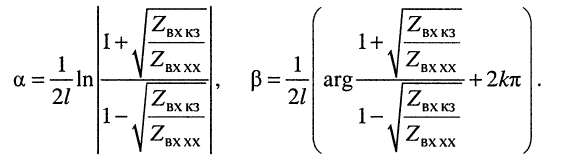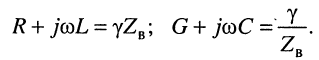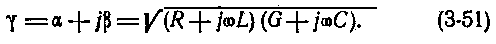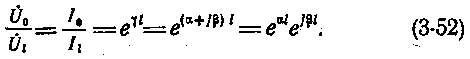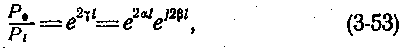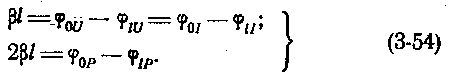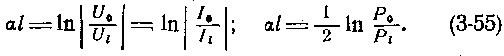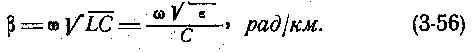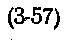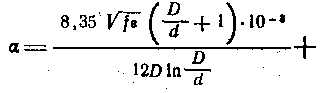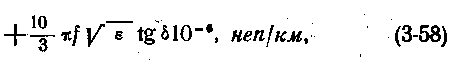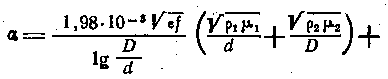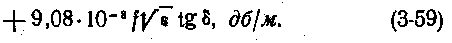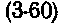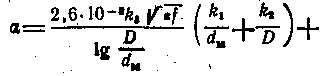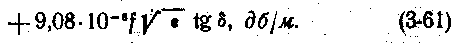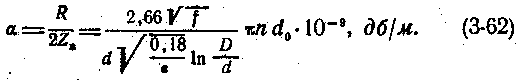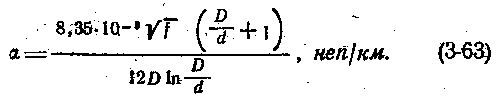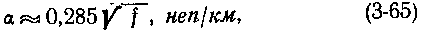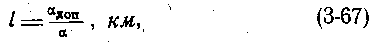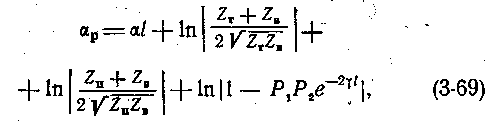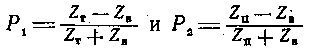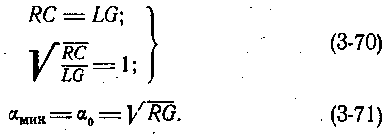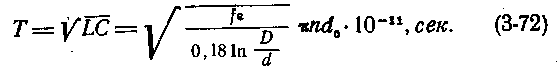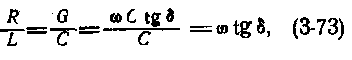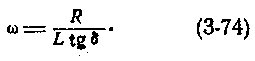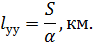Как найти коэффициент затухания фазы

Коэффициент

(20.11)

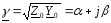
называют
постоянной
распространения;
в нем α – коэффициент
затухания,
β
– коэффициент
фазы.

Коэффициент
затухания
α
характеризует затухание падающей волны
на единицу длины линии (на 1 км), а
коэффициент фазы β
–
изменение фазы падающей волны на
единицу длины линии. Ток
определим из уравнения (7.15):

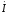
64. Почему коэффициент затухания, определяемый экспериментально, не равен нулю во всей полосе пропускания?

65. Что понимают под согласованной нагрузкой фильтра?

Что такое согласованная нагрузка

     В
учебной литературе согласование с
нагрузкой рассматривается чаще всего
применительно к волновым свойствам
длинной линии при передаче высокочастотного
сигнала. Но в [1] всё
же рассмотрены энергетические соотношения
при передаче энергии от активного
двухполюсника к пассивному.

     Активный
двухполюсник — это любой источник
электрической энергии, а пассивный — её
потребитель, который чаще всего именуют
нагрузкой. Возьмём в качестве активного
двухполюсника источник э.д.с. с известным
выходным сопротивлением (см. схему
на рис.1)
и посчитаем, при каком же сопротивлении
нагрузки мощность, передаваемая в
нагрузку, будет максимальной.

Рис.1.	Схема подключения нагрузки к источнику э.д.с.

     Согласно
закону Ома для полной электрической
цепи ток в нагрузке равен:

(1)

     где:

		— напряжение холостого хода активного двухполюсника;
		— выходное сопротивление активного двухполюсника;
		— сопротивление нагрузки.

     Напряжение
холостого хода активного двухполюсника
измеряется высокоомным вольтметром на
зажимах активного двухполюсника при
отключенной нагрузке.

     Напряжение
на нагрузке:

(2)

     Мощность
в нагрузке:

(3)

     Поскольку
обе величины иизмеряются
в омах, выразим для упрощения дальнейших
математических выкладок величинучерез
коэффициент пропорциональностиk,
показывающий, во сколько раз сопротивление
нагрузки отличается
от выходного сопротивления активного
двухполюсника:

(4)

     Тогда
после подстановки выражение для мощности
в нагрузке (3) примет
вид:

(5)

     Поскольку
левый множитель в последнем выражении
— величина постоянная, то максимум
мощности в нагрузке совпадёт с максимумом
правого множителя, то есть функции:

(6)

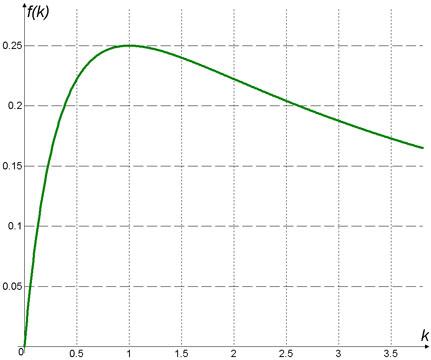
     Максимальное
значение функция f(k) примет
при таком k,
при котором будет равна нулю её производная
по k.
Производная частного двух функций
определена как:

     Следовательно:

(7)

     Очевидно,
что производная принимает нулевое
значение лишь при k=1,
то есть при выполнении равенства .
Максимум мощности в нагрузке приk=1 хорошо
виден на графике, приведенном на рис.2:

Рис.2.	Зависимость мощности в нагрузке от отношения сопротивления нагрузки к выходному сопротивлению активного двухполюсника

     Таким
образом максимальная мощность в нагрузку
передаётся при равенстве выходного
сопротивления активного двухполюсника
и сопротивления нагрузки. В этом случае
говорят, что сопротивление нагрузки
согласовано с выходным сопротивлением
источника электрической энергии или с
выходным сопротивлением источника
сигнала.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

характеризует изменение
амплитуд (действующих значений) и фаз напряжения и тока на единицу длины линии.
Его действительная часть α называется коэффициентом затухания, а мнимая
часть β – коэффициентом фазы.

Коэффициент затухания
определяет уменьшение амплитуды бегущей волны в направлении распространения,
существенно зависит от частоты передаваемого сигнала (рис. 2.4), измеряется в
неперах на единицу длины линии (Нп/км, Нп/м).

Рис. 2.4. Зависимость коэффициента
затухания от частоты

Коэффициент фазы
характеризует изменение фазы бегущей волны напряжения или тока на участке,
равном единице длины, определяет основные параметры бегущих волн: фазовую
скорость V_ф (2.12) и длину волны λ (2.13);
измеряется в радианах на единицу длины. Частотная зависимость коэффициента фазы
приведена на рис. 2.5.

Волновое сопротивление

                    (2.18)

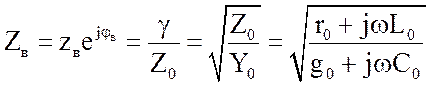
устанавливает соотношение между
комплексными значениями напряжения и

Рис. 2.5. Зависимость коэффициента
фазы от частоты

тока прямых и обратных волн в любой
точке линии:

                                     (2.19)

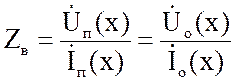
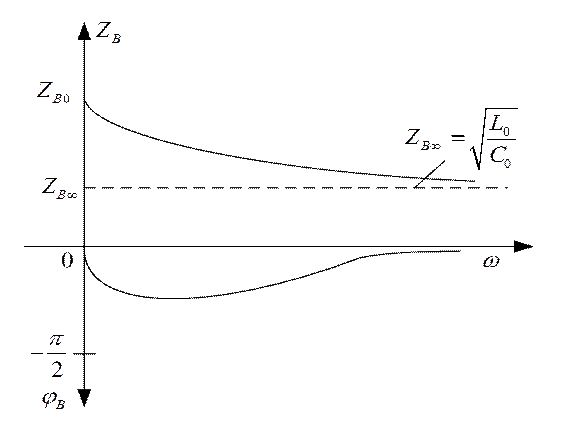
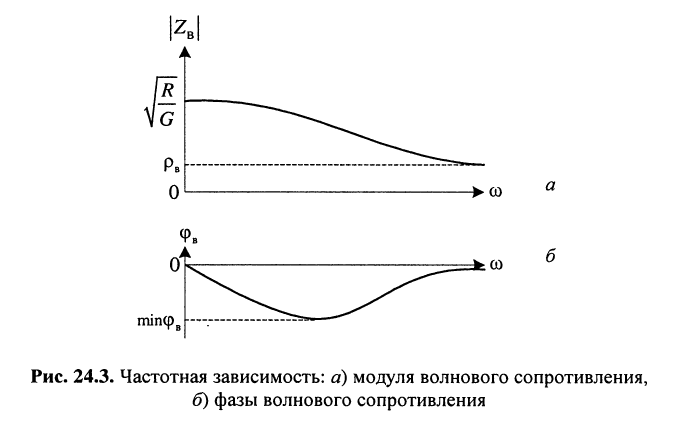
Частотная зависимость
модуля  и аргумента φ_В(ω) волнового сопротивления
приведены на рис. 2.6. На нулевой частоте (в линиях постоянного напряжения)
волновое сопротивление имеет наибольшее значение 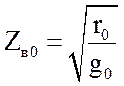. С
ростом частоты модуль волнового сопротивления стремится к своему пределу 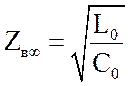, а аргумент φ_В → 0. Волновое
сопротивление в основном носит емкостный характер.

Рис. 2.6. Частотная зависимость
модуля и аргумента волнового сопротивления воздушной линии

2.6.
Расчетные уравнения линии

Коэффициенты  и  в
уравнениях (2.6) и (2.8) определяются из заданных граничных условий: напряжения
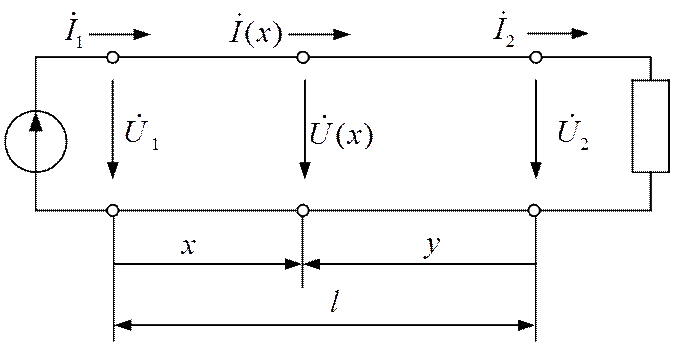
и тока на входе или выходе линии. На рис. 2.7 показана линия с входными  и выходными  значениями
напряжений и токов.

Рис. 2.7. Схема длинной линии

При выборе граничных
значений в начале линии: x = 0;
;  из
соотношений

                                             (2.20)

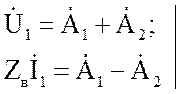
определяются коэффициенты

                                      (2.21)

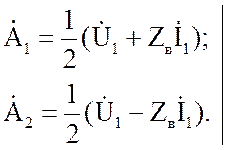
Расчетные уравнения
принимают вид:

                          (2.22)

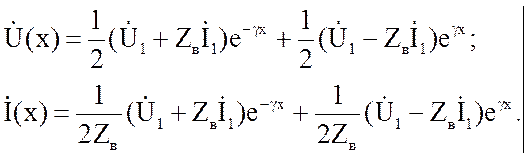
Полученные выражения
позволяют определить напряжение  и ток  в любой точке линии по заданным значениям  и  в
начале линии и отсчете координаты х от начала линии.

Уравнения (2.22) после
раскрытия скобок и перегруппировки слагаемых преобразуются к уравнениям с
гиперболическими функциями:

                          (2.23)

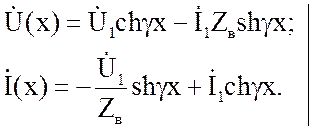
Часто граничные условия
выбирают в конце линии: напряжение  и ток  (или сопротивление нагрузки ). В этом случае отсчет координаты ведется
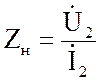
от конца линии и обозначается через y (рис. 2.7). При длине линии l координата х = l – y.

При выборе граничных
условий в конце линии х  = l из
соотношений:

                                     (2.24)

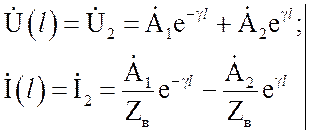
находятся коэффициенты

                                 (2.25)

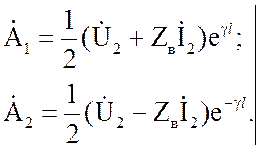
Подстановка коэффициентов
(2.25) в уравнения (2.6) и (2.8) при замене координаты х = l – y приводит уравнения к окончательному виду:

              (2.26)

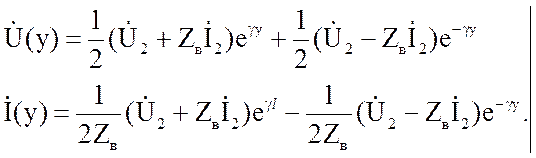
Первые слагаемые в
уравнениях (2.26) – прямые волны соответственно напряжения и тока, вторые
слагаемые – обратные волны.

Отношение обратной волны
напряжения к прямой в конце линии называется коэффициентом отражения:

                            (2.27)

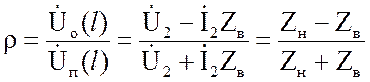
Уравнения (2.26) при
отсчете координаты у от конца линии преобразуются к уравнениям с
гиперболическими функциями:

                           (2.28)

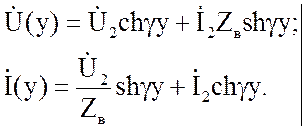
Согласно уравнениям
(2.28) однородную линию длиной l на
заданной частоте можно заменить симметричным четырехполюсником с
коэффициентами:

Характеристическое
сопротивление симметричного четырехполюсника
Z_c = Z_в. Постоянная передачи

2.7.
Входное сопротивление линии

Входное сопротивление
есть отношение комплексного напряжения к комплексному току в начале линии:

                                (2.29)

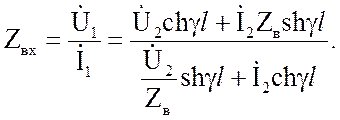
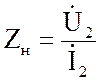
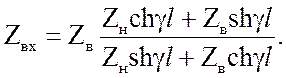
При заданной нагрузке  в конце линии

                                                  (2.30)

Содержание:

Волновые параметры длинной линии:

Полученные в предыдущей лекции уравнения передачи длинной линии (23.8) описывают комплексные амплитуды напряжения

Тогда для мгновенных значений напряжений и токов в линии получаем:

        (24.1)

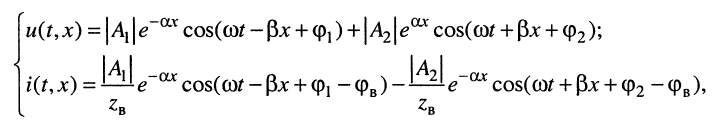
где 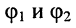— аргументы комплексных величин

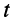
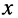
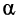
Решения (24.1) подтверждают, что напряжения и токи в длинной.линии являются функциями как времени , так и координаты (расстояния) . Каждое из уравнений представляет собой сумму двух слагаемых, структуры которых тождественны, но отличаются только знаками перед коэффициентами затухания и фазы Сначала рассмотрим левые слагаемые уравнений (24.1)

напряжений и токов, которые назовём падающими волнами напряжения и тока (смысл такого названия будет ясен из дальнейшего):

           (24.2)

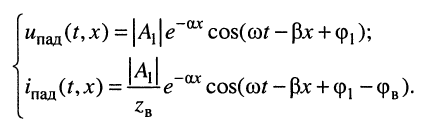
Из этих выражений следует:

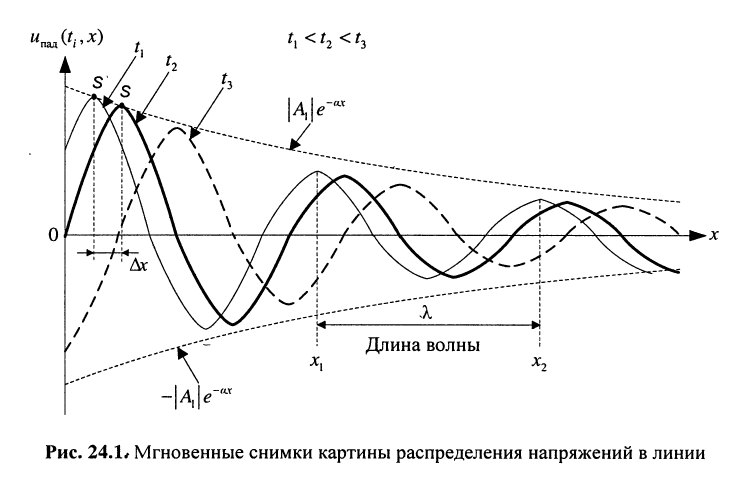
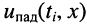
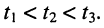
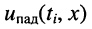
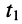
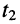
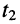
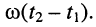
Сказанное демонстрируется на рис. 24.1, где представлено графическое распределение мгновенных значений напряжений по линии для трёх последовательных моментов времени: Эти графики можно рассматривать как последовательные мгновенные снимки картины распределения напряжений в указанные моменты времени. Они отображают волну, распространяющуюся от начала линии к концу. Например, рассматривая графики в моменты и , замечаем, что в момент фаза напряжения в каждой точке линии изменится на величину Огибающая процесса изображена пунктиром. Аналогичная картина имеет место и для тока.

Определение:

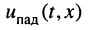
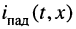
Совокупность волн напряжения и тока называется падающей волной.

Найдём длину 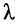и скорость распространения падающей волны в линии.

Под длиной волны понимают расстояние между смежными сечениями линии, фаза колебаний волны на которых отличается на 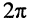(рис. 24.1):

откуда имеем равенство

из которого получаем формулу для вычисления длины волны:

               (24.3)

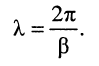
Определение:

Скоростью распространения, или фазовой скоростью, называют скорость 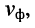с которой распространяется в линии состояние равной фазы волны; например, скорость, с которой перемещается вдоль линии нуль напряжения или тока.

Нуль напряжения достигается в точках, где функция косинуса равна нулю, поэтому условие состояния равной фазы можно записать в виде равенства:

при этом аргумент имеет значения:

Продифференцировав обе части полученного равенства по переменной t, найдём скорость распространения нуля

           (24.4)

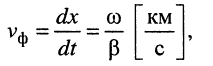
т. е. скорость распространения состояния равной фазы.

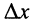
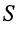
Фазовая скорость показывает, какое расстояние проходит точка в единицу времени (см. рис. 24.1), и равна отношению частоты колебания к коэффициенту фазы.

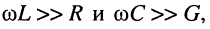
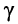
Рассмотрим, чему будет равен коэффициент фазы в наиболее характерной для практики области частот, когда  для чего разложим коэффициент распространения на вещественную и мнимую части:

Разложение в ряды полученных в правой части биномиальных сомножителей и удержание в разложениях лишь по два слагаемых даёт:

Раскрывая скобки и пренебрегая в произведении величиной второго порядка малости, получаем приближённое выражение для коэффициента распространения:

                     (24.5)

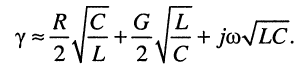
В линиях с хорошим диэлектриком проводимость чрезвычайно мала, поэтому второе вещественное слагаемое в выражении (24.5) оказывается очень малым по сравнению с первым, что позволяет записать формулы для коэффициентов затухания и фазы с хорошей степенью приближения:

                     (24.6)

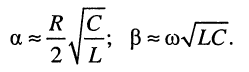
Тогда в указанной выше области частот фазовая скорость (24.4) согласно (24.6) оказывается равной

Подставляя сюда формулы значений первичных параметров длинной линии L и С (табл. 23.1), получаем:

                (24.7)

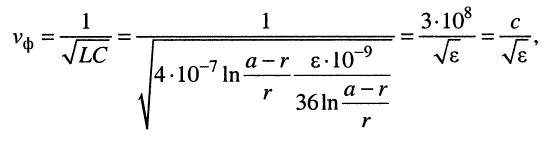
где с — скорость света.

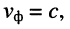
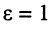
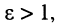
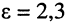
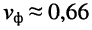
Из (24.7) ясно, что для воздушных линий  поскольку в этом случае можно считать . Для коаксиального кабеля, у которого всегда , фазовая скорость меньше скорости света в вакууме (например, при типовом значении имеем с).

Интересно, что в области низких частот значение фазовой скорости убывает с уменьшением частоты. Это объясняется меньшим проявлением скин-эффекта: волна больше проникает в проводник, и колеблющиеся частицы внутри проводника возбуждают вторичные волны. Поскольку частицы обладают некоторой инерцией, образуемые ими вторичные волны запаздывают по фазе относительно вынуждающей колебания волны, поэтому происходит запаздывание фазы результирующей волны и, как следствие, уменьшение фазовой скорости.

Обратимся теперь ко вторым слагаемым уравнений (24.1), которые назовём отражёнными волнами напряжения и тока:

                 (24.8)

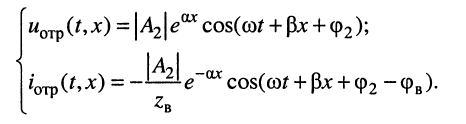
Проведя анализ этих слагаемых подобно тому, как это сделано для падающих волн, нетрудно убедиться, что они описывают затухающую волну такого же характера, как и падающая, но распространяющуюся в обратном направлении: от конца к началу линии.

Определение:

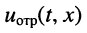
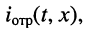
Волна напряжения и тока распространяющаяся от конца к началу линии, называется отражённой волной.

Соотношения между комплексными амплитудами падающих и отражённых волн

Из анализа, выполненного в разд. 24.1, следует:

• фазовая скорость отражённой волны совпадает с точностью до знака с фазовой скоростью падающей волны

Волновое сопротивление

Прежде всего отметим, что при любом jc, т. е. в любой точке линии согласно (24.9) справедливы равенства:

       (24.10)

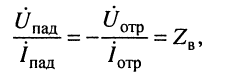
которое говорит о том, что в любом сечении линии .отношение комплексных амплитуд напряжения и тока падающей (отражённой) волны равно волновому сопротивлению линии

Свойства волнового сопротивления можно определить из выражений (24.10) и (23.6):

из которых следует:

модуль волнового сопротивления 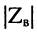представляет собой отношение амплитуды напряжения к амплитуде тока падающей (отражённой) волны;

фаза (угол) 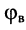волнового сопротивления представляет собой разность между фазами напряжения и тока падающей (отражённой) волны;

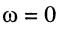
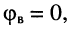
на частоте фаза а само волновое сопротивление чисто активно

при стремлении частоты  к бесконечности   фаза  и волновое сопротивление как и в предыдущем случае чисто активно 

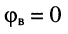
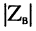
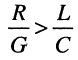
модуль волнового сопротивления | с увеличением частоты уменьшается, поскольку для реальных линий (рис. 24.3, а);

изменение фазы от нулевого значения при 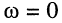до нулевого значения при говорит о том, что на одной из частот фаза будет минимальна (рис. 24.3, б), поскольку на всех частотах она является отрицательной.

Коэффициент отражения

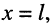
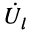
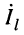
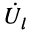
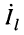
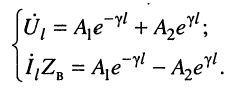
Что касается соотношения между комплексными амплитудами напряжения (тока) падающей и отражённой волн, то оно оказывается различным в различных сечениях линии. Установить эти соотношения можно из системы (23.8), положив при условии, что напряжение и ток  в конце линии известны. При этих условиях из (23.7) находятся два уравнения относительно комплексных амплитуд напряжения тока :

           (24.11)

Из системы (24.11) согласно правилу Крамера получаем значения постоянных 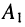и

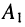
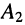
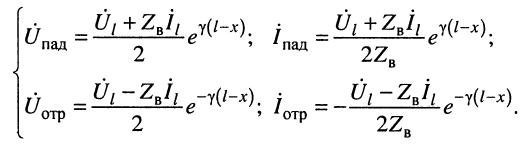
 Подстановка найденных значений i и в (24.9) приводит к частному решению:

            (24.12)

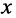
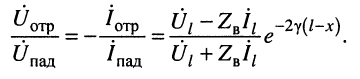
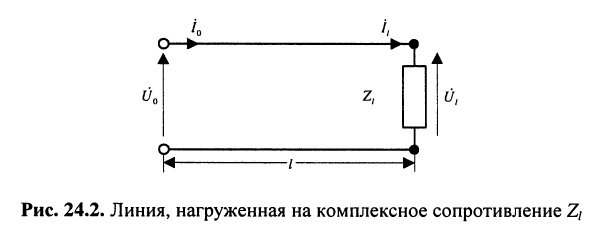
Система уравнений (24.12) позволяет записать отношение комплексных амплитуд напряжений и токов отражённой и падающей волн в сечении линии, расположенном на расстоянии от её начала:

         (24.13)

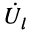
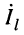
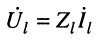
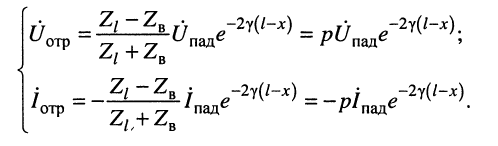
Но при выбранных направлениях отсчётов (рис. 24.2) напряжения  и тока имеет место равенство   поэтому из (24.13) окончательно получаем:

         (24.14)

Определение:

Отношение

          (24.15)

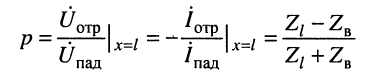
комплексной амплитуды напряжения отражённой волны к комплексной амплитуде напряжения падающей волны называется коэффициентом отражения.

Анализ соотношений (24.14) и (24.15) приводит к следующим выводам:

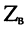
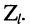
1.    Коэффициент отражения является комплексной величиной и полностью зависит от волнового сопротивления линии и сопротивления нагрузки .

2.    Коэффициент отражения по току отличается от коэффициента отражения по напряжению только знаком.

3.    При 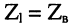коэффициент отражения равен нулю р = 0, поэтому отражённая волна отсутствует. Линия, сопротивление нагрузки которой равно её волновому сопротивлению, называется нагруженной согласованно, а сопротивление нагрузки — согласованным сопротивлением. Любая другая нагрузка приводит к появлению в линии отражённой волны.

4.    Отношение амплитуд отражённой и падающей волн (см. (24.14) и (24.15))

убывает с удалением от конца линии к её началу
 

5.    В режиме короткого замыкания, когда 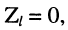коэффициент отражения по напряжению р = -1, а коэффициент отражения по току
р = 1. Это означает, что напряжения отражённой и падающей волн в конце линии находятся в противофазе:

а результирующее напряжение равно нулю

при этом токи падающей и отражённой волн оказываются в фазе

и результирующий ток равен удвоенному току падающей волны

6.    В режиме холостого хода, когда 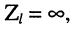коэффициент отражения по напряжению р = 1, поэтому имеет место ситуация, противоположная относительно вывода, указанного в п. 5: напряжения отражённой и падающей волн в конце линии находятся в фазе:

и результирующее напряжение равно удвоенному напряжению падающей волны

а ток равен нулю

Уравнения передачи согласованно нагруженной длинной линии

Ранее (см. разд. 23.3) были получены уравнения передачи длинной линии (23.8), которые представляют собой общее решение телеграфных уравнений и описывают закон распределения напряжений и токов по всей линии. Для решения же большинства практических задач достаточно знать соотношения лишь между напряжениями и токами на внешних зажимах линии и вовсе не интересоваться законом распределения напряжений и токов по длине линии. Иначе говоря, на практике вполне достаточно рассматривать линию как согласованно нагруженный четырёхполюсник, полностью описываемый соответствующими уравнениями передачи.

Поставим задачу найти уравнения передачи согласованно нагруженной линии, которые связывают комплексные амплитуды напряжений и токов на её внешних зажимах.

Воспользуемся уравнениями (24.12) для комплексных амплитуд напряжений и токов падающей и отражённой волн и подставим их в систему (24.9):

                             (24.16)

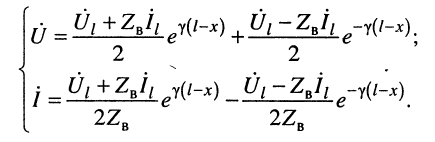
Если в систему (24.9) подставить выражения (24.14), получим

                         (24.17)

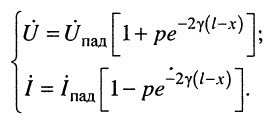
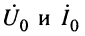
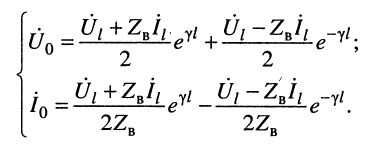
Системы (24.16) и (24.17) представляют собой системы уравнений передачи длинной линии. Обычно комплексные амплитуды напряжения и тока на входных зажимах линии (х = 0) обозначают через (см. рис. 24.2); при таких обозначениях из системы (24.16) получаем наиболее удобную форму записи уравнений передачи линии:

         (24.18)

В большинстве случаев уравнения (24.8) записывают в более компактном виде:

         (24.19)

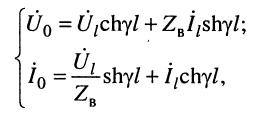
где
   —   гиперболический косинус

     —    гиперболический синус.
 

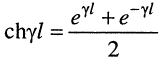
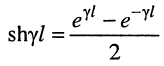
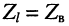
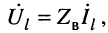
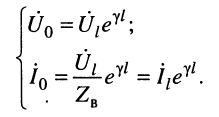
Для режима согласованной нагрузки, когда и т. е. когда отсутствует отражённая волна, из (24.18) получаем уравнения передачи согласованно нагруженной линии:

      (24.20)

Именно в такой режим и стремятся поставить линию связи, поскольку отражённые волны вызывают ряд нежелательных явлений, о чём речь пойдёт далее.

Постоянная передачи и частотные характеристики длинной линии

Постоянная передачи длинной линии:

Определение

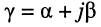
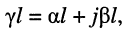
Безразмерная комплексная величина, равная произведению коэффициента распространения на длину линии

   (24.21)

называется постоянной передачи линии.

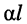
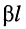
Вещественная часть постоянной передачи называется собственным, волновым или характеристическим затуханием линии, а мнимая часть — собственной, волновой или характеристической фазой.

Постоянная передачи и входящие в неё параметры характеризуют линию как таковую и не зависят от свойств генератора и нагрузки, между которыми линия может быть включена.

Поскольку режим согласованной нагрузки для линии является типовым, найдём указанные ранее параметры только для этого режима.

В таком случае постоянную передачи можно получить, прологарифмировав уравнения (24.20):

       (24.22)

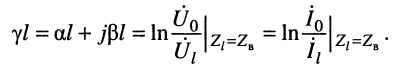
Подставляя отношения комплексных амплитуд

под знак логарифма, получаем:

на основании чего можно записать два равноправных выражения для коэффициента распространения

откуда имеем:

собственное затухание линии

      (24.3)

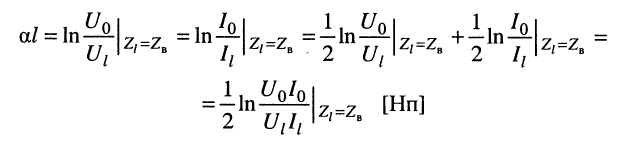
    и её собственную фазу

       (24.24)

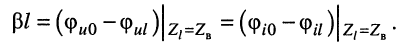
Из выражений (24.23) и (24.24) следует, что для согласованно нагруженной линии:

    собственное затухание линии 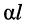 [Нп] равно натуральному логарифму отношения амплитуд или действующих значений напряжений (токов) на входе и выходе; оно равно также половине натурального логарифма отношения полных мощностей на входе и выходе;

    собственная фаза линии равна разности начальных фаз колебаний напряжений (токов) на входе и выходе.

Собственное затухание линии часто оценивается в децибелах:

         (24.25)

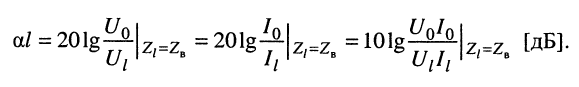
В этом случае нетрудно переформулировать зависимость собственного затухания, выраженного в децибелах, через десятичные логарифмы отношений амплитуд напряжений (токов) или полных мощностей.

Пример 24.1.

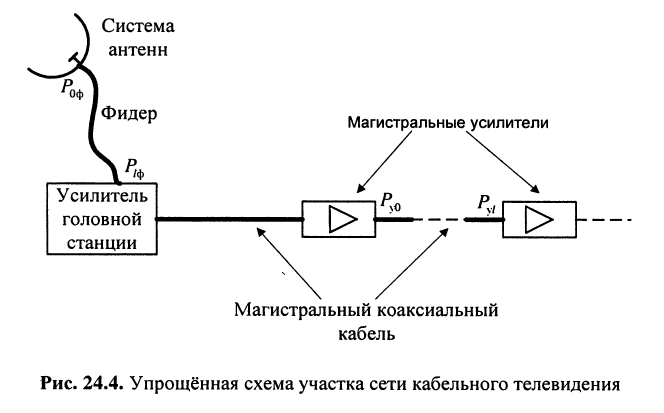
Оценим потери мощности телевизионного сигнала при распространении его в фидере’ от системы антенн до усилителя головной станции и в коаксиальном кабеле сети кабельного телевидения на отрезках магистральной линии между магистральными усилителями (рис. 24.4).

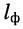
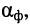
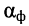
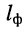
Решение. Затухание фидера зависит от его конструкции, длины и коэффициента затухания который измеряется на средней частоте частотного диапазона фидера. Обычный фидерный тракт имеет длину 50—150 м. Типовым кабелем, используемом при конструировании фидерных трактов, является кабель РК-75-24-51, имеющий полосу пропускания 50—600 МГц и коэффициент затухания = 0,002 дБ/м на частоте 300 МГц. Тогда при средней длине фидера = 100 его собственное затухание (24.25) оказывается равным

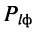
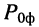
а отношение мощности сигнала на выходе фидера к мощности сигнала на входе фидера составляет

 т. е. потери мощности в фидере невелики.

 Фидер — линия для передачи электрических колебаний высокой частоты от радиопередатчика к антенне и от антенны к радиоприёмнику.

В то же время типовой магистральный коаксиальный кабель QR 540 JCA имеет полосу пропускания 5—1000 МГц и коэффициент затухания 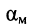= 0,0354 дБ/м на частоте 300 МГц.

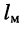
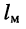
Расстояние между смежными усилителями магистрали обычно составляет до = 2 км. Следовательно, собственное затухание отрезка магистрального кабеля равно

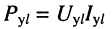
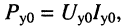
Последнее означает, что полная мощность на входе последующего усилителя меньше полной мощности которая отдаётся в линию предшествующим усилителем, в десятки миллионов раз, поскольку согласно (24.25)

Частотные характеристики (АЧХ и ФЧХ) согласованно нагруженной длинной линии

Исходя из уравнений передачи согласованно нагруженной линии (24.20) запишем её комплексную частотную характеристику через постоянную передачи линии:

        (24.26)

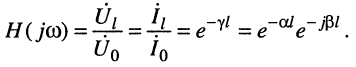
Отсюда нетрудно получить постоянную передачи через КЧХ линии:

        (24.27)

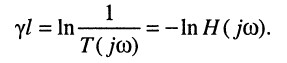
Амплитудно-частотная и фазочастотная характеристики определяются из (24.26): 

       (24.28)

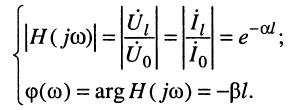
Для несогласованной нагруженной линии КЧХ можно найти из её уравнений передачи (24.18), подставив в них равенства:

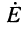
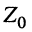
где и — комплексная амплитуда ЭДС и комплексное внутреннее сопротивление генератора, подключённого к линии.

Входное сопротивление длинной линии

Определение:

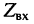
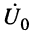
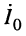
Входным сопротивлением линии называется отношение комплексной амплитуды напряжения к комплексной амплитуде тока , действующих на входе линии.

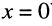
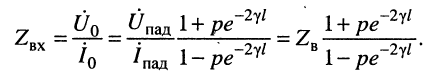
Формулу входного сопротивления для линии с произвольной нагрузкой можно получить из уравнений (24.17), если положить расстояние   и разделить первое уравнение на второе:

      (24’29)

Анализ формулы (24.29) показывает:

    при согласованной нагрузке входное сопротивление равно волновому, поскольку в данном случае 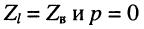(24.15);

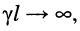
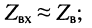
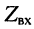
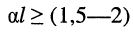
    если постоянная передачи линии стремится к бесконечности то входное и волновое сопротивления весьма близки по величине считают, что не зависит от нагрузки при собственном затухании линии Нп;

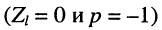
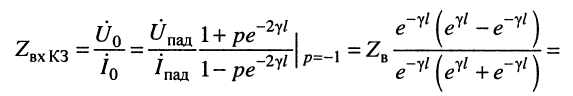
    в режиме КЗ получаем

         (24.30)

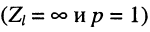
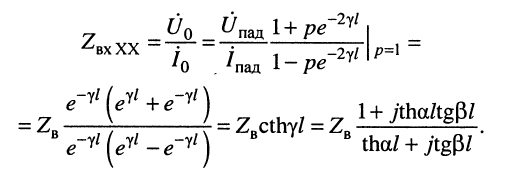
в режиме XX  имеем

          (24.31)

Вывод:

волновое сопротивление линии представляет собой предел, к которому стремится входное сопротивление при безграничном увеличении длины линии:

Этот факт объясняется тем, что при большом затухании линии значительная часть мощности, подводимой к её входу, рассеивается в самой линии и лишь небольшой остаток мощности поступает в нагрузку (см. пример 24.1). По этой причине энергетические соотношения на входе линии пренебрежимо мало зависят от энергетических соотношений на её выходе и, в частности, от сопротивления нагрузки линии.

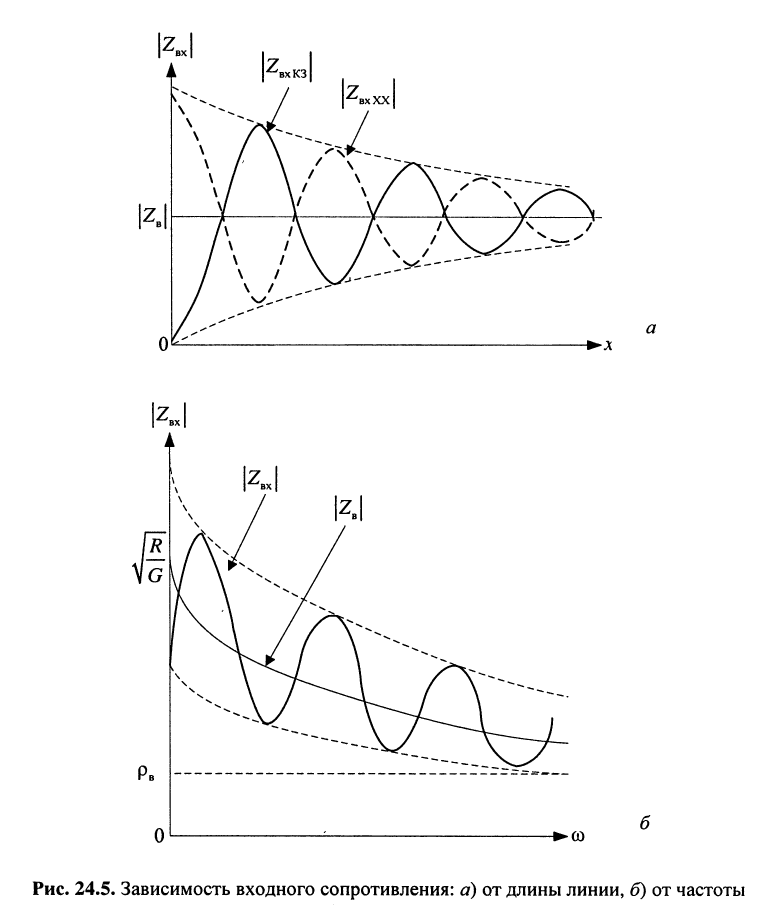
С увеличением длины линии увеличивается и её затухание, а потому уменьшается амплитуда отражённой волны на входе линии, что, в свою очередь, приводит к уменьшению отклонения входного сопротивления линии от её волнового сопротивления как по модулю, так и по фазе. В пределе входное сопротивление линии стремится к волновому сопротивлению. На рис. 24.5, а показаны зависимости модулей входных сопротивлений в режимах XX и КЗ. Колебательный характер волнового сопротивления при несогласованной нагрузке объясняется наличием падающих и отражённых волн.

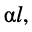
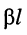
Входное сопротивление зависит не только от длины линии, но и от частоты (рис. 24.5, б). С ростом частоты увеличиваются как собственное затухание так и собственная фаза линии. Это приводит к весьма сложному волнообразному характеру изменения входного сопротивления линии относительно её волнового сопротивления.

Допустимые отклонения входного сопротивления линии от её волнового сопротивления строго нормированы, и при эксплуатации длинных линий необходимо придерживаться указываемых для линии обычно весьма жёстких норм.

Определение параметров линии методом холостого хода и короткого замыкания

Определение первичных и вторичных параметров линии наиболее просто осуществлять с помощью измерений входного сопротивления линии при двух граничных сопротивлениях нагрузки: холостом ходе и коротком замыкании.

Из уравнений (24.19) в режимах 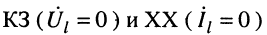 имеем

Совместное решение этих уравнений позволяет найти значения волновых параметров линии: волнового сопротивления и постоянной передачи.

Волновое сопротивление

      (24.32)

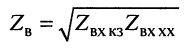
равно среднему геометрическому из входных сопротивлений короткозамкнутой и разомкнутой линии. Это выражение можно рассматривать как ещё одно определение волнового сопротивления длинной линии.

Гиперболический тангенс постоянной передачи

      (24.33)

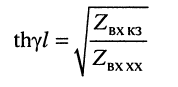
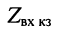
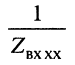
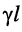
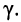
равен среднему геометрическому из сопротивления короткозамкнутой линии и проводимости — разомкнутой линии. Найдём из (24.33) постоянную передачи и коэффициент распространения Поскольку

то

Логарифмируя обе части последнего равенства, получаем постоянную передачи:
 

          (24.34)

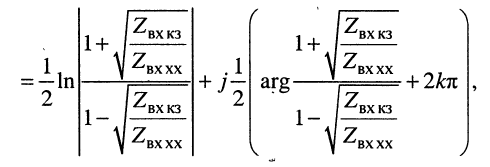
откуда легко находятся коэффициенты затухания и фазы:

Коэффициент 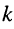равен целому числу волн, укладывающихся по длине линии.

Во всех формулах необходимо брать только арифметические корни.

Зная волновые параметры линии, нетрудно вычислить её первичные параметры путём приравнивания вещественных и мнимых частей равенств:

Замечание:

Метод холостого хода и короткого замыкания целесообразно применять в том случае, когда затухание линии не превышает
1 Нп (8,69 дБ), что характерно для большинства длинных линий.

Коэффициент распространения, затухания и фазы кабеля

Электромагнитная энергия, распространяясь вдоль кабеля, уменьшается по величине от начала к концу линии. Уменьшение или затухание энергии происходит вследствие потерь на нагревание жил и поляризацию молекул изоляции. С ростом частоты потери увеличиваются. Потери в изоляции учитываются посредством коэффициента распространения γ, являющегося комплексной величиной:

Приведенные выше уравнения для тока и напряжения можно представить в следующем виде:

Модуль этого выражения (е αt ) характеризует уменьшение абсолютного значения тока или напряжения при прохождении по линии длиной l. Аналогичны выражения для затухания мощности:

где α — коэффициент затухания (затухание на длине 1 км).

Угол φ = βl , характеризующий изменение угла вектора тока или напряжения на участке линии длиной l, называется коэффициентом фазы или фазовой постоянной:

Таким образом, коэффициент распространения одновременно определяет изменение сигнала как по абсолютной величине, так и по фазе на 1 км длины кабеля. Логарифмируя обе части уравнений (3-54), получаем формулы для расчета величины затухания:

Затухание принято измерять в неперах (неп) на 1 км. Затухание 1 неп — затухание кабельной цепи, у которой ток или напряжение в начале ее больше по абсолютной величине, чем ток или напряжение в конце, в 2,718 раза (е=2,718), т. е. αl = 1. В радиочастотных кабелях затухание обычно выражают в децибелах (дб) на 1 м (1 неп=8,65 дб; 1 дб = 0,115 неп).

Фазовая постоянная (коэффициент фазы)

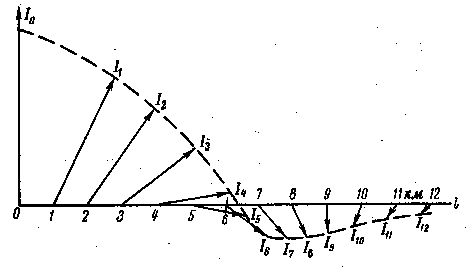
Рис. 3-8. Изменение тока вдоль однородной линии.

Фазовая постоянная измеряется в радианах на 1 км или градусах (1 рад = 57,3°).

Фазовая постоянная измеряется в радианах на 1 км или градусах (1 рад = 57,3°).

На рис. 3-8 приведена кривая изменения тока вдоль однородной линии. В табл. 3-1 приведены сокращенные формулы для подсчета α и β в различных диапазонах частот.

Затухание коаксиального радиочастотного кабеля

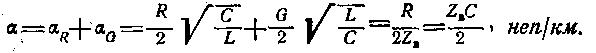
Подставив в (3-57) значения R, L,C и G, получим:

или после преобразований

Если внутренний и внешний проводники кабеля изготовлены из медной проволоки, то

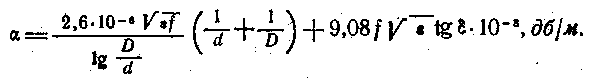
При многопроволочном внутреннем проводнике и оплетке — внешнем проводнике

Затухание спиральных радиочастотных кабелей (кабелей задержки)

Затухание коаксиальных кабелей связи

При оптимальном геометрическом отношении диаметров внешнего и внутреннего проводников D/d=3,6

Затухание коаксиального кабеля с полиэтиленовой шайбовой изоляцией

где f — частота, Мгц.

Затухание симметричного радиочастотного кабеля

На рис. 3-9 приведена зависимость затухания α и фазовой постоянной β от частоты. Дальность связи по кабельной линии

где α — коэффициент затухания кабеля, неп/км; α _доп — допустимое затухание кабельной линии, неп.

По существующим нормам затухание линий низкочастотной телефонной связи (НЧ) должно быть не более 3,3 неп, а высокочастотных линий (ВЧ) — 6 — 7 неп.

Предельно допустимая дальность связи по магистральным кабельным линиям

где τ — допустимое время прохождения сигнала, мксек; по нормам Международного консультативного комитета время прохождения сигналов от одного абонента к другому не должно превышать 250 мксек, а для кабельных линий, соединенных с международными магистралями, 100 мксек; Т — время пробега сигнала на участке линии длиной 1 км, мксек/км.

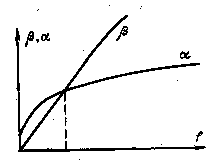
Рис. 3-9. Зависимость коэффициента затухания а и коэффициента фазы Р от частоты.

В неоднородных линиях затухание складывается из собственного затухания кабеля и затухания из-за неоднородности электрических характеристик. Дальность связи по такой кабельной линии будет обусловливаться ее рабочим затуханием α _р , являющимся затуханием кабельной линии в рабочих условиях (при любых нагрузочных сопротивлениях на концах). Кроме собственного затухания кабеля αl, рабочее затухание учитывает также несогласованность на соединениях кабелей с нагрузками Z _T и Z _n . Рабочее затухание определяется по формуле

— коэффициенты отражения на стыках генератор — кабель и приемник — кабель. Первое слагаемое в правой части этого уравнения — собственное затухание кабеля, второе и третье — дополнительные затухания вследствие несогласованности сопротивлений генератора и кабеля (Z _r ≠ Z _B ), приемника и кабеля (Z _n ≠ Z _B ), четвертое — дополнительное затухание вследствие взаимодействия нёсогласованностей в начале и конце линии.

Затухание линии имеет минимальное значение при следующих соотношениях первичных параметров:

На рис. 3 — 10 приведены изменения коэффициентов затухания в токопроводящих жилах α _ж и в изоляции α _и при различных значениях 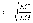. С ростом х затухание в токопроводящих жилах увеличивается, а затухание в изоляции уменьшается. При х = 1 потери в токопроводящих жилах равны потерям в изоляции (α _ш = α _и ) и затухание кабеля имеет наименьшую величину. В выпускаемых кабелях х > 1, так как RC значительно превосходят по величине LG (RC >> LG).

Таким образом, затухание кабеля может быть снижено путем уменьшения R, т. е. увеличения диаметра внутреннего проводника (токопроводящих жил) и соответствующего увеличения расхода меди; затем путем уменьшения G, т. е. применения изоляционных материалов с более высокими электроизоляционными свойствами, затем уменьшения С, т. е. увеличения толщины изоляции и соответственно увеличения расхода материалов, наконец, искусственного увеличения L.

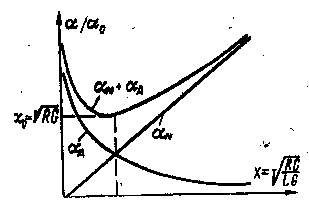
Рис. 3-10. Затухание в жилах и изоляции кабеля при различных соотношениях первичных параметров кабеля.

Известно несколько различных способов искусственного увеличения индуктивности кабельных линий: пупинизация (включение в кабель катушек индуктивности через определенные расстояния), крарупизация (нанесение на токопроводящую жилу проволоки или ленты из сплава с большой магнитной проницаемостью), биметаллизация (нанесение на токопроводящую жилу электролитическим путем слоя железа) и применение магнитодиэлектрика поверх токопроводящей жилы (например, полиэтилена, наполненного ферритом или альсифером). Практическое применение в кабельной технике получил способ пупинизации в низкочастотных кабелях связи, а способ искусственного увеличения индуктивности путем применения магнитодиэлектрика используют в спиральных радиочастотных кабелях (кабелях задержки) и помехозащищенных автомобильных проводах высокого напряжения.

В результате возникновения продольного магнитного поля, направленного вдоль оси спирального коаксиального кабеля, резко возрастает общее магнитное поле кабеля и соответственно увеличивается индуктивность его. Время распространения сигналов в таком кабеле

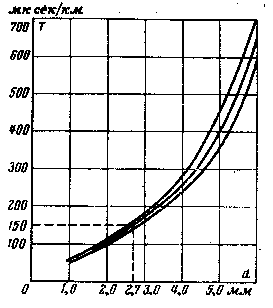
Рис. 3-11. Зависимость времени распространения сигналов Т от диаметра кабеля.

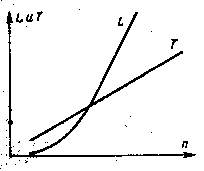
Рис. 3-12. Зависимость изменения времени распространения сигналов Т и индуктивности L от числа витков спирального кабеля.

На рис. 3-11 приведена зависимость времени распространения сигналов Т от диаметра кабеля. С увеличением диаметра спирального кабеля время распространения сигналов возрастает. На рис. 3-12 приведена зависимость времени распространения сигналов Т и индуктивности L от числа витков спирального кабеля. Возрастание индуктивности спирального кабеля находится в квадратичной зависимости от увеличения числа витков. Емкость и проводимость изоляции спиральных кабелей незначительно выше, чем у обычных коаксиальных радиочастотных кабелей. Активное сопротивление и затухание существенно возрастают с увеличением числа витков п, уменьшением диаметра эмалированного провода для изготовления спирального проводника кабеля и возрастанием частоты. По этой причине практическая максимальная частота спиральных кабелей не превышает 30 Мгц. С возрастанием частоты соотношение RC = LG в кабеле нарушается. Объясняется это увеличением проводимости изоляции с возрастанием частоты. Это условие выполняется только при определенной частоте (без искусственного повышения индуктивности):

Для симметричных кабелей связи частота f _ж = ω _х /2π находится в пределах 200-600 кгц.

Источник

Расчет проводимости изоляции симметричного кабеля

Согласно [1, формула 5.69], уравнение для расчета проводимости симметричного кабеля имеет вид:

С – емкость кабеля (рассчитано выше), Ф/км;

ω = 2πf – циклическая частота, Гц;

tg δ – тангенс угла диэлектрических потерь согласно, [2, таблица 3]);

G₀ – проводимость, обусловленная токами утечки, из за несовершенности материала. Так как современные изолирующие материалы достаточно качественны, то данное значение стремиться к нулю. В расчетах данным слагаемым пренебрегаем.

Подставим значения и произведем вычисления для f₁ = 12 кГц:

Расчеты для других частот проведем по аналогичной методикой табличным способом. Промежуточные и конечные результаты представим в таблице 1.

Расчет вторичных параметров:

5. Расчет коэффициента затухания симметричного кабеля:

Согласно [1, таблица 4.6], уравнение для расчета коэффициента затухания симметричного кабеля имеет вид:

R – километрическое сопротивление симметричного кабеля (рассчитано выше), Ом/мм 2 ·км;

L – километрическая индуктивность симметричного кабеля (рассчитано выше), Гн/км;

С – емкость симметричного кабеля (рассчитано выше), Ф/км;

G — проводимость симметричного кабеля (рассчитано выше), Ф/км.

Подставим значения и произведем вычисления для f₁ = 12 кГц:

Расчеты для других частот проведем по аналогичной методикой табличным способом. Конечные результаты представим в таблице 1.

6. Расчет коэффициента фазы симметричного кабеля:

Согласно [1, таблица 4.6], уравнение для расчета коэффициента фазы симметричного кабеля имеет вид:

ω = 2πf – циклическая частота, Гц;

L – километрическая индуктивность симметричного кабеля (рассчитано выше), Гн/км;

С – емкость симметричного кабеля (рассчитано выше), Ф/км;

Подставим значения и произведем вычисления для f₁ = 12 кГц:

Расчеты для других частот проведем по аналогичной методикой табличным способом. Конечные результаты представим в таблице 1.

7. Расчет волнового сопротивления симметричного кабеля:

Согласно [1, таблица 4.6], уравнение для расчета волнового сопротивления имметричного кабеля имеет вид:

L – километрическая индуктивность симметричного кабеля (рассчитано выше), Гн/км;

С – емкость симметричного кабеля (рассчитано выше), Ф/км;

Подставим значения и произведем вычисления для f₁ = 12 кГц:

Расчеты для других частот проведем по аналогичной методикой табличным способом. Конечные результаты представим в таблице 1.

Так как волновое сопротивления не зависит от частоты, то данное значение верно на всех заданных частотах.

8. Расчет фазовой скорости волны симметричного кабеля:

Согласно [1, таблица 4.6], уравнение для расчета скорости распространения волны в симметричном кабеле имеет вид:

L – километрическая индуктивность симметричного кабеля (рассчитано выше), Гн/км;

С – емкость симметричного кабеля (рассчитано выше), Ф/км;

Подставим значения и произведем вычисления для f₁ = 12 кГц:

Так как волновое сопротивления не зависит от частоты, то данное значение верно на всех заданных частотах.

Сведем все рассчитанные значения в итоговую таблицу 1 и построим графики.

Таблица 1 – Рассчитанные значения первичных и вторичных параметров передачи от различных значениях частоты в заданном диапазоне

Параметр	Частота f, кГц
Первичные параметры симметричного кабеля
R, Ом/км	119,699	164,424	219,585	291,239
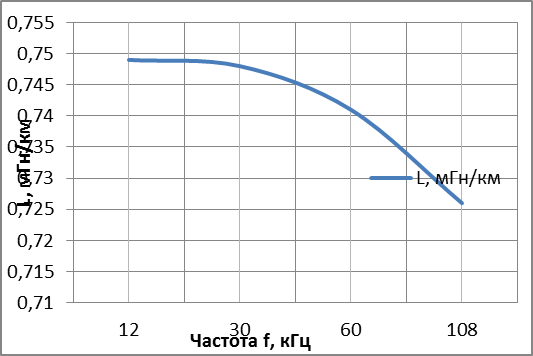
L, мГн/км	0,749	0,748	0,741	0,726
С, нФ/км	21,333	21,333	21,333	21,333
G, мкСм/км	0,723	2,813	8,038	21,704
Вторичные параметры симметричного кабеля
a, дБ/км	0,3194	0,4392	0,589	0,790
b, рад/км	0,301	0,7531	1,499	2,672
Zв, Ом	187,402	187,27	186,436	184,57
Vф, км/с	250,124	250,291	251,42	253,94

По рассчитанным значениям первичных и вторичных параметров симметричного кабеля, построим графики зависимостей коэффициентов передачи от частоты. Графики представлены на рисунках 1 и 2.

Рисунок 1 – Частотные зависимости первичных параметров симметричного кабеля
Рисунок 2 – Частотные зависимости вторичных параметров симметричного кабеля

Задача 2

Рассчитать защищенность между цепями симметричного кабеля на длине усилительного участка в заданном диапазоне частот и построить частотную зависимость данного параметра влияния.

Построить графики частотной зависимости защищенности на дальнем конце в заданном диапазоне частот. По результатам расчетов сделайте сравнение с нормами и дайте заключение о пригодности кабеля с данными симметричными цепями для заданной системы связи.

Параметр	S, дБ	К, пф/сд	Заданный диапазон, кГц	Частоты, кГц
f1	f2	f3	f4
Значение	12-108

Согласно [1, формулы 6,27; 6,28; 6,29] для симметричного кабеля характерины справедливы уравнения.

Переходное затухание на ближнем конце:

Переходное затухание на дальнем конце:

Защищенность симметричной линии:

l – длина участка регенерации, км;

a — кило метрическое затухание сигнала в кабеля (рассчитано в задаче 1);

N₁₂ – электромагнитная связь на ближнем конце;

F₁₂ – электромагнитная связь на дальнем конце;

N₁₂, F₁₂ упрощенно определяются согласно [1, стр. 264-265]:

Длину усилительного участка рассчитаем по приближенной формуле согласно [2, формула 3]:

a — коэффициент затухания цепи при частоте f (рассчитано 1 задачей);

S — энергетический потенциал аппаратуры.

Считаем, что оборудование ЦСП и следовательно S = 35 дБ.

Подставим значения и произведем вычисления для f₁ = 12 кГц:

Переходное затухание на ближнем конце:

Переходное затухание на дальнем конце:

Защищенность симметричной линии:

Расчеты для других частот проведем по аналогичной методикой табличным способом. Конечные результаты представим в таблице 2.

Таблица 2 – Рассчитанные значения переходных затуханий на ближнем, дальнем конце и защищённость симметричной линии связи в заданном диапазоне частот

Параметр	Частота, кГц
A0, дБ	78,061	71,492	66,789	81,99
Al, дБ	111,6	105,0307	100,328	115,537
Aз, дБ	76,6	70,03	65,32	80,537

По рассчитанным значениям переходных затуханий и защищённости симметричного кабеля, построим графики зависимостей рассчитанных параметров от частоты. Графики представлены на рисунке 3.

Рисунок 3 – График зависимости переходных затуханий от частоты

Приведем нормы на переходные затухания А₀ для симметричного кабеля и сравним рассчитанные параметры с нормативными приведенные в таблице 3 и сделаем вывод.

Таблица 3 – Нормативные и расчётные значение переходных затуханий

Параметр	Норма на НЧ симметричную, четырехпров. линия Aз, дБ	Частота, кГц
Нормативное значение, дБ	65,1+ al	100,1
Расчетное значение, дБ	76,6	70,03	65,32	80,53

Проверка показала, что нет необходимости повышать параметры взаимного влияния между симметричными цепями, так как они находятся в пределах нормы.

Задача 3

Рассчитать параметры двухслойных стеклянных волокон оптического кабеля. Разработать конструкцию кабеля и нарисовать эскиз поперечного сечения в масштабе 10:1.

Расчету подлежат: числовая апертура NА; нормированная частота ν; число типов волн N, распространяющихся в кабеле; диаметр сердцевины волокна для одномодовой передачи d, мкм; коэффициент затухания волны в волокне кабеляa, дБ/км; уширение импульса в кабеле t_и, мкс/км.

Параметр	Диаметр сердцев 2а, мкм	Диаметр оболочки 2в, мкм	Потери в сердцевине tgd·10 — 11	Длина волны l , мкм
Значение	1,2	1,5

Параметр	Коэффициент преломления сердцевины n1	Коэффициент преломления оболочки n2	Число волокон в кабеле, м	Длина регенерационного участка lр, км
Значение	1,5	1,48

Определим основные оптические параметры стекловолокна с точность до 4 цифры после запятой, согласно методике приведенной в [4, стр. 145-146] и в методических указаниях [2, формулы 6-9].

NA – числовая апертура ОВ;

n₁ и n₂ — коэффициент преломления сердцевины и оболочки;

Значение апертурного угла:

Θa = arcsin(NA) = arcsin(0,244) = 4,13, рад.

Значение нормированной частоты:

Так как v > 2,405, то можно сделать вывод, что для данного типа ОВ имеет место многомодовый режим работы.

Число типов волн (мод) N, которые одновременно распространяются по оптическому волокну, рассчитывают по формуле:

Полученное значение округлять до меньшей целой величины.

Для того чтобы по оптическому волокну распространялась только волна НЕ₁₁, диаметр сердцевины волокна должен выбираться из условия:

Затухание света в волокне оптического кабеля обусловлено поглощением энергии в материале стекловолокна, а также рассеянием в окружающее пространство. Приближенно суммарный коэффициент затухания вычислять по формуле:

Величину t_и рассчитать по формуле согласно [1, стр. 209] для заданной длины регенерационного участка:

с = 3·10 5 км/с – скорость света в вакууме.

Приведем возможную конструкцию волоконно-оптического кабеля в разрезе, учитывая число волокон и укажем основные элементы конструкции.

Эскиз поперечного разреза кабеля приведен на рисунке 4.

Рисунок 4 – Поперечный разрез волоконно-оптического кабеля

Список литературы

1. Гроднев И.И., Верник С.М. Линии связи. – М.: Радио и связь, 1988 г. -354 с.

2. Комаров Ю.З., Направляющие системы электросвязи: Методические указания и контрольные задания по выполнению домашней контрольной работы. – Екатеринбург: УрТИСИ ГОУ ВПО «СибГУТИ», 2006. -19 с.

3. Иванов А.Б. Волоконная оптика: компоненты, системы передачи, измерения – М.: Компания Сайрус Системс, 1999. -672 с.

4. Горлов Н.И., Микиденко А.В., Минина Е.А., Оптические линии связи и пассивные компоненты ВОСП: Учебное пособие. Новосибирск; Сиб.ГУТИ — 2003 г. –245 с.

5. Андреев В.А., Бурдин В.А., Попов Б.В., Польников А.И., Строительство и техническая эксплуатация волоконно-оптических линий связи: Учебник для ВУЗов, М.: Радио и связь, — 1995, -220 стр.

Источник