Как найти коэффициент затухания колебаний по уравнение
§6 Затухающие колебания
Декремент затухания. Логарифмический декремент затухания.
Добротность
Свободные колебания технических систем в реальных условиях протекают, когда на них действуют силы сопротивления. Действие этих сил приводит к уменьшению амплитуды колеблющейся величины.
Колебания, амплитуда которых из-за потерь энергии реальной колебательной системы уменьшается с течением времени, называются затухающими.
Наиболее часто встречается случаи, когда сила сопротивления пропорциональна скорости движения
где r — коэффициент сопротивления среды. Знак минус показывает, что FC направлена в сторону противоположную скорости.
Запишем уравнение колебаний в точке, колеблющийся в среде, коэффициент сопротивлений которой r . По второму закону Ньютона
где β — коэффициент затухания. Этот коэффициент характеризует скорость затухания колебаний, При наличии сил сопротивления энергия колеблющейся системы будет постепенно убывать, колебания будут затухать.
— дифференциальное уравнение затухающих колебаний.
— у равнение затухающих колебаний.
ω – частота затухающих колебаний:
Период затухающих колебаний:
Затухающие колебания при строгом рассмотрении не являются периодическими. Поэтому о периоде затухаюших колебаний можно говорить, когда β мало.
Если затухания выражены слабо (β→0), то . Затухающие колебания можно
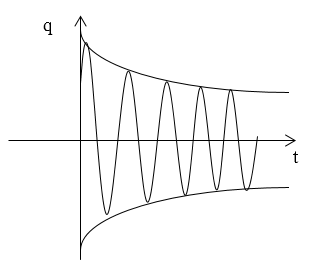
рассматривать как гармонические колебания, амплитуда которых меняется по экспоненциальному закону
В уравнении (1) А0 и φ0 — произвольные константы, зависящие от выбора момента времени, начиная е которого мы рассматриваем колебания
Рассмотрим колебание в течение, некоторого времени τ, за которое амплитуда уменьшится в е раз
τ — время релаксации.
Коэффициент затихания β обратно пропорционален времени, в течение которого амплитуда уменьшается в е раз. Однако коэффициента затухания недостаточна для характеристики затуханий колебаний. Поэтому необходимо ввести такую характеристику для затухания колебаний, в которую входит время одного колебаний. Такой характеристикой является декремент (по-русски: уменьшение) затухания D , который равен отношению амплитуд, отстоящих по времени на период:
Логарифмический декремент затухания равен логарифму D :
Логарифмический декремент затухания обратно пропорционален числу колебаний, в результате которых амплитуда колебаний уменьшилась в е раз. Логарифмический декремент затухания — постоянная для данной системы величина.
Еще одной характеристикой колебательной система является добротность Q .
Добротность пропорциональна числу колебаний, совершаемых системой, за время релаксации τ.
Добротность Q колебательной системы является мерой относительной диссипации (рассеивания) энергии.
Добротность Q колебательной системы называется число, показывающее во сколько раз сила упругости больше силы сопротивления.
Чем больше добротность, тем медленнее происходит затухание, тем затухающие колебания ближе к свободным гармоническим.
§7 Вынужденные колебания.
Резонанс
В целом ряде случаев возникает необходимость создания систем, совершающих незатухающие колебания. Получить незатухающие колебания в системе можно, если компенсировать потери энергии, воздействуя на систему периодически изменяющейся силой.
Запишем выражение для уравнения движения материальной точки, совершающей гармоническое колебательное движение под действием вынуждающей силы.
По второму закону Ньютона:
(1)
— дифференциальное уравнение вынужденных колебаний.
Это дифференциальное уравнение является линейным неоднородным.
Его решение равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения:
Найдем частное решение неоднородного уравнения. Для этого перепишем уравнение (1) в следующем виде:
(2)
Частное решение этого уравнения будем искать в виде:
т.к. выполняется для любого t , то должно выполняться равенство γ = ω , следовательно,
Это комплексное число удобно представить в виде
где А определяется по формуле (3 ниже), а φ — по формуле (4), следовательно, решение (2),в комплексной форме имеет вид
Его вещественная часть, являвшаяся решением уравнения (1) равна:
(3)
(4)
Слагаемое Хо.о. играет существенную роль только в начальной стадии при установлении колебаний до тех пор, пока амплитуда вынужденных колебаний не достигнет значения определяемого равенством (3). В установившемся режиме вынужденные колебания происходят с частотой ω и являются гармоническими. Амплитуда (3) и фаза (4) вынужденных колебаний зависят от частоты вынуждающей силы. При определенной частоте вынуждающей силы амплитуда может достигнуть очень больших значений. Резкое возрастание амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте механической системы, называется резонансом.
Частота ω вынуждающей силы, при которой наблюдается резонанс, называется резонансной. Для того чтобы найти значение ωрез, необходимо найти условие максимума амплитуды. Для этого нужно определить условие минимума знаменателя в (3) (т.е. исследовать (3) на экстремум).
Зависимость амплитуды колеблющейся величины от частоты вынуждающей силы называется резонансной кривой. Резонансная кривая будет тем выше, чем меньше коэффициент затухания β и с уменьшением β, максимум резонансных кривых смешается вправо. Если β = 0, то
При ω→0 все кривые приходят к значению — статическое отклонение.
Параметрический резонанс возникает в том случае, когда периодическое изменение одного из параметров система приводит к резкому увеличению амплитуды колеблющейся системы. Например, кабины, делающие «солнышко» за счет изменения положения центра тяжести система.(То же в «лодочках».) См. §61 .т. 1 Савельев И.В.
Затухающие колебания в контуре и их уравнение
Существуют колебания в системе без источника энергии, называемые затухающими. Рассмотрим реальный контур с сопротивлением не равным нулю. Для примера используют контур с включенным сопротивлением R , с емкостью конденсатора C , с катушкой индуктивности L , изображенный на рисунке 1 . Колебания, происходящие в нем, — затухающие.
Именно наличие сопротивления становится главной причиной их затухания. Данный процесс возможен посредствам потерь энергии на выделение джоулева тепла. Аналог сопротивления в механике – действие сил трения.
Характеристики затухающих колебаний
Затухающие колебания характеризуют коэффициентом затухания β . Применив второй закон Ньютона, получим:
m a = — k x — y v , d 2 x d t 2 + r m d x d t + k m x = 0 , ω 0 2 = k m , β = r 2 m .
Из записи видно, что β действительно является характеристикой контура. Реже вместо β применяют декремент затухания δ ,
Значение a ( t ) является амплитудой заряда, силы тока и так далее, δ равняется количеству колебаний, а N e — период времени уменьшения амплитуды в e раз.
Для R L C контура применима формула с ω частотой.
При небольшой δ ≪ 1 говорят, что β ≪ ω 0 ω 0 = 1 L C — собственная частота, отсюда ω ≈ ω 0 .
При рассмотрении затухающих колебаний последовательного контура колебательный контур характеризуется добротностью Q :
Q = 1 R L C = ω 0 L R , где R , L и C — сопротивление, индуктивность, емкость, а ω 0 — частота резонанса. Выражение L C называют характеристическим или волновым сопротивлением. Для параллельного контура формула примет вид:
Q = R L C = R ω 0 L .
R является входным сопротивлением параллельного контура.
Эквивалентное определение добротности применяется при слабых затуханиях. Его выражают через отношение энергий:
Q = ω 0 W P d = 2 π f 0 W P d , называемое общей формулой.
Уравнения затухающих колебаний
Рассмотрим рисунок 1 . Изменение заряда q на конденсаторе в таком контуре описывается дифференциальным уравнением:
q ( t ) = q 0 e ( — β t ) cos ω t + a ‘ 0 = q 0 e — β t cos ( ω t ) .
Если t = 0 , то заряд конденсатора становится равным q 0 , и ток в цепи отсутствует.
Если R > 2 L C изменения заряда не относят к колебаниям, разряд называют апериодическим.
Значение сопротивления, при котором колебания превращаются в апериодический разряд конденсатора, критическое R k .
Функция изображается аналогично рисунку 2 .
Записать закон убывания энергии, запасенной в контуре W ( t ) при W ( t = 0 ) = W 0 с затухающими колебаниями. Обозначить коэффициент затухания в контуре β , а собственную частоту — ω 0 .
Решение
Отправная точка решения – это применение формулы изменения заряда на конденсаторе в R L C — контуре:
q ( t ) = q 0 e ( — β t ) cos ω t + a ‘ 0 = q 0 e — β t cos ( ω t ) .
Предположим, что при t = 0 , a ‘ 0 = 0 . Тогда применим выражение
Для нахождения I ( t ) :
I ( t ) = — ω 0 q 0 e ( — 2 β t ) sin ( ω t + α ) , где t g α = β ω .
Очевидно, что электрическая энергия W q запишется как:
W q = q 2 2 C = q 0 2 2 C e ( — 2 β t ) cos 2 ( ω t ) = W 0 e ( — 2 β t ) cos 2 ( ω t ) .
Тогда значение магнитной энергии контура W m равняется:
W m = L 2 ω 0 2 q 0 2 e ( — 2 β t ) sin 2 ω t + a = W 0 e — 2 β t sin 2 ω t + a .
Запись полной энергии будет иметь вид:
W = W q + W m = W 0 e ( — 2 β t ) ( cos 2 ( ω t ) + sin 2 ( ω t + a ) ) = = W 0 e ( — 2 β t ) 1 + β ω 0 sin ( 2 ω t + α ) .
Где sin α = β ω 0 .
Ответ: W ( t ) = W 0 e ( — 2 β t ) 1 + β ω 0 sin ( 2 ω t + a ) .
Применив результат предыдущего примера, записать выражение для энергии, запасенной в контуре W ( t ) , при медленно затухающих колебаниях. Начертить график убывания энергии.
Решение
Если колебания в контуре затухают медленно, то:
Очевидно, выражение энергии, запасенной в контуре, вычислим из
W ( t ) = W 0 e ( — 2 β t ) 1 + β ω 0 sin ( 2 ω t + a ) , предварительно преобразовав до W ( t ) = W 0 e ( — 2 β t ) .
Такое упрощение возможно по причине выполнения условия β ω 0 ≪ 1 , sin ( 2 ω t + a ) ≤ 1 , что означает β ω 0 sin ( 2 ω t + a ) ≪ 1 .
Ответ: W ( t ) = W 0 e ( — 2 β t ) . Энергия в контуре убывает по экспоненте.
Лекция №8. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
5.6. Затухающие гармонические колебания.
Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних сил, то колебания будут затухать. Затухающие колебания − это колебания, амплитуда которых из-за потерь энергии реальной колебательной системой с течением времени уменьшается. В простейшем, и вместе с тем наиболее часто встречающемся случае, сила сопротивления, вызывающая затухание, зависит от скорости колебательного движения, т. е. ее можно считать прямо пропорциональной скорости
где μ − постоянная, называемая коэффициентом сопротивления.
Знак «минус» обусловлен тем, что сила и скорость имеют противоположные направления. Тогда второй закон Ньютона для гармонических колебаний при наличии сил сопротивления имеет вид
Учитывая , что a= $$d^2xover dt^2$$ , а υ= $$dxover dt$$ и разделив на массу m , получим
Применив обозначения $$ = ω_0<^2>$$ , $$ <μover m>= 2β$$ и $$ = f_0$$ получим
дифференциальное уравнение затухающих колебаний . Отметим, что ω0 представляет собой ту частоту, с которой совершались бы свободные колебания системы в отсутствие сопротивления среды. Эта частота называется собственной частотой .
Для решения уравнения (5.6.4) сделаем подстановку
Проведем замену переменных
Подставим (5.6.5 и 5.6.6) в выражение (5.6.4)
Преобразуем , сократив на e -βt
Рассмотрим случай, когда сопротивление среды настолько мало, что ω0 2 -β 2 >0 есть величина положи мы можем ввести тельная, и обозначение ω0 2 -β 2 =ω 2 , после чего уравнение (5.6.8) примает вид
В случае большого сопротивления среды ω0 2 -β 2 , движение становится непериодическим.
Решение уравнения (5.6.8) можно записать в виде
Окончательно, подставляя последнее уравнение в выражение (5.6.5), получаем общее решение дифференциального уравнения затухающих колебаний (5.6.4)
В соответствии с видом полученной функции движение можно рассматривать как гармоническое колебание с частотой
и амплитудой, изменяющейся по закону
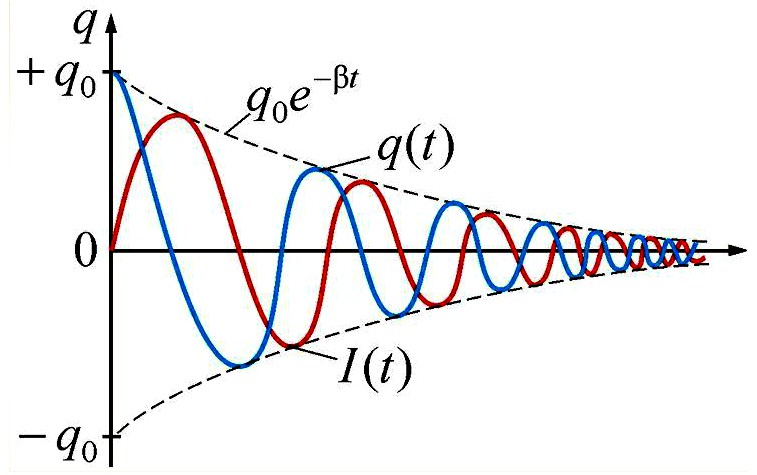
На рисунке показан график данной функции. Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки. Верхняя из пунктирных кривых дает график функции A(t) , причем величина A0 представляет собой амплитуду в начальный момент времени. Начальное смещение зависит от A0 и также от начальной фазы φ , т.е. x0=A0cosφ .
5.7. Коэффициент затухания и логарифмический декремент затухания.
Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно
и называется декрементом затухания .
Для характеристики системы обычно используется колебательной логарифмический декремент затухания , т.е. логарифм декремента затухания
Скорость затухания колебаний определяется величиной называем коэффициентом затухания $$β=<μover 2m>$$ .
Найдем время, называемое временем релаксации τ , за которое амплитуда уменьшается в e раз
т. е. коэффициент затухания обратен по величине промежутку времени, за который амплитуда колебаний уменьшается в e раз.
За время релаксации τ система успевает совершить $$N_e=<τover T>$$ колебаний
Следовательно, $$δ=<1over N_e>$$ логарифмический декремент затухания обратно пропорционален по величине числу колебаний, за которые амплитуда колебаний уменьшается в e раз.
Для характеристики колебательной системы используется величина
которая называется добротностью колебательной системы.
Величина Q , пропорциональная числу колебаний, совершаемых системой за время, в течение которого амплитуда колебаний уменьшается в e раз.
5.8. Вынужденные колебания.
До сих пор мы рассматривали свободные колебания, когда выведенная из положения равновесия система совершает колебания будучи предоставленной самой себе. Рассмотрим колебательную систему, которая подвергается действию внешней силы, изменяющейся по гармоническому закону F=F0cosωt . Колебания, возникающие под действием внешней периодически изменяющейся силы, называются вынужденными колебаниями . В этом случае уравнение второго закона Ньютона имеет вид
Учитывая , что a= $$d^2xover dt^2$$ , а υ= $$dxover dt$$ и разделив на массу m , получим
Применив обозначения $$ = ω_0<^2>$$ , $$ <μover m>= 2β$$ и $$ = f_0$$ получим
дифференциальное уравнение вынужденных колебаний.
Будем искать решение уравнения (5.8.3) в виде
предполагая, что результирующее колебание будет совершаться с частотой внешней вынуждающей силы.
Подставим (5.8.4) и (5.8.5) в уравнение (5.8.3)
Чтобы уравнение (69) обратилось в тождество необходимо, чтобы коэффициенты при cosωt и sinωt были равны нулю.
Из выражения (71) получаем
Возведем в квадрат уравнения (70) и сложим
Подставив полученные выражения (71) и (73) в выражение (64) получим уравнение вынужденных колебаний
5.9. Резонанс.
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой частоте амплитуда колебаний достигает максимального значения.
Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте, равной или близкой собственной частоте колебательной системы называется резонансом , а соответствующая частота − резонансной частотой.
Найдем резонансную частоту. Амплитуда вынужденных колебаний будет max, когда выражение $$(ω_0<^2>-ω^2)^2 + 4β^2ω^2$$ в уравнении $$A=-ω^2)^2 + 4β^2ω^2>>$$ (5.8.13) будет минимальным.
Продифференцируем это выражение по ω и приравняем к нулю
Полученное уравнение имеет три решения: ω=0 и ω=± $$sqrt <ω_0<^2>-2β^2>$$ . 2 . Первое решение соответствует максимуму знаменателя. Из остальных двух решений отрицательное не имеет физического смысла (частота не может быть отрицательной). Таким образом, резонансная циклическая частота
Подставив это значение в выражение для амплитуды (5.8.13), получим выражение для амплитуды при резонансе
Из последнего уравнения (5.9.3) следует, что при отсутствии сопротивления среды амплитуда при резонансе обращалась бы в бесконечность, а резонансная частота, согласно (5.9.2), при тех же условиях (при β=0 ), совпадала бы с собственной частотой колебаний системы ω0
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы показана графически на рис. 5.9.1. В соответствии с (5.9.2) и (5.9.3), чем меньше параметр β , тем выше и правее лежит максимум данной кривой. Изображенная на рис. 5.9.1 совокупность графиков функций (5.8.13), соответствующих различным значениям параметра β , называется резонансными кривыми .
При стремлении ω к нулю все кривые приходят к одному и тому же, отличному от нуля, предельному значению, равному f0ω0 2 . Это значение представляет собой смещение из положения равновесия, которое получает система под действием постоянной силы величины F0
При стремлении ω к бесконечности все кривые асимптотически стремятся к нулю, так как при большой частоте сила так быстро изменяет свое направление, что система не успевает заметно сместиться из положения равновесия.
Наконец, отметим, что чем меньше β , тем сильнее изменяется с частотой амплитуда вблизи резонанса, тем «острее» получается максимум. При малом затухании (т. е. β ) амплитуда при резонансе приближенно равна Apes≈f0/2βω0 . Разделим это выражение на смещение x0 из положения равновесия под действием постоянной силы F0 , равное x0=f0/ωp 2 . В результате получим
где δ = βТ – логарифмический декремент затухания (5.7.2); Q – добротность колебательной системы (5.7.6).
Таким образом, добротность Q показывает, во сколько раз амплитуда в момент резонанса превышает смещение системы из положения равновесия под действием постоянной силы той же величины, что и амплитуда вынуждающей силы. Следует отметить, что это справедливо лишь при небольшом затухании.
http://zaochnik.com/spravochnik/fizika/elektromagnitnye-kolebanija-volny/zatuhajuschie-kolebanija-v-konture/
http://physics.belstu.by/mechanics_lk/mechanics_lk8.html
Параллельный и последовательный колебательный контур
Что такое колебательный LC-контур? Принцип работы, формулы расчёта основных
параметров. Онлайн калькулятор резонансной
частоты колебательного контура,
добротности и коэффициента затухания в зависимости от величин индуктивности,
ёмкости и сопротивления потерь
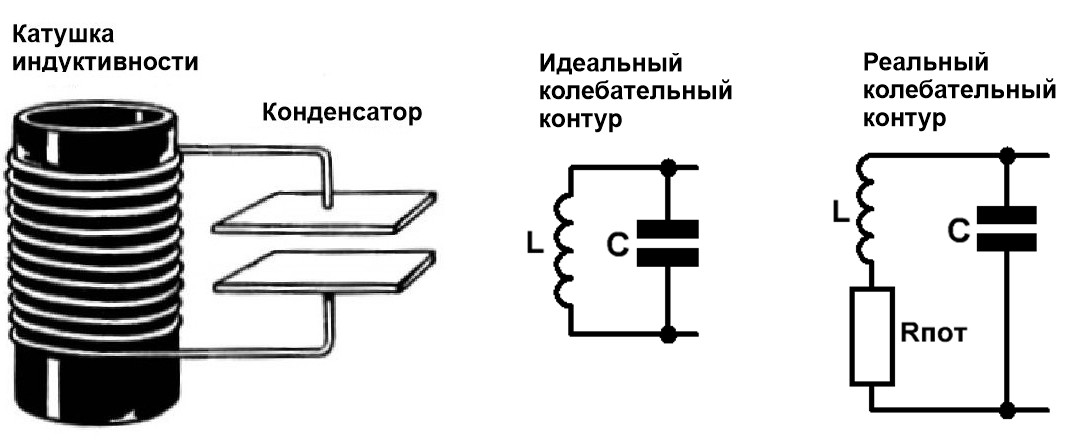
Колебательный контур – это пассивная электрическая цепь, состоящая из конденсатора и катушки индуктивности, в которой
возможно возбудить свободные электромагнитные колебания.
Если конденсатор и катушка соединены параллельно, то контур называется параллельным, при последовательном соединении элементов колебательный
контур называется последовательным.
Для начала рассмотрим параллельный колебательный контур, который в радиотехнике используется как основа частотно-избирательных цепей и встречается намного
чаще последовательного.
Рис.1 Параллельный колебательный контур, его изображение на схеме (идеальный
колебательный контур), реальный колебательный контур
При анализе цепи колебательного контура обычно используется реалистичная модель (Рис.1 справа), состоящая из идеальных пассивных элементов и активного
сопротивления потерь катушки – Rпот.
Сопротивление потерь катушки Rпот складывается из потерь в проводах, диэлектрике, сердечнике и экране (если он есть).
Поскольку потери в контурном конденсаторе на порядки меньше, чем потери в катушке, то его сопротивление потерь при расчётах обычно не учитывается.
Так, за счёт чего в колебательном контуре возникают свободные колебания? Для того чтобы ответить на этот вопрос, давайте соберём простейшую схему (Рис.2)
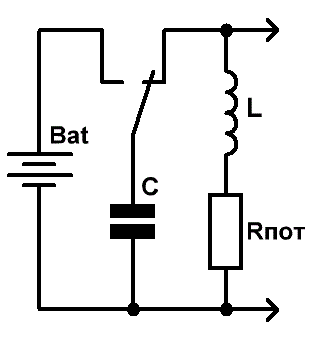
Рис.2 Колебательный процесс в параллельном колебательном контуре
Для возбуждения в контуре колебаний конденсатор следует предварительно зарядить, сообщая его обкладкам заряд
qmax от внешнего источника Bat напряжением
Umax.
После того как конденсатор будет заряжен, переводим переключатель в правое по схеме положение, отключая контур от источника, и наблюдаем возникшие в цепи затухающие
электромагнитные колебания, при которых происходит превращение энергии электрического поля в энергию магнитного поля и наоборот (Рис.2 справа).
Из-за потерь, возникающих в элементах контура, электромагнитные колебания в цепи всегда будут затухающими. Скорость их затухания зависит от величины этих потерь,
суммарное значение которых характеризуются параметром, называемым добротностью колебательного контура Q. Численно добротность равна числу
колебаний от момента возбуждения свободных колебаний до момента, когда их амплитуда уменьшится в
еπ = 23,14 раз. Для желающих поподробнее познакомиться с тем, что такое добротность и как её
измерить, имеет смысл посетить страницу – ссылка на страницу.
А мы тем временем рассмотрим последовательные фазы колебаний, происходящие в контуре после зарядки конденсатора.
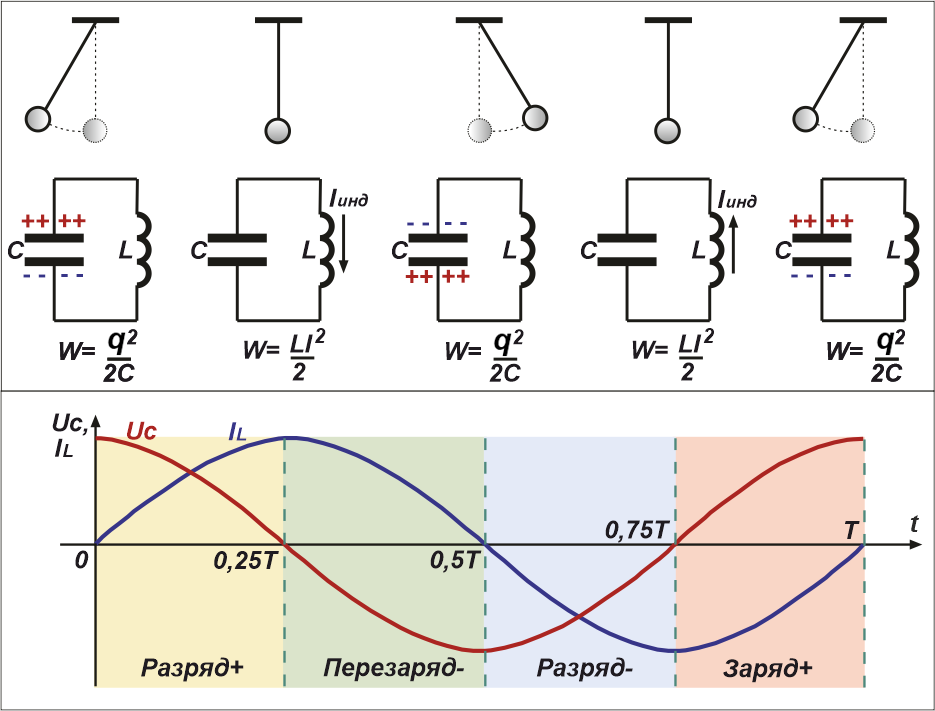
Рис.3 Фазы колебаний, происходящих в колебательном контуре за полный период
Электромагнитные колебания, а также описывающие их уравнения во многом подобны механическим колебаниям.
Опишем стадии колебательного процесса за полный период колебаний:
1. t = 0 – начало разрядки конденсатора (энергия электрического поля, запасённая в конденсаторе, равна
W = q2/2C ).
Через катушку начинает течь ток. При этом катушка оказывает сопротивление моментальному росту тока, поскольку в ней присутствует ЭДС
самоиндукции, препятствующая этому росту.
2. t = 0,25Т – конденсатор полностью разряжен.
Ток через катушку максимален, так как вся энергия из конденсатора перешла в энергию магнитного электрического поля катушки
W = L*I2/2.
Начиная с этого момента, эта энергия начинает опять перетекать в конденсатор, перезаряжая его потенциалом обратной полярности.
3. t = 0,5Т – конденсатор опять полностью заряжен, но потенциалом противоположной полярности. Ток через
катушку индуктивности равен нулю. Начинается фаза, описанная в п.1, но с током, текущем в обратном направлении.
4. t = 0,75Т – конденсатор вновь полностью разряжен, ток через катушку максимален и направлен
в противоположную (по отношению к п.2) сторону.
5. t = Т – всё начинается сначала, т. е. аналогично 1п.
А теперь – формулы, которые могут понадобиться при расчёте колебательного LC контура:
Период колебаний: T0 = 2π√LC ;
Частота: F0 = 1/T0 ;
Круговая (циклическая) частота: ω0 = 2π/T0 =
2πF0 ;
Максимальный заряд конденсатора: qmax = UmaxC ;
Максимальная сила тока через катушку: Imax = ωqmax .
Добротность колебательного контура:
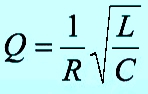
Мгновенные значения напряжения, силы тока и энергии можно рассчитать по формулам:
Заряд: q(t) = qmax cos(ωt) ;
Напряжение: U(t) = Umax cos(ωt) ;
Сила тока: I(t) = Imax sin(ωt) ;
Энергия: W(t) = I(t)2L/2 + q(t)2/(2C) .
Все приведённые формулы хороши для идеального колебательного контура, в котором нет потерь, а соответственно, и нет затухания колебаний. Для реальных же контуров
(с потерями) вводятся дополнительные параметры, характеризующие скорость затухания колебаний. Одними из таких параметров являются коэффициент затухания
β и логарифмический декремент колебаний λ.
Коэффициент затухания β – это величина, характеризующая скорость затухания колебаний и обратно
пропорциональная времени τ, по истечении которого амплитуда колебаний убывает в
е раз.
Для колебательного контура данная величина вычисляется по формуле:
β = Rпотерь /(2L).
Логарифмическим декрементом затухания λ называется величина, равная натуральному логарифму отношения
двух последовательных амплитуд, отстоящих друг от друга на период колебаний. Численно логарифмический декремент колебаний равен коэффициенту затухания,
умноженному на период колебаний:
λ = βT.
С учётом коэффициента затухания наши формулы приобретают следующий вид:
Заряд: q(t) = qmax cos(ωt) e(-βt) ;
Напряжение: U(t) = Umax cos(ωt) e(-βt) ;
Сила тока: I(t) = Imax sin(ωt) e(-βt) ;
Энергия: W(t) = I(t)2L/2 + q(t)2/(2C) ;
Период:
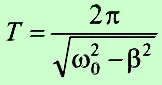
Круговая (циклическая) частота:
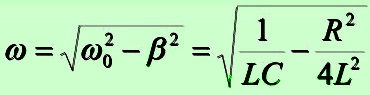
Добротность: Q = Lω/R .
При относительно высокой добротности цепи, то есть когда колебания затухают не слишком быстро и выполняется условие
β2 << ω02, круговая частота контура равна
ω ≈ ω0 ,
а формулы по расчёту резонансной частоты и добротности принимают привычный вид, приведённый выше на синем фоне.
Для проверки знаний, полученных в рамках данной статьи, приведём онлайн калькулятор для расчёта основных параметров колебательного контура.
РАСЧЁТ РЕЗОНАНСНОЙ ЧАСТОТЫ, ДОБРОТНОСТИ И КОЭФФИЦИЕНТА ЗАТУХАНИЯ КОНТУРА
Ёмкость конденсатора контура |
||
Индуктивность катушки контура L |
||
Сопротивление потерь Rпот |
||
Резонансная частота |
||
Добротность = кол-во колебаний |
||
Коэффициент затухания β (сек-1) |
Для последовательного колебательного контура резонансная частота (период и круговая частота) не зависит от сопротивления потерь, однако остальные приведённые
выше параметры описываются теми же формулами, что и для параллельного. При этом в составе частотно-избирательных цепей эти контуры ведут себя по-разному и
имеют значительно отличающиеся друг от друга передаточные характеристики. Какие это характеристики? – рассмотрим в рамках отдельной статьи.
А на следующей странице рассмотрим, как на добротность LC-контура влияют сопротивления нагрузки и источника сигнала.

(2.3.46)
.
Решением этого уравнения является выражение вида

Таким образом, заряд на обкладке конденсатора изменяется по гармоническому закону с собственной частотой контура ω0.
Для периода колебаний справедлива формула Томсона:
,

Продифференцируем (4.2.3) по времени и получим выражение для тока:
(2.3.49)
.
Напряжение на конденсаторе отличается от заряда на 1/С:
(2.3.50)
.
Таким образом, ток опережает по фазе напряжение на конденсаторе на π/2. На индуктивности, наоборот, напряжение опережает ток на π/2.
(2.3.51)
,
где 
Выражение (2.3.51) – это закон Ома для колебательного контура.
174
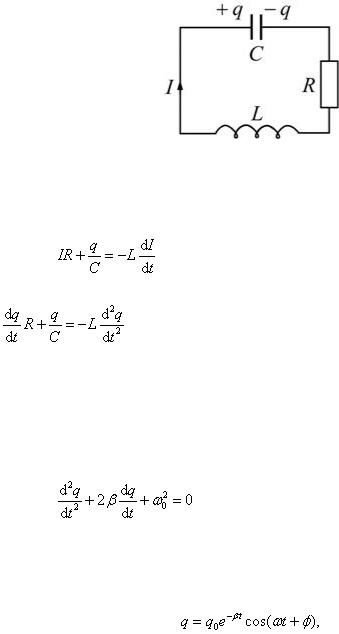
Всякий реальный контур обладает активным сопротивлением (рис. 2.3.20). Энергия, запасенная в контуре, постепенно расходуется в этом сопротивлении на нагревание, вследствие чего колебания затухают.
Рис. 2.3.20. Контур свободных затухающих колебаний
По второму закону Кирхгофа:
(2.3.52)
.
, или
Обозначим 
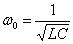
(2.3.53)
.
При 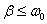

где 


175

Рис. 2.3.21
На рис. 2.3.21 показан вид затухающих колебаний заряда q и силы тока I. Если сравнить электрические затухающие колебания с механическими (рис. 2.3.14), то хорошо видны общие закономерности этих явлений: колебаниям q соответствует x – смещение маятника из положения равновесия, силе тока I – скорость υ.
Затухание принято характеризовать логарифмическим декрементом затухания χ:
(2.3.54)
,
где A – амплитуда I, U, q.
Найдём выражение χ для электрических колебаний. Т.к.


тогда

Поскольку R, L, ω определяются параметрами контура, следовательно χ является
характеристикой контура.
Если затухание невелико, т.е. 
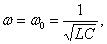
|
. |
(2.3.55) |
|
|
Колебательный контур часто характеризуют добротностью Q, которая определяется |
||
|
как величина, обратно пропорциональная χ: |
, а т.к. |
, где N – число |
176
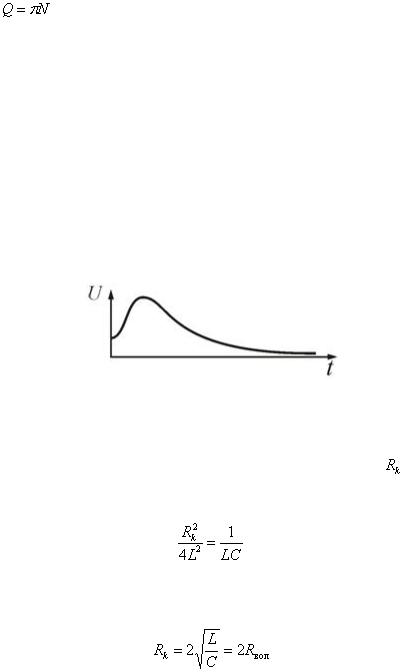
колебаний, то , т.е. добротность Q тем больше, чем больше колебаний успевает совершиться, прежде чем амплитуда уменьшится в е раз.
Добротность определяется и по-другому:

где W – энергия контура в данный момент, следующий за этим моментом.
(2.3.56)
W – убыль энергии за один период,
При 

Рис. 2.3.22
Сопротивление контура, при котором колебательный процесс переходит в
|
апериодический, называется критическим сопротивлением |
. Найдем это |
|
сопротивление из равенства: |
|
|
, |
|
|
отсюда |
|
|
, |
(2.3.57) |
где Rвол – волновое сопротивление, определяемое параметрами L и C.
177
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Рассмотрим две важные характеристики колебательных систем в механике и теории электричества и магнетизма: коэффициент затухания и логарифмический декремент затухания. Мы остановимся на так называемых затухающих колебаниях – таких колебаниях, амплитуда которых со временем уменьшается из-за потери энергии.
Чаще всего затухание происходит из-за трения — об воздух или поверхность, любую жидкую или газообразную среду, в которую помещено тело. Тело, проплывая в газе или жидкости или скользя по поверхности, передает этой среде внутреннюю энергию из за трения. Собственная суммарная кинетическая и потенциальная энергия при этом уменьшается. Соответственно уменьшается и скорость, а с ней — амплитуда.
Затухающие колебания можно поделить на свободные затухающие колебания и колебания, происходящие под действием внешних сил.
Как определить коэффициент затухания свободных затухающих механических колебаний
md2xdt2=−kx−rvmfrac{d^2x}{dt^2}=-kx-rv
mm — масса колеблющегося тела,
xx — его координата (смещение относительно точки равновесия x=0x=0),
−kx-kx — сила упругости, даваемая законом Гука для небольших смещений,
kk — коэффициент упругости,
−rv-rv — сила трения,
rr — коэффициент трения,
vv — скорость тела.
Это уравнение имеет решение:
x(t)=A0e−βtcos(ωt+φ)x(t)=A_0e^{-beta t}cos(omega t+varphi)
A0A_0 — амплитуда,
ωomega— циклическая частота,
φvarphi — начальная фаза,
βbeta — коэффициент затухания.
ω=ω02−β2omega=sqrt{omega_0^2-beta^2}
ω02=kmomega_0^2=frac{k}{m}
ω0omega_0 — собственная частота.
Коэффициент затухания βbeta – это величина, обратная времени, за которое амплитуда колебания уменьшилась в ee раз, где ee — основание натуральных логарифмов.
β=1NTbeta=frac{1}{NT}
NN — число колебаний после которых амплитуда уменьшилась в ee раз,
TT — период колебаний,
T=2πωT=frac{2pi}{omega}
Логарифмический декремент затухания свободных затухающих колебаний маятника
Маятник трется об воздух. И, казалось бы, как понять, какую он энергию отдает воздуху? Наверное, тут не обойтись без температуры, давления, плотности газообразной среды, и это долго, сложно, нудно… Может, и так. Но все это укладывается в коэффициент затухания ββ.
Определить логарифмический декремент затухания можно двумя способами — с помощью замеров амплитуды и с коэффициентом затухания. Для первого нужно лишь замерить две последовательные амплитуды. Тогда формула проста:
λ=lnA0e−βtA0e−β(t+T)lambda=lnfrac{A_0e^{-beta t}}{A_0e^{-beta (t+T)}}
Если же известен коэффициент затухания, амплитуда не нужна. Логарифмический декремент затухания будет равен его произведению на период колебаний:
λ=βTlambda=βT
Логарифмический декремент затухания электрического колебательного контура
Колебания в электрическом контуре возникают при отсутствии активного сопротивления в цепи, содержащей катушку индуктивности и конденсатор. Ток колеблется туда-сюда. Затухание этих колебаний удивительно похоже на затухание механических колебаний, потому, проведя несколько опытов, ученые пришли к выводу, что у электрического контура есть свой коэффициент затухания, и, соответственно, формула такая же, как для механических колебаний:
λ=βTlambda=βT
T=2πLCT=2πsqrt{LC}
LL — индуктивность катушки,
CC — емкость конденсатора.
Коэффициент затухания вынужденных механических колебаний
Конечно, в вынужденных колебаниях тоже существует затухание. Разница свободных и вынужденных колебаний в существовании добавочной силы, которая возвращает амплитуду к ее начальному значению, не давая маятнику остановиться, т.е. нивелирует работу силы трения.
Уравнение движения такой системы:
md2xdt2=−kx−rv+Fmfrac{d^2x}{dt^2}=-kx-rv+F.
Здесь все величины те же самые, что и в свободных колебаниях, но появляется внешняя сила FF:
F=mF0cos(ωt)F=mF_0cos(omega t).
F0F_0 имеет размерность силы, деленной на массу.
x=Asin(ωt+φ)x=Asin(omega t+varphi)
AA — амплитуда колебаний.
A=F0m(ω02−ω2)2+4β2ω2A=frac{F_0}{msqrt{{(omega_0^2-omega^2)^2}+4beta^2omega^2}{}}.
В случае затухающих вынужденных колебаний коэффициентом затухания снова является величина βbeta.
Тест по теме «Коэффициент и логарифмический декремент затухания»
Виталий Викторович Карабут
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Определение, характеристики затухающих колебаний
Определение 1
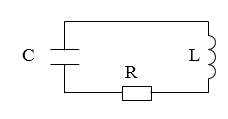
В реальном мире любые колебания в системе, где нет источника энергии, являются затухающими. Рассмотрим реальный контур, сопротивление которого отлично от нуля. Примером простейшей системы, которую рассматривают в таком случае может служить контур включают сопротивление $(R)$, конденсатор емкостью $C$, катушку индуктивности $L$, тогда такой контур имеет вид указанный на рис.1. Колебания в таком контуре являются затухающими.
Рисунок 1.
Причиной затухания колебаний в таком контуре является наличие сопротивления. Его существование ведет к тому, что в контуре происходят потери энергии на выделение джоулева тепла. В механике аналогом сопротивления являются силы трения.
Затухающие колебания характеризуют коэффициентом затухания ($beta $), равным:
Из выражения (1) видно, что $beta $ является характеристикой контура. Иногда для характеристики затухания используют логарифмический декремент затухания ($delta $), который равен:
где $aleft(tright)$- амплитуда какой — либо величины (заряда, силы тока и т.д.). $delta $ равен количеству колебаний ($N_e$) за время, в течение которого амплитуда уменьшается в e раз:
Для $RLC$ контура:
где $omega $ — частота.
Если затухание небольшое ($delta ll 1$), то полагают, что $beta ll {omega }_0$ (${omega }_0=sqrt{frac{1}{LC}}-собственнная частота$), тогда $omega approx {omega }_0$. В таком случае:
Рассматривая затухающие колебания, колебательный контур характеризуют его добротностью ($O$). Он равен:
Для слабого затухания добротность можно выразить как:
Также при слабом затухании электрических колебаний добротность можно выразить через отношение энергий:
где $W$ — энергия контура, $triangle W$- уменьшение энергии контура за одно колебание.
«Затухающие колебания в контуре и их уравнение» 👇
Уравнение затухающих колебаний
Обратимся вновь к контуру, который изображен на рис.1. Изменение заряда ($q$) на конденсаторе в таком контуре описывается дифференциальным уравнением вида:
Если сопротивление, которое входит в состав контура $R
[q(t)=A_0e^{left(-beta tright)}{sin left(omega t+{alpha }_0right)=A_0e^{left(-beta tright)}{cos left(omega t+{alpha ‘}_0right)=0left(10right) }, }]
где $omega =sqrt{frac{1}{LC}-frac{R^2}{4L^2}} cdot beta =frac{R}{2L}$. Амплитуда равна:
В том случае, если при $t=0$ заряд на конденсаторе равен $q_0$, тока в цепи нет, то для $A_0$ можно записать:
Начальная фаза колебаний (${alpha }_0$) равна:
При $R >2sqrt{frac{L}{C}}$ изменение заряда не является колебаниями, разряд конденсатора называют апериодическим.
Сопротивление, при котором колебания превращаются в апериодический разряд конденсатора называется критическим ($R_k$). Величина $R_k$ определяют условием:
График функции (10) изображают как на рис.2.
Рисунок 2.
Пример 1
Задание: Запишите закон убывания энергии, запасенной в контуре $(W(t))$, если $W(t=0)=W_0,$ колебания являются затухающими. Коэффициент затухания колебаний в контуре равен $beta $. Собственная частота ${omega }_0. $
Решение:
В качестве отправной точки для решения задачи используем уравнение изменения заряда на конденсаторе в $RLC$ -контуре в виде:
[qleft(tright)=q_0e^{left(-beta tright)}{cos left(omega t+{{alpha }’}_0right)=q_0e^{left(-beta tright)}cosleft(omega tright)left(1.1right) },]
в выражении (1.1) мы предположили, что при $t=0, {{alpha }’}_0=0$. Используя выражение:
[I=frac{dq}{dt}left(1.2right).]
Найдем $I(t)$, получим:
[I(t)=-{omega }_0q_0e^{left(-beta tright)}sinleft(omega t+alpha right)left(1.3right),]
где $tgalpha =frac{beta }{omega }.$
Следовательно, электрическая энергия контура ($W_q$) имеет вид:
[W_q=frac{q^2}{2C}=frac{{q_0}^2}{2C}e^{left(-2beta tright)}cos^2left(omega tright)=W_0e^{left(-2beta tright)}cos^2left(omega tright) left(1.4right).]
Магнитная энергия контура ($W_m$) равна:
[W_m=frac{L}{2}{omega_0}^2{q_0}^2e^{left(-2beta tright)}sin^2left(omega t+alpharight)=W_0e^{left(-2beta tright)}sin^2left(omega t+alpharight)left(1.5right).]
Полная энергия равна:
[W=W_q+W_m=W_0e^{left(-2beta tright)}left(cos^2left(omega tright)+sin^2left(omega t+alpha right)right)=W_0e^{left(-2beta tright)}left(1+frac{beta }{{omega }_0}{sin left(2omega t+alpha right) }right),]
где $sinalpha =frac{beta}{omega_0}.$
Ответ: $W(t)=W_0e^{left(-2beta tright)}left(1+frac{beta }{{omega }_0}{sin left(2omega t+alpha right) }right).$
Пример 2
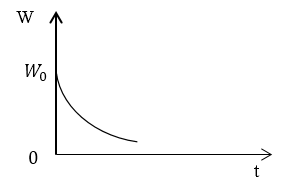
Задание: Используя результат Примера 1, запишите выражение для энергии, запасенной в контуре ($W(t)$), если колебания затухают в контуре очень медленно. Изобразите график убывания энергии запасенной в контуре.
Решение:
Если колебания в контуре затухают медленно, то это значит:
[frac{beta }{{omega }_0}ll 1 left(2.1right).]
Следовательно, выражение для энергии, запасенной в контуре:
[W(t)=W_0e^{left(-2beta tright)}left(1+frac{beta }{{omega }_0}{sin left(2omega t+alpha right) }right)(2.2)]
можно преобразовать к виду:
[Wleft(tright)=W_0e^{left(-2beta tright)}left(2.3right),]
так как выполняется условие (2.1), ${sin left(2omega t+alpha right) }le 1, $значит:
[{frac{beta }{{omega }_0}sin left(2omega t+alpha right)ll 1. }]
Рисунок 3.
Ответ: $Wleft(tright)=W_0e^{left(-2beta tright)}$. Энергия контура убывает по экспоненте.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме