Как найти коэффициенты функции кобба дугласа

Назначение производственной функции

Таким образом, это процесс создания товара и услуги, которая обладает определенной полезностью для покупателей. Любая деятельность по производству товаров и услуг является деятельностью направленной на удовлетворения потребностей отдельных индивидов или общества в целом.

Соотношение платежеспособного спроса на товары и предложения определяет цену товара или услуги. Количественной характеристикой предложения или объема производства и стоимости товаров является производственная функция. Производственный процесс оказывает прямое влияние на благосостояние общества в целом: чем выше степень удовлетворения индивидуальных и общественных потребностей и удельный вес среднего класса в общем численности населения, тем выше уровень национального благосостояния и развития.

Задача производственной функции состоит в том, чтобы объяснить рост благосостояния общества в процессе выпуска товаров и услуг.

Функция Кобба-Дугласа в системе производственных функций

Эти модели включают в себя такие показатели как объем производства в натуральном или стоимостном выражении, затраченные объемы ресурсов (факторов производства).

Различают две разновидности производственных функций:

• во-первых, однофакторные, устанавливающие зависимость объема производства от одного фактора. К этой разновидности относятся линейная, параболическая, степенная и показательная функции;
• во-вторых, двухфакторные устанавливающие зависимость объема производства от соотношения двух факторов. К этой разновидности относятся функции Кобба-Дугласа, Леонтьева, Солоу, Аллена.

«Производственная функция Кобба-Дугласа» 👇

Особенности производственной функции Кобба-Дугласа

В качестве двух основных факторов производства выступают капитал и труд. Определенная пропорциональность их сочетания создает условия для получения продукта. Назначение производственной функции Кобба-Дугласа состоит в том, чтобы отражать технологическое соотношение объема труда и капитала, необходимое для производства того или иного товара в необходимом количестве.

Данная производственная функция является двухфакторной. Впервые ее предложил шведский экономист Кнут Векселль, но статистическая проверка была выполнена в период с 1927 по 1947 год двумя учеными – Чарльзом Коббом и Полом Дугласом (в 1928 году вышла их работа под названием «Теория производства»). Именно фамилии этих ученых и дали название производственной функции.

Также термин «производственная функция Кобба-Дугласа» в узком смысле применяется для обозначения постоянной отдачи от масштаба.

Производственная функция, разработанная Коббом и Дугласом, представляет собой первую функцию агрегированного производства. Ее применение позволило осуществлять моделирование не только мелкомасштабных процессов, но и целых отраслей экономики. Статистическое подтверждение данной функции стало началом нового этапа макроэкономического развития, позволяющего дать оценку эффективности производства на уровне национального хозяйства.

Формула производственной функции Кобба-Дугласа

В формуле производственной функции Кобба-Дугласа отражается зависимость объем производства определенного товара от сочетания двух факторов производства – труда и капитала.
В общем виде формула имеет следующий вид:

$Q = A • L^α • K^β$, где:

• $Q$ – показатель объема производства, характеризующий реальную стоимость товаров и услуг, произведенных в определенный период времени;
• $A$ – общий показатель технологической продуктивности факторов. Этот показатель является наиболее трудным для определения и предусматривает с определенным уровнем погрешности возможность несовершенства оценки вклада труда и капитала, а также влияние иных факторов;
• $L$ – затраты труда в производство определенного объема продукции, выражающиеся в количестве человеко-часов, отработанных всеми работниками за указанный период времени;
• $K$ – затраты вложенного капитала в производство определенного объема продукции, выражающиеся в реальной стоимости оборудования и машин, используемых в производстве;
• $α$ – технологическая эластичность труда;
• $β$ – технологическая эластичность капитала.

Основу данной формулы составляют статистические расчеты, свидетельствующие о том, что для развитых стран характерны постоянные доли вкладов труда и капитала на протяжении длительного времени. Однако в настоящее время данное утверждение подвергается сомнению.

Эластичность факторов производства в производственной функции Кобба-Дугласа

Важнейшими показателя производственной функции Кобба-Дугласа являются показатели эластичности факторов производства, которые отражают влияние изменения их соотношения на физический объем производства при иных равных условиях.

Возможны три варианта значений, принимаемых коэффициентами эластичности в рамках формулы:

• $α + β = 1$, данное соотношение характеризует постоянную отдачу от масштаба, например, при росте затраченного труда и капитала на 100%, объем производства возрастет на те же 100%, то есть в два раза. производственная функция является линейно однородной;
• $α + β > 1$, данное соотношение характеризует возрастающую отдачу от масштаба, например, при росте затраченного труда и капитала на 100%, объем производства возрастет, допустим, на 120%, то есть более чем в два раза;
• $α + β$

Двухфакторная производственная функция Кобба-Дугласа

Теория
производственных функций была разработана
американскими учёными Д. Коббом
и П. Дугласом, опубликовавшими
в 1928 г. опубликовали работу «Теория
производства».

Эти
учёные предложили одну из наиболее
известных разновидностей производственных
функций, носящей название функции
Кобба-Дугласа.

Общий
вид функции Кобба-Дугласа:

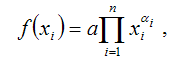
где
а – числовой параметр производственной
функции;

xi
– i-тый аргумент или i-ый фактор
производственной функции;

ai
– показатель степени i-го аргумента.

Наиболее
часто применяется двухфакторная форма
функции Кобба-Дугласа f(K,L):

Q=A*Ka*Lβ,

где
Q – объём выпущенной продукции (в
стоимостном или натуральном выражении);

K
– объём основного капитала или основных
фондов;

L
– объём трудовых ресурсов или трудовых
затрат (измеряемое количеством рабочих
или количеством человеко-дней).

A,a,β
– неизвестные числовые параметры
производственной функции, которые
подчиняются условиям:

1)
0≤а≤1;

2)
0≤β≤1;

3)
A›0;

4)
a+β=1.

На
основании четвёртного условия a+β=1,
функция Кобба-Дугласа может быть
представлена в виде:

Q=A*Ka*L1-а.

Данная
производственная функция позволяет
объяснить уровень совокупного выпуска
Q количествами затраченного капитала
K и труда L основных факторов
производства.

На
двухфакторную функцию Кобба-Дугласа
накладываются определённые ограничения,
которые необходимо учитывать при
спецификации модели:

1)

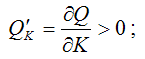
2)

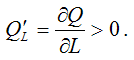
3)

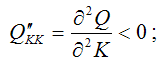
4)

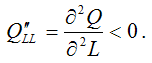
5)

6)

Первое
и второе ограничения означают, что объём
выпускаемой продукции увеличивается
при постоянном значении одного из
факторов и росте другого фактора. Однако
если один из факторов производства
фиксирован, а другой фактор возрастает,
то каждая дополнительная (предельная)
единица возрастающего фактора менее
полезна (с точки зрения прироста выпуска
продукции), чем предыдущая единица.

Третье
и четвёртное ограничения означают, что
при фиксированном значении одного из
факторов последовательное увеличение
другого фактора будет приводить к
сокращению прироста значения Q.

Пятое
и шестое ограничения означают, что
каждый из факторов производства необходим
в том смысле, что если один из факторов
равен нулю (K=0 или L=0), то и объём
производства также равен нулю Q=0.

51. Показатели двухфакторной производственной функции Кобба-Дугласа

Двухфакторную
производственную функцию Кобба-Дугласа
f(K,L) можно представить в виде:

Q=A*Ka*Lβ,

где
Q – объём выпущенной продукции (в
стоимостном или натуральном выражении);

K
– объём основного капитала или основных
фондов;

L
– объём трудовых ресурсов или трудовых
затрат (измеряемое количеством рабочих
или количеством человеко-дней).

A,
a, β – неизвестные числовые параметры
производственной функции, которые
подчиняются условиям:

1)
0≤а≤1;

2)
0≤β≤1;

3)
A›0;

4)
a+β=1.

Данная
производственная функция характеризуется
следующими показателями:

1)
частный коэффициент эластичности
производственной функции Кобба-Дугласа
по факторной переменной капитала K
рассчитывается по формуле:

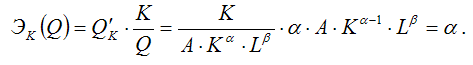
Таким
образом, ЭК(у)=а, т. е. частный
коэффициент эластичности функции
Кобба-Дугласа равен числовому параметру
а, и, следовательно, является
независимым от переменных К и L;

2)
частный коэффициент эластичности
производственной функции Кобба-Дугласа
по факторной переменной затрат труда
L рассчитывается по формуле:

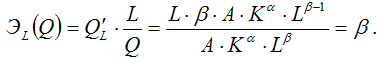
Таким
образом, ЭL(у)=β, т. е. частный коэффициент
эластичности функции Кобба-Дугласа
равен числовому параметру β, и,
следовательно, является независимым
от переменных К и L;

3)
коэффициент средней производительности
труда производственной функции
Кобба-Дугласа:

4)
коэффициент средней фондоотдачи
производственной функции Кобба-Дугласа:

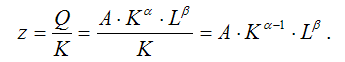
5)
коэффициент предельной производительности
труда производственной функции
Кобба-Дугласа:

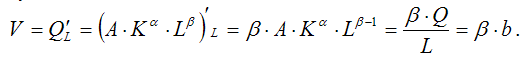
Данный
показатель характеризует величину
эффекта от каждой дополнительной единицы
затраченного труда. Он пропорционален
показателю средней производительности
труда, но всегда меньше его величины,
т. к. 0≤β≤1;

6)
коэффициент предельной фондоотдачи
производственной функции Кобба-Дугласа:

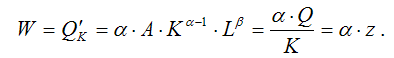
Данный
показатель характеризует величину
эффекта от каждой дополнительной единицы
основных фондов, использованной в
производстве. Он пропорционален
показателю средней производительности,
но всегда меньше его величины, т. к.
0≤а≤1;

7)
коэффициент предельной нормы технической
замены факторных переменных (замены
труда капиталом) производственной
функции Кобба-Дугласа:

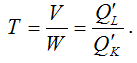
Данный
показатель характеризует, на сколько
единиц можно уменьшить объём используемого
капитала при увеличении объёма трудовых
затрат на единицу и фиксированном объёме
выпуска продукции.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

From Wikipedia, the free encyclopedia

In economics and econometrics, the Cobb–Douglas production function is a particular functional form of the production function, widely used to represent the technological relationship between the amounts of two or more inputs (particularly physical capital and labor) and the amount of output that can be produced by those inputs. The Cobb–Douglas form is developed and tested against statistical evidence by Charles Cobb and Paul Douglas between 1927 and 1947;^[1] according to Douglas, the functional form itself was developed earlier by Philip Wicksteed.^[2]

Formulation[edit]

In its most standard form for production of a single good with two factors, the function is

where:

• Y = total production (the real value of all goods produced in a year or 365.25 days)
• L = labour input (person-hours worked in a year or 365.25 days)
• K = capital input (a measure of all machinery, equipment, and buildings; the value of capital input divided by the price of capital)^{[clarification needed]}
• A = total factor productivity
• α and β are the output elasticities of capital and labor, respectively. These values are constants determined by available technology.

Output elasticity measures the responsiveness of output to a change in levels of either labor or capital used in production, ceteris paribus. For example, if α = 0.45, a 1% increase in capital usage would lead to approximately a .45% increase in output.

Sometimes the term has a more restricted meaning, requiring that the function display constant returns to scale, meaning that doubling the usage of capital K and labor L will also double output Y. This holds if

α + β = 1,

If

α + β < 1,

returns to scale are decreasing, means that a percentage increase in capital K and labor L will produce a smaller percentage increase in output Y,^[3]

and if

α + β > 1,

returns to scale are increasing, means that a percentage increase in capital K and labor L will produce a larger percentage increase in output Y.^[3] Assuming perfect competition and α + β = 1, α and β can be shown to be capital’s and labor’s shares of output.

In its generalized form, the Cobb–Douglas function models more than two goods. The Cobb–Douglas function may be written as^[4]

where

• A is an efficiency parameter
• n is the total number of input variables (goods)
• x₁, …, x_n are the (non-negative) quantities of good consumed, produced, etc.
• is an elasticity parameter for good i

History[edit]

Paul Douglas explained that his first formulation of the Cobb–Douglas production function was developed in 1927; when seeking a functional form to relate estimates he had calculated for workers and capital, he spoke with mathematician and colleague Charles Cobb, who suggested a function of the form Y = AL^βK^1−β, previously used by Knut Wicksell, Philip Wicksteed, and Léon Walras, although Douglas only acknowledges Wicksteed and Walras for their contributions.^[5] Not long after Knut Wicksell’s death in 1926, Paul Douglas and Charles Cobb implemented the Cobb-Douglas function in their work covering the subject manner of producer theory for the first time.^[6] Estimating this using least squares, he obtained a result for the exponent of labour of 0.75—which was subsequently confirmed by the National Bureau of Economic Research to be 0.741. Later work in the 1940s prompted them to allow for the exponents on K and L to vary, resulting in estimates that subsequently proved to be very close to improved measure of productivity developed at that time.^[7]

A major criticism at the time was that estimates of the production function, although seemingly accurate, were based on such sparse data that it was hard to give them much credibility. Douglas remarked «I must admit I was discouraged by this criticism and thought of giving up the effort, but there was something which told me I should hold on.»^[7] The breakthrough came in using US census data, which was cross-sectional and provided a large number of observations. Douglas presented the results of these findings, along with those for other countries, at his 1947 address as president of the American Economic Association. Shortly afterwards, Douglas went into politics and was stricken by ill health—resulting in little further development on his side. However, two decades later, his production function was widely used, being adopted by economists such as Paul Samuelson and Robert Solow.^[7] The Cobb–Douglas production function is especially notable for being the first time an aggregate or economy-wide production function had been developed, estimated, and then presented to the profession for analysis; it marked a landmark change in how economists approached macroeconomics from a microeconomics perspective.^[8]

Criticisms[edit]

The function has been criticised for its lack of foundation. Cobb and Douglas were influenced by statistical evidence that appeared to show that labor and capital shares of total output were constant over time in developed countries; they explained this by statistical fitting least-squares regression of their production function. There is now doubt over whether constancy over time exists.^{[citation needed]}. The production function contains a principal assumption that may not always provide the most accurate representation of a country’s productive capabilities and supply-side efficiencies. This assumption is a “constant share of labor in output”, which may not be effective when applied to cases of countries whose labor markets are growing at significant rates.^[9] Another issue within the fundamental composition the Cobb Douglas production function is the presence of simultaneous equation bias. When competition is presumed the simultaneous equation bias has impact on all function types involving firm decisions – including the Cobb Douglas function. In some cases this simultaneous equation bias doesn’t appear. However, it is apparent when least squares asymptotic approximations are used.^[10]

The Cobb–Douglas production function was not developed on the basis of any knowledge of engineering, technology, or management of the production process^{[citation needed]}. This rationale may be true given the definition of the Capital term. Labor hours and Capital need a better definition. If capital is defined as a building, labor is already included in the development of that building. A building is composed of commodities, labor and risks and general conditions. It was instead developed because it had attractive mathematical characteristics^{[citation needed]}, such as diminishing marginal returns to either factor of production and the property that the optimal expenditure shares on any given input of a firm operating a Cobb–Douglas technology are constant. Initially, there were no utility foundations for it. In the modern era, some economists try to build models up from individual agents acting, rather than imposing a functional form on an entire economy^{[citation needed]}. The Cobb–Douglas production function, if properly defined, can be applied at a micro-economic level, up to a macro- economic level.

However, many modern authors^[who?] have developed models which give microeconomically based Cobb–Douglas production functions, including many New Keynesian models.^[11] It is nevertheless a mathematical mistake to assume that just because the Cobb–Douglas function applies at the microeconomic level, it also always applies at the macroeconomic level. Similarly, it is not necessarily the case that a macro Cobb–Douglas applies at the disaggregated level. An early microfoundation of the aggregate Cobb–Douglas technology based on linear activities is derived in Houthakker (1955).^[12] The Cobb–Douglas production function is inconsistent with modern empirical estimates of the elasticity of substitution between capital and labor, which suggest that capital and labor are gross complements. A 2021 meta-analysis of 3186 estimates concludes that «the weight of evidence accumulated in the empirical literature emphatically rejects the Cobb-Douglas specification.»^[13]

Cobb–Douglas utilities[edit]

The Cobb–Douglas function is often used as a utility function.^[14][4] Utility is a function of the quantities of the goods consumed:

Utility functions represent ordinal preferences and do not have natural units, unlike production functions. As the result, a monotonic transformation of a utility function represents the same preferences. Unlike with a Cobb–Douglas production function, where the sum of the exponents determines the degree of economies of scale, the sum can be normalized to one for a utility function because normalization is a monotonic transformation of the original utility function. Thus, let us define and , so , and write the utility function as:

The consumer maximizes utility subject to the budget constraint that the cost of the goods is less than her wealth . Letting denote the goods’ prices, she solves:

It turns out that the solution for Cobb-Douglas demand is

Since , the consumer spends fraction of her wealth on good j. Note that this is the solution for either or since the same preferences generate the same demand.

The indirect utility function can be calculated by substituting the demands into the utility function. Define the constant ) and we get:

which is a special case of the Gorman polar form. The expenditure function is the inverse of the indirect utility function:^[15]: 112

Various representations of the production function[edit]

The Cobb–Douglas function form can be estimated as a linear relationship using the following expression:

where

The model can also be written as

As noted, the common Cobb–Douglas function used in macroeconomic modeling is

where K is capital and L is labor. When the model exponents sum to one, the production function is first-order homogeneous, which implies constant returns to scale—that is, if all inputs are scaled by a common factor greater than zero, output will be scaled by the same factor.

Relationship to the CES production function[edit]

The constant elasticity of substitution (CES) production function (in the two-factor case) is

in which the limiting case γ = 0 corresponds to a Cobb–Douglas function, with constant returns to scale.^[16]

To see this, the log of the CES function,

can be taken to the limit by applying l’Hôpital’s rule:

Therefore, .

Translog production function[edit]

The translog production function is an approximation of the CES function by a second-order Taylor polynomial in the variable about , i.e. the Cobb–Douglas case.^[17][18] The name translog stands for ‘transcendental logarithmic’. It is often used in econometrics for the fact that it is linear in the parameters, which means ordinary least squares could be used if inputs could be assumed exogenous.

In the two-factor case above the translog production function is

where , , , , and are defined appropriately. In the three factor case, the translog production function is:

where = total factor productivity, = labor, = capital, = materials and supplies, and = output.

See also[edit]

• Leontief production function
• Production–possibility frontier
• Production theory

References[edit]

Further reading[edit]

• Renshaw, Geoff (2005). Maths for Economics. New York: Oxford University Press. pp. 516–526. ISBN 0-19-926746-4.

External links[edit]

• Anatomy of Cobb-Douglas Type Production Functions in 3D
• Analysis of the Cobb-Douglas as a utility function
• Closed Form Solution for a firm with an N-input production function