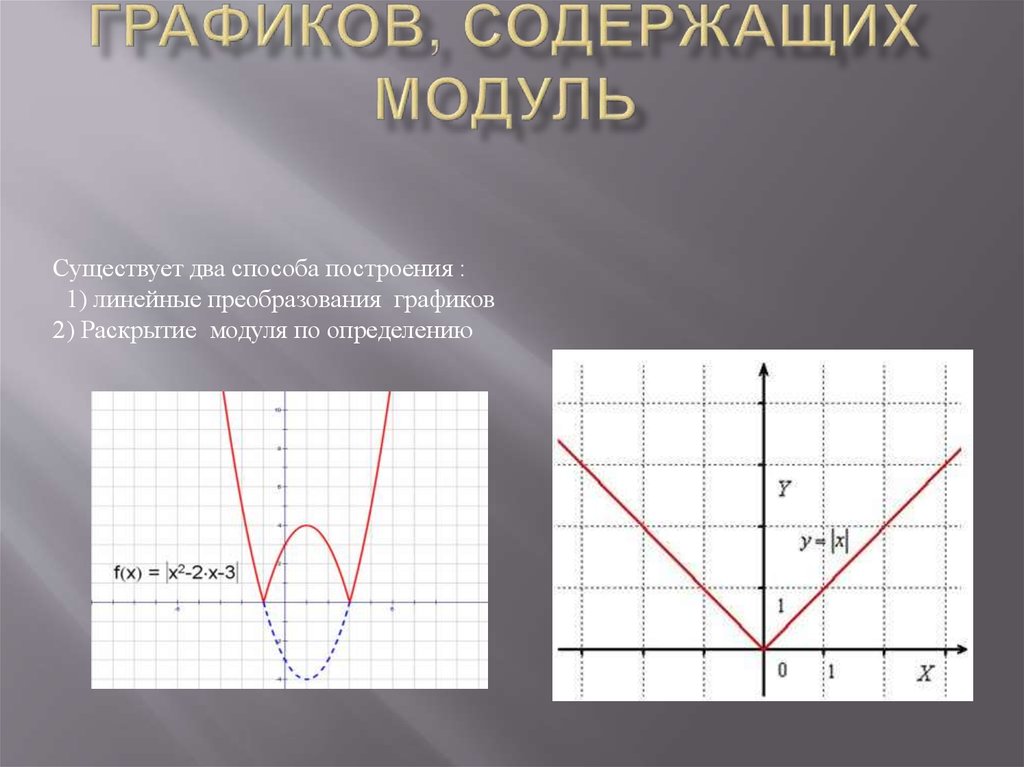
Описание презентации по отдельным слайдам:
-
1 слайд
ГРАФИК ЛИНЕЙНОЙ ФУНКЦИИ С МОДУЛЕМ
-
2 слайд
МОДУЛЬ
Модуль (лат. modulus )— «маленькая мера».
Абсолютной величиной (модулем) действительного числа называется само число , если оно неотрицательное, и число противоположное , если отрицательное. -
3 слайд
Линейной функцией называется функция вида
y = kx+ b, где k – угловой коэффициент (число), b – число, x – независимая переменная.
График линейной функции – есть прямая.
ОПРЕДЕЛЕНИЕ И СВОЙСТВА ЛИНЕЙНОЙ ФУНКЦИИ
Если k = 0, получим постоянную функцию y = b, график которой есть прямая, параллельная оси Ox, проходящая через точку с координатами
(0; b);2) Если b = 0, то получим функцию y = kx, которая есть прямая пропорциональность.
-
4 слайд
Построение графика линейной функции под знаком модуля
1) Построение графика функции у = |х| -
5 слайд
Построение графика линейной функции под знаком модуля
2) Построения графика функции y=|kx+b| -
6 слайд
Построение графика линейной функции под знаком модуля
3) Построения графика функции y=k|x|+b. -
7 слайд
Построение графика линейной функции под знаком модуля
4)Графики кусочно-линейных функций -
8 слайд
Линейная функция под знаком модуля в задачах ОГЭ
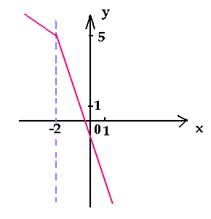
Постройте график функции и найдите все значения k, при которых прямая у = m имеет с графиком данной функции ровно одну общую точку.
Точки x=1 и x= -1 — разбивают числовую ось на 3 промежутка.
Раскрывая модули, получаем,
x ≤ — 1
y = 2;
y = — 2х
х ≥ 1
y= — 2
4) Находим значения m при которых прямая у = m имеет с графиком одну точку пересечения. Это будет промежуток (-2;2)
Ответ:
3) Изображаем график на координатной плоскости
Определение модуля
Алгебрагическое определение: | x |
=
Геометрическое определение: модулем
числа называется расстояние от точки,
изображающей это число, до начала отсчета.
Понятие модуля впервые вводится в 6 классе, в 7
классе рассматривается линейная функция и ее
график и уже можно показывать построение
несложных графиков функций, содержащих модуль.
Далее, по мере изучения различных функций, их
свойств, каждую такую тему можно заканчивать
рассмотрением более сложных графиков, в том
числе с модулем. В этой статье рассматриваются
основные приемы построения графиков таких
функций.
I. На алгебрагическом определении основан метод
«раскрытия модуля на промежутках».
Например: | x + 2 | = | x + 2 | =
метод можно применять при построении графиков
функций, содержащих один или более модулей.
Например, построим график функции у = | x + 2 | –
2x + 1 , предварительно упростив ее.
у = у
=
Если модулей несколько, то каждый из них
раскрываем на промежутках относительно точек,
обращающих каждый из них в нуль. Например,
построим график функции у = | 3 – x | – x
+ | x + 2 | + 1.
1. Если х < – 2, то у = 3 – х – х
– (х + 2) + 1, у = – 3х + 2.
< х < 3, то у = 3 – х – х + х
+ 2 + 1, у = – х + 6.
3. Если х > 3, то у = – (3 – х) – х
+ х + 2 + 1, у = х.
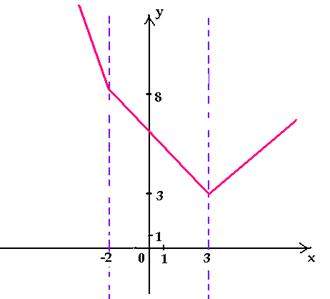
записываем как кусочно-заданную:
у =
Подобно тому, как числовая прямая точками – 2 и 3
разбивается на промежутки, координатная
плоскость прямыми х = – 2 и х = 3
разбивается на части («полосы»), в каждой из
которых строим свой график. Заметим, что данная
функция непрерывна, поэтому на «границах» части
графика должны соединяться.
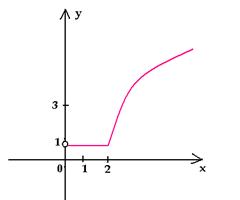
метод можно применять к функциям разных видов.
Например, построим график функции у = | log2
x – 1 | – log0,5 x.
Заметим, что х > 0.
1. Пусть log2x – 1 > 0, log2x >
1, x > 2, тогда у = log2 x – 1 +
log2 x; y = 2 log2 x – 1.
2. Пусть log2 x – 1 < 0, 0 < x < 2,
тогда у = – log2 x + 1 + log2 x; y
= 1.
Запишем функцию как кусочно-заданную:
у =
III. Рассмотрим некоторые частные случаи
функций, содержащих модуль.
1) у = | f(x) |.
По определению модуля имеем: | f(x) | =
Таким образом , для того, чтобы построить график
такой функции, необходимо взять часть графика,
лежащую не ниже оси абсцисс, а часть графика,
лежащую ниже этой оси отобразить относительно
нее в верхнюю полуплоскость. (Заметим, что «–»,
стоящий перед функцией означает симметричное
отображение графика относительно оси абсцисс).
Например, построим график функции у = | x2
– 2х – 3 |.
Построим сначала график функции у = х2
– 2х – 3. Графиком этой функции является
парабола, ветви которой направлены вверх.
Координаты ее вершины: х = 1, у = – 4. Точки
пересечения параболы с осями координат: (0; – 3); (–
1; 0); (3; 0). Далее выполняем отображение части
графика, лежащей в нижней полуплоскости,
относительно оси абсцисс.
2) у = f(| x |). Используем определение модуля: f(|
x |) =
Чтобы построить график такой функции строим
график функции у = f(x) и берем ту его
часть, где х > 0 (в правой полуплоскости).
Затем эту часть симметрично отображаем в левую
полуплоскость, где х < 0. (Заметим, что
построение графика функции f(– x) и
состоит в отображении части графика, лежащей в
правой полуплоскости в левую относительно оси
ординат).
Например, построим график функции у = х2
– 2| х | – 3. Сначала строим график функции у
= х2 – 2х – 3, далее выполняем
указанные преобразования.
3) Построим график функции y = | f(| x
|)|, например, y = | x2 – 2| х | – 3 |,
выполним последовательно преобразования,
рассмотренные в пунктах 2 и 1.
4. Рассмотрим зависимость | y | = f(x).
Ее нельзя назвать функцией, так как не
выполняется условие: каждому значению х должно
соответствовать единственное значение у.
Рассмотрим построение графика такой
зависимости (можно говорить «графика
уравнения»). Используем определение модуля: у
= f(x), если у > 0, – у = f(x),
y = – f(x), если у < 0
Получаем, чтобы построить такой график, сначала
строим график функции у = f(x) и
берем ту его часть, которая лежит в верхней
полуплоскости, где у > 0; чтобы
построить график в нижней полуплоскости (где у
< 0), нужно построенную часть отобразить
симметрично относительно оси абсцисс (знак «–»
перед функцией и означает такое отображение)
Например, построим график уравнения | y | = x2
– 2х – 3
Заметим, что графики, не относящиеся к
рассмотренным частным случаям, следует строить «
раскрывая модули на промежутках».
| x |
1 |
0 |
– 1 |
|
y |
0 |
|
|
IV. Приведем некоторые примеры
1. Построим график уравнения | y | = arccos| x
|.
2. Графическим способом можно решать и
неравенства с двумя переменными. Например,
решением неравенства | y | < arccos| x |
являются координаты точек закрашенной части
плоскости, включая границы.
Решим еще одно задание, предлагавшееся на ЕГЭ:
найти все целочисленные решения неравенства | y
| < | | x – 2 | – 3 | (х0; у0),
для которых х0 = у0. Построим
сначала график уравнения | y | = | | x – 2 | –
3 |. Решением данного неравенства будут являться
координаты точек закрашенной части плоскости,
включая границы.
Пары чисел (х0; у0),
являющиеся решениями неравенства, для которых y0
= x0, являются координатами точек,
лежащих на прямой у = х. Выберем точки с
целыми координатами: (0; – 1); (1; 0); (2; 1); (3; 2), они и
будут являться решениями данной задачи.
3. Определить, сколько корней имеет уравнение | 3
– x | + log3| x | = 2 – x.
Запишем уравнение в виде | 3 – x | + x = log3|
x | + 2. В одной системе координат построим
графики функций y = | 3 – x | = x (1) и y
= log3| x | = 2 (2). Функцию (1) запишем как
кусочно-заданную, раскрывая модуль на
промежутках:
y =
График функции (2) построим, выполняя
отображение графика y = log3x + 2
относительно оси ординат ( один из рассмотренных
частных случаев ).
Графики имеют две общие точки, следовательно,
данное уравнение имеет два корня.
V. Для повторения материала, его закрепления
предлагаем выполнить следующие задания.
1. Постройте графики функций и уравнений: y =
| y | =
; y = | | 2 – x
| – 4 |; y = | x2 – 4 | x | + 3 |; y = + 1.
2. Решите графически уравнения c одной и двумя
переменными: | 3 – x | – 3 = 2| x | – x2;
| y | = 2| x | – x2; = | x – 2,5 | –1,5.
3. Решите графически неравенства с двумя
переменными: | y | > x24x + 3;
| x | + | y | < 3.
4. Решите графически систему уравнений:
5. Найдите все значения а, при каждом из которых
уравнение | x + a | + | | x – 3 | – 4 | = 1
имеет ровно два корня.
На этой странице вы узнаете
- Как перевернуть график модуля?
- Одной ногой тут, другой там: к какому промежутку относить граничные точки?
- Может ли решением квадратного неравенства быть любое число, если дискриминант меньше 0?
Модуль числа — это великая математическая мудрость, которая показывает дружбу и соперничество противоположных знаков: минуса и плюса. О том, что держит число в рамках, узнаем в статье.
Модуль
Мы легко можем найти расстояние от точки до точки, достаточно просто измерить его линейкой. Но можно ли найти расстояние от 0 до любого числа?
Представим, что наш дом находится посередине между школой и магазином. И до школы, и до магазина 500 метров, но они стоят по разные стороны от дома.
Расположим их на координатной прямой. Поскольку и школа, и магазин располагаются на одинаковом расстоянии, то от дома до них мы будем идти 500 метров. Но на координатной прямой до школы мы пройдем −500 метров, поскольку движемся против направления оси, а до магазина 500 метров.

Будет ли являться полученный результат противоречием? Нет, поскольку когда мы ищем расстояние, нам неважно направление движения и знак. В математике существует специальное определение — это модуль, или абсолютная величина.
Модуль — расстояние от любой точки на координатной прямой до начала координат.
Поскольку на координатной прямой мы можем отложить расстояние в две стороны, то такое расстояние можно найти и с отрицательными точками, и с положительными. Расстояние измеряет длину отрезка, то есть оно всегда будет положительно.
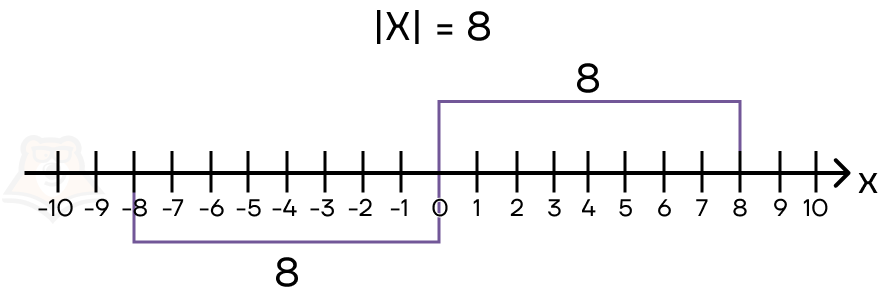
Можно сказать, что от любого числа модуль берет только цифры, а на знаки не обращает внимания. Например, |−8| = 8 и |8| = 8.
Может возникнуть вопрос: куда исчезает минус? Чтобы избавиться от минуса, достаточно умножить число на −1: (-8) * (-1) = 8. Значит, модуль просто умножает число на -1.
Отсюда получается, что модулем числа а называют выражение:

Возьмем два случая: a = 8 и a = -8. Для первого получаем |8| = 8, а для второго |-8| = -(-8) = 8, то есть определение выполняется.
Можно ли взять модуль функции? Да. Модулем произвольной функции называют выражение:
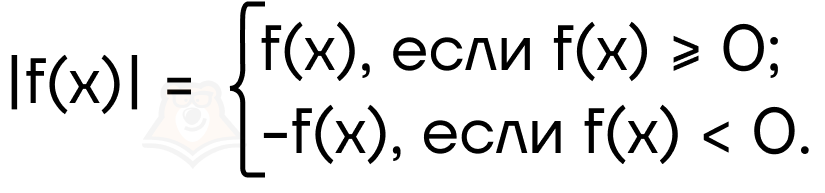
Свойства модуля
Модуль, как и все понятия в математике, обладает своими свойствами.
Свойство 1. |a| >= 0.
Как мы уже говорили, модуль всегда будет положительным числом, поскольку он не обращает внимания на знак числа.

Свойство 2. |a| = |-a|.
Это свойство также подтверждает рассуждения выше. Модули противоположных чисел, то есть чисел с разными знаками, равны.
Свойство 3. |a| >= a.
Если число а будет положительным, например, 5, то неравенство |5| >= 5 (rightarrow) 5 >= 5 выполняется, поскольку знак неравенства нестрогий.
Если число а будет отрицательным, например, -5, то неравенство |-5| >= -5 (rightarrow) 5 >= -5 выполняется, поскольку положительное число всегда больше отрицательного.
Свойство 4. |a * b| = |a| * |b|.
Пусть a = 5, b = -2, тогда |5 * (-2) | = |-10| = 10, и |5| * |-2| = 5 * 2 = 10, то есть выражения равны между собой.
Свойство 5. (|frac{a}{b}| = frac{|a|}{|b|}).
Рассуждения такие же, как и в предыдущем свойстве. Пусть a = 10, b = -5, тогда (|frac{10}{(-5)}| = |-2| = 2 и frac{|10|}{|-5|} = frac{10}{5} = 2).
Свойство 6. |a + b| <= |a| + |b|.
Почему появилось неравенство, а не уравнение, как в предыдущих двух свойствах? Разберем два примера.
Пусть a = 1, b = 2, тогда |1 + 2| = |3| = 3 и |1| + |2| = 1 + 2 = 3 — неравенство выполняется, поскольку знак нестрогий.
Но если a = -1, b = 2, тогда |-1 +2| = |1| = 1 и |-1| + |2| = 1 + 2 = 3, откуда получаем 1 < 3.
Свойство 7. (sqrt{a^2} = |a|).
Докажем это свойство. Пусть (sqrt{a^2} = x), тогда x0, поскольку квадратный «Корень» не может быть отрицательным. Возведем полученное уравнение в квадрат: a2 = x2
a2 — x2 = 0
(a — x)(a + x) = 0
Из уравнения x = a, из-за ограничений на x получаем a >= 0.
И x = -a, из-за ограничений на x получаем a < 0.
То есть получается выражение модуля.
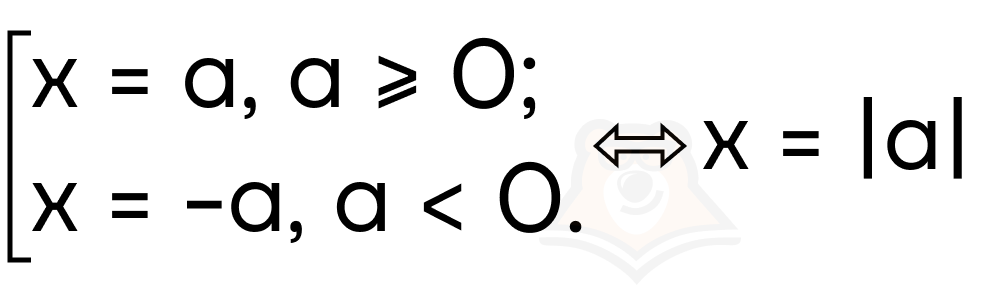
Свойство 8. |a|2 = a2.
Поскольку и модуль, и квадрат числа дают положительный результат, модуль в квадрате можно заменить просто квадратом числа.
График модуля
Как изобразить функцию с модулем? Для начала разберемся, что делает модуль с графиком функции.
Рассмотрим функцию y = x — это прямая. При этом у может быть и положительным, и отрицательным.
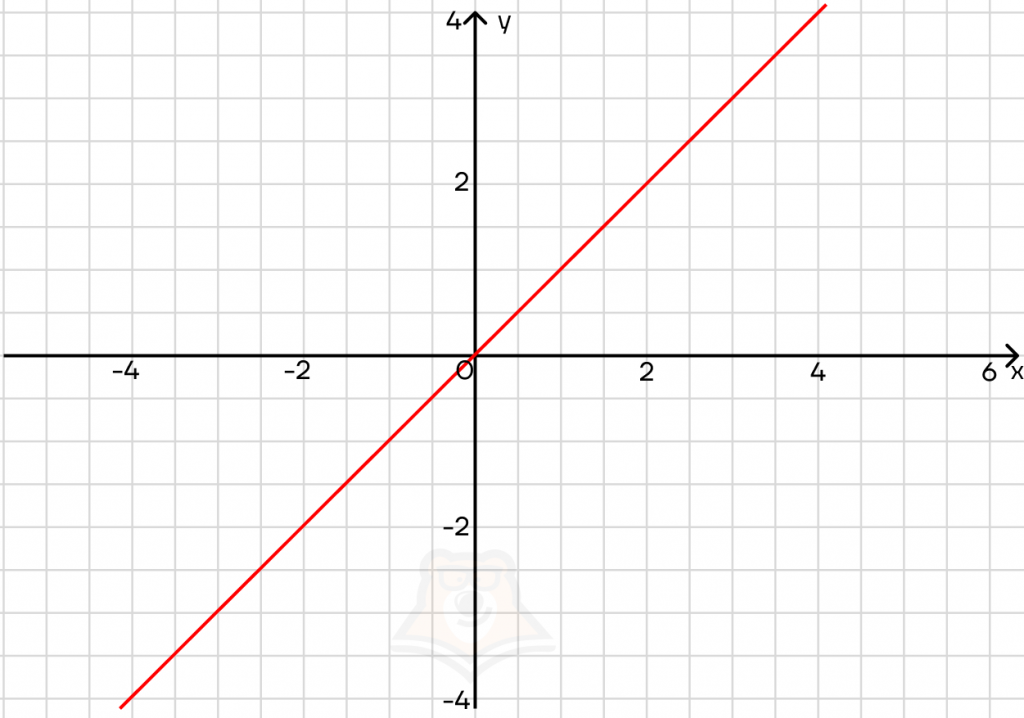
Занесем х под знак модуля: y = |x|. Теперь у может быть только положительным. Что происходит с частью графика, которая лежит ниже оси х? Она зеркально отражается. В итоге мы получаем галочку:
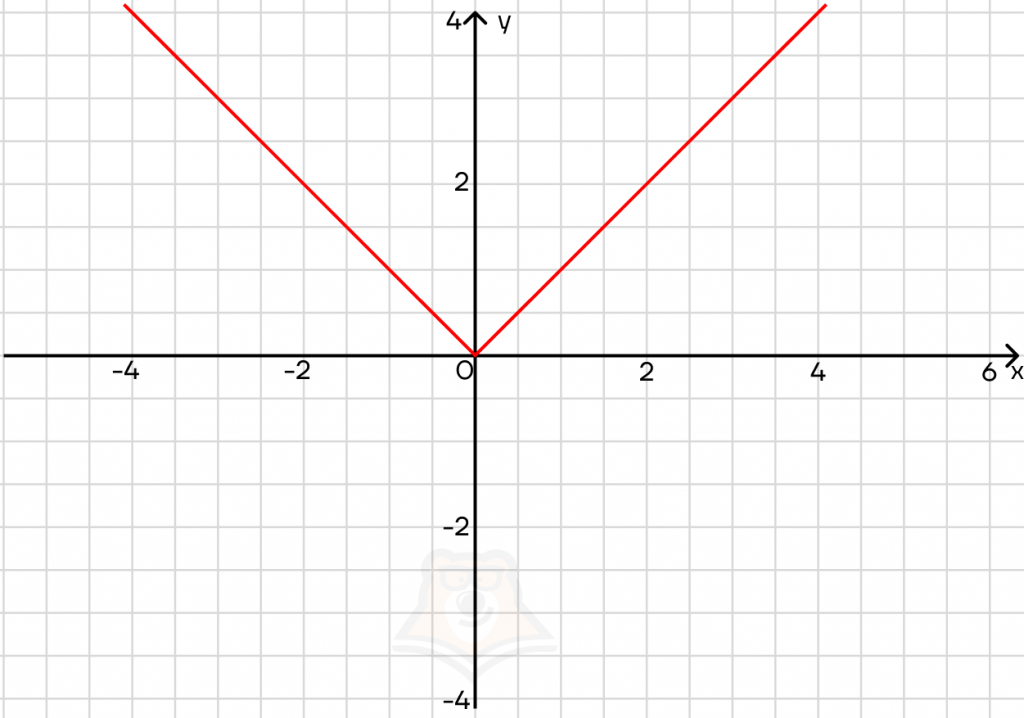
Модуль отражает любой график относительно оси х.
Что будет, если перед х будет стоять коэффициент? Построим графики:
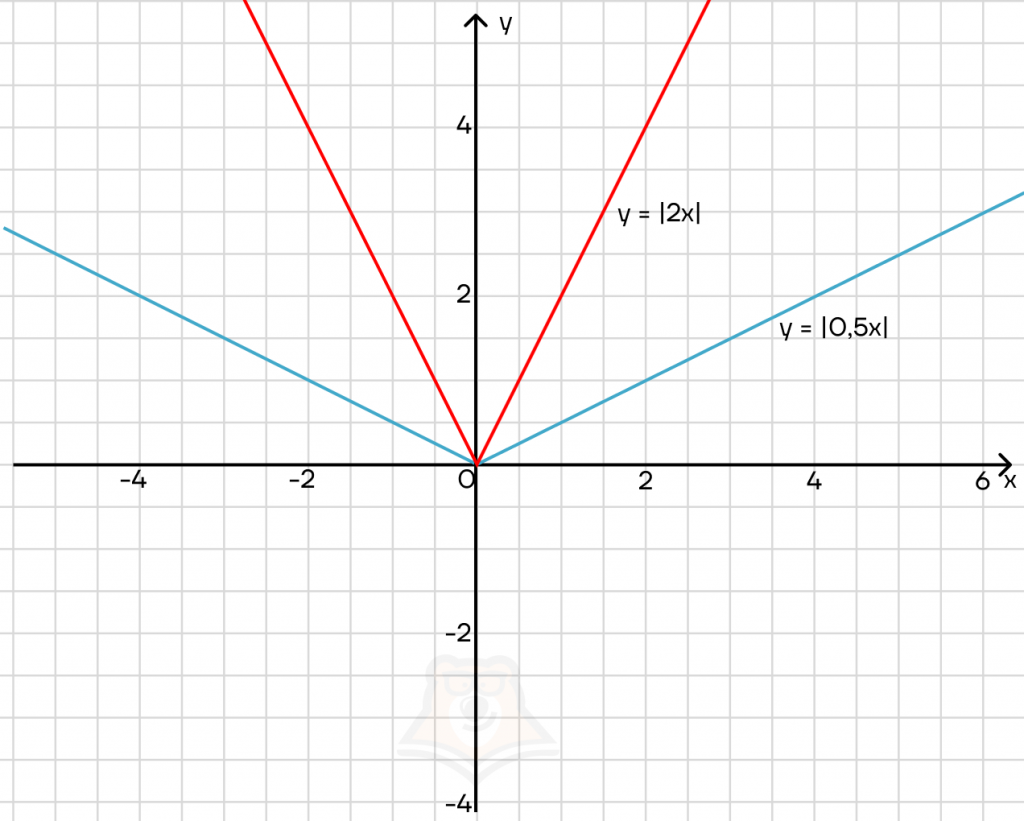
Галочка будет сужаться и расширяться. Причем чем больше коэффициент перед х, тем ýже будет галочка.
Попробуем добавить слагаемое к подмодульному выражению.
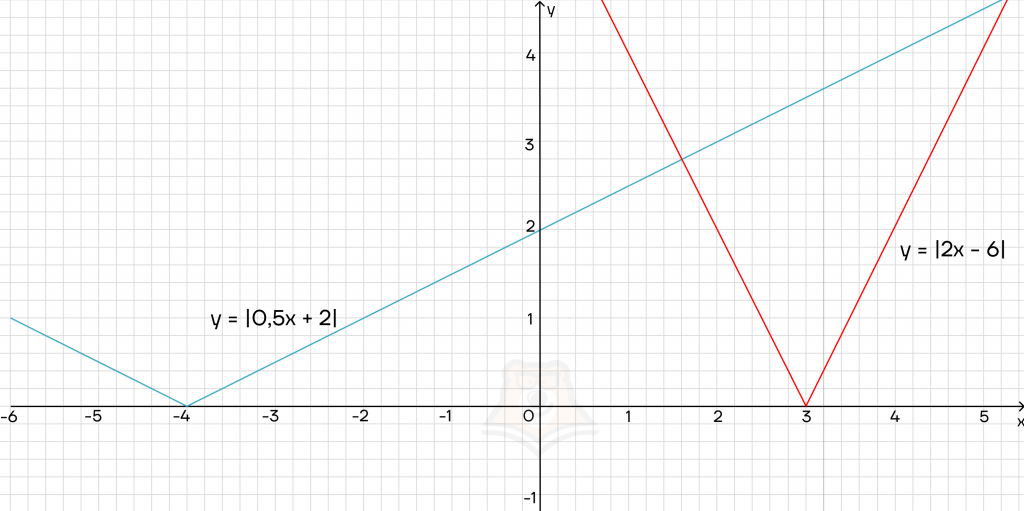
График модуля будет двигаться вдоль оси х. Причем:
- если мы прибавляем число, то график сдвигается влево;
- если мы вычитаем число, то график сдвигается вправо.
Добавим число к модулю, а не подмодульному выражению:
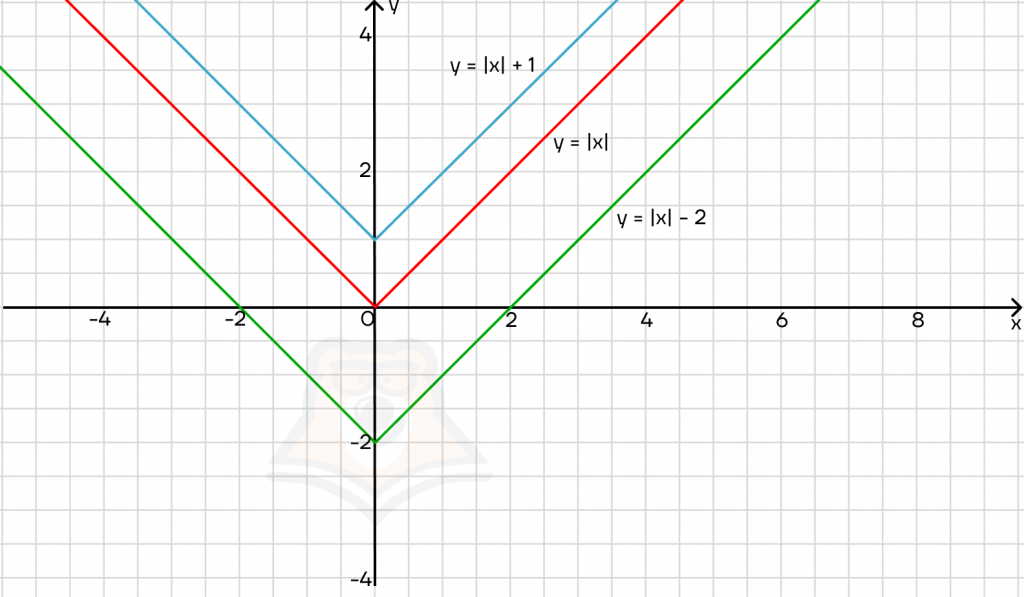
График будет двигаться вдоль оси у.
Для этого достаточно добавить перед модулем минус. Важно, чтобы минус стоял именно перед модулем, а не внутри него. Тогда график будет отзеркален относительно оси х и лежать только ниже нее.
Это легко проследить с помощью уравнений: если y = -|x|, то, при x = 3 получаем:
y = -|3| = -3
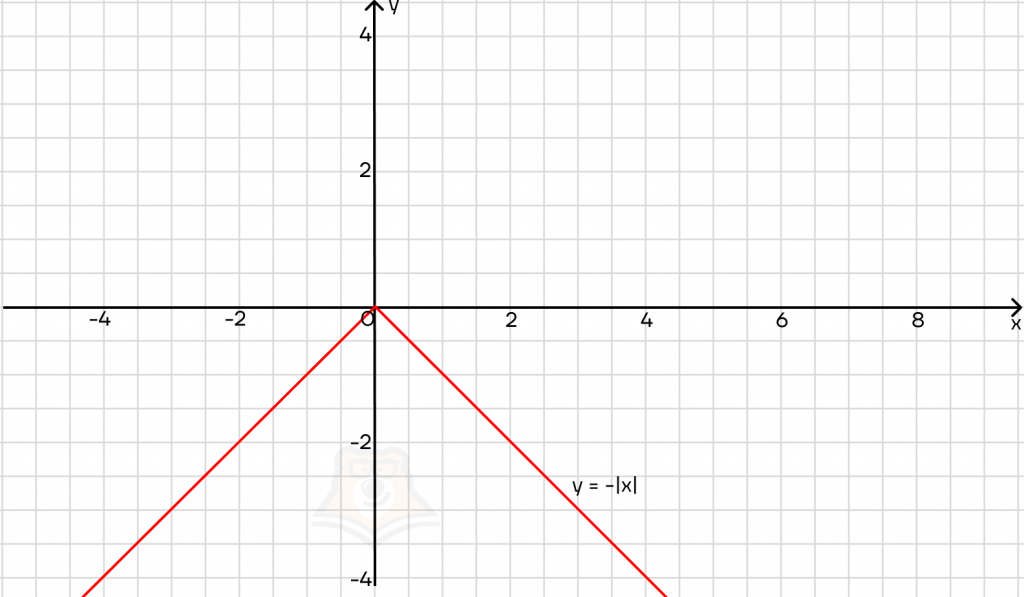
Уравнения с модулем
1. Возьмем уравнение вида |f(x)| = a. Поскольку модуль не может быть отрицательным, то и а не может быть отрицательным. Получаем следующий переход:
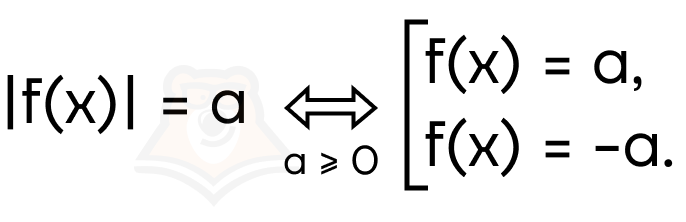
Пример 1. Решите уравнение |4x + 5| = 7.
Решение. В уравнении f(x) = 4x + 5, a = 7. Воспользуемся переходом:
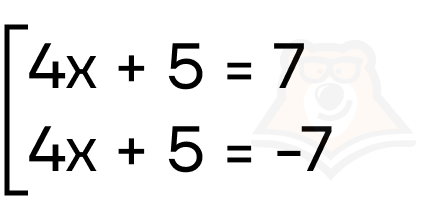
Из первого уравнения x = 0,5, а из второго уравнения x = -3.
Ответ: 0,5: -3.
2. В уравнениях и неравенствах можно встретить два разных модуля. Как быть в этом случае?
Шаг 1. Находим нули подмодульных выражений.
Шаг 2. Чертим числовую прямую и ищем знаки на промежутках для каждого модуля. Если подмодульное выражение отрицательно на промежутке, то ставится минус, если положительно — ставится плюс.
Шаг 3. Для каждого промежутка раскрываем модули. Если подмодульное выражение на промежутке отрицательно, то модуль раскрывается со знаком минус. Если положительно — модуль раскрывается со знаком плюс. Важно: полученные корни должны принадлежать промежуткам, на которых раскрывается модуль, иначе они не будут решениями уравнения.
Шаг 4. Записать все полученные корни в ответ.
Пример 2. Решите уравнение |x — 2| — |x + 2| = 4x — 5.
Решение. Найдем, в каких точках модули будут равны 0. Для этого подмодульное выражение также должно быть равно 0:
x — 2 = 0 (rightarrow) x = 2
x + 2 = 0 (rightarrow) x = -2
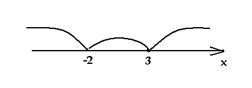
Нарисуем числовую прямую с этими точками:
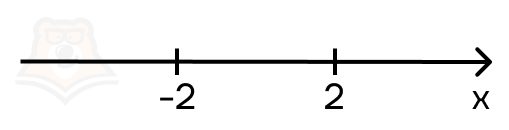
У нас получилось три промежутка:
- (-(infty);-2)
- [-2;2)
- [2;+(infty))
Обратим внимание, какие знаки имеет первый модуль на промежутках: x — 2 > 0 при x > 2. Следовательно, на первых двух промежутках модуль будет отрицательным, а на третьем положительным. Расставим его знаки красным цветом.
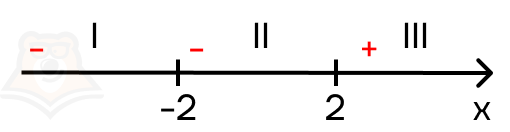
Проанализируем второй модуль: x + 2 > 0 (rightarrow) x>-2. Получается, подмодульное выражение будет положительно на втором и третьем промежутке, и отрицательным на первом промежутке. Расставим его знаки синим цветом.
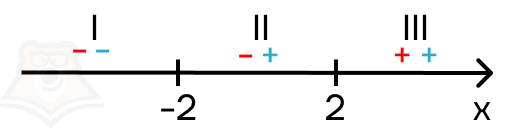
Теперь мы можем рассмотреть уравнение на всех трех промежутках. Однако для этого обязательно ввести ограничения: полученные точки должны принадлежать только этому промежутку, поскольку на следующем модули будут раскрываться уже по-другому.
2. Рассмотрим первый промежуток: x<-2. Оба модуля раскрываются с отрицательным знаком, и мы получаем следующее уравнение:
-(x — 2) — (-(x + 2)) = 4x — 5
-x + 2 + x + 2 = 4x — 5
4 = 4x — 5
4x = 9
x = 2,25
Точка не удовлетворяет ограничению, поскольку не лежит в промежутке (-(infty);-2):
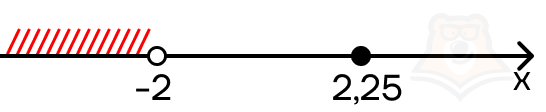
Рассмотрим второй промежуток: [-2;2). Первый модуль раскрывается с минусом, а второй с плюсом:
-(x — 2) — (x + 2) = 4x — 5
-x + 2 — x — 2 = 4x — 5
-2x = 4x — 5
6x = 5
(x = frac{5}{6})
Эта точка лежит в заданном промежутке и является решением уравнения.
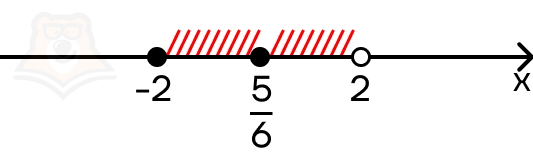
Рассмотрим третий промежуток [2;+(infty)). Оба модуля раскрываются со знаком плюс, мы получаем уравнение:
(x — 2) — (x + 2) = 4x — 5
x — 2 — x — 2 = 4x — 5
-4 = 4x — 5
4x = 1
x = 0,25 — эта точка не лежит в промежутке, то есть не является решением уравнения.
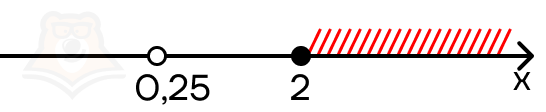
Решением уравнения будет только (x = frac{5}{6}).
Ответ: (frac{5}{6})
Разбивая прямую на промежутки, может возникнуть вопрос: а что делать с точками, в которых модуль равен 0? Их обязательно нужно проверять. Можно сделать это как отдельно, подставив точки в уравнение, так и сразу включить их в условие раскрытия модуля.
Если точки включаются в условие раскрытия модуля, то достаточно включить их только в один из двух промежутков. Включать их в два промежутка нецелесообразно: одна и та же точка будет проверяться дважды.

3. Уравнения вида |f(x)| = g(x)
Поскольку вместо функций могут стоять любые выражения, раскрыть модуль можно двумя способами. Выбор одного из них зависит от того, какая функция проще: f(x) или g(x).
Как можно раскрыть модуль?
- Можно раскрыть его в зависимости от знаков подмодульного выражения: если подмодульное выражение отрицательное, то модуль раскрывается с минусом, если положительное, то с плюсом.
- Можно возвести уравнение в квадрат. Но здесь необходимо ввести ограничения на g(x) — поскольку функция равна модулю, она не может быть отрицательной.
Для удобства можно пользоваться следующей схемой:
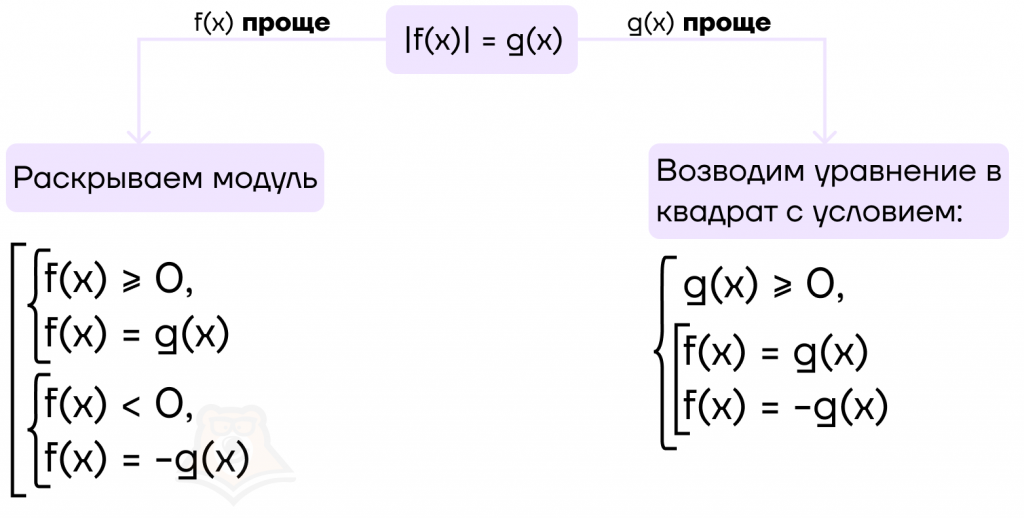
Пример 3. Решите уравнение |8 — x| = x2 — 5x + 11.
Решение. Заметим, что подмодульное выражение значительно проще функции справа, в этом случае удобнее будет раскрыть модуль. Получаем совокупность двух систем:
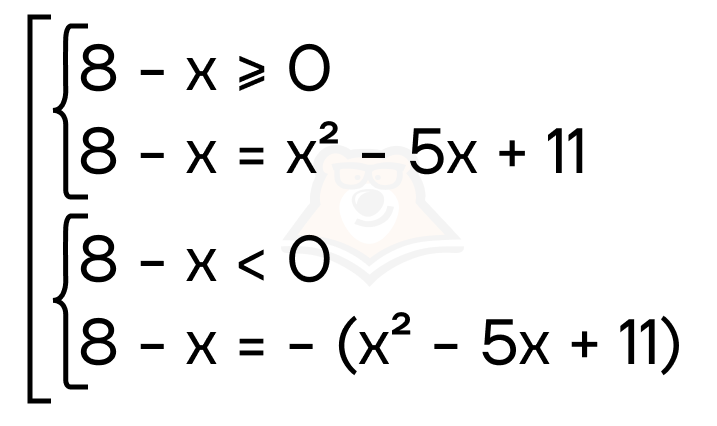
Рассмотрим первую систему.
8 — x >= 0 (rightarrow) x <= 8
Решим уравнение:
8 — x = x2 — 5x + 11
x2 — 4x + 3 = 0
D = 16 — 12 = 4
(x_1 = frac{4 + 2}{2} = 3)
(x_2 = frac{4 — 2}{2} = 1)
Оба корня уравнения удовлетворяют условию x <= 8, значит, решением системы будут 1 и 3.
Рассмотрим вторую систему.
8 — x < 0 (rightarrow) x > 8
Решим уравнение:
8 — x = -x2 + 5x — 11
x2 — 6x + 19 = 0
D = 36 — 76 = -40 — при отрицательном дискриминанте решения уравнений нет.
Решением всего уравнения будут x = 1 и x = 3.
Ответ: 1, 3
4. Разберем еще один тип уравнений, когда модуль равен модулю. Неужели придется рассматривать целых 4 случая раскрытия модуля? Нет, достаточно будет возвести в квадрат обе части уравнения. Таким образом, мы получаем следующий переход:
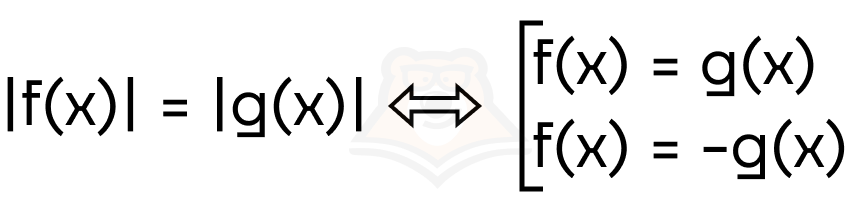
Пример 4. Решите уравнение |x — 2| = |2x + 8|.
Решение. Возведем обе части уравнения в квадрат. Для этого воспользуемся свойством 8.
(x — 2)2 = (2x + 
(x — 2)2 — (2x + 
Воспользуемся формулой сокращенного умножения:
((x — 2) — (2x + 8))((x — 2) + (2x + 
Если произведение множителей равно 0, то каждый множитель равен 0. Тогда:
x — 2 — (2x + 
x — 2 + (2x + 

Получаем совокупность:
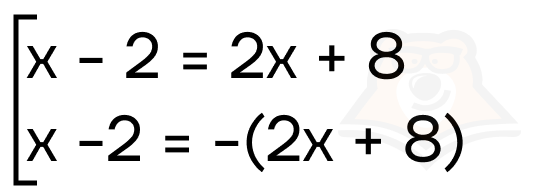
Решим первое уравнение совокупности:
x — 2 = 2x + 8
x = -10
Решим второе уравнение совокупности:
x — 2 = -2x — 8
3x = -6
x = -2
Решением уравнения будут x = -10 и x = -2
Ответ: -2, -10
Неравенства с модулем
Разобравшись, как решаются уравнения с модулем, можно приступать к неравенствам.
Пример 5. Решите неравенство x2 — |3x — 7| + 7 >= 0.
Решение. Найдем, при каких значениях х модуль равен 0. Получаем 3x = 7 (rightarrow) (x = frac{7}{3}).
Определим, с какими знаками модуль будет раскрываться на каждом промежутке.
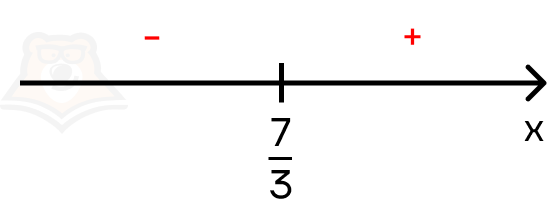
Осталось рассмотреть неравенство на двух промежутках.
1. (x leq frac{7}{3}), тогда
x2 — (-(3x — 7)) + 7 >= 0
x2 + 3x — 7 + 7 >= 0
x2 + 3x >= 0
x(x + 3) >= 0
Решим это неравенство «Методом интервалов». Сразу учтем ограничение (x leq frac{7}{3}).
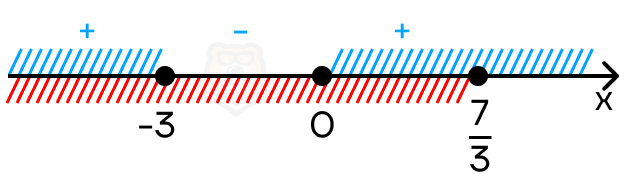
Получаем, что решением неравенства на заданном промежутке будет (x in (-infty; -3] U[0; frac{7}{3}]).
2. (x > frac{7}{3}), тогда
x2 — 3x + 7 + 7 >= 0
x2 — 3x + 14 >= 0
x2 — 3x + 14 = 0
D = 9 — 56 = -47 — корней на заданном отрезке не будет.
Вспомним, что корни квадратного уравнения — это точки пересечения параболы и оси х. Если парабола не пересекает ось х, то неизбежно лежит выше или ниже ее. Поскольку в нашем случае ветви параболы направлены вверх, мы можем нарисовать ее примерный график.
Так как парабола задается функцией y = x2 — 3x + 14, то неравенство будет выполняться при всех y >= 0. Парабола целиком попадает в эту область, а решением неравенства будет любое х.
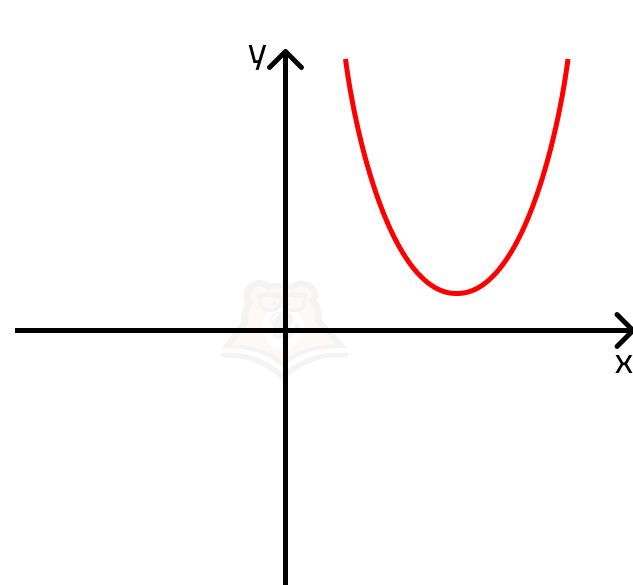
Однако не стоит забывать про ограничение (x > frac{7}{3}). Накладывая его, получаем решение ((frac{7}{3}; + infty)).
Осталось только объединить полученные на промежутках решения:
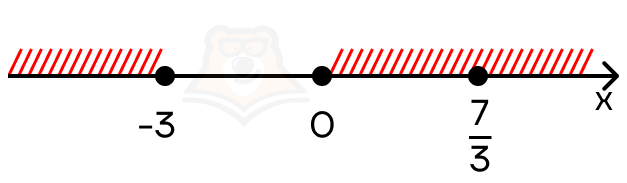
Получаем, что (x in (-infty;- 3] U [0; +infty)).
Ответ: (x in (-infty;- 3] U [0; +infty))
Рассмотрим неравенства вида |f(x)| > a и |f(x)| < a, где а — некоторое число и a >= 0. Модуль можно раскрыть двумя способами и получить два неравенства. Но будет это совокупность или система?
Это зависит от знака. Разберем случай |f(x)| > a. Заметим, что строгость знака может быть любой. Тогда модуль раскрывается как:
f(x) > a и -f(x) > a (rightarrow) f(x) < -a.
Отметим эти промежутки на числовой прямой:
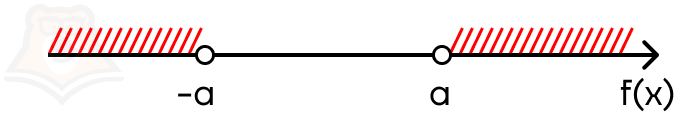
В ответе должны оказаться оба промежутка — их нужно объединить. В этом случае модуль раскрывается в совокупности.
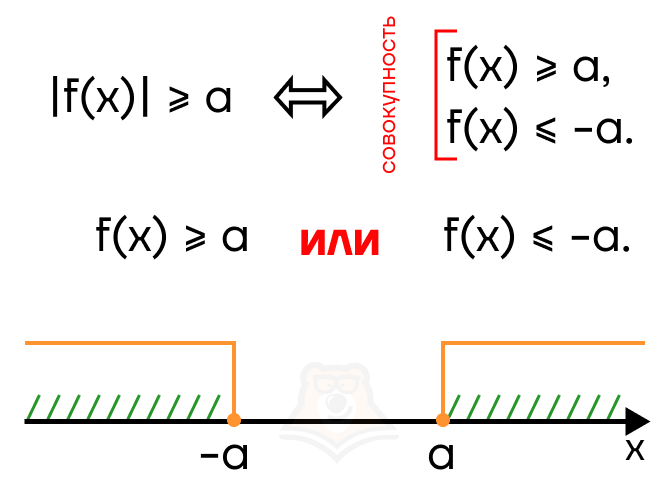
Рассмотрим случай |f(x)| < a, здесь строгость знака также может быть любой. Раскроем модуль: f(x) < 0 и -f(x) < a (rightarrow) f(x) > -a. На числовой прямой это будет выглядеть следующим образом:

В в ответе должен оказаться промежуток от —а до а. Следовательно, необходимо воспользоваться системой, чтобы “отсечь” лишние промежутки.
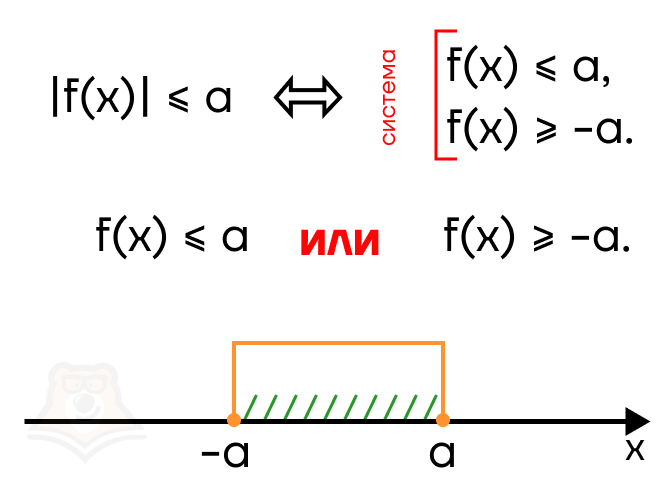
Можно ли обойтись в этом случае без раскрытия модуля? Да, но необходимо возвести неравенство в квадрат.
|f(x)| ⋁ a | (uparrow) 2 — вместо ⋁ может стоять любой знак неравенства.
f2(x) ⋁ a2
f2(x) — a2 ⋁ 0
Воспользуемся формулой сокращенного умножения:
(f(x) — a)(f(x) + a) ⋁ 0
Однако стоит помнить, что обе части неравенства можно возвести в квадрат только в том случае, если они неотрицательны. То есть обязательно должно выполняться условие a0.
Мы получили равносильный переход. Но существуют ли равносильные переходы, если вместо числа а стоит другая функция или даже модуль? Да. Они выводятся таким же способом, как и переход для неравенства с числом. Получаем еще два равносильных перехода:
- |f(x)| ⋁ g(x) (rightarrow) (f(x) — g(x))(f(x) + g(x)) ⋁ 0
g(x) обязательно должно быть неотрицательным, чтобы можно было возвести неравенства в квадрат.
- |f(x)| ⋁ |g(x)| (rightarrow) (f(x) — g(x))(f(x) + g(x)) ⋁ 0
Разберем на примере, как можно использовать равносильный переход. Для этого возьмем то же неравенство, что и в примере 5, но решим его по-другому.
Пример 6. Решите неравенство x2 — |3x — 7| + 7 >= 0.
Решение. Перенесем модуль в другую часть неравенства:
|3x — 7| <= x2 + 7. Модуль всегда неотрицателен. Правая часть неравенства неотрицательна, поскольку число в квадрате всегда положительно.
Повторим действия, чтобы прийти к равносильному переходу:
(3x — 7)2 <= (x2+7)2
(3x-7)2 — (x2 + 7)2 <= 0
(3x — 7 — (x2 + 7))(3x — 7 + x2 + 7) <= 0
(3x — 7 — x2 — 7)(3x + x2) <= 0
(-x2 + 3x — 14) * x(3 + x) <= 0
-(x2 — 3x + 14) * x(3 + x) <= 0
(x2 — 3x + 14) * x(3 + x) <= 0
Рассмотрим первую скобку:
x2 — 3x + 14 = 0
D = 9 — 56 = -47 — корней нет. Выражение всегда будет положительно, то есть на него можно разделить все неравенство. Получаем:
x(3 + x) <= 0

Тогда (x in (-infty;- 3] U [0; +infty))
Ответ: (x in (-infty;- 3] U [0; +infty))
При решении можно сразу использовать равносильный переход, не расписывая его.
Итак, неравенства с модулем можно решить двумя способами: раскрывать модуль и воспользоваться равносильным переходом. Выбор способа зависит от личных предпочтений и удобства решения.
Фактчек
- Модуль — расстояние от любой точки на координатной прямой до начала координат. Модуль обозначается двумя вертикальными черточками: |a| = a и |-a| = a.
- Модулем числа называют выражение:

- График модуля представляет собой “галочку”, которая лежит выше оси х. Модуль отражает график любой функции зеркально оси х так, что значения у всегда больше 0.
- Модуль можно раскрыть двумя способами. Этим свойством можно пользоваться при решении уравнений с модулем.
- При решении неравенств с модулем можно раскрывать его, либо воспользоваться равносильным переходом, если в неравенстве выполняются все условия для него.
Проверь себя
Задание 1.
Чему равно выражение |-16 * 2|?
- 32
- −32
- −16
- 16
Задание 2.
Какой график имеет функция y = |x|?
- Парабола
- Гипербола
- Прямая
- Галочка
Задание 3.
Решите уравнение |x| = -3.
- 3
- −3
- Решений нет
- 3 и −3
Задание 4.
Решите уравнение |x + 2| = 15.
- −13
- 17
- 13 и -17
- Решений нет
Задание 5.
Какой равносильный переход можно использовать для неравенства вида |f(x) |⋁ |g(x)|?
- f(x) ⋁ g(x)
- f(x) ⋀ g(x)
- f2(x) — 2 * f(x) * g(x) + g2(x) ⋁ 0
- (f(x) — g(x))(f(x) + g(x)) ⋁ 0
Ответы: 1. — 1 2. — 4 3. — 3 4. — 3 5. — 4
Знак модуля, пожалуй, одно из самых интересных явлений в математике. В связи с этим у многих школьников возникает вопрос, как строить графики функций, содержащих модуль. Давайте подробно разберем этот вопрос.
1. Построение графиков функций, содержащих модуль
Пример 1.
Построить график функции y = x2 – 8|x| + 12.
Решение.
Определим четность функции. Значение для y(-x) совпадает со значением для y(x), поэтому данная функция четная. Тогда ее график симметричен относительно оси Oy. Строим график функции y = x2 – 8x + 12 для x ≥ 0 и симметрично отображаем график относительно Oy для отрицательных x (рис. 1).
Пример 2.
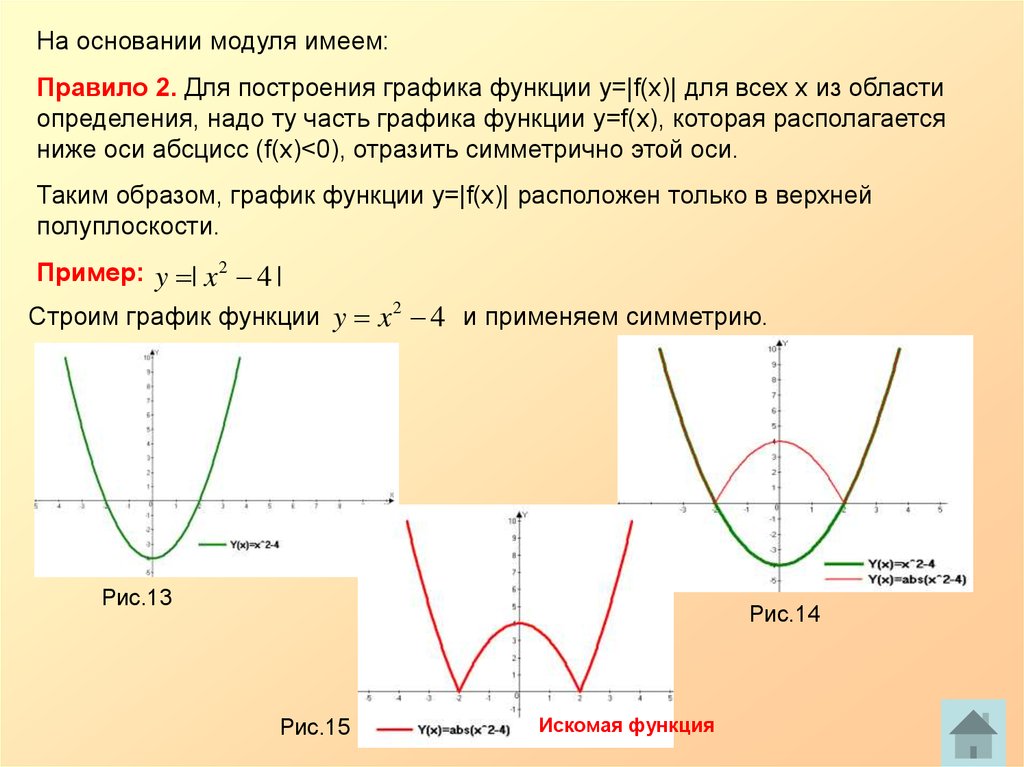
Следующий график вида y = |x2 – 8x + 12|.
– Какова область значений предложенной функции? (y ≥ 0).
– Как расположен график? (Над осью абсцисс или касаясь ее).
Это значит, что график функции получают следующим образом: строят график функции y = x2 – 8x + 12, оставляют часть графика, которая лежит над осью Ox, без изменений, а часть графика, которая лежит под осью абсцисс, симметрично отображают относительно оси Ox (рис. 2).
Пример 3.
Для построения графика функции y = |x2 – 8|x| + 12| проводят комбинацию преобразований:
y = x2 – 8x + 12 → y = x2 – 8|x| + 12 → y = |x2 – 8|x| + 12|.
Ответ: рисунок 3.
Рассмотренные преобразования справедливы для всех видов функций. Составим таблицу:
|
Функция |
Преобразование |
|
f(|x|) |
1) Для x ≥ 0, y = f(x) 2) Для x < 0 – преобразование симметрии относительно Oy графика y = f(x), для x ≥ 0 симметричные части графика из правой полуплоскости в левую |
|
|f(x)| |
1) Для f(x) ≥ 0, |f(x)| = f(x) 2) Для f(x) < 0, |f(x)| = -f(x) Симметричное отображение части графика из нижней полуплоскости в верхнюю относительно Ox |
|
|f(|x|)| |
f(x) → f(|x|) → |f(|x|)|. |
2. Построение графиков функций, содержащих в формуле «вложенные модули»
Мы уже познакомились с примерами квадратичной функции, содержащей модуль, а так же с общими правилами построения графиков функций вида y = f(|x|), y = |f(x)| и y = |f(|x|)|. Эти преобразования помогут нам при рассмотрении следующего примера.
СЛОЖНА-А-А 🙀 Ты же знаешь, что если не разобраться в теме сейчас, то потом придется исправлять оценки. Беги на бесплатное онлайн-занятие с репетитором (подробности тут + 🎁).
Пример 4.
Рассмотрим функцию вида y = |2 – |1 – |x|||. Выражение, задающее функцию, содержит «вложенные модули».
Решение.
Воспользуемся методом геометрических преобразований.
Запишем цепочку последовательных преобразований и сделаем соответствующий чертеж (рис. 4):
y = x → y = |x| → y = -|x| → y = -|x| + 1 → y = |-|x| + 1|→ y = -|-|x| + 1|→ y = -|-|x| + 1| + 2 → y = |2 –|1 – |x|||.
Рассмотрим случаи, когда преобразования симметрии и параллельного переноса не являются основным приемом при построении графиков.
Пример 5.
Построить график функции вида y = (x2 – 4)/√(x + 2)2.
Решение.
Прежде чем строить график, преобразуем формулу, которой задана функция, и получим другое аналитическое задание функции (рис. 5).
y = (x2 – 4)/√(x + 2)2 = (x– 2)(x + 2)/|x + 2|.
Раскроем в знаменателе модуль:
При x > -2, y = x – 2, а при x < -2, y = -(x – 2).
Область определения D(y) = (-∞; -2)ᴗ(-2; +∞).
Область значений E(y) = (-4; +∞).
Точки, в которых график пересекает с оси координат: (0; -2) и (2; 0).
Функция убывает при всех x из интервала (-∞; -2), возрастает при x от -2 до +∞.
Здесь нам пришлось раскрывать знак модуля и строить график функции для каждого случая.
Пример 6.
Рассмотрим функцию y = |x + 1| – |x – 2|.
Решение.
Раскрывая знак модуля, необходимо рассмотреть всевозможную комбинацию знаков подмодульных выражений.
Возможны четыре случая:
{x + 1 – x + 2 = 3, при x ≥ -1 и x ≥ 2;
{-x – 1 + x – 2 = -3, при x < -1 и x < 2;
{x + 1 + x – 2 = 2x — 1, при x ≥ -1 и x < 2;
{-x – 1 – x + 2 = -2x + 1, при x < -1 и x ≥ 2 – пустое множество.
Тогда исходная функция будет иметь вид:
{3, при x ≥ 2;
y = {-3, при x < -1;
{2x – 1, при -1 ≤ x < 2.
Получили кусочно-заданную функцию, график которой изображен на рисунке 6.
3. Алгоритм построения графиков функций вида
y = a1|x – x1| + a2|x – x2| + … + an|x – xn| + ax + b.
В предыдущем примере было достаточно легко раскрыть знаки модуля. Если же сумм модулей больше, то рассмотреть всевозможные комбинации знаков подмодульных выражений проблематично. Как же в этом случае построить график функции?
Заметим, что графиком является ломаная, с вершинами в точках, имеющих абсциссы -1 и 2. При x = -1 и x = 2 подмодульные выражения равны нулю. Практическим путем мы приблизились к правилу построения таких графиков:
Графиком функции вида y = a1|x – x1| + a2|x – x2| + … + an|x – xn| + ax + b является ломаная с бесконечными крайними звеньями. Чтобы построить такую ломаную, достаточно знать все ее вершины (абсциссы вершин есть нули подмодульных выражений) и по одной контрольной точке на левом и правом бесконечных звеньях.
Задача.
Построить график функции y = |x| + |x – 1| + |x + 1| и найти ее наименьшее значение.
Решение:
Нули подмодульных выражений: 0; -1; 1. Вершины ломаной (0; 2); (-1; 3); (1; 3). Контрольная точка справа (2; 6), слева (-2; 6). Строим график (рис. 7). min f(x) = 2.
Молодец! Раз ты дочитал это до конца, вероятно, ты все отлично усвоил. Но если вдруг что-то еще непонятно — попробуй онлайн-занятие с репетитором (подробности тут + 🎁).
Остались вопросы? Не знаете, как построить график функции с модулем?
Чтобы получить помощь репетитора – зарегистрируйтесь.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
«Графики функций, содержащих выражения под знаком модуля»
Министерство
образования РФ
Муниципальное
бюджетное общеобразовательное учреждение
«Средняя
общеобразовательная школа №7»
МО
«город Бугуруслан»
Исследовательская
работа на тему:
«Графики
функций, содержащих выражения под знаком модуля»
Городская
научно-исследовательская конференция
«Маленький шаг —
большая наука».
Выполнила:
Юсупова
Гузель Ильшатовна
Учащаяся
9 класса
МБОУ
СОШ №7.
Руководитель:
Мошнина Зульфия Равильевна
Учитель математики
МБОУ
СОШ №7
Бугуруслан
, 2018
Аннотация.
Автор
данной работы изучает различные виды графиков функций, содержащих выражения под
знаком модуля, составляет алгоритмы построения графиков
функций, аналитическое выражение которых содержит знак абсолютной величины; делает
выводы о том, что он узнал и чему научился, выполняя данную работу.
Тезисы.
Общие сведения об
учащемся: Юсупова Гузель Ильшатовна.
Муниципальное бюджетное
общеобразовательное учреждение
«Средняя
общеобразовательная школа №7»
муниципального
образования «город Бугуруслан»
Дата рождения:30
мая 2002 года.
Адрес: город
Бугуруслан, улица Монтажников дом 5 квартира 2
Общие сведения о
руководителе: Мошнина Зульфия Равильевна,
Муниципальное бюджетное
общеобразовательное учреждение
«Средняя
общеобразовательная школа №7»
муниципального
образования «город Бугуруслан»
Стаж работы в
данном учреждении: 6 лет.
Должность: учитель
математики.
Первая категория.
Адрес: г.
Бугуруслан, 1 микрорайон, дом 19, квартира 29.
Идея:
Изучить
соответствующие теоретические материалы, выявить алгоритм построения графиков
функций, аналитическое выражение которых содержит знак абсолютной величины.
Гипотеза: Если я
изучу свойства функций, то мне нетрудно будет выбрать рациональный способ
построения различных графиков.
Объект
исследования: Линейные и квадратичные функции,
аналитическое выражение которых содержит знак абсолютной величины.
Предмет изучения:
Свойства функций, содержащих знак модуля.
Тема:
Графики функций, содержащих выражения под знаком
модуля.
Цели:
Научиться строить графики функций, содержащих знак модуля.
Задачи:
Выявить алгоритм построения графиков функций, аналитическое выражение которых
содержит знак абсолютной величины, подобрать и изучить материал по выбранной
теме, провести анкетирование среди учеников класса и выяснить, сколько человек
умеет строить подобные графики, узнать какие виды графиков с модулем существуют,
и изучить каждый отдельно.
Методы
исследования: поисковый, аналитический.
Исследование
проведено по плану:
1.1. Историческая
справка. Определение модуля.
1.2
Функциональная зависимость.
Определения.
2.
графиков линейных функций со знаком модуля.
2.2.
Построение графиков линейных функций, содержащих несколько знаков модуля.
3.
Построение графика квадратичной функции, содержащей переменную под знаком
модуля.
Вывод: При выполнении исследовательской
работы я делала такие выводы:
—
сформировала алгоритмы построения графиков функций, аналитическое выражение
которых содержит знак абсолютной величины.
— научилась
работать с дополнительной литературой и материалами, производить отбор научных
сведений;
— приобрела
опыт выполнения графических работ на компьютере.
Содержание
Введение…………………………………………………………………………6
1. Графики
функций, аналитическое выражение которых содержит знак абсолютной
величины.……………………………………………..………….7
1.1. Историческая
справка. Определение модуля.……………………………7
1.2
Функциональная зависимость. Определения………………………………9
2.
функции и их построение. ……………………………………..10
2.1.Построение
графиков линейных функций со знаком модуля…………..11
2.2.
Построение графиков линейных функций, содержащих несколько знаков модуля…………………………………………………………………………..14
3.
Построение графика квадратичной функции, содержащей переменную под знаком
модуля………………………………………………………………….16
3.1. Подготовка к
ОГЭ…………………………………………………………22
Заключение……………………………………………………………………..23
Литература………………………………………………………………………25
Приложение………………………………………………………………………26
Введение.
В
курсе математики основной и средней школы незначительное место отводится
построению графиков функций, аналитическое выражение которых содержит знак
модуля.
Впервые
с модулем числа мы встречаемся в курсе математики 6 класса, и больше они не
упоминаются до 9 класса, и немного заданий на построение графиков таких
функций встречается в курсе алгебры и начала анализа 10 класса.
Поэтому
я считаю, что нужно научиться строить самому и научить других ребят строить
графики функций с модулем. Это очень интересная тема, но среди моих
одноклассников встречается очень много учеников, которые испытывают затруднения,
когда встречают в каких-либо тренировочных тестах подобные задания.
Также
я считаю, что любому человеку в дальнейшей жизни хоть раз но обязательно встретиться
задание подобного рода. Я хочу получить более широкие знания о модуле числа,
различных способах построения графиков, содержащих знак абсолютной величины.
Цель:
научиться строить разные графики функций с модулем.
Задачи:
-подобрать
и изучить материал по выбранной теме
-провести
анкетирование среди учеников класса и выяснить, сколько человек умеет строить
подобные графики
-узнать
какие виды графиков с модулем существуют, и изучить каждый отдельно
Методы
исследования: поисковый, аналитический.
1.
Графики функций, аналитическое выражение которых содержит знак абсолютной
величины.
1.1. Историческая
справка. Определение модуля.
Модуль – это целый мир геометрических
образов, простых и понятных часто очень
красивых и запоминающихся.
Знак
модуля, пожалуй, одно из самых интересных явлений в математике.
Буквенная
символика. До ХVI века в математике не было сколько-нибудь развитой единой
символики. Каждая операция записывалась полностью словами или специальными
знаками – сокращениями, которые использовал только один или несколько учёных. Неизвестные
коэффициенты и свободный член уравнения также не имели условных общепризнанных
обозначений. В ХVII веке французские учёные Франсуа Виет и Ренэ Декарт
разработали единую буквенную математическую символику, которая вскоре получила
всеобщее признание.
Введено было единое обозначение: неизвестных – последними
буквами латинского алфавита – x, y, z, известных – начальными буквами того же
алфавита – а, в, с,… и т. д.
После
введения единой буквенной символики стало возможным решать многие задачи по
формулам. Вместе с буквенной символикой в математику пришла идея изменения,
поскольку под каждой буквой стало возможным понимать различные значения.
Великое
открытие Декарта. К началу ХVII века алгебра была уже достаточно развитой
наукой. Трудами многих поколений учёных были подготовлены условия для нового
большого открытия в науке, которое послужило бы толчком к её дальнейшему
развитию. Таким открытием явилось введение в математику понятия переменной
величины и прямоугольной системы координат. Честь введения в математику
функциональной зависимости принадлежит французскому учёному Ренэ Декарту. (приложение
1)
Ренэ
Декарт придумал систему прямоугольных координат, которой пользуемся мы, ввёл её
в широкое употребление и положил начало развитию важной математической науки –
аналитической геометрии.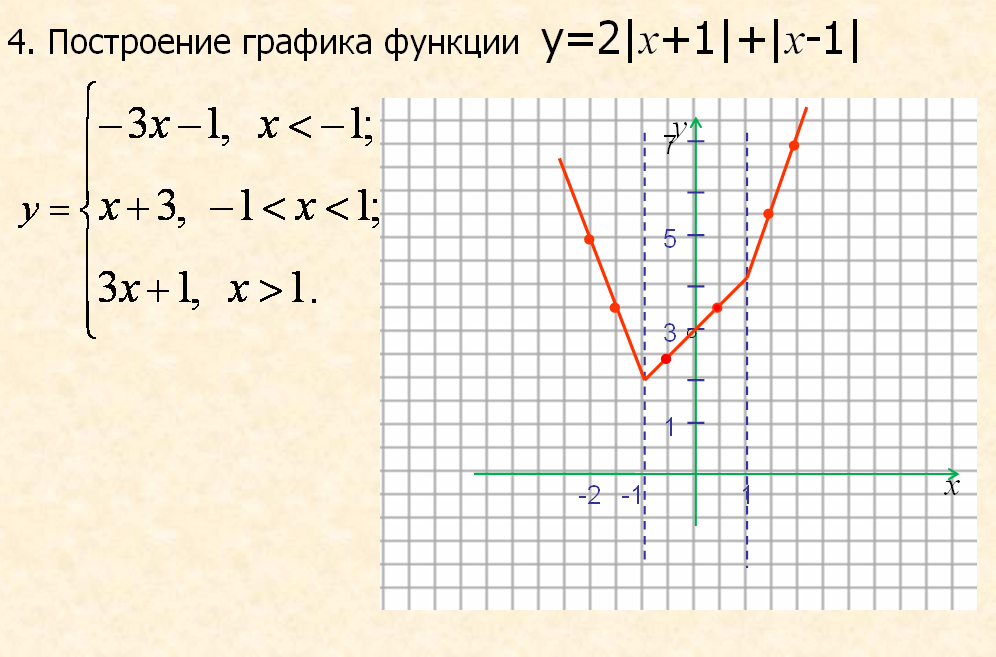
отрицательным числам, как отрезкам, имеющим определённое направление. Он сделал
очень много для усовершенствования алгебры: улучшил систему алгебраических
обозначений, предложил буквами х, у,z обозначать переменные, а буквами а, в, с
– постоянные; предложил записывать степени так, как пишем мы: а2, в3,с4 и т.
д., а алгебраические уравнения – в том виде, в каком пишем их мы. Он же дал
правило для определения числа положительных и отрицательных корней уравнения и
многое другое. Трудами Декарта алгебра была значительно усовершенствована. Термин
«функция» впервые встречается в письме немецкого математика Лейбница к
голландскому математику Гюйгенсу в 1694 г. В обычное употребление термин введён
в начале ХVIII в. Иоганном Бернулли.
Слово
«модуль» произошло от латинского слова «modulus»,
что в переводе означает «мера». Это многозначное слово (омоним), которое имеет
множество значений и применяется не только в математике, но и в архитектуре,
физике, технике, программировании и других точных науках.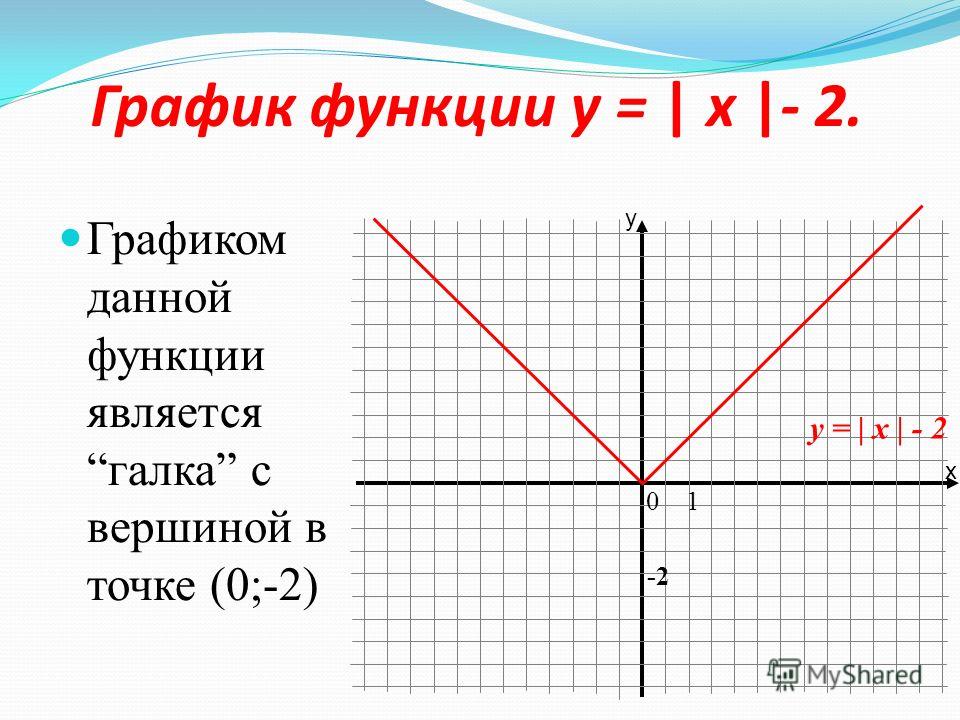
В
архитектуре — это исходная единица измерения, устанавливаемая
для данного архитектурного сооружения и служащая для выражения кратных
соотношений его составных элементов.
В
технике — это термин, применяемый в различных
областях техники, не имеющий универсального значения и служащий для обозначения
различных коэффициентов и величин, например модуль зацепления, модуль упругости
и .т.п.
Модуль объемного
сжатия( в физике)-отношение нормального напряжения в
материале к относительному удлинению.
Определение. Модуль числа a или абсолютная величина числа a равна a, если a больше или равно нулю и равна —a, если a меньше нуля:
Из определения следует, что для
любого действительного числа a,
1.2
Функциональная зависимость. Определения.
График
функции.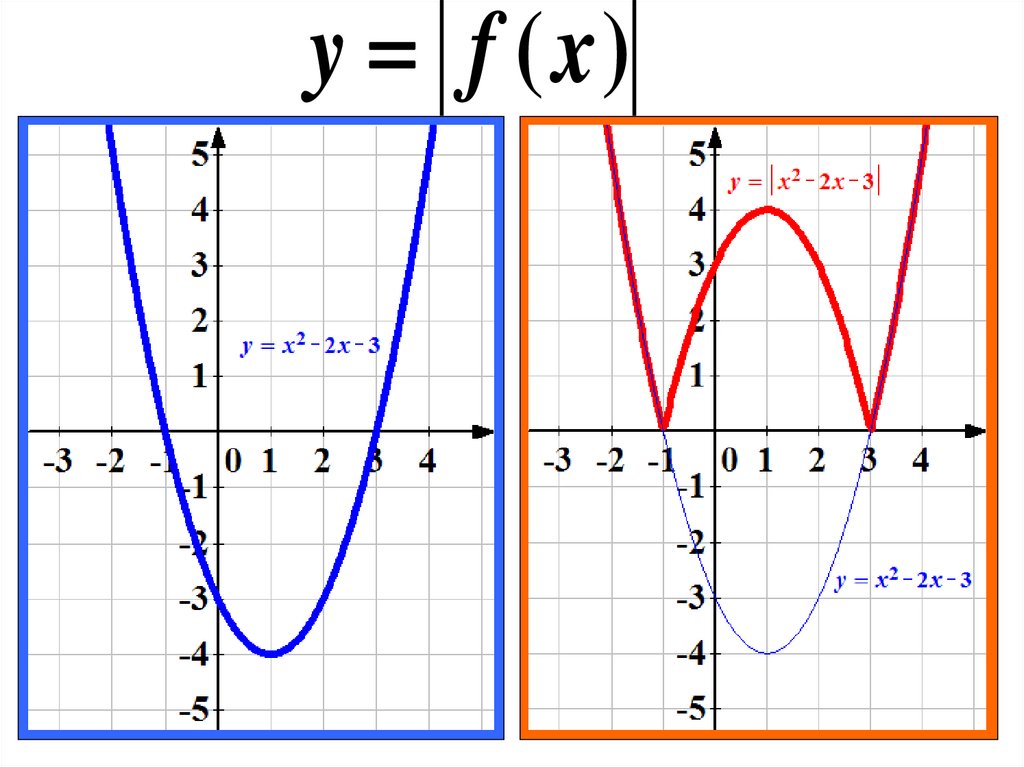
так что изменение одних из них влечёт за собой соответствующее изменение
других. В таких случаях говорят, что между переменными величинами существует
функциональная зависимость, причём одну величину называют функцией, или
зависимой переменной (её часто обозначают буквой у), а другую – аргументом, или
независимой переменной (её обозначают буквой х). Функциональную зависимость
между х и у принято обозначать символом у = f(х). Если каждому значению х
соответствует больше, чем одно значение у, то такая функция называется
многозначной. Исследование многозначных функций сводится обычно к исследованию
однозначных.
Определение
функции. Переменная величина у называется функцией аргумента х, т. е. у = f
(х), если каждому возможному значению х соответствует одно определённое
значение у.
Определение
графика функции. Графиком функции называется совокупность всех точек плоскости,
прямоугольные координаты которых х и у удовлетворяют уравнению у = f (х).
Горизонтальную
ось Ох называют осью абсцисс, вертикальную ось Оу – осью ординат.
Функциональная
зависимость, устанавливающая соответствие между значениями аргумента х и
функции у, может быть задана различными способами: табличным, словесным,
графическим, аналитическим. В математике чаще всего используется аналитический
способ задания функции, при котором известна формула, устанавливающая
зависимость между переменными х и у.
Множество значений
Х, при каждом из которых функции существует, называется областью определения
функции у = f (х) (проекция графика на ось абсцисс).Множество значений У, которые
принимает переменная у, называется областью изменения функции у = f (х).
Область изменения есть проекция графика функции у = f (х) на ось ординат.
2. Линейные
функции и их построение.
Функция
– одно из важнейших математических понятий.
переменной y от переменной x, при которой каждому значению переменной x
соответствует единственное значение переменной у.
Линейная
функция — функция вида y =kx+b (для функций одной переменной).
Основное
свойство линейных функций: приращение функции пропорционально приращению
аргумента. То есть функция является обобщением прямой пропорциональности.
Графиком
линейной функции является прямая линия, с чем и связано ее название. Это
касается вещественной функции одной вещественной переменной.
Частный
случай ~b=0 линейной функции называется однородными линейными функциями (это в
сущности синоним прямой пропорциональности), в отличие от b neq 0 —
неоднородных линейных функций. примеров
построения линейных функций множество. (приложение 2)
2.1.Построение
графиков линейных функций со знаком модуля.
График
функции получается из графика функции у=х следующим образом: часть графика,
лежащая НАД осью х сохраняется, а часть графика, лежащая ПОД осью х
отображается симметрично относительно данной оси.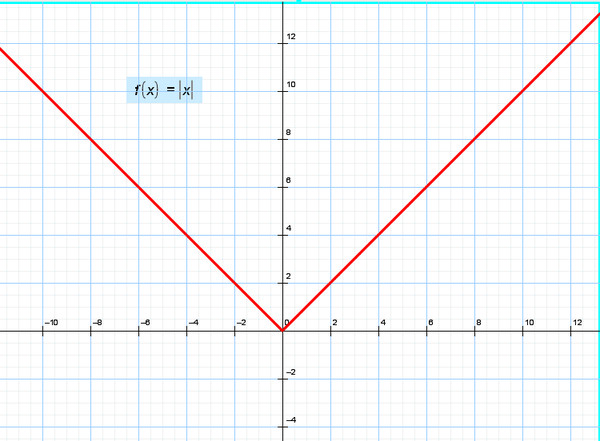
Сначала
начертим прямую, известную широкому кругу лиц:
Начинаем
строить график
Часть
графика, которая ВЫШЕ оси х, остаётся неизменной, а часть графика, которая НИЖЕ
оси х – отображается симметрично в верхнюю полуплоскость:
Аналогично
построим график функции
Сначала
изобразим график линейной функции :
Построение
графика, когда функция под модулем.
То,
что ВЫШЕ оси абсцисс – не трогаем, а то, что НИЖЕ – отобразим симметрично
относительно оси в верхнюю полуплоскость:
Почувствуем
разницу между графиками y = |х| — 3
и y = |х +3| .
y
= |х| — 3 y
= |х +3|
При
построении данных графиков функций можно воспользоваться знаниями, полученными
при преобразовании графиков функций y
=aх2+n c одной стороны, т. е. график функции y
= |х| — 3 можно получить из графика
y
= |х| с помощью параллельного переноса вдоль оси Оy
на три единицы масштаба вниз, а график функции y
= |х +3| из графика функции y
= |х| с помощью параллельного переноса вдоль оси Ох на три единицы масштаба
влево.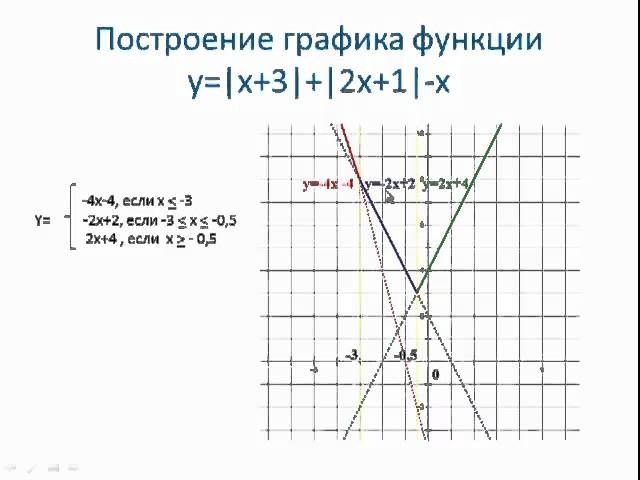
y
= |х — m|
y
= |х| + n
Вывод:
о построении графиков функций вида y
= |х| + n
; y
= |х — m|.
т. е. График функции y = |х| + n
можно получить из графика y
= |х| с помощью параллельного переноса вдоль оси Оy
на n единиц масштаба вниз или вверх, а график функции y = |х + m| из графика
функции y
= |х| с помощью параллельного переноса вдоль оси Ох на m единиц масштаба влево или вправо.
А
с другой стороны построить график функции y
= |х — m|
можно из графика функции y = х – m
, оставив без изменения все части графика, которые лежат выше оси абсцисс, а
части расположенные ниже её отобразить симметрично.
2.2.
Построение графиков линейных функций, содержащих несколько знаков модуля.
Построим график
уравнения y=|||х|-2|-2|.
Здесь при построении графика
удобно использовать сдвиги вдоль осей координат. Будем действовать по
следующему плану:
Построим “основной” график, т.е. график уравнения y=|х|;
Подвинем построенный график на 2 единицы вниз; получится график
уравнения y=|х|-2;
Часть графика, расположенную ниже оси х,
заменим ее “зеркальным отражением”, т.е. заменим ее линией, симметричной
относительно оси х; получится график уравнения y=||х|-2|;
Сдвинем построенный в п.3 график на 2 единицы вниз; получится
график уравнения y=||х|-2|-2;
Часть графика, расположенную ниже оси х,
отобразим симметрично относительно этой оси; получим график уравнения y=|||х|-2|-2|.
3.
Построение графика квадратичной функции, содержащей переменную под знаком
модуля.
…Математические
сведения могут применяться умело и с пользой только в том случае, если они
усвоены творчески, так, что учащийся видит сам, как можно было бы прийти к ним самостоятельно.
А.Н. Колмогоров.
Для
построения графиков функций, содержащих знак модуля, как и при решении
уравнений, сначала находят корни выражений, стоящих под знаком модуля. В
результате ось Ох разбивается на промежутки. Убираем знаки модуля, беря каждое
выражение в каждом промежутке с определённым знаком, которые находим методом
интервалов.
В
каждом промежутке получается функция без знака модуля. Строим график каждой
функции в каждом промежутке.
В
простейшем случае, когда только одно выражение стоит под знаком модуля и нет
других слагаемых без знака модуля, можно построить график функции, опустив знак
модуля, и затем часть графика, расположенную в области отрицательных значений
y, отобразить относительно оси Ох.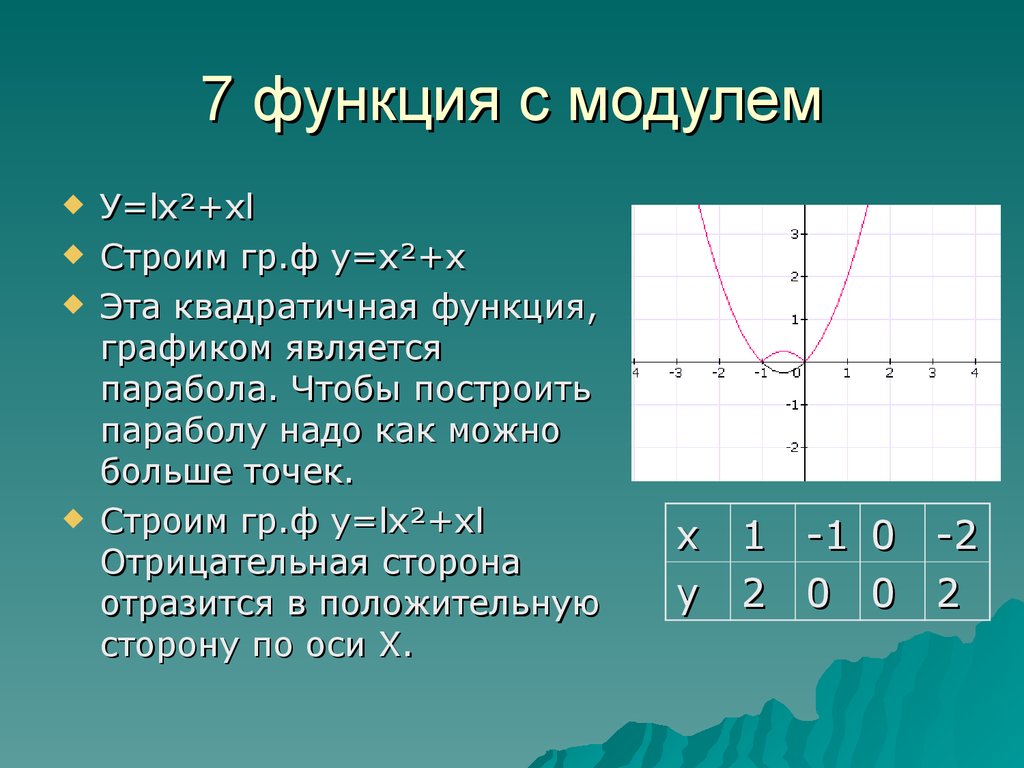
Покажем
на примерах некоторые приемы построения графиков функций с модулями.
Пример
1.
Построим
график функции у = |х2 – 6х +5|.
Сначала
построим параболу у= х2– 6х +5. Чтобы получить из неё график функции
у = |х2 — 6х + 5|, нужно каждую точку параболы с отрицательной
ординатой заменить точкой с той же абсциссой, но с противоположной
(положительной) ординатой. Иными словами, часть параболы, расположенную ниже
оси Ох, нужно заменить линией, ей симметричной относительно оси Ох.
Пример
2.
Рассмотрим
график функции у = |х|2– 6х +5.
Т.
к. |х| возводится в квадрат, то независимо от знака числа х после возведения в
квадрат он будет положительным. Отсюда следует, то график функции у =|х|2
— 6х +5 будет идентичен графику функции у = х2 — 6х +5, т.е. графику
функции, не содержащей знака абсолютной величины.
Пример
3.
Рассмотрим
график функции у = х2 – 6|х| +5.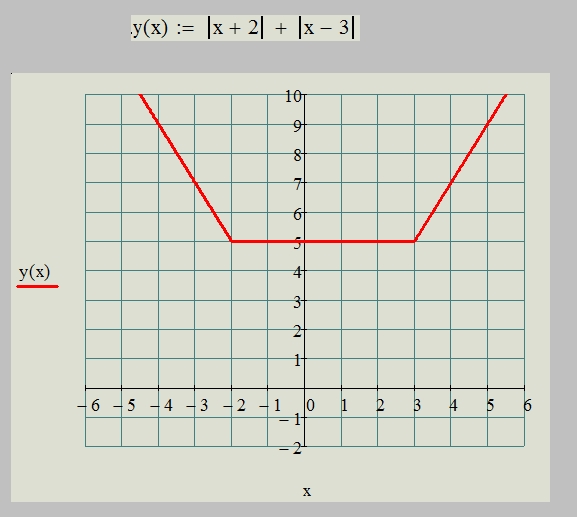
Воспользовавшись
определением модуля числа, заменим формулу
у
= х2 – 6|х| +5
Теперь
мы имеем дело с хорошо знакомым нам кусочным заданием зависимости. Строить
график будем так:
1)
построим параболу у = х2 — 6х +5 и обведём ту её часть, которая
соответствует неотрицательным значениям х, т.е. часть, расположенную правее оси
Оу.
2)
в той же координатной плоскости построим параболу у = х2 +6х +5 и
обведём ту её часть, которая соответствует отрицательным значениям х, т.е.
часть, расположенную левее оси Оу. Обведённые части парабол вместе образуют
график функции у = х2 — 6|х| +5.
Пример
4.
Рассмотрим
график функции у = |х|2 — 6|х|+5.
Т.к.
график уравнения у = |х|2 – 6х +5 такой же, как и график функции без
знака модуля (рассмотрено в примере 2) то следует, что график функции у = |х|2
– 6|х| +5 идентичен графику функции у = х2 – 6|х| +5, рассмотренному
в примере 3 .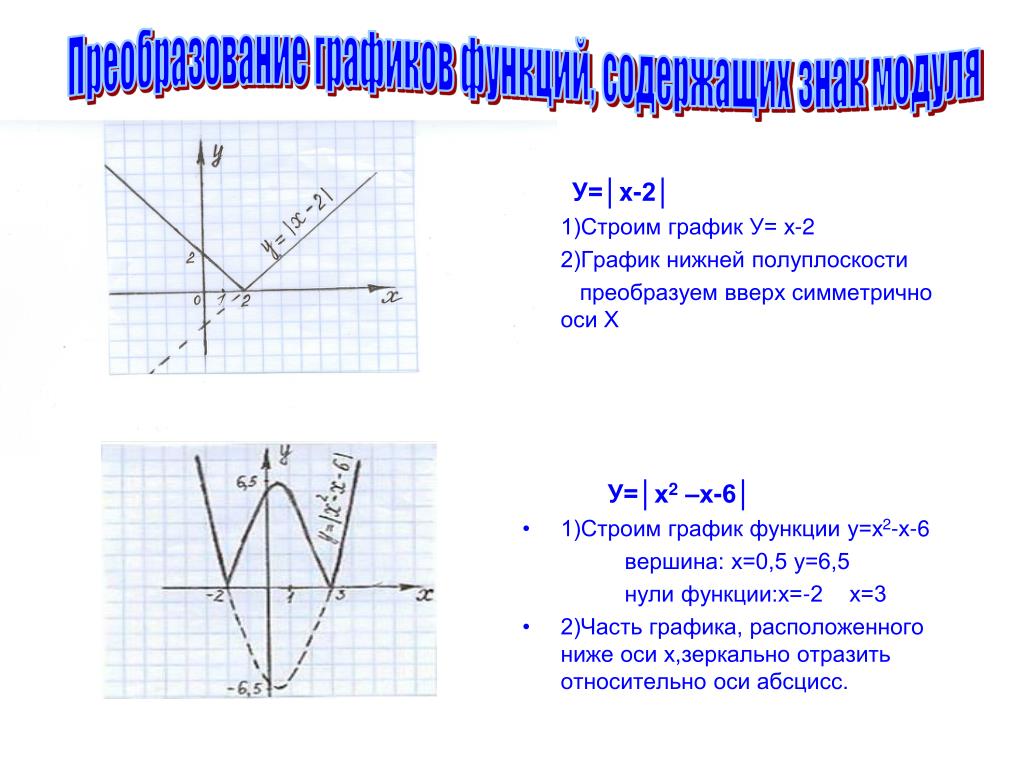
Пример
5.
Построим
график функции у = |х2 – 6х| +5.
Для
этого построим график функции у = х2 — 6х. Чтобы получить из неё
график функции у = |х2 — 6х|, нужно каждую точку параболы с
отрицательной ординатой заменить точкой с той же абсциссой, но с
противоположной (положительной) ординатой. Иными словами, часть параболы,
расположенную ниже оси х, нужно заменить линией ей симметричной относительно
оси х. Т.к. нам нужно построить график функции у = |х2 — 6х| +5, то
график рассмотренной нами функции у = |х2 — 6х| нужно просто поднять
по оси у на 5 единиц вверх.
Пример
6.
Построим
график функции у = х2 — |6х+5|. Для этого воспользуемся хорошо нам
известной кусочной функцией. Найдём нули функции
у
= 6х +5
6х
+ 5 = 0 при х = ̶
Рассмотрим
два случая:
1)Если
х ̶ , то
уравнение примет вид у = х2 – 6х -5. Построим эту параболу и обведём
ту её часть, где х ̶ .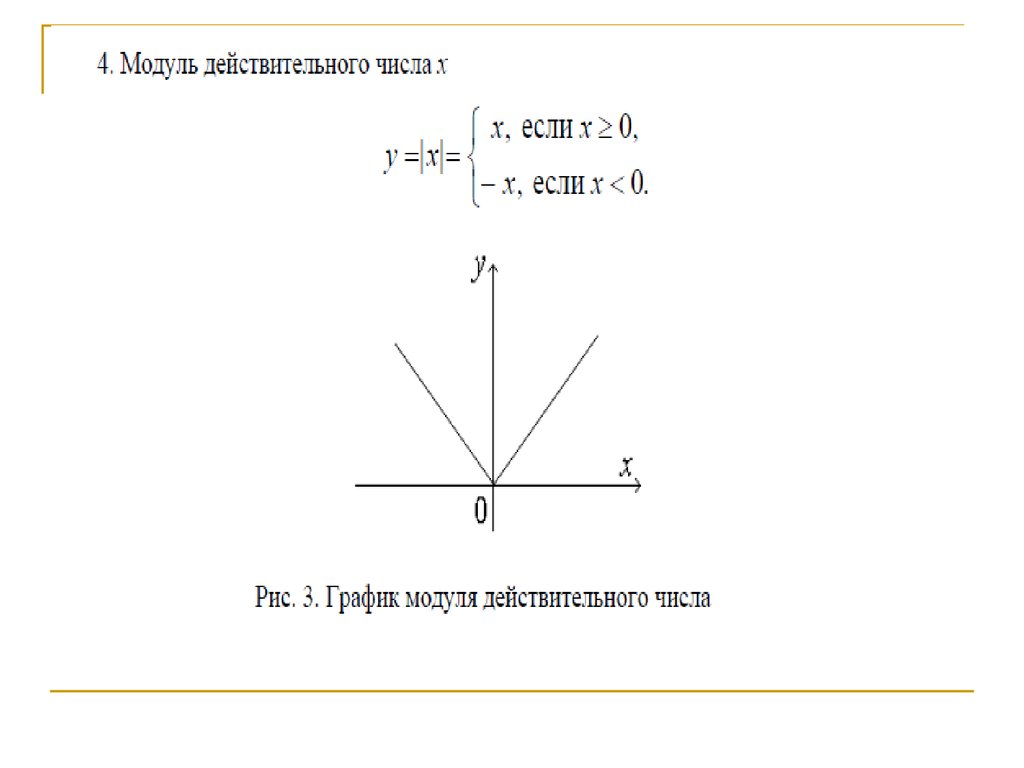
2)Если
х ̶ , то
уравнение принимает вид у = х2+ 6х +5. Построим эту параболу и
обведём ту её часть, которая расположена левее точки с координатами х = ̶.
Пример
7.
Построим
график функции у = |х2 – 6|х| +5|.
Для
этого мы построим график функции у =х2— 6|х| +5. Построение этого
графика мы проводили в примере 3. Т. к. наша функция полностью находится под
знаком модуля, то для того, чтобы построить график функции у = |х2 –
6|х| +5|, нужно каждую точку графика функции у = х2 – 6|х|+5 с
отрицательной ординатой заменить точкой с той же абсциссой, но с
противоположной (положительной) ординатой, т.е. часть параболы, расположенную
ниже оси Ох, нужно заменить линией ей симметричной относительно оси Ох.
3.1. Подготовка к ОГЭ. № 23. Постройте график функции у = х2 – 6|x| + 8. Какое наибольшее
число общих точек график данной функции может иметь с прямой, параллельной оси
абсцисс.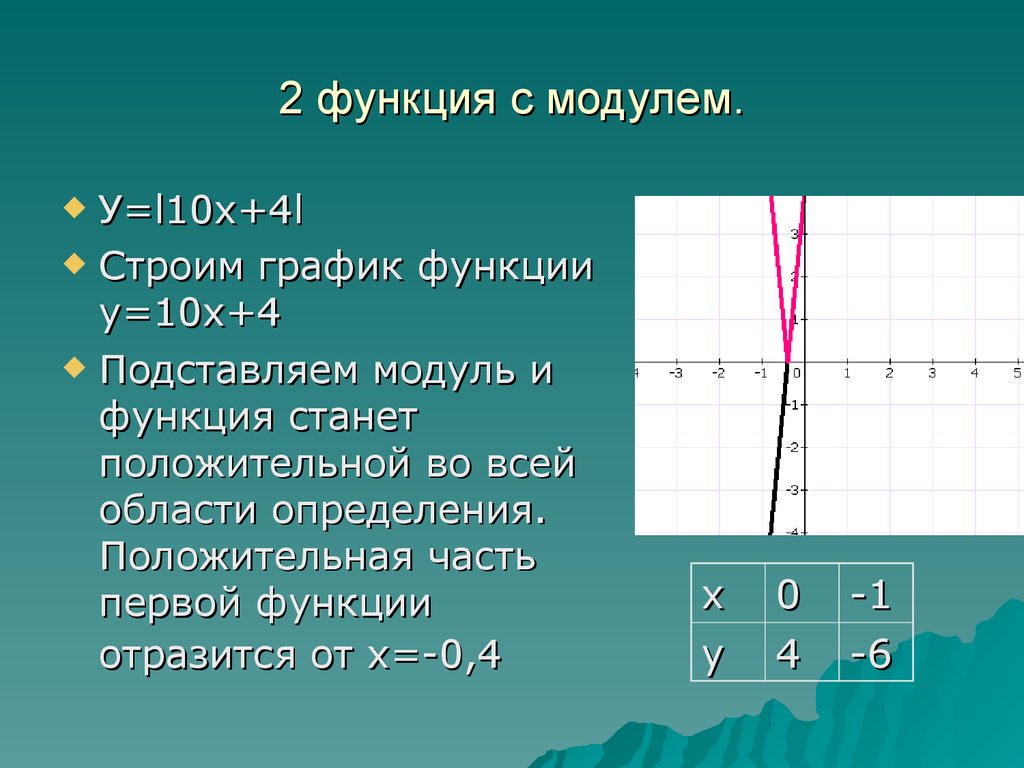
Решение.
Приложение 3.
Заключение.
При выполнении
исследовательской работы я делала такие выводы:
— сформировала алгоритмы
построения графиков функций, аналитическое выражение которых содержит знак
абсолютной величины.
Алгоритм
построения графика функции у=f |(х)|
1.Построить
график функции у=f(х) для х>0;
2.Построить для х<0 часть
графика, симметричную построенной относительно оси ОУ.
Алгоритм
построения графика функции у=|f(х) |
1.Построить график
функции у=f(х) ;
2. На участках,
где график расположен в нижней полуплоскости, т.е., где f(х) <0,
строить кривые, симметричные построенным графикам относительно оси абсцисс.
Алгоритм
построения графика функции у=|f |(х)| |
1. Построить
график функции у=f(х) для х>0.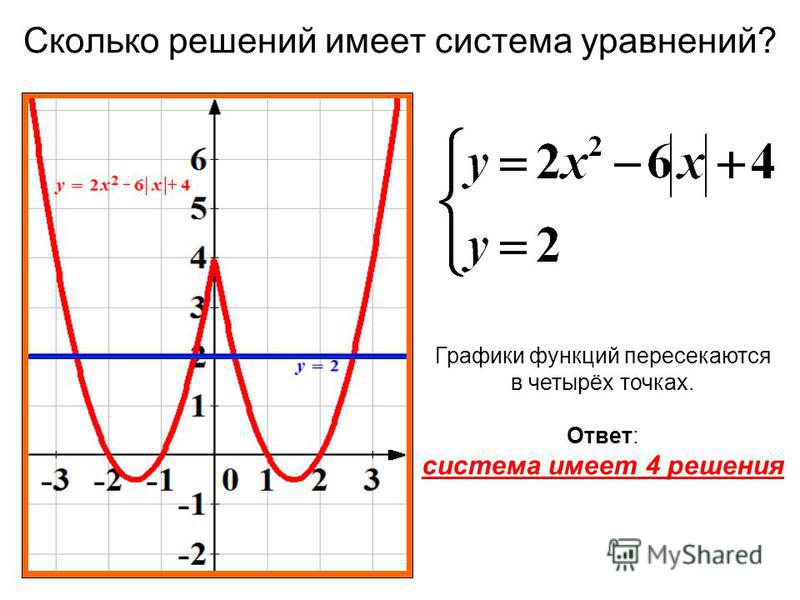
2. Построить
кривую графика, симметричную построенной относительно оси ОУ, т.к. данная
функция четная.
3. Участки графика,
расположенные в нижней полуплоскости, преобразовывать на верхнюю полуплоскость
симметрично оси ОХ.
— приобрела опыт
построения графиков таких функций, как:
у=f |(х)|; у = | f (х)|; у=|f |(х)|
|;
— научилась
работать с дополнительной литературой и материалами, производить отбор научных
сведений;
— приобрела
опыт выполнения графических работ на компьютере.
После
того как я провела опрос среди учеников школы я пришла к выводу что правильно
строить графики функций с модулем могут немногие. А именно среди учеников 7
класса всего 10 человек, среди 8 класса 6 человек, среди 9 класса 4 человека.
Теперь
мы можем сделать вывод, что графиков функций с модулем большое разнообразие,
и каждый человек должен знать самые основные, а кто интересуется графиками, тому
будет интересно рассмотреть примеры более трудных графиков.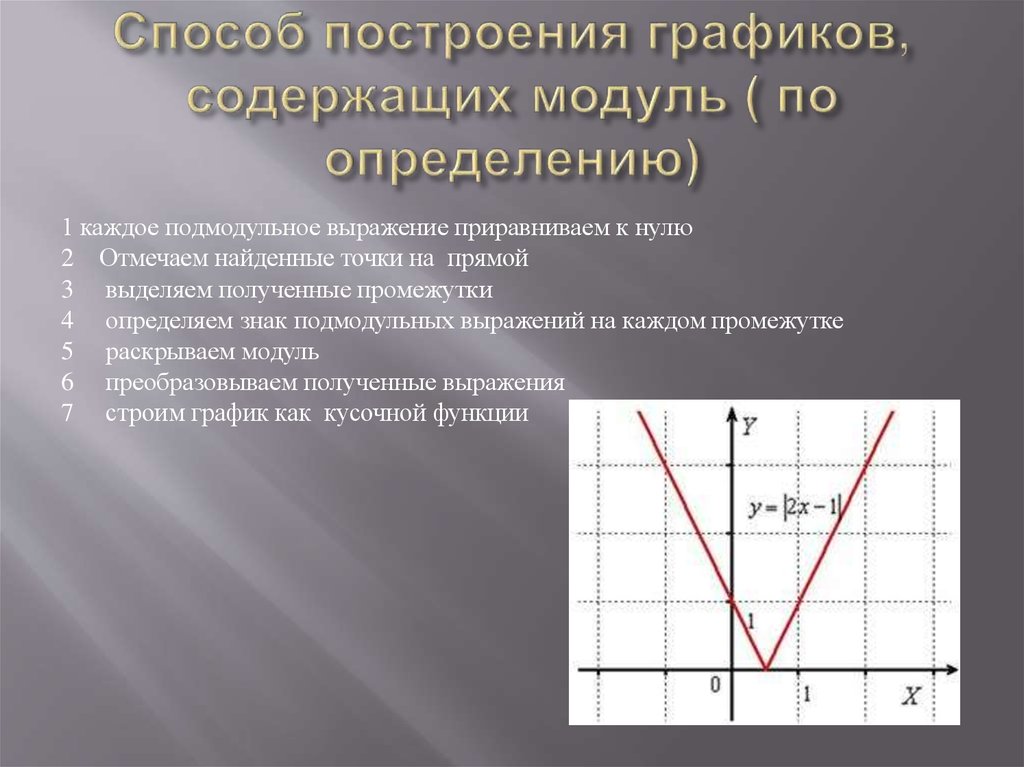
Литература
и интернет ресурсы
1.П.Ф. Севрюков,
А.Н. Смоляков. Уравнения и неравенства с модулями и методика их решения. Москва.
Ставрополь. 2005г.
2.Литвиненко В.Н.,
Мордкович А.Г.. Практикум по элементарной математике. Алгебра. Тригонометрия.
Москва. «Просвещение».1991г.
3.Сборник тестовых
заданий по алгебре к государственной (итоговой) аттестации в новой форме. Под
редакцией Е.А. Семенко. Краснодар.2006
4. ФИПИ.
Федеральный институт педагогических измерений http://5fan.info/qasotrjgeyfsbewpol.html
5. История математики под редакцией А. П.
Юшкевича в трёх томах, том II. — М.: Наука, 1970 Математика XVII столетия.
6. И. М.Гельфанд,
Е.Г. Глаголева. Функции и графики. Издательство «Наука»
7.
Р.А. Калнин. Алгебра и элементарные функции. Издательство «Наука»
8.
М.К. Потапов, С.Н. Олехник. Конкурсные задачи по математики, Москва.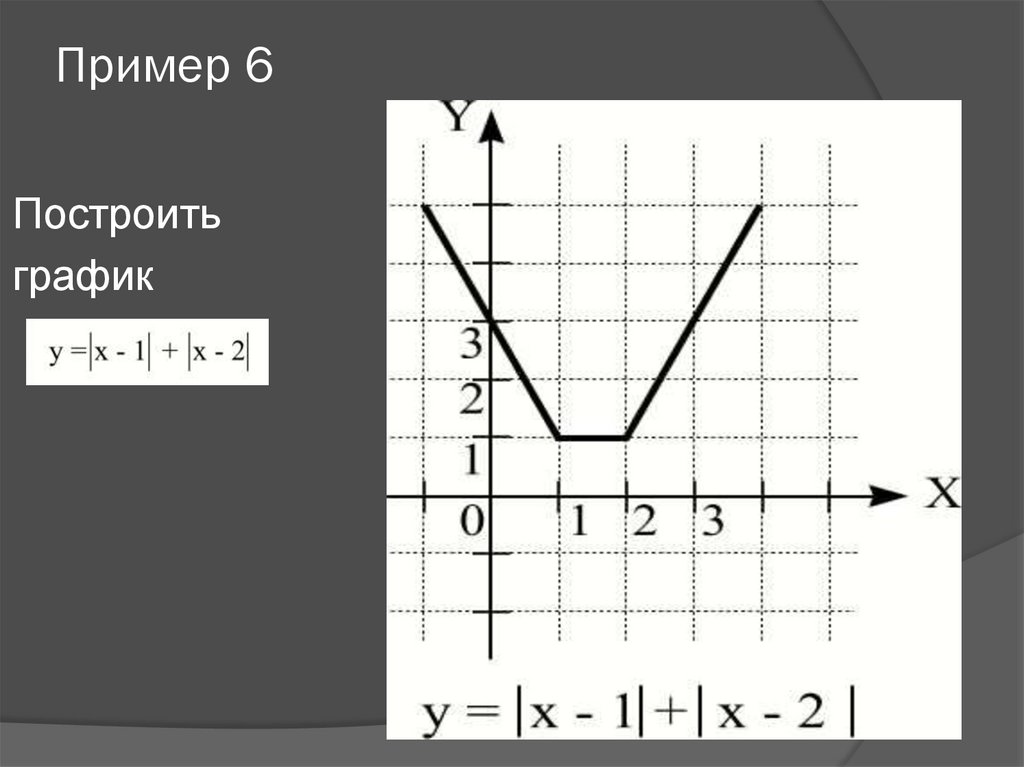
9.
Ю. Н.Макарычев, Н.Г. Миндюк. Дополнительные главы к школьному учебнику. Москва,
«Просвещение».
Приложение
1.
Приложение
2.
Приложение
3
Графики функций, содержащие знак модуля
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике.
1. Построение графиков функций, содержащих знак модуля
Десятниченко В. И.
2. ОПРЕДЕЛЕНИЕ МОДУЛЯ
f ( x), где f ( x) 0
f ( x)
f ( x), где f ( x) 0
3. Алгоритм построения графика функции
1.Строим график функции y=f(x).
2. Участки графика, лежащие выше
оси абсцисс, оставить без изменения.
3. Участки, лежащие ниже оси
абсцисс, зеркально отобразить
относительно этой оси.
4. Пример 1. Построить график функции
5. Алгоритм построения графика функции
1. Построим график функции y=f(x).
2. Удалим точки графика y=f(x),
находящиеся слева оси OY.
3. Все точки, лежащие на оси OY и
справа от неё, отразим симметрично
относительно оси OY.
6. Пример 2.Построить график функции
Выполняем последовательно
построения по алгоритму.
7. Пример 2.
Получим в итоге график.
8. Алгоритм построения графика функции
1. Построить график функции y=f(x) для
x>=0.
2. Отобразить построенную часть
графика симметрично относительно оси
ординат.
3. Участки полученного графика,
лежащие ниже оси абсцисс, зеркально
отобразить относительно этой оси.
9. Пример3. Построить график функции
1 способ.
10. 2 способ
11. Алгоритм построения графика
1. Строим график функции y=f(x).
2. Строим график функции
3. Осуществить его зеркальное
отображение относительно оси Ox.
12. Пример 4. Построить график функции
Строим по алгоритму.
13. Пример 5
Построить график
14. Алгоритм построения графика
1. Найдите абсциссы точек
«перелома» графика функции: x=x1,
x=x2,x=x3,…,x=xn.
2.Рассмотреть функцию на каждом из
полученных промежутков.
15. Пример 6
Построить
график
16. Алгоритм построения графика функции
1.
2.
Найти абсциссы точек «перелома»
графика функции.
Использовать способ, связанный с
геометрическими преобразованиями.
17. Пример 7
Построить
график
функции
k=2
b=1
c=2
18. Построение графиков функций аналитические выражения которых содержат знак модуля, выраженных неявно.
Рассмотрим пример. Построить график
функции
.По определению
абсолютной величины
. График этой
«функции» симметричен как относительно оси
Ох, так и относительно оси Oy. Построим его
лишь для первой координатной четверти, а
затем посредством двух зеркальных
отражений получим окончательный график.
19. Пример 8
Построить график
20. Следующий этап построения.
Строим график функции
21. Пример 9. Построить график функции
По определению модуля
Так как график «функции»
симметричен относительно двух осей,
построим его сначала для первой
координатной четверти. При этом
уравнение функции примет вид
22. Второе уравнение имеет решение х=2, y=0.
Рассмотрим первое уравнение.
а) y=x+2, при 0≤x≤2 и x-2≤0
б) y=6-x, при x>2 и x-2>0.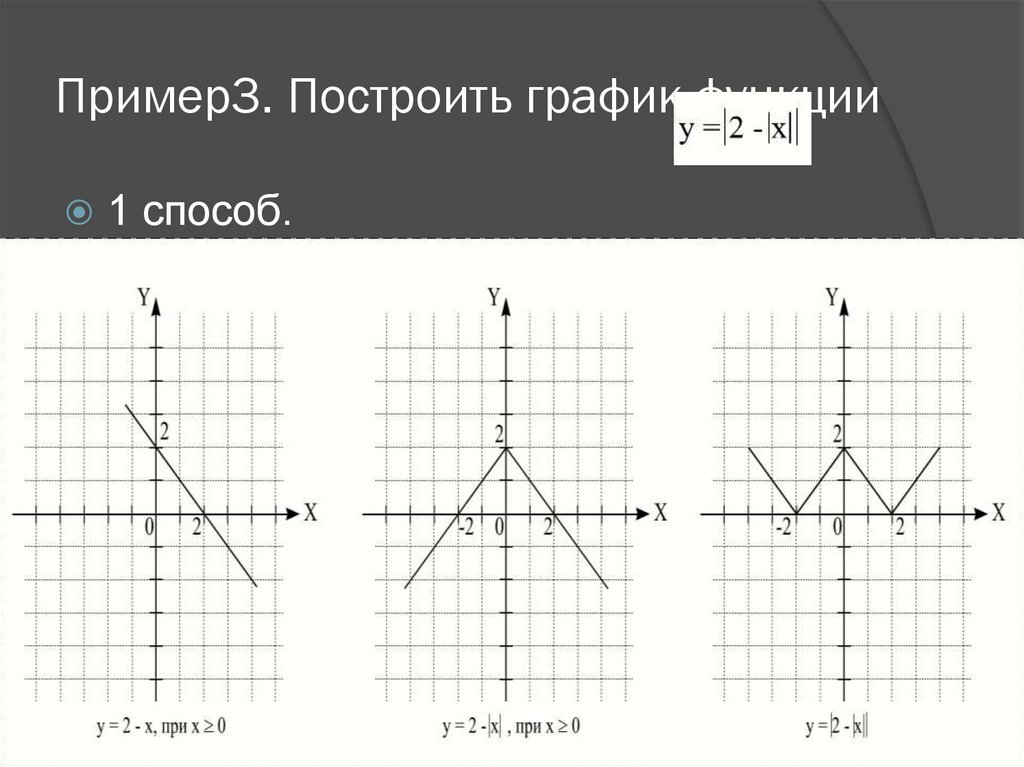
Строим графики полученных прямых
в первой четверти.
23. График функции
Строим в первой координатной
четверти.
x 2 y 4
24. Осуществим двукратное зеркальное отражение.
Относительно оси оX и относительно
оси оY. Получим в итоге следующий
график.
25. Итог работы.
В работе рассмотрены основные
случаи построения графиков
функций, которые содержат знак
модуля.
English
Русский
Правила
Графический модуль на Python
Графика – самая интересная тема для начала изучения любого языка программирования, особенно для детей и разработчиков графических игр. Применение графики в области программирования и компьютерных наук бесконечно.
Хотя в этой статье много говорится о Графика в Python , учащимся также важно иметь полное представление о Компьютерная графика как об отдельном предмете. Это потому, что каждый пиксель и разрешение экрана, соотношение сторон являются важными компонентами, которые компьютерная графика обслуживает в каждой системе.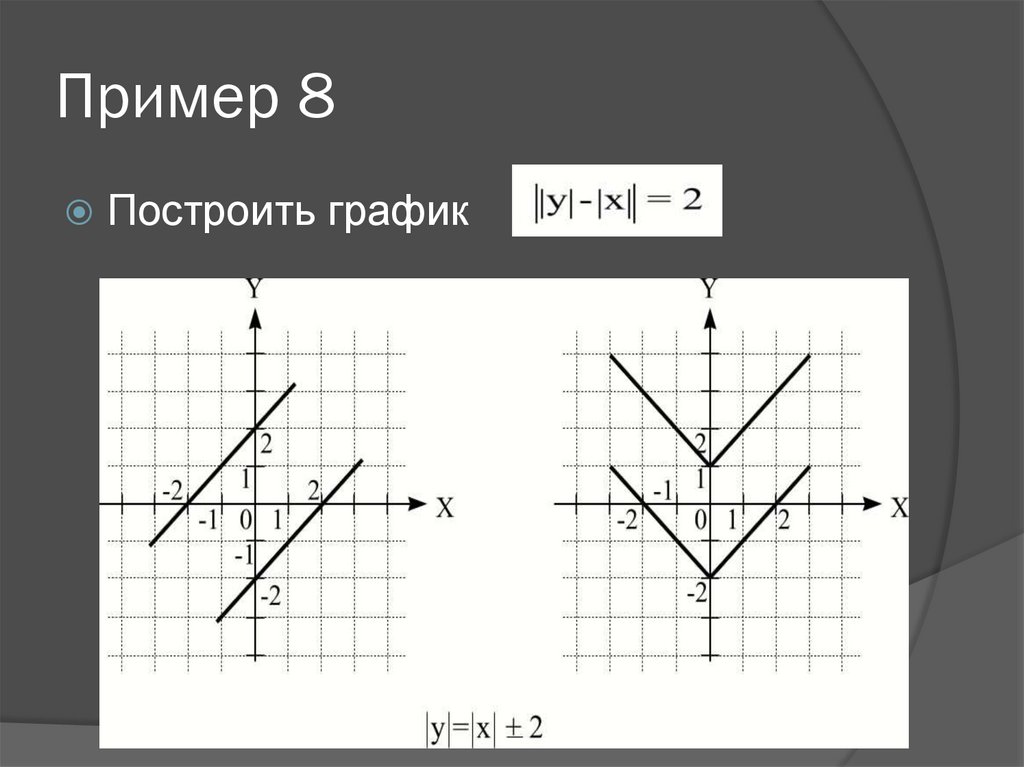
В этой статье вы узнаете, как графический модуль в Python позволяет рисовать простые объекты, используя функции , такие как GraphWin(), Point(), Circle() и многие другие. Вы будете создавать реальную графику с использованием этих объектов .
Ниже приведен список затронутых тем:
- Шаги по созданию графики в Python
- Особенности графического окна
- Создание различных типов графических объектов
- Реализация реальных графических примеров
Шаги для создания графики
Создание графики в Python содержит несколько основных и фиксированных шагов:
- Импорт всех библиотек из класса графики
- Создать объект окна
- Нарисуйте объекты в созданном окне.
- Закройте окно.
Например:
шаг 1: из импорта графики *
шаг 2: выигрыш = GraphWin()
шаг 3: pt = Point(100, 50) #100 указывает горизонтальную координату, а 50 указывает вертикальную координату pt. draw(win)
шаг 4: win.close()
draw(win)
шаг 4: win.close()
Графическое окно
Вы можете создать графику внутри окна, используя метод GraphWin() , который создает новое окно где-то под другим окном. Чтобы просмотреть его, вы можете перетащить его вверх. Это окно по умолчанию помечено как «Графическое окно» и создает окно по умолчанию 9.0003 Окно 200 X 200 пикселей.
пикселя (Элемент изображения) не что иное, как крошечный квадрат отображаемый на вашем экране, обычно на экране 1000 пикселей и больше количество пикселей в строке больше разрешение экрана и лучше качество изображения станет. Это потому, что каждый пиксель может хранить более детальный элемент изображения.
Графическое окно по умолчанию
Метод GraphWin() может принимать три аргументы :
- Заголовок графического окна.
- X-координата (длина графического окна).
- Y-координата (высота графического окна).
Например:
из импорта графики *
win = GraphWin("painting", 300, 300)
Вывод:
Графическое окно с рисованием этикетки и определенными координатами
Графические объекты
Точечный объект
Точка : для создания точечного объекта можно использовать метод Point() с координатами X и Y .
Пример:
баллов = точка (50, 50)
Чтобы отобразить точку в графическом окне, вы можете использовать pt.draw(win).
Выход:
Круг объект
Круг : Чтобы создать круг, вы можете использовать Circle() метод и иметь центр в определенной точке, pt = Point(50, 50) и радиус 50.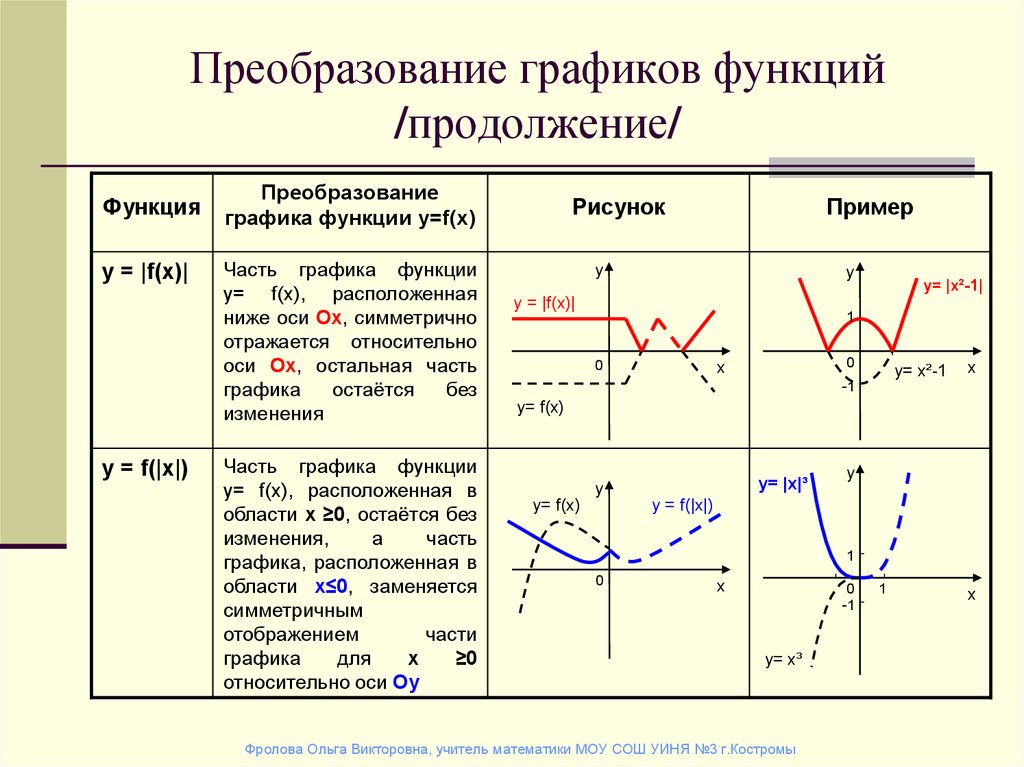
Пример:
cir = Круг (pt, 50)
cir.draw(win)
Вывод:
Цвет контурного круга по умолчанию черный. Вы можете использовать цвета для контура круга , а также внутри круга.
Например:
cir.setOutline('синий')
cir.setFill('pink')
Вывод:
Line Object
Line : Линия – это отрезок между двумя точками, поэтому для начертания линии вам потребуется определить две точки .
Например:
строка = Линия (Точка (100, 50), Точка (150, 100))
line.draw(win)
Прямоугольник Объект
Прямоугольник : Прямоугольник определяется двумя точками, и эти две точки должны располагаться по диагонали напротив друг друга.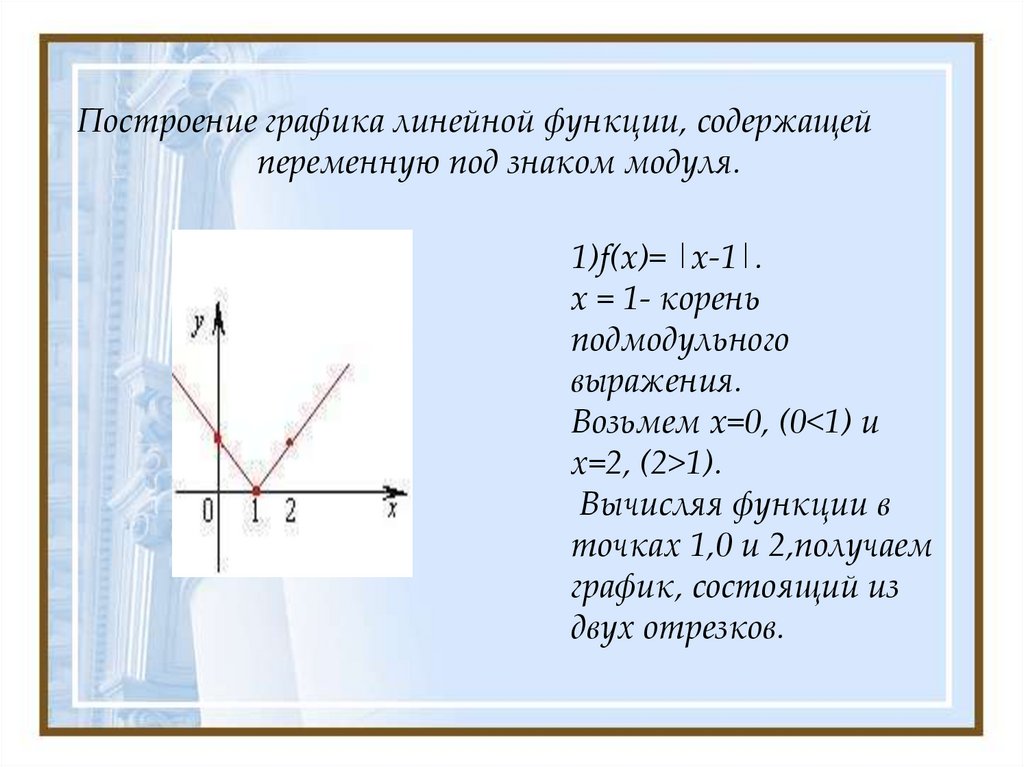
Например:
баллов = точка (50, 50)
прямоугольник = прямоугольник (точка (20, 10), точка)
rect.draw(win)
Вывод:
Овальный объект
Овал : Вы можете определить объект овальной формы, указав две точки, которые определяют ограничивающую рамку.
Например:
овал = овал(точка (30, 90), точка (50, 85))
oval.draw(win)
Вывод:
Графическая реализация
Теперь, когда вы узнали некоторые базовые реализации объектов . Вы можете использовать их для создания графики по вашему выбору. Рассмотрим пример создания человеческого лица. Для этого вам потребуется круг, линия и овальный объект, как показано в следующем коде.
из импорта графики *
#создание графического окна с именем Face и установка координат окна
выигрыш = ГрафикВыигрыш('Лицо', 200, 150)
win. setCoords(0,0,200,150)
#создание контура лица с помощью Circle() и закрашивание его розовым цветом
face = Circle(Point(40,100), 25) # установить центр и радиус
face.setFill("розовый")
face.draw(победа)
#создаем глаза из кругов и рисуем их синим цветом
глаз1 = Круг(Точка(30, 105), 5)
глаз1.setFill('синий')
eye1.draw(победа)
глаз2 = Круг(Точка(45, 105), 5)
eye2.setFill('синий')
eye2.draw(победа)
# Создание носа с помощью Line()
нос = Линия(Точка(35, 95), Точка(45, 95))
нос.setWidth(3)
нос.дро(победа)
# Создание рта с помощью Oval()
рот = овал (точка (30, 84), точка (50, 79))
рот.setFill ("красный")
рот.рисовать(победа)
выиграть.получитьмышь()
win.close()
setCoords(0,0,200,150)
#создание контура лица с помощью Circle() и закрашивание его розовым цветом
face = Circle(Point(40,100), 25) # установить центр и радиус
face.setFill("розовый")
face.draw(победа)
#создаем глаза из кругов и рисуем их синим цветом
глаз1 = Круг(Точка(30, 105), 5)
глаз1.setFill('синий')
eye1.draw(победа)
глаз2 = Круг(Точка(45, 105), 5)
eye2.setFill('синий')
eye2.draw(победа)
# Создание носа с помощью Line()
нос = Линия(Точка(35, 95), Точка(45, 95))
нос.setWidth(3)
нос.дро(победа)
# Создание рта с помощью Oval()
рот = овал (точка (30, 84), точка (50, 79))
рот.setFill ("красный")
рот.рисовать(победа)
выиграть.получитьмышь()
win.close()
Вывод:
Графика лица с использованием Python
Точно так же вы можете создавать более сложную и красивую графику, используя модуль Graphics и его методы.
Несколько случайных объектов
Если вы когда-либо использовали ОС Windows , вы, возможно, сталкивались с кругами разного цвета и размера , которые появляются на экране в качестве заставки .
Пример кода для создания случайных круглых объектов:
из импорта графики *
импорт случайный, время
win = GraphWin("Случайные круги", 300, 300)
#создание 75 случайных круглых объектов
для круга в диапазоне (75):
#randrange принимает один целочисленный аргумент, который определяет интенсивность красного, синего и зеленого цветов.
г = случайный.randrange(100)
b = случайный.randrange(100)
г = случайный.randrange(100)
цвет = color_rgb (г, б, г)
#создание круглых объектов с разным радиусом от 3 до 40
радиус = случайный.randrange(3, 40)
х = случайный.randrange(5, 295)
y = случайный.randrange(5, 295)
круг = круг (точка (x, y), радиус)
#раскрашивание круглых объектов разными цветами
круг. setFill(цвет)
Circle.draw (выигрыш)
#время, необходимое для появления каждого кругового объекта
time.sleep(.05)
setFill(цвет)
Circle.draw (выигрыш)
#время, необходимое для появления каждого кругового объекта
time.sleep(.05)
Вывод:
Заключение
Хотя есть много других модулей Python, таких как Turtle, Matplotlib, Tkinter, Deep Painterly Harmonization, Bokeh и т. д., которые помогают сделать потрясающую графику, но этот модуль является одним из самых быстрых и имеет широкий спектр методов, позволяющих с легкостью отображать любую графику.
В этой статье вы узнали о том, как графический модуль помогает вам рисовать с помощью Python, об основном наборе шагов, необходимых для любого типа создания графики, и о том, как создавать основные объекты.
Вы можете экспериментировать и исследовать больше с этими объектами и создавать сложную замечательную графику. Возможности и функциональные возможности Graphics безграничны, и каждый программист на Python должен иметь четкое представление о том, как реализовать его функцию и различные связанные с ней операции.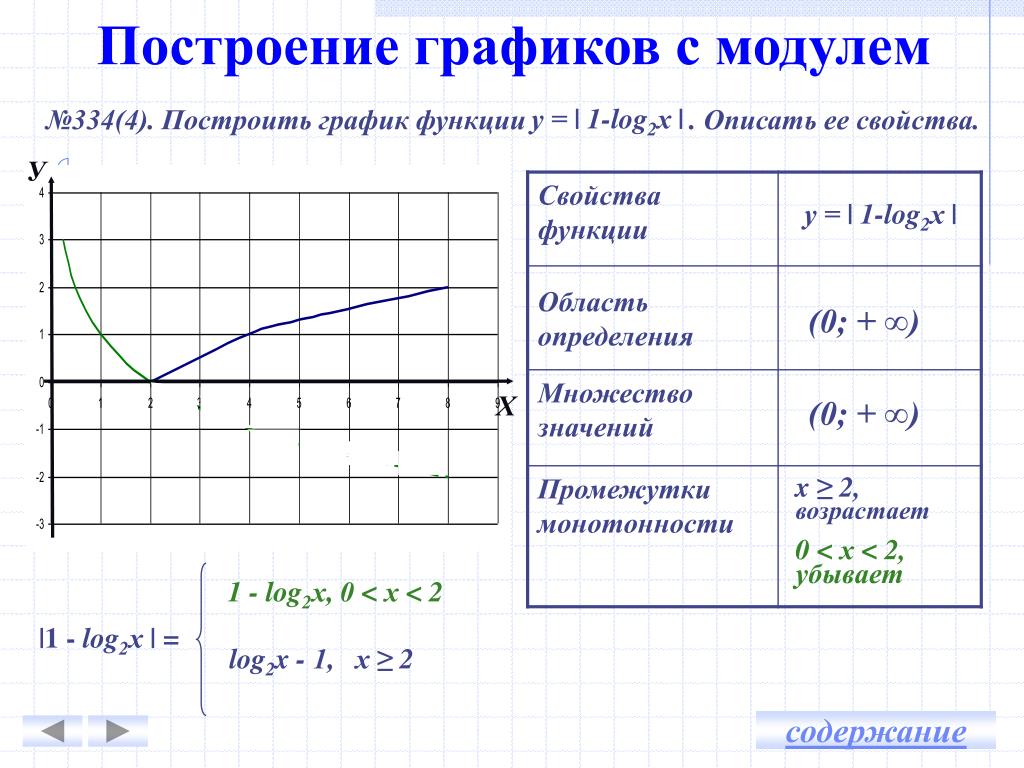
Графическая библиотека
Графическая библиотека
В этой главе описываются переносимые графические примитивы, которые поставляются
стандарт в реализации Caml Light на микрокомпьютерах.
- Unix:
- На рабочих станциях Unix с системой Windows X11
реализация графических примитивов доступна в
каталог contrib/libgraph в дистрибутиве. Посмотреть файл
README в этом каталоге для получения информации о сборке и использовании
camlgraph, система верхнего уровня, включающая графические примитивы,
и связывание автономных программ с библиотекой. Происходит розыгрыш
в отдельном окне, которое создается при вызове open_graph.
- Mac:
- Графический примитив доступен из автономного
приложение, которое запускает систему верхнего уровня. Они недоступны из
программы, скомпилированные camlc и работающие под оболочкой MPW. Рисунок
происходит в отдельном окне, которое можно сделать видимым с помощью кнопки
Пункт меню «Показать графическое окно».
- ПК:
- Графический примитив доступен из Windows
приложение, которое запускает систему верхнего уровня. Они недоступны из
программы, скомпилированные camlc и запущенные в командном окне DOS.
Рисование происходит в отдельном окне.
Экранные координаты интерпретируются, как показано на рисунке ниже.
Обратите внимание, что используемая система координат такая же, как и в математике:
y увеличивается от нижней части экрана к верхней части экрана,
а углы измеряются против часовой стрелки (в градусах).
Рисунок прикрепляется к экрану.
Вот спецификации графического режима, поддерживаемые open_graph на
различные реализации этой библиотеки.
- Unix:
- Аргумент open_graph имеет формат
отображаемое имя геометрия «,
где display-name — это имя дисплея X-windows для
подключиться и геометрия является стандартной геометрией X-windows
Технические характеристики. Два компонента разделены пробелом.Любой может
быть опущены, или и то, и другое. Примеры:- open_graph «foo:0»
- подключается к дисплею foo:0 и создает окно с геометрией по умолчанию
- open_graph «foo:0 300×100+50-0»
-
подключается к дисплею foo:0 и создает окно шириной 300 пикселей
на 100 пикселей в высоту, в месте (50,0) - open_graph » 300×100+50-0″
-
подключается к дисплею по умолчанию и создает окно шириной 300 пикселей
на 100 пикселей в высоту, в месте (50,0) - open_graph «»
-
подключается к дисплею по умолчанию и создает окно с
геометрия.
- Mac:
- Аргумент open_graph игнорируется.
- ПК:
- Аргумент open_graph имеет формат
ширина х высота » или
« ширина х высота + х + у «,
где ширина и высота начальные размеры
графические окна, а x и y — положение
верхнем левом углу графического окна.Если опущено,
( ширина , высота ) по умолчанию (600,400) и
( x , y ) по умолчанию (10, 10).
исключение Graphic_failure строки
- Вызывается приведенными ниже функциями, когда они обнаруживают ошибку.
Инициализации
значение open_graph: строка -> единица измерения
-
Показать графическое окно или переключить экран в графический режим.
Графическое окно очищается. Строковый аргумент используется для
передавать дополнительную информацию о желаемом графическом режиме,
размер графического окна и так далее. Его интерпретация
зависит от реализации. Если задана пустая строка, разумный
выбрано по умолчанию.
значение close_graph: единица измерения -> единица измерения
-
Удалите графическое окно или переключите экран обратно на
текстовый режим.
значение clear_graph : единица измерения -> единица измерения
-
Сотрите графическое окно.
значение size_x : единица измерения -> целое число значение size_y : единица измерения -> целое число
-
Возвращает размер графического окна. Координаты экрана
диапазон пикселей превышает 0 .. size_x()-1 и 0 .. size_y()-1.
Рисунки за пределами этого прямоугольника обрезаются, не вызывая
ошибка. Начало (0,0) находится в левом нижнем углу.
Цвета
тип цвет == int
-
Цвет определяется его компонентами R, G, B. Каждый компонент
находится в диапазоне 0..255. Три компонента упакованы в
int: 0xRRGGBB, где RR — две шестнадцатеричные цифры для
красный компонент, GG для зеленого компонента, BB для
синяя составляющая.
значение rgb: int -> int -> int -> цвет
-
rgb r g b возвращает целое число, кодирующее цвет с красным
компонент r, зеленый компонент g и синий компонент b.
r, g и b находятся в диапазоне 0..255.
значение set_color : цвет -> единица измерения
- Установите текущий цвет рисунка.
значение черный : цвет значение белый : цвет значение красный : цвет значение зеленый : цвет значение синий : цвет значение желтый : цвет значение голубой : цвет значение пурпурный : цвет
- Некоторые предустановленные цвета.
значение фона: цвет значение переднего плана: цвет
-
Цвета фона и переднего плана по умолчанию (обычно либо черный,
передний план на белом фоне или белый передний план на
черный фон).
clear_graph заполняет экран фоновым цветом.
Начальный цвет рисунка — передний план.
Рисование точками и линиями
график значений: int -> int -> unit
- Нанесите заданную точку текущим цветом рисунка.
значение point_color : int -> int -> цвет
-
Возвращает цвет заданной точки.
значение moveto : int -> int -> unit
- Разместите текущую точку.
значение current_point : unit -> int * int
- Возвращает позицию текущей точки.
значение lineto : int -> int -> unit
-
Нарисуйте линию с конечными точками текущей точки и заданной точки,
и переместить текущую точку в заданную точку.
значение draw_arc: int -> int -> int -> int -> int -> int -> unit
-
draw_arc x y rx ry a1 a2 рисует эллиптическую дугу с центром
x,y, горизонтальный радиус rx, вертикальный радиус ry, от угла
a1 на угол a2 (в градусах). Текущая точка не изменяется.
значение draw_ellipse: int -> int -> int -> int -> unit
-
draw_ellipse x y rx ry рисует эллипс с центром
x,y, горизонтальный радиус rx и вертикальный радиус ry.
Текущая точка не изменяется.
значение draw_circle: int -> int -> int -> unit
-
draw_circle x y r рисует круг с центром x,y и
радиус р.Текущая точка не изменяется.
значение set_line_width : int -> unit
-
Установите ширину точек и линий, нарисованных с помощью функций, описанных выше.
В X Windows set_line_width 0 выбирает ширину 1 пиксель.
и более быстрый, но менее точный алгоритм рисования, чем тот,
используется, когда указано set_line_width 1.
Текстовый рисунок
значение draw_char : char -> единица измерения значение draw_string : строка -> единица измерения
-
Нарисуйте символ или строку символов с нижним левым углом
в текущей позиции. После рисования устанавливается текущая позиция
в правый нижний угол нарисованного текста.
значение set_font : строка -> единица измерения значение set_text_size : int -> единица измерения
-
Установите шрифт и размер символов, используемые для рисования текста.
Интерпретация аргументов set_font и
set_text_size зависит от реализации.
значение text_size : строка -> int * int
-
Возвращает размеры данного текста, если он был нарисован с помощью
текущий шрифт и размер.
Наполнение
значение fill_rect : int -> int -> int -> int -> unit
-
fill_rect x y w h заполняет прямоугольник нижним левым углом
по x, y, ширине w и высоте h с текущим цветом.
значение fill_poly : (int * int) vect -> unit
-
Залейте заданный многоугольник текущим цветом. Массив
содержит координаты вершин многоугольника.
значение fill_arc : int -> int -> int -> int -> int -> int -> unit
-
Залейте эллиптический сектор пирога текущим цветом.
параметры такие же, как и для draw_arc.
значение fill_ellipse: int -> int -> int -> int -> unit
-
Залейте эллипс текущим цветом.
параметры такие же, как и для draw_ellipse.
значение fill_circle : int -> int -> int -> unit
-
Залейте круг текущим цветом.
параметры такие же, как и для draw_circle.
Изображения
введите изображение
-
Абстрактный тип для изображений во внутреннем представлении.
Внешне изображения представляются в виде матриц цветов.
значение трансп : цвет
-
В матрицах цветов этот цвет представляет собой «прозрачный»
точка: при рисовании соответствующего изображения все пиксели на
экран, соответствующий прозрачному пикселю изображения, будет
не изменяться, в то время как другим точкам будет присвоен цвет
соответствующей точки на изображении. Это позволяет накладывать
изображение поверх существующего фона.
значение make_image : вектор цвета вектор -> изображение
-
Преобразуйте данную цветовую матрицу в изображение.
Каждый подмассив представляет собой одну горизонтальную линию. Все подмассивы
должны иметь одинаковую длину; в противном случае исключение Graphic_failure
Поднялся.
значение dump_image : изображение -> цветной векторный вектор
- Преобразование изображения в цветовую матрицу.
значение draw_image : image -> int -> int -> unit
- Нарисуйте данное изображение с нижним левым углом в заданной точке.
значение get_image : int -> int -> int -> int -> изображение
-
Захват содержимого прямоугольника на экране в виде изображения.
Параметры такие же, как и для fill_rect.
значение create_image : int -> int -> изображение
-
create_image w h возвращает новое изображение шириной w пикселей и h
пикселей в высоту, для использования в сочетании с blit_image.
Исходное содержимое изображения является случайным.
значение blit_image : image -> int -> int -> unit
-
blit_image img x y копирует пиксели экрана в изображение img,
изменение img на месте.Скопированные пиксели находятся внутри
прямоугольник с нижним левым углом в точках x, y, шириной и высотой
равные изображениям.
События мыши и клавиатуры
введите статус =
{мышь_х: интервал; (*координата X мыши*)
мышь_у: интервал; (* Координата Y мыши *)
кнопка: логическое значение; (* верно, если нажата кнопка мыши *)
нажата клавиша: логическое значение; (* верно, если клавиша была нажата *)
key : char } (* символ нажатой клавиши *)
- Чтобы сообщать о событиях.
тип события =
Button_down (* Нажата кнопка мыши *)
| Button_up (*Кнопка мыши отпущена*)
| Key_pressed (* Нажата клавиша *)
| Mouse_motion (*Мышь перемещается*)
| Опрос (* Не ждите, вернитесь немедленно *)
- Чтобы указать события для ожидания.
значение wait_next_event : список событий -> статус
-
Подождите, пока не произойдет одно из событий, указанных в данном списке событий.
происходит, и возвращает состояние мыши и клавиатуры в
то время. Если опрос задан в списке событий, немедленно вернуться
с текущим статусом. Если курсор мыши находится за пределами
графическое окно, поля mouse_x и mouse_y события
вне диапазона 0..size_x()-1, 0..size_y()-1. Нажатия клавиш
ставятся в очередь и удаляются из очереди один за другим, когда Key_pressed
указывается событие.
Опрос мыши и клавиатуры
значение mouse_pos : unit -> int * int
-
Возвращает положение курсора мыши относительно
графическое окно. Если курсор мыши находится за пределами графики
window, mouse_pos() возвращает точку за пределами диапазона
0..size_x()-1, 0..size_y()-1.
значение button_down : единица -> логическое значение
- Возвращает true, если кнопка мыши нажата, иначе false.
значение read_key : единица измерения -> символ
-
Дождитесь нажатия клавиши и верните соответствующий
персонаж.









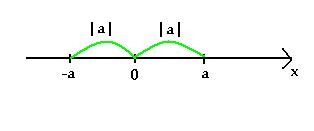
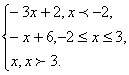
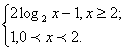
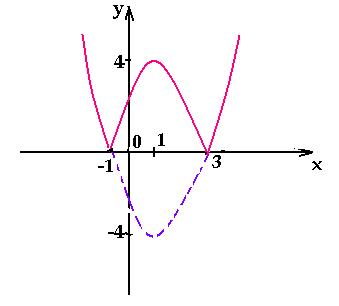
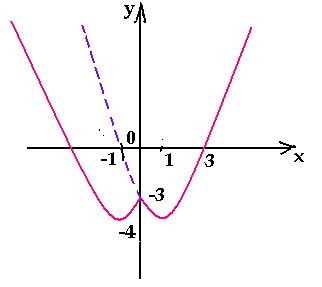
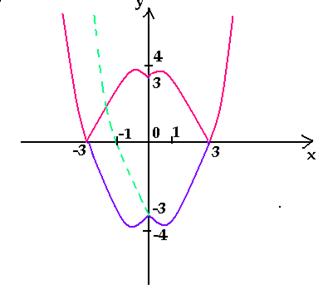
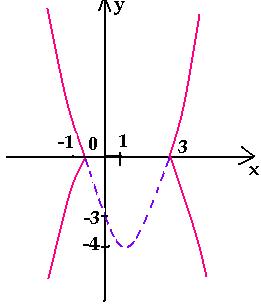
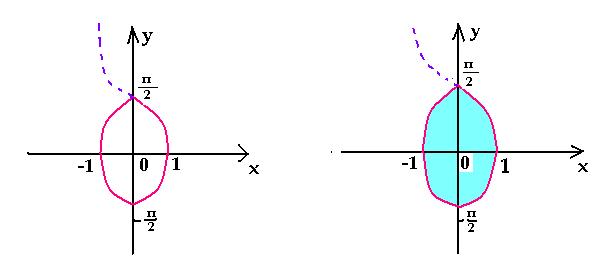
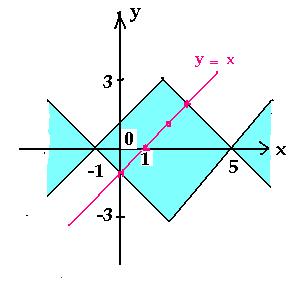
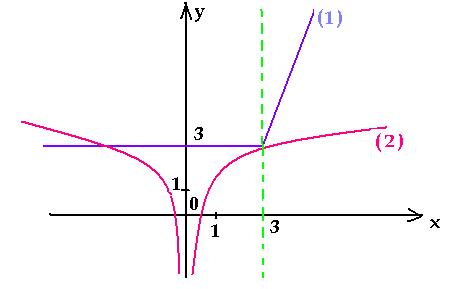
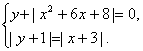
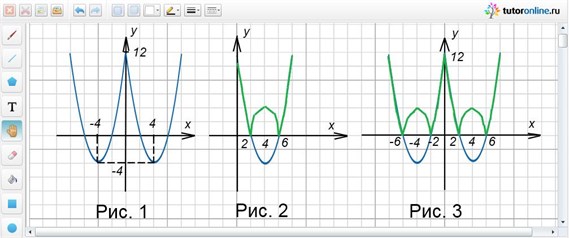
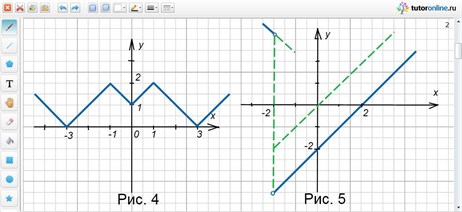
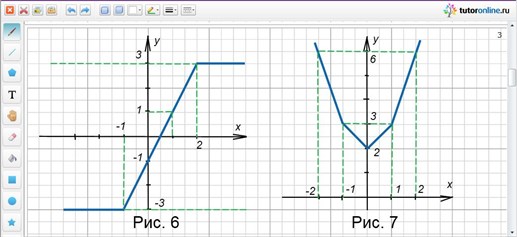

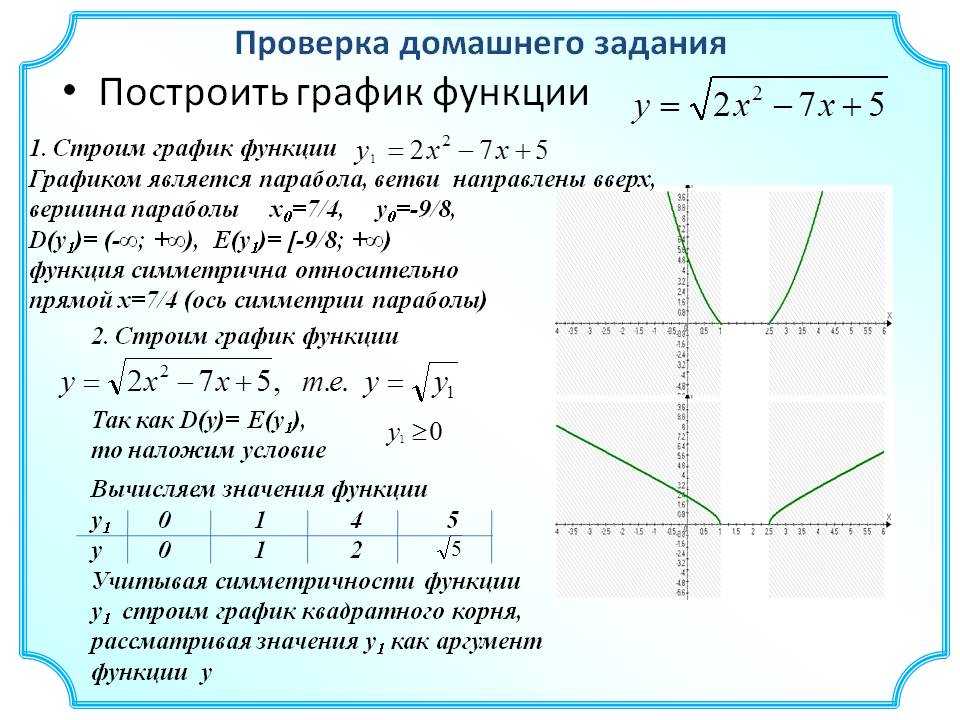
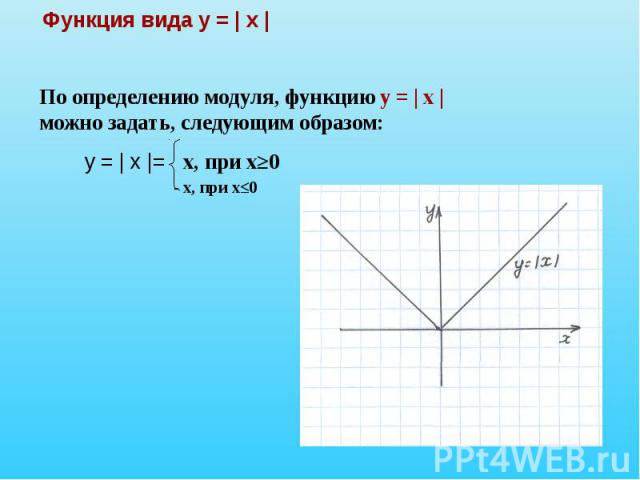
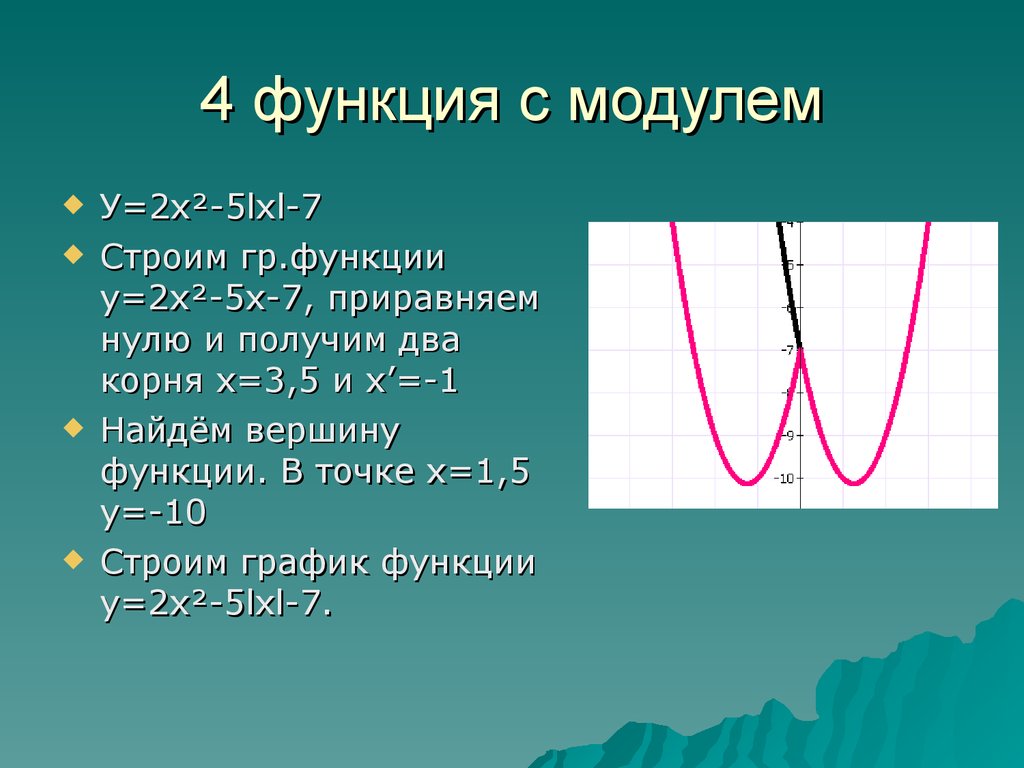

 draw(win)
шаг 4: win.close()
draw(win)
шаг 4: win.close() 
 setCoords(0,0,200,150)
#создание контура лица с помощью Circle() и закрашивание его розовым цветом
face = Circle(Point(40,100), 25) # установить центр и радиус
face.setFill("розовый")
face.draw(победа)
#создаем глаза из кругов и рисуем их синим цветом
глаз1 = Круг(Точка(30, 105), 5)
глаз1.setFill('синий')
eye1.draw(победа)
глаз2 = Круг(Точка(45, 105), 5)
eye2.setFill('синий')
eye2.draw(победа)
# Создание носа с помощью Line()
нос = Линия(Точка(35, 95), Точка(45, 95))
нос.setWidth(3)
нос.дро(победа)
# Создание рта с помощью Oval()
рот = овал (точка (30, 84), точка (50, 79))
рот.setFill ("красный")
рот.рисовать(победа)
выиграть.получитьмышь()
win.close()
setCoords(0,0,200,150)
#создание контура лица с помощью Circle() и закрашивание его розовым цветом
face = Circle(Point(40,100), 25) # установить центр и радиус
face.setFill("розовый")
face.draw(победа)
#создаем глаза из кругов и рисуем их синим цветом
глаз1 = Круг(Точка(30, 105), 5)
глаз1.setFill('синий')
eye1.draw(победа)
глаз2 = Круг(Точка(45, 105), 5)
eye2.setFill('синий')
eye2.draw(победа)
# Создание носа с помощью Line()
нос = Линия(Точка(35, 95), Точка(45, 95))
нос.setWidth(3)
нос.дро(победа)
# Создание рта с помощью Oval()
рот = овал (точка (30, 84), точка (50, 79))
рот.setFill ("красный")
рот.рисовать(победа)
выиграть.получитьмышь()
win.close()  setFill(цвет)
Circle.draw (выигрыш)
#время, необходимое для появления каждого кругового объекта
time.sleep(.05)
setFill(цвет)
Circle.draw (выигрыш)
#время, необходимое для появления каждого кругового объекта
time.sleep(.05) 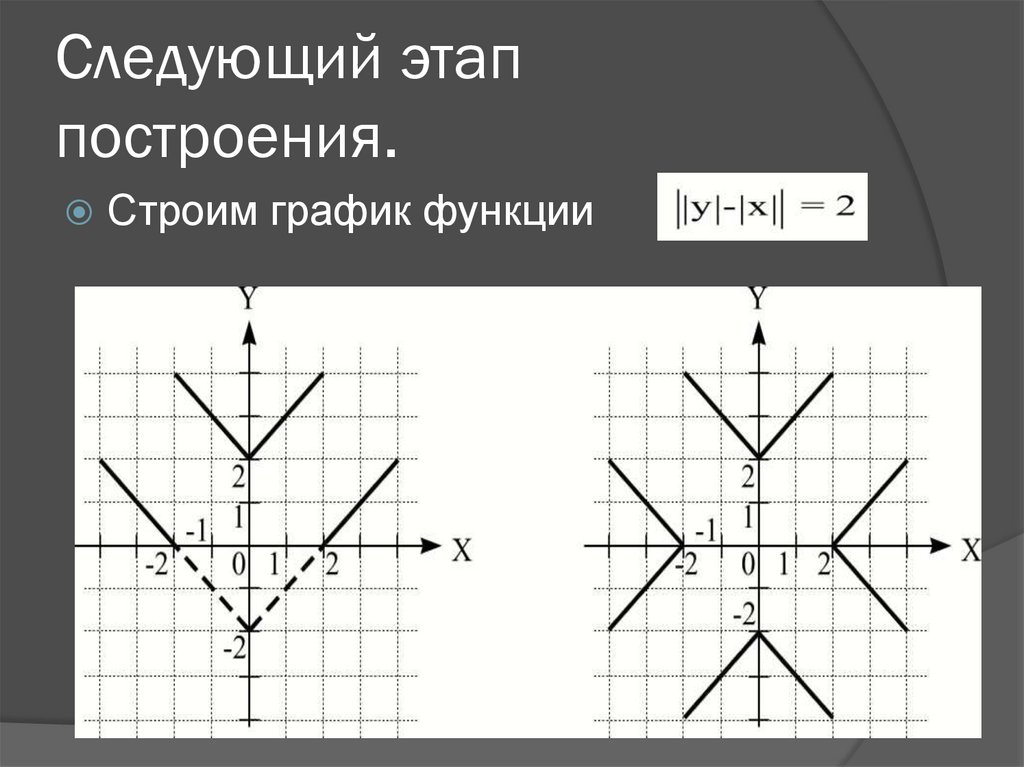
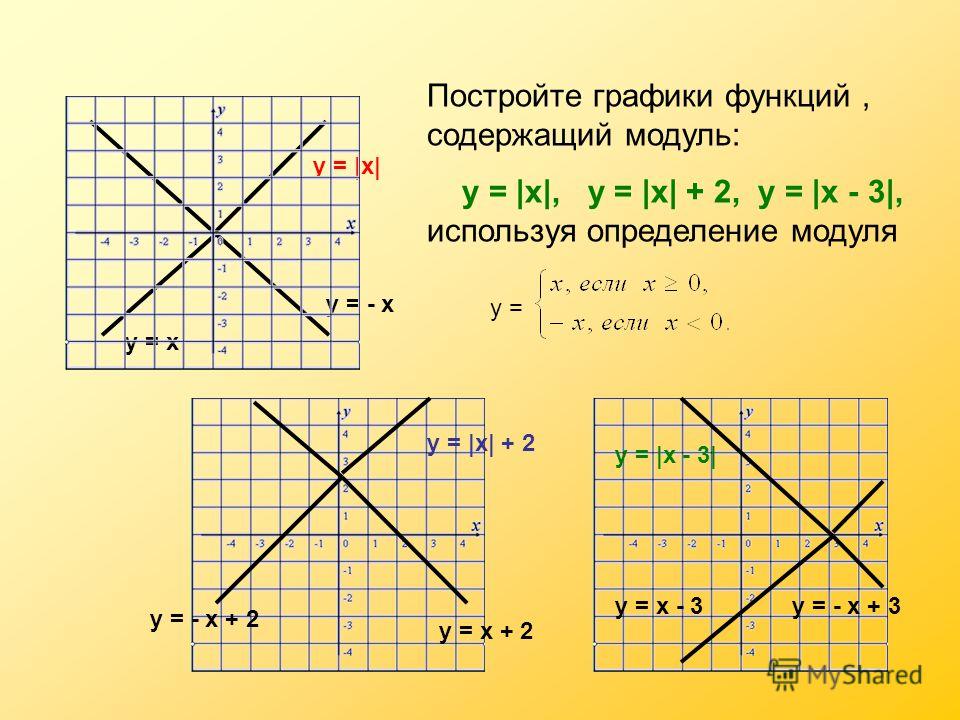 Любой может
Любой может Если опущено,
Если опущено,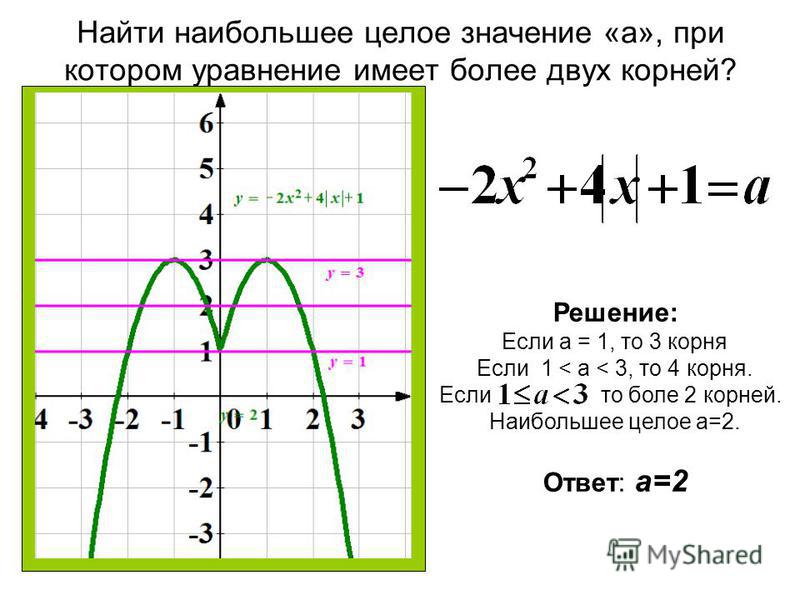
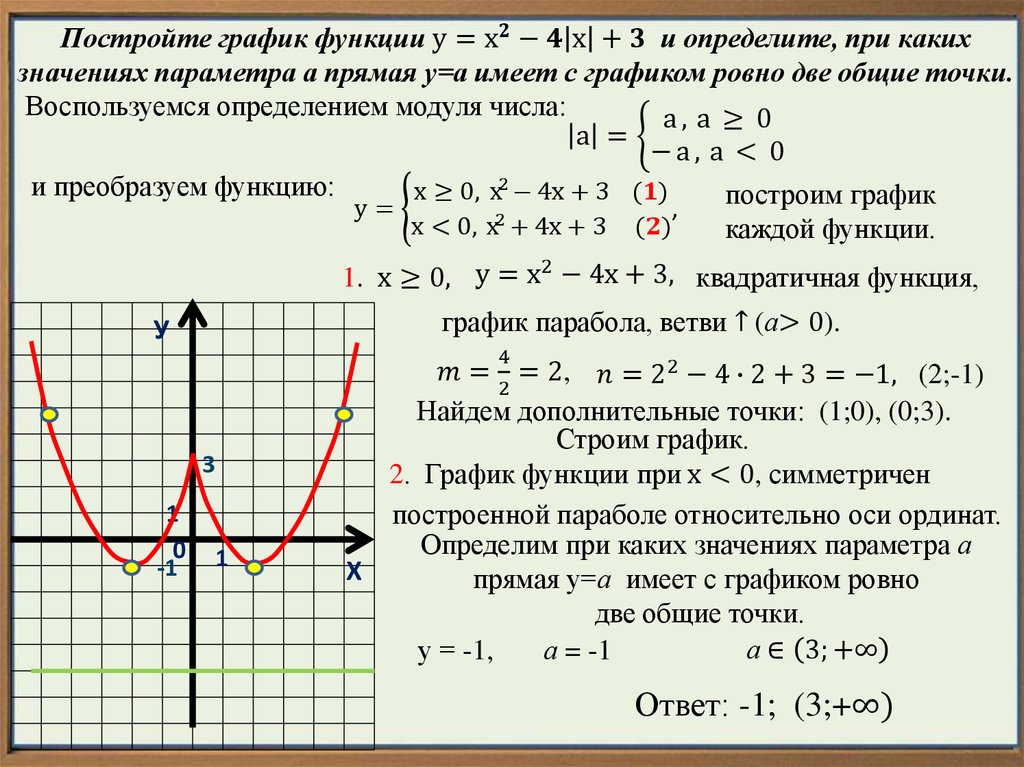 .255.
.255.
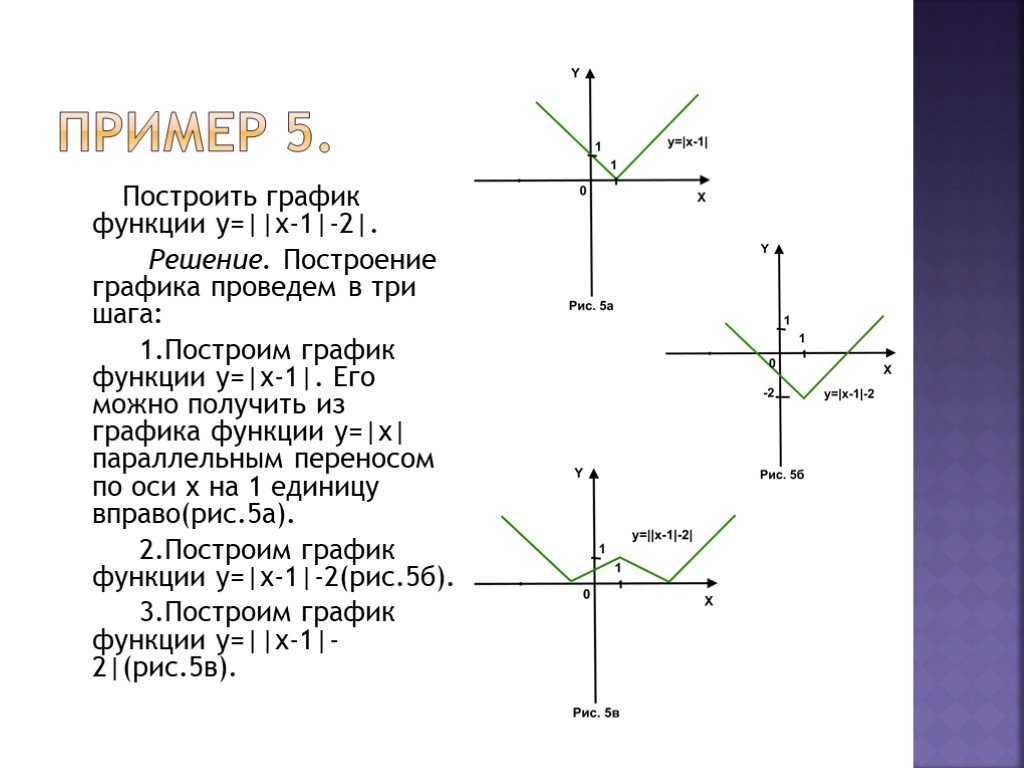
 Текущая точка не изменяется.
Текущая точка не изменяется.
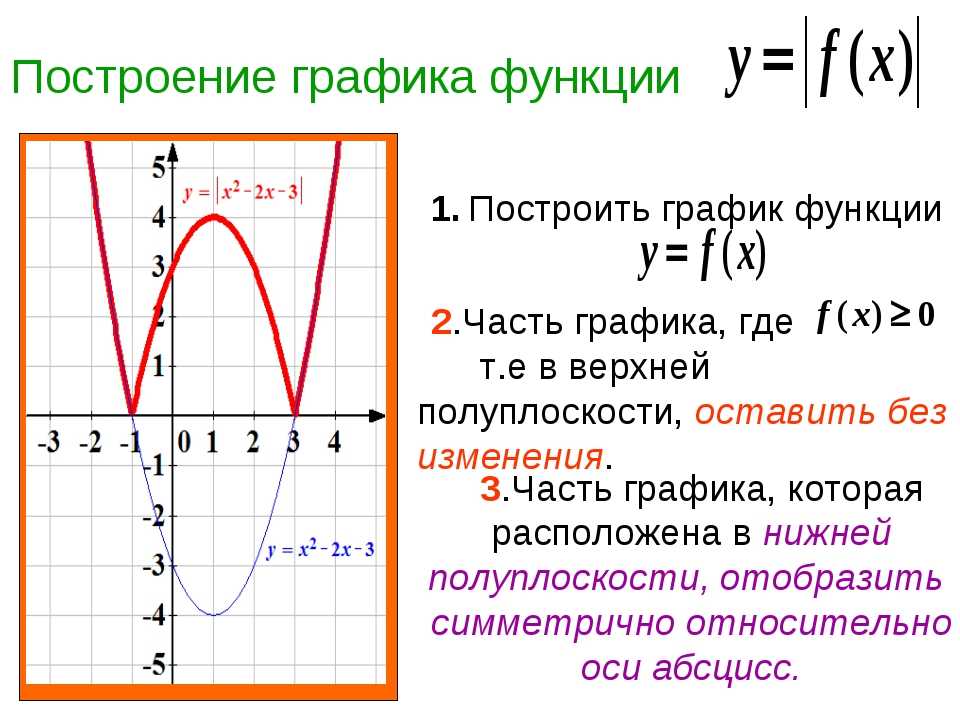
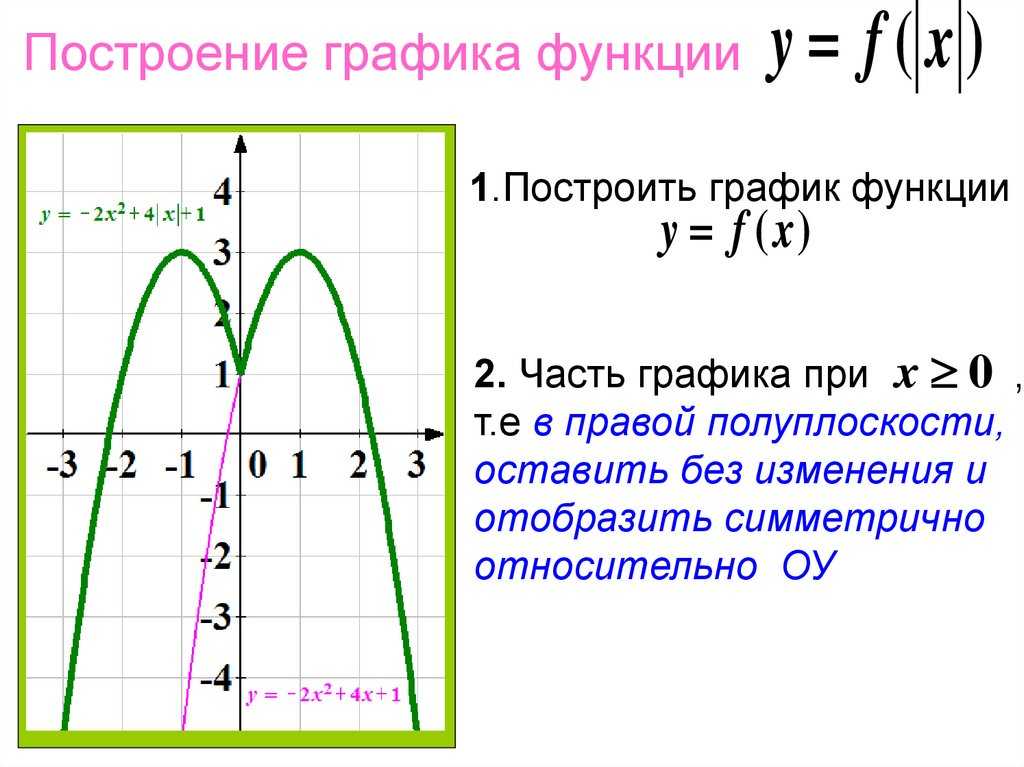
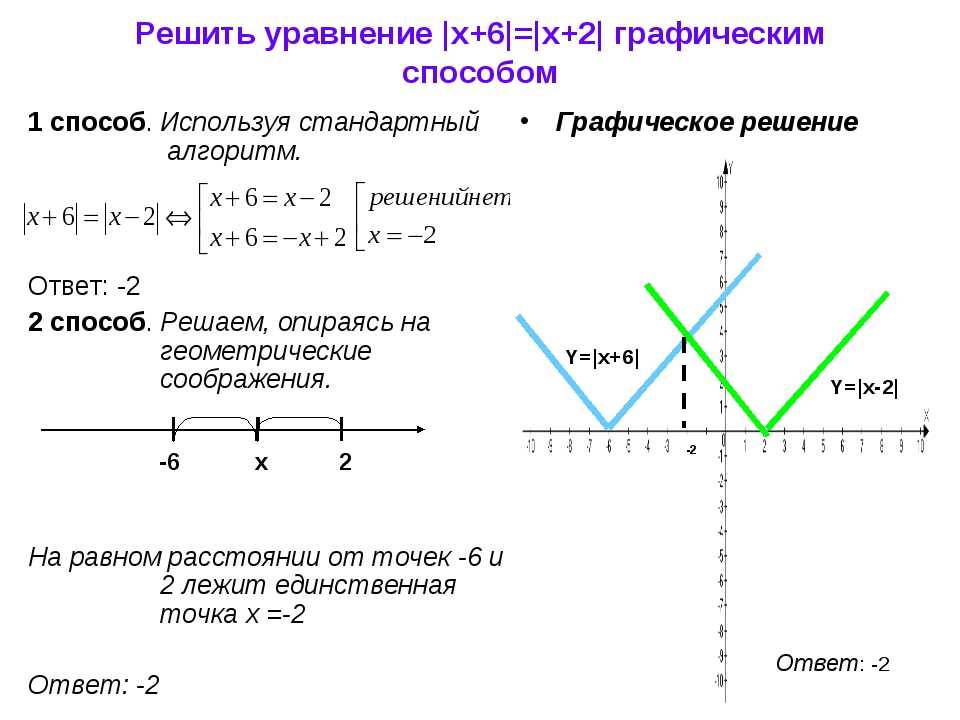
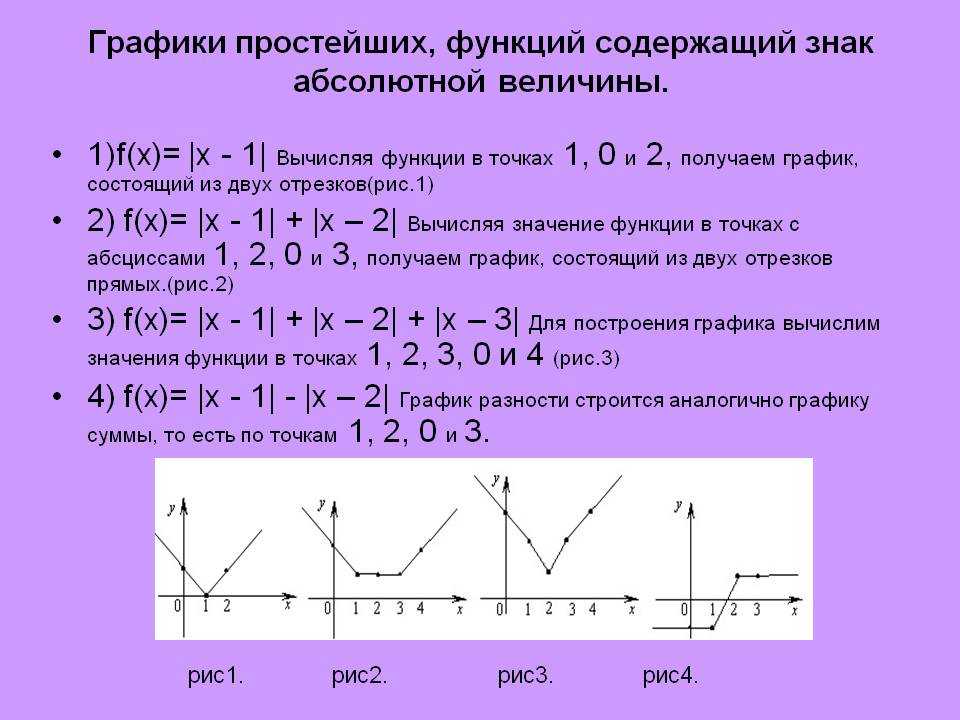 Скопированные пиксели находятся внутри
Скопированные пиксели находятся внутри