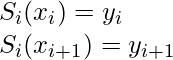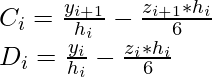Как найти коэффициенты кубического сплайна - Исправление недочетов и поиск решений вместе с Examum.ru

Нахождение коэффициентов естественного интерполяционного кубического сплайна

Из определения естественного
интерполяционного кубического сплайна
мы получаем систему линейных уравнений
с невырожденной матрицей, число уравнений
равно
.
Если мы будем решать эту систему линейных
уравнений методом Гаусса с частичным
выбором ведущего элемента, то нам
потребуется

арифметических действий и

памяти. Но известен устойчивый алгоритм
нахождения коэффициентов сплайна, для
реализации которого требуется

арифметических действий и

памяти. Опишем этот алгоритм.

По
явным формулам находятся коэффициенты
,
.
Коэффициенты

находятся из решения системы линейных
уравнений размерности

с невырожденной трехдиагональной
матрицей методом прогонки. Запишем эту
систему линейных уравнений для случая
равномерного шага

Условие на применение
метода прогонки для решения этой системы
уравнений следующее:
.
Это условие выполнено, если все узлы
сетки различны.

Зная

и
,
находим коэффициенты

и

по явным формулам:

Отметим, что для удобства записи
системы линейных уравнений, определен
дополнительный коэффициент
,
равный нулю. Уравнения

и

вытекают из равенства нулю второй
производной естественного интерполяционного
кубического сплайна на концах отрезка

Теорема (о сходимости).
Пусть функция

— непрерывная функция на отрезке
,
тогда интерполяционный кубический
сплайн

сходится к

при
,
стремящемся к нулю, для любой точки

из отрезка
,
то есть
,
где
,

Теорема (оценка погрешности).
Пусть
.
Тогда для любой точки

справедливы следующие оценки погрешности:

где
,
а положительные константы
,

,
и

не зависят от
.

Таким образом, при уменьшении
равномерного шага

в два раза, погрешность интерполяции
кубическим сплайном уменьшается в 16
раз.

Производная интерполяционного
кубического сплайна – это непрерывно
дифференцируемая кусочно-параболическая
функция, то есть параболический сплайн:

Отметим, что
производная интерполяционного кубического
сплайна не является интерполяционным
сплайном для производной функции.

Нахождение значений естественного интерполяционного кубического сплайна и его производных

Как и для параболического
сплайна, сначала находим номер

отрезка, содержащего точку
,
по формуле
.
Зная все коэффициенты
,

и номер отрезка
,
находим значение естественного
интерполяционного кубического сплайна
в точке,
принадлежащей отрезку
,

Для
вычисления значений сплайна и его
производных в точке
,
введем дополнительные коэффициенты:
,

.
Ранее уже был определен коэффициент
.

Значения первой и второй
производных естественного интерполяционного
кубического сплайна вычисляются по
формулам

Сложность
вычислительного алгоритма
построения интерполяционного кубического
сплайна та же, что и у параболического
и линейного сплайнов. Число арифметических
действий, необходимых для построения
интерполяционного кубического сплайна,
пропорционально числу отрезков (),
объем памяти также пропорционален числу
отрезков ().

Так как интерполяционный
кубический сплайн хорошо приближает
гладкие функции (теорема о сходимости,
оценка погрешности) и имеет минимальную
сложность, то на практике для гладких
функций при решении задач интерполяции
и численного дифференцирования
используется именно интерполяционный
кубический сплайн.

2.4.
B-сплайны

B-сплайны
(базовые, фундаментальные, базисные
сплайны) –
это функции, определенные на отрезке

и образующие некоторый базис, который
позволяет представить любой сплайн в
виде линейной комбинации соответствующих
B-сплайнов. Так же, как произвольный
вектор
,
принадлежащий плоскости
,
можно единственным образом представить
в виде линейной комбинации базисных
векторов

и
,
а именно
,
так и произвольный сплайн можно
единственным образом представить в
виде линейной комбинации соответствующих
базисных сплайнов.

B-сплайном нулевой степени,
построенным на отрезке

по сетке
,
называется функция вида:

B-сплайн

степени

может быть отличен от нуля только на

отрезках
,
примыкающих друг к другу. Например,
кубический B-сплайн

отличен от нуля на отрезке
,
а линейный B – сплайн отличен от нуля
на отрезке

(рис. 2.2).

Любой линейный сплайн на отрезке

можно представить в виде линейной
комбинации B-сплайнов первой степени:

Любой кубический
сплайн на отрезке

также может быть единственным образом
представлен в виде линейной комбинации
кубических B-сплайнов. Такой подход
позволяет уменьшить объем памяти,
необходимый для построения сплайна.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Материал из MachineLearning.

Перейти к: навигация, поиск

Содержание

1 Введение
- 1.1 Постановка математической задачи
2 Изложение метода
- 2.1 Метод прогонки
- 2.2 Пример: интерполирование неизвестной функции
3 Ошибка интерполяции
- 3.1 Пример: интерполяция синуса
4 Список литературы
5 См. также

Введение

Постановка математической задачи

Одной из основных задач численного анализа является задача об интерполяции функций.
Пусть на отрезке задана сетка $omega={x_i:x_0=a<x_1<cdots<x_i<cdots<x_n=b}$ и в её узлах заданы значения функции y(x) , равные . Требуется построить интерполянту — функцию f(x) , совпадающую с функцией y(x) в узлах сетки:

( 1 )

Основная цель интерполяции — получить быстрый (экономичный) алгоритм вычисления значений f(x) для значений , не содержащихся в таблице данных.

Интерполируюшие функции f(x) , как правило строятся в виде линейных комбинаций некоторых элементарных функций:

$f(x)=sum_{k=0}^N {c_kPhi_k(x)},$

где ${Phi_k(x)}$ — фиксированный линейно независимые функции, — не определенные пока коэффициенты.

Из условия (1) получаем систему из n+1 уравнений относительно коэффициентов ${c_k}$ :

$sum_{k=0}^N {c_kPhi_k(x_i)}=y_i, i=0,1,cdots,n.$

Предположим, что система функций такова, что при любом выборе узлов отличен от нуля определитель системы:

$Delta(Phi) = begin{vmatrix} Phi_0(x_0) & Phi_1(x_0) & cdots & Phi_n(x_0) \Phi_0(x_1) & Phi_1(x_1) & cdots & Phi_n(x_1)\ cdots & cdots & cdots & cdots \Phi_0(x_n) & Phi_1(x_n) & cdots & Phi_n(x_n)end{vmatrix}$ .

Тогда по заданным однозначно определяются коэффициенты .

Изложение метода

Интерполяция кубическими сплайнами является частным случаем кусочно-полиномиальной интерполцией. В этом специальном случае между любыми двумя соседними узлами функция интерполируется кубическим полиномом. его коэффициенты на каждом интервале определяются из условий сопряжения в узлах:

f_i=y_i,

f'(x_i-0)=f'(x_i+0),

f''(x_i-0)=f''(x_i+0), i=1, 2, cdots, n-1.

Кроме того, на границе при x=x_0 и x=x_n ставятся условия

( 2 )

Будем искать кубический полином в виде

( 3 )

$f(x)=a_i+b_i(x-x_{i-1})+c_i(x-x_{i-1})^2+d_i(x-x_{i-1})^3, x_{i-1}le xle x_i.$

Из условия f_i=y_i имеем

( 4 )

$f(x_{i-1})=a_i=y_{i-1}, f(x_i)=a_i+b_ih_i+c_ih_i^2+d_ih_i^3=y_i, h_i=x_i-x_{i-1}, i=1, 2, cdots, n-1.$

Вычислим производные:

$f'(x)=b_i+2c_i(x-x_{i-1})+3d_i(x-x_{i-1})^2, f''(x)=2c_i+6d_i(x-x_{i-1}), x_{i-1}le xle x_i,$

и потребуем их непрерывности при x=x_i :

( 5 )

$b_{i+1}=b_i+2c_ih_i + 3d_ih_i^2, c_{i+1}=c_i+3d_ih_i, i=1, 2, cdots, n-1.$

Общее число неизвестных коэффициентов, очевидно, равно , число уравнений (4) и (5) равно 4n-2 . Недостающие два уравнения получаем из условия (2) при x=x_0 и x=x_n :

Выражение из (5) $d_i=frac{c_{i+1}-c_i}{3h_i}$ , подставляя это выражение в (4) и исключая $a_i=y_{i-1}$ , получим

$b_i=[frac{y_i-y_{i-1}}h_i]-frac{1}{3}h_i(c_{i+1}+2c_i), i=1, 2, cdots, n-1, b_n=[frac{y_n-y_{n-1}}h_n]-frac{2}{3}h_nc_n,.$

Подставив теперь выражения для $b_i, b_{i+1}$ и d_i в первую формулу (5), после несложных преобразований получаем для определения c_i разностное уравнение второго порядка

( 6 )

$h_ic_i+2(h_i+h_{i+1})c_{i+1}+h_{i+1}c_{i+2}=3left(frac{y_{i+1}-y_i}{h_{i+1}} - frac{y_i-y_{i-1}}{h_i}right), i=1, 2, cdots, n-1.$

С краевыми условиями

( 7 )

$c_1=0, c_{n+1}=0.$

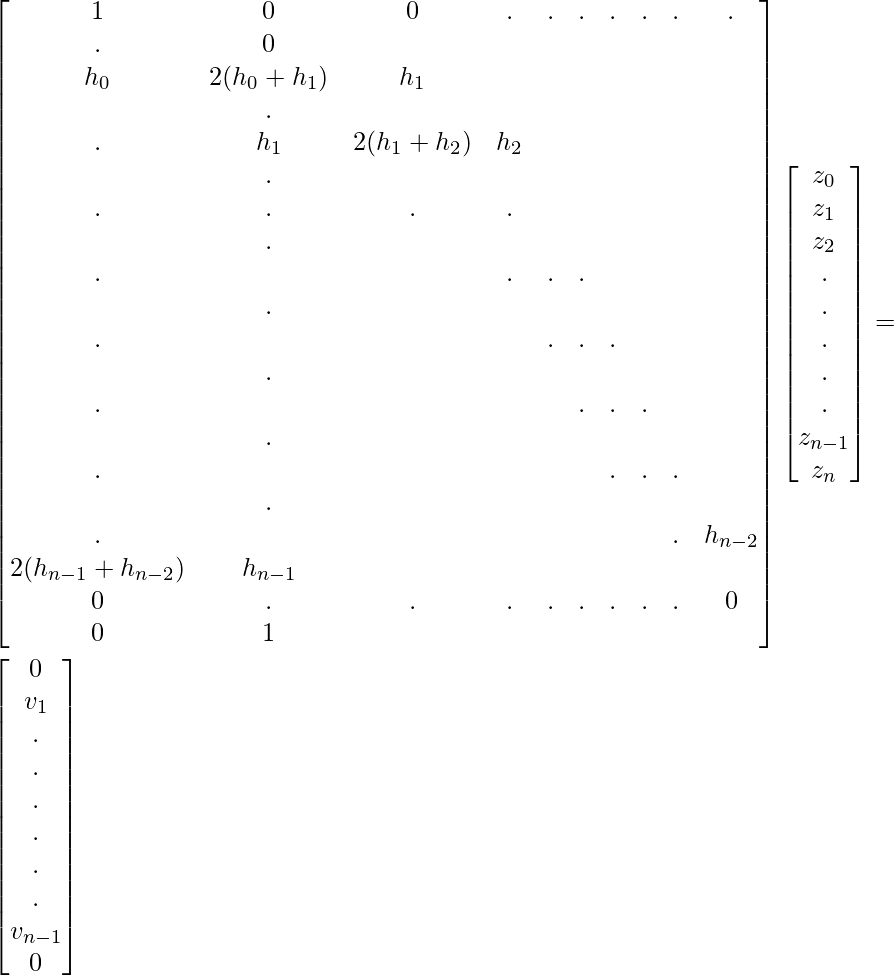
Условие $c_{n+1}=0$ эквивалентно условию и уравнению $c_{i+1} = c_i+d_ih_i$ . Разностное уравнение (6) с условиями (7) можно решить методом прогонки, представив в виде системы линейных алгебраических уравнений вида ~A*x=F , где вектор соответствует вектору ${c_i}$ , вектор поэлементно равен правой части уравнения (6), а матрица имеет следующий вид:

$A = begin{pmatrix} C_1 & B_1 & 0 & 0 & cdots & 0 & 0 \ A_2 & C_2 & B_2 & 0 & cdots & 0 & 0 \ 0 & A_3 & C_3 & B_3 & cdots & 0 & 0 \ cdots & cdots & cdots & cdots & cdots & cdots & cdots \ cdots & cdots & cdots & cdots & cdots & cdots & cdots \ cdots & cdots & cdots & cdots & cdots & cdots & B_{n-1} \ 0 & 0 & 0 & 0 & cdots & A_{n} & C_{n} end{pmatrix},$

где $A_i=h_i, i=2, cdots, n, B_i = h_{i+1}, i=1, cdots, n-1$ и $C_i=2(h_i+h_{i+1}), i =1, cdots, n$ .

Метод прогонки

Метод прогонки, основан на предположении, что искомые неизвестные связаны рекуррентным соотношением:

( 8 )

$x_i = alpha_{i+1}x_{i+1} + beta_{i+1}, i=1,cdots,n-1$

Используя это соотношение, выразим $x_{i-1}$ и x_i через $x_{i+1}$ и подставим в i-e уравнение:

$left(A_ialpha_ialpha_{i+1} + C_ialpha_{i+1} + B_iright)x_{i+1} + A_ialpha_ibeta_{i+1} + A_ibeta_i + C_ibeta_{i+1} - F_i = 0$

где F_i — правая часть i-го уравнения. Это соотношение будет выполняться независимо от решения, если потребовать

$A_ialpha_ialpha_{i+1} + C_ialpha_{i+1} + B_i = 0$

$A_ialpha_ibeta_{i+1} + A_ibeta_i + C_ibeta_{i+1} - F_i = 0$

Отсюда следует:

$alpha_{i+1} = {-B_i over A_ialpha_i + C_i}$

$beta_{i+1} = {F_i - A_ibeta_i over A_ialpha_i + C_i}$

Из первого уравнения получим:

$alpha_2 = {-B_1 over C_1}$

$beta_2 = {F_1 over C_1}$

После нахождения прогоночных коэффициентов alpha и beta , используя уравнение (1), получим решение системы. При этом,

$x_n = {F_n-A_nbeta_n over C_n+A_nalpha_n}$

Пример: интерполирование неизвестной функции

Построим интерполянту для для функции , заданной следующим образом:

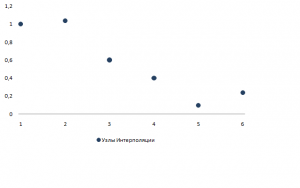
Вводные значения для задачи интерполяции


1	1.0002
2	1.0341
3	0.6
4	0.40105
5	0.1
6	0.23975

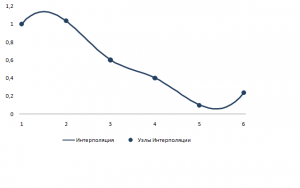
В результате интерполяции были рассчитаны следующие коэффициенты интерполянты:

Результат интерполяции


1,0002	-0,140113846	0,440979231	-0,266965385
1,0341	-0,291901538	-0,359916923	0,217718462
0,6	-0,22553	0,293238462	-0,266658462
0,40105	-0,100328462	-0,506736923	0,306015385
0,1	-0,134456154	0,411309231	-0,137103077

Ошибка интерполяции

Нас будет интересовать поведение максимального уклонения сплайна от интерполируемой функции в зависимости от максимального расстояния между соседними узлами интерполирования, т.е. зависимость величины

$parallel s-fparallel = max_{xin[a,b]}|s(x)-f(x)|$

от шага h, где $h = max_{k=1,2,cdots,n-1}|x_{k+1}-x_k|$ .

Известно, что если функция ƒ(x) имеет четыре непрерывные производные, то для ошибки интерполяции определенным выше кубическим сплайном s(x) верна следующая оценка

$parallel s-fparallel le frac{5}{384}h^4parallel frac{d^4f}{df^4}parallel$

причем константа $frac{5}{384}$ в этом неравенстве является наилучшей из возможных

Пример: интерполяция синуса

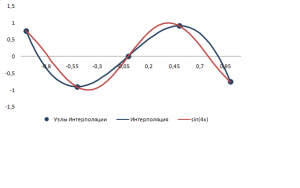
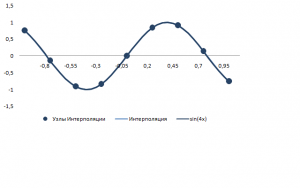
Постром интерполянту функции на отрезке [-1;1] , взяв равномерно отстоящие узлы с шагом 0.5 и шагом 0.25, и сравним полученные результаты.

	Ошибка интерполяции	Оценка ошибки	Иллюстрация
	0.429685	3.(3)	Результат интерполяции sin(4x) с шагом 0.5
	0.005167	0.208(3)	Результат интерполяции sin(4x) с шагом 0.25

Как видно из полученных иллюстрации, уже при шаге 0.25 интерполянта визуально ничем не отличается от исходной функции.

Код программы на языке С++ с помощью которой были произведены все расчеты, можно скачать тут.

Список литературы

А.А.Самарский, А.В.Гулин. Численные методы М.: Наука, 1989.
А.А.Самарский. Введение в численные методы М.: Наука, 1982.
Костомаров Д.П., Фаворский А.П. Вводные лекции по численным методам
Н.Н.Калиткин. Численные методы М.: Наука, 1978.

См. также

Интерполяция каноническим полиномом
Тригонометрическая интерполяция
Рациональная интерполяция
Проблема выбора узлов для интерполяции
Практикум ММП ВМК, 4й курс, осень 2008

Источник

Продолжаю делать свою лабораторную работу, которая посвящена сплайнам, последняя часть работы посвящена написанию программы, которая бы приближала функцию кубическим сплайном,
начал разбирать теорию, посвященную кубическому сплайну и запутался…
формула для вычисления сплайна:

[math]S_i(x)=x_i+b_i(x-x_i)+c_i(x-x_i)^2+d_i(x-x_i)^3, quad i=0,1,ldots,n-1[/math]

Как мне найти коэффициенты a,b,c и d ?

Источник

Время на прочтение
11 мин

Количество просмотров 77K

Доброго времени, Хабр!

Куча времени прошла с того момента, как я написал свою первую статью, и уже почти год с того момента, как пришла в голову идея для второй. В силу многих обстоятельств (в первую очередь – лени и забывчивости), эта идея так и не была реализована ранее, но сейчас я собрался, написал весь этот материал и готов представить его вашему вниманию.

Начну с небольшой вводной. Будучи студентом 4-го, на тот момент, курса бакалавриата, я изучал курс «Компьютерная графика». Много там было разных интересных (и не очень) заданий, но одно прямо особо запало мне в душу: интерполяция кубическими сплайнами с заданными первыми производными на концах интервала. Пользователь должен был задавать значения первых производных, а программа — считать и выводить на экран интерполяционную кривую. Особенность и основная сложность задания заключена в том, что задаются именно первые производные, а не вторые, как в классической постановке сплайн-интерполяции.
Как я ее решал, и к чему оно в итоге пришло, я как раз и изложу в этой статье. И да, если по описанию задачи вы не поняли ни в чем ее смысл, ни в чем сложность, не переживайте, все это я также постараюсь раскрыть. Итак, поехали.

А, нет, погодите один момент. Вот вам два числовых ряда:
a) 2, 4, 6, 8, ?
b) 1, 3, ?, 7, 9

Какие числа должны стоять на месте вопросов и почему? Вы действительно уверены в своем ответе?

Интерполяция

Интерполяция, интерполирование (от лат. inter-polis – «разглаженный, подновлённый, обновлённый; преобразованный») – в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. (с) Википедия

Поясню на примерах. Существуют задачи, когда нам требуется узнать, условно, «закон распределения» (взял в кавычки, так как это, вообще говоря, термин из другой области математики) некого параметра по нескольким известным его значениям. Чаще всего речь идет об изменении некого параметра во времени: координаты движущегося тела, температуры объекта, колебания курса валюты, etc. При этом в силу каких-либо обстоятельств у нас не было возможности наблюдать за этим параметром непрерывно, мы могли узнавать его значения лишь в какие-то отдельные моменты времени. Исходными данными в таком случае у нас является множество точек вида value(time), а целью задачи – восстановить кривую, проходящую через эти точки и непрерывно описывающую изменение этого параметра.

Следует понимать, что невозможность постоянного наблюдения за соответствующим параметром – это обычно какого-либо рода технологическое ограничение. С развитием техники таких ситуаций становится все меньше и меньше. Из современных задач такого плана – траектория движения, например, марсохода. Поддерживать непрерывный сеанс связи (пока что) все еще не представляется возможным, а контролировать его перемещение и рисовать красивые траектории хочется. Получается, что конкретные координаты можно узнать только в те моменты, когда связь все-таки налажена, а траекторию целиком приходится восстанавливать по полученным таким образом время от времени точкам.
Другой вариант применения интерполяции. Некоторые современные телевизоры показывают изображение с частотой обновления картинки до >=1000Гц (хотя это все еще запредельные значения). Большинство телевизоров так не умеет, но даже так многие отображают картинку на частоте 100Гц — такая величина уже вполне себе классика. А если верить википедии, то в кинематографе «частота 24 кадра в секунду является общемировым стандартом». Для того, чтобы превратить 24 кадра в секунду исходного видеопотока в 100 кадров в секунду результата, телевизор использует интерполяцию. А именно какие-нибудь алгоритмы в стиле «взять два соседних кадра 1 и 2, посчитать разницу между ними и сформировать из нее 3 дополнительных кадра, которые надо впихнуть между теми двумя изначальными» -> получаются кадры 1, 1_1, 1_2, 1_3, 2

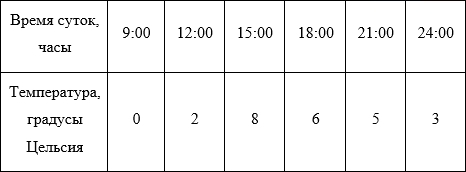
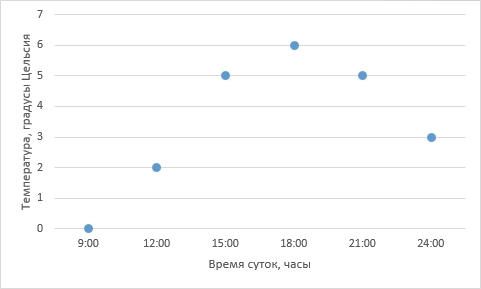
Для дальнейших рассуждений возьмем более простой пример. Представим себе, например, лабораторную работу по географии в каком-нибудь 6-ом классе (кстати, у меня когда-то и правда была такая). Необходимо каждые 3 часа измерять температуру воздуха и записывать данные, а потом сдать учителю график изменения температуры от времени суток. Допустим, по результатам измерений у нас получилась вот такая табличка (данные придуманы случайным образом и никак не претендуют на какую-либо правдоподобность):

Отобразим полученные данные на графике:

Собственно, данные записаны и отражены на графике. Мы вплотную подошли к задаче интерполяции – как по имеющимся точкам восстановить плавную кривую?

Количество условий и степень интерполирующего полинома

Можем ли мы вообще гарантировать, что такая функция, которая соединяет все заданные точки, вообще существует?

Да, такая функция гарантированно существует, и более того, таких функций будет бесконечно много. Для любого набора точек можно будет придумать сколько угодно много функций, которые через них будут проходить. И вот несколько примеров того, как две точки можно соединить разными способами:

Однако есть и способ задать интерполяционную кривую однозначно. В самом классическом случае, в качестве интерполяционной кривой берут полином:

$P_n(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0$

Для того, чтобы провести через имеющиеся точки такой полином единственным образом, необходимо и достаточно, чтобы степень полинома была на 1 меньше, чем количество условий (я специально выделил это слово, потому что в конце этого раздела я вернусь к этой формулировке). Пока что, простоты ради, условием будут являться координаты точки. Говоря человеческим языком, через 2 точки однозначным образом можно провести прямую (полином 1-ой степени), через 3 точки – параболу (полином 2-ой степени) и т.д.

Возвращаясь к нашей задаче с температурой – в ней мы определили 6 точек, значит, для того, чтобы провести полином единственным образом, он должен быть 5-ой степени

Интерполирующий полином тогда будет выглядеть так:

$-frac{x^5}{14580}+frac{13x^4}{1944}-frac{41x^3}{162}+frac{983x^2}{216}-frac{2273x}{60}+117$

А сейчас следует сделать важное замечание и пояснить, что я имел ввиду под «условием». Полином можно задать не только координатами точек, через которые он проходит, условиями могут быть любые параметры этого полинома. В простейшем случае это действительно координаты точек. Но в качестве условия можно взять, например, первую производную этого полинома в какой-либо из точек. Вторую производную. Третью производную. В общем, любую возможную производную в любой из точек, в которой этот полином существует. Поясню на примере:
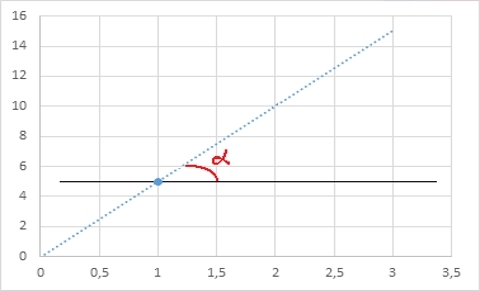
Прямую можно задать однозначно, как я уже говорил, двумя точками:

Ту же прямую, с другой стороны, можно определить координатой одной точки и углом наклона альфа к горизонтали:

С полиномами более высоких степеней можно использовать и более сложные условия (вторая производная, третья производная, etc.), и каждый такой параметр будет идти в общий счет количества условий, которые однозначным образом определят этот полином. Чтобы не быть голословным, вот еще пример:

Пусть нам заданы такие три условия:

Условий три, значит, мы хотим получить полином второй степени:

Подставляем

Считаем первую производную и считаем

Считаем вторую производную и считаем

Отсюда получаем, что наш полином выглядит так:

Интерполяция кубическими сплайнами

Вот, по тиху, мы и подбираемся к моей задаче. Полиномиальная интерполяция – не единственно возможный способ интерполяции. Среди всех прочих методов существует метод интерполяции кубическими сплайнами.

Принципиальное отличие идеи сплайн-интерполяции от интерполяции полиномом состоит в том, что полином один, а сплайн состоит из нескольких полиномов, а именно их количество равно количеству инервалов, внутри которых мы производим интерполяцию. В примере с нашей температурой воздуха, в которой у нас определено 6 точек, у нас будет 5 интервалов – соответственно, у нас будут 5 полиномов, каждый на своем интервале.

Каждый из этих полиномов – это полином третьей степени (строго говоря, степени не выше третьей, так как на каком-то из интервалов интерполирующая кривая может становиться квадратичной параболой или даже линейной функцией, но в общем случае это все-таки полином именно третьей степени). Записывая вышесказанное формульно, получим что все наши точки будут соединены некоей кривой

$S={S_1,S_2,S_3,S_4,S_5}$ , где каждый

$S_i$ – это полином третьей степени, а именно:

Возвращаясь к рассказанному в предыдущем пункте, для того, чтобы однозначно задать один полином 3-ей степени, необходимо 4 условия. В этой задаче у нас 5 полиномов, то есть, чтобы задать их все, нам нужно суммарно 5∙4=20 условий. И вот как они получаются:

1) Первый полином определен на первой и второй точках – это два условия. Второй полином определен на второй и третьей точках – еще два условия. Третий полином, четвертый, пятый – каждый из них определен на 2-х точках – суммарно это дает 10 условий.

2) Для каждой промежуточной точки из множества (а это 4 точки с временами 12:00, 15:00, 18:00, 21:00) должно выполняться условие, что первые и вторые производные для левого и правого полиномов должны совпадать. Формульно:

$S_{1}^{'}(x=12:00)=S_{2}^{'}(x=12:00)$

$S_{1}^{''}(x=12:00)=S_{2}^{''}(x=12:00)$

$etc.$

По два таких условия на каждую из промежуточных точек дает еще 8 условий. Следует добавить, что мы задаем только сам факт равенства, а какое конкретно значение они при этом принимают – это совершенно иная задача и считается она довольно сложно.

3) Остаются два условия, которые пока еще не определены. Это так называемые «граничные условия», от задания которых и зависит, какой именно сплайн получится. Обычно задают вторые производные на концах интервала равными 0:

$S_{1}^{''}(x=9:00)=0$

$S_{5}^{''}(x=21:00)=0$

Если сделать так, то мы получим так называемый «естественный сплайн». Для вычисления таких сплайнов написано уже огромное количество библиотек, бери и используй любую.

Отличие моего задания от классической постановки задачи, мои размышления над заданием и само решение

И вот мы подошли к условию моей задачи. Преподаватель придумал такое задание, что задаваться должны первые производные

$S_{1}^{'}(x_1)=k_1$ и

$S_{n-1}^{'}(x_n)=k_2$ на левом и правом концах интервала, а программа должна считать интерполирующую кривую. А для такого требования готовых алгоритмов я не нашел…
Я, разумеется, не стану описывать весь твой «творческий» путь от момента, когда я услышал задание, до того, как я его сдал. Расскажу лишь саму идею и покажу ее реализацию.

Сложность задания состоит в том, что, задавая первые производные на концах интервала, да, мы задаем этот сплайн. Теоретически. А вот посчитать его на практике – задача довольно сложная и совершенно неочевидная (желающие могут посмотреть код нахождения естественного сплайна на Вики – ru.wikipedia.org/wiki/Кубический_сплайн – и попробовать его понять хотя бы). Разумеется, я совершенно не хотел провести кучу времени, закопавшись в матан и пытаясь вывести нужные мне формулы. Я хотел более простое и элегантное решение. И я его нашел.
Рассмотрим наш сплайн и возьмем первый из его интервалов. На этом интервале уже заданы 3 условия:

$S_{1}^{'}(x_1 )=k_1$ — задается пользователем

Для того, чтобы однозначно задать кубический полином на этом интервале, нам не хватает еще лишь одного условия. Но мы можем его просто придумать! Возьмем вторую производную и положим ее равной, например, 0:

$S_{1}^{''}(x_1)=0$ — ничем не обоснованное предположение

Таким образом, зная эти 4 условия, мы полностью определяем этот полином. Зная все параметры этого полинома, мы можем вычислить значения первой и второй производных на второй точке, и поскольку они совпадают со значениями первой и второй производной для полинома на втором интервале, это приводит к тому, что мы также определяем и второй полином:

$S_{2}^{'}(x_2)=S_{1}^{'}(x_2)$ — вычисляется из

$S_1$

$S_{2}^{''}(x_2)=S_{1}^{''}(x_2)$ — вычисляется из

$S_1$

Аналогично мы считаем третий полином, четвертый, пятый и так далее, сколько бы их ни было. То есть, по факту, воссоздаем весь сплайн. Но поскольку мы взяли

$S_{1}^{''}(x_1)=0$ совершенно случайным образом, это приведет к тому, что производная

$k_2$ , заданная пользователем на правом конце сплайна, не будет совпадать с производной

$S_{n-1}^{'}(x_n)$ , которая получилась у нас в ходе таких вычислений. Но получается, что значение производной

$S_{n-1}^{'}(x_n)$ на правом конце сплайна – это функция, зависящая от значения второй производной

$S_{1}^{''}(x_1 )$ на левом конце:

$S_{n-1}^{'}(x_n)=f(S_{1}^{''}(x_1))$

А поскольку такой сплайн, который бы удовлетворял заданным условиям, гарантированно существует, и существует в единственном экземпляре, это значит, что мы можем рассмотреть разность:

$delta=S_{n-1}^{'}(x_n)-k_2$

и попытаться найти такое значение

$S_{1}^{''}(x_1)$ , при котором

$delta$ обращалась бы в 0 – и это будет тем самым правильным значением

$S_{1}^{''}(x_1)$ , которое строит искомый пользователем сплайн:

Самое замечательное в моей идее то, что эта зависимость оказалась линейной (вне зависимости от количества точек, через которые мы проводим сплайн. Этот факт доказан теоретическими подсчетами), а значит можно случайным образом взять любые два начальные значения

$S_{11}^{''}(x_1)$ и

$S_{12}^{''}(x_1)$ , посчитать

, и сразу же посчитать то самое верное значение, которое построит нам искомый сплайн:

$S_{REAL}^{''}(x_1)=-delta_2frac{S_{12}^{''}(x_1)-S_{11}^{''}(x_1)}{delta_2-delta_1}$

Итого, мы гарантированно находим искомый сплайн за 3 прогонки таких вычислений.

Немного кода и скриншотов программы

class CPoint
{
    public int X { get; }
    public int Y { get; }

    public double Df { get; set; }
    public double Ddf { get; set; }

    public CPoint(int x, int y)
    {
        X = x;
        Y = y;
    }
}

class CSplineSubinterval
{
    public double A { get; }
    public double B { get; }
    public double C { get; }
    public double D { get; }

    private readonly CPoint _p1;
    private readonly CPoint _p2;

    public CSplineSubinterval(CPoint p1, CPoint p2, double df, double ddf)
    {
        _p1 = p1;
        _p2 = p2;

        B = ddf;
        C = df;
        D = p1.Y;
        A = (_p2.Y - B * Math.Pow(_p2.X - _p1.X, 2) - C * (_p2.X - _p1.X) - D) / Math.Pow(_p2.X - _p1.X, 3);
    }

    public double F(int x)
    {
        return A * Math.Pow(x - _p1.X, 3) + B * Math.Pow(x - _p1.X, 2) + C * (x - _p1.X) + D;
    }

    public double Df(int x)
    {
        return 3 * A * Math.Pow(x - _p1.X, 2) + 2 * B * (x - _p1.X) + C;
    }

    public double Ddf(int x)
    {
        return 6 * A * (x - _p1.X) + 2 * B;
    }
}

class CSpline
{
    private readonly CPoint[] _points;
    private readonly CSplineSubinterval[] _splines;

    public double Df1
    {
        get { return _points[0].Df; }
        set { _points[0].Df = value; }
    }
    public double Ddf1
    {
        get { return _points[0].Ddf; }
        set { _points[0].Ddf = value; }
    }
    public double Dfn
    {
        get { return _points[_points.Length - 1].Df; }
        set { _points[_points.Length - 1].Df = value; }
    }
    public double Ddfn
    {
        get { return _points[_points.Length - 1].Ddf; }
        set { _points[_points.Length - 1].Ddf = value; }
    }

    public CSpline(CPoint[] points)
    {
        _points = points;
        _splines = new CSplineSubinterval[points.Length - 1];
    }

    public void GenerateSplines()
    {
        const double x1 = 0;
        var y1 = BuildSplines(x1);
        const double x2 = 10;
        var y2 = BuildSplines(x2);

        _points[0].Ddf = -y1 * (x2 - x1) / (y2 - y1);

        BuildSplines(_points[0].Ddf);

        _points[_points.Length - 1].Ddf = _splines[_splines.Length - 1].Ddf(_points[_points.Length - 1].X);
    }

    private double BuildSplines(double ddf1)
    {
        double df = _points[0].Df, ddf = ddf1;
        for (var i = 0; i < _splines.Length; i++)
        {
            _splines[i] = new CSplineSubinterval(_points[i], _points[i + 1], df, ddf);

            df = _splines[i].Df(_points[i + 1].X);
            ddf = _splines[i].Ddf(_points[i + 1].X);

            if (i < _splines.Length - 1)
            {
                _points[i + 1].Df = df;
                _points[i + 1].Ddf = ddf;
            }
        }
        return df - Dfn;
    }
}

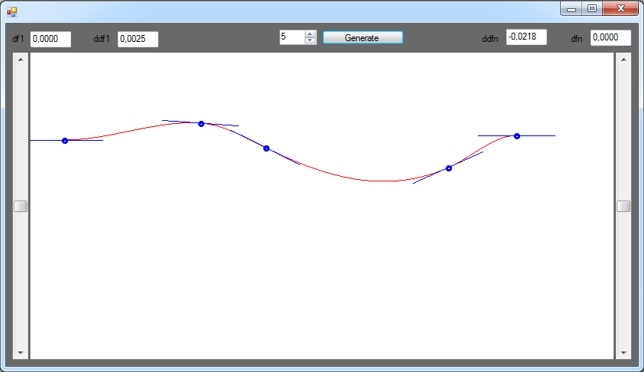
Синие отрезки — это первые производные сплайна в соответствующих его точках. Добавил такой вот графический элемент для большей наглядности.

Достоинства и недостатки алгоритма

Признаюсь честно, я не проводил сколь-либо серьезного анализа. По-хорошему стоило бы написать тесты, проверить, как оно работает в разных условиях (мало/много точек интерполяции, равное/произвольное между точками, линейные/квадратные/кубические/тригонометрические/etc. функции и так далее), но я этого не сделал, простите

Навскидку можно сказать, что сложность алгоритма — O(N), так как, как я уже говорил, вне зависимости от количества точек, достаточно двух прогонов вычислений, чтобы получить правильное значение второй производной на левом конце интервала, и еще одного, чтобы построить сплайн.

Впрочем, если кому-то захочется покопаться в коде и провести какой-нибудь более подробный анализ этого алгоритма, я буду только рад. Напишите мне разве что о результатах, мне было бы интересно.

Так а в чем провинились тесты IQ?

В самом начале статьи я написал два числовых ряда и попросил их продолжить. Это довольно частый вопрос во всяких IQ тестах. В принципе, вопрос как вопрос, но если копнуть чуть глубже, окажется, что он довольно бредовый, потому что при некотором желании можно доказать, что «правильного» ответа на него не имеется.

Рассмотрим для начала ряд «2, 4, 6, 8, ?»
Представим себе этот числовой ряд как множество пар значений

${x_i,y_i}$ :

, где в качестве

$y_i$ мы берем само число, а в качестве

$x_i $ – порядковый номер этого числа. Какое значение должно быть на месте

$y_5$ ?

Мысль, к которой я стараюсь плавно подвести – это то, что мы можем подставить абсолютно любое значение. Ведь что по факту проверяют такие задачи? Способность человека найти некое правило, которое связывает все имеющиеся числа, и по этому правилу вывести следующее число в последовательности. Говоря научным языком, здесь стоит задача экстраполяции (задача интерполяции состоит в том, чтобы найти кривую, проходящую через все точки внутри некоторого интервала, а задача экстраполяции – продолжить эту кривую за пределы интервала, «предсказав» таким образом поведение кривой в дальнейшем). Так вот, экстраполяция не имеет однозначного решения. Вообще. Никогда. Если бы было иначе, люди давным-давно бы предсказали прогноз погоды на всю историю человечества вперед, а скачки курса рубля никогда не были бы неожиданностью.

Разумеется, предполагается, что верный ответ в этой задаче все-таки есть и он равен 10, и тогда «закон», связывающий все эти числа, – это

Однако возьмем любое другое значение – и мы также сможем найти закон, который бы обосновывал именно его:

$y_5=12 to y=frac{x^4}{12}-frac{5x^3}{6}+frac{35x^2}{12}-frac{13x}{6}+2$

$y_5=16 to y=frac{x^4}{4}-frac{5x^3}{2}+frac{35x^2}{4}-frac{21x}{2}+6$

$y_5=-1 to y=-frac{11x^4}{24}+frac{55x^3}{12}-frac{385x^2}{24}+frac{299x}{12}-11$

Хорошо, с экстраполяцией разобрались, она не имеет однозначного решения даже теоретически. Но, быть может, мы сможем найти пропущенное число во втором ряду?

Я считаю, верный ответ

$y_3=1$ . Кто сможет оспорить?

Git-репозиторий

В прошлый раз меня ругали за то, что я выложил проект в виде архива в облаке, а не в виде кодов в репозиторий, поэтому в этот раз я исправляю эту свою ошибку: github.com/WieRuindl/Splines

Источник

Cubic Spline:

The cubic spline is a spline that uses the third-degree polynomial which satisfied the given m control points. To derive the solutions for the cubic spline, we assume the second derivation 0 at endpoints, which in turn provides a boundary condition that adds two equations to m-2 equations to make them solvable. The system of equations for the Cubic spline for 1-dimension can be given by:

$S_i (x) = a_i + b_i *x + c_i * x^{2} + d_i x^{3}$

We take a set of points [x_i, y_i] for i = 0, 1, …, n for the function y = f(x). The cubic spline interpolation is a piecewise continuous curve, passing through each of the values in the table.

Following are the conditions for the spline of degree K=3:
- The domain of s is in intervals of [a, b].
- S, S’, S” are all continuous function on [a,b].

$S(x) =begin{bmatrix} S_0 (x), x epsilon [x_0, x_1] \ S_1 (x), x epsilon [x_1, x_2] \ ... \ ... \ ... \ S_{n-1} (x), x epsilon [x_1, x_2] end{bmatrix}$

Here S_i(x) is the cubic polynomial that will be used on the subinterval [x_i, x_i+1].

Since, there are n intervals and 4 coefficients of each equation, for that we require a 4n parameters to solve the spline, we can get 2n equation from the fact that each of the cubic spline equation should satisfy the value at both ends:

$S_i(x_i) = y_i \ S_i(x_{i+1}) = y_{i+1}$

The above cubic spline equations should not only continuous and differentiable but also have defined first and second derivatives that are also continuous on control points.

$S_{i-1}^{'}(x_i) = S_{i}^{'}(x_i)$

and

$S_{i-1}^{''}(x_i) = S_{i}^{''}(x_i)$

For 1, 2, 3…n-1 provides the 2n -2 equation constraints. So, we need 2 more equations to solve the above cubic spline. For that, we will use some natural boundary conditions.

Natural Cubic Spline:

In Natural cubic spline, we assume that the second derivative of the spline at boundary points is 0:

$S^{''}(x_0) = 0 \ S^{''}(x_n) = 0$

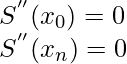
Now, since the S(x) is a third-order polynomial we know that S”(x) is a linear spline which interpolates. Hence, first, we construct S”(x) then integrate it twice to obtain S(x).

Now, let’s assume t_i = x_i for i= 0, 1,…n, and $z_i = S^{''}(x_i), i=0,1,2..n$ and from the natural boundary condition . Twice differentiating a cubic spline gives a linear spline which can be written as:

$S_i^{''}(x) = z_i frac{x- t_{i+1}}{t_i - t_{i+1}} + z_{i+1} frac{x - t_i}{t_{i+1} - t_i}$

where,

$h_i = t_{i+1} - t_i ; t=0,1, 2,...,n$

Now, the equation becomes:

$S''(x) = z_{i+1} frac{x- t_i}{h_i} + z_{i} frac{t_{i+1} - x}{h_i}$

Integrating this equation two times to obtain the cubic spline:

$S(x) =frac{z_{i+1}}{6h_i}(x - t_i)^{3} + frac{z_{i}}{6h_i}( t_{i+1} - x)^{3} + C_i(x_i -t) + D_i(t_{i+1} -x)$

where,

$C_i = frac{y_{i+1}}{h_i} - frac{z_{i+1} * h_i}{6} \ D_i = frac{y_{i}}{h_i} - frac{z_{i} * h_i}{6}$

Now, to check for the continuity of derivative at t_i i.e S^{‘}_{i}(t_i) = S^{‘}_{i-1}(t_{i}). We first need to find derivatives and put that condition:

$S'(x) = frac{z_{i+1}}{2h_i}(x - t_i)^{2} - frac{z_{i}}{2h_i}( t_{i+1} - x)^{2} + frac{1}{h_i}(y_{i+1}-y_i)- frac{h_i}{6}(z_{i+1} -z_i)$

where,

$b_i = frac{1}{h_i}(y_{i+1}-y_i)$

Putting the above equation for the continuity and solving it gives the following equation:

$6(b_i -b_{i-1}) = h_{i-1}z_{i-1} + 2(h_{i-1} + h_i)z_i + h_{i}z_{i+1}$

Take, v_i = 6(b_i – b_{i-1}) and the above equation can be written as form of matrix:

$begin{bmatrix} 1& 0 & 0& .& .& .& .& .& .& .& .& 0& \ h_0& 2(h_0 + h_1)& h_1& & & & & & & & & .& \ .& h_1 & 2(h_1 + h_2)& h_2& & & & & & & & .& \ .& .& .& .& & & & & & & & .& \ .& & & .& .& .& & & & & & .& \ .& & & & .& .& .& & & & & .& \ .& & & & & .& .& .& & & & .& \ .& & & & & & .& .& .& & & .& \ .& & & & & & & & .& h_{n-2}& 2(h_{n-1} + h_{n-2})& h_{n-1}& \ 0& .& .& .& .& .& .& .& .& 0& 0& 1& \ end{bmatrix} begin{bmatrix} z_0 \ z_1\ z_2\ .\ .\ .\ .\ .\ z_{n-1}\ z_{n} end{bmatrix} = begin{bmatrix} 0\ v_1 \ .\ .\ .\ .\ .\ .\ v_{n-1}\ 0 end{bmatrix}$

Implementation

In this implementation, we will be performing the spline interpolation for function f(x) = 1/x for points b/w 2-10 with cubic spline that satisfied natural boundary condition.

Python3

import matplotlib.pyplot as plt

import numpy as np

from scipy.interpolate import CubicSpline, interp1d

plt.rcParams['figure.figsize'] =(12,8)

x = np.arange(2,10)

y = 1/(x)

cs = CubicSpline(x, y, extrapolate=True)

ns = CubicSpline(x, y,bc_type='natural', extrapolate=True)

linear_int = interp1d(x,y)

xs = np.arange(2, 9, 0.1)

ys = linear_int(xs)

plt.plot(x, y,'o', label='data')

plt.plot(xs,ys, label="interpolation", color='green')

plt.legend(loc='upper right', ncol=2)

plt.title('Linear Interpolation')

plt.show()

xs = np.arange(1,15)

plt.plot(x, y, 'o', label='data')

plt.plot(xs, 1/(xs), label='true')

plt.plot(xs, cs(xs), label="S")

plt.plot(xs, ns(xs), label="NS")

plt.plot(xs, ns(xs,2), label="NS''")

plt.plot(xs, ns(xs,1), label="NS'")

plt.legend(loc='upper right', ncol=2)

plt.title('Cubic/Natural Cubic Spline Interpolation')

plt.show()

print("Value of double differentiation at boundary conditions are %s and %s"

%(ns(2,2),ns(10,2)))

Output:

Value of double differentiation at boundary conditions are -1.1102230246251565e-16 and -0.00450262550915248

Linear Interpolation

Cubic/Natural Spline Interpolation

References:

Natural Cubic Spline NTNU university

Last Updated :
18 Jul, 2021

Like Article

Save Article

Источник