Линейно зависимые и линейно независимые вектора.
Навигация по странице:
- Определение линейной комбинации векторов
- Определение линейно независимой комбинации векторов
- Определение линейно зависимой комбинации векторов
- Свойства линейно зависимых векторов
- Примеры задач на линейную зависимость и линейную независимость векторов
Определение. Линейной комбинацией векторов a1, …, an с коэффициентами x1, …, xn называется вектор
x1a1 + … + xnan.
Определение. Линейная комбинация x1a1 + … + xnan называется тривиальной, если все коэффициенты x1, …, xn равны нулю.
Определение. Линейная комбинация x1a1 + … + xnan называется нетривиальной, если хотя быбы один из коэффициентов x1, …, xn не равен нулю.
Определение. Вектора a1, …, an называются линейно независимыми, если не существует нетривиальной комбинации этих векторов равной нулевому вектору.
То есть вектора a1, …, an линейно независимы если x1a1 + … + xnan = 0 тогда и только тогда, когда x1 = 0, …, xn = 0.
Определение. Вектора a1, …, an называются линейно зависимыми, если существует нетривиальная комбинация этих векторов равная нулевому вектору.
Свойства линейно зависимых векторов:
-
Для 2-х и 3-х мерных векторов.
Два линейно зависимые вектора — коллинеарные. (Коллинеарные вектора — линейно зависимы.)
. -
Для 3-х мерных векторов.
Три линейно зависимые вектора — компланарные. (Три компланарные вектора — линейно зависимы.)
-
Для n -мерных векторов.
n + 1 вектор всегда линейно зависимы.
Примеры задач на линейную зависимость и линейную независимость векторов:
Пример 1. Проверить будут ли вектора a = {3; 4; 5}, b = {-3; 0; 5}, c = {4; 4; 4}, d = {3; 4; 0} линейно независимыми.
Решение:
Вектора будут линейно зависимыми, так как размерность векторов меньше количества векторов.
Пример 2. Проверить будут ли вектора a = {1; 1; 1}, b = {1; 2; 0}, c = {0; -1; 1} линейно независимыми.
Решение: Найдем значения коэффициентов при котором линейная комбинация этих векторов будет равна нулевому вектору.
x1a + x2b + x3c1 = 0
Это векторное уравнение можно записать в виде системы линейных уравнений
| x1 + x2 = 0 | |
| x1 + 2x2 — x3 = 0 | |
| x1 + x3 = 0 |
Решим эту систему используя метод Гаусса
1100
12-10
1010
~
из второй строки вычтем первую; из третей строки вычтем первую:
1100
1 — 12 — 1-1 — 00 — 0
1 — 10 — 11 — 00 — 0
~
1100
01-10
0-110
~
из первой строки вычтем вторую; к третей строке добавим вторую:
1 — 01 — 10 — (-1)0 — 0
01-10
0 + 0-1 + 11 + (-1)0 + 0
~
1010
01-10
0000
Данное решение показывает, что система имеет множество решений, то есть существует не нулевая комбинация значений чисел x1, x2, x3 таких, что линейная комбинация векторов a, b, c равна нулевому вектору, например:
—a + b + c = 0
а это значит вектора a, b, c линейно зависимы.
Ответ: вектора a, b, c линейно зависимы.
Пример 3. Проверить будут ли вектора a = {1; 1; 1}, b = {1; 2; 0}, c = {0; -1; 2} линейно независимыми.
Решение: Найдем значения коэффициентов при котором линейная комбинация этих векторов будет равна нулевому вектору.
x1a + x2b + x3c1 = 0
Это векторное уравнение можно записать в виде системы линейных уравнений
| x1 + x2 = 0 | |
| x1 + 2x2 — x3 = 0 | |
| x1 + 2x3 = 0 |
Решим эту систему используя метод Гаусса
1100
12-10
1020
~
из второй строки вычтем первую; из третей строки вычтем первую:
1100
1 — 12 — 1-1 — 00 — 0
1 — 10 — 12 — 00 — 0
~
1100
01-10
0-120
~
из первой строки вычтем вторую; к третей строке добавим вторую:
1 — 01 — 10 — (-1)0 — 0
01-10
0 + 0-1 + 12 + (-1)0 + 0
~
1010
01-10
0010
~
из первой строки вычтем третью; к второй строке добавим третью:
1 — 00 — 01 — 10 — 0
0 + 01 + 0-1 + 10 + 0
0010
~
1010
0100
0010
Данное решение показывает, что система имеет единственное решение x1 = 0, x2 = 0, x3 = 0, а это значит вектора a, b, c линейно независимые.
Ответ: вектора a, b, c линейно независимые.
Понятие
вектора
Определение
1. Вектором называется направленный
отрезок ( или, что то же, упорядоченная
пара точек).
Обозначают:
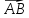
вектора) или одной буквой —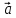
Определение
2. Длиной вектора (модулем)называется
расстояние между началом и концом
вектора. Длина вектора обозначается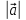
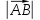
Определение
3. Нулевым вектором называется
вектор, у которого начало и конец
совпадают. Обозначают:
Определение
4. Единичным векторомназывается
вектор, длина которого равна единице.
Единичный
вектор, имеющий одинаковое направление
с данным вектором
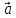
называется ортом вектора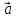
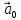
Определение
5. Векторы называютсяколлинеарными,
если они расположены на одной прямой
или на параллельных прямых. Нулевой
вектор считается коллинеарным любому
вектору.
Определение
6. Векторы называютсяравными,
если они коллинеарны, имеют одинаковые
длины и одинаковое направление.
Линейные
операции над векторами
Определение
7. Линейными операциями над вектораминазываются сложение векторов и умножение
вектора на число.
Определение
8. Суммой
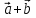
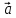

вектор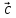
который идет из начала вектора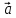
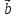
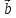
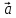
неколлинеарных векторов
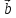
вместо правила треугольника использовать
правило параллелограмма: если векторы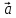
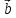
построен параллелограмм, то сумма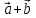
этого параллелограмма, идущего из общего
начала

Определение
9. Разностью
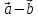
векторов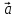
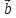
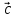
который в сумме с вектором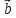
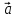
Если два вектора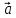
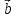
есть вектор, исходящий из конца вектора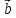

Определение
10. Два коллинеарных вектора равной
длины, направленные в противоположные
стороны, называются противоположными.
Вектор, противоположный вектору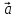
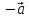
Произведение
вектора
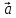
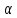
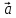
Некоторые
свойства линейных операций
1)
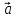
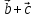
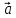
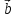
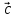
2)
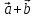
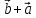
3)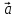
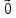

4)
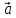
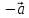
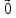
5)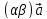

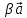
6)
7)


1·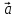
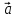
Теорема
1. (О коллинеарных векторах). Если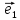

вектор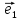
то существует единственное число х
такое, что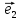
В
частности, ненулевой вектор
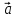
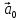

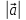
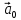
Сформулированные
свойства линейных операций позволяют
преобразовать выражения, составленные
из векторов, по обычным правилам алгебры:
можно раскрыть скобки, приводить подобные
члены, переносить некоторые члены в
другую часть равенства с противоположным
знаком и т.д.
Пример
1.
Доказать
равенства:
а)
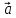
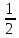


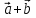
б)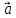
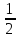

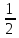
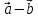
и
выяснить, каков их геометрический смысл.
Решение.
а) В левой части равенства раскроем
скобки, приведем подобные члены, получим
вектор в правой части. Поясним это
равенство геометрически. Пусть даны
два вектора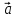
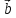
отложим их от общего начала и посмотрим
параллелограмм и его диагонали, получим:
§2 Линейная комбинация векторов
Векторный
базис на плоскости и в пространстве.
Определение
1. Линейной комбинацией векторов
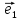
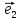
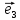
векторов на какие-нибудь числа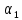
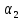

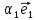
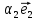
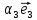
Определение
2. Векторным базисом в данной
плоскости называется любая пара
неколлинеарных векторов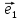
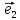
Вектор
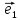
при этом первым базисным вектором,
вектор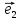
Справедлива
следующая теорема.
Теорема
1.Если базис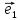
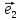
любой вектор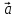
и притом единственным образом, в виде
линейной комбинации базисных векторов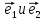
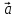
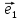
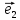
(*)
Определение
3. Равенство(*) называютразложением
вектора
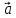
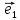
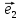
а числа х и у –координатами вектора
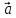
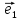
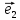
илиотносительно базиса

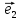
речь, то пишут кратко: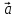
определения координат вектора относительно
базиса следует, что равные векторы имеют
соответственно равные координаты.
Два
и более векторов в пространстве называются
компланарными, если они параллельны
одной и той же плоскости или лежат в
этой плоскости.
Определение
4. Векторным базисом в пространстве
называют любые три вектора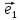

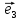
Вектор
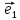
вектором,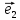
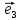
Замечание.
1. Три вектора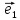
{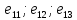
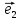
{
и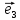

образуют базис пространства, если
определитель, составленный из их
координат, отличен от нуля :

2.
Основные положения теории определителей
и способы их вычисления рассмотрены в
модуле 1 «линейная алгебра».
Теорема
2. Пусть

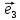
любой вектор
и притом единственным образом, в виде
линейной комбинации базисных векторов
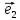
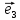
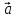
х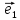
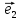
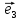
(**)
Определение
5. Равенство (**) называютразложением
вектора

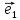
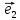

а числаx,y,z–координатами
(компонентами) вектора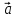
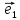
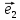
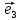
Если
заранее ясно, о каком базисе идет речь,
то пишут кратко:
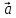
Определение
6. Базис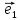
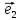
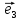
векторы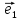
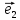
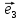
длину. В этом случае приняты обозначения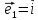
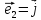
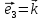
Действия
над векторами, заданными своими
координатами.
Теорема
3. Пусть на плоскости выбран векторный
базис
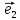
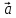
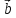
своими координатами: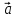

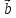
{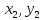
Тогда
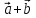
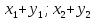
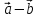
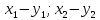
т.е. при сложении или вычитании векторов
складываются или вычитаются их одноименные
координаты;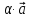
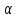
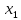
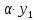
т.е. при умножении вектора на число его
координаты умножаются на это число.
Условие
коллинеарности двух векторов
Теорема
4. Вектор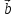
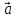
вектора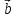
координатам вектора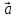
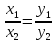
Линейные
операции над векторами, заданными своими
координатами в пространстве, производятся
аналогично.
Пример
1. Пусть даны векторы

= {1;0;1} в некотором векторном базисе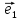

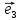
Найти координаты линейной комбинации
2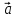
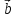
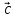
Решение.
Введем обозначение для линейной
комбинации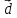
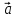

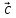
Коэффициенты
линейной комбинации
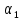
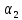

Запишем данное векторное равенство в
координатной форме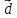
{x,y,z}=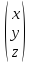
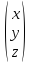
Очевидно,
что каждая координата линейной комбинации
векторов равна такой же линейной
комбинации одноименных координат, т.е.
х
= 2·1+3·3+(-4)·1=7,
у
= 2·2+3·2+(-4)·0=10,
z= 2·(-1)+3·1+(-4)·0=-3.
Координаты
вектора
в базисе
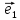
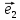
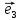

{7,10,-3}
Ответ: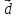
{7,10,-3}.
Общая
(аффинная) декартова система координат
Определение
7. Пусть О- некоторая фиксированная
точка, которую будем называтьначалом.
Если
М- произвольная точка, то вектор
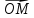
М по отношению к началу, коротко,
радиус-вектор точки М.
Декартовы
(аффинные) координаты на прямой
Пусть
дана в пространстве некоторая прямая
l.Выберем начало
О лежащим на этой прямой. Кроме того,
выберем на прямойl
ненулевой вектор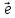
который будем называть базисным.
Определение
8. Пусть точка М лежит на прямойl.
Так как векторы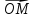
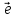
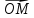

где х- некоторое число. Это число назовемкоординатой точки М на прямой.
Начало
О имеет положительные или отрицательные
координаты, в зависимости от того,
совпадают ли направления векторов
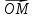
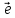
на которой координаты, будем называть
осью координат или осью ОХ.
Введение
координат на прямой соответствует
единственное число х, и наоборот,
существует единственная точка М, для
которой это число является координатой.
Декартовы
(аффинные) координаты на плоскости.
Выберем
на плоскости О два неколлинеарных
вектора
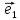
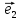
образующих некоторый базис . Очевидно,
что длины векторов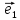
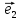
Определение
9. Совокупность {0;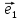
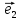
точки О и векторного базиса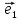

декартовой (аффинной) системой на
плоскости.
Две
прямые, проходящие через О и параллельные
соответственно векторам
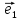
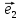
осями координат. Первую из них обычно
называют осью абсцисс и обозначают Ох,
вторую- осью ординат и обозначают Оу.
Будем
всегда изображать
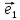
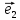
координат.
Определение
10. Координатами точки М на плоскости
относительно декартовой (аффинной)
системы координат {0;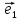
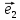
называют координаты ее радиус-вектора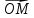
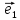
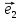
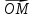
х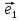
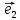
тогда числа х и у будет координатами М
относительно декартовой(аффинной)
системы координат {0;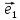
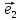
Координату х называютабсциссой точки
М, координату у-ординатой точки М.
Итак,
если выбрана система координат, {0;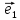
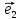
на плоскости, то каждой точке М плоскости
соответствует единственная точка М на
плоскости: эта точка является концом
вектора

х

Введение
системы координат лежит в основе метода
аналитической геометрии, сущность
которой состоит в том, чтобы уметь
сводить любую геометрическую задачу к
задачам арифметики или алгебры.
Определение
11. Координатами вектора
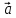
плоскости относительно декартовой
системы координат {0;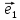
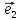
называют координаты этого вектора в
базисе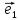
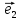
Чтобы
найти координаты вектора
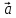
надо разложить его по базису

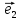
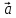
х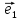
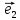
где коэффициенты х,у и будут координатами
вектора
относительно декартовой системы {0;

Декартова
(аффинная) система координат в пространстве.
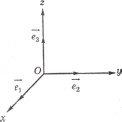
Пусть
в пространстве зафиксирована некоторая
точка О(начало) и выбран векторный базис

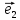
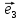
Определение
12. Совокупность {0;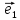
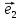
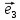
пространстве.
Определение
13. Три прямые проходящие через О и
параллельные соответственно векторам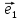
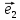
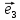
называютосями координат и обозначают
соответственно Оz,Oy,Oz.Мы
будем всегда изображать векторы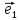
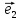
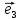
Определение
14. Координатами точки М в пространстве
относительно декартовой системы
координат {0;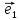
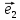
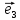
называют координаты ее радиус-вектора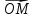
Иначе
говоря, координаты точки М – это такие
три числа х,у,zсоответственно
абсцисса и ордината точки М; третью
координатуzназывают
аппликатой точки М.
Введение
в пространстве декартовой системы
координат позволяет установить
взаимно-однозначное соответствие между
точками М пространства и упорядоченными
тройками чисел x,y,z.
Определение
15. Координатами вектора
в пространстве относительно декартовой
системы координат {0;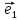
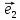
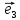
координаты этого вектора в базисе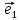
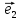
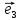
Пример
2.
Даны
три последовательные вершины
параллелограмма А(-2;1),В(1;3),С(4;0). Найти
четвертую его координату D.
Система координат аффинная.
Решение.
Векторы

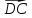
коэффициенты линейной комбинации):
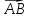
{3;2},


Значит,D(1;-2).
Ответ:D(1;-2).
Линейная
зависимость. Понятие базиса
Определение
16. Векторы
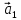

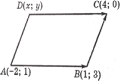
линейно зависимыми, если
существуют числа
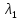
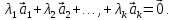
Это
определение линейной зависимости
векторов
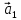
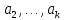
такому: векторы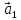
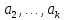
представить в виде линейной комбинации
остальных (или разложить по остальным).
Векторы
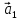
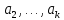
равенство (***) возможно в единственном
случае, когда
Понятие
линейной зависимости играет большую
роль в линейной алгебре. В векторной
алгебре линейная зависимость имеет
простой геометрический смысл.
-
Любые
два коллинеарных вектора линейно
зависимы, и наоборот, два неколлинеарных
вектора линейно независимы. -
Три
компланарных вектора линейно зависимы,
и наоборот, три некомпланарных вектора
линейно независимы. -
Каждые
четыре вектора линейно зависимы.
Определение
17. Три линейно
независимых вектора
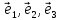
пространства, т.е.
любой вектор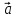
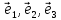
Определение
18. Два лежащих
в плоскости линейно независимых вектора
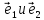
плоскости, т.е.
любой лежащий в этой плоскости вектор
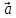
комбинации векторов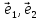
Задания
для самостоятельного решения.
-
Даны
три вектора
Найти
разложение векторапо
базису -
Даны
векторы
Вектор
–медиана
треугольникаOAB.
Разложить вектор
по
базису -
В
тетраэдре OABC
точки K,
L,
M,
N,
P,
Q
– середины рёбер OA,
OB,
OC,
AB,
AC,
BC
соответственно, S
– точка пересечения медиан треугольника
ABC.
Принимая за базисные
векторы
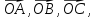
-
векторов
-
векторов
-
векторов
и
-
Точки
Mи
N
– середины сторон BCи
CDпараллелограмма
ABCD.
Разложить вектор
по
векторами
-
Дан
куб ABCDEFGH.
Разложить вектор
,
гдеK–
центр грани DHGC,
по векторам
,
-
На
плоскости даны вектора
Найти
разложение векторапо
базису,
-
На
плоскости даны три вектора
и
Определить разложение каждого из этих
трёх векторов, принимая в качестве
базиса два других. -
Принимая
в качестве базиса векторы
и
,
совпадающие со сторонами треугольникаABC,
определить разложение векторов,
приложенных в вершинах треугольника
и совпадающих с его медианами. -
Даны
четыре вектора
Найти координаты векторов – линейных
комбинаций: -
Даны
четыре вектора
,
Найти числа α, β, γ такие, что α
-
Проверить,
что векторы
образуют базис в пространстве. Найти
координаты векторов,
в
этом базисе. -
(Задача
об отрезке, разделённом в заданном
отношении.) Пусть точка C,
лежащая на отрезкеAB,
делит этот отрезок в отношении λ, т.е.
Выразить вектор
через векторы
и
-
Даны
две точки A(1;2;3).
B(7;2;5).
На прямой ABнайти
такую точку M,
чтобы точки Bи
Mбыли
расположены по разные стороны от точки
A и чтобы отрезок AMбыл
вдове длиннее отрезка AB.
Система координат аффинная. -
Вершина
Aпараллелепипеда
ABCD
принята за начало координат, а векторы
– за базисные векторы. Найти в этой
системе координаты всех вершин
параллелепипеда. -
Вершина
Oтетраэдра
OABCDпринята
за начало координат, а векторы
– за базисные векторы. Найти на этой
(аффинной) системе координаты точек
пересечения медиан граней тэтраэдра.
В данной публикации мы рассмотрим, что такое линейная комбинация векторов, какие векторы являются линейно зависимыми и независимыми, а также разберем пример задачи по этой теме.
- Определение линейной зависимости векторов
- Пример задачи
Определение линейной зависимости векторов
Линейная комбинация векторов a1, …, an – это вектор, заданный выражением x1a1 + … + xnan, где x1, …, xn – коэффициенты.
Представленная комбинация может быть:
- Тривиальная – все коэффициенты x1, …, xn равняются нулю.
- Нетривиальная – хотя бы один из коэффициентов x1, …, xn не равен нулю.
Векторы a1, …, an линейно независимы, если только их тривиальная комбинация равна нулевому вектору. То есть:
a1, …, an линейно независимы, если x1a1 + … + xnan = 0, исключительно когда x1 = 0, …, xn = 0.
Векторы a1, …, an линейно зависимы, если есть такая их нетривиальная комбинация, которая равняется нулевому вектору.
Свойства линейно зависимых векторов
- Линейно зависимые векторы в двух/трехмерном пространстве коллинеарны. Справедливо и обратное утверждение.
- В трехмерном пространстве три линейно зависимых вектора компланарны. Утверждение верно и в обратную сторону.
Пример задачи
Проверим, являются ли векторы a = {1; 2} и b = {2; 4} линейно зависимыми.
Решение:
Нам требуется найти значения коэффициентов, при которых линейная комбинация этих векторов равняется нулевому вектору.
xa + yb = 0
Полученное векторное уравнение можно представить в виде системы линейных уравнений:
Данная система имеет множество решений, при этом x = -2y.
То есть существует ненулевая комбинация коэффициентов x и y, при которых комбинация векторов a и b равняется нулевому вектору. Следовательно, заданные векторы линейно зависимы.

Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Линейная комбинация векторов
Например. Линейной комбинацией векторов с коэффициентами
и
есть выражение
Если все коэффициенты линейной комбинации (1) равны нулю одновременно: , то такая линейная комбинация называется тривиальной.
Например.
Если же хотя бы один из коэффициентов линейной комбинации (1) отличен от нуля, то такая линейная комбинация называется нетривиальной.
Например.
| Понравился сайт? Расскажи друзьям! | |
Регрессия и линейные комбинации векторов
Время на прочтение
8 мин
Количество просмотров 4.8K
Недавно я помогал вести курс по линейной алгебре, который организовали Тай-Даная Брэдли и Джек Хидари. Одним из вопросов, который периодически возникал у слушателей курса, был вопрос о том, почему программистов должна заботить тема линейной комбинации векторов.
Если кто не знает о том, что это такое — поясню. Предположим, имеются векторы 


Должен признать, что книги по математике оказывают своим читателям медвежью услугу, представляя концепцию линейной комбинации векторов не более чем теоретической идеей. В результате создаётся впечатление того, что эта концепция нужна лишь для математических доказательств, что самое ценное для практика — это умножение матриц и векторные произведения. Но, на самом деле, это не так. Линейная комбинация векторов лежит в самом сердце многих вариантов практического применения математических идей.
В некоторых случаях главной целью применения некоего алгоритма является лишь поиск «приемлемой» линейной комбинации набора векторов. Векторы — это строительные блоки (часто являющиеся базисом векторного пространства или подпространства), а набор линейных комбинаций векторов представляет собой законный способ комбинирования этих блоков. Более простые блоки допускают применение более простых и более эффективных алгоритмов, но их линейные комбинации менее выразительны. Вследствие этого и возникает компромисс.
Конкретный пример этого — регрессия. Большинство людей, говоря о регрессии, имеют в виду линейную регрессию. Речь идёт о поиске линейной функции, вроде 



Для того чтобы избежать сдвига функции на 



. В результате задача оптимизации, которую нужно решить, учитывая то, что 
В данном случае оптимизируемая функция, представляющая собой результат работы регрессии, не похожа на линейную комбинацию векторов. Но с технической точки зрения это — линейная комбинация векторов, хотя выполнена она с использованием не слишком интересного способа.
Более очевидной связь подобных задач с линейной комбинацией векторов становится тогда, когда пытаются моделировать нелинейные системы. Суть тут в том, чтобы определить класс функций, называемых базисными функциями 


Опять же, вместо того, чтобы умножать каждую координату входного вектора на коэффициент 
), это значит, что мы возвращаемся к линейной регрессии.
В результате задача оптимизации будет заключаться в том, чтобы выбрать коэффициенты, минимизирующие ошибку аппроксимации:
Рассмотрим пример. Предположим, что нам нужно выполнить регрессию на базисных функциях, представленных квадратичными полиномами. Базис для трёх входных переменных может выглядеть так:
Любой квадратичный полином от трёх переменных может быть представлен в виде линейной комбинации этих базисных функций. Кроме того, обратить внимание на то, что если рассматривать это как базис векторного пространства, тогда вектор будет представлен набором из 10 чисел — из десяти коэффициентов полинома. Это — то же самое, что 
Это — не те функции, которые обычно, на практике, используются в качестве базисных функций для полиномиальной регрессии (подробнее об этом смотрите в примечаниях, приведённых в конце статьи), но благодаря этим знаниям мы уже можем сделать кое-что полезное при реализации регрессионных алгоритмов.
Простой стохастический градиентный спуск
Хотя существуют аналитические решения многих регрессионных задач (включая задачу квадратичной регрессии, хотя и с небольшим изменением), градиентный спуск — это достаточно простое решение, позволяющее продемонстрировать то, как оптимизатор может находить «приемлемые» линейные комбинации векторов. Нижеприведённый код написан на Python 3.9, этот код можно найти на GitHub.
Начнём с объявления нескольких полезных псевдонимов типов:
from typing import Callable, Tuple, List
Input = Tuple[float, float, float]
Coefficients = List[float]
Gradient = List[float]
Hypothesis = Callable[[Input], float]
Dataset = List[Tuple[Input, float]]
Затем объявим простой класс-обёртку для базисных функций:
class QuadraticBasisPolynomials:
def __init__(self):
self.basis_functions = [
lambda x: 1,
lambda x: x[0],
lambda x: x[1],
lambda x: x[2],
lambda x: x[0] * x[1],
lambda x: x[0] * x[2],
lambda x: x[1] * x[2],
lambda x: x[0] * x[0],
lambda x: x[1] * x[1],
lambda x: x[2] * x[2],
]
def __getitem__(self, index):
return self.basis_functions[index]
def __len__(self):
return len(self.basis_functions)
def linear_combination(self, weights: Coefficients) -> Hypothesis:
def combined_function(x: Input) -> float:
return sum(
w * f(x)
for (w, f) in zip(weights, self.basis_functions)
)
return combined_function
basis = QuadraticBasisPolynomials()
Функция linear_combination возвращает функцию, которая вычисляет взвешенную сумму базисных функций. Теперь мы можем описать функции, вычисляющие ошибку для всего набора данных и для одной точки данных:
def total_error(weights: Coefficients, data: Dataset) -> float:
hypothesis = basis.linear_combination(weights)
return sum(
(actual_output - hypothesis(example)) ** 2
for (example, actual_output) in data
)
def single_point_error(
weights: Coefficients, point: Tuple[Input, float]) -> float:
return point[1] - basis.linear_combination(weights)(point[0])
Сейчас можно определить градиент функции ошибки по отношению к весам и к одной точке данных. Вспомним о том, что функция ошибок выглядит так:
Здесь 
Так как мы реализуем алгоритм стохастического градиентного спуска, формула вычисления ошибки немного упрощается. Мы вычисляем её не для всего набора данных, а только для одного, случайным образом выбранного элемента за раз. В результате функция ошибки будет выглядеть так:
Затем мы вычисляем градиент применительно к отдельным компонентам 


Ещё одна сильная сторона линейности заключается в том, что этой формуле безразлично содержимое исходных базисных функций. Это будет так до тех пор, пока веса не появятся в формуле для базисных функций. Попробуйте, в качестве упражнения, изменить эту реализацию так, чтобы в каждой из точек данных применялась бы собственная радиальная базисная функция (в конце статьи есть примечание о том, почему это, в реальной жизни, может быть непросто).
def gradient(weights: Coefficients, data_point: Tuple[Input, float]) -> Gradient:
error = single_point_error(weights, data_point)
dE_dw = [0] * len(weights)
for i, w in enumerate(weights):
dE_dw[i] = -2 * error * basis[i](data_point[0])
return dE_dw
И, наконец, реализуем ядро алгоритма градиентного спуска, в которое входят механизмы, упрощающие отладку кода:
import random
def print_debug_info(step, grad_norm, error, progress):
print(f"{step}, {progress:.4f}, {error:.4f}, {grad_norm:.4f}")
def gradient_descent(
data: Dataset,
learning_rate: float,
tolerance: float,
training_callback = None,
) -> Hypothesis:
weights = [random.random() * 2 - 1 for i in range(len(basis))]
last_error = total_error(weights, data)
step = 0
progress = tolerance * 2
grad_norm = 1.0
if training_callback:
training_callback(step, 0.0, last_error, 0.0)
while abs(progress) > tolerance or grad_norm > tolerance:
grad = gradient(weights, random.choice(data))
grad_norm = sum(x**2 for x in grad)
for i in range(len(weights)):
weights[i] -= learning_rate * grad[i]
error = total_error(weights, data)
progress = error - last_error
last_error = error
step += 1
if training_callback:
training_callback(step, grad_norm, error, progress)
return basis.linear_combination(weights)
Сгенерируем какой-нибудь простой набор данных и запустим оптимизацию:
def example_quadratic_data(num_points: int):
def fn(x, y, z):
return 2 - 4*x*y + z + z**2
data = []
for i in range(num_points):
x, y, z = random.random(), random.random(), random.random()
data.append(((x, y, z), fn(x, y, z)))
return data
if __name__ == "__main__":
data = example_quadratic_data(30)
gradient_descent(
data,
learning_rate=0.01,
tolerance=1e-06,
training_callback=print_debug_info
)
Алгоритму на то, чтобы сойтись, может понадобиться несколько тысяч шагов. Сколько именно — зависит от того, как отработал генератор случайных чисел при подготовке данных. Но обычно алгоритм сходится к решению, дающему ошибку меньше 1. Вот график, на котором показана связь ошибки и шагов алгоритма градиентного спуска для задачи квадратичной регрессии.
Ошибка и шаги алгоритма
Ядра и регуляризация
Я завершу этот материал пояснениями, на которые ссылался в статье.
Настоящее полиномиальное ядро. Мы решили использовать простой набор полиномиальных функций. Это тесно связано с концепцией «ядра», но «настоящее» полиномиальное ядро использует немного другие базисные функции. Оно масштабирует некоторые из базисных функций, используя 
Что не так с упражнением про радиальные базисные функции? В этом упражнении я предложил вам создать семейство базисных функций, по одной функции для каждой точки данных. Проблема тут заключается в том, что наличие настолько большого количества базисных функций делает пространство линейной комбинации векторов слишком выразительным. В ходе оптимизации произойдёт переобучение модели. В результате получится нечто, напоминающее справочную таблицу: каждой точке данных соответствует отдельная запись. При этом такая модель редко показывает хорошие результаты при обработке новых точек данных, которых не было в учебном наборе. Дело в том, что этих точек нет в найденной алгоритмом оптимизации «справочной таблице». На практике, для того чтобы справиться с этой проблемой, обычно, при расчёте ошибки, используют дополнительный компонент, соответствующий метрикам L1 или L2 вектора весовых коэффициентов. Это позволяет обеспечить то, что общий размер весов будет небольшим, то, что большинство весов, в случае с применением метрики L1, будут нулевыми, и то, что лишь немногие веса (самые важные) будут ненулевыми. Процесс введения «штрафов» за «размеры» линейных комбинаций векторов называют регуляризацией.
Что вы посоветовали бы почитать программистам, которые хотят с нуля освоить линейную алгебру?

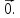
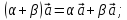
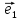
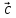
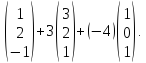



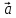
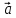

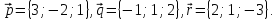 Найти
Найти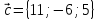 по
по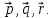
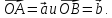 Вектор
Вектор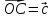 –медиана
–медиана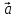 по
по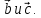

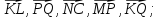
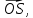 и
и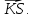
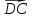 по
по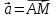 и
и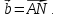
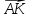 ,
,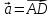 ,
,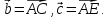
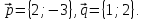 Найти
Найти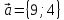 по
по ,
,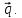
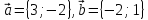 и
и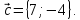 Определить разложение каждого из этих
Определить разложение каждого из этих и
и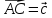 ,
,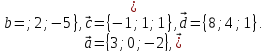 Найти координаты векторов – линейных
Найти координаты векторов – линейных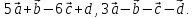
 ,
,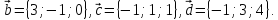 Найти числа α, β, γ такие, что α
Найти числа α, β, γ такие, что α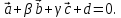
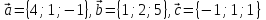 образуют базис в пространстве. Найти
образуют базис в пространстве. Найти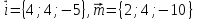 ,
,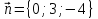 в
в Выразить вектор
Выразить вектор через векторы
через векторы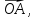 и
и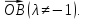

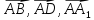
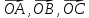 – за базисные векторы. Найти на этой
– за базисные векторы. Найти на этой












