Given $n+1$ points, you can uniquely fit a degree $n$ polynomial (e.g. with the help of Lagrange polynomials).
For a degree one polynomial, a line, you need two points (makes sense, right?). The formula looks like $$L(x) = dfrac{x-x_0}{x_1-x_0}f(x_1) + dfrac{x-x_1}{x_0-x_1}f(x_0),$$
Where the points are $(x_0,f(x_0)), (x_1,f(x_1))$
Notice here what happens to the left summand when we plug in $x_0$: we get zero contribution from this term; whereas, when we plug in $x_1$, we recover the function $f(x_1)$ that we’re trying to reach. Notice also that when we plugged in $x_0$ and $x_1$, the RHS went to $f(x_0)$ and $0$ respectively as well. Thus $L(x_1) = f(x_1)$ and $L(x_0) = f(x_0)$. We «constructed» a polynomial given two pairs of points that hits them with least degree needed.
For three points (quadratic), you want the similar cancellation effect:
$$L(x) = dfrac{x-x_0}{x_1-x_0}dfrac{x-x_2}{x_1-x_2}f(x_1) +dfrac{x-x_1}{x_0-x_1}dfrac{x-x_2}{x_0-x_2}f(x_0) + dfrac{x-x_1}{x_2-x_1}dfrac{x-x_0}{x_2-x_0}f(x_2)$$
See how the magic happens there? You should be able to construct the fourth degree polynomial from here. Hope this helps.
В [8] отмечается,
что в случае, когда характеристика
нелинейного элемента аппроксимируется
выражением, содержащим более трех точек,
значение функции целесообразно выбирать
при равноотстоящих значениях аргумента.
Кроме того, если число заданных точек
превышает число подлежащих определению
коэффициентов аппроксимации, рекомендуется
использовать «метод наименьших
квадратов», при котором среднеквадратичная
ошибка минимальна, т.е. при этом способе
сумма квадратов отклонений полинома
данной степени от кривой является
наименьшей.
В соответствии с
этим, несмотря на существующие компьютерные
программы, целесообразно привести
краткую рецептуру пользования этим
методом, что позволит студенту осмыслить
математическую суть метода и с помощью
простых микрокалькуляторов выполнить
любую аппроксимацию за оптимально
короткое время.
В [7] отмечается,
что вычислить коэффициенты полинома
по способу наименьших квадратов наиболее
рационально с помощью введенных Ю.Б.
Кобзаревым ортогональных полиномов
для заданного числа N
– равноотстоящих точек.
Обозначим через
полином степениl.
Тогда система полиномов будет ортогональной
для данного числа точек, если при любых
выполняется равенство
.
(16)
Воспользовавшись
известными ортогональными многочленами
Чебышева по методу Ю.Б. Кобзарева найдены
все семь полиномов, образующих такую
систему на отрезке
дляN=11
равноотстоящих точек [7, 9, 10], т.е. при
;
–0,8; … 0 … 0,8; 1,0 имеем:
(17)
Система (17)
ортогональных полиномов обладает тем
замечательным свойством, что разложение
по ним любой заданной функции дает
наилучшее приближение в смысле наименьших
квадратов. Поэтому вместо, например,
выражения (18) коэффициента передачи по
степеням напряжения
с неизвестными коэффициентами, можно
записать его, представив в виде суммы
(19) рассмотренных выше полиномов:
(18)
.
(19)
Здесь Р
– степень полинома; р
– целое число, равное номеру слагаемого;
– коэффициент, имеющий размерность
,
который можно назвать крутизной порядкар,
т.е.
есть крутизна нулевого порядка,
– первого порядка и т.д.
Входящая сюда
величина х
пропорциональна напряжению
,
отсчитываемому от середины участка
аппроксимации,
т.е. при изменениив пределах
,х
меняется от –1 до 1, поэтому
.
(20)
Для определения
коэффициента
в (19) умножим обе части равенства на
полиноми просуммируем по всем точкам
.
Тогда, используя свойство ортогональности
(16), находим
.
(21)
Отсюда
,
(22)
где
– нормированный полином
.
(23)
Так как нулевому
узлу соответствует левый конец участка
аппроксимации, т.е.
,
то сумму (22) удобно разбить на суммы, гдех<0
и х>0,
так как четные полиномы (р
= 0, 2, 4, 6) на
этих участках ничем не отличаются, а
нечетные (р=1,
3, 5, 7) отличаются лишь знаками. В связи
с этим целесообразно ввести нечетную
и четную
компоненты коэффициента усиленияК:
(24)
где
— шаг изменениях
(в нашем случае при N=11
);
— величина
коэффициента усиления в точках
.
Теперь вместо сумм
по положительным и отрицательным
значениям
можно взять суммы только по положительным
с использованием четной и нечетной
составляющей коэффициента усиления.
Тогда
(25)
Сведя в табл. 1
значения коэффициентов нормированных
полиномов
и используя их, легко найти коэффициенты
по формулам (25), далее в (19) сгруппировать
члены по степенямх
и перейти к представлению коэффициента
усиления в виде полинома по степеням
.
Коэффициенты этого полинома будут
подобраны наилучшим в смысле наименьших
квадратов способом, при котором
экспериментальная криваябудет практически сливаться с теоретической
кривой.
Вычисление
коэффициентов полинома, используемого
при гармоническом анализе для определения
коэффициентов и параметров нелинейности
и, в конечном итоге, для выбора оптимального
режима усилительного прибора рассмотрим
на конкретном примере.
Таблица
1
|
|
|
|
|
|
|
|
|
|
0 |
0,000000 |
-0,291375 |
0,000000 |
1,092658 |
0,000000 |
-5,1062086 |
0,000000 |
|
0,2 |
0,0454545 |
-0,262238 |
-0,339938 |
0,728439 |
2,003205 |
-1,5318624 |
-12,765522 |
|
0,4 |
0,0909091 |
-0,174825 |
-0,558470 |
-0,182110 |
2,003205 |
4,5955891 |
-0,9118072 |
|
0,6 |
0,1363636 |
-0,029138 |
-0,534189 |
-1,092658 |
-0,500801 |
3,7020048 |
15,045106 |
|
0,8 |
0,1818182 |
0,174825 |
-0,145688 |
-1,092658 |
-3,004808 |
-6,1274442 |
-10,485929 |
|
1,0 |
0,2272727 |
0,437063 |
0,728439 |
1,092658 |
1,502404 |
1,9148344 |
2,2795937 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Полиномиальное уравнение степени 3 

В алгебре кубическое уравнение с одной переменной — это уравнение вида
- ax 3 + bx 2 + cx + d = 0 { displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}
, в котором a не равно нулю.
Решения этого уравнения называются корнями кубической функции, определяемой левой частью уравнения. Если все коэффициенты a, b, c и d кубического уравнения имеют действительные числа, то оно имеет по крайней мере один действительный корень (это верно для всех нечетных степеней полиномиальные функции ). Все корни могут быть найдены алгоритмы алгоритмов:
- , то есть они могут быть выражены кубической формулой, включающей четыре коэффициента, основные арифметические операции и корни н — й степени (радикалы). (Это также верно для квадратичных (вторая степень) и четвертых (четвертой трех степеней), согласно теореме Абеля — Руффини.)
- числовые аппроксимации корней можно найти с помощью алгоритмов поиска корней, как таких метод Ньютона.
коэффициенты не обязательно должны быть действительными числами. Коэффициенты в любом поле с характеристикой, кроме 2 и 3. Решения некоторых кубических уравнений с рациональными коэффициентами имеют иррациональные (и даже ненастоящие) корни комплексные.
Содержание
- 1 История
- 2 Факторизация
- 3 Углубленная кубическая
- 4 Дискриминант и природа корней
- 4.1 Дискриминант
- 4.2 Природа корней
- 4.3 Множественный корень
- 4.4 Характеристика 2 и 3
- 5 Формула Кардано
- 6 Общая кубическая формула la
- 7 Тригонометрические и гиперболические решен ия
- 7.1 Тригонометрическое решение для трех действующих корней
- 7.2 Гиперболическое решение дл я одного действующего корня
- 8 Геометрические решения
- 8.1 Решение Омара Хайяма
- 8.2 Решение с трисектором угла
- 9 Геометрическая интерпретация корней
- 9.1 Три действительных корня
- 9.2 Один действительный корень
- 9.2.1 В декартовой плоскости
- 9.2.2 В комплексной плоскости
- 10 Группа Галуа
- 11 Получение корней
- 11.1 Метод Кардано
- 11.2 Подстановка Виета
- 11.3 Метод Лагранжа
- 11.3.1 Вычисление S и P
- 12 Приложений
- 12.1 В математике
- 12.2 В других науках
- 13 Примечания
- 14 Ссылки
- 15 Дополнительная литература
- 16 Внешние ссылки
История
Кубические уравнения были известны древним вавилонянам, грекам, китайцам, индийцам Вавилонские (20-16 вв. до н.э.) были найдены клинописи с таблицами для вычислений кубов и кубических корней. Вавилоняне могла использовать инструменты для решения кубических свойств, но нет никаких доказательств, подтверждающих это. Проблема удвоения куба включает простейшее и старейшее из изученных кубических уравнений, решение для которого древние египтяне не верили. В веке до нашей эры Гиппократ свел проблему к проблеме нахождения двух средних между одной линией и другой длиной, но не смог решить эту проблему с помощью линейки, задача, которая теперь известна как невыполнимая. Методы решения кубических представленных в Девяти главах математического искусства, китайском математическом тексте, составленном примерно во II веке нашей эры и прокомментированном Лю Хуэем в 3 век. В III веке нашей эры греческий математик Диофант нашел целочисленные или рациональные решения для некоторых двумерных кубических уравнений (Диофантовы уравнения ). Гиппократ, Менахм и Архимед, как полагают, точно подошли решение проблемы удвоения куба с помощью пересекающихся конических секций, хотя такие историки, как Ревиль Нетц, спорят, ли приводить к кубическим уравнениям или просто приводить к кубическим уравнениям. Некоторым другим нравится Т. Л. Хит, который перевел все работы Архимеда, не согласен, приводя доказательства того, что Архимед действительно решал кубические уравнения, используя пересечение двух коник, но также обсудил условия, при которых корни равны 0, 1 или 2.

В 7 веке династия Тан астроном-математик Ван Сяотун в своем математическом трактате под названием Цзигу Суаньцзин систематически обосновал и решил численно 25 кубических уравнений вида x + px + qx = N, 23 из них с p, q ≠ 0 и два из них с q = 0.
В 11 веке персидский поэт-математик Омар Хайям (1048–1131) добился значительных успехов в теории кубических уравнений. В одной из первых статей онил, что кубическое уравнение может иметь более одного решения, и обнаружено, что его нельзя решить с помощью компаса и линейки. Он также нашел геометрическое решение. В своей более поздней работе «Трактат о демонстрации проблемры» он написал классификацию кубических уравнений с общегеометрическими решениями, найденными с помощью пересекающихся конических сечений.
. В XII веке индийский математик Бхаскара II попытка решения кубических уравнений без общего успеха. Однако он привел один пример кубического уравнения: x + 12x = 6x + 35. В XII веке другой персидский математик, Шараф ад-Дин ат-Туси (1135–1135 гг.) 1213), создал Аль-Мухадалат (Трактат об уравнениях), в котором представлены восемь типов форм с положительными решениями и пять типов решений, которые не имеют положительных решений. Он использовал то, что позже будет известно как «метод Руффини — Хорнера », чтобы численно аппроксимировать корень кубического уравнения. Он также использует концепции максимумов и кривых для решения кубических уравнений, которые не имеют положительных решений. Он понимал важность дискриминанта кубического уравнения для нахождения алгебраических решений некоторых типов кубических уравнений.
В своей книге Flos Леонардо де Пиза, также известный как Фибоначчи (1170–1250), смог точно аппроксимировать положительное решение кубического уравнения x + 2x + 10x = 20. Записав вавилонскими, он дал результат 1,2,7, 42,33,4,40 (эквивалентно 1 + 22/60 + 7/60 + 42/60 + 33/60 + 4/60 + 40/60), что имеет относительную ошибку около 10.
В начале 16 века итальянский математик Принципионе дель Ферро (1465–1526) нашел метод решения класса кубических уравнений, а именно уравнения вида х + mx = п. Фактически, все кубические уравнения могут быть представлены в этой форме, если мы позволим m и n отрицать, но отрицательные числа ему не были известны в то время. Дель держал свои достижения в секрете до самой смерти, когда он рассказал об этом ученике Антонио Фьору.

В 1530 году Никколо Тарталья (1500–1557) получил от двух задач кубических условий и объявил, что может их решить. Вскоре ему бросил вызов Фиор, что произошло к известному состязанию между ними. Каждый участник должен внести определенную сумму и предложить сопернику ряд задач. Кто решит больше проблем в течение 30 дней, получит все деньги. Тарталья получил вопросы в форме x + mx = n, для которых он разработал общий метод. Фиор получил вопросы в форме x + mx = n, которые оказалось слишком сложно решить, и Тарталья выиграл конкурс.
Позже Джероламо Кардано (1501–1576) убедил Тарталья раскрыть свои секретные решения кубических уравнений. В 1539 году Тарталья сделал это только при условии, что Кардано никогда этого не раскроет и что, если он все-таки напишет книгу о кубиках, он даст Тарталье время для публикации. Несколько лет спустя Кардано узнал о предыдущей работе дельцов своей книги Ars Magna в 1545 году, что означает, что Кардано Тарталье шесть лет на публикации результатов (с признательностью Тартальи за независимое решение).). В обещании Кардано Тартальи говорилось, что он не будет публиковать работу Тартальи, и Кардано чувствовал, что публикует работу дель Ферро, чтобы обойти это обещание. Тем не менее, это привело к вызову Кардано из Тартальи, который Кардано отрицал. В конце концов, был принятый учеником Кардано Лодовико Феррари (1522–1565). Феррари выступил на соревновании лучше, чем Тарталья, и Тарталья потерял и свой престиж.
Кардано заметил, что метод Тартальи иногда требовал от него извлечения квадратного корня из отрицательного числа. Он даже включил вычисление с этим комплексными числами в Арс Магна, но на самом деле не понял этого. Рафаэль Бомбелли подробно изучил этот вопрос, поэтому его часто считают первооткрывателем комплексных чисел.
Франсуа Виет (1540–1603) независимо вывел тригонометрическое решение для кубики с тремя действующими корнями, а Рене Декарт (1596–1650) расширил работы Виете.
Факторизация
Если коэффициенты кубического уравнения представляют их рациональными числами, можно получить эквивалентное уравнение с целыми коэффициентами, умножив все коэффициенты на общее кратное <469 знаменателей. Такое уравнение
- ax 3 + bx 2 + cx + d = 0, { displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0,}
с целыми коэффициентами называется быть приводимым, если многочлен в левой части является произведением многочленов более низких степеней. Согласно лемме Гаусса, если уравнение приводимо, можно предположить, что множители имеют целые коэффициенты.
Найти корни приводимого кубического уравнения проще, чем решить общий случай. Фактически, уравнение сводится, один из множителей должен иметь степень и таким образом иметь
- qx — p { displaystyle qx-p}
, где q и p являются взаимно простыми целыми числами.. Тест на рациональный корень позволяет найти q и p, исследуя конечное число случаев (q должно быть делителем d).
Таким образом, один корень равенство x 1 = pq, { displaystyle textstyle x_ {1} = { frac {p} {q}},}
- aqx 2 + bq + apq 2 x + cq 2 + bpq + ap 2 q 3 { displaystyle { frac {a} {q}} x ^ {2} + { frac {bq + ap} {q ^ {2}}} x + { frac {cq ^ {2} + bpq + ap ^ {2}} {q ^ {3}}}}
(коэффициенты кажутся не цел, но должны быть целыми числами, если p / q является корнем.)
Тогда другие корни являются корнями этого квадратного многочлена и могут быть найдены с помощью квадратной формулы.
Углубленная кубическая
Кубическая форма
- t 3 + pt + q { displaystyle t ^ {3} + pt + q}
называется депрессивной. Они проще, чем общий кубики, простой анализ любой кубики может быть сведено простой заменой простой к изучению депрессивной кубики.
Пусть
- a x 3 + b x 2 + c x + d = 0 { displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}
— кубическое уравнение. Изменение модели
- x = t — b 3 a { displaystyle x = t — { frac {b} {3a}}}
приводит к кубике, у которой нет члена в t. После деления на единицу получаем угнетенное кубическое уравнение
- t 3 + pt + q = 0, { displaystyle t ^ {3} + pt + q = 0,}
с
- t = x + b 3 ap Знак равно 3 ac — b 2 3 a 2 q = 2 b 3-9 abc + 27 a 2 d 27 a 3. { displaystyle { begin {align} t = {} x + { frac {b} { 3a}} \ p = {} { frac {3ac-b ^ {2}} {3a ^ {2}}} \ q = {} { frac {2b ^ {3} -9abc + 27a ^ {2} d} {27a ^ {3}}}. end {align}}}
корни x 1, x 2, x 3 { displaystyle x_ {1}, x_ {2}, x_ {3}}

-
- xi = ti — b 3 a, { displaystyle x_ {i} = t_ {i} — { frac {b} {3a}},}
- xi = ti — b 3 a, { displaystyle x_ {i} = t_ {i} — { frac {b} {3a}},}
для i = 1, 2, 3 { displaystyle i = 1,2,3}
Дискриминант и природа корней
Природа (настоящая или нет, отличная или нет) корней кубики может быть определена без их явного вычислений, с помощью дискриминант.
Дискриминант
Дискриминант полинома функция его коэффициентов, которые равны нулю тогда и только тогда, когда полином имеет кратный корень, или, если он делится на квадрат непостоянного многочлена. Другими словами, дискриминант отличен от нуля тогда и только тогда, когда многочлен бесквадратный.
Если r 1, r 2, r 3 — три корня (не обязательно и не отдельные действительные ) кубического ax 3 + bx 2 + cx + d, { displaystyle ax ^ {3} + bx ^ {2} + cx + d,}
- a 4 (r 1 — r 2) 2 (r 1 — r 3) 2 (r 2 — r 3) 2. { displaystyle a ^ {4} (r_ {1} -r_ {2}) ^ {2} (r_ {1} -r_ {3}) ^ {2} (r_ {2} -r_ {3}) ^ {2}.}
Дискриминант депрессивной кубики t 3 + pt + q { displaystyle t ^ {3} + pt + q}
- — (4 p 3 + 27 кв 2). { displaystyle — left (4 , p ^ {3} +27 , q ^ {2} right).}
Дискриминант общей кубики ax 3 + bx 2 + cx + d { displaystyle ax ^ {3} + bx ^ {2} + cx + d}
- 18 abcd — 4 b 3 d + b 2 c 2 — 4 ac 3 — 27 a 2 d 2. { displaystyle 18 , abcd-4 , b ^ {3} d + b ^ {2} c ^ {2} -4 , ac ^ {3} -27 , a ^ {2} d ^ {2}.}
Это произведение a 4 { displaystyle a ^ {4}}
Чтобы выразить предыдущие формулы, можно использовать формулы Виета, чтобы выразить все как многочлены от r 1, r 2, r 3 и а. Затем доказательство приводит к проверке равенства двух многочленов.
Природа корней
Если коэффициенты полинома действительные числа и дискриминант Δ { displaystyle Delta}
- Если Δ>0, { displaystyle Delta>0,}
кубик имеет три различных реальных корня
- Если Δ < 0, {displaystyle Delta <0,}
кубик имеет вещественный корень
- Городской 469>. многочлен имеет три корня (не обязательно разные) по основной теореме алгебры, крайней мере один корень должен быт ь действительным.
Как указано выше, если r 1, r 2, r 3 тремя корнями кубической ax 3 + bx 2 + cx + d { displaystyle ax ^ {3} + bx ^ {2} + cx + d }
, то дискриминант равенство
- Δ знак рав но a 4 (r 1 — r 2) 2 (r 1 — r 3) 2 (r 2 — r 3) 2 { displaystyle Delta = а ^ {4} (г_ {1} -r_ {2}) ^ {2} (r_ {1} -r_ {3}) ^ {2} (r_ {2} -r_ {3}) ^ {2}}
Если три корня действительны и различны, дискриминант является произведением положительных вещественных чисел, то есть Δ>0. { displaystyle Delta>0.}
Если только один корень, скажем, r 1, действителен, то r 2 и r 3 являются комплексно сопряженными, что означает, что r 2 — r 3 является чисто мнимым числом, и, таким образом, (r 2 — r 3) является действительным и отрицательным. С другой стороны, r 1 — r 2 и r 1 — r 3 являются комплексными, и их документ является сопроводительным и положительным. Таким, дискриминант произведен образом одного отрицательного числа и нескольких положительных чисел, Кубика кратный корень, кроме того, ее коэффициенты действительны, то все ее коэффициенты действительны, то все ее корни действитель ны.
Дискриминантивной депрессивной кубики t 3 + pt + д { Displaystyle ; t ^ {3} + pt + q ;}
равно нулю, если 4 p 3 + 27 д 2 = 0. { displaystyle 4p ^ {3} + 27q ^ {2} = 0 ;.}
Если p также равно нулю, то p = q = 0, а 0 — тройной корень кубики. Если 4 п 3 + 27 q 2 знак равно 0, { displaystyle ; 4p ^ {3} + 27q ^ {2} = 0 ;,}
и p ≠ 0, то кубическая имеет простой корень
- t 1 = 3 qp { displaystyle t_ {1} = { frac {, 3q ,} {p}}}
и двойной корень
- t 2 = t 3 = — 3 q 2 п. { displaystyle t_ {2} = t_ {3} = — { frac {, 3q ,} {2p}} ~.}
Другими словами,
- t 3 + pt + q = (t — 3 qp) (t + 3 q 2 p) 2. { displaystyle t ^ {3} + pt + q = left (t — { frac {3q} {p}} right) left (t + { frac {, 3q ,} {2p}} справа) ^ {2} ;.}
Этот результат может быть доказан путем расширения последнего произведения или получен путем решения довольно простой системы уравнений, полученной из формул Виета.
По использованию редукции угнетенной кубики, эти результаты можно распространить на общую кубику. Это дает: Если дискриминант кубической ax 3 + bx 2 + cx + d { displaystyle ; ax ^ {3} + bx ^ {2} + cx + d ;}
равно нулю, то
- либо, если b 2 = 3 ac, { displaystyle b ^ {2 } = 3ac ;,}
кубика имеет тройной корень
-
- x 1 = x 2 = x 3 = — b 3 a, { displaystyle x_ {1} = x_ {2} = x_ {3 } = — { frac {b} {, 3a ,}} ~,}
- x 1 = x 2 = x 3 = — b 3 a, { displaystyle x_ {1} = x_ {2} = x_ {3 } = — { frac {b} {, 3a ,}} ~,}
- и
- ax 3 + bx 2 + cx + d = a (x + b 3 a) 3 { displaystyle ax ^ {3} + bx ^ {2} + cx + d = a left (x + { frac {b} {, 3a ,}} right) ^ {3}}
- ax 3 + bx 2 + cx + d = a (x + b 3 a) 3 { displaystyle ax ^ {3} + bx ^ {2} + cx + d = a left (x + { frac {b} {, 3a ,}} right) ^ {3}}
- или, если б 2 ≠ 3 переменного тока, { Displaystyle ; Ь ^ {2} neq 3ac ;,}
кубика имеет двойной корень
-
- x 2 = x 3 = 9 ad — bc 2 (b 2 — 3 ac), { displaystyle x_ {2} = x_ {3} = { frac {9ad-bc} {, 2 (b ^ {2} -3ac) ,}} ~,}
- x 2 = x 3 = 9 ad — bc 2 (b 2 — 3 ac), { displaystyle x_ {2} = x_ {3} = { frac {9ad-bc} {, 2 (b ^ {2} -3ac) ,}} ~,}
- и простой корень,
- x 1 = 4 abc — 9 a 2 d — b 3 а ( б 2 — 3 ас). { displaystyle x_ {1} = { frac {, 4abc-9a ^ {2} db ^ {3} ,} {a (b ^ {2} -3ac)}} ~.}
- x 1 = 4 abc — 9 a 2 d — b 3 а ( б 2 — 3 ас). { displaystyle x_ {1} = { frac {, 4abc-9a ^ {2} db ^ {3} ,} {a (b ^ {2} -3ac)}} ~.}
- и, Следовательно,
- ах 3 + bx 2 + cx + d = a (x — x 1) (x — x 2) 2. { displaystyle ax ^ {3} + bx ^ {2} + cx + d = a , left (x-x_ {1} right) left (x-x_ {2} right) ^ {2} ~.}
- ах 3 + bx 2 + cx + d = a (x — x 1) (x — x 2) 2. { displaystyle ax ^ {3} + bx ^ {2} + cx + d = a , left (x-x_ {1} right) left (x-x_ {2} right) ^ {2} ~.}
Характеристика 2 и 3
Приведенные выше результаты действительны, если коэффициенты принадлежат полюса характеристики, кроме 2 или 3, но должны быть измененными для характеристик 2 или 3 из-за задействованных делений на 2 и 3.
Редукция до пониженной формы работает для характеристик 2, но не для характеристик 3. В обоих случаях это проще установить и определить для общей кубики. Основным инструментом для этого является тот факт, что кратный корень является общим корнем многочлена и его формальной производной. В этих характеристиках, если производная не константой, она имеет единственный корень, введенный линейным в характеристике 3, или квадрат линейного полинома в характеристике 2. Это позволяет вычислить кратный корень, а третий корень может быть выведен из суммы корней, которая предоставляется формулами Виета.
Отличие от других характеристик состоит в том, что в характеристике 2 формула двойного корня включает квадратный корень, а в характеристике 3 формула для тройной корень включает кубический корень.
Формуле Кардано
Джероламо Кардано приписывают публикацию первой формулы для решения кубических формул, приписывая ее Принципионе дель Ферро. Формула применима к кубикам с углублением, но, как показано в § Кубика с углублением, она позволяет решать все кубические уравнения.
Результат Кардано таков: если
- x 3 + px + q = 0 { displaystyle x ^ {3} + px + q = 0}
— это кубическое уравнение, такое что p и q являются действительными числами такими, что 4 p 3 + 27 q 2>0, { displaystyle 4p ^ {3} + 27q ^ {2}>0,}
тогда уравнение имеет реальный корень <6>- q 2 + q 2 4 + p 3 27 3 + — q 2 — q 2 4 + p 3 27 3. { Displaystyle { sqrt [{3}] {- { frac {q} {2}} + { sqrt {{ frac {q ^ {2}} {4}} + { frac {p ^ {3}} {27}}}}}} + { sqrt [{3}] {- { frac {q} {2}} — { sqrt {{ frac {q ^ {2}} {4}} + { frac {p ^ {3}} {27}}}}}}.}. }
См. § Получение корней ниже, чтобы узнать о нескольких методах получения этого результата.
Как показано в § Природа корней, два других В этом случае корни — это не действительные комплексно-сопряженные числ а. Позже было показано (Кардано не знал комплексных чисел ), что два других корня получаются умножением одного из корней куба на примитивный кубический корень из единицы — 1 + i 3 2, { displaystyle { frac {-1 + i { sqrt {3}}} {2}},}
и корень другого куба на — 1 — i 3 2. { displaystyle { frac {-1-i { sqrt {3}}} {2}}.}
Если 4 p 3 + 27 q 2 < 0, {displaystyle 4p^{3}+27q^{2}<0,}
существует три действительных корня, но теория Галуа позволяет доказать, что они не могут быть выражены алгебраическим выражением, включающим только действительные числа. Следовательно, в этом случае уравнение не может быть решено с учетом времени Кардано. Таким образом, этот падеж был назван casus unducibilis, что на латыни означает неприводимый падеж.
В случае использования casus irducibilis формула Кардано все еще может найти, но при использовании кубических корней требуется некоторая осторожность. Первый метод — определить символы { displaystyle { sqrt {{~} ^ {~}}}}
и 3 { displaystyle { sqrt [{3}] {{~ } ^ {~}}}}
как представление основных значений основная функция (то есть корня, имеющая наибольшую действующую часть). С этим соглашением формула Кардано для трех корней остается в силе, но не является чисто алгебраической, обозначением главной части не является чисто алгебраическим, поскольку оно включает неравенство для сравнения действительных частей. Кроме того, использование главного корня куба может дать неверный результат, если коэффициенты не являются действительными комплексными числами. Более того, если коэффициенты принадлежат другому полю , главный корень куба, как правило, не определено.
Второй способ сделать формулу Кардано всегда правильный — это отметить, что произведение двух корней куба должно быть –p / 3. В результате корень уравнения равенство
- C — p 3 C с C = — q 2 + q 2 4 + п 3 27 3. { displaystyle C — { frac {p} {3C}} quad { text {with}} quad C = { sqrt [{3}] {- { frac { q} {2}} + { sqrt {{ frac {q ^ {2}} {4}} + { frac {p ^ {3}} {27}}}}}}.}
В формуле символов { displaystyle { sqrt {{~} ^ {~}}}}
и 3 { displaystyle { sqrt [{3}] {{~} ^ { ~}}}}
обозначают любой квадратный корень и любой кубический корень. Остальные корни уравнения получаются либо заменой кубического корня, либо умножением кубического корня на примитивный кубический корень из единицы, то есть — 1 ± — 3 2. { displaystyle textstyle { frac {-1 pm { sqrt {- — 3}}} {2}}.}
Эта формула для корней всегда верна, кроме случаев, когда p = q = 0, при условии, если q = 0, выбора квадратного корня для того, чтобы иметь C ≠ 0. Однако формула бесполезна в этих случаях может быть выражена без кубического корня. Точно так же формула бесполезна и в других случаях, когда кубический корень не нужен, то есть когда 4 p 3 + 27 q 2 = 0 { displaystyle 4p ^ {3} + 27q ^ {2} = 0}
и когда кубический многочлен не неприводимый.
Эта формула также верна, когда p и q принадлежат любому полю характеристики кроме 2 или 3.
Общая кубическая формула
Кубическая формула для корней общего кубического уравнения (с a ≠ 0)
- ax 3 + bx 2 + cx + d = 0 { displaystyle ax ^ {3} + bx ^ { 2} + cx + d = 0}
можно вывести из любого варианта формулы Кардано путем сведения к угнетенной кубической. Представленный здесь вариант действителен не только для реальных коэффициентов, но и для коэффициентов a, b, c, d, принадлежащих любому полю характеристики, отличной от 2 и 3.
Формула довольно сложна, поэтому стоит разбить ее на более мелкие формулы.
Пусть
- Δ 0 = b 2 — 3 ac, Δ 1 = 2 b 3 — 9 abc + 27 a 2 d, { displaystyle { begin {align} Delta _ {0} = b ^ {2} -3ac, \ Delta _ {1} = 2b ^ {3} -9abc + 27a ^ {2} d, end {align}}}
и
- C = Δ 1 ± Δ 1 2 — 4 Δ 0 3 2 3, { displaystyle C = { sqrt [{3}] { frac { Delta _ {1} pm { sqrt { Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}}}} {2}}},}
где символы { displaystyle { sqrt {{~} ^ {~}}}}
и 3 { displaystyle { sqrt [{3}] {{~} ^ {~}}}}
интерпретируются как любой квадратный корень и любой кубический корень соответственно. Знак «±» перед квадратным корнем означает «+» или «-»; выбор почти произвольный, и его изменение равносильно выбору другого квадратного корня. Однако, если выбор дает C = 0, тогда должен быть выбран другой знак. Тогда один из корней равен
- x = — 1 3 a (b + C + Δ 0 C). { displaystyle x = — { frac {1} {3a}} left (b + C + { frac { Delta _ {0}} {C}} right) { text {.}}}
Два других корня можно получить, изменить выбор кубического корня в определении C или, что то же самое, умножив C на примитивный кубический корень из единицы, то есть –1 ± √ — 3 / 2. Другими словами, три корня:
- xk = — 1 3 a (b + ξ k C + Δ 0 ξ k C), k ∈ {0, 1, 2}, { displaystyle x_ {k} = — { frac { 1} {3a}} left (b + xi ^ {k} C + { frac { Delta _ {0}} { xi ^ {k} C}} right), qquad k in {0,1,2 } { text {,}}}
где ξ = –1 + √ — 3/2.
Что касается особого случая углубления кубики, формула применима, когда корни могут быть выражены без кубических корней.
Тригонометрические и гиперболические решения
Тригонометрическое решение для трех действующих корней
Когда кубическое уравнение с действующими коэффициентами имеет три действительных корня, формулы, выражающие эти корни черезлы, включая сложные числа. Теория Галуа позволяет доказать, что когда три корня действительны и ни один из них не является рациональным (casus unducibilis ), нельзя выразить корни в терминах реальных радикалов. Тем не менее, реальные выражения могут быть получены с помощью тригонометрических функций, в частности, в терминах косинусов и арккосинусов. Точнее, корни угнетенной кубической
- t 3 + pt + q = 0 { displaystyle t ^ {3} + p , t + q = 0}
равны
- tk = 2 — p 3 соз [1 3 arccos (3 q 2 p — 3 p) — 2 π k 3] для k = 0, 1, 2. { displaystyle t_ {k} = 2 , { sqrt {- { frac {, P ,} {3}} ;}} , cos left [, { frac {1} {3}} , arccos left ({ frac {, 3q ,} {2p}} , { sqrt {{ frac {-3 ;} {p}} ,}} , справа) — { frac {, 2 pi k ,} { 3}} , right] qquad { text {for}} ~ k = 0,1,2 ;.}
Это формула принадлежит François Viète. Это чисто реально, когда уравнение имеет три действительных корня (то есть 4 p 3 + 27 q 2 < 0 {displaystyle 4,p^{3}+27,q^{2}<0,}
). В противном случае это все еще правильно, но включает сложные косинусы и арккосинусы, когда есть только один действительный корень, и бессмысленно (деление на ноль), когда p = 0).
Эту формулу можно напрямую преобразовать в формулу для корней общего кубического уравнения, используя обратную подстановку, описанную в § Углубленная кубическая. Это можно доказать следующим образом:
Исходя из уравнения t + p t + q = 0, положим t = u cos θ. Идея состоит в том, чтобы выбрать u, чтобы уравнение совпадало с тождеством
- 4 cos 3 θ — 3 cos θ — cos (3 θ) = 0. { displaystyle 4 , cos ^ {3} theta -3 , cos theta — cos (, 3 theta ,) = 0 ;.}
Для этого выберите u = 2 — p 3, { displaystyle u = 2 , { sqrt {- { frac {, p ,} {3}} ;}} ,,}
и разделить уравнение по u 3 4. { displaystyle { гидроразрыв {; u ^ {3} ,} {4}} ,.}
Это дает
- 4 cos 3 θ — 3 cos θ — 3 q 2 р — 3 р = 0. { displaystyle 4 , cos ^ {3} theta -3 , cos theta — { frac {, 3q ,} {2p}} , { sqrt {{ frac {-3 ;} {p}} ,}} = 0 ;.}
В сочетании с указанным выше тождеством получаем
- cos (3 θ) = 3 q 2 p — 3 p, { displaystyle cos (3 theta) = { frac {, 3q ,} {2p}} { sqrt {{ frac {-3 ;} {p}} ,}} ;,}
и Таким образом, корни равны
- tk = 2 — p 3 cos [1 3 arccos (3 q 2 p — 3 p) — 2 π k 3] для k = 0, 1, 2. { displaystyle t_ {k} = 2 , { sqrt {, — { frac {, p ,} {3}} ;}} , cos left [{ frac {1} {3}} , arccos left ({ frac {, 3q ,} {2p}} , { sqrt {{ frac {-3 ;} {p}} ,}} right) — { frac {, 2 pi k ,} {3}} right] qquad { text {for}} ~ k = 0,1,2 ;.}
Гиперболическое решение для одного действительного корня
Когда есть только один действительный корень (и p ≠ 0), этот корень можно аналогичным образом представить с помощ ью гиперболических функций, как
- t 0 = — 2 | q | q — p 3 ch [1 3 arcosh (- 3 | q | 2 p — 3 p)], если 4 p 3 + 27 q 2>0 и p < 0, t 0 = − 2 p 3 sinh [ 1 3 arsinh ( 3 q 2 p 3 p) ] if p>0. { displaystyle { begin {align} t_ {0} = — 2 { frac {| q |} {q}} { sqrt {- { frac {p} {3}}}} cosh left [{ frac {1} {3}} operatorname {arcosh} left ({ frac {-3 | q |} {2p}} { sqrt { frac {-3} {p}}} right) right] qquad { text {if}} ~ 4p ^ {3} + 27q ^ {2}>0 ~ { text {and}} ~ p <0;,\t_{0}=-2{sqrt {frac {p}{3}}}sinh left[{frac {1}{3}}operatorname {arsinh} left({frac {3q}{2p}}{sqrt {frac {3}{p}}}right)right]qquad {text{if }}~p>0 ;. end {выровнено}}}
Если p ≠ 0 и неравенства справа не выполняются (трех случайных действительных корней), формулы остаются действительными, но включают комплексные величины.
Когда p = ± 3, приведенные выше значения t 0 иногда называют кубическим корнем Чебышева. Точнее, значения с косинусами и гиперболическими косинусами определяют, когда p = −3, ту же аналитическую функцию, обозначенную C 1/3 ( q), которая является правильным кубическим корнем Чебышева. Значение, включающее гиперболические sines аналогично обозначается S 1/3 (q), когда p = 3.
Геометрические решения
Решение Омара Хайяма
Геометрическое решение Омара Хайяма кубического уравнения для случая m = 2, n = 16, дающее корень 2. Пересечение вертикальной линии на оси x в центре круг является случайностью проиллюстрированного примера.
Для решения кубического уравнения x + mx = n, где n>0, Омар Хайям построил параболу y = x / m, круг, который имеет диаметр отрезка [0, n / m] на положительной оси x и вертикальная линия, проходящая через точку пересечения окружности и параболы над осью x. Решение определяется длиной горизонтального отрезка от начала координат до пересечения вертикальной линии и оси x (см. Рисунок).
Простое современное доказательство состоит в следующем. Умножение уравнения на x / m и перегруппировка членов дает
- x 4 m 2 = x (n m 2 — x). { displaystyle { frac {x ^ {4}} {m ^ {2}}} = x left ({ frac {n} {m ^ {2}}} — x right).}
В левой части находится значение y на параболе. Уравнение круга: y + x (x — n / m) = 0, правая часть — это значение y на круге.
Решение с трисектором угла
Кубическое уравнение с действительными коэффициентами может быть решено геометрически с использованием циркуля, линейки и трисектора угла тогда и только тогда. если у него три действительных корня.
Кубическое уравнение может быть решено с помощью построения циркуля и линейки (без трисектора) тогда и только тогда, когда оно имеет рациональный корень. Это означает, что старые проблемы трисекции угла и удвоения куба, поставленные древнегреческими математиками, не могут быть решены с помощью построения циркуля и линейки.
Геометрическая интерпретация корней
Три действительных корня
Для кубики (1)с тремя действительными корнями корни — это проекции на ось x вершин A, B и C равностороннего треугольника . Центр треугольника имеет ту же x-координату, что и точка перегиба .
. Тригонометрическое выражение корней Виете в случае трех действительных корней поддается геометрической интерпретации в терминах круга. Когда кубика записана в форме скобки (2), t + pt + q = 0, как показано выше, решение может быть выражено как
- tk = 2 — p 3 cos (1 3 arccos (3 q 2 p — 3 p) — k 2 π 3) для k = 0, 1, 2. { displaystyle t_ {k} = 2 { sqrt {- { frac {p} {3}}}} cos left ({ frac {1} {3}} arccos left ({ frac { 3q} {2p}} { sqrt { frac {-3} {p}}} right) -k { frac {2 pi} {3}} right) quad { text {for}} quad k = 0,1,2 ,.}
Здесь arccos (3 q 2 p — 3 p) { displaystyle arccos left ({ frac {3q} {2p}} { sqrt { frac {-3} {p}}} right)}
— угол в единичной окружности; взятие 1/3 этого угла соответствует извлечению кубического корня из комплексного числа; добавление −k2π / 3 для k = 1, 2 находит другие корни куба; и умножение косинусов этих результирующих углов на 2 — p 3 { displaystyle 2 { sqrt {- { frac {p} {3}}}}}}
корректирует масштаб.
В случае без депрессии (1)(показанного на прилагаемом графике) депрессивный случай, как указано ранее, получается путем определения таким образом, что x = t — b / 3a, поэтому t = x + b / 3а. Графически это соответствует простому смещению графика по горизонтали при переключении между переменными t и x без изменений угловых изменений. Этот сдвиг перемещает точку перегиба и центр круга на ось y. Следовательно, сумма корней уравнения по t равна нулю.
Один действительный корень
В декартовой плоскости
Наклон прямой RA в два раза больше, чем RH. Обозначая комплексные корни кубики как g ± hi, g = OM (здесь отрицательное значение) и h = √tan ORH = √ наклон прямой RH = BE = DA.
Когда график кубической функции отображается в декартовой плоскости, если есть только один действительный корень, это абсцисса (координата x) горизонтального пересечения кривой (точка R на рисунок). Кроме того, если комплексно сопряженные корни записаны как g ± hi, то вещественная часть g является абсциссой точки касания H касательной линии к кубике, проходящей через x- перехват R кубики (то есть длина RM со знаком, на рисунке отрицательная). Мнимые части ± h являются квадратными корнями из тангенса угла между этой касательной и горизонтальной осью.
В комплексной плоскости
С одним действительным и два комплексных корня, три корня могут быть представлены в виде точек на комплексной плоскости, как и два корня производной кубики. Между всеми этими корнями существует интересная геометрическая связь.
Точки на комплексной плоскости, представляющие три корня, пейзаж вершины равнобедренного треугольника. (Треугольник является равнобедренным, потому что один корень находится на горизонтальной (действительной) оси, являясь комплексно сопряженными, симметрично выше и ниже действительной оси.) Теорема Мардена гласит, что точки, представляющие корни производной кубики — это фокусы эллипса Штейнера треугольника — уникального эллипса, который касается треугольника в серединах его сторон. Если угол при вершине на действующей оси меньше, чем π / 3, тогда большая ось эллипса лежит на действительной оси, как и его фокусы и, следовательно, корни производной. Если этот угол больше π / 3, большая ось вертикальна, а ее фокусы, корни производной, являются комплексно сопряженными. И если этот угол равен π / 3, треугольник равносторонний, эллипс Штейнера — это просто вписанная окружность треугольника, его фокусы совпадают друг с другом в центре, который лежит на действительной оси, и, следовательно, производная имеет повторяющиеся действительные корни.
Группа Галуа
Для кубического неприводимого многочлена над полем k характеристики, отличной от 2 и 3, группа Галуа над k — это группа полевых автоморфизмов, фиксирующих k наименьшего расширения k (поле расщепления ). Эти автоморфизмы должны переставлять корни многочленов, эта группа является либо группой S 3 всех шести перестановок трех корней, либо группой A 3 трех круговых перестановок.
Дискриминант Δ кубики — это квадрат
- Δ = a 2 (r 1 — r 2) (r 1 — r 3) (r 2 — r 3), { displaystyle { sqrt { Delta }} = a ^ {2} (r_ {1} -r_ {2}) (r_ {1} -r_ {3}) (r_ {2} -r_ {3}),}
где a — старший коэффициент кубики, а r 1, r 2 и r 3 — три корня кубики. <Времен375>Δ { displaystyle { sqrt { Delta}}}
меняет знак при обмене двумя корнями, Δ { displaystyle { sqrt { Delta}}}
фиксированной группой Галуа, только если группа Галуа — A 3. Другими словами, группа Галуа является A 3 тогда и только тогда, когда дискриминант является квадратом элемента k.
Большинство целых чисел не являются квадратами, при работе с полем Q из рациональных чисел группа Галуа наиболее неприводимых кубических многочленов является группой S 3 с шестью элементами. Пример группы Галуа A 3 с тремя элементами дается формулой p (x) = x — 3x — 1, дискриминант с равенством 81 = 9.
Вывод корней
В этом раздел собраны несколько методов вывода формулы Кардано.
метод Кардано
Этот метод принадлежит Принципионе дель Ферро и Тарталье, но назван в честь Джероламо Кардано, который первым опубликовал его в своей книге Арс Магна (1545).
Этот метод применяется к вогнутой кубике t + pt + q = 0. Идея состоит в том, чтобы сделать две переменные u и v так, чтобы u + v = t, и подставить их в депрессивную кубику, получив
- U 3 + v 3 + (3 uv + p) (u + v) + q = 0. { displaystyle u ^ {3} + v ^ {3} + (3uv + p) (u + v) + q = 0.}
На этом этапе Кардано наложил условие 3uv + p = 0. Это убирает третий член в предыдущем равенстве, что приводит к системе уравнений
- u 3 + v 3 = — quv = — p 3. { displaystyle { begin {align} u ^ {3} + v ^ {3} = — q \ uv = — { frac {p} {3}}. end {align}}}
Зная сумма и произведение u и v, можно сделать вывод, что они являются двумя решениями квадратного уравнения
- (x — u 3) (x — v 3) = x 2 — (u 3 + v 3) Икс + U 3 v 3 знак равно Икс 2 — (U 3 + v 3) Икс + (УФ) 3 = 0, { Displaystyle (xu ^ {3}) (xv ^ {3 }) = х ^ {2} — (u ^ {3} + v ^ {3}) x + u ^ {3} v ^ {3} = x ^ {2} — (u ^ {3} + v ^ {3}) x + (uv) ^ {3} = 0,}
поэтому
- x 2 + qx — p 3 27 = 0, { displaystyle x ^ {2} + qx — { frac { p ^ {3}} {27}} = 0,}
Дискриминант этого уравнения равен Δ = q 2 + 4 p 3 27 { displaystyle Delta = q ^ {2} + { frac {4p ^ {3}} {27}}}
, и в предположении, что он положительные, действительные решения этого уравнения (после складывания деления на 4 под квадратным корнем):
- — q 2 ± q 2 4 + p 3 27. { displaystyle — { frac {q} {2}} pm { sqrt {{ frac {q ^ {2}} {4}} + { frac {p ^ {3}} {27}}}}.}
Итак (без ограничения общности выбора u v):
- u = — q 2 + q 2 4 + p 3 27 3. { displaystyl eu = { sqrt [{3}] {- { frac {q} {2}} + { sqrt {{ frac {q ^ {2}} {4}} + { frac {p) ^ { 3}} {27}}}}}}.}
- v = — q 2 — q 2 4 + p 3 27 3. { displaystyle v = { sqrt [{3}] {- { frac { q} {2}} — { sqrt {{ frac {q ^ {2}} {4}} + { frac {p) ^ {3}} {27}}}}}}.}
Сумма кубических корней этих решений является корнем уравнений. То есть
- t = — q 2 + q 2 4 + p 3 27 3 + — q 2 — q 2 4 + p 3 27 3 { displaystyle t = { sqrt [{3}] {- {q более 2} + { sqrt {{q ^ {2} over 4} + {p ^ {3} over 27}}}}} + { sqrt [{3}] {- {q over 2} — { sqrt {{q ^ {2} over 4} + {p ^ {3} over 27}}}}}}
— корень уравнения; это формула Кардано.
Это хорошо работает, когда 4 p 3 + 27 q 2>0, { displaystyle 4p ^ {3} + 27q ^ {2}>0,}
но, если 4 стр.. 3 + 27 q 2 < 0, {displaystyle 4p^{3}+27q^{2}<0,}
квадратный корень, фигурирующий в формуле, не является действительным. Форма комплексное число имеет три кубических корня, использование формулы Кардано без осторожности даст девять корней, кубическое уравнение не Это было впервые разъяснено Рафаэлем Бомбелли в его книге L’Algebra (1572). Решение состоит в том, что uv = –p / 3, то есть v = — p / 3u. Это означает, что можно вычислить только один кубический корень, и приводит ко второй формуле, приведенной в § Формула Кардано.
Другие корни уравнения могут быть получены путем изменения кубического корня, или эквивалентно, умножением кубического корня ня на каждый из двух примитивных кубических корней из единицы, которые равны — 1 ± — 3 2. { displaystyle { frac {-1 pm { sqrt {-3}}} { 2}}.}
Подстановка Виета
Подстановка Виета — это метод, представленный Франсуа Виетом (Виета — его латинское имя) в тексте, опубликованном посмертно в 1615 году, который непосредственно используется вторую формулу § метода Кардано и позволяет избежать проблемы вычислений двух разных кубических корней.
Начало с угнетенной кубики t + pt + q = 0, замена Виета имеет вид t = w — p / 3w.
Подстановка t = w — p / 3w преобразует угнетенную кубику в
- w 3 + q — p 3 27 w 3 = 0. { displaystyle w ^ {3} + q — { frac {p ^ {3}} {27w ^ {3}}} = 0.}
Умножая на w, получаем квадратное уравнение w:
- (w 3) 2 + q (w 3) — p 3 27 = 0. { displaystyle (w ^ {3}) ^ {2} + q (w ^ {3)}) — { frac {p ^ {3}} {27}} = 0.}
Пусть
- W = — q 2 ± p 3 27 + q 2 4 { displaystyle W = — { frac {q} {2}} pm { sqrt {{ frac {p ^ {3}} {27}} + { frac {q ^ {2}} {4}}}}}
быть любым ненулевой корень этого квадратного уравнения. Если w 1, w 2 и w 3 тремя кубическими корнями из W, то корни исходной депрессивной кубической системы равны w 1 — p / 3w 1, w 2 — p / 3w 2 и w 3 — п / 3w 3. Другой корень квадратного уравнения равенство — p 3 27 Вт. { displaystyle textstyle — { frac {p ^ {3}} {27W}}.}
Это означает, что изменение знака квадратного корня меняет местами w i и — p / 3w i для i = 1, 2, 3 и, следовательно, не меняет корни. Этот метод не работает только тогда, когда оба корня квадратного уравнения равны нулю, то есть когда p = q = 0, и в этом случае единственная корень углубленной кубики равен 0.
Метод Лагранжа
В своей статье Рефлексии на основе алгебраических решений уравнений («Мысли об алгебраическом решении уравнений») Джозеф Луи Лагранж представил новый метод решений низкой степени единообразным образом, с надеждой, что он мог обобщить это для более высоких степеней. Этот метод хорошо работает для кубических четвертой степени, но Лагранжу не удалось применить его к уравнению пятой степени, поскольку он требует решения резольвентного полинома не менее шестой степени. За исключением того, что решить задачу ранее никому не удавалось, это было первым признаком алгебраической формулы для степеней 5 и выше. Позже это было доказано и названо теоремой Абеля — Руффини. Тем не менее, современные методы решения уравнений пятой степени основаны в основном на методе Лагранжа.
В случае кубических условий метод Лагранжа дает то же решение, что и метод Кардано. Метод Лагранжа может быть применен непосредственно к общему кубическому уравнению ax + bx + cx + d = 0, но проще с кубическим уравнением с депрессией, t + pt + q = 0.
Основная идея Лагранжа заключалась в для работы с дискретным преобразованием Фурье корней вместо самих корней. Точнее, пусть ξ будет примитивным корнем третьей степени из единицы, то есть таким числом, что ξ = 1 и ξ + ξ + 1 = 0 (при работе в пространстве комплексных чисел, один имеет ξ = — 1 ± i 3 2 = е 2 я π / 3, { displaystyle textstyle xi = { frac {-1 pm i { sqrt {3}}} {2}} = e ^ {2i pi / 3},}
, но эта сложная интерпретация здесь не используется). Обозначая x 0, x 1 и x 2 три корня кубического уравнения, которое нужно решить, пусть
- s 0 = x 0 + x 1 + Икс 2, s 1 знак равно Икс 0 + ξ Икс 1 + ξ 2 Икс 2, s 2 = Икс 0 + ξ 2 Икс 1 + ξ Икс 2, { Displaystyle { begin {Выровнено} s_ {0} = x_ { 0} + x_ {1} + x_ {2}, \ s_ {1} = x_ {0} + xi x_ {1} + xi ^ {2} x_ {2}, \ s_ {2} = x_ {0} + xi ^ {2} x_ {1} + xi x_ {2}, end {align}}}
— дискретное преобразование Фурье корней. Если s 0, s 1 и s 2 известны, корни могут быть восстановлены из них с помощью обратного преобразования Фурье, состоящего из обращения этого линейного преобразования; то есть
- x 0 = 1 3 (s 0 + s 1 + s 2), x 1 = 1 3 (s 0 + ξ 2 s 1 + ξ s 2), x 2 = 1 3 (s 0 + ξ s 1 + ξ 2 s 2). { displaystyle { begin {align} x_ {0} = { tfrac {1} {3}} (s_ {0} + s_ {1} + s_ {2}), \ x_ {1} = { tfrac {1} {3}} (s_ {0} + xi ^ {2} s_ {1} + xi s_ {2}), \ x_ {2} = { tfrac {1} { 3}} (s_ {0} + xi s_ {1} + xi ^ {2} s_ {2}). End {align}}}
По формулам Виета, s 0, как известно, равняется нулю в случае кубики с углублением и −b / a для общей кубики. Таким образом, необходимо вычислить только s 1 и s 2. Они не являются симметричными функциями корней (обмен x 1 и x 2 также меняет s 1 и s 2), но некоторые простые симметричные функции s 1 и s 2 также симметричны по корням решаемого кубического уравнения. Таким образом, эти симметричные функции могут быть выражены через (известные) коэффициенты исходной кубики, и это позволяет в конечном итоге выразить s и как корни многочлена с известными коэффициентами.
В случае кубического уравнения такими симметричными многочленами являются P = s 1s2и S = s 1 + s 2 (см. Ниже). Отсюда следует, что s 1 и s 2 являются двумя корнями квадратного уравнения z — Sz + P = 0. Таким образом, разрешение уравнения может быть завершено точно так же, как с методом Кардано., с s 1 и s 2 вместо u и v.
В случае вдавленной кубики x 0 = 1/3 (s 1 + s 2) и s 1s2= −3p, в то время как в методе Кардано мы установили x 0 = u + v и uv = −1 / 3шт. Таким образом, до обмена u и v s 1 = 3u и s 2 = 3v. Другими словами, в этом случае метод Лагранжа вычисляет в точности одни и те же вещи с помощью трех вспомогательных чисел, причем главное состоит в том, что метод Лагранжа объясняет, почему эти вспомогательные переменные появляются в задаче.
Вычисление S и P
Прямое вычисление с использованием использования ξ = 1 и ξ + ξ + 1 = 0
- P = s 1 s 2 = x 0 2 + x 1 2 + x 2 2 — (x 0 x 1 + x 1 x 2 + x 2 x 0), S = s 1 3 + s 2 3 = 2 (x 0 3 + x 1 3 + x 2 3) — 3 (Икс 0 2 Икс 1 + Икс 1 2 Икс 2 + Икс 2 2 Икс 0 + Икс 0 Икс 1 2 + Икс 1 Икс 2 2 + Икс 2 Икс 0 2) + 12 Икс 0 Икс 1 Икс 2. { displaystyle { begin {align} P = s_ {1} s_ {2} = x_ {0} ^ {2} + x_ {1} ^ {2} + x_ {2} ^ {2} — (x_ {0} x_ {1 } + x_ {1} x_ {2} + x_ {2} x_ {0}), \ S = s_ {1} ^ {3} + s_ {2} ^ {3} = 2 (x_ {0} ^ {3} + x_ {1} ^ {3} + x_ {2} ^ {3}) — 3 (x_ {0} ^ {2} x_ {1} + x_ {1} ^ {2} x_ {2 } + x_ {2} ^ {2} x_ {0} + x_ {0} x_ {1} ^ {2} + x_ {1} x_ {2} ^ {2} + x_ {2} x_ {0} ^ {2}) + 12x_ {0} x_ {1} x_ {2}. End {align}}}
Это показывает, что P и Q являются симметричными функциями корней. Используя тождества Ньютона, их просто выразить в терминах элементарных симметричных функций корней, давая
- P = e 1 2 — 3 e 2, S = 2 е 1 3–9 е 1 е 2 + 27 е 3, { displaystyle { begin {выровнено} P = e_ {1} ^ {2} -3e_ {2}, \ S = 2e_ {1} ^ {3} -9e_ {1 } e_ {2} + 27e_ {3}, end {align}}}
с e 1 = 0, e 2 = p и e 3 = −q в случае вдавленной кубики и e 1 = −b / a, e 2 = c / a и e 3 = −d / a, в общем случае.
Приложения
Кубические уравнения в различных контекстах.
В математике
- Трисекция угла и удвоение куба — это две древние проблемы геометрии, которые, как было доказано, не решаемы линейка и компас, поскольку они эквивалентны решению кубического уравнения.
- Теорема Мардена трех утверждает, что фокусы эллипса Штайнера любого треугольника можно найти с помощью кубических функций, корни которых являются координатами в комплексной плоскости вершин треугольника. Корни первой производной этой кубики являются комплексными координатами этих фокусов.
- Площадь правильного семиугольника может быть выражена с точки зрения корней кубика. Кроме того, отношения длинного диагонали к стороне, стороны к короткой диагонали и отрицательного значения соответствуют определенному кубическому уравнению. Кроме того, внутренним радиусом к описанным радиусу для семи тогоугольного треугольника является одним из решений кубического уравнения. Значения тригонометрических функций угловых, связанных с 2 π / 7 { displaystyle 2 pi / 7}
, удовлетворяют кубическим уравнениям.
- Данный косинус (или другую тригонометрическую функцию) произвольного угла, косинус одной трети этого угла является одним из корней кубики.
- Решение общего уравнения четвертой степени опирается на решение его резольвентной кубики.
- . Собственные значения матрицы 3 × 3 являются корнями кубического многочлена, который является характерным многочленом матрицы.
- характеристическое уравнение для постоянных коэффициентов третьего порядка линейное дифференциальное уравнение или разностное уравнение является кубическим уравнением.
- Точки пересечения кубической кривой Безье и прямые линии могут быть вычислены с использованием прямого кубического уравнения, представляющего кривую Безье.
В других науках
- В аналитической химии, уравнение Шарло, которое можно использовать для найти pH буферных растворов, можно решить с помощью кубического уравнения.
- В термодинамике, уравнения состояния (связанные с давлением, объемом и температурой вещества) кубичны по объему.
- Кинематические уравнения, включающие линейные скорости ускорения, кубические.
- Скорость сейсмических волн Рэлея — это решение кубического уравнения волны Рэлея.
Примечания
Ссылки
- Гильбо, Люси (1930), «История решения кубического уравнения», «Новости математики», 5 (4): 8–12, doi : 10.2307 / 3027812, JSTOR 3027812
Дополнительная литература
- Энглин, WS; Ламбек, Иоахим (1995), «Математика в эпоху Возрождения», Наследие Фалеса, Спрингерс, стр. 125–131, ISBN 978-0-387-94544 -6 гл. 24.
- Денс, Т. (ноябрь 1997 г.), «Кубика, хаос и метод Ньютона», Mathematical Gazette, Mathematical Association, 81(492): 403–408, doi : 10.2307 / 3619617, ISSN 0025-5572, JSTOR 3619617
- Даннет, Р. (ноябрь 1994 г.), «Ньютон — Рафсон и кубик», Mathematical Gazette, Mathematical Association, 78(483): 347–348, doi : 10.2307 / 3620218, ISSN 0025-5572, JSTOR 3620218
- Джейкобсон, Натан (2009), Базовая алгебра, 1 (2-е изд.), Довер, ISBN 978-0-486-47189-1
- Митчелл, DW (ноябрь 2007 г.), «Решение кубиков путем решения треугольников », Mathematical Gazette, Mathematical Association, 91: 514–516, doi : 10.1017 / S0025557200182178, ISSN 0025- 5572
- Митчелл, DW (ноябрь 2009 г.), «Степени φ как корни кубики», Mathematical Gazette, Mathematical Association, 93, ISSN 0025-5572
- Press, WH; Теукольский, С. А.; Vetterling, W. T.; Фланнери, Б.П. (2007), «Раздел 5.6 Квадратные и кубические уравнения», Численные рецепты: Искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521-88068-8
- Рехтшаффен, Эдгар (июль 2008 г.), «Действительные корни кубики: явная формула для квазирешений», Mathematical Gazette, Mathematical Association, 92: 268 –276, doi : 10.1017 / S0025557200183147, ISSN 0025-5572
- Zucker, IJ (июль 2008 г.), «Кубическое уравнение — новый взгляд на неприводимый случай », Mathematical Gazette, Mathematical Association, 92: 264–268, doi : 10.1017 / S0025557200183135, ISSN 0025 -5572
Внешние ссылки
На Викискладе есть материалы, связанные с Кубическими функциями. - Δ знак рав но a 4 (r 1 — r 2) 2 (r 1 — r 3) 2 (r 2 — r 3) 2 { displaystyle Delta = а ^ {4} (г_ {1} -r_ {2}) ^ {2} (r_ {1} -r_ {3}) ^ {2} (r_ {2} -r_ {3}) ^ {2}}
Содержание
Полином одной переменной
§
Полиномы нескольких переменных рассматриваются
☞
ЗДЕСЬ.
Будем обозначать через $ mathbb A_{} $ какое-либо из множеств $ mathbb Z,mathbb Q, mathbb R_{} $ или
$ mathbb C_{} $.
Общая информация
Функция вида
$$
f(x)=a_0x^n+a_1x^{n-1}+dots+a_n = sum_{j=0}^n a_jx^{n-j}
$$
при $ n_{} in {0,1,dots } $ и $ {a_{0},dots,a_n}subset mathbb A $ относительно переменной $ x_{} $ называется
полиномом1)
или многочленом от указанной переменной над множеством $ mathbb A_{} $. Число $ a_{j} $
называется коэффициентом2) полинома (при $ (n-j)_{} $-й степени переменной),
выражение $ a_{j}x^{n-j} $ — членом (одночленом) полинома,
$ a_{n} $ — свободным членом, $ x_{}^{n-j} $ — мономом.
П
Пример. Выражения
$$ x^{2}+2,x-679, x^{2}+sqrt{2}x-pi , {mathbf i} , x^{3}- 2,x +sqrt{3} $$
являются полиномами; а
$$ x^{-2}+3, x +x^{2} , x^{x}, sum_{j=0}^{infty} x^{j}/j_{} $$
полиномами не являются.
Если $ a_{0}ne 0 $, то член $ a_0x^{n} $ называется ведущим членом, а
$ a_{0} $ — старшим коэффициентом полинома. При этом
число $ n_{} $ называется степенью полинома и обозначается3) $ deg f_{}(x) $.
Полином первой степени называется линейным полиномом.
Полином, все коэффициенты которого, кроме, возможно, $ a_{n} $, равны нулю,
называется константой4); будем обозначать его const.
Очевидно, что степень константы равна нулю; исключительным для этого
утверждения является случай когда константа является нулем.
Если все коэффициенты полинома равны нулю,
то такой полином называется (тождественно) нулевым. В этом
случае его степень не определяется.
На переменную $ x_{} $ мы пока не накладываем ни какого ограничения: она может
принимать значения из любого указанного выше множества — не обязательно
из того, которому принадлежат коэффициенты полинома. Обозначим область
определения полинома через $ mathbb B_{} $.
Значением полинома при (или в точке) $ cin mathbb B_{} $ называется число
$$
f(c) = a_0c^n+a_1c^{n-1}+dots+a_n .
$$
Два полинома
$$ f(x)=a_0x^n+dots+a_n u g(x)=b_0x^m+dots+b_m $$
с коэффициентами из $ mathbb A $ называются (тождественно) равными:
$$ f(x)equiv g(x) $$
если совпадают множества их членов; или, что то же, равны их степени
и равны коэффициенты при одинаковых степенях переменной.
Это определение отличается от привычного определения равенства двух функций:
две функции $ F_{}(x) $ и $ G(x)_{} $ называются равными на множестве $ mathbb B_{} $ если
совпадают их значения при любом $ x in mathbb B_{} $.
На самом деле, для случая полиномов эти два определения — алгебраическое и функциональное — эквивалентны.
Т
Теорема. $ f_{}(x)equiv g(x) $ тогда и только тогда, когда
$ f(c)=g(c)_{} $ для $ forall cin mathbb B_{} $.
Одним из следствий теоремы является тот факт, что для полинома совершенно
не важен порядок следования его членов; в частности, наряду с записью
полинома по убывающим степеням переменной, мы имеем право
записывать его и по возрастающим: $ f_{}(x)= sum_{j=0}^n a_{n-j}x^{j} $.
Форма полинома, в которой его разложение записывается
по убывающим степеням переменной, называется его канонической формой.
Кроме того, теорема дает нам право на операцию, называемую
приведением подобных членов:
$$ ax^{j}+bx^j equiv (a+b)x^j, quad ax^jcdot bx^k=ab x^{j+k} .$$
Имея в виду этот факт, определим теперь две основные операции для полиномов:
сложение и умножение.
Суммой двух полиномов $ f_{}(x) $ и $ g_{}(x) $ называется полином, составленный как сумма всех одночленов, входящих в состав
$ f_{}(x) $ и $ g_{}(x) $:
$$ f(x) + g(x) = (a_n+b_m) + (a_{n-1}+b_{m-1})x+dots +
left{begin{array}{ll}
(a_0+b_0)x^n & npu m=n, \
a_0x^n & npu m<n, \
b_0x^m & npu m>n.
end{array} right.
$$
Т
Теорема. $ deg (f+g_{})le max (deg f, deg g) $.
Произведением двух полиномов $ f_{}(x) $ и $ g_{}(x) $ называется полином, составленный как сумма всевозможных попарных произведений членов первого полинома на члены второго:
$$
begin{matrix}
f(x)g(x) &=& a_0b_0x^{n+m}+(a_1b_0+a_0b_1)x^{n+m-1}
+(a_2b_0+a_1b_1+a_0b_2)x^{n+m-2}+ \
& &+dots + (a_0b_k+a_1b_{k-1}+dots+a_kb_0)x^{n+m-k}+ dots + a_nb_m .
end{matrix}
$$
(В записи коэффициента при $ x^{n+m-k} $ мы полагаем $ a_{j}= 0 $ при $ j>n_{} $ и
$ b_{ell} = 0 $ при $ ell>m_{} $).
Т
Теорема. Если $ f_{}(x) notequiv 0 $ и $ g_{}(x) notequiv 0 $,
то $ deg (fcdot g_{})= deg f + deg g_{} $.
Фактическое выполнение операции перемножения полиномов возможно по схеме,
напоминающей алгоритм умножения целых чисел «столбиком»: это позволяет
сэкономить время на выписывание степеней переменной.
П
Пример. Перемножить полиномы
$$ x^{5}+x^3-2,x^2+3 quad mbox{ и } quad 2, x^{4}-3,x^3 +4,x^2-1 , . $$
Решение. Представим полиномы наборами их коэффициентов, расположив
один из них горизонтально, а второй — вертикально. Умножение полинома
$ f_{}(x) $ на $ b_{j}x^{n-j} $ сводится к умножению набора $ (a_{0},dots,a_n) $
на $ b_{j} $; результат следующего умножения — на $ b_{j+1}x^{n-j-1} $ —
получается аналогичным образом, но записывается со сдвигом на одну позицию
вправо. Получившиеся ряды суммируются по столбцам.
$$
begin{array}{r|rrrrrrrrrr}
&1 & 0 & 1 & -2& 0 & 3 \
hline
2 & 2 & 0 & 2 & -4 & 0 & 6 \
-3& & -3 & 0 & -3 & 6 & 0 & -9 \
4 & & & 4 & 0 & 4 & -8 & 0 & 12 \
0 & & & \
-1 &&&&& -1 & 0 & -1 & 2 & 0 & -3 \
hline& 2 & -3 & 6 & -7 & 9 & -2 & -10 & 14 & 0 & -3
end{array}
$$
(В отличие от перемножения чисел здесь результаты сложения в столбиках не
переносятся в следующий разряд.)
Ответ. $ 2,x^{9}-3,x^8+6,x^7-7,x^6+9,x^5-2,x^4-10,x^3+14,x^2 — 3 $.
Множество всех полиномов от переменной $ x_{} $ с коэффициентами из $ mathbb A_{} $
будем обозначать $ mathbb A_{} [x] $.
§
Способы более эффективного умножения полиномов излагаются
☞
ЗДЕСЬ
Схема Хорнера
Задача. Вычислить значение полинома в точке $ c $.
Схема вычисления, заложенная в самом определении, «стóит» $ 3n_{}-1 $ операции:
$$ begin{array}{rrrrr}
& &c^2=ctimes c, & dots, & c^n=c^{n-1}times c , \
&a_{n-1} times c, & a_{n-2} times c^2, & dots, & a_0 times c^n ,\
a_n & +a_{n-1} times c & + a_{n-2} times c^2 & + dots & + a_0 times c^n,
end{array}
$$
т.е. $ 2n_{}-1 $ операции умножения и $ n_{} $ операций сложения. Организуем теперь
вычисления по-другому:
$$
begin{matrix}
f(c)&=&a_n+a_{n-1}c+a_{n-2}c^2+dots +a_1c^{n-1}+a_0c^n = \
&=&a_n+cleft(a_{n-1}+a_{n-2}c+ dots + a_0c^{n-1} right) = \
&= &a_n+cleft(a_{n-1}+cleft(a_{n-2}+dots + a_0c^{n-2} right) right) = \
&=& dots = \
&=&a_n+cleft(a_{n-1}+cleft(a_{n-2}+dots + c(a_1+ a_0c)dots right) right) .
end{matrix}
$$
Начинаем вычислять с самой внутренней скобки:
$${mathfrak b}_1= a_1+ a_0c, {mathfrak b}_2= a_2+ {mathfrak b}_1 c,dots,
{mathfrak b}_{n-1} = a_{n-1} +{mathfrak b}_{n-2}c,, {mathfrak b}_{n} = a_{n} +{mathfrak b}_{n-1}c=f(c)
$$
Вычисление каждой величины $ {mathfrak b}_{k} $ «стоит» $ 2_{} $ операции — одного
сложения и одного умножения (при условии, что предварительно вычислено $ {mathfrak b}_{k-1}^{} $).
Приведем компактную запись алгоритма:
$$
{mathfrak b}_k = a_k + {mathfrak b}_{k-1}c quad npu quad {mathfrak b}_0 = a_0 quad u quad
kin {1,dots,n }
.
$$
«Стоимость» вычисления значения $ f_{}(c) $ по этой схеме Хорнера составляет
$ 2n_{} $ операций. Налицо экономия по сравнению с прямым способом вычисления $ f_{}(c) $.
Вычисления удобно производить с помощью таблицы, стартовое состояние которой следующее:
$$
begin{array}{c|ccccccc}
& a_0 & a_1 & a_2 & dots & a_{n-2} & a_{n-1} & a_n \
hline
c & a_0
end{array}
$$
Будем отсчитывать строки сверху вниз, начиная от горизонтальной черты, т.е.
нулевой строкой будем считать строку из коэффициентов полинома.
Вычисление значения $ {mathfrak b}_{1} $ в первой строке производится по схеме: предыдущее число умножается на $ c_{} $ и складывается с верхним, т.е.
$$
begin{array}{c|ccccccc}
& a_0 & a_1 & a_2 & dots & a_{n-2} & a_{n-1} & a_n \
hline
c & a_0 & underbrace{a_1+ca_0}_{{mathfrak b}_1}
end{array}
$$
Далее вычисления идут по тому же правилу:
$$
begin{array}{c|ccccccc}
& a_0 & a_1 & a_2 & dots & a_{n-2} & a_{n-1} & a_n \
hline
c & a_0 &{mathfrak b}_1&underbrace{a_2+c{mathfrak b}_1}_{{mathfrak b}_2}
end{array}
$$
и т.д. Величина, получившаяся в последнем столбце, и будет искомым значением $ f_{}(c) $:
$$
begin{array}{c|ccccccc}
& a_0 & a_1 & a_2 & dots & a_{n-2} & a_{n-1} & a_n \
hline
c & a_0 &{mathfrak b}_1&{mathfrak b}_2&dots &{mathfrak b}_{n-2} & {mathfrak b}_{n-1}&
underbrace{a_n+c{mathfrak b}_{n-1}}_{{mathfrak b}_n=f(c)}
end{array}
$$
П
Пример. Вычислить значение полинома $ x^{5}-3, x +1 $ в точке $ 2+ mathbf i_{} $.
Решение.
$$
begin{array}{c|cccccc}
& 1 & 0 & 0 & 0 & -3 & 1 \
hline
2+ mathbf i & 1& 2+mathbf i &3+4 mathbf i &2+11 mathbf i & -10+24mathbf i& -43+38mathbf i
end{array}
$$
Ответ. $ -43+38mathbf i_{} $.
Выясним теперь смысл коэффициентов $ {mathfrak b}_{1},dots, {mathfrak b}_{n-1} $
первой строки схемы Хорнера.
Т
Теорема. Пусть $ cin mathbb B_{} $ и $ mathbb Bsubset mathbb A_{} $. Полином
$ f_{}(x)in mathbb A[x] $ допускает единственное представление в виде:
$$
f(x)equiv (x-c)q(x)+r npu r=constin mathbb A, q(x)in mathbb A[x],
deg q = deg f — 1 .
$$
Доказательство. Будем искать константу $ r_{} $ и полином $ q_{}(x) $ методом неопределенных
коэффициентов:
$ q(x)= q_{0}x^{n-1}+q_1x^{n-2}+ dots + q_{n-1} $. Подставим его в правую часть доказываемого
тождества, приведем подобные и приравняем коэффициенты
полученного полинома коэффициентам полинома $ f_{}(x) $. Получим линейные уравнения,
из которых последовательно определяем $ q_{0},q_1, dots, q_{n-1} $ :
$$
begin{array}{l|lll}
x^n& a_0&=q_0, & \
x^{n-1}& a_1&=q_1-q_0c &Rightarrow q_1=a_1+q_0c, \
x^{n-2}& a_2&=q_2-q_1c &Rightarrow q_2=a_2+q_1c, \
vdots & & dots & \
x & a_{n-1}&=q_{n-1}-q_{n-2}c &Rightarrow q_{n-1}=a_{n-1}+q_{n-2}c,\
1 & a_n&=qquad -q_{n-1}c+r & Rightarrow r=a_n+q_{n-1}c.
end{array}
$$
Видим, что формулы, определяющие коэффициенты $ q_{k} $, полностью совпадают
с формулами, определяющими элементы первой строки
схемы Хорнера, т.е. $ q_0={mathfrak b}_{0},dots,q_{n-1}={mathfrak b}_{n-1} $.
Но тогда $ r=a_n+q_{n-1}c=a_{n}+{mathfrak b}_{n-1}c={mathfrak b}_{n}=f(c) $.
♦
Итак, имеем:
$$q(x)={mathfrak b}_0x^{n-1}+dots+{mathfrak b}_{n-1}, r={mathfrak b}_{n} , $$
при этом все коэффициенты вычисляются по схеме Хорнера, а старший коэффициент
полинома $ q_{}(x) $ совпадает со старшим коэффициентом $ f_{}(x) $. Так, для полинома приведенного выше примера имеет место тождество:
$$x^5-3, x +1 equiv
$$
$$
equiv (x-2-mathbf i)left(x^4+ (2+mathbf i)x^3+(3+4,mathbf i)x^2+ (2+11,mathbf i)x
-10+24,mathbf i right) -43+38 mathbf i .
$$
Фактически результат предыдущей теоремы говорит о возможности деления полинома $ f_{}(x) $ на линейный полином $ (x-c)_{} $ с остатком. Строгое определение операции деления полиномов дается
☟
НИЖЕ.
Алгоритм схемы Хорнера можно развить и до вычисления значений производных от полинома $ f(x_{}) $ в точке $ c_{} $. См.
☞
ЗДЕСЬ.
Корни
Если значение полинома $ f_{}(x) $ при $ x=cin mathbb B_{} $ равно нулю, то число $ c_{} $ называется корнем полинома $ f_{}(x) $.
Иными словами, корень полинома $ f_{}(x) $ — это решение уравнения $ f_{}(x)=0 $, принадлежащее множеству
$ mathbb B_{} $.
«Корень»
как название неизвестной величины, которую требуется определить («извлечь») из уравнения,
является переводом арабского слова
ریشه
«джизр, джазир» — буквально означающего
«корень растения». В свою очередь, арабский вариант, по-видимому, является переводом санскритского слова «мула», применявшегося индийскими
учеными для обозначения квадратного корня.
Уравнение $ f_{}=0 $, в левой части которого стоит полином одной или
нескольких переменных, называется алгебраическим.
Задача. Выяснить количество корней полинома $ f_{}(x)in mathbb A[x] $,
принадлежащих множеству $ mathbb B_{} $, и вычислить их.
Решить алгебраическое уравнение $ f_{}(x)=0 $ над множеством
$ mathbb B $ означает найти все корни $ f_{}(x) $, принадлежащие $ mathbb B_{} $.
На основании теоремы из предыдущего пункта имеет место следующая
Т
Теорема [Безу]. Пусть $ mathbb B subset mathbb A_{} $ и $ cin mathbb B_{} $ — корень полинома $ f_{}(x), deg fge 1 $. Тогда полином $ f_{}(x)in mathbb A [x] $ допускает представление в виде произведения:
$$
f(x)equiv (x-c)f_1(x) ,
$$
где полином $ f_{1}(x)in mathbb A [x], deg f_1 = deg f — 1 $ определяется единственным образом.
Итак, теорема Безу утверждает, что в случае существования корня полинома,
возможно разложение этого полинома в произведение двух полиномов — одного
первой степени и одного полинома степени, на единицу меньшей исходного.
Тем самым, задача о нахождении корней полинома $ f_{}(x) $ сведется к аналогичной
задаче для полинома $ f_{1}(x) $; вторая задача может оказаться более простой
за счет понижения степени.
Фактическое нахождение полинома $ f_{1}(x) $ возможно произвести с помощью схемы Хорнера.
П
Пример. Решить уравнение
$$ x^{3}+3 mathbf i, x^2-3(1+2 mathbf i)x+10-5 mathbf i =0 $$
над множеством $ mathbb C_{} $, если известно, что число $ (-1-2 mathbf i)_{} $ — одно из его решений.
Решение. Строим схему Хорнера:
$$
begin{array}{c|cccc}
& 1& 3mathbf i & -3(1+2 mathbf i) & 10-5 mathbf i \
hline
-1-2 mathbf i & 1& -1+ mathbf i & -5 mathbf i & 0
end{array}
$$
Видим, что число $ (-1-2 mathbf i)_{} $ действительно является корнем полинома, и, следовательно, последний раскладывается в произведение двух полиномов: линейного и квадратичного. Коэффициенты квадратичного полинома выбираются из той же схемы:
$$ (x+1+2 mathbf i )(x^2 + (-1+ mathbf i )x- 5 mathbf i) . $$
Квадратное уравнение над $ mathbb C_{} $ можно решить (см.
☞
ЗДЕСЬ ), его корни:
$ (-1-2 mathbf i)_{} $ и $ 2+mathbf i_{} $.
Ответ. $ (-1-2 mathbf i), 2+ mathbf i_{} $.
Если полином $ f_{}(x) $ раскладывается в произведение $ f_{}(x)equiv (x-c)f_1(x) $, то полином $ (x-c) $ называется линейным множителем для $ f_{}(x) $ над множеством $ mathbb B_{} $.
=>
Для того, чтобы $ (x-c)_{} $ был линейным множителем для $ f_{}(x) $ необходимо и достаточно чтобы число $ c_{} $ было корнем $ f_{}(x) $.
Начиная с этого места, корни полинома будем обозначать греческими буквами: $ lambda, mu_{} $ и т.д.
Примеры показывают, что не для всякого полинома и множества $ mathbb B_{} $
корни существуют. Очевидно не имеет корней полином нулевой степени
(константа, отличная от нуля); любой полином первой степени над $ mathbb A_{} $
имеет единственный корень, принадлежащий $ mathbb A_{} $.
Квадратный полином $ x^{2}+1 $ не имеет вещественных корней,
но имеет мнимые.
Основная теорема высшей алгебры
Т
Теорема. Любой полином с комплексными коэффициентами, степень которого больше нуля, имеет хотя бы один корень, в общем случае, комплексный.
Эта теорема гарантирует существование корня $ lambda_{1}in mathbb C $.
На основании теоремы Безу, можно утверждать, что $ f_{}(x) $ допускает представление
$$ f(x)equiv (x-lambda_1)f_1(x) quad npu quad f_1(x)in mathbb C [x], deg f_1(x)=deg f(x) -1 .$$
Если $ deg f_{1}(x) ge 1 $, то, по той же теореме, полином $ f_{1}(x) $
также должен обладать корнем, который мы обозначим5) $ lambda_{2} $; теорема Безу гарантирует тогда представление
$$
f(x)equiv (x-lambda_1)(x-lambda_2)f_2(x) quad npu quad f_2(x)in mathbb C [x], deg f_2(x)=deg f(x) -2
.$$
Продолжая процесс далее, мы за $ n_{} $ шагов придем к представлению
$$
f(x)equiv (x-lambda_1)(x-lambda_2)times dots times (x-lambda_n)f_n(x) quad npu quad f_n(x)in mathbb C[x], deg f_n(x)=0
,$$
т.е. полином $ f_{n}(x)^{} $ представляет собой константу. На основании условия
тождественного равенства полиномов утверждаем, что $ f_{n}(x) equiv a_0 $.
Таким образом приходим к следующей альтернативной версии основной теоремы высшей алгебры.
Т
Теорема. Для произвольного полинома $ f_{}(x) $ степени $ n_{}ge 1 $
существует его представление в виде произведения линейных множителей
$$
f(x)equiv a_0(x-lambda_1)(x-lambda_2)times dots times (x-lambda_n) ;
$$
это представление единственно с точностью до перестановки сомножителей.
Как уже отмечалось в доказательстве теоремы, в этом представлении
могут встречаться одинаковые линейные сомножители. Собрав их вместе, получим
иной вид этого представления
$$
f(x)equiv a_0(x-lambda_1)^{{mathfrak m}_{1}}times
dots times
(x-lambda_{mathfrak r})^{{mathfrak m}_{{mathfrak r}}} , npu
{mathfrak m}_{1}+{mathfrak m}_{2}+dots+{mathfrak m}_{mathfrak r}=n
$$
и все числа $ lambda_{1},dots,lambda_{mathfrak r} $ теперь различны. Эта
формула называется формулой разложения полинома $ f_{}(x) $ на линейные сомножители или линейным представлением полинома $ f_{}(x) $; при этом число
$ {mathfrak m}_{j}^{}in mathbb N $ называется кратностью линейного сомножителя
$ x-lambda_{j} $ или кратностью корня $ lambda_{j} $ в полиноме $ f_{}(x) $.
Корень $ lambda_{j} $ называется простым, если $ {mathfrak m}_{j}=1_{} $ и
кратным кратности $ {mathfrak m}_{j}^{} $ если $ {mathfrak m}_{j}>1_{} $ (двойным или двукратным, если $ {mathfrak m}_{j}=2_{} $, тройным или трехкратным если $ {mathfrak m}_{j}=3_{} $ и т.д.)
Здесь имеет место неоднозначность математической терминологии:
простой корень — не обязательно простое число!
П
Пример. Найти линейное представление полинома
$$ f(x)=x^{6}-2, x^3+1 , .$$
Решение. Линейное представление легко получить если сначала заметить, что $ f(x)equiv (x^3-1)^{2} $, а затем использовать
выражения для корней кубических из единицы:
$$f(x)equiv (x-1)^2 left(x- frac{-1+ mathbf i sqrt{3}}{2} right)^2
left(x- frac{-1 — mathbf i sqrt{3}}{2} right)^2
.
$$
Все корни полинома имеют вторую кратность.
♦
§
Выведение условия наличия кратного корня (в терминах коэффициентов полинома)
☞
ЗДЕСЬ. При известном корне, нахождение его кратности
☞
ЗДЕСЬ.
Т
Теорема. Два полинома, степени которых
не превосходят $ n_{} $, равны тождественно если они имеют равные значения более
чем при $ n_{} $ различных значениях переменной.
Доказательство необходимости очевидно. Если полиномы $ f_{}(x) $ и $ g_{}(x) $ удовлетворяют условию теоремы, то полином $ f(x)-g_{}(x) $ должен иметь более,
чем $ n_{} $ корней, что, ввиду основной теоремы высшей алгебры, возможно лишь если он тождественно
нулевой.
♦
Теорема утверждает, что полином $ f_{}(x) $ степени,
$ le n_{} $, однозначно определяется своими значениями при более чем $ n_{} $
различных значениях переменной. Можно ли эти значения задавать произвольно?
Оказывается задание $ (n+1)_{} $-й пары $ (x_{1},y_1),dots,(x_{n+1},y_{n+1}) $
при всех различных $ x_{1},dots,x_{n+1} $ позволяет однозначно определить
полином $ f_{}(x) $ такой, что $ f(x_{1})=y_1,dots,f(x_{n+1})=y_{n+1} $ и
$ deg f_{} le n $. Практические способы решения этой задачи обсуждаются в разделе
☟
Интерполяция
Раздел находится
☞
ЗДЕСЬ.
Корни и коэффициенты полинома
Симметрические функции корней
Разложение полинома $ f_{}(x) $ на линейные множители дает интересные
соотношения между корнями полинома и его коэффициентами. Сначала выведем их
для малых степеней. Для $ n_{}=2 $:
$$a_0x^2+a_1x+a_2equiv a_0(x-lambda_1)(x-lambda_2)equiv
a_0x^2-a_0(lambda_1+lambda_2)x+a_0lambda_1lambda_2
Rightarrow
$$
$$
Rightarrow
left{ begin{array}{ccr}
lambda_1+lambda_2&=&-a_1/a_0, \
lambda_1lambda_2&=&a_2/a_0,
end{array}
right.
$$
т.е. получили формулы известные из школьного курса алгебры. Далее, для $ n_{}=3 $:
$$a_0x^3+a_1x^2+a_2x+a_3equiv a_0(x-lambda_1)(x-lambda_2)(x-lambda_3)equiv $$
$$equiv
a_0x^3-a_0(lambda_1+lambda_2+lambda_3)x^2+a_0(lambda_1lambda_2
+ lambda_1lambda_3+lambda_2lambda_3)x-a_0lambda_1lambda_2lambda_3
Rightarrow
$$
$$
Rightarrow
left{ begin{array}{ccr}
lambda_1+lambda_2+lambda_3&=&-a_1/a_0, \
lambda_1lambda_2+lambda_1lambda_3+lambda_2lambda_3&=&a_2/a_0,\
lambda_1lambda_2lambda_3&=&-a_3/a_0.
end{array}
right.
$$
Т
Теорема. Для корней $ lambda_{1},dots,lambda_n $ полинома
$$ f(x)=a_{0}x^n+a_1x^{n-1}+dots+a_n,, a_0ne 0 $$
справедливы формулы Виета
$$
sum_{1 le jle n} lambda_j = lambda_1+ dots+ lambda_n= -frac{a_1}{a_0},
$$
$$
sum_{1le j_1<j_2le n} lambda_{j_1} lambda_{j_2}= lambda_1 lambda_2 +
lambda_1 lambda_3 +dots + lambda_2 lambda_3
+ dots+ lambda_{n-1}lambda_n= frac{a_2}{a_0},
$$
$$
sum_{1le j_1<j_2<j_3le n} lambda_{j_1} lambda_{j_2} lambda_{j_3}=
lambda_1 lambda_2 lambda_3+ lambda_1 lambda_2 lambda_4 + dots+
lambda_{n-2} lambda_{n-1} lambda_n = -frac{a_3}{a_0},
$$
$$
dots
$$
$$
lambda_{1} lambda_{2}times dots timeslambda_{n-1}
+ lambda_{1} lambda_{2} times dots times lambda_{n-2} lambda_n
+ dots + lambda_{2} lambda_{3}times dots times lambda_n
= (-1)^{n-1} frac{a_{n-1}}{a_0},
$$
$$ lambda_{1} lambda_{2}times dots times lambda_{n}= (-1)^{n} frac{a_{n}}{a_0} .$$
Здесь в левой части $ k_{} $-й формулы стоит сумма всевозможных
произведений из $ k_{} $ чисел, выбранных из $ lambda_{1},dots,lambda_n $ (корни учитываются в
соответствии с их кратностями); в правой части формулы стоит $ (-1)^ka_{k}/a_0 $.
Доказательство
☞
ЗДЕСЬ.
И
Биографические заметки о Виете
☞
ЗДЕСЬ
П
Пример. Найти все корни полинома $ 3,x^3-16,x^2+23,x-6 $,
если известно, что произведение двух из них равно $ 1_{} $.
Решение. Имеем:
$$
left{ begin{array}{ccl}
lambda_1+lambda_2+lambda_3&=&16/3, \
lambda_1lambda_2+lambda_1lambda_3+lambda_2lambda_3
&=&23/3,\
lambda_1lambda_2lambda_3&=&6/3=2.
end{array}
right.
$$
Вдобавок к этим уравнениям, мы должны записать дополнительное условие:
$$lambda_1 lambda_2=1 .$$
Из третьего уравнения системы получаем тогда $ lambda_3=2 $. Подставив его
в два оставшихся, придем к двум идентичным:
$$lambda_1 + lambda_2=10/3 .$$
Теперь для нахождения неизвестных $ lambda_{1} $ и $ lambda_{2} $ можем воспользоваться
формулами Виета «в обратном порядке», составив квадратный полином,
имеющий их корнями:
$$t^2-10/3,t+1 .$$
Ответ. $ 2,,3,, 1/3 $.
?
Можно ли использовать формулы Виета для решения уравнения ?
Ответ
☞
ЗДЕСЬ.
Обдумаем еще раз результаты основной теоремы высшей алгебры и формул Виета. С одной
стороны, задав коэффициенты $ a_{0},a_1,dots,a_n $ мы однозначно определяем
набор из $ n_{} $ комплексных чисел $ lambda_{1},dots,lambda_n $ — корней этого
полинома. С другой стороны, задав произвольным образом набор корней
$ lambda_{1},dots,lambda_n $, по формулам Виета однозначно определим
величины $ a_1/a_0,dots,a_n/a_0 $. Для простоты, рассмотрим подмножество
полиномов степени $ n_{} $, имеющих старший коэффициент равным $ 1_{} $. Получаем
тогда взаимно-однозначное соответствие:
$$ (a_1,dots,a_n) leftrightarrow (lambda_1,dots,lambda_n) . $$
Итак, каждый корень $ lambda_{j} $ полинома является какой-то функцией его
коэффициентов $ a_1,dots,a_{n} $, т.е. формально говоря, функцией от многих
переменных. Относительно этой функции мы пока ничего сказать не можем; более того, как мы узнаем НИЖЕ, для степеней полинома бóльших $ 4_{} $ не существует
«хороших» общих формул, выражающих корни полинома через его
коэффициенты. Несмотря на это, формулы Виета подтверждают, что
некоторые комбинации этих неизвестных нам функций оказываются равными
коэффициентам полинома. Какова основная отличительная особенность этих
комбинаций?
Функция $ Phi(x_1,dots,x_n) $ называется симметрической функцией своих переменных, если ее значение не меняется ни при какой перестановке этих переменных:
$$Phi(x_1,dots,x_n) equiv Phi(x_{j_1},dots,x_{j_n}) $$
при всех различных $ j_1,dots, j_n in {1,dots,n} $.
П
Пример. Функции
$$ sqrt{1+x_1x_2x_3} , frac{x_1x_2}{x_3}+frac{x_1x_3}{x_2}+frac{x_2x_3}{x_1} $$
являются симметрическими функциями переменных $ x_1,x_2,x_3 $, а функция
$$ x_1^2x_2x_3+x_1x_2^2x_3 $$
симметрической функцией не является, поскольку ее значения меняются при перестанове $ (x_1,x_2,x_3) leftrightarrow (x_3,x_2,x_1) $.
В левых частях формул Виета как раз и стоят симметрические полиномы
относительно $ lambda_{1},dots,lambda_n $. Оказывается результат теоремы
допускает следующее обобщение.
Т
Теорема [Гаусс]. Значение любого симметрического полинома
$ Phi(x_1,dots,x_n) $ на корнях $ lambda_1,dots,lambda_n $ полинома
$ x^n+a_1x^{n-1}+ dots+a_n $ является полиномиальной функцией от $ a_{1},dots,a_n $:
$$
Phi(lambda_1,dots,lambda_n) equiv {mathfrak F}(a_1,dots,a_n) .
$$
П
Пример. Пусть $ lambda_{1} $ и $ lambda_{2} $
означают корни полинома $ x^2+a_1x+a_2 $.
Выразить
$$lambda_1^2+lambda_2^2-3,lambda_1^2lambda_2-3,lambda_1lambda_2^2$$
через коэффициенты полинома.
Решение. Поскольку выражения для корней квадратного уравнения нам известны:
$$
lambda_1= frac{-a_1+sqrt{a_1^2-4,a_2}}{2} quad u quad
lambda_2= frac{-a_1-sqrt{a_1^2-4,a_2}}{2} ,
$$
то непосредственной подстановкой их в заданный полином, получаем
$$ a_1^2-2,a_2+3,a_1a_2 . $$
♦
П
Пример. Пусть $ lambda_1,, lambda_2,, lambda_3 $
означают корни полинома $ x^3+a_1x^2+a_2x+a_3 $.
Выразить
$$lambda_1^2lambda_2+lambda_1^2lambda_3+lambda_1lambda_2^2+
lambda_1lambda_3^2+lambda_2^2lambda_3+lambda_2lambda_3^2
-lambda_1^2-lambda_2^2-lambda_3^2
$$
через коэффициенты полинома.
Решение. Выделим в требуемом выражении комбинации
корней, стоящие в левых частях формул Виета.
Первые $ 6_{} $ слагаемых можно представить в виде
$$(lambda_1lambda_2+lambda_1lambda_3+lambda_2lambda_3)
(lambda_1+lambda_2+lambda_3)-3lambda_1lambda_2lambda_3 , $$
а
$$lambda_1^2+lambda_2^2+lambda_3^2=
left(lambda_1+lambda_2+lambda_3 right)^2-2, (lambda_1lambda_2+
lambda_1lambda_3+lambda_2lambda_3) .$$
Далее применяем формулы Виета.
Ответ. $ 3,a_3-a_1a_2-a_1^2+2, a_2 $.
Существуют общие алгоритмы нахождения полинома $ {mathfrak F} $ по заданному полиному $ Phi $: см.
[3], [4]. Однако в своей практике я встречал необходимость в подобном представлении лишь для некоторых классов полиномов $ Phi_{} $; сейчас их и рассмотрим.
Суммы Ньютона
Для полинома $ f(x)=a_{0}x^n+a_1x^{n-1}+dots+a_n, (a_0ne 0) $ его $ k_{} $-й суммой Ньютона называется сумма $ k_{} $-х степеней его корней:
$$
s_k=lambda_1^k + dots + lambda_n^k .
$$
При этом обычно считают $ k_{} in {mathbb N} $ (хотя формально можно определить суммы Ньютона и для отрицательных индексов $ k_{} $ при условии $ a_{n} ne 0 $). Для однообразия полагают также $ s_{0}=n $.
T
Теорема. Суммы Ньютона выражаются рационально через коэффициенты полинома $ f_{}(x) $ посредством следующих рекуррентных формул Ньютона:
$$s_0=n, s_1=-a_1/a_0, $$
$$
s_k=left{begin{array}{lr}
-(a_1s_{k-1}+a_2s_{k-2}+dots+a_{k-1}s_1+a_kk)/a_0,
&npu kle n ;\
-(a_1s_{k-1}+a_2s_{k-2}+dots+a_ns_{k-n})/a_0
& npu k > n.
end{array}
right.
$$
П
Пример.
$$
s_2=(a_1^2-2, a_0a_2) big/ a_0^2 ,
$$
$$
s_3=-(a_1s_2+a_2s_1+3,a_3)big/ a_0=
$$
$$
=-left(a_1 (a_1^2-2, a_0a_2) big/ a_0^2 +a_2 (-a_1 big/ a_0)+3,a_3 right)
big/ a_0=
$$
$$
=left(-a_1^3+3,a_0a_1a_2-3,a_0^2a_3 right) big/ a_0^3 .
$$
♦
§
Подробнее о суммах Ньютона
☞
ЗДЕСЬ.
Результант и дискриминант
Пусть $ g(x)=b_0x^m+dots + b_{m} $ — произвольный полином из $ mathbb A_{} [x] $. Тогда выражение
$$ g(lambda_1) times dots times g(lambda_n) $$
является симметрическим полиномом от корней $ lambda_{1},dots,lambda_n $ полинома $ f_{}(x) $.
По теореме Гаусса, оно должно рационально выражаться через коэффициенты $ a_{0},dots,a_n $. С другой стороны, очевидно, это выражение обращается в нуль тогда и только тогда, когда хотя бы один сомножитель обратится в нуль, т.е. будет существовать общий корень полиномов $ f_{}(x) $ и $ g_{}(x) $. Выражение
$$ a_0^m prod_{j=1}^n g(lambda_j) $$
называется результантом полиномов $ f_{}(x) $ и $ g_{}(x) $.
§
Способы вычисления результанта, его свойства и применения
☞
ЗДЕСЬ.
В частном случае, когда $ g_{}(x) $ совпадает с производной полинома $ f_{}(x) $ результант переходит в дискриминант — выражение отличающееся от
$$ a_0^{n-1} prod_{j=1}^n f^{prime}(lambda_j) $$
только сомножителем $ (-1)^{n(n-1)/2}/a_0 $ и
обращающееся в нуль тогда и только тогда, когда $ f^{prime}(x) $ имеет общий корень с $ f_{}(x) $.
Как мы увидим НИЖЕ, последнее условие оказывается необходимым и достаточным наличия у полинома $ f_{}(x) $ кратного корня.
П
Пример. Для $ f(x)=a_{0}x^2+a_1x+a_2 $ указанное произведение оказывается равным
$$ (2a_0lambda_1 +a_1)(2a_0lambda_2 +a_1)=(4a_0^2lambda_1 lambda_2+2a_0a_1(lambda_1 +lambda_2)+a_1^2)=
$$
$$
=left(4a_0^2 frac{a_2}{a_0}-2a_0a_1frac{a_1}{a_0}+a_1^2right)=4a_0a_2-a_1^2,
$$
т.е. привычному «школьному» понятию.
§
Способы вычисления дискриминанта, его свойства и применения
☞
ЗДЕСЬ.
Преобразования корней
Если $ lambda_{1},dots,lambda_n $ — корни полинома $ f(x)=a_0x^n+a_1x^{n-1}+dots+a_{n} $, то
1.
корнями полинома
$$ f(-x)=(-1)^nleft(a_0x^n-a_1x^{n-1}+dots+(-1)^na_nright) = $$
$$ =(-1)^n sum_{j=0}^n (-1)^ja_jx^{n-j} $$
являются $ -lambda_1, dots, -lambda_n $;
2.
корнями полинома
$$f(x- {color{Red} alpha })=a_0(x-{color{Red} alpha } )^n+a_1(x-{color{Red} alpha })^{n-1}+dots+a_n=
$$
$$
= sum_{j=0}^n a_j(x-{color{Red} alpha })^{n-j}
$$
являются $ {color{Red} alpha }+lambda_1, dots, {color{Red} alpha }+lambda_n $;
3.
при дополнительном условии, что $ a_{n} ne 0 $, корнями полинома
$$f^{ast}(x)= x^nfleft(1/x right) equiv a_0+a_1x+dots+a_nx^n =
$$
$$
=sum_{j=0}^n a_jx^{j}
$$
являются $ 1/{lambda_1}, dots, 1/{lambda_n} $.
Преобразования
1-3
часто используются как при выводе теоретических результатов так и в практике вычислений.
Поясним идею этих применений. Корни исходного и корни преобразованного полинома остаются неизвестными. Допустим, мы получили какой-то результат, касающийся оценки положительных корней полинома $ f_{}(x) in mathbb R[x] $, и хотим распространить эту оценку и на отрицательные корни (см., к примеру,
☟
НИЖЕ ). Производится замена переменной $ x rightarrow — x $, которая меняет знаки всех корней: отрицательные становятся положительными, и к новому полиному применяется полученный результат. В приложениях возникают и более сложные преобразования корней: когда, к примеру, все их надо «загнать» в ограниченную область комплексной плоскости — скажем, в круг $ |x|le 1 $ (см.
☟
НИЖЕ ).
П
Пример. Построить полином $ F_{}(x) $, корни которого равны квадратам корней полинома $ f_{}(x) $.
Решение. Составим выражение
$$
f(sqrt{x})f(-sqrt{x}) .
$$
С одной стороны, используя линейное представление полинома $ f_{}(x) $ получим
$$
f(sqrt{x})f(-sqrt{x})=(-1)^n a_0^2(x-lambda_1^2)times dots times (x-lambda_n^2) ,
$$
т.е. полином с требуемыми корнями. С другой стороны, мы можем найти выражения для коэффициентов этого полинома:
$$
begin{matrix}
f(sqrt{x})&equiv & a_n+a_{n-1} sqrt{x} +a_{n-2} x + a_{n-3} x sqrt{x}+dots equiv \
& equiv & (a_n+a_{n-2} x +a_{n-4} x^2 +dots ) + sqrt{x} (a_{n-1}+ a_{n-3} x + a_{n-5} x^2+ dots ) ;\
f(-sqrt{x})&equiv & (a_n+a_{n-2} x +a_{n-4} x^2 +dots ) — sqrt{x} (a_{n-1}+ a_{n-3} x + a_{n-5} x^2+ dots ) .
end{matrix}
$$
В результате, искомый полином представляется в виде
$$
F(x)=(a_n+a_{n-2} x +a_{n-4} x^2 +dots )^2-x(a_{n-1}+ a_{n-3} x + a_{n-5} x^2+ dots )^2 .
$$
Это преобразование иногда называется квадрированием корней полинома $ f_{}(x) $; оно применяется в методе Греффе-Лобачевского вычисления корней полинома.
♦
Общий метод построения полинома $ F_{}(x) $ , корни которого связаны с корнями $ f_{}(x) $ соотношением вида $ Lambda_j = g(lambda_j) $ при $ g_{}(x) $ — произвольном полиноме
☞
ЗДЕСЬ.
Непрерывность корней
Т
Теорема [5]. Корни полинома
$$ f(x)=x^n+a_1x^{n-1}+dots+a_n in mathbb C[x],quad nge 1 $$
являются непрерывными функциями его коэффициентов. Строго говоря,
если $ lambda_1,dots,lambda_{n} $ — корни этого полинома,
а $ {tilde lambda_1},dots,{tilde lambda_n} $ — корни полинома
$${tilde f}(x)=x^n+{tilde a}_1x^{n-1}+dots+{tilde a}_n in mathbb C[x]
,
$$
то эти корни можно перенумеровать таким образом, чтобы
$$ |lambda_j-{tilde lambda}_j| < 2n varepsilon quad npu quad jin{1,dots,n} . $$
Здесь
$$varepsilon= sqrt[n]{sum_{k=1}^n|a_k-{tilde a}_k| gamma^{n-k} } quad
npu quad gamma = max_{jin {1,dots,n}}
left( sqrt[j]{|a_j|} ,
sqrt[j]{|{tilde a}_j|} right) . $$
П
Пример. Для полинома
$$ f(x)=192,x^5+[(259-173{mathbf i}){color{Red} alpha }+211-413{mathbf i}]x^4 +
$$
$$
+[(80-320{mathbf i}){color{Red} alpha }-304-704{mathbf i}]x^3
+384{mathbf i},x^2-192-192,{mathbf i}
$$
исследовать динамику корней при изменении значений параметра $ {color{Red} alpha }_{} $ от $ -2_{} $ до $ 3_{} $.
Решение. На рисунке

показаны следы, «заметаемые» корнями на комплексной плоскости. Направления движений указаны стрелками.
Сначала посмотрим на начало процесса. При $ {color{Red} alpha }=-2 $ полином имеет следующие
корни:
$$ lambda_1approx-1.0726-0.5122 {mathbf i}, lambda_{2}approx -0.7337+0.1972{mathbf i},
lambda_{3}approx 0.3557+0.9054 {mathbf i},
$$
$$
lambda_4 approx 0.5028-0.3812 {mathbf i}, lambda_5 approx 2.5467+0.1398 {mathbf i} .
$$
Эти стартовые точки отмечены отрезками
|
|
|
|
|
. При увеличении значений $ {color{Red} alpha }_{} $ от $ -2 $ до $ -1_{} $ происходит «дрейф» корней — плавный, но разный по скорости. К примеру, синий и фиолетовый корни меняются очень медленно, а вот зеленый и малиновый быстро сближаются пока не столкнутся при значении $ {color{Red} alpha }=-1 $:
$$ lambda_1approx -1.5096-0.4133 {mathbf i}, lambda_2 approx -0.6768+0.1479 {mathbf i},
lambda_3 approx 0.4364-0.4845 {mathbf i}, lambda_4 = 1+ {mathbf i},
$$
$$
lambda_5 =1+ {mathbf i} .
$$
Что происходит при дальнейшем увеличении $ {color{Red} alpha }_{} $? Число корней должно остаться инвариантным — по основной теореме высшей алгебры оно продолжает совпадать со степенью полинома, т.е. корни не
аннигилируют. Поэтому столкнувшиеся корни порождают два новых — голубой и коричневый — которые начинают расходиться. При $ {color{Red} alpha }=1 $ ситуация следующая:
$$
lambda_1 approx -2.3350+0.4836 {mathbf i}, lambda_2 approx -0.5794+0.1185{mathbf i}, lambda_3 approx 0.2721-0.4926 {mathbf i},
$$
$$
lambda_4 approx -0.3888+2.5945 {mathbf i},
lambda_5 approx 0.5832+0.3480 {mathbf i} .
$$
Имея перед глазами полную картину истории, понимаем, что корни, обозначенные $ lambda_{1} $ (красный) и $ lambda_{4} $ (голубой), стремятся к столкновению — и оно действительно происходит при $ {color{Red} alpha }=2 $:
$$ lambda_1 = -2+2{mathbf i}, lambda_2 approx -0.5458+0.1142 {mathbf i}, lambda_3 approx 0.2296-0.4712 {mathbf i}, lambda_4 = -2+2{mathbf i},
$$
$$
lambda_5 approx 0.5193+0.3101 {mathbf i} .
$$
Дальнейшую динамику можем предсказать «по прецеденту» — столкнувшиеся корни должны разойтись. При $ {color{Red} alpha }=3_{} $:
$$
lambda_1 approx -4.0682+3.6140 {mathbf i}, lambda_2 approx -0.5184+0.1116 {mathbf i},
lambda_3 approx 0.2007-0.4506{mathbf i},
$$
$$
lambda_4 approx -1.2359+1.2927{mathbf i},
lambda_5 approx 0.4759+0.2864{mathbf i} .
$$
♦
?
К какому числу стремится желтый корень при $ {color{Red} alpha } to +infty $ ?
Последний пример наводит на еще одну гипотезу: мы видим, что графики корней получились гладкими, за исключением, возможно, некоторых специфических точек.
Т
Теорема. Корни полинома
$$ f(x)=x^n+a_1x^{n-1}+dots+a_n in mathbb C[x] $$
являются непрерывно дифференцируемыми функциями коэффициентов за исключением тех наборов значений коэффициентов, которые определяют кратные корни.
Доказательство
☞
ЗДЕСЬ.
§
Условие наличия кратного корня у полинома $ f_{}(x) $ может быть получено в виде явного условия на его коэффициенты. См.
☞
ДИСКРИМИНАНТ.
Теоремы настоящего пункта имеют теоретический, качественный характер. Для оценки реального влияния изменений коэффициентов полинома на динамику его корней приходится проводить отдельные — и весьма кропотливые — исследования: см.
☞
ЧУВСТВИТЕЛЬНОСТЬ КОРНЕЙ.
Поиск корней алгебраических уравнений: решение в радикалах
Можно ли выразить корни полинома $ f(x)in mathbb C[x] $ в виде «хороших» функций от его коэффициентов? Вспомним, что для квадратного уравнения
существует общая формула вычисления корней:
$$x^2+ax+b=0 Rightarrow lambda_{1,2}=frac{-apm sqrt{a^2-4b}}{2}
.
$$
Эта формула включает в себя элементарные алгебраические операции
$ +,- ,times, div $ и операцию извлечения квадратного корня. По аналогии
можно сформулировать и общую задачу.
Задача. Найти выражения корней полинома степени $ n_{}>2 $ в виде функций его коэффициентов; при этом функции должны представлять конечную комбинацию элементарных алгебраических
операций и операций извлечения корней произвольных (целых) степеней.
Поставленная задача называется задачей о разрешимости уравнения в радикалах6).
Оказывается, что любое уравнение третьей или четвертой степени разрешимо в радикалах. Перед тем, как изложить способы их решения, сделаем два упрощения. Первое из них заключается в том, что уравнение $ f_{}(x)=0 $ делится на старший коэффициент полинома $ f_{}(x) $.
Полином называется нормализованным7), если его старший коэффициент равен $ 1_{} $. Операция деления полинома на его старший коэффициент называется нормализацией полинома.
Очевидно, что нормализованный полином имеет те же корни, и в тех же кратностях, что и
исходный. Для простоты обозначений, будем считать, что полином уже
нормализован:
$$ f(x)=x^n+a_1x^{n-1}+dots+a_n .$$
Второе упрощение заключается в замене переменной (подстановке): $ x=y+{color{Red} alpha } $.
Ее результатом будет новый полином той же степени, что и исходный, относительно
переменной $ y_{} $:
$$ F(y)equiv f(y+{color{Red} alpha }) , . $$
Корни нового полинома связаны (cм. преобразование
2
☞
ЗДЕСЬ ) с корнями старого
по формуле $ lambda_j = Lambda_j+{color{Red} alpha } $; так что, найдя корни одного полинома,
легко установим и корни другого. Подберем теперь параметр $ {color{Red} alpha } $ так,
чтобы обратить в нуль коэффициент при $ y^{n-1} $ в полиноме $ F_{}(y) $.
Используя формулу бинома Ньютона, получаем
$$
begin{matrix}
f(x)&=&x^n+a_1x^{n-1}+a_2x^{n-2}+dots+a_n= \
&=&(y+{color{Red} alpha })^n +a_1(y+{color{Red} alpha })^{n-1}+a_2(y+{color{Red} alpha })^{n-2}+dots+a_n = \
&=&y^n + C_n^1 {color{Red} alpha } y^{n-1} +C_n^2 {color{Red} alpha }^2 y^{n-2}+dots+
{color{Red} alpha }^n + \
& & qquad + a_1y^{n-1}+a_1 C_{n-1}^1 {color{Red} alpha } y^{n-2}+dots
+a_1{color{Red} alpha }^{n-1} + \
& & quad qquad qquad +a_2y^{n-2} + dots + a_n.
end{matrix}
$$
Понятно, что если положить $ {color{Red} alpha }= — a_1/n $, то коэффициент при $ y^{n-1} $
исчезнет. Для простоты обозначений, будем считать, что полином уже
предварительно подвергнут такому преобразованию:
$$ f(x)=x^n qquad +a_2x^{n-2}+dots+a_n .$$
Уравнение третьей степени
Рассмотрим уравнение третьей степени:
$$
x^3+p,x+q=0
$$
Сделаем в этом уравнении замену переменной: $ x=u+v $, введя две неизвестные
$ u_{} $ и $ v_{} $; получим:
$$
u^3+v^3+3,uv(u+v)+p(u+v)+q=0 .
$$
Сгруппируем:
$$
u^3+v^3+(3,uv+p)(u+v)+q=0 .
$$
Подчиним теперь неизвестные $ u_{} $ и $ v_{} $ условию
$$
3,uv+p=0 iff uv=-frac{p}{3} .
$$
Тогда предыдущее уравнение приведется к виду
$$u^3+v^3=-q . $$
Итак, для определения неизвестных величин $ u_{} $ и $ v_{} $ мы получили систему
уравнений
$$
u^3+v^3=-q,
uv=-frac{p}{3} .
$$
Возведя последнее уравнение в куб, получим
$$
u^3v^3=-frac{p^3}{27} .
$$
Два полученных равенства, связывающие $ u^3 $ и $ v^3 $,
позволяет утверждать, что эти величины являются решениями квадратного
уравнения:
$$t^2+q,t- frac{p^3}{27}=0 .$$
Выражение
$$
Delta = frac{q^2}{4}+frac{p^3}{27}
$$
называется дискриминантом кубического уравнения.
Решив квадратное уравнение, получим:
$$
u^3=-frac{q}{2}+ sqrt{Delta}, v^3=-frac{q}{2}- sqrt{Delta} .
$$
В итоге имеем формулу для решений уравнения:
$$
x=u+v=sqrt[3]{-frac{q}{2}+sqrt{frac{q^2}{4}+frac{p^3}{27}}}+
sqrt[3]{-frac{q}{2}-sqrt{frac{q^2}{4}+frac{p^3}{27}}} ;
$$
она называется формулой Кардано.
Формула Кардано не очень удобна для практических вычислений.
Вспомним, что корень кубический из комплексного числа может принимать три различных значения.
Решение же, представленное формулой Кардано, имеет в правой части
комбинацию из двух кубических корней. Таким образом, получаем
9 всевозможных комбинаций из значений корней кубических. С другой стороны, основная теорема высшей алгебры утверждает, что кубическое уравнение должно иметь только
три решения. Для того, чтобы установить соответствие между значениями $ u_{} $
и $ v_{} $, обратимся к условию $ uv=-p/3 $ . Согласно этому условию, задание
значений для $ u_{} $ позволит однозначно восстановить $ v_{} $. Пусть
$$
u_1=sqrt[3]{-frac{q}{2}+sqrt{frac{q^2}{4}+frac{p^3}{27}}}
$$
какое-то одно из трех возможных значений корня кубического. Два оставшихся значения корня кубического получаются домножением $ u_1 $ на корни кубические из единицы:
$$u_2=u_1varepsilon_1, u_3=u_1varepsilon_2 $$
при
$$varepsilon_1=cos frac{2pi}{3} + {mathbf i} sin frac{2pi}{3}=
frac{-1}{2}+
{mathbf i} frac{sqrt{3}}{2} u
varepsilon_2=cos frac{4pi}{3} + {mathbf i} sin frac{4pi}{3}=
frac{-1}{2}-
{mathbf i} frac{ sqrt{3}}{ 2}
.
$$
Если теперь взять
$$
v_1=-frac{p}{3u_1} ,
$$
то решения кубического уравнения можно выразить в виде комбинаций
$ u_1 $ и $ v_1 $:
$$
begin{array}{ccl}
lambda_1&=&u_1+v_1, \
lambda_2&=&u_2+v_2=u_2-frac{displaystyle p}{displaystyle 3u_2}=u_1varepsilon_1-frac{displaystyle p}{displaystyle 3u_1varepsilon_1}
=u_1varepsilon_1-frac{displaystyle pvarepsilon_2}{displaystyle 3u_1}=u_1varepsilon_1+v_1varepsilon_2,\
lambda_3&=&u_3+v_3=u_1varepsilon_2+v_1varepsilon_1 .
end{array}
$$
Окончательно получаем формулы для вычисления корней:
$$
left{
begin{array}{lcl}
lambda_1&=&u_1+v_1, \
lambda_2&=&-frac{scriptstyle 1}{scriptstyle 2}(u_1+v_1)
+{mathbf i} frac{scriptstyle sqrt{3}}{scriptstyle 2} (u_1-v_1),\
lambda_3&=&-frac{scriptstyle 1}{scriptstyle 2}(u_1+v_1)
-{mathbf i} frac{scriptstyle sqrt{3}}{scriptstyle 2} (u_1-v_1),
end{array} right.
$$
где $ u_1 $ — одно из значений корня кубического, а $ v_1 $ связано с ним
соотношением $ v_1=-p/(3u_1) $.
П
Пример [2]. Решить уравнение $ x^3-6{mathbf i},x^2-10,x+8 {mathbf i}=0 $.
Решение. Подстановка $ x=y+2 {mathbf i} $ приводит уравнение к виду
$$y^3+2,y+4{mathbf i} =0 , $$
т.е. $ p=2,,q=4 {mathbf i} $. Далее
$$Delta=-frac{100}{27} Rightarrow sqrt{Delta} = pm frac{10 {mathbf i}}{3sqrt{3}}
Rightarrow u_1=sqrt[3]{left(-2 + frac{10}{3sqrt{3}} right){mathbf i}}
.
$$
Одно из значений последнего корня:
$$u_1=-{mathbf i}, sqrt[3]{-2 + frac{10}{3sqrt{3}}} , $$
это выражение можно упростить, если повезет заметить, что подкоренное выражение
равно $ left(-1+1/{sqrt{3}}right)^3 $:
$$u_1={mathbf i}left(1-frac{1}{sqrt{3}}right) Rightarrow
v_1=-frac{p}{3u_1}= {mathbf i} left(1+frac{1}{sqrt{3}}right) .
$$
Получаем:
$$mu_1=2, {mathbf i} , mu_2=1- {mathbf i}, mu_3=-1- {mathbf i} .$$
Значения корней исходного уравнения получатся «сдвигом» на
$ 2 {mathbf i} $.
Ответ. $ 4{mathbf i},, 1 + {mathbf i},, -1+ {mathbf i} $.
§
Дальнейший анализ формулы Кардано
☞
ЗДЕСЬ
Уравнение четвертой степени
$$ x^4+a_1x^3+a_2x^2+a_3x+a_4 = 0 $$
также может быть решено в радикалах. Идея решения заключается в сведении задачи к решению некоторого кубического уравнения. Ее реализация
☞
ЗДЕСЬ.
Уравнения высших степеней
Успех в решении уравнений третьей и четвертой степени побудил
исследователей искать подобные формулы для уравнений высших степеней.
Методология подхода была очевидна: свести решение уравнения $ n $-й
степени к решению уравнения $ (n-1) $-й степени. Однако, несмотря на почти трехвековые усилия лучших математиков, решить уравнение пятой степени не удавалось. Наконец, в начале
XIX века был получен отрицательный результат.
Т
Теорема [Руффини, Абель]. Уравнение степени выше четвертой в общем
случае неразрешимо в радикалах.
П
Пример. Уравнение $ x^5-4, x -2=0 $ не разрешимо в радикалах.
Установить разрешимо или нет данное конкретное уравнение в радикалах возможно с помощью теории, развитой французским математиком Галуа.
П
Пример. Уравнение $ x^5+x+1=0 $ разрешимо в радикалах, поскольку
$$ x ^5+x+1equiv (x^2+x+1)(x^3-x^2+1) , .$$
Отрицательный характер результата теоремы Руффини-Абеля не должен слишком уж
разочаровывать. Он означает только лишь то, что корни полинома нельзя представить в виде
формулы, состоящей из конечного набора сравнительно простых функций. Тем не
менее, если расширить класс допустимых в формуле функций (или допустить бесконечность числа операций), представление для корня можно найти (см., к примеру,
☞
ЗДЕСЬ ). Наконец, для практических задач часто более важна не столько «красивая»
аналитическая формула для корня, сколько приближенное его значение с требуемой точностью.
Поиск корней алгебраических уравнений: возможность упрощений
Для некоторых классов уравнений удается упростить задачу: свести решение исходного уравнения к решению уравнения меньшей степени 
Возвратное уравнение
Так называется уравнение вида
$ a_0z^n+a_1z^{n-1}+dots+a_{n-1}z+a_n=0, a_0ne 0 $, у которого набор коэффициентов
$ (a_0,a_1,dots, a_{n-1},a_n) $ симметричен относительно
середины:
$$ a_0=a_{n},a_1=a_{n-1},dots, a_{j}=a_{n-j} dots $$
П
Пример. Уравнения
$$ z^2-3,z+1=0,quad -sqrt{2}z^5+2,z^4+mathbf i z^3+2,z-sqrt{2},quad z^n+1=0 , $$ $$ z^n+z^{n-1}+z^{n-2}+dots + z^2 +z+1=0 $$
являются возвратными.
§
Методы упрощения подобных уравнений
☞
ЗДЕСЬ.
Делимость полиномов
Здесь $ mathbb A_{} $ означает какое-то из множеств $ mathbb Q, mathbb R $ или $ mathbb C_{} $.
Т
Теорема. Для полиномов $ f_{}(x) $ и $ g(x)not equiv 0 $ из $ mathbb A[x] $
существует единственная пара полиномов $ q_{}(x) $ и $ r_{}(x) $ из
$ mathbb A[x] $ таких, что
$$
f(x) equiv g(x) q(x) + r(x) quad mbox{ и } quad
deg r < deg g .
$$
Доказательство
☞
ЗДЕСЬ.
В этом представлении полином $ f_{}(x) $ называется делимым, $ g_{}(x) $ — делителем,
$ r_{}(x) $ — остатком от деления $ f_{}(x) $ на $ g_{}(x) $, а $ q_{}(x) $ —
частным9).
При $ r(x) equiv 0 $, говорят, что полином $ f_{}(x) $ делится (нацело)
на $ g_{}(x) $, а полином $ g_{}(x) $ называется делителем $ f_{}(x) $. Тривиальными делителями полинома $ f_{}(x) $ называют сам полином $ f_{}(x) $ и полином тождественно равный $ 1_{} $ (оба — с точностью до домножения на ненулевую константу). Любой другой делитель полинома (если существует) называется нетривиальным.
П
Пример [1]. Найти частное и остаток от деления
$$f(x)=2, x^5 +x^4 -x^2 +2, x +1 quad mbox{ на } quad
g(x)=x^3+2, x^2 — x -1 .$$
Решение.
$$
begin{array}{rrrrrrr|l}
2,x^5&+ x^4 &+0x^3 &-x^2 &+2x &+1 && x^3+2,x^2-x-1\
2,x^{5}&+4 x^4&-2,x^3&-2x^2&& && overline{ 2,x^2 -3, x +8 quad } \
hline
&-3,x^4&+2,x^3&+x^2&+2,x& \
&-3,x^{4}&-6,x^3&+3,x^2&+3,x& \
hline
&&8,x^{3}&-2,x^2&-x&+1 \
&&8,x^{3}&+16,x^2&-8,x&-8 \
hline
&&& -18x^{2}&+7,x&+9
end{array}
$$
Ответ. $ q(x)=2, x^2 -3, x + 8, r(x)=-18, x^2 + 7, x +9 $.
Фактическое выполнение операции деления полиномов можно производить, действуя лишь над наборами их коэффициентов — подобно тому, как мы производили их умножение.
П
Пример. Найти частное и остаток от деления
$$f(x)=x^8+x^7+3,x^4-1 quad mbox{ на } quad g(x)=x^4-3, x^3 +4, x +1 .$$
Решение.
$$
begin{array}{rrrrrrrrrr|l}
1& 1 &0&0&3&0 &0 & 0&-1 &&1 -3 0 4 1\
1&-3 &0&4&1& & & & && overline{ 1 4 12 32 82} \
hline
&4 & 0 &-4 & 2 & 0 & {} \
&4 &-12& 0 & 16 & 4& {} \
hline
&& 12& -4 &-14 & -4 & 0 & {} \
&& 12& -36 & 0 & 48 & 12 & {} \
hline
&&& 32 & -14& -52&-12 & 0 & {} \
&&& 32 & -96& 0 & 128& 32 & {} \
hline
&&&&82&-52&-140&-32&-1 \
&&&&82&-246&0&328&82 \
hline
&&&&&194&-140&-360&-83
end{array}
$$
Ответ. $ q(x)=x^4+4,x^3+12,x^2+32, x+82,, r(x)=194, x^3-140, x^2-360, x -83 $.
Свойства.
1.
Если $ m le n $ при $ a_0ne 0, b_0 ne 0 $, то $ deg q(x) =n-m $ и ведущий член $ q_{}(x) $ равен $ {a_0}/{b_0}, x^{n-m} $.
2.
Если $ g(x)equiv x-c $, то коэффициенты частного $ q_{}(x) $ найдутся из схемы Хорнера.
Наибольший общий делитель
Рассмотрим множество всех общих делителей полиномов $ f_{}(x) $ и $ g_{}(x) $:
$$
mathbb D={d_1(x) in mathbb A[x] , | f(x) mbox{ делится на } d_1(x), g(x) mbox{ делится на } d_1(x) } .
$$
Наибольшим общим делителем полиномов $ f_{}(x) $ и $ g_{}(x) $ называется полином $ d_{}(x) $, который является делителем как $ f_{}(x) $, так и $ g_{}(x) $ и, вместе с тем, сам делится на любой другой общий делитель этих полиномов:
$$ operatorname{HOD} (f(x),g(x)) = d(x) iff d(x) in mathbb D
, d(x) mbox{ делится на } forall d_1(x) in mathbb D
.
$$
Рассмотрим множество всех полиномов, которые делятся и на $ f_{}(x) $ и на $ g_{}(x) $:
$$
mathbb K={k_1(x) in mathbb A[x] , | k_1(x) mbox{ делится на } f(x), k_1(x) mbox{ делится на } g(x) } .
$$
Наименьшим общим кратным полиномов $ f_{}(x) $ и $ g_{}(x) $ называется полином $ k_{}(x) $, который делится как на $ f_{}(x) $, так и на $ g_{}(x) $ и, вместе с тем, сам является делителем любого другого полинома, который делится на $ f_{}(x) $ и $ g_{}(x) $:
$$ operatorname{HOK} (f(x),g(x)) = k(x) iff k(x) in mathbb K
, forall k_1(x) in mathbb K
mbox{ делится на } k(x) .
$$
Пока открытым является вопрос существования $ operatorname{HOD} (f,g)_{} $ и $ operatorname{HOK} (f,g)_{} $. Для первого случая этот вопрос решается
конструктивно — построением $ operatorname{HOD} (f,g)_{} $ с помощью алгоритма, позаимствованного из
☞
ТЕОРИИ ЧИСЕЛ.
Алгоритм Евклида.
Пусть $ f(x) not equiv 0 $ и $ g(x) not equiv 0 $ — полиномы из $ mathbb A_{}[x] $ . Поделим $ f_{}(x) $ на $ g_{}(x) $:
$ f(x)=g(x)q_{1}(x)+r_1(x) $, пусть остаток $ r_{1}(x) not equiv 0 $, тогда
$ 0 le deg r_{1}(x)< deg g(x) $. Поделим делитель на
этот остаток: $ g(x)=r_{1}(x)q_2(x)+r_2(x) $, предположим, что остаток
$ r_{2}(x) not equiv 0 $, тогда $ 0 le deg r_{2}(x)< deg r_1(x) $.
Снова разделим делитель на остаток и продолжим процесс далее
до тех пор, пока на каком-то шаге не произойдет деление нацело, т.е.
остаток будет тождественно равен нулю (это обязательно случится за конечное число
шагов, т.к. степени полиномов $ r_{j}(x) $ уменьшаются). Запишем процедуру в виде схемы:
$$
begin{array}{lcl}
f(x)&=&g(x)q_1(x)+r_1(x) , quad 0 le deg r_1(x)< deg g(x) , \
g(x)&=&r_1(x)q_2(x)+r_2(x) , quad 0 le deg r_2(x)< deg r_1(x), \
r_1(x)&=&r_2(x)q_3(x)+r_3(x) , quad 0 le deg r_3(x)< deg r_2(x), \
dots && dots \
r_{j-2}(x)&=&r_{j-1}(x)q_{j}(x)+r_{j}(x) , quad
0 le deg r_j(x)< deg r_{j-1}(x) , \
dots && dots \
r_{k-2}(x)&=&r_{k-1}(x)q_{k}(x)+r_{k}(x) , quad 0 le deg r_k(x)< deg r_{k-1}(x) , \
r_{k-1}(x)&=&r_{k}(x)q_{k+1}(x) .
end{array}
$$
Т
Теорема. Последний не равный нулю остаток в алгоритме Евклида совпадает с $ operatorname{HOD}(f(x),g_{}(x)) $.
Доказательство полностью аналогично доказательству соответствующего результата из теории целых чисел.
♦
П
Пример. Вычислить
$$ operatorname{HOD} left( x^4+3, x^3 -x^2 -4, x -3, ,
3, x^3 +10, x^2 +2, x -3 right) , . $$
Решение.
$$
begin{array}{rrrrrr|l}
x^4 &+3,x^3 &-x^2 &-4,x &-3 && 3,x^3+10,x^2+2,x-3\
x^4&+10/3, x^3&+2/3, x^2&-, x &
&& overline{ 1/3 x -1/9 quad } \
hline
&-1/3,x^3&-
5/3,x^2&-3,x&-3 \
&-1/3,x^3&-10/9,x^2&
-2/9,x&{}
+1/3 \
hline
&&-5/9,,x^2&
-25/9,x&-10/3
end{array}
$$
В обозначениях алгоритма Евклида, имеем:
$$ q_{1}(x)=1/3, x -1/9, r_{1}(x)=-5/9, x^2 -25/9, x-10/3 . $$
Поскольку $ r_{1}(x) notequiv 0 $, делим $ g_{}(x) $ на этот остаток:
$$
begin{array}{rrrrr|l}
3,x^3 &+10,x^2 &+2,x &-3 && -5/9,,x^2
-25/9,x-10/3 \
3, x^3&+15, x^2&+18, x & &&,
overline{-27/5, x +9 quad } \
hline
&-5,x^2&-16,x&-3 \
&-5,x^2&-25,x&-30 \
hline
&&9,x&+27
end{array}
$$
Здесь $ q_{2}(x)=-27/5, x +9, r_2(x)=9x+27 notequiv 0 $ и алгоритм деления продолжается:
$$
begin{array}{rrrr|l}
-5/9,,x^2&
-25/9,x&
-10/3 && 9,x+27 \
-5/9,,x^2&
-5/3,x& && ,
overline{ -5/81, x
— 10/81 quad } \
hline
&-10/9,x&
-10/3 \
&-10/9,x&-10/3 \
hline
& & 0
end{array}
$$
Здесь остаток получился равным нулю, следовательно $ r_{2}(x)=operatorname{HOD}(f(x),g(x)) $.
Ответ. $ 9(x+3)_{} $.
Легко видеть, что если $ d_{}(x) = operatorname{HOD} (f(x),g(x)) $, то и $ Ccdot d(x)_{} $
также будет $ operatorname{HOD} (f(x),g(x)) $ при любой константе $ C ne 0 $. Так, в только
что решенном примере мы имели право записать ответ в виде $ operatorname{HOD}(f,g)=x+3 $
или $ operatorname{HOD} (f,g)=mathbf{i} x+3, mathbf{i} $ и т.д.
Обычно, получив какое-то представление $ d_{}(x) $ для $ operatorname{HOD} (f(x),g(x)) $,
подбирают константу $ C_{} $ так, что либо — в случае $ d(x)in mathbb{Q}[x] $ —
полином $ C_{}d(x) $ имел коэффициенты целыми:
$$ Cd(x) in mathbb{Z}[x] $$
(например, положив $ C_{} $ равным наименьшему общему кратному знаменателей коэффициентов $ d_{}(x) $ ;
либо же так, чтобы $ C_{}d(x) $ был нормализован (имел старший коэффициент равным $ 1_{} $):
$$C=1/(mbox{старший коэффициент } d(x)) .$$
Еще один способ нахождения $ operatorname{HOD} $ для полиномов из $ mathbb{C}[x] $ вытекает из основной теоремы высшей алгебры.
Т
Теорема. Пусть множество $ { (x-lambda_1),dots,(x-lambda_{mathfrak r}) } $ представляет собой объединение множеств линейных сомножителей полиномов $ f_1(x),dots,f_k(x) $. Выпишем «универсальное» разложение каждого $ f_j $ на линейные сомножители:
$$ f_j(x)equiv a_{0j} (x-lambda_1)^{{mathfrak m}_{1j}}(x-lambda_2)^{{mathfrak m}_{2j}}times
dots times
(x-lambda_{mathfrak r})^{{mathfrak m}_{{mathfrak r}j}}
$$
(здесь возможно, что некоторые из кратностей $ {mathfrak m}_{ij} $ равны 0). Тогда
$$ operatorname{HOD} left(f_1(x),dots,f_k(x) right)=
(x-lambda_1)^{{mathfrak m}_1}(x-lambda_2)^{{mathfrak m}_2}times cdots times (x-lambda_{mathfrak r})^{{mathfrak m}_{mathfrak r}} ,
$$
$$
operatorname{HOK} left(f_1(x),dots,f_k(x) right)=
(x-lambda_1)^{{mathfrak M}_1}(x-lambda_2)^{{mathfrak M}_2}times cdots times (x-lambda_{mathfrak r})^{{mathfrak M}_{mathfrak r}}
$$
где $ displaystyle {mathfrak m}_{ell} = min_{jin{1,dots, k}} {mathfrak m}_{ell j}, displaystyle {mathfrak M}_{ell} = max_{jin{1,dots, k}} {mathfrak m}_{ell j} $.
П
Пример. Вычислить $ operatorname{HOD} left(x^2-1,, x^3+1 right) $ .
Решение. Выписываем разложения полиномов на линейные сомножители:
$$x^2-1equiv (x-1)(x+1), quad x^3+1 equiv(x+1)
left(x-left( 1/2 — sqrt{3}/2 mathbf{i} right) right)
left(x- left( 1/2 + sqrt{3}/2 mathbf{i} right) right) .$$
Ответ. $ x+1 $.
Разумеется, этот способ нахождения $ operatorname{HOD} $ имеет
лишь теоретическое значение, поскольку, как было указано
☞
ЗДЕСЬ, получить выражение корней полинома в радикалах, как правило, не удается.
Т
Теорема. Существуют полиномы $ u(x)_{} $ и $ v(x)_{} $ из
$ mathbb A[x] $, удовлетворяющие уравнению линейного представления $ operatorname{HOD} $:
$$
v(x)f(x)+u(x)g(x)equiv operatorname{HOD}(f,g) .
$$
Доказательство этого результата и практический способ построения полиномов $ u(x)_{} $ и $ v(x)_{} $ можно скопировать из соответствующего раздела теории чисел.
§
Явное представление $ operatorname{HOD} (f(x),g(x)) $ через коэффициенты полиномов с помощью аппарата определителей приведено
☞
ЗДЕСЬ.
Алгоритм Евклида имеет приложение и к задаче локализации корней полинома $ f(x) $ с вещественными коэффициентами, т.е. к нахождению числа всех вещественных корней и точного количества их на произвольном интервале вещественной оси. Подробне
☟
ЗДЕСЬ.
Взаимно простые полиномы
— это полиномы, у которых
нормализованный $ operatorname{HOD} $ равен $ 1_{} $ (тождественно). Подробное рассмотрение этого случая
☞
ЗДЕСЬ.
Производные от полинома
Для случая произвольной функции
$ F(x): mathbb R mapsto mathbb R $ это определение строится на предельном переходе:
$$ frac{d, F}{d, x} bigg|_{_{x=c}}
= F^{prime}(c) = lim_{hto 0} frac{F(c+h)-F(c)}{h} .$$
Пусть $ F(x)equiv x^k $ при $ kin mathbb N_{} $. Тогда, с помощью формулы бинома Ньютона
получаем:
$$(c+h)^k-c^k=kc^{k-1}h+C_k^2c^{k-2}h^2+dots+h^k $$
и
$$frac{F(c+h)-F(c)}{h} to kc^{k-1} quad npu hto 0 . $$
Отсюда следует, что функция $ x^{k} $ дифференцируема в любой точке $ xinmathbb R_{} $
и ее производная равна $ kx^{k-1} $. Обобщим это определение и на комплексную
плоскость $ mathbb C^{} $ . Всюду в предыдущих рассуждениях допустим, что и точка
$ c_{} $ и приращение $ h_{} $ могут быть комплексными. Окончательный вывод не изменится:
формула
$$(x^k)^{prime}= kx^{k-1} $$
остается справедливой и для $ xin mathbb C_{} $. С помощью этой формулы, а также с
помощью основных правил дифференцирования функций:
$$
left(F_1pm F_2 right)^{prime}=F_1^{prime}pm F_2^{prime},
left(cFright)^{prime}=cF^{prime},
left(F_1F_2 right)^{prime}=F_1^{prime}F_2+F_1F_2^{prime}
$$
получаем
$$ f^{prime}(x)=(a_0x^n+a_1x^{n-1}+dots+a_{n-1}x+a_n)^{prime}
= na_0x^{n-1}+(n-1)a_1x^{n-2}+dots +a_{n-1} . $$
Таким образом, $ f^{prime}(x) $ также будет полиномом над $ mathbb A_{} $ и
$ deg f^{prime} = deg f — 1 $. Кроме того, обобщая по индукции
формулу дифференцирования произведения, выводим:
$$
left(f_1f_2times dots times f_k right)^{prime}=
f_1^{prime}f_2times dots times f_k+f_1f_2^{prime}times dots times f_k+
dots+ f_1f_2times dots times f_k^{prime} .
$$
Если применить ее к формуле разложения полинома на линейные
множители, то получим формулу
$$
begin{matrix}
f^{prime}(x)&=&a_0(x-lambda_2)(x-lambda_3)times dots times (x-lambda_n)+
\
&+&a_0(x-lambda_1)(x-lambda_3)times dots times (x-lambda_n)+ \
&+ & dots + \
&+& a_0(x-lambda_1)(x-lambda_2)times dots times (x-lambda_{n-1}).
end{matrix}
$$
Из нее, в частности, следует, что
$$
f^{prime}(lambda_j)=a_0(lambda_j-lambda_1)times dots times
(lambda_j-lambda_{j-1})(lambda_j-lambda_{j+1})
times dots times (lambda_j-lambda_{n})=
$$
$$
=a_0
prod_{1le k le n atop
scriptstyle kne j} (lambda_j — lambda_k) .
$$
Последняя формула, впрочем, может быть получена и напрямую из определения производной:
$$
f^{prime}(lambda_j)=lim_{xto lambda_j} frac{f(x)-f(lambda_j)}{x-lambda_j}
=lim_{xto lambda_j} frac{a_0(x-lambda_1)timesdotstimes (x-lambda_n)}{x-lambda_j} .
$$
Производные высших порядков вводятся определением
$$F^{(k)}(x)= left(F^{(k-1)}(x) right)^{prime} npu k>1 ; $$
для однотипности обозначений считают также нулевой производной сам полином:
$$F^{(0)}(x)= F(x) .$$
В дальнейшем нам пригодится следующая формула Лейбница:
$$left(F_1 F_2 right)^{(k)}=sum_{j=0}^k C_k^j F_1^{(k-j)}F_2^{(j)}=$$
$$
=F_1^{(k)}F_2+ C_k^1F_1^{(k-1)}F_2^{prime}
+ C_k^2F_1^{(k-2)}F_2^{prime prime }+ dots +F_1F_2^{(k)} ,
$$
где $ C_k^{j} $ означает биномиальный коэффициент.
Для полинома $ f(x)_{} $ степени $ n_{} $ имеем:
$$f^{(k)}(x)=n(n-1)times dots times (n-k+1)a_0x^{n-k}+dots+k!a_{n-k}
npu kle n $$
и $ deg f^{(k)} = deg f — k $. Очевидно $ f^{(k)}(x)equiv 0 $ при $ k> n_{} $.
Т
Теорема. Простой корень полинома не является корнем его производной. Кратный корень полинома кратности $ mathfrak m $ является корнем его производной кратности $ ({mathfrak m}-1) $.
Доказательство. Если $ x=lambda_{} in mathbb C $ — простой корень для $ f_{}(x) $, то
$ f(x)equiv (x-lambda)tilde{f}(x) $ при $ tilde{f}(lambda) ne 0 $.
Дифференцируя и подставляя $ x=lambda $, получаем
$$
f^{prime}(x)equiv tilde{f}(x) +(x-lambda)tilde{f}^{prime}(x)
Rightarrow f^{prime}(lambda)=tilde{f}(lambda)ne 0
$$
по предположению.
Если $ x=lambda_{} $ — кратный корень кратности $ mathfrak m $ для $ f_{}(x) $, то
$ f(x)equiv (x-lambda)^{mathfrak m}widehat{f}(x) $ при $ widehat{f}(lambda) ne 0 $. Снова дифференцируем:
$$
f^{prime}(x)={mathfrak m}(x-lambda)^{{mathfrak m}-1} widehat{f}(x)+
(x-lambda)^{{mathfrak m}}widehat{f}^{prime}(x)=
$$
$$
=(x-lambda)^{{mathfrak m}-1}
underbrace{left({mathfrak m}widehat{f}(x)
+(x-lambda)widehat{f}^{prime}(x)
right)}_{= H(x)} .
$$
Из этого представления следует, что $ x=lambda_{} $ является корнем $ f^{prime}(x) $
кратности, не меньшей $ ({mathfrak m}-1) $. Если бы кратность была
больше этого значения, то необходимо $ H(lambda)=0 $. Однако, этого не
может быть, т.к. $ widehat{f}(lambda) ne 0 $.
♦
=>
Полином $ f(x)_{} $ имеет кратный корень тогда и только
тогда, когда он имеет нетривиальный наибольший общий делитель со своей производной
$$ operatorname{HOD} (f(x),f^{prime}(x)) notequiv const . $$
П
Пример. При каком условии на коэффициенты $ p_{} $ и $ q_{} $ полином
$$ x^3+p,x+q $$
имеет кратный корень?
Решение. На основании теоремы на этом корне $ x=lambda_{} $
должно быть выполнено
$$lambda^3+p,lambda+q=0 , quad 3, lambda^2 + p=0 .$$
Из второго равенства выражаем $ lambda^2 $ и подставляем в первое:
$$lambda^2=-frac{p}{3} Rightarrow lambda left(-frac{p}{3} right)
+p,lambda+q=0 Rightarrow lambda=-frac{3,q}{2,p} $$
при $ pne 0 $.
Подставляя это значение в любое из исходных равенств, получаем:
$$
frac{27,q^2+4,p^3}{4, p^2} =0 Rightarrow
left(frac{q}{2} right)^2 + left(frac{p}{3} right)^3 =0 .
$$
Это условие уже встречалось нам ВЫШЕ при анализе формулы решения уравнения третьей степени.
При $ p=0 $ кратный корень может встретиться лишь при $ q=0 $, т.е. опять же
при обращении в нуль дискриминанта кубического уравнения.
Ответ. $ left( p/3 right)^3 + left( q/2 right)^2=0 $.
Предыдущий пример позволяет выявить общую закономерность:
наличие у полинома $ f_{}(x) $ кратного корня является ситуацией исключительной,
наблюдаемой только тогда, когда коэффициенты полинома связаны некоторым
условием типа равенства. Общий способ получения этого условия
☞
ЗДЕСЬ
?
При каком условии на коэффициенты $ p_{} $ и $ q_{} $ полином
а) $ x^4+p,x+q $ ; б) $ x^5+p,x+q $
имеет кратный корень?
П
Пример. Найти все значения параметра $ {color{Red} alpha } $, при которых полином
$$ x^4-5,x^2+{color{Red} alpha },x+28 $$
имеет кратный корень.
Решение. На основании следствия к теореме для выполнения
условия необходимо и достаточно, чтобы был нетривиален
$ operatorname{HOD} (f(x),f^{prime}(x)) $. Ищем его по алгоритму Евклида, делим $ f(x) $ на $ f^{prime}(x) $:
$$
f(x)equiv frac{1}{4} , x, f^{prime}(x) +
overbrace{left(-frac{5}{2}, x^2
+frac{3}{4}, {color{Red} alpha }, x +28 right)}^{r_1(x)}
,
$$
затем $ f^{prime}(x) $ на полученный остаток $ r_{1}(x) $:
$$
f^{prime}(x) equiv left(-frac{8}{5},x-
frac{12}{25}, {color{Red} alpha } right) r_1(x) +
overbrace{left(frac{3}{25},(3, {color{Red} alpha }^2 + 290),x+
frac{361}{25}, {color{Red} alpha } right)}^{r_2(x)}
,
$$
и, при дополнительном предположении $ 3, {color{Red} alpha }^2 + 290ne 0 $, делим $ r_{1}(x) $ на $ r_{2}(x) $:
$$
r_1(x) equiv frac{25}{36left(3, {color{Red} alpha }^2 +290 right)^2}
left[-30,left(3, {color{Red} alpha }^2 +290 right) x +
alpha, (27, {color{Red} alpha }^2 + 6220) right] r_2(x) +
$$
$$
+ frac{25, left(-27, {color{Red} alpha }^4 -19660, {color{Red} alpha }^2 + 3390912right)
}{36, left(3, {color{Red} alpha }^2 +290 right)^2} .
$$
$ operatorname{HOD} (f(x),f^{prime}(x)) $ может быть нетривиальным (равным $ r_{2}(x) $)
только при условии
$$-27, {color{Red} alpha }^4 -19660, {color{Red} alpha }^2 + 3390912=0 . $$
Решить последнее уравнение легко если заменить
переменную $ A = {color{Red} alpha }^2 $:
$$( A-144)(27, A +23548)=0 .$$
При $ 3, {color{Red} alpha }^2 + 290= 0 $ будет
$ operatorname{HOD} (f(x),f^{prime}(x))= r_2(x)not equiv 0 $, так что
при этих значениях параметра кратных корней у $ f(x)_{} $ быть не может.
Ответ. $ {color{Red} alpha } in { pm 12, pm {scriptstyle 58}/{scriptstyle 3} sqrt{{scriptstyle 7}/{scriptstyle 3}}, mathbf i } $.
=>
Число $ lambda_{} $ является корнем кратности $ mathfrak m_{} $ для $ f(x)_{} $ тогда и
только тогда, когда выполнены условия:
$$
underbrace{f^{(0)}(lambda)=0,dots, f^{({mathfrak m}-1)}(lambda)=0}_{mathfrak m},,
f^{({mathfrak m})}(lambda)ne 0 .
$$
Доказательство необходимости следует из теоремы. Достаточность вытекает из результатов следующего пункта (формализация способа проверки приводится
☞
ЗДЕСЬ).
Формула Тейлора
Представление полинома $ f(x)_{}in mathbb A[x] $ в канонической форме $ a_{0}x^n+a_1x^{n-1}+dots + a_n $ не является единственно возможным способом задания полинома. В конце концов,
полином можно представить и с помощью разложения на линейные сомножители — разумеется, если известен набор его корней. Саму
эту каноническую форму можно описать как разложение полинома по
степеням переменной $ x_{} $. Пусть теперь $ cin mathbb A_{} $ — произвольная константа.
Любую степень $ x^{k} $ можно «переразложить» по степеням линейного полинома
$ x-c_{} $ с помощью формулы бинома Ньютона:
$$ x^kequiv left[c+(x-c) right]^kequiv c^k +kc^{k-1}(x-c)+
frac{k(k-1)}{2}c^{k-2}(x-c)^2+dots+ (x-c)^k .$$
Если это сделать для каждого монома полинома $ f(x)_{} $, то
получим разложение $ f(x)_{} $ по степеням $ x-c_{} $ в виде
$$
f(x)equiv A_0+A_1(x-c)+A_2(x-c)^2+dots+A_n(x-c)^n .
$$
Задача. Найти коэффициенты $ A_{0},dots,A_n $ в этом разложении.
Для решения этой задачи продифференцируем несколько раз последнее тождество:
$$
begin{matrix}
f^{prime}(x)&=&A_1+2,A_2(x-c)+3,A_3(x-c)^2+dots+nA_n(x-c)^{n-1} , ,\
f^{prime prime}(x)&=&2,A_2+3cdot 2,A_3(x-c)+dots +n(n-1)A_n(x-c)^{n-2}, ,\
f^{prime prime prime}(x)&=&3cdot 2,A_3+dots +n(n-1)(n-2)A_n(x-c)^{n-3}, ,\
dots & & dots
end{matrix}
$$
Подстановка в эти формулы $ x=c_{} $ дает:
$$f^{prime}(c)=A_1, f^{prime prime}(c)=2,A_2, f^{prime prime prime}(c)=
3cdot 2,A_3,dots $$
Т
Теорема. Разложение полинома $ f_{}(x) $ по степеням $ x-c_{} $ имеет вид
$$
f(x) equiv f(c)+
frac{f^{prime}(c)}{1!} (x-c) + frac{f^{prime prime }(c)}{2!} (x-c)^2+
dots + frac{f^{(n)}(c)}{n!} (x-c)^{n} =
$$
$$
=sum_{j=0}^n frac{f^{(j)}(c)}{j!} (x-c)^{j} ;
$$
это тождество называется формулой Тейлора для полинома $ f_{}(x) $ в точке $ x=c $.
Доказательство и алгоритм эффективного вычисления коэффициентов формулы Тейлора (схема Хорнера)
☞
ЗДЕСЬ.
Формула Тейлора имеет гораздо большее значение,
чем просто переразложение полинома $ f_{}(x) $ по степеням заданного линейного полинома.
Она связана с задачей о приближении, аппроксимации функций.
Пусть функция $ F_{}(x) $ неизвестной заранее структуры описывает поведение
какого-то природного процесса. Мы имеем возможность провести серию (конечное
число) экспериментов (наблюдений), чтобы на их основе найти приближенное значение функции в произвольной точке $ x_{} $. Экспериментальные серии могут различаться по своему типу. Это могут быть серии экспериментов
-
однотипных, когда, например, удается узнать (засечь) положение спутника в разные моменты времени $ x_1,x_{2},dots $ на неизвестной орбите;
-
разнотипных, когда для того же спутника мы имеем возможность измерения большого количества различных параметров движения (положения, скорости, ускорения, ускорения ускорения, и пр.), но только в один фиксированный момент времени $ x=c_{} $.
На основании этих серий мы должны предсказать величину $ F(x)_{} $.
Самой простой функцией, решающей задачи в таких постановках, является
полином. Если этот полином $ f(x)_{} $ удается построить, то именно его
мы и будем считать приближением неизвестной нам функции $ F(x)_{} $.
Задача построения такого полинома для серии экспериментов первого типа обсуждается
☞
ЗДЕСЬ. А формула Тейлора позволяет найти полином $ f(x)_{} $ для серии
экспериментов второго типа. Геометрически: неизвестный нам заранее график функции $ y=F(x)_{} $ (красный) приближается (аппроксимируется) либо прямой (зеленый), либо параболой (серый), либо кубикой (фиолетовый) — и все кривые приближения строятся только на основании информации о функции $ F(x)_{} $ в одной-единственной точке $ c_{} $.
П
Пример. Найти приближенное значение $ F(1)_{} $, если известно, что
$$F(-1)=F^{prime}(-1)=F^{prime prime}(-1)=F^{prime prime prime}(-1)=0.367
.$$
Решение. По формуле Тейлора получаем полином
$$f(x)=0.367+0.367(x+1) + frac{0.367}{2} (x+1)^2+frac{0.367}{6} (x+1)^3 $$
и $ f(1)=2.324(3) $.
Ответ. $ F(1)approx 2.324 $.
Полиномы с вещественными коэффициентами
Рассмотрим теперь случай полинома с вещественными коэффициентами
$ f(x)=a_0x^n+a_1x^{n-1}+ dots + a_n in mathbb R [x] $.
Т
Теорема. Значения полинома $ f(x) in mathbb R [x] $ от комплексно-сопряженных значений переменной будут также комплексно-сопряженными:
$$ mbox{если} f(c)=A+mathbf i B mbox{при} {A,B} subset mathbb R, mbox{то} f(overline{c})=A-mathbf i B , . $$
Доказательство. Действительно, поскольку $ a_jin mathbb R $,
то $ overline{a_j}=a_j $ для $ forall jin {0,1,dots,n} $, и тогда
$$
begin{matrix}
fleft(overline{c} right)&=&a_0 overline{c}^n + a_1 overline{c}^{n-1} +
dots + a_n = overline{a_0} overline{c^n} +
overline{a_1} overline{c^{n-1}}+ dots +
overline{a_n}= \
&=&overline{a_0c^n+a_1c^{n-1}+ dots + a_n}=A-mathbf i B .
end{matrix}
$$
=>
Если мнимое число
$ c=alpha + mathbf i beta , beta ne 0 $ является корнем $ f_{}(x) $, то и
ему комплексно-сопряженное $ overline c = alpha — mathbf i beta $ также
является корнем $ f_{}(x) $.
Иными словами, мнимые корни полинома $ f_{}(x) $ с вещественными коэффициентами «ходят пáрами»:
$ alpha pm mathbf i beta $. Геометрический смысл: на комплексной плоскости точки,
изображающие корни $ f_{}(x) $, расположены симметрично относительно вещественной
оси.

Как следствие предыдущей теоремы и основной теоремы высшей алгебры, получим
Т
Теорема. Любой полином $ f_{}(x)in mathbb R [x] $ может быть представлен в виде произведения вещественных полиномов степеней не выше второй:
$$
begin{array}{rl}
f(x) & equiv a_0 (x- lambda_1)^{{mathfrak m}_1} times dots times
(x- lambda_r)^{{mathfrak m}_r} times \
& times (x^2 +p_1x+ q_1)^{{mathfrak M}_1} times dots times
(x^2 +p_{ell}x+ q_{ell})^{{mathfrak M}_{ell}} .
end{array}
$$
Здесь $ lambda_1 , dots , lambda_r $ — различные вещественные числа,
а квадратные трехчлены
$$ {x^2 +p_1x+ q_1, dots , x^2 +p_{ell}x+ q_{ell}} subset mathbb R [x] $$
— различные с отрицательными дискриминантами
$ mathcal D_j=p_j^2-4q_j<0 $. Это представление единственно с точностью до перестановки множителей.
П
Пример. Разложить полином
$$
x^7-sqrt{3}x^6+(-3+2sqrt{3})x^5+(2+sqrt{3})x^4+(3-6sqrt{3})x^3+(-12+11sqrt{3})x^2+
$$
$$
+(10-8sqrt{3})x+4sqrt{3}-6
$$
на вещественные множители.
Ответ. $ (x+sqrt{3})(x+(1-sqrt{3}))^2(x^2-x+1)^2 $.
=>
Полином $ f_{}(x) $ с вещественными коэффициентами нечетной степени имеет хотя бы один вещественный корень, а, в общем случае, нечетное число вещественных корней (с учетом их кратностей ).
Геометрия
Полиномы с вещественными коэффициентами удобны тем, что теоретические результаты, полученные в предыдущих пунктах, получают геометрическую интерпретацию. Прежде всего, следует отметить, что полином является частным случаем непрерывной функции и на него распространяются все результаты математического анализа, разработанные для подобных функций. Итак, полином $ f_{}(x) $ — непрерывная функция при любых $ x in mathbb R $. Более того, поскольку производные полинома снова оказываются полиномами, то свойство непрерывности наследуется при дифференцировании: полином является непрерывно-дифференцируемой функцией. Из этого следует, что на плоскости $ (x_{},y) $ график полинома $ y=f_{}(x) $ представляет из себя непрерывную и гладкую кривую (ни разрывов, ни углов!) — касательная к графику существует в любой его точке.
Далее, вещественному корню $ x=lambda_{} $ полинома $ f_{}(x) $ на плоскости
$ (x_{},y) $ соответствует точка пересечения графика $ y=f_{}(x) $ с осью абсцисс.

По основной теореме высшей алгебры, таких точек может быть только конечное число: их — не более степени полинома $ deg f (x) $. Далее, между каждой парой $ lambda_j, lambda_k $ вещественных корней полинома $ f_{}(x) $, его график обязан иметь «впадину» или «горб». Обращаясь к языку математического анализа, можно сказать (и доказать), что между двумя вещественными корнями полинома находится точка его локального минимума или локального максимума. В этой точке касательная к графику функции параллельна оси абсцисс и, следовательно, тангенс угла наклона касательной должен быть равен нулю. Иными словами, точки $ mu_1,mu_2,dots $, в которых полином имеет локальный минимум или максимум, должны быть корнями его производной. См. следующий ПУНКТ.
К сожалению, не имеется наглядной интерпретации мнимых корней полинома .
§
Дальнейшие геометрические свойства полинома с вещественными коэффициентами см.
☞
ЗДЕСЬ.
Экстремумы
Говорят, что полином $ f(x)in mathbb R[x] $ имеет в точке
$ c_{} $ (локальный) минимум если существует некоторое $ delta>0 $, что при всех значениях аргументов из $ delta_{} $-окрестности точки $ c_{} $, т.е. при всех $ x_{} $, удовлетворяющих неравенству $ |x-c|<delta $
будет выполнено $ f(x)> f(c) $.
Если последнее неравенство изменить на противоположное, то получим
определение (локального) максимума. Говорят, что полином
имеет в точке $ c_{} $ (локальный) экстремум10) если он имеет в этой точке либо максимум либо минимум.
Т
Теорема [Ферма для полиномов]. Если полином $ f_{}(x) $ имеет в точке
$ c_{} $ экстремум, то в этой точке его производная обращается в нуль:
$$
f'(c)=0 .
$$
Геометрический смысл этого результата пояснен в предыдущем пункте. Обращение производной полинома в нуль в точке $ c_{} $ является условием необходимым для существования в ней экстремума. Для выяснения будет ли в этой точке минимум, максимум или же экстремум отсутствует, следует обратиться к формуле Тейлора. Рассмотрим эту формулу в точке $ c_{} $ «подозрительной на экстремум», т.е. в такой, где $ f'(c)=0 $:
$$
f(x)-f(c)=frac{1}{2}f»(c)(x-c)^2+frac{1}{6}f»'(c)(x-c)^3+dots+frac{1}{n!}f^{(n)}(c)(x-c)^n
.
$$
Если $ f»(c)ne 0 $, то можем переписать эту разность в виде
$$
f(x)-f(c)=(x-c)^2underbrace{left[frac{1}{2}f»(c)+frac{1}{6}f»'(c)(x-c)+dots+frac{1}{n!}f^{(n)}(c)(x-c)^{n-2}right]}_{P(x)} .
$$
Полином $ P(x) $ в точке $ c_{} $ имеет значение $ frac{1}{2}f»(c) $, и его знак в некоторой окрестности точки $ c_{} $ полностью определяется знаком этого числа. Таким образом, в той же окрестности имеем:
$$ operatorname{sign} (f(x)-f(c)) = operatorname{sign} (f»(c)) . $$
=>
Если в точке $ c_{} $ выполнены условия $ f'(c)=0, f»(c)> 0 $ то в этой точке полином имеет локальный минимум; если же в ней выполнены условия $ f'(c)=0, f»(c)< 0 $, то в этой точке полином имеет локальный максимум.
Остался нерассмотренным случай $ f'(c)=0, f»(c)= 0 $ — крайне исключительный. Эта исключительность будет понятной если обратиться к результатам пункта о производных полинома: вероятность того, чтобы случайным образом выбранный полином $ f_{}(x) $ обладал такой точкой $ c_{} $ — нулевая. Тем не менее, надо довести исследование до конца и в этом случае. Если $ f»'(c) ne 0 $, то из той же формулы Тейлора имеем формулу:
$$
f(x)-f(c)=(x-c)^3underbrace{left[frac{1}{6}f»'(c)+dots+frac{1}{n!}f^{(n)}(c)(x-c)^{n-3}right]}_{Q(x)} .
$$
Вне зависимости от знака $ f»'(c) $ эта разность принимает значения разных знаков в произвольной окрестности точки $ c_{} $:
$$ operatorname{sign} (f(x)-f(c)) = left{ begin{array}{r}
operatorname{sign} f»'(c) quad npu x > c \
— operatorname{sign} f»'(c) quad npu x < c
end{array}
right.
$$
В точке $ c_{} $ полином не имеет ни минимума, ни максимума. По аналогии рассматривается и общий случай.
Т
Теорема. Для того, чтобы в точке $ c_{} $ полином $ f_{}(x) $ имел экстремум необходимо и достаточно, чтобы в этой точке были выполнены условия
$$ f'(c)=0,f»(c)=0,dots, f^{(k)}(c)=0,f^{(k+1)}(c)ne 0 $$
при произвольном нечетном $ k_{} $. При этом в точке $ c_{} $ полином будет иметь локальный минимум при $ f^{(k+1)}(c)>0 $ и локальный максимум при $ f^{(k+1)}(c)<0 $.
При известной точке $ c_{} $ условия теоремы удобно проверять с помощью схемы Хорнера.
Еще одним аспектом проблемы является вычисление собственно экстремальных значений полинома, т.е. величин $ f(c) $. В самом деле, поставим, например, задачу нахождения абсолютного (глобального) максимума полинома на всем множестве вещественных чисел. Такая постановка задачи имеет смысл при дополнительном условии, что полином $ f_{}(x) $ имеет четную степень и отрицательный старший коэффициент (только при этом условии при $ x to + infty $ и при $ x to -infty $ значения полинома не будут неограниченно возрастать). В соответствии с теоремой Ферма, нам нужно найти все вещественные корни производной полинома, т.е. решить уравнение $ f'(x)=0 $, подставить найденные величины в сам полином и ранжировать полученные значения по возрастанию. Вспомним, однако, что для корней полинома, как правило, не получить точных формул (см.
☞
ЗДЕСЬ ), поэтому оценить корни полинома $ f'(x) $ мы можем, разве что, приближенно. После их нахождения, приближенные значения подставляются в полином $ f_{}(x) $ и ошибка вычислений накапливается… Можно ли избежать этого накопления? — Частично, да. Для полинома $ f_{}(x) $ (четной) степени $ n_{} $ можно построить новый полином степени $ n-1 $ по новой переменной $ z_{} $:
$$ mathcal F(z) = (z-f(mu_1))times dots times(z-f(mu_{n-1})) , $$
где $ mu_1,dots,mu_{n-1} $ — корни $ f'(x) $. При этом коэффициенты нового полинома $ mathcal F(z) $ будут рационально выражаться через коэффициенты полинома $ f'(x) $ на основании теоремы Гаусса о симметрических полиномах. Подробности конструктивного построения см.
☞
ЗДЕСЬ. Как правило, максимальный вещественный корень полинома $ mathcal F(z) $ и будет давать значение $ max f(x) $.
П
Пример. Найти
$$ max_{xin mathbb R} (-x^6+12,x^2+12,x+2) , . $$
Решение. Если идти по традиционной схеме математического анализа, то мы должны сначала найти корни производной полинома $ f(x)=-x^6+12,x^2+12,x+2 $, т.е. решить уравнение
$ x^5-4,x-2=0 $. В радикалах это уравнение не решается, так что приходится применять приближенные методы поиска вещественных корней: $ mu_1approx -1.24359, mu_2 approx — 0.50849, mu_3 approx 1.51851 $. Наконец, требуется сравнить по величине $ f(mu_1), f(mu_2), f(mu_3) $.
В альтернативу этому подходу, можно избежать нахождения корней производной и построить (хоть и кропотливо, но зато безошибочно) полином
$$ mathcal F(z)= -z^5+10,z^4+472,z^3+16208,z^2-16272,z-32800 , $$
найти один его (максимальный вещественный) корень $ approx 35.6321 $ — он и будет искомым максимумом.
Проверка: $ max f = f(mu_3) approx 35.6321 $.
Подчеркнем, что указанная возможность гарантирована только полиномиальностью рассматриваемой экстремальной задачи и на произвольные (неполиномиальные) функции предлагаемый метод не распространяется.
Приводимость
Полином $ Phi(x) in mathbb A[x] $, отличный от константы, называется неприводимым в (или неприводимым над) $ mathbb A_{} $ если у $ Phi(x) $ нет нетривиального делителя в $ mathbb A[x] $. В противном случае $ Phi(x) $ называется приводимым в (или приводимым над) $ mathbb A_{} $. Полином $ Phi(x) in mathbb A[x] $ неприводим над $ mathbb A_{} $ тогда и только тогда, когда $ operatorname{HOD} (Phi(x),g(x)) equiv const in mathbb A_{} $ для любого полинома $ g(x)in mathbb A_{}[x], deg g(x) < deg Phi (x) $.
Понятие неприводимости полинома является аналогом понятия простоты числа в теории (целых) чисел.
Т
Теорема. Любой полином $ f(x) in mathbb A [x] $ можно представить в виде
$$
begin{array}{rl}
f(x) & equiv a_0 (x- lambda_1)^{{mathfrak m}_1} times dots times
(x- lambda_r)^{{mathfrak m}_r} times \
& times (x^2 +p_1x+ q_1)^{{mathfrak M}_1} times dots times
(x^2 +p_{ell}x+ q_{ell})^{{mathfrak M}_{ell}} .
end{array}
$$
где $ Phi_1(x),dots , Phi_K(x) $ — различные нормализованные и неприводимые в $ mathbb A_{} $ полиномы, а $ { {mathfrak m}_1,dots,{mathfrak m}_K } subset mathbb N $.
Последнее тождество называется каноническим разложением $ f(x)_{} $ над $ mathbb A_{} $.
П
Пример. Полином $ x^{2}-2 $ неприводим в $ mathbb Q_{} $, но приводим в $ mathbb R_{} $:
$$ x^2-2 equiv left(x-sqrt{2} right) left(x + sqrt{2} right) , .$$
Полином $ x^{2}+2 $ неприводим в $ mathbb Q_{} $, но приводим в $ mathbb C_{} $:
$$ x^2+2 equiv left(x+mathbf i sqrt{2} right) left(x — mathbf i sqrt{2} right) , .$$
Полином $ x^{4}+4 $ не имеет вещественных корней, но, тем не менее, приводим в $ mathbb Q_{} $, т.к.
$$ x^4+4equiv (x^2+2, x +2)(x^2-2, x +2) , . $$
Т
Теорема. Любой полином $ f(x)in mathbb C [x] $ степени большей $ 1_{} $ приводим в $ mathbb C_{} $.
Доказательство следует из основной теоремы высшей алгебры.
♦
Т
Теорема. Любой полином $ f(x)in mathbb R [x] $ степени большей $ 2_{} $ приводим в $ mathbb R_{} $. Неприводимыми в $ mathbb R_{} $ являются полиномы вида
$$ x+a quad mbox{и} quad x^2+p, x +q_{} quad mbox{при} quad {a,p,q } subset mathbb R, p^2 — 4q <0 , .$$
Каноническое разложение в $ mathbb R_{} $ произвольного полинома $ f(x)in mathbb R [x] $
имеет вид
$$
f(x)equiv a_0 (x- lambda_1)^{{mathfrak m}_1} times dots times
(x- lambda_r)^{{mathfrak m}_r} times
$$
$$
times (x^2 +p_1x+ q_1)^{{mathfrak M}_1} times dots times
(x^2 +p_{ell}x+ q_{ell})^{{mathfrak M}_{ell}} ,
$$
где $ lambda_{1} , dots , lambda_r $ — различные вещественные числа, а квадратные трехчлены $ {x^2 +p_1x+ q_1, dots , x^2 +p_{ell}x+ q_{ell}} subset mathbb R [x] $ — различные с отрицательными дискриминантами $ mathcal D_j=p_j^2-4q_j<0 $.
Фактически, эта теорема является переформулировкой результата, приведенного
☞
ЗДЕСЬ.
Рассмотрим теперь полином с рациональными коэффициентами:
$$f(x)=a_0x^n+a_1x^{n-1}+dots+a_n in mathbb Q [x] , a_0 ne 0 . $$
Если полином $ f_{}(x) $ приводим в $ mathbb Q_{} $, то будет приводимым и
полином $ Ccdot f_{}(x) $ при $ forall C in mathbb Q, C ne 0 $; верно и обратное.
Представив коэффициенты $ a_{0},dots, a_n $ в виде несократимых дробей,
возьмем
$$ C=operatorname{HOK}(mbox{ знаменатель } a_{0},dots, mbox{ знаменатель } a_n ) , $$
тогда приводимость (или неприводимость) полинома $ f_{}(x) $ в $ mathbb Q_{} $
эквивалентна приводимости (соответственно, неприводимости)
в $ mathbb Q_{} $ полинома $ Ccdot f(x) $ с целыми коэффициентами. Поэтому в дальнейшем
будем сразу предполагать
$ f(x)in mathbb Z[x] $. Можно ли пойти дальше и утверждать, что приводимость
такого полинома в $ mathbb Q_{} $ эквивалентна приводимости его в $ mathbb Z_{} $, т.е.
полином раскладывается на произведение полиномов меньших степеней с рациональными коэффициентами тогда и
только тогда, когда он раскладывается на произведение полиномов меньших степеней с целыми коэффициентами?
Т
Теорема. Полином $ f(x)in mathbb Z[x] $ неприводимый в $ mathbb Z_{} $ будет неприводимым и в $ mathbb Q_{} $.
Приводимость полинома с целыми коэффициентами $ f(x)in mathbb Z[x] $ в $ mathbb Z_{} $ означает, что он раскладывается на два множителя с целыми коэффициентами:
$$
a_0x^n+a_1x^{n-1}+ dots + a_n equiv (b_0x^k+b_1x^{k-1} + dots + b_k)
(c_0x^{ell}+c_1x^{ell-1} + dots + c_{ell})
$$
при $ k<n, ell < n, k+ell = n $. Для практического решения вопроса о существовании такого разложения, сначала установим условия его существования для случая, когда один из
сомножителей — линейный полином.
Т
Теорема. Если полином
$$f(x)=a_0x^n+a_1x^{n-1} + dots + a_n in mathbb Z[x] , a_0 ne 0,a_n ne 0 $$
имеет рациональный корень, представленный в виде несократимой дроби $ lambda=mathfrak p/mathfrak q,, {{mathfrak p}, {mathfrak q}}subset mathbb Z $, то ее числитель $ {mathfrak p} $ является делителем свободного члена $ a_{n} $, а знаменатель $ {mathfrak q}_{} $ — делителем старшего коэффициента $ a_{0} $.
Доказательство
☞
ЗДЕСЬ
.
♦
Итак, для поиска рациональных корней полинома $ f_{}(x) $ надо выписать множество всех натуральных делителей $ {{mathfrak p}_1=1,dots,{mathfrak p}_{s}} $ числа $ |a_n| $, и множество всех натуральных делителей $ {{mathfrak q}_1=1,dots,{mathfrak q}_{t}} $ числа $ |a_0| $, и после этого организовать вычисление $ fleft(pm {mathfrak p}_j/{mathfrak q}_i right) $
при всех возможных значениях индексов $ jin {1,dots,s }, i in {1,dots, t } $. Если ни одно из полученных чисел не равно нулю, то рациональных корней полином не имеет.
=>
Если нормализованный полином $ f(x) in mathbb Z[x] $ имеет рациональные корни, то они — только целые и находятся среди делителей свободного члена.
П
Пример. Найти рациональные корни полинома
$$f(x)=6,x^6-55, x^5+331, x^3-86,x^4+289,x^2-25,x+350 . $$
Решение. Выписываем множества делителей
для $ 350 : quad {1,, 2 ,, 5 ,, 7,, 10,, 14,, 25
,, 35,, 50,, 70,, 175 } $ и для $ 6 : {1,, 2,, 3,, 6 } $.
Составляем всевозможные несократимые дроби:
$$ left{
begin{array}{ccccccccccc}
1,& 2 ,& 5 ,& 7,& 10,& 14,& 25 ,& 35,& 50,& 70,& 175, \
{scriptstyle 1}/{scriptstyle 2},& &
{scriptstyle 5}/{scriptstyle 2} ,& {scriptstyle 7}/{scriptstyle 2}, &
& & {scriptstyle 25}/{scriptstyle 2}
& {scriptstyle 35}/{scriptstyle 2}, & & &
{scriptstyle 175}/{scriptstyle 2}, \
{scriptstyle 1}/{scriptstyle 3},& {scriptstyle 2}/{scriptstyle 3},&
{scriptstyle 5}/{scriptstyle 3},& {scriptstyle 7}/{scriptstyle 3},&
{scriptstyle 10}/{scriptstyle 3},&
{scriptstyle 14}/{scriptstyle 3},& {scriptstyle 25}/{scriptstyle 3},&
{scriptstyle 35}/{scriptstyle 3},& {scriptstyle 50}/{scriptstyle 3},&
{scriptstyle 70}/{scriptstyle 3},& {scriptstyle 175}/{scriptstyle 3}, \
{scriptstyle 1}/{scriptstyle 6},& &
{scriptstyle 5}/{scriptstyle 6}, & {scriptstyle 7}/{scriptstyle 6}, &
& &
{scriptstyle 25}/{scriptstyle 6},& {scriptstyle 35}/{scriptstyle 6},& &
& {scriptstyle 175}/{scriptstyle 6}
end{array}
right}
$$
Подставляем все эти значения со знаками $ +_{} $ и $ — $ в $ f(x)_{} $ и проверяем (например, с использованием схемы Хорнера ) на равенство нулю.
Ответ. $ 10,, {scriptstyle 5}/{scriptstyle 2},, -{scriptstyle 7}/{scriptstyle 3} $.
Из того факта, что полином $ f(x) in mathbb Z[x] $ не имеет рациональных корней не
следует, что он неприводим в $ mathbb Z_{} $: в разложении $ f(x)equiv f_{1}(x)f_2(x) $ сомножители
могут оказаться и нелинейными — например, как указанный выше полином $ x^{2}+4 $. Как найти эти сомножители?
§
Подробнее о приводимости и неприводимости полиномов в $ mathbb Z_{} $
☞
ЗДЕСЬ.
Локализация корней
Границы расположения корней
Т
Теорема [Маклорен].11) Все корни полинома
$$f(x)=a_0x^n+a_1x^{n-1}+dots+a_n in mathbb C [x], a_0 ne 0$$
удовлетворяют неравенству
$$
|lambda_j|<1+ A,quad npu quad A=
max_{kin{1,dots,n}} left| frac{a_k}{a_0} right| .
$$
Оценка Маклорена довольно грубая и для корней полиномов с вещественными коэффициентами
чаще применяется другой критерий.
Т
Теорема [Лагранж]. Все вещественные корни полинома
$$f(x)=a_0x^n+a_1x^{n-1}+dots+a_n in mathbb R [x], a_0>0$$
удовлетворяют неравенству
$$
lambda_j<1+ sqrt[r]{A},quad npu quad
A=max_{kin {1,dots,n}} left| frac{a_k}{a_0} right| ,
$$
где $ r $ — номер первого отрицательного коэффициента.
Оценка Лагранжа, являясь оценкой вещественных корней сверху, фактически ограничивает возможные положительные корни.
?
А как получить нижнюю оценку возможных отрицательных корней?
Это можно сделать с помощью преобразования
1
полинома, рассмотренного
☞
ЗДЕСЬ.
В самом деле, отрицательные корни полинома $ f(x) $ являются положительными
корнями полинома $ f(-x) $. Найдя верхнюю границу последних с помощью любого
из приведенных выше критериев, мы меняем у нее знак и в результате получаем
нижнюю оценку отрицательных корней $ f(x) $.
Преобразование
3
,
рассмотренное в том же пункте, позволяет получить отдельные
интервалы для возможных положительных и отрицательных корней.
П
Пример. Найти оценки положительных и отрицательных корней полинома
$$
f(x)=x^8+2, x^7-2, x^6 +6, x^5 -80, x^4 + 100, x^3 -400, x^2 + 15, x +30
.
$$
Решение. Сначала ограничим положительные корни сверху. В теореме
Лагранжа имеем $ r=2,, A=400 $, следовательно $ lambda_j<21 $.
Теперь ограничим отрицательные корни снизу.
$$
f(-x)=x^8-2, x^7-2, x^6 -6, x^5 -80, x^4 — 100, x^3 -400, x^2 — 15, x +30
,
$$
и теперь $ r=1,, A=400 $, следовательно $ -lambda_j<401 Rightarrow
lambda_j > -401 $. Формируем полином
$$
f^{ast}(x) = x^8f(1/x)=
1+2, x-2, x^2 +6, x^3 -80, x^4 + 100, x^5 -400, x^6 + 15, x^7 +30,x^8
$$
для оценки нижней границы положительных корней:
$$1/lambda_j < 1 + sqrt{400/30}
Rightarrow lambda_j > frac{1}{1 +sqrt{40/3}}
.
$$
Наконец, оценка Лагранжа для полинома $ f^{ast}(-x) $:
$$-1/lambda_j < 1+ 40/3
Rightarrow lambda_j < — frac{1}{1 +40/3}
$$
позволяет ограничить сверху отрицательные корни полинома $ f(x) $.
Ответ. Положительные корни находятся в интервале $ ]0.214, ,21[ $,
а отрицательные — в интервале $ ]-401,-0.06[ $.
Проверка. Вещественные корни полинома:
$$-4.324358112, -0.2473416673, 0.3027275675, 2.716544138 .$$
Правило знаков Декарта
Для полиномов с вещественными коэффициентами следующий полезный результат очень прост в проверке.
Будем использовать сокращение $ operatorname{nrr} $ для числа вещественных корней12).
Т
Теорема [Декарт]. Число положительных корней полинома
$$f(x)=a_0x^n+a_1x^{n-1}+dots+a_{n-1}x+a_n in mathbb R[x], quad (a_0> 0,a_n ne 0)$$
с учетом их кратностей равно или меньше на четное число числа знакоперемен в ряду его коэффициентов:
$$
operatorname{nrr} { f(x)=0 mid x>0 } = {mathcal V}(a_0,a_1,dots,a_n)-2 k , quad
kin {0,1,2, dots } .
$$
Доказательство
☞
ЗДЕСЬ.
С помощью преобразования корней полинома (см. пункт
1
☞
ЗДЕСЬ ) можно доказать следствие:
=>
Число отрицательных корней полинома
$$f(x)=a_0x^n+a_1x^{n-1}+dots+a_{n-1}x+a_n, quad (a_0> 0,a_n ne 0)$$
с учетом их кратностей можно оценить по формуле
$$
operatorname{nrr} { f(x)=0 mid x<0 } = {mathcal V}(a_0,-a_1,a_2,dots,(-1)^na_n)-2 k’
,
$$
а если среди коэффициентов $ a_{j} $ нет нулевых, то — по формуле
$$
operatorname{nrr} { f(x)=0 mid x<0 } = {mathcal P}(a_0,a_1,a_2,dots,a_n)-2 k’ ,
$$
где $ k’in {0,1,2, dots } $ и $ {mathcal P} $ обозначает число знакопостоянств.
П
Пример. Оценить число положительных и число отрицательных корней
полинома
$$ f(x)=x^5-2, x^4-8,x^3-x^2-9, x+1 , .$$
Решение. $ {mathcal V}(1,-2,-8,-1,-9,1)=2 $.
$$ operatorname{nrr} { f(x)=0 mid x>0 } =2-2k ge 0
,$$
следовательно $ f_{}(x) $ имеет либо два, либо ни одного положительного
корня. Далее, по следствию:
$$
operatorname{nrr} { f(x)=0 mid x<0 } = {mathcal P}(1,-2,-8,-1,-9,1)=3-2k’ge 0
,
$$
следовательно $ f_{}(x) $ имеет либо три, либо один отрицательный корень.
Проверка. Вещественные корни полинома: $ -2.23233, 0.10863, 4.12369 $.
=>
Если каким-то образом заранее известно, что все корни полинома вещественны, то число положительных из них определяется по правилу знаков Декарта однозначно:
$$ operatorname{nrr} { f(x)=0 mid x>0 } = {mathcal V}(a_0,a_1,dots,a_n) . $$
П
Пример. Характеристический полином вещественной симметричной матрицы удовлетворяет условию следствия. См.
☞
ЗДЕСЬ.
Не смотря на кажущуюся грубость (приблизительность) оценки, правило знаков Декарта позволяет иногда делать достаточно глубокие выводы относительно корней полинома. В частности, из него следует, что чем больше коэффициентов полинома $ f_{}(x) $ обращается в нуль13), тем меньше у него потенциальных возможностей иметь вещественные корни!
Корни полинома в областях комплексной плоскости
Задача. Для полинома14) $ f(z) $ получить точную информацию о числе его корней в заданной области $ mathbb S $ комплексной плоскости $ mathbb C $.
Оказывается, для достаточно широкого класса областей $ mathbb S $ эту информацию можно получить без
применения численных, т.е. приближенных методов. Существуют алгоритмы,
позволяющие за конечное число элементарных алгебраических операций
($ +,-,times, div $) над коэффициентами $ f(z) $ установить количество корней
этого полинома в таких областях, как, к примеру,
$$
begin{array}{ccl}
mathbb S&=&{ zin mathbb R big| a<z<b } npu {a,b} subset mathbb R , \
&& \
mathbb S&=&{ zin mathbb C big| Re e (z) <0 } , \
&& \
mathbb S&=&{ zin mathbb C big| |z| <1 } .
end{array}
$$
Интервал вещественной оси
Задача. Для полинома $ f(x)_{}in mathbb R[x] $ установить точное число его
корней на заданном интервале $ ]a,b[ $:
$$ operatorname{nrr} {f(x)=0 | a<x<b } .$$
Система полиномов Штурма
Для полинома $ f_{}(x) $ система полиномов
$$
f_0(x)equiv f(x), f_1(x),dots, f_K(x)
$$
называется системой полиномов Штурма15) на заданном интервале $ ]a,b[ $ если на этом
интервале
1.
cоседние полиномы $ f_j(x) $ и $ f_{j+1}(x) $ не имеют общих корней;
2.
$ f_K(x)ne 0 $;
3.
если $ f_j(x_0)=0 $ при $ x_0 in ]a,b[ $ и $ jin {1,dots,k-1} $, то
числа $ f_{j-1}(x_0) $ и $ f_{j+1}(x_0) $ имеют разные знаки:
$ f_{j-1}(x_0)f_{j+1}(x_0)<0 $;
4.
произведение $ f_{0}(x)f_{1}(x) $ меняет знак с отрицательного на положительный когда $ x_{} $, возрастая, проходит корень $ lambdain ]a,b[ $ полинома $ f_0(x)equiv f(x) $.
Число знакоперемен
$$
{mathcal V}_x= {mathcal V}(f_0(x), f_1(x),dots, f_K(x))
$$
при $ x_{} $ возрастающем от $ a_{} $ к $ b_{} $, будет меняться когда $ x_{} $ проходит через
корень какого-либо полинома системы. Доказывается, что это число может
разве лишь уменьшаться, и уменьшается на единицу тогда и только тогда,
когда $ x_{} $ проходит через корень начального полинома системы, т.е. через корень $ f(x)_{} $.
Т
Теорема [Штурм]. Если $ f(a)ne 0, f(b)ne 0 $, и система $ f_0(x), f_1(x),dots, f_K(x) $
является системой полиномов Штурма для $ f(x_{}) $, то
$$
operatorname{nrr} {f(x)=0 mid a<x<b }= {mathcal V}_a — {mathcal V}_b=
$$
$$
={mathcal V}(f_0(a), f_1(a),dots, f_K(a))-
{mathcal V}(f_0(b), f_1(b),dots, f_K(b)) .
$$
Самый распространенный способ построение системы полиномов Штурма основан на алгоритме Евклида нахождения наибольшего общего делителя полинома $ f_{}(x) $ и его производной $ f{‘}(x) $.
Предположим, что $ f_{}(x) $ не имеет кратных корней. Это равносильно
тому, что $ operatorname{HOD} (f(x),f'(x))= const ne 0 $ (см.
☞
ЗДЕСЬ ). Установить этот факт можно по алгоритму Евклида нахождения $ operatorname{HOD} $. Оказывается, что в качестве полиномов системы Штурма можно взять последовательность остатков из алгоритма Евклида, если только домножить некоторые из них на $ -1_{} $. Именно, возьмем
$$f_1(x) equiv f'(x) .$$
Поделим $ f_{0}(x) equiv f(x) $ на $ f_{1}(x) $ и обозначим через $ f_{2}(x) $ остаток,
домноженный на $ -1_{} $:
$$f_0(x)equiv q_1(x) f_1(x)-f_2(x), quad deg f_2 < n-1 .$$
Поделим $ f_{1}(x) $ на $ f_{2}(x) $ и обозначим через $ f_{3}(x) $ остаток,
домноженный на $ -1_{} $:
$$f_1(x)equiv q_2(x) f_2(x)-f_3(x), quad deg f_3 < deg f_2 .$$
Продолжаем алгоритм далее, в конце концов дойдем до последнего ненулевого
остатка $ f_{K}(x) $, который совпадает с $ operatorname{HOD} (f(x),f'(x)) $. По предположению, этот последний $ f_{K}(x)equiv const ne 0 $.
§
Если на интервале $ ]a,b[ $ полином $ f_{}(x) $ имеет корень четной кратности, то построение системы полиномов Штурма невозможно.
П
Пример. Отделить корни полинома $ f (x)=x^{4}-x-1 $.
Решение. $ f_1=f'(x)=4, x^{3}-1 $.
$$
begin{array}{rrrrrr|l}
x^4+ &{}0x^3 +&{}0x^2 &-x &-1 &&,4, x^3-1\
x^{4}+& & &
— frac{scriptstyle 1}{scriptstyle 4} x & &&,
overline{quad frac{scriptstyle 1}{scriptstyle 4}, x quad } \
hline
& & &- frac{scriptstyle 3}{scriptstyle 4} , x &-1 \
end{array}
$$
Полагаем $ f_2(x)= frac{scriptstyle 3}{scriptstyle 4} , x+1 $.
$$
begin{array}{rrrrr|l}
4x^3 +&{}0x^2 &+0x &-{}1 &&frac{scriptstyle 3}{scriptstyle 4}, x+1\
4x^3 +&frac{scriptstyle 16}{scriptstyle 3}, x^2 & & &
& overline{ frac{scriptstyle 16}{scriptstyle 3},x^{2}-frac{scriptstyle 64}{scriptstyle 9}, x+
frac{scriptstyle 256}{scriptstyle 27}} \
hline
&-frac{scriptstyle 16}{scriptstyle 3}, x^{2} & &{}-1 \
&-frac{scriptstyle 16}{scriptstyle 3}, x^2 &-frac{scriptstyle 64}{scriptstyle 9}, x & \
hline
& & frac{scriptstyle 64}{scriptstyle 9}, x & -1 \
& & frac{scriptstyle 64}{scriptstyle 9}, x & +frac{scriptstyle 256}{scriptstyle 27} \
hline
& & & — frac{scriptstyle 283}{scriptstyle 27}
end{array}
$$
Полагаем $ f_3(x)=frac{scriptstyle 283}{scriptstyle 27} $.
| $ x_{} $ | $ f_{}(x) $ | $ f_{1}(x) $ | $ f_{2}(x) $ | $ f_{3}(x) $ | $ {mathcal V}_x $ | Комментарии |
|---|---|---|---|---|---|---|
| $ -infty $ | $ +_{} $ | — | — | $ +_{} $ | $ 2_{} $ | сначала устанавливаем |
| $ +infty $ | $ +_{} $ | $ +_{} $ | $ +_{} $ | $ +_{} $ | $ 0_{} $ | число вещественных корней, |
| $ 0_{} $ | — | — | $ +_{} $ | $ +_{} $ | $ 1_{} $ | затем положительных и отрицательных, |
| $ -1 $ | $ +_{} $ | — | $ +_{} $ | $ +_{} $ | $ 2_{} $ | затем просто дробим |
| $ 1_{} $ | — | $ +_{} $ | $ +_{} $ | $ +_{} $ | $ 1_{} $ | промежутки, отыскивая такие, |
| $ 2_{} $ | $ +_{} $ | $ +_{} $ | $ +_{} $ | $ +_{} $ | $ 0_{} $ | чтобы на каждом $ {mathcal V}_{a}-{mathcal V}_{b}=1 $ |
Ответ. Полином $ f_{}(x) $ имеет два различных вещественных корня, один на
интервале $ ]-1,0_{}[ $, другой — на $ ]1,2_{}[ $.
§
Более подробный анализ алгоритма, а также альтернативный способ локализации корней полинома, основанный на ганкелевых матрицах
☞
ЗДЕСЬ
Левая полуплоскость: устойчивость
Полином $ f(z) $ с комплексными коэффициентами называется устойчивым, если все его корни удовлетворяют условию $ {mathfrak Re}(z)<0 $.
Понятие устойчивого полинома важно в теории оптимального управления.
Т
Теорема [Раус, Гурвиц]. Для устойчивости
полинома $ f(z)=a_0z^n+a_1z^{n-1}+dots+a_n $ с вещественными коэффициентами и $ a_0 > 0 $ необходимо и достаточно, чтобы были выполнены неравенства
$$
a_1>0, left| begin{array}{ll} a_1 & a_3 \
a_0 & a_2
end{array}
right|>0,
left| begin{array}{lll} a_1 & a_3 & a_5\
a_0 & a_2 & a_4 \
0 & a_1 & a_3
end{array}
right|>0,dots,
left| begin{array}{lllcl} a_1 & a_3 & a_5 & dots & 0\
a_0 & a_2 & a_4 & dots & 0 \
0 & a_1 & a_3 & dots & 0 \
0 & a_0 & a_2 & dots & 0 \
dots & & & ddots & dots \
dots & & & dots & a_n
end{array}
right|>0 .
$$
Условия теоремы Рауса-Гурвица являются избыточными: примерно от половины неравенств можно избавиться. См.
☞
Теорема Льенара-Шипара ).
Единичный круг
Единичным кругом на комплексной плоскости назовем круг $ |z|le 1 $.
Задача. Найти необходимые и достаточные условия на коэффициенты
полинома $ f(z)=a_0z^n+dots+ a_n $, при которых все его корни $ lambda_1,dots, lambda_n $
находятся внутри единичного круга, т.е. удовлетворяют условию $ |z|<1 $.
По аналогии с предыдущим случаем, иногда такой полином называют дискретно устойчивым; также употребляется и название устойчивый по Шуру.
Решить эту задачу можно сведением ее к задаче установления критерия
устойчивости некоторого вспомогательного полинома.
Т
Теорема. Замена переменной
$$ z = frac{w+1}{w-1} $$
производит взаимно-однозначное отображение внутренности единичного круга
плоскости $ z $ в левую полуплоскость плоскости $ w $.

Т
Теорема. Полином $ f(z)=a_0z^n+dots+a_n $ имеет все свои корни
лежащими внутри единичного круга тогда и только тогда, когда полином
$$
F(w) = (w-1)^n fleft( frac{w+1}{w-1} right) =
a_0(w+1)^n+a_1(w+1)^{n-1}(w-1)+dots+a_n(w-1)^n
$$
будет устойчив.
П
Пример. Определить все вещественные значения параметра
$ {color{Red} alpha } $, при которых полином
$$f(z)=3,z^3+{color{Red} alpha } , z^2+z+2 $$
будет иметь все корни лежащими внутри единичного круга.
Решение. Строим полином из теоремы
$$
F(w)=underbrace{(6+{color{Red} alpha })}_{A_0}w^3+underbrace{(2+{color{Red} alpha })}_{A_1}w^2
+underbrace{(14-{color{Red} alpha })}_{A_2}w+underbrace{2-{color{Red} alpha }}_{A_3} .
$$
Теорема Льенара-Шипара дает условия устойчивости $ F(w) $
в виде
$$A_0>0, A_1>0, A_2>0, A_3>0, A_1A_2-A_0A_3>0 ; $$
и
$$A_0<0, A_1<0, A_2<0, A_3<0, A_1A_2-A_0A_3>0 .$$
Подставляя сюда выражения для коэффициентов, получим, что первая система ограничений
имеет решение $ -1< {color{Red} alpha } < 2 $, вторая же — несовместна.
Косвенной проверкой истинности полученного интервала могут служить его границы:
$$
f(z)equiv
left{ begin{array}{rl}
(3z+2)(z^2-z+1)
& npu {color{Red} alpha }=-1 ; \
(z+1)(3,z^2-z+2)
& npu {color{Red} alpha }=2 .
end{array}
right.
$$
В обоих случаях имеются корни, удовлетворяющие условию $ |z|=1 $: в первом
случае это будет комплексно-сопряженная пара
$ 1/2 pm {mathbf i} sqrt{3}/2 $,
во втором — корень $ (-1) $.
Ответ. $ -1< {color{Red} alpha } < 2 $.
Известен еще один результат, позволяющий решить поставленную задачу.
Т
Теорема [Шур, Кон]. Полином $ f(z)=a_0z^n+dots+a_n $ с вещественными коэффициентами имеет все свои корни лежащими внутри единичного круга тогда и только тогда, когда
$$
|mbox{ старший коэффициент } f(z) |>|mbox{ свободный член } f(z)| ,
$$
т.е. $ |a_0| > |a_n| $, и полином
$$
f_1(z) = frac{a_0f(z)-a_nf^{*}(z)}{z} quad npu quad f^{*}(z) = z^nf(1/z) equiv a_0+a_1z+dots+a_nz^n
$$
имеет все свои корни лежащими внутри единичного круга.
На первый взгляд, конструктивность этого результата не очень очевидна:
исходная задача для полинома $ f(z) $ сводится к аналогичной задаче для
полинома $ f_1(z) $. Обратим, однако, внимание на то, что полином
$$
begin{matrix}
f_1(z)&=& left[a_0(a_0z^n+dots+a_n)-a_n (a_0+a_1z+dots+a_nz^n) right] big/ z = \
&=& left[(a_0^2-a_n^2)z^n+(a_0a_1-a_{n-1}a_n)z^{n-1} + dots +
(a_0a_{n-1}-a_{1}a_n)z right] big/ z = \
&=& (a_0^2-a_n^2)z^{n-1}+(a_0a_1-a_{n-1}a_n)z^{n-2} + dots +
(a_0a_{n-1}-a_{1}a_n)
end{matrix}
$$
имеет степень меньшую, чем $ deg f $. Таким образом, алгоритм конструктивен
в том смысле, что он сводит исходную задачу к более простой. Применяя
к полиному $ f_1(z) $ снова критерий Шура-Кона, получим следующее необходимое
условие
$$
|mbox{ старший коэффициент } f_1(z) | > | mbox{ свободный член }
f_1(z)|
iff quad |a_0^2-a_n^2| > |a_0a_{n-1}-a_{1}a_n| ,
$$
при выполнении которого дальнейшему исследованию подлежит полином
$$
f_2(z) = frac{(a_0^2-a_n^2)f_1(z)-(a_0a_{n-1}-a_{1}a_n)f^{*}_1(z)}{z} .
$$
Продолжая процедуру, за конечное число шагов мы дойдем до полинома первой
степени. Окончательно, необходимые и достаточные условия нахождения
всех корней полинома $ f(z) $ степени $ n_{} $ внутри единичного круга получаются
объединением $ n_{} $ условий
$$
|mbox{ старший коэффициент } f(z) |>|mbox{ свободный член } f(z)|
,
$$
$$
|mbox{ старший коэффициент } f_1(z) | > |mbox{ свободный член } f_1(z)|
,
$$
$$
vdots qquad qquad qquad vdots
$$
$$
|mbox{ старший коэффициент } f_{n-1}(z) |>|mbox{ свободный член }
f_{n-1}(z)| .
$$
§
Пример на применение этой теоремы
☞
ЗДЕСЬ.
Численные методы поиска корней полинома
Как упоминалось
☝
ВЫШЕ, корни полинома $ f_{}(z) $, как правило,
не выражаются в радикалах уже при $ deg f=5 $ . Но даже в тех случаях, когда
выражаются, как, например,
$$lambda=frac{sqrt{5}-1 + sqrt{10- sqrt{20}}}{2} quad mbox{ для }
f(x)=x^4+2x^3-6x^2-2x+1 ,
$$
толку от такого представления мало: на каком интервале вещественной оси лежит $ lambda $?
Поэтому наряду с поиском аналитических формул для корней полиномов
практический интерес представляет нахождение их приближенных значений.
Эту задачу будем решать, в основном, для полиномов над $ mathbb R_{} $ (т.е. полиномов с вещественными коэффициентами), с которыми чаще всего и приходится иметь дело на практике.
Задачу поиска мнимых корней таких полиномов можно свести к поиску вещественных решений системы алгебраических уравнений от двух переменных и специальными приемами свести к поиску вещественных корней одного уравнения от одной переменной. Подробнее см.
☞
ЗДЕСЬ. Имеются и другие способы поиска мнимых корней, (например, метод Греффе-Лобачевского), но я о них еще нескоро напишу.
Нас, прежде всего, будут интересовать именно вещественные корни полиномов. В дальнейшем переменную этих полиномов будем обозначать через $ x_{} $ и считать ее вещественной. Для поиска вещественных корней полинома, как правило, требуется их предварительно отделить, т.е. найти интервалы
$ ]a,b_{}[ $, каждый из которых содержит только один корень $ f_{}(x) $. Поиск такого интервала
можно производить разными способами, самый общий из которых изложен
☝
ВЫШЕ. Однако, для предварительного понимания изложенных ниже методов, достаточно будет ориентироваться на теорему Больцано: полином имеет корень на $ ]a,b_{}[ $, если на концах интервала он принимает значения разных знаков.
Этот корень будет единственным, если дополнительно предположить, что функция $ f_{}(x) $ монотонна на $ ]a,b_{}[ $.
Последнее условие будет очевидно выполнено, если производная $ f^{prime}(x) $ не меняет знака на $ ]a,b_{}[ $, т.е. полином $ f^{prime}(x) $
не имеет корней на рассматриваемом интервале. Действительно, если
предположить существование двух корней у $ f_{}(x) $ на $ ]a,b_{}[ $, то, по соображениям, упомянутым
☞
ЗДЕСЬ16), должна существовать точка этого интервала, в которой $ f^{prime}(x) $ обращается в нуль. Анализ знака $ f^{prime}(x) $ на $ ]a,b_{}[ $ часто удается произвести элементарными рассуждениями.
Метод Руффини-Хорнера
Метод Лагранжа (непрерывных дробей)
Метод Ньютона
Универсальный метод: подходит не только для полиномов.
Рассматривается
☞
ЗДЕСЬ.
Метод Бернулли и его развитие
Подходит для полиномов в том числе и с комплексными коэффициентами (и мнимые корни тоже ищет). Не предполагает предварительного отделения корней. Рассматривается
☞
ЗДЕСЬ.
Характеристический полином матрицы
рассматривается
☞
ЗДЕСЬ
Полином нескольких переменных
рассматривается
☞
ЗДЕСЬ
Задачи
Источники
3 способа расчета полинома в Excel.
Автор: Алексей Батурин.
Есть 3 способа расчета значений полинома в Excel:
- 1-й способ с помощью графика;
- 2-й способ с помощью функции Excel =ЛИНЕЙН();
- 3-й способ с помощью Forecast4AC PRO;
Подробнее о полиноме и способе его расчета в Excel далее в нашей статье.
Полиномиальный тренд применяется для описания значений временных рядов, попеременно возрастающих и убывающих. Полином отлично подходит для анализа большого набора данных нестабильной величины (например, продажи сезонных товаров).
Что такое полином? Полином — это степенная функция y=ax 2 +bx+c (полином второй степени) и y=ax 3 +bx 2 +cx+d (полином третей степени) и т.д. Степень полинома определяет количество экстремумов (пиков), т.е. максимальных и минимальных значений на анализируемом промежутке времени.
У полинома второй степени y=ax 2 +bx+c один экстремум (на графике ниже 1 максимум).
У Полинома третьей степени y=ax 3 +bx 2 +cx+d может быть один или два экстремума.
Один экстремум
Два экстремума
У Полинома четвертой степени не более трех экстремумов и т.д.
Как рассчитать значения полинома в Excel?
Есть 3 способа расчета значений полинома в Excel:
- 1-й способ с помощью графика;
- 2-й способ с помощью функции Excel =ЛИНЕЙН;
- 3-й способ с помощью Forecast4AC PRO;
1-й способ расчета полинома — с помощью графика
Выделяем ряд со значениями и строим график временного ряда.
На график добавляем полином 6-й степени.
Затем в формате линии тренда ставим галочку «показать уравнение на диаграмме»
После этого уравнение выводится на график y = 3,7066x 6 — 234,94x 5 + 4973,6x 4 — 35930x 3 — 7576,8x 2 + 645515x + 5E+06 . Для того чтобы последний коэффициент сделать читаемым, мы зажимаем левую кнопку мыши и выделяем уравнение полинома
Нажимаем правой кнопкой и выбираем «формат подписи линии тренда»
В настройках подписи линии тренда выбираем число и в числовых форматах выбираем «Числовой».
Получаем уравнение полинома в читаемом формате:
y = 3,71x 6 — 234,94x 5 + 4 973,59x 4 — 35 929,91x 3 — 7 576,79x 2 + 645 514,77x + 4 693 169,35
Из этого уравнения берем коэффициенты a, b, c, d, g, m, v, и вводим в соответствующие ячейки Excel
Каждому периоду во временном ряду присваиваем порядковый номер, который будем подставлять в уравнение вместо X.
Рассчитаем значения полинома для каждого периода. Для этого вводим формулу полинома y = 3,71x 6 — 234,94x 5 + 4 973,59x 4 — 35 929,91x 3 — 7 576,79x 2 + 645 514,77x + 4 693 169,35 в первую ячейку и фиксируем ссылки на коэффициенты тренда (см. статью как зафиксировать ссылки)
Получаем формулу следующего вида:
= R2C8 *RC[-3]^6+ R3C8 *RC[-3]^5+ R4C8 *RC[-3]^4+ R5C8 *RC[-3]^3+ R6C8 *RC[-3]^2+ R7C8 *RC[-3]+ R8C8
в которой коэффициенты тренда зафиксированы и вместо «x» мы подставляем ссылку на номер текущего временного ряда (для первого значение 1, для второго 2 и т.д.)
Также «X» возводим в соответствующую степень (значок в Excel «^» означает возведение в степень)
=R2C8*RC[-3] ^6 +R3C8*RC[-3] ^5 +R4C8*RC[-3] ^4 +R5C8*RC[-3] ^3 +R6C8*RC[-3] ^2 +R7C8*RC[-3]+R8C8
Теперь протягиваем формулу до конца временного ряда и получаем рассчитанные значения полиномиального тренда для каждого периода.
2-й способ расчета полинома в Excel — функция ЛИНЕЙН()
Рассчитаем коэффициенты линейного тренда с помощью стандартной функции Excel =ЛИНЕЙН()
Для расчета коэффициентов в формулу =ЛИНЕЙН(известные значения y, известные значения x, константа, статистика) вводим:
- «известные значения y» (объёмы продаж за периоды),
- «известные значения x» (порядковый номер временного ряда),
- в константу ставим «1»,
- в статистику «0»
Получаем следующего вида формулу:
Теперь, чтобы формула Линейн() рассчитала коэффициенты полинома, нам в неё надо дописать степень полинома, коэффициенты которого мы хотим рассчитать.
Для этого в часть формулы с «известными значениями x» вписываем степень полинома:
- ^ <1:2:3:4:5:6>— для расчета коэффициентов полинома 6-й степени
- ^ <1:2:3:4:5>— для расчета коэффициентов полинома 5-й степени
- ^ <1:2>— для расчета коэффициентов полинома 2-й степени
Получаем формулу следующего вида:
Вводим формулу в ячейку, получаем 3,71 —- значение (a) для полинома 6-й степени y=ax^6+bx^5+cx^4+dx^3+gx^2+mx+v
Для того, чтобы Excel рассчитал все 7 коэффициентов полинома 6-й степени y=ax^6+bx^5+cx^4+dx^3+gx^2+mx+v, необходимо:
1. Установить курсор в ячейку с формулой и выделить 7 соседних ячеек справа, как на рисунке:
2. Нажать на клавишу F2
3. Затем одновременно — клавиши CTRL + SHIFT + ВВОД (т.е. ввести формулу массива, как это сделать читайте подробно в статье «Как ввести формулу массива»)
Получаем 7 коэффициентов полиномиального тренда 6-й степени.
Рассчитаем значения полиномиального тренда с помощью полученных коэффициентов. Подставляем в уравнение y=3,7* x ^ 6 -234,9* x ^ 5 +4973,5* x ^ 4 -35929,9 * x^3 -7576,7 * x^2 +645514,7* x +4693169,3 номера периодов X, для которых хотим рассчитать значения полинома.
Каждому периоду во временном ряду присваиваем порядковый номер, который будем подставлять в уравнение полинома вместо X.
Рассчитаем значения полиномиального тренда для каждого периода. Для этого вводим формулу полинома в первую ячейку и фиксируем ссылки на коэффициенты тренда (см. статью как зафиксировать ссылки)
Получаем формулу следующего вида:
= R2C8 *RC[-3]^6+ R3C8 *RC[-3]^5+ R4C8 *RC[-3]^4+ R5C8 *RC[-3]^3+ R6C8 *RC[-3]^2+ R7C8 *RC[-3]+ R8C8
в которой коэффициенты тренда зафиксированы и вместо «x» мы подставляем ссылку на номер текущего временного ряда (для первого значение 1, для второго 2 и т.д.)
Также «X» возводим в соответствующую степень (значок в Excel «^» означает возведение в степень)
=R2C8*RC[-3] ^6 +R3C8*RC[-3] ^5 +R4C8*RC[-3] ^4 +R5C8*RC[-3] ^3 +R6C8*RC[-3] ^2 +R7C8*RC[-3]+R8C8
Теперь протягиваем формулу до конца временного ряда и получаем рассчитанные значения полиномиального тренда для каждого периода.
2-й способ точнее, чем первый, т.к. коэффициенты тренда мы получаем без округления, а также этот расчет быстрее.
3-й способ расчета значений полиномиальных трендов — Forecast4AC PRO
Устанавливаем курсор в начало временного ряда
Заходим в настройки Forecast4AC PRO, выбираем «Прогноз с ростом и сезонностью», «Полином 6-й степени», нажимаем кнопку «Рассчитать».
Заходим в лист с пошаговым расчетом «ForPol6», находим строку «Сложившийся тренд»:
Копируем значения в наш лист.
Получаем значения полинома 6-й степени, рассчитанные 3 способами с помощью:
- Коэффициентов полиномиального тренда выведенных на график;
- Коэффициентов полинома рассчитанных с помощью функцию Excel =ЛИНЕЙН
- и с помощью Forecast4AC PRO одним нажатием клавиши, легко и быстро.
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel .
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Полином одной переменной
Полиномы нескольких переменных рассматриваются ☞ ЗДЕСЬ.
Будем обозначать через $ mathbb A_<> $ какое-либо из множеств $ mathbb Z,mathbb Q, mathbb R_<> $ или $ mathbb C_<> $.
Общая информация
Функция вида $$ f(x)=a_0x^n+a_1x^+dots+a_n = sum_^n a_jx^ $$ при $ n_<> in <0,1,dots >$ и $ ,dots,a_n>subset mathbb A $ относительно переменной $ x_<> $ называется полиномом 1) или многочленом от указанной переменной над множеством $ mathbb A_<> $. Число $ a_ $ называется коэффициентом 2) полинома (при $ (n-j)_<> $-й степени переменной), выражение $ a_x^ $ — членом (одночленом) полинома, $ a_ $ — свободным членом, $ x_<>^ $ — мономом.
Пример. Выражения
$$ x^<2>+2,x-679, x^<2>+sqrt<2>x-pi , <mathbf i>, x^<3>- 2,x +sqrt <3>$$ являются полиномами; а $$ x^<-2>+3, x +x^ <2>, x^, sum_^ <infty>x^/j_<> $$ полиномами не являются.
Если $ a_<0>ne 0 $, то член $ a_0x^ $ называется ведущим членом, а $ a_ <0>$ — старшим коэффициентом полинома. При этом число $ n_<> $ называется степенью полинома и обозначается 3) $ deg f_<>(x) $. Полином первой степени называется линейным полиномом. Полином, все коэффициенты которого, кроме, возможно, $ a_ $, равны нулю, называется константой 4) ; будем обозначать его const. Очевидно, что степень константы равна нулю; исключительным для этого утверждения является случай когда константа является нулем. Если все коэффициенты полинома равны нулю, то такой полином называется (тождественно) нулевым. В этом случае его степень не определяется.
На переменную $ x_<> $ мы пока не накладываем ни какого ограничения: она может принимать значения из любого указанного выше множества — не обязательно из того, которому принадлежат коэффициенты полинома. Обозначим область определения полинома через $ mathbb B_<> $.
Значением полинома при (или в точке) $ cin mathbb B_<> $ называется число $$ f(c) = a_0c^n+a_1c^+dots+a_n . $$
Два полинома $$ f(x)=a_0x^n+dots+a_n u g(x)=b_0x^m+dots+b_m $$ с коэффициентами из $ mathbb A $ называются (тождественно) равными: $$ f(x)equiv g(x) $$ если совпадают множества их членов; или, что то же, равны их степени и равны коэффициенты при одинаковых степенях переменной.
Это определение отличается от привычного определения равенства двух функций: две функции $ F_<>(x) $ и $ G(x)_<> $ называются равными на множестве $ mathbb B_<> $ если совпадают их значения при любом $ x in mathbb B_<> $. На самом деле, для случая полиномов эти два определения — алгебраическое и функциональное — эквивалентны.
Теорема. $ f_<>(x)equiv g(x) $ тогда и только тогда, когда $ f(c)=g(c)_<> $ для $ forall cin mathbb B_<> $.
Одним из следствий теоремы является тот факт, что для полинома совершенно не важен порядок следования его членов; в частности, наряду с записью полинома по убывающим степеням переменной, мы имеем право записывать его и по возрастающим: $ f_<>(x)= sum_^n a_x^ $. Форма полинома, в которой его разложение записывается по убывающим степеням переменной, называется его канонической формой. Кроме того, теорема дает нам право на операцию, называемую приведением подобных членов: $$ ax^+bx^j equiv (a+b)x^j, quad ax^jcdot bx^k=ab x^ .$$ Имея в виду этот факт, определим теперь две основные операции для полиномов: сложение и умножение.
Суммой двух полиномов $ f_<>(x) $ и $ g_<>(x) $ называется полином, составленный как сумма всех одночленов, входящих в состав $ f_<>(x) $ и $ g_<>(x) $: $$ f(x) + g(x) = (a_n+b_m) + (a_+b_)x+dots + left<begin (a_0+b_0)x^n & npu m=n, \ a_0x^n & npu m n. end right. $$
Теорема. $ deg (f+g_<>)le max (deg f, deg g) $.
Произведением двух полиномов $ f_<>(x) $ и $ g_<>(x) $ называется полином, составленный как сумма всевозможных попарных произведений членов первого полинома на члены второго: $$ begin f(x)g(x) &=& a_0b_0x^+(a_1b_0+a_0b_1)x^ +(a_2b_0+a_1b_1+a_0b_2)x^+ \ & &+dots + (a_0b_k+a_1b_+dots+a_kb_0)x^+ dots + a_nb_m . end $$ (В записи коэффициента при $ x^ $ мы полагаем $ a_= 0 $ при $ j>n_<> $ и $ b_ <ell>= 0 $ при $ ell>m_<> $).
Теорема. Если $ f_<>(x) notequiv 0 $ и $ g_<>(x) notequiv 0 $, то $ deg (fcdot g_<>)= deg f + deg g_<> $.
Фактическое выполнение операции перемножения полиномов возможно по схеме, напоминающей алгоритм умножения целых чисел «столбиком»: это позволяет сэкономить время на выписывание степеней переменной.
Пример. Перемножить полиномы
Решение. Представим полиномы наборами их коэффициентов, расположив один из них горизонтально, а второй — вертикально. Умножение полинома $ f_<>(x) $ на $ b_x^ $ сводится к умножению набора $ (a_<0>,dots,a_n) $ на $ b_ $; результат следующего умножения — на $ b_x^ $ — получается аналогичным образом, но записывается со сдвигом на одну позицию вправо. Получившиеся ряды суммируются по столбцам. $$ begin &1 & 0 & 1 & -2& 0 & 3 \ hline 2 & 2 & 0 & 2 & -4 & 0 & 6 \ -3& & -3 & 0 & -3 & 6 & 0 & -9 \ 4 & & & 4 & 0 & 4 & -8 & 0 & 12 \ 0 & & & \ -1 &&&&& -1 & 0 & -1 & 2 & 0 & -3 \ hline& 2 & -3 & 6 & -7 & 9 & -2 & -10 & 14 & 0 & -3 end $$ (В отличие от перемножения чисел здесь результаты сложения в столбиках не переносятся в следующий разряд.)
Ответ. $ 2,x^<9>-3,x^8+6,x^7-7,x^6+9,x^5-2,x^4-10,x^3+14,x^2 — 3 $.
Множество всех полиномов от переменной $ x_<> $ с коэффициентами из $ mathbb A_<> $ будем обозначать $ mathbb A_<> [x] $.
Способы более эффективного умножения полиномов излагаются ☞ ЗДЕСЬ
Схема Хорнера
Задача. Вычислить значение полинома в точке $ c $.
Схема вычисления, заложенная в самом определении, «стóит» $ 3n_<>-1 $ операции: $$ begin & &c^2=ctimes c, & dots, & c^n=c^times c , \ &a_ times c, & a_ times c^2, & dots, & a_0 times c^n ,\ a_n & +a_ times c & + a_ times c^2 & + dots & + a_0 times c^n, end $$ т.е. $ 2n_<>-1 $ операции умножения и $ n_<> $ операций сложения. Организуем теперь вычисления по-другому: $$ begin f(c)&=&a_n+a_c+a_c^2+dots +a_1c^+a_0c^n = \ &=&a_n+cleft(a_+a_c+ dots + a_0c^ right) = \ &= &a_n+cleft(a_+cleft(a_+dots + a_0c^ right) right) = \ &=& dots = \ &=&a_n+cleft(a_+cleft(a_+dots + c(a_1+ a_0c)dots right) right) . end $$ Начинаем вычислять с самой внутренней скобки: $$<mathfrak b>_1= a_1+ a_0c, <mathfrak b>_2= a_2+ <mathfrak b>_1 c,dots, <mathfrak b>_ = a_ +<mathfrak b>_c,, <mathfrak b>_ = a_ +<mathfrak b>_c=f(c) $$ Вычисление каждой величины $ <mathfrak b>_ $ «стоит» $ 2_<> $ операции — одного сложения и одного умножения (при условии, что предварительно вычислено $ <mathfrak b>_^<> $). Приведем компактную запись алгоритма: $$ <mathfrak b>_k = a_k + <mathfrak b>_c quad npu quad <mathfrak b>_0 = a_0 quad u quad kin <1,dots,n > . $$ «Стоимость» вычисления значения $ f_<>(c) $ по этой схеме Хорнера составляет $ 2n_<> $ операций. Налицо экономия по сравнению с прямым способом вычисления $ f_<>(c) $.
Вычисления удобно производить с помощью таблицы, стартовое состояние которой следующее: $$ begin & a_0 & a_1 & a_2 & dots & a_ & a_ & a_n \ hline c & a_0 end $$ Будем отсчитывать строки сверху вниз, начиная от горизонтальной черты, т.е. нулевой строкой будем считать строку из коэффициентов полинома. Вычисление значения $ <mathfrak b>_ <1>$ в первой строке производится по схеме: предыдущее число умножается на $ c_<> $ и складывается с верхним, т.е. $$ begin & a_0 & a_1 & a_2 & dots & a_ & a_ & a_n \ hline c & a_0 & underbrace_<<mathfrak b>_1> end $$ Далее вычисления идут по тому же правилу: $$ begin & a_0 & a_1 & a_2 & dots & a_ & a_ & a_n \ hline c & a_0 &<mathfrak b>_1&underbrace_1>_<<mathfrak b>_2> end $$ и т.д. Величина, получившаяся в последнем столбце, и будет искомым значением $ f_<>(c) $: $$ begin & a_0 & a_1 & a_2 & dots & a_ & a_ & a_n \ hline c & a_0 &<mathfrak b>_1&<mathfrak b>_2&dots &<mathfrak b>_ & <mathfrak b>_& underbrace_>_<<mathfrak b>_n=f(c)> end $$
Пример. Вычислить значение полинома $ x^<5>-3, x +1 $ в точке $ 2+ mathbf i_<> $.
Решение. $$ begin & 1 & 0 & 0 & 0 & -3 & 1 \ hline 2+ mathbf i & 1& 2+mathbf i &3+4 mathbf i &2+11 mathbf i & -10+24mathbf i& -43+38mathbf i end $$
Ответ. $ -43+38mathbf i_<> $.
Выясним теперь смысл коэффициентов $ <mathfrak b>_<1>,dots, <mathfrak b>_ $ первой строки схемы Хорнера.
Теорема. Пусть $ cin mathbb B_<> $ и $ mathbb Bsubset mathbb A_<> $. Полином $ f_<>(x)in mathbb A[x] $ допускает единственное представление в виде:
$$ f(x)equiv (x-c)q(x)+r npu r=constin mathbb A, q(x)in mathbb A[x], deg q = deg f — 1 . $$
Доказательство. Будем искать константу $ r_<> $ и полином $ q_<>(x) $ методом неопределенных коэффициентов: $ q(x)= q_<0>x^+q_1x^+ dots + q_ $. Подставим его в правую часть доказываемого тождества, приведем подобные и приравняем коэффициенты полученного полинома коэффициентам полинома $ f_<>(x) $. Получим линейные уравнения, из которых последовательно определяем $ q_<0>,q_1, dots, q_ $ : $$ begin x^n& a_0&=q_0, & \ x^& a_1&=q_1-q_0c &Rightarrow q_1=a_1+q_0c, \ x^& a_2&=q_2-q_1c &Rightarrow q_2=a_2+q_1c, \ vdots & & dots & \ x & a_&=q_-q_c &Rightarrow q_=a_+q_c,\ 1 & a_n&=qquad -q_c+r & Rightarrow r=a_n+q_c. end $$ Видим, что формулы, определяющие коэффициенты $ q_ $, полностью совпадают с формулами, определяющими элементы первой строки схемы Хорнера, т.е. $ q_0=<mathfrak b>_<0>,dots,q_=<mathfrak b>_ $. Но тогда $ r=a_n+q_c=a_+<mathfrak b>_c=<mathfrak b>_=f(c) $. ♦
Итак, имеем: $$q(x)=<mathfrak b>_0x^+dots+<mathfrak b>_, r=<mathfrak b>_ , $$ при этом все коэффициенты вычисляются по схеме Хорнера, а старший коэффициент полинома $ q_<>(x) $ совпадает со старшим коэффициентом $ f_<>(x) $. Так, для полинома приведенного выше примера имеет место тождество: $$x^5-3, x +1 equiv $$ $$ equiv (x-2-mathbf i)left(x^4+ (2+mathbf i)x^3+(3+4,mathbf i)x^2+ (2+11,mathbf i)x -10+24,mathbf i right) -43+38 mathbf i . $$
Корни
Если значение полинома $ f_<>(x) $ при $ x=cin mathbb B_<> $ равно нулю, то число $ c_<> $ называется корнем полинома $ f_<>(x) $. Иными словами, корень полинома $ f_<>(x) $ — это решение уравнения $ f_<>(x)=0 $, принадлежащее множеству $ mathbb B_<> $.
Уравнение $ f_<>=0 $, в левой части которого стоит полином одной или нескольких переменных, называется алгебраическим.
Задача. Выяснить количество корней полинома $ f_<>(x)in mathbb A[x] $, принадлежащих множеству $ mathbb B_<> $, и вычислить их.
Решить алгебраическое уравнение $ f_<>(x)=0 $ над множеством $ mathbb B $ означает найти все корни $ f_<>(x) $, принадлежащие $ mathbb B_<> $.
На основании теоремы из предыдущего пункта имеет место следующая
Теорема [Безу]. Пусть $ mathbb B subset mathbb A_<> $ и $ cin mathbb B_<> $ — корень полинома $ f_<>(x), deg fge 1 $. Тогда полином $ f_<>(x)in mathbb A [x] $ допускает представление в виде произведения:
$$ f(x)equiv (x-c)f_1(x) , $$ где полином $ f_<1>(x)in mathbb A [x], deg f_1 = deg f — 1 $ определяется единственным образом.
Итак, теорема Безу утверждает, что в случае существования корня полинома, возможно разложение этого полинома в произведение двух полиномов — одного первой степени и одного полинома степени, на единицу меньшей исходного. Тем самым, задача о нахождении корней полинома $ f_<>(x) $ сведется к аналогичной задаче для полинома $ f_<1>(x) $; вторая задача может оказаться более простой за счет понижения степени.
Фактическое нахождение полинома $ f_<1>(x) $ возможно произвести с помощью схемы Хорнера.
Пример. Решить уравнение
$$ x^<3>+3 mathbf i, x^2-3(1+2 mathbf i)x+10-5 mathbf i =0 $$ над множеством $ mathbb C_<> $, если известно, что число $ (-1-2 mathbf i)_<> $ — одно из его решений.
Решение. Строим схему Хорнера: $$ begin & 1& 3mathbf i & -3(1+2 mathbf i) & 10-5 mathbf i \ hline -1-2 mathbf i & 1& -1+ mathbf i & -5 mathbf i & 0 end $$ Видим, что число $ (-1-2 mathbf i)_<> $ действительно является корнем полинома, и, следовательно, последний раскладывается в произведение двух полиномов: линейного и квадратичного. Коэффициенты квадратичного полинома выбираются из той же схемы: $$ (x+1+2 mathbf i )(x^2 + (-1+ mathbf i )x- 5 mathbf i) . $$ Квадратное уравнение над $ mathbb C_<> $ можно решить (см. ☞ ЗДЕСЬ ), его корни: $ (-1-2 mathbf i)_<> $ и $ 2+mathbf i_<> $.
Ответ. $ (-1-2 mathbf i), 2+ mathbf i_<> $.
Если полином $ f_<>(x) $ раскладывается в произведение $ f_<>(x)equiv (x-c)f_1(x) $, то полином $ (x-c) $ называется линейным множителем для $ f_<>(x) $ над множеством $ mathbb B_<> $.
Для того, чтобы $ (x-c)_<> $ был линейным множителем для $ f_<>(x) $ необходимо и достаточно чтобы число $ c_<> $ было корнем $ f_<>(x) $.
Примеры показывают, что не для всякого полинома и множества $ mathbb B_<> $ корни существуют. Очевидно не имеет корней полином нулевой степени (константа, отличная от нуля); любой полином первой степени над $ mathbb A_<> $ имеет единственный корень, принадлежащий $ mathbb A_<> $. Квадратный полином $ x^<2>+1 $ не имеет вещественных корней, но имеет мнимые.
Основная теорема высшей алгебры
Теорема. Любой полином с комплексными коэффициентами, степень которого больше нуля, имеет хотя бы один корень, в общем случае, комплексный.
Эта теорема гарантирует существование корня $ lambda_<1>in mathbb C $. На основании теоремы Безу, можно утверждать, что $ f_<>(x) $ допускает представление $$ f(x)equiv (x-lambda_1)f_1(x) quad npu quad f_1(x)in mathbb C [x], deg f_1(x)=deg f(x) -1 .$$ Если $ deg f_<1>(x) ge 1 $, то, по той же теореме, полином $ f_<1>(x) $ также должен обладать корнем, который мы обозначим 5) $ lambda_ <2>$; теорема Безу гарантирует тогда представление $$ f(x)equiv (x-lambda_1)(x-lambda_2)f_2(x) quad npu quad f_2(x)in mathbb C [x], deg f_2(x)=deg f(x) -2 .$$ Продолжая процесс далее, мы за $ n_<> $ шагов придем к представлению $$ f(x)equiv (x-lambda_1)(x-lambda_2)times dots times (x-lambda_n)f_n(x) quad npu quad f_n(x)in mathbb C[x], deg f_n(x)=0 ,$$ т.е. полином $ f_(x)^<> $ представляет собой константу. На основании условия тождественного равенства полиномов утверждаем, что $ f_(x) equiv a_0 $. Таким образом приходим к следующей альтернативной версии основной теоремы высшей алгебры.
Теорема. Для произвольного полинома $ f_<>(x) $ степени $ n_<>ge 1 $ существует его представление в виде произведения линейных множителей
$$ f(x)equiv a_0(x-lambda_1)(x-lambda_2)times dots times (x-lambda_n) ; $$ это представление единственно с точностью до перестановки сомножителей.
Как уже отмечалось в доказательстве теоремы, в этом представлении могут встречаться одинаковые линейные сомножители. Собрав их вместе, получим иной вид этого представления $$ f(x)equiv a_0(x-lambda_1)^<<mathfrak m>_<1>>times dots times (x-lambda_<mathfrak r>)^<<mathfrak m>_<<mathfrak r>>> , npu <mathfrak m>_<1>+<mathfrak m>_<2>+dots+<mathfrak m>_<mathfrak r>=n $$ и все числа $ lambda_<1>,dots,lambda_ <mathfrak r>$ теперь различны. Эта формула называется формулой разложения полинома $ f_<>(x) $ на линейные сомножители или линейным представлением полинома $ f_<>(x) $; при этом число $ <mathfrak m>_^<>in mathbb N $ называется кратностью линейного сомножителя $ x-lambda_ $ или кратностью корня $ lambda_ $ в полиноме $ f_<>(x) $. Корень $ lambda_ $ называется простым, если $ <mathfrak m>_=1_<> $ и кратным кратности $ <mathfrak m>_^<> $ если $ <mathfrak m>_>1_<> $ (двойным или двукратным, если $ <mathfrak m>_=2_<> $, тройным или трехкратным если $ <mathfrak m>_=3_<> $ и т.д.)
Пример. Найти линейное представление полинома $ f(x)=x^<6>-2, x^3+1 $.
Решение. Линейное представление легко получить если сначала заметить, что $ f(x)equiv (x^3-1)^ <2>$, а затем использовать выражения для корней кубических из единицы: $$f(x)equiv (x-1)^2 left(x- frac<-1+ mathbf i sqrt<3>> <2>right)^2 left(x- frac<-1 — mathbf i sqrt<3>> <2>right)^2 . $$ Все корни полинома имеют вторую кратность. ♦
Выведение условия наличия кратного корня (в терминах коэффициентов полинома) ☞ ЗДЕСЬ. При известном корне, нахождение его кратности ☞ ЗДЕСЬ.
Теорема. Два полинома, степени которых не превосходят $ n_<> $, равны тождественно если они имеют равные значения более чем при $ n_<> $ различных значениях переменной.
Доказательство необходимости очевидно. Если полиномы $ f_<>(x) $ и $ g_<>(x) $ удовлетворяют условию теоремы, то полином $ f(x)-g_<>(x) $ должен иметь более, чем $ n_<> $ корней, что, ввиду основной теоремы высшей алгебры, возможно лишь если он тождественно нулевой. ♦
Теорема утверждает, что полином $ f_<>(x) $ степени, $ le n_<> $, однозначно определяется своими значениями при более чем $ n_<> $ различных значениях переменной. Можно ли эти значения задавать произвольно? Оказывается задание $ (n+1)_<> $-й пары $ (x_<1>,y_1),dots,(x_,y_) $ при всех различных $ x_<1>,dots,x_ $ позволяет однозначно определить полином $ f_<>(x) $ такой, что $ f(x_<1>)=y_1,dots,f(x_)=y_ $ и $ deg f_<> le n $. Практические способы решения этой задачи обсуждаются в разделе ☟
Интерполяция
Корни и коэффициенты полинома
Симметрические функции корней
Разложение полинома $ f_<>(x) $ на линейные множители дает интересные соотношения между корнями полинома и его коэффициентами. Сначала выведем их для малых степеней. Для $ n_<>=2 $: $$a_0x^2+a_1x+a_2equiv a_0(x-lambda_1)(x-lambda_2)equiv a_0x^2-a_0(lambda_1+lambda_2)x+a_0lambda_1lambda_2 Rightarrow $$ $$ Rightarrow left< begin lambda_1+lambda_2&=&-a_1/a_0, \ lambda_1lambda_2&=&a_2/a_0, end right. $$ т.е. получили формулы известные из школьного курса алгебры. Далее, для $ n_<>=3 $: $$a_0x^3+a_1x^2+a_2x+a_3equiv a_0(x-lambda_1)(x-lambda_2)(x-lambda_3)equiv $$ $$equiv a_0x^3-a_0(lambda_1+lambda_2+lambda_3)x^2+a_0(lambda_1lambda_2 + lambda_1lambda_3+lambda_2lambda_3)x-a_0lambda_1lambda_2lambda_3 Rightarrow $$ $$ Rightarrow left< begin lambda_1+lambda_2+lambda_3&=&-a_1/a_0, \ lambda_1lambda_2+lambda_1lambda_3+lambda_2lambda_3&=&a_2/a_0,\ lambda_1lambda_2lambda_3&=&-a_3/a_0. end right. $$
Теорема. Для корней $ lambda_<1>,dots,lambda_n $ полинома
$$ f(x)=a_<0>x^n+a_1x^+dots+a_n,, a_0ne 0 $$ справедливы формулы Виета $$ sum_ <1 le jle n>lambda_j = lambda_1+ dots+ lambda_n= -frac, $$ $$ sum_<1le j_1 ☞ ЗДЕСЬ.
Биографические заметки о Виете ☞ ЗДЕСЬ
Пример. Найти все корни полинома $ 3,x^3-16,x^2+23,x-6 $, если известно, что произведение двух из них равно $ 1_<> $.
Решение. Имеем: $$ left< begin lambda_1+lambda_2+lambda_3&=&16/3, \ lambda_1lambda_2+lambda_1lambda_3+lambda_2lambda_3 &=&23/3,\ lambda_1lambda_2lambda_3&=&6/3=2. end right. $$ Вдобавок к этим уравнениям, мы должны записать дополнительное условие: $$lambda_1 lambda_2=1 .$$ Из третьего уравнения системы получаем тогда $ lambda_3=2 $. Подставив его в два оставшихся, придем к двум идентичным: $$lambda_1 + lambda_2=10/3 .$$ Теперь для нахождения неизвестных $ lambda_ <1>$ и $ lambda_ <2>$ можем воспользоваться формулами Виета «в обратном порядке», составив квадратный полином, имеющий их корнями: $$t^2-10/3,t+1 .$$
Ответ. $ 2,,3,, 1/3 $.
Можно ли использовать формулы Виета для решения уравнения ?
Ответ ☞ ЗДЕСЬ.
Обдумаем еще раз результаты основной теоремы высшей алгебры и формул Виета. С одной стороны, задав коэффициенты $ a_<0>,a_1,dots,a_n $ мы однозначно определяем набор из $ n_<> $ комплексных чисел $ lambda_<1>,dots,lambda_n $ — корней этого полинома. С другой стороны, задав произвольным образом набор корней $ lambda_<1>,dots,lambda_n $, по формулам Виета однозначно определим величины $ a_1/a_0,dots,a_n/a_0 $. Для простоты, рассмотрим подмножество полиномов степени $ n_<> $, имеющих старший коэффициент равным $ 1_<> $. Получаем тогда взаимно-однозначное соответствие: $$ (a_1,dots,a_n) leftrightarrow (lambda_1,dots,lambda_n) . $$ Итак, каждый корень $ lambda_ $ полинома является какой-то функцией его коэффициентов $ a_1,dots,a_ $, т.е. формально говоря, функцией от многих переменных. Относительно этой функции мы пока ничего сказать не можем; более того, как мы узнаем НИЖЕ, для степеней полинома бóльших $ 4_<> $ не существует «хороших» общих формул, выражающих корни полинома через его коэффициенты. Несмотря на это, формулы Виета подтверждают, что некоторые комбинации этих неизвестных нам функций оказываются равными коэффициентам полинома. Какова основная отличительная особенность этих комбинаций?
Функция $ Phi(x_1,dots,x_n) $ называется симметрической функцией своих переменных, если ее значение не меняется ни при какой перестановке этих переменных: $$Phi(x_1,dots,x_n) equiv Phi(x_,dots,x_) $$ при всех различных $ j_1,dots, j_n in <1,dots,n>$.
Пример. Функции
$$ sqrt <1+x_1x_2x_3>, frac+frac+frac $$ являются симметрическими функциями переменных $ x_1,x_2,x_3 $, а функция $$ x_1^2x_2x_3+x_1x_2^2x_3 $$ симметрической функцией не является, поскольку ее значения меняются при перестанове $ (x_1,x_2,x_3) leftrightarrow (x_3,x_2,x_1) $.
В левых частях формул Виета как раз и стоят симметрические полиномы относительно $ lambda_<1>,dots,lambda_n $. Оказывается результат теоремы допускает следующее обобщение.
Теорема [Гаусс]. Значение любого симметрического полинома $ Phi(x_1,dots,x_n) $ на корнях $ lambda_1,dots,lambda_n $ полинома $ x^n+a_1x^+ dots+a_n $ является полиномиальной функцией от $ a_<1>,dots,a_n $: $$ Phi(lambda_1,dots,lambda_n) equiv <mathfrak F>(a_1,dots,a_n) . $$
Пример. Пусть $ lambda_ <1>$ и $ lambda_ <2>$ означают корни полинома $ x^2+a_1x+a_2 $. Выразить
$$lambda_1^2+lambda_2^2-3,lambda_1^2lambda_2-3,lambda_1lambda_2^2$$ через коэффициенты полинома.
Решение. Поскольку выражения для корней квадратного уравнения нам известны: $$ lambda_1= frac<-a_1+sqrt> <2>quad u quad lambda_2= frac<-a_1-sqrt> <2> , $$ то непосредственной подстановкой их в заданный полином, получаем $$ a_1^2-2,a_2+3,a_1a_2 . $$ ♦
Пример. Пусть $ lambda_1,, lambda_2,, lambda_3 $ означают корни полинома $ x^3+a_1x^2+a_2x+a_3 $. Выразить
$$lambda_1^2lambda_2+lambda_1^2lambda_3+lambda_1lambda_2^2+ lambda_1lambda_3^2+lambda_2^2lambda_3+lambda_2lambda_3^2 -lambda_1^2-lambda_2^2-lambda_3^2 $$ через коэффициенты полинома.
Решение. Выделим в требуемом выражении комбинации корней, стоящие в левых частях формул Виета. Первые $ 6_<> $ слагаемых можно представить в виде $$(lambda_1lambda_2+lambda_1lambda_3+lambda_2lambda_3) (lambda_1+lambda_2+lambda_3)-3lambda_1lambda_2lambda_3 , $$ а $$lambda_1^2+lambda_2^2+lambda_3^2= left(lambda_1+lambda_2+lambda_3 right)^2-2, (lambda_1lambda_2+ lambda_1lambda_3+lambda_2lambda_3) .$$ Далее применяем формулы Виета.
Ответ. $ 3,a_3-a_1a_2-a_1^2+2, a_2 $.
Существуют общие алгоритмы нахождения полинома $ <mathfrak F>$ по заданному полиному $ Phi $: см. [3], [4]. Однако в своей практике я встречал необходимость в подобном представлении лишь для некоторых классов полиномов $ Phi_<> $; сейчас их и рассмотрим.
Суммы Ньютона
Для полинома $ f(x)=a_<0>x^n+a_1x^+dots+a_n, (a_0ne 0) $ его $ k_<> $-й суммой Ньютона называется сумма $ k_<> $-х степеней его корней: $$ s_k=lambda_1^k + dots + lambda_n^k . $$ При этом обычно считают $ k_<> in <mathbb N>$ (хотя формально можно определить суммы Ньютона и для отрицательных индексов $ k_<> $ при условии $ a_ ne 0 $). Для однообразия полагают также $ s_<0>=n $.
Теорема. Суммы Ньютона выражаются рационально через коэффициенты полинома $ f_<>(x) $ посредством следующих рекуррентных формул Ньютона:
Пример.
$$ s_2=(a_1^2-2, a_0a_2) big/ a_0^2 , $$ $$ s_3=-(a_1s_2+a_2s_1+3,a_3)big/ a_0= $$ $$ =-left(a_1 (a_1^2-2, a_0a_2) big/ a_0^2 +a_2 (-a_1 big/ a_0)+3,a_3 right) big/ a_0= $$ $$ =left(-a_1^3+3,a_0a_1a_2-3,a_0^2a_3 right) big/ a_0^3 . $$ ♦
Подробнее о суммах Ньютона ☞ ЗДЕСЬ.
Результант и дискриминант
Пусть $ g(x)=b_0x^m+dots + b_ $ — произвольный полином из $ mathbb A_<> [x] $. Тогда выражение $$ g(lambda_1) times dots times g(lambda_n) $$ является симметрическим полиномом от корней $ lambda_<1>,dots,lambda_n $ полинома $ f_<>(x) $. По теореме Гаусса, оно должно рационально выражаться через коэффициенты $ a_<0>,dots,a_n $. С другой стороны, очевидно, это выражение обращается в нуль тогда и только тогда, когда хотя бы один сомножитель обратится в нуль, т.е. будет существовать общий корень полиномов $ f_<>(x) $ и $ g_<>(x) $. Выражение $$ a_0^m prod_^n g(lambda_j) $$ называется результантом полиномов $ f_<>(x) $ и $ g_<>(x) $.
Способы вычисления результанта, его свойства и применения ☞ ЗДЕСЬ.
В частном случае, когда $ g_<>(x) $ совпадает с производной полинома $ f_<>(x) $ результант переходит в дискриминант — выражение отличающееся от $$ a_0^ prod_^n f^<prime>(lambda_j) $$ только сомножителем $ (-1)^/a_0 $ и обращающееся в нуль тогда и только тогда, когда $ f^<prime>(x) $ имеет общий корень с $ f_<>(x) $. Как мы увидим НИЖЕ, последнее условие оказывается необходимым и достаточным наличия у полинома $ f_<>(x) $ кратного корня.
Пример. Для $ f(x)=a_<0>x^2+a_1x+a_2 $ указанное произведение оказывается равным
$$ (2a_0lambda_1 +a_1)(2a_0lambda_2 +a_1)=(4a_0^2lambda_1 lambda_2+2a_0a_1(lambda_1 +lambda_2)+a_1^2)= $$ $$ =left(4a_0^2 frac-2a_0a_1frac+a_1^2right)=4a_0a_2-a_1^2, $$ т.е. привычному «школьному» понятию.
Способы вычисления дискриминанта, его свойства и применения ☞ ЗДЕСЬ.
Преобразования корней
Если $ lambda_<1>,dots,lambda_n $ — корни полинома $ f(x)=a_0x^n+a_1x^+dots+a_ $, то
1. корнями полинома $$ f(-x)=(-1)^nleft(a_0x^n-a_1x^+dots+(-1)^na_nright) = $$ $$ =(-1)^n sum_^n (-1)^ja_jx^ $$ являются $ -lambda_1, dots, -lambda_n $;
2. корнями полинома $$f(x- <coloralpha >)=a_0(x- <coloralpha > )^n+a_1(x- <coloralpha >)^+dots+a_n= $$ $$ = sum_^n a_j(x- <coloralpha >)^ $$ являются $ <coloralpha >+lambda_1, dots, <coloralpha >+lambda_n $;
3. при дополнительном условии, что $ a_ ne 0 $, корнями полинома $$f^<ast>(x)= x^nfleft(1/x right) equiv a_0+a_1x+dots+a_nx^n = $$ $$ =sum_^n a_jx^ $$ являются $ 1/<lambda_1>, dots, 1/ <lambda_n>$.
Преобразования 1-3 часто используются как при выводе теоретических результатов так и в практике вычислений.
Поясним идею этих применений. Корни исходного и корни преобразованного полинома остаются неизвестными. Допустим, мы получили какой-то результат, касающийся оценки положительных корней полинома $ f_<>(x) in mathbb R[x] $, и хотим распространить эту оценку и на отрицательные корни (см., к примеру, ☟ НИЖЕ ). Производится замена переменной $ x rightarrow — x $, которая меняет знаки всех корней: отрицательные становятся положительными, и к новому полиному применяется полученный результат. В приложениях возникают и более сложные преобразования корней: когда, к примеру, все их надо «загнать» в ограниченную область комплексной плоскости — скажем, в круг $ |x|le 1 $ (см. ☟ НИЖЕ ).
Пример. Построить полином $ F_<>(x) $, корни которого равны квадратам корней полинома $ f_<>(x) $.
Непрерывность корней
Теорема [5]. Корни полинома
$$ f(x)=x^n+a_1x^+dots+a_n in mathbb C[x],quad nge 1 $$ являются непрерывными функциями его коэффициентов. Строго говоря, если $ lambda_1,dots,lambda_ $ — корни этого полинома, а $ <tilde lambda_1>,dots, <tilde lambda_n>$ — корни полинома $$<tilde f>(x)=x^n+<tilde a>_1x^+dots+<tilde a>_n in mathbb C[x] , $$ то эти корни можно перенумеровать таким образом, чтобы $$ |lambda_j-<tilde lambda>_j| | | | | | . При увеличении значений $ <coloralpha >_<> $ от $ -2 $ до $ -1_<> $ происходит «дрейф» корней — плавный, но разный по скорости. К примеру, синий и фиолетовый корни меняются очень медленно, а вот зеленый и малиновый быстро сближаются пока не столкнутся при значении $ <coloralpha >=-1 $: $$ lambda_1approx -1.5096-0.4133 <mathbf i>, lambda_2 approx -0.6768+0.1479 <mathbf i>, lambda_3 approx 0.4364-0.4845 <mathbf i>, lambda_4 = 1+ <mathbf i>, $$ $$ lambda_5 =1+ <mathbf i> . $$ Что происходит при дальнейшем увеличении $ <coloralpha >_<> $? Число корней должно остаться инвариантным — по основной теореме высшей алгебры оно продолжает совпадать со степенью полинома, т.е. корни не аннигилируют. Поэтому столкнувшиеся корни порождают два новых — голубой и коричневый — которые начинают расходиться. При $ <coloralpha >=1 $ ситуация следующая: $$ lambda_1 approx -2.3350+0.4836 <mathbf i>, lambda_2 approx -0.5794+0.1185<mathbf i>, lambda_3 approx 0.2721-0.4926 <mathbf i>, $$ $$ lambda_4 approx -0.3888+2.5945 <mathbf i>, lambda_5 approx 0.5832+0.3480 <mathbf i>. $$ Имея перед глазами полную картину истории, понимаем, что корни, обозначенные $ lambda_ <1>$ (красный) и $ lambda_ <4>$ (голубой), стремятся к столкновению — и оно действительно происходит при $ <coloralpha >=2 $: $$ lambda_1 = -2+2<mathbf i>, lambda_2 approx -0.5458+0.1142 <mathbf i>, lambda_3 approx 0.2296-0.4712 <mathbf i>, lambda_4 = -2+2<mathbf i>, $$ $$ lambda_5 approx 0.5193+0.3101 <mathbf i>. $$ Дальнейшую динамику можем предсказать «по прецеденту» — столкнувшиеся корни должны разойтись. При $ <coloralpha >=3_<> $: $$ lambda_1 approx -4.0682+3.6140 <mathbf i>, lambda_2 approx -0.5184+0.1116 <mathbf i>, lambda_3 approx 0.2007-0.4506<mathbf i>, $$ $$ lambda_4 approx -1.2359+1.2927<mathbf i>, lambda_5 approx 0.4759+0.2864 <mathbf i>. $$ ♦
К какому числу стремится желтый корень при $ <coloralpha > to +infty $ ?
Последний пример наводит на еще одну гипотезу: мы видим, что графики корней получились гладкими, за исключением, возможно, некоторых специфических точек.
Теорема. Корни полинома
$$ f(x)=x^n+a_1x^+dots+a_n in mathbb C[x] $$ являются непрерывно дифференцируемыми функциями коэффициентов за исключением тех наборов значений коэффициентов, которые определяют кратные корни.
Доказательство ☞ ЗДЕСЬ.
Условие наличия кратного корня у полинома $ f_<>(x) $ может быть получено в виде явного условия на его коэффициенты. См. ☞ ДИСКРИМИНАНТ.
Поиск корней алгебраических уравнений: решение в радикалах
Можно ли выразить корни полинома $ f(x)in mathbb C[x] $ в виде «хороших» функций от его коэффициентов? Вспомним, что для квадратного уравнения существует общая формула вычисления корней: $$x^2+ax+b=0 Rightarrow lambda_<1,2>=frac<-apm sqrt> <2> . $$ Эта формула включает в себя элементарные алгебраические операции $ +,- ,times, div $ и операцию извлечения квадратного корня. По аналогии можно сформулировать и общую задачу.
Задача. Найти выражения корней полинома степени $ n_<>>2 $ в виде функций его коэффициентов; при этом функции должны представлять конечную комбинацию элементарных алгебраических операций и операций извлечения корней произвольных (целых) степеней.
Поставленная задача называется задачей о разрешимости уравнения в радикалах 6) .
Оказывается, что любое уравнение третьей или четвертой степени разрешимо в радикалах. Перед тем, как изложить способы их решения, сделаем два упрощения. Первое из них заключается в том, что уравнение $ f_<>(x)=0 $ делится на старший коэффициент полинома $ f_<>(x) $.
Полином называется нормализованным 7) , если его старший коэффициент равен $ 1_<> $. Операция деления полинома на его старший коэффициент называется нормализацией полинома.
Очевидно, что нормализованный полином имеет те же корни, и в тех же кратностях, что и исходный. Для простоты обозначений, будем считать, что полином уже нормализован: $$ f(x)=x^n+a_1x^+dots+a_n .$$
Второе упрощение заключается в замене переменной (подстановке): $ x=y+ <coloralpha > $. Ее результатом будет новый полином той же степени, что и исходный, относительно переменной $ y_<> $: $$ F(y)equiv f(y+ <coloralpha >) , . $$ Корни нового полинома связаны (cм. преобразование 2 ☞ ЗДЕСЬ ) с корнями старого по формуле $ lambda_j = Lambda_j+ <coloralpha > $; так что, найдя корни одного полинома, легко установим и корни другого. Подберем теперь параметр $ <coloralpha > $ так, чтобы обратить в нуль коэффициент при $ y^ $ в полиноме $ F_<>(y) $. Используя формулу бинома Ньютона, получаем $$ begin f(x)&=&x^n+a_1x^+a_2x^+dots+a_n= \ &=&(y+ <coloralpha >)^n +a_1(y+ <coloralpha >)^+a_2(y+ <coloralpha >)^+dots+a_n = \ &=&y^n + C_n^1 <coloralpha > y^ +C_n^2 <coloralpha >^2 y^+dots+ <coloralpha >^n + \ & & qquad + a_1y^+a_1 C_^1 <coloralpha > y^+dots +a_1 <coloralpha >^ + \ & & quad qquad qquad +a_2y^ + dots + a_n. end $$ Понятно, что если положить $ <coloralpha >= — a_1/n $, то коэффициент при $ y^ $ исчезнет. Для простоты обозначений, будем считать, что полином уже предварительно подвергнут такому преобразованию: $$ f(x)=x^n qquad +a_2x^+dots+a_n .$$
Уравнение третьей степени
Рассмотрим уравнение третьей степени: $$ x^3+p,x+q=0 $$ Сделаем в этом уравнении замену переменной: $ x=u+v $, введя две неизвестные $ u_<> $ и $ v_<> $; получим: $$ u^3+v^3+3,uv(u+v)+p(u+v)+q=0 . $$ Сгруппируем: $$ u^3+v^3+(3,uv+p)(u+v)+q=0 . $$ Подчиним теперь неизвестные $ u_<> $ и $ v_<> $ условию $$ 3,uv+p=0 iff uv=-frac
<3> . $$ Тогда предыдущее уравнение приведется к виду $$u^3+v^3=-q . $$ Итак, для определения неизвестных величин $ u_<> $ и $ v_<> $ мы получили систему уравнений $$ u^3+v^3=-q, uv=-frac
<3>. $$ Возведя последнее уравнение в куб, получим $$ u^3v^3=-frac <27> . $$ Два полученных равенства, связывающие $ u^3 $ и $ v^3 $, позволяет утверждать, что эти величины являются решениями квадратного уравнения: $$t^2+q,t- frac<27>=0 .$$
Выражение $$ Delta = frac<4>+frac <27>$$ называется дискриминантом кубического уравнения.
Решив квадратное уравнение, получим: $$ u^3=-frac<2>+ sqrt<Delta>, v^3=-frac
<2>- sqrt <Delta> . $$ В итоге имеем формулу для решений уравнения: $$ x=u+v=sqrt[3]<-frac
<2>+sqrt<frac<4>+frac<27>>>+ sqrt[3]<-frac
<2>-sqrt<frac<4>+frac<27>>> ; $$ она называется формулой Кардано.
Формула Кардано не очень удобна для практических вычислений. Вспомним, что корень кубический из комплексного числа может принимать три различных значения. Решение же, представленное формулой Кардано, имеет в правой части комбинацию из двух кубических корней. Таким образом, получаем 9 всевозможных комбинаций из значений корней кубических. С другой стороны, основная теорема высшей алгебры утверждает, что кубическое уравнение должно иметь только три решения. Для того, чтобы установить соответствие между значениями $ u_<> $ и $ v_<> $, обратимся к условию $ uv=-p/3 $ . Согласно этому условию, задание значений для $ u_<> $ позволит однозначно восстановить $ v_<> $. Пусть $$ u_1=sqrt[3]<-frac<2>+sqrt<frac<4>+frac<27>>> $$ какое-то одно из трех возможных значений корня кубического. Два оставшихся значения корня кубического получаются домножением $ u_1 $ на корни кубические из единицы: $$u_2=u_1varepsilon_1, u_3=u_1varepsilon_2 $$ при $$varepsilon_1=cos frac<2pi> <3>+ <mathbf i>sin frac<2pi><3>= frac<-1><2>+ <mathbf i>frac<sqrt<3>> <2> u varepsilon_2=cos frac<4pi> <3>+ <mathbf i>sin frac<4pi><3>= frac<-1><2>- <mathbf i>frac< sqrt<3>> < 2> . $$ Если теперь взять $$ v_1=-frac
<3u_1> , $$ то решения кубического уравнения можно выразить в виде комбинаций $ u_1 $ и $ v_1 $: $$ begin lambda_1&=&u_1+v_1, \ lambda_2&=&u_2+v_2=u_2-frac<displaystyle p><displaystyle 3u_2>=u_1varepsilon_1-frac<displaystyle p> <displaystyle 3u_1varepsilon_1>=u_1varepsilon_1-frac<displaystyle pvarepsilon_2><displaystyle 3u_1>=u_1varepsilon_1+v_1varepsilon_2,\ lambda_3&=&u_3+v_3=u_1varepsilon_2+v_1varepsilon_1 . end $$ Окончательно получаем формулы для вычисления корней: $$ left< begin lambda_1&=&u_1+v_1, \ lambda_2&=&-frac<scriptstyle 1><scriptstyle 2>(u_1+v_1) + <mathbf i>frac<scriptstyle sqrt<3>> <scriptstyle 2>(u_1-v_1),\ lambda_3&=&-frac<scriptstyle 1><scriptstyle 2>(u_1+v_1) — <mathbf i>frac<scriptstyle sqrt<3>> <scriptstyle 2>(u_1-v_1), end right. $$ где $ u_1 $ — одно из значений корня кубического, а $ v_1 $ связано с ним соотношением $ v_1=-p/(3u_1) $.
Пример [2]. Решить уравнение $ x^3-6<mathbf i>,x^2-10,x+8 <mathbf i>=0 $.
Решение. Подстановка $ x=y+2 <mathbf i>$ приводит уравнение к виду $$y^3+2,y+4 <mathbf i>=0 , $$ т.е. $ p=2,,q=4 <mathbf i>$. Далее $$Delta=-frac<100> <27> Rightarrow sqrt <Delta>= pm frac<10 <mathbf i>><3sqrt<3>> Rightarrow u_1=sqrt[3]<left(-2 + frac<10><3sqrt<3>> right)<mathbf i>> . $$ Одно из значений последнего корня: $$u_1=-<mathbf i>, sqrt[3]<-2 + frac<10><3sqrt<3>>> , $$ это выражение можно упростить, если повезет заметить, что подкоренное выражение равно $ left(-1+1/<sqrt<3>>right)^3 $: $$u_1=<mathbf i>left(1-frac<1><sqrt<3>>right) Rightarrow v_1=-frac
<3u_1>= <mathbf i>left(1+frac<1><sqrt<3>>right) . $$ Получаем: $$mu_1=2, <mathbf i>, mu_2=1- <mathbf i>, mu_3=-1- <mathbf i> .$$ Значения корней исходного уравнения получатся «сдвигом» на $ 2 <mathbf i>$.
Дальнейший анализ формулы Кардано ☞ ЗДЕСЬ
Уравнение четвертой степени
$ x^4+a_1x^3+a_2x^2+a_3x+a_4 = 0 $ также может быть решено в радикалах. Идея решения заключается в сведении задачи к решению некоторого кубического уравнения. Ее реализация ☞ ЗДЕСЬ.
Уравнения высших степеней
Успех в решении уравнений третьей и четвертой степени побудил исследователей искать подобные формулы для уравнений высших степеней. Методология подхода была очевидна: свести решение уравнения $ n $-й степени к решению уравнения $ (n-1) $-й степени. Однако, несмотря на почти трехвековые усилия лучших математиков, решить уравнение пятой степени не удавалось. Наконец, в начале XIX века был получен отрицательный результат.
Теорема [Руффини, Абель]. Уравнение степени выше четвертой в общем случае неразрешимо в радикалах.
Пример. Уравнение $ x^5-4, x -2=0 $ не разрешимо в радикалах.
Установить разрешимо или нет данное конкретное уравнение в радикалах возможно с помощью теории, развитой французским математиком Галуа.
Пример. Уравнение $ x^5+x+1=0 $ разрешимо в радикалах, поскольку
Отрицательный характер результата теоремы Руффини-Абеля не должен слишком уж разочаровывать. Он означает только лишь то, что корни полинома нельзя представить в виде формулы, состоящей из конечного набора сравнительно простых функций. Тем не менее, если расширить класс допустимых в формуле функций (или допустить бесконечность числа операций), представление для корня можно найти (см., к примеру, ☞ ЗДЕСЬ ). Наконец, для практических задач часто более важна не столько «красивая» аналитическая формула для корня, сколько приближенное его значение с требуемой точностью.
Поиск корней алгебраических уравнений: возможность упрощений
Для некоторых классов уравнений удается упростить задачу: свести решение исходного уравнения к решению уравнения меньшей степени 
Возвратное уравнение
Так называется уравнение вида $ a_0z^n+a_1z^+dots+a_z+a_n=0, a_0ne 0 $, у которого набор коэффициентов $ (a_0,a_1,dots, a_,a_n) $ симметричен относительно середины: $$ a_0=a_,a_1=a_,dots, a_=a_ dots $$
Пример. Уравнения
$$ z^2-3,z+1=0,quad -sqrt<2>z^5+2,z^4+mathbf i z^3+2,z-sqrt<2>,quad z^n+1=0 , $$ $$ z^n+z^+z^+dots + z^2 +z+1=0 $$ являются возвратными.
Методы упрощения подобных уравнений ☞ ЗДЕСЬ.
Делимость полиномов
Здесь $ mathbb A_<> $ означает какое-то из множеств $ mathbb Q, mathbb R $ или $ mathbb C_<> $.
Теорема. Для полиномов $ f_<>(x) $ и $ g(x)not equiv 0 $ из $ mathbb A[x] $ существует единственная пара полиномов $ q_<>(x) $ и $ r_<>(x) $ из $ mathbb A[x] $ таких, что
$$ f(x) equiv g(x) q(x) + r(x) quad mbox < и >quad deg r ☞ ЗДЕСЬ.
В этом представлении полином $ f_<>(x) $ называется делимым, $ g_<>(x) $ — делителем, $ r_<>(x) $ — остатком от деления $ f_<>(x) $ на $ g_<>(x) $, а $ q_<>(x) $ — частным 9) . При $ r(x) equiv 0 $, говорят, что полином $ f_<>(x) $ делится (нацело) на $ g_<>(x) $, а полином $ g_<>(x) $ называется делителем $ f_<>(x) $. Тривиальными делителями полинома $ f_<>(x) $ называют сам полином $ f_<>(x) $ и полином тождественно равный $ 1_<> $ (оба — с точностью до домножения на ненулевую константу). Любой другой делитель полинома (если существует) называется нетривиальным.
Пример [1]. Найти частное и остаток от деления
$$f(x)=2, x^5 +x^4 -x^2 +2, x +1 quad mbox < на >quad g(x)=x^3+2, x^2 — x -1 .$$
Ответ. $ q(x)=2, x^2 -3, x + 8, r(x)=-18, x^2 + 7, x +9 $.
Фактическое выполнение операции деления полиномов можно производить, действуя лишь над наборами их коэффициентов — подобно тому, как мы производили их умножение.
Пример. Найти частное и остаток от деления
$$f(x)=x^8+x^7+3,x^4-1 quad mbox < на >quad g(x)=x^4-3, x^3 +4, x +1 .$$
Решение. $$ begin 1& 1 &0&0&3&0 &0 & 0&-1 &&1 -3 0 4 1\ 1&-3 &0&4&1& & & & && overline < 1 4 12 32 82>\ hline &4 & 0 &-4 & 2 & 0 & <> \ &4 &-12& 0 & 16 & 4& <> \ hline && 12& -4 &-14 & -4 & 0 & <> \ && 12& -36 & 0 & 48 & 12 & <> \ hline &&& 32 & -14& -52&-12 & 0 & <> \ &&& 32 & -96& 0 & 128& 32 & <> \ hline &&&&82&-52&-140&-32&-1 \ &&&&82&-246&0&328&82 \ hline &&&&&194&-140&-360&-83 end $$
Ответ. $ q(x)=x^4+4,x^3+12,x^2+32, x+82,, r(x)=194, x^3-140, x^2-360, x -83 $.
Свойства.
1. Если $ m le n $ при $ a_0ne 0, b_0 ne 0 $, то $ deg q(x) =n-m $ и ведущий член $ q_<>(x) $ равен $ /, x^ $.
2. Если $ g(x)equiv x-c $, то коэффициенты частного $ q_<>(x) $ найдутся из схемы Хорнера.
Наибольший общий делитель
Рассмотрим множество всех общих делителей полиномов $ f_<>(x) $ и $ g_<>(x) $: $$ mathbb D= d_1(x), g(x) mbox < делится на > d_1(x) > . $$ Наибольшим общим делителем полиномов $ f_<>(x) $ и $ g_<>(x) $ называется полином $ d_<>(x) $, который является делителем как $ f_<>(x) $, так и $ g_<>(x) $ и, вместе с тем, сам делится на любой другой общий делитель этих полиномов: $$ operatorname (f(x),g(x)) = d(x) iff d(x) in mathbb D , d(x) mbox< делится на > forall d_1(x) in mathbb D . $$ Рассмотрим множество всех полиномов, которые делятся и на $ f_<>(x) $ и на $ g_<>(x) $: $$ mathbb K= f(x), k_1(x) mbox < делится на > g(x) > . $$ Наименьшим общим кратным полиномов $ f_<>(x) $ и $ g_<>(x) $ называется полином $ k_<>(x) $, который делится как на $ f_<>(x) $, так и на $ g_<>(x) $ и, вместе с тем, сам является делителем любого другого полинома, который делится на $ f_<>(x) $ и $ g_<>(x) $: $$ operatorname (f(x),g(x)) = k(x) iff k(x) in mathbb K , forall k_1(x) in mathbb K mbox< делится на > k(x) . $$ Пока открытым является вопрос существования $ operatorname (f,g)_<> $ и $ operatorname (f,g)_<> $. Для первого случая этот вопрос решается конструктивно — построением $ operatorname (f,g)_<> $ с помощью алгоритма, позаимствованного из ☞ ТЕОРИИ ЧИСЕЛ.
Пусть $ f(x) not equiv 0 $ и $ g(x) not equiv 0 $ — полиномы из $ mathbb A_<>[x] $ . Поделим $ f_<>(x) $ на $ g_<>(x) $: $ f(x)=g(x)q_<1>(x)+r_1(x) $, пусть остаток $ r_<1>(x) not equiv 0 $, тогда $ 0 le deg r_<1>(x)
Теорема. Последний не равный нулю остаток в алгоритме Евклида совпадает с $ operatorname(f(x),g_<>(x)) $.
Доказательство полностью аналогично доказательству соответствующего результата из теории целых чисел. ♦
Пример. Вычислить
$$ operatorname left( x^4+3, x^3 -x^2 -4, x -3, , 3, x^3 +10, x^2 +2, x -3 right) , . $$
Решение. $$ begin x^4 &+3,x^3 &-x^2 &-4,x &-3 && 3,x^3+10,x^2+2,x-3\ x^4&+10/3, x^3&+2/3, x^2&-, x & && overline < 1/3 x -1/9 quad >\ hline &-1/3,x^3&- 5/3,x^2&-3,x&-3 \ &-1/3,x^3&-10/9,x^2& -2/9,x&<> +1/3 \ hline &&-5/9,,x^2& -25/9,x&-10/3 end $$ В обозначениях алгоритма Евклида, имеем: $$ q_<1>(x)=1/3, x -1/9, r_<1>(x)=-5/9, x^2 -25/9, x-10/3 . $$ Поскольку $ r_<1>(x) notequiv 0 $, делим $ g_<>(x) $ на этот остаток: $$ begin 3,x^3 &+10,x^2 &+2,x &-3 && -5/9,,x^2 -25/9,x-10/3 \ 3, x^3&+15, x^2&+18, x & &&, overline <-27/5, x +9 quad >\ hline &-5,x^2&-16,x&-3 \ &-5,x^2&-25,x&-30 \ hline &&9,x&+27 end $$ Здесь $ q_<2>(x)=-27/5, x +9, r_2(x)=9x+27 notequiv 0 $ и алгоритм деления продолжается: $$ begin -5/9,,x^2& -25/9,x& -10/3 && 9,x+27 \ -5/9,,x^2& -5/3,x& && , overline < -5/81, x — 10/81 quad >\ hline &-10/9,x& -10/3 \ &-10/9,x&-10/3 \ hline & & 0 end $$ Здесь остаток получился равным нулю, следовательно $ r_<2>(x)=operatorname(f(x),g(x)) $.
Ответ. $ 9(x+3)_<> $.
Еще один способ нахождения $ operatorname $ для полиномов из $ mathbb[x] $ вытекает из основной теоремы высшей алгебры.
Теорема. Пусть множество $ < (x-lambda_1),dots,(x-lambda_<mathfrak r>) > $ представляет собой объединение множеств линейных сомножителей полиномов $ f_1(x),dots,f_k(x) $. Выпишем «универсальное» разложение каждого $ f_j $ на линейные сомножители:
Пример. Вычислить $ operatorname left(x^2-1,, x^3+1 right) $ .
Решение. Выписываем разложения полиномов на линейные сомножители: $$x^2-1equiv (x-1)(x+1), quad x^3+1 equiv(x+1) left(x-left( 1/2 — sqrt<3>/2 mathbf right) right) left(x- left( 1/2 + sqrt<3>/2 mathbf right) right) .$$
Ответ. $ x+1 $.
Теорема. Существуют полиномы $ u(x)_<> $ и $ v(x)_<> $ из $ mathbb A[x] $, удовлетворяющие уравнению линейного представления $ operatorname $:
Доказательство этого результата и практический способ построения полиномов $ u(x)_<> $ и $ v(x)_<> $ можно скопировать из соответствующего раздела теории чисел.
Явное представление $ operatorname (f(x),g(x)) $ через коэффициенты полиномов с помощью аппарата определителей приведено ☞ ЗДЕСЬ.
Взаимно простые полиномы
— это полиномы, у которых нормализованный $ operatorname $ равен $ 1_<> $ (тождественно). Подробное рассмотрение этого случая ☞ ЗДЕСЬ.
Производные от полинома
Для случая произвольной функции $ F(x): mathbb R mapsto mathbb R $ это определение строится на предельном переходе: $$ frac bigg|_<_> = F^<prime>(c) = lim_ frac .$$ Пусть $ F(x)equiv x^k $ при $ kin mathbb N_<> $. Тогда, с помощью формулы бинома Ньютона получаем: $$(c+h)^k-c^k=kc^h+C_k^2c^h^2+dots+h^k $$ и $$frac to kc^ quad npu hto 0 . $$ Отсюда следует, что функция $ x^ $ дифференцируема в любой точке $ xinmathbb R_<> $ и ее производная равна $ kx^ $. Обобщим это определение и на комплексную плоскость $ mathbb C^<> $ . Всюду в предыдущих рассуждениях допустим, что и точка $ c_<> $ и приращение $ h_<> $ могут быть комплексными. Окончательный вывод не изменится: формула $$(x^k)^<prime>= kx^ $$ остается справедливой и для $ xin mathbb C_<> $. С помощью этой формулы, а также с помощью основных правил дифференцирования функций: $$ left(F_1pm F_2 right)^<prime>=F_1^<prime>pm F_2^<prime>, left(cFright)^<prime>=cF^<prime>, left(F_1F_2 right)^<prime>=F_1^<prime>F_2+F_1F_2^ <prime>$$ получаем $$ f^<prime>(x)=(a_0x^n+a_1x^+dots+a_x+a_n)^ <prime>= na_0x^+(n-1)a_1x^+dots +a_ . $$ Таким образом, $ f^<prime>(x) $ также будет полиномом над $ mathbb A_<> $ и $ deg f^ <prime>= deg f — 1 $. Кроме того, обобщая по индукции формулу дифференцирования произведения, выводим: $$ left(f_1f_2times dots times f_k right)^<prime>= f_1^<prime>f_2times dots times f_k+f_1f_2^<prime>times dots times f_k+ dots+ f_1f_2times dots times f_k^ <prime>. $$ Если применить ее к формуле разложения полинома на линейные множители, то получим формулу $$ begin f^<prime>(x)&=&a_0(x-lambda_2)(x-lambda_3)times dots times (x-lambda_n)+ \ &+&a_0(x-lambda_1)(x-lambda_3)times dots times (x-lambda_n)+ \ &+ & dots + \ &+& a_0(x-lambda_1)(x-lambda_2)times dots times (x-lambda_). end $$ Из нее, в частности, следует, что $$ f^<prime>(lambda_j)=a_0(lambda_j-lambda_1)times dots times (lambda_j-lambda_)(lambda_j-lambda_) times dots times (lambda_j-lambda_)= a_0 prod_ <1le k le n atop scriptstyle kne j>(lambda_j — lambda_k) . $$ Последняя формула, впрочем, может быть получена и напрямую из определения производной: $$ f^<prime>(lambda_j)=lim_ frac =lim_ frac . $$ Производные высших порядков вводятся определением $$F^<(k)>(x)= left(F^<(k-1)>(x) right)^ <prime> npu k>1 ; $$ для однотипности обозначений считают также нулевой производной сам полином: $$F^<(0)>(x)= F(x) .$$ В дальнейшем нам пригодится следующая формула Лейбница: $$left(F_1 F_2 right)^<(k)>=sum_^k C_k^j F_1^<(k-j)>F_2^ <(j)>=F_1^<(k)>F_2+ C_k^1F_1^<(k-1)>F_2^ <prime>+ C_k^2F_1^<(k-2)>F_2^<prime prime >+ dots +F_1F_2^ <(k)> , $$ где $ C_k^ $ означает биномиальный коэффициент.
Для полинома $ f(x)_<> $ степени $ n_<> $ имеем: $$f^<(k)>(x)=n(n-1)times dots times (n-k+1)a_0x^+dots+k!a_ npu kle n $$ и $ deg f^ <(k)>= deg f — k $. Очевидно $ f^<(k)>(x)equiv 0 $ при $ k> n_<> $.
Теорема. Простой корень полинома не является корнем его производной. Кратный корень полинома кратности $ mathfrak m $ является корнем его производной кратности $ (<mathfrak m>-1) $.
Доказательство. Если $ x=lambda_<> in mathbb C $ — простой корень для $ f_<>(x) $, то $ f(x)equiv (x-lambda)tilde(x) $ при $ tilde(lambda) ne 0 $. Дифференцируя и подставляя $ x=lambda $, получаем $$ f^<prime>(x)equiv tilde(x) +(x-lambda)tilde^<prime>(x) Rightarrow f^<prime>(lambda)=tilde(lambda)ne 0 $$ по предположению.
Если $ x=lambda_<> $ — кратный корень кратности $ mathfrak m $ для $ f_<>(x) $, то $ f(x)equiv (x-lambda)^<mathfrak m>widehat(x) $ при $ widehat(lambda) ne 0 $. Снова дифференцируем: $$ f^<prime>(x)=<mathfrak m>(x-lambda)^<<mathfrak m>-1> widehat(x)+ (x-lambda)^<<mathfrak m>>widehat^<prime>(x)= (x-lambda)^<<mathfrak m>-1> underbrace<left(<mathfrak m>widehat(x) +(x-lambda)widehat^<prime>(x) right)>_ <= H(x)> . $$ Из этого представления следует, что $ x=lambda_<> $ является корнем $ f^<prime>(x) $ кратности, не меньшей $ (<mathfrak m>-1) $. Если бы кратность была больше этого значения, то необходимо $ H(lambda)=0 $. Однако, этого не может быть, т.к. $ widehat(lambda) ne 0 $. ♦
Полином $ f(x)_<> $ имеет кратный корень тогда и только тогда, когда он имеет нетривиальный наибольший общий делитель со своей производной $$ operatorname (f(x),f^<prime>(x)) notequiv const . $$
Пример. При каком условии на коэффициенты $ p_<> $ и $ q_<> $ полином
$$ x^3+p,x+q $$ имеет кратный корень?
Решение. На основании теоремы на этом корне $ x=lambda_<> $ должно быть выполнено $$lambda^3+p,lambda+q=0 , quad 3, lambda^2 + p=0 .$$ Из второго равенства выражаем $ lambda^2 $ и подставляем в первое: $$lambda^2=-frac
<3> Rightarrow lambda left(-frac
<3>right) +p,lambda+q=0 Rightarrow lambda=-frac<3,q> <2,p>$$ при $ pne 0 $. Подставляя это значение в любое из исходных равенств, получаем: $$ frac<27,q^2+4,p^3> <4, p^2>=0 Rightarrow left(frac <2>right)^2 + left(frac
<3>right)^3 =0 . $$ Это условие уже встречалось нам ВЫШЕ при анализе формулы решения уравнения третьей степени. При $ p=0 $ кратный корень может встретиться лишь при $ q=0 $, т.е. опять же при обращении в нуль дискриминанта кубического уравнения.
Ответ. $ left( p/3 right)^3 + left( q/2 right)^2=0 $.
При каком условии на коэффициенты $ p_<> $ и $ q_<> $ полином
а) $ x^4+p,x+q $ ; б) $ x^5+p,x+q $
имеет кратный корень?
Пример. Найти все значения параметра $ <coloralpha > $, при которых полином
$$ x^4-5,x^2+ <coloralpha >,x+28 $$ имеет кратный корень.
Решение. На основании следствия к теореме для выполнения условия необходимо и достаточно, чтобы был нетривиален $ operatorname (f(x),f^<prime>(x)) $. Ищем его по алгоритму Евклида, делим $ f(x) $ на $ f^<prime>(x) $: $$ f(x)equiv frac<1> <4>, x, f^<prime>(x) + overbrace<left(-frac<5><2>, x^2 +frac<3><4>, <coloralpha >, x +28 right)>^ , $$ затем $ f^<prime>(x) $ на полученный остаток $ r_<1>(x) $: $$ f^<prime>(x) equiv left(-frac<8><5>,x- frac<12><25>, <coloralpha > right) r_1(x) + overbrace<left(frac<3><25>,(3, <coloralpha >^2 + 290),x+ frac<361><25>, <coloralpha > right)>^ , $$ и, при дополнительном предположении $ 3, <coloralpha >^2 + 290ne 0 $, делим $ r_<1>(x) $ на $ r_<2>(x) $: $$ r_1(x) equiv frac<25> <36left(3, <coloralpha >^2 +290 right)^2> left[-30,left(3, <coloralpha >^2 +290 right) x + alpha, (27, <coloralpha >^2 + 6220) right] r_2(x) + $$ $$ + frac <25, left(-27, <coloralpha >^4 -19660, <coloralpha >^2 + 3390912right) > <36, left(3, <coloralpha >^2 +290 right)^2> . $$ $ operatorname (f(x),f^<prime>(x)) $ может быть нетривиальным (равным $ r_<2>(x) $) только при условии $$-27, <coloralpha >^4 -19660, <coloralpha >^2 + 3390912=0 . $$ Решить последнее уравнение легко если заменить переменную $ A = <coloralpha >^2 $: $$( A-144)(27, A +23548)=0 .$$
При $ 3, <coloralpha >^2 + 290= 0 $ будет $ operatorname (f(x),f^<prime>(x))= r_2(x)not equiv 0 $, так что при этих значениях параметра кратных корней у $ f(x)_<> $ быть не может.
Число $ lambda_<> $ является корнем кратности $ mathfrak m_<> $ для $ f(x)_<> $ тогда и только тогда, когда выполнены условия:
Доказательство необходимости следует из теоремы. Достаточность вытекает из результатов следующего пункта (формализация способа проверки приводится ☞ ЗДЕСЬ).
Формула Тейлора
Представление полинома $ f(x)_<>in mathbb A[x] $ в канонической форме $ a_<0>x^n+a_1x^+dots + a_n $ не является единственно возможным способом задания полинома. В конце концов, полином можно представить и с помощью разложения на линейные сомножители — разумеется, если известен набор его корней. Саму эту каноническую форму можно описать как разложение полинома по степеням переменной $ x_<> $. Пусть теперь $ cin mathbb A_<> $ — произвольная константа. Любую степень $ x^ $ можно «переразложить» по степеням линейного полинома $ x-c_<> $ с помощью формулы бинома Ньютона: $$ x^kequiv left[c+(x-c) right]^kequiv c^k +kc^(x-c)+ frac<2>c^(x-c)^2+dots+ (x-c)^k .$$ Если это сделать для каждого монома полинома $ f(x)_<> $, то получим разложение $ f(x)_<> $ по степеням $ x-c_<> $ в виде $$ f(x)equiv A_0+A_1(x-c)+A_2(x-c)^2+dots+A_n(x-c)^n . $$
Задача. Найти коэффициенты $ A_<0>,dots,A_n $ в этом разложении.
Для решения этой задачи продифференцируем несколько раз последнее тождество: $$ begin f^<prime>(x)&=&A_1+2,A_2(x-c)+3,A_3(x-c)^2+dots+nA_n(x-c)^ , ,\ f^<prime prime>(x)&=&2,A_2+3cdot 2,A_3(x-c)+dots +n(n-1)A_n(x-c)^, ,\ f^<prime prime prime>(x)&=&3cdot 2,A_3+dots +n(n-1)(n-2)A_n(x-c)^, ,\ dots & & dots end $$ Подстановка в эти формулы $ x=c_<> $ дает: $$f^<prime>(c)=A_1, f^<prime prime>(c)=2,A_2, f^<prime prime prime>(c)= 3cdot 2,A_3,dots $$
Теорема. Разложение полинома $ f_<>(x) $ по степеням $ x-c_<> $ имеет вид
$$ f(x) equiv f(c)+ frac(c)> <1!>(x-c) + frac(c)> <2!>(x-c)^2+ dots + frac(c)> (x-c)^ = $$ $$ =sum_^n frac(c)> (x-c)^ ; $$ это тождество называется формулой Тейлора для полинома $ f_<>(x) $ в точке $ x=c $.
Доказательство и алгоритм эффективного вычисления коэффициентов формулы Тейлора (схема Хорнера) ☞ ЗДЕСЬ.
На основании этих серий мы должны предсказать величину $ F(x)_<> $. Самой простой функцией, решающей задачи в таких постановках, является полином. Если этот полином $ f(x)_<> $ удается построить, то именно его мы и будем считать приближением неизвестной нам функции $ F(x)_<> $. Задача построения такого полинома для серии экспериментов первого типа обсуждается ☞ ЗДЕСЬ. А формула Тейлора позволяет найти полином $ f(x)_<> $ для серии экспериментов второго типа. Геометрически: неизвестный нам заранее график функции $ y=F(x)_<> $ (красный) приближается (аппроксимируется) либо прямой (зеленый), либо параболой (серый), либо кубикой (фиолетовый) — и все кривые приближения строятся только на основании информации о функции $ F(x)_<> $ в одной-единственной точке $ c_<> $.
Пример. Найти приближенное значение $ F(1)_<> $, если известно, что
Решение. По формуле Тейлора получаем полином $$f(x)=0.367+0.367(x+1) + frac<0.367> <2>(x+1)^2+frac<0.367> <6>(x+1)^3 $$ и $ f(1)=2.324(3) $.
Ответ. $ F(1)approx 2.324 $.
Полиномы с вещественными коэффициентами
Рассмотрим теперь случай полинома с вещественными коэффициентами $ f(x)=a_0x^n+a_1x^+ dots + a_n in mathbb R [x] $.
Теорема. Значения полинома $ f(x) in mathbb R [x] $ от комплексно-сопряженных значений переменной будут также комплексно-сопряженными:
$$ mbox <если> f(c)=A+mathbf i B mbox <при> subset mathbb R, mbox <то> f(overline)=A-mathbf i B , . $$
Доказательство. Действительно, поскольку $ a_jin mathbb R $, то $ overline=a_j $ для $ forall jin <0,1,dots,n>$, и тогда $$ begin fleft(overline right)&=&a_0 overline^n + a_1 overline^ + dots + a_n = overline overline + overline overline>+ dots + overline= \ &=&overline+ dots + a_n>=A-mathbf i B . end $$
Если мнимое число $ c=alpha + mathbf i beta , beta ne 0 $ является корнем $ f_<>(x) $, то и ему комплексно-сопряженное $ overline c = alpha — mathbf i beta $ также является корнем $ f_<>(x) $.
Иными словами, мнимые корни полинома $ f_<>(x) $ с вещественными коэффициентами «ходят пáрами»: $ alpha pm mathbf i beta $. Геометрический смысл: на комплексной плоскости точки, изображающие корни $ f_<>(x) $, расположены симметрично относительно вещественной оси.
Как следствие предыдущей теоремы и основной теоремы высшей алгебры, получим
Теорема. Любой полином $ f_<>(x)in mathbb R [x] $ может быть представлен в виде произведения вещественных полиномов степеней не выше второй:
$$ begin f(x) & equiv a_0 (x- lambda_1)^<<mathfrak m>_1> times dots times (x- lambda_r)^<<mathfrak m>_r> times \ & times (x^2 +p_1x+ q_1)^<<mathfrak M>_1> times dots times (x^2 +p_<ell>x+ q_<ell>)^<<mathfrak M>_<ell>> . end $$ Здесь $ lambda_1 , dots , lambda_r $ — различные вещественные числа, а квадратные трехчлены $$ x+ q_<ell>> subset mathbb R [x] $$ — различные с отрицательными дискриминантами $ mathcal D_j=p_j^2-4q_j
Полином $ f_<>(x) $ с вещественными коэффициентами нечетной степени имеет хотя бы один вещественный корень, а, в общем случае, нечетное число вещественных корней (с учетом их кратностей ).
Геометрия
Полиномы с вещественными коэффициентами удобны тем, что теоретические результаты, полученные в предыдущих пунктах, получают геометрическую интерпретацию. Прежде всего, следует отметить, что полином является частным случаем непрерывной функции и на него распространяются все результаты математического анализа, разработанные для подобных функций. Итак, полином $ f_<>(x) $ — непрерывная функция при любых $ x in mathbb R $. Более того, поскольку производные полинома снова оказываются полиномами, то свойство непрерывности наследуется при дифференцировании: полином является непрерывно-дифференцируемой функцией. Из этого следует, что на плоскости $ (x_<>,y) $ график полинома $ y=f_<>(x) $ представляет из себя непрерывную и гладкую кривую (ни разрывов, ни углов!) — касательная к графику существует в любой его точке.
Далее, вещественному корню $ x=lambda_<> $ полинома $ f_<>(x) $ на плоскости $ (x_<>,y) $ соответствует точка пересечения графика $ y=f_<>(x) $ с осью абсцисс.
По основной теореме высшей алгебры, таких точек может быть только конечное число: их — не более степени полинома $ deg f (x) $. Далее, между каждой парой $ lambda_j, lambda_k $ вещественных корней полинома $ f_<>(x) $, его график обязан иметь «впадину» или «горб». Обращаясь к языку математического анализа, можно сказать (и доказать), что между двумя вещественными корнями полинома находится точка его локального минимума или локального максимума. В этой точке касательная к графику функции параллельна оси абсцисс и, следовательно, тангенс угла наклона касательной должен быть равен нулю. Иными словами, точки $ mu_1,mu_2,dots $, в которых полином имеет локальный минимум или максимум, должны быть корнями его производной. См. следующий ПУНКТ.
К сожалению, не имеется наглядной интерпретации мнимых корней полинома .
Дальнейшие геометрические свойства полинома с вещественными коэффициентами см. ☞ ЗДЕСЬ.
Экстремумы
Говорят, что полином $ f(x)in mathbb R[x] $ имеет в точке $ c_<> $ (локальный) минимум если существует некоторое $ delta>0 $, что при всех значениях аргументов из $ delta_<> $-окрестности точки $ c_<> $, т.е. при всех $ x_<> $, удовлетворяющих неравенству $ |x-c| f(c) $. Если последнее неравенство изменить на противоположное, то получим определение (локального) максимума. Говорят, что полином имеет в точке $ c_<> $ (локальный) экстремум 10) если он имеет в этой точке либо максимум либо минимум.
Теорема [Ферма для полиномов]. Если полином $ f_<>(x) $ имеет в точке $ c_<> $ экстремум, то в этой точке его производная обращается в нуль: $$ f'(c)=0 . $$
Геометрический смысл этого результата пояснен в предыдущем пункте. Обращение производной полинома в нуль в точке $ c_<> $ является условием необходимым для существования в ней экстремума. Для выяснения будет ли в этой точке минимум, максимум или же экстремум отсутствует, следует обратиться к формуле Тейлора. Рассмотрим эту формулу в точке $ c_<> $ «подозрительной на экстремум», т.е. в такой, где $ f'(c)=0 $: $$ f(x)-f(c)=frac<1><2>f»(c)(x-c)^2+frac<1><6>f»'(c)(x-c)^3+dots+frac<1>f^<(n)>(c)(x-c)^n . $$ Если $ f»(c)ne 0 $, то можем переписать эту разность в виде $$ f(x)-f(c)=(x-c)^2underbrace<left[frac<1><2>f»(c)+frac<1><6>f»'(c)(x-c)+dots+frac<1>f^<(n)>(c)(x-c)^right]>_ . $$ Полином $ P(x) $ в точке $ c_<> $ имеет значение $ frac<1><2>f»(c) $, и его знак в некоторой окрестности точки $ c_<> $ полностью определяется знаком этого числа. Таким образом, в той же окрестности имеем: $$ operatorname (f(x)-f(c)) = operatorname (f»(c)) . $$
Если в точке $ c_<> $ выполнены условия $ f'(c)=0, f»(c)> 0 $ то в этой точке полином имеет локальный минимум; если же в ней выполнены условия $ f'(c)=0, f»(c) c \ — operatorname f»'(c) quad npu x нечетном $ k_<> $. При этом в точке $ c_<> $ полином будет иметь локальный минимум при $ f^<(k+1)>(c)>0 $ и локальный максимум при $ f^<(k+1)>(c) ☞ ЗДЕСЬ ), поэтому оценить корни полинома $ f'(x) $ мы можем, разве что, приближенно. После их нахождения, приближеные значения подставляются в полином $ f_<>(x) $ и ошибка вычислений накапливается… Можно ли избежать этого накопления? — Частично, да. Для полинома $ f_<>(x) $ (четной) степени $ n_<> $ можно построить новый полином степени $ n-1 $ по новой переменной $ z_<> $: $$ mathcal F(z) = (z-f(mu_1))times dots times(z-f(mu_)) , $$ где $ mu_1,dots,mu_ $ — корни $ f'(x) $. При этом коэффициенты нового полинома $ mathcal F(z) $ будут рационально выражаться через коэффициенты полинома $ f'(x) $ на основании теоремы Гаусса о симметрических полиномах. Подробности конструктивного построения см. ☞ ЗДЕСЬ. Как правило, максимальный вещественный корень полинома $ mathcal F(z) $ и будет давать значение $ max f(x) $.
Пример. Найти $ displaystyle max_ (-x^6+12,x^2+12,x+2) $.
Решение. Если идти по традиционной схеме математического анализа, то мы должны сначала найти корни производной полинома $ f(x)=-x^6+12,x^2+12,x+2 $, т.е. решить уравнение $ x^5-4,x-2=0 $. В радикалах это уравнение не решается, так что приходится применять приближенные методы поиска вещественных корней: $ mu_1approx -1.24359, mu_2 approx — 0.50849, mu_3 approx 1.51851 $. Наконец, требуется сравнить по величине $ f(mu_1), f(mu_2), f(mu_3) $.
В альтернативу этому подходу, можно избежать нахождения корней производной и построить (хоть и кропотливо, но зато безошибочно) полином $$ mathcal F(z)= -z^5+10,z^4+472,z^3+16208,z^2-16272,z-32800 , $$ найти один его (максимальный вещественный) корень $ approx 35.6321 $ — он и будет искомым максимумом.
Проверка: $ max f = f(mu_3) approx 35.6321 $.
Подчеркнем, что указанная возможность гарантирована только полиномиальностью рассматриваемой экстремальной задачи и на произвольные (неполиномиальные) функции предлагаемый метод не распространяется.
Приводимость
Полином $ Phi(x) in mathbb A[x] $, отличный от константы, называется неприводимым в (или неприводимым над) $ mathbb A_<> $ если у $ Phi(x) $ нет нетривиального делителя в $ mathbb A[x] $. В противном случае $ Phi(x) $ называется приводимым в (или приводимым над) $ mathbb A_<> $. Полином $ Phi(x) in mathbb A[x] $ неприводим над $ mathbb A_<> $ тогда и только тогда, когда $ operatorname (Phi(x),g(x)) equiv const in mathbb A_<> $ для любого полинома $ g(x)in mathbb A_<>[x], deg g(x) ♦
Теорема. Любой полином $ f(x)in mathbb R [x] $ степени большей $ 2_<> $ приводим в $ mathbb R_<> $. Неприводимыми в $ mathbb R_<> $ являются полиномы вида
$$ x+a quad mbox <и>quad x^2+p, x +q_<> quad mbox <при>quad subset mathbb R, p^2 — 4q ☞ ЗДЕСЬ .
Рассмотрим теперь полином с рациональными коэффициентами: $$f(x)=a_0x^n+a_1x^+dots+a_n in mathbb Q [x] , a_0 ne 0 . $$ Если полином $ f_<>(x) $ приводим в $ mathbb Q_<> $, то будет приводимым и полином $ Ccdot f_<>(x) $ при $ forall C in mathbb Q, C ne 0 $; верно и обратное. Представив коэффициенты $ a_<0>,dots, a_n $ в виде несократимых дробей, возьмем $$ C=operatorname(mbox< знаменатель > a_<0>,dots, mbox< знаменатель > a_n ) , $$ тогда приводимость (или неприводимость) полинома $ f_<>(x) $ в $ mathbb Q_<> $ эквивалентна приводимости (соответственно, неприводимости) в $ mathbb Q_<> $ полинома $ Ccdot f(x) $ с целыми коэффициентами. Поэтому в дальнейшем будем сразу предполагать $ f(x)in mathbb Z[x] $. Можно ли пойти дальше и утверждать, что приводимость такого полинома в $ mathbb Q_<> $ эквивалентна приводимости его в $ mathbb Z_<> $, т.е. полином раскладывается на произведение полиномов меньших степеней с рациональными коэффициентами тогда и только тогда, когда он раскладывается на произведение полиномов меньших степеней с целыми коэффициентами?
Теорема. Полином $ f(x)in mathbb Z[x] $ неприводимый в $ mathbb Z_<> $ будет неприводимым и в $ mathbb Q_<> $.
Приводимость полинома с целыми коэффициентами $ f(x)in mathbb Z[x] $ в $ mathbb Z_<> $ означает, что он раскладывается на два множителя с целыми коэффициентами: $$ a_0x^n+a_1x^+ dots + a_n equiv (b_0x^k+b_1x^ + dots + b_k) (c_0x^<ell>+c_1x^ <ell-1>+ dots + c_<ell>) $$ при $ k ☞ ЗДЕСЬ . ♦
Итак, для поиска рациональных корней полинома $ f_<>(x) $ надо выписать множество всех натуральных делителей $ <<mathfrak p>_1=1,dots,<mathfrak p>_> $ числа $ |a_n| $, и множество всех натуральных делителей $ <<mathfrak q>_1=1,dots,<mathfrak q>_> $ числа $ |a_0| $, и после этого организовать вычисление $ fleft(pm <mathfrak p>_j/<mathfrak q>_i right) $ при всех возможных значениях индексов $ jin <1,dots,s >, i in <1,dots, t >$. Если ни одно из полученных чисел не равно нулю, то рациональных корней полином не имеет.
Если нормализованный полином $ f(x) in mathbb Z[x] $ имеет рациональные корни, то они — только целые и находятся среди делителей свободного члена.
Пример. Найти рациональные корни полинома
Подробнее о приводимости и неприводимости полиномов в $ mathbb Z_<> $ ☞ ЗДЕСЬ.
Локализация корней
Границы расположения корней
Теорема [Маклорен]. 11) Все корни полинома
$$f(x)=a_0x^n+a_1x^+dots+a_n in mathbb C [x], a_0 ne 0$$ удовлетворяют неравенству $$ |lambda_j| 0$$ удовлетворяют неравенству $$ lambda_j положительные корни.
А как получить нижнюю оценку возможных отрицательных корней?
Это можно сделать с помощью преобразования 1 полинома, рассмотренного ☞ ЗДЕСЬ. В самом деле, отрицательные корни полинома $ f(x) $ являются положительными корнями полинома $ f(-x) $. Найдя верхнюю границу последних с помощью любого из приведенных выше критериев, мы меняем у нее знак и в результате получаем нижнюю оценку отрицательных корней $ f(x) $. Преобразование 3 , рассмотренное в том же пункте, позволяет получить отдельные интервалы для возможных положительных и отрицательных корней.
Пример. Найти оценки положительных и отрицательных корней полинома
$$ f(x)=x^8+2, x^7-2, x^6 +6, x^5 -80, x^4 + 100, x^3 -400, x^2 + 15, x +30 . $$
Решение. Сначала ограничим положительные корни сверху. В теореме Лагранжа имеем $ r=2,, A=400 $, следовательно $ lambda_j -401 $. Формируем полином $$ f^<ast>(x) = x^8f(1/x)= 1+2, x-2, x^2 +6, x^3 -80, x^4 + 100, x^5 -400, x^6 + 15, x^7 +30,x^8 $$ для оценки нижней границы положительных корней: $$1/lambda_j frac<1><1 +sqrt<40/3>> . $$ Наконец, оценка Лагранжа для полинома $ f^<ast>(-x) $: $$-1/lambda_j 12) .
Теорема [Декарт]. Число положительных корней полинома
$$f(x)=a_0x^n+a_1x^+dots+a_x+a_n in mathbb R[x], quad (a_0> 0,a_n ne 0)$$ с учетом их кратностей равно или меньше на четное число числа знакоперемен в ряду его коэффициентов: $$ operatorname < f(x)=0 mid x>0 > = <mathcal V>(a_0,a_1,dots,a_n)-2 k , quad kin <0,1,2, dots > . $$
Доказательство ☞ ЗДЕСЬ.
С помощью преобразования корней полинома (см. пункт 1 ☞ ЗДЕСЬ ) можно доказать следствие:
Число отрицательных корней полинома
$$f(x)=a_0x^n+a_1x^+dots+a_x+a_n, quad (a_0> 0,a_n ne 0)$$ с учетом их кратностей можно оценить по формуле $$ operatorname < f(x)=0 mid x 0 >=2-2k ge 0 ,$$ следовательно $ f_<>(x) $ имеет либо два, либо ни одного положительного корня. Далее, по следствию: $$ operatorname < f(x)=0 mid x
Если каким-то образом заранее известно, что все корни полинома вещественны, то число положительных из них определяется по правилу знаков Декарта однозначно:
Пример. Характеристический полином вещественной симметричной матрицы удовлетворяет условию следствия. См. ☞ ЗДЕСЬ.
Корни полинома в областях комплексной плоскости
Задача. Для полинома 14) $ f(z) $ получить точную информацию о числе его корней в заданной области $ mathbb S $ комплексной плоскости $ mathbb C $.
Оказывается, для достаточно широкого класса областей $ mathbb S $ эту информацию можно получить без применения численных, т.е. приближенных методов. Существуют алгоритмы, позволяющие за конечное число элементарных алгебраических операций ($ +,-,times, div $) над коэффициентами $ f(z) $ установить количество корней этого полинома в таких областях, как, к примеру, $$ begin mathbb S&=&< zin mathbb R big| a 15) на заданном интервале $ ]a,b[ $ если на этом интервале
1. cоседние полиномы $ f_j(x) $ и $ f_(x) $ не имеют общих корней;
2. $ f_K(x)ne 0 $;
3. если $ f_j(x_0)=0 $ при $ x_0 in ]a,b[ $ и $ jin <1,dots,k-1>$, то числа $ f_(x_0) $ и $ f_(x_0) $ имеют разные знаки: $ f_(x_0)f_(x_0) 4. произведение $ f_<0>(x)f_<1>(x) $ меняет знак с отрицательного на положительный когда $ x_<> $, возрастая, проходит корень $ lambdain ]a,b[ $ полинома $ f_0(x)equiv f(x) $.
Число знакоперемен $$ <mathcal V>_x= <mathcal V>(f_0(x), f_1(x),dots, f_K(x)) $$ при $ x_<> $ возрастающем от $ a_<> $ к $ b_<> $, будет меняться когда $ x_<> $ проходит через корень какого-либо полинома системы. Доказывается, что это число может разве лишь уменьшаться, и уменьшается на единицу тогда и только тогда, когда $ x_<> $ проходит через корень начального полинома системы, т.е. через корень $ f(x)_<> $.
Теорема [Штурм]. Если $ f(a)ne 0, f(b)ne 0 $, и система $ f_0(x), f_1(x),dots, f_K(x) $ является системой полиномов Штурма для $ f(x_<>) $, то
$$ operatorname $. Оказывается, что в качестве полиномов системы Штурма можно взять последовательность остатков из алгоритма Евклида, если только домножить некоторые из них на $ -1_<> $. Именно, возьмем $$f_1(x) equiv f'(x) .$$ Поделим $ f_<0>(x) equiv f(x) $ на $ f_<1>(x) $ и обозначим через $ f_<2>(x) $ остаток, домноженный на $ -1_<> $: $$f_0(x)equiv q_1(x) f_1(x)-f_2(x), quad deg f_2 ☞ ЗДЕСЬ
Левая полуплоскость: устойчивость
Полином $ f(z) $ с комплексными коэффициентами называется устойчивым, если все его корни удовлетворяют условию $ <mathfrak Re>(z) 0 $ необходимо и достаточно, чтобы были выполнены неравенства
$$ a_1>0, left| begin a_1 & a_3 \ a_0 & a_2 end right|>0, left| begin a_1 & a_3 & a_5\ a_0 & a_2 & a_4 \ 0 & a_1 & a_3 end right|>0,dots, left| begin a_1 & a_3 & a_5 & dots & 0\ a_0 & a_2 & a_4 & dots & 0 \ 0 & a_1 & a_3 & dots & 0 \ 0 & a_0 & a_2 & dots & 0 \ dots & & & ddots & dots \ dots & & & dots & a_n end right|>0 . $$
Единичный круг
Единичным кругом на комплексной плоскости назовем круг $ |z|le 1 $.
Задача. Найти необходимые и достаточные условия на коэффициенты полинома $ f(z)=a_0z^n+dots+ a_n $, при которых все его корни $ lambda_1,dots, lambda_n $ находятся внутри единичного круга, т.е. удовлетворяют условию $ |z| 0, A_1>0, A_2>0, A_3>0, A_1A_2-A_0A_3>0 ; $$ и $$A_0 0 .$$ Подставляя сюда выражения для коэффициентов, получим, что первая система ограничений имеет решение $ -1 |mbox < свободный член >f(z)| , $$ т.е. $ |a_0| > |a_n| $, и полином $$ f_1(z) = frac(z)> quad npu quad f^<*>(z) = z^nf(1/z) equiv a_0+a_1z+dots+a_nz^n $$ имеет все свои корни лежащими внутри единичного круга.
На первый взгляд, конструктивность этого результата не очень очевидна: исходная задача для полинома $ f(z) $ сводится к аналогичной задаче для полинома $ f_1(z) $. Обратим, однако, внимание на то, что полином $$ begin f_1(z)&=& left[a_0(a_0z^n+dots+a_n)-a_n (a_0+a_1z+dots+a_nz^n) right] big/ z = \ &=& left[(a_0^2-a_n^2)z^n+(a_0a_1-a_a_n)z^ + dots + (a_0a_-a_<1>a_n)z right] big/ z = \ &=& (a_0^2-a_n^2)z^+(a_0a_1-a_a_n)z^ + dots + (a_0a_-a_<1>a_n) end $$ имеет степень меньшую, чем $ deg f $. Таким образом, алгоритм конструктивен в том смысле, что он сводит исходную задачу к более простой. Применяя к полиному $ f_1(z) $ снова критерий Шура-Кона, получим следующее необходимое условие $$ |mbox < старший коэффициент >f_1(z) | > | mbox < свободный член >f_1(z)| iff quad |a_0^2-a_n^2| > |a_0a_-a_<1>a_n| , $$ при выполнении которого дальнейшему исследованию подлежит полином $$ f_2(z) = frac<(a_0^2-a_n^2)f_1(z)-(a_0a_-a_<1>a_n)f^<*>_1(z)> . $$ Продолжая процедуру, за конечное число шагов мы дойдем до полинома первой степени. Окончательно, необходимые и достаточные условия нахождения всех корней полинома $ f(z) $ степени $ n_<> $ внутри единичного круга получаются объединением $ n_<> $ условий $$ |mbox < старший коэффициент >f(z) |>|mbox < свободный член >f(z)| , $$ $$ |mbox < старший коэффициент >f_1(z) | > |mbox < свободный член >f_1(z)| , $$ $$ vdots qquad qquad qquad vdots $$ $$ |mbox < старший коэффициент >f_(z) |>|mbox < свободный член >f_(z)| . $$
Пример на применение этой теоремы ☞ ЗДЕСЬ.
Численные методы поиска корней полинома
Как упоминалось ☝ ВЫШЕ, корни полинома $ f_<>(z) $, как правило, не выражаются в радикалах уже при $ deg f=5 $ . Но даже в тех случаях, когда выражаются, как, например, $$lambda=frac<sqrt<5>-1 + sqrt<10- sqrt<20>>> <2>quad mbox < для > f(x)=x^4+2x^3-6x^2-2x+1 , $$ толку от такого представления мало: на каком интервале вещественной оси лежит $ lambda $? Поэтому наряду с поиском аналитических формул для корней полиномов практический интерес представляет нахождение их приближенных значений. Эту задачу будем решать, в основном, для полиномов над $ mathbb R_<> $ (т.е. полиномов с вещественными коэффициентами), с которыми чаще всего и приходится иметь дело на практике.
Нас, прежде всего, будут интересовать именно вещественные корни полиномов. В дальнейшем переменную этих полиномов будем обозначать через $ x_<> $ и считать ее вещественной. Для поиска вещественных корней полинома, как правило, требуется их предварительно отделить, т.е. найти интервалы $ ]a,b_<>[ $, каждый из которых содержит только один корень $ f_<>(x) $. Поиск такого интервала можно производить разными способами, самый общий из которых изложен ☝ ВЫШЕ. Однако, для предварительного понимания изложенных ниже методов, достаточно будет ориентироваться на теорему Больцано: полином имеет корень на $ ]a,b_<>[ $, если на концах интервала он принимает значения разных знаков. Этот корень будет единственным, если дополнительно предположить, что функция $ f_<>(x) $ монотонна на $ ]a,b_<>[ $. Последнее условие будет очевидно выполнено, если производная $ f^<prime>(x) $ не меняет знака на $ ]a,b_<>[ $, т.е. полином $ f^<prime>(x) $ не имеет корней на рассматриваемом интервале. Действительно, если предположить существование двух корней у $ f_<>(x) $ на $ ]a,b_<>[ $, то, по соображениям, упомянутым ☞ ЗДЕСЬ 16) , должна существовать точка этого интервала, в которой $ f^<prime>(x) $ обращается в нуль. Анализ знака $ f^<prime>(x) $ на $ ]a,b_<>[ $ часто удается произвести элементарными рассуждениями.
Полиномиальные уравнения (с решенными упражнениями)
полиномиальные уравнения являются утверждением, которое поднимает равенство двух выражений или членов, где хотя бы один из членов, составляющих каждую сторону равенства, является полиномом P (x). Эти уравнения названы в соответствии со степенью их переменных.
В общем, уравнение — это утверждение, которое устанавливает равенство двух выражений, где хотя бы в одном из них есть неизвестные величины, которые называются переменными или неизвестными. Хотя существует много типов уравнений, они обычно подразделяются на два типа: алгебраические и трансцендентные..
Полиномиальные уравнения содержат только алгебраические выражения, в которых может быть одно или несколько неизвестных, участвующих в уравнении. В соответствии с показателем степени (степени) они могут быть классифицированы на: первую степень (линейную), вторую степень (квадратичную), третью степень (кубическую), четвертую степень (квартальную), большую или равную пяти и иррациональную.
- 1 Характеристики
- 2 типа
- 2.1 Первый класс
- 2.2 Вторая степень
- 2.3 Резолвер
- 2.4 Высшая оценка
- 3 упражнения выполнены
- 3.1 Первое упражнение
- 3.2 Второе упражнение
- 4 Ссылки
черты
Полиномиальные уравнения — это выражения, которые образованы равенством двух полиномов; то есть с помощью конечных сумм умножений между неизвестными значениями (переменными) и фиксированными числами (коэффициентами), где переменные могут иметь показатели степени, а их значение может быть положительным целым числом, включая ноль.
Показатели степени определяют степень или тип уравнения. Тот член выражения, который имеет наивысший показатель степени, будет представлять абсолютную степень многочлена.
Полиномиальные уравнения также известны как алгебраические уравнения, их коэффициенты могут быть действительными или комплексными числами, а переменные представляют собой неизвестные числа, представленные буквой, например: «x».
Если подставить значение для переменной «x» в P (x), результат будет равен нулю (0), то говорят, что это значение удовлетворяет уравнению (это решение) и обычно называется корнем многочлена..
Когда разработано полиномиальное уравнение, вы хотите найти все корни или решения.
тип
Существует несколько типов полиномиальных уравнений, которые дифференцируются по количеству переменных, а также по степени их степени..
Таким образом, полиномиальные уравнения, где первый член является полиномом с единственным неизвестным, учитывая, что его степень может быть любым натуральным числом (n), а второй член равен нулю, можно выразить следующим образом:
— вN, вн-1 и0, они действительные коэффициенты (числа).
— вN это отличается от нуля.
— Показатель n представляет собой положительное целое число, которое представляет степень уравнения.
— х — это переменная или неизвестная, которую нужно искать.
Абсолютная или большая степень полиномиального уравнения — это показатель большей ценности среди всех тех, которые образуют полином; таким образом, уравнения классифицируются как:
Первый класс
Уравнения полиномов первой степени, также известные как линейные уравнения, — это уравнения, в которых степень (наибольший показатель степени) равна 1, а полином имеет форму P (x) = 0; и он состоит из линейного члена и независимого члена. Это написано следующим образом:
— a и b — действительные числа и a ≠ 0.
— ax — линейный член.
— б независимый термин.
Например, уравнение 13x — 18 = 4x.
Чтобы решить линейные уравнения, все члены, содержащие неизвестный x, должны быть переданы в одну сторону равенства, а те, которые не имеют, перемещены в другую сторону, чтобы очистить его и получить решение:
Таким образом, данное уравнение имеет единственное решение или корень, который равен x = 2.
Второй класс
Полиномиальные уравнения второй степени, также известные как квадратные уравнения, — это те, в которых степень (наибольший показатель степени) равна 2, полином имеет форму P (x) = 0 и состоит из квадратичного члена один линейный и один независимый. Это выражается следующим образом:
топор 2 + bx + c = 0.
— a, b и c — действительные числа и a ≠ 0.
— топор 2 является квадратичным членом, а «a» является коэффициентом квадратичного члена.
— bx — линейный член, а «b» — коэффициент линейного члена..
— с является независимым термином.
resolvente
Как правило, решение этого типа уравнений дается путем очистки х из уравнения, и оно оставляется следующим образом, который называется резольвер:
Там, (б 2 — 4ac) называется дискриминантом уравнения, и это выражение определяет количество решений, которые может иметь уравнение:
— Да (б 2 — 4ac) = 0, уравнение будет иметь одно решение, которое является двойным; то есть у вас будет два равных решения.
— Да (б 2 — 4ac)> 0, уравнение будет иметь два разных реальных решения.
— Да (б 2 — 4ac) 2 + 10x — 6 = 0, чтобы разрешить его, сначала определите термины a, b и c, а затем замените его в формуле:
Существуют случаи, когда полиномиальные уравнения второй степени не имеют трех членов, и поэтому они решаются по-разному:
— В случае, если квадратные уравнения не имеют линейного члена (то есть b = 0), уравнение будет выражено как ось 2 + с = 0. Чтобы решить это, очищается х 2 и квадратные корни применяются в каждом члене, помня, что рассматриваются два возможных признака, которые может иметь неизвестное:
Например, 5 х 2 — 20 = 0.
— Если квадратное уравнение не имеет независимого члена (т. Е. С = 0), уравнение будет выражено как ось 2 + bx = 0. Чтобы решить его, мы должны извлечь общий множитель неизвестного x в первом члене; поскольку уравнение равно нулю, верно, что хотя бы один из факторов будет равен 0:
Таким образом, вы должны:
Например: у вас есть уравнение 5x 2 + 30x = 0. Первый фактор:
Генерируются два фактора: х и (5х + 30). Считается, что одно из них будет равно нулю, а другое решение будет дано:
Степень магистра
Полиномиальные уравнения большей степени — это те, которые идут от третьей степени и далее, которые могут быть выражены или разрешены с помощью общего полиномиального уравнения для любой степени:
Это используется потому, что уравнение со степенью больше двух является результатом факторизации полинома; то есть оно выражается как умножение многочленов степени один или больше, но без реальных корней.
Решение этого типа уравнений является прямым, потому что умножение двух факторов будет равно нулю, если любой из факторов равен нулю (0); следовательно, каждое из найденных полиномиальных уравнений должно быть разрешено, сопоставляя каждый из его факторов с нулем.
Например, у вас есть уравнение третьей степени (куб) х 3 + х 2 +4x + 4 = 0. Чтобы решить эту проблему, необходимо выполнить следующие шаги:
х 3 + х 2 +4x + 4 = 0
(х 3 + х 2 ) + (4x + 4) = 0.
— Конечности разбиты, чтобы получить общий фактор неизвестного:
х 2 (х + 1) + 4 (х + 1) = 0
— Таким образом, получаются два фактора, которые должны быть равны нулю:
— Видно, что коэффициент (х 2 + 4) = 0 не будет иметь реального решения, а коэффициент (x + 1) = 0 да. Таким образом, решение является:
Решенные упражнения
Решите следующие уравнения:
Первое упражнение
решение
В этом случае уравнение выражается в виде умножения полиномов; то есть это факторизовано. Для ее решения каждый фактор должен быть равен нулю:
— 2x 2 + 5 = 0, не имеет решения.
Таким образом, данное уравнение имеет два решения: x = 3 и x = -1.
Второе упражнение
решение
Ему был дан полином, который можно переписать как разность квадратов, чтобы прийти к более быстрому решению. Таким образом, уравнение остается:
Чтобы найти решение уравнений, оба фактора равны нулю:
(х 2 + 6) = 0, не имеет решения.
Таким образом, исходное уравнение имеет два решения:
http://vmath.ru/vf5/polynomial
http://ru.thpanorama.com/articles/matemticas/ecuaciones-polinmicas-con-ejercicios-resueltos.html


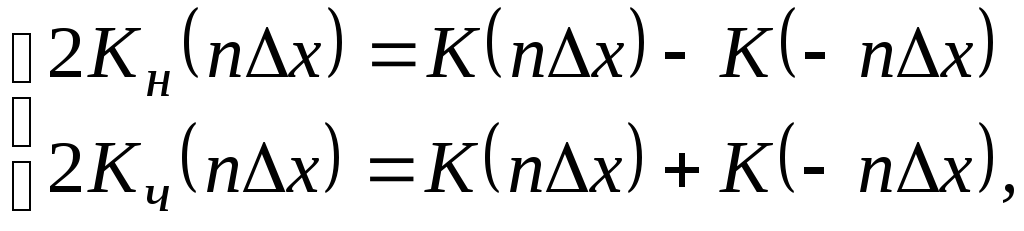
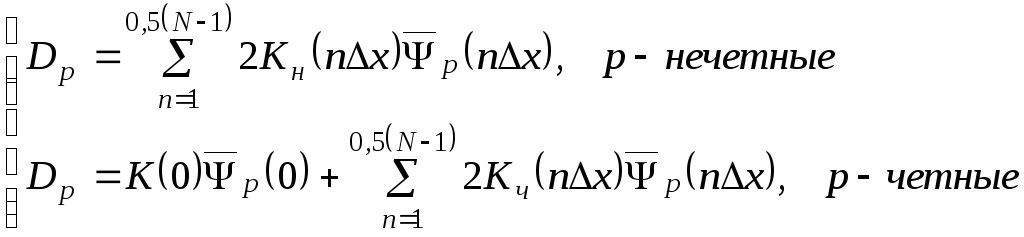











 кубик имеет три различных реальных корня
кубик имеет три различных реальных корня  кубик имеет вещественный корень
кубик имеет вещественный корень 

 равно нулю, если 4 p 3 + 27 д 2 = 0. { displaystyle 4p ^ {3} + 27q ^ {2} = 0 ;.}
равно нулю, если 4 p 3 + 27 д 2 = 0. { displaystyle 4p ^ {3} + 27q ^ {2} = 0 ;.} Если p также равно нулю, то p = q = 0, а 0 — тройной корень кубики. Если 4 п 3 + 27 q 2 знак равно 0, { displaystyle ; 4p ^ {3} + 27q ^ {2} = 0 ;,}
Если p также равно нулю, то p = q = 0, а 0 — тройной корень кубики. Если 4 п 3 + 27 q 2 знак равно 0, { displaystyle ; 4p ^ {3} + 27q ^ {2} = 0 ;,} и p ≠ 0, то кубическая имеет простой корень
и p ≠ 0, то кубическая имеет простой корень


 равно нулю, то
равно нулю, то кубика имеет тройной корень
кубика имеет тройной корень

 кубика имеет двойной корень
кубика имеет двойной корень



 тогда уравнение имеет реальный корень <6>- q 2 + q 2 4 + p 3 27 3 + — q 2 — q 2 4 + p 3 27 3. { Displaystyle { sqrt [{3}] {- { frac {q} {2}} + { sqrt {{ frac {q ^ {2}} {4}} + { frac {p ^ {3}} {27}}}}}} + { sqrt [{3}] {- { frac {q} {2}} — { sqrt {{ frac {q ^ {2}} {4}} + { frac {p ^ {3}} {27}}}}}}.}. }
тогда уравнение имеет реальный корень <6>- q 2 + q 2 4 + p 3 27 3 + — q 2 — q 2 4 + p 3 27 3. { Displaystyle { sqrt [{3}] {- { frac {q} {2}} + { sqrt {{ frac {q ^ {2}} {4}} + { frac {p ^ {3}} {27}}}}}} + { sqrt [{3}] {- { frac {q} {2}} — { sqrt {{ frac {q ^ {2}} {4}} + { frac {p ^ {3}} {27}}}}}}.}. }![{ displaystyle { sqrt [{3}] {- { frac {q} {2}} + { sqrt {{ fr ac {q ^ {2}} {4}} + { frac {p ^ {3}} {27}}}}}} + { sqrt [{3}] {- { frac {q} {2} } - { sqrt {{ frac {q ^ {2}} {4}} + { frac {p ^ {3}} {27}}}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56ea527f89e3bdb66eca0e1c1a5bb4a5512358df)
 и корень другого куба на — 1 — i 3 2. { displaystyle { frac {-1-i { sqrt {3}}} {2}}.}
и корень другого куба на — 1 — i 3 2. { displaystyle { frac {-1-i { sqrt {3}}} {2}}.}
 существует три действительных корня, но теория Галуа позволяет доказать, что они не могут быть выражены алгебраическим выражением, включающим только действительные числа. Следовательно, в этом случае уравнение не может быть решено с учетом времени Кардано. Таким образом, этот падеж был назван casus unducibilis, что на латыни означает неприводимый падеж.
существует три действительных корня, но теория Галуа позволяет доказать, что они не могут быть выражены алгебраическим выражением, включающим только действительные числа. Следовательно, в этом случае уравнение не может быть решено с учетом времени Кардано. Таким образом, этот падеж был назван casus unducibilis, что на латыни означает неприводимый падеж. и 3 { displaystyle { sqrt [{3}] {{~ } ^ {~}}}}
и 3 { displaystyle { sqrt [{3}] {{~ } ^ {~}}}}![{ displaystyle { sqrt [{3}] {{~} ^ {~}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24d9ec8c0118de0d1a1c4002b6edfa9a90209ddf) как представление основных значений основная функция (то есть корня, имеющая наибольшую действующую часть). С этим соглашением формула Кардано для трех корней остается в силе, но не является чисто алгебраической, обозначением главной части не является чисто алгебраическим, поскольку оно включает неравенство для сравнения действительных частей. Кроме того, использование главного корня куба может дать неверный результат, если коэффициенты не являются действительными комплексными числами. Более того, если коэффициенты принадлежат другому полю , главный корень куба, как правило, не определено.
как представление основных значений основная функция (то есть корня, имеющая наибольшую действующую часть). С этим соглашением формула Кардано для трех корней остается в силе, но не является чисто алгебраической, обозначением главной части не является чисто алгебраическим, поскольку оно включает неравенство для сравнения действительных частей. Кроме того, использование главного корня куба может дать неверный результат, если коэффициенты не являются действительными комплексными числами. Более того, если коэффициенты принадлежат другому полю , главный корень куба, как правило, не определено.![{ displaystyle C- { frac {p} {3C}} quad { text {with}} quad C = { sqrt [{3}] {- { frac {q} {2}} + { sqrt {{ гидроразрыв {q ^ {2}} {4}} + { frac {p ^ {3}} {27}}}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c87abe575ce3101b7076ebb7dd0b960d85195d3f)

 и когда кубический многочлен не неприводимый.
и когда кубический многочлен не неприводимый.
![{ displaystyle C = { sqrt [{3}] { frac { Delta _ {1} pm { sqrt { Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}}}} {2}} },}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57102b328503b04914d43ce3ab469e53c6fad58d)



![{ displaystyle t_ {k} = 2 , { sqrt {- { frac {, p ,} {3 }} ;}} , cos left [, { frac {1} {3}} , arccos left ({ frac {, 3q ,} {2p}} , { sqrt {{ frac {-3 ;} {p}} ,}} , right) - { frac {, 2 pi k ,} {3}} , right] qquad { текст {for}} ~ к = 0,1,2 ;.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c0227de94b75d9be59155e564abdef28db6b334)
 ). В противном случае это все еще правильно, но включает сложные косинусы и арккосинусы, когда есть только один действительный корень, и бессмысленно (деление на ноль), когда p = 0).
). В противном случае это все еще правильно, но включает сложные косинусы и арккосинусы, когда есть только один действительный корень, и бессмысленно (деление на ноль), когда p = 0).
 и разделить уравнение по u 3 4. { displaystyle { гидроразрыв {; u ^ {3} ,} {4}} ,.}
и разделить уравнение по u 3 4. { displaystyle { гидроразрыв {; u ^ {3} ,} {4}} ,.} Это дает
Это дает

![{ displaystyle t_ {k} = 2 , { sqrt {, - { frac {, p ,} {3}} ;}} , cos left [{ frac {1} {3}} , arccos left ({ frac {, 3q ,} {2p}} , { sqrt {{ frac {-3 ;} {p}} ,}} right) - { frac {, 2 pi k ,} {3 }} right] qquad { text {for}} ~ k = 0,1,2 ;.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8375a40f286157be686b55bbc46020f2184b1c92)
![{displaystyle {begin{aligned}t_{0}=-2{frac {|q|}{q}}{sqrt {-{frac {p}{3}}}}cosh left[{frac {1}{3}}operatorname {arcosh} left({frac {-3|q|}{2p}}{sqrt {frac {-3}{p}}}right)right]qquad {text{if }}~4p^{3}+27q^{2}>0 ~ { text {и}} ~ p <0;,\t_{0}=-2{sqrt {frac {p}{3}}}sinh left[{frac {1}{3}}operatorname {arsinh} left({frac {3q}{2p}}{sqrt {frac {3}{p}}}right)right]qquad {text{if }}~p>0 ;. End {align}}}](https://alphapedia.ru/w/%20//wikimedia.org/api/rest_v1/media/math/render/svg/ac9eb577ab0165f79a1c5bf4ee5e99e850582cbe)
 Геометрическое решение Омара Хайяма кубического уравнения для случая m = 2, n = 16, дающее корень 2. Пересечение вертикальной линии на оси x в центре круг является случайностью проиллюстрированного примера.
Геометрическое решение Омара Хайяма кубического уравнения для случая m = 2, n = 16, дающее корень 2. Пересечение вертикальной линии на оси x в центре круг является случайностью проиллюстрированного примера. 
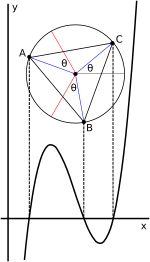 Для кубики (1)с тремя действительными корнями корни — это проекции на ось x вершин A, B и C равностороннего треугольника . Центр треугольника имеет ту же x-координату, что и точка перегиба .
Для кубики (1)с тремя действительными корнями корни — это проекции на ось x вершин A, B и C равностороннего треугольника . Центр треугольника имеет ту же x-координату, что и точка перегиба .
 — угол в единичной окружности; взятие 1/3 этого угла соответствует извлечению кубического корня из комплексного числа; добавление −k2π / 3 для k = 1, 2 находит другие корни куба; и умножение косинусов этих результирующих углов на 2 — p 3 { displaystyle 2 { sqrt {- { frac {p} {3}}}}}}
— угол в единичной окружности; взятие 1/3 этого угла соответствует извлечению кубического корня из комплексного числа; добавление −k2π / 3 для k = 1, 2 находит другие корни куба; и умножение косинусов этих результирующих углов на 2 — p 3 { displaystyle 2 { sqrt {- { frac {p} {3}}}}}} корректирует масштаб.
корректирует масштаб. Наклон прямой RA в два раза больше, чем RH. Обозначая комплексные корни кубики как g ± hi, g = OM (здесь отрицательное значение) и h = √tan ORH = √ наклон прямой RH = BE = DA.
Наклон прямой RA в два раза больше, чем RH. Обозначая комплексные корни кубики как g ± hi, g = OM (здесь отрицательное значение) и h = √tan ORH = √ наклон прямой RH = BE = DA. 
 меняет знак при обмене двумя корнями, Δ { displaystyle { sqrt { Delta}}}
меняет знак при обмене двумя корнями, Δ { displaystyle { sqrt { Delta}}}



 , и в предположении, что он положительные, действительные решения этого уравнения (после складывания деления на 4 под квадратным корнем):
, и в предположении, что он положительные, действительные решения этого уравнения (после складывания деления на 4 под квадратным корнем):
![{ displaystyle u = { sqrt [{3}] {- { frac {q} {2 }} + { sqrt {{ frac {q ^ {2}} {4}} + { frac {p ^ {3}} {27}}}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d5bf9eaebfd5896d4f8dde09d59ff00381d33a9)
![{ displaystyle v = { sqrt [{3}] {- { frac {q} {2}} - { sqrt {{ frac {q ^ {2}} {4}} + { frac {p ^ { 3}} {27}}}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a7232f72d8ec7b6cee76973ccfc6189a981b1dd)
![{ displaystyle t = { sqrt [{3}] {- {q over 2} + { sqrt {{q ^ {2} over 4} + {p ^ {3} over 27}}}}} + { sqrt [{3}] {- {q over 2} - { sqrt {{q ^ {2} over 4} + {p ^ {3} over 27}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d62f2e04f38bbf3c00fc86f15fe1a717fa25d82)




 Это означает, что изменение знака квадратного корня меняет местами w i и — p / 3w i для i = 1, 2, 3 и, следовательно, не меняет корни. Этот метод не работает только тогда, когда оба корня квадратного уравнения равны нулю, то есть когда p = q = 0, и в этом случае единственная корень углубленной кубики равен 0.
Это означает, что изменение знака квадратного корня меняет местами w i и — p / 3w i для i = 1, 2, 3 и, следовательно, не меняет корни. Этот метод не работает только тогда, когда оба корня квадратного уравнения равны нулю, то есть когда p = q = 0, и в этом случае единственная корень углубленной кубики равен 0. , но эта сложная интерпретация здесь не используется). Обозначая x 0, x 1 и x 2 три корня кубического уравнения, которое нужно решить, пусть
, но эта сложная интерпретация здесь не используется). Обозначая x 0, x 1 и x 2 три корня кубического уравнения, которое нужно решить, пусть



 , удовлетворяют кубическим уравнениям.
, удовлетворяют кубическим уравнениям.