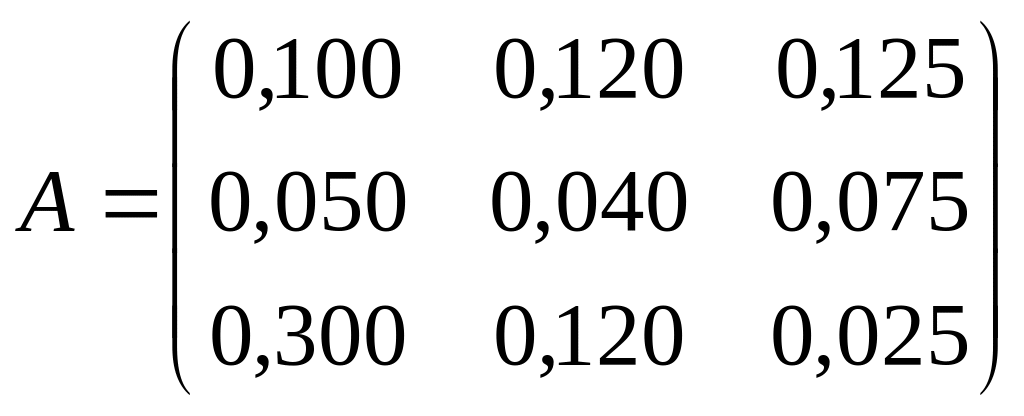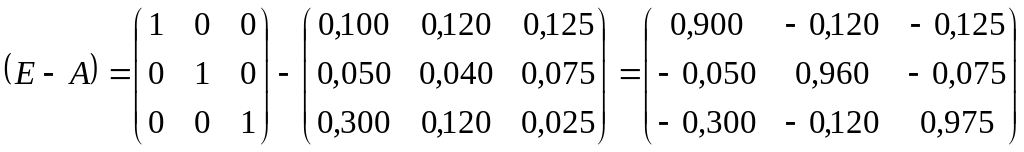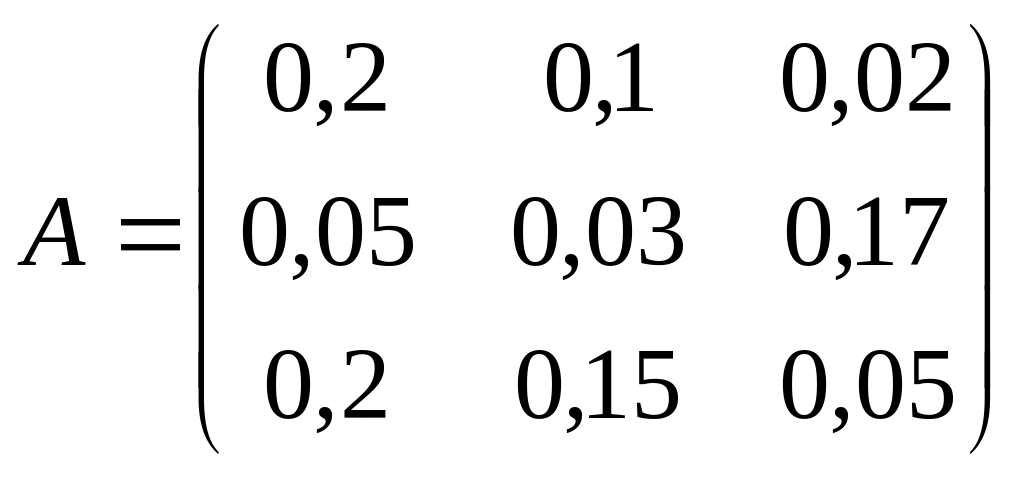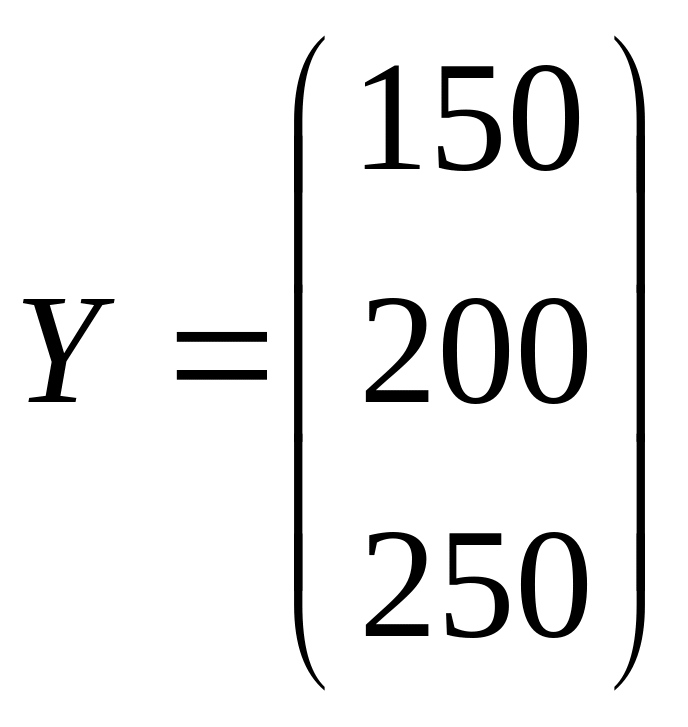Как найти коэффициенты полных материальных затрат

Перейдем к построе­нию математической модели. Для этого введем понятие коэффициентов прямых материальных затрат:

                                  (1)

Коэффициент aij показывает, какое количество i-го продукта затрачивается на производство единицы j-го продукта.

Поскольку продукция измеряется в стоимостных единицах, коэффици­енты прямых затрат являются величинами безразмерными. Кроме того, из (1) следует, что

                                 (2)

Считая коэффициенты прямых материальных затрат постоянными, запишем систему балансовых соотношений

следующим образом:

Перенося yi в правую часть, а xi в левую и меняя знаки на противопо­ложные, получаем

В матричной форме эта система уравнений выглядит следующим обра­зом:

X — AX = Y  или  (E — A) X = Y,

где Е — единичная матрица n-го порядка;

 — матрица коэффициентов прямых материальных затрат.

Итак, мы получили систему уравнений межотраслевого баланса, кото­рую называют моделью Леонтьева. Используя эту модель, можно ответить на основной вопрос межотраслевого анализа — каким должно быть валовое производство каждой отрасли для того, чтобы экономическая система в целом произвела заданное количество конечной продукции?

Следует отметить одно важное свойство А — сумма элементов любого ее столбца меньше единицы:

                                 (3)

Для доказательства разделим обе части балансового соотношения

на хj и, выполнив простейшие преобразования, полу­чим

где vj / xj= — доля условно-чистой продукции в единице валового выпуска.

Очевидно, что >0, так как в процессе производства не может не создавать­ся новой стоимости. Из этого следует справедливость соотношения (3).

Свойства (2) и (3) матрицы А играют ключевую роль в доказательстве ее продуктивности, т. е. в доказательстве того, что при любом неотрицатель­ном Y система

X — AX = Y  или  (E — A) X = Y,

имеет единственное и неотрицательное решение Х=(Е-А)-1Y. Матрицу (Е-А)-1 обозначают через В и называют матрицей коэффициентов полных материальных затрат, или обратной матрицей Леонтьева. Коэф­фициент bij этой матрицы показывает, каким должен быть валовой выпуск i-й отрасли для того, чтобы обеспечить производство единицы конечного продукта j-й отрасли. Используя матрицу В, можем записать

Х = ВY

или в развернутом виде

Преимущество такой формы записи балансовой модели состоит в том, что, вычислив матрицу В лишь однажды, мы можем многократно использовать ее для вычисления Х прямым счетом, т.е. умножением В на Y. Это гораздо проще, чем каждый раз решать систему линейных уравнений.

Обратную матрицу В можно вычислить, используя метод обращения с применением формулы разложения ее в матричный ряд:

В=Е+А+А2+…+Аk+…                                             (4)

Число членов ряда, необходимое для получения достаточно точного приближения, зависит от матрицы А, но в любом случае приемлемый результат достигается при k 30.

Формула (4) имеет строгое математическое доказательство. Но мы ограничимся тем, что попытаемся осмыслить ее, рассматривая Х как результат некоторого гипотетического процесса последовательного уточне­ния промежуточной продукции, необходимой для создания заданного конечного продукта.

Итак, вектор конечной продукции, которую должна произвести эконо­мическая система, равен Y. Будем считать, что это и есть первоначальное задание отраслям, т. е. Х0 =Y. Для выполнения собственного задания каждая отрасль нуждается в продукции других отраслей. Если бы все отрасли подсчитали потребности и подали заявки в некоторый центр, то оказалось бы, что суммарная потребность составляет X1 =АХ0=АY. Вектор X1 можно рассматривать как промежуточную продукцию, необходимую для производства Х0. Но под обеспечение производства X1 тоже нужна проме­жуточная продукция: X2 =АХ1 =А2Y. Рассуждая так и далее, мы приходим к выводу, что

Х=Х0+Х1+Х2+…+Хk+… = Y+АY+А2Y+…+AkY+… =

= (Е+А+А2+…+Аk+…)Y.

Полные затраты можно разложить на прямую и косвенную составля­ющие.  Прямые затраты осуществляются непосредственно при производстве данного продукта, а косвенные А2+А3+…+Аk+… относятся к предшествую­щим стадиям производства. Они осуществляются не прямо, а через посред­ство других ингредиентов, входящих в данный продукт. Элементы матрицы А2 представляют собой косвенные затраты первого порядка, элементы матрицы А3 — косвенные затраты второго порядка и т. д.

Пример 1. Рассматривается трехотраслевой МОБ. Известна матрица коэффициен­тов прямых материальных затрат и задан вектор конечного продукта:

.

Определить валовое производство X, обеспечивающее заданный конеч­ный продукт.

Для ответа на поставленный вопрос необходимо составить и решить систему линейных уравнений (Е-А)Х = Y.

Получим соответствующую систему уравнений

Решим систему методом Крамера. Если определитель системы  отличен от нуля, то система имеет единственное решение, которое находится по формулам

где  — определитель, который получается из  заменой j-го столбца столбцом свободных членов.

 

    

Применяя формулы Крамера, получаем решение системы:

  

Пример 2. Вычислить изменение межотраслевых потоков, если известна матрица коэффициентов полных материальных затрат и задан вектор изменения ко­нечного продукта:

Изменение межотраслевых потоков вычисляется по формулам

Вектор изменения валового производства определяется следующим образом:

Кроме того, нам необходимо знать матрицу А. Из формулы В=(Е-А)-1 следует, что

Теперь, отвечая на поставленный вопрос, получаем:

 

 и т.д.

Источник: https://lms2.sseu.ru

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

1. Коэффициенты прямых и полных материальных затрат.

При исследовании
модели межотраслевого баланса сначала
нужно рассмотреть основные свойства
матрицы коэффициентов прямых материальных
затрат A.

Основные свойства
матрицы коэффициентов прямых материальных
затрат

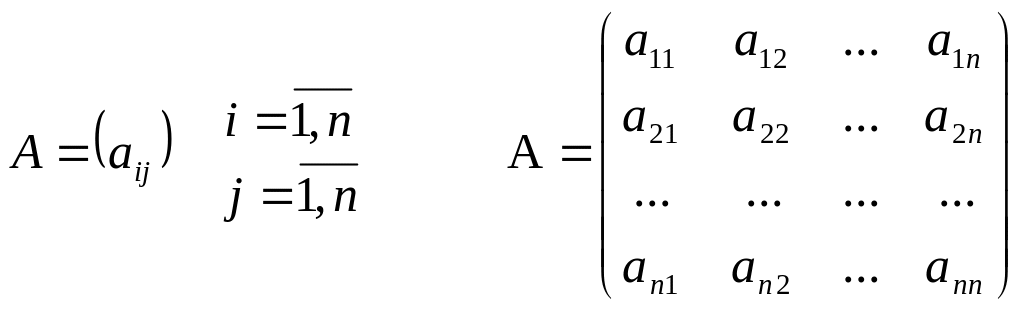
1. Коэффициенты
прямых затрат по определению являются
неотрицательными

,
поэтому матрица А
в целом может быть названа неотрицательной:

.

2. Диагональные
элементы матрицы А
меньше единицы

,
так как процесс воспроизводства нельзя
было бы осуществлять, если бы для
собственного воспроизводства в отрасли
затрачивалось больше количество
продукта, чем создавалось.

Система уравнений
межотраслевого баланса является
отражением реальных экономических
процессов, в которых содержательный
смысл могут иметь лишь неотрицательные
значения валовых выпусков. Значит,
вектор валовой продукции состоит из
неотрицательных компонентов и называется
неотрицательным, т.е.

.

Экономическая
система способна обеспечить положительный
конечный выпуск по всем отраслям, если
матрица коэффициентов прямых материальных
затрат А
является продуктивной.

Продуктивность
матрицы А.

Неотрицательную
матрицу А
называют продуктивной, если существует
такой неотрицательный вектор

,
что справедливо:

(13)

Это условие означает
существование положительного вектора
конечной продукции

для модели межотраслевого баланса

(7).

Существует несколько
способов
проверки продуктивности матрицы А.

Матрица коэффициентов
прямых материальных затрат А продуктивна,
если выполняется одно из условий:

1. Матрица

неотрицательно обратима, т.е существует
обратная матрица

.

2. Матричный ряд

сходится и его сумма равна обратной
матрице

.

3. Наибольшее по
модулю собственное значение

матрицы А
меньше 1.

Собственные числа
матрицы А
– корни характеристического уравнения

.

4. Все главные
миноры матрицы

,
т.е. определители матриц, образованные
элементами первых строк и первых столбцов
этой матрицы, порядка от 1 до n,
положительны.

Наиболее простым,
но только достаточным признаком
продуктивности матрицы А
является ограничение на величину ее
нормы, т.е. на величину наибольшей из
сумм элементов матрицы А
в каждом столбце. Если норма матрицы А
строго меньше единицы, то эта матрица
продуктивна.

Но эти условия
являются только достаточными, т.е.
матрица А
может быть продуктивной и в случае,
когда ее норма больше единицы.

Пример № 1.

Проверить
продуктивность матрицы

.
Найдем матрицу

.

Найдем определитель
матрицы

Находим элементы
присоединенной матрицы

;

Сначала найдем
транспонированную матрицу

:

обозначим ее через
D.

,
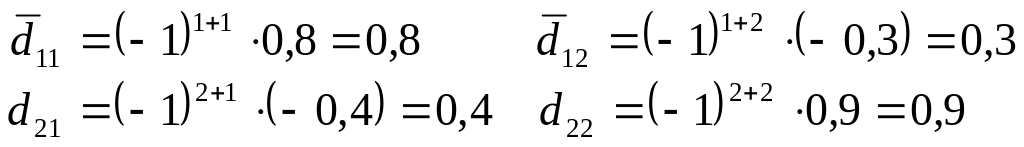
значит, матрица А
продуктивна.

Пример № 2.

Проверить
продуктивность матрицы

.

Найдем главные
миноры матрицы

;

.

Главный минор
I-ого
порядка: 0,900 > 0/

Главный минор
II-ого
порядка:

> 0.

Главный минор
III-его
порядка:

> 0.

Итак: все главные
миноры матрицы

положительны, значит матрица А
является продуктивной.

Анализ матрицы
коэффициентов полных материальных
затрат.

Матрица

— матрица коэффициентов полных материальных
затрат

.

Ранее было дано
определение коэффициента b_ij
полных материальных затрат, что b_ij
показывает сколько нужно произвести
продукции i-той
отрасли, чтобы с учетом прямых и косвенных
материальных затрат, получить единицу
конечной продукции отрасли j.

Дадим другое
определение коэффициента полных
материальных затрат, исходя из того,
что, кроме прямых затрат существуют
косвенные затраты той или иной продукции
при производстве продукции данной
отрасли.

Например,
при производстве автомобиля в виде
прямых затрат расходуется уголь, стальной
прокат, цветные металлы, электроэнергия
и т.д. Но на производство стального
проката также расходуется уголь. Это
будут косвенные затраты I-го
порядка при производстве автомобиля.
При производстве стального проката
расходуются цветные металлы, для
производства которых также расходуется
уголь. Но при производстве автомобиля
это будут косвенные затраты II-го
порядка и т.д.

В связи с этим
имеет место следующее определение:
коэффициентом
полных материальных затрат (с_ij)
называется сумма прямых затрат продукции
i-той
отрасли для производства единицы
продукции j-той
отрасли через все промежуточные продукты
на всех предшествующих стадиях
производства.

Обозначим коэффициент
косвенных материальных затрат k-го
порядка через

,
тогда имеет место равенство:

(14)

Если ввести в
рассмотрение матрицу коэффициентов
полных материальных затрат

и матрицы коэффициентов материальных
затрат различных порядков:

,
то можно записать формулу:

(15)

где А
– матрица коэффициентов прямых
материальных затрат;

А⁽¹⁾
– матрица коэффициентов косвенных
материальных затрат I-го
порядка;

А⁽²⁾
– матрица коэффициентов косвенных
материальных затрат II-го
порядка и т.д.;

А^(k)
– матрица коэффициентов косвенных
материальных затрат k-го
порядка.

;

и т.д.

.

Итак:

(16)

Если матрица
коэффициентов прямых материальных
затрат А
является продуктивной, то из второго
условия продуктивности следует, что
существует матрица

,
которая является суммой сходящегося
матричного ряда:

(17)

Тогда сопоставляя
соотношения (16) и (17), можно сделать вывод
о связи между двумя матрицами коэффициентов
полных материальных затрат.

(18)

или

Экономический
смысл различия между коэффициентами
матриц В
и С:
в отличие от коэффициентов матрицы С,
которые учитывают только затраты на
производство продукции, коэффициенты
матрицы В
включают в себя кроме затрат также саму
единицу конечной продукции, которая
выходит за сферу производства.

Таким образом,
если матрица А
продуктивна, то для нахождения
матрицы В
можно использовать способы:

1. По формулам
обращения матриц:

(19)

2. Приближенный
способ по формулам разложения в матричный
ряд:

(20)

В этом случае
обычно ограничиваются косвенными
затратами до некоторого порядка
включительно.

Пример.

Дана матрица
коэффициентов прямых материальных
затрат и вектор конечной продукции:

.

Найти коэффициенты
полных материальных затрат, вектор
валовой продукции, заполнить схему
межотраслевого баланса.

Решение:

1. Определитель
матрицы

:

;

2. Транспонируем
матрицу

:

.

3. Находим
алгебраические дополнения для элементов
матрицы

:

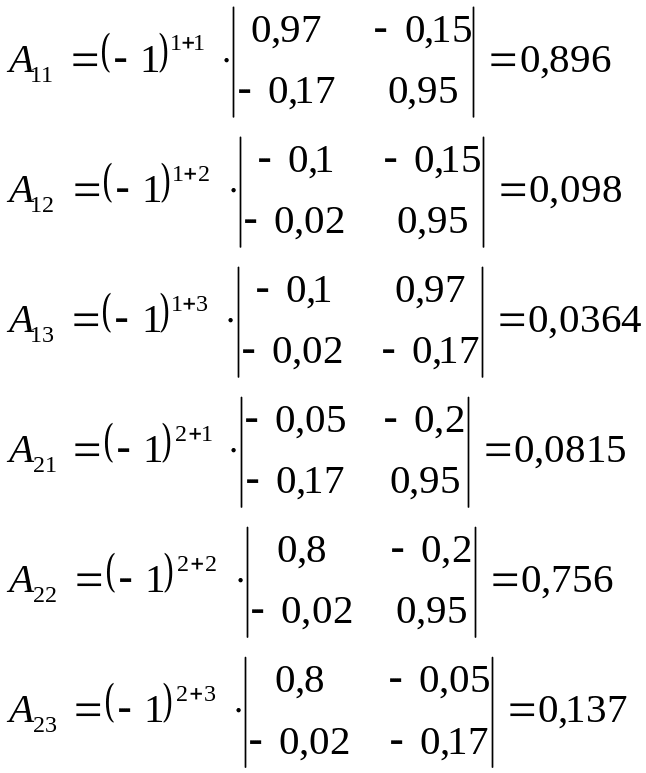
Присоединенная
матрица:

Найдем вектор
валовой продукции по формуле:

Для заполнения
схемы межотраслевого баланса, необходимо
найти:

Находим условно-чистую
продукцию отраслей:

Межотраслевой
баланс производства и распределения
продукции:

Производящие отрасли	Потребляющие отрасли	Конечная продукция	Валовая продукция
1	2	3
1 2 3	46,32 11,58 46,32	28,05 8,415 42,075	7,124 60,554 17,81	150 200 250	231,6 280,5 356,2
Условно-чистая продукция	127,38	201,96	270,712	600,0
Валовая продукция	231,6	280,5	356,2		868,3

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Задача

Экономика
представлена двумя отраслями производства: промышленностью и сельским
хозяйством. За отчетный период получены следующие данные о межотраслевых
поставках

 и векторе объемов конечного использования

.

Требуется:

Указание:
При вычислениях производить округление с точностью до тысячных.

Решение

Матрица прямых затрат

Найдем
валовые выпуски отраслей, просуммировав в каждой строке межотраслевые поставки
и координату вектора

:

Найдем
матрицу прямых затрат. Ее элементы можно найти по формуле:

Подставляя
числовые значения, получаем:

Матрица «Затраты — выпуск»

Найдем матрицу
«Затраты — выпуск»

Вектор конечного использования Y для валового объема выпуска X

Вектор
конечного использования Y для валового объема выпуска X определим на основе
балансового соотношения: 

Для этого выполним умножение двух матриц

Матрица полных затрат

Найдем
матрицу коэффициентов полных материальных затрат

 -она будет равна обратной матрице

:

Определитель матрицы

:

Алгебраические
дополнения:

Обратная матрица:

Вектор валового объема выпуска X для конечного использования Y

Вектор валового объема выпуска

 для конечного продукта

 определим формуле:

Приросты валовых объемов выпуска

Найдем
приросты валовых объемов выпуска, если конечное потребление должно изменяться
на

 по сравнению с

:

Матрица полных затрат ресурсов S

Найдем
матрицу полных затрат ресурсов S для заданной матрицы ее прямых затрат M:

Суммарная потребность в ресурсах

Суммарная  потребность в ресурсах для вектора Y₀:

Суммарная  потребность в ресурсах для вектора Y_n:

Матрицы косвенных затрат и сумма затрат

Найдем
матрицы косвенных затрат первого, второго и третьего порядка

Сумма затрат:

Разность
матриц:

Вектор потребности в продукции

Найдем
вектор потребности в продукции всех отраслей материального производства b_ij
для получения единицы конечного продукта b_j вида. Для этого
просуммируем столбцы матрицы полных затрат:

Это значит, что для производства
единицы конечного продукта в первой отрасли во всех отраслях надо расходовать
продукции на сумму 1,913 ден.ед., для производства единицы конечного продукта
во второй отрасли -на 2,021 ден.ед.