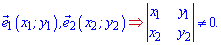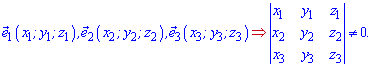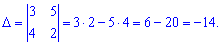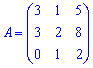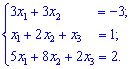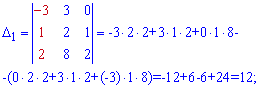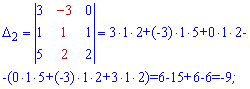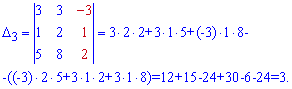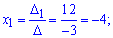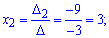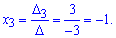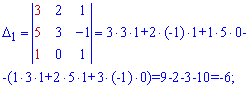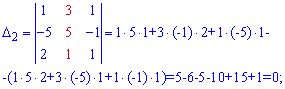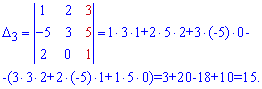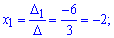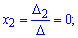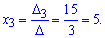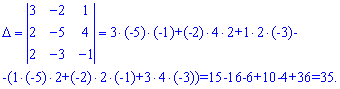Составим систему линейных уравнений, используя векторы из условия задачи:
$$ begin{cases} 10= 2alpha + 3 beta + 5 gamma \ 3=3 alpha + 7 beta + 4 gamma \ 3 = 1 alpha + 2 beta + 2 gamma end{cases} $$
Запишем систему в привычном виде:
$$ begin{cases} 2alpha + 3 beta + 5 gamma = 10 \ 3 alpha + 7 beta + 4 gamma = 3 \ alpha + 2 beta + 2 gamma = 3 end{cases} $$
Решив систему уравнений любым методом, найдем неизвестные $ alpha, beta, gamma $. К примеру, возьмём метод Крамера.
Найдем главный определитель:
$$ Delta = begin{vmatrix} 2 & 3 & 5 \ 3 & 7 & 4 \ 1 & 2 & 2 end{vmatrix} = $$
$$ = 2 cdot 7 cdot 2 + 3 cdot 4 cdot 1 + 3 cdot 2 cdot 5 — 5 cdot 7 cdot 1 — 4 cdot 2 cdot 2 — 3 cdot 3 cdot 2 = $$
$$ = 28 + 12 + 30 — 35 — 16 — 18 = 1 $$
Так как $ Delta = 1 $ не равно нулю, то СЛАУ имеет единственное решение.
Вычислим дополнительные определители составленные из столбцов главного путём поочередной замены одного из столбцов на свободные члены системы:
$$ Delta_1 = begin{vmatrix} 10 & 3 & 5 \ 3 & 7 & 4 \ 3 & 2 & 2 end{vmatrix} = $$
$$ = 10 cdot 7 cdot 2 + 3 cdot 4 cdot 3 + 3 cdot 2 cdot 5 — 5 cdot 7 cdot 3 — 4 cdot 2 cdot 10 — 3 cdot 3 cdot 2 = $$
$$ = 140 + 36 + 30 — 105 — 80 — 18 = 3 $$
$$ Delta_2 = begin{vmatrix} 2 & 10 & 5 \ 3 & 3 & 4 \ 1 & 3 & 2 end{vmatrix} = $$
$$ = 2 cdot 3 cdot 2 + 10 cdot 4 cdot 1 + 3 cdot 3 cdot 5 — 5 cdot 3 cdot 1 — 4 cdot 3 cdot 2 — 10 cdot 3 cdot 2 = $$
$$ = 12 + 40 + 45 — 15 — 24 — 60 = -2 $$
$$ Delta_3 = begin{vmatrix} 2 & 3 & 10 \ 3 & 7 & 3 \ 1 & 2 & 3 end{vmatrix} = $$
$$ = 2 cdot 7 cdot 3 + 3 cdot 3 cdot 1 + 3 cdot 2 cdot 10 — 10 cdot 7 cdot 1 — 3 cdot 2 cdot 2 — 3 cdot 3 cdot 3 = $$
$$ = 42 + 9 + 60 — 70 — 12 — 27 = 2 $$
Теперь вычислим коэффициенты $ alpha, beta, gamma $:
$$ alpha = frac{Delta_1}{Delta} = frac{3}{1} = 3 $$
$$ beta = frac{Delta_2}{Delta} = frac{-2}{1} = -2 $$
$$ gamma = frac{Delta_3}{Delta} = frac{2}{1} = 2 $$
Зная постоянные $ alpha, beta, gamma $, запишем разложение вектора $ overline{x} $ по векторам $ overline{p}, overline{q}, overline{r} $:
$$ overline{x} = 3overline{p} — 2overline{q} + 2overline{r} $$
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
План урока:
Разложение векторов
Координаты векторов
Сложение и вычитание векторов
Признак коллинеарности векторов
Разложение векторов
Заметим, что если два вектора a и b коллинеарны, то обязательно найдется такое число k, для которого будет справедливо равенство:
Длина а составляет 6 клеток, а длина b – 9 клеток, при этом они сонаправлены. Получается, что b длиннее a в 9/6 = 1,5 раза, а потому можно записать:
Мы смогли выразить b через а. Иначе можно сказать, что мы разложили вектор b по вектору a. Можно и наоборот, выразить b через a:
Теперь посмотрим на вектора с и d. Их длины составляют 4 и 8 клеток, то есть отличаются в 2 раза, при этом они противоположно направлены. Поэтому эти вектора можно выразить так:
Обратите внимание, что выразить, например, а через с не удастся. Действительно, предположим, что есть такое число k, что
Тогда, по определению операции умножения вектора на число, вектора а и c должны быть коллинеарными, но они таковыми не являются.
Вектор можно раскладывать не на один, а на два вектора, которые ему не коллинеарны. Покажем это на примере:
Здесь вектора р, а и b не коллинеарны, при этом р выражен через а и b:
В данном случае говорят, что р разложен на вектора а и b, а числа 2 и 4 именуют коэффициентами разложения.
Верно следующее утверждение:
Продемонстрируем, как можно осуществить такое разложение. Пусть заданы вектора с, а и b, и требуется разложить c на а и b:
На первом шаге просто отложим все три вектора от одной точки. Далее построим прямые, проходящие через вектора а и b:
Далее через конец вектора с проведем прямые, параллельные построенным на предыдущем шаге прямым. В результате у нас получится некоторый параллелограмм АВСD:
Заметим, что вектор с оказался диагональю в этом параллелограмме. Тогда, согласно правилу параллелограмма, можно записать:
Ясно, что вектора АВ и b коллинеарны, так как лежат на одной и той же прямой. Тогда найдется такое число k, для которого будет верно отношение:
Конкретно в данном случае видно по рисунку, что АВ вдвое длиннее вектора b, поэтому
Аналогично коллинеарными являются вектора а и АD, поэтому существует число m, при котором справедливо равенство:
Понятно, что числа k и m определяются единственным образом. В общем случае они могут быть не только целыми, но и дробными (в том числе иррациональными) и даже отрицательными числами. Проще говоря, они могут быть любыми действительными числами.
Задание. Найдите коэффициенты разложения вектора d на вектора e и f:
Решение. Отложим все три вектора от одной точки. Далее проведем прямые, на которых лежат вектора e и f:
Теперь через конец d проводим ещё две прямые, параллельные двум уже построенным прямым, и в результате получаем параллелограмм:
Вектор d можно представить в виде суммы:
Особняком стоит случай, когда раскладываемый вектор коллинеарен одному из тех векторов, на которые он раскладывается. В этом случае один из коэффициентов разложения оказывается равным нулю. Например, пусть с надо разложить на а и b:
Строить параллелограмм в данном случае не нужно. Так как а и с коллинеарны, то найдется некоторое число k, при котором будет выполняться равенство:
Координаты векторов
Из курса алгебры нам известна прямоугольная система координат. В ней есть оси Ох и Оу, а каждая отмеченная на плоскости точка имеет свои координаты:
Естественно, что на координатной плоскости можно отметить и вектора. Построим два вектора, которые начинаются в начале координат, имеют длину, равную единице, и направление которых совпадает с направлениями осей координат. Тот вектор, который лежит на оси Ох, обозначают буквой i, а тот, который лежит на оси Оу, обозначают как j.
Эти вектора называют единичными векторами, или ортами (ещё используется термин координатный вектор). Они не коллинеарны друг другу, а это означает, что любой вектор на плоскости можно разложить на единичные вектора. Коэффициенты такого разложения как раз и являются координатами вектора.
Посмотрим на примере, как находить координаты вектора. Пусть задан вектор а:
Нам надо разложить а по векторам i и j. Для этого их следует отложить от одной точки. Удобно перенести вектор а к началу координат:
Теперь надо через конец а провести прямые, параллельные векторам iи j. В результате получится прямоугольник АВСD:
Можно записать равенство:
Значит, и координаты данного вектора – это числа 3 и 2. Записывается это так:
Обратите внимание, что порядок чисел в скобках принципиально важен. Первое число – это коэффициент разложения, стоящий перед вектором i. Эту координату можно называть координатой х (по аналогии с координатами точек). Второе число – это коэффициент при векторе j, оно является координатой у. Также заметим очевидный факт, что координаты равных векторов одинаковы.
В приведенном выше примере легко заметить, что после того, как мы перенесли вектор в начало координат, координаты его конца (он обозначен точкой С) совпали с координатами самого вектора. Действительно, точка С имеет координаты (3; 2).
Это правильно несколько упрощает определение координат вектора. Достаточно просто отложить вектор от точки начала координат, после чего посмотреть на координаты его конечной точки. Отметим, что вектор, чье начало совпадает с началом координат, имеет особое название – радиус-вектор.
Задание. Определите координаты векторов a, b, c и d, отмеченных на рисунке:
Решение. Во всех случаях будем просто переносить вектора к началу координат, получая радиус вектора. Далее будем просто смотреть, каковы координаты конца радиус-вектора. Начнем с а:
После переноса а его конец оказался в точке А(4; 3), поэтому и координаты всего вектора можно записать так:
После переноса вершина радиус-вектора попала в точку B (1; – 3), поэтому вектор имеет координаты {1; – 3}.
Выполним построение и для с:
Конец вектора попал в точку С (3,5; 0), а потому и координаты вектора составляют {3,5; 0}.
Осталось рассмотреть d:
Здесь координаты вектора будут равны {– 2,5; – 2,5}, так как такие же координаты имеет точка D.
Ответ: а{4;3}; b{1; – 3}; с{3,5; 0}; d{– 2,5; – 2,5}.
Рассмотрим решение обратной задачи, в которой необходимо построить вектор по заранее заданным координатам.
Задание. Даны координаты вектора:
Постройте по три вектора, имеющие заданные координаты.
Решение. Проще всего построить радиус-вектор, вершина которого будет иметь те же координаты, что и требуемый вектор:
Чтобы построить ещё два вектора с такими же координатами, надо просто отложить уже построенный вектор от любых других точек:
Аналогично поступаем и во второй задаче – сначала откладываем радиус-вектор с заданными координатами, а потом добавляем ещё два равных ему вектора, отложенных от других точек:
Отдельно отметим нулевой вектор. Очевидно, что все его координаты равны нулю, так как для него можно записать такое разложение на орты:
Также можно сказать, что если отложить нулевой вектор от начала координат, то его конец также будет находиться в начале координат (так как у нулевого вектора начало и конец совпадают), то есть в точке с координатами (0; 0).
Сложение и вычитание векторов
Пусть у нас есть векторы a{x1; у1} и b{x2; у2}. Можно ли, зная только их координаты, определить их сумму и разность? Оказывается, можно. Действительно, по определению координат векторов (напомним, они являются коэффициентами разложения вектора на орты) можно записать:
Эта запись означает, что с имеет координаты {х1 + х2; у1 + у2}. В результате мы можем сформулировать правило сложения векторов:
Проиллюстрируем правило на примере. Пусть надо сложить вектора а {2; 3} и b {4; 5}. Понятно, что в результате получится новый вектор, который мы обозначим как с {х; у}. Чтобы найти его первую координату, надо сложить первые координаты векторов a и b:
x = 2 + 4 = 6
Для нахождения второй координаты складываем соответственно вторые координаты векторов:
y = 3 + 5 = 8
В итоге получился вектор с {6; 8}.
Задание. Сложите вектора, имеющие координаты:
Решение. Сначала просто складываем первые числа в скобках (и получаем координату х), а потом – вторые (и получаем координату у):
Теперь попытаемся понять, как вычислять разность двух векторов. Пусть есть вектора с заранее заданными координатами a{x1; у1} и b{x2; у2}. Снова запишем их разложение на единичные вектора:
Теперь мы можем сформулировать правило вычитания векторов:
Например, пусть надо вычесть из вектора а{5; 3} вектор b{2;1}. Искомая разность будет представлять собой вектор, чья координата х будет равна разности первых координат векторов а и b:
x = 5 — 2 = 3
Аналогично вычисляем и координату у:
y = 3 — 1 = 2
В итоге получили вектор с координатами {3; 2}.
Задание. Вычтите из вектора а вектор b, если известны их координаты:
Решение. Во всех случаях мы сначала из первой координаты вектора а вычитаем первую координату b, в результате чего получаем координату х искомого вектора. Далее повторяем процесс со второй координатой (то есть с у):
Далее рассмотрим такую операцию, как умножение вектора на число. Снова запишем, что вектор а с координатами х1и у1 можно разложить на орты следующим образом:
Это означает, что при умножении вектора на число надо просто умножить на это число каждую его координату.
Например, есть вектор а{3; 7}, который надо умножить на 5. Умножим на 5 по отдельности каждую координату:
x = 5*3 = 15
y = 5*7 = 35
В результате получился вектор {15; 35}.
Задание. Умножьте вектор а на число k, если известно, что:
Решение. Надо всего лишь умножить каждую координату а на число k, и таким образом получить новые координаты:
Признак коллинеарности векторов
Напомним, что если два вектора (обозначим их как a и b) коллинеарны, то обязательно существует такое число k, что
Из равенства (1) и рассмотренного нами правила умножения вектора на число вытекают два соотношения между этими координатами:
x1 = k * x2
y1 = k * y2
Если числа х2 и у2 не равны нулю, то можно выразить из каждого уравнения число k, после чего выражения можно будет приравнять:
Получили соотношение, которое можно считать свойством коллинеарных векторов. Это правило работает и в обратную сторону – если координаты векторов удовлетворяют выведенному отношению, то можно смело утверждать, что вектора – коллинеарны.
Примечание. Формулировка «тогда и только тогда» означает, что правило действует в обе стороны – из пропорциональности координат следует коллинеарность векторов, а из коллинеарности векторов следует пропорциональность координат.
Покажем, как пользоваться этим признаком коллинеарности векторов. Пусть вектор а имеет координаты {8; 5}, а у вектора b они равны {24; 15}. Нам надо определить, коллинеарны ли они. Для этого поделим друг на друга их координаты х:
24:8 = 3
Получили число 3. Далее поделим и координаты у:
15:5 = 3
Снова получили тройку. То, что в обоих случаях получилось одно и тоже число, указывает на то, что вектора коллинеарны. Более того, можно даже записать, что вектор b втрое больше a:
В данном примере мы делили координаты второго вектора b на координаты первого вектора a. Но можно было поступить и наоборот, делить координаты а на координаты b:
Естественно, снова получилось одинаковое число.
Особняком стоит случай, когда одна из координат вектора равна нулю. Например, пусть вектор имеет координаты {0; у1}, причем у1≠ 0. Любой коллинеарный ему вектор можно получить, умножив вектор на какое-то число k. В этом случае его координаты {x2; у2} составят:
Получается, что и у коллинеарного вектора координата х обязательно будет равняться нулю. В свою очередь координаты у2 и у1 могут быть любыми, ведь мы всегда можем найти такое число k, для которого будет выполняться условие
y2 = ky1
Например, есть вектор {0; 5}. Можно сказать, что ему будет коллинеарен любой вектор, у которого первая координата также равна нулю, в частности,
Но любой вектор, у которого координата х НЕ равна нулю, НЕ будет коллинеарен вектору {0; 5}. В частности, ему не будут коллинеарны вектора:
Аналогичная логика действует и тогда, когда нулю равна не координата х, а координата у.
Если же у вектора обе координаты равны нулю, то он является нулевым вектором, то есть точкой. Напомним, что такой вектор считается коллинеарным любому другому вектору.
Задание. Определите, являются ли коллинеарными два вектора, если их координаты равны:
Решение. В первых пяти случаях все координаты – ненулевые, а поэтому надо просто проверить их пропорциональность. Для этого надо делить координаты друг на друга:
Числа различны, поэтому вектора НЕ коллинеарны.
В следующих примерах как минимум одна из координат равна нулю, поэтому делить координаты уже не нужно.
е) {0; 5} и {0; 12}
У обоих векторов координаты х нулевые, этого достаточно, чтобы утверждать, что они коллинеарны.
ж) {0; 3} и {2; 6}
У первого вектора координата х – нулевая, в то время как у второго нет. Значит, они не коллинеарны.
з) {9; 0} и {4; 0}
У первого вектора координата х – нулевая, в то время как у второго нет. Значит, они не коллинеарны.
и) {0; 3} и {12; 0}
Здесь у первого вектора нулю равна координата х, а у второго она ненулевая, поэтому вектора не коллинеарны.
к) {0; 0} и {5; 8}
Здесь имеет место особый случай, ведь первый вектор – нулевой, то есть представляющий собой точку. Считается, что он коллинеарен любому вектору, поэтому в данном примере вектора коллинеарны.
Ответ: а) да; б) нет; в) да; г) да; д) нет; е) да; ж) нет; з) да; и) нет; к) да.
Пока что мы рассматривали задачи, в которых фигурируют только вектора. Однако в будущем мы научимся с помощью метода координат решать и другие задачи, в которых рассматриваются отрезки, треугольники, окружности и прочие геометрические фигуры.
Математика
Тема 5: Метод координат
Урок 4: Координаты вектора. Разложение вектора по двум неколлинеарным векторам
- Видео
- Тренажер
- Теория
Заметили ошибку?
Координаты вектора. Разложение вектора по двум неколлинеарным векторам.
Если векторы a⃗ и b⃗ коллинеарны и a⃗≠0⃗, то существует такое число k, что b⃗=ka⃗.
Пусть a⃗ и b⃗ – два данных вектора. Если вектор p представлен в виде p⃗=xa⃗+yb⃗, где x и y – некоторые числа, то говорят, что вектор p⃗ разложен по векторам a⃗ и b⃗. Числа x и y называются коэффициентами разложения.
Теорема
На плоскости любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.
Напомню, что для задания прямоугольной системы координат нужно провести две взаимно перпендикулярные прямые, на каждой из них выбрать направление (оно обозначается стрелкой) и выбрать единицу измерения отрезков. При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом.
В дальнейшем под длиной отрезка мы будем понимать это число.
Отложим от начала координат O единичные векторы (т.е. векторы, длины которых равны единице) i⃗ и j⃗ так, чтобы направление вектора i⃗совпало с напралением оси Ox, а направление вектора j⃗ – с направлением оси Oy. Векторы i⃗ и j⃗ назовем координатными векторами.
Координатные векторы не коллинеарны, поэтому любой вектор p⃗ можно разложить по координатным векторам, т.е. представить в виде p⃗=xi⃗+yj⃗, причем коэффициенты разложения (числа x и y) определяются единственным образом. Коэффициенты разложения вектора p⃗ по координатным векторамназываются координатными векторамиp⃗ в данной системе координат. Координаты вектора будем записывать в фигурных скобках после обозначения вектора: p⃗{x;y}.
Так как нулевой вектор можно представить в виде 0⃗=0.i⃗+0.j⃗, то его координаты равны нулю: 0⃗{0;0}. Если векторы a⃗=x1i⃗+y1j⃗ и b⃗=x2i⃗+y2j⃗ равны, то x1 = x2 и y1 = y3. Таким образом, координаты равных векторов соответственно равны.
Рассмотрим правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число.
-
Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.
Докажем это утверждение для двух векторов. Рассмотрим векторы a{x1;y1} и b{x2;y2}. Так как a⃗=x1i⃗+y1j⃗ и b ⃗=x2i⃗ +y2j⃗ ,то, пользуясь свойствами сложения векторов и умножения вектора на число, получим:
a⃗+b⃗=x1i⃗+y1j⃗+x2i⃗+y2j⃗=(x1+x2)i⃗+(y1+y2)j⃗ .
Следовательно, что координаты вектора a⃗+b⃗ равны {x1+x2; y1+y2}.
Аналогично доказывается следующее утверждение:
-
Каждая координата разности двух или более векторов равна разности соответствующих координат этих векторов.
Иными словами, если a⃗{x1;y1} и b⃗{x2;y2} – данные векторы, то вектор a⃗–b⃗ имеет координаты {x1-x2;y1-y2}.
-
Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
В самом деле, пусть вектор a⃗ имеет координаты {x;y}. Найдем координаты вектора ka⃗, гдеk – произвольное число. Так как a⃗=xi⃗+yj⃗, то kxi⃗+kyj⃗. Отсюда следует, что координаты вектора ka⃗ равны {kx;ky}.
Рассмотренные правила позволяют определить координаты любого вектора, представленного в виде алгебраической суммы данных векторов с известными координатами.
Найти координаты вектора a⃗+b⃗,если a⃗{3;2},b⃗{2;5}
Чтобы найти координаты вектора суммы, надо сложить соответствующие координаты данных векторов, получим:
a⃗+b⃗ имеет координаты {3 + 2; 2 + 5}, то есть {5; 7}
Найти координаты вектора 2a⃗, если a⃗{3;2}
Значит, вектор 2a⃗ имеет координаты {2 ⋅ 3; 2 ⋅ 2}, то есть {6;4}
Итак, сегодня мы узнали, что любой вектор можно разложить по двум неколлинеарным векторам, ввели понятие координат вектора и рассмотрели правила, позволяющие находить координаты суммы, разности векторов, и произведения вектора на число. А в следующий раз мы найдем связь между координатами вектора и координатами его начала и конца.
Заметили ошибку?
Расскажите нам об ошибке, и мы ее исправим.
Чтобы разложить, вектор b по базисным векторам a1, …, an, необходимо найти коэффициенты x1, …, xn, при которых линейная комбинация векторов a1, …, an равна вектору b:
x1a1 + … + xnan = b,
при этом коэффициенты x1, …, xn, называются координатами вектора b в базисе a1, …, an.
Пример задачи на разложение вектора по базисным векторам
Пример 1. Разложить вектор b = {8; 1} по базисным векторам p = {1; 2} и q = {3; 1}.
Решение: Составим векторное уравнение:
xp + yq = b,
которое можно записать в виде системы линейных уравнений
| 1x + 3y = 8 | |
| 2x + 1y = 1 |
из первого уравнения выражаем x
| x = 8 — 3y | |
| 2x + y = 1 |
Подставим x во второе уравнение
| x = 8 — 3y | |
| 2(8 — 3y) + y = 1 |
| x = 8 — 3y | |
| 16 — 6y + y = 1 |
| x = 8 — 3y | |
| 5y = 15 |
| x = 8 — 3y | |
| y = 3 |
| x = 8 — 3·3 | |
| y = 3 |
| x = -1 | |
| y = 3 |
Ответ: b = —p + 3q.
Базисом пространства называют такую систему векторов в которой все остальные векторы пространства можно представить в виде линейной комбинации векторов, входящих в базис.
На практике это все реализуется достаточно просто. Базис, как правило, проверяют на плоскости или в пространстве, а для этого нужно найти определитель матрицы второго, третьего порядка составленный из координат векторов. Ниже схематически записаны условия, при которых векторы образуют базис
Чтобы разложить вектор b по базисным векторам
e[1],e[2]…,e[n] необходимо найти коэффициенты x[1], …, x[n] при которых линейная комбинация векторов e[1],e[2]…,e[n] равна вектору b:
x1*e[1]+ … + x[n]*e[n] = b.
Для этого векторное уравнение следует преобразовать к системе линейных уравнений и найти решения. Это также достаточно просто реализовать.
Найденные коэффициенты x[1], …, x[n] называются координатами вектора b в базисе e[1],e[2]…,e[n].
Перейдем к практической стороне темы.
Разложение вектора по векторам базиса
Задача 1. Проверьте, образуют ли векторы a1, a2 базис на плоскости
1) a1 (3; 5), a2 (4; 2)
Решение: Составляем определитель из координат векторов и вычисляем его
Определитель не равен нулю, следовательно векторы линейно независимы, а значит образуют базис.
2) a1 (2; -3), a2 (5;-1)
Решение: Вычисляем детерминант составленный из векторов
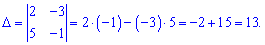
Определитель равен 13 (не равен нулю) — из этого следует что векторы a1, a2 является базисом на плоскости.
—=================—
Рассмотрим типичные примеры из программы МАУП по дисциплине «Высшая математика».
Задача 2. Показать, что векторы a1, a2, a3 образуют базис трехмерного векторного пространства, и разложить вектор b по этому базису (при решении системы линейных алгебраических уравнений использовать метод Крамера).
1) a1 (3; 1; 5), a2 (3; 2; 8), a3 (0; 1; 2), b (−3; 1; 2).
Решение: Сначала рассмотрим систему векторов a1, a2, a3 и проверим определитель матрицы А
построенной на векторах отличных от нуля. Матрица содержит один нулевой элемент, поэтому детерминант целесообразнее вычислять как расписание по первому столбцу или третей строчке.
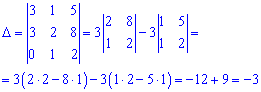
В рекзультаье вычислений получили что определитель отличен от нуля, следовательно векторы a1, a2, a3 линейно независимы.
Согласно определению векторы образуют базис в R3. Запишем расписание вектора b по базису
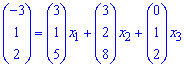
Векторы равны, когда их соответствующие координаты равны.
Поэтому из векторного уравнения получим систему линейных уравнений
Решим СЛАУ методом Крамера . Для этого запишем систему уравнений в виде
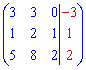
Главный определитель СЛАУ всегда равен определителю составленному из векторов базиса
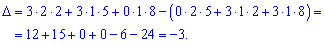
Поэтому на практике его не исчисляют дважды. Для нахождения вспомогательных определителей ставим столбец свободных членов на место каждого столбца главного определителя. Определители вычисляем по правилу треугольников
Подставим найденые определители в формулу Крамера
Итак, разложение вектора b по базису имеет вид b=-4a1+3a2-a3. Координатами вектора b в базисе a1, a2, a3 будут (-4,3,-1).
2) a1 (1; -5; 2), a2 (2; 3; 0), a3 (1; -1; 1), b (3; 5; 1).
Решение: Проверяем векторы на базис — составляем определитель из координат векторов и вычисляем его
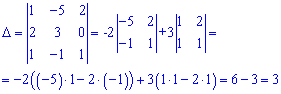
Определитель 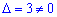
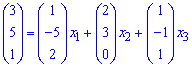
и преобразуем к системе линейных уравнений
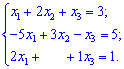
Записываем матричное уравнение
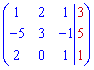
Далее для формул Крамера находим вспомогательные определители
Применяем формулы Крамера
Итак заданный вектора b имеет расписание через два вектора базиса b=-2a1+5a3, а его координаты в базисе равны b(-2,0, 5).
Задача 3. Доказать что векторы a1, a2, a3 образуют базис в пространстве
1) a1 (3;-2;1), a2 (2; -5; 4) , a3 (2; -3; -1)
Решение: Записываем координаты в определитель и применяем правило треугольников для определителя
Поскольку определитель (=35) не равен нулю то векторы образуют базис в пространстве.
2) a1 (1; 1;1), a2 (2; -3; 2) , a3 (3; 4; 1)
Решение: Вычисляем определитель составленный из векторов
Det=1*(-3)*1+1*2*3+1*2*4-(1*(-3)*3+1*2*1+1*2*4)=-3+6+8+9-2-8=10 .
Векторы a1, a2, a3 линейно независимы (Det=10), а значит образуют базис в пространстве.
Теперь Вы знаете как проверить, что векторы образуют базис и сможете без проблем разложить вектор по базису.
Посмотреть материалы:
- Длина вектора. Угол между векторами
- Разложение вектора по базису
- Смешанное произведение векторов
- Деление отрезка в заданном отношении
- Треугольная пирамида