Как найти коэффициенты уравнения плоскости

Во многих стереометрических задачах, связанных с нахождением расстояния от точки до плоскости или расстояния между скрещивающимися прямыми, или угла между плоскостями, требуется найти уравнение плоскости. В этой статье я расскажу, как найти уравнение плоскости, если известны координаты трех точек, через которые она проходит.

Уравнение плоскости имеет вид: , где , , и  — числовые коэффициенты.

Пусть  нам нужно написать уравнение плоскости, которая проходит через точки , и  

Так как точки принадлежат плоскости, то при подстановке их координат в уравнение плоскости, мы получим верные равенства.

Так как у нас три точки, мы должны получить систему из трех уравнений с четырьмя неизвестными. Примем коэффициент  равным 1. Для этого разделим уравнение плоскости на  .  Получим:

Мы можем переписать  это уравнение в виде: 

Внимание! Если плоскость проходит через начало координат, то принимаем d=0.

Чтобы найти коэффициенты А, В и С, подставим координаты точек , и   в уравнение плоскости .

Получим систему уравнений:

Решив ее, мы найдем значения коэффициентов А, В и С.

Решим задачу.

В правильной четырехугольной призме  со стороной основания 12 и высотой 21 на ребре  взята точка  так, что  равно 8. на ребре  взята точка  так, что  равно 8. Написать уравнение плоскости :

Поскольку для нахождения уравнения плоскости нам понадобятся координаты точек, я сразу помещаю призму в систему координат:

Запишем координаты точек:

Подставим их в систему уравнений:

Отсюда:

Подставим найденные коэффициенты в уравнение плоскости:

Чтобы избавиться от дробных коэффициентов, умножим обе части уравнения плоскости на . Получим:

Ответ: уравнение плоскости   

И.В. Фельдман, репетитор по математике.

Общее уравнение плоскости

В данной статье мы рассмотрим общее уравнение плоскости в пространстве. Определим понятия полного и неполного уравнения плоскости. Для построения общего уравнения плоскости пользуйтесь калькулятором уравнение плоскости онлайн.

Пусть задана произвольная декартова прямоугольная система координат Oxyz. Общим уравнением плоскости называется линейное уравнение вида:

где A, B, C, D − некоторые постоянные, причем хотя бы один из элементов A , B и C отлично от нуля.

Мы покажем, что линейное уравнение (1) в пространстве определяет плоскость и любой плоскость в пространстве можно представить линейным уравнением (1). Докажем следующую теорему.

Теорема 1. В произвольной декартовой прямоугольной системе координат в пространстве каждая плоскость α может быть задана линейным уравнением (1). Обратно, каждое линейное уравнение (1) в произвольной декартовой прямоугольной системе координат в пространстве определяет плоскость.

Доказательство. Достаточно доказать, что плоскость α определяется линейным уравнением при какой нибудь одной декартовой прямоугольной системе координат, поскольку тогда она будет определяться линейным уравнением и при любом выборе декартовой прямоугольной системы координат.

Пусть в пространстве задана плоскость α. Выберем оси Ox и Oy так, чтобы они располагались на плоскости α, а ось Oz направим перпендикулярно к этой плоскости. Тогда линейное уравнение z=0 будет уравнением плоскости, т.к. координаты любой точки, принадлежащей этой плоскости удовлетворяют уравнению z=0, а координаты любой точки, не лежащей на этой плоскости − нет. Первая часть теоремы доказана.

Пусть фиксирована произвольная декартова прямоугольная система координат Oxyz. Рассмотрим линейное уравнение (1), где хотя бы один из элементов A , B и C отлично от нуля. Тогда уравнение (1) имеет хотя бы одно решение x₀, y₀, z₀. Действительно. Пусть из коэффициентов A≠0. Возьмем произвольные числа y₀, z₀. Тогда

.

Таким образом, существует точка M₀(x₀, y₀, z₀), координаты которой удовлетворяют уравнению (1):

Вычитая из уравнения (1) тождество (2), получим

A(x−x0)+B(y−y0)+С(z−z0)=0,

(3)

которая эквивалентна уравнению (1).

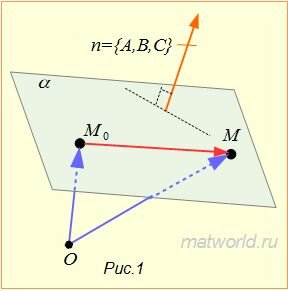
Покажем, что (3) определяет некоторую плоскость, проходящую через точку M₀(x₀, y₀, z₀) и перпендикулярную вектору n=<A,B,C> (n≠0, так как хотя бы один из чисел A,B,C отлично от нуля).

Если точка M₀(x₀, y₀, z₀) принадлежит плоскости α, то ее координаты удовлетворяют уравнению (3), т.к. векторы n=<A,B,C> и перпендикулярны (Рис.1) и их скалярное произведение равно нулю:

Если же точка M(x, y, z) не лежит на плоскости α, то векторы n=<A,B,C> и не ортогональны. Тогда их скалярное произведение не равно нулю, т.е. координаты точки M(x, y, z) не удовлетворяют условию (3). Теорема доказана.

Одновременно с доказательством теоремы 1 мы получили следующее утверждение.

Утверждение 1. В декартовой прямоугольной системе координат вектор с компонентами (A,B,C) перпендикулярен плоскости Ax+By+Cz+D=0.

Вектор n=(A,B,C) называется нормальным вектором плоскости , определяемой линейным уравнением (1).

Утверждение 2. Если два общих уравнения плоскости

определяют одну и ту же плоскость, то найдется такое число λ, что выпонены равенства

A2=A1λ, B2=B1λ, C2=C1λ, D2=D1λ.

(6)

Умножая уравнение (7) на λ и вычитая из него уравнение (8) получим:

(A₁λ−A₂)x₀+(B₁λ−B₂)y₀+(C₁λ−C₂)z₀+(D₁λ−D₂)=0.

Так как выполнены первые три равенства из выражений (6), то D₁λ−D₂=0. Т.е. D₂=D₁λ. Утверждение доказано.

Неполные уравнения плоскости

Определение 1. Общее уравнение плоскости (1) называется полным , если все коэффициенты A, B, C, D отличны от нуля. Если же хотя бы один из коэффициентов A, B, C, D равен нулю, то общее уравнение плоскости называется неполным .

Рассмотрим все возможные варианты неполных уравнений плоскости:

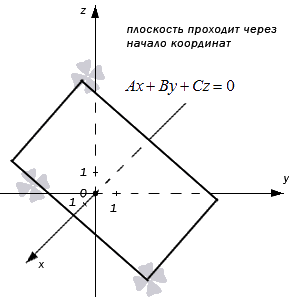
При D=0, имеем уравнение плоскости Ax+By+Cz=0, проходящей через начало координат (Рис.2). Действительно, точка O(0,0,0) удовлетворяет этой системы линейных уравнений.

При A=0, имеем уравнение плоскости By+Cz+D=0, которая параллельна оси Ox (Рис.3). В этом случае нормальный вектор плоскости n=<0,B,C> лежит на координатной плоскости Oyz.

При B=0, имеем уравнение плоскости Ax+Cz+D=0, которая параллельна оси Oy (Рис.4).

При C=0, имеем уравнение плоскости Ax+By+D=0, которая параллельна оси Oz (Рис.5).

При A=0,B=0 имеем уравнение плоскости Cz+D=0, которая параллельна координатной плоскости Oxy (Рис.6).

При B=0,C=0 имеем уравнение плоскости Ax+D=0, которая параллельна координатной плоскости Oyz (Рис.7).

При A=0,C=0 имеем уравнение плоскости By+D=0, которая параллельна координатной плоскости Oxz (Рис.8).

При A=0,B=0,D=0 имеем уравнение плоскости Cz=0, которая совпадает с координатной плоскостью Oxy (Рис.9).

При B=0,C=0,D=0 имеем уравнение плоскости Ax=0, которая совпадает с координатной плоскостью Oyz (Рис.10).

При A=0,C=0,D=0 имеем уравнение плоскости By=0, которая совпадает с координатной плоскостью Oxz (Рис.11).

Рассмотрим примеры построения общего уравнения плоскости.

Пример 1. Построить общее уравнение плоскости, проходящей через точку M(4,−1,2) параллельной координатной плоскости Oxy.

Решение. Общее уравнение плоскости, проходящей через некоторую точку M(x₀,y₀,z₀) имеет вид (3). Подставляя координаты точки M в (3), получим:

A(x−4)+B(y−(−1))+C(z−2)=0

(9)

Так как плоскость параллельна координатной плоскости Oxy, то направляющий вектор имеет следующий вид n=<A,B,C>=<0,0,1>, т.е. A=0, B=0, C=1.

Подставляя коэффициенты A,B,C в (9), получим:

0(x−4)+0(y−(−1))+1(z−2)=0

(9)

Пример 2. Построить общее уравнение плоскости, проходящей через начало координат и имеющий нормальный вектор n==<2,3,1>.

Решение. Начало координат имеет коэффициенты (0,0,0). Общее уравнение плоскости, проходящей через некоторую точку M(x₀,y₀,z₀) имеет вид (3). Подставляя коэффициенты начальной точки в (3), получим:

A(x−0)+B(y−0)+C(z−0)=0

(10)

Так как плоскость имеет нормальный вектор n=<A,B,C>=<2,3,1>, т.е. A=2, B=3, C=1, подставляя коэффициенты A,B,C в (10), получим:

2(x−0)+3(y−0)+1(z−0)=0

(9)

Онлайн калькулятор для построения общего уравнения плоскости находится здесь. Там же вы найдете примеры построения общего уравнения плоскости, если известны три точки этой плоскости или если известна одна точка и нормальный вектор этой плоскости.

Общее уравнение плоскости в пространстве геометрический смысл его коэффициентов

Выяснить геометрический смысл коэффициентов A, B и C в общем уравнении плоскости Ax + By + Cz + D = 0.

1. Рассмотрим вектор с проекциями на координатные оси, соответственно равными A, B и C, т. е. .

2. Возьмем на плоскости Ax + By + Cz + D = 0 две произвольные точки M( x₁, y₁, z₁) и N( x₂, y₂, z₂) и рассмотрим вектор . Этот вектор лежит в плоскости Ax + By + Cz + D = 0. Его проекции на координатные оси соответственно равны x₂ — x₁, y₂ — y₁, z₂ — z₁ и .

3. Так как точки M и N лежат в плоскости Ax + By + Cz + D = 0, то имеют место равенства

Вычитая первое уравнение из второго, получим

Скалярное произведение вектора на вектор равно

Так как на основании (1) это скалярное произведение равно нулю, то вектор перпендикулярен вектору , а тем самым и той плоскости, в которой лежит этот вектор, т. е. вектор перпендикулярен плоскости Ax + By + Cz + D = 0.

Геометрическое значение коэффициентов A, B и C в общем уравнении плоскости Ax + By + Cz + D = 0 состоит в том, что они являются проекциями на координатные оси Ox, Oy, Oz вектора, перпендикулярного этой плоскости.

Общее уравнение плоскости : описание, примеры, решение задач

В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.

Общее уравнение плоскости: основные сведения

Перед началом разбора темы вспомним, что такое уравнение плоскости в прямоугольной системе координат в трёхмерном пространстве. Пусть нам дана прямоугольная система координат O x y z в трехмерном пространстве, уравнением плоскости в заданной системе координат будет такое уравнение с тремя неизвестными x , y , и z , которому отвечали бы координаты всех точек этой плоскости и не отвечали бы координаты никаких прочих точек. Иначе говоря, подставив в уравнение плоскости координаты некоторой точки этой плоскости, получаем тождество. Если же в уравнение подставить координаты какой-то другой точки, не принадлежащей заданной плоскости, равенство станет неверным.

Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.

Любую плоскость, заданную в прямоугольной системе координат O x y z трехмерного пространства, можно определить уравнением A x + B y + C z + D = 0 . В свою очередь, любое уравнение A x + B y + C z + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A , B , C , D – некоторые действительные числа, и числа A , B , C не равны одновременно нулю.

Теорема состоит из двух частей. Разберем доказательство каждой из них.

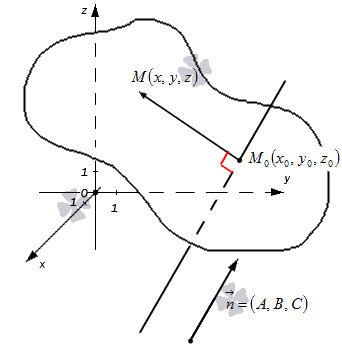
1. Первая часть теоремы гласит, что любую заданную плоскость возможно описать уравнением вида A x + B y + C z + D = 0 . Допустим, задана некоторая плоскость и точка M 0 ( x 0 , y 0 , z 0 ) , через которую эта плоскость проходит. Нормальным вектором этой плоскости является n → = ( A , B , C ) . Приведем доказательство, что указанную плоскость в прямоугольной системе координат O x y z задает уравнение A x + B y + C z + D = 0 .

Возьмем произвольную точку заданной плоскости M ( x , y , z ) .В таком случае векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю:

n → , M 0 M → = A x — x 0 + B ( y — y 0 ) + C ( z — z 0 ) = A x + B y + C z — ( A x 0 + B y 0 + C z 0 )

Примем D = — ( A x 0 + B y 0 + C z 0 ) , тогда уравнение преобразуется в следующий вид: A x + B y + C z + D = 0 . Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.

1. Во второй части теоремы утверждается, что любое уравнение вида A x + B y + C z + D = 0 задает некоторую плоскость в прямоугольной системе координат O x y z трехмерного пространства. Докажем это.

В теореме также указано, что действительные числа А , B , C одновременно не являются равными нулю. Тогда существует некоторая точка M 0 ( x 0 , y 0 , z 0 ) , координаты которой отвечают уравнению A x + B y + C z + D = 0 , т.е. верным будет равенство A x 0 + B y 0 + C z 0 + D = 0 . Отнимем левую и правую части этого равенства от левой и правой частей уравнения A x + B y + C z + D = 0 . Получим уравнение вида

A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 , и оно эквивалентно уравнению A x + B y + C z + D = 0 . Докажем, что уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает некоторую плоскость.

Уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 являет собой условие, необходимое и достаточное для перпендикулярности векторов n → = ( A , B , C ) и M 0 M → = x — x 0 , y — y 0 , z — z 0 . Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 множество точек M ( x , y , z ) задает плоскость, у которой нормальный вектор n → = ( A , B , C ) . При этом плоскость проходит через точку M ( x 0 , y 0 , z 0 ) . Иначе говоря, уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает в прямоугольной системе координат O x y z трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение A x + B y + C z + D = 0 также определяет эту плоскость. Теорема доказана полностью.

Уравнение вида A x + B y + C z + D = 0 называют общим уравнением плоскости в прямоугольной системе координат O x y z трехмерного пространства.

Допустим, задано некоторое общее уравнение плоскости λ · A x + λ · B y + λ · C z + λ · D = 0 , где λ – некое действительное число, не равное нулю. Это уравнение также задает в прямоугольной системе координат некоторую плоскость, совпадающую с плоскостью, определяемую уравнением A x + B y + C z + D = 0 , поскольку описывает то же самое множество точек трехмерного пространства. Например, уравнения x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 задают одну и ту же плоскость, поскольку им обоим отвечают координаты одних и тех же точек трехмерного пространства.

Раскроем чуть шире смысл теорем.

В пределах заданной системы координат плоскость и общее уравнение, ее определяющее, неразрывно связаны: каждой плоскости отвечает общее уравнение плоскости вида A x + B y + C z + D = 0 ( при конкретных значениях чисел A , B , C , D ). В свою очередь, этому уравнению отвечает заданная плоскость в заданной прямоугольной системе координат.

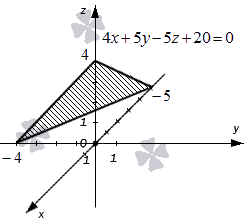
Укажем пример как иллюстрацию этих утверждений.

Ниже приведен чертеж, на котором изображена плоскость в фиксированной прямоугольной системе координат трехмерного пространства. Заданной плоскости отвечает общее уравнение вида 4 x + 5 y – 5 z + 20 = 0 , и ему соответствуют координаты любой точки этой плоскости. В свою очередь, уравнение 4 x + 5 y – 5 z + 20 = 0 описывает в заданной системе координат множество точек, которые составляют изображенную плоскость.

Общее уравнение плоскости, проходящей через точку

Повторимся: точка M 0 ( x 0 , y 0 , z 0 ) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением A x + B y + C z + D = 0 в том случае, когда подставив координаты точки M 0 ( x 0 , y 0 , z 0 ) в уравнение A x + B y + C z + D = 0 , мы получим тождество.

Заданы точки M 0 ( 1 , — 1 , — 3 ) и N 0 ( 0 , 2 , — 8 ) и плоскость, определяемая уравнением 2 x + 3 y — z — 2 = 0 . Необходимо проверить, принадлежат ли заданные точки заданной плоскости.

Решение

Подставим координаты точки М 0 в исходной уравнение плоскости:

2 · 1 + 3 · ( — 1 ) — ( — 3 ) — 2 = 0 ⇔ 0 = 0

Мы видим, что получено верное равенство, значит точка M 0 ( 1 , — 1 , — 3 ) принадлежит заданной плоскости.

Аналогично проверим точку N 0 . Подставим ее координаты в исходное уравнение:

2 · 0 + 3 · 2 — ( — 8 ) — 2 = 0 ⇔ 12 = 0

Равенство неверно. Таким, образом, точка N 0 ( 0 , 2 , — 8 ) не принадлежит заданной плоскости.

Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит.

Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n → = ( A , B , C ) — нормальный вектор для плоскости, определяемой уравнением A x + B y + C z + D = 0 . Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости.

В прямоугольной системе координат задана плоскость 2 x + 3 y — z + 5 = 0 . Необходимо записать координаты всех нормальных векторов заданной плоскости.

Решение

Мы знаем, что заданные общим уравнением коэффициенты при переменных x , y , z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n → исходной плоскости имеет координаты 2 , 3 , — 1 . В свою очередь, множество нормальных векторов запишем так:

λ · n → = λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0

Ответ: λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0

Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.

Очевидным фактом является то, что нормальный вектор n → = ( A , B , C ) является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M 0 ( x 0 , y 0 , z 0 ) , принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали.

Общее уравнение плоскости с нормальным вектором n → = ( A , B , C ) будет выглядеть так: A x + B y + C z + D = 0 . По условию задачи точка M 0 ( x 0 , y 0 , z 0 ) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство: A x 0 + B y 0 + C z 0 + D = 0

Вычитая соответственно правые и левые части исходного уравнения и уравнения A x 0 + B y 0 + C z 0 + D = 0 , получим уравнение вида A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 . Оно и будет уравнением плоскости, проходящей через точку M 0 ( x 0 , y 0 , z 0 ) и имеющей нормальный вектор n → = ( A , B , C ) .

Возможно получить это уравнение другим способом.

Очевидным фактом является то, что все точки М ( x , y , z ) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю:

n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0

Задана точка М 0 ( — 1 , 2 , — 3 ) , через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n → = ( 3 , 7 , — 5 ) . Необходимо записать уравнение заданной плоскости.

Решение

Рассмотрим два способа решения.

1. Исходные условия позволяют получить следующие данные:

x 0 = — 1 , y 0 = 2 , z 0 = — 3 , A = 3 , B = 7 , C = — 5

Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0

3 ( x — ( — 1 ) ) + 7 ( y — 2 ) — 5 ( z — ( — 3 ) ) = 0 ⇔ 3 x + 7 y — 5 z — 26 = 0

1. Допустим, М ( x , y , z ) – некоторая точки заданной плоскости. Определим координаты вектора M 0 M → по координатам точек начала и конца:

M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) = ( x + 1 , y — 2 , z + 3 )

Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:

n → , M 0 M → = 0 ⇔ 3 ( x + 1 ) + 7 ( y — 2 ) — 5 ( z + 3 ) = 0 ⇔ ⇔ 3 x + 7 y — 5 z — 26 = 0

Ответ: 3 x + 7 y — 5 z — 26 = 0

Неполное общее уравнение плоскости

Выше мы говорили о том, что, когда все числа А , B , C , D отличны от нуля, общее уравнение плоскости A x + B y + C z + D = 0 называют полным. В ином случае общее уравнение плоскости является неполным.

Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.

1. В случае, когда D = 0 , мы получаем общее неполное уравнение плоскости: A x + B y + C z + D = 0 ⇔ A x + B y + C z = 0

Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О ( 0 , 0 , 0 ) , то придем к тождеству:

A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0

1. Если А = 0 , В ≠ 0 , С ≠ 0 , или А ≠ 0 , В = 0 , С ≠ 0 , или А ≠ 0 , В ≠ 0 , С = 0 , то общие уравнения плоскостей имеют вид соответственно: B y + C z + D = 0 , или A x + C z + D = 0 , или A x + B y + D = 0 . Такие плоскости параллельны координатным осям О x , O y , O z соответственно. Когда D = 0 , плоскости проходят через эти координатные оси соответственно. Также заметим, что неполные общие уравнения плоскостей B y + C z + D = 0 , A x + C z + D = 0 и A x + B y + D = 0 задают плоскости, которые перпендикулярны плоскостям O y z , O x z , O z y соответственно.

1. При А = 0 , В = 0 , С ≠ 0 , или А = 0 , В ≠ 0 , С = 0 , или А ≠ 0 , В = 0 , С = 0 получим общие неполные уравнения плоскостей: C z + D = 0 ⇔ z + D C = 0 ⇔ z = — D C ⇔ z = λ , λ ∈ R или B y + D = 0 ⇔ y + D B = 0 ⇔ y = — D B ⇔ y = λ , λ ∈ R или A x + D = 0 ⇔ x + D A = 0 ⇔ x = — D A ⇔ x = λ , λ ∈ R соответственно.

Эти уравнения определяют плоскости, которые параллельны координатным плоскостям O x y , O x z , O y z соответственно и проходят через точки 0 , 0 , — D C , 0 , — D B , 0 и — D A , 0 , 0 соответственно. При D = 0 уравнения самих координатных плоскостей O x y , O x z , O y z выглядят так: z = 0 , y = 0 , x = 0

Задана плоскость, параллельная координатной плоскости O y z и проходящая через точку М 0 ( 7 , — 2 , 3 ) . Необходимо составить общее уравнение заданной плоскости.

Р​​ешение

У​​​​​словием задачи определено, что заданная плоскость параллельна координатной плоскости O y z , а, следовательно, может быть задана общим неполным уравнением плоскости A x + D = 0 , A ≠ 0 ⇔ x + D A = 0 . Поскольку точка M 0 ( 7 , — 2 , 3 ) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости x + D A = 0 , иначе говоря, должно быть верным равенство 7 + D A = 0 . Преобразуем: D A = — 7 , тогда требуемое уравнение имеет вид: x — 7 = 0 .

Задачу возможно решить еще одним способом.

Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости O y z . Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости O y z : i → = ( 1 , 0 , 0 ) . Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости:

A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 ⇔ ⇔ 1 · ( x — 7 ) + 0 · ( y + 2 ) + 0 · ( z — 3 ) = 0 ⇔ ⇔ x — 7 = 0

Ответ: x — 7 = 0

Задана плоскость, перпендикулярная плоскости O x y и проходящая через начало координат и точку М 0 ( — 3 , 1 , 2 ) .

Решение

Плоскость, которая перпендикулярна координатной плоскости O x y определяется общим неполным уравнением плоскости A x + B y + D = 0 ( А ≠ 0 , В ≠ 0 ) . Условием задачи дано, что плоскость проходит через начало координат, тогда D = 0 и уравнение плоскости принимает вид A x + B y = 0 ⇔ x + B A y = 0 .

Найдем значение B A . В исходных данных фигурирует точка М 0 ( — 3 , 1 , 2 ) , координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: — 3 + B A · 1 = 0 , откуда определяем B A = 3 .

Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x + 3 y = 0 .

Для начала стоит напомнить, как выглядит общее уравнение плоскости:

$Ax cdot + By + Cz + D = 0left(1right)$,

при этом: ${A; B; C}$ — координаты нормального вектора данной плоскости, а $D$ — свободный член.

В общем уравнении коэффициенты $A, B, C$ не могут быть одновременно равны нулю, если же один из коэффициентов нулевой — уравнение называется неполным. При $D=0$ плоскость проходит через центр осей координат.

Также в дальнейшем нам пригодится уравнение плоскости, заданной точкой, лежащей в данной плоскости и нормальным вектором:

$A(x-x_0)+B(y-y_0) + C(z-z_0)=0left(2right)$,

здесь $(x_0; y_0; z_0)$ — координаты точки плоскости.

Теперь непосредственно к делу.

Уравнение плоскости через три точки можно выразить несколькими способами: с помощью смешанного произведения векторов и выразив сначала нормальный вектор плоскости и используя одну точку.

Уравнение плоскости, проходящей через 3 точки, через смешанное произведение векторов

Рассмотрим три точки $M_1, M_2, M_3$, не находящиеся на одной прямой. Соответственно аксиоме стереометрии о том, что три точки задают плоскость, и притом только одну, все эти точки лежат в одной плоскости $α$.

Рассмотрим точку $M$, лежащую в плоскости $α$. Если описать плоскость $α$ как множество точек $M$, вектора $vec{M_1M_2}$, $vec{M_1M_3}$ и $vec{M_1M}$ должны быть компланарны между собой. А как известно, вектора компланарны между собой если их смешанное произведение равно нулю.

Соответственно, для того чтобы вычислить это смешанное произведение, необходимо вычислить определитель третьего порядка, каждая строка которого является координатами вышеперечисленных векторов.

«Уравнение плоскости через 3 точки» 👇

Пусть координаты точек $M, M_1, M_2, M_3$ — $(x; y; z), (x_1;y_1; z_1), (x_2;y_2; z_2), (x_3;y_3;z_3)$ соответственно. Тогда координаты каждого из вышеперечисленных векторов составят:

$vec{M_1M_2}={x_2-x_1; y_2-y_1; z_2-z_1}$;

$vec{M_1M_3}= {x_3-x_1; y_3-y_1; z_3-z_1}$;

$vec{M_1M} = {x-x_1; y-y_1; z-z_1}$.

Составим определитель, описывающий смешанное произведение векторов:

$begin{array}{|ccc|} x-x_1 && y-y_1 && z-z_1 \ x_2-x_1 && y_2-y_1 && z_2-z_1 \ x_3-x_1 && y_3-y_1 &&z_3-z_1 \ end{array}=0$ — уравнение плоскости через 3 точки.

При вычислении этого определителя получается общее уравнение плоскости, проходящей через три точки. Это можно увидеть, раскрыв определитель по первой строке:

$begin{array}{|cc|} y_2-y_1 && z_2-z_1 \ y_3-y_1 &&z_3-z_1 \ end{array} cdot ( x-x_1) + begin{array}{|cc|} x_2-x_1 && z_2-z_1 \ x_3-x_1 &&z_3-z_1 \ end{array} cdot (y-y_1) + begin{array}{|cc|} x_2-x_1 && y_2-y_1 \ x_3-x_1 && y_3-y_1 \ end{array} cdot (z-z_1) = 0left(3right)$.

Коэффициенты из уравнения $(3)$ также совпадают с координатами векторного произведения $vec{M_1M_2}×vec{M_1M_3}$ и, так как два этих вектора неколлинеарны и параллельны рассматриваемой плоскости $α$, данное векторное произведение представляет собой нормальный вектор к плоскости, для которой составляется уравнение.

Уравнение плоскости, заданной 3 точками, через нормальный вектор и точку

Другим альтернативным методом задания плоскости является использование нормального вектора плоскости и точки, принадлежащей данной плоскости.

Для того чтобы воспользоваться данным методом, найдём векторное произведение векторов $vec{M_1M_2}$ и $vec{M_1M_3}$:

$[vec{M_1M_2} × vec{M_1M_3}]= begin{array}{|ccc|} vec{i} &&vec{j} &&vec{k} \ x_2-x_1 &&y_2-y_1 &&z_2-z_1 \ x_3-x_1 &&y_3-y_1 &&z_3-z_1 \ end{array}=0$.

Данное произведение является нормальным вектором плоскости, для которой составляется уравнение. Полученные координаты нормального вектора можно использовать непосредственно для составления уравнения плоскости.

Зная точку, принадлежащую этой плоскости, можно подставить координаты нормального вектора и координаты точки в уравнение $(2)$ и получить уравнение плоскости:

$n_x(x-x_3)+n_y(y-y_3)+n_z(z-z_3)=0$.

В этом уравнении $n_x; n_y; n_z$ — координаты нормального вектора, определённого из векторного произведения векторов $vec{M_1M_2}$ и $vec{M_1M_3}$, а $(x_3; y_3; z_3)$ — некая точка, принадлежащая данной плоскости.

К данной задаче можно также свести задачу с нахождением уравнения плоскости по уравнениям лежащих в ней параллельных и пересекающихся прямых.

– уравнение плоскости, проходящей через заданную точку
перпендикулярно заданному вектору.

Раскроем скобки: После обозначения получим
общее уравнение плоскости:

Ax+By+Cz+D=0.                                                                                                                                                                           (2.39)

Равенство
(2.39) имеет смысл при условии, что 
его  коэффициенты  не равны

нулю
одновременно, то есть   A²+B²+ C² ≠ 0.

Предположим, что все коэффициенты уравнения (2.39)
отличны от нуля, тогда  Ax+By+Cz = –D. Поделив это равенство на  , имеем  После обозначений;
 получим
уравнение плоскости в отрезках, отсекаемых ею на осях координат: 

                                                                                                                                                                   (2.40)

1).
Докажем, что  α – длина отрезка, отсекаемого плоскостью α на
оси  0x (при  y=z=0). В этом случае уравнение (2.40)
принимает вид: .

2). Докажем, что b – длина отрезка, отсекаемого плоскостью α на оси 0y (при x=z=0): уравнение (2.40) 
  3). Докажем, что c – длина отрезка, отсекаемого
плоскостью α на оси
0z (при x=y=0):
уравнение (2.40)    (рис. 2.19).  

Известно, что плоскость в пространстве
единственным образом задаётся тремя точками. Пусть точка M(x;y;z) – текущая точка на плоскости α. Тогда векторы 
компланарны и
исходят из одного начала (рис. 2.20).

     

 По теореме 2.6 необходимым и достаточным условием
компланарности трех векторов является равенство нулю их смешанного
произведения:  Согласно
теореме 2.7 и формуле (2.35) получаем

                                                                                                                                                          (2.41)

– уравнение
плоскости, проходящей  через три заданные
точки (см. рис. 2.20).

Пусть положение плоскости α в пространстве определяется заданием единичного вектора, имеющего направление перпендикуляра, опущенного на
плоскость из начала координат, и длиной  p этого
перпендикуляра. Пусть α, β, γ – углы,
образованные единичным вектором  с осями
координат 0x, 0y, 0z
соответственно. Тогда 

Возьмем на
плоскости произвольную точку М(x;y;z) и соединим
ее с началом координат, при этом образуем вектор    При любом положении точки М  на плоскости α проекция  на направление
вектора

 всегда равна p, то есть  или скалярное
произведение векторов   Зная координаты векторов, с помощью теоремы (2.3)
можно записать:

                                                                                                                                                 (2.42)

Уравнение (2.42) называется нормальным уравнением плоскости.

Заметим, что общее уравнение плоскости (2.39) можно
привести к нормальному уравнению (2.42) так, как это уже делалось для уравнения
прямой на плоскости. А именно: умножить обе части уравнения (2.39) на нормирующий
множитель , где знак берется противоположным знаку свободного
члена D  общего уравнения плоскости.

Пример 2.14.
Составить общее уравнение плоскости, проходящей через три точки: A(–1;2;3), B(4;0;–1), C(1;5;–2). Найти длины отрезков, отсекаемых ею на осях
координат.

Решение. Пусть точки  тогда по уравнению (2.41) получим:

Разложим данный определитель с помощью
теоремы Лапласа по первой строке (смотри формулу (1.3)):

                                                                 –
общее уравнение искомой плоскости.

Разделим данное уравнение на свободный член 69,
получим уравнение плоскости в отрезках вида (2.40):

Отсюда длины отрезков, отсекаемых плоскостью на осях координат,
соответственно равны: 

Пусть задано уравнение (2.39) – общее уравнение плоскости  в пространстве: Ax+By+Cz+D=0. Рассмотрим различные варианты коэффициентов данного уравнения.

1. При          A=0  –  плоскость α паралельна оси 0x;                  

              B=0 –  плоскость α паралельна оси 0y;

              C=0 –  плоскость α паралельна оси 0z;

              D=0 –  плоскость  проходит через начало координат.

2. При          A=D=0 –  плоскость  проходит  через ось 0x;

              B=D=0  –  плоскость α проходит  через ось 0y;

             C=D=0   –  плоскость α проходит  через ось 0z.

3. При  плоскость α перпендикулярна   0z;

 плоскость α перпендикулярна оси  0y;  

 плоскость α перпендикулярна оси  0x.

4. При  –  уравнение  плоскости  x0y;

      –  уравнение  плоскости  y0z;        

      –  уравнение  плоскости  x0z.

Если все коэффициенты (2.39) отличны от нуля,  то плоскость в пространстве пересекает оси координат произвольным образом.

 Пример 2.15. Составить уравнение плоскости проходящей через ось 0x и точку P(1,–1,3).

Решение. Так как по условию плоскость проходит через ось 0x, то в  уравне­нии (2.39) коэффициенты A=D=0. Следовательно, общее уравнение искомой плоскости имеет вид By+Cz=0. По условию точка P принадлежит плоскости, значит, ее координаты удовлетворяют последнему равенству, то есть –B+3C=0  или  B=3C.

Подставляя найденное соотношение коэффициентов в уравнение By+Cz=0, получим 3Cy+Cz=0 . После сокращения на C искомое уравнение принимает вид: 3y+x=0.

Вопросы для самопроверки