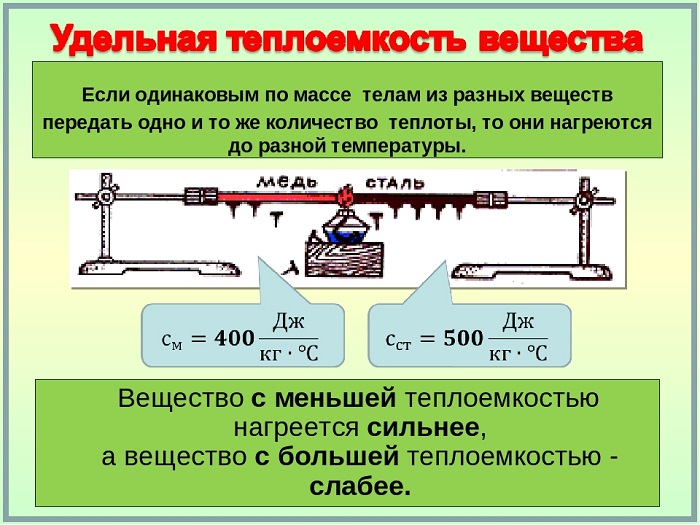
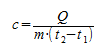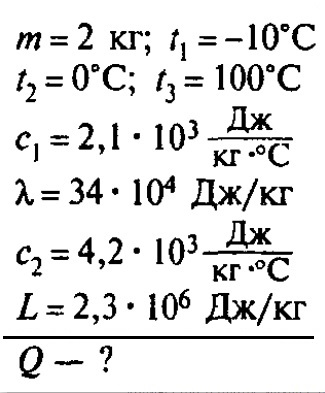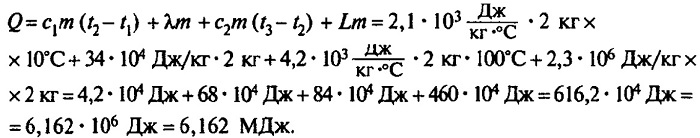Физика под удельной теплоемкостью понимает количество теплоты, которое термодинамическое вещество или система способно поглотить до повышения температуры.
Определение из учебника говорит, что это количество тепла, необходимое для создания температуры при нагревании.
Количество теплоты
Единица измерения — джоуль. Другой распространенной формой измерения является использование калорий.
Обозначается латинской буквой Q.
Удельная теплоемкость вещества
Это физическая величина, выражающая количество тепла, необходимое веществу на единицу массы для повышения температуры на одну единицу.
Таким образом, удельная теплоёмкость является свойством вещества, поскольку его значение является репрезентативным для каждого вещества, каждое из которых, в свою очередь, имеет различные значения в зависимости от того, в каком состоянии оно находится (жидкое, твердое или газообразное).
Удельная теплоёмкость обозначается маленькой буквой c и измеряется в Дж/кг∗°С, представляет собой коэффициент повышения температуры в одной единице всей системы или всей массы вещества.
Кроме того, удельная теплоёмкость меняется в зависимости от физического состояния вещества, особенно в случае твердых частиц и газов, поскольку его молекулярная структура влияет на теплопередачу в системе частиц. То же самое относится и к условиям атмосферного давления: чем выше давление, тем ниже удельное тепло.
Основной состав удельной теплоты вещества должен быть с = С/m, т. е. удельная теплота равна соотношению калорийности и массы. Однако когда это применяется к данному изменению температуры, говорят о средней удельной теплоемкости, которая рассчитывается на основе следующей формулы:
где:
Q — передача тепловой энергии между системой и средой (Дж);
m — масса системы (кг);
Δt или (t2 — t1) — повышение температуры, которой она подвергается (°C).
Формула для нахождения количества теплоты Q:
Q = c∗m(t2 — t1)
Чем выше удельная теплоёмкость вещества, тем больше тепловой энергии потребуется, чтобы его температура повысилась. Например, для нагрева воды (своды = 4200 Дж/кг∗°С) потребуется больше тепловой энергии, чем для нагрева свинца (ссвинца = 140 Дж/кг∗°С).
Уравнение теплового баланса:
Q отданное + Q полученное = 0.
Ниже представлена таблица значений удельной теплоёмкости некоторых веществ:
Примеры решения задач
Следующие задачи покажут примеры расчета необходимого количества теплоты.
Задача №1
Сколько теплоты нужно, чтобы изо льда массой 2 кг, взятого при температуре -10°С, получить пар при 100°С?
Решение:
Ответ: чтобы изо льда массой 2 кг, взятого при температуре -10°С, получить пар при 100°С, нужно взять 6,162 мегаджоулей теплоты.
Задача №2
В железный котёл массой 5 кг налита вода массой 10 кг. Какое количество теплоты нужно передать котлу с водой для изменения их температуры от 10 до 100°С?
Начнем решение и отметим, что нагреваться будет и котёл, и вода. Разница температур составит 1000С — 100С = 900С. Т. е. и температура котла изменится на 90 градусов, и температура воды также изменится на 90 градусов.
Количества теплоты, которые получили оба объекта (Q1
– для котла и Q2 — для воды), не будут одинаковыми. Мы найдем общее количество теплоты по формуле теплового баланса Q = Q1 + Q2.
На практике часто приходится проводить различные тепловые расчёты. Для увеличения эргономичности тепловой системы жилых домов измеряют количество тепловой энергии, рассеиваемой через вентиляцию, окна, расщелины.
Для расчёта количества тепловой энергии нужно измерить массу (m), разность температуры в начале и в конце процесса
Δt=tкон−tнач
, а также знать теплоёмкость (c) данного вещества.
Чтобы нагреть некоторое вещество массой (1) кг на (1°C), необходимо затратить количество теплоты, равное удельной теплоёмкости (c) данного вещества.
Количество теплоты, получаемое веществом при нагревании, прямо пропорционально удельной теплоёмкости вещества, его массе и разности температур, то есть:
Q=cmΔt
или
Данная формула даёт возможность найти и выделяемую при охлаждении вещества теплоту.
Чтобы рассчитать количество теплоты, необходимое для нагревания вещества (или выделяемое им при охлаждении), следует удельную теплоёмкость вещества умножить на его массу и на разность между конечной и начальной температурой вещества.
Так как конечная температура остывающего вещества меньше его начальной температуры:
то изменение температуры оказывается отрицательным числом:
Значит, и выделяемое веществом количество теплоты выражается отрицательным числом:
Последний факт обозначает не рост, а убыль внутренней энергии вещества.
Содержание:
- Определение и формула количества теплоты
- Формула расчета теплоты при изменении температуры
- Формула количества теплоты при фазовых переходах
- Единицы измерения количества теплоты
- Примеры решения задач
Определение и формула количества теплоты
Внутреннюю энергию термодинамической системы можно изменить двумя способами:
- совершая над системой работу,
- при помощи теплового взаимодействия.
Передача тепла телу не связана с совершением над телом макроскопической работы. В данном случае изменение внутренней энергии вызвано тем,
что отдельные молекулы тела с большей температурой совершают работу над некоторыми молекулами тела, которое имеет меньшую температуру. В этом
случае тепловое взаимодействие реализуется за счет теплопроводности. Передача энергии также возможна при помощи излучения. Система
микроскопических процессов (относящихся не ко всему телу, а к отдельным молекулам) называется теплопередачей. Количество энергии,
которое передается от одного тела к другому в результате теплопередачи, определяется количеством теплоты, которое предано от одного тела другому.
Определение
Теплотой называют энергию, которая получается (или отдается) телом в процессе теплообмена с окружающими телами (средой).
Обозначается теплота, обычно буквой Q.
Это одна из основных величин в термодинамике. Теплота включена в математические выражения первого и второго начал термодинамики.
Говорят, что теплота – это энергия в форме молекулярного движения.
Теплота может сообщаться системе (телу), а может забираться от нее. Считают, что если тепло сообщается системе, то оно положительно.
Формула расчета теплоты при изменении температуры
Элементарное количество теплоты обозначим как $delta Q$. Обратим внимание,
что элемент тепла, которое получает (отдает) система при малом изменении ее состояния не является полным дифференциалом.
Причина этого состоит в том, что теплота является функцией процесса изменения состояния системы.
Элементарное количество тепла, которое сообщается системе, и температура при этом меняется от Tдо T+dT, равно:
$$delta Q=C d T(1)$$
где C – теплоемкость тела. Если рассматриваемое тело однородно, то формулу (1) для количества теплоты можно представить как:
$$delta Q=c m d T=nu c_{mu} d T(2)$$
где $c=frac{C}{m}$ – удельная теплоемкость тела, m – масса тела,
$c_{mu}=c cdot mu$ — молярная теплоемкость,
$mu$ – молярная масса вещества,
$nu=frac{m}{mu}$ – число молей вещества.
Если тело однородно, а теплоемкость считают независимой от температуры, то количество теплоты
($Delta Q$), которое получает тело при увеличении его температуры на величину
$Delta t = t_2 — t_1$ можно вычислить как:
$$Delta Q=c m Delta t(3)$$
где t2, t1 температуры тела до нагрева и после. Обратите внимание, что температуры при нахождении разности
($Delta t$) в расчетах можно подставлять как в градусах Цельсия, так и в кельвинах.
Формула количества теплоты при фазовых переходах
Переход от одной фазы вещества в другую сопровождается поглощением или выделением некоторого количества теплоты,
которая носит название теплоты фазового перехода.
Так, для перевода элемента вещества из состояния твердого тела в жидкость ему следует сообщить количество теплоты
($delta Q$) равное:
$$delta Q=lambda d m$$
где $lambda$ – удельная теплота плавления, dm – элемент массы тела.
При этом следует учесть, что тело должно иметь температуру, равную температуре плавления рассматриваемого вещества.
При кристаллизации происходит выделение тепла равного (4).
Количество теплоты (теплота испарения), которое необходимо для перевода жидкости в пар можно найти как:
$$delta Q=r d m$$
где r – удельная теплота испарения. При конденсации пара теплота выделяется. Теплота испарения равна теплоте конденсации одинаковых масс вещества.
Единицы измерения количества теплоты
Основной единицей измерения количества теплоты в системе СИ является: [Q]=Дж
Внесистемная единица теплоты, которая часто встречается в технических расчетах. [Q]=кал (калория). 1 кал=4,1868 Дж.
Примеры решения задач
Пример
Задание. Какие объемы воды следует смешать, чтобы получить 200 л воды при температуре t=40С, если температура
одной массы воды t1=10С, второй массы воды t2=60С?
Решение. Запишем уравнение теплового баланса в виде:
$$Q=Q_{1}+Q_{2}(1.1)$$
где Q=cmt – количество теплоты приготовленной после смешивания воды; Q1=cm1t1 —
количество теплоты части воды температурой t1 и массой m1;
Q2=cm2t2— количество теплоты части воды температурой t2 и массой m2.
Из уравнения (1.1) следует:
$$
begin{array}{l}
mathrm{cmt}=mathrm{cm}_{1} t_{1}+mathrm{~cm}_{2} t_{2} rightarrow mathrm{mt}=mathrm{m}_{1} t_{1}+mathrm{~m}_{2} t_{2} rightarrow \
rightarrow rho mathrm{Vt}=rho V_{1} t_{1}+rho mathrm{V}_{2} t_{2} rightarrow mathrm{Vt}=V_{1} t_{1}+V_{2} t_{2}(1.2)
end{array}
$$
При объединении холодной (V1) и горячей (V2) частей воды в единый объем (V) можно принять то, что:
$$$
V=V_{1}+V_{2}(1.3)
$$$
Так, мы получаем систему уравнений:
$$
left{begin{array}{c}
V t=V_{1} t_{1}+V_{2} t_{2} \
V=V_{1}+V_{2}
end{array}right.
$$
Решив ее получим:
$$
begin{array}{l}
V_{1}=frac{left(t_{2}-tright)}{t_{2}-t_{1}} V \
V_{2}=frac{left(t-t_{1}right)}{t_{2}-t_{1}} V
end{array}
$$
Проведем вычисления (это можно сделать, не переходя в систему СИ):
$$
begin{array}{l}
V_{1}=frac{(60-40)}{60-10} 200=80 text { (л) } \
V_{2}=frac{(40-10)}{60-10} 200=120 text { (л) }
end{array}
$$
Ответ. V1=80 л, V2=120 л.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
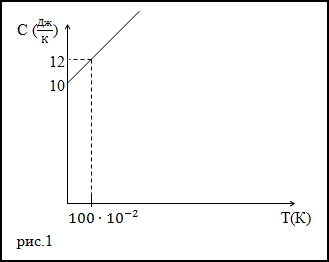
Задание. Теплоемкость тела изменяется по линейному закону (рис.1) в зависимости от абсолютной температуры в
рассматриваемом интервале $T_{1} leq T leq T_{2}$ .
Какое количество теплоты получает тело, если T1=300 К, T2=400 К.
Решение. Исследуя график функции теплоемкости (C(T)) (рис.1) запишем его аналитическое выражение, оно получится:
$C(T)=10+2 cdot 10^{-2} T$ (Дж/К)
Основой для решения задачи послужит формула для количества теплоты в виде:
$$delta Q=C d T(2.2)$$
Подставим полученное выражение для теплоемкости (2.1) в формулу (2.2) поведем интегрирование в заданном интервале температур:
$$
begin{array}{c}
Delta Q=int_{300}^{400}left(10+2 cdot 10^{-2} Tright) d T=left.left(10 cdot T+10^{-2} T^{2}right)right|_{300} ^{400}= \
=left(10 cdot 400+10^{-2} cdot(400)^{2}right)-left(10 cdot 300+10^{-2} cdot(300)^{2}right)=1700left(mathrm{~A}^{*}right)
end{array}
$$
Ответ. $Delta Q$=1700 Дж
Читать дальше: Формула напряженности магнитного поля.
Количество теплоты — еще один изученный нами вид энергии. Эту энергию тело получает или отдает при теплопередаче. Мы установили, что количество теплоты, необходимое для нагревания тела, зависит от массы тела, разности температур и рода вещества. Нам известен физический смысл удельной теплоемкости и некоторые ее табличные значения для разных веществ. В этом уроке мы перейдем к численному расчету количества теплоты, необходимой для нагревания тела или выделяемого им при охлаждении.
Зачем это нужно? На самом деле, на практике очень часто используют подобные расчеты.
При строительстве зданий и проектировании систем отопления важно знать, какое количество теплоты необходимо отдавать для полного обогрева всех помещений. С другой стороны, также необходима информация о том, какое количество теплоты будет уходить через окна, стены и двери.
Формула для расчета количества теплоты
Допустим, на нужно узнать, какое количество теплоты получила при нагревании железная деталь. Масса детали $3 space кг$. Деталь нагрелась от $20 degree C$ до $300 degree C$.
Возьмем значение теплоемкости железа из таблицы — $460 frac{Дж}{кг cdot degree C}$. Объясним смысл этой величины: на нагревание куска железа массой $1 space кг$ на $1 degree C$ необходимо затратить количество теплоты, равное $460 space Дж$.
- Масса детали у нас в 3 раза больше, значит, на ее нагрев потребуется в 3 раза большее количество теплоты — $1380 space Дж$
- Температура изменилась не на $1 degree C$, а на $280 degree C$
- Значит, необходимо в 280 раз большее количество теплоты: $1380 space Дж cdot 280 = 386 400 space Дж$
Тогда, формула для расчета количества теплоты, необходимой для нагревания тела или выделяемого им при охлаждении примет вид:
$Q = cm(t_2 — t_1)$,
где $Q$ — количество теплоты,
$c$ — удельная теплоемкость вещества, из которого состоит тело,
$m$ — масса тела,
$t_1$ — начальная температура тела,
$t_2$ — конечная температура тела.
Чтобы рассчитать количество теплоты, которое необходимо затратить для нагревания тела или выделяемое им при охлаждении, нужно удельную теплоемкость умножить на массу тела и на разность конечной и начальной температур.
Рассмотрим подробнее особенности расчета количества теплоты на примерах решения задач.
Расчет количества теплоты, затраченного на нагревание двух тел
В железный котелок массой $4 space кг$ налили воду массой $10 space кг$ (рисунок 1). Их температура $25 degree C$. Какое количество теплоты нужно затратить, чтобы нагреть котелок и воду до температуры $100 degree C$?
Обратите внимание, что нагреваться будут сразу два тела: и котелок, и вода в нем. Между постоянно будет происходить теплообмен. Поэтому их температуры мы можем считать одинаковыми.
Отметим, что массы котелка и воды различные. Также они имеют различные теплоемкости. Значит, полученные ими количества теплоты будет различными.
Теперь мы можем записать условие задачи и решить ее.
Дано:
$m_1 = 4 space кг$
$c_1 = 460 frac{Дж}{кг cdot degree C}$
$m_2 = 10 space кг$
$c_2 = 4200 frac{Дж}{кг cdot degree C}$
$t_1 = 25 degree C$
$t_2 = 100 degree C$
Q-?
Посмотреть решение и ответ
Скрыть
Решение:
Для расчета полученного количества теплоты используем формулу $Q = cm(t_2 — t_1)$.
Запишем эту формулу для количества теплоты, полученного котелком:
$Q_1 = c_1m_1(t_2 — t_1)$.
Рассчитаем это количество теплоты:
$Q_1 = 460 frac{Дж}{кг cdot degree C} cdot 4 space кг cdot (100 degree C — 25 degree C) = 1840 frac{Дж}{degree C} cdot 75 degree C = 138 000 space Дж = 138 space кДж$.
Количество теплоты, полученное водой при нагревании будет равно:
$Q_2 = c_2m_2(t_2 — t_1)$.
Подставим численные значения и рассчитаем:
$Q_2 = 4200 frac{Дж}{кг cdot degree C} cdot 10 space кг cdot (100 degree C — 25 degree C) = 42000 frac{Дж}{degree C} cdot 75 degree C = 3 150 000 space Дж = 3150 space кДж$.
Общее количество теплоты, затраченное на нагревание котелка и воды:
$Q = Q_1 +Q_2$,
$Q = 138 space кДж + 3150 space кДж = 3288 space кДж$.
Ответ: $Q = 3288 space кДж$.
Расчет количества теплоты при смешивании жидкостей
Горячую воду разбавили холодной и получили температуру смеси $30 degree C$. Горячей воды с температурой $100 degree C$ при этом было $0.3 space кг$. Холодная вода имела массу $1.4 space кг$ и температуру $15 degree C$. Рассчитайте, какое количество теплоты было отдано горячей водой при остывании и получила холодная вода при нагревании. Сравните эти количества теплоты.
Дано:
$c_1 = c_2 = c = 4200 frac{Дж}{кг cdot degree C}$
$m_1 = 0.3 space кг$
$m_2 = 1.4 space кг$
$t_1 = 100 degree C$
$t_2 = 15 degree C$
$t = 30 degree C$
$Q_1 — ?$
$Q_2 — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Запишем формулу для расчета количества теплоты, отданного горячей водой при остывании от $100 degree C$ до $30 degree C$:
$Q_1 = cm_1(t_1 — t)$.
Рассчитаем эту величину:
$Q_1 = 4200 frac{Дж}{кг cdot degree C} cdot 0.3 space кг cdot (100 degree C — 30 degree C) = 1260 frac{Дж}{degree C} cdot 70 degree C = 88 200 space Дж = 88.2 space кДж$.
Запишем формулу для расчета количества теплоты, полученного холодной водой при нагревании от $15 degree C$ до $30 degree C$:
$Q_2 = cm_2(t — t_2)$.
Рассчитаем эту величину:
$Q_1 = 4200 frac{Дж}{кг cdot degree C} cdot 1.4 space кг cdot (30 degree C — 15 degree C) = 5880 frac{Дж}{degree C} cdot 15 degree C = 88 200 space Дж = 88.2 space кДж$.
$Q_1 = Q_2 = 88.2 space кДж$.
Ответ: $Q_1 = Q_2 = 88.2 space кДж$.
В ходе решения этой задачи мы увидели, что количество теплоты, отданное горячей водой, и количество теплоты, полученное холодной водой, равны. Другие опыты дают схожие результаты.
Значит,
Если между телами происходит теплоообмен, то внутренняя энергия всех нагревающихся тел увеличивается на столько, на сколько уменьшается внутренняя энергия остывающих тел.
На практике часто получается так, что отданная горячей водой энергия больше, чем полученная холодной. На самом деле, горячая вода при охлаждении передает какую-то часть своей внутренней энергии воздуху и сосуду, в котором происходит смешивание.
Есть 2 способа учесть этот фактор:
- Если мы максимально сократим потери энергии, то добьемся приблизительного равенства отданной и полученной энергий
- Если рассчитать и учесть потери энергии, то можно получить точное равенство
Расчет температуры при известной величине количества теплоты
При нагревании куска меди было затрачено $22 space кДж$. Масса этого куска составляет $300 space г$. Начальная температура была равна $20 degree C$. До какой температуры нагрели кусок меди?
Дано:
$m = 300 space г$
$t_1 = 20 degree C$
$c = 400 frac{Дж}{кг cdot degree C}$
$Q = 22 space кДж$
СИ:
$0.3 space кг$
$22 000 space Дж$
$t_2 — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Запишем формулу для расчета количества теплоты:
$Q = cm(t_2 — t_1)$.
Постепенно выразим из этой формулы искомую температуру $t_2$:
$t_2 — t_1 = frac{Q}{cm}$,
$t_2 = frac{Q}{cm} + t_1$.
Рассчитаем $t_2$:
$t_2 = frac{22 000 space Дж}{400 frac{Дж}{кг cdot degree C} cdot 0.3 space кг} + 20 degree C approx 183 degree C + 20 degree C approx 203 degree C$.
Ответ: $t_2 approx 203 degree C$.
«Количество теплоты. Удельная теплоёмкость»
Количество теплоты
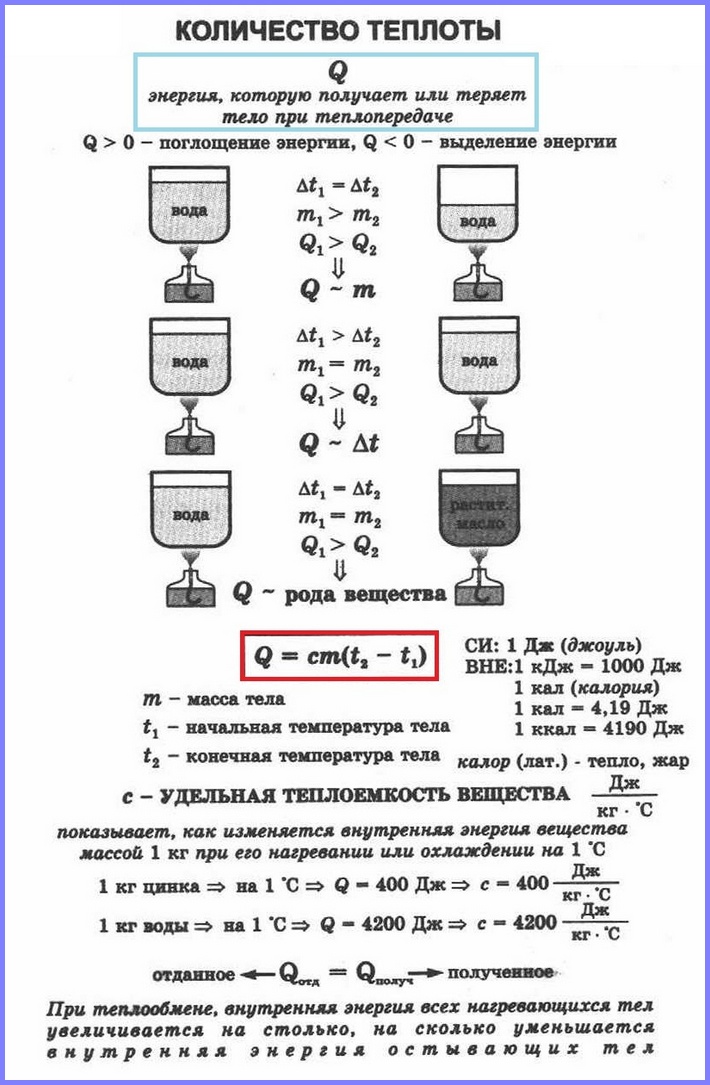
Изменение внутренней энергии путём совершения работы характеризуется величиной работы, т.е. работа является мерой изменения внутренней энергии в данном процессе. Изменение внутренней энергии тела при теплопередаче характеризуется величиной, называемой количествоv теплоты.
Количество теплоты – это изменение внутренней энергии тела в процессе теплопередачи без совершения работы. Количество теплоты обозначают буквой Q.
Работа, внутренняя энергия и количество теплоты измеряются в одних и тех же единицах — джоулях (Дж), как и всякий вид энергии.
В тепловых измерениях в качестве единицы количества теплоты раньше использовалась особая единица энергии — калория (кал), равная количеству теплоты, необходимому для нагревания 1 грамма воды на 1 градус Цельсия (точнее, от 19,5 до 20,5 °С). Данную единицу, в частности, используют в настоящее время при расчетах потребления тепла (тепловой энергии) в многоквартирных домах. Опытным путем установлен механический эквивалент теплоты — соотношение между калорией и джоулем: 1 кал = 4,2 Дж.
При передаче телу некоторого количества теплоты без совершения работы его внутренняя энергия увеличивается, если тело отдаёт какое-то количество теплоты, то его внутренняя энергия уменьшается.
Если в два одинаковых сосуда налить в один 100 г воды, а в другой 400 г при одной и той же температуре и поставить их на одинаковые горелки, то раньше закипит вода в первом сосуде. Таким образом, чем больше масса тела, тем большее количество тепла требуется ему для нагревания. То же самое и с охлаждением.
Количество теплоты, необходимое для нагревания тела зависит еще и от рода вещества, из которого это тело сделано. Эта зависимость количества теплоты, необходимого для нагревания тела, от рода вещества характеризуется физической величиной, называемой удельной теплоёмкостью вещества.
Удельная теплоёмкость
Удельная теплоёмкость – это физическая величина, равная количеству теплоты, которое необходимо сообщить 1 кг вещества для нагревания его на 1 °С (или на 1 К). Такое же количество теплоты 1 кг вещества отдаёт при охлаждении на 1 °С.
Удельная теплоёмкость обозначается буквой с. Единицей удельной теплоёмкости является 1 Дж/кг °С или 1 Дж/кг °К.
Значения удельной теплоёмкости веществ определяют экспериментально. Жидкости имеют большую удельную теплоёмкость, чем металлы; самую большую удельную теплоёмкость имеет вода, очень маленькую удельную теплоёмкость имеет золото.
Поскольку кол-во теплоты равно изменению внутренней энергии тела, то можно сказать, что удельная теплоёмкость показывает, на сколько изменяется внутренняя энергия 1 кг вещества при изменении его температуры на 1 °С. В частности, внутренняя энергия 1 кг свинца при его нагревании на 1 °С увеличивается на 140 Дж, а при охлаждении уменьшается на 140 Дж.
Количество теплоты Q, необходимое для нагревания тела массой m от температуры t1°С до температуры t2°С, равно произведению удельной теплоёмкости вещества, массы тела и разности конечной и начальной температур, т.е.
Q = c ∙ m (t2 — t1)
По этой же формуле вычисляется и количество теплоты, которое тело отдаёт при охлаждении. Только в этом случае от начальной температуры следует отнять конечную, т.е. от большего значения температуры отнять меньшее.
Это конспект по теме «Количество теплоты. Удельная теплоёмкость». Выберите дальнейшие действия:
- Перейти к следующему конспекту: «Уравнение теплового баланса»
- Вернуться к списку конспектов по Физике
- Посмотреть решение типовых задач на количество теплоты