Как найти количество целых решений уравнения

Метод подсчёта количества решений

Линейные алгебраические уравнения — одни из самых простых уравнений, которые мы можем решить. Если в уравнении только одна переменная, решение тривиально, в то время как для системы линейных уравнений существует множество способов найти уникальные решения.

В этой статье нас интересует частный случай линейного уравнения с несколькими переменными. Хорошо известно, что подобное уравнение имеет бесконечное число решений. Мы наложим определённые ограничения и в значительной степени сократим количество решений.

Общая форма интересующего нас уравнения:

где n и m — положительные целые числа.

Наша задача — найти число решений этого уравнения, предполагая, что xᵢ являются целыми числами. Это предположение значительно снижает число решений заданного уравнения.

Нам нужен метод

Давайте начнём с частного случая общего уравнения:

Нетрудно найти все решения этого уравнения методом простого счёта. Решения заданы парами (x₁, x₂):

Мы видим, что уравнение имеет шесть решений. Также нетрудно предположить, что, если мы заменим правую часть определённым положительным целым числом m, решения будут выглядеть так:

и мы сможем подсчитать число решений — m+1.

Это было просто, верно?

Теперь возьмём немного более сложный вариант с тремя переменными, скажем:

С несколько большими усилиями, чем в предыдущем примере, находим решения в виде наборов из трёх чисел (x₁, x₂, x₃):

Число решений в этом случае равно 10.

Легко представить, что метод прямого счёта может стать очень утомительным для уравнения с большим количеством переменных. Он также становится утомительным, если целое число в правой части уравнения становится больше — например, если в правой части у нас будет 8, а не 3, решений будет уже 45. Разумеется, не хотелось бы искать все эти решения методом прямого счёта.

Значит, нужен эффективный метод.

Разрабатываем метод

Существует ещё один способ, которым можно решить предыдущие два уравнения. Давайте снова начнём с этого уравнения:

Одним из решений было (5, 0). Давайте преобразуем его в:

Мы разложили решение на нули и единицы, соответствующие каждому числу. Ненулевую часть (в данном случае 5) мы разложили на соответствующее число единиц, а ноль преобразовали в ноль. Таким же образом мы можем разложить и другое решение:

Мы поменяли прежнее расположение нуля, чтобы получить новое решение. Итак, два числа в парах (обозначенные красным и голубым) разделены нулём (чёрный) в разложенном виде. Таким же образом запишем оставшиеся решения:

Записав решения таким образом, видим закономерность. Кажется, все решения — это просто перестановки нулей и единиц. Вопрос о том, сколько существует решений, становится эквивалентным вопросу как много таких перестановок нулей и единиц может быть сделано, начиная с любой из конфигураций.

В данном случае у нас есть 6 местоположений в разложенной конфигурации для размещения нулей и единиц. Мы можем выбрать простейшее решение в качестве начальной конфигурации:

Теперь всё, что нам нужно найти, это общее число способов, которыми можно заполнить шесть местоположений пятью единицами и одним нулём.

Подобные задачи подсчёта мы можем решить различными способами, но наиболее эффективным будет способ, разработанный в такой области математики как комбинаторика, которая даёт нам формулу для числа способов перестановки r объектов в n местоположений:

где n! (читается как “n факториал”) определяется как произведение всех целых чисел от 1 до n, т.е. n! = 1 × 2 × 3 × ⋅ ⋅ ⋅ × n. Мы также определяем 0! = 1.

Эта формула обычно записывается в компактной форме как:

Теперь, возвращаясь к задаче, мы можем использовать эту формулу для нахождения числа способов перестановки пяти единиц в шести местоположениях:

Это то же самое число, что мы получили методом прямого счёта!

Выглядит многообещающе, поэтому давайте проверим, сможем ли мы найти таким способом число решений второго линейного уравнения:

Некоторые решения можно записать в разложенном виде:

В этот раз нам нужно заполнить тремя единицами и двумя нулями пять местоположений. Используя формулу мы можем найти число способов расположения чисел:

И опять то же число, что мы получили методом прямого счёта. Мы можем также найти число решений для нерешённого случая, где в правой части уравнения 8 вместо 3. Одним из решений будет:

а нам нужно найти число способов разместить 8 единиц в 10 местоположениях, и это будет:

как и утверждалось выше.

Если мы уверены в том, что этот метод работает для всех случаев, нам нужна общая формула. Напомним, что общее уравнение имеет вид:

Простейшее решение этого уравнения:

Поскольку существует n переменных, количество нулей в этом решении равно n-1. Таким образом, разложение выглядит так:

В разложенной конфигурации видим m и n-1 нулей (как утверждалось выше).

Следовательно, общее число местоположений, которые нужно заполнить, равно (m+n-1). Единственное, что остаётся — найти число способов, которыми можно заполнить m+n-1 местоположений m единиц, что определяется по формуле:

math4school.ru

Уравнения в целых числах

Немного теории

Уравнения в целых числах – это алгебраические уравнения с двумя или более неизвестными переменными и целыми коэффициентами. Решениями такого уравнения являются все целочисленные (иногда натуральные или рациональные) наборы значений неизвестных переменных, удовлетворяющих этому уравнению. Такие уравнения ещё называют диофантовыми, в честь древнегреческого математика Диофанта Александрийского, который исследовал некоторые типы таких уравнений ещё до нашей эры.

Современной постановкой диофантовых задач мы обязаны французскому математику Ферма. Именно он поставил перед европейскими математиками вопрос о решении неопределённых уравнений только в целых числах. Наиболее известное уравнение в целых числах – великая теорема Ферма: уравнение

не имеет ненулевых рациональных решений для всех натуральных n > 2.

Теоретический интерес к уравнениям в целых числах достаточно велик, так как эти уравнения тесно связаны со многими проблемами теории чисел.

В 1970 году ленинградский математик Юрий Владимирович Матиясевич доказал, что общего способа, позволяющего за конечное число шагов решать в целых числах произвольные диофантовы уравнения, не существует и быть не может. Поэтому следует для разных типов уравнений выбирать собственные методы решения.

При решении уравнений в целых и натуральных числах можно условно выделить следующие методы:

способ перебора вариантов;

применение алгоритма Евклида;

представление чисел в виде непрерывных (цепных) дробей;

разложения на множители;

решение уравнений в целых числах как квадратных (или иных) относительно какой-либо переменной;

метод бесконечного спуска.

Задачи с решениями

1. Решить в целых числах уравнение x 2 – xy – 2y 2 = 7.

Запишем уравнение в виде (x – 2y)(x + y) = 7.

Так как х, у – целые числа, то находим решения исходного уравнения, как решения следующих четырёх систем:

1) x – 2y = 7, x + y = 1;

2) x – 2y = 1, x + y = 7;

3) x – 2y = –7, x + y = –1;

4) x – 2y = –1, x + y = –7.

Решив эти системы, получаем решения уравнения: (3; –2), (5; 2), (–3; 2) и (–5; –2).

Ответ: (3; –2), (5; 2), (–3; 2), (–5; –2).

2. Решить в целых числах уравнение:

а) 20х + 12у = 2013;

в) 201х – 1999у = 12.

а) Поскольку при любых целых значениях х и у левая часть уравнения делится на два, а правая является нечётным числом, то уравнение не имеет решений в целых числах.

Ответ: решений нет.

б) Подберём сначала некоторое конкретное решение. В данном случае, это просто, например,

Поскольку числа 5 и 7 взаимно простые, то

Значит, общее решение:

х = 1 + 7k, у = 2 – 5k,

где k – произвольное целое число.

Ответ: (1+7k; 2–5k), где k – целое число.

в) Найти некоторое конкретное решение подбором в данном случае достаточно сложно. Воспользуемся алгоритмом Евклида для чисел 1999 и 201:

НОД(1999, 201) = НОД(201, 190) = НОД(190, 11) = НОД(11, 3) = НОД(3 , 2) = НОД(2, 1) = 1.

Запишем этот процесс в обратном порядке:

1 = 2 – 1 = 2 – (3 – 2) = 2·2 – 3 = 2· (11 – 3·3) – 3 = 2·11 – 7·3 = 2·11 – 7(190 – 11·17) =

= 121·11 – 7·190 = 121(201 – 190) – 7·190 = 121·201 – 128·190 =

= 121·201 – 128(1999 – 9·201) = 1273·201 – 128·1999.

Значит, пара (1273, 128) является решением уравнения 201х – 1999у = 1. Тогда пара чисел

x₀ = 1273·12 = 15276, y₀ = 128·12 = 1536

является решением уравнения 201х – 1999у = 12.

Общее решение этого уравнения запишется в виде

х = 15276 + 1999k, у = 1536 + 201k, где k – целое число,

или, после переобозначения (используем, что 15276 = 1283 + 7·1999, 1536 = 129 + 7·201),

х = 1283 + 1999n, у = 129 + 201n, где n – целое число.

Ответ: (1283+1999n, 129+201n), где n – целое число.

3. Решить в целых числах уравнение:

а) x 3 + y 3 = 3333333;

б) x 3 + y 3 = 4(x 2 y + xy 2 + 1).

а) Так как x 3 и y 3 при делении на 9 могут давать только остатки 0, 1 и 8 (смотрите таблицу в разделе «Делимость целых чисел и остатки»), то x 3 + y 3 может давать только остатки 0, 1, 2, 7 и 8. Но число 3333333 при делении на 9 даёт остаток 3. Поэтому исходное уравнение не имеет решений в целых числах.

Ответ: целочисленных решений нет.

б) Перепишем исходное уравнение в виде (x + y) 3 = 7(x 2 y + xy 2 ) + 4. Так как кубы целых чисел при делении на 7 дают остатки 0, 1 и 6, но не 4, то уравнение не имеет решений в целых числах.

Ответ: целочисленных решений нет.

а) в простых числах уравнение х 2 – 7х – 144 = у 2 – 25у;

б) в целых числах уравнение x + y = x 2 – xy + y 2 .

а) Решим данное уравнение как квадратное относительно переменной у. Получим

у = х + 9 или у = 16 – х.

Поскольку при нечётном х число х + 9 является чётным, то единственной парой простых чисел, которая удовлетворяет первому равенству, является (2; 11).

Так как х, у – простые, то из равенства у = 16 – х имеем

С помощью перебора вариантов находим остальные решения: (3; 13), (5; 11), (11; 5), (13; 3).

Ответ: (2; 11), (3; 13), (5; 11), (11; 5), (13; 3).

б) Рассмотрим данное уравнение как квадратное уравнение относительно x:

x 2 – (y + 1)x + y 2 – y = 0.

Дискриминант этого уравнения равен –3y 2 + 6y + 1. Он положителен лишь для следующих значений у: 0, 1, 2. Для каждого из этих значений из исходного уравнения получаем квадратное уравнение относительно х, которое легко решается.

Ответ: (0; 0), (0; 1), (1; 0), (1; 2), (2; 1), (2; 2).

5. Существует ли бесконечное число троек целых чисел x, y, z таких, что x 2 + y 2 + z 2 = x 3 + y 3 + z 3 ?

Попробуем подбирать такие тройки, где у = –z. Тогда y 3 и z 3 будут всегда взаимно уничтожаться, и наше уравнение будет иметь вид

Чтобы пара целых чисел (x; y) удовлетворяла этому условию, достаточно, чтобы число x–1 было удвоенным квадратом целого числа. Таких чисел бесконечно много, а именно, это все числа вида 2n 2 +1. Подставляя в x 2 (x–1) = 2y 2 такое число, после несложных преобразований получаем:

y = xn = n(2n 2 +1) = 2n 3 +n.

Все тройки, полученные таким образом, имеют вид (2n 2 +1; 2n 3 +n; –2n 3 – n).

6. Найдите такие целые числа x, y, z, u, что x 2 + y 2 + z 2 + u 2 = 2xyzu.

Число x 2 + y 2 + z 2 + u 2 чётно, поэтому среди чисел x, y, z, u чётное число нечётных чисел.

Если все четыре числа x, y, z, u нечётны, то x 2 + y 2 + z 2 + u 2 делится на 4, но при этом 2xyzu не делится на 4 – несоответствие.

Если ровно два из чисел x, y, z, u нечётны, то x 2 + y 2 + z 2 + u 2 не делится на 4, а 2xyzu делится на 4 – опять несоответствие.

Поэтому все числа x, y, z, u чётны. Тогда можно записать, что

и исходное уравнение примет вид

Теперь заметим, что (2k + 1) 2 = 4k(k + 1) + 1 при делении на 8 даёт остаток 1. Поэтому если все числа x₁, y₁, z₁, u₁ нечётны, то x₁ 2 + y₁ 2 + z₁ 2 + u₁ 2 не делится на 8. А если ровно два из этих чисел нечётно, то x₁ 2 + y₁ 2 + z₁ 2 + u₁ 2 не делится даже на 4. Значит,

и мы получаем уравнение

Снова повторив те же самые рассуждения, получим, что x, y, z, u делятся на 2 n при всех натуральных n, что возможно лишь при x = y = z = u = 0.

7. Докажите, что уравнение

(х – у) 3 + (y – z) 3 + (z – x) 3 = 30

не имеет решений в целых числах.

Воспользуемся следующим тождеством:

(х – у) 3 + (y – z) 3 + (z – x) 3 = 3(х – у)(y – z)(z – x).

Тогда исходное уравнение можно записать в виде

(х – у)(y – z)(z – x) = 10.

Обозначим a = x – y, b = y – z, c = z – x и запишем полученное равенство в виде

Кроме того очевидно, a + b + c = 0. Легко убедиться, что с точностью до перестановки из равенства abc = 10 следует, что числа |a|, |b|, |c| равны либо 1, 2, 5, либо 1, 1, 10. Но во всех этих случаях при любом выборе знаков a, b, c сумма a + b + c отлична от нуля. Таким образом, исходное уравнение не имеет решений в целых числах.

8. Решить в целых числах уравнение 1! + 2! + . . . + х! = у 2 .

если х = 1, то у 2 = 1,

если х = 3, то у 2 = 9.

Этим случаям соответствуют следующие пары чисел:

Заметим, что при х = 2 имеем 1! + 2! = 3, при х = 4 имеем 1! + 2! + 3! + 4! = 33 и ни 3, ни 33 не являются квадратами целых чисел. Если же х > 5, то, так как

5! + 6! + . . . + х! = 10n,

можем записать, что

1! + 2! + 3! + 4! + 5! + . . . + х! = 33 + 10n.

Так как 33 + 10n – число, оканчивающееся цифрой 3, то оно не является квадратом целого числа.

Ответ: (1; 1), (1; –1), (3; 3), (3; –3).

9. Решите следующую систему уравнений в натуральных числах:

a 3 – b 3 – c 3 = 3abc, a 2 = 2(b + c).

3abc > 0, то a 3 > b 3 + c 3 ;

таким образом имеем

b 2 2 + х = у 4 + у 3 + у 2 + у.

Разложив на множители обе части данного уравнения, получим:

х(х + 1) = у(у + 1)(у 2 + 1),

х(х + 1) = (у 2 + у)(у 2 + 1)

Такое равенство возможно, если левая и правая части равны нулю, или представляют собой произведение двух последовательных целых чисел. Поэтому, приравнивая к нулю те или иные множители, получим 4 пары искомых значений переменных:

Произведение (у 2 + у)(у 2 + 1) можно рассматривать как произведение двух последовательных целых чисел, отличных от нуля, только при у = 2. Поэтому х(х + 1) = 30, откуда х₅ = 5, х₆ = –6. Значит, существуют ещё две пары целых чисел, удовлетворяющих исходному уравнению:

Ответ: (0; 0), (0; –1), (–1; 0), (–1; –1), (5; 2), (–6; 2.)

Задачи без решений

1. Решить в целых числах уравнение:

б) х 2 + у 2 = х + у + 2.

2. Решить в целых числах уравнение:

а) х 3 + 21у 2 + 5 = 0;

б) 15х 2 – 7у 2 = 9.

3. Решить в натуральных числах уравнение:

4. Доказать, что уравнение х 3 + 3у 3 + 9z 3 = 9xyz в рациональных числах имеет единственное решение

5. Доказать, что уравнение х 2 + 5 = у 3 в целых числах не имеет решений.

Линейные диофантовы уравнения с двумя переменными

Калькулятор решает линейные диофантовы уравнения с двумя переменными.

Сначала калькулятор, теория под ним.

Линейные диофантовы уравнения с двумя переменными

Диофантово уравнение с двумя неизвестными имеет вид:

где a, b, c — заданные целые числа, x и y — неизвестные целые числа.

Для нахождения решений уравнения используется Расширенный алгоритм Евклида (исключая вырожденный случай, когда a = b = 0 и уравнение имеет либо бесконечно много решений, либо же не имеет решений вовсе).
Если числа a и b неотрицательны, тогда с помощью расширенного алгоритма Евклида мы можем найти их наибольший общий делитель g, а также такие коэффициенты и , что:
.

Утверждается, что если число c делится на g, то диофантово уравнение имеет решение; в противном случае диофантово уравнение решений не имеет. Это следует из очевидного факта, что линейная комбинация двух чисел по-прежнему должна делиться на их общий делитель.

То есть если c делится на g, тогда выполняется соотношение:

т. е. одним из решений диофантова уравнения являются числа:

Если одно из чисел a и b или они оба отрицательны, то можно взять их по модулю и применить к ним алгоритм Евклида, как было описано выше, а затем изменить знак найденных коэффициентов и в соответствии с настоящим знаком чисел a и b соответственно.

Если мы знаем одно из решений, мы можем получить выражение для всех остальных решений, которых бесконечное множество.

Итак, пусть g = НОД (a,b), выполняется условие:
.

Тогда, прибавив к число и одновременно отняв от , мы не нарушим равенства:

Этот процесс можно повторять сколько угодно, т. е. все числа вида:

,
где k принадлежит множеству целых чисел, являются множеством всех решений диофантова уравнения.

Линейные алгебраические уравнения — одни из самых простых уравнений, которые мы можем решить. Если в уравнении только одна переменная, решение тривиально, в то время как для системы линейных уравнений существует множество способов найти уникальные решения. 

В этой статье нас интересует частный случай линейного уравнения с несколькими переменными. Хорошо известно, что подобное уравнение имеет бесконечное число решений. Мы наложим определённые ограничения и в значительной степени сократим количество решений. 

Общая форма интересующего нас уравнения: 

где n и m — положительные целые числа.

Наша задача — найти число решений этого уравнения, предполагая, что xᵢ являются целыми числами. Это предположение значительно снижает число решений заданного уравнения. 

Нам нужен метод

Давайте начнём с частного случая общего уравнения: 

Нетрудно найти все решения этого уравнения методом простого счёта. Решения заданы парами (x₁, x₂):

Мы видим, что уравнение имеет шесть решений. Также нетрудно предположить, что, если мы заменим правую часть определённым положительным целым числом m, решения будут выглядеть так:

и мы сможем подсчитать число решений — m+1.

Это было просто, верно?

Теперь возьмём немного более сложный вариант с тремя переменными, скажем:

С несколько большими усилиями, чем в предыдущем примере, находим решения в виде наборов из трёх чисел (x₁, x₂, x₃):

Число решений в этом случае равно 10.

Легко представить, что метод прямого счёта может стать очень утомительным для уравнения с большим количеством переменных. Он также становится утомительным, если целое число в правой части уравнения становится больше — например, если в правой части у нас будет 8, а не 3, решений будет уже 45. Разумеется, не хотелось бы искать все эти решения методом прямого счёта.

Значит, нужен эффективный метод.

Разрабатываем метод

Существует ещё один способ, которым можно решить предыдущие два уравнения. Давайте снова начнём с этого уравнения: 

Одним из решений было (5, 0). Давайте преобразуем его в:

Мы разложили решение на нули и единицы, соответствующие каждому числу. Ненулевую часть (в данном случае 5) мы разложили на соответствующее число единиц, а ноль преобразовали в ноль. Таким же образом мы можем разложить и другое решение:

Мы поменяли прежнее расположение нуля, чтобы получить новое решение. Итак, два числа в парах (обозначенные красным и голубым) разделены нулём (чёрный) в разложенном виде. Таким же образом запишем оставшиеся решения:

Записав решения таким образом, видим закономерность. Кажется, все решения — это просто перестановки нулей и единиц. Вопрос о том, сколько существует решений, становится эквивалентным вопросу как много таких перестановок нулей и единиц может быть сделано, начиная с любой из конфигураций. 

В данном случае у нас есть 6 местоположений в разложенной конфигурации для размещения нулей и единиц. Мы можем выбрать простейшее решение в качестве начальной конфигурации:

Теперь всё, что нам нужно найти, это общее число способов, которыми можно заполнить шесть местоположений пятью единицами и одним нулём. 

Подобные задачи подсчёта мы можем решить различными способами, но наиболее эффективным будет способ, разработанный в такой области математики как комбинаторика, которая даёт нам формулу для числа способов перестановки r объектов в n местоположений:

где n! (читается как “n факториал”) определяется как произведение всех целых чисел от 1 до n, т.е. n! = 1 × 2 × 3 × ⋅ ⋅ ⋅ × n. Мы также определяем 0! = 1.

Эта формула обычно записывается в компактной форме как:

Теперь, возвращаясь к задаче, мы можем использовать эту формулу для нахождения числа способов перестановки пяти единиц в шести местоположениях:

Это то же самое число, что мы получили методом прямого счёта!

Выглядит многообещающе, поэтому давайте проверим, сможем ли мы найти таким способом число решений второго линейного уравнения:

Некоторые решения можно записать в разложенном виде:

В этот раз нам нужно заполнить тремя единицами и двумя нулями пять местоположений. Используя формулу мы можем найти число способов расположения чисел:

И опять то же число, что мы получили методом прямого счёта. Мы можем также найти число решений для нерешённого случая, где в правой части уравнения 8 вместо 3. Одним из решений будет:

а нам нужно найти число способов разместить 8 единиц в 10 местоположениях, и это будет:

как и утверждалось выше.

Если мы уверены в том, что этот метод работает для всех случаев, нам нужна общая формула. Напомним, что общее уравнение имеет вид:

Простейшее решение этого уравнения:

Поскольку существует n переменных, количество нулей в этом решении равно n-1. Таким образом, разложение выглядит так:

В разложенной конфигурации видим m и n-1 нулей (как утверждалось выше).

Следовательно, общее число местоположений, которые нужно заполнить, равно (m+n-1). Единственное, что остаётся — найти число способов, которыми можно заполнить m+n-1 местоположений m единиц, что определяется по формуле:

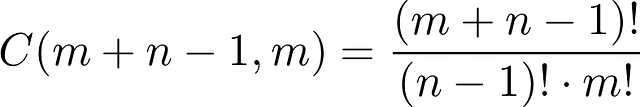
Это наш конечный результат.

---

Originally published at https://physicsgarage.com on April 26, 2020.

Читайте также:

• Связный список в деталях
• 7 способов раскрыть жульничество аналитика данных
• Лучшие фреймворки для ИИ и машинного обучения в веб-разработке

---

Перевод статьи Julia Fisher: A Method of Counting The Number of Solutions

Уравнения в целых числах – уравнения с двумя и более неизвестными переменными и целыми коэффициентами. Решениями таких уравнений являются целые числа. Также такие уравнения называются диофантовыми, в честь древнегреческого математика Диофанта Александрийского, который изучал такие уравнения еще до нашей эры.

При решении уравнений в целых и натуральных числах можно выделить следующие способы.

1 способ. Метод перебора вариантов.

Решим уравнение  $ (x-2)(y+3)=4 $  в целых числах.

Так как x и у целые числа, совершим перебор вариантов:

$ {x-2=1;; y+3=4rightarrow;x=3;;y=1\ x-2=4;; y+3=1rightarrow;x=6;;y=-2\ x-2=-1;; y+3=-4rightarrow;x=1;;y=-7\ x-2=-4;; y+3=-1rightarrow;x=-2;;y=-4\ x-2=2;; y+3=2rightarrow;x=4;;y=-1\ x-2=-2;; y+3=-2rightarrow;x=0;;y=-5\} $

Ответ: (3; 1), (6; -2), (1; -7), (-2; -4), (4; -1), (0; -5).

Решим уравнение 10х + 10у = 2019 в целых числах.

Поскольку при любых целых значениях х и у левая часть уравнения делится на два, а правая является нечётным числом, то уравнение не имеет решений в целых числах.

Ответ: решений нет.

Пусть нужно решить уравнение в целых числах:  $ 5x+4y=22. $

Методом перебора находим решение  $ x_1=2;;y_1=3. $

Получаем систему уравнений:

$ {begin{cases}5x=4y=22\5cdot2=4cdot3=22end{cases}\ 5(x-2)=4(y-3)=0\ 5(x-2)=-4(y-3)} $

$ x-2=frac{-4(y-3)}{5} $

Из полученного равенства видно, что число (х – 2) будет целым тогда и только тогда, когда (у – 3) делится на 5, т.е. у – 3 = 5n, где n какое-нибудь целое число.

Имеем:

$ { y=3+5n\ x-2=-4cdotfrac{5n}{5}=-4n\ x=2-4n} $

Тем самым все целые решения исходного уравнения можно записать в таком виде:

$ (2-4n;;3=5n),; где; n in Z. $

Ответ:  $ (2-4n;;3=5n),; где; n in Z. $

2 способ. Алгоритм Евклида

Пусть нужно решить уравнение в целых числах:  $ 5x+7y=6. $

Сделаем это с помощью Алгоритма Евклида. Ищем НОД чисел 5 и 7 с помощью него:

НОД (5, 7) = НОД (5, 7-5) = НОД (5, 2) = НОД (5 — 2∙2, 2) = НОД (1, 2) = 1

Запишем этот процесс в обратном порядке:

$ 1=2-1=2-(5-2cdot2)=2cdot3-5cdot1=(7-5)cdot3-5cdot1=7cdot3-5cdot4. $

То есть:

$ 1=5cdot(-4)+7cdot3 $

Тогда:

$ { 1cdot6=5cdot(-4)cdot6+7cdot3cdot6\ 6=5cdot(-24)+7cdot18\ 6=5x+7y} $

Тогда  $ { x=-24 ;и ; y=18} $  является решением уравнения.

Общее решение записывается в виде:

$ { x=-24+7n; ; y=18+5n,} $  где n – любое целое число.

Выполним проверку:

$ { 5(-24+7n)+7(18+5n)=6\ -120+35n+126+35n=6\ 70n=0} $

$ { n} $  – любое целое.

Верно.

Это не всевозможные способы решения. Зачастую для решения диофантовых уравнений требуются более тонкие рассуждения, связанные с делимостью, перебором остатков, оценками частей уравнения, тождественными преобразованиями и т.п.

Пример.

Решим уравнение:

$ 3^{x}+4^{y}=5^{z} $

Разложить на множители и выразить переменную мы здесь не можем. Воспользуемся методом перебора остатков.

Если левая часть уравнения в целых числах кратна какому-то числу, то и другая обязательно должна быть кратна этому же числу. Отсюда следует, что и остатки от деления обеих частей уравнения на одно и то же число будут давать одинаковые остатки.

Будем делать выводы о делимости одной части уравнения на какое-либо число (или смотреть, какой остаток от деления при этом получается) и проверять, при каких значениях переменных вторая часть уравнения также делится на это число (либо даёт такой же остаток).

Левая часть кратна 5. И остатки от деления на 5 у обеих частей также будут равны.

Про пятёрку уже сказали, что правая часть делится на неё без остатка, значит и левая тоже должна делиться.

Рассмотрим остатки от деления на 4.

Z	$ 5^{z} $	Остаток при делении на 4
1	5	1
2	25	1
3	125	1
4	625	1

Видим простую закономерность, что 5 в любой степени при делении на 4 будет давать остаток 1.

Теперь левая часть: будет делиться на 4 без остатка.

Рассмотрим остатки от деления на 4 числа  $ 3^{x} $

Z	$ 3^{x} $	Остаток при делении на 4
1	3	3
2	9	1
3	27	3
4	81	1
5	243	3

И так далее. Закономерность: при чётных х остаток 1, при нечётных остаток 3.

Отсюда делаем вывод, что х — число чётное, значит, мы можем представить его как х = 2n.

Теперь рассмотрим остатки при делении обеих частей на 3.

Правая часть:

Z	$ 5^{z} $	Остаток при делении на 3
1	5	2
2	25	1
3	125	2
4	625	1

И так далее. Видим закономерность, что при чётных z остаток равен 1, при нечетных z остаток равен 2.

Рассмотрим левую часть. Число  $ 3^{x} $  даёт остаток 0 при делении на 3.

Рассмотрим остатки от деления на 3 числа  $ 4^{y} $

Z	$ 4^{y} $	Остаток при делении на 3
1	4	1
2	16	1
3	64	1
4	256	1
5	1024	1

Получается, что левая часть при делении на 3 может давать только остаток 1. Значит, и правая тоже. Это происходит при чётных z.

Вернёмся к нашему уравнению  $ 3^{x}+4^{y}=5^{z} $

Рассмотрев все остатки от деления, мы делаем выводы, что х и z — чётные числа. Тогда х = 2n, z = 2m, где m, n натуральные. Подставим в уравнение:

$ 3^{2n}+4^{y}=5^{2m} $ , заметим также, что  $ 4^{y}=2^{2y} $

Теперь мы можем разложить на множители, используя формулу разности квадратов:

$ 2^{2y}=5^{2m}-3^{2n} $

$ (5^{m}-3^{n})(5^{m}+3^{n})=2^{2y} $ . Получается, что обе скобки должны быть степенями двойки. Мы не можем сделать никаких обоснованных выводов. Наша группировка неудачная. Попробуем иначе:

$ { 5^{2m}-2^{2y}=3^{2n}\ (5^{m}-2^{y})(5^{m}+2^{y})=3^{2n}} $

Теперь у нас обе скобки являются произведением троек. Рассмотрим такую ситуацию,

$ acdot b=3^{2n} $ , это означает, что и а, и b кратны 3. Либо одно из чисел кратно 3, а другое равно 1.

Рассмотрим случай, когда и а, и b кратны трём. Вспомним основные свойства делимости.

Ключевым признаком здесь будет второй: в нашем случае разность a-b также будет делиться на 3.

Рассмотрим разность скобок:

$ 5^{m}+2^{y}-(5^{m}-2^{y})=2cdot 2^{y} $  — это число никогда не будет кратно 3. Значит, в нашем произведении один из множителей равен 1, а другой равен 3²ⁿ. Так как  $ 5^{m}+2^{y}> 1 $ ,

$ 5^{m}-2^{y}=1,5^{m}+2^{y})=3^{2n} $ Итак, мы с вами уже решаем немного другое уравнение, с переменными m и n, которые зависят от х и у. И пришли к выводу, что  $ 5^{m}+2^{y}=1 $

m	$ 5^{m} $	y	$ 2^{y} $
0	1	0	1
1	5	1	2
2	25	2	4
3	125	3	8

Эта таблица показывает, что  $ 5^{m}+2^{y}=1 $  только в одном случае при m = 1, y = 2. При их увеличении разница между и будет всё больше, поэтому это единственное решение.

Тогда z = 2m = 2, x = 2.

Ответ: (2, 2, 2)

СПОСОБЫ РЕШЕНИЙ УРАВНЕНИЙ В ЦЕЛЫХ ЧИСЛАХ

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение.

Объект исследования.

Исследования касаются одного из наиболее интересных разделов теории чисел — решения уравнений в целых числах.

Предмет исследования.

Решение в целых числах алгебраических уравнений с целыми коэффициентами более чем с одним неизвестным представляет собой одну из труднейших и древнейших математических задач и не достаточно глубоко представлена в школьном курсе математики. В своей работе я представлю достаточно полный анализ уравнений в целых числах, классификацию данных уравнений по способам их решения, описание алгоритмов их решения, а также практические примеры применения каждого способа для решения уравнений в целых числах.

Цель.

Познакомиться со способами решения уравнений в целых числах.

Задачи:

Изучить учебную и справочную литературу;

Собрать теоретический материал по способам решения уравнений;

Разобрать алгоритмы решения уравнений данного вида;

Описать способы решения;

Рассмотреть примеры решения уравнений с применением данных способов.

Гипотеза:

Столкнувшись с уравнениями в целых числах в олимпиадных заданиях, я предположила, что трудности в их решении обусловлены тем, что далеко не все способы их решения мне известны.

Актуальность:

Решая примерные варианты заданий ЕГЭ, я заметила, что часто встречаются задания на решение уравнений первой и второй степени в целых числах. Кроме того олимпиадные задания различных уровней также содержат уравнения в целых числах или задачи, которые решаются с применением умений решать уравнения в целых числах. Важность знания способов решения уравнений в целых числах и определяет актуальность моих исследований.

Методы исследования

Теоретический анализ и обобщение сведений научной литературы об уравнениях в целых числах.

Классификация уравнений в целых числах по методам их решения.

Анализ и обобщение методов решения уравнений в целых числах.

Результаты исследования

В работе описаны способы решений уравнений, рассмотрен теоретический материал теоремы Ферма, теорема Пифагора, алгоритма Евклида, представлены примеры решений задач и уравнений различных уровней сложности.

2.История уравнений в целых числах

Диофант – ученый – алгебраист Древней Греции, по некоторым данным он жил до 364 года н. э. Он специализировался на решении задач в целых числах. Отсюда и пошло название Диофантовы уравнения. Наиболее известной, решенной Диофантом, является задача «о разложении на два квадрата». Ее эквивалентом является известная всем теорема Пифагора. Жизнь и деятельность Диофанта протекала в Александрии, он собирал и решал известные и придумывал новые задачи. Позднее он объединил их в большом труде под названием «Арифметика». Из тринадцати книг, входивших в состав «Арифметики», только шесть сохранились до Средних веков и стали источником вдохновения для математиков эпохи Возрождения.«Арифметика» Диофанта — это сборник задач, каждая включает в себя решение и необходимое пояснение. В собрание входят разнообразные задачи, а их решение часто в высшей степени остроумно. Диофанта интересуют только положительные целые и рациональные решения. Иррациональные решения он называет «невозможными» и тщательно подбирает коэффициенты так, чтобы получились искомые положительные, рациональные решения.

Для решения уравнений в целых числах применяется теорема Ферма. История доказательства которой достаточно интересная. Над полным доказательством Великой теоремы работало немало выдающихся математиков, и эти усилия привели к получению многих результатов современной теории чисел. Считается, что теорема стоит на первом месте по количеству неверных доказательств.

Замечательный французский математик Пьер Ферма высказал утверждение, что уравнение при целом n ≥ 3 не имеет решений в целых положительных числах x, y, z ( xyz = 0 исключается положительностью x, y, z.Для случая n = 3 эту теорему в X веке пытался доказать среднеазиатский математик ал-Ходжанди, но его доказательство не сохранилось. Несколько позже сам Ферма опубликовал доказательство частного случая для n = 4.

Эйлер в 1770 доказал теорему для случая n = 3, Дирихле и Лежандр в 1825 — для n = 5,Ламе — для n = 7. Куммер показал, что теорема верна для всех простых n, меньших 100, за возможным исключением 37, 59, 67.

В 1980-х годах появился новый подход к решению проблемы. Из гипотезы Морделла, доказанной Фальтингсом в 1983 году, следует, что уравнение

при n > 3 может иметь лишь конечное число взаимно простых решений.

Последний, но самый важный, шаг в доказательстве теоремы был сделан в сентябре 1994 года Уайлсом. Его 130-страничное доказательство было опубликовано в журнале «AnnalsofMathematics». Доказательство основано на предположении немецкого математика Герхарда Фрая о том, что Великая теорема Ферма является следствием гипотезы Таниямы — Симуры (это предположение было доказано Кеном Рибетом при участии Ж.‑П.Серра. ).Первый вариант своего доказательства Уайлс опубликовал в 1993 году (после 7 лет напряжённой работы), но в нём вскоре обнаружился серьёзный пробел; с помощью Ричарда Лоуренса Тейлора пробел удалось достаточно быстро ликвидировать. В 1995 году был опубликован завершающий вариант. 15 марта 2016 года Эндрю Уайлз получает премию Абеля. В настоящее время премия составляет 6 миллионов норвежских крон, то есть примерно 50 миллионов рублей. По словам Уайлса, присуждение премии стало для него «полной неожиданностью».

3.Линейные уравнения в целых числах

Линейные уравнения – самые простые из всех диофантовых уравнений .

Уравнение вида ах=b, где a и b – некоторые числа, а х- неизвестная переменная, называется линейным уравнением с одной неизвестной. Здесь требуется найти только целые решения уравнения. Можно заметить, что если а ≠ 0, то целочисленное решение уравнение будет иметь только в том случае, когда b нацело делится на а и это решение х= b/ф. Если же а=0, то целочисленное решение уравнение будет иметь тогда, когда b=0 и в этом случае х любое число.

Примеры:

4х=12

т.к. 12 нацело делится на 4, то

х=12/4

х=3

0х=0

Т.к. а=о и b=0, то х любое число

10х=7

Т.к. 7 нацело не делится на 10, то решений нет.

4. Способ перебора вариантов.

В способе перебора вариантов необходимо учитывать признаки делимости чисел, рассмотреть все возможные варианты равенства конечного перебора. Этот способ можно применить решая данные задачи:

№1 Найти множество всех пар натуральных чисел, которые являются решением уравнения 49x+69y=602

Решение:

49x+69y=602

Выражаем из уравнения х =,

Т.к. x и y натуральные числа, то х = ≥ 1, умножаем все уравнение на 49, чтобы избавиться от знаменателя:

602-51y ≥ 49,

Переносим 602 в левую сторону:

51y ≤ 553, выражаем y, y= 10

1 ≤ y ≤ 10

Полный перебор вариантов показывает, что натуральными решениями уравнения являются x=5, y=7.

Ответ:(5,7).-

№2 Решить задачу

Из цифр 2, 4, 7 следует составить трёхзначное число, в котором ни одна цифра не может повторяться более двух раз.

Решение.

Найдем количество всех трехзначных чисел, которые начинаются с цифры 2: (224, 242, 227, 272, 247, 274, 244, 277) – их 8.

Аналогично находим все трехзначные цифры начинающиеся с цифр 4 и 7: (442, 424, 422, 447, 474, 427, 472, 477).

(772, 774, 727, 747, 722, 744, 724, 742) – их тоже по 8 чисел. Следует всего 24 числа.

Ответ: 24 числа.

5. Цепная дробь и алгоритм Евклида

Цепной дробью называется выражение обыкновенной дроби в виде

где q₁ – целое число, а q₂, … ,qn – натуральные числа. Такое выражение называется цепной (конечной непрерывной) дробью. Различают конечные и бесконечные цепные дроби.

Для рациональных чисел цепная дробь имеет конечный вид. Кроме того, последовательность a_i— это ровно та последовательность частных, которая получается при применении алгоритма Евклида к числителю и знаменателю дроби.

Решая уравнения цепной дробью, я составила общий алгоритм действий для данного способа решения уравнений в целых числах.

Алгоритм

1) Составить отношение коэффициентов при неизвестных в виде дроби

2) Преобразовать выражение в неправильную дробь

3) Выделить целую часть неправильной дроби

4) Правильную дробь заменить равной ей дробью

5) Проделать 3,4 с полученной в знаменателе неправильной дробью

6) Повторять 5 до конечного результата

7) У полученного выражения отбросить последнее звено цепной дроби, превратить получающуюся при этом новую цепную дробь в простую и вычесть ее из исходной дробь.

Пример №1 Решить в целых числах уравнение 127x- 52y+ 1 = 0

Решение:

Преобразуем отношение коэффициентов при неизвестных.

Прежде всего, выделим целую часть неправильной дроби ; = 2 +

Правильную дробь заменим равной ей дробью .

Откуда = 2+

Проделаем такие же преобразования с полученной в знаменателе неправильной дробью.

Теперь исходная дробь примет вид: .Повторяя те же рассуждения для дроби получим Выделяя целую часть неправильной дроби, придем к окончательному результату:

Мы получили выражение, которое называется конечной цепной или непрерывной дробью. Отбросив последнее звено этой цепной дроби — одну пятую, превратим получающуюся при этом новую цепную дробь в простую и вычтем ее из исходной дроби :

2+;

Приведем полученное выражение к общему знаменателю и отбросим его.

Откуда 127∙9–52∙22+1=0. Из сопоставления полученного равенства с уравнением 127x- 52y+1 = 0 следует, что тогда x= 9, y= 22 — решение исходного уравнения, и согласно теореме все его решения будут содержаться в прогрессиях x= 9+ 52t, y= 22+ 127t, где t=( 0; ±1; ±2…..).Полученный результат наводит на мысль о том, что и в общем случае для нахождения решения уравнения ax+by+c=0 надо разложить отношение коэффициентов при неизвестных в цепную дробь, отбросить ее последнее звено и проделать выкладки, подобные тем, которые были приведены выше.

Для доказательства этого предположения будут нужны некоторые свойства цепных дробей.

Рассмотрим несократимую дробь . Обозначим через q₁ частное и через r₂ остаток от деления a на b. Тогда получим:

Пусть, далее, q₂ – частное и r₃ – остаток от деления b на r₂.

Тогда b=q₂r₂+r₃,

Точно так же

r₂=q₃r₃+r₄, ;

r₃=q₄r₄+r₅,;

………………………………..

Величины q₁, q₂,… называются неполными частными. Приведенный выше процесс образования неполных частных называется алгоритмом Евклида. Остатки от деления r₂, r₃,…удовлетворяют неравенствам

т.е. образуют ряд убывающих неотрицательных чисел.

Пример№2 Решить уравнение170х+190у=3000 в целых числах

После сокращения на 10 уравнение выглядит так,

17х+19у=300.

Для нахождения частного решения воспользуемся разложением дроби в цепную дробь

Свернув предпоследнюю подходящую к ней дробь в обыкновенную

Частное решение данного уравнения имеет вид

Х₀= (-1)4300∙9=2700, y₀=(-1)5300∙8=-2400,

а общее задается формулой

х=2700-19k, y= -2400+17k.

откуда получаем условие на параметр k

Т.е. k=142, x=2, y=14. .

6. Метод разложения на множители

Метод перебора вариантов неудобный способ, так как бывают случаи когда найти перебором всецелые решения, невозможно, так как таких решений бесконечное множество. Метод разложения на множители очень интересный прием и встречается он как и в элементарной математике так и в высшей.

Суть состоит в тождественном преобразовании. Смысл любого тождественного преобразования — это запись выражения в другом виде с сохранением его сути. Рассмотрим примеры применения данного метода.

№1 Решить уравнение в целых числах y³ — x³ = 91.

Решение:

Используя формулы сокращенного умножения, разложим правую часть уравнения на множители:

(y — x)(y² + xy + x²) = 91

Выписываем все делители числа 91: ± 1; ± 7; ± 13; ± 91

Замечаем, что для любых целых x и y число

y² + yx + x² ≥ y² — 2|y||x| + x² = (|y| — |x|)² ≥ 0,

следовательно, оба сомножителя в левой части уравнения должны быть положительными. Тогда исходное уравнение равносильно совокупности систем уравнений:

; ; ;

Решив системы, отбираем те корни, которые являются целыми числами.

Получаем решения исходного уравнения: (5; 6), (-6; -5); (-3; 4),(-4;3).

Ответ: (5; 6); (-6; -5); (-3; 4); (-4;3).

№2 Найти все пары натуральных чисел, удовлетворяющих уравнению х² –у²= 69

Решение:

Разложим левую часть уравнения на множители и запишем уравнение в виде

.

Т.к. делителями числа 69 являются числа 1, 3, 23 и 69, то 69 можно получить двумя способами: 69=1·69 и 69=3·23. Учитывая, что х-у > 0, получим две системы уравнений, решив которые мы сможем найти искомые числа:

или

Выразив одну переменную и подставив ее в второе уравнение находим корни уравнений.Первая система имеет решение x=35;y=34 , а вторая система имеет решение x=13, y=10.

Ответ: (35; 34), (13; 10).

№3 Решить уравнение х+у =ху в целых числах:

Решение:

Запишем уравнение в виде

Разложим левую часть уравнения на множители. Получим

Произведение двух целых чисел может равняться 1 только в двух случаях: если оба они равны 1 или -1. Получим две системы:

или

Первая система имеет решение х=2, у=2, а вторая система имеет решение х=0, у=0.Ответ: (2; 2), (0; 0).

№4 Доказать, что уравнение (x — y)³ + (y — z)³ + (z — x)³ = 30 не имеет решений в целых числах.

Решение:

Разложим левую часть уравнения на множители и обе части уравнения разделим на 3, в результате получим уравнение:

( x — y)(y — z)(z — x) = 10

Делителями 10 являются числа ±1, ±2, ±5, ±10. Заметим также, что сумма сомножителей левой части уравнения равна 0. Нетрудно проверить, что сумма любых трех чисел из множества делителей числа 10, дающих в произведении 10, не будет равняться 0. Следовательно, исходное уравнение не имеет решений в целых числах.

7. Метод остатков

Основная задача метода — находить остаток от деления обоих частей уравнения на целое число, на основе полученных результатов. Часто полученная информация уменьшает возможности множеств решений уравнения. Рассмотрим примеры:

№1 Доказать, что уравнение x² = 3y + 2 не имеет решений в целых числах.

Доказательство.

Рассмотрим случай, когда x, y ∈ N. Рассмотрим остатки от деления обоих частей на 3. Правая часть уравнения дает остаток 2 при делении на 3 при любом значении y. Левая же часть, которая является квадратом натурального числа, при делении на 3 всегда дает остаток 0 или 1. Исходя из этого получаем, что решения данного уравнения в натуральных числах нет.

Рассмотрим случай, когда одно из чисел равно 0. Тогда очевидно, решений в целых числах нет.

Случай, когда y — целое отрицательное не имеет решений, т.к. правая часть будет отрицательна, а левая — положительна.

Случай, когда x — целое отрицательное, также не имеет решений, т.к. попадает под один из рассмотренных ранее случаев ввиду того, что (-x)² = (x)².

Получается, что указанное уравнение не имеет решений в целых числах, что и требовалось доказать.

№2 Решите в целых числах 3^х= 1 + y² .

Не сложно заметить, что (0; 0) — решение данного уравнения. Остаётся доказать, что других целых корней уравнение не имеет.

Рассмотрим случаи:

1) Если x∈N, y∈N, то З делится на три без остатка, а 1 + y²при делении на 3 дает

остаток либо 1, либо 2. Следовательно, равенство при натуральных

значениях х, у невозможно.

2) Если х— целое отрицательное число,y∈Z , тогда 0< 3^х< 1, а 1 + y² ≥ 0 и

равенство также невозможно. Следовательно, (0; 0) — единственное

решение.

Ответ: (0; 0).

№3 Решить уравнение 2х² -2ху+9х+у=2 в целых числах:

Выразим из уравнения то неизвестное, которое входит в него только в первой степени, то есть переменную у:

2х² +9х-2=2ху-у, откуда

У =

Выделим у дроби целую часть с помощью правила деления многочлена на многочлен «углом». Получим:

Очевидно, разность 2х-1 может принимать только значения -3, -1, 1 и 3.

Осталось перебрать эти четыре случая, в результате чего получаем решения: (1;9), (2;8), (0;2), (-1;3)

Ответ: (1;9), (2;8), (0;2), (-1;3)

8.Пример решения уравнений с двумя переменными в целых числах как квадратных относительно одной из переменных

№1 Решить в целых числах уравнение 5х²+5у² + 8ху+2у-2х +2=0

Данное уравнение можно решить методом разложения на множители, однако этот способ применительно к данному уравнению достаточно трудоёмкий. Рассмотрим более рациональный способ.

Запишем уравнение в виде квадратного относительно переменной х:

5x²+(8y-2)x+5y²+2y+2=0

Находим его корни.

Х_1,2=

Данное уравнение имеет решение тогда и только тогда, когда дискриминант

этого уравнения равен нулю, т.е. — 9(у+1)² =0, отсюда у= — 1.

Если у= -1,то х= 1.

Ответ: (1; — 1).

9.Пример решения задач с помощью уравнений в целых числах.

№ 1. Решить в натуральных числах уравнение: где n>m

Решение:

Выразим переменную n через переменную m:

Найдем делители числа 625: это 1; 5; 25; 125; 625

1) если m-25 =1, то m=26, n=25+625=650

2) m-25 =5, то m=30, n=150

3) m-25 =25, то m=50, n=50

4) m-25 =125, то m=150, n=30

5) m-25 =625, то m=650, n=26

Ответ: m=150, n=30

m=650, n=26

№ 2. Решить уравнение в натуральных числах: mn +25 = 4m

Решение: mn +25 = 4m

1) выразим переменную 4m через n:

4m – mn =25

m(4-n) =25

m =

2) найдем натуральные делители числа 25: это 1; 5; 25

если 4-n =1, то n=3, m=25

4-n=5, то n=-1, m=5; 4-n =25, то n=-21, m=1 (посторонние корни)

Ответ: (25;3)

Помимо заданий решить уравнение в целых числах, встречаются задания на доказательство того факта, что уравнение не имеет целых корней.

При решении таких задач, необходимо помнить следующие свойства делимости:

1) Если n Z; n делится на 2, то n = 2k, k ∈ Z.

2) Если n ∈ Z; n не делится на 2, то n = 2k+1, k ∈ Z.

3) Если n ∈ Z; n делится на 3, то n = 3k, k ∈ Z.

4) Если n ∈ Z; n не делится на 3, то n = 3k±1, k ∈ Z.

5) Если n ∈ Z; n не делится на 4, то n = 4k+1; n = 4k+2; n = 4k+3. k ∈ Z.

6) Если n ∈ Z; n(n+1) делится на 2, то n (n+1)(n+2) делится на 2;3;6.

7) n; n+1 – взаимно простые.

№3 Доказать, что уравнение x²– 3у = 17 не имеет целых решений.

Решение:

Доказательство:

x²– 3у = 17

Пусть x; y – решения уравнения

x²= 3у – 17

x² = 3(у+6)-1 Т.к. y ∈ Z то y+6 ∈ Z , значит 3(y+6) делится на 3, следовательно, 3(y+6)-1 не делится на 3, следовательно, x² не делится на 3, следовательно, x не делится на 3, значит x = 3k±1, k ∈ Z.

Подставим это в исходное уравнение.

.

Получили противоречие. Значит у уравнения нет целых решений, что и требовалось доказать.

10.Формула Пика

Формула Пика была открыта австрийским математиком Георгом Пиком в 1899 году. Формула связанна с уравнениями в целых числах тем, что из многоугольников берут только целые узлы, как и целые числа в уравнениях.

При помощи этой формулы можно находить площадь фигуры построенной на листе в клетку (треугольник, квадрат, трапеция, прямоугольник, многоугольник).

В этой формуле будем находить целые точки внутри многоугольника и на его границе.

В задачах, которые будут на ЕГЭ есть целая группа заданий, в которых дан многоугольник построенный на листе в клетку и стоит вопрос о нахождении площади. Масштаб клетки это один квадратный сантиметр.

Пример№1

М – количество узлов на границе треугольника (на сторонах и вершинах)

N – количество узлов внутри треугольника.

*Под «узлами» имеется ввиду пересечение линий. Найдём площадь треугольника:

Отметим узлы:

M = 15 (обозначены красным)

N = 34 (обозначены синим)

Пример №2

Найдём площадь многоугольника: Отметим узлы:

M = 14 (обозначены красным)

N = 43 (обозначены синим)

12.Метод спуска

Один из методов решений уравнений в целых числах – метод спуска — опирается на теорему Ферма.

Методом спуска называется метод, который заключается в построении одного решения бесчисленной последовательности решений с неограниченно убывающим положительным z.

Алгоритм этого метода рассмотрим на примере решения конкретного уравнения.

Пример 1. Решить уравнение в целых числах 5x + 8y = 39.

1) Выберем неизвестное, имеющее наименьший коэффициент (в нашем случае это х), и выразим его через другое неизвестное:

2) Выделим целую часть: Очевидно, что х будет целым, если выражение окажется целым, что, в свою очередь, будет иметь место тогда, когда число 4 – 3y без остатка делится на 5.

3) Введем дополнительную целочисленную переменную z следующим образом: 4 –3y = 5z. В результате получим уравнение такого же типа, как и первоначальное, но уже с меньшими коэффициентами.

4) Решаем его уже относительно переменной y, рассуждая точно также как в п.1, 2: Выделяя целую часть, получим:

5) Рассуждая аналогично предыдущему, вводим новую переменную u: 3u = 1 – 2z.

6) Выразим неизвестную с наименьшим коэффициентом, в этом случае переменную z: . Требуя, чтобы было целым, получим: 1 – u = 2v, откуда u = 1 – 2v. Дробей больше нет, спуск закончен (процесс продолжаем до тез пор, пока в выражении для очередной переменной не останется дробей).

7) Теперь необходимо «подняться вверх». Выразим через переменную v сначала z, потом y и затем x:

Формулы x = 3+8v и y = 3 – 5v, где v – произвольное целое число, представляют общее решение исходного уравнения в целых числах.

Таким образом, метод спуска предполагает сначала последовательное выражение одной переменой чрез другую, пока в представлении переменной не останется дробей, а затем, последовательное «восхождение» по цепочке равенств для получения общего решения уравнения.

12.Заключение

В результате исследования подтвердилась гипотеза о том, что трудности при решении уравнений в целых числах обусловлены тем, что далеко не все способы их решения были мне известны. В ходе исследований мне удалось отыскать и описать малоизвестные способы решения уравнений в целых числах, проиллюстрировать их примерами. Результаты моих исследований могут быть полезны всем ученикам, интересующимся математикой.

13.Библиография

Книжные ресурсы:

1. Н. Я. Виленкин и др., Алгебра и математический анализ/10класс, 11 класс// М., «Просвещение», 1998 год;

2. А. Ф. Иванов и др., Математика. Учебно-тренировочные материалы для подготовки к экзамену// Воронеж, ГОУВПО ВГТУ, 2007 год

3. А. О. Гельфонд, Математика, теория чисел// Решение уравнений в целых числах// Книжный дом «ЛИБРОКОМ»

Ресурсы сети интернет:

4. Демонстрационные варианты контрольных измерительных материалов единого государственного экзамена по математике http://fipi.ru/

5. Примеры решений уравнений в целых числахhttp://reshuege.ru

6. Примеры решений уравнений в целых числахhttp://mat-ege.ru

7.История Диофантовых уравнений http://www.goldenmuseum.com/1612Hilbert_rus.html

8. История Диофанта http://nenuda.ru/%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D1%8F-%D1%81-%D0%B4%D0%B2%D1%83%D0%BC%D1%8F-%D0%BD%D0%B5%D0%B8%D0%B7%D0%B2%D0%B5%D1%81%D1%82%D0%BD%D1%8B%D0%BC%D0%B8-%D0%B2-%D1%86%D0%B5%D0%BB%D1%8B%D1%85-%D1%87%D0%B8%D1%81%D0%BB%D0%B0%D1%85.htm

9.История Диофантовых уравненийhttp://dok.opredelim.com/docs/index-1732.html

10. История Диофанта http://www.studfiles.ru/preview/4518769/

11. http://pandia.ru/text/78/004/3180.php

Просмотров работы: 26485

Решение уравнений в целых числах является одной из древнейших математических задач. 

Уравнения в целых числах – это алгебраические уравнения с двумя или более неизвестными переменными и целыми коэффициентами. Решениями такого уравнения являются все целочисленные (иногда натуральные или рациональные) наборы значений неизвестных переменных, удовлетворяющих этому уравнению. Такие уравнения ещё называют диофантовыми, в честь древнегреческого математика Диофанта Александрийского, который исследовал некоторые типы таких уравнений ещё до нашей эры.

Теоремы о числе решений линейного диофантового уравнения

Приведем здесь формулировки теорем, на основании которых может быть составлен алгоритм решения неопределенных уравнений первой степени от двух переменных в целых числах.

Теорема 1. Если в уравнении (ax + by) = 1,  (a,b) = 1, то уравнение имеет, по крайней мере, одно решение.

Теорема 2. Если в уравнении (ax + by) = с , (a,b) = d >1  и с не делится на d , то уравнение целых решений не имеет.

Теорема 3. Если в уравнении (ax + by) = с , (a,b) = d >1 , и  d⋮c, то оно равносильно уравнению (a₁x + b₁y) = 1 , в котором (a₁,b₁) = 1.

Теорема 4. Если в уравнении (ax + by) = 1, (a,b) = 1, то все целые решения этого уравнения заключены в формулах:

x = x₀c + bt

y = y₀c — at

где х₀ , у₀ – целое решение уравнения  (ax + by) = 1,  t- любое целое число.

Cформулируем на основании этих теорем алгоритм решения уравнения

Алгоритм решения уравнения в целых числах

Сформулированные теоремы позволяют составить следующий алгоритм решения в целых числах уравнения вида (ax + by) = с .

1. Найти наибольший общий делитель чисел a и b ,

если (a,b) = d >1  и с не делится на d , то уравнение целых решений не имеет;

если (a,b) = d >1  и  c⋮d , то переходим к этапу 2.

2. Разделить почленно уравнение (ax + by) = с  на d, получив при этом уравнение (a₁x + b₁y) = c₁ , в котором (a₁,b₁) = 1.

3. Найти целое решение (х₀ , у₀ ) уравнения (a₁x + b₁y) = 1 путем представления 1 как линейной комбинации чисел  a и b ;

4. Составить общую формулу целых решений данного уравнения

x = x₀c + bt

y = y₀c — at

где х₀ , у₀ – целое решение уравнения (ax + by) = 1, t- любое целое число.

Способы решения уравнений

При решении уравнений в целых и натуральных числах можно условно выделить следующие методы:

1. Алгоритм Евклида.

2. Способ перебора вариантов.

3. Метод разложения на множители.

4. Метод остатков.

5. Решение уравнений в целых числах как квадратных относительно какой-либо переменной.

6. Цепные дроби.

7. Метод бесконечного спуска.

Применение способов решения уравнений

Примеры решения уравнений.

Алгоритм Евклида.

Решить в целых числах уравнение:

а) 20х + 12у = 2013;

б) 5х + 7у = 19;

в) 201х – 1999у = 12.

Решение

а) 20х + 12у = 2013 Поскольку при любых целых значениях х и у левая часть уравнения делится на два, а правая является нечётным числом, то уравнение не имеет решений в целых числах.

Ответ: решений нет.

б) 5х + 7у = 19 Подберём сначала некоторое конкретное решение. В данном случае, это просто, например,

x₀= 1, y₀ = 2.

Тогда 5x₀ + 7y₀ = 19,

откуда 5(х – x₀) + 7(у – y₀) = 0,

5(х – x₀) = –7(у – y₀).

Поскольку числа 5 и 7 взаимно простые, то

х – x₀ = 7k, у – y₀ = –5k.

Значит, общее решение:

х = 1 + 7k, у = 2 – 5k,

где k – произвольное целое число.

Ответ: (1+7k; 2–5k), где k – целое число.

в) 201х – 1999у = 12 Найти некоторое конкретное решение подбором в данном случае достаточно сложно. Воспользуемся алгоритмом Евклида для чисел 1999 и 201:

НОД(1999, 201) = НОД(201, 190) = НОД(190, 11) = НОД(11, 3) = НОД(3 , 2) = НОД(2, 1) = 1.

Запишем этот процесс в обратном порядке:

1 = 2 – 1 = 2 – (3 – 2) = 2·2 – 3 = 2· (11 – 3·3) – 3 = 2·11 – 7·3 = 2·11 – 7(190 – 11·17) =

= 121·11 – 7·190 = 121(201 – 190) – 7·190 = 121·201 – 128·190 =

= 121·201 – 128(1999 – 9·201) = 1273·201 – 128·1999.

Значит, пара (1273, 128) является решением уравнения 201х – 1999у = 1. Тогда пара чисел

x₀= 1273·12 = 15276, y₀ = 128·12 = 1536

является решением уравнения 201х – 1999у = 12.

Общее решение этого уравнения запишется в виде

х = 15276 + 1999k, у = 1536 + 201k, где k – целое число,

или, после переобозначения (используем, что 15276 = 1283 + 7·1999, 1536 = 129 + 7·201),

х = 1283 + 1999n, у = 129 + 201n, где n – целое число.

Ответ: (1283+1999n, 129+201n), где n – целое число.

Решить уравнение в целых числах 407х – 2816y = 33.

Воспользуемся составленным алгоритмом.

1. Используя алгоритм Евклида, найдем наибольший общий делитель чисел 407 и 2816:

2816 = 407·6 + 374;

407 = 374·1 + 33;

374 = 33·11 + 11;

33 = 11·3

Следовательно (407,2816) = 11, причем 33 делится на 11

2. Разделим обе части первоначального уравнения на 11, получим уравнение 37х – 256y = 3, причем (37, 256) = 1

3. С помощью алгоритма Евклида найдем линейное представление числа 1 через числа 37 и 256.

256 = 37·6 + 34;

37 = 34·1 + 3;

34 = 3·11 + 1

Выразим 1 из последнего равенства, затем последовательно поднимаясь по равенствам будем выражать 3; 34 и полученные выражения подставим в выражение для 1.

1 = 34 – 3·11 = 34 – (37 – 34·1) ·11 = 34·12 – 37·11 = (256 – 37·6) ·12 – 37·11 =

– 83·37 – 256·(–12)

Таким образом, 37·(– 83) – 256·(–12) = 1, следовательно пара чисел х₀ = – 83 и у₀ = – 12 есть решение уравнения 37х – 256y = 3.

4. Запишем общую формулу решений первоначального уравнения

х = — 83с + bt = -83*3 — 256 t = -249 — 256t

y = -12c — at = -12*3 — 37t = -36 — 37t

где t — любое целое число.

2 Способ перебора вариантов.

Задача 2. В клетке сидят cобаки и кошки, всего у них 18 ног. Узнать, сколько в клетке тех и других?

Решение: Составляется уравнение с двумя неизвестными переменными, в котором х – число собак , у – число кошек:

4х + 2у = 18, или 2х + у = 9.

Выразим у через х : у = 9 – 2х.

Далее воспользуемся методом перебора:

х = 1__2__3__4__

у = 7__5__3__1__

Таким образом, задача имеет четыре решения.

Ответ: (1; 7), (2; 5), (3; 3), (4; 1).

3 Метод разложения на множители.

Перебор вариантов при нахождении натуральных решений уравнения с двумя переменными оказывается весьма трудоемким. Кроме того, если уравнение имеет целые решения, то перебрать их невозможно, так как таких решений бесконечное множество. Поэтому покажем еще один прием — метод разложения на множители.

Задача 3. Решить уравнение в целых числах y³ — x³ = 91.

Решение. 1) Используя формулы сокращенного умножения, разложим правую часть уравнения на множители:

(y — x )(y² + xy + x² ) = 91

2) Выпишем все делители числа 91: ± 1; ± 7; ± 13; ± 91

3) Проводим исследование. Заметим, что для любых целых x и y число

y² + yx + x² ≥ y ² — 2|y ||x | + x ²= (|y | — |x |)² ≥ 0,

следовательно, оба сомножителя в левой части уравнения должны быть положительными. Тогда уравнение (y — x )(y² + xy + x² ) = 91 равносильно совокупности систем уравнений:

(у — х) = 1

(y² + xy + x² ) =91 

(у — х) = 91

(y² + xy + x² ) =1 

(у — х) = 7

(y² + xy + x² ) =13 

(у — х) = 13

(y² + xy + x² ) =7

4) Решив системы, получим: первая система имеет решения (5; 6), (-6; -5); третья (-3; 4),(-4;3); вторая и четвертая решений в целых числах не имеют.

Ответ: уравнение имеет четыре решения (5; 6); (-6; -5); (-3; 4); (-4;3).

Задача 4. Найти все пары натуральных чисел, удовлетворяющих уравнению

x² — у² = 69

Решение. Разложим левую часть уравнения на множители и запишем уравнение в виде

(х-у)(х +у) = 69

Т.к. делителями числа 69 являются числа 1, 3, 23 и 69, то 69 можно получить двумя способами: 69=1·69 и 69=3·23. Учитывая, что , получим две системы уравнений, решив которые мы сможем найти искомые числа:

Первая система имеет решение

(х — у) = 1

(х+у) = 69

х = 35, у = 34

 , а вторая система имеет решение .

(х — у) = 3

(х+у) = 23

х = 13 , у = 10

Ответ: (13;10) (35;34)  .

Задача 4. Найти все пары натуральных чисел, удовлетворяющих уравнению

x² — у² = 13

Решение. Разложим левую часть уравнения на множители и запишем уравнение в виде

(х-у)(х +у) = 13

Т.к. делителями числа 13 являются числа 1, и 13, то получим только одну систему уравнений:

(х — у) = 1

(х+у) = 13

х = 7, у = 6

Ответ: (7;6) 

Решить в целых числах уравнение x² – xy – 2y² = 7.

Решение

Запишем уравнение в виде (x – 2y)(x + y) = 7.

Так как х, у – целые числа, то находим решения исходного уравнения, как решения следующих четырёх систем:

1) x – 2y = 7, x + y = 1;

2) x – 2y = 1, x + y = 7;

3) x – 2y = –7, x + y = –1;

4) x – 2y = –1, x + y = –7.

Решив эти системы, получаем решения уравнения: (3; –2), (5; 2), (–3; 2) и (–5; –2).

Ответ: (3; –2), (5; 2), (–3; 2), (–5; –2).

Метод остатков

 Решить в целых числах уравнение:

а) x³ + y³ = 3333333;

б) x³ + y³ = 4(x²y + xy² + 1).

Решение

а) Так как x³ и y³ при делении на 9 могут давать только остатки 0, 1 и 8 , то x³+ y³ может давать только остатки 0, 1, 2, 7 и 8. Но число 3333333 при делении на 9 даёт остаток 3. Поэтому исходное уравнение не имеет решений в целых числах.

Ответ: целочисленных решений нет.

б) Перепишем исходное уравнение в виде (x + y)³ = 7(x²y + xy²) + 4. Так как кубы целых чисел при делении на 7 дают остатки 0, 1 и 6, но не 4, то уравнение не имеет решений в целых числах.

Ответ: целочисленных решений нет.

Решить в целых числах уравнение 1! + 2! + . . . + х! = у².

Решение

Очевидно, что

если х = 1, то у² = 1,

если х = 3, то у² = 9.

Этим случаям соответствуют следующие пары чисел:

х₁ = 1, у₁ = 1;

х₂ = 1, у₂ = –1;

х₃ = 3, у₃ = 3;

х₄ = 3, у₄ = –3.

Заметим, что при х = 2 имеем 1! + 2! = 3, при х = 4 имеем 1! + 2! + 3! + 4! = 33 и ни 3, ни 33 не являются квадратами целых чисел. Если же х > 5, то, так как

5! + 6! + . . . + х! = 10n,

можем записать, что

1! + 2! + 3! + 4! + 5! + . . . + х! = 33 + 10n.

Так как 33 + 10n – число, оканчивающееся цифрой 3, то оно не является квадратом целого числа.

Ответ: (1; 1), (1; –1), (3; 3), (3; –3).

ЕЩЕ УРАВНЕНИЯ)))

Сколько пар натуральных чисел удовлетворяет равенству 2x+5y=60?

Решение задачи

Так как (2x+5y)⋮5, то 2x⋮5, x⋮5. Аналогично можно показать, что y⋮2. Сделаем замену x=5x₀,y=2y₀. Тогда уравнение примет вид x₀+y₀ = 6. Очевидно, что это уравнение имеет в натуральных числах ровно 5 решений. Поэтому и исходное уравнение имеет ровно 5 решений.

Найдите количество целых решений уравнения xy + 6 = 2x + 3y, если x и y принадлежат отрезку [0;2014].

Перенесём все слагаемые в левую часть и разложим полученное выражение на множители:

xy + 6 = 2x+3y⇔xy − 2x−3y+6 = 0⇔ (x−3)(y−2) = 0.

Заметим, что, если x = 3, то y — любое, а если y = 2, то x — любое. (Так при умножении на 0 получается 0) Поэтому количество целых пар решений равно 2015 + 2015−1 = 4029.

Отметим, что решением исходного уравнения являются две прямые y=2 и x=3.

Найти все пары простых чисел x и y, удовлетворяющих уравнению:

x²−2y² = 1

В ответе запишите максимальное значение xx.

Решение задачи

Переписав исходное уравнение в виде

x² = 1+ 2y²,

заключаем, что x — нечетное число. Теперь, приводя исходное уравнение к виду

(x−1)(x+1)=2y²,

заметим, что числа x−1 и x+1 четные, а из (x−1)(x+1)=2y²

следует, что y четное. Значит, y = 2 (это единственное простое четное число). Следовательно, x = 3.