$begingroup$
Just an addition to Ross Millikan’s answer:
Remember that the highest power of a prime $p$ dividing $n!$ is given by the procedure:
- Greatest integer less than or equal to $frac{n}{p}$
- Greatest integer less than or equal to $frac{n}{p^2}$
- Greatest integer less than or equal to $frac{n}{p^3}$
- Repeat until the greatest integer less than or equal to $frac{n}{p^k}$ is $0$.
- Add all of your numbers up!
Example: Power of $3$ in the factorization of $100!$:
- Greatest integer less than or equal to $frac{100}{3}$ is $33$
- Greatest integer less than or equal to $frac{100}{3^2}$ is $11$
- Greatest integer less than or equal to $frac{100}{3^3}$ is $3$
- Greatest integer less than or equal to $frac{100}{3^4}$ is $1$
- Greatest integer less than or equal to all the fractions after this is zero: $frac{100}{3^5} > frac{100}{3^6} > cdots$
- Add: $33 + 11 + 3 + 1 = 48$.
I would assume you would do this for every prime under $n$ and use the formula in Ross’s answer.
answered Jun 2, 2015 at 23:18
AntAnt
2,3671 gold badge15 silver badges29 bronze badges
$endgroup$
4
$begingroup$
You have to assess the powers of all the primes less than $n$ in $n!$ and use the formula you cite. For example, $8!=40320=2^7cdot3^2cdot 5 cdot 7$, so it has $(7+1)(2+1)(1+1)(1+1)=96$ factors. The way to calculate the power of the primes is given here
answered Jun 2, 2015 at 23:13
Ross MillikanRoss Millikan
369k27 gold badges252 silver badges444 bronze badges
$endgroup$
You must log in to answer this question.
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.
Делители факториала
По заданному натуральному числу N необходимо вычислить количество натуральных чисел, которые являются делителями N! (факториала числа N).
Например, при N=4, N!=4⋅3⋅2⋅1=24. Это число имеет следующие делители: 1,2,3,4,6,8,12,24. Таким образом, искомое количество составляет 8.
Напишите программу, которая по натуральному N находит количество делителей его факториала.
Ввод 4
Вывод 8
n = int(input())
d=1
factorial = 1
while n > 1:
factorial *= n
n -= 1
numb = factorial
count_of_dividers = 2
for i in range(numb - 1, 1, -1):
if (numb % i == 0):
count_of_dividers += 1
print(count_of_dividers)
Программа выполняется долго…
Часто в олимпиадных задачах, чтобы оценить асимптотику алгоритма, требуется знать примерное число делителей поступающего на вход числа. Точнее, требуется знать максимальное число делителей среди всех чисел до, скажем, миллиарда.
Самая грубая оценка — O (sqrt(N)), а именно, не более двух квадратных корней из N.
Но часто это оказывается слишком грубой оценкой, неоправданно завышенной.
Обычная используемая мной оценка — O(кубического корня из N). Эту таинственную оценку я услышал когда-то давно от кого-то, и никогда её не понимал, но пользовался ей, и она работала.
Совсем недавно мы делали стресс-тест, и на числах до миллиарда она подтвердилась — число делителей не превосходит двух кубических корней из числа. Этого «доказательства» вполне достаточно, чтобы и дальше применять эту оценку на практике. Но найти ей математическое объяснение ну никак не получалось.
Сегодня в очередной раз решил поискать на эту тему в интернете. На этот раз нашёл то. что нужно, на удивление быстро: en.wikipedia.org/wiki/Divisor_function. Здесь много всякого интересного, но вот главная вещь, поразительная для меня формула:
«для любого eps>0 выполняется: d(n) = o(n^eps)»
Выходит, на самом деле число делителей ведёт себя на бесконечности не только лучше квадратного, кубического и прочего корней из числа n; оно вообще является субполиномиальной величиной!
Другие оценки:
- Wigert: «d(n) ~ n ^ (log2 / log log n)» (ну я примерно передал порядок, на самом деле там формула посложнее)
- Дирихле: «СУММА_{i=1..n} d(i) / n ~ log n + 2 gamma — 1»
P.S. Некоторым это может показаться бояном, но я знаю, что многие до сих пор даже не знают, что число делителей меньше квадратного корня, не говоря уже о таких «крутых» оценках 
P.P.S. Для олимпиад, где обычно в таких задачах мы имеем дело с числами до 10^9 — 10^12, эти оценки малополезны (здесь надо по-прежнему брать корень кубический), но они интересны чисто как математический факт.
#статьи
- 19 май 2023
-
0
Что такое факториал и как его вычислить
Статья, после которой вы начнёте щёлкать факториалы как орешки.
Иллюстрация: Катя Павловская для Skillbox Media
Любитель научной фантастики и технологического прогресса. Хорошо сочетает в себе заумного технаря и утончённого гуманитария. Пишет про IT и радуется этому.
Даже если вы уже давно окончили школу, факториалы всё равно могут доставить немало приятных флешбэков — например, если вы обучаетесь программированию и знакомитесь с задачками на рекурсию или комбинаторику. Поэтому мы решили максимально просто объяснить, что такое факториал, как его вычислять и зачем он вообще нужен.
Эта статья будет полезна как опытным программистам, которые хотят освежить знания, так и тем, кто ещё учится: школьникам, студентам и совсем зелёным джунам.
Содержание:
- Что такое факториал
- Для чего он нужен
- Основные свойства и формулы
- Шпаргалка: таблица факториалов
- Решаем задачи на факториалы
- Что запомнить
Факториал числа n — это произведение всех натуральных чисел от единицы до n. Обозначается факториал символом восклицательного знака: !.
Это определение из учебника, и оно пока звучит сложновато — неясно, зачем эти факториалы вообще нужны и как они могут пригодиться в науке и технике. Но об этом чуть позже — для начала давайте посмотрим на примеры факториалов:
Чтобы вычислить их, нам нужно перемножить все числа от единицы до числа, стоящего под знаком факториала — так гласит определение. Получаем выражения:
Ещё в математическом определении сказано, что факториал не может быть отрицательным или дробным — то есть вот такие факториалы вычислить нельзя:
Факториалы незаменимы там, где нужно быстро посчитать количество комбинаций и сочетаний разных предметов. В математике этому посвящён даже целый раздел — комбинаторика. Её методы используют много где: от лингвистики до криптографии и анализа ДНК. И во всех этих сферах факториал помогает упрощать сложные вычисления.
Разберём на примере, как это работает.
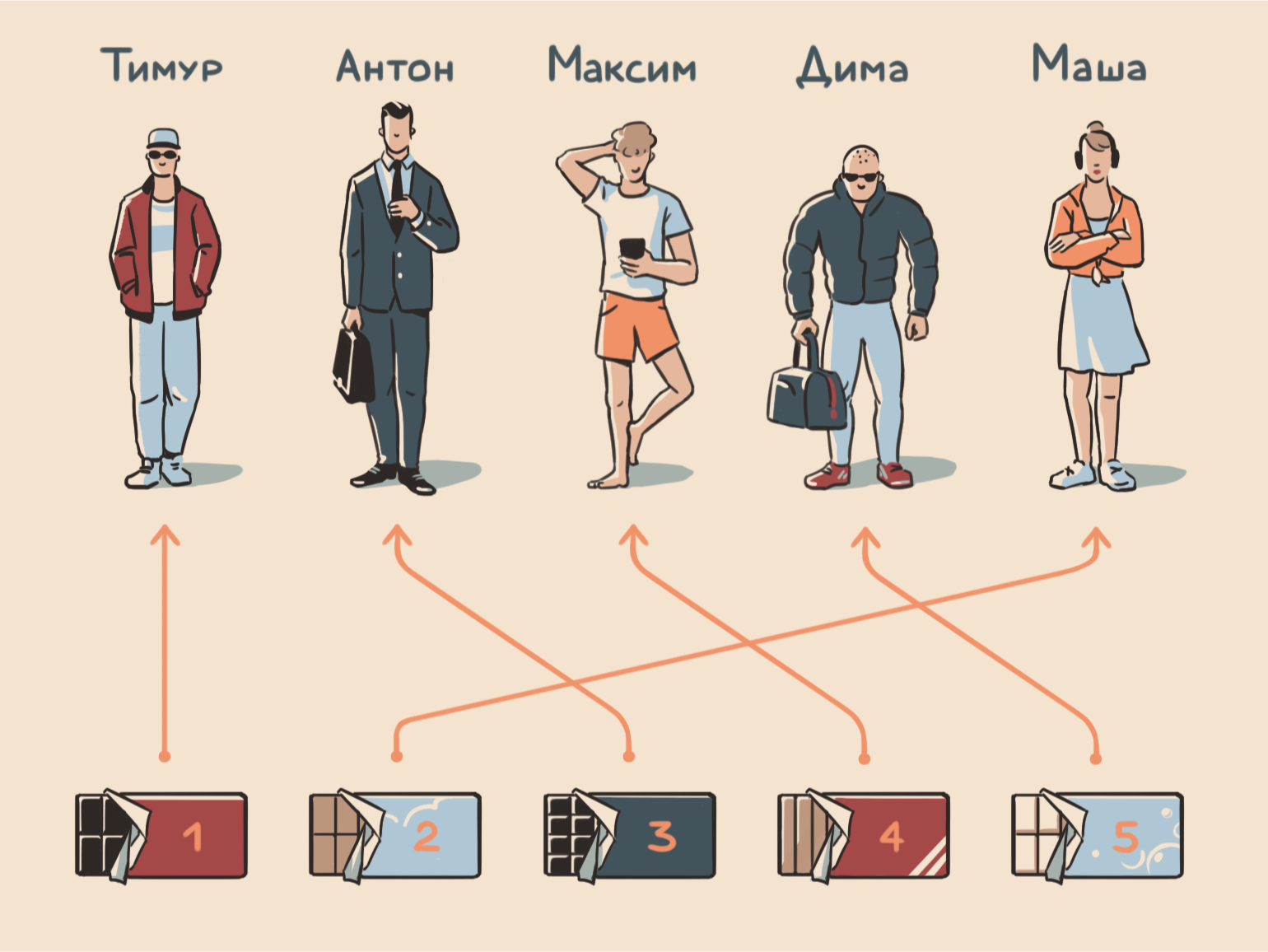
Допустим, у вас есть пять шоколадок и вы решили раздать их пяти друзьям — каждому по одной. Задача — выяснить, сколько существует способов раздать эти шоколадки. Начинаем размышлять:
- первую шоколадку можно отдать одному из пяти друзей;
- вторую — одному из четырёх друзей, потому что один уже получил свою шоколадку;
- третью — одному из трёх, потому что двое уже наслаждаются своими шоколадками;
- четвёртую — одному из двух;
- пятую — последнему другу.
Получается, что способов раздать первую шоколадку — 5, вторую — 4, третью — 3, четвёртую — 2, а пятую — всего 1. По правилам математики, чтобы выяснить общее количество всех вариантов, нужно перемножить их между собой. Ну а кто мы такие, чтобы с этими правилами спорить?
Смотрим на выражение выше и понимаем: ведь оно идеально вписывается в определение факториала — произведение натуральных чисел от одного до n (в нашем случае n равно 5). Следовательно, это выражение можно коротко и изящно записать в виде факториала:
Выходит, что всего способов раздать пять шоколадок пяти друзьям существует 120. Вот как может выглядеть один из них:
Конечно, в жизни вам вряд ли придётся считать количество способов раздать друзьям шоколадки. Но, например, в статистике, теории вероятностей, матанализе и программировании факториалы используют сплошь и рядом. Так что, если видите себя в будущем на матмехе или, на худой конец, в IT, то лучше познакомиться с ними хотя бы бегло.
Так как факториалы используются в разных областях математики, свойств у них довольно много — каждая область привносит какие-то свои методы вычислений. Одно из свойств вы уже знаете: факториал — это всегда целое положительное число. Вот ещё несколько, которые стоит запомнить:
- Факториал нуля равен единице — 0! = 1.
- Факториал единицы тоже равен единице: 1! = 1.
- Рекурсия: n! = (n – 1)! × n. Это основное свойство факториалов, о нём мы чуть подробнее поговорим дальше.
Мы видим, что каждое свойство описывается какой-то формулой — и некоторые из этих формул могут быть весьма полезны. Они позволяют нам находить факториалы проще и быстрее, чем простым перемножением натуральных чисел. Разберём эти формулы тоже.
Чтобы вычислить факториал, не используя так много операций умножения, придумали формулу Стирлинга. Вот как она выглядит:
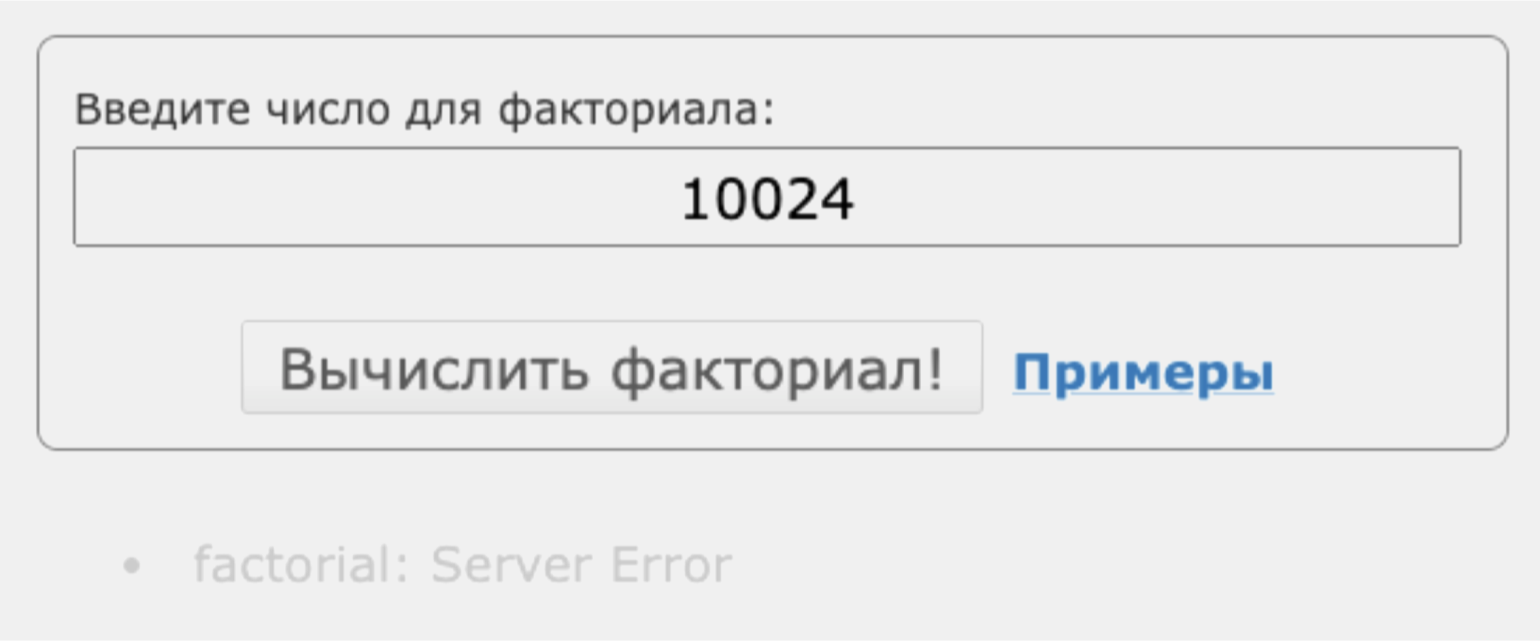
Выглядит страшно, но на самом деле она очень полезная. Её используют, когда хотят приблизительно узнать факториал большого числа. Обычным способом это будет сделать сложно даже мощному компьютеру — например, попробуйте посчитать в онлайн-калькуляторе факториал числа 10 024 (спойлер: это может занять несколько часов и даже дней).
Скришнот: «Контрольная работа РУ — калькуляторы онлайн» / Skillbox Media
Давайте попробуем вычислить факториал числа 6 по этой формуле:
Число e примерно равно 2,71, а π — 3,14. Подставляем их в выражение и получаем ответ:
Получили приближённое значение настоящего факториала, который равен 720. Но можно сделать ответ и более точным. Для этого нужно добавить больше знаков после запятой всем переменным — например, если взять 20 знаков, то ответ будет таким:
Это уже больше похоже на правду. Хотя погрешность всё равно есть.
Рекуррентная формула позволяет вычислить факториал числа n, основываясь на факториале предыдущего числа — (n – 1). Выглядит она так:
В целом рекуррентная формула не приносит нам большой пользы, так как всё равно приходится вычислять факториал предыдущего числа. Если он равен какому-то большому числу (например, 100), то использование формулы теряет смысл — слишком уж много вычислений это потребует.
Рекуррентная формула основана на главном свойстве факториалов — рекурсии: n! = (n – 1)! × n. Это свойство особенно полезно при решении задач по комбинаторике: так мы можем быстро сокращать факториалы и упрощать выражения.
Однако рекуррентная формула хорошо подходит для алгоритмов — в частности, для программирования. Мы можем задать начальное значение: например, что 0! = 1 или 1! = 1, а затем считать следующие факториалы по формуле:
Получим алгоритм для вычисления факториалов. Не очень эффективный, но простой.
Давайте вычислим по этой формуле факториал числа 4. Сначала распишем рекуррентную формулу до базового значения — факториала числа 1:
Можно записать это и в сокращённом виде:
Теперь последовательно подставляем значение факториала, которое мы уже знаем, и вычисляем результат:
Получили ответ — 24. Ничего сложного, просто перемножаем числа.
Кстати, всю эту формулу можно обернуть в реально работающую функцию на языке Python:
def factorial(n): # Определяем функцию if n == 0 or n == 1: # Базовый случай return 1 else: # Рекуррентный случай return factorial(n-1) * n # Вызываем эту же функцию, но с меньшим аргументом print(factorial(4)) # Печатаем факториал 4 # Вывод: # 24
Можете попробовать запустить её в онлайн-интерпретаторе и посмотреть, как работает. Тут есть один нюанс: Python не даст вам посчитать факториал числа больше 998, так как у него есть ограничение на количество вызовов функции — в программировании это называется глубиной рекурсии.
Чтобы быстро находить, чему равен факториал, можно запомнить или сохранить в заметки вот такую табличку. Она рассчитана всего на 12 чисел, но для большинства учебных задач этого хватит.
| 1! | 1 |
| 2! | 2 |
| 3! | 6 |
| 4! | 24 |
| 5! | 120 |
| 6! | 720 |
| 7! | 5040 |
| 8! | 40 320 |
| 9! | 362 880 |
| 10! | 3 628 800 |
| 11! | 39 916 800 |
| 12! | 479 001 600 |
С теорией вроде разобрались — теперь попробуем решить несколько задач с факториалами, чтобы закрепить знания на практике.
Задача: перемножить два факториала.
Решение:
Сперва нужно вычислить значения факториалов, а затем перемножить полученные значения:
Обратите внимание: во второй строке мы применили рекуррентную формулу, чтобы быстрее вычислить факториал числа 7.
Задача: вычесть из одного факториала другой.
Решение:
Используем тот же подход, что и в предыдущей задаче: сначала вычисляем факториалы, а затем получаем ответ на всё выражение.
Вроде бы ничего сложного, главное — не запутаться в умножении.
Задача: умножить один факториал на другой:
Решение:
Вычисляем факториалы, потом перемножаем их значения:
Во второй строке мы воспользовались таблицей выше и быстро нашли значение факториала от числа 8.
Задача: сократить дробь и вычислить её значение.
Решение:
Здесь мы воспользуемся рекуррентной формулой для вычисления факториала и разложим верхний факториал на множители:
В первой строке мы применили рекуррентную формулу два раза, а во второй — просто сократили одинаковые факториалы в числителе и в знаменателе.
Задача: сократить дробь.
Решение:
Хотя здесь нет конкретных чисел, но принцип решения остаётся таким же: используем рекуррентную формулу и сокращаем одинаковые значения в числителе и знаменателе.
Главное — не запутаться и правильно применить рекуррентную формулу.
- Факториал — это произведение всех натуральных чисел от 1 до данного числа. Например, факториал числа 5 будет равен 1 × 2 × 3 × 4 × 5 = 120.
- Его используют во многих областях науки — например, комбинаторике, теории вероятностей и математическом анализе.
- Помимо стандартной формулы для вычисления факториала можно использовать формулы Стирлинга и рекуррентную формулу.
- Формула Стирлинга нужна для того, чтобы посчитать факториал без большого числа операций умножения.
- Рекуррентная формула позволяет вычислить факториал на основе предыдущего факториала.

Научитесь: Профессия Data Scientist
Узнать больше
Что такое факториал числа 20? – Обзоры Вики
Ответ: Факториал числа 20 равен 2432902008176640000.
Факториал n обозначается через n!
Аналогично, как вычислить факториал? Расчет факториала. Факториал n обозначается через n! и вычисляется целыми числами от 1 до n. Формула для n факториала: n! =n×(nu22121)!
Какие есть факториалы числа 12? Небольшой список
| n | n! |
|---|---|
| 9 | 362,880 |
| 10 | 3,628,800 |
| 11 | 39,916,800 |
| 12 | 479,001,600 |
Что такое факториал числа 15? Что такое факториал числа 15? 15! знак равно 1307674368000.
Во-вторых, как найти факториал 18? Что такое факториал числа 18? 18! знак равно 6402373705728000.
Насколько велик факториал 52?
52! является приблизительно 8.0658e67. Чтобы получить точное представление, просмотрите факториальную таблицу или попробуйте калькулятор «новой школы», который понимает длинные целые числа.
Чему равен факториал n 1? Таблица факториалов чисел от 1 до 10
| n | Факториал числа n! | Значение |
|---|---|---|
| 1 | 1! | 1 |
| 2 | 2! | 2 |
| 3 | 3! | 6 |
| 4 | 4! | 24 |
Что такое факториал 100000?
100000! =100000×99999×99998×99997×… × 3 × 2 × 1 .
Сколько стоит 8.06 е67? способами, которыми мы можем составить колоду карт. 52! чертовски большое число, равное 8.06e+67. 80,658,175,170,943,878,571,660,636,856,403,766,975,289,505,440,883,277,824,000,000,000,000 68 XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX XNUMX, если быть точным.
Как решить 3 факториалов?
Что такое факториал 10? Значение факториала 10 равно 3628800, т.е. 10!
Как быстро вычислить факториал?
Как решить 5 факториалов?
Чтобы найти факториал 5 или 5!, просто используйте формулу; то есть перемножьте все целые числа от 5 до 1. Когда мы используем формулу для нахождения 5!, мы получаем 120. Итак, 5! = 120.
Чему равен факториал меньше 100? Приблизительное значение 100! является 9.

Что такое триллион факториала?
Один миллиард факториала составляет примерно 1.57637137 × 108,565,705,531.
Каковы шансы перетасовать колоду по порядку? Если вы действительно рандомизируете колоду, шансы на то, что карты окажутся в идеальном порядке — пики, затем червы, бубны и трефы — равны примерно 1 из 10 в степени 68 (или 1 с последующими 68 нулями). Это огромное число, примерно равное количеству атомов в нашей галактике. Тем не менее, карточные игроки сообщают, что это происходит.
Каждая тасовка карт уникальна?
Хотя вполне возможно, что две колоды карт могли быть перетасованы в одном и том же порядке, шансы на то, что это произошло, на самом деле ничтожны, и да, очень вероятно, что каждая правильно перетасованная колода действительно является уникальной вариацией этих 52 карт. … Цель полная правильная перетасовка почти наверняка уникальна каждый раз.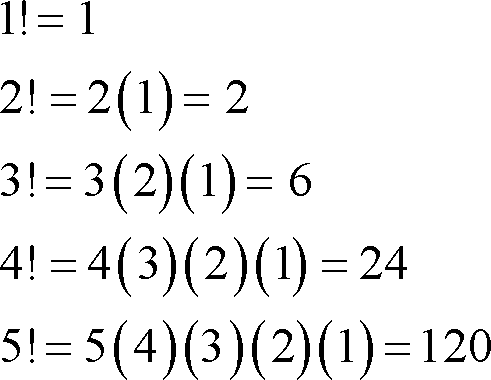
Сколько существует комбинаций перетасовки колод? Шансы на то, что кто-либо когда-либо перетасовывал колоду карт (справедливо) таким же образом дважды в мировой истории или когда-либо еще перетасует, ничтожно малы. Количество возможных способов заказать колоду из 52 карт равно ‘52! ‘ («факториал 52»), что означает умножение 52 на 51 на 50… вплоть до 1.
Можно ли умножать факториалы?
Факториалы, обозначаемые a. … Вы также можете умножить факториалы вручную. Самый простой способ сделать это — вычислить каждый факториал по отдельности, а затем перемножить их произведения вместе. Вы также можете использовать определенные правила факториалов для извлечения общих множителей, что может упростить процесс умножения.
Как посчитать факториал 100? 0
Что такое факториал 9?
Ответ: Факториал числа 9 равен 362,880.
Можно ли умножать факториалы?
Факториалы, обозначаемые a. … Вы также можете умножить факториалы вручную. Самый простой способ сделать это — вычислить каждый факториал по отдельности, а затем перемножить их произведения вместе.
python — Как найти n делителей факториала?
Вопрос задан
11 месяцев назад
Изменён
11 месяцев назад
Просмотрен
225 раз
Есть факториал числа(n!). Как найти n делителей факториала, чтобы их сумма была рана факториалу
Пример:
3! = 1*2*3 = 6 = 1+2+3 (1, 2, 3 — делители 6) 4! = 1*2*3*4 = 24 = 1+3+8+12 (1, 3, 8, 12 — делители 24)
- python
- алгоритм
- математика
5
Пусть N! = sum(a[i]), тогда (N + 1)! = (N + 1) * sum(a[i]).
a[i] делит
N!, то (n + 1) * a[i] делит (N + 1)!. Таким образом, по разложению N! в сумму N делителей мы можем построить разложение (N + 1)! в сумму N делителей. Осталось как-то добавить один делитель.
Рассмотрим первые разложения:
3! = 3 + 2 + 14! = 12 + 8 + 3 + 15! = 60 + 40 + 15 + 4 + 1
Пусть минимальным делителем в разложении N будет 1, тогда в разложении (N + 1)! на N делителей минимальным будет N + 1. Причем его можно разбить на сумму N и 1, которые очевидно являются делителями (N + 1)! и при этом не встречаются в разложении до этого, так как меньше N + 1, который был минимальным.
Получаем следующий алгоритм:
N = 10
a = [3, 2, 1]
for n in range(3, N):
for i in range(n):
a[i] *= n + 1
a[i] -= 1
a. append(1)
print(a) #[1814400, 1209600, 453600, 120960, 25200, 4320, 630, 80, 9, 1]
# CHECK
from math import factorial
F = factorial(N)
print(sum(a) == F and len(a) == N and len(set(a)) == N and all(F % i == 0 for i in a)) #True
append(1)
print(a) #[1814400, 1209600, 453600, 120960, 25200, 4320, 630, 80, 9, 1]
# CHECK
from math import factorial
F = factorial(N)
print(sum(a) == F and len(a) == N and len(set(a)) == N and all(F % i == 0 for i in a)) #True
1
from math import factorial, ceil, sqrt
numb = int(input('Введите число: '))
находим факториал введенного числа
a = factorial(numb)
функция нахождения делителей
def get_all_dividers(num):
first_half_dividers = [x for x in range(1, ceil(sqrt(num)) + 1)
if num % x == 0]
second_half_dividers = [int(num / x) for x in reversed(first_half_dividers)
if int(num / x) not in first_half_dividers]
return first_half_dividers + second_half_dividers
list_of_fact = get_all_dividers(a)
Удаляем последний элемент списка, иначе он будет выводится в конце при выводе всех вариантов
del list_of_fact[-1]
def subset_sum(numbers, target, partial=[]):
s = sum(partial)
if s == target:
print(partial)
if s >= target:
return
for i in range(len(numbers)):
n = numbers[i]
remaining = numbers[i + 1:]
subset_sum(remaining, target, partial + [n])
выводим все возможные комбинации сумм делителей
subset_sum(list_of_fact, a)
Зарегистрируйтесь или войдите
Регистрация через Google
Регистрация через Facebook
Регистрация через почту
Отправить без регистрации
Почта
Необходима, но никому не показывается
Отправить без регистрации
Почта
Необходима, но никому не показывается
Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки
чему равен факториал 20?
Калькулятор факториала До 10 000
Здесь вы можете найти ответы на такие вопросы, как: что такое факториал числа 20? Чему равен факториал числа 20? Каковы последние цифры факториала числа 20? Сколько нулей в конце факториала 20? Сколько цифр в факториале 20? Воспользуйтесь приведенным выше калькулятором факториала, чтобы найти факториал любого натурального числа в диапазоне от 0 до 10 000.
Что такое факториал?
Определение факториала
Факториал — это величина, определенная для любого целого числа n, большего или равного 0.
Факториал — это произведение всех целых чисел, меньших или равных n, но больших или равных 1. Значение факториала 0 равно определение равно 1. Для отрицательных целых чисел факториалы не определены. Факториал можно рассматривать как результат умножения последовательности убывающих натуральных чисел (например, 3 × 2 × 1).
Символ факториала — восклицательный знак!.
Формула факториала
Если n — натуральное число, большее или равное 1, то
n! = n x (n — 1) x (n — 2) x (n — 3) … 3 x 2 x 1
Если n = 0, то n! = 1, по соглашению.
Пример: 6! = 6 x 5 x 4 x 3 x 2 x 1 = 720
Ярлык для поиска конечных нулей в факториале
Конечные нули представляют собой последовательность нулей в десятичном представлении числа, после которой не следуют никакие другие цифры.
Таблица факториалов до 30
| нет | нет! |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5040 |
| 8 | 40320 |
| 9 | 362880 |
| 10 | 3628800 |
| 11 | 39916800 |
| 12 | 47
00 |
| 13 | 6227020800 |
| 14 | 87178291200 |
| 15 | 1307674368000 |
| 16 | 20922789888000 |
| 17 | 355687428096000 |
| 18 | 6402373705728000 |
| 19 | 121645100408832000 |
| 20 | 2432 |
| 21 | 51090942171709440000 |
| 22 | 1124000727777607680000 |
| 23 | 25852016738884976640000 |
| 24 | 620448401733239439360000 |
| 25 | 15511210043330985984000000 |
| 26 | 403291461126605635584000000 |
| 27 | 10888869450418352160768000000 |
| 28 | 304888344611713860501504000000 |
| 29 | 8841761993739701954543616000000 |
| 30 | 265252859812191058636308480000000 |
8176640000
Factorial Calculator
Please ссылка на эту страницу! Просто щелкните правой кнопкой мыши на изображении выше, выберите «Скопировать адрес ссылки», а затем вставьте его в HTML-код.
Пример расчета факториала.
- Factorial of 600
- Factorial of 710
- Factorial of 512
- Factorial of 940
- Factorial of 1000
- Factorial of 460
- Factorial of 610
- Factorial of 770
- Factorial of 80
Отказ от ответственности
Несмотря на то, что мы прилагаем все усилия для обеспечения точности информации, представленной на этом веб-сайте, ни этот веб-сайт, ни его авторы не несут ответственности за какие-либо ошибки или упущения. Поэтому содержимое этого сайта не подходит для любого использования, связанного с риском для здоровья, финансов или имущества.
Калькулятор — факториал(20) — Solumaths
Факториал, расчет онлайн
Резюме:
Факториал натурального числа n — это произведение натуральных чисел, меньших или равных n. Калькулятор факториала позволяет найти это число.
факториал онлайн
Описание:
Онлайн-калькулятор факториала имеет функцию факториала .
что позволяет вычислить онлайн факториал целого числа.
Восклицательный знак обычно используется как обозначение факториала, калькулятор позволяет использовать это обозначение.
Например, для , вычисляющего факториал 5 , используйте следующий синтаксис
факториал(`5`),
после расчета возвращается результат 120.
Следующий синтаксис также можно использовать для вычисления факториала 5!
Для небольших чисел калькулятор может выдать детали расчетов факториала.
Синтаксис:
factorial(n), где n — целое число.
Можно использовать восклицательный знак для вычисления факториала n!
Примеры:
factorial(`5`), возвращает 120
Расчет онлайн с факториалом (факторный калькулятор)
См.
Список связанных калькуляторов:
-
Номер расстановки комплекта вычислителя : расстановка.
Вычислить онлайн количество расположения p элементов множества из n элементов.
- Расчет биномиальных коэффициентов: binomial_coefficient. Калькулятор биномиального коэффициента, который позволяет вычислить биномиальный коэффициент из двух целых чисел.
- Чтобы подсчитать количество комбинаций: комбинация. Вычислить количество k элементов части множества из n элементов.
- Преобразователь base-n : base_converter. Калькулятор позволяет выполнять десятичные, двоичные, шестнадцатеричные преобразования и, в более общем случае, преобразование в любое основание n от 2 до 36.
- Калькулятор простой факторизации: prime_factorization. Функция prime_factorization используется для онлайн-расчета разложения целого числа на простые множители.
- Калькулятор частного и остатка: euclidean_division. Калькулятор позволяет найти в режиме онлайн частное и остаток при евклидовом делении двух многочленов или двух целых чисел.
- Четность числа: is_odd. Функция Is_odd возвращает true, если переданное число нечетное, иначе false.
- Четность числа: is_even. Функция Is_even возвращает 1, если число четное, иначе 0.
- Калькулятор факториала: факториал. Факториал натурального числа n — это произведение натуральных чисел, меньших или равных n. Калькулятор факториала позволяет найти это число.
- Калькулятор перестановок: перестановка. Подсчитать онлайн количество перестановок набора из n элементов.
- Расчет НОД онлайн: НОД. Калькулятор НОД, который использует алгоритм Евклида для определения шагов вычисления НОД.
- Наименьшее общее кратное: lcm. Калькулятор LCM для расчета наименьшего общего кратного (НОК).
- Калькулятор теоремы Пифагора: пифагорейский. Калькулятор использует теорему Пифагора, чтобы проверить прямоугольность треугольника или найти длину одной стороны прямоугольного треугольника.
- Решатель обратного отсчета: arithmetic_solver. Этот решатель обратного отсчета позволяет найти целевое число из набора целых чисел с помощью арифметических операций.



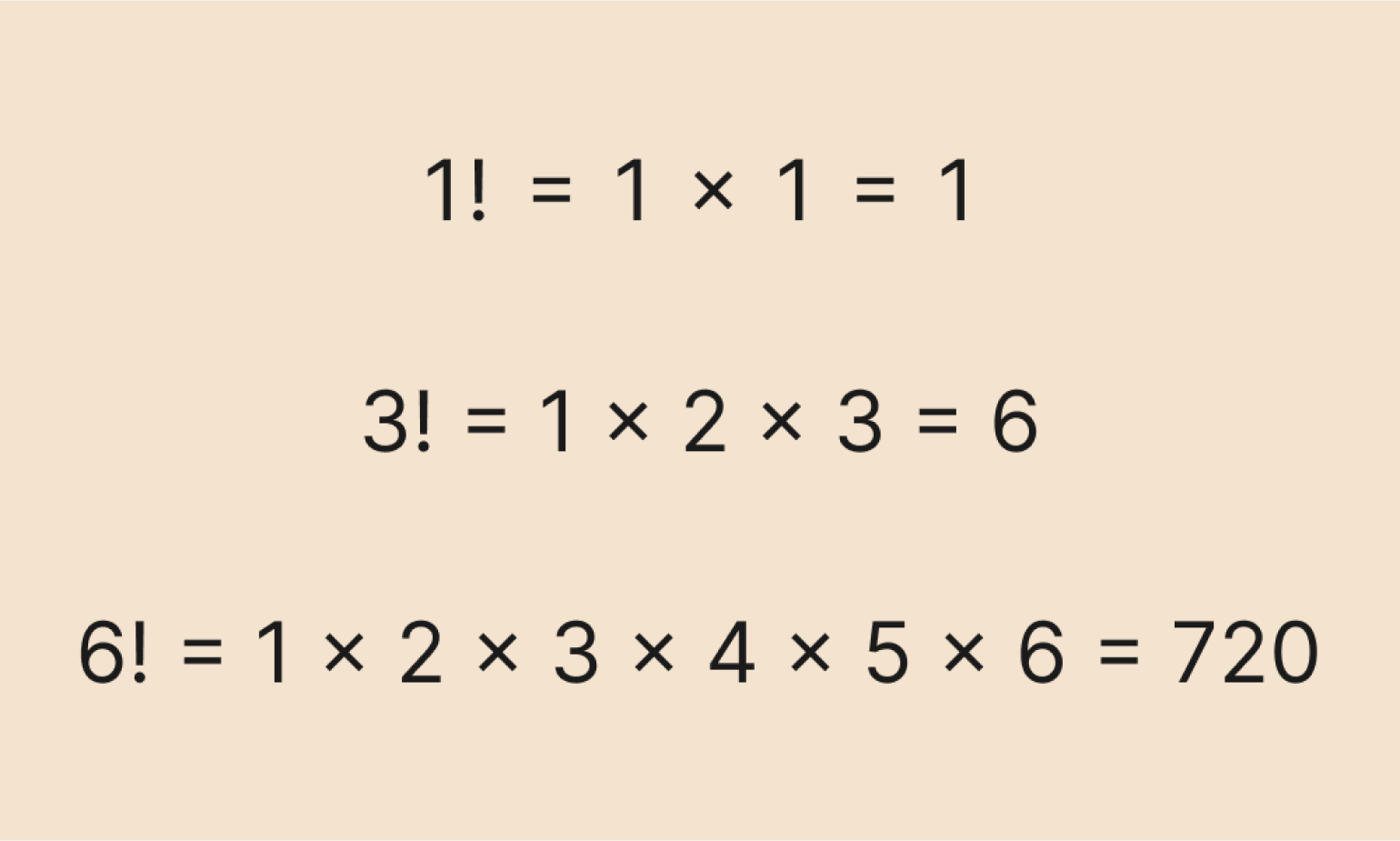

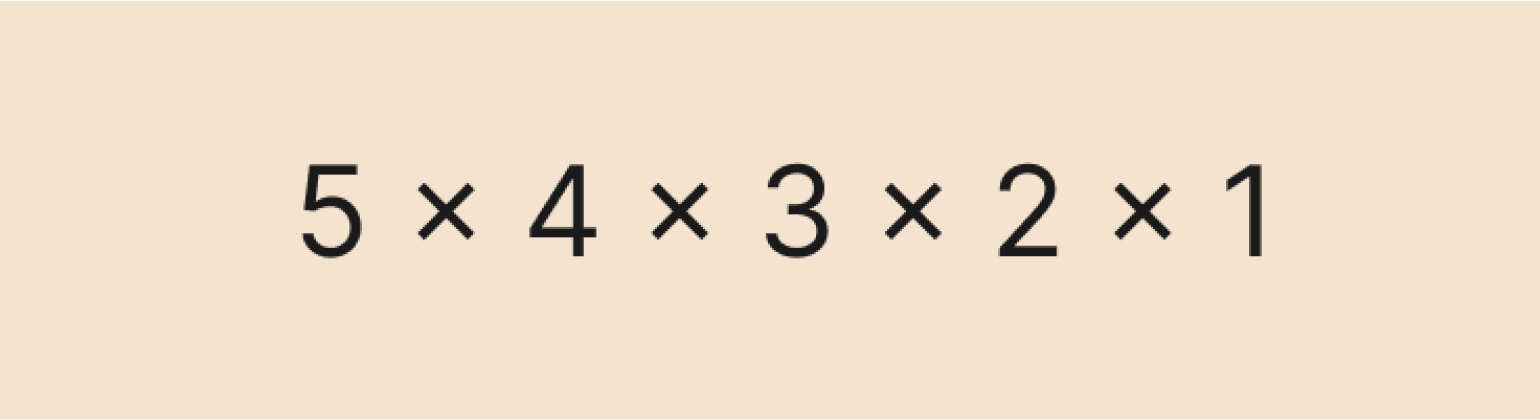
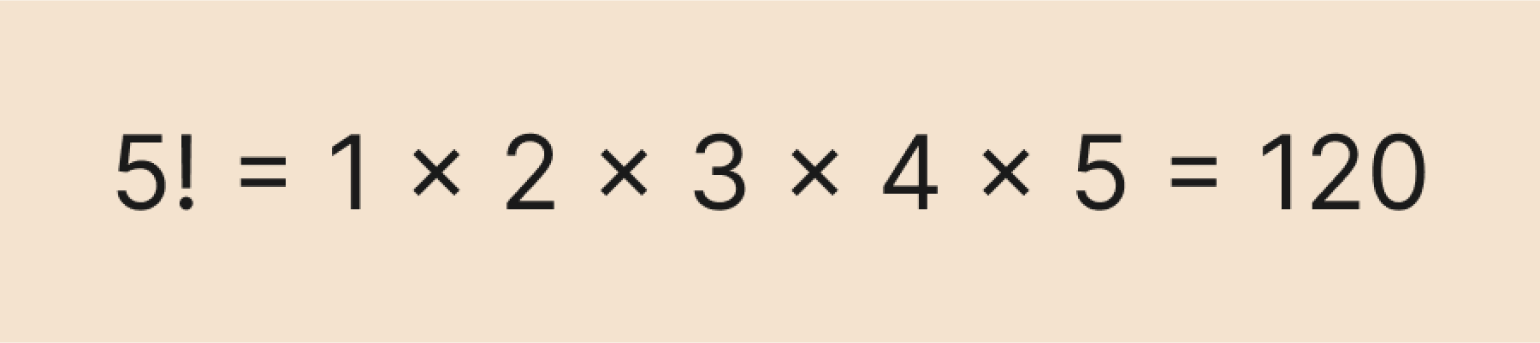
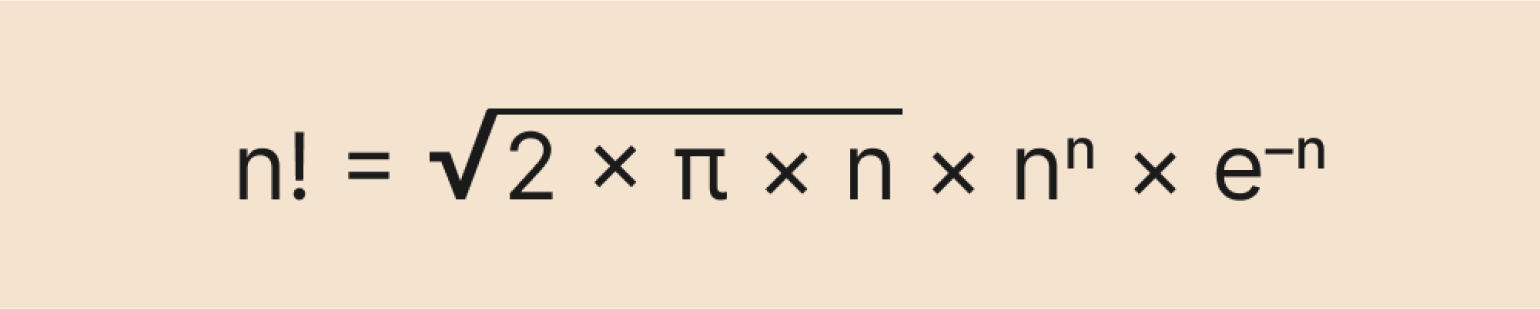
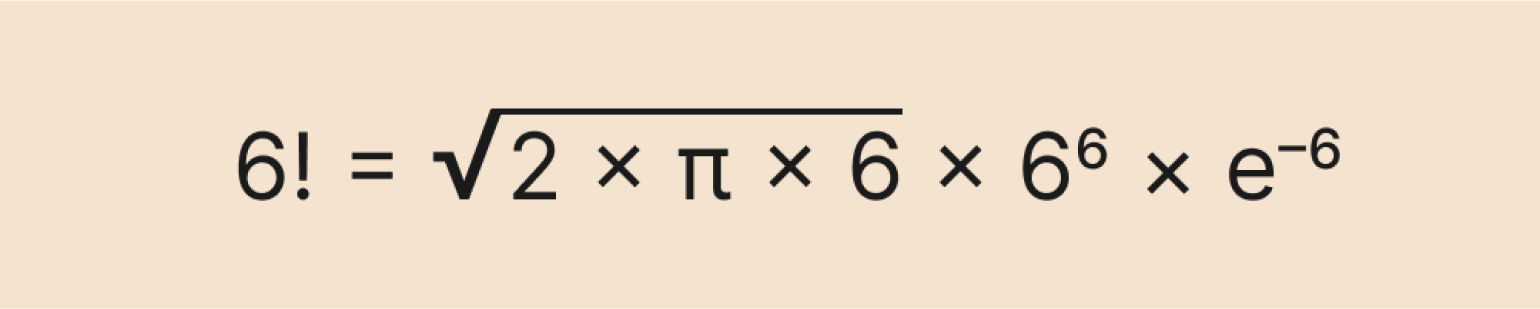
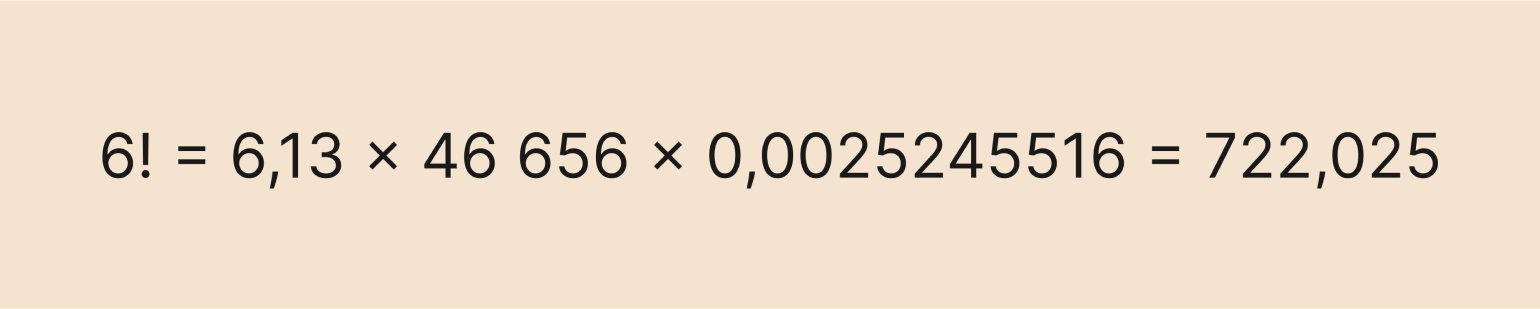

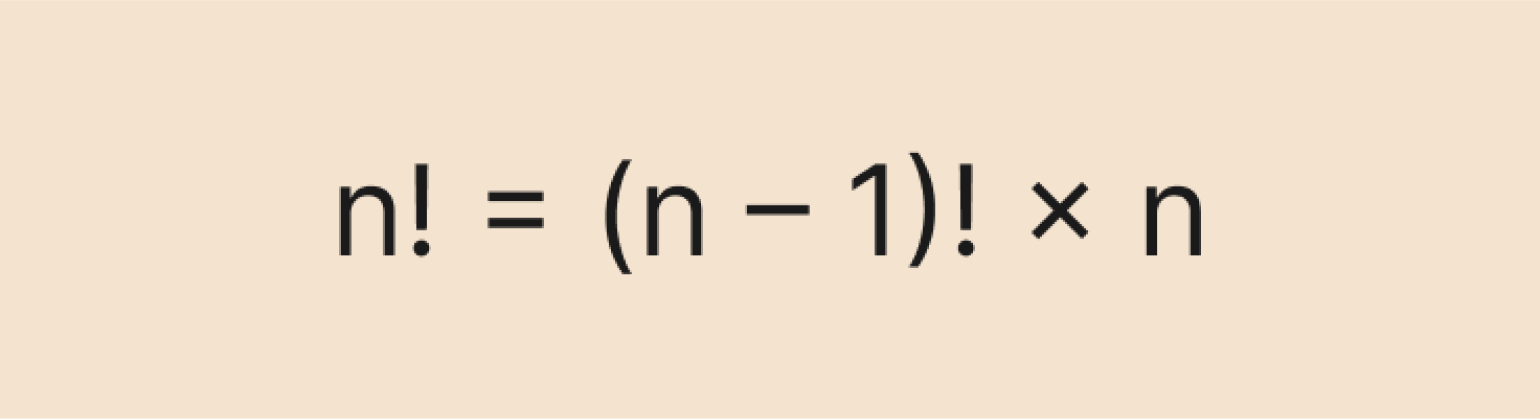

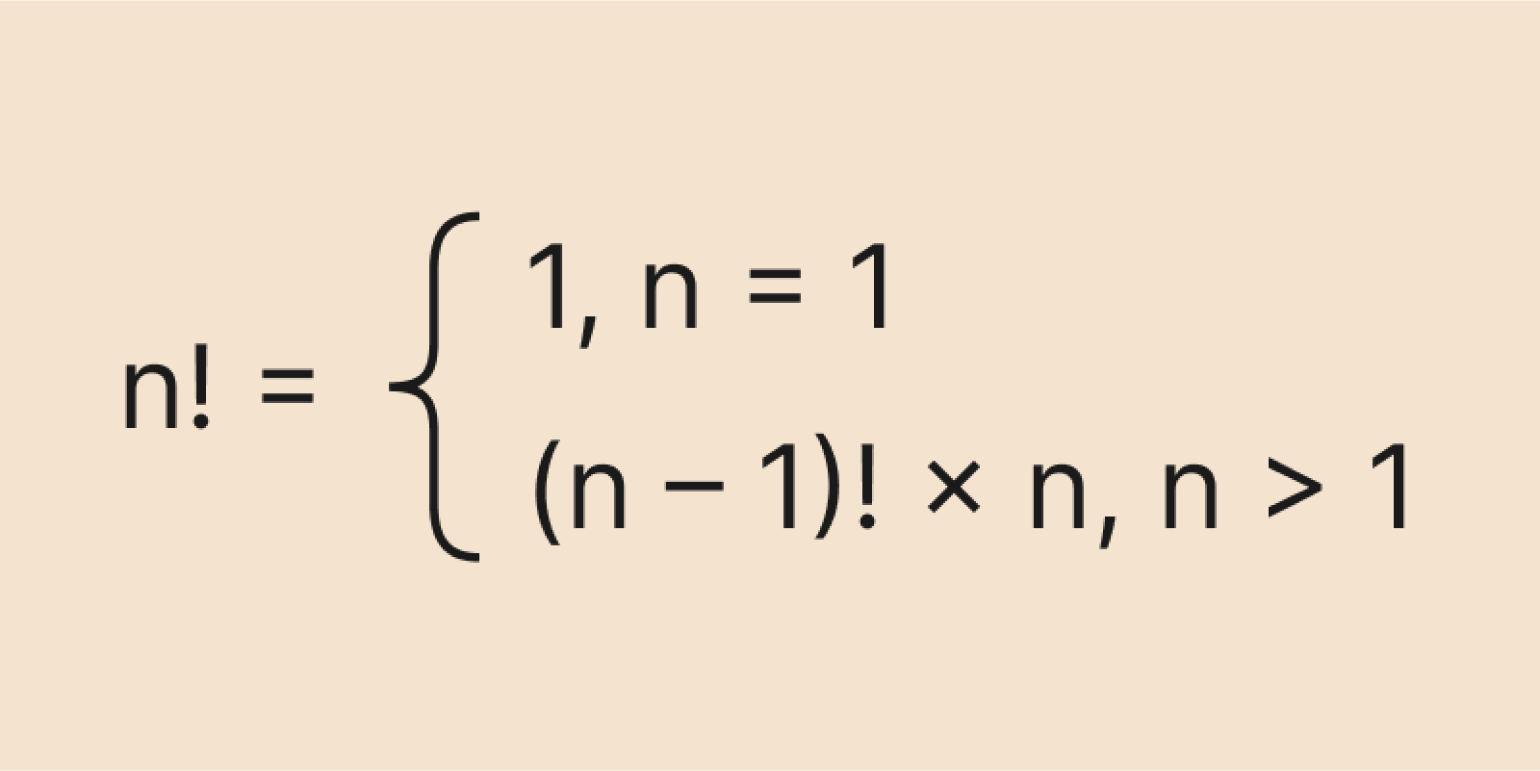
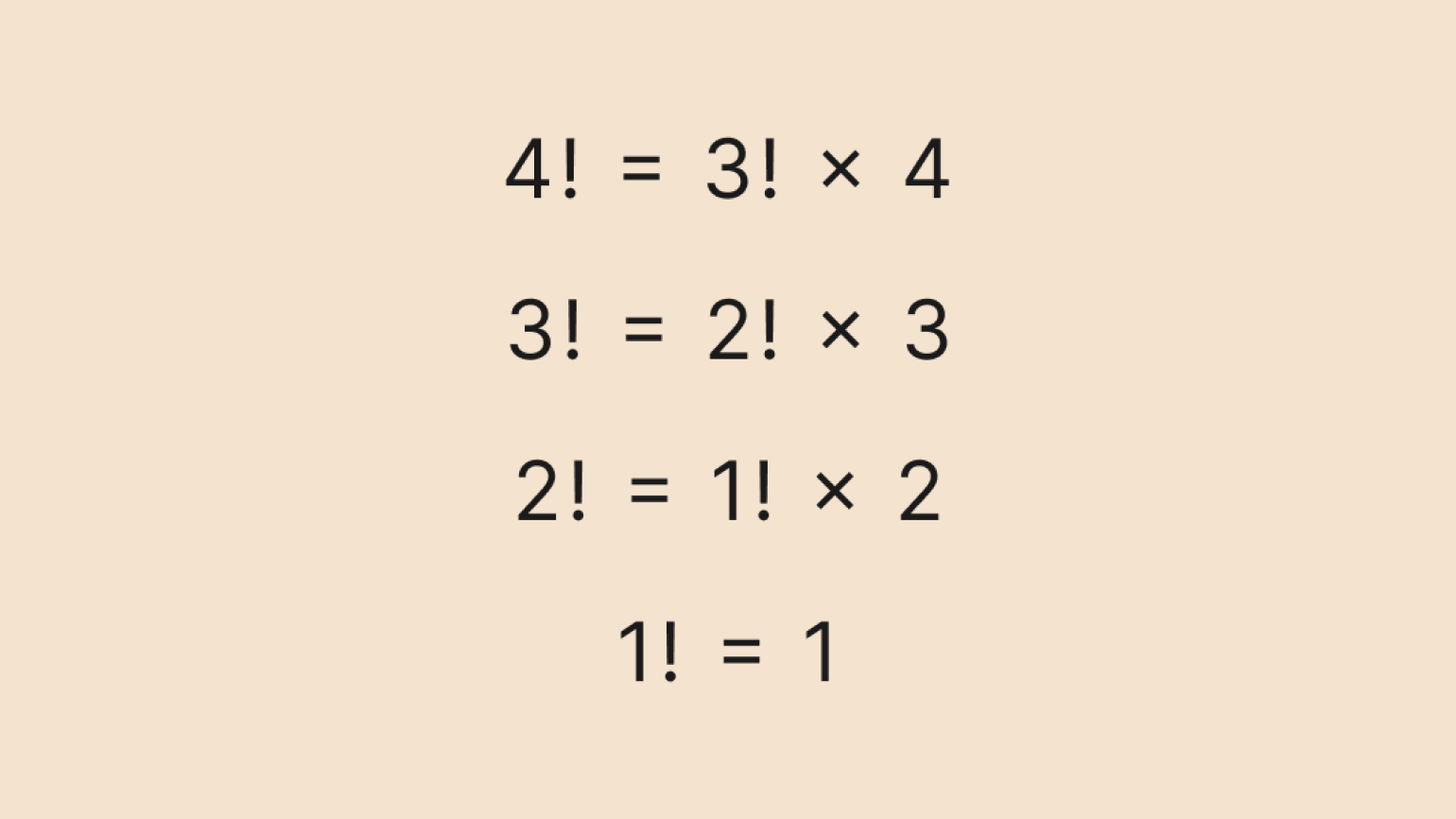
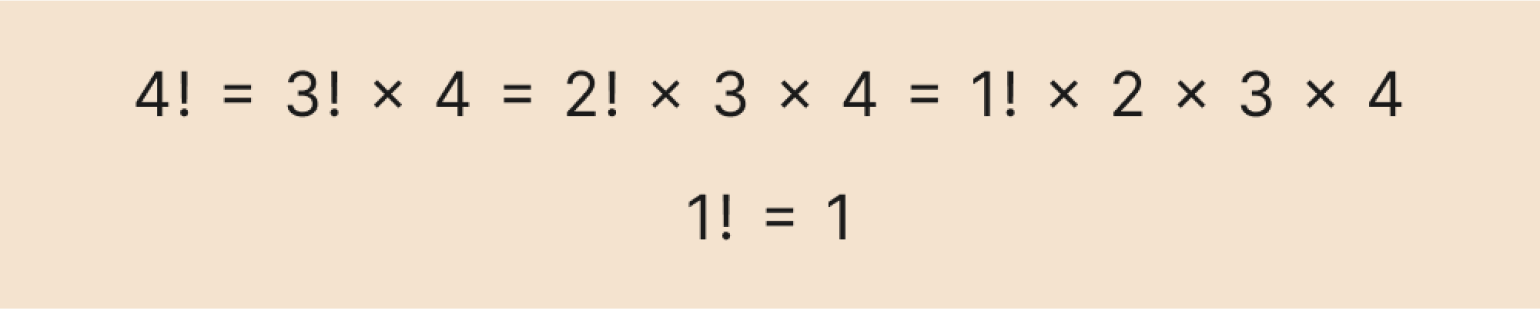
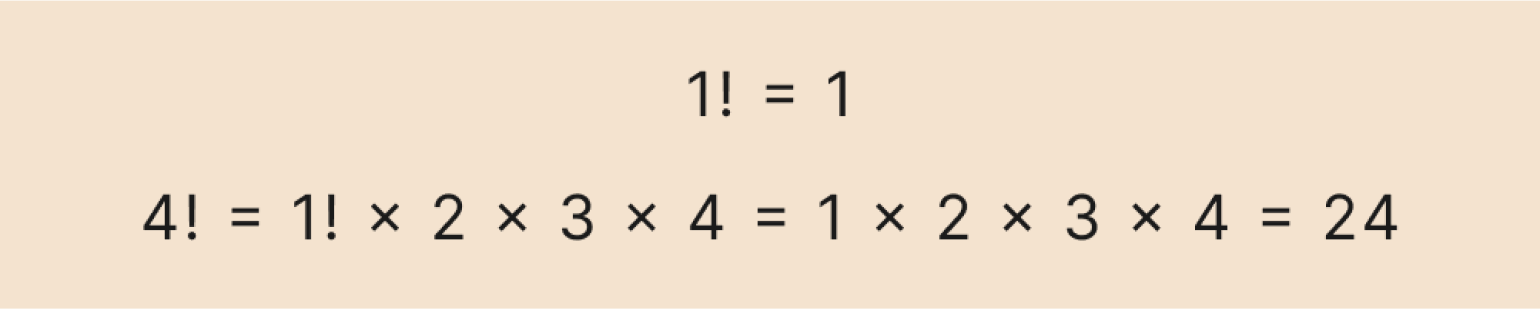


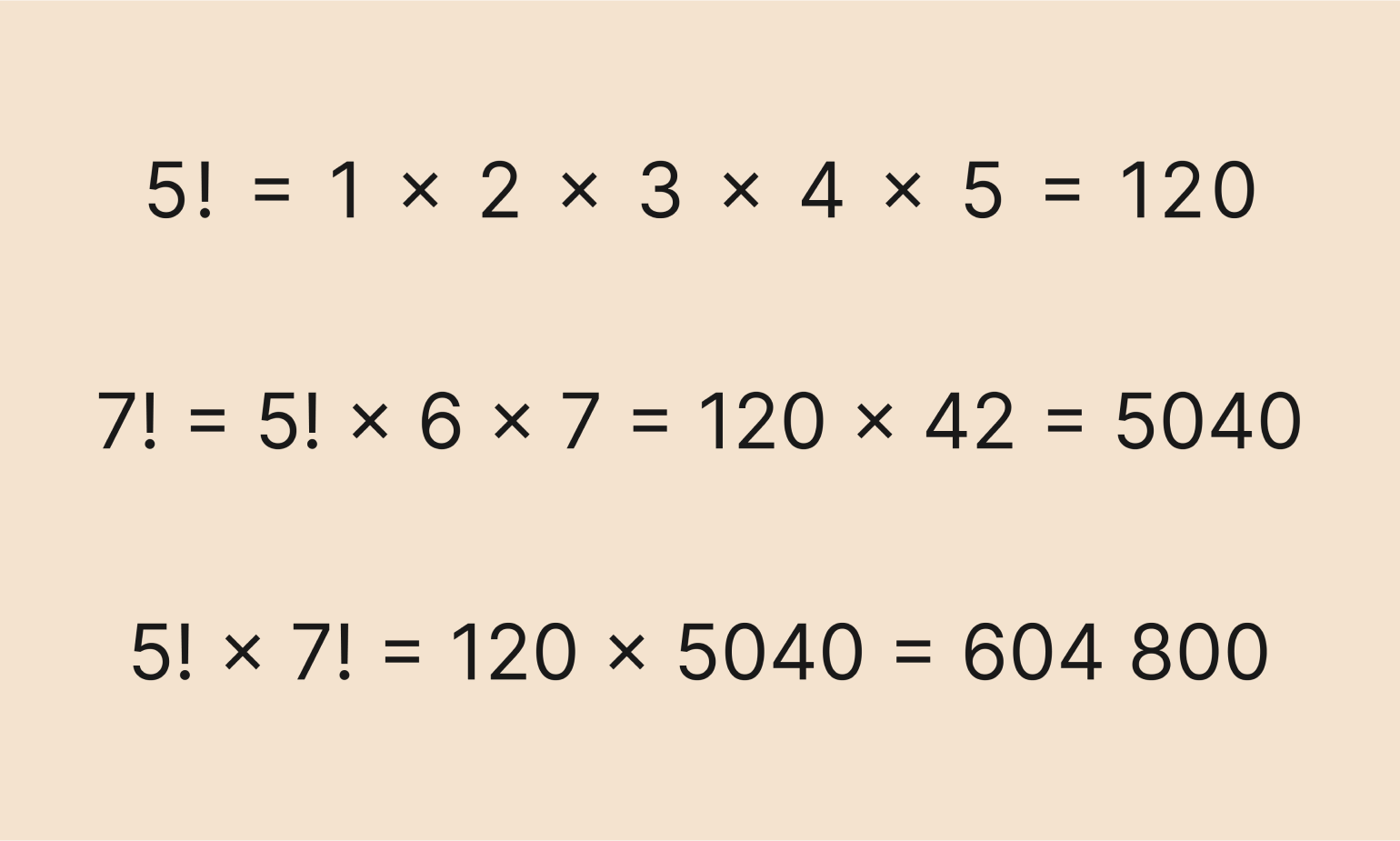

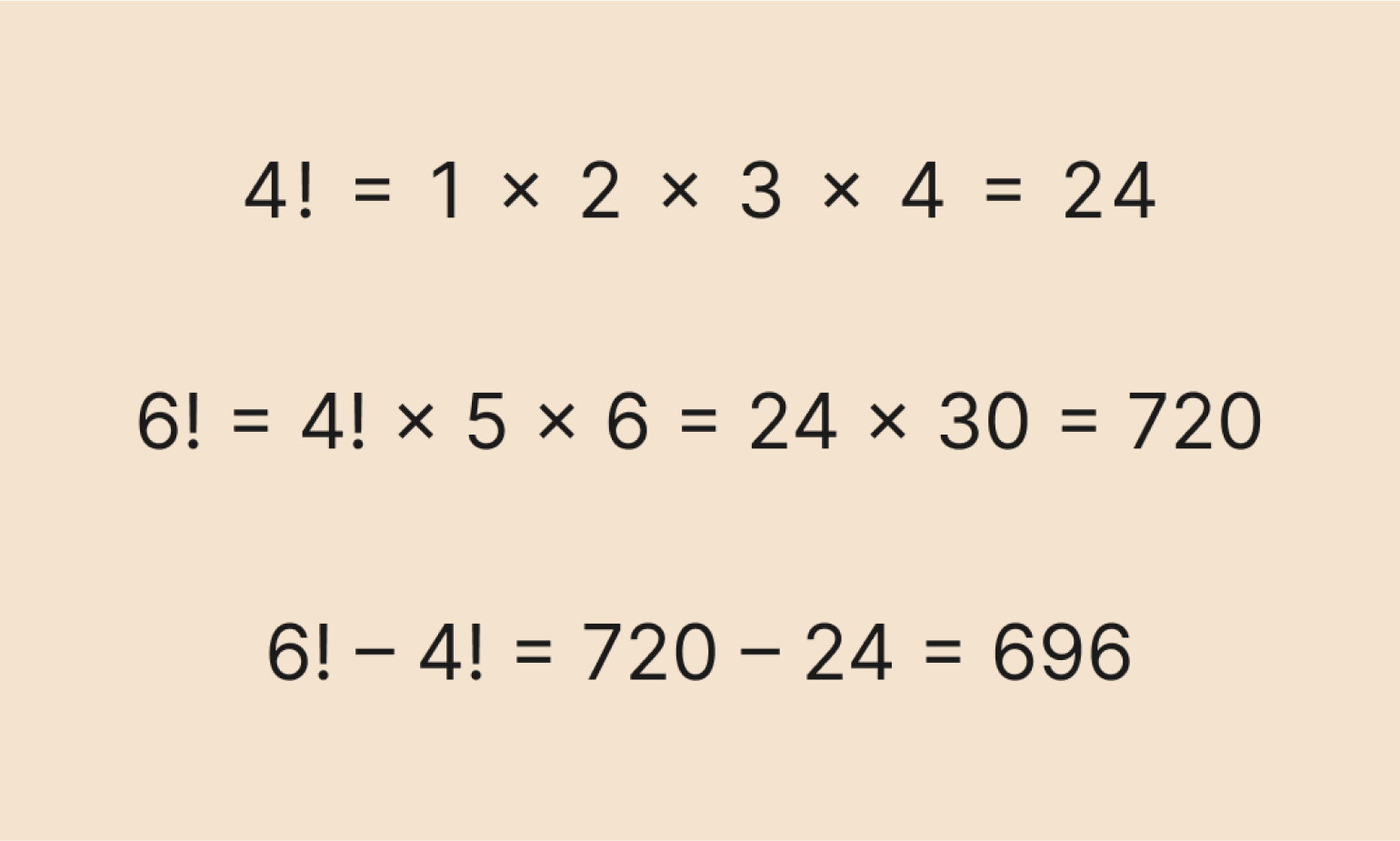

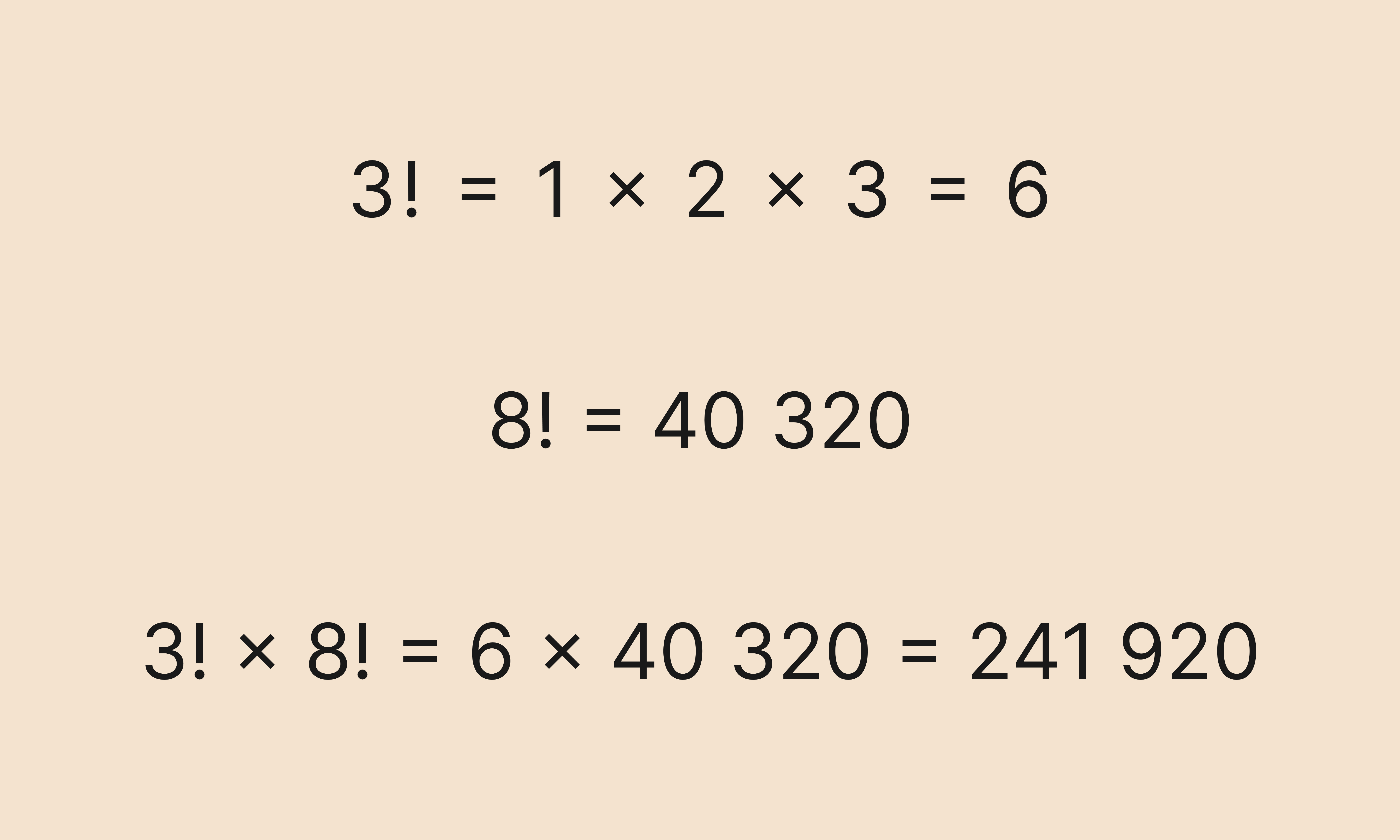

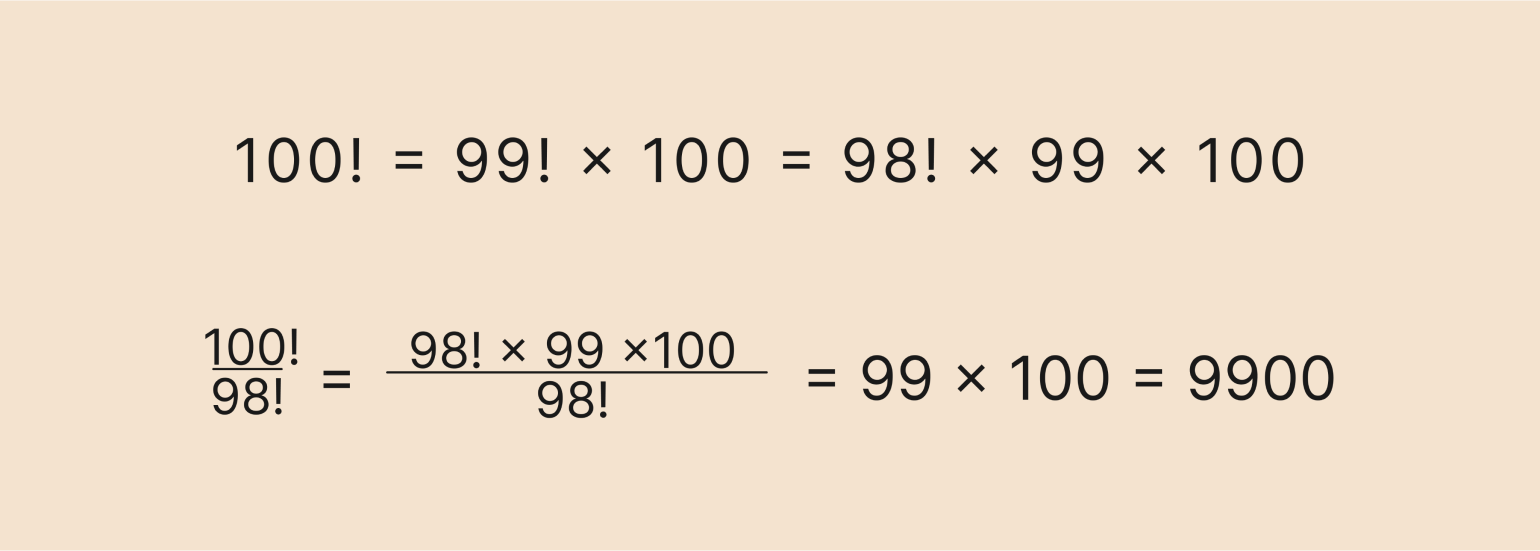
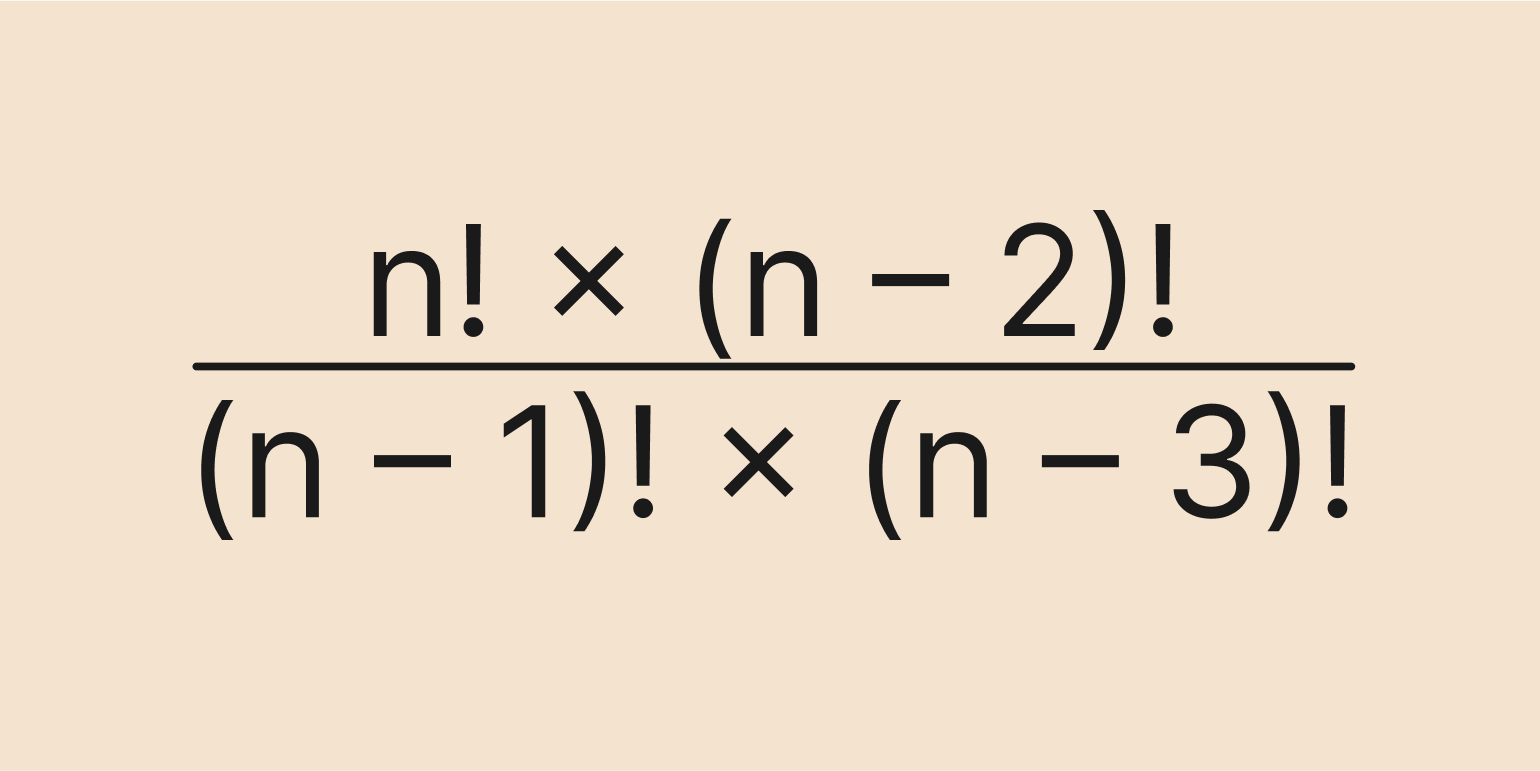
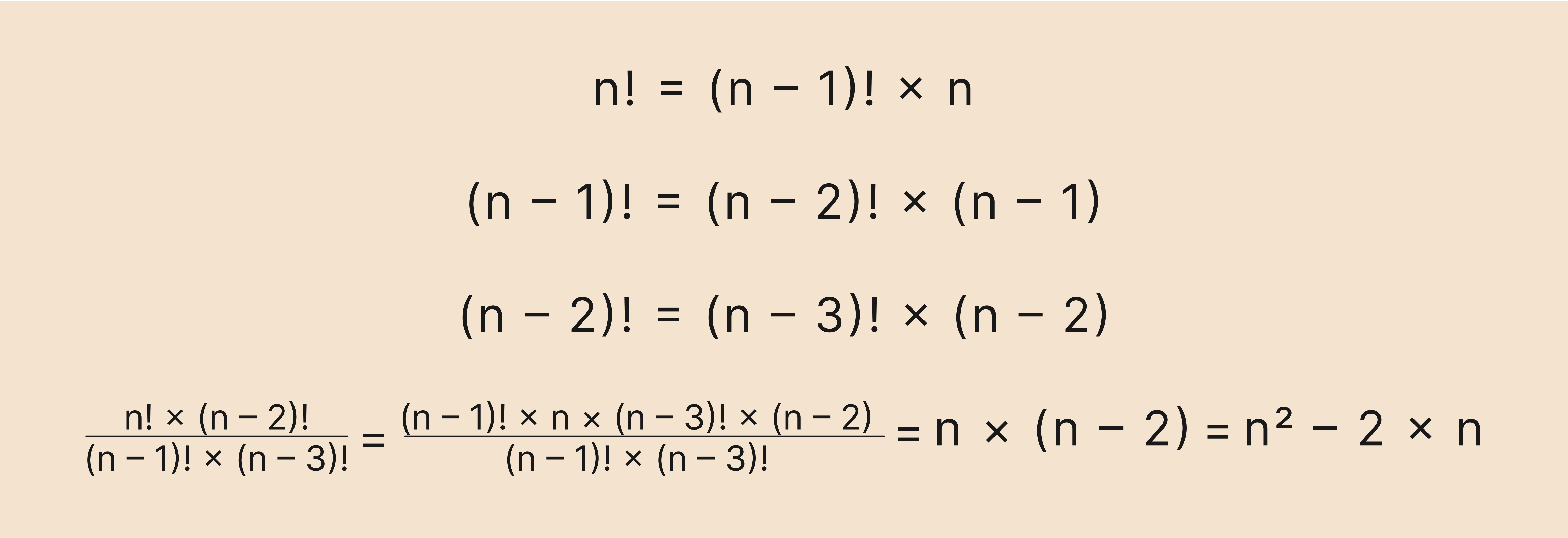
 append(1)
print(a) #[1814400, 1209600, 453600, 120960, 25200, 4320, 630, 80, 9, 1]
# CHECK
from math import factorial
F = factorial(N)
print(sum(a) == F and len(a) == N and len(set(a)) == N and all(F % i == 0 for i in a)) #True
append(1)
print(a) #[1814400, 1209600, 453600, 120960, 25200, 4320, 630, 80, 9, 1]
# CHECK
from math import factorial
F = factorial(N)
print(sum(a) == F and len(a) == N and len(set(a)) == N and all(F % i == 0 for i in a)) #True
 Вычислить онлайн количество расположения p элементов множества из n элементов.
Вычислить онлайн количество расположения p элементов множества из n элементов. 
