Как найти количество максимумов в массиве

Вы можете определить функцию, которая будет находить любое количество максимальных элементов в целочисленном массиве. Для этого просто нужно передавать в функцию массив нужной размерности для хранения максимальных значений.

Функция возвращает число максимальных элементов, так как в общем случае вы можете запросить найти больше максимальных элементов, чем общее количество элементов имеется в массиве, или, например, когда вам передается пустой массив.

Ниже приведена демонстрационная программа

#include <stdlib.h>
#include <stdio.h>
#include <string.h>
#include <time.h>

size_t max_elements(const int *a, size_t n, int *max, size_t m)
{
    size_t k = 0;

    for (size_t i = 0; i < n; i++)
    {
        size_t j = 0;

        while (j < k && !(a[i] > max[j])) j++;

        if (j == k )
        {
            if ( k < m ) max[k++] = a[i];
        }
        else
        {
            memmove(max + j + 1, max + j, 
                    ( k < m ? k - j: k - j - 1 ) * sizeof(int));
            max[j] = a[i];
            if (k < m) ++k;
        }
    }

    return k;
}

#define N1  10
#define M   3

int main()
{
    int a[N1];
    int max[M];

    srand((unsigned int)time(NULL));

    for (size_t i = 0; i < N1; i++) a[i] = rand() % (2 * N1);

    for (size_t i = 0; i < N1; i++) printf("%d ", a[i]);
    printf("n");

    size_t k = max_elements(a, N1, max, M);

    if (k != 0)
    {
        printf("%zu max elements are ", k);
        for (size_t i = 0; i < k; i++) printf("%d ", max[i]);
        printf("n");
    }
}

Ее вывод на консоль может выглядеть следующим образом:

13 17 8 9 14 10 2 15 3 19
3 max elements are 19 17 15

Аналогичным образом вы можете найти минимальные элементы. Все, что вам для этого требуется это изменить условие в этом цикле

while (j < k && !(a[i] > max[j])) j++;
                ^^^^^^^^^^^^^^^^  

Без сортировки задача может быть решена, например, так. Создаем рабочий массив длины m и заполняем его начальными значениями. В общем случае можно в качестве такого значения выбрать минимальное значение int/integer для соответствующей среды программирования. А если известна нижняя граница значений исходного массива, то можно взять любое число, меньшее этой границы.

Итак рабочий массив заполнен одинаковыми значениями. Теперь берем элемент за элементом исходного массива и вставляем его в нужное место рабочего массива. При этом длину рабочего массива сохраняем равной m (после вставки последний элемент пропадает). Если очередной элемент меньше последнего значения рабочего массива, то он просто пропускается. Этот процесс имеет вычислительную сложность O(nm). Тогда как сортировка в лучшем случае описывается асимптотикой O(n*og(n)). Асимптотики показывают, как ведет себя функция (в данном случае — время сортировки) при стремлении параметров к бесконечности. Можно сказать, что время описанного алгоритма при стремлении n к бесконечности задается формулой t1=k1*O(n), а время сортировки t2=k2*O(n*log(n)). Здесь k1 и k2 — некие константы, зависящие от процессора, языка программирования, операционной системы и других факторов.

Я построил три системы тестов (для Питона, Java и VBA). Все тесты устроены по сути одинаково: строились массивы возрастающих размеров, заполнялись случайными числами задаваемого диапазона, сортировались с фиксацией времени и прогонялись через описанный выше алгоритм тоже с фиксацией времени. Каждый тест повторялся 10 раз и время усреднялось. В Питоне и Java использовалась встроенная сортировка, в VBA — реализация QuickSort.

Питон

Ниже показан код питоновских тестов.

import time
from random import randint
    
def max_n_1(arr,n):
    return sorted(arr,reverse=True)[0:n]
    
def max_n_2(arr,n):
    res=[-1 for _ in range(n)]
    for x in arr:
        if x > res[n-1]:
            i=n-1
            j=i-1
            while(j>=0 and res[j]<x):
                res[i]=res[j]
                i=i-1
                j=j-1
            res[i]=x
    return res  
    
def start():
    k=10
    n=10000
    print("k=",k)
    while(n<=500000):
        print("n=",n,end=' ')

        t1=0.0
        for i in range(10):
            arr=[randint(1,2000) for _ in range(n)]
            start_time = time.time()
            z1=max_n_1(arr,k)
            fin_time = time.time()
            t1=t1+(fin_time-start_time)
        print(t1/10.0,end=' ')
    
        t2=0.0
        for i in range(10): 
            arr=[randint(1,2000) for _ in range(n)]
            start_time = time.time()
            z2=max_n_2(arr,k)
            fin_time = time.time()
            t2=t2+(fin_time-start_time)
        print(t2/10.0)
    
        n+=10000
        
start()

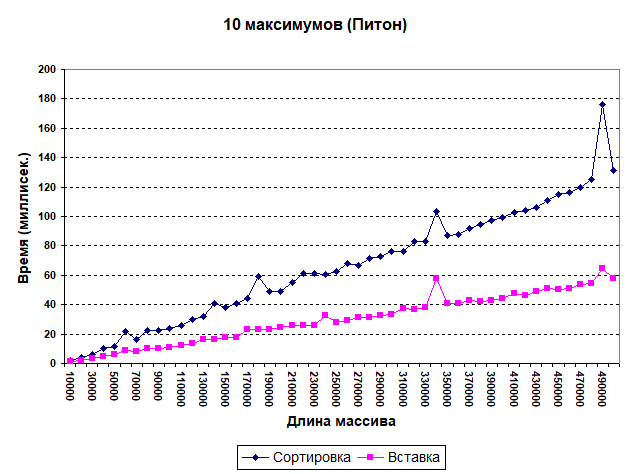
Размеры массива менялись от 10 до 500 тыс. элементов с шагом 10 тыс. Было выполнено два прогона: определение пяти и десяти максимумов. Результат для 10 максимумов показан ниже.

Время здесь приведено в миллисекундах. Что видим? Сортировка отстает (на краю интервала — вдвое). Для пяти максимумов картина аналогична. И надо заметить, что хотя питоновская сортировка очень эффективна, простой алгоритм оказывается быстрее. Заметны резкие провалы в производительности (зубцы на графиках). Они, вероятно, объясняются влиянием внутренних процессов (типа сборки мусора). Это же замечание относится и к другим графикам.

Java

Код тестов выглядел так:

import java.util.*;

class Start
{
   public static void main(String [] args)
   {   
    Random random = new Random();
    Scanner inp = new Scanner(System.in);
    long startTime,endTime,tot1,tot2;
    int i,a,b,n,m,x,ii,jj,u;
	
    a=1;
    b=3000; // диапазон случайных чисел [a,b]
    m=10;
    
    System.out.println(a+" "+b+" "+m);
    for (n=50000; n<=5000000; n+=50000)
    {
	    int arr[] = new int[n];
      int ma[]  = new int[m];
	
      tot1=0;
      for (u=0; u<10; u++)
      {        
	      for (i=0; i<n; i++)
	      {
		     arr[i]=a+random.nextInt(b-a+1);
	      }
        startTime = System.currentTimeMillis();
        Arrays.sort(arr);
        endTime = System.currentTimeMillis();
        tot1=tot1+(endTime-startTime);
      }

      tot2=0;
      for (u=0; u<10; u++)
      {        
	      for (i=0; i<n; i++)
	      {
		      arr[i]=a+random.nextInt(b-a+1);
	      }
   
        startTime = System.currentTimeMillis();
	      for (i=0; i<m; i++) ma[i]=-999999;
	      for (i=0; i<n; i++)
	      {
            x=arr[i];        
            if (x >= ma[m-1])
            {
              ii=m-1;
              jj=ii-1;
              while(jj>=0 && ma[jj]<x)
              {
                ma[ii]=ma[jj];
                ii--;
                jj--;
              }  
              ma[ii]=x;
            }
          }
          endTime = System.currentTimeMillis();
          tot2=tot2+(endTime-startTime);
        }
      System.out.println(n+" "+tot1+" "+tot2); 	
  	}
  } 
}

Здесь размер массива тоже менялся от 10 тыс. до 500 тыс. элементов. Время — в миллисекундах. Результат оказался весьма похожим на питоновский (только сортировка Javа, увы, медленнее).

VBA

В этом языке нет универсальной встроенной сортировки (можно, правда, сортировать ячейки листа, но в этом случае будут велики накладные расходы, связанные с загрузкой и выгрузкой данных). Поэтому пришлось реализовать QuickSort вручную. Все это выглядит так:

Private Declare Function GetTickCount Lib "kernel32" () As Long

'::: Собственно сортировка
Sub QSort(A() As Long, Optional b As Long = 1, Optional e As Long = 0)
    If b > e Then Exit Sub
    i& = b
    j& = e
    w& = A((i& + j&) / 2)
    Do While (True)
      Do While (A(i&) < w&)
         i& = i& + 1
      Loop
      Do While (A(j&) > w&)
         j& = j& - 1
      Loop
      If i& <= j& Then
         Tmp& = A(i&)
         A(i&) = A(j&)
         A(j&) = Tmp&
         i& = i& + 1
         j& = j& - 1
      End If
      If i& > j& Then Exit Do
    Loop
    
    If j& > b Then QSort A, b, j&
    If i& < e Then QSort A, i&, e

End Sub

'::: Проверка успешности сортировки 
Function check(X() As Long) As Boolean
     n& = UBound(X)
     For i& = 1 To n& - 1
         If X(i& + 1) < X(i&) Then
            Debug.Print "Err! i=" + CStr(i&)
            check = False
            Exit Function
         End If
     Next i&
     check = True
End Function

'::: Вставка в упорядоченный массив
Sub ins_in_arr(X As Long, A() As Long, n As Integer)
    If X < A(n) Then Exit Sub
    For i% = 1 To n
        If X > A(i%) Then
           For j% = n To i% + 1 Step -1
               A(j%) = A(j% - 1)
           Next j%
           A(i%) = X
           Exit Sub
        End If
    Next i%
End Sub

'::: Собственно тест
Sub test()
Const sz = 500
Dim X() As Long
Dim Ma(1 To sz) As Long
    Randomize
    ooo& = 1

    For n& = 10000 To 500000 Step 10000
        
        t1# = 0
        For nc% = 1 To 10
                    
            ReDim X(1 To n&) As Long
            For i& = 1 To n&
                X(i&) = Rnd() * 5000
            Next i&
            s1& = GetTickCount
            For i& = 1 To sz
                Ma(i&) = -2147483647
            Next i&
            For i& = 1 To n&
                ins_in_arr X(i&), Ma, 10
            Next i&
            s2& = GetTickCount
            t1# = t1# + s2& - s1&
        
        Next nc%
                
        Cells(ooo&, 1).Value = n&
        Cells(ooo&, 2).Value = t1# / 10
                
        t2# = 0
        
        For nc% = 1 To 10
        
            ReDim X(1 To n&) As Long
            For i& = 1 To n&
                X(i&) = Rnd() * 5000
            Next i&
            s1& = GetTickCount
            QSort X, 1, n&
            s2& = GetTickCount
            If Not check(X) Then
               MsgBox "Ошибка при сортировке!"
               Exit Sub
            End If
            t2# = t2# + s2& - s1&

        Next nc%

        Cells(ooo&, 3).Value = t2# / 10
        ooo& = ooo& + 1
        
    Next n&

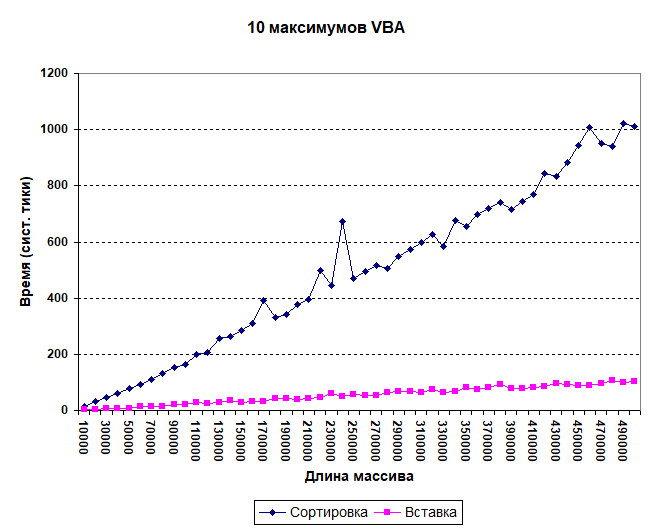
End Sub

На каждом витке цикла корректность сортировки проверяется. Время проверки, естественно, не включается в общий хронометраж. Набор исходных данных тот же — от 10 до 500 тыс. целых чисел. Получает, в общем, похожая картина:

Представляет некоторый интерес изучить зависимость времени от количества искомых максимумов (при фиксированном размере массива). Здесь, очевидно, сортировка будет тем выгоднее, чем больше максимумов требуется найти. А вставка в упорядоченный массив будет тем медленнее, чем массив больше.

Самым невыгодным случаем будет являться, как ни странно, входной массив, уже упорядоченный по возрастанию. В этом случае количество сравнений при вставке достигнет максимума и будет равно n*m. Массив, упорядоченный по убыванию, напротив, весьма выгоден. Число сравнений здесь будет ~ m+n.

Описанный в самом начале статьи алгоритм, можно ускорить, если вместо простого упорядоченного массива использовать древовидную или пирамидальную структуру. Именно так и реализована в Питоне в модуле heapq функция nsmallest.

Для небольших массивов (несколько тысяч элементов и менее) разница в подходах представляется несущественной. И если нужно быстро написать код, то сортировка — вполне приемлемое решение. Для больших массивов выгоднее от сортировки отказаться.

Вот и все, что я хотел рассказать об этой задаче. Спасибо, что дочитали до конца. С наступившим 2021-м годом!

Аннотация: в данной работе раскрыт способ реализации общих реконструкций обучению учащихся программированию к задачам на массивы.

Ключевые слова: программирование; массив; обучение решению задач.

На уроках информатики в современной системе обучения уделяется большое внимание изучению программирования. Понятие операций над массивами входит в образовательный стандарт, учащиеся должны уметь писать алгоритмы, требующие обработку массива.

При ознакомлении учащихся с массивами актуальным стал вопрос о методике работы над задачей. В достаточной мере вопрос раскрыт не был не в одном из источников [1],[2],[5]. При решение задач различных видов, основной целью для учителя должно являться максимальное понимание учащимися алгоритма решения каждой из задач. На примере некоторых задач на массивы систематизируем информацию таким образом, чтобы каждый из последующих этапов вытекал из предыдущего.

Существуют 4 этапа работы над задачей:

1. Анализ условия задачи
2. Поиск способа решения
3. Оформление решения
4. Подведение итогов

Каждый из этапов необходимо раскрыть полостью для достижения поставленной цели.

На уроке были рассмотрены способы поиска максимального элемента в массиве, подсчет количества элементов с заданным параметром. На практическом занятии была предложена задача на подсчет количества максимальных элементов массива. Рассмотрим методику работы с задачей на конкретном примере.

Задача. Дан массив из десяти целых чисел. Определите, сколько элементов этого массива имеют максимальное значение [3].

На этапе анализа условия задачи задаем вопросы, которые могут помочь в поиске известных элементов, по итогу которых мы сможем составить краткую запись. Из диалога с учащимися устанавливаем, что в программе должен появиться массив, состоящий из десяти целочисленных элементов. Требуется определить количество элементов, удовлетворяющих условию. Краткая запись может выглядеть следующим образом:

Дано:  Массив из 10 целочисленных элементов.
Найти:  Количество максимальных элементов.

Следующим этапом становится поиск способа решения данной задачи. Учащимся требуется ответить на вопрос: «Какие переменные потребуются в программе?». Исходя из условия, приходим к выводу, что в разделе описания переменных потребуются следующие переменные: i, max, a, k; где i – индекс элемента в массиве, max – максимальный элемент, a — массив, k – счетчик элементов, равных данному.

var i, max, k: integer;
     a: array [1..10] of integer;

Следующий этап  — этап выявления, используемых алгоритмических конструкций.

Учитель: «Какие алгоритмические конструкции потребуются для решения данной задачи?»

Учащийся: «Заполнение массива, поиск максимального элемента, подсчет количества элементов, равных данному.»

Учитель: «Какие способы заполнения массива нам известны?»

Ранее на уроках с учащимися были рассмотрены способы заполнения массива:

• for i:=1 to 10 do read ( a [ i ] ); {ввод значений элементов массива с клавиатуры};
• for i:=1 to 10 do a [ i ] := i; {заполнение массива при помощи оператора присваивания};
• for i:=1 to 10 do a [ i ] := random (100); {заполнение массива случайными числами, значение которых изменяется в диапазоне от 0 до 99}.

Заполнить массив учащиеся выбрали при помощи оператора randomize. В этом случае стоит отметить, что обязательно для проверки работы программы необходимо массив вывести на экран.

for i:= 1 to 10 do
begin
     randomize;
     a[i]=random(100);
     writeln (a[i], ‘_’);

Следующая алгоритмическая конструкция, которая понадобится нам, для решения нашей задачи направлена на поиск максимального элемента массива.

Учитель: «Каким способом можно организовать поиск максимального элемента?»

Учащиеся: «Присвоить максимальному элементу значение первого, в случае, если последующий больше, то присвоить максимальному значение этого элемента.»

Учитель: «Как организовать это в программе?»

max:=a[1];
     for i:=2 to 10 do
          if a[i]>max then max:=a[i];

После того, как программа нашла максимальный элемент требуется подсчитать количество элементов равных данному. Последней алгоритмической конструкцией, которая необходима для достижения цели – это подсчет количества элементов равных данному.

Подсчет количества элементов осуществляется следующим образом:

k:=0;
     for i:=1 to 10 do
          if a[i]=max then k:=k+1;
     writeln (k ‘_’);

На этапе оформления решения учащимся самостоятельно предлагается составить программу: оформить ее решение в тетради в виде целостной программы, набрать программу на компьютере. Программа может выглядеть следующим образом:

var i, max, k: integer;
     a: array [1..10] of integer;
begin
     for i:= 1 to 10 do
begin
randomize;
     a[i]=random(100);
     writeln (a[i], ‘_’);
end;
max:=a[1];
     for i:=2 to 10 do
          if a[i]>max then max:=a[i];
k:=0;
     for i:=1 to 10 do
          if a[i]=max then k:=k+1;
writeln (k ‘_’);
end.

На этапе подведения итогов важно построить вопросы так, чтобы ученики смогли выстроить логическую цепочку того важного, что они вынесли с данного урока. Результатом решения данной задачи становится алгоритм, который можно будет применить при решении  различного вида задач.

Учитель:  «Каков алгоритм для решения данной задачи мы можем составить?»

Учащиеся: «1. Анализ условия; 2. Переменные, которые потребуются для решения задачи, исходя из краткой записи; 3.Алгоритмические конструкции, решающие подзадачи; 4. Составление программы. »

Исходя из слов учащихся составляем алгоритм решения задачи. Для того, чтобы данный алгоритм был полезен учащимся в дальнейшем при решении задач на программирование немного корректируем и записываем в виде:

1. Анализ условия и составление краткой записи;
2. Исходя из краткой записи определяем переменные, которые потребуются для решения задачи;
3. Определение подзадач, решаемых в программе;
4. Описание алгоритмических конструкций;
5. Составление программы.

Задан массив из n целых чисел. Найти количество максимальных элементов массива.

Входные данные

В первой строке записано число n (n ≤ 100). В следующей строке записано n целых чисел, не превосходящих по модулю 100.

Выходные данные

Вывести количество максимальных элементов массива.

Алгоритм решения задачи

• В первом цикле находим максимальное значение;
• Во втором цикле сравниваем все элементы массива с максимальным, и увеличиваем счетчик при совпадении.

Решение

using System;

class Program
{
    static void Main(string[] args)
    {
        var n = Convert.ToInt32(Console.ReadLine());
        var array = Array.ConvertAll(Console.ReadLine().Split(new[] { " " }, StringSplitOptions.RemoveEmptyEntries), s => int.Parse(s));

        int max = array[0];
        for (int i = 1; i < array.Length; i++)
        {
            if (max < array[i])
            {
                max = array[i];
            }
        }

        var count = 0;

        foreach (var current in array)
        {
            if (current == max)
            {
                count++;
            }
        }

        Console.WriteLine(count);
    }
}