Сайт переезжает. Большинство статей уже перенесено на новую версию.
Скоро добавим автоматические переходы, но пока обновленную версию этой статьи можно найти там.
Задача
Дан ориентированный граф (G = (V, E)), а также вершина (s).
Найти длину кратчайшего пути от (s) до каждой из вершин графа. Длина пути — количество рёбер в нём.
BFS
BFS — breadth-first search, или же поиск в ширину.
Этот алгоритм позволяет решать следующую задачу.
Алгоритм работает следующим образом.
- Создадим массив (dist) расстояний. Изначально (dist[s] = 0) (поскольку расстояний от вершины до самой себя равно (0)) и (dist[v] = infty) для (v neq s).
- Создадим очередь (q). Изначально в (q) добавим вершину (s).
- Пока очередь (q) непуста, делаем следующее:
- Извлекаем вершину (v) из очереди.
- Рассматриваем все рёбра ((v, u) in E). Для каждого такого ребра пытаемся сделать релаксацию: если (dist[v] + 1 < dist[u]), то мы делаем присвоение (dist[u] = dist[v] + 1) и добавляем вершину (u) в очередь.
Визуализации:
-
https://visualgo.net/mn/dfsbfs
-
https://www.hackerearth.com/practice/algorithms/graphs/breadth-first-search/visualize/
Интуитивное понимание алгоритма
Можно представить, что мы поджигаем вершину (s). Каждый шаг алгоритма — это распространение огня на соседние вершины. Понятно, что огонь доберётся до вершины по кратчайшему пути.
Заметьте, что этот алгоритм очень похож на DFS — достаточно заменить очередь на стек и поиск в ширину станет поиском в глубину. Действительно, оба алгоритма при обработке вершины просто записывают всех непосещенных соседей, в которые из неё есть ребро, в структуру данных, и после этого выбирает следующую вершину для обработки в структуре данных. В DFS это стек (благодаря рекурсии), поэтому мы сначала записываем соседа, идем в обрабатываем его полностью, а потом начинаем обрабатывать следующего соседа. В BFS это очередь, поэтому мы кидаем сразу всех соседей, а потом начинаем обрабатывать вообще другую вершину — ту непосещенную, которую мы положили в очередь раньше всего.
Оба алгоритма позволяют обойти граф целиком — посетить каждую вершину ровно один раз. Поэтому они оба подходят для таких задач как: * поиск компонент связности * проверка графа на двудольность * построение остова
Реализация на C++
n — количество вершин в графе; adj — список смежности
vector<int> bfs(int s) {
// длина любого кратчайшего пути не превосходит n - 1,
// поэтому n - достаточное значение для "бесконечности";
// после работы алгоритма dist[v] = n, если v недостижима из s
vector<int> dist(n, n);
dist[s] = 0;
queue<int> q;
q.push(s);
while (!q.empty()) {
int v = q.front();
q.pop();
for (int u : adj[v]) {
if (dist[u] > dist[v] + 1) {
dist[u] = dist[v] + 1;
q.push(u);
}
}
}
return dist;
}Свойства кратчайших путей
Обозначение: (d(v)) — длина кратчайшего пути от (s) до (v).
Лемма 1. > Пусть ((u, v) in E), тогда (d(v) leq d(u) + 1).
Действительно, существует путь из (s) в (u) длины (d(u)), а также есть ребро ((u, v)), следовательно, существует путь из (s) в (v) длины (d(u) + 1). А значит кратчайший путь из (s) в (v) имеет длину не более (d(u) + 1),
Лемма 2. > Рассмотрим кратчайший путь от (s) до (v). Обозначим его как (u_1, u_2, dots u_k) ((u_1 = s) и (u_k = v), а также (k = d(v) + 1)).
> Тогда (forall (i < k): d(u_i) + 1 = d(u_{i + 1})).
Действительно, пусть для какого-то (i < k) это не так. Тогда, используя лемму 1, имеем: (d(u_i) + 1 > d(u_{i + 1})). Тогда мы можем заменить первые (i + 1) вершин пути на вершины из кратчайшего пути из (s) в (u_{i + 1}). Полученный путь стал короче, но мы рассматривали кратчайший путь — противоречие.
Корректность
Утверждение. > 1. Расстояния до тех вершин, которые были добавлены в очередь, посчитаны корректно. > 2. Вершины лежат в очереди в порядке неубывания расстояния, притом разность между кратчайшими расстояними до вершин в очереди не превосходит (1).
Докажем это по индукции по количеству итераций алгоритма (итерация — извлечение вершины из очереди и дальнейшая релаксация).
База очевидна.
Переход. Сначала докажем первую часть. Предположим, что (dist[v] + 1 < dist[u]), но (dist[v] + 1) — некорректное расстояние до вершины (u), то есть (dist[v] + 1 neq d(u)). Тогда по лемме 1: (d(u) < dist[v] + 1). Рассмотрим предпоследнюю вершину (w) на кратчайшем пути от (s) до (u). Тогда по лемме 2: (d(w) + 1 = d(u)). Следовательно, (d(w) + 1 < dist[v] + 1) и (d(w) < dist[v]). Но тогда по предположению индукции (w) была извлечена раньше (v), следовательно, при релаксации из неё в очередь должна была быть добавлена вершина (u) с уже корректным расстоянием. Противоречие.
Теперь докажем вторую часть. По предположению индукции в очереди лежали некоторые вершины (u_1, u_2, dots u_k), для которых выполнялось следующее: (dist[u_1] leq dist[u_2] leq dots leq dist[u_k]) и (dist[u_k] — dist[u_1] leq 1). Мы извлекли вершину (v = u_1) и могли добавить в конец очереди какие-то вершины с расстоянием (dist[v] + 1). Если (k = 1), то утверждение очевидно. В противном случае имеем (dist[u_k] — dist[u_1] leq 1 leftrightarrow dist[u_k] — dist[v] leq 1 leftrightarrow dist[u_k] leq dist[v] + 1), то есть упорядоченность сохранилась. Осталось показать, что ((dist[v] + 1) — dist[u_2] leq 1), но это равносильно (dist[v] leq dist[u_2]), что, как мы знаем, верно.
Время работы
Из доказанного следует, что каждая достижимая из (s) вершина будет добавлена в очередь ровно (1) раз, недостижимые вершины добавлены не будут. Каждое ребро, соединяющее достижимые вершины, будет рассмотрено ровно (2) раза. Таким образом, алгоритм работает за (O(V+ E)) времени, при условии, что граф хранится в виде списка смежности.
Неориентированные графы
Если дан неориентированный граф, его можно рассматривать как ориентированный граф с двумя обратными друг другу ориентированными рёбрами.
Восстановление пути
Пусть теперь заданы 2 вершины (s) и (t), и необходимо не только найти длину кратчайшего пути из (s) в (t), но и восстановить какой-нибудь из кратчайших путей между ними. Всё ещё можно воспользоваться алгоритмом BFS, но необходимо ещё и поддерживать массив предков (p), в котором для каждой вершины будет храниться предыдущая вершина на кратчайшем пути.
Поддерживать этот массив просто: при релаксации нужно просто запоминать, из какой вершины мы прорелаксировали в данную. Также будем считать, что (p[s] = -1): у стартовой вершины предок — некоторая несуществующая вершина.
Восстановление пути делается с конца. Мы знаем последнюю вершину пути — это (t). Далее, мы сводим задачу к меньшей, переходя к нахождению пути из (s) в (p[t]).
Реализация BFS с восстановлением пути
// теперь bfs принимает 2 вершины, между которыми ищется пути
// bfs возвращает кратчайший путь из s в t, или же пустой vector, если пути нет
vector<int> bfs(int s, int t) {
vector<int> dist(n, n);
vector<int> p(n, -1);
dist[s] = 0;
queue<int> q;
q.push(s);
while (!q.empty()) {
int v = q.front();
q.pop();
for (int u : adj[v]) {
if (dist[u] > dist[v] + 1) {
p[u] = v;
dist[u] = dist[v] + 1;
q.push(u);
}
}
}
// если пути не существует, возвращаем пустой vector
if (dist[t] == n) {
return {};
}
vector<int> path;
while (t != -1) {
path.push_back(t);
t = p[t];
}
// путь был рассмотрен в обратном порядке, поэтому его нужно перевернуть
reverse(path.begin(), path.end());
return path;
}Проверка принадлежности вершины кратчайшему пути
Дан ориентированный граф (G), найти все вершины, которые принадлежат хотя бы одному кратчайшему пути из (s) в (t).
Запустим из вершины (s) в графе (G) BFS — найдём расстояния (d_1). Построим транспонированный граф (G^T) — граф, в котором каждое ребро заменено на противоположное. Запустим из вершины (t) в графе (G^T) BFS — найдём расстояния (d_2).
Теперь очевидно, что (v) принадлежит хотя бы одному кратчайшему пути из (s) в (t) тогда и только тогда, когда (d_1(v) + d_2(v) = d_1(t)) — это значит, что есть путь из (s) в (v) длины (d_1(v)), а затем есть путь из (v) в (t) длины (d_2(v)), и их суммарная длина совпадает с длиной кратчайшего пути из (s) в (t).
Кратчайший цикл в ориентированном графе
Найти цикл минимальной длины в ориентированном графе.
Попытаемся из каждой вершины найти кратчайший цикл, проходящий через неё, с помощью BFS. Это делается аналогично обычному BFS: мы должны найти расстояний от вершины до самой себя, при этом не считая, что оно равно (0).
Итого, у нас (|V|) запусков BFS, и каждый запуск работает за (O(|V| + |E|)). Тогда общее время работы составляет (O(|V|^2 + |V| |E|)). Если инициализировать массив (dist) единожды, а после каждого запуска BFS возвращать исходные значения только для достижимых вершин, решение будет работать за (O(|V||E|)).
Задача
Дан взвешенный ориентированный граф (G = (V, E)), а также вершина (s). Длина ребра ((u, v)) равна (w(u, v)). Длины всех рёбер неотрицательные.
Найти длину кратчайшего пути от (s) до каждой из вершин графа. Длина пути — сумма длин рёбер в нём.
Алгоритм Дейкстры
Алгоритм Дейкстры решает приведённую выше задачу. Он работает следующим образом.
- Создать массив (dist) расстояний. Изначально (dist[s] = 0) и (dist[v] = infty) для (v neq s).
- Создать булёв массив (used), (used[v] = 0) для всех вершин (v) — в нём мы будем отмечать, совершалась ли релаксация из вершины.
- Пока существует вершина (v) такая, что (used[v] = 0) и (dist[v] neq infty), притом, если таких вершин несколько, то (v) — вершина с минимальным (dist[v]), делать следующее:
- Пометить, что мы совершали релаксацию из вершины (v), то есть присвоить (used[v] = 1).
- Рассматриваем все рёбра ((v, u) in E). Для каждого ребра пытаемся сделать релаксацию: если (dist[v] + w(v, u) < dist[u]), присвоить (dist[u] = dist[v] + w(v, u)).
Иными словами, алгоритм на каждом шаге находит вершину, до которой расстояние сейчас минимально и из которой ещё не была произведена релаксация, и делает её.
Посчитаем, за сколько работает алгоритм. Мы (V) раз ищем вершину минимальным (dist), поиск минимума у нас линейный за (O(V)), отсюда (O(V^2)). Обработка ребер у нас происходит суммарно за (O(E)), потому что на каждое ребро мы тратим (O(1)) действий. Так мы находим финальную асимптотику: (O(V^2 + E)).
Реализация на C++
Рёбра будем хранить как pair<int, int>, где первое число пары — куда оно ведёт; а второе — длина ребра.
// INF - infinity - бесконечность
const long long INF = (long long) 1e18 + 1;
vector<long long> dijkstra(int s) {
vector<long long> dist(n, INF);
dist[s] = 0;
vector<bool> used(n);
while (true) {
// находим вершину, из которой будем релаксировать
int v = -1;
for (int i = 0; i < n; i++) {
if (!used[i] && (v == -1 || dist[i] < dist[v])) {
v = i;
}
}
// если не нашли подходящую вершину, прекращаем работу алгоритма
if (v == -1) {
break;
}
for (auto &e : adj[v]) {
int u = e.first;
int len = e.second;
if (dist[u] > dist[v] + len) {
dist[u] = dist[v] + len;
}
}
}
return dist;
}Восстановление пути
Восстановление пути в алгоритме Дейкстры делается аналогично восстановлению пути в BFS (и любой динамике).
Дейкстра на сете
Искать вершину с минимальным (dist) можно гораздо быстрее, используя такую структуру данных как очередь с приоритетом. Нам нужно хранить пары ((dist, index)) и уметь делать такие операции: * Извлечь минимум (чтобы обработать новую вершину) * Удалить вершину по индексу (чтобы уменьшить (dist) до какого-то соседа) * Добавить новую вершину (чтобы уменьшить (dist) до какого-то соседа)
Для этого используют, например, кучу или сет. Удобно помимо сета хранить сам массив dist, который его дублирует, но хранит элементы по порядку. Тогда, чтобы заменить значение ((dist_1, u)) на ((dist_2, u)), нужно удалить из сета значение ((dist[u], u)), сделать (dist[u] = dist_2;) и добавить в сет ((dist[u], u)).
Данный алгоритм будет работать за (V O(log V)) извлечений минимума и (O(E log V)) операций уменьшения расстояния до вершины (может быть сделано после каждого ребра). Поэтому алгоритм работает за (O(E log V)).
Заметьте, что этот алгоритм не лучше и не хуже, чем без сета, который работает за (O(V^2 + E)). Ведь если (E = O(V^2)) (граф почти полный), то Дейкстра без сета работает быстрее, а если, наример, (E = O(V)), то Дейкстра на сете работает быстрее. Учитывайте это, когда выбираете алгоритм.
Уровень сложности
Средний
Время на прочтение
3 мин
Количество просмотров 2.4K
Введение
Здравствуйте, дорогие читатели! Я рад представить вам алгоритм, который разработал для решения задачи нахождения кратчайших путей в графе, когда использование алгоритма Дейкстры было неэффективно из-за ограничений по памяти. Этот алгоритм имеет ряд преимуществ перед традиционным алгоритмом Дейкстры. В данной статье мы рассмотрим ключевые особенности этого алгоритма, его преимущества и недостатки, а так же примеры реализации.
Описание алгоритма
Алгоритм использует матрицу размером 5xN для хранения информации о графе и вычисления кратчайших путей. Каждая строка матрицы содержит следующую информацию:
-
Номер исходящего узла
-
Номер входящего узла
-
Длина пути между узлами
-
Сумма пути до текущего узла
-
Флаг, который меняет значения в зависимости от прохождения по разным ребрам графа
Преимущества алгоритма
-
Экономия памяти: По сравнению с базовым алгоритмом Дейкстры, который использует матрицу NxN, алгоритм использует матрицу размером 5xN, что позволяет сэкономить память, особенно при работе с большими графами.
-
Скорость вычисления: В некоторых случаях алгоритм может быть быстрее, так как он работает с меньшим количеством данных и может более эффективно обрабатывать изменения в структуре графа.
-
Гибкость: Благодаря использованию флага, который меняет значения в зависимости от прохождения по разным ребрам графа, алгоритм может быть более гибким и адаптивным для решения различных задач нахождения кратчайших путей.
Пример класса на PHP
<?php
namespace GraphMatrix5xN;
class Graph
{
private array $nodes = []; // Массив для хранения узлов и их соединений (ребер)
private array $matrix = []; // Массив для хранения матричного представления графа
// Добавляет узел в граф
public function addNode(string $node): void
{
if (!isset($this->nodes[$node])) {
$this->nodes[$node] = [];
}
}
// Добавляет ребро между двумя узлами с указанным весом
public function addEdge(string $from, string $to, int $weight): void
{
$this->nodes[$from][$to] = $weight;
$this->nodes[$to][$from] = $weight;
}
// Находит кратчайший путь между начальным и конечным узлами
public function findShortestPath(string $start, string $end): array
{
$visited = []; // Массив для хранения статуса посещения каждого узла
$distances = []; // Массив для хранения текущего кратчайшего расстояния до каждого узла
$previousNodes = []; // Массив для хранения предыдущего узла в пути для каждого узла
$nodes = array_keys($this->nodes);
// Инициализация массивов значениями по умолчанию
foreach ($nodes as $node) {
$visited[$node] = false;
$previousNodes[$node] = null;
$distances[$node] = INF;
}
$distances[$start] = 0;
$currentNode = $start;
// Основной цикл для обработки каждого узла
while ($currentNode !== null) {
$neighbors = $this->nodes[$currentNode];
$currentDistance = $distances[$currentNode];
// Обработка соседей текущего узла
foreach ($neighbors as $neighbor => $weight) {
$newDistance = $currentDistance + $weight;
// Обновление расстояния до соседа, если найден более короткий путь
if ($newDistance < $distances[$neighbor]) {
$distances[$neighbor] = $newDistance;
$previousNodes[$neighbor] = $currentNode;
}
}
// Отмечаем текущий узел как посещенный
$visited[$currentNode] = true;
// Находим следующий непосещенный узел с кратчайшим расстоянием
$currentNode = null;
$minDistance = INF;
foreach ($nodes as $node) {
if (!$visited[$node] && $distances[$node] < $minDistance) {
$currentNode = $node;
$minDistance = $distances[$node];
}
}
}
// Восстанавливаем кратчайший путь из массива предыдущих узлов
$path = [];
$currentNode = $end;
while ($currentNode !== null) {
$path[] = $currentNode;
$currentNode = $previousNodes[$currentNode];
}
// Разворачиваем путь и возвращаем его вместе с общим весом
$path = array_reverse($path);
return [
'path' => $path,
'totalWeight' => $distances[$end],
];
}
}
?>Пример реализации
<?php
require_once 'vendor/autoload.php';
use GraphMatrix5xNGraph;
$graph = new Graph();
$graph->addNode('A');
$graph->addNode('B');
$graph->addNode('C');
$graph->addEdge('A', 'B', 5);
$graph->addEdge('B', 'C', 7);
$graph->addEdge('A', 'C', 10);
$result = $graph->findShortestPath('A', 'C');
print_r($result);
?>
//Array
//(
// [path] => Array
// (
// [0] => A
// [1] => C
// )
//
// [totalWeight] => 10
//)Недостатки алгоритма
Алгоритм рассчитан на графы с положительной длинной ребер, так же на разряженные графы, если у узлов будет большое количество связей, то алгоритм будет не так эффективен.
Заключение
Алгоритм имеет преимущества по сравнению с классическим алгоритмом Дейкстры при решении задач в области искусственного интеллекта, транспортной логистики, сетевой оптимизации и других сферах. Благодаря более эффективному использованию памяти, увеличенной скорости вычислений и гибкости в применении, данный алгоритм становится превосходным инструментом для анализа текстов, выделения семантических связей между словами, а также решения многочисленных проблем поиска кратчайших путей в самых разных областях.
Исходные коды примеров на PHP
Исходные коды на GoLang
1. Нахождение кратчайших путей. Алгоритм Дейкстры
Пусть G={S,U,Ω}
– ориентированный граф со взвешенными
дугами. Обозначим s –
вершину – начало пути и t
– вершину конец пути. Веса дуг должны
быть положительными.
Этап
1.
Нахождение
длины кратчайшего пути.
Шаг 1.
Присвоение вершинам
начальных меток.
Полагаем
и считаем эту метку постоянной (постоянные
метки помечаются сверху звёздочкой).
Для остальных вершин
полагаем
d(x)
= ∞ и считаем эти метки временными. Пусть
обозначение
текущей вершины.
Шаг 2.
Изменение меток.
Для каждой вершины xi
с временной меткой, непосредственно
следует за вершиной
,
меняет её метку в соответствии со
следующим правилом:
(1)
Шаг
3.
Превращение
метки
из
временной
в
постоянную.
Из всех вершин с временными метками
выбираем вершину
с наименьшим значением метки:
(2)
Превращаем
эту метку в постоянную и полагаем
.
Шаг 4.
Проверка на
завершение первого
этапа.
Если
—
длина кратчайшего пути от S
до t. В противном случае
происходит возвращение ко второму шагу.
Этап 2.
Построение кратчайшего
пути.
Шаг
5.
Последовательный
поиск
дуг
кратчайшего
пути.
Среди вершин, непосредственно
предшествующих вершине
с постоянными метками, находим вершину
хi,
удовлетворяющую соотношению
.
(3)
Включаем дугу
в
искомый путь и полагаем
.
Шаг
6.
Проверка
на
завершение
второго
этапа.
Если
,
то кратчайший путь найден – его образует
последовательность дуг, полученных на
пятом шаге и выстроенных в обратном
порядке. В противном случае возвращаемся
к пятому шагу.
Пример. Задана весовая
матрица Ω сети G:
Рис.
34
Найти
минимальный путь из вершины х1
в вершину х6 по алгоритму
Дейкстры.
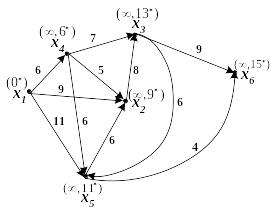
Решение. Т.к. в данном
графе есть цикл между вершинами х2,
х3 и х5, то
вершины графа нельзя упорядочить по
алгоритму Фалкерсона.
Этап 1.
Шаг 1.
Полагаем
.
Первая итерация.
Шаг 2.
Множество вершин, непосредственно
следующих за
с
временными метками
.
Пересчитываем временные метки этих
вершин.
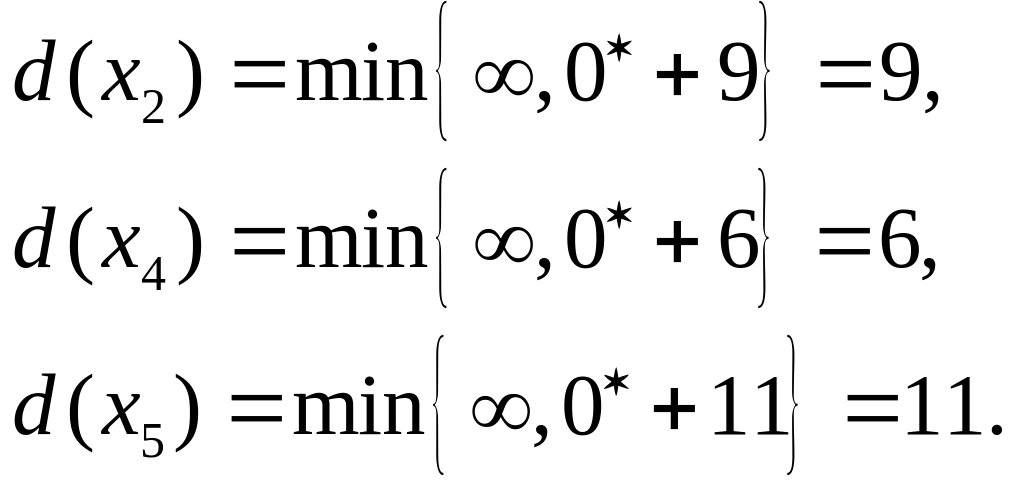
Шаг 3.
Одна из временных меток превращается
в постоянную:
Шаг 4.
происходит возвращение на второй шаг.
Вторая итерация.
Шаг 2.
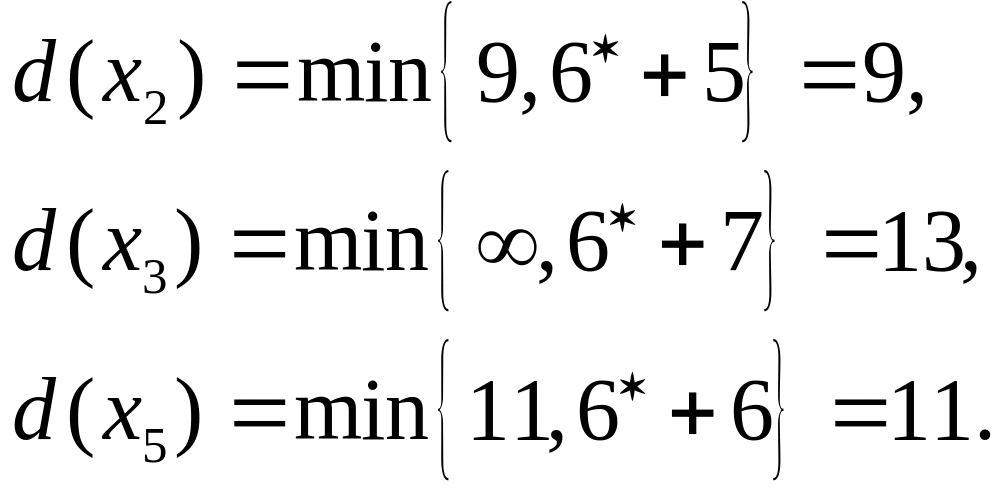
Шаг 3.
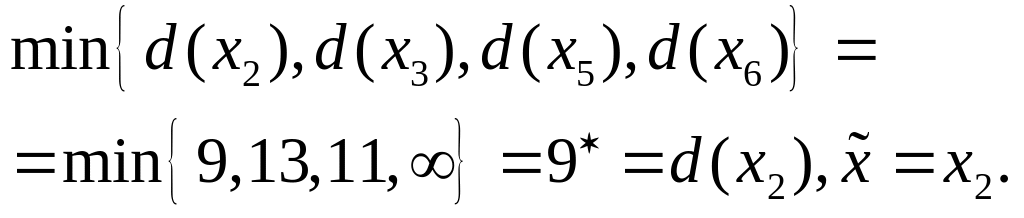
Шаг 4.
,
возвращение на 2-ой шаг.
Третья итерация.
Шаг 2.
Шаг 3.
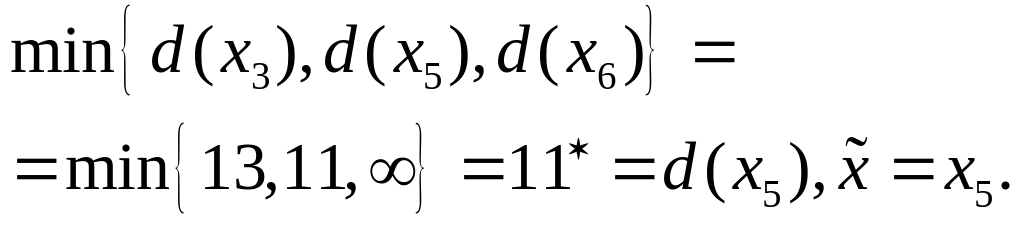
Шаг 4.
возвращение
на 2-ой шаг.
Четвёртая итерация.
Шаг 2.
Шаг 3.
Шаг 4.
возвращение
на 2-ой шаг.
Пятая итерация.
Шаг 2.
Шаг 3.
Шаг 4.
конец
1-го этапа.
Этап 2.
Первая итерация.
Шаг 5.
Составим множество вершин, непосредственно
предшествующих
с постоянными метками
Проверим для
этих двух вершин выполнение равенства
(3):
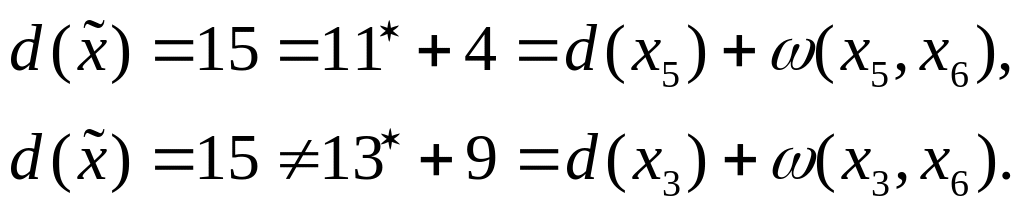
Включаем дугу
(х5,х6) в
кратчайший путь.
.
Шаг 6.
,
возвращение на 5-ый шаг.
Вторая
итерация.
Шаг5.
Включаем дугу (х1,х5)
в кратчайший путь.
.
Шаг 6.
,
завершение второго этапа.
Итак
кратчайший путь от вершины х1
до вершины х6
построен. Его длина (вес) равен 15, сам
путь образует следующая последовательность
дуг:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Кратчайший путь (A, B, D, F) между вершинами A и F в неориентированном графе без весов.
Кратчайший путь (A, C, E, D, F) между вершинами A и F во взвешенном ориентированном графе.
Зада́ча о кратча́йшем пути́ (англ. shortest path problem) — задача поиска самого короткого пути (цепи) между двумя точками (вершинами) на графе, в которой минимизируется сумма весов ребер, составляющих путь.
Кратчайшая (простая) цепь часто называется геодезической [1].
Задача о кратчайшем пути является одной из важнейших классических задач теории графов. Сегодня известно множество алгоритмов для её решения[⇨].
У данной задачи существуют и другие названия: задача о минимальном пути или, в устаревшем варианте, задача о дилижансе.
Значимость данной задачи определяется её различными практическими применениями[⇨]. Например в GPS-навигаторах, где осуществляется поиск кратчайшего пути между двумя перекрестками. В качестве вершин выступают перекрестки, а дороги являются ребрами, которые лежат между ними. Сумма расстояний всех дорог между перекрестками должна быть минимальной, тогда найден самый короткий путь.
Содержание
- 1 Определение
- 2 Задача о кратчайшем пути с учетом дополнительных ограничений
- 3 Алгоритмы
- 4 Задача поиска кратчайшего пути из одной вершины во все остальные
- 4.1 Взвешенный ориентированный граф
- 4.2 Ориентированный граф с неотрицательными весами
- 4.3 Ориентированный граф с произвольными весами
- 5 Задача о кратчайшем пути между всеми парами вершин
- 6 Применение
- 6.1 Картографические сервисы
- 6.2 Недетерминированная машина
- 6.3 Сети дорог
- 7 Похожие задачи
- 8 Постановка задачи линейного программирования
- 9 См. также
- 10 Примечания
- 11 Литература
Определение[править | править вики-текст]
Задача поиска кратчайшего пути на графе может быть определена для неориентированного, ориентированного или смешанного графа. Далее будет рассмотрена постановка задачи в самом простом виде для неориентированного графа. Для смешанного и ориентированного графа дополнительно должны учитываться направления ребер.
Граф представляет собой совокупность непустого множества вершин и ребер (наборов пар вершин). Две вершины на графе смежны, если они соединяются общим ребром. Путь в неориентированном графе представляет собой последовательность вершин 








Пусть 










Существуют различные постановки задачи о кратчайшем пути:
- Задача о кратчайшем пути в заданный пункт назначения. Требуется найти кратчайший путь в заданную вершину назначения t, который начинается в каждой из вершин графа (кроме t). Поменяв направление каждого принадлежащего графу ребра, эту задачу можно свести к задаче о единой исходной вершине (в которой осуществляется поиск кратчайшего пути из заданной вершины во все остальные).
- Задача о кратчайшем пути между заданной парой вершин. Требуется найти кратчайший путь из заданной вершины u в заданную вершину v.
- Задача о кратчайшем пути между всеми парами вершин. Требуется найти кратчайший путь из каждой вершины u в каждую вершину v. Эту задачу тоже можно решить с помощью алгоритма, предназначенного для решения задачи об одной исходной вершине, однако обычно она решается быстрее.
В различных постановках задачи, роль длины ребра могут играть не только сами длины, но и время, стоимость, расходы, объем затрачиваемых ресурсов (материальных, финансовых, топливно-энергетических и т. п.) или другие характеристики, связанные с прохождением каждого ребра. Таким образом, задача находит практическое применение в большом количестве областей (информатика, экономика, география и др.).
Задача о кратчайшем пути с учетом дополнительных ограничений[править | править вики-текст]
Задача о кратчайшем пути очень часто встречается в ситуации, когда необходимо учитывать дополнительные ограничения. Наличие их может значительно повысить сложность задачи[2]. Примеры таких задач:
- Кратчайший путь, проходящий через заданное множество вершин. Можно рассматривать два ограничения: кратчайший путь должен проходить через выделенное множество вершин, и кратчайший путь должен содержать как можно меньше невыделенных вершин. Первое из них хорошо известна в теории исследования операций[3].
- Минимальное покрытие вершин ориентированного графа путями. Осуществляется поиск минимального по числу путей покрытия графа, а именно подмножества всех s-t путей, таких что, каждая вершина ориентированного графа принадлежит хотя бы одному такому пути[4].
- Задача о требуемых путях. Требуется найти минимальное по мощности множество s-t путей
такое, что для любого
найдется путь
, накрывающий его.
— множество некоторых путей в ориентированном графе G[5].
- Минимальное покрытие дуг ориентированного графа путями. Задача состоит в отыскании минимального по числу путей подмножества всех путей, такого, что каждая дуга принадлежит хотя бы одному такому пути. При этом возможно дополнительное требование о том, чтобы все пути исходили из одной вершины[6].
Алгоритмы[править | править вики-текст]
В связи с тем, что существует множество различных постановок данной задачи, есть наиболее популярные алгоритмы для решения задачи поиска кратчайшего пути на графе:
- Алгоритм Дейкстры находит кратчайший путь от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса[7].
- Алгоритм Беллмана — Форда находит кратчайшие пути от одной вершины графа до всех остальных во взвешенном графе. Вес ребер может быть отрицательным.
- Алгоритм поиска A* находит маршрут с наименьшей стоимостью от одной вершины (начальной) к другой (целевой, конечной), используя алгоритм поиска по первому наилучшему совпадению на графе.
- Алгоритм Флойда — Уоршелла находит кратчайшие пути между всеми вершинами взвешенного ориентированного графа[7].
- Алгоритм Джонсона находит кратчайшие пути между всеми парами вершин взвешенного ориентированного графа.
- Алгоритм Ли (волновой алгоритм) основан на методе поиска в ширину. Находит путь между вершинами s и t графа (s не совпадает с t), содержащий минимальное количество промежуточных вершин (ребер). Основное применение — трассировки электрических соединений на кристаллах микросхем и на печатных платах. Так же используется для поиска кратчайшего расстояния на карте в стратегических играх.
- Поиск кратчайшего пути на основе алгоритма Килдала[8].
В работе (Черкасский и др., 1993)[9] представлено ещё несколько алгоритмов для решения этой задачи.
Задача поиска кратчайшего пути из одной вершины во все остальные[править | править вики-текст]
В такой постановке задачи осуществляется поиск кратчайшего пути из вершины v во все остальные вершины на графе.
Взвешенный ориентированный граф[править | править вики-текст]
| Алгоритм | Сложность | Автор |
|---|---|---|
| Поиск в ширину | O(E) |
Ориентированный граф с неотрицательными весами[править | править вики-текст]
| Алгоритм | Сложность | Автор |
|---|---|---|
| — | O(V2EL) | Форд 1956 |
| Алгоритм Беллмана — Форда | O(VE) | Беллман 1958[10], Мур 1959[11] |
| — | O(V2 log V) | Данциг 1958, Данциг 1960, Minty (cf. Pollack&Wiebenson 1960), Whiting&Hillier 1960 |
| Алгоритм Дейкстры со списком. | O(V2) | Leyzorek et al. 1957[12], Дейкстра 1959[13] |
| Алгоритм Дейкстры с модифицированной двоичной кучей | O((E + V) log V) | — |
| . . . | . . . | . . . |
| Алгоритм Дейкстры с использованием фибоначчиевой кучи | O(E + V log V) | Фридман&Тарьян 1984[14], Фридман&Тарьян 1987[15] |
| — | O(E log log L) | Джонсон 1982, Карлссон&Поблете 1983 |
| Алгоритм Габова | O(E logE/V L) | Габов 1983, Габов 1985 |
| — | O(E + V√log L) | Ахуджа et al. 1990 |
Ориентированный граф с произвольными весами[править | править вики-текст]
| Алгоритм | Сложность | Автор |
|---|---|---|
| Алгоритм Беллмана — Форда | O(VE) | Беллман[10], Мур[16] |
Задача о кратчайшем пути между всеми парами вершин[править | править вики-текст]
Задача о кратчайшем пути между всеми парами вершин для невзвешенного ориентированного графа была поставлена Симбелом в 1953 году[17], который обнаружил, что она может быть решена за линейное количество манипуляций (умножения) с матрицей. Сложность такого алгоритма O(V4).
Так же для решения данной задачи существуют другие более быстрые алгоритмы, такие как Алгоритм Флойда — Уоршелла со сложностью O(V3), и Алгоритм Джонсона (является комбинацией алгоритмов Бэллмана-Форда и Дейкстры) со сложностью O(VE + V2 log V).
Применение[править | править вики-текст]
Задача о поиске кратчайшего пути на графе может быть интерпретирована по-разному и применяться в различных областях. Далее приведены примеры различных применений задачи. Другие применения изучаются в дисциплине, которая занимается исследованием операций[18].
Картографические сервисы[править | править вики-текст]
Алгоритмы нахождения кратчайшего пути на графе применяются для нахождения путей между физическими объектами на таких картографических сервисах, как карты Google или OpenStreetMap. В обучающем видео от Google можно узнать различные эффективные алгоритмы, которые применяются в данной сфере[19].
Недетерминированная машина[править | править вики-текст]
Если представить недетерминированную абстрактную машину как граф, где вершины описывают состояния, а ребра определяют возможные переходы, тогда алгоритмы поиска кратчайшего пути могут быть применены для поиска оптимальной последовательности решений для достижения главной цели. Например, если вершинами являются состояния Кубика Рубика, а ребром представляет собой одно действие над кубиком, тогда алгоритм может быть применен для поиска решения с минимальным количеством ходов.
Сети дорог[править | править вики-текст]
Задача поиска кратчайшего пути на графе широко используется при определении наименьшего расстояния в сети дорог.
Сеть дорог можно представить в виде графа с положительными весами. Вершины являются дорожными развязками, а ребра дорогами, которые их соединяют. Веса ребер могут соответствовать протяженности данного участка, времени необходимому для его преодоления или стоимости путешествия по нему. Ориентированные ребра можно использовать для представления односторонних улиц. В таком графе можно ввести характеристику, которая указывает на то, что одни дороги важнее других для длительных путешествий (например автомагистрали). Она была формализована в понятии (идее) о магистралях[20].
Для реализации подхода, где одни дороги важнее других, существует множество алгоритмов. Они решают задачу поиска кратчайшего пути намного быстрее, чем аналогичные на обычных графах. Подобные алгоритмы состоят из двух этапов:
- этап предобработки. Производится предварительная обработка графа без учета начальной и конечной вершины (может длиться до нескольких дней, если работать с реальными данными). Обычно выполняется один раз и потом используются полученные данные.
- этап запроса. Осуществляется запрос и поиск кратчайшего пути, при этом известны начальная и конечная вершина.
Самый быстрый алгоритм может решить данную задачу на дорогах Европы или Америки за доли микросекунды[21].
Другие подходы (техники), которые применяются в данной сфере:
- ALT
- Arc Flags
- Contraction hierarchies
- Transit Node Routing
- Reach based Pruning
- Labeling
Похожие задачи[править | править вики-текст]
Существуют задачи, которые похожи на задачу поиска кратчайшего пути на графе.
- Поиск кратчайшего пути в вычислительной геометрии (см. евклидов кратчайший путь).
- Задача коммивояжёра. Требуется найти кратчайший маршрут, проходящий через указанные города (вершины) хотя бы по одному разу с последующим возвратом в исходный город. Данная задача относится к классу NP-трудных задач в отличие от задачи поиска кратчайшего пути, которая может быть решена за полиномиальное время в графах без циклов. Задача коммивояжёра решается неэффективно для больших наборов данных.
- Задача канадского путешественника и задача стохастического поиска кратчайшего пути являются обобщением рассматриваемой задачи, в которых обходимый граф заранее полностью неизвестен и изменяется во времени или следующий проход по графу вычисляется на основе вероятностей.
- Задача поиска кратчайшего пути, когда в графе происходят преобразования. Например, изменяется вес ребра или удаляется вершина[22].
Постановка задачи линейного программирования[править | править вики-текст]
Пусть дан направленный граф (V, A), где V — множество вершин и A — множество ребер, с начальной вершиной обхода s, конечной t и весами wij для каждого ребра (i, j) в A. Вес каждого ребра соответствует переменной программы xij.
Тогда задача ставится следующим образом: найти минимум функции 

См. также[править | править вики-текст]
- IEEE 802.1aq
- Транспортная сеть
- Двунаправленный поиск
Примечания[править | править вики-текст]
- ↑ Теория графов (Харари), 1973
- ↑ Применение теории графов в программировании, 1985
- ↑ Применение теории графов в программировании, 1985, с. 138-139
- ↑ Применение теории графов в программировании, 1985, с. 139-142
- ↑ Применение теории графов в программировании, 1985, с. 144-145
- ↑ Применение теории графов в программировании, 1985, с. 145-148
- ↑ 1 2 Дискретная математика. Комбинаторная оптимизация на графах, 2003
- ↑ Применение теории графов в программировании, 1985, с. 130-131
- ↑ Cherkassky Goldberg, 1996
- ↑ 1 2 Bellman Richard
- ↑ Moore
- ↑ M. Leyzorek
- ↑ Dijkstra
- ↑ Michael Fredman Lawrence 1984
- ↑ Fredman Michael 1987
- ↑ Moore E. F.
- ↑ Shimbel
- ↑ Developing algorithms and software for geometric path planning problems
- ↑ Fast route planning
- ↑ Highway Dimension
- ↑ A Hub-Based Labeling Algorithm
- ↑ Ladyzhensky Y., Popoff Y. Algorithm
Литература[править | править вики-текст]
- Евстигнеев В. А. Глава 3. Итеративные алгоритмы глобального анализа графов. Пути и покрытия // Применение теории графов в программировании / Под ред. А. П. Ершова. — Москва: Наука. Главная редакция физико-математической литературы, 1985. — С. 138-150. — 352 с.
- Алексеев В.Е., Таланов В.А. Глава 3.4. Нахождения кратчайших путей в графе // Графы. Модели вычислений. Структуры данных. — Нижний Новгород: Издательство Нижегородского гос. университета, 2005. — С. 236-237. — 307 с. — ISBN 5–85747–810–8.
- Галкина В.А. Глава 4. Построение кратчайших путей в ориентированном графе // Дискретная математика. Комбинаторная оптимизация на графах. — Москва: Издательство «Гелиос АРВ», 2003. — С. 75-94. — 232 с. — ISBN 5–85438–069–2.
- Берж К. Глава 7. Задача о кратчайшем пути // Теория графов и её применения = Theorie des graphes et ses applications / Под ред. И. А. Вайнштейна. — Москва: Издательство иностранной литературы, 1962. — С. 75-81. — 320 с.
- Ойстин Оре. Теория графов / Под ред. И. М. Овчинниковой. — Издательство наука, 1980. — 336 с.
- Cherkassky Boris V.,Goldberg Andrew V. , Radzik Tomasz. Shortest paths algorithms: theory and experimental evaluation (англ.) // Mathematical Programming. — 1996. — No. 73. — P. 129–174. — DOI:10.1016/0025-5610(95)00021-6.
- Харари Ф. Глава 2. Графы // Теория графов / Под ред. Г. П. Гаврилова. — Издательство мир, 1973. — С. 27. — 300 с. — ISBN 5-354-00301-6.
- Ричард Беллман (1958). «On a routing problem». Quarterly of Applied Mathematics 16: 87–90.
- Dijkstra E. W. A note on two problems in connexion with graphs // Numer. Math — Springer Science+Business Media, 1959. — Vol. 1, Iss. 1. — P. 269—271. — ISSN 0029-599X; 0945-3245 — doi:10.1007/BF01386390
- E. F. Moore (April 2–5, 195). «The shortest path through a maze» (Harvard University Press): 285–292.
- M. Leyzorek, R. S. Gray, A. A. Gray, W. C. Ladew, S. R. Meaker, R. M. Petry, R. N. Seitz. Investigation of Model Techniques — First Annual Report — 6 June 1956 — 1 July 1957 — A Study of Model Techniques for Communication Systems. — Cleveland, Ohio: Case Institute of Technology, 1957.
- Michael Fredman Lawrence, Роберт Андре Тарьян (1984). «Fibonacci heaps and their uses in improved network optimization algorithms» (IEEE): 338–346. DOI:10.1109/SFCS.1984.715934.
- Michael Fredman Lawrence, Роберт Андре Тарьян (1987). «Fibonacci heaps and their uses in improved network optimization algorithms». Journal of the Association for Computing Machinery 34 (3): 596–615. DOI:10.1145/28869.28874.
- Shimbel, Alfonso (1953). «Structural parameters of communication networks». Bulletin of Mathematical Biophysics 15 (4): 501–507. DOI:10.1007/BF02476438.
- Sanders, Peter (March 23, 2009). «Fast route planning» (Google Tech Talk).
- Chen, Danny Z. (December 1996). «Developing algorithms and software for geometric path planning problems». ACM Computing Surveys 28 (4es): 18. DOI:10.1145/242224.242246.
- Abraham, Ittai; Fiat, Amos; Goldberg, Andrew V.; Werneck, Renato F. (2010). «Highway Dimension, Shortest Paths, and Provably Efficient Algorithms». ACM-SIAM Symposium on Discrete Algorithms: 782-793.
- Abraham, Ittai; Delling, Daniel; Goldberg, Andrew V.; Werneck, Renato F. (2011). «A Hub-Based Labeling Algorithm for Shortest Paths on Road Networks. Symposium on Experimental Algorithms]»: 230-241.
- Kroger, Martin (2005). «Shortest multiple disconnected path for the analysis of entanglements in two- and three-dimensional polymeric systems». Computer Physics Communications 168 (168): 209–232. DOI:10.1016/j.cpc.2005.01.020.
- Ladyzhensky Y., Popoff Y. (2006). «Algorithm to define the shortest paths between all nodes in a graph after compressing of two nodes. Proceedings of Donetsk national technical university, Computing and automation. Vol.107. Donetsk»: 68–75.
Автор — Лада Борисовна Есакова.
Подсчет путей в ориентированном графе. ЗАДАЧА № 15.
В этой задаче требуется подсчитать количество путей, ведущих из одной вершины графа в другую. Обычно задачу решают преобразованием графа в дерево. Однако, при сложной структуре графа такое решение становится очень трудоемким. Велика вероятность ошибки.
Рассмотрим простой и эффективный способ решения.
В этой задаче мы имеем дело с ориентированным графом (графом, у которого ребра имеют направление). Т.е. ребра имеют вид стрелок. Две вершины, соединенные напрямую стрелкой, называются смежными. Вершина, из которой выходит стрелка, называется предком, а вершина, в которую входит стрелка – потомком.
Несложно понять, что количество путей, которыми можно попасть в некоторую вершину, равно сумме количеств путей предков этой вершины.
Пример:
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?
Решение:
Каждой вершине, начиная с начальной (A), поставим в соответствие индекс, равный количеству путей, которыми можно попасть в эту вершину. Для вершины A (начало пути) индекс всегда равен 1 (в начало пути можно попасть единственным образом – никуда не двигаясь). Теперь сформулируем правило: индекс вершины равен сумме индексов его предков. Исходя из этого индекс Б равен 1 (предок у Б один – вершина A).
У вершины Д предками являются А и Б, значит индекс вершины Д равен 1+1=2.
Очевидно, что мы можем посчитать индекс только тех вершин, индексы предков которых уже посчитаны. Например, мы не можем посчитать индекс Г, пока не посчитан индекс В. Двигаясь последовательно, мы рассчитаем индексы всех вершин.
Индекс вершины Ж и будет ответом задачи.
Ответ: 11
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задача №15. Графы. Поиск количества путей.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
07.05.2023

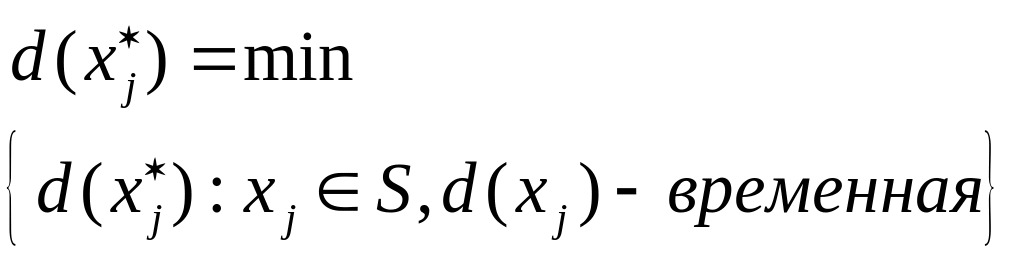
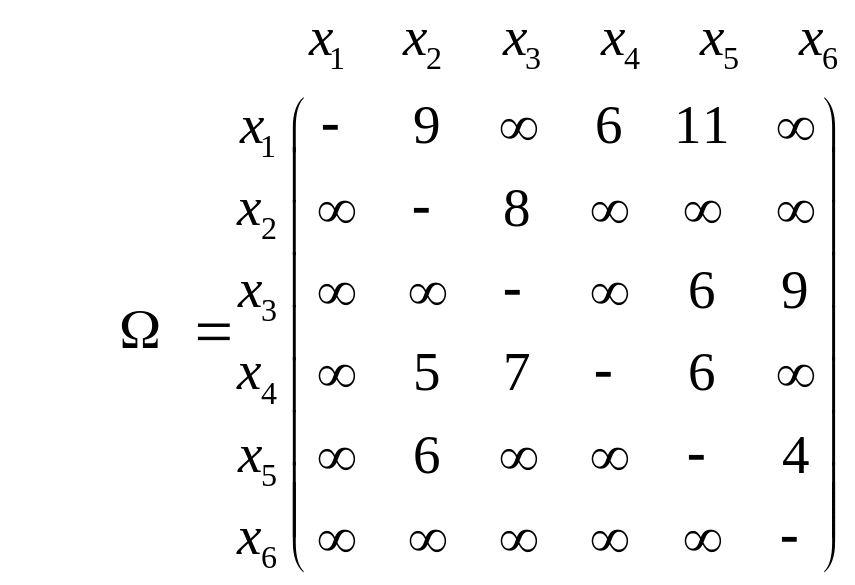


 такое, что для любого
такое, что для любого  найдется путь
найдется путь  , накрывающий его.
, накрывающий его.  — множество некоторых путей в ориентированном графе G[5].
— множество некоторых путей в ориентированном графе G[5].


