Как найти количество путей в неориентированном графе

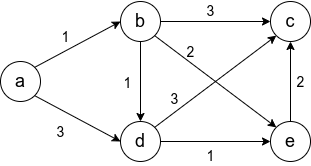
Given a weighted undirected graph G and an integer S, the task is to print the distances of the shortest paths and the count of the number of the shortest paths for each node from a given vertex, S.

Examples:

Input: S =1, G = 

Output: Shortest Paths distances are : 0 1 2 4 5 3 2 1 3 
              Numbers of the shortest Paths are: 1 1 1 2 3 1 1 1 2 
Explanation:

1. The distance of the shortest paths to vertex 1 is 0 and there is only 1 such path, which is {1}.
2. The distance of the shortest paths to vertex 2 is 1 and there is only 1 such path, which is {1→2}.
3. The distance of the shortest paths to vertex 3 is 2 and there is only 1 such path, which is {1→2→3}.
4. The distance of the shortest paths to vertex 4 is 4 and there exist 2 such paths, which are {{1→2→3→4}, {1→2→3→6→4}}.
5. The distance of the shortest paths to vertex 5 is 5 and there exist 3 such paths, which are {{1→2→3→4→5}, {1→2→3→6→4→5}, {1→2→3→6→5}}.
6. The distance of the shortest paths to vertex 6 is 3 and there is only 1 such path, which is {1→2→3→6}.
7. The distance of the shortest paths to vertex 7 is 2 and there is only 1 such path, which is {1→8→7}.
8. The distance of the shortest paths to vertex 8 is 1 and there is only 1 such path, which is {1→8}.
9. The distance of the shortest paths to vertex 9 is 3 and there exist 2 such paths, which are {{1→8→9}, {1→2→3→9}}.

Recommended: Please try your approach on {IDE} first, before moving on to the solution.

Approach: The given problem can be solved using the Dijkstra Algorithm. Follow the steps below to solve the problem:

• Form the adjacency List of the given graph using ArrayList<ArrayList<>> and store it in a variable, say adj.
• Initialize two integers, Arrays say Dist[] and Paths[] all elements as 0 to store the shortest distances of each node and count of paths with the shortest distance from the source Node, S.
• Define a function, say Dijkstra() to find the shortest distances of each node and count the paths with the shortest distance:
  • Initialize a min PriorityQueue say PQ and a HashSet of Strings say settled to store if the edge is visited or not.
  • Assign 0 to Dist[S] and 1 to Paths[S].
  • Now iterate until PQ is not empty() and perform the following operations:
    • Find the top Node of the PQ and store the Node value in a variable u.
    • Pop the top element of PQ.
    • Iterate over the ArrayList adj[u] and perform the following operations
      • Store the adjacent node in a variable say to and edge cost in a variable say cost:
      • If edge {u, to} is visited, then continue.
      • If dist[to] is greater than dist[u]+cost, then assign dist[u]+cost to dist[to] and then assign Paths[u] to Paths[to].
      • Otherwise, if dist[to] is equal to dist[u]+cost, then increment Paths[to] by 1.
      • Now, Mark, the current edge {u, to} visited in settled.
• Call the function Dijkstra().
• Finally, print the Arrays dist[] and Paths[].

Below is the implementation of the above approach:

Shortest Paths distances are : 0 1 2 4 5 3 2 1 3 
Numbers of the shortest Paths are: 1 1 1 2 3 1 1 1 2

Time Complexity: O(M + N * log(N))  
Auxiliary Space: O(M)

Last Updated :
12 Mar, 2023

Like Article

Save Article

Введение

Если G является неориентированным графом, то путём в графе G будет такой конечный или бесконечный набор последовательных рёбер и вершин S = (…, a0, E0, a1, E1, …, En-1, an), для которого пара соседних рёбер Ei и Ei-1 обладают общей вершиной ai. То есть справедливы следующие выражения E0 = (a0, a1), E1 = (a1, a2), …, En = (an, an+1)

Следует заметить, что возможна неоднократная встреча с одним и тем же ребром при прохождении путевого маршрута. В случае, когда нет рёбер, которые предшествуют E0, то a0 считается исходной вершиной S. А когда не существует рёбер, которые идут за E(n-1), то an считается последней вершиной S. Все вершины, которые принадлежат паре соседних рёбер, считаются внутренними.

Следует заметить, что поскольку возможно повторение рёбер и вершин при прохождении путевого маршрута, то внутренняя вершина может быть, как начальной, так и конечной вершиной.

При совпадении начальной и конечной вершин, путь считается циклическим. В случае, когда каждое ребро графа при обходе путевого маршрута, попадается всего один раз (повтор вершин допускается), такой путь считается цепью, а циклический путь считается циклом.

Путь, при котором нет рёбер графа, соединяющих две вершины пути, носит название индуцированного пути. Пара путей считается независимой в смысле вершин, когда у них нет одинаковых внутренних вершин. И по аналогии пара путей считается независимой в плане рёбер, когда у них нет общих внутренних рёбер.

Количество путей в графе

В случае, когда в город S возможно доехать лишь из городов X, Y, и Z, то количество разнообразных путевых маршрутов из города А в город S равняется суммарному количеству разных путей движения из А в Х, из А в Y и из А в Z, что можно выразить следующей формулой:

$N_S = N_X + N_Y + N_Z$

Обозначим как NM количество путевых маршрутов из вершины А в некую вершину М. Количество путей будет конечным, если в графе отсутствуют замкнутые пути, то есть циклы. Рассмотрим конкретный пример. Имеется структурная схема дорог, которые соединяют города А, Б, В, Г, Д, Е, Ж, И, К, Л. Передвижение по всем дорогам возможно только в одну сторону, в которую указывает стрелка. Необходимо определить количество возможных путей из города А в город Л.

Обозначим как $N_X$ число разных маршрутов из города А в город Х. Считаем, что город А является исходным пунктом путевого маршрута, и, следовательно, NA = 1. А для произвольно выбранного города Х число путей $N_X$ возможно определить по формуле:

$N_X = N_Y + … + N_Z$.

Здесь суммарный путь принят по всем вершинам, имеющим прямую связь с вершиной Х, то есть, к примеру:

$N_Л = N_Д + N_И + N_Ж + N_К$

Сформируем таблицу, где каждому городу сопоставлено общее число прямых маршрутов в этот город. Вычислим общее число путей из начальной точки маршрута, города А.

В пункты Б и В ведут единственные дороги из А. В пункт В можно попасть из пунктов А, Б, и Г, т.е. $N_В = N_А + N_Б + N_Г = 3$.

В пункт Е можно попасть только из Г, количество путей равно количеству путей в пункт Г. В пункт Ж ведут прямые пути из пунктов Е и В, т.е. $N_Ж = N_В + N_Е = 4$. В пункт Д ведут прямые пути из пунктов Б и В, т.е. $N_Д = N_В + N_Б = 4$.

В пункт И можно попасть только из Д, количество путей равно количеству путей в пункт Д = 4. В пункт К ведет путь только из пункта Е, т.е. $N_К = N_Е = 1$. В пункт Л ведут прямые пути из пунктов Д, И, Ж и К, т.е. $N_Л = N_Д + N_И + N_Ж + N_К = 13$.

Итоговый результат тринадцать путей.

Автор — Лада Борисовна Есакова.

Подсчет путей в ориентированном графе. ЗАДАЧА № 15.

В этой задаче требуется подсчитать количество путей, ведущих из одной вершины графа в другую. Обычно задачу решают преобразованием графа в дерево. Однако, при сложной структуре графа такое решение становится очень трудоемким. Велика вероятность ошибки.

Рассмотрим простой и эффективный способ решения.

В этой задаче мы имеем дело с ориентированным графом (графом, у которого ребра имеют направление). Т.е. ребра имеют вид стрелок. Две вершины, соединенные напрямую стрелкой, называются смежными. Вершина, из которой выходит стрелка, называется предком, а вершина, в которую входит стрелка – потомком.

Несложно понять, что количество путей, которыми можно попасть в некоторую вершину, равно сумме количеств путей предков этой вершины.

Пример:

На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?

Решение:

Каждой вершине, начиная с начальной (A), поставим в соответствие индекс, равный количеству путей, которыми можно попасть в эту вершину. Для вершины A (начало пути) индекс всегда равен 1 (в начало пути можно попасть единственным образом – никуда не двигаясь). Теперь сформулируем правило: индекс вершины равен сумме индексов его предков. Исходя из этого индекс Б равен 1 (предок у Б один – вершина A).

У вершины Д предками являются А и Б, значит индекс вершины Д равен 1+1=2.

Очевидно, что мы можем посчитать индекс только тех вершин, индексы предков которых уже посчитаны. Например, мы не можем посчитать индекс Г, пока не посчитан индекс В. Двигаясь последовательно, мы рассчитаем индексы всех вершин.

Индекс вершины Ж и будет ответом задачи.

Ответ: 11

3 ответа

Лучший ответ

import numpy as np

def count_paths(v, n, a):
    # v: number of vertices, n: expected path length
    paths = 0    
    b = np.array(a, copy=True)

    for i in range(n-2):
        b = np.dot(b, a)

    c = np.dot(b, a)
    x = c - b

    for i in range(v):
        for j in range(i+1, v):
            if x[i][j] == 1:
                paths = paths + 1

    return paths

print count_paths(5, 2, np.array([
                np.array([0, 1, 0, 0, 0]),
                np.array([1, 0, 1, 0, 1]),
                np.array([0, 1, 0, 1, 0]),
                np.array([0, 0, 1, 0, 0]),
                np.array([0, 1, 0, 0, 0])
            ])

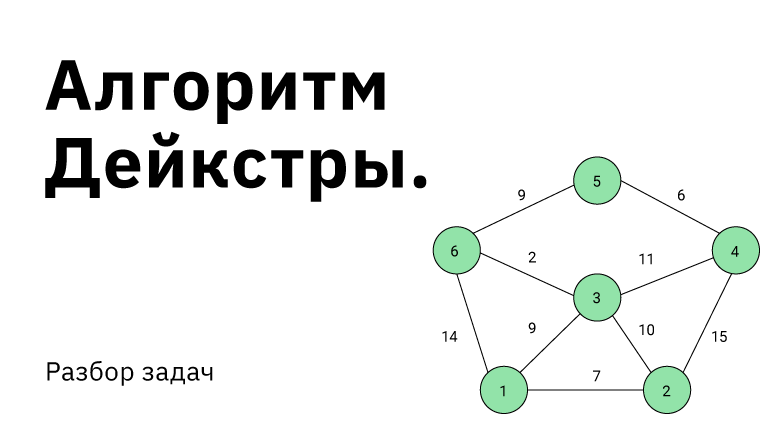
Алгоритм Дейкстры. Разбор Задач

Поиск оптимального пути в графе. Такая задача встречается довольно часто и в повседневной жизни, и в мире технологий. Справиться с такими вызовами помогает подход, который должен быть в арсенале каждого программиста — алгоритм Дейкстры.

Если вы хотите найти ответить на вопросы, чем этот алгоритм лучше BFS (поиска в ширину), при каких условиях алгоритм применим, и какие теоретические и практические задачи можно с его помощью решать, читайте далее.

Введение

Для каждого ребра в графе задан неотрицательный вес , а также вершина, из которой осуществляется поиск оптимальных путей.

Алгоритм Дейкстры может найти кратчайший путь между вершинами и в графе, только если существует хотя бы один путь между этими вершинами. Если это условие не выполняется, то алгоритм отработает корректно, вернув значение «бесконечность» для пары несвязанных вершин.

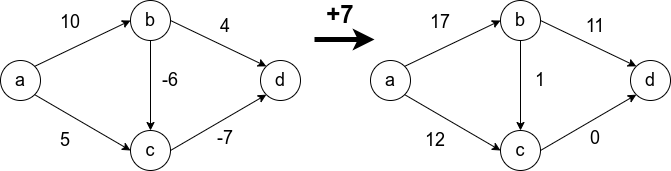
Условие неотрицательности весов рёбер крайне важно и от него нельзя просто избавиться. Не получится свести задачу к решаемой алгоритмом Дейкстры, прибавив наибольший по модулю вес ко всем рёбрам. Это может изменить оптимальный маршрут. На рисунке видно, что в первом случае оптимальный путь между и (сумма рёбер на пути наименьшая) изменяется при такой манипуляции. В оригинале путь проходит через , а после добавления семёрки ко всем рёбрам, оптимальный путь проходит через

Как ведёт себя алгоритм Дейкстры на исходном графе, мы разберём, когда выпишем алгоритм. Но для начала зададимся другим вопросом: «почему не применить поиск в ширину для нашего графа?». Известно, что метод BFS находит оптимальный путь от произвольной вершины в ориентированном графе до любой другой вершины, но это справедливо только для рёбер с единичным весом.

Свести задачу к решаемой BFS можно, но если заменить все рёбра неединичной длины рёбрами длины , то граф очень разрастётся, и это приведёт к огромному числу действий при вычислении оптимального маршрута.

Чтобы этого избежать предлагается использовать алгоритм Дейкстры. Опишем его:

Инициализация:

Основный цикл алгоритма:

• Пока все вершины не исследованы (или формально ), повторяем:

В итоге исполнения этого алгоритма, массив будет содержать все оптимальные пути, исходящие из .

Примеры работы

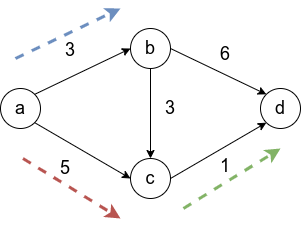
Рассмотрим граф выше, в нём будем искать пути от до всего остального.

Первый шаг алгоритма определит, что кратчайший путь до проходит по направлению синей стрелки и зафиксирует кратчайший путь. Второй шаг рассмотрит, все возможные варианты и окажется, что оптимальный вариант двигаться вдоль красной стрелки, поскольку меньше, чем и Добавляется длина кратчайшего пути до . И наконец, третьим шагом, когда три вершины уже лежат в , остается рассмотреть только два ребра и выбрать, лежащее вдоль зеленой стрелки.

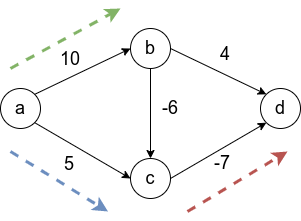
Теперь рассмотрим граф с отрицательными весами, упомянутый выше. Напомню, алгоритм Дейкстры на таком графе может работать некорректно.

Первым шагом отбирается ребро вдоль синей стрелки, поскольку это ребро наименьшего веса из исходной вершины. Затем выбирается ребро Это зафиксирует навсегда неверный путь от к , в то время как оптимальный путь проходит через центр с отрицательным весом. Последним шагом, будет добавлена вершина .

Оценка сложности алгоритма

К этому моменту мы разобрали сам алгоритм, ограничения, накладываемые на его работу и ряд примеров его применения. Давайте упомянем какова вычислительная сложность этого алгоритма, поскольку это пригодится нам для решения задач, ради которых затевалась эта статья.
Базовый подход, основанный на циклах, предполагает проход по всем рёбрам каждого узла, что приводит к сложности .

Эффективная реализация предполагает использование кучи. Об этой структуре данных можно сказать коротко: она позволяет выполнять две операции за логарифмическое время. Первая операция — получение узла в дереве, с наименьшим ключом, и, вторая операция, вставка нового узла в дерево с новым ключом.

Что еще можно сказать о куче:

• это сбалансированное бинарное дерево,
• ключ текущего узла всегда меньше, либо равен ключей дочерних узлов.

Интересную задачу с использованием куч я разбирал ранее в этом посте.

Используя кучу в алгоритме Дейкстры, где в качестве ключей используются расстояния от вершины в неисследованной части графа (в алгоритме это ), до ближайшей вершины в уже покрытом (это множество вершин ), можно сократить вычислительную сложность до Доказательство справедливости этих оценок я оставляю за пределами этой статьи.

Далее перейдём к разбору задач!

Задача №1

Будем называть узким местом пути в графе ребро максимальной длины в этом пути. Путём с минимальным узким местом назовём такой путь между вершинами и , что не существует другого пути , чьё узкое место меньше по длине. Требуется построить алгоритм, который вычисляет путь с минимальным узким местом для двух данных вершин в графе. Асимптотическая сложность такого алгоритма должна быть

Решение

По условию задачи ребро с большим весом трактуется как узкое место. Вес в этом случае можно воспринимать как цену за проход по ребру. В результате решения задачи хотелось бы получить алгоритм, способный строить маршруты между узлами так, чтобы, если мы захотим провести любой другой путь, он будет содержать более тяжелые рёбра.

В случае классической задачи, поиска пути минимальной длины между двумя вершинами графа, мы поддерживаем в каждой посещенной алгоритмом вершине графа минимальную длину пути до этой вершины. Здесь стоит оговориться, что будем именовать множество посещенными вершинами, а часть графа, для которой еще нужно найти величину пути или узкого места.

В отличии от классического алгоритма, решение этой задачи должно поддерживать величину актуального узкого места пути, приводящего в вершину . А при добавлении новой вершины из , мы должны смотреть не увеличивает ли ребро величину узкого места пути, которое теперь приводит в .
Если ребро увеличивает узкое место, то лучше рассмотреть вершину , ребро до которой легче . Поиск неувеличивающих узкое место ребёр нужно осуществлять не только среди соседей определенного узла , но и среди всех , поскольку отдавая предпочтение вершине, путь в которую имеет наименьшее узкое место в данный момент, мы гарантируем, что мы не ухудшаем ситуацию для других вершин.

Последнее можно проиллюстрировать примером: если путь, оканчивающийся в вершине имеет узкое место величины , и есть вершина с ребром веса , и с ребром веса , то предпочтение отдаётся , алгоритм даст верный результат в обоих случая, если существует веса или веса .

В результате разбора выше, предлагается руководствоваться следующей формулой при выборе очередной вершины из непосещенных и обновлении величин, которые мы поддерживаем.

Стоит пояснить, что поиск по осуществляется, только для существующих связей а это вес ребра .

Задача №2

Предлагается решить более практическую задачу. Пусть городов, между ними существуют пути, заданные массивом edges[i] = [city_a, city_b, distance_ab], а также дано целое число mileage.

Требуется найти такой город из данных, из которого можно добраться до наименьшего числа городов не превысив mileage.

Стоит отметить, что граф неориентированый, т.е. по пути между городами можно двигаться в обе стороны, а длина пути между городами a и c может быть получена как сумма длин путей a -> b и b -> c, если есть маршрут a -> b -> c

Решение

С решением данной проблемы нам поможет алгоритм Дейкстры и описанная выше реализация с помощью кучи. Поставщиком этой структуры данных станет библиотека heapq в Python.

Будем использовать алгоритм Дейкстры для того, чтобы подсчитать количество соседних городов, расстояние до которых меньше mileage, для каждого из городов. Соберем количества соседей в в одном месте и найдем минимум из них.

Поскольку наш граф неориентированный, то из любой его вершины можно добраться до произвольной вершины . Будем использовать алгоритм Дейкстры для того, чтобы для каждого из городов в графе построить кратчайшие пути до всех остальных городов, мы это уже умеем делать в теории. И чтобы, оптимизировать этот процесс, будем в его течении сразу отвергать пути, которые превышают mileage, а не делать постфактум, когда все пути получены.

Давайте опишем функцию решения:

def least_reachable_city(n, edges, mileage):
        """
        входные параметры:
            n --- количество городов,
            edges --- тройки (a, b, distance_ab),
            mileage --- максимально допустимое расстояние между городами 
            для соседства
        """
        # заполняем список смежности (adjacency list), в нашем случае это 
        # словарь, в котором ключи это города, а значения --- пары 
        # (<другой_город>, <расстояние_до_него>)

        graph = {}
        for u, v, w in edges:
            if graph.get(u, None) is None:
                graph[u] = [(v, w)]
            else:
                graph[u].append((v, w))
            if graph.get(v, None) is None:
                graph[v] = [(u, w)]
            else:
                graph[v].append((u, w))
        
        # локально объявим функцию, которая будет считать кратчайшие пути в 
        # графе от вершины, до всех вершин, удовлетворяющих условию
        def num_reachable_neighbors(city):
            # создаем кучу, из одного элемента с парой, задающей нулевую 
            # длину пути до самого исходного города
            heap = [(0, city)]
            # и массив, содержащий города и кратчайшие 
            # расстояния до них от исходного
            distances = {}
            # затем, пока куча не пуста, извлекаем ближайший 
            # от посещенных городов город
            while heap:
                currDist, neighb = heapq.heappop(heap)
                # если кратчайшее ребро ведет к городу, где мы уже знаем 
                # оптимальный маршрут, то завершаем итерацию
                if neighb in distances:
                    continue
                # в остальных случаях, и если сосед не является отправным 
                # городом, мы добавляем новую запись в массив кратчайших расстояний
                if neighb != city:    
                    distances[neighb] = currDist
                # обрабатываем всех смежных городов с соседом, добавляя их в кучу 
                # но только если: а) до них еще не известен кратчайший маршрут и б) путь до них через neighb не выходит за пределы mileage
                for node, d in graph[neighb]:
                    if node in distances:
                        continue
                    if currDist + d <= mileage:
                        heapq.heappush(heap, (currDist + d, node))
            # возвращаем количество городов, прошедших проверку
            return len(distances)
        
        # выполним поиск соседей для каждого из городов
        cities_neighbors = {num_reachable_neighbors(city): city for city in range(n)}
        # вернём номер города, у которого наименьшее число соседей
        # в пределах досигаемости
        return cities_neighbors[min(cities_neighbors)]

В функции выше, в комментариях, подробно описывается, как метод Дейкстры, реализованный на куче позволяет найти расстояния до всех городов, в пределах `mileage`. Основную сложность для понимания предстваляет цикл, работающий с кучей.

Заключение

Алгоритм Дейкстры это мощный инструмент в мире работы с графами, область применения его крайне широка. С его помощью можно оценить даже целесообразность добавления новой ветки метро, новой дороги или маршрута в компьютерной сети. Он прост в исполнении и интуитивно понятен, как другие жадные (greedy) алгоритмы. Вычислительная сложность решений задач с его помощью зачастую не выше . При некоторых условиях может достигать линейной сложности (существует алгоритм линейной сложности, решающий первую задачу, при условии, что граф неориентированный).

Стоит еще раз отметить, что алгоритм не работает, когда в графе существуют отрицательные веса. Для этого существует подход динамического программирования — алгоритм Беллмана – Форда, что может послужить темой другой статьи. Несмотря на это, алгоритм Дейкстры является представителем идеального баланса простоты и мощи, для решения прикладных задач.

Статья подготовлена в преддверии старта курса «Алгоритмы для разработчиков». Узнать о курсе подробнее, а также зарегистрироваться на бесплатный демоурок можно по ссылке.

Информация

[1] Условия задач взяты из книги «Algorithms Illuminated: Part 2: Graph Algorithms and Data Structures» от Tim Roughgarden,
[2] и с сайта leetcode.com.
[3] Решения авторские.