Как найти количество ребер в неориентированном графе - Исправление недочетов и поиск решений вместе с Examum.ru

Improve Article

Save Article

Like Article

Read

Discuss

Improve Article

Save Article

Like Article

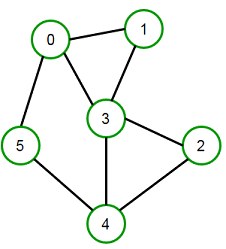
Given an adjacency list representation undirected graph. Write a function to count the number of edges in the undirected graph. Expected time complexity : O(V) Examples:

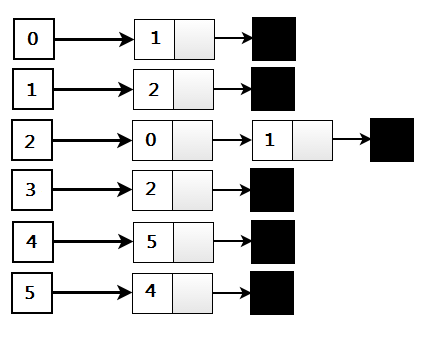
Input : Adjacency list representation of
        below graph.  
Output : 9

Recommended: Please try your approach on {IDE} first, before moving on to the solution.

Idea is based on Handshaking Lemma. Handshaking lemma is about undirected graph. In every finite undirected graph number of vertices with odd degree is always even. The handshaking lemma is a consequence of the degree sum formula (also sometimes called the handshaking lemma)

So we traverse all vertices, compute sum of sizes of their adjacency lists, and finally returns sum/2. Below implementation of above idea

C++

#include<bits/stdc++.h>

using namespace std;

class Graph

{

int V ;

list < int > *adj;

public :

Graph( int V )

{

this->V = V ;

adj = new list<int>[V];

}

void addEdge ( int u, int v ) ;

int countEdges () ;

};

void Graph :: addEdge ( int u, int v )

{

adj[u].push_back(v);

adj[v].push_back(u);

}

int Graph :: countEdges()

{

int sum = 0;

for (int i = 0 ; i < V ; i++)

sum += adj[i].size();

return sum/2;

}

int main()

{

int V = 9 ;

Graph g(V);

g.addEdge(0, 1 );

g.addEdge(0, 7 );

g.addEdge(1, 2 );

g.addEdge(1, 7 );

g.addEdge(2, 3 );

g.addEdge(2, 8 );

g.addEdge(2, 5 );

g.addEdge(3, 4 );

g.addEdge(3, 5 );

g.addEdge(4, 5 );

g.addEdge(5, 6 );

g.addEdge(6, 7 );

g.addEdge(6, 8 );

g.addEdge(7, 8 );

cout << g.countEdges() << endl;

return 0;

}

Java

import java.io.*;

import java.util.*;

class Graph

{

int V;

Vector<Integer>[] adj;

Graph(int V)

{

this.V = V;

this.adj = new Vector[V];

for (int i = 0; i < V; i++)

adj[i] = new Vector<Integer>();

}

void addEdge(int u, int v)

{

adj[u].add(v);

adj[v].add(u);

}

int countEdges()

{

int sum = 0;

for (int i = 0; i < V; i++)

sum += adj[i].size();

return sum / 2;

}

class GFG

{

public static void main(String[] args) throws IOException

{

int V = 9;

Graph g = new Graph(V);

g.addEdge(0, 1);

g.addEdge(0, 7);

g.addEdge(1, 2);

g.addEdge(1, 7);

g.addEdge(2, 3);

g.addEdge(2, 8);

g.addEdge(2, 5);

g.addEdge(3, 4);

g.addEdge(3, 5);

g.addEdge(4, 5);

g.addEdge(5, 6);

g.addEdge(6, 7);

g.addEdge(6, 8);

g.addEdge(7, 8);

System.out.println(g.countEdges());

}

Python3

class Graph:

def __init__(self, V):

self.V = V

self.adj = [[] for i in range(V)]

def addEdge (self, u, v ):

self.adj[u].append(v)

self.adj[v].append(u)

def countEdges(self):

Sum = 0

for i in range(self.V):

Sum += len(self.adj[i])

return Sum // 2

if __name__ == '__main__':

V = 9

g = Graph(V)

g.addEdge(0, 1 )

g.addEdge(0, 7 )

g.addEdge(1, 2 )

g.addEdge(1, 7 )

g.addEdge(2, 3 )

g.addEdge(2, 8 )

g.addEdge(2, 5 )

g.addEdge(3, 4 )

g.addEdge(3, 5 )

g.addEdge(4, 5 )

g.addEdge(5, 6 )

g.addEdge(6, 7 )

g.addEdge(6, 8 )

g.addEdge(7, 8 )

print(g.countEdges())

C#

using System;

using System.Collections.Generic;

class Graph

{

public int V;

public List<int>[] adj;

public Graph(int V)

{

this.V = V;

this.adj = new List<int>[V];

for (int i = 0; i < V; i++)

adj[i] = new List<int>();

}

public void addEdge(int u, int v)

{

adj[u].Add(v);

adj[v].Add(u);

}

public int countEdges()

{

int sum = 0;

for (int i = 0; i < V; i++)

sum += adj[i].Count;

return sum / 2;

}

class GFG

{

public static void Main(String[] args)

{

int V = 9;

Graph g = new Graph(V);

g.addEdge(0, 1);

g.addEdge(0, 7);

g.addEdge(1, 2);

g.addEdge(1, 7);

g.addEdge(2, 3);

g.addEdge(2, 8);

g.addEdge(2, 5);

g.addEdge(3, 4);

g.addEdge(3, 5);

g.addEdge(4, 5);

g.addEdge(5, 6);

g.addEdge(6, 7);

g.addEdge(6, 8);

g.addEdge(7, 8);

Console.WriteLine(g.countEdges());

}

Javascript

class Graph {

constructor(V) {

this.V = V;

this.adj = new Array(V);

for (let i = 0; i < V; i++) {

this.adj[i] = [];

}

addEdge(u, v) {

this.adj[u].push(v);

this.adj[v].push(u);

}

countEdges() {

let sum = 0;

for (let i = 0; i < this.V; i++) {

sum += this.adj[i].length;

}

return sum / 2;

}

function main() {

let V = 9;

let g = new Graph(V);

g.addEdge(0, 1);

g.addEdge(0, 7);

g.addEdge(1, 2);

g.addEdge(1, 7);

g.addEdge(2, 3);

g.addEdge(2, 8);

g.addEdge(2, 5);

g.addEdge(3, 4);

g.addEdge(3, 5);

g.addEdge(4, 5);

g.addEdge(5, 6);

g.addEdge(6, 7);

g.addEdge(6, 8);

g.addEdge(7, 8);

console.log(g.countEdges());

}

main();

Output:

Time Complexity: O(V) This article is contributed by Nishant Singh. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.

Last Updated :
06 Feb, 2023

Like Article

Save Article

Источник

Все, что познается, имеет число, ибо невозможно ни понять ничего, ни познать без него – Пифагор

В этой статье:

Матрица смежности

Матрица инцидентности

Список смежности (инцидентности)

Взвешенный граф (коротко)

Итак, мы умеем задавать граф графическим способом. Но есть еще два способа как можно задавать граф, а точнее представлять его. Для экономии памяти в компьютере граф можно представлять с помощью матриц или с помощью списков.

Матрица является удобной для представления плотных графов, в которых число ребер близко к максимально возможному числу ребер (у полного графа).

Другой способ называется списком. Данный способ больше подходит для более разреженных графов, в котором число ребер намного меньше максимально возможного числа ребер (у полного графа).

Перед чтением материала рекомендуется ознакомится с предыдущей статьей, о смежности и инцидентности, где данные определения подробно разбираются.

Матрица смежности

Но тем кто знает, но чуть забыл, что такое смежность есть краткое определение.

Смежность – понятие, используемое только в отношении двух ребер или в отношении двух вершин: два ребра инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными.

Матрица (назовем ее L) состоит из n строк и n столбцов и поэтому занимает n^2 места.

Каждая ячейка матрицы равна либо 1, либо 0;

Ячейка в позиции L (i, j) равна 1 тогда и только тогда, когда существует ребро (E) между вершинами (V) i и j. Если у нас положение (j, i), то мы также сможем использовать данное правило. Из этого следует, что число единиц в матрице равно удвоенному числу ребер в графе. (если граф неориентированный). Если ребра между вершинами i и j не существует, то ставится 0.

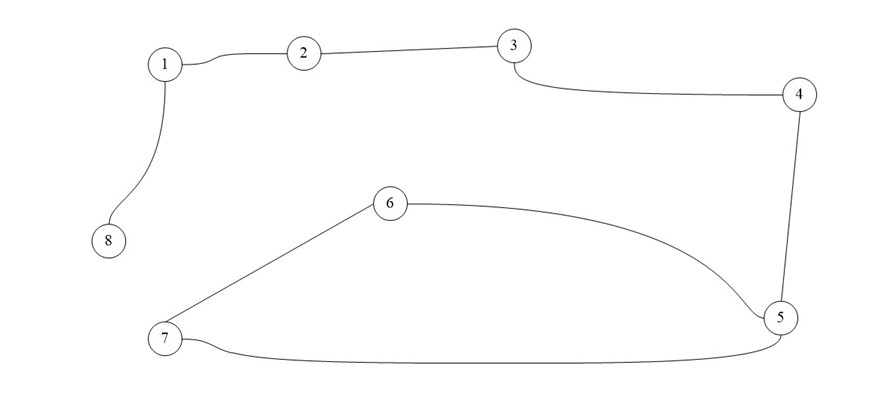
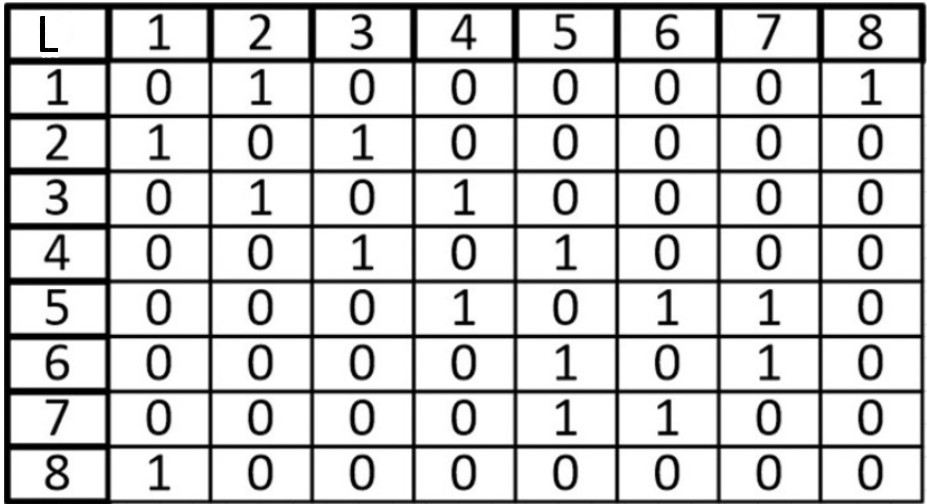
Для практического примера возьмем самый обыкновенный неориентированный граф:

А теперь представим его в виде матрицы:

Ячейки, расположенные на главной диагонали всегда равны нулю, потому что ни у одной вершины нет ребра, которое и начинается, и заканчивается в ней только если мы не используем петли. То есть наша матрица симметрична относительно главной диагонали. Благодаря этому мы можем уменьшить объем памяти, который нам нужен для хранения.

С одной стороны объем памяти будет:

Но используя вышеописанный подход получается:

Потому что нижнюю часть матрицы мы можем создать из верхней половины матрицы. Только при условии того, что у нас главная диагональ должна быть пустой, потому что при наличии петель данное правило не работает.

Если граф неориентированный, то, когда мы просуммируем строку или столбец мы узнаем степень рассматриваемой нами вершины.

Если мы используем ориентированный граф, то кое-что меняется.

Здесь отсутствует дублирование между вершинами, так как если вершина 1 соединена с вершиной 2, наоборот соединена она не может быть, так у нас есть направление у ребра.

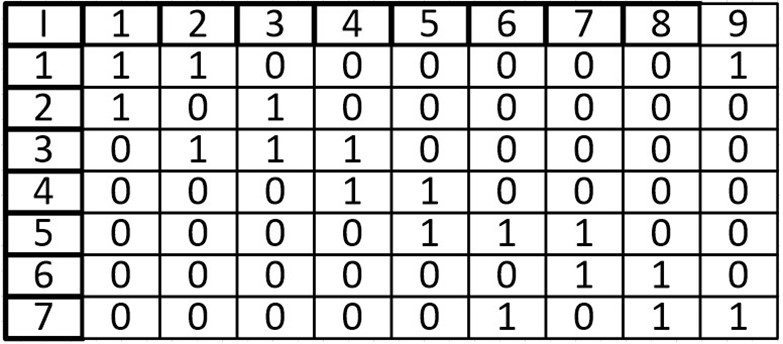
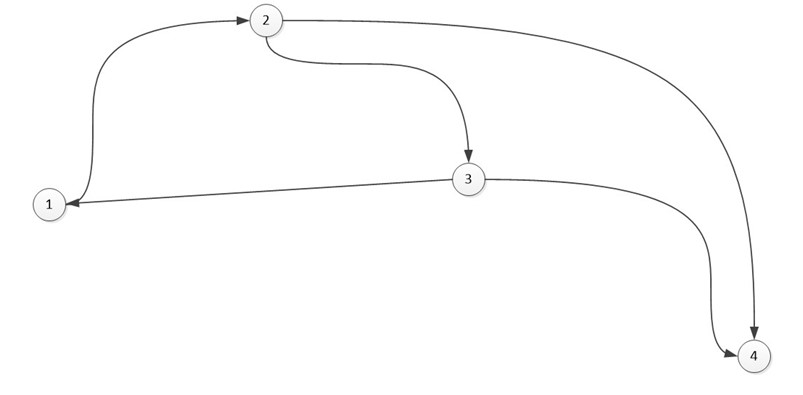
Возьмем в этот раз ориентированный граф и сделаем матрицу смежности для него:

В виде матрицы:

Если мы работаем со строкой матрицы, то мы имеем элемент из которого выходит ребро, в нашем случаи вершина 1 входит в вершину 2 и 8. Когда мы работаем со столбцом то мы рассматриваем те ребра, которые входят в данную вершину. В вершину 1 ничего не входит, значит матрица верна.

Объем памяти:

Если бы на главной диагонали была бы 1, то есть в графе присутствовала петля, то мы бы работали уже не с простым графом, с каким мы работали до сих пор.

Используя петли мы должны запомнить, что в неориентированном графе петля учитывается дважды, а в ориентированном — единожды.

Матрица инцидентности

Инцидентность – понятие, используемое только в отношении ребра и вершины: две вершины (или два ребра) инцидентными быть не могут.

Матрица (назовем ее I) состоит из n строк которое равно числу вершин графа, и m столбцов, которое равно числу ребер. Таким образом полная матрица имеет размерность n x m. То есть она может быть, как квадратной, так и отличной от нее.

Ячейка в позиции I (i, j) равна 1 тогда, когда вершина инцидентна ребру иначе мы записываем в ячейку 0, такой вариант представления верен для неориентированного графа.

Сразу же иллюстрируем данное правило:

В виде матрицы:

Сумма элементов i-ой строки равна степени вершины.

При ориентированным графе, ячейка I (i, j) равна 1, если вершина V (i) начало дуги E(j) и ячейка I (i, j) равна -1 если вершина V (i) конец дуги E (j), иначе ставится 0.

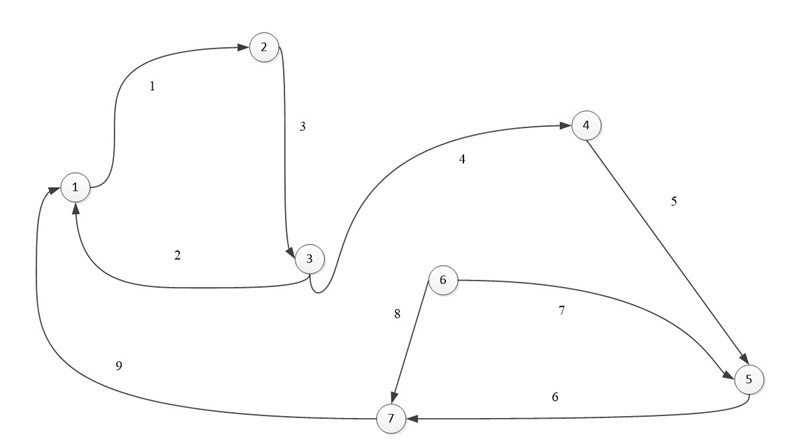
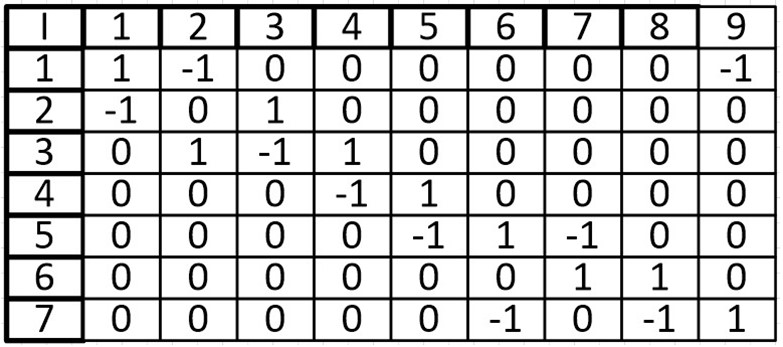
Ориентированный граф:

В виде матрицы:

Одной из особенностей данной матрицы является то, что в столбце может быть только две ненулевых ячейки. Так как у ребра два конца.

При суммировании строки, ячейки со значением -1, могут складываться только с ячейками, также имеющими значение -1, то же касается и 1, мы можем узнать степень входа и степень выхода из вершины. Допустим при сложении первой вершины, мы узнаем, что из нее исходит 1 ребро и входят два других ребра. Это является еще одной особенностью (при том очень удобной) данной матрицы.

Объем памяти:

Список смежности (инцидентности)

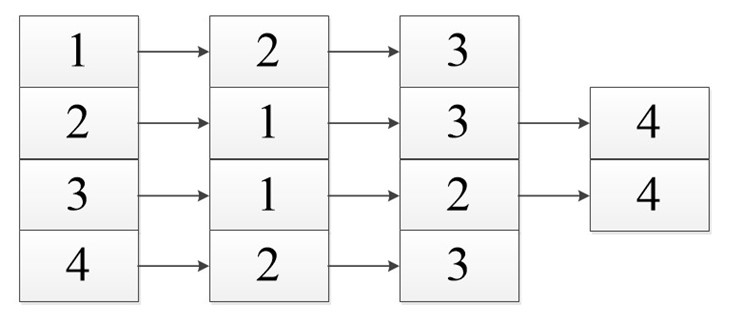
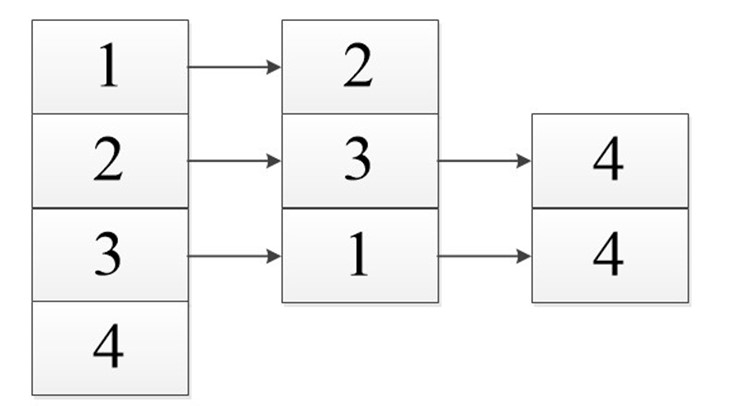
Список смежности подразумевает под собой, то что мы работаем с некоторым списком (массивом). В нем указаны вершины нашего графа. И каждый из них имеет ссылку на смежные с ним вершины.

В виде списка это будет выглядеть так:

Неважно в каком порядке вы расположите ссылку так как вы рассматриваете смежность относительно первой ячейки, все остальные ссылки указывают лишь на связь с ней, а не между собой.

Так как здесь рассматривается смежность, то здесь не обойдется без дублирования вершин. Поэтому сумма длин всех списков считается как:

Объем памяти:

Когда мы работаем с ориентированным графом, то замечаем, что объем задействованной памяти будет меньше, чем при неориентированном (из-за отсутствия дублирования).

В виде списка:

Сумма длин всех списков:

Объем памяти:

Со списком инцидентности все просто. Вместо вершин в список (массив) вы вставляете рёбра и потом делаете ссылки на те вершины, с которыми он связан.

К недостатку списка смежности (инцидентности) относится то что сложно определить наличие конкретного ребра (требуется поиск по списку). А если у вас большой список, то удачи вам и творческих успехов! Поэтому, чтобы работать максимальной отдачей в графе должно быть мало рёбер.

Взвешенность графа

Взвешенный граф — это граф, в котором вместо 1 обозначающее наличие связи между вершинами или связи между вершиной и ребром, хранится вес ребра, то есть определённое число с которым мы будем проводить различные действия.

К примеру, возьмем граф с весами на ребрах:

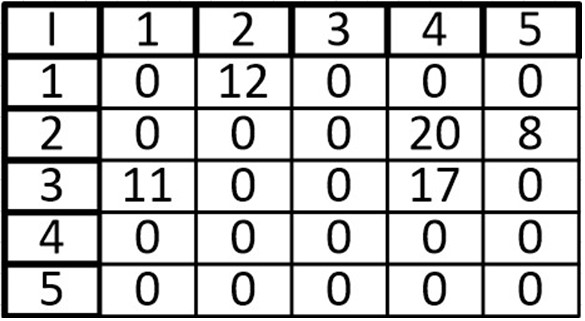
И сделаем матрицу смежности:

В ячейках просто указываем веса ребра, а в местах где отсутствует связь пишем 0 или -∞.

Более подробно данное определение будет рассмотрено при нахождении поиска кратчайшего пути в графе.

Итак, мы завершили разбор представления графа с помощью матрицы смежности и инцидентности и списка смежности (инцидентности). Это самые известные способы представления графа. В дальнейшем мы будем рассматривать и другие матрицы, и списки, которые в свою очередь будут удобны для представления графа с определёнными особенностями.

Если заметили ошибку или есть предложения пишите в комментарии.

Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.

На каком языке программирования проводить операции с графами

21.28%
Использовать оба
10

Проголосовали 47 пользователей.

Воздержались 8 пользователей.

Источник

2 / 2 / 0

Регистрация: 15.11.2015

Сообщений: 12

Подсчет количества ребер неориентированного графа

25.11.2015, 17:44. Показов 10357. Ответов 1

Простой неориентированный граф задан матрицей смежности. Найдите количество ребер в графе.

На вход программы поступает число n ( из отрезка [0;100]) – количество вершин в графе, а затем n строк по n чисел, каждое из которых равно 0 или 1, – его матрица смежности.

Выведите одно число – количество ребер заданного графа.

Jabbson

5889 / 3347 / 1033

Регистрация: 03.11.2009

Сообщений: 9,974

25.11.2015, 18:32

Сообщение было отмечено Olya652 как решение

Решение

Python

1
2
3

m = (map(int, input().split()) for _ in range(int(input('Num of nodes: '))))
a = {frozenset([ci+1, ni+1]) for ni, ne in enumerate(m) for ci, ce in enumerate(ne) if ce == 1}
print('Num of edges:', len(a))

Название: graph.png
Просмотров: 180

Размер: 2.0 Кб

Код

Num of nodes: 6
1 1 0 0 1 0
1 0 1 0 1 0
0 1 0 1 0 0
0 0 1 0 1 1
1 1 0 1 0 0
0 0 0 1 0 0
Num of edges: 8

Источник

Теория графов представляет собой раздел математики, имеющий широкое
практическое применение во многих
областях человеческой деятельности. Математика, физика, химия, теория связи,
электротехника, архитектура, исследование операций, генетика, психология – вот
далеко не полный список областей ее применения
Теория графов становится одной из существенных частей
математического аппарата кибернетики, языком дискретной математики.

Граф G задается с помощью пары множеств G = (V, R), где V есть множество вершин,
а R –
множество линий, соединяющих пары вершин. Линии со стрелками называются дугами, без стрелок – ребрами. Обычно граф представляют с помощью
схемы, на которой некоторые вершины соединены ребрами (дугами).

Вершинами могут служить объекты любой природы: будь то
населенные пункты, компьютерные сети, элементы блок- схем алгоритмов. Под
ребром могут подразумеваться дороги между соседними городами, линии связи между
компьютерами.

Вершины называются смежными, если их соединяет ребро.
Например, на рис. смежны вершины V₁ и V₂

, так как их соединяет ребро R₁₂

Множество V,
R являются конечными –
мы можем перечислить все вершины и ребра
графа. Количество вершин и количество ребер графа определяют мощности множеств V и R. Так, количество вершин графа G ровно 5, а количество ребер
равно 8.

Ребро и любая из его двух вершин называются инцидентными.
Под степенью вершин подразумевается количество инцидентных ей ребер. Так,
степень вершин V₁ равно 3, а степень вершин V₅

равна 4.

Последовательность чередующихся ребер и вершин графа называется маршрутом.
В графах можно выделить различные
маршруты. Маршрут называется замкнутым, если вершины начала и конца маршрута
совпадают. Если ребра и вершины, образующие маршрут различны, то такой маршрут
называется цепью. Путь в ориентированном графе — это
последовательность дуг, в которой конечная вершина всякой дуги, отличной от
последней, является начальной вершиной следующей.

Длина маршрута равна количеству ребер, входящих в него.

Граф называется связным, если любые две его вершины
можно соединить маршрутом (или путем).

Ориентированные
графы.

Граф, в котором направление линий принципиально называется ориентированным
(орграф). В орграфе каждое ребро имеет одно направление. Такие ребра называются
дугами. Для орграфа вводятся такие понятия, как входящая и исходящая
степени вершины. Это соответственно число входящих в вершину дуг и число исходящих из
нее дуг.

Взвешенные графы.

Взвешенный граф – это граф, в котором с
вершинами и линиями связана некоторая дополнительная информация. Эта информация
называется весом вершины или линии. Вес позволяет отобразить на графе не
только структуру системы, но и различные свойства компонент или связей,
количественная характеристика. Вес сети равен сумме весов ее ребер.

Полный граф
Граф называется полным, если каждые две различные вершины его соединены одним и только одним ребром. В полном графе каждая его вершина принадлежит одному и тому же числу ребер. Для задания полного графа достаточно знать число его вершин. Полный граф с n
вершинами обычно обозначается через K_n.

Граф, не являющийся полным, можно преобразовать в полный с теми же вершинами, добавив недостающие ребра. Вершины графа G и ребра, которые добавлены, тоже образуют граф. Такой граф называют дополнением графа и обозначают его G .

Двудольный граф

Допустим, что множество вершин графа можно разбить на два
непересекающихся подмножества V₁и V₂

, так,
что каждое ребро в G соединяет
какую-нибудь вершину из V₁ с какой-либо
вершиной из V₂ , тогда G называем двудольным
графом. Такие графы иногда обозначают G(V₁, V₂

) , если хотят выделить два указанных
подмножества. Двудольный граф можно определить и по-другому: в терминах
раскраски его вершин двумя цветами, скажем, красным и синим. При этом граф
называется двудольным, если каждую его вершину можно окрасить красным или синим
цветом так, чтобы любое ребро имело один конец красный, а другой — синий.
Следует подчеркнуть, что в двудольном графе совсем не обязательно каждая
вершина из V₁ соединена с каждой вершиной
из V₂

; если же это так и если при этом граф G простой, то он называется полным двудольным графом и обычно обозначается K_m,n

, где m, n
— число вершин соответственно
в V₁ и V₂ .

Заметим, что граф K_m,n имеет ровно m + n вершин и m*n ребер.

Плоский граф

Плоским графом называется граф, изображенный на плоскости
так, что никакие два его ребра (или, вернее, представляющие их кривые)
геометрически не пересекаются нигде, кроме инцидентной им обоим вершины. Граф,
изоморфный плоскому графу, называется
планарным. Планарный граф можно определить еще так: граф
планарен, если его можно уложить на плоскости. Рисунок графа, в котором никакие
два его ребра не пересекаются, если не считать точками пересечения общие
вершины, называют плоским представлением графа. Ясно, что плоское
представление имеет только плоский граф. Обратно, у всякого плоского графа
непременно найдется плоское представление. Плоские графы — это простые циклы,
деревья, лес, а также граф, содержащий цикл, из вершин которого
«выходят» деревья.

Примером неплоского графа
может служить полный граф с пятью вершинами. Любые попытки начертить его
плоское представление обернутся неудачей.

В качестве характеристики плоского
представления графа вводится понятие грани. Гранью в плоском представлении
графа G называется
часть плоскости, ограниченная простым циклом и не содержащая внутри других
циклов.

На рисунке показано плоское
представление графа G с тремя гранями: (1, 5,4,1), (1, 3, 2,4,1), (1,2,3,1). Часть плоскости, ограниченная простым циклом (1,2,4,1), гранью не является, так как содержит
цикл (1, 2, 3,1). Простой цикл,
ограничивающий грань, называется границей грани. Две грани будем называть
соседними, если их границы имеют хотя бы одно общее ребро.

В данном графе часть плоскости,
ограниченная простым циклом (1,2,3,4,1), является
гранью, так как ребро (4,5), расположенное
внутри грани, не образует цикла.

Не является гранью заштрихованная
часть плоскости в данном примере, так как она содержит цикл, да к тому же эта
часть плоскости не ограничена циклом. Ребро (1,2) является
мостом, соединяющим циклы. Такие мосты называются перегородками.

В качестве грани можно
рассматривать и часть плоскости, расположенную «вне» плоского
представления графа. Она ограничена «изнутри» простым циклом и не
содержит других циклов. Эту часть плоскости называют бесконечной гранью.

На рисунке часть бесконечной грани
заштрихована. Всякое плоское представление графа либо не имеет бесконечной
грани, либо имеет в точности одну бесконечную грань. Как особый случай вводится
бесконечная грань в плоском представлении дерева и леса. В плоском
представлении дерева и леса за грань принимают всю плоскость рисунка.

Два графа гомеоморфны (или
тождественны с точностью до вершин степени 2), если они оба могут быть получены
из одного и того же графа «включением» в его ребра новых вершин
степени 2.

Изображенные графы гомеомофны, и то же самое можно
сказать о любых двух циклических графах.

Гомеоморфность графов является отношением эквивалентности. Ясно, что введение термина
«гомеоморфны» удобно только с технической точки зрения — включение
или удаление вершин степени 2 не имеет никакого отношения к планарности.
Добавление (включение) одной вершины, скажем V_,
в какое-нибудь ребро, например е, осуществляется
следующим образом: пусть ребро е инцидентно
вершинам w и х
. Тогда ребро е удаляется из графа,
но добавляются два новых ребра: е₁инцидентное
вершинам V и w, и е₂,
инцидентное вершинам V и x.

Введение понятия гомеоморфности графов позволяет установить следующий важный результат, известный как теорема Куратовского (точнее, как теорема Понтрягина-Куратовского, так как Л.С.Понтрягин доказал, но не опубликовал, эту теорему еще в 1927 году), которая дает необходимое и достаточное условие планарности графа.

Гомеоморфные графы

Теорема (Куратовский, 1930) Граф
планарен тогда и только тогда, если не содержит подграфов, гомеоморфных К₅или Кз,з.

Поскольку доказательство теоремы Куратовского
довольно длинное и сложное, здесь оно не приводится (см. Ф.Харари. Теория
графов. М.: «Мир». 1973). Тем не менее, воспользуемся теоремой
Куратовского для получения другого критерия планарности. Рассмотрим еще два
определения.

Элементарным
стягиванием называется такая процедура: берем ребро е (вместе с
инцидентными ему вершинами, например, V и W) и»стягиваем»
его, то есть удаляем е и отождествляем V и
W. Полученная при этом вершина инцидентна тем ребрам (отличным от
е ), которым первоначально были инцидентны V или W.

Граф G называется стягиваемым к графу Н,
если Н можно получить из G с помощью
некоторой последовательности элементарных стягиваний.

Граф планарен тогда и
только тогда, если он не содержит подграфов, стягиваемых в К₅или к К_з.з.

Формула Эйлера

Для всякого
плоского представления связного плоского графа без перегородок число вершин (V), число ребер (Е)
и число граней с учетом бесконечной (R) связаны
соотношением V –Е + R = 2.

Пусть граф G — связный, плоский граф без перегородок. Определим
значение алгебраической суммы V –Е + R для его произвольного плоского представления.

Преобразуем данный
граф в дерево, содержащее все его вершины. Для этого удалим некоторые ребра
графа G, разрывая поочередно все его
простые циклы, причем так, чтобы граф оставался связным и без перегородок.

Заметим, что при
таком удалении одного ребра число граней уменьшается на 1, так как при этом либо пропадет один простой цикл, либо два
простых цикла преобразуются в один. Следовательно, значение разности Е — R при этом остается неизменным.

На рисунке ребра,
которые мы удаляем, изображены кривыми. В полученном дереве обозначим число
вершин — V_d , число
ребер — E_d, число граней — R_d . Справедливо
равенство Е
— R
= E_d — R_d.

В дереве одна грань, то есть Е — R = E_d
— 1. Операция
удаления ребер из графа не меняет число его вершин, то есть V = V_d. По теореме в дереве V_d
— E_d = 1. Отсюда V — E_d = 1, то есть E_d
= V — 1, а потому Е-R = V — 2 или V — Е + R = 2.

Итак, доказано, что если в плоском
представлении связного графа без перегородок V вершин, Е ребер
и R граней,
то V — Е + R = 2. Полученная формула называется
формулой Эйлера.

Триангулированный граф

Рассмотрим плоский граф G с пятью вершинами.

Если добавить к нему ребра (1, 3) и (1,5) и, то полученный новый граф G тоже будет плоским.

К этому графу не удается добавить ни
одного ребра так, чтобы новый граф тоже был плоским.

Плоский граф называется максимально
плоским, если невозможно добавить к нему ни одного ребра так, чтобы полученный
граф был плоским. Изображенный граф является максимально плоским.

Каждая грань в плоском представлении
максимально плоского графа имеет 3 вершины. Поэтому максимально плоский граф
называют триангулированным. Операция
добавления новых ребер, в результате которой в плоском представлении каждая
грань имеет ровно 3 вершины, называется триангуляцией
графа.

Подграфы и деревья.

Подграфом графа G называется граф, у которого все вершины принадлежат
графу G.

Остовной связный подграф – это подграф графа G, который содержит все его вершины и
каждая его вершина достижима из любой другой.

Дерево — это граф, в котором нет циклов, то
есть граф, в котором нельзя из некоторой вершины пройти по нескольким различным
ребрам и вернуться в ту же вершину. Остовным связным деревом называется
подграф, включающий все вершины исходного графа G, каждая вершина которого достижима из
любой другой, и притом не содержащий циклов.

Преобразование графа
в остовное связное дерево минимального веса.

Пусть G = (V, R) – связный взвешенный неориентированный граф, где V — множество вершин, а R – множество
ребер. Ребра графа не ориентированы, то
есть ребра R_nkи R_knсчитаются одним и тем же ребром, поэтому в матрице
смежности не учитываются дублирующие друг друга ребра. В результате граф G можно представить с помощью матрицы
смежности, содержащей значения весов десяти ребер.

Введем понятие цикломатического числа y, показывающего, сколько ребер графа нужно удалить, чтобы в нем не
осталось ни одного цикла. Цикломатическое число y равно увеличенной на
единицу разности между количеством ребер и количеством вершин графа:

y = m – n +1, где m – количество ребер, n — количество
вершин.

Для каждого графа обычно существует несколько осотвных
связных деревьев, которые обладают различными весами.

Для построения остовного связного дерева минимального веса
используют алгоритм Крускала:

Первоначально
из графа удаляются все ребра, получается остовной подграф, где все вершины
изолированы. Каждая вершина такого графа помещается в одноэлементное
подмножество.
Ребра
сортируются по возрастанию весов.
Ребра
последовательно, по возрастанию их весов, включаются в оставное дерево.
Существуют четыре случая:

а) обе вершины включаемого графа
принадлежат одноэлементным подмножествам, тогда они объединяются в новое,
связное подмножество.

б) одна из вершин принадлежит
связному подмножеству, а другая нет, тогда включаем вторую в подмножество,
которому принадлежит первая.

в) обе вершины принадлежат разным
связным подмножествам, тогда объединяем подмножества.

г) обе вершины принадлежат одному
связному подмножеству, тогда исключаем данное ребро.

4. Алгоритм заканчивает работу, когда все
вершины будут объединены ы одно множество, при этом оставшиеся ребра не
включаются в оставное дерево.

Источник

В этом посте обсуждаются основные определения в терминологии, связанной с Graphми, и рассматриваются представления списка смежности и матрицы смежности структуры данных Graph.

Что такое Graph?

graph представляет собой упорядоченную пару G = (V, E) состоящий из набора V вершин или узлов и набор пар вершин из V, известные как ребра графа. Например, для Graphа ниже.

V = { 1, 2, 3, 4, 5, 6 }
E = { (1, 4), (1, 6), (2, 6), (4, 5), (5, 6) }

Graph

Типы Graphов

1. Неориентированный graph

Неориентированный graph (граф) — это graph, в котором ребра не имеют ориентации. Край (x, y) идентичен краю (y, x), т. е. они не являются упорядоченными парами. Максимальное количество ребер, возможное в неориентированном Graph без петли, равно n×(n-1)/2.

2. Ориентированный graph

Ориентированный graph (орграф) — это graph, в котором ребра имеют ориентации, т. е. ребро (x, y) не идентичен ребру (y, x).

3. Направленный ациклический graph (DAG)

Направленный ациклический graph (DAG) — это ориентированный graph, не содержащий циклов.

DAG

4. Мультиграф

Мультиграф — это неориентированный graph, в котором допускается несколько ребер (а иногда и петель). Множественные ребра — это два или более ребра, соединяющие одни и те же две вершины. Петля — это ребро (направленное или ненаправленное), соединяющее вершину с самой собой; это может быть разрешено или нет.

5. Простой Graph

Простой граф — это неориентированный граф, в котором не допускаются множественные ребра и петли, в отличие от мультиграфа. На простом Graphе с n вершин, степень каждой вершины не более n-1.

6. Взвешенный и невзвешенный Graph

Взвешенный граф связывает значение (вес) с каждым ребром в Graph. Мы также можем использовать слова стоимость или длина вместо веса.

Невзвешенный граф не имеет никакого значения (веса), связанного с каждым ребром в Graph. Другими словами, невзвешенный граф — это взвешенный граф со всеми весами ребер, равными 1. Если не указано иное, все графы по умолчанию считаются невзвешенными.

7. Полный Graph

Полный graph — это graph, в котором каждые две вершины смежны: присутствуют все ребра, которые могут существовать.

8. Связный graph

Связный graph имеет путь между каждой парой вершин. Другими словами, недостижимых вершин нет. Несвязный graph — это несвязный graph.

Наиболее часто используемые термины в graphиках

Ан edge является (вместе с вершинами) одной из двух основных единиц, из которых строятся graphы. Каждое ребро имеет две вершины, к которым оно присоединено, называемые его endpoints.
Две вершины называются adjacent если они являются концами одного ребра.
Outgoing edges вершины являются направленными ребрами, исходными точками которых является вершина.
Incoming edges вершины — это направленные ребра, к которым вершина относится.
The degree вершины Graph — это общее количество инцидентных ей ребер.
В ориентированном Graph out-degree вершины — общее количество исходящих ребер, а in-degree — общее количество входящих ребер.
Вершина с нулевой степенью вхождения называется исходной вершиной, а вершина с нулевой степенью исхода называется вершиной-приемником.
Изолированная вершина — это вершина с нулевой степенью, которая не является конечной точкой ребра.
Path представляет собой последовательность чередующихся вершин и ребер, такую, что ребро соединяет каждую последующую вершину.
Cycle это путь, который начинается и заканчивается в одной вершине.
Simple path путь с различными вершинами.
Graph Strongly Connected если он содержит направленный путь из u к v и направленный путь от v к u для каждой пары вершин u, v.
Ориентированный graph называется Weakly Connected если замена всех его ориентированных ребер неориентированными ребрами дает связный (неориентированный) граф. Вершины в слабосвязном Graph имеют исходящую или входящую степень не менее 1.
Connected component максимальный связный подграф несвязного Graph.
А bridge — ребро, удаление которого разъединило бы graph.
Forest graph без циклов.
Tree является связным graphом без циклов. Если мы удалим все циклы из DAG (направленный ациклический graph), он станет деревом, а если мы удалим любое ребро в дереве, оно станет лесом.
Spanning tree неориентированного Graph — это подграф, то есть дерево, включающее все вершины Graph.

Связь между количеством ребер и вершин

Для простого Graph с m края и n вершин, если graph

направленный, то m = n×(n-1)
ненаправленный, то m = n×(n-1)/2
подключен, то m = n-1
дерево, то m = n-1
лес, то m = n-1
завершить, то m = n×(n-1)/2

Следовательно, O(m) может варьироваться между O(1) а также O(n²), в зависимости от того, насколько плотен graph.

Graph представление

1. Матричное представление смежности:

Матрица смежности — это квадратная матрица, используемая для представления конечного Graph. Элементы матрицы указывают, являются ли пары вершин смежными или нет в Graph.

Определение:

Для простого невзвешенного Graph с множеством вершин V, матрица смежности представляет собой квадрат |V| × |V| матрица A такой, что его элемент:

A_ij = 1, когда есть ребро из вершины i к вершине j, а также
A_ij = 0, когда нет края.

Каждая строка в матрице представляет исходные вершины, а каждый столбец представляет вершины назначения. Все диагональные элементы матрицы равны нулю, поскольку ребра ведут из вершины в саму себя, т. е. в простых graphs не допускаются петли. Если граф неориентированный, матрица смежности будет симметричной. Кроме того, для взвешенного графа A_ij может представлять веса ребер.

Матрица смежности сохраняет значение (1/0/edge-weight) для каждой пары вершин, независимо от того, существует ребро или нет, поэтому требуется n² пространство. Их можно эффективно использовать только тогда, когда graph плотный.

2. Представление списка смежности:

Представление Graph списком смежности связывает каждую вершину Graph с набором соседних вершин или ребер, т. е. каждая вершина хранит список смежных вершин. Существует множество вариантов представления списка смежности в зависимости от реализации. Эта структура данных позволяет хранить дополнительные данные о вершинах, но практически очень эффективна, когда граф содержит только несколько ребер. т.е. граф разреженный.

Также см:

Реализовать структуру данных Graph в C

Реализация Graph на C++ (без использования STL)

Реализация Graph на C++ с использованием STL

Реализация Graph в Java с использованием коллекций

Использованная литература:

1. http://www.csl.mtu.edu/cs2321/www/newLectures/24_Graph_Terminology.html

2. https://en.wikipedia.org/wiki/Graph_(discrete_mathematics)

Источник