Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (−3; 5). Найдите количество решений уравнения f(x) = 0 на отрезке [−2; 4].
2
На рисунке изображён график некоторой функции
(два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2), где F(x) — одна из первообразных функции f(x).
3
На рисунке изображён график функции y = f(x). Функция
— одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.
4
На рисунке изображён график некоторой функции y = f(x). Функция
— одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
Пройти тестирование по этим заданиям
Как найти количество решений уравнения на графике
Покажем, как задачи с параметрами можно решать графически.
Найдём количество решений уравнения
в зависимости от $$ a$$.
Искомое количество решений совпадает с числом точек пересечения графиков функций
График первой функции получается из графика функции, который был построен в предыдущем примере. Для этого нужно воспользоваться преобразованием вида ПР1 то есть график $$ y=_<1>left(xright)$$ имеет такой вид, как показано на рис. 43 $$ fleft(0right)=sqrt<5>$$.
Графиком функции $$ y=a$$ будет прямая, параллельная оси $$ Ox$$ (рис. 43). При этом она пересекает ось ординат в точке $$ (0,a)$$. Легко видеть, что при $$a 3$$ прямая $$ y=a$$ не имеет пересечений с графиком $$ y=_<1>left(xright)$$, при $$ a=3$$ и $$ ain [0;sqrt<5>)$$ есть две точки пересечения, а при $$ ain [sqrt<5>;3)$$ – четыре общие точки и при $$ a=sqrt<5>$$ – три общие точки. Остаётся лишь сформулировать ответ.
При $$ ain (-infty ;0)bigcup (3;+infty )$$ решений нет, при $$ ain [0;sqrt<5>)bigcup left<3right>$$ – два решения, при $$ ain left<sqrt<5>right>$$ – три решения, при $$ ain (sqrt<5>;3)$$ – четыре решения.
Найдём количество решений уравнения в зависимости от $$ a$$:
Методом интервалов нетрудно построить график функции
Количество решений уравнения совпадает с числом точек пересечения этого графика с прямой $$ fleft(xright)=a$$ (рис. 44).
Проанализировав график, несложно выписать ответ.
При $$ ain (8;+infty )$$ уравнение имеет 2 решения, при $$ a=8$$ уравнение имеет бесконечно много решений, при $$ ain (-infty ;8)$$ решений нет.
Рассмотрим ещё один пример задач с параметром, где используется построение множеств, задаваемых уравнениями с модулем. Напомним, что графиком уравнения называют линию на плоскости, на которой лежат те и только те точки, координаты которых удовлетворяют этому уравнению.
Найдём количество решений системы уравнений
в зависимости от $$ a$$.
Для решения необходимо построить график уравнения $$ left|xright|+left|yright|=4$$. Это можно сделать, последовательно выполнив построения таких графиков:
График второго уравнения – окружность с центром в точке $$ O(0;0)$$ и радиусом $$ left|aright|$$. Изобразим оба этих графика на координатной плоскости $$ xOy$$.
Как видим, при $$|a| 4$$ графики не пересекаются. При $$ left|aright|=2sqrt<2>$$ или $$ left|aright|=4$$ есть 4 точки пересечения. При остальных $$ a$$ есть 8 точек пересечения. Таким образом, можно сформулировать ответ.
При $$ ain (-infty ;-4)cup (-2sqrt<2>;2sqrt<2>)cup (4;+infty )$$ система не имеет решений;
при $$ ain <-4;-2sqrt<2>;2sqrt<2>;4>$$ система имеет 4 решения;
при $$ ain (-4;-2sqrt<2>)cup (2sqrt<2>;4)$$ система имеет 8 решений.
В следующей задаче нам потребуется понятие локального экстремума функции. Говорят, что функция $$ y=fleft(xright)$$ имеет локальный максимум в точке $$ _<0>$$, если для некоторого числа $$ε > 0$$ при $$|x − x_0| 0$$ при $$|x − x_0| 0$$ график $$ y=at-3$$ касается линии $$ y=sqrt$$ (cм. рис. 46). Уравнение $$ D=0$$ имеет единственный положительный корень `a=1/4`. Следовательно, `a_2=1/4`. Если $$dfrac3<16>leq a 1/4` они не имеют общих точек.
Рассмотрим пример использования этого правила в задаче.
Найдём все значения параметра $$ a$$, при которых система
имеет хотя бы одно решение.
Неравенство системы после выделения полных квадратов можно записать в виде $$ ^<2>-8left|xright|+16+^<2>-8left|yright|+16le 1$$ или $$ left(right|x|-4<)>^<2>+(left|yright|-4<)>^<2>le 1$$. Множество $$ E$$ решений этого неравенства – объединение кругов $$ _<1>$$, $$ _<2>$$, $$ _<3>$$, $$ _<4>$$ (вместе с их границами) радиуса $$ 1$$ (см. рис. 47) с центрами $$ _<1>(4;4)$$, $$ _<2>(4;-4)$$, $$ _<3>(-4;-4)$$, $$ _<4>(-4;4)$$. Запишем уравнение системы в виде
Это уравнение задаёт окружность $$ L$$ радиуса $$ left|aright|$$ с центром в точке $$ M(0;1)$$, или точку $$ (0;1)$$ при $$ a=0$$. Исходная система имеет хотя бы одно решение при тех значениях $$ a$$, при которых окружность $$ L$$ имеет общие точки с множеством $$ E$$. При этом ввиду симметричного расположения соответствующих пар кругов относительно оси ординат достаточно выяснить, при каких значениях $$ a$$ окружность $$ L$$ имеет общие точки с кругами, центрами которых являются точки $$ _<1>$$ и $$ _<2>$$. Проведём из точки $$ M$$ лучи $$ _<1>$$ и $$ _<2>$$ в направлении точек $$ _<1>$$ и $$ _<2>$$. Пусть $$ _<1>$$ и $$ _<1>$$ – точки пересечения $$ _<1>$$ и окружности с центром $$ _<1>$$, $$ _<2>$$ и $$ _<2>$$ – точки пересечения $$ _<2>$$ и окружности с центром $$ _<2>$$. Тогда из геометрических соображений имеем:
При $$ 4le left|aright|le 6$$ окружность с центром $$ M$$ имеет общие точки с кругом $$ <omega >_<1>$$ , а при $$ sqrt<41>-1le left|aright|le sqrt<41>+1$$ – с кругом $$ <omega >_<2>$$.
а) Если $$b 0$$. Эта система не имеет решений при $$ a=0$$ и поэтому $$b 0$$. Теперь мы прибегнем к графическому методу. Рассмотрим два случая: $$0 1$$. Если $$b > 1$$, то $$sqrt Эта система не имеет решений, так как прямая $$ y=x-b$$ не пересекает график функции $$ y=|^<2>-b|$$ (см. рис. 48). Если $$0 0$$).
В завершении разберём несколько задач с параметрами, которые удобно решать методом областей на координатной плоскости.
Найдём все значения `a`, при каждом из которых уравнение
Рассмотрим функции `f(x)-a|x-3|` и `g(x)=5/(x+2)`.
Если построить график функции `f(x)` для разных `a` (рис. 50) и график функции `g(x)` (рис. 51), то можно без проблем исследовать на промежутке `[0;+oo)` уравнение `f(x)=g(x)`.
При `a При `a>0` функция `f(x)` возрастает на промежутке `(3;+oo)`. Функция `g(x)` убывает на этом промежутке, поэтому уравнение `f(x)=g(x)` всегда имеет ровно одно решение на промежутке `(3;+oo)`, поскольку `f(3) g(3+1/a)`. На промежутке `[0;3]` уравнение `f(x)=g(x)` принимает вид `3a-ax=5/(x+2)`. Это уравнение сводится к уравнению `ax^2-ax+(5-6a)=0`. Будем считать, что `a>0`, поскольку случай `a
Пусть уравнение имеет два корня, то есть `a>4/5`. Тогда оба корня меньше `3`, поскольку при `x>=3` значения функции `3a-ax` неположительны, а значения функции `5/(x+2)` положительны. По теореме Виета сумма корней равна `1`, а произведение равно `5/6-6`. Значит, больший корень всегда принадлежит промежутку `[0;3]`, а меньший принадлежит этому промежутку тогда и только тогда, когда `5/a-6>=0`, то есть `a 5/6`;
– три корня при `4/5
В завершении разберём несколько задач с параметрами, которые удобно решать методом областей на координатной плоскости. В следующем примере будем использовать известный подход к задачам, содержащим некоторые переменные в квадрате. Суть этого подхода — рассмотрение выражения как квадратичной функции относительно какой-нибудь переменной (остальные переменные при этом считаются параметрами) с последующим использованием известных свойств квадратичной функции.
Найдём все значения параметра $$ a$$, при каждом из которых система уравнений
имеет ровно три решения.
Первое уравнение данной системы равносильно совокупности двух уравнений $$ |y+9|+|x+2|=2$$ и $$ ^<2>+^<2>=3$$. Первое из них задаёт квадрат $$ G$$ с центром $$ (-2;-9)$$, диагонали которого равны $$ 4$$ и параллельны осям координат. Второе задаёт окружность $$ S$$ с центром $$ (0;0)$$ радиуса $$ sqrt<3>$$ (см. рис. 52).
Второе уравнение исходной системы при $$a > 0$$ задаёт окружность $$ Omega $$ с центром $$ (-2;-4)$$ радиуса $$ R=sqrt$$.
Отметим, что при $$a Рассмотрев случаи внешнего и внутреннего касания окружностей $$ Omega $$ и $$ S$$, можно заключить, что они имеют ровно `1` общую точку при $$ R=sqrt<20>pm sqrt<3>$$, ровно `2` общие точки при $$ Rin (sqrt<20>-sqrt<3>;sqrt<20>+sqrt<3>)$$ и ни одной общей точки при остальных $$ R$$. Поскольку центры окружности $$ Omega $$ и квадрата $$ G$$ лежат на прямой $$ x=-2$$, то $$ Omega $$ и $$ G$$ имеют ровно `1` общую точку при $$ R=3$$ или $$ R=7$$, ровно `2` общие точки при $$ Rin (3;7)$$ и ни одной общей точки при остальных значениях $$ R$$. Для того чтобы у системы было 3 решения, необходимо и достаточно, чтобы окружность $$ Omega $$ имела `2` общие точки с квадратом $$ G$$ и `1` общую точку с окружностью $$ S$$ или наоборот. Рассмотрим значения $$ R$$, при которых окружность $$ Omega $$ имеет с квадратом $$ G$$ или окружностью $$ S$$ ровно `1` общую точку.
1) $$ R=sqrt<20>+sqrt<3>$$. Тогда есть ровно `1` общая точка с окружностью $$ S$$, и ровно `2` общие точки с квадратом $$ G$$ (т. к. $$3 sqrt <20>+ sqrt<3>$$), т. е. у системы 1 решение.
Итак, подходят $$ R=3$$ и $$ R=sqrt<20>+sqrt<3>$$. Тогда искомые значения параметра $$ a=<3>^<2>=9$$ и $$ a=(sqrt<20>+sqrt<3><)>^<2>=23+4sqrt<15>$$.
03. В9. На рисунке изображен график первообразной y=F(x) некоторой функции y=f(x), определенной на интервале (-16; -2).
Задача.
На рисунке изображен график первообразной y=F(x) некоторой функции y=f(x), определенной на интервале (-16; -2). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-14;-8].
Решение:
По определению первообразной имеем F′(x) = f(x).
Нас просят найти количество точек, в которых f(x) = 0, то есть F′(x) = 0.
На рисунке изображен график функции у = F(x). Производная этой функции F′(x) равна нулю в точках максимума и минимума.
На отрезке [-14; -8] таких точек всего две — это х1 = -13 — точка минимума и х2 = -9 — точка максимума.
Поэтому F′(x) равно нулю в этих точках на отрезке [-14; -8].
Значит, количество решений уравнения f(x) = 0 или что тоже самое F′(x) = 0 будет иметь 2 решения.
Метод подсчёта количества решений
Линейные алгебраические уравнения — одни из самых простых уравнений, которые мы можем решить. Если в уравнении только одна переменная, решение тривиально, в то время как для системы линейных уравнений существует множество способов найти уникальные решения.
В этой статье нас интересует частный случай линейного уравнения с несколькими переменными. Хорошо известно, что подобное уравнение имеет бесконечное число решений. Мы наложим определённые ограничения и в значительной степени сократим количество решений.
Общая форма интересующего нас уравнения:
где n и m — положительные целые числа.
Наша задача — найти число решений этого уравнения, предполагая, что xᵢ являются целыми числами. Это предположение значительно снижает число решений заданного уравнения.
Нам нужен метод
Давайте начнём с частного случая общего уравнения:
Нетрудно найти все решения этого уравнения методом простого счёта. Решения заданы парами (x₁, x₂):
Мы видим, что уравнение имеет шесть решений. Также нетрудно предположить, что, если мы заменим правую часть определённым положительным целым числом m, решения будут выглядеть так:
и мы сможем подсчитать число решений — m+1.
Это было просто, верно?
Теперь возьмём немного более сложный вариант с тремя переменными, скажем:
С несколько большими усилиями, чем в предыдущем примере, находим решения в виде наборов из трёх чисел (x₁, x₂, x₃):
Число решений в этом случае равно 10.
Легко представить, что метод прямого счёта может стать очень утомительным для уравнения с большим количеством переменных. Он также становится утомительным, если целое число в правой части уравнения становится больше — например, если в правой части у нас будет 8, а не 3, решений будет уже 45. Разумеется, не хотелось бы искать все эти решения методом прямого счёта.
Значит, нужен эффективный метод.
Разрабатываем метод
Существует ещё один способ, которым можно решить предыдущие два уравнения. Давайте снова начнём с этого уравнения:
Одним из решений было (5, 0). Давайте преобразуем его в:
Мы разложили решение на нули и единицы, соответствующие каждому числу. Ненулевую часть (в данном случае 5) мы разложили на соответствующее число единиц, а ноль преобразовали в ноль. Таким же образом мы можем разложить и другое решение:
Мы поменяли прежнее расположение нуля, чтобы получить новое решение. Итак, два числа в парах (обозначенные красным и голубым) разделены нулём (чёрный) в разложенном виде. Таким же образом запишем оставшиеся решения:
Записав решения таким образом, видим закономерность. Кажется, все решения — это просто перестановки нулей и единиц. Вопрос о том, сколько существует решений, становится эквивалентным вопросу как много таких перестановок нулей и единиц может быть сделано, начиная с любой из конфигураций.
В данном случае у нас есть 6 местоположений в разложенной конфигурации для размещения нулей и единиц. Мы можем выбрать простейшее решение в качестве начальной конфигурации:
Теперь всё, что нам нужно найти, это общее число способов, которыми можно заполнить шесть местоположений пятью единицами и одним нулём.
Подобные задачи подсчёта мы можем решить различными способами, но наиболее эффективным будет способ, разработанный в такой области математики как комбинаторика, которая даёт нам формулу для числа способов перестановки r объектов в n местоположений:
где n! (читается как “n факториал”) определяется как произведение всех целых чисел от 1 до n, т.е. n! = 1 × 2 × 3 × ⋅ ⋅ ⋅ × n. Мы также определяем 0! = 1.
Эта формула обычно записывается в компактной форме как:
Теперь, возвращаясь к задаче, мы можем использовать эту формулу для нахождения числа способов перестановки пяти единиц в шести местоположениях:
Это то же самое число, что мы получили методом прямого счёта!
Выглядит многообещающе, поэтому давайте проверим, сможем ли мы найти таким способом число решений второго линейного уравнения:
Некоторые решения можно записать в разложенном виде:
В этот раз нам нужно заполнить тремя единицами и двумя нулями пять местоположений. Используя формулу мы можем найти число способов расположения чисел:
И опять то же число, что мы получили методом прямого счёта. Мы можем также найти число решений для нерешённого случая, где в правой части уравнения 8 вместо 3. Одним из решений будет:
а нам нужно найти число способов разместить 8 единиц в 10 местоположениях, и это будет:
как и утверждалось выше.
Если мы уверены в том, что этот метод работает для всех случаев, нам нужна общая формула. Напомним, что общее уравнение имеет вид:
Простейшее решение этого уравнения:
Поскольку существует n переменных, количество нулей в этом решении равно n-1. Таким образом, разложение выглядит так:
В разложенной конфигурации видим m и n-1 нулей (как утверждалось выше).
Следовательно, общее число местоположений, которые нужно заполнить, равно (m+n-1). Единственное, что остаётся — найти число способов, которыми можно заполнить m+n-1 местоположений m единиц, что определяется по формуле:
http://dnevnikanet.ru/b8-resheniya/87-03-v8-na-risunke-izobrazhen-grafik-pervoobraznoj-y-f-x-nekotoroj-funktsii-y-f-x-opredelennoj-na-intervale-16-2
На этой странице вы узнаете
- Где проходит граница между теплом и холодом?
- Почему успех фильма не всегда зависит от наличия экшн-сцен?
- Чем кофе похож на функцию, ее первообразную и производную?
Многие из нас чем-то похожи на родителей. Не являясь их точной копией, мы перенимаем определенные черты. То же самое происходит и с графиками. О том, какие особенности “наследуют” друг у друга графики функции, производной и первообразной, поговорим в статье.
Связь графика функции и производной
Подготовим карандаши и линейки, мы начинаем погружение в мир графиков. Почему графики — это круто? Они дают нам наглядное представление о функции. Мы можем проанализировать ее, не прибегая к сложным формулам и трудоемким вычислениям.
Воспринимать визуальную информацию всегда легче. А графики — это как раз визуальное описание функции.
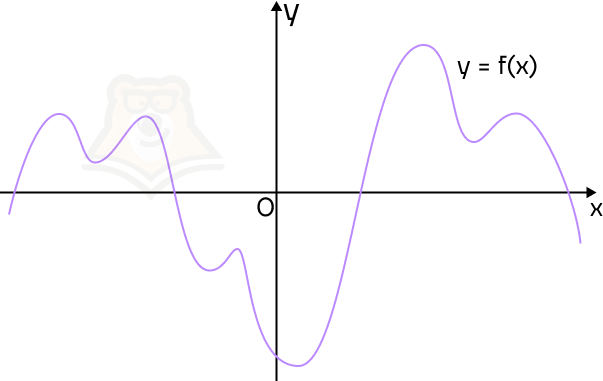
Возьмем график произвольной функции.
Прежде чем приступать к дальнейшему изучению материала, рекомендуем ознакомиться с «Определением и графиком функции», а также «Производной».
Мы точно видим, на каких промежутках график будет возрастать, а на каких убывать. Если представить, что мы пойдем по направлению оси х, то график будет возрастать на подъемах в горку и убывать на спусках с нее. Отметим промежутки возрастания зеленым фоном, а промежутки убывания красным.
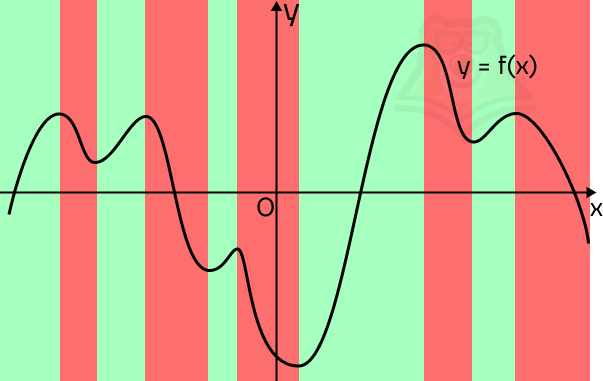
В зеленых промежутках производная будет положительна, а в красных отрицательна. Пока что просто запомним этот факт.
Обратим внимание на границы между зелеными и красными зонами. В этих точках функция будет менять свой знак с положительного на отрицательный или обратно. Такие точки называются точками экстремума.
Экстремум — это точка, в которой достигается максимальное или минимальное значение функции на заданном отрезке.
Точки экстремума — точки, в которых достигается экстремум.
В точках экстремума производная равна 0.
Теперь попробуем построить примерный график производной. Для начала опустим точки экстремума. Где они будут лежать на графике производной? На оси х.
Вспомним, что в точках экстремума производная функции будет равна 0. Пусть график будет задан
y = f'(x), тогда в точках экстремума получаем y = 0. Это и есть ось х.
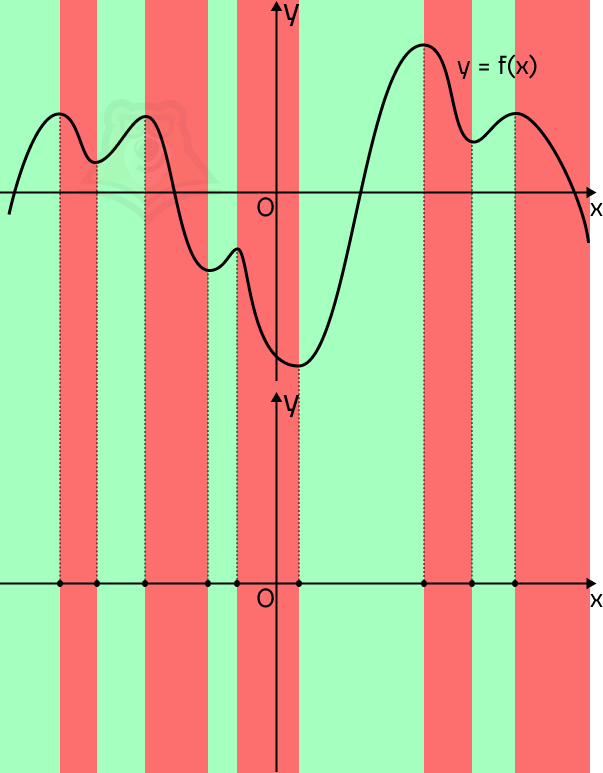
Так мы получили целых 9 точек, через которые пройдет производная. Осталось провести через них примерный график.
Вспомним, что:
- производная положительна на промежутках возрастания функции;
- производная отрицательна на промежутках убывания функции.
Как понять, что все точки на графике производной будут положительны или отрицательны? Достаточно посмотреть на то, с какой стороны от оси х они располагаются.
Положительные значения всегда будут лежать выше оси х. Это связано со значением y: значения функции будут положительны при положительных значениях у, и отрицательны при отрицательных значениях у.
Можно представить, что ось х — это полюс, который разделяет тропики и льды. Над осью х всегда будет светить солнце, а температура будет положительной. А вот под осью х всегда будут льды и снега, и температура — отрицательной.
Следовательно, знак производной на ее графике будет совпадать со знаком температуры в тропиках или льдах.
Итак, как нам нарисовать график производной? На зеленых участках ее график будет лежать над осью х, а на красных участках — под ней.
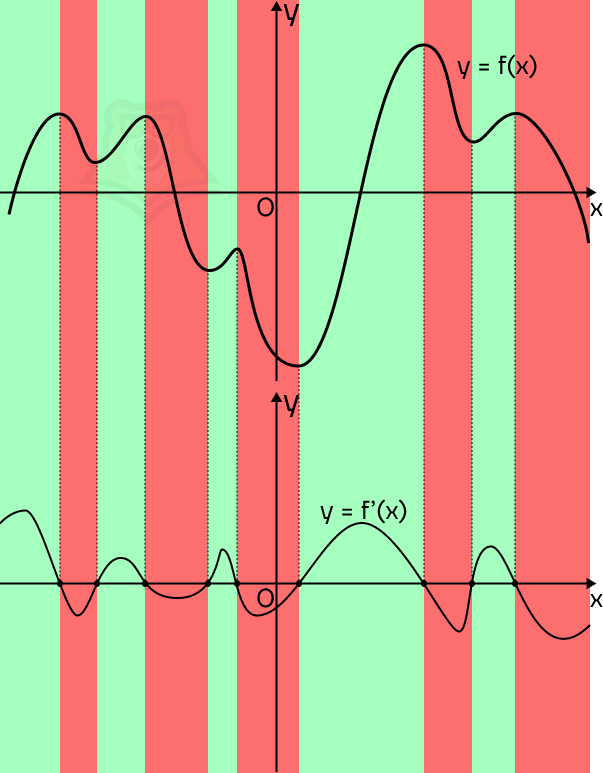
Подведем итоги:
- В точках экстремума функции график производной будет проходить через ось х.
- На промежутках возрастания функции график производной будет лежать выше оси х.
- На промежутках убывания функции график производной будет лежать ниже оси х.
Эти зависимости можно отследить на любых графиках функции и ее производной.
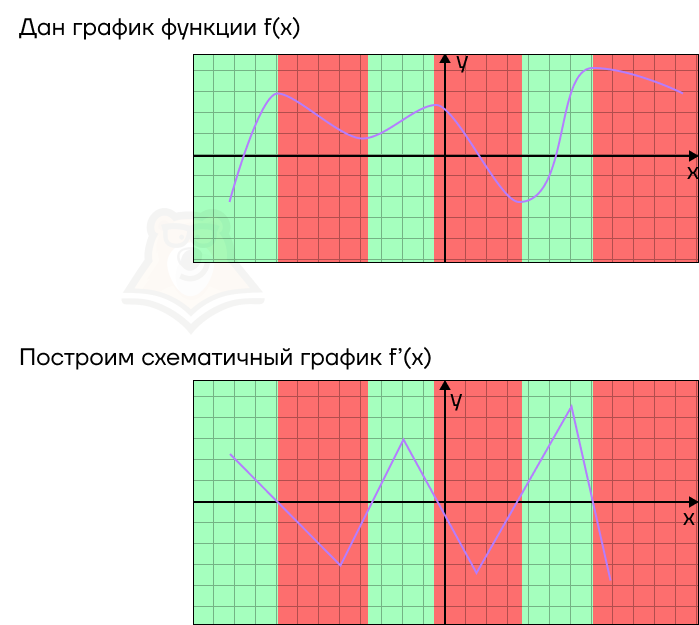
Если провести обратные рассуждения, то по графику производной можно восстановить примерный график функции. В этом случае:
- В точках, где график производной пересекает ось х, будут лежать точки экстремума. При этом если в точке производная меняет значение с положительного на отрицательное, то это точка максимума, а если с отрицательного на положительное, то это точка минимума.
- На промежутках, где график производной будет лежать выше оси х, функция будет возрастать.
- На промежутках, где график производной будет лежать ниже оси х, функция будет убывать.
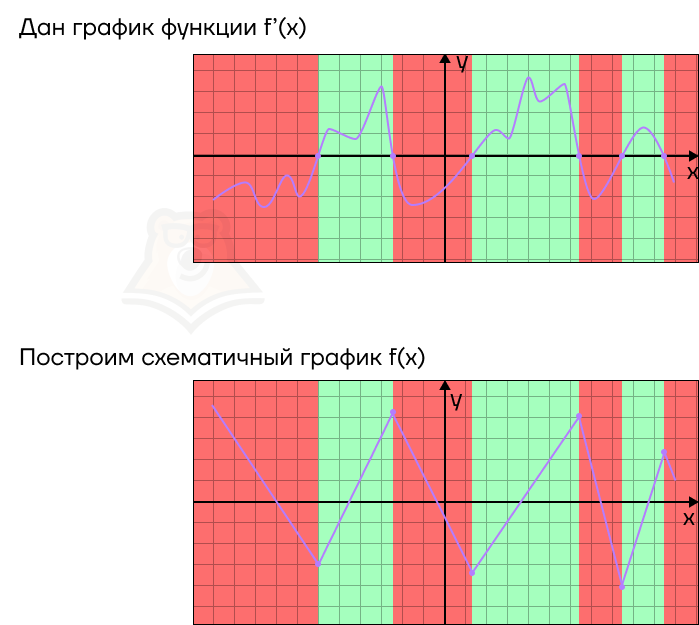
Разберем несколько примеров, где можно применить эти знания.
Пример 1. На рисунке изображен график функции f(x) и отмечены пять точек на оси абсцисс: x1, x2, x3, x4, x5. В скольких из этих точек производная функции отрицательна?
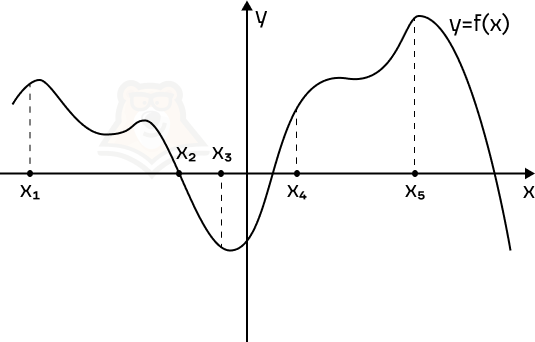
Решение. Производная отрицательна на промежутках убывания функции. Отметим такие промежутки.
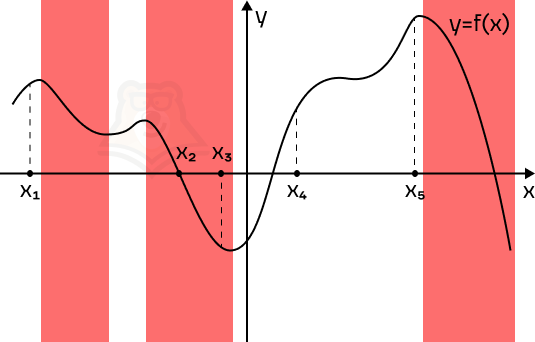
В точках, которые попали в эти промежутки, производная отрицательная. Всего таких точек 2.
Ответ: 2
Пример 2. На рисунке изображен график функции y = f'(x) — производной функции f(x), определенной на интервале (-5; 3). Найдите точку максимума функции f(x).
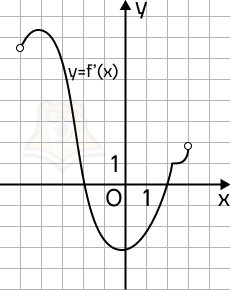
Решение. Точки экстремума на графике производной лежат на оси х. На данном графике таких точки две: x = -2, x = 2.
Точка максимума — это точка, в которой производная меняет знак с положительного на отрицательный. По графику определяем, что это точка x = -2.
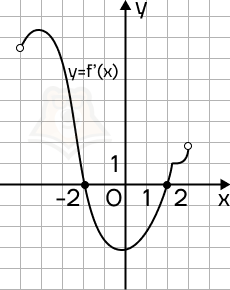
Ответ: -2
Представим, что мы составили графики “Заинтересованность зрителей фильмом” и “Наличие в фильме экшн-сцен”. Совпадут ли эти графики? Скорее всего, нет.
Экшн-сцены могут вызывать интерес у зрителей, равно как и романтические сцены или смешные повороты сюжета. Получается, что наличие экшн-сцен и заинтересованность фильмом — это разные величины в кинематографе, хотя и связаны между собой.
Также и графики производной и функции: они зависят друг от друга, но иллюстрируют совсем разные свойства функции, поэтому сильно отличаются.
Связь графика функции и первообразной
Мы разобрались, как связаны графики функции и ее производной. Есть ли связь между графиком функции и «Первообразной»?
Вспомним один важный факт: если взять производную от первообразной, то получим функцию.
F'(x) = f(x)
Похоже на функцию и ее производную, верно? На самом деле, ситуации ничем не отличаются.
В этом случае изначальной функцией будет первообразная, а ее производной — функция. Для наглядности составим таблицу.
| Было | Взяли производную | Стало | |
| Функция и производная | f(x) | f'(x) | f'(x) |
| Функция и первообразная | F(x) | F'(x) | f(x) |
Получается, для функции и первообразной будут действовать почти те же правила, что и для функции и ее производной.
При решении заданий с графиками первообразной достаточно проанализировать уравнение F'(x) = f(x). Рассмотрим несколько примеров.
Пример 3. На рисунке изображен график функции y = F(x) — одной из первообразных функции f(x) и отмечены шесть точек на оси абсцисс x1, x2, x3, x4, x5, x6. В скольких из этих точек функция f(x) отрицательна?
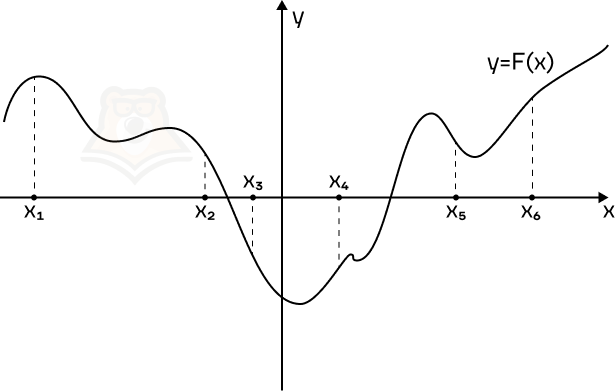
Решение. Поскольку F'(x) = f(x), то функция f(x) будет отрицательна в тех же точках, в которых будет отрицательна F'(x).
Поскольку на графике изображена функция y = F(x), то ее производная будет отрицательна на промежутках убывания функции. Отметим их красным.
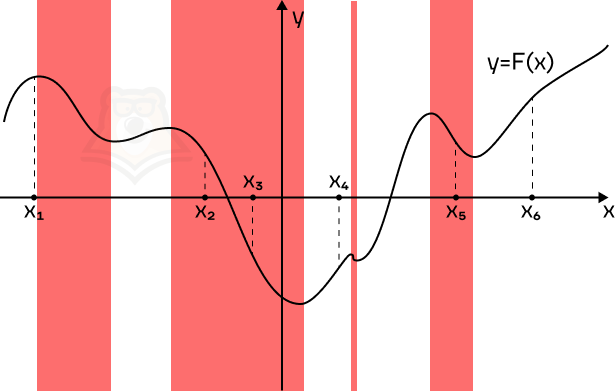
В эти промежутки попадают 3 из 6 точек.
Ответ: 3.
Пример 4. На рисунке изображен график функции y = F(x) — одной из первообразных функции f(x), определенной на интервале (-6; 7). Пользуясь рисунком, определите количество решений уравнения f(x) = 0 на отрезке [-5; 4].
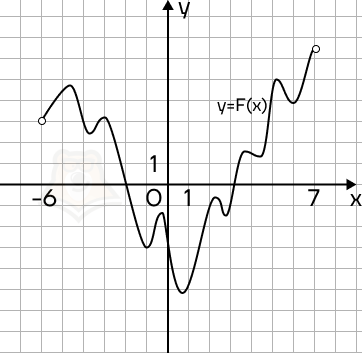
Решение. Вспомним, что F'(x) = f(x). Тогда если f(x) = 0, то и F'(x) = 0. Следовательно, на заданном промежутке нужно найти точки экстремума.
Отметим заданный промежуток красными линиями. На промежутке всего 9 точек экстремума, значит, в 9 точках f(x) будет равна 0.
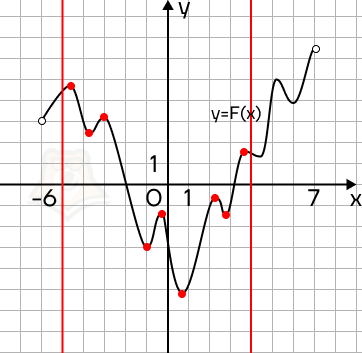
Ответ: 9
Представим, что в качестве функции у нас выступают кофейные зерна. Тогда производная — то, что мы получаем в результате их переработки — это вкусный напиток.
Из чего получаются сами кофейные зерна? Их собирают с кофейного дерева. То есть зерна будут производной от кофейного дерева, а кофейное дерево — это первообразная.
Так мы можем отследить следующую цепочку: кофейное дерево → кофейные зерна → кофе. И эта цепочка наглядно иллюстрирует связь первообразной, функции и ее производной.
Фактчек
- Графики функции, производной и первообразной связаны между собой.
- В точках экстремума функции график производной будет проходить через ось х.
- На промежутках возрастания функции график производной будет лежать выше оси х.
- На промежутках убывания функции график производной будет лежать ниже оси х.
- Для решения задач с первообразной необходимо вспомнить, что F'(x) = f(x). Любой график можно проанализировать с помощью этого уравнения также, как анализируются графики функции и ее производной.
Проверь себя
Задание 1.
На каких промежутках будет производная функции будет положительна?
- На промежутках убывания функции.
- На промежутках возрастания функции.
- В точках экстремума.
- Невозможно определить по графику.
Задание 2.
На каких промежутках производная функции будет отрицательна?
- На промежутках возрастания функции.
- На промежутках убывания функции.
- В точках экстремума.
- Невозможно определить по графику.
Задание 3.
На рисунке изображен график производной функции f(x), на котором отмечена точка. Чем будет являться эта точка для функции f(x)?
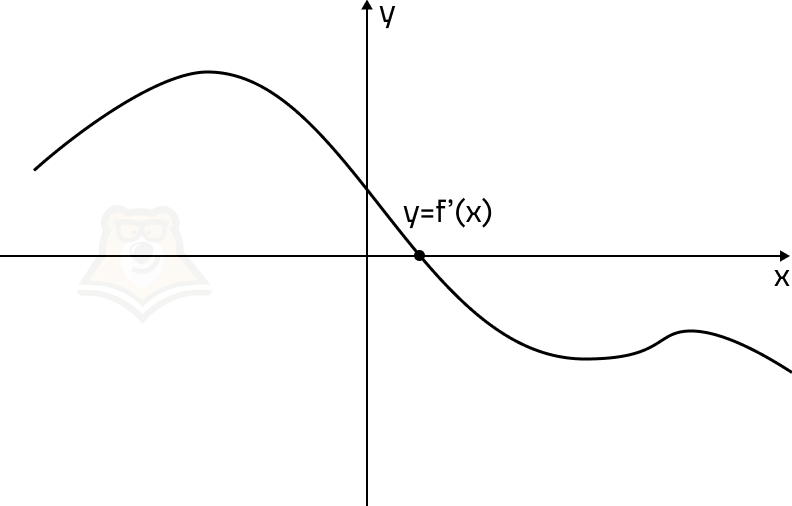
- Точка максимума функции.
- Точка минимума функции.
- Любая произвольная точка на функции.
- Невозможно определить по графику.
Задание 4.
Выберите верный вариант:
- F(x) = f'(x)
- F(x) = f(x)
- F'(x) = f'(x)
- F'(x) = f(x)
Ответы: 1. — 2 2. — 2 3. — 1 4. — 4
Графики в задачах с параметрами
Покажем, как задачи с параметрами можно решать графически.
Найдём количество решений уравнения
$$ sqrt{5+4left|xright|-{x}^{2}}=a$$
в зависимости от $$ a$$.
Искомое количество решений совпадает с числом точек пересечения графиков функций
$$ {f}_{1}left(xright)=sqrt{5+4left|xright|-{x}^{2}}$$ и $$ {f}_{2}left(xright)=a$$.
График первой функции получается из графика функции, который был построен в предыдущем примере. Для этого нужно воспользоваться преобразованием вида ПР1 то есть график $$ y={f}_{1}left(xright)$$ имеет такой вид, как показано на рис. 43 $$ fleft(0right)=sqrt{5}$$.
Графиком функции $$ y=a$$ будет прямая, параллельная оси $$ Ox$$ (рис. 43). При этом она пересекает ось ординат в точке $$ (0,a)$$. Легко видеть, что при $$a < 0$$ и $$a > 3$$ прямая $$ y=a$$ не имеет пересечений с графиком $$ y={f}_{1}left(xright)$$, при $$ a=3$$ и $$ ain [0;sqrt{5})$$ есть две точки пересечения, а при $$ ain [sqrt{5};3)$$ – четыре общие точки и при $$ a=sqrt{5}$$ – три общие точки. Остаётся лишь сформулировать ответ.
При $$ ain (-infty ;0)bigcup (3;+infty )$$ решений нет, при $$ ain [0;sqrt{5})bigcup left{3right}$$ – два решения, при $$ ain left{sqrt{5}right}$$ – три решения, при $$ ain (sqrt{5};3)$$ – четыре решения.
Найдём количество решений уравнения в зависимости от $$ a$$:
$$ |x+5|+|x-3|=a$$.
Методом интервалов нетрудно построить график функции
$$ fleft(xright)=|x+5|+|x-3|$$.
Количество решений уравнения совпадает с числом точек пересечения этого графика с прямой $$ fleft(xright)=a$$ (рис. 44).
Проанализировав график, несложно выписать ответ.
При $$ ain (8;+infty )$$ уравнение имеет 2 решения, при $$ a=8$$ уравнение имеет бесконечно много решений, при $$ ain (-infty ;8)$$ решений нет.
Рассмотрим ещё один пример задач с параметром, где используется построение множеств, задаваемых уравнениями с модулем. Напомним, что графиком уравнения называют линию на плоскости, на которой лежат те и только те точки, координаты которых удовлетворяют этому уравнению.
Найдём количество решений системы уравнений
$$ left{begin{array}{l}left|xright|+left|yright|=4;\ {x}^{2}+{y}^{2}={a}^{2}end{array}right.$$
в зависимости от $$ a$$.
Для решения необходимо построить график уравнения $$ left|xright|+left|yright|=4$$. Это можно сделать, последовательно выполнив построения таких графиков:
График второго уравнения – окружность с центром в точке $$ O(0;0)$$ и радиусом $$ left|aright|$$. Изобразим оба этих графика на координатной плоскости $$ xOy$$.
Как видим, при $$|a| < 2sqrt{2}$$ и $$|a| > 4$$ графики не пересекаются. При $$ left|aright|=2sqrt{2}$$ или $$ left|aright|=4$$ есть 4 точки пересечения. При остальных $$ a$$ есть 8 точек пересечения. Таким образом, можно сформулировать ответ.
При $$ ain (-infty ;-4)cup (-2sqrt{2};2sqrt{2})cup (4;+infty )$$ система не имеет решений;
при $$ ain {-4;-2sqrt{2};2sqrt{2};4}$$ система имеет 4 решения;
при $$ ain (-4;-2sqrt{2})cup (2sqrt{2};4)$$ система имеет 8 решений.
В следующей задаче нам потребуется понятие локального экстремума функции. Говорят, что функция $$ y=fleft(xright)$$ имеет локальный максимум в точке $$ {x}_{0}$$, если для некоторого числа $$ε > 0$$ при $$|x − x_0| < ε$$ (т. е. числа $$ x$$ и $$ {x}_{0}$$ достаточно близки) верно неравенство $$ fleft(xright)le fleft({x}_{0}right)$$. Если же для некоторого числа $$ε > 0$$ при $$|x − x_0| < ε$$ верно $$ fleft(xright)ge fleft({x}_{0}right)$$, то говорят, что функция $$ y=fleft(xright)$$ имеет локальный минимум в точке $$ {x}_{0}$$. Точки локального максимума или минимума называют точками локального экстремума функции. В случае выполнения неравенств $$ fleft(xright)le fleft({x}_{0}right)$$ или $$ fleft(xright)ge fleft({x}_{0}right)$$ для произвольного $$ x$$ точку $$ {x}_{0}$$ называют точкой глобального экстремума функции. Ясно, что всякий глобальный экстремум будет локальным. Примером такой точки для квадратичной функции будет точка, соответствующая вершине параболы.
При каких $$ a$$ функция $$ fleft(xright)={x}^{2}-3|x-{a}^{2}|-5x$$ имеет более двух точек локального экстремума?
$$left|x-{a}^{2}right|=left{begin{array}{l}x-{a}^{2}, mathrm{если} xge {a}^{2},\ {a}^{2}-x, mathrm{если} x<{a}^{2}.end{array}right.$$
$$fleft(xright)=left{begin{array}{l}{x}^{2}-8x+3{a}^{2}, mathrm{если} xge {a}^{2},\ {x}^{2}-2x-3{a}^{2}, mathrm{если} x<{a}^{2}.end{array}right.$$
При $$ xge {a}^{2}$$ график функции $$ fleft(xright)$$ есть часть параболы $$ y={x}^{2}-8x+3{a}^{2}$$, лежащая справа от $$ x={a}^{2}$$, а при $$x < a^2$$ $$ fleft(xright)={x}^{2}-2x-3{a}^{2}$$ и графиком функции будет часть параболы $$ y={x}^{2}-2x-3{a}^{2}$$ в полуплоскости слева от прямой $$ x={a}^{2}$$. Наибольшее возможное количество точек экстремума этой функции равно `3` (две вершины парабол и точка их пересечения, см. рис. 45).
Это возможно при условии $$1 < a^2 < 4$$, то есть $$ ain (-2;-1)bigcup (1;2)$$.
$$ ain (-2;-1)bigcup (1;2)$$.
Найдём все значения $$ a$$, при которых уравнение
$$ sqrt{x-9}=ax+7a-3$$
имеет единственное решение.
Полагая $$ x+7=t$$, получим уравнение $$ sqrt{t-16}=at-3$$. (1)
Требуется найти все значения $$ a$$, при которых графики функций $$ y=sqrt{t-16}$$ и $$ y=at-3$$ имеют единственную общую точку. Заметим, что все прямые, задаваемые уравнением $$ y=at-3$$ проходят через $$ (0;-3)$$ (рис. 46).
Ясно, что если $$ ale 0$$, то прямая $$ y=at-3$$ не имеет общих точек с параболой $$ y=sqrt{t-16}$$. Угловой коэффициент прямой $$ y=at-3$$ равен $$ a$$. Найдем угловые коэффициенты $$ {a}_{1}$$ и $$ {a}_{2}$$ прямых $$ {l}_{1}$$ и $$ {l}_{2}$$ (см. рис. 46) (обе задаются уравнением вида $$ y=at-3$$), первая из которых проходит через точку $$ (16;0)$$, а вторая имеет ровно одну общую точку (касается) с параболой $$ y=sqrt{t-16}$$. Подставляя в уравнение прямой значения $$ t=16$$, $$ y=0$$, находим $$ {a}_{1}={displaystyle frac{3}{16}}$$. И при `0<a<3/16` уравнение (1) имеет единственное решение. Число `a_2` является ещё одним значением `a`, при котором уравнение (1) имеет единственный корень `t_1>16`. Возводя обе части (1) в квадрат, получаем уравнение $$ {a}^{2}{t}^{2}-(6a+1)t+25=0$$, дискриминант которого $$ D=(6a+1{)}^{2}-(10a{)}^{2}$$. При $$ D=0$$ и $$a > 0$$ график $$ y=at-3$$ касается линии $$ y=sqrt{t-16}$$ (cм. рис. 46). Уравнение $$ D=0$$ имеет единственный положительный корень `a=1/4`. Следовательно, `a_2=1/4`. Если $$dfrac3{16}leq a<dfrac14$$, то прямая $$ y=at-3$$ и парабола $$ y=sqrt{t-16}$$ имеют две общих точки, а при `a > 1/4` они не имеют общих точек.
`0<a<3/16`, `a=1/4`.
В следующем примере нам необходимо будет изобразить точки на координатной плоскости, координаты которых удовлетворяют некоторому неравенству $$ f(x,y)le {a}_{0}$$ для заданной функции двух переменных $$ f$$ и некоторого фиксированного числа $$ {a}_{0}$$. Для этого нужно сначала выяснить вид множества точек $$ f(x,y)=a$$ при различных значениях $$ a$$ и заштриховать все точки координатной плоскости, принадлежащие линиям $$ f(x,y)=a$$ при $$ ale {a}_{0}$$. Часто это бывает область на плоскости внутри, либо вне некоторой фигуры, которая задаётся равенством $$ f(x,y)=a$$. Например, неравенство $$ f(x,y)=(x-1{)}^{2}+(y+1{)}^{2}le 1$$ задаёт круг радиуса $$ 1$$ с центром в точке $$ А(1,–1)$$.
Рассмотрим пример использования этого правила в задаче.
Найдём все значения параметра $$ a$$, при которых система
$$ left{begin{array}{l}{x}^{2}+{y}^{2}+31le 8left(right|x|+|yleft|right),\ {x}^{2}+{y}^{2}-2y={a}^{2}-1end{array}right.$$
имеет хотя бы одно решение.
Неравенство системы после выделения полных квадратов можно записать в виде $$ {x}^{2}-8left|xright|+16+{y}^{2}-8left|yright|+16le 1$$ или $$ left(right|x|-4{)}^{2}+(left|yright|-4{)}^{2}le 1$$. Множество $$ E$$ решений этого неравенства – объединение кругов $$ {K}_{1}$$, $$ {K}_{2}$$, $$ {K}_{3}$$, $$ {K}_{4}$$ (вместе с их границами) радиуса $$ 1$$ (см. рис. 47) с центрами $$ {O}_{1}(4;4)$$, $$ {O}_{2}(4;-4)$$, $$ {O}_{3}(-4;-4)$$, $$ {O}_{4}(-4;4)$$. Запишем уравнение системы в виде
$$ {x}^{2}+(y-1{)}^{2}={a}^{2}$$.
Это уравнение задаёт окружность $$ L$$ радиуса $$ left|aright|$$ с центром в точке $$ M(0;1)$$, или точку $$ (0;1)$$ при $$ a=0$$. Исходная система имеет хотя бы одно решение при тех значениях $$ a$$, при которых окружность $$ L$$ имеет общие точки с множеством $$ E$$. При этом ввиду симметричного расположения соответствующих пар кругов относительно оси ординат достаточно выяснить, при каких значениях $$ a$$ окружность $$ L$$ имеет общие точки с кругами, центрами которых являются точки $$ {O}_{1}$$ и $$ {O}_{2}$$. Проведём из точки $$ M$$ лучи $$ {l}_{1}$$ и $$ {l}_{2}$$ в направлении точек $$ {O}_{1}$$ и $$ {O}_{2}$$. Пусть $$ {A}_{1}$$ и $$ {B}_{1}$$ – точки пересечения $$ {l}_{1}$$ и окружности с центром $$ {O}_{1}$$, $$ {A}_{2}$$ и $$ {B}_{2}$$ – точки пересечения $$ {l}_{2}$$ и окружности с центром $$ {O}_{2}$$. Тогда из геометрических соображений имеем:
$$ M{O}_{1}=5$$, $$ M{O}_{2}=sqrt{25+16}=sqrt{41}$$,
$$ M{A}_{1}=4$$, $$ M{B}_{1}=6$$, $$ M{A}_{2}=sqrt{41}-1$$, $$ M{B}_{2}=sqrt{41}+1$$.
При $$ 4le left|aright|le 6$$ окружность с центром $$ M$$ имеет общие точки с кругом $$ {omega }_{1}$$ , а при $$ sqrt{41}-1le left|aright|le sqrt{41}+1$$ – с кругом $$ {omega }_{2}$$.
Так как $$4 < sqrt{41} − 1 < 6$$, то объединение отрезков $$ [4;6]$$ и $$ [sqrt{41}-1;sqrt{41}+1]$$ есть отрезок $$ [4;sqrt{41}+1]$$, а искомое множество значений $$ a$$ определяется неравенством $$ 4le left|aright|le sqrt{41}+1$$.
$$ 4le left|aright|le sqrt{41}+1$$.
Найдём все значения параметра $$ b$$, при которых система уравнений
$$ left{begin{array}{l}y=|b-{x}^{2}|,\ y=a(x-b)end{array}right.$$
имеет решение при любом значении параметра $$ a$$.
Рассмотрим три возможных случая: $$b < 0$$, $$ b=0$$,а также $$b > 0$$.
а) Если $$b < 0$$, то запишем систему в виде $$ left{begin{array}{l}y={x}^{2}+d,\ y=a(x+d),end{array}right.$$ где $$d = −b > 0$$. Эта система не имеет решений при $$ a=0$$ и поэтому $$b < 0$$ не подходит.
б) Если $$ b=0$$, то система примет вид $$ left{begin{array}{l}y={x}^{2},\ y=ax.end{array}right.$$
Легко видеть, что она имеет решение $$ (0;0)$$ при любом $$ a$$, т.е. значение $$ b=0$$ подходит.
в) Пусть $$b > 0$$. Теперь мы прибегнем к графическому методу. Рассмотрим два случая: $$0 < b ≤ 1$$ и $$b > 1$$. Если $$b > 1$$, то $$sqrt{b} < b$$. Пусть $$ a=1$$, тогда система примет вид $$ left{begin{array}{l}y=|{x}^{2}-b|,\ y=x-b.end{array}right.$$
Эта система не имеет решений, так как прямая $$ y=x-b$$ не пересекает график функции $$ y=|{x}^{2}-b|$$ (см. рис. 48). Если $$0 < b ≤ 1$$, то $$ sqrt{b}ge b$$. В этом случае прямая $$ y=a(x-b)$$ пересекает график функции $$ y=|{x}^{2}-b|$$ при любом $$ a$$ (на рис. 49) представлен случай $$a > 0$$).
$$ 0le ble 1$$.
В завершении разберём несколько задач с параметрами, которые удобно решать методом областей на координатной плоскости.
Найдём все значения `a`, при каждом из которых уравнение
`a|x-3|=5/(x+2)`
на промежутке `{0;+oo)` имеет ровно два корня.
Рассмотрим функции `f(x)-a|x-3|` и `g(x)=5/(x+2)`.
Если построить график функции `f(x)` для разных `a` (рис. 50) и график функции `g(x)` (рис. 51), то можно без проблем исследовать на промежутке `[0;+oo)` уравнение `f(x)=g(x)`.
При `a<=0` все значения функции `f(x)` на промежутке `[0;+oo)` неположительны, а все значения функции `g(x)` – положительны, поэтому при `a<=0` уравнение `f(x)=g(x)` не имеет решений на промежутке `[0;+oo)`. При `a>0` функция `f(x)` возрастает на промежутке `(3;+oo)`. Функция `g(x)` убывает на этом промежутке, поэтому уравнение `f(x)=g(x)` всегда имеет ровно одно решение на промежутке `(3;+oo)`, поскольку `f(3)<g(3)` и `f(3+1/a)>g(3+1/a)`. На промежутке `[0;3]` уравнение `f(x)=g(x)` принимает вид `3a-ax=5/(x+2)`. Это уравнение сводится к уравнению `ax^2-ax+(5-6a)=0`. Будем считать, что `a>0`, поскольку случай `a<=0` был рассмотрен ранее. Дискриминант квадратного уравнения `D=a^2-4a(5-6a)=25a^2-20a`, поэтому при `0<a<4/5` это уравнение не имеет корней; при `a=4/5` уравнение имеет единственный корень, равный `1/2`; при `a>4/5` уравнение имеет два корня.
Пусть уравнение имеет два корня, то есть `a>4/5`. Тогда оба корня меньше `3`, поскольку при `x>=3` значения функции `3a-ax` неположительны, а значения функции `5/(x+2)` положительны. По теореме Виета сумма корней равна `1`, а произведение равно `5/6-6`. Значит, больший корень всегда принадлежит промежутку `[0;3]`, а меньший принадлежит этому промежутку тогда и только тогда, когда `5/a-6>=0`, то есть `a<=5/6`.
Таким образом, уравнение `a|x-3|=5/(x+2)` имеет следующее количество корней на промежутке `[0;+oo):
– нет корней при `a<=0`;
– один корень при `0<a<4/5`;
– два корня при `a=4/5` и `a>5/6`;
– три корня при `4/5<a<=5/6`.
`a=4/5`, `a>5/6`.
В завершении разберём несколько задач с параметрами, которые удобно решать методом областей на координатной плоскости. В следующем примере будем использовать известный подход к задачам, содержащим некоторые переменные в квадрате. Суть этого подхода — рассмотрение выражения как квадратичной функции относительно какой-нибудь переменной (остальные переменные при этом считаются параметрами) с последующим использованием известных свойств квадратичной функции.
Найдём все значения параметра $$ a$$, при каждом из которых система уравнений
$$ left{begin{array}{l}left(right|y+9|+|x+2|-2)({x}^{2}+{y}^{2}-3)=0,\ (x+2{)}^{2}+(y+4{)}^{2}=aend{array}right.$$
имеет ровно три решения.
Первое уравнение данной системы равносильно совокупности двух уравнений $$ |y+9|+|x+2|=2$$ и $$ {x}^{2}+{y}^{2}=3$$. Первое из них задаёт квадрат $$ G$$ с центром $$ (-2;-9)$$, диагонали которого равны $$ 4$$ и параллельны осям координат. Второе задаёт окружность $$ S$$ с центром $$ (0;0)$$ радиуса $$ sqrt{3}$$ (см. рис. 52).
Второе уравнение исходной системы при $$a > 0$$ задаёт окружность $$ Omega $$ с центром $$ (-2;-4)$$ радиуса $$ R=sqrt{a}$$.
Отметим, что при $$a < 0$$ второе уравнение задаёт пустое множество, при $$ a=0$$ одну точку $$ (-2;-4)$$. Поэтому при $$ ale 0$$ трёх решений быть не может.
Рассмотрев случаи внешнего и внутреннего касания окружностей $$ Omega $$ и $$ S$$, можно заключить, что они имеют ровно `1` общую точку при $$ R=sqrt{20}pm sqrt{3}$$, ровно `2` общие точки при $$ Rin (sqrt{20}-sqrt{3};sqrt{20}+sqrt{3})$$ и ни одной общей точки при остальных $$ R$$. Поскольку центры окружности $$ Omega $$ и квадрата $$ G$$ лежат на прямой $$ x=-2$$, то $$ Omega $$ и $$ G$$ имеют ровно `1` общую точку при $$ R=3$$ или $$ R=7$$, ровно `2` общие точки при $$ Rin (3;7)$$ и ни одной общей точки при остальных значениях $$ R$$. Для того чтобы у системы было 3 решения, необходимо и достаточно, чтобы окружность $$ Omega $$ имела `2` общие точки с квадратом $$ G$$ и `1` общую точку с окружностью $$ S$$ или наоборот. Рассмотрим значения $$ R$$, при которых окружность $$ Omega $$ имеет с квадратом $$ G$$ или окружностью $$ S$$ ровно `1` общую точку.
1) $$ R=sqrt{20}+sqrt{3}$$. Тогда есть ровно `1` общая точка с окружностью $$ S$$, и ровно `2` общие точки с квадратом $$ G$$ (т. к. $$3<sqrt{20}+sqrt3<7$$), т. е. у системы 3 решения.
2) $$ R=sqrt{20}-sqrt{3}$$. Тогда есть ровно `1` общая точка с окружностью $$ S$$ и нет общих точек с квадратом $$ G$$ (т. к. $$sqrt{20}-sqrt3<3$$), т. е. у системы 1 решение.
3) $$ R=3$$. Тогда есть ровно `1` общая точка с квадратом $$ G$$ и ровно `2` общие точки с окружностью $$ S$$ (т. к. $$sqrt{20} − sqrt{3} < 3 < sqrt{20} + sqrt{3}$$), т. е. у системы 3 решения.
4) $$ R=7$$. Тогда есть ровно `1` общая точка с квадратом $$ G$$ и нет общих точек с окружностью $$ S$$ (т. к. $$7 > sqrt{20} + sqrt{3}$$), т. е. у системы 1 решение.
Итак, подходят $$ R=3$$ и $$ R=sqrt{20}+sqrt{3}$$. Тогда искомые значения параметра $$ a={3}^{2}=9$$ и $$ a=(sqrt{20}+sqrt{3}{)}^{2}=23+4sqrt{15}$$.
$$ a=9$$, $$ a=23+4sqrt{15}$$.
В зависимости от значений параметра а найдём количество решений уравнения
`a+[x]=sqrt(2x-x^2)`.
Количество решений соответствует количеству общих точек графиков `y=a+[x]` и `y=sqrt(2x-x^2)`.
$$ y=sqrt{2x-{x}^{2}}iff left{begin{array}{l}yge 0,\ {left(x-1right)}^{2}+{y}^{2}=1.end{array}right.$$ (Рис. 53)
График функции `y=a+[x]` представлен на рисунке ниже (Рис. 54).
Общие точки возможны лишь при `x in [0;2]`. Рассмотрим несколько случаев расположения графиков.
1) Если `0<=x<1`, то `y=a+[x]=a`. В этом случае возможна одна общая точка с полуокружностью `y=sqrt(2x-x^2)` при `0<=a<1`.
2) Если `1<=x<2`, то `y=a+[x]=a+1`. Теперь одна общая точка возможна при `0<a+1<=1`, то есть `-1<a<=0`.
3) Если `x=2`, то `y=a+[x]=a+2`. Точка `(2;a+2)` лежит на графике `y=sqrt(2x-x^2) iff a=-2`.
При `a in (-oo;-2)uu(-2;-1]uu[1;+oo)` нет решений;
при `a in {-2}uu(-1;0)uu(0;1)` одно решение;
при `a=0` два решения.
Необходимая теория:
Производная функции
Таблица производных
Первообразная функции
Задание 7 Профильного ЕГЭ по математике — это задачи на геометрический и физический смысл производной. Это задачи о том, как производная связана с поведением функции. И еще (правда, очень редко) в этих задачах встречаются вопросы о первообразной.
Геометрический смысл производной
Вспомним, что производная — это скорость изменения функции.
Производная функции в точке
равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Производная также равна тангенсу угла наклона касательной.
1. На рисунке изображён график функции и касательная к нему в точке с абсциссой
Найдите значение производной функции
в точке
Производная функции в точке
равна тангенсу угла наклона касательной, проведенной в точке
.
Достроив до прямоугольного треугольника АВС, получим:
Ответ: 0,25.
2. На рисунке изображён график функции и касательная к нему в точке с абсциссой
Найдите значение производной функции в точке
Начнём с определения знака производной. Мы видим, что в точке функция убывает, следовательно, её производная отрицательна. Касательная в точке
образует тупой угол
с положительным направлением оси
. Поэтому из прямоугольного треугольника мы найдём тангенс угла
, смежного с углом
.
Мы помним, что тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему: Поскольку
, имеем:
Ответ: −0, 25.
Касательная к графику функции
3. Прямая является касательной к графику функции
Найдите абсциссу точки касания.
Запишем условие касания функции и прямой
в точке
При значения выражений
и
равны.
При этом производная функции равна угловому коэффициенту касательной, то есть
.
Из второго уравнения находим или
Первому уравнению удовлетворяет только
.
Физический смысл производной
Мы помним, что производная — это скорость изменения функции.
Мгновенная скорость — это производная от координаты по времени. Но это не единственное применение производной в физике. Например, cила тока — это производная заряда по времени, то есть скорость изменения заряда. Угловая скорость — производная от угла поворота по времени.
Множество процессов в природе, экономике и технике описывается дифференциальными уравнениями — то есть уравнениями, содержащими не только сами функции, но и их производные.
4. Материальная точка движется прямолинейно по закону , где
— расстояние от точки отсчета в метрах,
— время в секундах, измеренное с начала движения. Найдите ее скорость (в м/с) в момент времени
с.
Мгновенная скорость движущегося тела является производной от его координаты по времени. Это физический смысл производной. В условии дан закон изменения координаты материальной точки, то есть расстояния от точки отсчета:
Найдем скорость материальной точки как производную от координаты по времени:
В момент времени
получим:
.
Ответ: 3.
Применение производной к исследованию функций
Каждый год в вариантах ЕГЭ встречаются задачи, в которых старшеклассники делают одни и те же ошибки.
Например, на рисунке изображен график функции — а спрашивают о производной. Кто их перепутал, тот задачу не решил.
Или наоборот. Нарисован график производной — а спрашивают о поведении функции.
И значит, надо просто внимательно читать условие. И знать, как же связана производная с поведением функции.
Если , то функция
возрастает.
Если , то функция
убывает.
В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».
В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».
| возрастает | точка максимума | убывает | точка минимума | возрастает | |
| 0 | 0 |
5. На рисунке изображен график функции , определенной на интервале
Найдите количество точек, в которых производная функции
равна 0.
Производная функции в точках максимума и минимума функции
Таких точек на графике 5.
Ответ: 5.
6. На рисунке изображён график — производной функции
, определённой на интервале
. В какой точке отрезка
функция
принимает наибольшее значение?
Не спешим. Зададим себе два вопроса: что изображено на рисунке и о чем спрашивается в этой задаче?
Изображен график производной, а спрашивают о поведении функции. График функции не нарисован. Но мы знаем, как производная связана с поведением функции.
На отрезке производная функции
положительна.
Значит, функция возрастает на этом отрезке. Большим значениям х соответствует большее значение
Наибольшее значение функции достигается в правом конце отрезка, то есть в точке 3.
Ответ: 3.
7. На рисунке изображён график функции , определённой на интервале
. Найдите количество точек, в которых касательная к графику функции параллельна прямой
Прямая параллельна оси абсцисс. Найдем на графике функции
точки, в которых касательная параллельна оси абсцисс, то есть горизонтальна. Таких точек на графике 7. Это точки максимума и минимума.
Ответ: 7.
8. На рисунке изображен график производной функции , определенной на интервале
Найдите количество точек максимума функции
на отрезке
Очень внимательно читаем условие задачи. Изображен график производной, а спрашивают о точках максимума функции. В точке максимума производная равна нулю и меняет знак с «плюса» на «минус». На отрезке такая точка всего одна! Это
Ответ: 1.
9. На рисунке изображен график производной функции , определенной на интервале
Найдите точку экстремума функции
на отрезке
Точками экстремума называют точки максимума и минимума функции. Если производная функции в некоторой точке равна нулю и при переходе через эту точку меняет знак, то это точка экстремума. На отрезке график производной (а именно он изображен на рисунке) пересекает ось абсцисс в точке
В этой точке производная меняет знак с минуса на плюс.
Значит, является точкой экстремума.
Первообразная и формула Ньютона-Лейбница
Функция , для которой
является производной, называется первообразной функции
Функции вида
образуют множество первообразных функции
10. На рисунке изображён график — одной из первообразных некоторой функции
, определённой на интервале
Пользуясь рисунком, определите количество решений уравнения
на отрезке
Функция для которой
является производной, называется первообразной функции
Это значит, что на графике нужно найти такие точки, принадлежащие отрезку , в которых производная функции
равна нулю. Это точки максимума и минимума функции
На отрезке
таких точек 4.
Ответ: 4.
Больше задач на тему «Первообразная. Площадь под графиком функции» — в этой статье
Первообразная функции. Формула Ньютона-Лейбница.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задание №7. Производная. Поведение функции. Первообразная u0026#8212; профильный ЕГЭ по Математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023



































