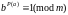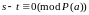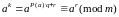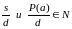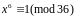-
Линейные сравнения: критерий разрешимости и количество решений.
Теорема.
Пусть НОД(a,m)
= d.
Сравнение ax≡b(mod
m)
имеет решение т.и.т когда d
делит b.
Если b:d,
то сравнение имеет d
решений.
Цепные
дроби
=a1
+

×
=
Pn×Qn-1-QnPn-1=(-1)n
m×Qn-1
— a× Pn-1=(-1)n
–a×
Pn-1≡(–1)n
(mod
m)
a×
Pn-1≡(–1)n-1
(mod m) или
(–1)n-1
a× Pn-1
≡1
(mod
m)
(–1)n-1
a×
Pn-1
≡b
(mod
m)
получаем
x≡(–1)n-1
b×
Pn-1
(mod
m)
– решение сравнения первой степени с
одним неизвестным.
Пример:
111x≡75(mod
321) |:3|
37x≡25(mod
107)
d
= 3 => три
решения
=
2
+
=2
+
= 2 +

=
1
+
= 1+
=
8 +
= 8 +
n=4
-
2
1
8
4
qs
ps
1
2
3
26
107
-
Метод
подбора решения линейных сравнений.
1)5x
7(mod

НОД(5,8)=1
=> 1- решение
Проверим
числа с помощью системы вычетов по mod
8
0;
±1; ±2; ±3; 4;
x≡3(mod

2)
6x≡7(mod
15)
НОД(6,15)=3,
но 7 не кратно 3 => сравнение не имеет
решений
3)
15x≡35(mod
55)
3x≡7(mod
11)
x≡6(mod
11); x≡6(mod
55); x≡17(mod
55)
x≡39(mod
55);
x≡50(mod
55);
-
Решение
линейных сравнений с помощью теоремы
Эйлера.
λ≡aɸ(m)–1b(mod
m)
1)9x≡8(mod
34)
x≡aɸ(m)–1b(mod
m),
НОД(9, 34)=1 – значит сравнение имеет
единственное решение
ɸ(34)=ɸ(2×17)=1×16=16
x≡916×8(mod
34) |:| x≡330×8(mod
34)
x≡314×8(mod
34)
x≡3–2×8(mod
34)
x≡232×8(mod
34)≡529×8(mod 34)
-
Решение
линейных сравнений методом преобразования
коэффициентов.
1)
5x≡7(mod

5x≡15(mod


2)7x≡6(mod
15)
7x≡21(mod
15) => x≡3(mod
15)
3)17x≡25(mod
28)
45x≡25(mod
28)
9x≡5(mod
28) => 9x≡5–140(mod
28) =>
9x≡–135(mod
28)
x≡–15(mod
28) => x≡13(mod
28)
-
Порядок
числа по данному модулю.

Теорема.
(НОД(a,m)=1).
Если
,
то P(a)=P(b).
Док-во.
,
по определению
,
а значит
,
P(a)
P(b).
,
Если
числа сравнимы по модулю, то их порядки
одинаковы. ч.т.д.
Следствие.
Все числа одного и того же класса имеют
одни и те же порядки.
Теорема.
Если
Док-во:

Cледствие.
Порядок элемента делит
,
т.е.
.
Это следует из теоремы Эйлера.
Теорема.
as
at
когда
.
Д-во:
НЕОБХОДИМОСТЬ:
as
at
s
и
t – натуральные,
.
Разделим
=>
,
.
Достаточность:
,
тогда
,
k
Z.
=>
.
Теорема.
Все
числа последовательности а,
а2,
… , аk,
… (1), все аk
P(a)
классам, и вычетами которой в каждом
классе будет а, а2,
… , аP(a)
(2). Док-во:
Все числа последов-сти (2) попарно
несравнимы по модулю m,
.
Теорема.
Порядок
элемента P(as)=P(a)
НОД (s,
P(a))=1.
Док-во: пусть НОД (s,
P(a))=1.
Рассмотрим у – такая степень элемента,
что
as
,
=> (as)y
,
=>
,
но по условию НОД (s,
P(a))=1
и
.
Если же НОД (s,
P(a))=d
> 1, то порядок аs
не совпадает с порядком P(a),
покажем это
.
Рассмотрим
.
Теорема.
Обозначим
порядок P(a)=k.
Тогда классы
представляют
различные решения сравнения
,
эти все классы различны. Док-во: Если
.
Пример.
m=36,
P(5)=6,
тогда
.
Решение.
.
Замечание.
Если m=p
– простое число, то других решений НЕТ,
оно имеет не больше чем k
решений.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
Отдельно рассмотрим сравнение по модулю 4 и по модулю 25.
Поскольку многочлен разложим на множители: $%x^3+2x+3=(x+1)(x^2-x+3)$%, а второе из чисел нечётно, то $%xequiv3pmod4$%.
Теперь рассмотрим сравнение по модулю 25. Легко видеть, что если $%x+1$% делится на 5, то и второй сомножитель тоже делится, так как $%(-1)^2-(-1)+3=5$%. Значит, остатки 4, 9, 14, 19, 24 подходят. Если же $%x+1$% не делится на 5, то $%x^2-x+3$% делится на 25. В частности, это число делится и на 5, а по модулю 5 оно сравнимо с $%x^2+4x+3=(x+1)(x+3)$%. Тогда $%x+3$% кратно 5. Положим $%x=5y+2$% и подставим в многочлен. Это даст $%25y^2+15y+5$%. Следовательно, $%3y+1$% делится на 5, а это значит, что $%y=5z+3$%. Итого $%x=5(5z+3)+2=25z+17$%, и мы получаем шестое значение остатка, равное 17.
Из соображений китайской теоремы об остатках, получается, что по модулю 100 решений тоже шесть. Их нетрудно выписать: для первых пяти значений $%x+1$% делится на 20, что даёт 19, 39, 59, 79, 99. Для особого значения получается 67 (это 17+25+25; остаток 3 от деления на 4).
1.2.5 Сравнения первой степени
Любое сравнение первой степени с одним неизвестным 
 |
( 1.4) |
где 
Выясним условия, при которых сравнение (1.4) имеет:
- единственное решение,
- несколько решений,
- не имеет решений.
Теорема 1.17 Для того, чтобы сравнение (1.4) имело хотя бы одно решение, необходимо и достаточно, чтобы число 

Пример 1.24 Сравнение 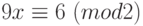
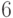

Пример 1.25 Сравнение 

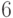
Теорема 1.18 Пусть сравнение (1.4) разрешимо и 
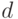




Пример 1.26 Сравнение 
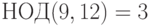



Пример 1.27 Сравнение 


Покажем, как решать сравнение первой степени. Рассмотрим случай 


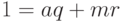
Умножим обе части этого равенства на 
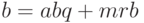

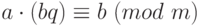
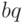
Другой способ: использовать теорему Эйлера. Пусть, снова, 





Допустим теперь, что 









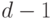
Итак, если 



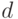

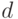
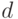
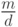
Пример 1.28 Решим сравнение: 
Вычисляем 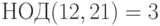
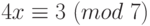
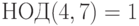

Поясним:



Таким образом, 6 — это одно из решений сравнения 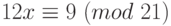
Проверка: 
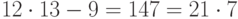

Пример 1.29 
Так как 

Пример 1.30 
Поскольку 
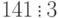
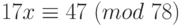
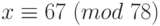
Решения исходного сравнения найдём по теореме 1.18: