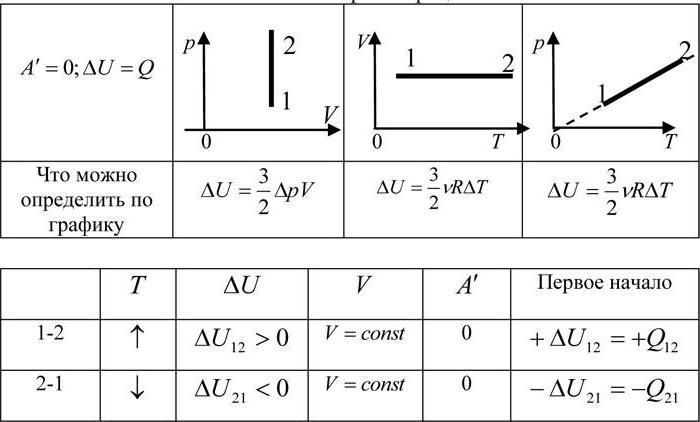
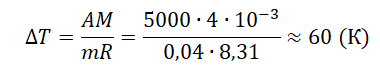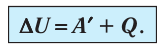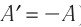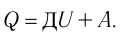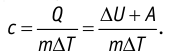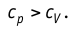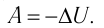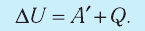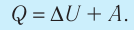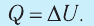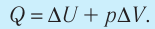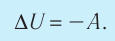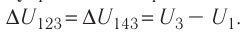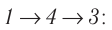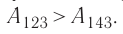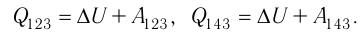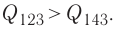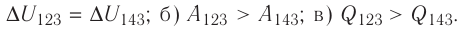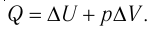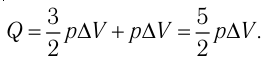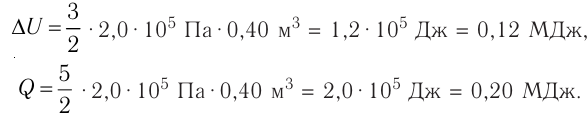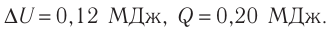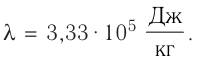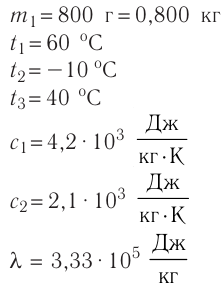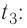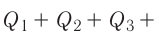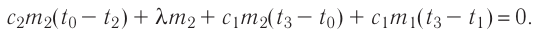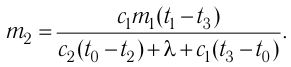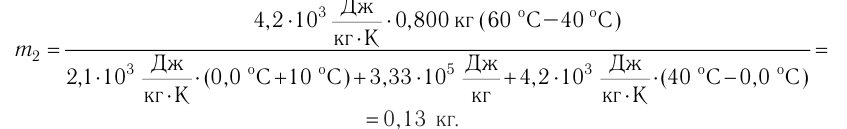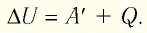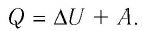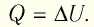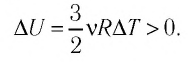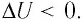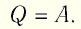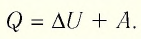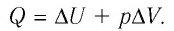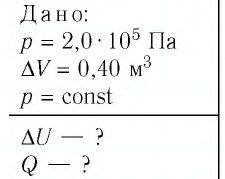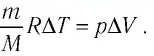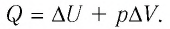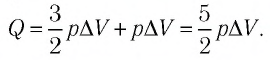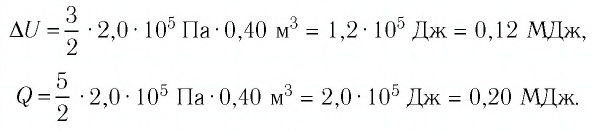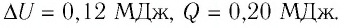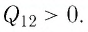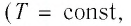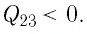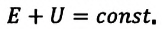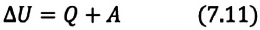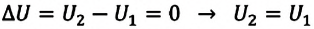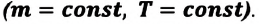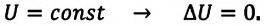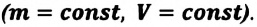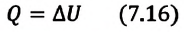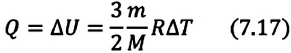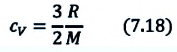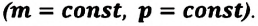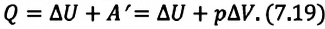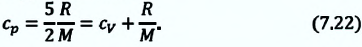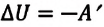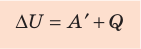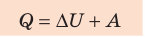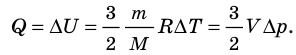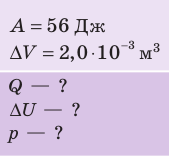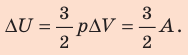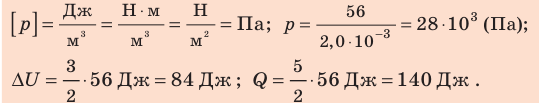Первое начало термодинамики (первый закон термодинамики) представляет собой закон сохранения энергии в тепловых процессах.
Первое начало термодинамики
Внутренняя энергия идеального газа изменяется двумя способами: за счет теплопередачи или при совершении работы.
±ΔU=±Q±A‘
Пояснение:
- +∆U — внутренняя энергия газа увеличивается.
- –∆U — внутренняя энергия газа уменьшается.
- +Q — газ нагревают (газу передают количество теплоты).
- –Q — газ охлаждается (газ отдает тепло окружающей среде).
- +A’ — газ сжимает внешняя сила.
- –A’ — газ расширяется, совершая работу.
Внимание! Знак перед работой показывает, как процесс совершения работы влияет на изменение внутренней энергии газа.
Пример №1. В некотором процессе внутренняя энергия газа уменьшилась на 300 Дж, а газ совершил работу 500 Дж. Какое количество теплоты было сообщено газу?
Чтобы рассчитать количество теплоты, сообщенное газу, нужно найти разность между изменением внутренней энергии и работой, совершенным газом. Для этого нужно правильно определить их знаки. Так как внутренняя энергия уменьшилась, она отрицательна. Но работа положительна. Поэтому газу было сообщено следующее количество теплоты:
Q = A – U = 500 – 300 = 200 (Дж)
Зависимость физических величин
Выясним, от чего зависят величины, входящие в формулу первого начала термодинамики. Изменение внутренней энергии идеального газа зависит от изменения температуры:
ΔU=32νRΔT
Работа идеального газа зависит от изменения его объема:
A‘=pΔV
Первое начало термодинамики для изопроцессов
| Изотермический процесс (T = const) |
ΔU=0, Q=A‘ |
| Изохорный процесс (V = const) |
A‘=0, ΔU=Q |
| Изобарное расширение газа (p = const) |
ΔU=Q−pΔV ΔU=Q−νRΔT |
| Адиабатный (система не получает тепло извне и не отдает его окружающей среде, или Q = 0) |
Q=0, ΔU=A‘ |
Пример №2. Идеальный одноатомный газ находится в сосуде с жесткими стенками объемом 0,6 куб. м. При нагревании его внутренняя энергия увеличилась на 18 кДж. На сколько возросло давление газа?
18 кДж = 18000 Дж
Внутреннюю энергию газа можно определить по формуле:
ΔU=32νRΔT
Отсюда изменение температуры равно:
ΔT=2ΔU3νR
Уравнение состояния идеального газа для 1 и 2 состояния:
p1V=νRT1
p2V=νRT2
Отсюда давления равны:
p1=νRT1V
p2=νRT2V
Разность давлений:
p2−p1=νRT2V−νRT1V=νRVΔT=νRV·2ΔU3νR=2ΔU3V
p2−p1=2·180003·0,6=20000 (Па)=20 (кПа)
Графические задачи на первое начало термодинамики
Рассмотрим графический способ решения задачи на первое начало термодинамики на конкретном примере.
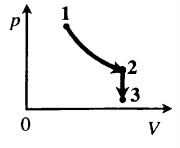
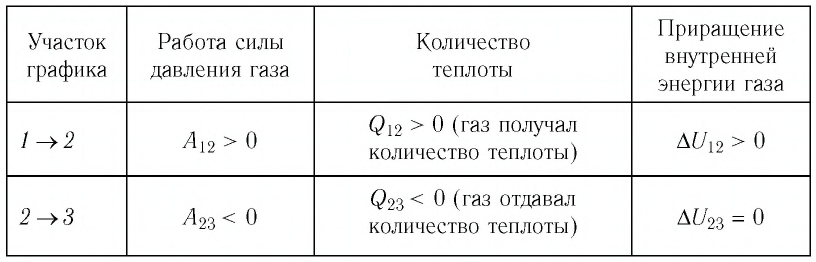
Задача: Один моль идеального одноатомного газа сначала изотермически расширился (T1 = 300 К). Затем газ охладили, понизив давление в 3 раза (см. рисунок). Какое количество теплоты отдал газ на участке 2–3?
Порядок решения:
1. Определить температуры для всех указанных точек, учитывая графики процессов, масштаб и условие задачи.
T1 = T2 = 300 К; T3 = 100 К
2. Определить, к какому изопроцессу относится тот участок графика, о котором спрашивают в задаче.
Участок 2–3 на графике — это изохорный процесс, так как давление остается постоянным.
3. Записать для него первое начало термодинамики.
В данном процессе:
ΔU=Q
4. Учитывая характер изменения величин, правильно расставить знаки: −ΔU=−Q.
5. Подставляя в первое начало термодинамики формулы для расчета изменения внутренней энергии и работы газа, решить задачу.
Формула изменения внутренней энергии газа:
ΔU=32νRΔT
Формула работы газа:
A‘=pΔV
Так как процесс изохорный, работа газа равна нулю. Поэтому количество теплоты, отданное газом на участке 2–3, равно изменению внутренней энергии газа:
Изменение внутренней энергии равно:
Q23=32νRΔT23=32·1·8,31·200=2493 (Дж)
Задание EF17492
- A
- B
- C
- D
Алгоритм решения
- Определить тип теплопередачи.
- Вспомнить, как происходит этот тип теплопередачи.
- Сделав анализ рисунка, установить, какой брусок имеет указанную в задаче температуру.
Решение
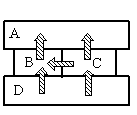
Так как это твердые тела, поверхности которых соприкасаются друг с другом, и перенос тепла происходит без переноса вещества, то этот вид теплопередачи является теплопроводностью. Тепло всегда направлено от более нагретого тела к менее нагретому.
На рисунке видно, что самым нагретым телом является нижний брусок, так как он только отдает тепло, но не принимает его. Средний брусок справа менее нагрет, чем нижний, так как принимает от него тепло. Но он более теплый по сравнению со средним бруском слева, так как он делится с ним теплом. И оба этих бруска отдают свою энергию верхнему бруску, который сам только принимает тепло, но не отдает его. Следовательно, именно он имеет температуру +40 оС.
Ответ: A
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17758
Один моль аргона, находящийся в цилиндре при температуре T1=600 K и давлении p1=4⋅105 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p2=105 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?
Алгоритм решения
1.Записать исходные данные.
2.Записать уравнение состояния идеального газа.
3.Записать формулу для расчета внутренней энергии газа.
4.Используя первое начало термодинамики, выполнить общее решение задачи.
5.Подставив известные данные, вычислить неизвестную величину.
Решение
Запишем исходные данные:
• Начальная температура газа: T1 = 600 К.
• Начальное давление: p1 = 4∙105 Па.
• Конечное давление: p2 = 105 Па.
• Работа, совершенная газом: A = 2493 Дж.
Аргон является одноатомным газом. Поэтому для него можно использовать уравнение состояния идеального газа:
pV=νRT
Внутренняя энергия одноатомного идеального газа пропорциональна температуре:
U=32νRT
Внутренняя энергия аргона до расширения и после него:
U1=32νRT1
U2=32νRT2
Согласно условию задачи, температура при расширении обратно пропорциональна объёму. Следовательно:
T=constV
T1V1=T2V2
Выразим конечную температуру:
T2=T1V1V2
Составим уравнение состояния газа для состояний аргона 1 и 2:
p1V1=νRT1
p2V2=νRT2
Отсюда:
νR=p1V1T1=p2V2T2
Отсюда отношение объема аргона в состоянии 1 к объему газа в состоянии 2 равно:
V1V2=p2T1p1T2
Подставим это отношение в формулу для конечной температуры:
T2=T1V1V2=p2T12p1T2
Отсюда:
T2=T1√p2p1
Отсюда внутренняя энергия газа в состоянии 2 равна:
U2=32νRT1√p2p1
Уменьшение внутренней энергии аргона составило (изначально она была выше):
ΔU=U1−U2=32νRT1−32νRT1√p2p1=32νRT1(1−√p2p1)
В соответствии с первым началом термодинамики уменьшение внутренней энергии равно сумме совершённой работы и количества теплоты, отданного газом:
ΔU=Q+A
Следовательно, газ отдал следующее количество теплоты:
Q=ΔU−A=32νRT1(1−√p2p1)−A
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17562
Газу передали изохорно количество теплоты 300 Дж. Как изменилась его внутренняя энергия в этом процессе?
Ответ:
а) увеличилась на 300 Дж
б) уменьшилась на 300 Дж
в) увеличилась на 600 Дж
г) уменьшилась на 600 Дж
Алгоритм решения
1.Записать исходные данные.
2.Записать первое начало термодинамики.
3.Установить, как меняется внутренняя энергия идеального газа.
Решение
Запишем исходные данные:
• Количество теплоты, переданное газу: Q = 300 Дж.
Первое начало термодинамики:
ΔU=Q+A
Так как по условию задачи это изохорный процесс, то работа равна 0. Следовательно, изменение внутренней энергии газа равно количеству теплоты:
ΔU=Q=300 (Дж)
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17597
Находясь в цилиндре двигателя, газ получил от нагревателя количество теплоты, равное 10 кДж. Затем он расширился, совершив работу 15 кДж. В результате всех этих процессов внутренняя энергия газа уменьшилась на
Ответ:
а) 5 кДж
б) 10 кДж
в) 15 кДж
г) 25 кДж
Алгоритм решения
1.Записать исходные данные.
2.Записать первое начало термодинамики.
3.Установить, как меняется внутренняя энергия идеального газа.
Решение
Запишем исходные данные:
• Количество теплоты, переданное газу: Q = 10 кДж.
• Работа, совершенная газом: A = 15 кДж.
Первое начало термодинамики:
ΔU=Q+A
В этой формуле за работу принимается та работа, что совершается над газом. Но в данном случае газ сам совершает работу. Поэтому первое начало термодинамики примет вид:
ΔU=Q−A=10−15=−5 (кДж)
Знак «–» указывает на то, что внутренняя энергия газа уменьшилась на 5 кДж.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17579
При постоянном давлении гелий нагрели, в результате чего он совершил работу 5 кДж? Масса гелия 0,04 кг. Насколько увеличилась температура газа?
Ответ:
а) 60 К
б) 25 К
в) 15 К
г) 3 К
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Записать первое начало термодинамики.
3.Записать формулу для расчета работы газа.
4.Выполнить решение задачи в общем виде.
5.Подставить известные данные и выполнить вычисления искомой величины.
Решение
Запишем исходные данные:
• Газ совершил работу: A = 5 кДж.
• Масса гелия: m = 0,04 кг.
5 кДж = 5000 Дж
Первое начало термодинамики:
ΔU=Q+A
Учтем, что не над газом совершают работу, а сам газ совершает ее:
Отсюда:
ΔU=Q−A
Так как газ нагревали изобарно, часть тепла ушла на изменение внутренней энергии газа, а часть — на совершение этим газом работы.
Работа, совершенная газом, равна:
A=pΔV=mMRΔT
Молярная масса гелия равна 4∙10–3 кг/моль.
Отсюда:
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 3.9k
Основы термодинамики
В
основе термодинамики лежат три
фундаментальных закона, называемых
началами термодинамики.
Первое
начало термодинамики:
Количество
теплоты, сообщённое газу, идёт на
приращение внутренней энергии газа и
на совершение газом работы над внешними
телами.
—
первое начало термодинамики.
Определим физические
величины, входящие в этот закон.
а)
Внутренняя
энергия
идеального газа равна
,
где
— количество вещества,
i
– число степеней свободы молекул газа.
Тогда
изменение внутренней энергии газа равно
—
изменение внутренней энергии
газа.
Рис.
1
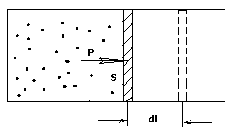
б) Вычислим теперь
работу, совершаемую
газом при изменении объёма. Для этого
рассмотрим газ, находящийся в цилиндре
под поршнем, который может свободно
перемещаться. При нагревании давление
газа P
, будет оставаться постоянным, и, как
видно из рисунка, работа, которую
совершает газ, будет равна:
,
где
dV
= S
dl
— изменение объема газа.
работа,
совершаемая газом при изменении его
объема
—
в)
Наконец, найдём формулу для подсчёта
количества теплоты, сообщенной газу
массы
при его нагревании на
.
Для этого введем понятие молярной
теплоёмкости газа
.
Молярная теплоёмкость газа – это
количество теплоты, сообщённой 1 молю
газа, для увеличения его температуры
на
.
Тогда формула
для подсчёта теплоты будет иметь вид
—
теплота,
сообщённая газу для
увеличения его
температуры на dT.
Применим первое начало термодинамики
к изопроцессам в газе.
Изопроцесс — это процесс, происходящий
в газе, когда один из параметров,
описывающих газ, является постоянным.
1. Термодинамика
изохорического процесса: V=const
Рассмотрим
закон, описывающий этот процесс и его
график в координатах (P,V).
Этот закон является частным случаем
уравнения состояния идеального газа:
PV
= RT.
Рис.
2

— закон Шарля.
Так как
,
то
и
,
т.е
работа
совершаемая газом при изохорическом
процессе равна нулю.
—
первое
начало термодинамики для изохорического
процесса.
Тогда
—
Поскольку
количество теплоты, сообщенное газу,
равно
,
где
—
молярная теплоёмкость газа при постоянном
объёме, то мы получаем полезную формулу
для подсчёта приращения внутренней
энергии газа:
изменение
внутренней энергии газа.
—
Сравнивая
эту формулу с другой формулой
получим
выражение для молярной теплоёмкости
газа при постоянном объёме:
.
-
Термодинамика
изобарического процесса: P=const.
Соседние файлы в папке Курс лекций по Физике
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Два
моля идеального одноатомного газа сначала расширяются изобарно, а затем
изохорно переходят в состояние с начальной температурой 300 K. Определите количество теплоты, переданной газу, если объем в
этом процессе увеличился в 6 раз.
Решение.
Согласно
первому началу термодинамики количество теплоты, сообщенное системе,
расходуется на увеличение ее внутренней энергии и на работу, совершаемую
системой против внешних сил: Q = DU + A. В частности, при изобарном расширении газа Q1 = DU1 + A1 , где изменение внутренней
энергии газа DU1.
T – температура газа
после завершения этого процесса. При изохорном процессе Q2 = DU2 + A2 = DU2.
Тогда
полное количество переданной газу теплоты Q
= Q2 + Q2 = A1 = (n-1)vRT1 = 5•2,0•8,31•300 = 25
кДж.
Ответ:
Q = 25 кДж.
Источник: Подготовка к тестированию по физике. Шепелевич. В. Г.
Содержание:
Первый закон термодинамики:
При изучении физики в 9 классе вы узнали, что полная механическая энергия замкнутой системы тел сохраняется только при отсутствии трения, а при наличии трения она уменьшается. Куда девается механическая энергия? Если бутылку, заполненную до половины водой при комнатной температуре, встряхивать в течение нескольких минут, то окажется, что вода нагрелась на 1—2 °С. Каким образом нагрелась вода?
В середине XIX века известный английский физик Дж. Джоуль (1818— 1889), проведя многочисленные опыты, показал, что совершённая при перемешивании воды механическая работа практически равна увеличению её внутренней энергии. Опыты Джоуля, а также исследования немецкого врача и естествоиспытателя Р. Майера (1814—1878), немецкого профессора физиологии и одного из самых знаменитых физиков второй половины XIX века Г. Гельмгольца (1821 —1894) позволили сформулировать закон сохранения и превращения энергии, распространив его на все явления природы. Согласно этому закону при любых взаимодействиях материальных объектов энергия не исчезает и не возникает из ничего, она только передаётся от одних объектов к другим или превращается из одной формы в другую.
Для термодинамических систем (в термодинамике обычно рассматривают макроскопически неподвижные системы) закон сохранения и превращения энергии называют первым законом термодинамики. Согласно первому закону термодинамики, приращение внутренней энергии термодинамической системы при переходе из одного состояния в другое равно алгебраической сумме работы, совершённой внешними силами, и количества теплоты, полученного или отданного системой при взаимодействии с внешними телами:
Поскольку работа внешних сил равна работе, совершаемой термодинамической системой, взятой с противоположным знаком (
Если система представляет собой действующее устройство, периодически возвращающееся в исходное состояние, то при этом AU-0 и A-Q. Механизм, который мог бы совершать работу без изменения состояния составляющих его тел и без теплопередачи от внешних тел, называют «вечным двигателем первого рода». Поэтому первый закон термодинамики можно сформулировать и следующим образом: невозможен вечный двигатель первого рода, т. е. такой двигатель, который при неизменном значении собственной внутренней энергии совершал бы работу большую, чем энергия, получаемая им извне.
Применим первый закон термодинамики к различным изопроцессам, происходящим с идеальным одноатомным газом.
Изохорный процесс
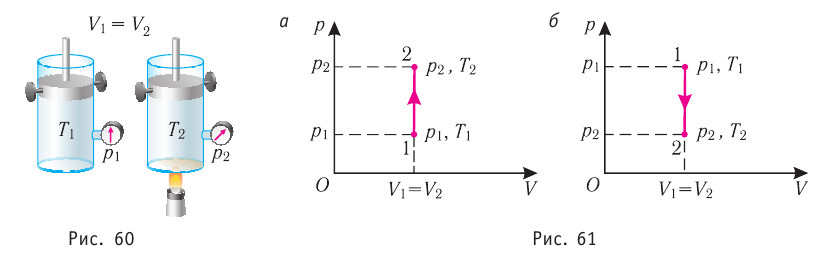
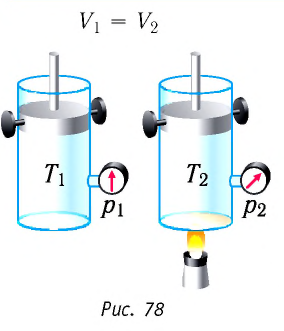
Пусть идеальный одноатомный газ находится в цилиндрическом сосуде, закрытом неподвижным поршнем (V = const). Нагреем сосуд с газом. Объём газа остаётся практически постоянным (тепловым расширением сосуда пренебрегаем) (рис. 60), следовательно, работа силы давления газа А= 0. Тогда первый закон термодинамики примет вид
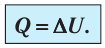
Это означает, что всё передаваемое газу количество теплоты идёт на увеличение его внутренней энергии. При этом приращение внутренней энергии газа 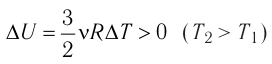
процессе отдаёт количество теплоты, то его внутренняя энергия убывает:
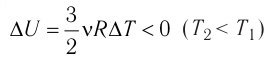
Изотермический процесс
Пусть цилиндрический сосуд с газом под поршнем находится в термостате — устройстве, в котором поддерживается постоянная температура. В этом случае внутренняя энергия идеального одноатомного газа 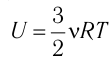
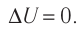
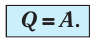
Какие выводы следуют из этого? Если с помощью внешнего устройства медленно перемещать поршень в сосуде так, чтобы объём газа увеличивался (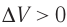
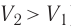
Если же внешнее устройство обеспечивает медленное уменьшение объёма газа в сосуде (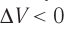
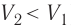
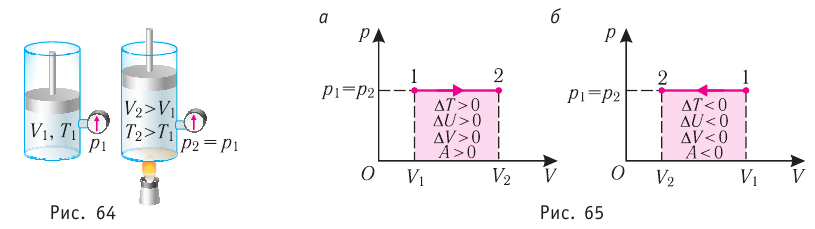
Изобарный процесс
Пусть газ находится в цилиндрическом сосуде, закрытом поршнем, который может свободно или под постоянной нагрузкой перемещаться (рис. 64). Нагреем газ, передав ему некоторое количество теплоты (Q > 0). Согласно первому закону термодинамики (11.2) переданное газу количество теплоты частично расходуется на увеличение внутренней энергии 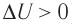
При изобарном процессе работа расширения (сжатия) газа 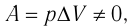
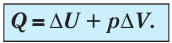
При изобарном сжатии газа внешние силы совершают работу А’ > 0. Чтобы давление газа при этом оставалось постоянным, газ необходимо охлаждать, т. е. он должен отдавать в окружающую среду некоторое количество теплоты (Q < 0). Понижение температуры газа при изобарном сжатии приводит к уменьшению его внутренней энергии (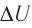
Удельная теплоёмкость вещества зависит не только от его свойств, но и от характера осуществления процесса теплопередачи. Действительно, из формулы (10.4) следует, что удельная теплоемкость
Тогда согласно первому закону термодинамики при изохорном процессе (11.3)
удельная теплоёмкость идеального газа 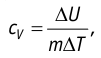
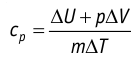
Это объясняется тем, что при постоянном давлении часть подводимой энергии расходуется на совершение силой давления газа работы при расширении.
Расширение жидких и твёрдых тел при нагревании при постоянном давлении значительно меньше, чем газов, поэтому для них 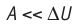
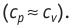
Адиабатный процесс
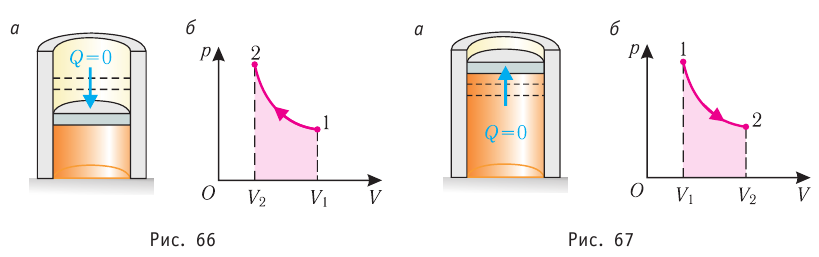
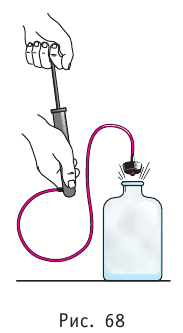
Адиабатным называют процесс, в ходе которого термодинамическая система не получает и не отдаёт энергию путём теплопередачи. Таким образом, при адиабатном процессе
Q = 0.
Применяя к этому процессу первый закон термодинамики, получим:
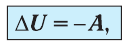
или
При адиабатном процессе изменение внутренней энергии системы происходит только за счёт совершения работы. Если внешние силы совершают работу по сжатию газа (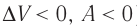
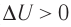
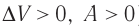
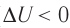
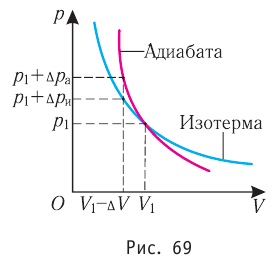
Если процесс протекает очень быстро, то теплопередача практически не сказывается. Очень нагляден опыт, иллюстрирующий уменьшение температуры газа при его адиабатном расширении. Используя насос, через отверстие в пробке будем накачивать в стеклянный сосуд воздух (рис. 68). Через некоторый промежуток времени накачивания сжатый воздух совершит работу по преодолению силы трения, с которой сосуд действует на пробку, и силы атмосферного давления. Теплопередача между сосудом и окружающими телами не успевает проявиться за тот малый промежуток времени, пока пробка вылетает из сосуда. Уменьшение внутренней энергии воздуха в сосуде выражается в понижении его температуры, что приводит к конденсации водяных паров, т. е. к образованию тумана.
В качестве примера адиабатного процесса можно привести охлаждение воздуха в атмосфере. Нагретый возле поверхности Земли воздух при быстром подъёме в верхние слои атмосферы расширяется почти адиабатно и при этом резко охлаждается. Водяной пар в нём конденсируется в маленькие капли воды и кристаллики льда, образуя облака. Близкий к адиабатному процесс используют в двигателях внутреннего сгорания.
Обратимый адиабатный процесс относят к изопроцессам, так как он характеризуется постоянством функции состояния, называемой энтропией. В отличие от остальных изопроцессов при обратимом адиабатном процессе происходят изменения давления, объёма и температуры. График адиабатного процесса в координатах (р, V) похож на график изотермического процесса (рис. 69). Однако одному и тому же изменению объёма 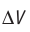
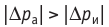
Это объясняется тем, что в случае адиабатного расширения давление 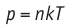
1. Приращение внутренней энергии термодинамической системы при
переходе из одного состояния в другое равно алгебраической сумме работы, совершённой внешними силами, и количества теплоты, полученного или отданного системой при взаимодействии с внешними телами:
2. Количество теплоты, полученное или отданное термодинамической системой при взаимодействии с внешними телами при её переходе из одного состояния в другое, идёт на приращение внутренней энергии системы и на работу, которую система совершает при расширении:
3. При изохорном процессе всё передаваемое системе количество теплоты идёт на увеличение её внутренней энергии:
4. При изотермическом процессе работа расширения или сжатия идеального газа сопровождается теплопередачей между газом и термостатом:
A=Q.
5. При изобарном процессе переданное идеальному газу количество теплоты частично расходуется на увеличение внутренней энергии газа и частично идёт на совершение работы газом при его расширении:
6. При адиабатном процессе приращение внутренней энергии газа равно работе, которую совершает сила давления газа, взятой с противоположным знаком:
Пример №1
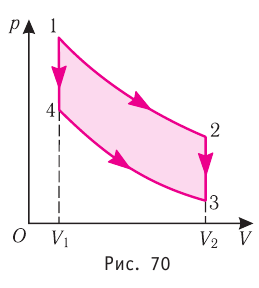
Идеальный газ, масса которого постоянна, переводят из состояния / в состояние 3 двумя различными способами: 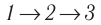
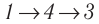
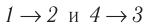
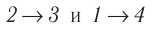
Решение, а) Так как начальное и конечное состояния для обоих переходов одинаковы, то будут одинаковы и приращения внутренней энергии:
б) Из рисунка 70 видно, что площадь фигуры, ограниченной осью OV, изотермой и изохорами, проходящими через точки 3 и 4, меньше площади фигуры, ограниченной осью ОV, изотермой и изохорами, проходящими через точки 1 и 2. Следовательно, в процессе перехода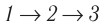
в) Из первого закона термодинамики следует:
Поскольку приращения внутренней энергии в обоих случаях одинаковы, а совершённая силой давления газа работа больше при переходе 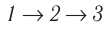
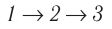
Ответ: а)
Пример №2
Идеальный одноатомный газ, давление которого 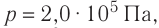
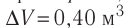
Дано:
р = 2,0 • 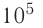
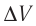
р =const
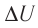
Решение. Приращение внутренней энергии идеального одноатомного газа 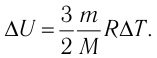
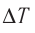
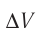
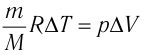
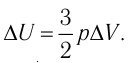
Отсюда
Ответ:
Пример №3
В сосуд налита вода массой 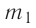
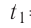
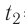
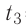
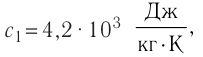
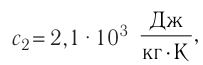
Дано
Решение. Если пренебречь потерями энергии в окружающую среду, то термодинамическая система «сосуд—вода—лёд» является изолированной. Поэтому учитываем только обмен энергией между входящими в систему телами при теплопередаче. Рассмотрим тепловые процессы, происходящие в системе: 1) нагревание льда от температуры 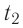
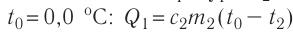
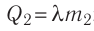
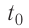
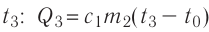
массой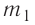
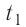
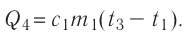
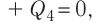
Отсюда масса льда
Ответ: 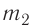
Первый закон термодинамики
В 9-м классе вы узнали, что полная механическая энергия замкнутой системы тел сохраняется только при отсутствии трения, а при наличии трения она уменьшается. Куда девается механическая энергия?
Закон сохранения энергии
В середине XIX в. известный английский физик Дж. Джоуль (1818—1889), проведя многочисленные опыты, показал, что совершённая при перемешивании воды механическая работа практически равна увеличению её внутренней энергии. Опыты Джоуля, а также исследования немецкого врача и естествоиспытателя Р. Майера (1814—1878), немецкого профессора физиологии и одного из самых знаменитых физиков второй половины XIX в. Г. Гельмгольца (1821 — 1894) позволили сформулировать закон сохранения и превращения энергии, распространив его на все явления природы.
Закон сохранения и превращения энергии: при любых взаимодействиях материальных объектов энергия не исчезает и не возникает из ничего, она только передаётся от одних объектов к другим или превращается из одной формы в другую.
Закон сохранения и превращения энергии является всеобщим законом природы и связывает воедино все физические явления. Этот закон выполняется абсолютно точно, на нём базируется всё современное естествознание.
Первый закон термодинамики:
В предыдущих параграфах мы рассматривали процессы, в которых внутренняя энергия системы изменялась или при совершении работы, или в результате теплообмена. Однако чаще всего при переходе системы из одного состояния в другое внутренняя энергия изменяется как за счёт совершения работы, так и за счёт теплообмена с окружающими телами.
Для термодинамических систем закон сохранения и превращения энергии называют первым законом термодинамики.
Первый закон термодинамики: приращение внутренней энергии термодинамической системы при переходе из одного состояния в другое равно алгебраической сумме работы, совершённой внешними силами, и количества теплоты, полученного (или отданного) системой при взаимодействии с внешними телами.
Поскольку работа внешних сил равна работе, совершаемой термодинамической системой, взятой с противоположным знаком 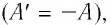
Количество теплоты, полученное (или отданное) термодинамической системой при взаимодействии с внешними телами при её переходе из одного состояния в другое, идёт на приращение внутренней энергии системы и на работу, которую она совершает против внешних сил:
Применим первый закон термодинамики к различным изопроцессам изменения состояния идеального одноатомного газа.
Рассмотрим в качестве термодинамической системы идеальный одноатомный газ, находящийся в цилиндрическом сосуде, закрытом поршнем.
Изохорный процесс:
Если сосуд закрыт неподвижным поршнем, то при нагревании объём газа остаётся постоянным 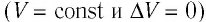
При изохорном процессе всё передаваемое газу количество теплоты идёт на увеличение его внутренней энергии:
Если газ при изохорном процессе отдаёт количество теплоты, то его внутренняя энергия убывает:
Изотермический процесс:
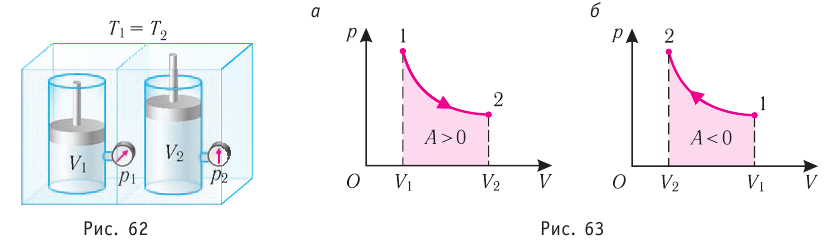
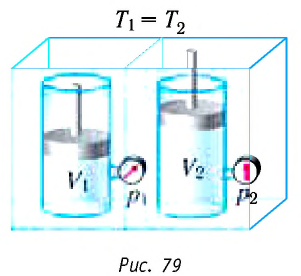
Поместим сосуд с газом, находящимся под подвижным поршнем, в термостат — устройство, в котором поддерживается постоянная температура (рис. 79). С помощью внешнего устройства медленно переместим поршень в сосуде так, чтобы объём газа увеличился (или уменьшился). Значения температуры газа в начальном и конечном состояниях одинаковы. В этом случае внутренняя энергия идеального одноатомного газа 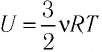
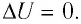
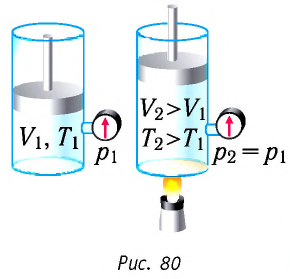
При изотермическом процессе переданное газу количество теплоты расходуется на совершение газом работы.
Изобарный процесс:
Если сосуд закрыт подвижным поршнем, то при нагревании увеличится как температура газа, так и его объём (рис. 80). Тогда первый закон термодинамики имеет вид:
При изобарном процессе переданное газу количество теплоты частично расходуется на увеличение внутренней энергии системы и частично идёт на совершение работы силой давления газа при его расширении.
С учётом того, что при изобарном процессе работа расширения (сжатия) газа 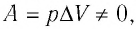
Пример №4
Идеальный одноатомный газ, давление которого 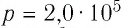
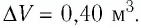
Решение. 11риращение внутренней энергии идеального одноатомного газа 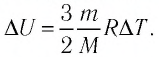
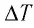
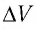
Тогда 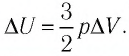
Следовательно,
Ответ:
Пример №5
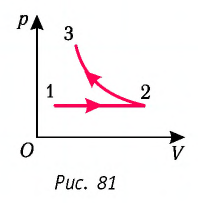
На рисунке 81 представлен график процесса изменения состояния некоторой массы идеального газа (участок 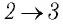
Решение. Участок 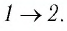
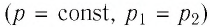
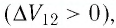
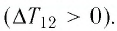
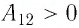
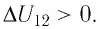
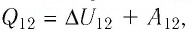
Участок 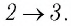
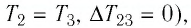
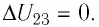
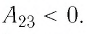
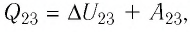
Ответ:
Определение первого закона термодинамики
Невозможно представить себе повседневную жизнь без разноцелевой техники, облегчающей нашу жизнь. При помощи этой техники люди вспахивают землю, добывают нефть, газ, руду и другие полезные ископаемые, «сокращают» большие расстояния и т.д. Главное свойство всей техники — способность совершения ими работы.
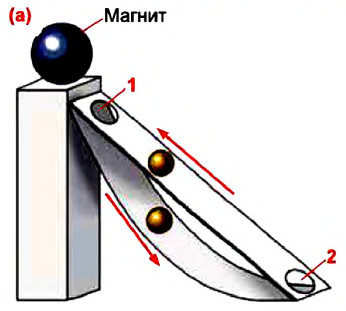
По этой причине еще с древних времен люди пытались создать способный работать вечно perpetuum mobile, то есть вечный двигатель. Как одну из интересных работ в этом направлении можно показать оригинальный проект, предложенный английским священником Джоном Уилкенсином в XVII веке, основанный на действии магнитного поля. По идее проекта, вечный двигатель должен работать так: шарообразный магнит помещен на высокую опору, к которой прикрепляются две наклонные плоскости, верхняя плоскость прямолинейная, а нижняя изогнутая (а).
В результате притяжения магнитом шарик, помещенный в нижней части прямой плоскости, начинает подниматься вверх и проваливается на нижнюю плоскость через отверстие 1 в верхней части плоскости. Затем, скатываясь вниз по изогнутой плоскости, снова попадает на прямую плоскость через отверстие 2, и всё повторяется снова.
Первый закон термодинамики:
Согласно одному из фундаментальных законов природы — закону сохранения энергии, полная энергия (механическая и внутренняя энергия) замкнутой системы остается постоянной при всех процессах, происходящих внутри этой системы:
Закон сохранения энергии, применяемый к тепловым процессам, называют первым законом термодинамики:
Изменение внутренней энергии термодинамической системы равно количеству теплоты, переданному этой системе, и работе внешних сил, совершенной над системой:
Над замкнутой и изолированной системой внешние силы не совершают работу 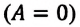
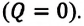
Так как работа, совершаемая системой над внешними силами, равна работе, совершаемой внешними силами над системой с противоположным знаком: 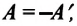
Количество теплоты, сообщенное термодинамической системе, затрачивается на изменение ее внутренней энергии и работу, которую система совершает против внешних сил:
После открытия закона сохранения энергии стала очевидной невозможность создания вечного двигателя первого рода:
Вечный двигатель первого рода (perpetuum mobile I) — это двигатель, который будучи однажды приведен в действие и не получая энергию извне, совершает работу вечно.
Согласно выражению (7.11), для совершения работы система или должна получать энергию извне, или использовать свою внутреннюю энергию:
В противном случае, то есть если 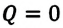
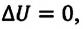
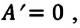
Применение первого закона термодинамики к разным процессам
1. Изотермический процесс
Так как в этом процессе температура системы остается постоянной, то и ее внутренняя энергия остается постоянной, изменение же внутренней энергии равно нулю:
Из выражений первого закона термодинамики (7.11) и (7.12) получаем:
• При изотермическом процессе все количество теплоты, переданное системе, затрачивается на совершение работы.
2. Изохорный процесс
Так как в этом процессе объем системы остается постоянным, то из выражения (7.10) следует, что работа не совершается 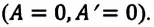
Для одноатомного идеального газа:
• При изохорном процессе количество теплоты, переданное системе, целиком затрачивается на изменение внутренней энергии.
Удельная теплоемкость одноатомного идеального газа, при постоянном объеме
Если в выражении (7.17) учесть выражения внутренней энергии одноатомного идеального газа (7.7) и количества теплоты (7.4), то получим формулу для удельной теплоемкости при постоянном объеме:
3. Изобарный процесс
В этом процессе давление системы остается постоянным, а температура и объем изменяются. Для этого процесса первый закон термодинамики записывается, так:
• При изобарном процессе (расширении) переданное системе количество теплоты затрачивается на увеличение его внутренней энергии и на совершение газом работы против внешних сил.
Удельная теплоемкость одноатомного идеального газа при постоянном давлении
Приняв в (7.19) во внимание выражения для одноатомного идеального газа:
получим:
С учетом этих выражений можно определить удельную теплоемкость одноатомного идеального газа при постоянном давлении как:
Из сравнения выражений (7.20) и (7.21) видно, что при изобарном процессе для одноатомного идеального газа существуют следующие соотношения между переданным количеством теплоты, изменением внутренней энергии и совершенной работой:
4. Адиабатный процесс
Адиабатный процесс — это процесс, происходящий без теплообмена системы с окружающей средой.
Так как в этом процессе отсутствует теплообмен системы со сторонними телами, то первый закон термодинамики можно записать так:
или
При адиабатном расширении газа его температура и внутренняя энергия уменьшаются, то есть газ охлаждается, а при адиабатном же сжатии, наоборот, его температура и внутренняя энергия увеличиваются, то есть газ нагревается.
История первого закона термодинамики
Один из фундаментальных законов природы — закон сохранения и превращения энергии. Первым этот закон сформулировал немецкий врач и физик Юлиус Роберт фон Майер (1814–1878). интересно, что к открытию ученого подтолкнули наблюдения над цветом крови у людей. Майер заметил, что венозная кровь у жителей тропиков светлее, чем у жителей его страны, и по цвету напоминает артериальную. он сделал вывод, что разница в цвете обусловлена количеством потребления кислорода, или «силой процесса сгорания», происходящего в организме. независимо от Майера и совсем иначе к открытию закона сохранения энергии пришли английский промышленник и ученый Джеймс Прескотт Джоуль (1818–1889) и немецкий физик, физиолог и психолог Герман Людвиг Фердинанд фон Гельмгольц (1821–1894). закон сохранения и превращения энергии управляет всеми явлениями природы, неизвестно ни одного случая, когда бы этот закон не выполнялся.
В термодинамике рассматривают системы, механическая энергия которых при переходе из одного термодинамического состояния в другое не изменяется. Тогда, если внешние силы совершили работу A′ и одновременно системе передано определенное количество теплоты Q, вся энергия идет на изменение внутренней энергии системы (∆U) . Закон сохранения и превращения энергии в таком случае называют первым законом (началом) термодинамики:
Изменение внутренней энергии системы ( ∆U) при переходе из одного термодинамического состояния в другое равно сумме работы A′ внешних сил и количества теплоты Q, сообщенного системе или переданного системой окружающим телам в процессе теплообмена:
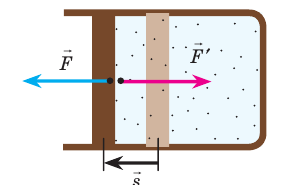
Рис. 38.1. согласно третьему закону ньютона сила 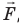
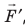
Обратите внимание! Если система получает некоторое количество теплоты, то в приведенной формуле Q берется со знаком «+», если отдает, то со знаком «–». На практике чаще рассматривают не работу A′ внешних сил, а работу A совершаемую данной системой против внешних сил. Учитывая, что A = −A ′ (рис. 38.1), первый закон (начало) термодинамики можно сформулировать так:
Количество теплоты Q, переданное системе, идет на изменение внутренней энергии системы (∆U) и на совершение системой работы A против внешних сил:
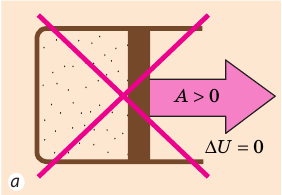
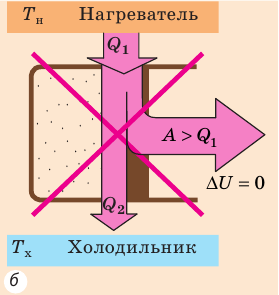
Согласно первому закону термодинамики невозможно создать вечный двигатель первого рода — циклическое устройство, которое совершало бы механическую работу без потребления энергии извне (рис. 38.2, а) или совершало бы работу большую, чем потребляемая им энергия (рис. 38.2, б).
Рис. 38.2. Циклические процессы, которые невозможны с точки зрения первого закона термодинамики
Какой вид имеет первый закон термодинамики для изопроцессов
Рассмотрим, какой вид принимает первый закон термодинамики в случаях, когда идеальному газу неизменной массы передают некоторое количество теплоты таким образом, что один из макроскопических параметров газа (V, p или T) остается неизменным.
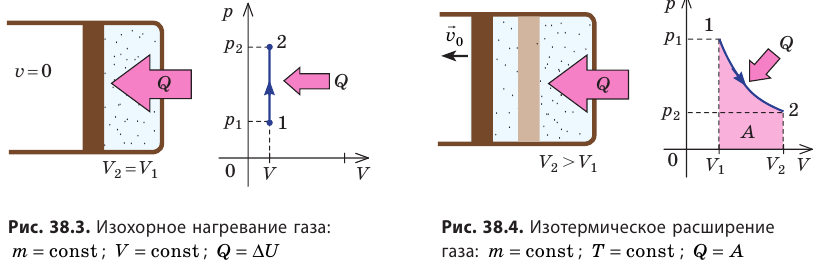
- Изохорный процесс (рис. 38.3). В ходе изохорного процесса объем газа не изменяется (∆V=0) и газ работу не совершает (A = 0), поэтому уравнение первого закона термодинамики имеет вид: Q=∆U . При изохорном процессе все переданное газу количество теплоты расходуется на увеличение внутренней энергии газа. Если идеальный газ одноатомный, то количество теплоты, переданное газу, равно:
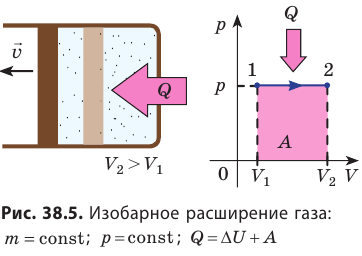
- Изотермический процесс (рис. 38.4). В ходе изотермического процесса температура, а значит, и внутренняя энергия газа не изменяются (∆U=0), поэтому уравнение первого закона термодинамики имеет вид: Q=A.
При изотермическом процессе все переданное газу количество теплоты идет на совершение механической работы.
Каковы особенности адиабатного процесса
Адиабатный процесс — это процесс, который происходит без теплообмена с окружающей средой. При адиабатном процессе количество теплоты Q, переданное системе, равно нулю, поэтому первый закон термодинамики имеет вид: Q=∆U + A, или A = −∆U.
При адиабатном расширении газ совершает положительную работу за счет уменьшения внутренней энергии; температура газа уменьшается.
Поскольку p =nkT, при адиабатном сжатии давление газа возрастает намного быстрее, чем при изотермическом, ведь одновременно с увеличением концентрации молекул газа увеличивается и его температура (рис. 38.6).
Рис. 38.6. изменение давления газа в ходе адиабатного сжатия. синим цветом показана адиабата, красным — изотермы
Аналогично при адиабатном расширении давление падает быстрее, чем при изотермическом, ведь одновременно уменьшаются и концентрация, и температура газа.
В реальных условиях процесс, близкий к адиабатному, можно осуществить, если газ будет находиться в оболочке с очень хорошими термоизоляционными свойствами. Адиабатными можно считать и процессы, которые происходят очень быстро: в таком случае газ не успевает обменяться теплотой с окружающей средой (например, расширение и сжатие воздуха при распространении звуковых волн, расширение газа при взрыве).
Увеличение температуры при резком сжатии воздуха используется в дизельном двигателе, в котором нет системы зажигания горючей смеси.
Пример №6
При изобарном расширении неон совершил работу 56 Дж. Какое количество теплоты передано газу? Каково изменение его внутренней энергии? При каком давлении происходил процесс, если объем газа увеличился на 2,0 л?
Решение:
Для изобарного процесса работа газа равна: A=p∆V. Отсюда 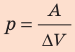
Согласно первому закону термодинамики: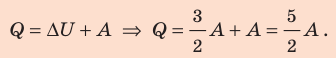
Ответ: Q = 140 Дж; ∆U = 84 Дж; p = 28 кПа.
Выводы:
- Закон сохранения энергии, записанный для тепловых процессов, называют первым законом (началом) термодинамики: количество теплоты, переданное системе, идет на изменение внутренней энергии системы и на совершение системой работы против внешних сил: Q=∆U + A.
- При изохорном процессе газ не выполняет работу (A = 0 ) , поэтому вся теплота, переданная газу, идет на увеличение его внутренней энергии: Q=∆U.
- При изотермическом процессе внутренняя энергия газа не изменяется (∆U=0), поэтому вся теплота, переданная газу, идет на совершение газом работы: Q=A.
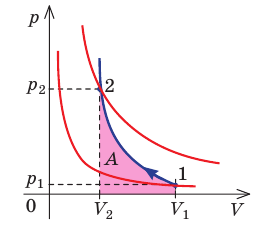
- При изобарном процессе теплота, переданная газу, идет как на увеличение внутренней энергии газа, так и на совершение газом работы: Q=∆U + A.
- При адиабатном процессе газ не получает теплоты (Q = 0) , поэтому увеличение его внутренней энергии происходит за счет совершения над газом работы (адиабатное сжатие): ∆U=A′. Если газ сам совершает работу (адиабатное расширение), его внутренняя энергия уменьшается: A = −∆U.
- Второй закон термодинамики
- Тепловые двигатели и их КПД
- Тепловое состояние тел
- Изменение агрегатного состояния вещества
- Необратимость тепловых процессов
- Адиабатический процесс
- Молекулярно-кинетическая теория
- Работа в термодинамике
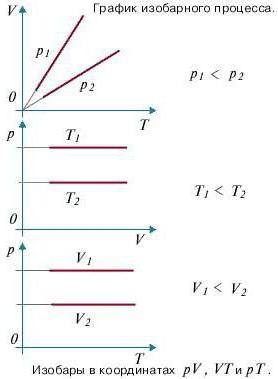
Изобарный процесс, связанные с ним уравнения и вывод формулы работы
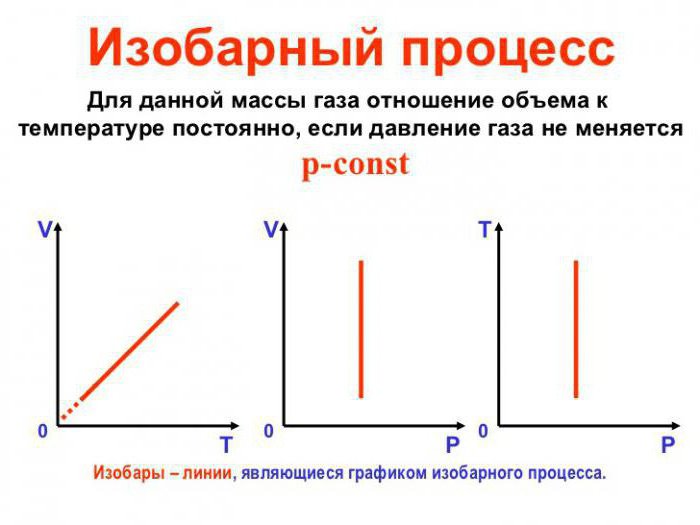
Изобарный процесс (также называемый изобарическим процессом) является одним из термодинамических процессов, которые происходят при постоянном показателе давления. Масса газа системы при этом также остается постоянной. Наглядное представление о графике, демонстрирующем изобарный процесс, дает термодинамическая диаграмма в соответствующей системе координат.
Примеры
Наиболее простым примером изобарического процесса можно назвать нагревание некоторого объема воды в открытом сосуде. В качестве еще одного примера можно привести расширение идеального газа в цилиндрическом объеме, где поршень имеет свободный ход. В каждом из этих случаев давление будет постоянным. Оно равно обыкновенному атмосферному давлению, что вполне очевидно.
Обратимость
Изобарный процесс можно считать обратимым в том случае, если давление в системе совпадает с внешним давлением и равно во все моменты времени процесса (то есть оно постоянно по своему значению), а температура изменяется очень медленно. Таким образом, термодинамическое равновесие в системе сохраняется в каждый момент времени. Именно совокупность вышеперечисленных факторов дает нам возможность считать изобарный процесс обратимым.
Чтобы осуществить в системе изобарический процесс, теплоту к ней нужно или подводить, или отводить. При этом теплота должна расходоваться на работу расширения идеального газа и на изменение его внутренней энергии. Формулу, демонстрирующую зависимость величин друг от друга при изобарном процессе, называют законом Гей-Люссака. Она показывает, что объем пропорционален температуре. Давайте выведем эту формулу на основании поверхностных знаний.
Вывод закона Гей-Люссака (первичное понимание)
Человек, хотя бы немного разбирающийся в молекулярной физике, знает, что многие задачи связаны с определенными параметрами. Имя им – давление газа, объем газа и температура газа. В тех или иных случаях в ход идут молекулярная и молярная масса, количество вещества, универсальная газовая постоянная и другие показатели. И здесь есть определенная связь. Давайте поговорим об универсальной газовой постоянной подробнее. На тот случай, если кто-то не знает, каким образом ее получили.
Получение универсальной газовой постоянной
Эту константу (постоянное число с определенной размерностью) принято также называть постоянной Менделеева. Она присутствует также в уравнении Менделеева-Клапейрона для идеального газа. Как же получил наш знаменитый физик эту константу?
Как мы знаем, уравнение идеального газа имеет следующую форму: PV/T (что озвучивается так: “произведение давления на объем, деленное на температуру”). По отношению к универсальной газовой постоянной применим так называемый закон Авогадро. Он гласит о том, что если мы возьмем любой газ, то одинаковое его количество молей при одинаковой температуре и одинаковом давлении займет одинаковый объем.
По сути дела, это есть словесная формулировка уравнения состояния идеального газа, которое было записано в виде формулы немного ранее. Если мы возьмем нормальные условия (а это когда температура газа равна 273,15 Кельвинов, давление равно 1 атмосфере, соответственно, 101325 Паскалей, а объем моля газа равен 22,4 литра) и подставим их в уравнение, все перемножим и разделим, то получим, что совокупность подобных действий дает нам численный показатель, равный 8,31. Размерность дается в Джоулях, деленных на произведение моля на Кельвин (Дж/моль*К).
Уравнение Менделеева-Клапейрона
Давайте возьмем уравнение состояния идеального газа и перепишем его в новом виде. Изначальное уравнение, напомним, имеет вид PV/T=R. А теперь умножим обе части на температурный показатель. Получим формулу PV(м)=RT. То есть произведение давления на объем равно произведению универсальной газовой постоянной на температуру.
Теперь умножим обе части уравнения на то или иное количество молей. Обозначим их количество буквой, скажем, X. Таким образом, получим следующую формулу: PV(м)X=XRT. Но ведь мы знаем, что произведение V с индексом “м” дает нам в результате просто объем V, а число молей X раскрывается в виде деления частной массы на молярную массу, то есть имеет вид m/M.
Таким образом, конечная формула будет выглядеть следующим образом: PV=MRT/m. Это и есть то самое уравнение Менделеева-Клапейрона, к которому пришли оба физика практически одновременно. Мы можем умножить правую часть уравнения (и в то же время разделить) на число Авогадро. Тогда получим: PV = XN(a)RT/N(a). Но ведь произведение количества молей на число Авогадро, то есть XN(a), дает нам не что иное, как общее число молекул газа, обозначаемое буквой N.
В то же время частное от универсальной газовой постоянной и числа Авогадро – R/N(a) даст постоянную Больцмана (обозначается k). В итоге мы получим еще одну формулу, но уже в несколько другом виде. Вот она: PV=NkT. Можно раскрыть эту формулу и получить следующий результат: NkT/V=P.
Работа газа при изобарном процессе
Как мы выяснили ранее, изобарным процессом называется термодинамический процесс, при котором давление остается величиной постоянной. А чтобы выяснить, как будет определяться работа при изобарном процессе, нам придется обратиться к первому началу термодинамики. Общая формула выглядит следующим образом: dQ = dU + dA, где dQ — это количество теплоты, dU – изменение внутренней энергии, а dA – работа, совершаемая в ходе выполнения термодинамического процесса.
Теперь рассмотрим конкретно изобарный процесс. Примем во внимание тот фактор, что давление остается постоянным. Теперь попытаемся переписать первое начало термодинамики для изобарного процесса: dQ = dU + pdV. Чтобы получить наглядное представление о процессе и работе, нужно изобразить его в системе координат. Ось абсцисс обозначим p, ось ординат V. Пускай объем будет увеличиваться. В двух отличных друг от друга точках с соответствующим значением p (конечно же, фиксированным) отметим состояния, представляющие собой V1 (первоначальный объем) и V2 (конечный объем). В этом случае график будет представлять собой прямую линию, параллельную оси абсцисс.
Найти работы в таком случае проще простого. Это будет просто площадь фигуры, ограниченная с двух сторон проекциями на ось абсцисс, а с третьей стороны – прямой линией, соединяющей точки, лежащие, соответственно, в начале и конце изобарной прямой. Попробуем вычислить значение работы при помощи интеграла.
Он будет вычисляться следующим образом: A = p (интеграл в пределах от V1 до V2) dV. Раскроем интеграл. Получим, что работа будет равна произведению давления на разность объемов. То есть выглядеть формула будет следующим образом: A = p (V2 – V1). Если мы раскроем некоторые величины, то получим еще одну формулу. Она выглядит так: A = xR (T2 – T2), где x – количество вещества.
Универсальная газовая постоянная и ее смысл
Можно сказать, что последнее выражение будет определять физический смысл R – универсальной газовой постоянной. Чтобы было понятнее, давайте обратимся к конкретным числам. Возьмем для проверки один моль какого-либо вещества. В то же время пускай температурная разница будет составлять 1 Кельвин. В этом случае легко заметить, что работа газа будет равна универсальной газовой постоянной (или же наоборот).
Заключение
Этот факт можно подать немного в другом свете, перефразировав формулировку. Например, универсальная газовая постоянная будет численно равна работе, совершаемой при изобарном расширении одним молем идеального газа, если он нагревается на один Кельвин. Вычислить работу при других изопроцессах будет несколько сложнее, но главное — при этом применять логику. Тогда все быстро встанет на свои места, и вывод формулы окажется проще, чем вы думаете.
Изобарический процесс
Вы будете перенаправлены на Автор24
Что такое изобарический процесс
Изобарическим (или изобарным) процессом называется процесс, происходящий в неизменной массе газа при постоянном давлении.
Запишем уравнение для двух состояний идеального газа:
[pV_1=nu RT_1left(1right),] [pV_2=nu RT_2 left(2right).]
Разделим уравнение (2) на уравнение (1), получим уравнение изобарного процесса:
Уравнение (4) называют законом Гей-Люссака.
Внутренняя энергия и количество теплоты изобарического процесса
Этот процесс происходит с подводом тепла, если объем увеличивается, или его отводом, чтобы уменьшать объем. Запишем первое начало термодинамики, последовательно получим выражения для работы, внутренней энергии и количества теплоты изобарного процесса:
где $delta Q $- элементарное тепло, подводимое к системе, $dU$- изменение внутренней энергии газа в проводимом процессе, $dA$- элементарная работа, которую совершает газ в процессе, i-число степеней свободы молекулы газа, R — универсальная газовая постоянная, d — количество молей газа.
Изменение внутренней энергии газа:
Уравнение (8) определяет работу для изобарного процесса. Вычтем из (2) уравнение (1), получим еще одно уравнение для работы газа в изобарном процессе:
[p<(V>_2-V_1)=nu R<(T>_2-T_1)to A=nu R<(T>_2-T_1) (9)] [triangle Q=frac<2>нR<(T>_2-T_1)+nu R<(T>_2-T_1)=c_<mu p>nu triangle T (10),]
где $c_<mu p>$ — молярная теплоёмкость газа при изобарном процессе. Уравнение (10) определяет количество теплоты, сообщаемое газу массы m в изобарном процессе при увеличении температуры на $triangle T.$
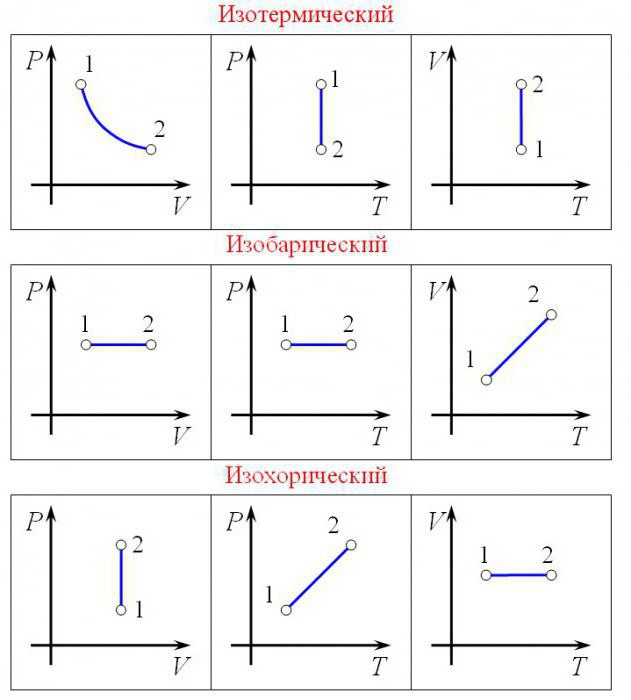
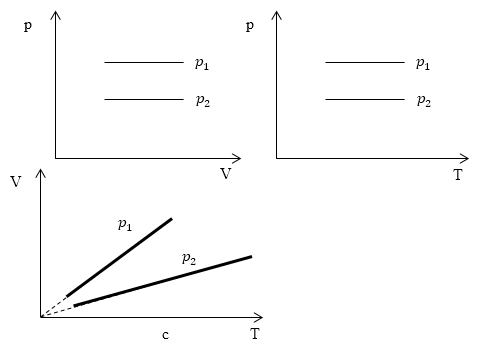
Изопроцессы очень часто изображают на термодинамических диаграммах. Так, линия, изображающая на такой диаграмме изобарический процесс, называется изобарой (рис.1).
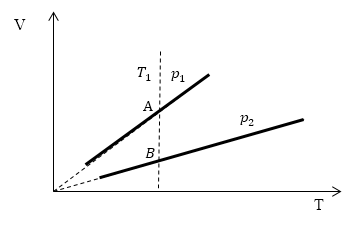
Задание: Определите, как соотносятся давления $p_1$ и $p_2$ на диаграмме V(T) рис 1с.
Проведем изотерму $T_1$
В точках А и В температуры одинаковы, следовательно, газ подчиняется закону Бойля — Мариотта:
[p_AV_A=p_BV_B (1.2)] [V_A > V_Bto p_A Ответ: Давления $p_1 > p_2$.
Готовые работы на аналогичную тему
Задание: При неизменном давлении p=3$cdot <10>^5$Па газ расширился от объема $V_1=2л$ до $V_2=4л.$ Найти работу, совершаемую газом.
За основу решения задачи примем формулу работы при расширении газа в изобарном процессе:
Переведем данные объемы в СИ: $V_1=2л=2<cdot 10>^<-3>м^3$, $V_2=4л=4<•10>^<-3>м^3$
Ответ: Работа газа в изобарном процессе 600 Дж.
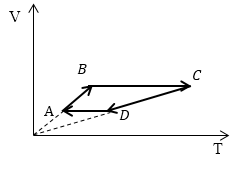
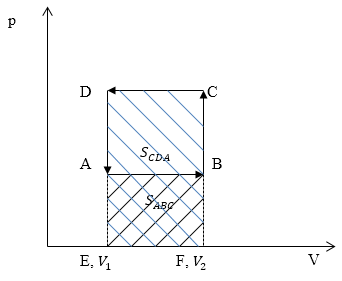
Задание: Сравните работу газа в процессе ABC и работу над газом в процессе CDA рис 3.
За основу решения примем формулу, определяющую работу газа:
Из геометрического смысла определенного интеграла известно, что работа — есть площадь фигуры, которая ограничена функцией подынтегрального выражения, осью абсцисс, и изохорами в точках $V_1 и V_2$ (оси p(V)). Переведем графики процессов в оси p(V).
Рассмотрим каждый отрезок графиков процессов изображенных на рисунке (3).
АВ: Изохорный процесс (p=const), $Vuparrow left( Объем растетright), Tuparrow $;
ВС: Изохорный процесс (V =const), $Tuparrow $ (из графика), p$uparrow $, из закона для изохорного процесса ($frac
=const$);
CD: (p=const), $Vdownarrow , Tdownarrow ;$
DA: (V =const), $Tdownarrow , pdownarrow .$
Изобразим графики процессов в осях p(V) (рис.4):
Работа газа $A_=S_$ ($S_$ — площадь прямоугольника ABFE) (рис. 3). Работа над газом $A_=S_$ ($S_$)$ -площадь прямоугольника $EFCD.Очевидно, что $A_>A_.$
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 18 12 2021
Первый закон термодинамики — формулы и определение с примерами
Содержание:
Первый закон термодинамики:
При изучении физики в 9 классе вы узнали, что полная механическая энергия замкнутой системы тел сохраняется только при отсутствии трения, а при наличии трения она уменьшается. Куда девается механическая энергия? Если бутылку, заполненную до половины водой при комнатной температуре, встряхивать в течение нескольких минут, то окажется, что вода нагрелась на 1—2 °С. Каким образом нагрелась вода?
В середине XIX века известный английский физик Дж. Джоуль (1818— 1889), проведя многочисленные опыты, показал, что совершённая при перемешивании воды механическая работа практически равна увеличению её внутренней энергии. Опыты Джоуля, а также исследования немецкого врача и естествоиспытателя Р. Майера (1814—1878), немецкого профессора физиологии и одного из самых знаменитых физиков второй половины XIX века Г. Гельмгольца (1821 —1894) позволили сформулировать закон сохранения и превращения энергии, распространив его на все явления природы. Согласно этому закону при любых взаимодействиях материальных объектов энергия не исчезает и не возникает из ничего, она только передаётся от одних объектов к другим или превращается из одной формы в другую.
Для термодинамических систем (в термодинамике обычно рассматривают макроскопически неподвижные системы) закон сохранения и превращения энергии называют первым законом термодинамики. Согласно первому закону термодинамики, приращение внутренней энергии термодинамической системы при переходе из одного состояния в другое равно алгебраической сумме работы, совершённой внешними силами, и количества теплоты, полученного или отданного системой при взаимодействии с внешними телами:
Поскольку работа внешних сил равна работе, совершаемой термодинамической системой, взятой с противоположным знаком (
Если система представляет собой действующее устройство, периодически возвращающееся в исходное состояние, то при этом AU-0 и A-Q. Механизм, который мог бы совершать работу без изменения состояния составляющих его тел и без теплопередачи от внешних тел, называют «вечным двигателем первого рода». Поэтому первый закон термодинамики можно сформулировать и следующим образом: невозможен вечный двигатель первого рода, т. е. такой двигатель, который при неизменном значении собственной внутренней энергии совершал бы работу большую, чем энергия, получаемая им извне.
Применим первый закон термодинамики к различным изопроцессам, происходящим с идеальным одноатомным газом.
Изохорный процесс
Пусть идеальный одноатомный газ находится в цилиндрическом сосуде, закрытом неподвижным поршнем (V = const). Нагреем сосуд с газом. Объём газа остаётся практически постоянным (тепловым расширением сосуда пренебрегаем) (рис. 60), следовательно, работа силы давления газа А= 0. Тогда первый закон термодинамики примет вид 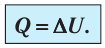
Это означает, что всё передаваемое газу количество теплоты идёт на увеличение его внутренней энергии. При этом приращение внутренней энергии газа 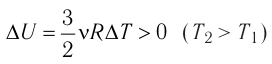
процессе отдаёт количество теплоты, то его внутренняя энергия убывает:
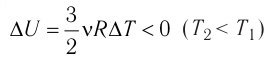
Изотермический процесс
Пусть цилиндрический сосуд с газом под поршнем находится в термостате — устройстве, в котором поддерживается постоянная температура. В этом случае внутренняя энергия идеального одноатомного газа 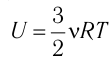
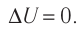
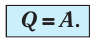
Какие выводы следуют из этого? Если с помощью внешнего устройства медленно перемещать поршень в сосуде так, чтобы объём газа увеличивался (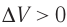
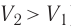
Если же внешнее устройство обеспечивает медленное уменьшение объёма газа в сосуде (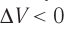
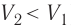
Изобарный процесс
Пусть газ находится в цилиндрическом сосуде, закрытом поршнем, который может свободно или под постоянной нагрузкой перемещаться (рис. 64). Нагреем газ, передав ему некоторое количество теплоты (Q > 0). Согласно первому закону термодинамики (11.2) переданное газу количество теплоты частично расходуется на увеличение внутренней энергии 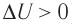
При изобарном процессе работа расширения (сжатия) газа , и первый закон термодинамики принимает вид
(11.5)
При изобарном сжатии газа внешние силы совершают работу А’ > 0. Чтобы давление газа при этом оставалось постоянным, газ необходимо охлаждать, т. е. он должен отдавать в окружающую среду некоторое количество теплоты (Q
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://spravochnick.ru/fizika/molekulyarnaya_fizika/izobaricheskiy_process/
http://www.evkova.org/pervyij-zakon-termodinamiki