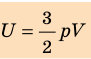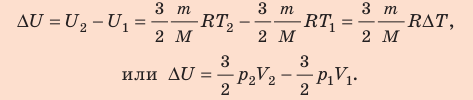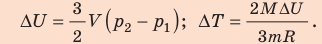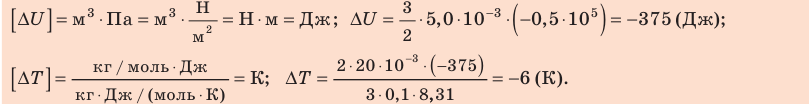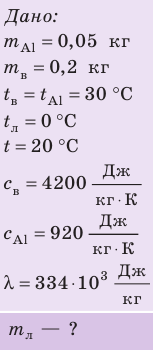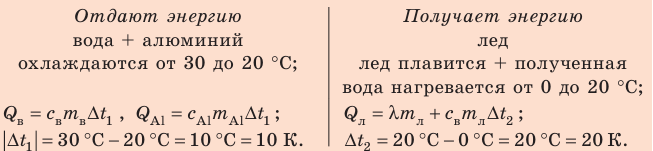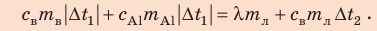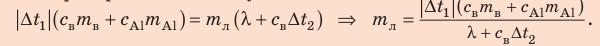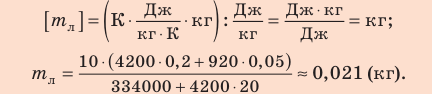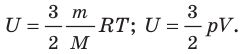Содержание:
Внутренняя энергия:
Вы знаете, что движущееся тело обладает кинетической энергией. А если оно еще и взаимодействует с другим телом, то обладает потенциальной энергией. Оба вида энергии представляют собой механическую энергию. Они взаимно превращаемы: кинетическая энергия может переходить в потенциальную и наоборот. Кроме того, вы знаете, что любое тело имеет дискретную структуру, т. е. состоит из частиц (атомов, молекул). Частицы находятся в непрерывном хаотическом движении. А частицы жидкости и твердого тела еще и взаимодействуют между собой. Следовательно, частицы обладают кинетической, а частицы жидкости и твердых тел — еще и потенциальной энергией. Сумма кинетической и потенциальной энергий всех частиц тела называется внутренней энергией. Внутренняя энергия измеряется в джоулях. Чем отличается внутренняя энергия от механической? В чем ее особенности? Может ли механическая энергия переходить во внутреннюю?
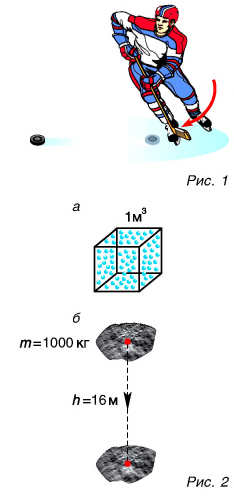
Для ответа на эти вопросы рассмотрим пример. Шайба, двигавшаяся горизонтально по льду (рис. 1), остановилась. Как изменилась ее механическая энергия относительно льда?
Кинетическая энергия шайбы уменьшилась до нуля. Положение шайбы над уровнем льда не изменилось, шайба не деформировалась. Значит, изменение потенциальной энергии равно нулю. Означает ли это, что се механическая (кинетическая) энергия исчезла бесследно? Нет. Механическая энергия шайбы перешла во внутреннюю энергию шайбы и льда.
А может ли внутренняя энергия тела, как механическая, быть равной нулю? Движение частиц, из которых состоит тело, не прекращается даже при самых низких температурах. Значит, тело всегда (подчеркиваем, всегда) обладает некоторым запасом внутренней энергии. Его можно либо увеличить, либо уменьшить — и только!
Велико ли значение внутренней энергии тела? Энергия одной частицы, например кинетическая, в силу незначительности ее массы чрезвычайно мала. Расчеты для средней энергии поступательного движения молекулы кислорода показывают, что ее значение при комнатной температуре
Главные выводы:
- Независимо от того, есть у тела механическая энергия или нет, оно обладает внутренней энергией.
- Внутренняя энергия тела равна сумме кинетической и потенциальной энергий частиц, из которых оно состоит.
- Внутренняя энергия тела всегда не равна нулю.
Способы изменения внутренней энергии
Чтобы изменить механическую энергию тела, надо изменить скорость его движения, взаимодействие с другими телами или взаимодействие частей тела. Вы уже знаете, что это достигается совершением работы.
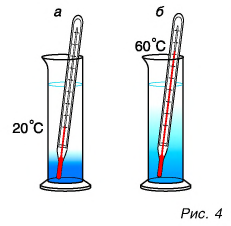
Как можно изменить (увеличить или уменьшить) внутреннюю энергию тела? Рассуждаем логически. Внутренняя энергия определяется как сумма кинетической и потенциальной энергий частиц. Значит, нужно изменить либо скорость движения частиц, либо их взаимодействие (изменить расстояния между ними). Очевидно, можно изменить и скорость, и расстояния между частицами одновременно. Изменить скорость частиц тела можно, увеличив или уменьшив его температуру. Действительно, наблюдения за диффузией показывают, что быстрота ее протекания увеличивается при нагревании (рис. 4, а, б).
Значит, увеличивается средняя скорость движения частиц, а следовательно, их средняя кинетическая энергия. Отсюда следует важный вывод: температура является мерой средней кинетической энергии частиц.
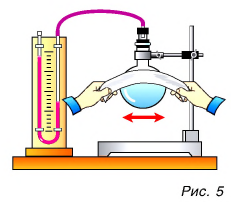
Как изменить кинетическую энергию частиц тела? Существуют два способа. Рассмотрим их на опытах. Будем натирать колбу с воздухом полоской сукна (рис. 5).
Через некоторое время уровень жидкости в правом колене манометра (см. рис. 5) опустится, т. е. давление воздуха в колбе увеличится. Это говорит о нагревании воздуха. Значит, увеличилась скорость движения и кинетическая энергия его молекул, а следовательно, и внутренняя энергия. Но за счет чего? Очевидно, за счет совершения механической работы при трении сукна о колбу. Нагрелась колба, а от нее — газ.
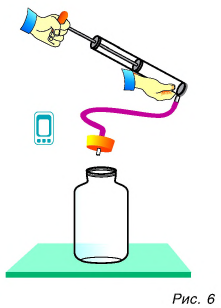
Проведем еще один опыт. В толстостенный стеклянный сосуд нальем немного воды (чайную ложку для увлажнения воздуха в нем. Насосом (рис. 6) будем накачивать в сосуд воздух. Через несколько качков пробка вылетит, а в сосуде образуется туман. Из наблюдений за окружающей средой мы знаем, что туман появляется тогда, когда после теплого дня наступает холодная ночь. Образование тумана в сосуде свидетельствует об охлаждении воздуха, т. е. об уменьшении его внутренней энергии. Но почему уменьшилась энергия? Потому что за ее счет совершена работа по выталкиванию пробки из сосуда.
Сравним результаты опытов. В обоих случаях изменилась внутренняя энергия газа, но в первом опыте она увеличилась, так как работа совершалась внешней силой (над колбой с газом), а во втором — уменьшилась, ибо работу совершала сила давления самого газа.
А можно ли, совершая работу, изменить потенциальную энергию взаимодействия молекул?
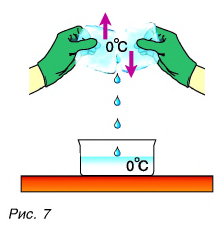
Опять обратимся к опыту. Два куска льда при О °C будем тереть друг о друга (рис. 7).
Лед превращается в воду, при этом температура воды и льда остается постоянной, равной О °C (см. рис. 7). На что тратится механическая работа силы трения?
Конечно же, на изменение внутренней энергии!
Но кинетическая энергия молекул не изменилась, так как температура не изменилась. Лед превратился в воду. При этом изменились силы взаимодействия молекул 
Совершение механической работы — один из способов изменения внутренней энергии тела.
А есть ли возможность изменить внутреннюю энергию тела, не совершая механическую работу?
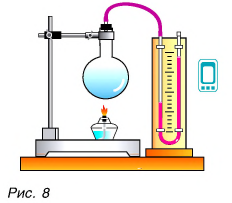
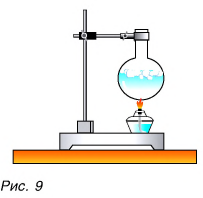
Да, есть. Нагреть воздух в колбе (рис. 8), расплавить лед (рис. 9) можно с помощью спиртовки, передав и воздуху, и льду теплоту. В обоих случаях внутренняя энергия увеличивается.
При охлаждении тел (если колбы со льдом и воздухом поместить в морозильник) их внутренняя энергия уменьшается. Теплота от тел передается окружающей среде.
Процесс изменения внутренней энергии тела, происходящий без совершения работы, называется теплопередачей (теплообменом).
Таким образом, совершение механической работы и теплопередача — два способа изменения внутренней энергии тела.
Величину, равную изменению внутренней энергии при теплопередаче, называют количеством теплоты (обозначается Q). Единицей количества теплоты, как работы и энергии, в СИ является 1 джоуль.
Для любознательных:
Физики XVIII в. и первой половины XIX в. рассматривали теплоту не как изменение энергии, а как особое вещество — теплород — жидкость (флюид), которая может перетекать от одного тела к другому. Если тело нагревалось, то считалось, что в него вливался теплород, а если охлаждалось — то выливался. При нагревании тела расширяются. Это объяснялось тем, что теплород имеет объем. Но если теплород — вещество, то тела при нагревании должны увеличивать свою массу. Однако взвешивания показывали, что масса тела не менялась. Поэтому теплород считали невесомым. Теорию теплорода поддерживали многие ученые, в том числе и такой гениальный ученый, как Г. Галилей. Позже Дж. Джоуль на основании проведенных им опытов пришел к выводу, что теплород не существует и что теплота есть мера изменения кинетической и потенциальной энергий движущихся частиц тела.
В дальнейшем выражение «сообщить телу количество теплоты» мы будем понимать как «изменить внутреннюю энергию тела без совершения механической работы, т. е. путем теплообмена». А выражение «нагреть тело» будем понимать как «повысить его температуру» любым из двух способов.
Главные выводы:
- Внутреннюю энергию тела можно изменить путем совершения механической работы или теплопередачи (теплообмена).
- Изменение внутренней энергии при нагревании или охлаждении тела при постоянном объеме связано с изменением средней кинетической энергии его частиц.
- Изменение внутренней энергии тела при неизменной температуре связано с изменением потенциальной энергии его частиц.
Основы термодинамики
МКТ стала общепризнанной на рубеже XIX и XX веков. Задолго до ее создания исследованием тепловых процессов занималась термодинамика — раздел физики, изучающий превращение внутренней (тепловой) энергии в другие виды энергии и наоборот, а также количественные соотношения при таких превращениях.
- Заказать решение задач по физике
Внутренняя энергия и ее особенности
Внутренняя энергия макроскопического тела определяется характером движения и взаимодействия всех микрочастиц, из которых состоит тело (система тел). Таким образом, к внутренней энергии следует отнести:
- кинетическую энергию хаотического (теплового) движения частиц вещества (атомов, молекул, ионов);
- потенциальную энергию взаимодействия частиц вещества;
- энергию взаимодействия атомов в молекулах (химическую энергию);
- энергию взаимодействия электронов и ядра в атоме и энергию взаимодействия нуклонов в ядре (внутриатомную и внутриядерную энергии).
Однако для описания тепловых процессов важно не столько значение внутренней энергии, как ее изменение. При тепловых процессах химическая, внутриатомная и внутриядерная энергии практически не изменяются. Именно поэтому внутренняя энергия в термодинамике определяется как сумма кинетических энергий хаотического (теплового) движения частиц вещества (атомов, молекул, ионов), из которых состоит тело, и потенциальных энергий их взаимодействия.
Внутреннюю энергию обозначают символом U.
Единица внутренней энергии в СИ — джоуль: [U]=1 Дж (J).
Особенности внутренней энергии идеального газа
- Атомы и молекулы идеального газа практически не взаимодействуют друг с другом, поэтому внутренняя энергия идеального газа равна кинетической энергии поступательного и вращательного движений его частиц.
- Внутренняя энергия данной массы идеального газа прямо пропорциональна его абсолютной температуре. Докажем данное утверждение для одноатомного газа. Атомы такого газа движутся только поступательно, поэтому, чтобы определить его внутреннюю энергию, следует среднюю кинетическую энергию поступательного движения атомов умножить на количество атомов:
Итак, для одноатомного идеального газа:
. Используя уравнение состояния
, выражение для внутренней энергии идеального одноатомного газа можно представить так:
- Внутренняя энергия — функция состояния системы, то есть она однозначно определяется основными макроскопическими параметрами (p, V, T), характеризующими систему. Независимо от того, каким образом система переведена из одного состояния в другое, изменение внутренней энергии будет одинаковым.
- Внутреннюю энергию можно изменить двумя способами: совершением работы и теплопередачей.
Какие существуют виды теплопередачи
Теплопередача (теплообмен) — процесс изменения внутренней энергии тела или частей тела без совершения работы. Процесс теплопередачи возможен только при наличии разности температур. Самопроизвольно тепло всегда передается от более нагретого тела к менее нагретому. Чем больше разность температур, тем быстрее — при прочих равных условиях — протекает процесс передачи тепла.
| Виды теплопередачи | ||
|---|---|---|
| Теплопроводность | Конвекция | Излучение |
|
Вид теплопередачи, который обусловлен хаотическим движением частиц вещества и не сопровождается переносом этого вещества. Лучшие проводники тепла — металлы, плохо проводят тепло дерево, стекло, кожа, жидкости (за исключением жидких металлов); самые плохие проводники тепла — газы. Передача энергии от горячей воды к батарее отопления, от поверхности воды до ее нижних слоев и т. д. происходит благодаря теплопроводности. |
Вид теплопередачи, при котором тепло переносится потоками жидкости или газа. Теплые потоки жидкости или газа имеют меньшую плотность, поэтому под действием архимедовой силы поднимаются, а холодные потоки — опускаются. Благодаря конвекции происходит циркуляция воздуха в помещении, нагревается жидкость в стоящей на плите кастрюле, существуют ветры и морские течения и т. д. В твердых телах конвекция невозможна. | Вид теплопередачи, при котором энергия передается посредством электромагнитных волн. Излучение — универсальный вид теплопередачи: тела всегда излучают и поглощают инфракрасное (тепловое) излучение. Это единственный вид теплообмена, возможный в вакууме (энергия от Солнца передается только излучением). Лучше излучают и поглощают энергию тела с темной поверхностью. |
Как определить количество теплоты
Количество теплоты Q — это физическая величина, равная энергии, которую тело получает (или отдает) в ходе теплопередачи.
Единица количества теплоты в СИ — джоуль: [П] =1 Дж (J).
Из курса физики 8 класса вы знаете, что количество теплоты, которое поглощается при нагревании вещества (или выделяется при его охлаждении), вычисляют по формуле: Q=cm∆Т=cm∆t , где c — удельная теплоемкость вещества; m — масса вещества; 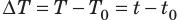
Обратите внимание! Произведение удельной теплоемкости на массу вещества, из которого изготовлено тело, называют теплоемкостью тела: C=cm . Если известна теплоемкость C тела, то количество теплоты, которое получает тело при изменении температуры на ∆T, вычисляют по формуле: Q=C∆T .
| Расчет количества теплоты при фазовых переходах | |
|---|---|
| Кристаллическое состояние ↔ Жидкое состояние | Жидкое состояние ↔ Газообразное состояние |
|
Температуру, при которой происходят фазовые переходы «кристалл → жидкость» и «жидкость → кристалл», называют температурой плавления. Температура плавления зависит от рода вещества и внешнего давления. Количество теплоты Q, которое поглощается при плавлении кристаллического вещества (или выделяется при кристаллизации жидкости), вычисляют по формуле: Q = λm, где m — масса вещества; λ — удельная теплота плавления. |
Фазовые переходы «жидкость → пар» и «пар → жидкость» происходят при любой температуре. Количество теплоты Q, которая поглощается при парообразовании (или выделяется при конденсации), вычисляют по формуле: Q=rm (Q=Lm), где m — масса вещества; r (L) — удельная теплота парообразования при данной температуре (обычно в таблицах представлена удельная теплота парообразования при температуре кипения жидкости). |
| Напомним: и при плавлении, и при кипении температура вещества не изменяется. |
Пример решения задачи №1
Неон массой 100 г находится в колбе объемом 5,0 л. В процессе изохорного охлаждения давление неона уменьшилось с 100 до 50 кПа. На сколько при этом изменились внутренняя энергия и температура неона?
Решение:
Неон — одноатомный газ; для таких газов изменение внутренней энергии равно:
Поскольку охлаждение изохорное, объем неона не изменяется: 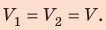
Проверим единицы, найдем значения искомых величин:
Анализ результатов. Знак «–» свидетельствует о том, что внутренняя энергия и температура неона уменьшились, — это соответствует изохорному охлаждению. Ответ: ∆U = –375 Дж; ∆T = –6 К.
Пример решения задачи №2
Внутренний алюминиевый сосуд калориметра имеет массу 50 г и содержит 200 г воды при температуре 30 °С. В сосуд бросили кубики льда при температуре 0 °С, в результате чего температура воды в калориметре снизилась до 20 °С. Определите массу льда. Удельные теплоемкости воды и алюминия: 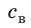
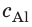
Анализ физической проблемы.
Калориметр имеет такое устройство, что теплообмен с окружающей средой практически отсутствует, поэтому для решения задачи воспользуемся уравнением теплового баланса. В теплообмене участвуют три тела: вода, внутренний сосуд калориметра, лед.
Решение:
Запишем уравнение теплового баланса:
После преобразований получим:
Проверим единицу, найдем значение искомой величины:
Ответ: 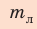
Выводы:
- В термодинамике под внутренней энергией U тела понимают сумму кинетических энергий хаотического движения частиц вещества, из которых состоит тело, и потенциальных энергий их взаимодействия. Внутренняя энергия однозначно определяется основными макроскопическими параметрами (p, V, T), характеризующими термодинамическую систему. Внутреннюю энергию идеального одноатомного газа определяют по формулам:
- Внутреннюю энергию можно изменить двумя способами: совершением работы и теплопередачей. Существует три вида теплопередачи: теплопроводность, конвекция, излучение.
- Физическую величину, равную энергии, которую тело получает или отдает при теплопередаче, называют количеством теплоты (Q): Q=cm∆T = С∆T — количество теплоты, которое поглощается при нагревании тела (или выделяется при его охлаждении); Q = λm — количество теплоты, которое поглощается при плавлении вещества (или выделяется при кристаллизации); Q=rm (Q=Lm) — количество теплоты, которое поглощается при парообразовании вещества (или выделяется при конденсации).
- Теплопроводность в физике
- Конвекция в физике
- Излучение тепла в физике
- Виды излучений в физике
- Машины и механизмы в физике
- Коэффициент полезного действия (КПД) механизмов
- Тепловые явления в физике
- Тепловое движение в физике и его измерение
Введение
Все тела состоят из атомов и молекул, которые непрерывно движутся и взаимодействуют между собой. Нас интересует суммарная энергия их движения (кинетическая) и взаимодействия (потенциальная) – внутренняя энергия тела.
Внутреннюю энергию можно изменить двумя способами: выполняя работу и с помощью теплообмена.
Про механическую работу мы уже говорили, в ответвлении подробнее рассмотрим, как это связано с изменением внутренней энергии.
Механическая работа и превращение энергии
В механике мы использовали закон сохранения механической энергии:
Полная механическая энергия системы, в которой действуют только консервативные силы, остается постоянной.
Под полной механической энергией мы понимаем сумму кинетической и потенциальной энергии. Значит, энергия превращается из кинетической в потенциальную, и наоборот, чтобы их сумма оставалась постоянной (см. рис. 1).
Рис. 1. Превращение кинетической и потенциальной энергий
Изменение кинетической энергии равно изменению потенциальной энергии со знаком минус – это значит, на сколько увеличилась кинетическая энергия, на столько же уменьшилась потенциальная. А работа консервативных сил равна этому изменению:
Что же происходит с энергией тела, если на него действуют неконсервативные силы, например сила трения? Механическая энергия не сохраняется, она превращается в другие виды энергии, в частности в тепловую (или внутреннюю энергию тела) (см. рис. 2).
Рис. 2. Превращение механической энергии в тепловую
Работа неконсервативной силы равна изменению механической энергии (а оно равно изменению внутренней энергии со знаком минус, для превращения кинетической энергии в потенциальную мы записывали так же).
При изучении тепловых явлений нас как раз интересует изменение внутренней энергии.
Передача энергии от более теплого объекта к менее теплому
Рассмотрим второй способ изменения внутренней энергии тела – это передача энергии от более теплого объекта к менее теплому. Назвали это теплопередачей и выделили виды теплопередачи: через излучение и через соударения молекул, назвав это теплопроводностью (см. рис. 3).
Рис. 3. Виды теплопередачи
Теплопередача может сопровождаться перемещением вещества, этот процесс мы назвали конвекцией.
Но для того чтобы количественно описывать тепловые процессы, нам недостаточно знать сам факт, что теплота передается.
Предположим, что в системе тел неконсервативные силы не совершают механическую работу. Рассмотрим энергию, которую передает или получает тело в результате теплообмена. Вследствие этого изменяется его внутренняя энергия. Эту полученную энергию, равную изменению внутренней энергии, назовем теплотой, а для ее количественного выражения часто будем употреблять название количество теплоты.
О терминах «теплота» и «количество теплоты»
Мы определили теплоту как энергию, которую передает или получает тело в процессе теплообмена. Это физическая величина, единицы измерения у нее те же, что и для энергии. То есть можно сказать «теплота равна 10 Дж» и т. д. Но в русском языке сложилась такая ситуация: если о многих других величинах можно сказать «какая масса?», «какая скорость?», то к теплоте более естественно применить вопрос «сколько?». То есть не «чему равна теплота?», а «сколько теплоты?», или, другими словами: «какое количество теплоты?». Это понятие, «количество теплоты», мы применяем наряду с понятием «теплота», но стоит помнить, что подразумевается одна и та же физическая величина. Просто иногда удобнее сказать «теплота передалась», а иногда «количество теплоты равно 10 Дж».
Обратите внимание: теплота равна изменению внутренней энергии тела. То есть мы не будем говорить об абсолютном количестве теплоты, а только о его изменении. То есть отвечать на вопрос: «Сколько теплоты получило или передало тело?». А привычные нам понятия «тепло/холодно» лучше всего описывает такая физическая величина, как температура.
Ощущаем ли мы температуру?
Касаясь чашки с горячим чаем, вы чувствуете ее тепло (см. рис. 4).
Рис. 4. Чашка с горячим чаем
Кажется, что мы определяем ее температуру и можем судить о внутренней энергии. А попробуйте провести следующий опыт: опустите одну руку в теплую воду, другую – в холодную, чтобы руки «привыкли» к температуре (см. рис. 5).
Рис. 5. Проведение эксперимента
А затем поместите их обе в воду комнатной температуры. Одной рукой вы почувствуете холод, другой – тепло. Получается, что наши ощущения связаны не с абсолютным значением температуры тела, а с разностью температур тела и нашей руки и с направлением теплообмена между ними.
Одна рука чувствует тепло, поскольку теплота передается от воды к руке. А вторая рука чувствует холод, поскольку тепло передается от руки к воде. При этом в случае холодной воды это не вода передает руке холод, а рука отдает воде тепло.
Конечно, мы иногда говорим «закрой дверь – холод напустишь» (как будто подразумеваем передачу именно холода), но это обывательский оборот, который закрепился в языке.
Например, при игре в пятнашки мы всегда двигаем сами «костяшки», но часто говорим о перемещении пустой клетки.
Мы говорим: «становится темно». Хотя темнота – это отсутствие света. Августин Блаженный говорил: «Нет зла, есть недостаток добра».
Так и с холодом – это отсутствие тепла. Нет передачи холода, есть теплопередача в том или ином направлении. Поэтому и лед, и чай, укутанные в шубу, будут некоторое время сохранять температуру, здесь у шубы одна и та же функция – теплоизоляция.
Количество теплоты
Обычно количество теплоты обозначается буквой Q. Количество теплоты – это изменение внутренней энергии при теплообмене, значит, эта величина измеряется, как и энергия, в джоулях: [Q] = Дж.
Обозначим внутреннюю энергию U. Тогда определение количества теплоты можно записать следующим образом:
Q = ΔU при равной нулю механической работе внешних сил (о чем мы договорились в начале урока).
Если тело получило 10 Дж теплоты и если тело потеряло 10 Дж теплоты – это не одно и то же (см. рис. 6).
Рис. 6. Получение и потеря теплоты
Как это обозначить? Для этого можем использовать удобный математический инструмент – отрицательные числа. Мы его уже использовали для обозначения направления движения. Если рассматривать прямолинейное движение вдоль одной прямой, удобно выбрать ось координат и одно направление считать положительным (см. рис. 7).
Рис. 7. Выбор положительного направления
В проекции на эту ось скорости тел 5 м/с и –5 м/с означают, что тела движутся со скоростью 5 м/с в противоположных направлениях.
Так и здесь: договоримся, что если тело получает теплоту (наши руки получили от теплой воды 10 Дж тепла), то Q положительно (запишем Q = 10 Дж), а если отдает – отрицательно, запишем Q = –10 Дж.
Остановимся пока на изучении тех случаев, когда агрегатное состояние вещества не меняется. Тогда если передать тепло телу, то оно нагреется, увеличится его температура (см. рис. 
.
Рис. 8. Агрегатное состояние вещества не изменяется при получении теплоты
Разберемся, как количественно описать этот процесс.
Чайник закипит быстрее, если в него залить теплую воду, а не холодную (см. рис. 9).
Рис. 9. Закипание чайника с теплой и холодной водой
То есть чем большей разности конечной и начальной температур нужно достичь, тем больше нужно передать энергии. Полный чайник будет закипать дольше, чем почти пустой (см. рис. 10).
Рис. 10. Закипание полного чайника и полупустого
То есть чем больше масса воды, тем больше нужно передать энергии, чтобы ее нагреть. И наверняка есть разница, нагреть на одни и те же 10 градусов килограмм воды или килограмм железа – это тоже нужно учесть (см. рис. 11).
Рис. 11. Нагревание разных веществ
Можно провести эксперименты и установить более точные закономерности.
Оказывается, количество теплоты, которое необходимо передать телу, прямо пропорционально изменению температуры: , где
обозначает изменение температуры: конечная температура минус начальная
.
Если тело отдает тепло, то оно охлаждается. Конечная температура будет меньше начальной: . Тогда
. Количество теплоты также будет
. Это согласуется с введенным понятием количества теплоты: если тело отдает тепло, то
.
Экспериментально также было установлено, что: (количество теплоты, которое необходимо передать телу, прямо пропорционально массе тела).
Почему изменение внутренней энергии пропорционально массе?
Количество теплоты, которое получает тело, идет на увеличение его внутренней энергии. Внутренняя энергия – это суммарная энергия частиц вещества: атомов или молекул. Значит, изменение внутренней энергии должно быть пропорционально количеству частиц: .
Однако таким параметром, как количество молекул, мы пользуемся редко. Более удобной характеристикой, эквивалентной количеству частиц данного вещества, является масса.
Масса вещества равна массе одной частицы (атома или молекулы), умноженной на количество частиц: , тогда количество молекул равно
.
Получаем, что или
, т. к. масса одной молекулы – величина постоянная для данного вещества и она будет заложена в коэффициенте пропорциональности, который определяется отдельно для каждого вещества и учитывает его параметры: массу молекул, связь между ними, связь кинетической энергии молекул и температуры и т. д.
Удельная теплоемкость
Количество теплоты пропорционально массе тела и изменению его температуры:
Кроме того, количество теплоты, необходимое для нагревания данной массы на данную температуру, зависит от вещества: для спирта нужно меньше теплоты, чем для воды (см. рис. 12), а для золота – меньше, чем для железа (см. рис. 13).
Рис. 12. Количество теплоты для нагревания воды и спирта
Рис. 13. Количество теплоты для нагревания железа и золота
Для данного вещества количество теплоты, которое нужно передать для нагревания данной m на данную , оказалось постоянной величиной.
Отношение назвали удельной теплоемкостью, которую принято обозначать буквой c. Это количество теплоты, которое нужно передать 1 кг вещества, чтобы нагреть его на 1 °С (или 1 К, потому что мы говорим об изменении температуры, а цена деления этих двух шкал одинакова (см. рис. 14)).
Рис. 14. Шкалы температур Цельсия и Кельвина
Для разных веществ это отношение отличается.
Единицы измерения удельной теплоемкости:
Различные вещества имеют различные удельные теплоемкости. Почему это так – поговорим в ответвлении.
c = const
Удельная теплоемкость с зависит от температуры t. Чтобы нагреть один и тот же железный шарик с 10 градусов до 11 и с 200 до 201 – нужно разное количество теплоты (см. рис. 15).
Рис. 15. Нагрев одного и того же шарика на 1 градус
Изменение удельной теплоемкости с изменением температуры достаточно мало, поэтому для решения задач мы можем считать, что с = const и зависимость линейная (на участках, где не изменяется агрегатное состояние вещества (см. рис. 16)).
Рис. 16. Линейная зависимость на участках, где не изменяется агрегатное состояние вещества
На самом деле, с, кроме температуры, зависит и от давления, но обычно мы будем решать задачи, в которых описаны процессы при нормальном атмосферном давлении, поэтому и здесь можно считать с = const.
Почему у веществ различные удельные теплоемкости
Почему для нагревания одной и той же массы на одну и ту же температуру для разных веществ нужно разное количество энергии?
Мы определили внутреннюю энергию тела как сумму кинетической и потенциальной энергии всех частиц тела. Когда теплота передается телу, часть ее идет на увеличение кинетической энергии (а значит, увеличение температуры), а часть – на увеличение потенциальной энергии частиц (см. рис. 17).
Рис. 17. Внутренняя энергия тела
У разных веществ соотношение этих частей разное.
Например, двум разным телам передали 100 Дж теплоты (см. рис. 18).
Рис. 18. Нагревание разных тел
У одного тела 40 Дж ушло в кинетическую энергию, а 60 – в потенциальную. У другого в кинетическую энергию перешло 20 Дж, 80 – в потенциальную. Итого тела получили одинаковое количество теплоты, но первое тело нагрелось больше, чем второе, т. к. кинетическая энергия его частиц увеличилась сильнее (40 Дж > 20 Дж). Это значит, что удельная теплоемкость второго вещества больше – ведь его труднее нагреть, чем первое.
Для разных веществ полученная энергия может распределяться по-разному – для нас это не ново.
Возьмем три мяча (см. рис. 19): хорошо накачанный, спущенный и деревянный.
Рис. 19. Опыт с тремя мячами
Если ударить по ним, сообщив одинаковую энергию, полетят они с разной скоростью. Часть переданной энергии пойдет на неупругую деформацию мяча и обуви бьющего, а часть – на увеличение кинетической энергии мяча. Для перечисленных мячей соотношение этих частей будет разное.
Значения удельных теплоемкостей различных веществ уже измерены, их можно найти в соответствующих таблицах.
Итак, на основе всего вышесказанного можно записать формулу для расчета количества теплоты, необходимого для нагревания тела:
Процессы нагревания и охлаждения отличаются лишь знаком , так что формулу можно использовать и для расчета количества теплоты, которое выделяет тело при охлаждении.
Для задач, которые мы будем решать в ближайшее время, нам достаточно такого очевидного утверждения: тепло передается от тела с большей температурой к телу с меньшей температурой до тех пор, пока температуры этих тел не уравняются (см. рис. 20).
Рис. 20. Теплообмен между телами с разной температурой
Более точно эта закономерность сформулирована в виде законов термодинамики, но их мы будем подробно изучать позже.
Тепловой баланс
Мы сейчас рассматриваем изменение внутренней энергии тел через передачу теплоты. Если выделить систему тел, которые будем рассматривать вместе в рамках решения конкретной задачи, то возможны два варианта.
Первый – энергия может быть получена извне этой системы (см. рис. 21)
Рис. 21. Теплообмен с другими телами вне системы
(например, теплообмен с другими телами вне системы, превращение механической энергии в тепловую и т. д.). Второй вариант – считаем, что энергия передается посредством теплообмена только внутри системы, тогда суммарная энергия системы не меняется (см. рис. 22).
Рис. 22. Теплообмен только внутри системы
Рассмотрим первый случай, когда тепло передается системе тел извне.
Задача 1
В алюминиевой кастрюле массой 1,5 кг находится 5 кг воды при температуре 20 °С (см. рис. 23).
Рис. 23. Задача 1
Найти количество теплоты, необходимое для нагревания воды до температуры кипения. Передачей тепла в окружающую среду пренебречь.
Имеется два тела: кастрюля и вода. Нужно передать какое-то количество теплоты, чтобы нагреть их. Потерями тепла в окружающую среду пренебрегаем – значит, все тепло пойдет на нагревание кастрюли с водой.
Потери тепла
Предположим, что для выполнения условия задачи мы поставили кастрюлю с водой на электроплиту. Понятно, что часть тепла, которое выделяет плита, будет тратиться на нагревание кастрюли, окружающего воздуха и самой электроплиты (см. рис. 24).
Рис. 24. Потери тепла на нагревание кастрюли, окружающего воздуха и самой электроплиты
Это ненужные нам «потери тепла», как их называют. Но без них не обойтись – кастрюля и окружающий воздух неизбежно будут греться вместе с водой.
Обычно потери тепла незначительные и мы их можем не учитывать. Если в задаче отдельно не оговорено иное, потерями при решении пренебрегаем. Если же мы хотим получить более точное решение, придется учитывать (и рассчитывать) эти потери.
В нашей задаче в условии прямо сказано: «Передачей тепла в окружающую среду пренебречь».
Если бы в условии не были даны материал и масса кастрюли, то подразумевалось бы, что нагреванием самой кастрюли тоже можно пренебречь. Однако в данной конкретной задаче сказано, что кастрюля алюминиевая (то есть можно найти ее удельную теплоемкость по таблице), а также дана масса кастрюли. Значит, можно и нужно посчитать, какое количество теплоты пойдет на нагревание самой кастрюли.
Для нагревания алюминиевой кастрюли нужно:
Для нагревания воды нужно:
Всего нужно передать:
Массы воды и кастрюли даны в условии, удельные теплоемкости можно найти в таблице. Вода должна нагреться от до кипения, то есть до
. Кастрюля нагревается вместе с водой, поэтому изменение ее температуры будет таким же:
Осталось подставить численные данные и найти ответ.
Решение задачи
Итак, мы получили систему уравнений:

Численные данные из условия:
Из таблицы:
Вычисляем:
Ответ: .
В предыдущем ответвлении мы говорили о том, учитывать ли потери теплоты. В данной задаче мы пренебрегли потерями на нагревание окружающего воздуха, но учли нагрев кастрюли. Если решить задачу, не учитывая нагрев кастрюли, останется количество теплоты, необходимое для нагревания только воды:
Как видим, этот результат отличается от полученного ранее приблизительно на 6 %. Много это или мало – зависит от цели. Если мы греем воду для чая, то погрешностью в 6 % можно пренебречь. Если же вода нужна для выращивания клеток в биологической лаборатории со строгим температурным режимом, то 6 % могут оказаться очень большой разницей и пренебрегать нельзя.
Теперь рассмотрим модель, в которой можно не учитывать теплообмен системы тел с окружающими телами: тепло только передается от одного тела к другому.
Задача 2
В чашке находится горячий чай при температуре 95 °С (см. рис. 25).
Рис. 25. Задача 2
Масса чая – 150 г. Определите массу холодной воды, которую нужно долить в чашку с чаем, чтобы понизить температуру чая до 60 °С. Температура холодной воды – 5 °С. Теплоемкость чая считать равной теплоемкости воды, потерями тепла пренебречь.
Почему чай будет остывать? Мы долили в чашку холодную воду, поэтому чай будет отдавать тепло, его температура будет уменьшаться (см. рис. 26).
Рис. 26. Доливание холодной воды в чашку
Вода будет получать тепло, ее температура будет увеличиваться. В некоторый момент температура воды станет равной температуре чая, теплообмен прекратится. В условии сказано, что потерями тепла можно пренебречь, значит, все тепло, которое отдал чай, получит вода.
Чай отдал , вода получила
. Тогда
.
Откуда в формуле появились модули
Было оговорено, что направление теплопередачи обозначать знаком количества теплоты: плюс – если тело получает теплоту, и минус – если отдает (см. рис. 27).

Рис. 27. Получение (слева) и отдача (справа) теплоты
Если записывать как
, знак Q получится таким, как мы договорились.
Можно использовать такой подход: записать общее количество теплоты для всех тел ( и приравнять его к нулю – суммарная внутренняя энергия системы не изменилась, теплообмен вне системы равен нулю:
Q чая и воды имеют противоположные знаки.
Можно направление теплообмена учесть по-другому: записать модули и
(то есть при вычислении
просто от большей температуры отнимаем меньшую), но перенести в правую часть уравнения переданную теплоту, оставив в левой части полученную:
То есть сколько тепла отдал горячий чай, столько и получила холодная вода.
Решать задачи можно любым удобным способом, главное, чтобы направление теплообмена было учтено правильно.
Из условия: ; изменения температур:
,
. На этом физическая часть решения закончена, осталось лишь выразить неизвестную величину, подставить численные значение и получить ответ.
Решение задачи
Имеем систему уравнений:
Уравнений много, но все они очень простые. Подставим значения и найдем изменение температуры:
Второе и третье уравнение подставим в первое:
С учетом , сократим на теплоемкость:
Подставим численные значения:
Если в задаче будет больше тел, то алгоритм решения будет аналогичным:
1) определить, какие тела получают тепло, а какие отдают;
2) записать общее количество теплоты, которое было отдано и которое было получено телами;
3) приравнять модули полученного и отданного тепла.
Либо же не брать модули, оставить разные знаки Q для разных направлений теплообмена и сумму Q внутри замкнутой системы приравнять нулю, как мы показали в ответвлении.
А дальше останется только техника – математические расчеты.
Итоги
В подобных задачах всегда есть баланс: сколько теплоты одни тела отдают, столько другие тела получают. Они так и называются: задачи на тепловой баланс. В этом уроке мы рассмотрели процессы, при которых изменялась температура, но не рассмотрели процессы изменения агрегатного состояния вещества. Но мы можем взять лед при температуре 0 ℃, расплавить его и получить воду при 0 ℃ – ∆t равно нулю (см. рис. 28).
Рис. 28. Плавление льда
Греть его для этого нужно, энергии этот процесс требует. Значит, здесь что-то другое, модель не работает.
Например, тепло полученное от солнца, идет на то, чтобы расплавить лед в замерзших лужах. Другой пример: если надолго оставить на плите кастрюлю с водой, то тепло будет тратиться на испарение воды, превращение ее в пар. Как решать задачи с процессами агрегатных превращений – плавлением, парообразованием и пр. – мы рассмотрим на следующем уроке.
Список литературы
- Соколович Ю.А., Богданова Г.С. Физика: справочник с примерами решения задач. – 2-е издание, передел. – X.: Веста: издательство «Ранок», 2005. – 464 с.
- А.В. Перышкин. Физика 8 кл.: учеб. для общеобразоват. учреждений. – М.: Дрофа, 2013. – 237 с.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Сайт объединения учителей Санкт-Петербурга (Источник)
- Интернет-сайт «Класс!ная физика — для любознательных» (Источник)
- 3Интернет-сайт «Класс!ная физика — для любознательных» (Источник)
Домашнее задание
- Какие вы знаете способы изменения внутренней энергии?
- Назовите 3 вида теплопередачи. В каком из них теплопередача может сопровождаться перемещением вещества?
- Что такое количество теплоты, в каких единицах оно измеряется?
- Что такое удельная теплоемкость вещества? В каких единицах она измеряется? Где ее можно посмотреть?
- Металлическую деталь, масса которой 200 г, нагрели до 100
, а затем опустили в воду массой 800 г и температурой 20
. Через некоторое время температура воды и детали стала равна 25 °С. Определите удельную теплоемкость металлической детали. Тепловыми потерями пренебречь.
Условие задачи:
Найти количество теплоты, выделившееся при лобовом абсолютно неупругом ударе двух свинцовых шаров массой 1 кг каждый, скользящих без вращения по абсолютно гладкой поверхности. До удара шары двигались по одной прямой в одном направлении. Скорость первого шара равна 10 см/с, скорость второго – 20 см/с.
Задача №2.10.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(m=1) кг, (upsilon_1=10) см/с, (upsilon_2=20) см/с, (Q-?)
Решение задачи:
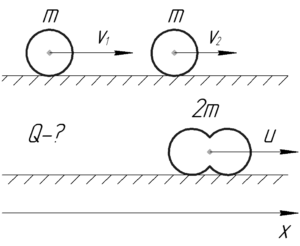
- закон сохранения импульса (ЗСИ) в проекции на ось (x), поскольку система, состоящая из двух шаров замкнута в этом направлении;
- закон сохранения энергии (ЗСЭ), но учтем, что часть начальной кинетической энергии шаров при абсолютно неупругом ударе переходит в теплоту (Q).
[left{ begin{gathered}
m{upsilon _1} + m{upsilon _2} = 2mu hfill \
frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{2m{u^2}}}{2} + Q hfill \
end{gathered} right.]
Из ЗСИ выразим скорость шаров после удара:
[u = frac{{{upsilon _1} + {upsilon _2}}}{2}]
Полученное выражение подставим в ЗСЭ:
[frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{2m}}{2}{left( {frac{{{upsilon _1} + {upsilon _2}}}{2}} right)^2} + Q]
Раскроем квадрат суммы в правой части уравнения:
[frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{2m}}{2}left( {frac{{upsilon _1^2 + 2{upsilon _1}{upsilon _2} + upsilon _2^2}}{4}} right) + Q]
Откроем скобки:
[frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{mupsilon _1^2}}{4} + frac{{m{upsilon _1}{upsilon _2}}}{2} + frac{{mupsilon _2^2}}{4} + Q]
[Q = frac{{mupsilon _1^2}}{4} – frac{{m{upsilon _1}{upsilon _2}}}{2} + frac{{mupsilon _2^2}}{4} = frac{m}{4}left( {upsilon _1^2 – 2{upsilon _1}{upsilon _2} + upsilon _2^2} right)]
[Q = frac{m}{4}{left( {{upsilon _1} – {upsilon _2}} right)^2}]
Получилась “красивая” формула для расчета ответа. Переведем скорости в единицы системы СИ.
[10; см/с = frac{{10}}{{100}}; м/с = 0,1; м/с]
[20; см/с = frac{{20}}{{100}}; м/с = 0,2; м/с]
Считаем ответ:
[Q = frac{1}{4}{left( {0,1 – 0,2} right)^2} = 2,5 cdot 10^{-3}; Дж = 2,5; мДж]
Ответ: 2,5 мДж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.10.2 Тележка массой 100 кг движется со скоростью 2 м/с. Когда она проезжает мимо
2.10.4 Охотник стреляет из ружья. Определить силу отдачи, если масса дроби 35 г
2.10.5 Шары массами 1 и 2 кг движутся навстречу друг другу. Скорость первого шара 5 м/с
Тепловое равновесие и уравнение теплового баланса
Тела, температура которых отличается, могут обмениваться тепловой энергией. То есть, между телами будет происходить теплообмен. Самостоятельно тепловая энергия переходит от более нагретых тел к менее нагретым.
Что такое теплообмен и при каких условиях он происходит
Тела, имеющие различные температуры, будут обмениваться тепловой энергией. Этот процесс называется теплообменом.
Теплообмен – процесс обмена тепловой энергией между телами, имеющими различные температуры.
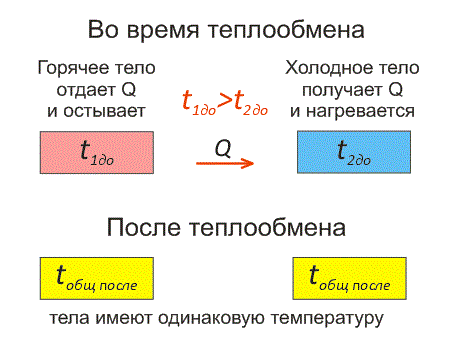
Рассмотрим два тела, имеющие различные температуры (рис. 1).
Тело, имеющее более высокую температуру, будет остывать и отдавать тепловую энергию телу, имеющему низкую температуру. А тело с низкой температурой будет получать количество теплоты и нагреваться.
На рисунке, горячее тело имеет розовый оттенок, а холодное изображено голубым цветом.
Когда температуры тел выравниваются, теплообмен прекращается.
Чтобы теплообмен происходил, нужно, чтобы тела имели различные температуры.
Когда температура тел выравняется, теплообмен прекратится.
Тепловое равновесие — это состояние, при котором тела имеют одинаковую температуру.
Уравнение теплового баланса и сохранение тепловой энергии
Когда тело остывает, оно отдает тепловую энергию (теплоту). Утерянное количество теплоты Q имеет знак «минус».
А когда тело нагревается – оно получает тепловую энергию. Приобретенное количество теплоты Q имеет знак «плюс».
Эти факты отражены на рисунке 2.
Закон сохранения тепловой энергии: Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом.
Примечание: Существует и другая формулировка закона сохранения энергии: Энергия не появляется сама собой и не исчезает бесследно. Она переходит из одного вида в другой.
Уравнение теплового баланса
Тот факт, что тепловая энергия сохраняется, можно записать с помощью математики в виде уравнения. Такую запись называют уравнением теплового баланса.
Запишем уравнение теплового баланса для двух тел, обменивающихся тепловой энергией:
(large Q_<text<остывания горяч>> left( text <Дж>right) ) – это количество теплоты горячее тело теряет.
(large Q_<text<нагревания холод>> left( text <Дж>right) ) – это количество теплоты холодное тело получает.
В левой части уравнения складываем количество теплоты каждого из тел, участвующих в теплообмене.
Записываем ноль в правой части уравнения, когда теплообмен с окружающей средой отсутствует. То есть, теплообмен происходит только между рассматриваемыми телами.
В некоторых учебниках применяют сокращения:
[large Q_ <1>+ Q_ <2>= 0 ]
Примечание: Складывая два числа мы получим ноль, когда эти числа будут:
- равными по модулю и
- имеют различные знаки (одно число — знак «плюс», а второе – знак «минус»).
Если несколько тел участвуют в процессе теплообмена
Иногда в процессе теплообмена участвуют несколько тел. Тогда, для каждого тела нужно записать формулу количества теплоты Q. А потом все количества теплоты подставить в уравнение для теплового баланса:
[large boxed < Q_<1>+ Q_ <2>+ Q_ <3>+ ldots + Q_ = 0 > ]
- Q для каждого нагреваемого тела будет обладать знаком «+»,
- Q для каждого охлаждаемого тела — знаком «-».
Пример расчетов для теплообмена между холодным и горячим телом
К горячей воде, массой 200 грамм, имеющей температуру +80 градусов Цельсия, добавили холодную воду, в количестве 100 грамм при температуре +15 градусов Цельсия. Какую температуру будет иметь смесь после установления теплового равновесия? Считать, что окружающая среда в теплообмене не участвует.
Примечание: Здесь мы рассматриваем упрощенную задачу, для того, чтобы облегчить понимание закона сохранения энергии. Мы не учитываем в этой задаче, что вода содержится в емкости. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.
При решении других задач обязательно учитывайте, что емкость, в которой будет содержаться вещество, имеет массу. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.
Решение:
В условии сказано, что окружающая среда в теплообмене не участвует. Поэтому, будем считать рассматриваемую систему замкнутой. А в замкнутых системах выполняются законы сохранения. Например, закон сохранения энергии.
Иными словами, с сосудом и окружающим воздухом теплообмен не происходит и, все тепловая энергия, отданная горячей водой, будет получена холодной водой.
1). Запишем уравнение теплового баланса, в правой части которого можно записать ноль:
2). Теперь запишем формулу для каждого количества теплоты:
Примечания:
- (large c_<text<воды>> ) – удельную теплоемкость воды находим в справочнике;
- Массу воды переводим в килограммы;
- Горячая вода остывает и отдает тепловую энергию. Поэтому, разность (large (t_<text<общ>> — t_<text<горяч>> ) ) будет иметь знак «минус», потому, что конечная температура горячей воды меньше ее начальной температуры;
- Холодная вода получает тепловую энергию и нагревается. Из-за этого, разность (large (t_<text<общ>> — t_<text<холодн>> ) ) будет иметь знак «плюс», потому, что конечная температура холодной воды больше ее начальной температуры;
3). Подставим выражения для каждого Q в уравнение баланса:
4). Для удобства, заменим символы числами:
[large 4200 cdot 0,2 cdot (t_<text<общ>> — 80 ) + 4200 cdot 0,1 cdot (t_<text<общ>> — 15 ) = 0 ]
[large 840 cdot (t_<text<общ>> — 80 ) + 420 cdot (t_<text<общ>> — 15 ) = 0 ]
Раскрыв скобки и решив это уравнение, получим ответ:
Ответ: Температура смеси после прекращения теплообмена будет равна 58,33 градуса Цельсия.
Задача для самостоятельного решения:
В алюминиевом калориметре массой 100 грамм находится керосин массой 250 грамм при температуре +80 градусов Цельсия. В керосин поместили свинцовый шарик, массой 300 грамм. Начальная температура шарика +20 градусов Цельсия. Найдите температуру тел после установления теплового равновесия. Внешняя среда в теплообмене не участвует.
Примечание к решению: В левой части уравнения теплового баланса теперь будут находиться три слагаемых. Потому, что мы учитываем три количества теплоты:
- (large Q_ <1>) – охлаждение алюминия от температуры +80 градусов до конечной температуры;
- (large Q_ <2>) – охлаждение керосина от температуры +80 градусов до конечной температуры;
- (large Q_ <3>) – нагревание свинца от температуры +20 градусов до конечной температуры;
А справа в уравнение теплового баланса запишем ноль. Так как внешняя среда в теплообмене не участвует.
Уравнения баланса энергии и теплоты
Ключевые слова конспекта: количество теплоты, уравнение теплового баланса, закон сохранения энергии в тепловых процессах.
Для механических явлений при определённых условиях выполняется закон сохранения механической энергии: полная механическая энергия системы тел сохраняется, если они взаимодействуют силами тяготения или упругости. Если действуют силы трения, то полная механическая энергия тел не сохраняется, часть её (или вся) превращается в их внутреннюю энергию.
При изменении состояния тела (системы) меняется его внутренняя энергия. Состояние тела и соответственно его внутреннюю энергию можно изменить двумя способами: в процессе теплопередачи или путём совершения внешними силами работы над телом (работа, например, силы трения). Мерой изменения внутренней энергии тела в процессе теплообмена выступает количество теплоты (Q).
Уравнение теплового баланса
В изолированной системе при смешивании горячей и холодной воды, количество теплоты Q1, отданное горячей водой, равно количеству теплоты Q2, полученному холодной водой, т.е.: |Q1|= |Q2| . Q1 (выделенное) 0.
Qотданное + Qполученное = 0
Записанное равенство называется уравнением теплового баланса (эта формула и уравнение, используемое в 8 классе!). Определение: суммарное количества теплоты, которое выделяется в теплоизолированной системе равно суммарному количеству теплоты, которое в этой системе поглощается.
Уравнение теплового баланса связывает количество теплоты, полученное одним телом, и количество теплоты, отданное другим телом при теплообмене. При этом в теплообмене могут участвовать не два тела, а три и более: Q1 + Q2 + Q3 + … = 0
Уравнение теплового баланса – это закон сохранения энергии для процессов теплообмена в термоизолированных системах. Оно даёт возможность определить те или иные величины. В частности, значения удельной теплоёмкости веществ определяют из уравнения теплового баланса.
◊◊◊ Обратите внимание! В более старших классах используется следующее определение «уравнения теплового баланса»: Если в изолированной системе тел не происходит никаких превращений энергии кроме теплообмена, то количество теплоты, отданное телами, внутренняя энергия которых уменьшается, равно количеству теплоты, полученному телами, внутренняя энергия которых увеличивается. При этом суммарная энергия системы не изменяется«. А также используется другая формула уравнения (с учетом интегральной формы Первого начала термодинамики):
Закон сохранения энергии в тепловых процессах
Закон сохранения энергии в тепловых процессах выполняется при нагревании тел за счёт энергии, выделяющейся при сгорании топлива. Топливо — это природный газ, дрова, уголь, нефть. При его сгорании происходит химическая реакция окисления — атомы углерода соединяются с атомами кислорода, содержащимися в воздухе, и образуется молекула оксида углерода (углекислого газа) С02. При этом выделяется энергия.
При сгорании различного топлива одинаковой массы выделяется разное количество теплоты. Например, хорошо известно, что природный газ является энергетически более выгодным топливом, чем дрова. Это значит, что для получения одного и того же количества теплоты, масса дров, которые нужно сжечь, должна быть существенно больше массы природного газа. Следовательно, различные виды топлива с энергетической точки зрения характеризуются величиной, называемой удельной теплотой сгорания топлива.
Конспект урока «Уравнение теплового баланса».
Уравнение теплового баланса — формула, суть и примеры решений
Общие сведения
Баланс в переводе на русский язык означает равновесие. Когда теплоизолированная система приходит в состояние теплового равновесия, то температура всех тел, образующих эту совокупность, становится одинаковой. Такую ситуацию называют законом теплового равновесия или нулевым уравнением термодинамики.
Впервые с уравнением теплового баланса знакомят в средней школе на уроке физики. Ученикам в седьмом классе предлагается решить несколько простых заданий, используя равенство. Формула и определение даётся без доказательства, так как для понимания процесса нужно знать понятия, которые разбираются в выпускных классах школы. Например, то, что теплоёмкость не является характеристикой вещества, при этом она может быть разной в зависимости от проходящих процессов.
Закон теплового баланса позволяет утверждать, что когда в изолированной системе физических тел происходит только теплообмен, то часть тепла, переданного телами, внутреннее состояние энергии которых уменьшается, численно равняется теплу, полученному объектами с возрастающей внутренней энергии. Математически уравнение записывается в виде следующей формулы: Q 1 + Q 2 + Q 3 + …+ Qn = 0, где:
- n — число тел, находящихся в теплоизолированной системе;
- Q — полученное количество теплоты.
Если предположить, что имеется совокупность, состоящая из двух тел, из которых одно отдаёт тепло, а другое принимает его, то справедливо будет записать: Q1 = Q2. Таким образом, теплоотдача всегда равняется теплоприёму. Поэтому этот закон и называют правилом сохранения энергии в тепловых процессах.
Когда тела два, то понять, какое из них отдаёт тепло, а какое получает, несложно. То, что имеет большее нагревание, — будет отдавать. Если же объектов три и более, и некоторые из них имеют промежуточную температуру, определить, какие из них принимают тепло, довольно сложно. Вот тут на помощь и приходит уравнение термодинамики.
Изменение внутренней энергии объясняется теплопередачей, то есть случаем, когда работа не совершается. Поэтому в физике уравнение теплового баланса используется при анализе процессов теплопередачи, нахождении КПД. Это равенство можно применять как при рассмотрении твёрдых тел, так и жидкости.
Суть уравнения
Следует рассмотреть процесс установления теплового равновесия в теплоизолированной системе. Это такая совокупность, в которой объекты взаимодействуют только друг с другом. Простейшая система будет состоять из двух тел. Например, в термос налит сок и в него вброшен лёд. В этом случае термос является изолятором от внешнего воздействия. Пусть первое тело имеет температуру t1, а второе t2. Допустим, что t1 больше t2. Это допущение не является принципиальным, поэтому его можно использовать.
В начальный момент времени тела находятся далеко друг от друга и теплообмен между ними не происходит. Как только, они соприкоснутся — начнётся взаимодействие. Так как температура первого тела больше, то оно начнёт остывать, а второе нагреваться. Происходит теплопередача. В какой-то момент времени она прекратится и наступит тепловое равновесие. То есть температура двух тел станет одинаковой: t1 = t2.
Получившаяся температура называется равновесной. Обозначается она греческой буквой тета — θ. Так как раньше первое тело имело большую температуру, то получается, что в процессе взаимодействия оно отдало тепло. Записать это можно как Q1 — — количество теплоты, отданное первым телом. Второй же объект в процессе подогрелся — увеличил температуру. Обозначить это можно как +Q2 — количество теплоты, полученное вторым телом.
Получить тепло второй объект мог только от первого тела, так как рассматриваемая система изолированная. Соответственно, и отдать определённое количество теплоты первое тело могло только второму. Отсюда можно сделать вывод, что если система теплоизолированная, то эти два количества теплоты одинаковы: Q1 — = +Q2. Фактически это есть уравнение баланса.
Такая запись даётся в школьных учебниках. Но профессиональные физики записывают его в другой форме. Для термодинамики неважно, какой объект отдаёт, а какой получает тепло. Наука изучает только количество теплоты, полученное в процессе. Взяв простую аналогию с весом, когда о похудевшем человеке на два килограмма можно сказать, что он поправился на минус два кило, будет верным записать: Q1 — = -Q1 или -Q1 = Q2.
Если собрать два слагаемых таким образом, чтобы они находились с одной стороны знака равенства, то можно записать: Q1 + Q2 = 0.
Суммарное количество теплоты, образуемое при теплообмене тел в теплоизолированной системе, равно нулю. При этом это правило будет справедливо и для энного количества объектов.
Доказательство закона
Пусть имеется теплоизолированная система, состоящая из нескольких помещённых в неё объектов. Сами тела могут обмениваться теплом только друг с другом. Первый закон термодинамики для системы в целом можно записать как Q = А’ + Δ U. То есть количество теплоты, полученное всей системой, равняется суммарной работе, совершённой всеми телами в совокупности над внешним миром, складывающейся с изменением энергии всех тел внутри системы.
По условию задачи внутренняя энергия меняется не за счёт совершения работы. Поэтому А’ = 0. С другой же стороны, теплоизоляция обозначает, что Q = 0. Иными словами, количество энергии, поступающее из окружения Земли, равняется нулю. Следовательно, изменение внутренней энергии всех тел в системе будет нулевым: Δ U = 0.
Энергия системы состоит из внутренних энергий каждого из входящих в неё тел: U = U1 + U2 +…+ Un. Изменение же её Δ U = Δ U 1 + Δ U 2 + … + Δ Un. Отсюда следует, что если внутренняя энергия остаётся неизменной, то сумма Δ U будет нулевой: Δ U 1 + Δ U 2 + … + Δ Un = 0.
Первый закон термодинамики персонально для каждого из тел входящих в систему можно записать как следующую систему:
Все уравнения, входящие в неё, можно сложить почленно. При этом распределив слагаемые для удобства дальнейшего анализирования: Q1 + Q2 +…+ Q n = (А n1′ + А n2′ + … + А n’) + (Δ U1 + Δ U2 + … + Δ Un). Из полученного выражения можно сделать вывод, что сумма дельт второго члена в правой части равняется нулю. В первом же члене с правой стороны каждое слагаемое также равняется нулю. Поэтому можно записать: Q1 + Q2 +…+ Q n = 0. Что и следовало доказать.
Для решения задач полезно вспомнить, на что может идти полученное тепло. К таким частным случаям относят:
- Процессы, при которых нет фазовых переходов. В таком случае полученное количество идёт на увеличение теплоты потенциальной и кинетической энергии: Q = c * m * ΔT (изохорная теплоёмкость).
- Плавление. Например, есть тающий лёд, к которому подводят тепло, при этом кинетическая энергия остаётся постоянной. Значит, изменяется только потенциальная мощность. В этом случае происходит превращение льда в воду. Это действие называют плавлением — переход кристаллического вещества из твёрдого состояния в жидкое: Q = λ * m.
- Парообразование. Выделение из жидкости пара: Q = L * m.
Типовое задание
Явление теплового баланса используется как в изучении процессов при переходе из одного агрегатного состояния в другое, так и для твёрдых или жидких тел, не изменяющих решётку. Существуют типовые задания, входящие в школьную программу. Ученик, решая их, научится находить удельные параметры и сможет понять всю важность выражения теплового баланса.
В латунный котёл массой 128 граммов, содержащий 240 граммов воды, при 8,4 градусах опущено металлическое тело массой 192 грамма, нагретое до 120 градусов Цельсия. Окончательная установившаяся температура составила 21,5 градус. Определить удельную теплоёмкость рассматриваемого тела. Для решения задачи необходимо из справочника взять значение энергетической теплоёмкости латуни. Она составляет 400 Дж/ кг *С 0 . При этом нужно учитывать, что котёл теплоизолирован.
Температуру, которая установилась через время, обозначают буквой θ. Решение подобных задач начинают с установления количества тел, участвующих в теплообмене. В этом примере их три: вода, котёл, испытываемое тело. Количество тепла, полученное всеми тремя объектами, согласно закону, будет равняться нулю: Qв + Qк +Qт = 0. Теперь следует каждое слагаемое расписать отдельно:
- Qв = mв * cв * Св (θ — Tв).
- Qк = mк * cл * (θ — Tв).
- Qт = mт * cт * (θ — Tк).
Полученные формулы нужно подставить в исходное уравнение. При этом следует обратить внимание, что при подстановке образуется общий множитель (θ — T в), который можно вынести за скобки: (m в * c в + m к * c л) * (θ — T в) + m т * c т * (θ — T к) = 0.
Из условия задачи известно, что у тела температура 100 градусов, а равновесная температура меньше. Поэтому последняя скобка будет отрицательной. Значит, есть смысл перенести это слагаемое вправо, поменяв местами вычитаемое и уменьшаемое: (m в * c в + m к * c л) * (θ — T в) = m т * c т * (T к — θ). Отсюда можно выразить удельную теплоёмкость массы тела. Она будет равняться: C т = (m в * c в + m к * c л) * (θ — T в) / m т * (T к — θ) .
Все данные, используемые в формуле, известны. Остаётся только провести расчёты, подставив значения: Cт = (0,24 кг * 4,2 кДж/кг*С + 0,128 кг * 0,4 кДж/кг*С *(21,5 — 8,4) С) / 0,192 кг * (100 — 21,5)С = 0,921 кДж/ кг *С 0 . Полученное вещество является алюминием.
Примеры высокого уровня
Эти задачи рассчитаны на подготовленных учащихся, понимающих суть процессов и знающих уравнение баланса. Например, электрическая установка с мощностью P = 350 Вт не может нагреть воду массой 0,6 кг до кипения. Убедившись в этом, её выключают. Нужно определить, каким останется конечный нагрев воды через 15 секунд.
Из условия можно утверждать, что мощность теплопотерь равняется мощности нагревателя: Pпот = P. По сути, мощность теплопотерь это количество тепла, отдаваемое телом в единицу времени. То есть: P пот = Q — / ΔT. С другой стороны, отданное тепло находится из формулы: Q — = c * m * (-ΔT). Отсюда можно записать: P = — c * m * ΔT / Δt. Из последнего выражения легко выразить искомый параметр: ΔT = -(P * Δt) / (c * m). Все необходимые данные есть в условии и их необходимо просто подставить: ΔT = — 350 Вт * 15 с / 4200 Дж * 0,6 кг = — 2,1 С 0 . Минус в ответе показывает, что температура понижается. Задача решена.
Вот ещё одна задача, для решения которой необходимо вначале исследовать ситуацию. В ёмкость поместили смесь, состоящую из пяти килограммов воды и трёх килограммов льда. Затем туда пустили 0,2 кг водяного пара при температуре 100 0 С. Нужно определить, что произойдёт.
По условию задачи даны три массы mв, mл, mп. Можно предположить, что при смешении в момент запуска пара температура в системе была нулевой. Это исходит из того, что в ёмкости одновременно находится лёд и вода. Поступающий пар конденсирует, и из него образуется вода. Через время она остывает до нуля. Поэтому в начальный момент выделившаяся энергия идёт только на таяние льда. Cуществует три варианта развития события:
- Лёд не растает ( θ =0 0 С).
- Лёд полностью растает (0 0 С).
- Вода начнёт кипеть ( θ = 100 0 С) .
Для того чтобы выяснить, какой вариант верный, нужно найти выделившуюся энергию: Qпл = λ * m = 330 * 3 = 990 кДж. Получается, чтобы растопить лёд, нужно 990 кДж теплоты. Пар, вступая в реакцию, отдаёт: Q- = L* m + cв * mв (Tпар – Tпл) = 2300 + 0,2 + 4,2 * 0,2 * 100 = 544 кДж. Учитывая два полученных результата, можно утверждать, что при конденсации основного пара выделившейся теплоты будет недостаточно для расплавления льда. Следовательно θ = 0 0 С.
http://nauka.club/fizika/uravneni%D0%B5-teplovogo-balansa.html
Условие задачи:
Найти количество теплоты, выделившейся при абсолютно неупругом ударе свинцового шара массой 1 кг об очень тяжелую стенку, движущуюся со скоростью 5 см/с. Шар до удара двигался не вращаясь перпендикулярно стенке, навстречу ей со скоростью 10 см/с.
Задача №2.10.26 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
(m=1) кг, (u=5) см/с, (upsilon=10) см/с, (M gg m), (Q-?)
Решение задачи:
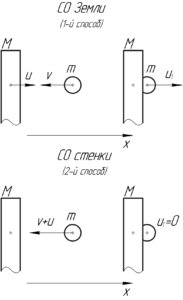
Первый способ. Запишем закон сохранения импульса в проекции на ось (x) и закон сохранения энергии для системы тел «шар — стенка» в системе отсчета (СО) Земли. Замечу, что этот способ достаточно трудоёмкий, по сравнению со вторым.
Из равенства (1) выразим скорость стенки с шаром (u_1) после удара:
Полученное выражение для скорости (u_1) подставим в (2).
Оставим искомое количество теплоты (Q) в одной стороне, все остальные члены перенесем в другую, где приведем их под общий знаменатель.
Раскроем в числителе скобки и квадрат разности:
Вынесем в числителе общий множитель (mM) за скобки:
Воспользуемся основным свойством дроби и поделим и числитель и знаменатель на (M).
Так как по условию стенка очень тяжелая, то есть (M gg m), то отношение (<frac>) стремится к нулю, значит им можно пренебречь. В итоге конечная формула такая:
Второй способ. Перейдем в систему отсчета (СО), связанную с массивной стенкой. В этой СО скорость свинцового шарика равна (upsilon + u) и направлена к стенке. После удара скорость шарика станет такой же, как и у стенки, то есть в этой СО станет равной нулю. Получается, что вся кинетическая энергия шарика в этой СО перейдет в теплоту:
Как Вы видите, второй способ решения этой задачи существенно короче.
Переведем скорости в систему СИ, а уже потом будет считать ответ:
Ответ: 11,25 мДж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Вследствие изменения полной механической энергии системы может выделяться теплота.
Наличие сил трения (сопротивления) между телами замкнутой системы приводит к выделению энергии в виде теплоты:
где E 1 — полная механическая энергия системы в начальном состоянии; E 2 — полная механическая энергия системы в конечном состоянии.
Если теплота в механической системе выделяется в результате совершения работы силами трения, то количество выделившейся при этом теплоты может быть рассчитано по формуле
где A тр — работа, совершенная силами трения.
Превращение части механической энергии в теплоту происходит при абсолютно неупругом столкновении (ударе) двух и более тел.
Абсолютно неупругий удар — это столкновение тел, в результате которого тела объединяются и продолжают двигаться как единое целое.
Для абсолютно неупругого удара двух тел:
- выполняется закон сохранения импульса:
m 1 v → 1 + m 2 v → 2 = ( m 1 + m 2 ) u → ;
- не выполняется закон сохранения полной механической (кинетической) энергии:
m 1 v 1 2 2 + m 2 v 2 2 2 ≠ ( m 1 + m 2 ) u 2 2 ,
где m 1 и m 2 — массы соударяющихся тел; v → 1 и v → 2 — скорости тел до столкновения; ( m 1 + m 2 ) — масса тела, образовавшегося в результате удара; u → — скорость тела, образовавшегося в результате удара.
Разность энергий до и после столкновения равна теплоте, выделившейся в процессе столкновения:
Q = m 1 v 1 2 2 + m 2 v 2 2 2 − ( m 1 + m 2 ) u 2 2 .
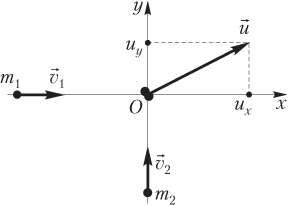
Пример 36. Какая доля энергии двух движущихся с равными по модулю скоростями тел, направленными под прямым углом друг к другу, перейдет в теплоту при абсолютно неупругом ударе? Массы тел относятся как 1:2.
Решение. На рисунке показаны два положения системы тел: до удара и сразу после удара. До удара тела движутся: первое — в положительном направлении оси Ox , второе — в положительном направлении оси Oy . Столкновение тел (абсолютно неупругий удар) происходит в начале системы координат. В результате абсолютно неупругого удара тела объединяются и движутся как единое целое со скоростью u → .
Полная механическая энергия системы является кинетической энергией:
E 1 = W k 1 + W k 2 ;
где W k 1 = m 1 v 1 2 2 — кинетическая энергия первого тела до удара; W k 2 = m 2 v 2 2 2 — кинетическая энергия второго тела до удара; m 1 — масса первого тела; m 2 — масса второго тела; v 1 — модуль скорости первого тела до удара; v 2 — модуль скорости второго тела до удара; W k = ( m 1 + m 2 ) u 2 2 — кинетическая энергия объединенного тела после удара; ( m 1 + m 2 ) — масса объединенного тела после удара; u — модуль скорости объединенного тела после удара.
Теплота, выделившаяся в результате абсолютно неупругого удара, определяется разностью полных механических энергий системы до удара и после него:
Для ее вычисления необходимо определить скорость объединенного тела.
Воспользуемся законом сохранения импульса, записав его в виде:
m 1 v → 1 + m 2 v → 2 = ( m 1 + m 2 ) u → ,
или в проекциях на координатные оси,
O x : m 1 v 1 = ( m 1 + m 2 ) u x ; O y : m 2 v 2 = ( m 1 + m 2 ) u y . >
Выразим отсюда проекции скорости объединенного тела:
u x = m 1 v 1 m 1 + m 2 u y = m 2 v 2 m 1 + m 2 >
и подставим их в формулу, определяющую квадрат скорости объединенного тела:
u 2 = u x 2 + u y 2 = ( m 1 v 1 m 1 + m 2 ) 2 + ( m 2 v 2 m 1 + m 2 ) 2 .
Полная механическая энергия объединенного тела, таким образом, определяется формулой
E 2 = ( m 1 + m 2 ) u 2 2 = ( m 1 + m 2 ) 2 [ ( m 1 v 1 m 1 + m 2 ) 2 + ( m 2 v 2 m 1 + m 2 ) 2 ] .
- равенства модулей скоростей тел до удара:
- соотношения между массами тел:
запишем полные механические энергии системы:
E 1 = m 1 v 1 2 2 + m 2 v 2 2 2 = m v 2 2 + 2 m v 2 2 = 3 2 m v 2 ;
E 2 = ( m 1 + m 2 ) 2 [ ( m 1 v 1 m 1 + m 2 ) 2 + ( m 2 v 2 m 1 + m 2 ) 2 ] = 5 6 m v 2 .
Количество теплоты, выделившейся после абсолютно неупругого удара, определяется формулой
Q = E 1 − E 2 = 3 2 m v 2 − 5 6 m v 2 = 2 3 m v 2 .
Доля механической энергии, превратившейся в теплоту в результате абсолютно неупругого удара,
η = Q E 1 = 2 m v 2 3 2 3 m v 2 = 4 9 ≈ 0,44 .
При абсолютно неупругом ударе двух тел с заданными соотношениями масс и скоростей в теплоту перешло около 44 % механической энергии системы.
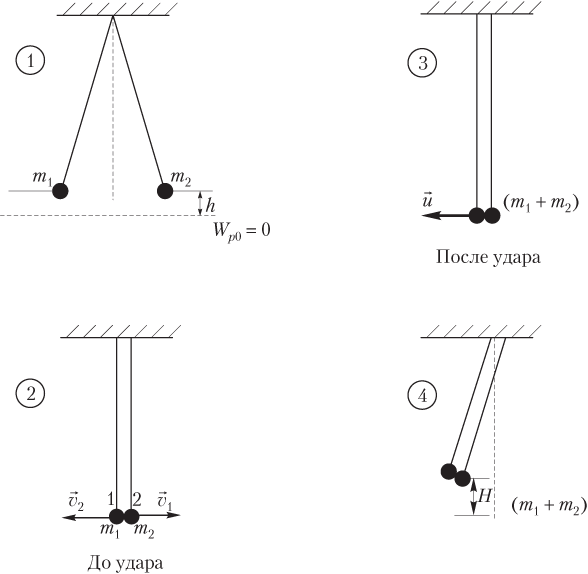
Пример 37. Два пластилиновых шарика, массы которых соотносятся как 1:5, подвешены на нитях одинаковой длины. Шарики симметрично разводят в противоположные стороны и отпускают. Какая часть механической энергии перейдет в теплоту при абсолютно неупругом ударе?
Решение. На рисунке показаны четыре состояния системы тел:
1) шарики симметрично разведены в стороны, при этом они подняты на высоту h над нулевым уровнем потенциальной энергии; полная механическая энергия системы является потенциальной:
E 1 = m 1 gh + m 2 gh ,
или с учетом соотношения масс ( m 1 = m , m 2 = 5 m ):
где g — модуль ускорения свободного падения; h — первоначальная высота шариков над нулевым уровнем потенциальной энергии;
2) шарики подлетают друг к другу (но соударения еще не происходит); полная механическая энергия системы является кинетической:
E 2 = m 1 v 1 2 2 + m 2 v 2 2 2 ,
или с учетом соотношения масс ( m 1 = m , m 2 = 5 m ):
E 2 = m 2 ( v 1 2 + 5 v 2 2 ) ,
где v 1 — модуль скорости первого шарика; v 2 — модуль скорости второго шарика;
3) шарики после абсолютно неупругого удара объединяются и движутся как единое целое с некоторой скоростью; полная механическая энергия системы является кинетической:
E 3 = ( m 1 + m 2 ) u 2 2 ,
или с учетом соотношения масс ( m 1 = m , m 2 = 5 m ):
где u — модуль скорости объединенного тела непосредственно после удара;
4) объединенное тело поднимается на некоторую высоту, полная механическая энергия системы является потенциальной:
E 4 = ( m 1 + m 2 ) gH ,
или с учетом соотношения масс ( m 1 = m , m 2 = 5 m ):
где H — максимальная высота, на которую может подняться объединенное тело.
При переходе системы из первого состояния во второе полная механическая энергия сохраняется как для всей системы, так и для каждого шарика в отдельности:
m 1 g h = m 1 v 1 2 2 ; m 2 g h = m 2 v 2 2 2 . >
Отсюда следует равенство модулей скоростей шариков перед абсолютно неупругим ударом:
v = v 1 = v 2 = 2 g h .
С учетом этого равенства полная механическая энергия системы перед ударом определяется формулой
При переходе системы из второго состояния в третье полная механическая энергия системы не сохраняется (при абсолютно неупругом ударе часть энергии переходит в теплоту), однако импульс системы сохраняется:
m 1 v → 1 + m 2 v → 2 = ( m 1 + m 2 ) u → ,
в проекции на направление скорости объединенного тела
− m 1 v 1 + m 2 v 2 = ( m 1 + m 2 ) u ,
или с учетом соотношения масс ( m 1 = m , m 2 = 5 m ) и равенства модулей скоростей ( v = v 1 = v 2 ):
Отсюда найдем отношение модулей скоростей шариков до и после удара:
Искомой величиной является доля механической энергии, которая перейдет в результате абсолютно неупругого удара в теплоту, т.е.
η = Q E 2 = E 2 − E 3 E 2 = 1 − E 3 E 2 ,
где E 2 — полная механическая энергия системы до удара (состояние 2); E 3 — полная механическая энергия системы после удара (состояние 3).
Подстановка в формулу соответствующих энергий и отношения скоростей ( u / v ) дает искомую долю:
η = 1 − 3 m u 2 3 m v 2 = 1 − u 2 v 2 = 1 − ( u v ) 2 = 1 − ( 2 3 ) 2 = 5 9 ≈ 0,56 .
Таким образом, при абсолютно неупругом ударе шариков с заданным соотношением масс в теплоту превращается около 56 % их суммарной механической энергии.
Пример 38. Тело массой 2,0 кг влетает в вязкую среду со скоростью 10 м/c. Определить кинетическую энергию тела при вылете из среды, если 30 % его механической энергии в среде превращается в теплоту.
Решение. На рисунке показаны два положения тела:
1) перед попаданием в вязкую среду; тело имеет полную механическую (кинетическую) энергию E 1 ;
2) после вылета из вязкой среды; тело имеет полную механическую (кинетическую) энергию E 2 .
Теплота, которая выделяется при движении тела в вязкой среде, определяется разностью
где Q = 0,3 E 1 — по условию задачи.
Выразим искомую кинетическую энергию тела при вылете из вязкой среды:
Замена Q = 0,3 E 1 преобразует формулу к виду:
E 2 = E 1 − 0,3 E 1 = 0,7 E 1 ,
где E 1 = m v 1 2 2 — кинетическая энергия тела перед его попаданием в вязкую среду; m — масса тела; v 1 — модуль первоначальной скорости тела.
Окончательная формула для расчета искомой кинетической энергии имеет следующий вид:
Скорость брошенного мяча непосредственно перед ударом об абсолютно гладкую стену была вдвое больше его скорости сразу после удара. Какое количество теплоты выделилось при ударе, если перед ударом кинетическая энергия мяча была равна 20 Дж? (Ответ дайте в джоулях.)
Кинетическая энергия пропорциональна квадрату скорости. Поскольку скорость после удара уменьшилась в 2 раза, кинетическая энергия мяча уменьшилась в 4 раза и стала равна 5 Дж. По закону сохранения, количество теплоты, выделившееся после удара равняется убыли кинетической энергии:
Для приведенного здесь решения задачи существенно, что стенка, о которую ударяется мяч, абсолютно гладкая. Действительно, в противном случае на мяч во время удара может дейстовать еще и сила трения со стороны стенки, которая приведет к тому, что мяч после удара будет вращаться поэтому кинетическая энергия шара после удара будет состоять из энергии поступательного и вращательного движений. Следовательно, судить о величине выделившегося тепла будет невозможно.

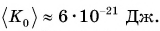
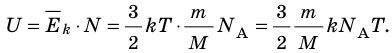 Итак, для одноатомного идеального газа:
Итак, для одноатомного идеального газа: 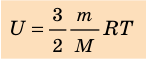 . Используя уравнение состояния
. Используя уравнение состояния 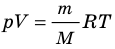 , выражение для внутренней энергии идеального одноатомного газа можно представить так:
, выражение для внутренней энергии идеального одноатомного газа можно представить так: